A low-power band of neuronal spiking activity dominated by local single units improves the performance of brain–machine interfaces

Abstract

The large power requirement of current brain-machine interfaces is a major hindrance to their clinical translation. In basic behavioural tasks, the downsampled magnitude of the 300-1,000 Hz band of spiking activity can predict movement similarly to the threshold crossing rate (TCR) at 30 kilo-samples per second. However, the relationship between such a spiking-band power (SBP) and neural activity remains unclear, as does the capability of using the SBP to decode complicated behaviour. By using simulations of recordings of neural activity, here we show that the SBP is dominated by local single-unit spikes with spatial specificity comparable to or better than that of the TCR, and that the SBP correlates better with the firing rates of lower signal-to-noise-ratio units than the TCR. With non-human primates, in an online task involving the one-dimensional decoding of the movement of finger groups and in an offline two-dimensional cursor-control task, the SBP performed equally well or better than the TCR. The SBP may enhance the decoding performance of neural interfaces while enabling substantial cuts in power consumption.

Brain–machine interfaces have the potential to treat many neurological diseases and disorders. By translating brain activity into user intent, they can enable self-feeding, independent movement and computer control for people with paralysis^1–4. Some of these advances were demonstrated more than a decade ago, but they have not yet been translated to widespread clinical use. A fundamental barrier to clinical systems is the high power and computation requirements for high-bandwidth neural recording. Consequently, modern high-performance solutions have required transcutaneous connections to a large cart of computers recording, processing and decoding the neural activity. This renders existing clinical implantable recording systems, such as closed-loop deep-brain stimulation implants, unfeasible as replacements, as they record from too few channels with too small of a bandwidth.

To predict complicated behaviour, brain-machine interfaces typically use estimates of the firing rates of relevant neurons. To extract these, they record from approximately 100 transcutaneous electrodes at 20 kSps to isolate units via thresholding. In an attempt to eliminate the infection risks associated with persistent transcutaneous connections and free the user from being tethered to the necessary computational hardware, several groups have investigated wireless, fully implantable neural interfaces. In particular, some devices wirelessly transmitted broadband neural recordings from ~100 electrodes^5,6. Unfortunately, power delivery generated unsafe tissue temperatures and the devices did not have decoding capabilities to translate the neural activity, which would require the user to remain within the wireless range of the processing computers. In the case of controlling functional electrical stimulation, additional wireless links would be required to interact with the implanted stimulating hardware, requiring more power-hungry, wireless, implantable devices.

To resolve the power consumption issue, many groups have developed application-specific integrated circuits to optimally perform the necessary computations^7–18. In particular, a promising 8mW wireless implantable chip accommodating acquisition, spike sorting and transmission of 15.7 kSps neural data from 100 electrodes was demonstrated¹⁹. However, the amplifiers used were nearly optimal between the noise efficiency factor (4.0) and current usage (16 μA per channel), implying devices must optimize power consumption through alternative means²⁰. In addition, while radio-frequency transmission of neural data and power has become a common solution for these groups, one found that it cannot accommodate micrometre-scale recording modules due to power loss through tissue and the inefficiencies of integrated components²¹. It seems even the optimizations of customized integrated circuitry may still require new techniques to further cut power consumption. These challenges have resulted in very few low-power integrated solutions being functional enough for animal use before being considered for safety verification in humans.

One potential way to lower power is to identify neural features that maintain the decoding capabilities of intracortical spike recordings but using less bandwidth. Using threshold crossing events is a common solution^4,22–28, but this only saves power after digitization, leaving the high-bandwidth, low-noise amplifier included. Local field potentials have also been demonstrated to contain much movement information from recordings as invasive as threshold crossings^29–31. The frequency content of such signals is appropriately low bandwidth for power reductions, and several groups have shown their usefulness towards open-loop decoding^32–39 and closed-loop decoding^4,27,40–43. However, owing to their intracortical nature, it is inconclusive how much of the performance is impacted by low-pass filtered spikes instead of potentials alone. Therefore, although most studies show that local field potential decoders can achieve peak performance levels comparable to but lower than spike-based features, we do not know whether that is an artefact of spikes present in the signals.

Electrocorticography (2 kSps sampling rate) has also been proposed as a less invasive neural feature for brain-machine interfaces. Several groups have shown open-loop^44–47 and closed-loop⁴⁸ decoding, and the average correlation coefficient of these studies is 0.67. While comparable to spike-based neural features, these tasks were simple, where the multiple degrees of freedom (if present) moved mostly along one dimension to minimally varying displacements. This suggests that the decoders were dominated by the presence of movement. It is unclear how well electrocorticography decoders will perform at predicting more complex tasks that have systematically varied target locations and displacements, such as the continuous centre-out-and-back or the point-to-point tasks.

Another interesting neural feature is the integration of multiple unit activity, sometimes called ‘spiking-band power’ (SBP), which was originally suggested in the 1960s before the age of cheap electronics, leaving it uninvestigated during the rise of brain-machine interfaces⁴⁹. More recently, it has been demonstrated that the power in the 300–6,000 Hz band of spiking activity is not just equivalent to local field potentials, threshold crossing rate (TCR) and sorted unit firing rate at predicting movement direction, but superior³². Further, our group has demonstrated that the bandwidth over which the signal is integrated can be drastically lowered to 300–1,000 Hz while maintaining 95% of the decoding performance⁵⁰. However, these studies only investigated offline decoding of relatively simple tasks, where population activity may decode as well as single units. The spatial specificity of SBP is not well understood, which makes the ultimate decoding limitations difficult to predict from fundamentals.

Here we use a combination of simulated and in vivo neural recordings from non-human primates and rats to compare the specificity of the 300–1,000 Hz spiking band with signals containing spikes. These simulations indicate that SBP results primarily from spike waveforms themselves, weighted by their amplitude, which creates a highly spatially specific signal. In addition, the simulations suggest that the spiking band can extract accurate spike information at low signal-to-noise ratios (SNRs) below typical thresholds, implying that SBP may represent neural activity that cannot be extracted by the TCR or sorted units. We believe that these analyses explain the findings of our previous work and its foundational work^32,50. Further, the outcomes of these simulations suggest that this very-low-power approach will fare as well or better than unit-based methods at decoding more complex tasks. Thus, we evaluate this claim using a variety of decoded tasks in non-human primates: recalibrated feedback intention-trained (ReFIT) Kalman filters to control one-dimensional index and middle-ring-small (MRS) fingers in closed loop, support vector machines to classify two-dimensional individuated movements of unrestricted fingers in open loop, and standard Kalman filters to predict two-dimensional centre-out-and-back arm reaches in open loop.

Results

Visualizing single spikes in the spiking band.

We began by investigating the frequency content of typical motor cortical biphasic spike waveforms to find a spectral basis for the 300–1,000 Hz pass band optimized in our previous work⁵⁰. We identified two units representing narrow and broad spikes, plotted in Fig. 1a, from 30 kSps recordings from a 96-channel Utah microelectrode array implanted into primary motor cortex in a rhesus macaque (monkey W, see Supplementary Fig. 1 for placement). Analysing both narrow (putative inter-neurons with higher frequencies) and wide (putative pyramidal neurons with lower frequencies) spikes, which are expected waveforms and have been reported previously in premotor and motor areas in rhesus monkeys^51,52, should approximate the range of power belonging to the 300–1,000 Hz spiking band for any motor cortical spike. We extracted the averaged spikes, processed their interpolated fast Fourier transforms, and approximated the total amount of signal power belonging to each of the 1–300 Hz, 0.3–1 kHz and 1–15 kHz bands. Although most of the power in both spikes existed above 1 kHz, we found that the 300–1,000 Hz band contained a substantial amount, between 25% and 45% of the total, as shown in the green band of Fig. 1a.

Fig. 1 |. Representation of spikes in the 300–1,000 Hz band.

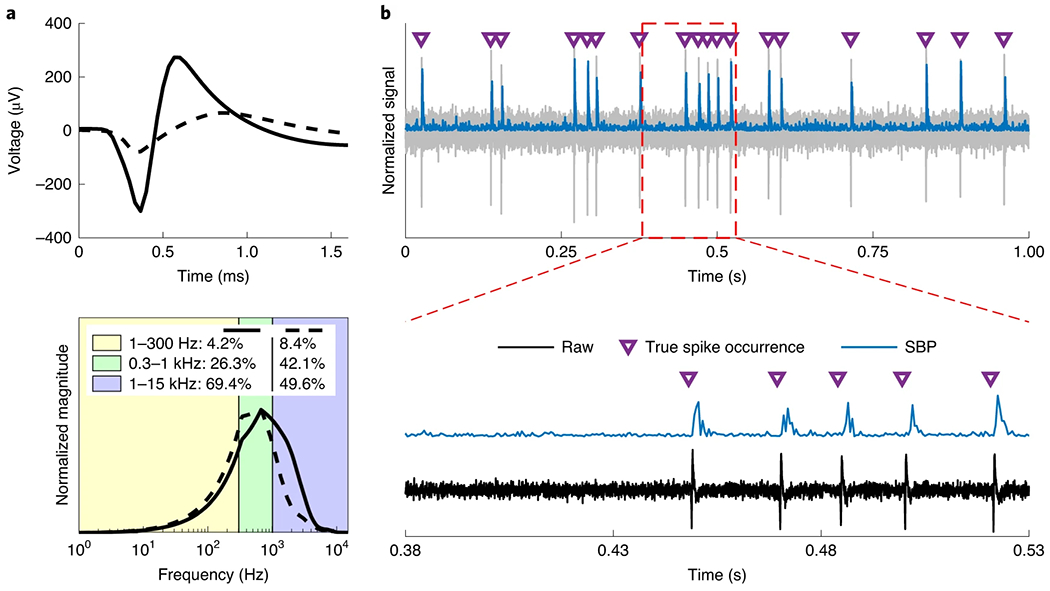
a, Frequency spectrum of two averaged neural spikes (solid line, narrow/putative inter-neuron; dashed line, wide/putative pyramidal neuron) extracted from intracortical non-human primate recordings. Top: averaged neural spike waveforms. Bottom: interpolated fast Fourier transform of the above waveforms split by relevant frequency bands, normalized to the maximum value for each transform. The numbers in the legend indicate the amount of power belonging to each frequency band, with the solid line represented by the left-most set of percentages. b, Single-unit simulated recording of the solid-line unit in a at an SNR of 10. Top: raw simulated noisy signal (grey) with spike occurrences (purple triangles) and SBP (blue) overlaid. Bottom: a snippet of the top plot with the SBP manually offset vertically to avoid occlusion.

With substantial power in the spiking band, we expect at least high SNR single-unit recordings to maintain strong spike representations after filtering to 300–1,000 Hz. Figure 1b shows a simulated recording of the solid-line unit from Fig. 1a (which had the least amount of power in the spiking band) firing spontaneously at an SNR of 10. The purple triangles represent the true simulated spike occurrences of this unit, while the blue trace represents the absolute value of the raw simulated signal filtered with a 300–1,000 Hz second-order Butterworth filter, re-sampled at the Nyquist sampling rate of 2 kSps. After smoothing both signals with a 50 ms Gaussian window filter, SBP exhibited a 0.95 correlation with the true firing rate of the unit. In the unsmoothed signal energy on the bottom of Fig. 1b, there is a clear burst at each instance of a spike with a small lag resulting from the filter’s non-zero-phase characteristics. This resembles an envelope of the broadband signal, showing how the neural activity is captured on a spike-by-spike basis. While this first example represents a best-case scenario, the SBP trace does not look unusual for a single-unit electrode and starts to suggest that the spikes are dominating the SBP signal. Interestingly, though only obvious to us in hindsight, the SNR of the spiking-band trace in Fig. 1b is approximately twice as high (SNR = 19.52) as the SNR of the broadband trace. The small pass band of SBP cuts the noise level by a factor of about two while taking advantage of the spike’s energy above and below zero, suggesting SBP may be more robust to noise than single-ended broadband TCR.

We further explored this idea by simulating single neuron recordings under a variety of conditions to estimate the operational space of SBP for predicting true unit firing rates and compared it with that of TCR. In these simulations, the SBP and TCR feature extraction pipelines received the same simulated recording, including identical noise and spike timings. In addition, our simulations did not estimate the true firing rate by thresholding; rather, the true firing rate was known absolutely because the timings of the simulated spikes were known. Figure 2a shows these results in a grid for optimized TCR and SBP, where the colour represents the correlation with smoothed true firing rate. We found that the correlation is low for both features when the SNR or firing rate are very low (lower left corner). In contrast, the correlation is high when the SNR or firing rate are high (upper right corner). However, surprisingly, SBP maintains high correlation for lower SNRs and lower firing rates compared with optimized TCR.

Fig. 2 |. SBP, TCR (optimized threshold set at −3.75 × r.m.s.) and low-bandwidth TCR (optimized threshold set at 2.75 × r.m.s.) prediction of true firing rate.

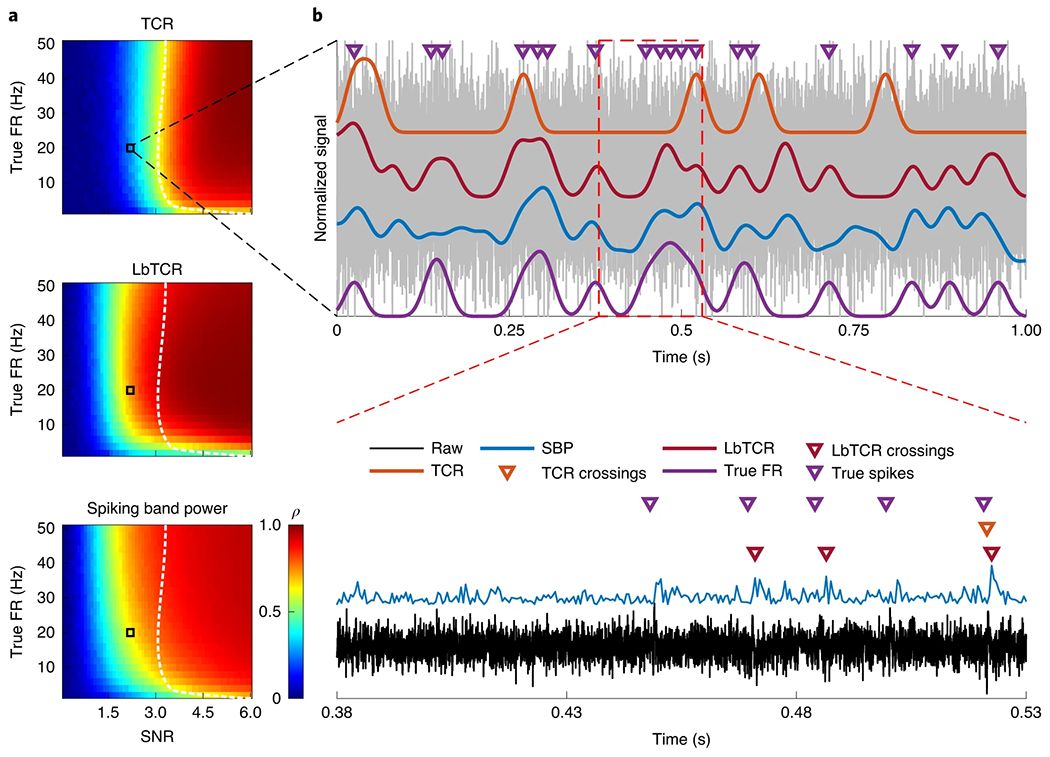
a, Predictive capability of the three features of various true firing rates from various recording SNRs. The colour bar represents the Pearson’s correlation coefficient (ρ) between the smoothed neural feature and the unit’s smoothed true firing rate. Zero-phase smoothing used a 50 ms Gaussian window. The black boxes indicate the simulated recording conditions in b, and the white dotted lines track the yellow region of the TCR plot to better compare performance. The averages of 100 simulations with random spike timings and noise are shown, with each simulation containing 144,000 samples at 30 kSps and 9,600 samples at 2 kSps. b, The same simulated unit plotted in Fig. 1b but with an SNR of 2.25. Spike occurrences are overlaid as purple triangles along with smoothed TCR (orange), smoothed low-bandwidth TCR (LbTCR; red), SBP (blue) and true firing rate (true FR; purple).

However, we consider it unfair to directly compare SBP and TCR, as the reduced SBP pass band eliminates much of the higher-frequency noise components. Thus, we also compare SBP to a low-bandwidth form of TCR, which is extracted by thresholding the SBP. We found that SBP achieved similar low firing rate and low-SNR prediction performance to low-bandwidth TCR. This suggests that the small bandwidth is indeed a major contributing factor towards the single-unit firing rate estimation performance.

An example from this region of high SBP and low-bandwidth TCR correlation but low TCR correlation is shown in Fig. 2b, where we recreated the same recording from Fig. 1b but with an SNR of 2.25. SBP in blue and low-bandwidth TCR in red maintained relatively high correlations with the unit’s true firing rate in purple (0.62 and 0.69, respectively) and are rarely falsely ‘activated’ by noise. In comparison, the firing rate predicted by crossings of an optimized −3.75 × root-mean-square (r.m.s.) threshold in purple had a 0.34 correlation and more frequently missed true spikes. Although this may seem unfair to TCR detecting just one of the five spikes in the bottom of Fig. 2b, we found that lowering the threshold level to acquire more spikes resulted in more false detections. This reduced the overall predictive performance for TCR, even when the unit had a high SNR and a high firing rate. In addition, SBP required no trained parameters, while we found it necessary to optimize both TCR and low-bandwidth TCR to fairly compare the three features (Methods). To capture the low-SNR spikes via thresholding, substantial time must be spent optimizing that threshold, whereas a fixed −4.5 r.m.s. threshold that is used frequently for closed-loop brain-machine interface experiments would miss virtually all of the low-SNR spikes, a claim suggested by the worse low-SNR prediction performance in the TCR plot of Fig. 2a. Overall, this illustrates that the spiking band may be better able to extract firing rates of low-SNR or low-firing-rate units despite its much lower bandwidth, ones that high-bandwidth detectors may ignore.

SBP predicts firing rates of local units.

The simulations presented thus far have only represented simulated recordings from one unit. In practice, electrodes record from many units simultaneously. Consequently, we investigated how well SBP tracks the true firing rates when there are multiple units surrounding an electrode. We first simulated recording of five neurons spiking spontaneously and independently at 20 Hz in different arrangements surrounding the simulated recording electrode, similar to past simulation work⁵³. Each neuron’s amplitude was attenuated based on its simulated displacement from the recording point according to the monopole equation (equation (2) in Methods) and the result of Holt and Koch’s simulations⁵⁴. Figure 3 illustrates the results of these simulations, where a red colour represents high correlation between that specific neuron’s firing rate and the recording’s SBP (blue is low correlation). First, we simulated a simple arrangement of the neurons cumulatively displaced by 50 μm in Fig. 3a. These waveform amplitudes fall off with the inverse of the distance according to the monopole equation. As a result, SBP strongly predicts the firing rate of just the highest-amplitude unit, 50 μm away. We then simulated a more realistic scenario with five units spaced out in a constant density around the electrode, which means that there are fewer close neurons and more distant neurons, and found an even stronger preference of SBP to the highest-amplitude unit (Fig. 3b). Third, in Fig. 3c, we simulated a highly active electrode, where multiple neurons correlated with SBP. However, the correlation was weighted by amplitude towards the highest-amplitude units, leaving less representation of the lower amplitude units still visible above noise. Lastly, in Fig. 3d, to illustrate that firing rate is also factored into the representation, we simulated the scenario in Fig. 3c again, but with the highest-amplitude unit spiking at just 1 Hz. We found that SBP cannot detect the firing rate of the highest-amplitude unit accurately (as predicted by lower firing rates in Fig. 2a and Supplementary Fig. 4) but shifts to a more specific prediction of the firing rate of the next largest amplitude unit that is active (or the highest r.m.s.-based SNR unit according to the r.m.s.-based SNR analysis; Supplementary Information). In all simulations, we found that SBP is a spatially local signal (see the monopole equation variant in Methods), dominated by the firing rates of the highest-amplitude single units that are reasonably active, regardless of where they are with respect to any voltage threshold.

Fig. 3 |. Correlation between the true firing rate of individual units and the field’s SBP.

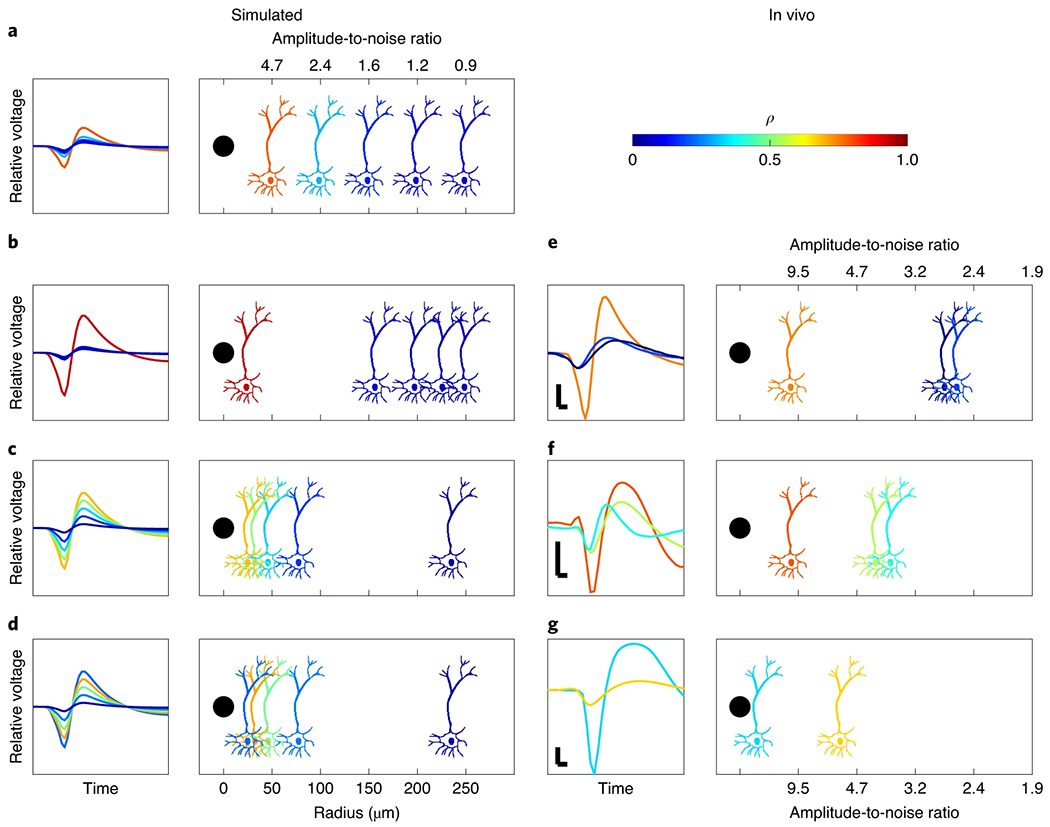
a–g, Each rectangle represents an arrangement of neurons distributed as shown. The schematic of the neurons and their corresponding spikes to the left are coloured according to their firing rate’s Pearson’s correlation with the recording’s SBP. a–d, Simulated arrangements. e–g, In vivo recording arrangements estimated by amplitude. Simulated neurons all fire at 20 Hz, unless otherwise specified. The averages of 100 simulations with random spike timings and noise are shown, with each simulation containing 144,000 samples at 30 kSps and 9,600 samples at 2 kSps. The in vivo analyses on the right are similar in relative amplitude content to the simulations immediately to the left. Vertical and horizontal scale bars are 100 μV and 0.1 ms, respectively. Firing rates listed below are ordered from left to right as shown. The black dots in the panels represent the electrode. a, Neurons are cumulatively displaced by 50 μm. b, Neurons spaced in a constant volumetric density around the electrode. c, Neurons organized with amplitude to noise ratios of 9, 7, 5, 3 and 1. d, The same as c, but the highest relative amplitude neuron fires at 1 Hz. e, In vivo recording from monkey W with units firing at 25, 34 and 7 Hz. f, In vivo recording from a carbon fibre electrode in rat motor cortex with units firing at 9, 12 and 9 Hz. g, In vivo recording from a carbon fibre electrode in rat motor cortex with the units firing at 0.5 and 15 Hz.

To compare with realistic voltage traces that include multiple sortable units, we used three recordings captured in vivo and performed the same analysis. These include one channel from monkey W’s motor array (Fig. 3e) and two from carbon fibre electrodes implanted acutely into rat motor cortex (Fig. 3f,g). Overall, we found similar results to the simulations, validating that SBP is tuned strongly to the firing rates of higher-amplitude units, while mostly ignoring low-amplitude units. This suggests that while SBP may not be a single-unit signal, it maintains the spatial specificity of broadband spike-related features like TCR or sorted units.

Improved decoding with SBP.

In previous work, we and others demonstrated that SBP can be used to predict gross movements offline^32,50. Specifically for fingers, we showed that SBP from 300 to 1,000 Hz had very similar performance to TCR⁵⁰. If the unit specificity suggested by the simulations above is correct, this would predict that the performance equivalence will be maintained in more complex tasks, specifically the control of multiple fingers, which we evaluate here. We trained three non-human primates, monkeys L, W and N, to perform a one-dimensional task requiring them to move virtual fingers into virtual targets by moving their physical fingers (Supplementary Fig. 2). In these datasets, monkeys L and W performed the task with all four fingers moving together and monkey N moving just his index finger. We first trained four Kalman filters for each monkey, one each for SBP, low-bandwidth TCR, TCR and single-unit firing rate, to decode the neural activity into finger positions offline. Each dataset was tenfold cross-validated, and so each decoder was always trained and tested on neural and behavioural data in which the monkey was moving the same finger(s). We found that SBP achieved correlations between its prediction and the actual finger movements statistically as high or higher than all other features (P < 1 × 10⁻⁴; see ‘Open-loop decoding analysis’ in the Supplementary Information). These results were comparable to those found by others and our group, but with a more challenging task to decode than our previous study due to more target locations and randomized target order^30,50,55. Offline, we also compared the importance of SBP, low-bandwidth TCR and TCR channels for decoding in Supplementary Fig. 5b and found that SBP generally had more channels that resulted in a drop in decode performance when individually excluded. This suggests SBP is extracting more valuable information from the available channels than TCR methods, which follows from the result of the low-SNR simulations in Fig. 2a.

With a functional offline SBP decoder, we tested SBP as a closed-loop neural feature in real time to gauge its usability in neuroprosthetic applications. We trained monkeys W and N to perform the same one-dimensional finger task as the offline task, except using the index finger alone or the MRS fingers as a group (as described previously⁵⁶). During each experiment, we trained ReFIT Kalman filters to decode TCR or SBP into finger positions and velocities⁵⁶. The closed-loop decoders the monkeys used for a specific finger group were always trained on neural data and behavioural data associated with movements of that finger group. Figure 4a shows predicted finger traces with visual feedback provided to monkey W using only his MRS fingers and monkey N using only his index finger (Supplementary Videos 1 and 2 are of monkeys W and N using their other finger groups, recording conditions displayed in Supplementary Fig. 3). Across all ReFIT decoders for any combination of finger groups, both monkeys achieved significantly higher bit rates (1.1 bps to 1.5 bps, P < 1 × 10⁻²⁵ for monkey W; 1.0 bps to 1.1 bps, P < 1 × 10⁻⁴ for monkey N; single-tailed two-sample t-test) when using the SBP decoders compared with TCR decoders, though only monkey W acquired targets in significantly less time (1.9 s to 1.3 s, P < 1 × 10⁻³⁰; single-tailed two-sample t-test; Fig. 4b). This suggests that ReFIT Kalman filters can decode SBP into individual finger motions at least as well as TCR. For completeness, monkey W also used a ReFIT Kalman filter trained to decode 300–6,000 Hz SBP (that is, from previous studies³²) to characterize any losses from the bandwidth reduction. With SBP allowing an improved acquisition time (1.4 s to 1.3 s, P < 1 × 10⁻³; single-tailed two-sample t-test) and no significant difference in bit rate (1.5 bps, P = 0.51; two-tailed two-sample t-test) over 300–6,000 Hz SBP, we suggest that the 300–1,000 Hz spiking band is sufficient for optimal closed-loop SBP decoding.

Fig. 4 |. Comparison between the decoding performances of SBP and TCR.

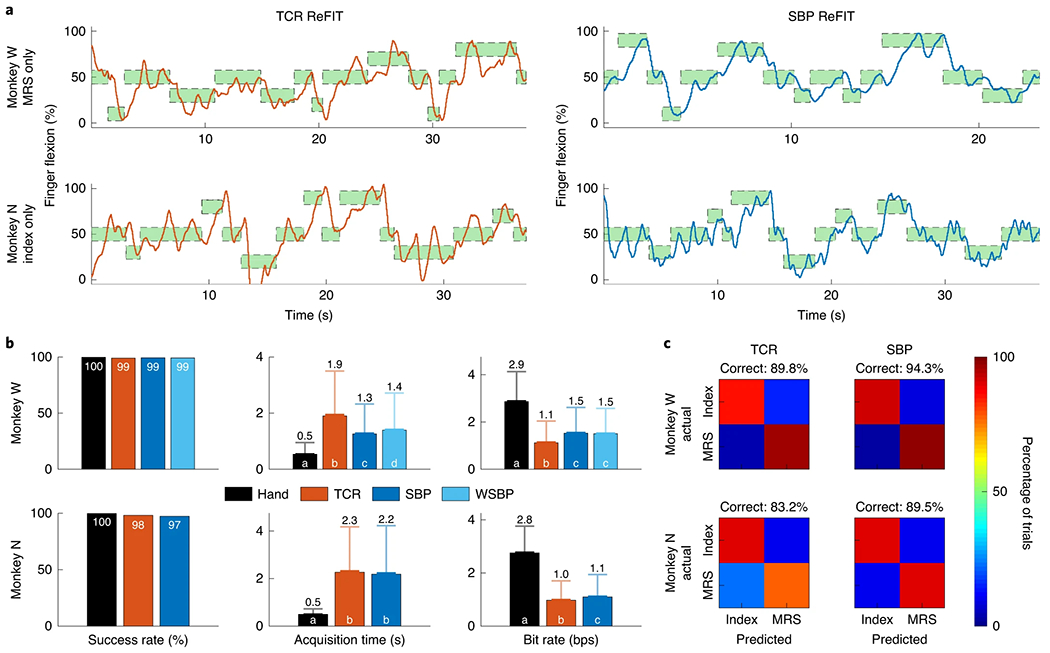
a, Closed-loop decode traces from translating TCR in orange (left) or SBP in blue (right) for 15 targets of each decoder. The top panels are for monkey W and the bottom panels are for monkey N. Targets are green (for successful acquisition) and surrounded by a dashed line. b, Success rate, acquisition time and bit-rate statistics for all methods of closed-loop virtual hand control. Columns represent mean with standard error shown by the darker error bars (very small, so the error bars are difficult to distinguish from the mean bar) and standard deviation shown by the lighter error bars. These statistics resulted from 4,659 hand trials, 1,084 TCR decoder trials, 2,042 SBP decoder trials and 2,428 wideband SBP (WSBP) decoder trials from monkey W and 1,556 hand trials, 1,256 TCR decoder trials, and 1,915 SBP decoder trials from monkey N. Bars in a group labelled with the same letter are statistically similar. For example, in monkey W’s bit-rate statistics, for the case where the virtual hand was controlled directly by physical hand movements, it was exclusively labelled ‘a’ because it was statistically different. TCR control’s bit rate was also statistically different than all others, so it was exclusively labelled ‘b’. However, the bit rates for SBP and WSBP control were statistically similar to each other, so they share label ‘c’. P < 1 × 10⁻³ between SBP and WSBP for monkey W acquisition time and between SBP and TCR for monkey N bit rate. P < 1 × 10⁻¹⁸ otherwise. All statistical tests were single-tailed, two-sample t-tests. The legend represents trials in which the virtual fingers were controlled by the monkey’s physical hand movements or the TCR, SBP or WSBP (300–6,000 Hz pass band) decoders, respectively. c, Support vector machine confusion matrices from classifying finger movements as index or MRS.

With the ability to use SBP to decode movements of individual finger groups, we sought to validate that SBP could maintain high performance in two-dimensional tasks. First, we attempted to classify which finger group was moving when both were given unrestricted mobility. We trained the monkeys to acquire two targets simultaneously in a two-dimensional finger task, one exclusively for each finger group, and presented targets such that only one group was moved from rest to a flexion position at a time while the other group remained at rest. We trained two support vector machines to classify which finger moved in a given trial, one using TCR and the other using SBP. The SBP machine achieved the higher prediction performance (average >5% improvement for both monkeys), as shown in Fig. 4c and similar to that found previously for TCR⁵⁶. Second, we predicted offline continuous hand position in a two-dimensional centre-out-and-back cursor-control task using a standard Kalman filter in non-human primates, similar to what has been done in other work⁵⁷. We found that SBP achieved statistically higher correlation coefficients between the predicted and actual hand positions and statistically similar hand velocity correlation coefficients compared with TCR and low-bandwidth TCR (for SBP, TCR and low-bandwidth TCR, respectively: 0.86, 0.84, 0.84 X position; 0.94, 0.93, 0.93 Y position; 0.74, 0.73, 0.74 X velocity; 0.84, 0.82, 0.82 Y velocity for monkey J; 0.84, 0.81, 0.81 X position; 0.77, 0.72, 0.75 Y position; 0.76, 0.71, 0.73 X velocity; 0.77, 0.73, 0.74 Y velocity for monkey L; P < 1 × 10⁻³, two-tailed two-sample z-test; see ‘Two-dimensional cursor control’ in the Supplementary Information).

These results, consistent with our one-dimensional finger task, suggest that SBP exceeds the performance of threshold crossing-based features at multidimensional control tasks despite the drastically reduced bandwidth, similar to what was found previously by others³². We also investigated the impacts of increasing the recording noise on decoding performance in the Supplementary Information (‘Two-dimensional cursor control’), and found that SBP could tolerate almost two times the noise level as TCR to maintain at least 80% of their no-noise decode performances.

Discussion

Here we have compared single-unit firing patterns and the 300–1,000 Hz SBP. Specifically, we have shown that the single-unit specificity of the SBP is comparable to sorted units despite the reduction in bandwidth, likely explaining the mechanism that yielded the outcomes of our previous work and that of others. We also believe that the specificity of SBP improves its decoding performance to be comparable or better than standard high-bandwidth methods, such as TCR, and comparable to sorted unit firing rates. Finally, we believe our results extend our previous findings as well as those of others to suggest that the decode performance improvements of SBP are maintained in complicated behaviours, higher dimensions and closed loop.

The results of our simulations suggest that SBP, sampled at only 2 kSps, is a highly spatially specific neural feature. It is dominated by spikes, and to extract neural information, it requires spikes to be present. Compared with TCR, SBP requires no specific tuning for it to function optimally. It is ‘parameter free,’ without requiring adjustable thresholds or any programming to implement spike sorting that must be done daily for optimal TCR performance. From a device perspective, TCR would require programmable and receiver circuitry to, at the least, optimize the thresholds that we found varied substantially between animals and across days within one animal (see ‘Open-loop decoding analysis’ in the Supplementary Information). However, SBP would need no additional circuitry while maintaining performance levels. In a medical application, this implies a reduction in training time without a required daily parameter search of the best threshold and overall greater ease of use as a medical device. In addition, lower device complexity and power consumption without any required receiver hardware would imply an increased battery life of SBP devices. As a result, SBP may become broadly applicable to other closed-loop, low-power neural applications, such as bladder-state monitoring, deep-brain stimulation and seizure prevention.

Importantly, these results suggest that SBP can accurately extract single-unit firing rates at lower SNRs than TCR, suggesting that more activity can be extracted on channels that may not have visible spikes. This has major implications for the longevity of implanted microelectrode arrays in human patients, as it has been reported that the quantity of electrodes displaying spikes visible above noise wanes over time⁵⁸. We performed an analysis (‘Two-dimensional cursor control’ in the Supplementary Information) in which we injected noise into the recorded neural activity to investigate the impacts of fewer visible neural spikes on decoding. Through this analysis, we validated that SBP maintains better decoding performance than TCR as visible spike presence on an array drops off. In fact, some groups conducting human clinical trials have already made use of this approach to extend the lifetime of their arrays^25,59,60. In particular, high-frequency band power (essentially 250–3,000 Hz SBP) was added to the spike counts for their brain-controlled functional electrical stimulation prosthesis²⁵. Others also used 250–5,000 Hz SBP in addition to spike counts for their virtual typing task in human patients⁶⁰. In neighbouring fields, groups that implant deep-brain electrodes utilize SBP to detect when electrodes have entered the grey matter of the subthalamic nucleus⁶¹. We believe that our findings suggest a potential mechanism explaining why their methods work, and we hypothesize that SBP’s capabilities of extracting low-SNR unit activity may extend the usable, high-performance lifetime of such a neuroprosthesis even once the spikes are indiscernible above broadband noise.

While most high-performance brain-machine interfaces rely on visible spikes to decode, many groups have experienced performance issues as the spike amplitudes wane over time or are invisible above noise^39,62,63. Consequently, local field potentials and electrocorticography have been investigated as replacement and supplemental feature sources, as they represent local neural activity even with lacking spikes. As many local field potential studies have shown performances comparable to but lower than spike-based features^{4,27,32,34–38,40–43}, it is inconclusive how much of the performance is a result of low-pass filtered spikes. However, the results we have presented clearly demonstrate that SBP, while dependent on spikes, exceeds the performance of high-bandwidth spike-based features. Further, the average electrocorticography open-loop decode correlations of 0.67 (refs. ^44–48) are similar to the offline analyses we have presented here for SBP and TCR. However, the simplicity of the tasks in the electrocorticography studies suggests that the decoders may be predicting the presence of movement effort rather than the movement itself. In contrast, our one- and two-dimensional centre-out-and-back decoding results using SBP demonstrate SBP’s capability of predicting the movement directly with performance as good or better than TCR.

One of the major benefits of SBP as a reduced-bandwidth, highly specific neural feature is the power savings it enables compared with higher-bandwidth devices previously presented^5,6,64. In our analysis presented in ‘Integrated circuit simulations’ in the Supplementary Information, we simulated the power consumptions of optimized, custom integrated circuits that extract 2 kSps low-bandwidth features or 20 kSps high-bandwidth features to estimate the power savings that can be attributed to the reduction in recording bandwidth. On the basis of those results, which showed a 90% reduction in power consumption from 11 mW to 1.1 mW, we believe the greatest improvement to the power consumption of neural interfaces can be made only through changes to the analogue front-end. However, such a wide bandwidth is not optimized for power consumption and is much larger than what is necessary to accurately estimate firing rates with threshold crossings. While reducing the TCR bandwidth to the spiking band would save equivalent amounts of amplifier power, such a circuit would be suboptimal, as the SBP decodes always out-performed low-bandwidth TCR. In addition, the low-bandwidth TCR circuit would require a receiver and programmable circuits for the thresholds that SBP does not require. Such circuitry would increase the power consumption of a low-bandwidth TCR circuit (though not investigated here) and be a major hindrance in applicability to neural dust-like chiplets that have intermittent power supplies and would benefit greatly from having no programmable, power-consuming memory for threshold levels that would otherwise be forgotten each power cycle. The factor of ten reduction in power consumption predicted by the circuit simulations implies a substantial increase in battery life of SBP devices while enhancing decoding performance over the equivalent TCR circuit.

The lower power requirements of SBP would not only reduce the consumptions of current acquisition technologies but also have implications for the future of cellular-scale neural recording. State-of-the-art front-end designs are being presented that require a small number of transistors^65–67. With simpler front-end amplifiers, it becomes much more plausible to have electronics mounted on the array itself or have modular, wireless ‘chiplets’ with single-unit-level specificity^66,68. This also suggests that existing application-specific integrated circuits developed for local field potentials and electrocorticography may be sufficient for brain-machine interface applications, so long as there are spikes present on the electrodes^69–71. Overall, the minimal hardware and small supply requirements of SBP may help enable a path towards recording thousands to tens of thousands of channels with similar performance to single-unit-based systems.

Methods

All procedures were approved by the University of Michigan Institutional Animal Care and Use Committee.

Array implants.

We implanted three male rhesus macaques with Utah microelectrode arrays (Blackrock Microsystems) in the hand area of primary motor cortex, as described previously^26,56. Pictures of the implants are illustrated in Supplementary Fig. 1. Only motor cortex arrays were used in this study, and only monkey N’s most rostral array was used.

In addition, we obtained previously recorded offline datasets (L120502 and J121009, a centre-out-and-back arm reaches behavioural task performed by monkey J using the same implants as described in the original work) for our two-dimensional cursor-control analysis⁵⁷. All surgical and animal care procedures for these animals were performed in accordance with National Institutes of Health guidelines and were approved by the Stanford University Institutional Animal Care and Use Committee. Monkeys J and L were adult male rhesus macaques implanted with 96 electrode Utah arrays using standard neurosurgical techniques. Electrode arrays were implanted in primary motor cortex (M1) as visually estimated from local anatomical landmarks. Monkey J had two arrays, one in M1 and one in dorsal premotor cortex (PMd; unused in this study), while Monkey L had one array implanted on the M1/PMd border.

We also obtained recordings using carbon fibre electrodes in the rat motor cortex⁷². Each carbon fibre (~6.8 μm) was insulated with parylene C, cut to expose the carbon recording surface, and then coated to reduce impedance to near 30 kΩ (refs. ^72,73). We obtained acute electrophysiology recordings from layer V of one male wild-type Long Evans rat’s motor cortex following previously established methods⁷³. Three minutes of electrophysiological data were acquired from two separate carbon fibres using a TDT RX5 Pentusa recording system (Tucker-Davis Technologies).

Feature extraction.

All processing was done in Matlab v.2012b, 2016a or 2018a (Mathworks), except where noted.

The band power neural features presented here are similar to those used previously, but in less computationally expensive forms^32,49. The raw data were collected from the monkeys using a Cerebus v1.0 using firmware version 6.03.01.00 (Blackrock Microsystems) digitizing at 30 kSps and from the rat using the RX5 Pentusa digitizing at 24.414 kSps. We first applied a second-order Butterworth filter to the raw data with a 300–1,000 Hz pass band for SBP. Then, we extracted the magnitude of the signal and downsampled it to 2 kSps or 2.4414 kSps for the Cerebus or RX5 Pentusa, respectively. Lastly, we smoothed this signal using a 50 ms Gaussian window for simulations or averaged the signal in non-overlapping 50 ms bins for open-loop decoding.

For closed-loop decoding, we extracted SBP differently for simpler processing in real time. We configured the Cerebus to band-pass filter the raw signals to 300–1,000 Hz using the Digital Filter Editor feature included in the Central programme (Blackrock Microsystems), then sampled at 2 kSps for SBP.

The continuous data was streamed to a computer running xPC Target (Mathworks), which took the absolute value of the incoming data and averaged it in 50 ms bins for decoding.

To extract TCR in simulation, we first high-pass filtered the raw, simulated 30 kSps recordings using a zero-phase second-order Butterworth filter with a 250 Hz cut-off frequency. We set a threshold at −3.75 r.m.s. and smoothed the binary result using a 50 ms Gaussian window. We optimized the −3.75 r.m.s. threshold for Fig. 2 from the threshold that achieved similar low firing rate prediction performance to SBP (we found more negative thresholds further reduced TCR’s low-SNR prediction performance, which, at all thresholds, was worse than SBP).

To decode TCR, we configured the Cerebus to extract voltage snippets that crossed a −4.5 r.m.s. threshold. Then, these waveforms were streamed to the computer running xPC Target, which logged the time of each spike’s arrival (for later open-loop decode processing) and counted the number of spikes in 50 ms bins (for closed-loop decoding).

We also sought to compare SBP to a lower-bandwidth form of TCR to validate that the improvements in decode performance were not artefacts of the restricted noise bands. To extract low-bandwidth TCR, we thresholded the absolute value of the 300–1,000 Hz band. We chose to threshold only the spiking band since our primary goal with using SBP is to reduce front-end bandwidth to save the most power, with a secondary goal of maintaining decode performance.

When comparing SBP to sorted units to mimic the multiple unit simulation, we imported the relevant recordings into Offline Sorter (Plexon). Then, we high-pass filtered the recordings with a four-pole Butterworth filter with a cut-off frequency set to 250 Hz. To sort units of all amplitudes for validation of the multiple unit simulation results, we manually chose a reasonable threshold and sorted the spikes crossing the threshold individually and in combination with principal component analysis and visual inspection. For the power spectrum analyses we performed, we decided it was necessary to extract the averaged units without any influence from the lower frequency, higher signal power 1–300 Hz band. The random phases of the spikes in that band could confound the averaged spike waveforms, despite the possibility that action potentials could contain power in that band.

To sort units for offline decoding, we imported into Offline Sorter spike waveforms and timings extracted by the Cerebus with a −4.5 r.m.s. threshold during a behavioural task. Then, we eliminated all waveforms that were clearly artefactual, determined by extraneously large amplitudes, extraneously fast timescales or waveform shape. We manually sorted the remaining waveforms into single units by analysing the three strongest principal components, the density of waveforms in the principal component space and the visual patterns of the waveforms. For all channels with distinguishable units, we added one additional unit, termed the neural hash in this manuscript, containing the remaining unsorted waveforms that were not deemed artefact. After unit isolation, we synchronized the timings of the waveforms of each unit with the behavioural data and binned each unit’s spiking rates in 50 ms bins.

In all simulations, we compared each estimate of firing rate with the true firing rate of each simulated unit (‘True spike occurrence’ in Fig. 1 and ‘True FR’ in Fig. 2). We defined true firing rate as the indicator function of the initiation of a spike smoothed by a 50 ms Gaussian window, with the timings of all simulated spikes known based on the methods detailed in the subsequent paragraph.

In addition, several simulations were also performed with 100 ms Gaussian smoothing windows or exponential smoothing windows of various time lengths for all features, which yielded similar results and are subsequently not presented.

Simulation design and parameters.

In Matlab, we simulated 30 kSps recordings of neural activity to investigate the origins and characteristics of SBP. We simulated spontaneously firing neurons as point current sources with an action potential waveform averaged from a 3 ms sorted unit from one of monkey W’s intracortical recordings digitized at 30 kSps. To emulate spontaneous neural firing patterns, we first selected a reasonable firing rate, FR, representative of typical neural activity and a simulation duration, T. Then, we subtracted the total number of samples occupied by spikes (that is, 3 ms of samples times the firing rate times the duration, or 3 × 30 × FR × T) from the 30,000 × T samples in each simulation and randomly partitioned the remaining samples into FR × T + 1 parts. Then, these randomly sized partitions were placed between spikes to generate a random spiking pattern with known timings. As such, simulated single-unit recordings never had overlapping spikes. When simulated spikes from multiple units overlapped in time on one simulated recording, we superimposed the recorded voltages as was done by others⁵³.

We simulated our recording electrode as a point current sink. For a noise model, we generated additive 6.23 μV thermal white noise as was determined typical of intracortical recording simulations previously by others⁵³. We found this value similar to the noise level of our Cerebus recording hardware. We did not include any biological noise since such a noise source with frequency characteristics similar to the spikes being simulated could confound the results. Thus, the same simulated 30 kSps signals, 6.23 μV noise included, were used as inputs to both the TCR and SBP feature extraction pipelines. For simulations, we defined the SNR as the maximum of the absolute value of the noiseless signal divided by the r.m.s. value of the isolated noise:

$$\text{SNR}=\frac{\text{max}\left(\right|\text{signal}\left|\right)}{\text{r}.\text{m}.\text{s}.\left(\text{noise}\right)}$$ (1)

This allowed us to evaluate simulated signal SNRs for unrectified broadband recordings and their corresponding rectified SBP using the same metric. In addition, we have also performed all simulations using another SNR definition based on signal r.m.s. to better represent the total spiking signal power of a recording (results in the ‘r.m.s.-based SNR analysis’ section in the Supplementary Information):

$${\text{SNR}}_{\text{r}.\text{m}.\text{s}.}\text{=}\frac{\text{r}.\text{m}.\text{s}.\left(\text{signal}\right)}{\text{r}.\text{m}.\text{s}.\left(\text{noise}\right)}$$

To transition between a simulated unit’s SNR and the estimated displacement from a recording electrode, we applied a variation of the monopole equation:

$$r=\frac{I_{\text{0}}}{4\pi \sigma \times \text{SNR}\times \text{r}.\text{m}.\text{s}.\left(\text{noise}\right)}$$ (2)

where r is the estimated displacement between the point current source neuron and the point current sink recording electrode, I₀ is the maximum of the absolute value of the current source, which we set to a realistic 5 nA, and σ is the simulated conductivity of grey matter of 0.27 S m⁻¹ (ref. ⁷⁴). By this derivation of the monopole equation, we assume that displacement is inversely proportional to the SNR, as was suggested by the simulation results of Holt and Koch⁵⁴. Thus, to convert to voltage when necessary, we multiplied the SNR value of each sample by the 6.23 μV noise r.m.s. level according to equation (1).

All simulations in this study were performed 100 times to avoid any effects of random noise and random spike timings, and the averages of those simulations are presented in these results. Correlations were computed from two window lengths into the simulated recording to two window lengths from the end of the simulated recording to avoid any impacts of onset and offset transients on the filters. Each simulated neural recording was 5 s long, resulting in n = 150,000 samples at 30 kSps and n = 10, 000 samples at 2 kSps per simulated recording.

Behavioural task.

We trained monkeys L, W and N, to acquire virtual targets with virtual fingers by moving their physical fingers, as illustrated in Supplementary Fig. 2. During all sessions, the monkeys sat in a shielded chamber with their right arms fixed at their sides flexed at 90° at the elbow, resting on a table. Monkeys W and N had their hands placed in the manipulandum described previously, while monkey L had his hand lightly restrained facing left in a simple stanchion⁵⁶. Finger movements were measured by flex sensors (FS-L-0073-103-ST, Spectra Symbol) attached to both doors of the manipulandum or directly to the index finger of monkey L’s right hand. Position measurements were recorded by a computer running real-time xPC Target. The computer monitor directly in front of the monkey displayed a virtual monkey hand model (MusculoSkeletal Modeling Software) which was controlled by the xPC Target computer to mirror the monkey’s hand movements⁷⁵.

For closed-loop decoding experiments presented in this work, monkeys W and N performed trials in which either the MRS door or the index door was locked at full extension and the other was free to move, or both doors were locked together to keep the monkeys’ fingers moving together. Later, monkeys W and N were trained to acquire two targets simultaneously, one specifically with their index finger and the other specifically with their MRS fingers, to classify which fingers are being moved for each target acquisition. Both groups of fingers moved freely and independently in this movement style. Monkey L had no finger restrictions and voluntarily moved all four fingers together.

Each trial began with a spherical target(s) appearing along the path of the virtual finger(s) of interest, where each target occupied 15% of the full arc of motion of the virtual finger(s). For a successful trial, the monkey was required to move its fingers such that the corresponding virtual finger(s) of interest moved into the target(s) and remained there for 500–750 ms. On successful trial completion, the monkeys received a juice reward. For closed-loop decoding, the targets were presented in a centre-out pattern for one finger group, as detailed previously⁵⁶.

For finger movement classification, four target arrangements were presented in a pattern similar to centre-out, where both targets defaulted to the rest position (50% between full extension and full flexion) and, randomly, only the index, only the MRS or both groups had targets presented at 80% flexion on the non-rest trials.

Open-loop decoding.

For all open-loop decoding, we applied a standard position/velocity Kalman filter with a position/velocity neural tuning model and optimizations as we described previously to predict the movements the monkeys made in the behavioural task²⁶. We trained Kalman filters individually for each neural feature and conducted tenfold cross-validation. In the analyses presented in the Supplementary Information (‘Open-loop decoding analysis’), we performed open-loop decodes of all six neural features in Matlab: SBP, wideband SBP (that is, 300–6,000 Hz pass band³²), low-bandwidth TCR, TCR, single-unit firing rate and single-unit firing rate with neural hash. All decodes used bin sizes of 50 ms, no common-average referencing, the optimal quantity of additional historical bins per channel or unit determined for that set of data, the optimal bin lag between the neural activity and behaviour determined for that set of data, and all available channels as previously described. In addition, to most fairly compare low-bandwidth TCR as the alternative power-efficient feature, we found the optimal r.m.s. threshold for each set of data to compare to the other features. For each decode, we calculated Pearson’s correlation coefficient and the r.m.s. error between the predicted and actual finger positions using Matlab. We transformed all correlation coefficients between the predicted and actual movements to their Fisher’s z-scores and performed two-tailed, two-sample z-tests to compare the statistical differences between all features. To determine statistical significance between r.m.s. errors of the different features, we calculated the r.m.s. errors of bins of ten distinct samples from the predictions/true movements, yielding vectors of errors representing subsets of the predictions. Then, between these vectors, we performed one-tailed, two-sample Wilcoxon rank-sum tests to determine significance.

To estimate the value of each channel or unit for each decoder, we omitted each channel or unit from the decoder and calculated the corresponding correlation between the predicted and actual finger positions. Then, we subtracted the correlation of the decoder that had access to all neural data from the correlation of the decoder missing one channel or unit to gauge the impact on performance⁷⁶.

Closed-loop decoding.

To quantify how well a system decoding SBP would perform in a neuroprosthetic application, we gave monkeys W and N visual feedback of the decoders’ outputs during the behavioural task. For each closed-loop experimental session, the monkeys began by completing at least 350 target presentations with the virtual hand controlled directly by the physical hand’s movements. The monkeys were required to acquire and hold the target for 750 ms continuously for a successful trial. The behavioural data (that is, finger kinematics) were measured synchronously with the neural features by the xPC Target computer. Then, we trained a standard Kalman filter on this data. Subsequently, we used it to predict the finger movements exclusively from the neural features and actuate the virtual hand accordingly in real time. These types of trials are what we call closed-loop experiments. For a successful closed-loop trial, the virtual finger had to remain within the target continuously for 500 ms.

The monkeys completed at least 250 target presentations using the standard Kalman filter. Then, we trained a ReFIT Kalman filter using the data from the standard Kalman filter set of trials. ReFIT Kalman filter recalibration followed the same procedure and optimization as we previously described⁵⁶. Finally, we enabled the monkeys to complete at least 150 target presentations using the ReFIT Kalman filter in closed-loop form. An entire experimental session, from the initial hand-controlled training data through standard Kalman filter and ReFIT Kalman filter training and testing, occurred within a few consecutive hours, always on the same day.

We compared success rate, target acquisition time and Fitts’ law bit rate of closed-loop decoders using exclusively SBP, TCR or wideband SBP. All decoders used a bin size of 50 ms, a bin lag of 0, 1 or 2 bins for monkey W and 2 or 3 bins for monkey N, and channel masking as needed, which were determined optimal for each decoder on each day during training²⁶. We calculated Fitts’ law bit rate using the following formula:

$$\text{Bit rate}=\frac{{\text{log}}_{\text{2}}\left(\text{1}+\frac{D_{\text{i}}{-R}_{\text{T}}}{{2\times R}_{\text{T}}}\right)}{t_{\text{acq}}}$$

where D₁ is the n-dimensional displacement between the finger’s starting position to the centre of the target, R_T is the radius of the target and t_acq is the time the monkey took to successfully complete the trial minus the required holding time⁷⁷. All failed trials were given a bit rate of 0. To best compare closed-loop decoding performance among the three neural features, we aligned the training sets of data as best as possible. The SBP and TCR standard Kalman filters were trained on the same set of synchronized behavioural data and neural activity. As the Cerebus used could apply only one filter at a time to continuous data and the xPC Target computer could not additionally filter all incoming data quickly enough in real time, the SBP and wideband SBP standard Kalman filters were compared using different synchronized behavioural and neural data acquired consecutively within the same experiment. We randomly switched the neural feature for which we would synchronize behavioural data first in a day’s experiment to avoid any biases associated with the cumulative amount of training time for each set.

The closed-loop decode statistics were calculated with single-tailed, two-sample t-tests between all combinations of virtual hand control methods. The statistics resulted from monkey W performing 4,659 trials using his hand, 1,084 trials using the TCR decoder, 2,042 trials using the SBP decoder and 2,428 trials using the wideband SBP decoder and monkey N performing 1,556 trials using his hand, 1,256 trials using the TCR decoder and 1,915 trials using the SBP decoder. Closed-loop experiments were performed in eight sessions across one month for monkey W and four sessions across nine days for monkey N.

Finger classification.

To characterize SBP in a more complex neural decoding scenario, we classified which of index or MRS groups were moving in a given trial. A support vector machine with a Gaussian kernel function and L₁ regularization was chosen as the classifier and tested using tenfold cross-validation in Matlab. Only trials in which the monkeys flexed one finger after both fingers were at the rest position were used for training and testing. The classifier translated 160 ms bins of neural activity from active channels from 50 ms before to 250 ms after movement onset with 20 ms steps between the start of each bin⁷⁸. Movement onset was determined by smoothing the moving finger’s position using a second-order Savitzky–Golay filter with a frame duration of 200 ms, deriving the velocity, and finding the first point of incline towards the maximum velocity, which is assumed to be involved in the initial movement towards a target. The results in Fig. 4c were based on 88 trials from monkey W and 95 trials from monkey N.

Reporting Summary.

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Data availability

The main data supporting the results in this study are available within the paper and its Supplementary Information. The raw and analysed datasets generated during the study are too large to be publicly shared, yet they are available for research purposes from the corresponding authors on reasonable request.

Code availability

The code used in this study is available from the corresponding author upon reasonable request.