Abstract
Temporal enhanced ultrasound (TeUS), comprising the analysis of variations in backscattered signals from a tissue over a sequence of ultrasound frames, has been previously proposed as a new paradigm for tissue characterization. In this paper, we propose to use deep recurrent neural networks (RNN) to explicitly model the temporal information in TeUS. By investigating several RNN models, we demonstrate that long short-term memory (LSTM) networks achieve the highest accuracy in separating cancer from benign tissue in the prostate. We also present algorithms for in-depth analysis of LSTM networks. Our in vivo study includes data from 255 prostate biopsy cores of 157 patients. We achieve area under the curve, sensitivity, specificity, and accuracy of 0.96, 0.76, 0.98, and 0.93, respectively. Our result suggests that temporal modeling of TeUS using RNN can significantly improve cancer detection accuracy over previously presented works.
Keywords: Temporal enhanced ultrasound, deep learning, recurrent neural network, long short-term memory, prostate cancer, cancer detection
I. Introduction
Prostate cancer (PCa) is amongst the most commonly diagnosed forms of cancer in men. The American Cancer Society estimates 161,360 new cases to be diagnosed in 2017 in the United States. Early stage PCa detection followed by treatment results in a five-year survival rate of above 95% [1]. Core needle biopsy, the current gold standard for PCa detection, is performed under transrectal ultrasound (TRUS) guidance where ultrasound is used for anatomical navigation rather than for targeting PCa.
In the past four decades, ultrasound (US) imaging has been increasingly used for tissue characterization and non-invasive detection of disease. Ultrasound-based tissue typing has been investigated extensively to enable targeted biopsy [2]. Most of the research in this field has focused on the analysis of texture and spectral features [3] of a single ultrasound image. Additionally, elastography [4] and Doppler imaging [5] have been explored to determine changes in tissue stiffness and blood flow associated with PCa, respectively. Fusion of TRUS with multi-parametric MRI (mp-MRI) has also been used for PCa detection [6]–[8], where lesions identified on mp-MRI are registered to TRUS images and used for targeted biopsy.
Temporal Enhanced Ultrasound (TeUS), comprising a time series of ultrasound images, has been reported as an alternative tissue characterization technique (Fig. 1) [2], [9], [10]. TeUS utilizes an underlying machine learning framework to extract information from the backscattered ultrasound data obtained in a time span of few seconds without any imposed mechanical excitation. We demonstrated that ultrasound-induced thermal effects [11] and tissue micro-vibrations [12] influence the backscattered ultrasound data. Furthermore, we independently analyzed the effects of tissue elasticity and micro-vibration [12], [13], and presented an analytical model linking elasticity to TeUS measurements, which showed that TeUS signature is both dependent on the scattering function of the medium and the inverse of tissue elasticity. Since 2007, TeUS has been successfully used for characterization of prostate cancer in ex vivo [2], [14] and in vivo [15]–[19] studies. Comparison of the TeUS framework with the analysis of a single Radio Frequency (RF) ultrasound frame indicates that the two approaches are complementary [2], [16], with TeUS showing higher overall area under the curve (AUC).
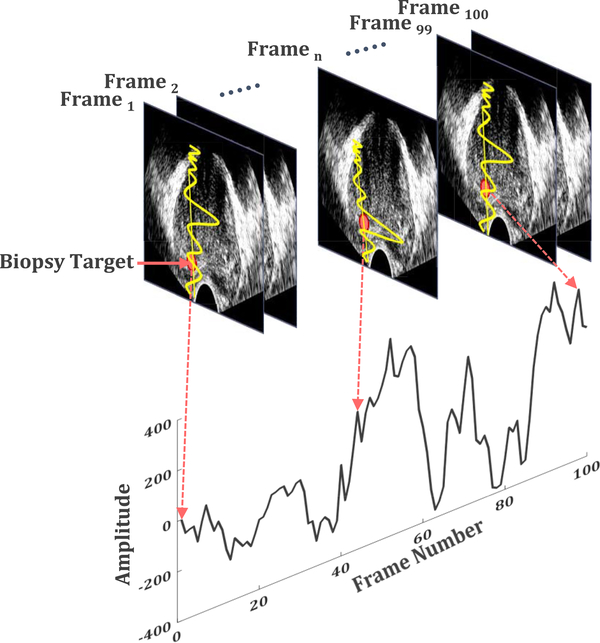
Fig. 1.
A schematic diagram of Temporal Enhanced Ultrasound (TeUS) data generation. A time series of a fixed point in an image frame, shown as a red dot, is analyzed over a sequence of ultrasound frames to determine tissue characteristics [38].
Previously, manually engineered feature representations extracted from RF TeUS data [16], [20], [21] have been used with shallow discriminant models such as Support Vector Machines (SVMs) [2], Random Forest [22], [23], Bayesian classifiers [24] and multi-layer feed-forward perceptron networks [14], to differentiate tissue types [25]. Moradi et al. [14], [24] used fractal dimension with Bayesian classifiers and feed-forward neural networks for ex vivo characterization of prostate tissue. More recently, Imani et al. [15], [16] combined extracted features from Discrete Fourier and Wavelet transforms of TeUS data and fractal dimension to characterize in vivo prostate tissue using SVMs. Ghavidel et al. [23] used spectral features of TeUS data and performed feature selection using Random Forests to classify lower grade prostate cancer from higher cancer grades.
Deep neural networks [26], [27] have been recently established as a powerful machine learning paradigm. Our group has applied deep networks for automatic feature selection from TeUS spectrum [17], [18] to address the so-called “cherry picking” of the features [21]. This framework exploited Deep Belief Networks (DBN) [28] to automatically learn a high-level latent feature representation from TeUS data. We subsequently extended our work from detecting PCa to its grading [29]. We also examined Convolutional Neural Networks (CNNs) to combine temporal and spatial information from TeUS data to detect high-risk prostate cancer. Additionally, we utilized deep-learning-based features to examine the physical phenomenon governing TeUS [12], [17], [30]. These features pointed to the presence of a strong backscattered ultrasound signal in frequency range of 0 − 2 Hz. This observation led to a hypothesis that tissue micro-vibration, possibly due to pulsation in major blood vessels surrounding the prostate, at the heartbeat frequency (∼ 1.2 Hz) is a key contributor to TeUS. To-date, our efforts have mainly focused on spectral analysis as the key pre-processing step for feature extraction from TeUS data [17]. Most recently, analysis of TeUS in the temporal domain using probabilistic methods, such as Hidden Markov Models (HMMs), have shown significant promise [31], [32].
In this paper, we propose to use Recurrent Neural Networks (RNNs) [33]–[35] to explicitly analyze TeUS data in temporal domain. Specifically, we use Long Short-Term Memory (LSTM) networks [33] and Gated Recurrent Units (GRUs) [36], [37], the classes of RNNs, to effectively learn long-term dependencies in the data. In an in vivo study with 157 patients, we analyze data from 255 suspicious cancer foci obtained during MRI-TRUS fusion biopsy. We achieve AUC, sensitivity, specificity and accuracy of 0.96, 0.76, 0.98, and 0.93, respectively. Our results indicate that RNN can identify temporal patterns in the data that may not be readily observable in spectral analysis of TeUS [17], leading to significant improvements in detection of PCa.
II. Background: Recurrent Neural Networks
RNNs are a category of neural networks that are “deep” in temporal dimension and have been used extensively in time-sequence modeling [39]. Unlike a conventional neural network, RNNs are able to process sequential data points through a recurrent hidden state whose activation at each step depends on that of a previous step. Generally, given sequence data x = (x1,, …, xT), an RNN updates its recurrent hidden state ht by:
| (1) |
where xt and ht are data values and the recurrent hidden state at time step t, respectively, and φ(.) represents the nonlinear activation function of a hidden layer, such as a sigmoid or hyperbolic tangent. Optionally, the RNN may have an output y = (y1,, …, yT). In the traditional RNN model aka vanilla, the update rule of the recurrent hidden state in (1) is implemented as:
| (2) |
where W and U are the coefficient matrices of the input at the present step and the recurrent hidden units activation at the previous step, respectively. We can further expand Equation (2) to calculate the hidden vector sequence h = (h1,, …, hT):
| (3) |
where t = 1 to T, Wih denotes the input-hidden weight vector, Whh represents the weight matrix of the hidden layer, and bh is the hidden layer bias vector.
It has been observed that using the traditional RNN implementation, gradients decrease significantly for deeper temporal models. This is referred to as the vanishing gradient, and makes learning of long-term sequence data a challenging task for RNNs. To address it, other types of recurrent hidden units such as LSTM and GRU have been proposed. As shown in Equations (2) and (3), traditional RNN simply applies a transformation to a weighted linear sum of inputs. In contrast, an LSTM-based recurrent layer creates a memory cell c at each time step whose activation is computed as:
| (4) |
where ot is the output gate that determines the portion of the memory cell content in time step t (ct) to be exposed at the next time step [33]. The recursive equation for updating ot is:
| (5) |
where σ(.) is the logistic sigmoid function, Woi is the input-output weight matrix, Woh is the hidden layer-output weight matrix, and Woc is the memory-output weight matrix. The memory cell, ct, is updated by adding new content, , and discarding part of the present memory:
| (6) |
where ⨀ is an element-wise multiplication and is calculated as:
| (7) |
In this equation, the W term represents weight matrices; e.g., Wci is the input-memory weight matrix. Input gate i, and forget gate f determine the degree that new information is to be added and current information is to be removed, respectively, as follows:
| (8) |
| (9) |
All weight matrices, W, and biases, b, are free parameters that are shared between cells across time. Figure 2 shows a graphical model of an LSTM cell. A slightly different version of LSTMs are GRUs [36] which have fewer number of parameters to avoid over-fitting in the lack of sufficient training samples. GRUs combine the forget and input gates into a single update gate, u, and merge the cell memory and hidden state to a reset gate, r. The activation of ht of the GRU at time t is a linear interpolation between the previous activation, ht−1, and the updated activation, :
| (10) |
where ut, the update gate at time step t, determines how much the unit updates its activation or content. The update gate can be calculated as follows:
| (11) |
where Wui is the input-update weight matrix and Wuh denotes the update-hidden weight matrix. The updated activation, , is computed similarly to the traditional RNN in Equation (2) as follows:
| (12) |
Finally, the reset gate, rt, is computed as:
| (13) |
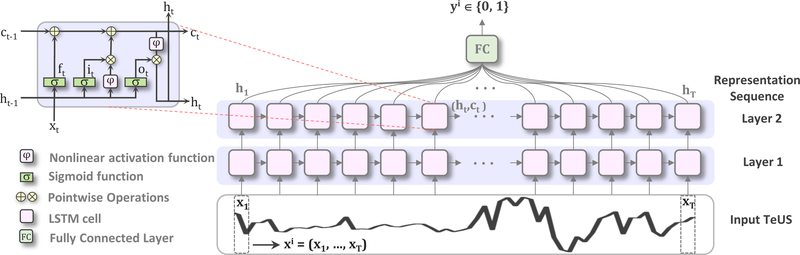
Fig. 2.
Overview of the proposed method. We use two layers of RNNs with LSTM cells to model the temporal information in a sequence of TeUS data. x(i) = (x1,, …,xT), T = 100 indicates the ith sequence data, while xt refers to the tth time step.
III. Materials
A. TeUS Data Acquisition and Histopathology Labeling
TeUS data was acquired from 157 subjects during fusion prostate biopsy. All subjects provided informed consent to participate, and the study was approved by the institutional research ethics board. Data from 255 biopsy targets of the subjects, that were identified as suspicious for cancer in preoperative mp-MRI examination, were used. Through a consensus, two radiologists assigned an overall MR suspicious level score of “low”, “moderate” and “high” to each target [6]. These scores are based on findings on each mp-MRI sequence using previously described criteria [6], which indicate both the presence of prostate cancer and tumor grade. The standardized PI-RADS criteria were not used for this study. Subsequently, subjects underwent MRI-guided ultrasound biopsies using UroNav (Invivo Corp., FL) MR-US fusion system [40]. Prior to biopsy sampling from each target, the ultrasound transducer was held steady freehand for 5 seconds to obtain T = 100 frames of beam-formed RF data (i.e., prior to envelope detection and compression). For this purpose, an endocavity curvilinear probe (Philips C9–5ec) with frequency of 6.6 MHz was used. This procedure was followed by firing the biopsy gun to acquire a tissue sample. Histopathology information of each biopsy core is used as the gold-standard for generating a label for that core. Histopathology reports include the length of cancer in the biopsy core and a Gleason Score (GS) [41]. The GS is reported as a summation of the Gleason grades of the two most common cancer patterns in the tissue specimen. Gleason grades range from 1 (resembling normal tissue) to 5 (aggressive cancerous tissue).
In our dataset, 83 biopsy cores are cancerous with GS 3+3 or higher, where 31 of those are labeled as clinically significant cancer with GS ≥ 4+3. The remaining 172 cores are non-cancerous and include benign or fibromuscular tissue, chronic inflammation, atrophy and Prostatic Intraepithelial Neoplasia (PIN) [29].
B. Preprocessing and Data Augmentation
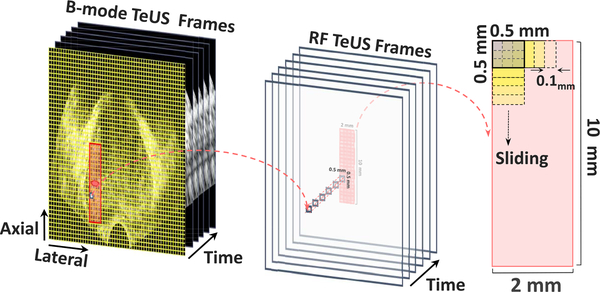
The biopsy needle path is mechanically constrained by the biopsy guide attached to the ultrasound transducer. For each biopsy target, we analyze an area of 2 mm × 10 mm around the target location, along the projected needle path (Fig. 3). We divide this region to 80 equally-sized Regions of Interest (ROIs) of 0.5 mm ×0.5 mm. For each ROI, we generate a sequence of TeUS data, , T = 100 by averaging over all time series values within a given ROI of an ultrasound frame. We augment the training data by creating ROIs using a sliding window of size 0.5 mm × 0.5 mm over the target region, which results in 1,536 ROIs per target (see Fig. 3). The number of averaged time series within an ROI depends on the axial and lateral resolution of the system at the ROI location.
Fig. 3.
Preprocessing and ROI selection: the target region is divided to 80 ROIs of size 0.5 mm × 0.5 mm and then a sliding window is used for the data augmentation.
IV. Method
A. Proposed Discriminative Method
Our overarching objective is to develop a deep learning model to discriminate cancer and benign prostate regions in TeUS data. Let represent a collection of all labeled ROIs, where x(i) is the ith TeUS sequence and y(i) indicates the corresponding label. An individual TeUS sequence of length T, , is composed of signal-amplitude values for each time step, t, and is labeled as yi ∈ {0, 1}, where zero and one indicate benign and cancer outcome, respectively in histopathology (see Fig. 1). We aim to learn a mapping from x(i) to y(i) in a supervised framework by using RNNs to explicitly model the temporal information in TeUS. Our sequence classification approach is built with connected RNN layers followed by a softmax layer to map the sequence to a posterior over classes. Each RNN layer includes T = 100 homogeneous hidden units (i.e., traditional/vanilla RNN, LSTM or GRU cells) to capture temporal changes in TeUS data. The model learns a distribution over classes P(y|x1,, …, xT) given a time-series sequence x1,, …, xT rather than a single, time independent input. Figure 2 shows an overview of the proposed architecture with LSTM cells.
Given the input sequence x = (x1,, …, xT), RNN computes the hidden vector sequence h = (h1,, …, hT) in the sequence learning step. As discussed in Section II, h is a function of the input sequence x, model parameters, Θ, and time, t: φ(x; Θ, t). denotes the sequence learning model parameters, where is the set of weights and is the set of biases in Eq. (3) for vanilla RNN cells, in Eq. (4) for LSTM cells, and in Eq. (10) for GRU cells through time steps, t = 0 to t = T. All weight matrices, , and biases, , are free parameters that are shared across time. The final node generates the posterior probability for the given sequence:
| (14) |
| (15) |
where is the softmax function, which in our binary classification case is equivalent to the logistic function, and indicates the predicted label. The optimization criterion for the network is to maximize the probability of the training labels or equivalently, to minimize the negative log-likelihood defined as a the loss function. This function is the binary cross-entropy between y(i) and over all training samples, :
| (16) |
where . During training, the loss function is minimized through a proper gradient optimization algorithm like stochastic gradient descent (SGD), root mean square propagation (RMSprop) or adaptive moment estimation (Adam) [42].
B. Cancer Classification
The RNN models learn a probability distribution over classes, P(y|x1,, …, xT), given a time-series sequence, x1,, …, xT. Let represent the collection of all labeled ROIs surrounding a target core, where , , x(i) represents the ith TeUS sequence of the core, and y(i) indicates the corresponding label. Using the probability output of the classifier for each ROI, we assign a binary label to each target core. The label is calculated using a majority vote based on the predicted labels of all ROIs surrounding the target. For this purpose, we define the predicted label for each ROI, , as 1, when P(y(i)|x(i)) ≥ 0.5, and as 0 otherwise. The probability of a given core being cancerous based on the cancerous ROIs within that core is:
| (17) |
A binary label of 1 is assigned to a core, when .
C. Network Analysis
To better understand the temporal information in TeUS, we examine the LSTM gates. For this purpose, following training, we use the learned weights and biases to regenerate the network behavior for any given sequence of length T. First, the state of each cell is set to zero. Then, the full learning formula (Eqs. (4)–(9)) along with the model parameters are recursively applied for T = 100 time steps. A summary of the steps is presented in Algorithms 1 and 2. Finally, the on-and-off behavior of the hidden activation in the last layer of the network is used to analyze the high level learned features.
Algorithm 1.
Examination of the LSTM Gates
| Input: Trained model parameters “”, input data “X ”, number of time-steps “T”, number of input sequence “N”. |
| Output: States activation “”, gates activation “” |
| Initialization: Set the state of each cell “inStates” to zero. |
| 1: for i = 0 to N do |
| 2: for t = 0 to T do |
| 3: x ←X(i, :) |
| 4: |
| 5: |
| 6: end for |
| 7: end for |
| 8: return , |
Algorithm 2.
Recurrent Step Function of the LSTM
| Input: Trained model parameters “”, input sequence “x”, input states of time step (t − 1) “”. |
| Output: States activation of the current time step (t) “”, gates activation of the current time step (t) “” |
| 1: procedure |
| 2: Woi, Woh, Woc, Wci, Wch, Wix, Wih, Wf x, Wf h, |
| 3: bo, bc, bi, |
| 4: ht−1, |
| 5: it ← σ(Wix x + Wihht−1 + Wicct−1 + bi) |
| 6: ft ← σ(Wf x x + Wf hht−1 + Wf cct−1 + b f) |
| 7: ot ← σ(Woi x + Wohht−1 + Wocct−1 + bo) |
| 8: |
| 9: |
| 10: ht ← otφ(ct) |
| 11: |
| 12: |
| 13: return , |
V. Experiments
A. Data Division
Data is divided into mutually exclusive training, , and test sets, . Training data is made up of 84 cores with the following histopathology label distribution: benign: 42 cores; GS 3+3: 2; GS 3+4: 14; GS 4+3: 3; GS 4+4: 18; and, GS 4+5: 5 cores. Training cores were selected from those with homogeneous tissue regions (See [38] for more details). Therefore, the training data are selected from biopsy cores with at least 4.0 mm of cancer in a typical core length of 18.0 mm, 26 of which are labeled as clinically significant cancer with GS ≥ 4+3. Benign cores are randomly selected from all available non-cancerous cores.
The test data consists of 171 cores, where 130 cores are labeled as benign, 29 cores with GS ≤ 3+4, and 12 cores with GS ≥ 4+3. Given the data augmentation strategy in Section III-B (Fig. 3), we obtain a total number of 84 × 1,536 = 129, 024 training samples .
B. Hyper-Parameter Selection and Network Structure
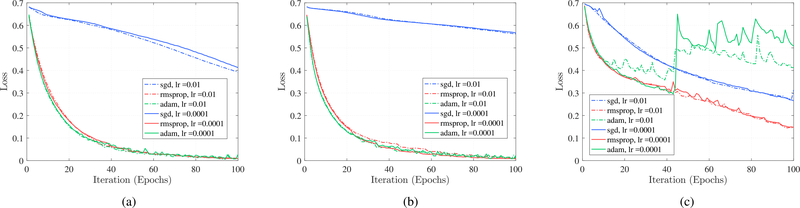
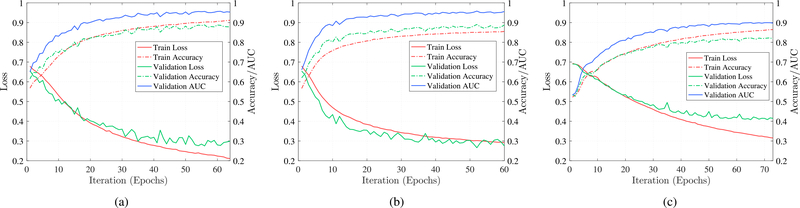
The performance of deep RNNs, similar to other deep learning approaches, are affected by their hyper-parameters. In practice, hyper-parameter selection can be constrained as a generalization-error minimization problem. Solutions are often based on running trials with different hyper-parameter settings, and choosing the setting that results in the best performing model (Fig. 4). We optimize the hyper-parameters through a grid search, which is an exhaustive search through a prespecified subset of the hyper-parameter space of the learning algorithm.
Fig. 4.
Comparison between optimizer performance for different RNN cells: Each curve corresponds to an RNN network structure with two hidden layers, batch size of 128 with dropout rate of 0.2 and regularization term of 0.0001. (a) LSTM. (b) GRU. (c) Vanilla RNN.
The grid search starts with randomly partitioning the selected training dataset, , into training (80%) denoted by and held-out validation sets (20%) denoted by . This partitioning results in training samples and held-out validation samples. To guide the grid search algorithm, we track the loss, accuracy and AUC on both and . Loss is defined using Eq. (16) as the binary cross-entropy between the predicted label and the true label, while accuracy is the percentage of the correctly predicted labels. To stabilize learning and prevent the model from over-fitting on the training data, we use regularization and dropout, two of the most effective proposed strategies [43]. Regularization adds a penalty term to the loss function (Equation (16)) to prevent the coefficients from getting too large. Here, we use L2 regularization in the form of , where we search for λ as the hyper-parameter. Dropout prevents co-adaptations on training data. In each step of training, a dropout layer removes some units of its previous layer from the network, which means the network architecture changes in every training step. These units are chosen randomly based on the probability parameter of the dropout layer as another hyper-parameter. We perform a grid search over the number of RNN hidden layers, nh ∈ {1, 2}, batch size, bs ∈ {64, 128}, and initial learning rate, lr ∈ {0.01 − 0.0001} with three different optimization algorithms, SGD, RMSprop and Adam [42]. We also experiment with various levels of dropout rate, dr ∈ {0.2, 0.4} and L2-regularization term (λ), lreg ∈ {0.0001, 0.0002}. These result in 96 different hyper-parameter settings for the proposed approach. All models are trained with the same number of iterations and training is stopped after 100 epochs. Models benefit from reducing the learning rate by a factor once learning stagnates [43]. For this purpose, we monitor the validation loss and if no improvement is observed over 10 epochs, the learning rate is reduced by lrnew = lr × factor, where factor = 0.9.
C. Model Training and Evaluation
Once the optimum hyper-parameters are identified, the entire training set, , is used to learn the final model. Loss is used as the performance measure for early stopping to avoid over fitting. Training is stopped if the loss as we defined in Eq. (16) increases or if it does not decrease after 10 epochs. An absolute change of less than δ = 0.0004 is considered as no improvement in loss. We also record the model performance for to track its behavior in a random subset of training data.
To assess the performance of our method, we report its sensitivity, specificity, and accuracy in detecting cancerous tissue samples in the test data, . All cancerous target cores are considered as the positive class (labeled as 1), and non-cancerous cores as the negative class (labeled as 0). Sensitivity or recall is defined as the percentage of cancerous cores that are correctly identified, while specificity is the proportion of non-cancerous cores that are correctly classified. Accuracy is the ratio of the true results (both true positives and true negatives) over the total number of cores. The overall performance of the models are reported using AUC. The curve depicts a relative trade-off between sensitivity and specificity. The maximum value for AUC is 1, where higher values indicate better classification performance.
D. Implementation
We implement the RNNs in Keras [44] using the Tensorflow [45] back-end. Training is performed on a GeForce GTX 980 Ti GPU with 6 GB of memory, hosted by a machine running Ubuntu 16.04 operating system on a 3.4 GHz Intel Core™ i7 CPU with 16 GB of memory. Training of vanilla RNN, LSTM and GRU network structures with 100 epochs takes 1.1, 8.1 and 3.3 hours, respectively. Early stopping and calculation of additional performance metrics are implemented using Keras callbacks and the Tensorflow back-end to evaluate internal states and statistics of the model during training. The proposed network analysis method in Algorithms 1 and 2, is implemented independently of Keras or Tensorflow in Python 2.7, executed on CPU.
VI. Results and Discussion
A. Model Selection
Results from hyper-parameter search demonstrate that network structures with two RNN hidden layers outperform other architectures. Furthermore, for the vanilla RNN, bs = 128, lr = 0.0001; for LSTM, bs = 64, lr = 0.0001; and for GRU, bs = 128, lr = 0.01 generate the optimum models. For all models, dr = 0.2 and lr eg = 0.0001 generate the lowest loss and the highest accuracy for both and . The learning curves for different optimization algorithms and initial learning rates on are shown in Fig. 4. Each curve corresponds to an RNN network structure with two hidden layers, the batch size of 128 with the dropout rate of 0.4 and regularization term of λ = 0.0001, where the vertical axis is the loss and the horizontal axis is the number of iterations. It is clear that RMSprop substantially outperforms SGD optimization for all of the RNN cell types while RMSprop and Adam have similar performance for GRU and LSTM cells. RMSprop leads to a better performance on our data.
Learning curves of the different RNN cells using the optimum hyper-parameters are shown in Fig. 5. The right-vertical axis represents the loss value while the left-vertical axis shows the accuracy and AUC, and the horizontal axis is the number of iterations. We observe that all models converge after 65±7 epochs, and GRU and LSTM cells outperform vanilla RNN cells in terms of accuracy. Comparing Fig. 5(a) and (b) demonstrates that the network with GRU cells has a steeper learning curve and converges faster than the network with LSTM cells. One possible reason could be fewer number of parameters to be learned in GRU cells compared to LSTM cells. Fig. 5 shows that the network with LSTM cells leads to a lower loss value and a higher accuracy.
Fig. 5.
Learning curves of different RNN cells using the optimum hyper-parameters in our search space. All of the models use the RMSprop optimizer and converge after 65 ± 7 epochs. (a) LSTM. (b) GRU. (c) Vanilla RNN.
B. Model Performance
Table I shows the classification results in the test dataset, , including 171 target cores. Models with LSTM and GRU cells consistently achieve higher performance compared to vanilla RNN and the spectral method proposed in [17]. A paired t-test shows statistically significant improvement in AUC (p < 0.05) with LSTM and GRU cells. Moreover, the LSTM configuration has the highest performance for detection of cancer. Using the LSTM model as the best configuration, we achieve specificity and sensitivity of 0.98 and 0.76, respectively, where we classify 31 out of 41 cancerous cores correctly. Table II shows performance of models for classification of cores in for different MR suspicious levels as explained in Section III. For samples with moderate MR suspicious level (70% of all cores), we achieve AUC of 0.97 using the LSTM-RNN structure. In this group, our sensitivity, specificity, and accuracy are 0.78, 0.98, and 0.95, respectively. For samples with high MR suspicious level, we consistently achieve higher sensitivity result compared to those with moderate MR suspicious level.
TABLE I.
Model Performance for Classification of Cores in the Test Data (N = 171)
| Method | Specificity | Sensitivity | Accuracy | AUC |
|---|---|---|---|---|
| LSTM | 0.98 | 0.76 | 0.93 | 0.96 |
| GRU | 0.95 | 0.70 | 0.86 | 0.92 |
| Vanilla RNN | 0.72 | 0.69 | 0.75 | 0.76 |
| Spectral [17] | 0.73 | 0.63 | 0.78 | 0.76 |
TABLE II.
Model Performance for Classification of Cores in the Test Data for Different MR Suspicious Levels. N Indicates Number of Cores in Each Group
| MR suspicious levels | Moderate MR suspicious level (N = 115) |
High MR suspicious level (N = 20) |
||||||
|---|---|---|---|---|---|---|---|---|
| Specificity | Sensitivity | Accuracy | AUC | Specificity | Sensitivity | Accuracy | AUC | |
| LSTM | 0.98 | 0.78 | 0.95 | 0.97 | 0.86 | 0.92 | 0.90 | 0.97 |
| GRU | 0.95 | 0.70 | 0.89 | 0.91 | 0.80 | 1.00 | 0.90 | 0.92 |
| Vanilla RNN | 0.82 | 0.70 | 0.82 | 0.73 | 0.85 | 0.67 | 0.70 | 0.68 |
| Spectral [17] | 0.70 | 0.78 | 0.80 | 0.80 | 0.83 | 0.90 | 0.85 | 0.95 |
C. Comparison with Other Methods
The best results to-date involving TeUS are based on spectral analysis as proposed in [17]. We compare our RNN-based approach with this method as the most related work. As reported in Table I and Table II, the LSTM-RNN models consistently outperform spectral analysis of TeUS with a paired t-test showing statistically significant improvement in sensitivity, specificity, accuracy, and AUC (p < 0.05) for LSTM-RNN. Datasets used in a few other studies are different from the current work so a detailed comparison is not feasible. However, the proposed network architectures outperform Imani et al. [46], who used cascade CNNs, and Uniyal et al. [22], who applied random forests for TeUS based PCa detection, both on data from 14 patients. While analysis of a single RF ultrasound frame is not possible in the context of our current clinical study, previously, we have shown that TeUS is complementary to this information and generally outperforms analysis of single RF frames [2], [11]. The best results reported using a single RF frame analysis [47] involve 64 subjects with an AUC of 0.84, where they used PSA as an additional surrogate. In a recent study, Nahlawi et al. [31], [48] used Hidden Markov Models (HMMs) to model the temporal information of TeUS data for prostate cancer detection. In a limited clinical study including 14 subjects, they identified cancerous regions with an accuracy of 0.85.
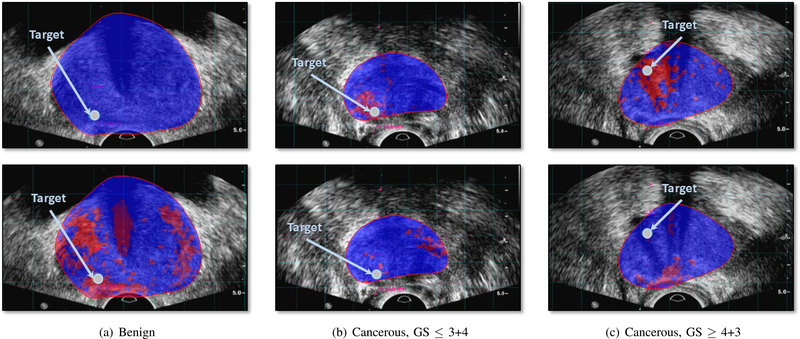
Furthermore, we qualitatively compare the cancer likelihood colormap resulting from LSTM-RNN with the spectral analysis of TeUS [17]. Figure 6 shows two examples of the cancer likelihood maps from the test dataset. There is an observable improvement in identifying cancerous regions around the biopsy target that match the gold-standard label.
Fig. 6.
Cancer likelihood maps overlaid on B-mode ultrasound images, along the projected needle path in the TeUS data, and centered on the target. Red indicates predicted labels as cancer, and blue indicates predicted benign regions. The boundary of the segmented prostate in MRI is overlaid on TRUS data. The arrow points to the target location. The top row shows the result of LSTM and the bottom row shows the result of spectral analysis [17] for benign targets (a), and cancer targets (b) and (c).
D. Network Analysis
To analyze the network behavior and identify LSTM cells that contribute most to differentiating between benign and cancerous tissue, we examine the final high-level feature representation for cancerous and benign samples. By generating the difference map between the final activation of the network (ht at t = 100) for TeUS data from benign and cancerous samples, we identify 20 cells with the highest activation difference. This refers to cells whose activation level change the most between benign and cancer samples.
In these cells, we observe the evolution of high-level feature representations. Specifically, as per Algorithm 1, input TeUS data from benign and cancerous ROIs in are forward propagated in the models. Activation of the input gate (i(t)), the output gate (o(t)) and the cell state (c(t)) for the top 20 active cells are studied.
We observe cell states c(t) evolve over time and gradually learn discriminative information. Moreover, the input gate i(t) evolves so that it attenuates parts of the input TeUS sequence and detects the important information from the sequence. Interestingly, the input gate reduces the contribution of TeUS data to model learning around time step 50, for both cancerous and benign samples. The evolution and attenuation patterns of c(t) and i(t) suggest that the most discriminative features for distinguishing cancerous and benign tissue samples are captured within the first half of TeUS sequence. These finding match those reported by Nahlawi et al. [31], [48].
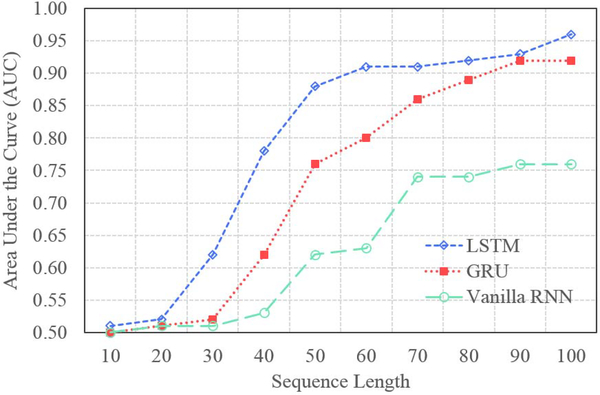
To further examine this, we evaluate the evolving behavior of LSTM-RNN by training and testing the RNN models with different TeUS sequence lengths. Figure 7 shows the performance of the models evaluated by AUC for different TeUS sequence lengths. For each case, using the training procedure explained in Section V-C, we trained an RNN-based deep network with 10–100 RNN cells corresponding to TeUS length. Similar to previous observations, the vanilla RNN-based model has the lowest performance compared to GRU and LSTM based models. By increasing the length of input TeUS sequence, the performance of the models improve. However, for TeUS sequence length more than 50, the improvement saturates. Using a paired t-test, the DeLong test, and bootstrapping, we demonstrate that for sequence length of over 50, there is no statistically significant improvement in performance using the LSTM-RNN model (p > 0.05).
Fig. 7.
Sequence length effect.
VII. Conclusion
In this paper, we present an accurate approach for detecting PCa from TeUS data collected during MRI-TRUS guided biopsy. We utilize deep RNNs to explicitly model the temporal information of TeUS. Our investigation of several RNN structures shows that LSTM-based RNN can efficiently capture temporal patterns in TeUS data with statistically significant improvement in accuracy over our previously proposed spectral analysis approach [17]. In a large clinical study including 255 suspicious cancer foci obtained from 157 patients, we achieve AUC, sensitivity, specificity and accuracy of 0.96, 0.76, 0.98, and 0.93, respectively. We also presented algorithms for in-depth analysis of high-level latent features of LSTM-based RNN. A transformational finding, achieved through this analysis, is that the most discriminative features for detection of PCa can be learned from a fraction of the full TeUS time series. Specifically, in our data, less than 50 ultrasound frames were required to build models that accurately detect PCa. This information can be used to optimize TeUS data acquisition for clinical translation [38], [49]. Cancer likelihood maps can be used to guide systematic biopsies and potentially increase the yield of high grade cancer. For fusion biopsies, the map can help compensate for small mis-registrations between MRI and ultrasound. Eventually, the approach can enable monitoring of active surveillance patients by detecting changes in prostate tissue over time.
Acknowledgments
This work was supported in part by the Natural Sciences and Engineering Research Council of Canada and in part by the Philips Research North America, Cambridge, MA, USA.
Contributor Information
Shekoofeh Azizi, Department of Electrical and Computer Engineering, The University of British Columbia, Vancouver, BC V6T 1Z4, Canada.
Sharareh Bayat, Department of Electrical and Computer Engineering, The University of British Columbia, Vancouver, BC V6T 1Z4, Canada.
Pingkun Yan, Rensselaer Polytechnic Institute, Troy, NY 12180 USA.
Amir Tahmasebi, Philips Research North America, Cambridge, MA 02141 USA.
Jin Tae Kwak, Department of Computer Engineering, Sejong University, Seoul 143-747, South Korea.
Sheng Xu, National Institutes of Health Research Center, Bethesda, MD 20892 USA.
Baris Turkbey, National Institutes of Health Research Center, Bethesda, MD 20892 USA.
Peter Choyke, National Institutes of Health Research Center, Bethesda, MD 20892 USA.
Peter Pinto, National Institutes of Health Research Center, Bethesda, MD 20892 USA.
Bradford Wood, National Institutes of Health Research Center, Bethesda, MD 20892 USA.
Parvin Mousavi, School of Computing, Queen’s University, Kingston, ON K7L 3N6, Canada.
Purang Abolmaesumi, Department of Electrical and Computer Engineering, The University of British Columbia, Vancouver, BC V6T 1Z4, Canada.
References
- [1].Barentsz JO et al. , “ESUR prostate MR guidelines 2012,” Eur. Radiol, vol. 22, no. 4, pp. 746–757, April. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Moradi M, Abolmaesumi P, Siemens DR, Sauerbrei EE, Boag AH, and Mousavi P, “Augmenting detection of prostate cancer in transrectal ultrasound images using SVM and RF time series,” IEEE Trans. Biomed. Eng, vol. 56, no. 9, pp. 2214–2224, September. 2009. [DOI] [PubMed] [Google Scholar]
- [3].Oelze ML and Mamou J, “Review of quantitative ultrasound: Envelope statistics and backscatter coefficient imaging and contributions to diagnostic ultrasound,” IEEE Trans. Ultrason., Ferroelect., Freq. Control, vol. 63, no. 2, pp. 336–351, February. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Salcudean SE et al. , “Viscoelasticity modeling of the prostate region using vibro-elastography,” in Proc. Int. Conf. Med. Image Comput. Comput.-Assist. Intervent Berlin, Germany: Springer-Verlag, 2006, pp. 389–396. [DOI] [PubMed] [Google Scholar]
- [5].Sauvain J-L et al. , “Value of transrectal power Doppler sonography in the detection of low-risk prostate cancers,” Diagnostic Interventional Imag, vol. 94, no. 1, pp. 60–67, 2013. [DOI] [PubMed] [Google Scholar]
- [6].Siddiqui MM et al. , “Comparison of MR/ultrasound fusion–guided biopsy with ultrasound-guided biopsy for the diagnosis of prostate cancer,” J. Amer. Med. Assoc, vol. 313, no. 4, pp. 390–397, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Kasivisvanathan V et al. , “Prostate evaluation for clinically important disease: Sampling using image-guidance or not?” Eur. Urology Supplements, vol. 17, no. 2, pp. e1716–e1717, 2018. [Google Scholar]
- [8].Ahmed HU et al. , “Diagnostic accuracy of multi-parametric MRI and TRUS biopsy in prostate cancer (PROMIS): A paired validating confirmatory study,” Lancet, vol. 389, no. 10071, pp. 815–822, 2017. [DOI] [PubMed] [Google Scholar]
- [9].Lin C-Y, Yi T, Gao Y-Z, Zhou J-H, and Huang Q-H, “Early detection and assessment of liver fibrosis by using ultrasound RF time series,” J. Med. Biol. Eng, vol. 37, no. 5, pp. 717–729, 2017. [Google Scholar]
- [10].Lin Q et al. , “Ultrasonic RF time series for early assessment of tumor response to chemotherapy: First in vivo studies on mice breast cancer model,” Ultrasound Med. Biol, vol. 43, p. S3, January. 2017. [Google Scholar]
- [11].Daoud MI, Mousavi P, Imani F, Rohling R, and Abolmaesumi P, “Tissue classification using ultrasound-induced variations in acoustic backscattering features,” IEEE Trans. Biomed. Eng, vol. 60, no. 2, pp. 310–320, February. 2013. [DOI] [PubMed] [Google Scholar]
- [12].Bayat S et al. , “Tissue mimicking simulations for temporal enhanced ultrasound-based tissue typing,” Proc. SPIE, vol. 10139, p. 101390D, March. 2017. [Google Scholar]
- [13].Bayat S et al. , “Investigation of physical phenomena underlying temporal-enhanced ultrasound as a new diagnostic imaging technique: Theory and simulations,” IEEE Trans. Ultrason., Ferroelectr., Freq. Control, vol. 65, no. 3, pp. 400–410, March. 2018. [DOI] [PubMed] [Google Scholar]
- [14].Moradi M, Abolmaesumi P, and Mousavi P, “Tissue typing using ultrasound RF time series: Experiments with animal tissue samples,” Med. Phys, vol. 37, no. 8, pp. 4401–4413, 2010. [DOI] [PubMed] [Google Scholar]
- [15].Imani F et al. , “Ultrasound-based characterization of prostate cancer using joint independent component analysis,” IEEE Trans. Biomed. Eng, vol. 62, no. 7, pp. 1796–1804, July. 2015. [DOI] [PubMed] [Google Scholar]
- [16].Imani F et al. , “Computer-aided prostate cancer detection using ultrasound RF time series: In vivo feasibility study,” IEEE Trans. Med. Imag, vol. 34, no. 11, pp. 2248–2257, November. 2015. [DOI] [PubMed] [Google Scholar]
- [17].Azizi S, Imani F, Tahmasebi A, Wood B, Mousavi P, and Abolmaesumi P, “Detection of prostate cancer using temporal sequences of ultrasound data: A large clinical feasibility study,” Int. J. Comput. Assist. Radiol. Surg, vol. 11, no. 6, pp. 947–956, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Azizi S et al. , “Ultrasound-based detection of prostate cancer using automatic feature selection with deep belief networks,” in Proc. Int. Conf. Med. Image Comput. Comput.-Assist. Intervent Cham, Switzerland: Springer, 2015, pp. 70–77. [Google Scholar]
- [19].Moradi M, Mahdavi SS, Nir G, Jones EC, Goldenberg SL, and Salcudean SE, “Ultrasound RF time series for tissue typing: First in vivo clinical results,” Proc. SPIE, vol. 8670, p. 86701I, March. 2013. [Google Scholar]
- [20].Imani F et al. , “Ultrasound-based characterization of prostate cancer: An in vivo clinical feasibility study,” in Proc. Int. Conf. Med. Image Comput. Comput.-Assist. Intervent Berlin, Germany: Springer-Verlag, 2006, pp. 279–286. [DOI] [PubMed] [Google Scholar]
- [21].Imani F et al. , “Augmenting MRI-transrectal ultrasound-guided prostate biopsy with temporal ultrasound data: A clinical feasibility study,” Int. J. Comput. Assist. Radiol. Surg, vol. 10, no. 6, pp. 727–735, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Uniyal N et al. , “Ultrasound-based predication of prostate cancer in MRI-guided biopsy,” in Proc. Int. Conf. Med. Image Comput. Comput.-Assist. Intervent.-Workshop Clin. Image-Based Procedures Cham, Switzerland: Springer, 2014, pp. 142–150. [Google Scholar]
- [23].Ghavidel S et al. , “Classification of prostate cancer grade using temporal ultrasound: In vivo feasibility study,” Proc. SPIE, vol. 9786, p. 97860K, March. 2016. [Google Scholar]
- [24].Moradi M, Mousavi P, Isotalo PA, Siemens DR, Sauerbrei EE, and Abolmaesumi P, “A new approach to analysis of RF ultrasound echo signals for tissue characterization: Animal studies,” Proc. SPIE, vol. 6513, p. 65130P, March. 2007. [Google Scholar]
- [25].Moradi M, Mousavi P, and Abolmaesumi P, “Computer-aided diagnosis of prostate cancer with emphasis on ultrasound-based approaches: A review,” Ultrasound Med. Biol, vol. 33, no. 7, pp. 1010–1028, 2007. [DOI] [PubMed] [Google Scholar]
- [26].Hinton GE and Salakhutdinov RR, “Reducing the dimensionality of data with neural networks,” Science, vol. 313, no. 5786, pp. 504–507, 2006. [DOI] [PubMed] [Google Scholar]
- [27].Litjens G et al. (2017). “A survey on deep learning in medical image analysis.” [Online]. Available: https://arxiv.org/abs/1702.05747 [DOI] [PubMed]
- [28].Bengio Y, Lamblin P, Popovici D, and Larochelle H, “Greedy layer-wise training of deep networks,” in Advances in Neural Information Processing Systems, vol. 19. Cambridge, MA, USA: MIT Press, 2007, p. 153. [Google Scholar]
- [29].Azizi S et al. , “Classifying cancer grades using temporal ultrasound for transrectal prostate biopsy,” in Proc. Int. Conf. Med. Image Comput. Comput.-Assist. Intervent Springer, 2016, pp. 653–661. [Google Scholar]
- [30].Azizi S et al. , “Detection and grading of prostate cancer using temporal enhanced ultrasound: combining deep neural networks and tissue mimicking simulations,” Int. J. Comput. Assist. Radiol. Surg, vol. 12, no. 8, pp. 1293–1305, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Nahlawi L et al. , “Prostate cancer: Improved tissue characterization by temporal modeling of radio-frequency ultrasound echo data,” in Proc. Int. Conf. Med. Image Comput. Comput.-Assist. Intervent Springer, 2016, pp. 644–652. [Google Scholar]
- [32].Nahlawi L et al. , “Models of temporal enhanced ultrasound data for prostate cancer diagnosis: The impact of time-series order,” Proc. SPIE, vol. 10135, p. 101351D, March. 2017. [Google Scholar]
- [33].Gers FA, Schmidhuber J, and Cummins F, “Learning to forget: Continual prediction with LSTM,” Neural Comput, vol. 12, no. 10, pp. 2451–2471, 2000. [DOI] [PubMed] [Google Scholar]
- [34].Chen H et al. , “Automatic fetal ultrasound standard plane detection using knowledge transferred recurrent neural networks,” in Proc. Int. Conf. Med. Image Comput. Comput.-Assist. Intervent. Springer, 2015, pp. 507–514. [Google Scholar]
- [35].Kong B, Zhan Y, Shin M, Denny T, and Zhang S, “Recognizing end-diastole and end-systole frames via deep temporal regression network,” in Proc. Int. Conf. Med. image Comput. Comput.-Assist. Intervent Springer, 2016, pp. 264–272. [Google Scholar]
- [36].Chung J, Gulcehre C, Cho K, and Bengio Y. (2014). “Empirical evaluation of gated recurrent neural networks on sequence modeling.” [Online]. Available: https://arxiv.org/abs/1412.3555 [Google Scholar]
- [37].Cho K and Van Merrienboer B, Bahdanau D, and Bengio Y. (2014). “On the properties of neural machine translation: Encoder-decoder approaches.” [Online]. Available: https://arxiv.org/abs/1409.1259 [Google Scholar]
- [38].Azizi S et al. , “Transfer learning from RF to B-mode temporal enhanced ultrasound features for prostate cancer detection,” Int. J. Comput. Assist. Radiol. Surg, vol. 12, no. 7, pp. 1111–1121, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Graves A, Mohamed A-R, and Hinton G, “Speech recognition with deep recurrent neural networks,” in Proc. IEEE Int. Conf. Acoust., Speech and Signal Process, May 2013, pp. 6645–6649. [Google Scholar]
- [40].Marks L, Young S, and Natarajan S, “MRI-ultrasound fusion for guidance of targeted prostate biopsy,” Current Opinion Urol, vol. 23, no. 1, pp. 43–50, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Epstein JI, Feng Z, Trock BJ, and Pierorazio PM, “Upgrading and downgrading of prostate cancer from biopsy to radical prostatectomy: Incidence and predictive factors using the modified gleason grading system and factoring in tertiary grades,” Eur. Urol, vol. 61, no. 5, pp. 1019–1024, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Kingma D and Ba J. (2014). “Adam: A method for stochastic optimization.” [Online]. Available: https://arxiv.org/abs/1412.6980
- [43].Hinton G, “A practical guide to training restricted Boltzmann machines,” Momentum, vol. 9, no. 1, p. 926, 2012. [Google Scholar]
- [44].Chollet F. (2015). Keras. [Online]. Available: https://github.com/fchollet/keras
- [45].Abadi M et al. (2016). “Tensorflow: Large-scale machine learning on heterogeneous distributed systems.” [Online]. Available: https://arxiv.org/abs/1603.04467
- [46].Imani F et al. , “Fusion of multi-parametric MRI and temporal ultrasound for characterization of prostate cancer: In vivo feasibility study,” Proc. SPIE, vol. 9785, p. 97851K, March. 2016. [Google Scholar]
- [47].Feleppa E, Porter C, Ketterling J, Dasgupta S, Ramachandran S, and Sparks D, “Recent advances in ultrasonic tissue-type imaging of the prostate,” in Acoustical Imaging. Dordrecht, The Netherlands: Springer, 2007, pp. 331–339. [Google Scholar]
- [48].Nahlawi L et al. , “Stochastic modeling of temporal enhanced ultrasound: Impact of temporal properties on prostate cancer characterization,” IEEE Trans. Biomed. Eng, to be published. [Online]. Available: https://ieeexplore.ieee.org/document/8120142/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Azizi S et al. , “Toward a real-time system for temporal enhanced ultrasound-guided prostate biopsy,” Int. J. Comput. Assist. Radiol. Surg, pp. 1–9, March. 2018. [Online]. Available: https://link.springer.com/article/10.1007%2Fs11548-018-1749-z#citeas [DOI] [PMC free article] [PubMed] [Google Scholar]