Abstract
In Bayesian disease mapping, spatial random effects are used to account for confounding in the data so that reasonable estimates for the fixed effects can be obtained. Typically, the spatial random effects are mapped and qualitative comments are made related to an increase or decrease in risk for certain areas. The approach outlined here illustrates how a quantitative secondary assessment can be applied to make more useful and applicable inference related to these spatial random effects. We are able to recover important but unmeasured or unincluded risk factors via a secondary model fit. Results from the secondary model fit can determine association between spatial region-level risk factors and the estimated spatial random effects. We believe this work presents a useful, quantitative technique highlighting the importance and applicability of spatial random effects as well as illustrates how these methods lead to more interpretable conclusions.
Keywords: spatial epidemiology, disease mapping, random effects, INLA
1. Introduction
It has long been established that geographic location offers important information for the prediction and modeling of disease risk. Within spatial epidemiology, this spatial modeling of diseases, coined disease mapping (1), has gained in popularity following the technological improvements of geographic information system and statistical development of the conditional autoregressive (CAR)(2, 3) model. An extensive literature supports the relevance and importance of considering geographic location in applications from observational assessment of aggregated disease counts to individual-level survival following diagnosis (2, 4–8).
Despite the abundance of literature, there was no consistent, quantitative method of interpreting spatial heterogeneity estimates. In these studies, random effects typically represented latent combinations of unmeasured spatially-varying risk factors, and in general, studies simply estiamted the random effects, produced maps, and qualitatively commented on increased or decreased risk in certain areas of the map. In our proposed approach, a next step was performed wherein a true risk factor association within the random effects was quantitatively addressed and tested via a secondary model fit.
In this work, the purpose of the secondary model fit was to demonstrate a quantitative method that determined which risk factors the estimated random effects were representing. We accomplished this goal via a simulation study and real data case study. The simulation study involved aggregated count data and accomplished the goal of illustrating that random effects could represent risk factors that were not included in the primary model. Alternatively, the real data case study involved breast cancer (BrCa)-specific mortality in Louisiana SEER data (9); this was our motivating example as this registry failed to include individual level information on several known risk factors for BrCa. These methods could be applied to any scenario where a spatial random effect was estimated, regardless of the underlying primary statistical model.
2. Statistical Methods
2.1. Spatial Heterogeneity Assessment
We proposed a secondary assessment with the goal of quantitatively interpreting the spatial heterogeneity estimated as in typical spatial epidemiology studies via a primary model. The primary model used for estimating the random effects could range from fitting an aggregated count outcome (10) to an outcome on the individual-level (9). This secondary assessment compared distributions of potential risk factors across ranked categorizations of the spatial random effect. However, the regular methods for independent observations, such as two-sample t-test or Wilcoxon rank sum test, did not apply here due to the imposed correlation between nearby spatial areas as well as the inherent spatial correlation in risk factors of interest. To account for spatial correlation, we proposed to assess the difference through a secondary model fit in the Bayesian paradigm such that:
| (1) |
where xi was the risk factor of interest, Qi was the design matrix associated with the spatial random effect from the primary model which we will discuss in detail later, a was the intercept defined by a~Norm(0,1), b was a vector of parameter estimates (all b ∈ b, were independent and given a prior distribution such that b~N(0,1)) which represented the mean difference between categories, and zi was a spatial random effect term defined as zi = ui + vi. In this formulation, ui was the uncorrelated spatial heterogeneity with prior distribution N(0, τu), and vi was the correlated spatial heterogeneity with a prior distribution represented by the intrinsic CAR model often written as CAR(τv) (1–3). Both precision parameters (τu, τv) followed a gamma prior distribution, Gamma(2,1). The spatial random effect, zi, was included in this secondary model fit to account for the spatial correlation and dependence between the counties being examined; if this random effect were excluded, this test would essentially have been equivalent to a pairwise t test. Note that we assumed a spatially correlated structure for zi since the risk factors of interest had a strong spatially-structured distribution. The spatial random effect in the primary model could be spatially correlated or uncorrelated. All prior distributions were chosen such that they are non-informative.
In this secondary fit, Qi was created from a categorical variable, qi, which represented if a spatial area was contained in the first (qi = 0), second (qi = 1), third (qi = 2), or fourth (qi = 3) quartile of the spatial random effect. An example of the relationship between qi, Qi, and b is included in the Supplemental Materials. Alternatively, qi could be defined with respect to other categorization criteria (terciles, continuous for a trend test, etc).
Ultimately, this secondary model fit tested a null hypothesis of bj = 0 for j = 1,2,3, i.e. no difference in risk factor x for the counties contained in the corresponding level of q compared to the reference. A rejection of the null hypothesis indicated an association between the risk factor under examination and the spatial random effect. Therefore, it could be stated that the random effect at least partially represented this risk factor in the primary model fit. We could also do subgroup analysis if the interest was in the comparison of the first and fourth quartiles as this tested a difference in the extremes of the spatial random effect’s distribution. This method could be useful as a type of variable selection; if a large number of risk factors were of interest, the secondary model fits could be informative about which risk factors should be included in the final model.
2.2. Computation and Evaluation Techniques
These secondary model fits were performed with the statistical software R, specifically using the R package INLA (11–14). The integrated nested Laplace approximation (INLA) furnished a computationally efficient alternative to the Markov chain Monte-Carlo approach that has been shown to be comparable to other methods when appropriate specifications were implemented (15). Code for the spatial heterogeneity assessment is included in the appendix and has been incorporated as a function (assessmap) in the R package fillmap available on GitHub via user carrollrm.
3. Simulation Study
To show that our proposed secondary assessment was valid and useful in capturing risk factors associated with observed spatial heterogeneity, we performed some simulation studies.
3.1. Simulated Data
Here, we gave an example where an aggregated spatial-level count outcome was simulated under a Poisson model. Specifically, the count outcome was represented as yi for the ith small area (i = 1, … , n) with expected rate ei and relative risk θi (1). Therefore, the Poisson outcome with mean μi was defined as:
In this formulation, the expected rate was assumed known and constant across all spatial areas (ei = 1).
To mimic a real data situation, we used county-level risk factors from the state of Georgia, USA obtained via the Area Health Resources Files (16) as the true covariates: x1 - percent African American population, x2 - percent among persons 25 years and older who had completed 4+ years of college education (high education), x3 - total number of hospitals, and x4 - median household income. Supplemental Figure 1 displays maps of these variables and Supplemental Table 1 shows the correlation matrix for all of them. From these displays, it was obvious that these variables had spatial structure in their distributions and a range of low (ρ(x3, x4) = 0.13) to high (ρ(x2, x4) = 0.75) correlation.
Different combinations of mean-centered versions of these variables led to the following scenarios for defining the true model of the relative risk used to complete this illustration:
| NULL) |
| S1) |
| S2) |
| S3) |
| S4) |
Here, NULL was used for comparison and was defined by an intercept plus identical and independently distributed error (ϵi~N(0,1)). S1 considered a scenario in which the simulation assumed a mixture of variables with high and low correlation, while S2 and S3 furnished an examination of having pairs of variables with either low or high correlation, respectively. Finally, S4 offered an example where a single variable decided the risk. A total of 50 simulated data sets were created for each scenario and the posterior mean estimates were averaged for inference.
Fitting the Simulated Data
To fit the primary spatial model, we assumed the same Poisson data model with known expected rate and relative risk defined as:
where was the design matrix for including the known and measured risk factors and a, β, and wi were as in a, b, and zi in Section 2.1. The fixed effect contents of the models fitted for this illustration were based on the simulation scenario: all risk factors in the simulation model, subset(s) of the simulation model risk factors, or no risk factor adjustment. R-INLA was also used for these primary model fits to gain the spatial risk factor estimates for use in the secondary assessment. With the estimated wi’s from the primary model fit, we performed the proposed secondary assessments to understand the spatial heterogeneity.
3.2. Simulation Results
Table 1 allows for an examination of the estimated fixed effect parameter estimates for several combinations of fitted models per simulated data scenario. These risk factor sets were selected to examine a wide range of possible misspecifications as well as the case when all risk factors were adjusted for. The left-most column indicates specifically which risk factors, in addition to spatial random effects, were adjusted for in each of the different primary models, and the simulated data scenario is listed in the single-cell rows for identifying the rows that follow. In general and in the presence of spatial random effects, the parameter estimates were recovered appropriately, even when only a subset of true risk factors were included in the fitted model (e.g. the two fits for S2). Similarly, when additional risk factors were adjusted for (e.g. adjusting for x2 in addition to x4 with S4), the associated fixed effect parameter estimate was not significant; this suggested that it could be removed from the primary model. Finally, when highly correlated risk factors were part of the true simulation model and only one was considered or the incorrect one was adjusted for (e.g. adjusting for only x2 with S3 or S4 respectively), the associated parameter estimate was significant and appropriately accounted for the variation in the data by capturing the information from the missing risk factor (e.g. the parameter estimate associated with x2 in the fit adjusting for only x2 with outcome S3 appeared to be the sum of the true parameter values for that simulation scenario: 0.1 + 0.1 = 0.2). These results suggested the importance of including a spatial random effect in the primary model.
Table 1:
Fixed effect estimates averaged over the 50 simulated data sets.
| Risk factors adjusted for | Mean (95% CI) | Mean (95% CI) | Mean (95% CI) | Mean (95% CI) |
|---|---|---|---|---|
| True Model NULL: | ||||
| x1 | 0.00 (−0.01, 0.01) | |||
| True Model S1: | ||||
| x1, x2, x3, x4 | 0.10 (0.09, 0.11) | 0.10 (0.07, 0.13) | 0.10 (0.03, 0.17) | 0.10 (0.08, 0.12) |
| x3, x4 | 0.44 (0.33, 0.56) | 0.07 (0.04, 0.09) | ||
| x1 | 0.06 (0.04, 0.09) | |||
| True Model S2: | ||||
| x3, x4 | 0.20 (0.15, 0.25) | 0.20 (0.19, 0.21) | ||
| x4 | 0.20 (0.19, 0.22) | |||
| True Model S3: | ||||
| x2, x4 | 0.10 (0.08, 0.12) | 0.10 (0.09, 0.12) | ||
| x2 | 0.20 (0.18, 0.23) | |||
| True Model S4: | ||||
| x2, x4 | 0.00 (−0.02, 0.02) | 0.20 (0.19, 0.22) | ||
| x4 | 0.20 (0.19, 0.21) | |||
| x2 | 0.21 (0.17, 0.26) | |||
Table 2 shows the secondary model fit b3 estimates for comparing the first and fourth quartiles of the spatial random effect in models that adjusted for different sets of risk factors as in Table 1 plus the no risk factor adjustment case (“---“). The entire set of b estimates are included in Supplemental Table 2. Also as in Table 1, the left-most column indicates the primary models that were fitted to estimate the spatial frailties and the single-cell rows indicate the simulated data scenario. When all simulation model factors were adjusted for, none of the secondary models indicated that the potential risk factors were associated with the random effects from the primary models (second rows of S1, S2, S3, and S4). Conversely and except for S1, when no risk factors were adjusted for, the secondary models indicated that the appropriate risk factors were significantly associated with the spatial random effects from the primary model. Finally, the fits with the NULL simulated data scenario were performed for comparison of assessing an association between the risk factors and an outcome that was simulated independently, and, appropriately, no association was detected here.
Table 2:
Secondary model fit posterior mean b3 estimates for comparing the first vs. fourth quartiles associated with each risk factor and simulated model. Bold b estimates indicate statistical significance at the 0.05 level.
| Risk factors adjusted for | x1 Mean (95% CI) | x2 Mean (95% CI) | x3 Mean (95% CI) | x4 Mean (95% CI) |
|---|---|---|---|---|
| True Model NULL: | ||||
| --- | 0.18 (−0.12, 0.49) | −0.04 (−0.23, 0.15) | −0.08 (−0.51, 0.34) | −0.08 (−0.43, 0.27) |
| x1 | 0.28 (−1.46, 2.02) | 0.39 (−1.11, 1.90) | 0.46 (−0.25, 1.17) | −0.05 (−1.67, 1.56) |
| True Model S1: | ||||
| --- | 1.39 (−0.40, 3.16) | 3.14 (1.54, 4.71)* | 1.35 (0.64, 2.06)* | 1.60 (−0.07, 3.27) |
| x1, x2, x3, x4 | 0.53 (−1.26, 2.32) | −0.38 (−1.99, 1.22) | 0.04 (−0.74, 0.81) | −0.45 (−2.14, 1.24) |
| x3, x4 | 1.89 (0.09, 3.68)* | 1.68 (0.08, 3.26)* | 0.64 (−0.11, 1.39) | 0.38 (−1.30, 2.05) |
| x1 | −0.17 (−1.96, 1.62) | 3.84 (2.13, 5.51)* | 1.42 (0.71, 2.12)* | 3.15 (1.36, 4.92)* |
| True Model S2: | ||||
| --- | −1.23 (−3.03, 0.57) | −2.54 (0.90, 4.17)* | 1.05 (0.29, 1.80)* | 4.36 (2.54, 6.15)* |
| x3, x4 | −0.69 (−2.43, 1.04) | 0.58 (−0.92, 2.07) | −0.01 (−0.72, 0.69) | 0.88 (−0.73, 2.49) |
| x4 | 0.94 (−0.82, 2.69) | −0.33 (−1.20, 1.85) | 1.84 (1.17, 2.51)* | −0.63 (−2.27, 1.00) |
| True Model S3: | ||||
| --- | −1.18 (−2.98, 0.62) | 3.26 (1.60, 4.91)* | 0.87 (0.10, 1.63)* | 4.16 (2.35, 5.94)* |
| x2, x4 | −0.06 (−1.81, 1.68) | −0.41 (−1.93, 1.11) | 0.24 (−0.46, 0.95) | −0.18 (−1.81, 1.44) |
| x4 | −1.68 (−3.49, 0.13) | −0.01 (−1.59, 1.57) | −2.03 (−2.82, -1.20)* | 3.53 (1.76, 5.28)* |
| True Model S4: | ||||
| --- | −1.46 (−3.27, 0.35) | 2.16 (0.51, 3.80)* | 0.77 (0.00, 1.53) | 4.36 (2.53, 6.16)* |
| x2, x4 | 0.09 (−1.69, 1.86) | 0.89 (−0.67, 2.44) | −0.31 (−1.04, 0.43) | 0.23 (−1.43, 1.90) |
| x4 | −0.34 (−2.06, 1.38) | −0.30 (−1.77, 1.17) | 0.15 (−0.55, 0.86) | 0.15 (−1.44, 1.74) |
| x2 | −1.96 (−3.77, -0.15)* | 0.25 (−1.32, 1.82) | −2.15 (−2.94, -1.32)* | 3.92 (2.16, 5.66)* |
Indicates a significant 95% credible interval.
In terms of interpretation of Table 2 and the secondary model fit results, for each of the situations where a fitted model recovered a true association between the risk factor and random effect, we concluded that an increased risk in disease was related to increased percent African American population (x1), increased education (x2), increased access to healthcare (x3), and/or increased median household income (x4). These conclusions were consistent with the simulated data scenarios since all true fixed effect parameters were selected to be positive, indicating a positive association between those risk factors and the outcome. An issue related to risk factor correlation arose when we considered the interpretation of the secondary results for certain simulated/fitted model combinations. Take x3 in simulation scenario S4 for example. x3 was not part of the simulation model; however, it appeared to be associated with the random effect when only x2 was adjusted for. The direction of x3’s significant association with the random effect was reversed from the nearly significant estimate in the fitted model that adjusted for no risk factors with simulated data scenario S4. On the surface, this change was baffling as the correlation between x2 and x3 was also positive, though much stronger than that of x3 and x4. Interestingly, x3 did differ from both x2 and x4 in that it was positively correlated with x1; thus, the change in direction could be a result of that relationship coupled with x3’s stronger, positive association with x2 being adjusted away. Ultimately, this discovery suggested that these results should be used with caution and that correlations between the risk factors of interest should be considered.
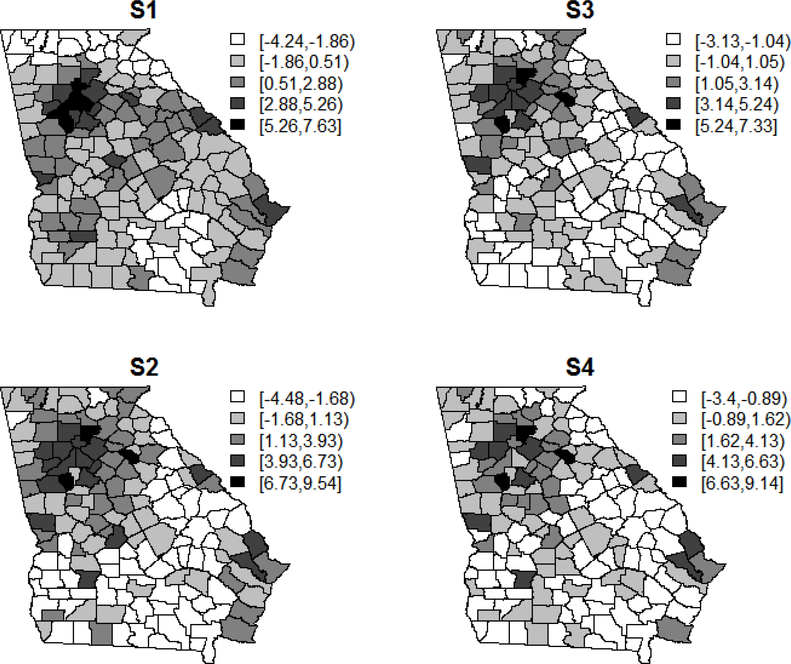
Figure 1 displays the random effect estimates (wi) for a single simulated data set from S1-S4 models that did not adjust for any of the risk factors. From these maps, it was easy to deduce that the random effect estimates represented latent combinations of the variables used in the simulated data scenarios. In fact, for S4, the image was nearly identical to that of median household income in Supplemental Figure 1, as expected. In a typical analysis, the conclusion for scenario S1 could be that there was an elevated risk in the Atlanta region as well as among some of the counties along the borders. However, with the knowledge gained from the secondary model fit, we concluded that this elevation in risk was associated with race, socio-economic status, and access to healthcare.
Figure 1:
Maps of the random effect estimates (wi) for each of the simulated data scenarios when not adjusting for any risk factors (log(θi) = α + wi).
4. Real Data Case Study
The motivating example for this secondary assessment technique involved individual-level BrCa-specific mortality in Louisiana SEER data (17). The SEER data contained mostly clinical and some demographic variables but did not include individual information on risk factors such as socio-economic status or access to healthcare. To solve this issue, we could have imputed individual-level risk factors based on the Federal Information Processing Standard codes given by SEER. Instead, we previously only included the measured individual level risk factors in the primary model and added a spatial random effect, or frailty in the survival context, to represent the unmeasured spatial risk factors (9). The frailty was given an uncorrelated structure as this was the best fitting model for the data. Then, we performed a simpler type of secondary assessment using two sample t-tests with these data and detected several risk factor associations with the spatial frailty. Now, we have explored a re-analysis with our proposed secondary assessment.
With these data, we performed a survival analysis and gained spatial frailty estimates for the parishes of Louisiana via an accelerated failure time model that adjusted for known, available risk factors of interest. The details of this model and results were omitted here since the focus was on the interpretation of the spatial random effects but can be found in our previous paper (9). For the paper at hand, we employed this more intensive secondary model fit assessment which demonstrated the use of this method in a data set with unknown risk factors. Many of the parish-level risk factors employed here came from the Area Health Resources Files (16). Specifically: percent of persons 25 years or older with four or more years of college education; total number of hospitals (public or private); number of hospitals per square mile; total number of hospitals with BrCa screening and mammography machines; number of BrCa screening hospitals with mammography machines per square mile; median household income; percent Medicaid eligible persons; percent urban population; percent farmland; percent of persons living in poverty; and percent persons working in agriculture, forestry, fishing, hunting, or mining.
Figure 2 displays the spatial frailty estimate and Table 3 displays the secondary assessment results for this frailty. Ultimately, the results in Table 3 suggested that survival time was associated with access to and quality of care, availablility of fresh food, socio-economic status, and percent of the population working in agriculture, forestry, fishing, hunting, or mining.
Figure 2:
Spatial frailty estimate for the case study data
Table 3:
Secondary assessment results for the case study data
| Risk Factor | Mean (95% CI) a |
|---|---|
| Access to care | |
| Total Hospitals | 0.78 (0.15, 1.40)* |
| Hospitals per square mile | 0.85 (0.24, 1.45)* |
| BrCa Hospitals b | 0.38 (−0.25, 1.01) |
| BrCa Hospitals per square mile b | 0.71 (0.11, 1.32)* |
| Quality of Care c | |
| ACS program | 0.57 (−0.06, 1.19) |
| ACS program per square mile | 0.69 (0.10, 1.28)* |
| Medicare certification | 0.61 (0.002, 1.21)* |
| Medicare certification per square mile | 0.69 (0.10, 1.26)* |
| Availability of Fresh Food | |
| Total Number of Groceries | 0.56 (−0.07, 1.19) |
| Groceries per square mile | 0.67 (0.06, 1.27)* |
| Socio-economic Status | |
| Median Income d | 0.59 (−0.03, 1.21) |
| % High Education e | 0.79 (0.17, 1.40)* |
| % Medicaid Eligible | −0.23 (−0.87, 0.41) |
| % Poverty f | −0.26 (−0.91, 0.39) |
| % Urban Population | 0.47 (−0.17, 1.10) |
| % Farmland | 0.00 (−1.96, 1.96) |
| % African American | 0.25 (−0.39, 0.89) |
| % Agriculture etc Work g | −0.83 (−1.42, -0.24)* |
Indicates statistical significance.
The estimates are from the secondary model fit using the spatial frailty estimate from the best model, S+T1.
BrCa hospitals are a subset of total hospitals which perform BrCa screenings and have mammography machines.
Hospital quality risk factors based on: number of hospitals with ACS cancer programs, number of hospitals with Medicare certifications, and a hospital quality ranking based on health factors.
Median household income in thousands of dollars
Percent of persons 25 years or older with four or more years of college education
Percent of persons living in poverty
This includes workers in: agriculture, forestry, fishing, hunting, and mining industries
These select chemicals are emissions from agriculture and forestry sources
5. Discussion and Conclusion
The results in this illustrative set of simulations and real data case study demonstrated that spatial random effects were important for representing unadjusted for spatial risk factors and that the secondary fit uncovered the omitted risk factors. Additionally, the results illustrated that once important risk factors were adjusted for in the primary fitted model, they no longer suggested an association with the random effects via the secondary model fit. This could be important for studies with individual level data that lack individual information on some potential risk factors, as in our real data case study. Here, the random effects were used to account for the unknown information, as a latent combination of spatially-varying risk factors, in a way that improved upon including them additively in the primary model. The idea that population-level representations of risk factors could inform on individual-level outcomes was not new (18) and was supported by the information presented in this paper. In terms of the case study, the spatial risk factor conclusions were consistent with what was documented in the BrCa literature for individual survival (19, 20). However, as a precaution, causation could not be concluded from these post hoc assessments of the spatial differences and correlations between risk factors of interest should be considered, as illustrated in the simulation results section.
In this exploration, we demonstrated the usefulness of employing a secondary fit in two settings and assessed random effect estimates for risk factors of interest. There were many statistical tests that could have accomplished similar goals. In addition to the secondary fit, we also examined permutation tests, two sample t tests, paired t tests, two sample Wilcoxon signed rank tests, and paired Wilcoxon signed rank tests. With the paired tests, counties in the first and fourth quartiles were paired by closest distance. We examined these alternative tests to determine if the correlation structure compromised the test validity, and there were some extraneous results. Thus, the employed secondary model fit option resulted in the best recovery of the simulation models, where a correlation structure was assumed for the spatial random effect. We also believed that the secondary assessment outlined in this paper furnished an improvement over using two sample t-tests in the case study data where there was no correlation structure assumed for the frailty because it also accounted for the inherent spatial correlation in the risk factors of interest.
The choice of risk factor was also important to consider in analyses such as this. All the risk factors we considered here were continuous. Though, our technique could have examined those that were binary or categorical as well. Our results also suggested that correlation between risk factors led to results that differed somewhat from the truth defined by the simulation models. However, this was expected as the correlation indicated that these risk factors explained similar disparities, e.g. correlation between percent high education and median household income. Thus, it was not false to draw the conclusion that education was associated with increased risk when median household income was included in the simulation model since the two were noted as correlated. However, if the step that followed this detection of association involved fitting a model that adjusted for both risk factors, results would have suggested that it was unnecessary to include education in addition to median income.
In conclusion, this work illustrated how to quantitatively explore random effect estimates and their associations in terms of risk factors beyond those that were adjusted for in two types of disease mapping models. The simulations demonstrated that a secondary assessment recovered the truth associated with increased risk of disease and that random effects appropriately represented potential risk factors. This technique was demonstreated as widely applicable in the disease mapping framework and led to more interpretable, useful results and conclusions related to spatial random effects.
Supplementary Material
Highlights.
Spatial random effects are an important aspect of spatial epidemiology.
There is no consistent way in the literature to draw inferences from spatial random effects.
Formal statistical modeling and testing can be applied for that purpose.
Results from these models and tests lead to more interpretable conclusions.
Acknowledgements
This research was supported by the Intramural Research Program of NIH, National Institute of Environmental Health Sciences.
References
- 1.Lawson AB. Bayesian disease mapping: Hierarchical modeling in spatial epidemiology. 2 ed. Boca Raton, FL: CRC Press; 2013. [Google Scholar]
- 2.Besag J, Green PJ. Spatial statistics and Bayesian computation. J Roy Stat Soc B 1993;55(1):25–37. [Google Scholar]
- 3.Besag J, York J, Mollie A. Bayesian image restoration, with two applications in spatial statistics. Ann Inst Stat Math. 1991;43(1):1–20. [Google Scholar]
- 4.Carroll R, Lawson AB, Voronca D, Rotejanaprasert C, Vena JE, Aelion CM, et al. Spatial environmental modeling of autoantibody outcomes among an African American population. Int J Environ Res Public Health. 2014;11(3):2764–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Guillot G, Leblois R, Coulon A, Frantz AC. Statistical methods in spatial genetics. Mol Ecol. 2009;18(23):4734–56. [DOI] [PubMed] [Google Scholar]
- 6.Henderson R, Shimakura S, Gorst D. Modeling Spatial Variation in Leukemia Survival Data. J Am Stat Assoc 2002;97(460):965–72. [Google Scholar]
- 7.Lawson AB, Carroll R, Castro M. Joint spatial Bayesian modeling for studies combining longitudinal and cross-sectional data. Stat Methods Med Res 2014;23(6):611–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lawson AB, Ellerbe C, Carroll R, Alia K, Coulon S, Wilson DK, et al. Bayesian latent structure modeling of walking behavior in a physical activity intervention. Stat Methods Med Res 2016;25(6):2634–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Carroll R, Lawson AB, Jackson CL, Zhao S. Assessment of spatial variation in breast cancer-specific mortality using Louisiana SEER data. Soc Sci Med 2017;193(11):1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lawson AB, Banerjee S, Haining R, Ugarte MD. Handbook of Spatial Epidemiology. Fitzmaurice G, editor. Boca Raton, FL: CRC Press; 2016. [Google Scholar]
- 11.Blangiardo M, Cameletti M, Baio G, Rue H. Spatial and spatio-temporal models with R-INLA. Spat Spatiotemporal Epidemiol 2013;4:33–49. [DOI] [PubMed] [Google Scholar]
- 12.Martins TG, Simpson D, Lindgren F, Rue H. Bayesian computing with INLA: New features. Comput Stat Data An 2013;67:68–83. [Google Scholar]
- 13.Schrödle B, Held L. A primer on disease mapping and ecological regression using INLA. Computation Stat 2010;26(2):241–58. [Google Scholar]
- 14.Rue H, Martino S, Chopin N. Approximate Bayesian inference for latent Gaussian models using integrated nested Laplace approximations (with discussion). J R Stat Soc B 2009;71:319–92. [Google Scholar]
- 15.Carroll R, Lawson AB, Faes C, Kirby RS, Aregay M, Watjou K. Comparing INLA and OpenBUGS for hierarchical Poisson modeling in disease mapping. Spat Spatiotemporal Epidemiol 2015;14–15:45–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bureau of Health Workforce. Area Health Resource Files (AHRF) Rockville, MD: US Department of Health and Human Services, Health Resources and Services Administration; 2015. [Available from: http://ahrf.hrsa.gov/. [Google Scholar]
- 17.Surveillance Epidemiology and End Results (SEER) Program. S EER*Stat Database: Incidence - SEER 9 Regs Research Data, Nov 2015 Sub (1973–2013). Bethesda, MD: 2015. [Available from: www.seer.cancer.gov. [Google Scholar]
- 18.Warnecke RB, Oh A, Breen N, Gehlert S, Paskett E, Tucker KL, et al. Approaching health disparities from a population perspective: the National Institutes of Health Centers for Population Health and Health Disparities. Am J Public Health. 2008;98(9):1608–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.American Cancer Society. Breast Cancer Facts & Figures 2017–2018 Atlanta: American Cancer Society, Inc; 2017. [Available from: http://www.cancer.org/acs/groups/content/@research/documents/document/acspc-046381.pdf. [Google Scholar]
- 20.Breastcancer.org. Healthy eating after diagnosis improves survival. Ardmore, PA: 2014. [Available from: http://www.breastcancer.org/research-news/healthy-eating-improves-survival. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.