Trends in colorectal cancer incidence and survival in Iowa SEER data: The timing of it all

Abstract

Colorectal cancer (CRC) is common worldwide with 140,250 diagnoses and 50,630 deaths estimated for the United States in 2018. Guidelines current to the most recent individuals in our analysis suggested regular screenings beginning at age 50 have reduced the incidence of colorectal cancer. However, incidence continues to rise among those under 50. Less is known about survival following CRC diagnosis, but research has suggested that younger cases may also have worse survival. However, we hypothesize that younger individuals are generally healthier with fewer comorbidities leading to the potential for better survival following diagnosis. We utilize the Surveillance, Epidemiology, and End Results data to estimate and assess both spatial and temporal variation in age-specific colorectal cancer incidence and survival in Iowa. Both overall and older-onset colorectal cancer incidence began to decline in the early 2000s, while younger-onset incidences decreased until the late 1980s but then increased steeply through the 2000s. The risk for those younger than 50 years of age first exceeded the risk for those 50 years or older in 2007. Survival times did increase for overall CRC, older-onset CRC, and young-onset CRC throughout the study period, with young-onset CRC increasing at a higher rate. The spatial variation assessment indicated that the survival was positively associated with several variables of interest, most notably disparities including better access to healthcare and higher socio-demographic status. In conclusion, results suggest that regular colorectal screenings could reduce incidence and mortality in people under 50.

1. Introduction

Colorectal cancer (CRC) is one of the most diagnosed cancers in the United States. The American Cancer Society estimated that 140,250 individuals will be diagnosed with CRC in 2018 (1). Strong recommendations were made by the American Cancer Society in 1996 suggesting that all adults over the age of 50 should submit to regular screenings for CRC every 10 years. This change has resulted in an overall decline in CRC incidence (2). However, recent studies have suggested an increase in incidence remains for individuals less than 50 years of age (2–5). Specifically, the American Cancer Society stated that incidence rates for CRC among individuals older than 50 years declined by 3.8% annually from 2005 to 2010 while CRC rates for individuals younger than 50 years increased by 1.4% over the same time frame (1). For these analyses, we consider CRC diagnosis prior to the age of 50 as young-onset CRC and CRC diagnosis after the age of 50 to be older-onset CRC.

Survival following CRC diagnosis in different age groups has not been explored as thoroughly though studies suggest that treatment improvements lead to better survival overall (6, 7). The American Cancer Society estimated that, in 2018, 50,630 individuals’ underlying cause of death will be CRC but did not offer age-specific mortality information (1). Further, age group-sepecific survival following CRC diagnosis has not been assessed much with respect to changes over calendar time.

In this paper we utilized information related to CRC incidence and survival following diagnosis recorded in the Iowa Surveillance Epidemiology and End Results (SEER) registry between the years 1973 and 2013, with the goal to understand the differences to younger and older individuals separately. To assess incidence of CRC, we employed a Bayesian Poisson Knorr-Held model (8, 9) which produced estimates for the temporal trend after accounting for several aggregated, county-level risk factors as well as the underlying spatial and spatio-temporal variation. Similarly, temporal trends in survival following CRC diagnosis were assessed after adjusting for individual-level risk factors as well as the underlying spatial and spatio-temporal variation via a spatio-temporal Bayesian accelerated failure time model (AFT) (10–12).

Previous work has demonstrated improvements in the modeling of rare diseases by borrowing information from related, more common diseases (13, 14). While CRC as a whole is not a rare disease, young onset CRC is. And, since young and older onset CRC do have similarities in terms of risk factors, we believed that a multivariate approach with shared random effects could be adopted for the purpose of this analysis as we were interested in quantifying and comparing the temporal trends of incidence and survival for those under age 50 versus those over age 50.

2. Materials and Methods

2.1. Iowa SEER data

The SEER program offers publicly available cancer data from 17 registries across the US. The specific registry that provides CRC data for Iowa currently includes individuals diagnosed between January 1, 1973 and December 31, 2013. The Iowa registry was selected for the long follow up, which is not available for all SEER registries. To model the CRC incidence, a Poisson model was used, based on the county level incidence calculated as a count of the number of individuals diagnosed in each county for a given year. The county population across the study years was also accounted for as an offset in the Poisson model. Since Iowa has 99 counties and 41 years were considered, the count outcome was a matrix with 99 rows and 41 columns. To model survival following CRC diagnosis, we combined the documented individual survival time in months together with a CRC mortality underlying cause of death indicator (ICD-10: C18, C26.0, and C19-C20). Thus, an individual was considered censored either at their last follow-up time, at the end of the study period (December 31, 2013), or at the time of their death due to other causes. The final number of individuals diagnosed with CRC and considered for analysis was reduced from 83,664 to 82,828 based on requiring known survival time. This removed only 1% (n=836) from the total analysis, 0.4% (n=18) from young onset and 1% (n=818) from older onset.

To determine an individual’s location, we utilized the SEER registry-provided Federal Information Processing Standard county code. With this information, we assigned an individual to one of the 99 Iowa counties. On average, there were 20.6 (range: 0–227) incidences per county per year. There were four counties with no CRC diagnosed ever across the study time; all these were smaller counties, as they were consistently in the 12^th or less percentile of counties for year-specific population size. When reducing the outcome to either above or below the age of 50, the average number of incidences within a county per year were 19.5 (range: 0–210) and 1.1 (range: 0–30) respectively. There were four county-year combinations without older onsets, and 2014 without young onsets.

The demographic and clinical covariates considered in the analysis of CRC survival were selected for their known associations with CRC mortality (15) and their availability in the SEER database. There was some missing in the covariates considered in the survival model. However, it was important to include this information so that we could maximize the number of individuals contributing within each county and year for the spatial and temporal components, particularly for the young onset age group. Thus, we incorporated unknown categories when needed. Specifically, the covariates included were: race (White vs. other), marital status at diagnosis (single, currently married, separate/divorced/widowed/unknown), age at diagnosis, high cancer grade (yes, no/unknown), previous history of reportable malignant, in situ, benign, and borderline primary tumors (no, yes), CRC surgery (no/unknown, yes), and radiation therapy (no/unknown, yes). For marital status, the large majority (80%, n=23416) of the third category was widowed individuals. Cancer grade had the highest amount of missing (23%, n=19,216) and the next highest was marital status (2%, n=1622). We considered grade as our best available measure to account for severity of cancer among age groups. Other potential variables for this were: stage at diagnosis, anatomic location, or histologic behavior; however, stage at diagnosis was missing for a large majority of individuals (84%, n=70,286), a laterality variable offered no information about placement of the tumor, and a comparison of histological behavior showed no difference between the age groups.

2.2. County level data

We used county level data as a means to adjust for risk factors in the Poisson model, and these data were collected from the following sources: the Area Health Resources Files (16), the University of Wisconsin Population Health Institute’s County Health Rankings and Roadmaps (17), and the Center for Disease Control and Prevention (18). The risk factors included for this purpose were chosen based on their association with increased risk of CRC (15), and specifically, these were: percent white population, percent current smokers, percent of individuals with high education (4 year of college or more), median home value (in 10,000s), percent urban population, and county-level diabetes rate. Note that these risk factors were only available for a single year, and not all were from the same year; we made an attempt to account for such discrepancies within the statistical model.

2.3. Statistical Methods

2.3.1. Incidence model

A Bayesian Poisson model was utilized in the assessment of temporal trends in CRC incidence. In this model, the mean of the Poisson distribution is defined as the expected rate times the relative risk (e_ijθ_ij) and both are specified for each Iowa county (i = 1, …, 99) and available year (j = 1, …, 41 corresponding to the years 1973 to 2013). The expected rate is the offset term and is calculated as the year-specific county incidence divided by the county population for the same year (19, 20). Then, the fixed and random effects of interest are related to the relative risk through a log link: log(θ_ij) = X_iβ_j* + w_i + γ_j + ϕ_ij where X_i represents the county-level risk factors of interest and the β_j* coefficients capture fixed effects of those factors that are specific to time intervals, with j* = 1, …, 8 corresponding to every 5 years (19, 20). Also, w_i is the correlated spatial random effect, γ_j is the temporal random effect, and ϕ_ij is the spatio-temporal interaction term. We used the 5-year timeframe for the fixed effect parameter (β_j*) to minimize the identifiablility issues with the temporal random effect and to have a more interpretable number of parameters.

A multivariate specification for this Poisson model was used to separately model individuals with young and older onset CRC. The parameterization of this model is as follows for h = 1,2 corresponding to the young and older onset incidences respectively:

$$y_{ijh}~Poisson({\mu }_{ijh})$$

$${\mu }_{ijh}=e_{ijh}{\theta }_{ijh}$$

$$\log ({\theta }_{ijh})=X_i{\beta }_{j^{\mathrm{*}}h}+w_i+{\gamma }_{jh}+{\varphi }_{ij}$$

Here, the spatial random effect and spatio-temporal interaction term are shared between the multivariate outcomes as a means to improve the fit for the rarer outcome, incidence of CRC for those younger than 50. Note that the offset terms are specific to the corresponding age-based subpopulations. This allows fixed effect parameter estimates and temporal random effect estimates to be specific to the age group, but the spatial and temporal effect to be the same for these two age groups, which is a reasonable assumption in practice.

2.3.2. Survival model

To assess CRC survival time following diagnosis, we use the accelerated failure time (AFT) model (21). This model allows for a direct relationship of the logarithm of survival time with both the risk factors and the spatial, temporal, and spatio-temporal random effects (22–24). This capability along with the models’ general flexibility in terms of assumptions has led to the AFT model’s increase in popularity and, for our purposes, an ideal interpretation of the spatial, temporal, and spatio-temporal frailty estimates. The AFT model for an individual k diagnosed in county i at time j can be written as: log(t_ijk) = λ_ijk + σϵ_ijk where t_ijk is the survival time, λ_ijk is the linear predictor of interest, ϵ_ijk’s are the independent random errors, and σ is a scale parameter. A single parameterization of λ_ijk is considered, and it is such that λ_ijk = X_ijkβ + w_i + γ_j + ϕ_ij. This parameterization is used in both univariate and multivariate settings where, similar to the Poisson model, a multivariate analysis is constrained to share random effects between the two age-specific case groups to gain age-group-specific temporal random effect estimates. The multivariate specification is as follows: λ_ijkh = X_ijkβ_h + w_i + γ_jh + ϕ_ij where h = 1,2 for the two age groups considered. From here on model results specific to the univariate, multivariate for younger onset, and the multivariate for older onset will be referred to as “all,” “<50,” and “≥50.”

3. Results

3.1. Incidence assessment results

Figure 1 displays maps of the county level risk factors that were adjusted for in these Poisson models for assessing incidence, and Supplemental Table 1 shows the correlation matrix for these risk factors. Together, these illustrated that the distribution of these county-level variables was spatially structured since closer counties were more alike, and there were some similarities in the spatial distributions across variables since some correlations were fairly high. Specifically, the highest Pearson correlation is between median home value and percent high education (ρ = 0.73). The high correlation suggested that some of these variables could be representing similar characteristics.

Figure 1:

Iowa county-level risk factors adjusted for in the Poisson models for assessing CRC incidence. Here, lighter shading indicates lower values and darker shading indicates higher values of the given variable.

Figure 2 displays the temporal random effect estimates for the “all” as well as both age subgroup incidence models. From this figure, it is clear that the “all” model estimates (black line) were dominated by the ≥50 age group (blue line). In the multivariate setting, we were able to separate the temporal trends for the age groups of interest. From these, it was clear that the ≥50 model (blue line) suggested an increase in risk until about 1990, then risk was level throughout the 90s, and risk began to decline in the early 2000s. By contrast, the <50 model (red line) decreased until the 1990s. Following that, the risk began increasing drastically and appeared to level off somewhat towards the end of the study time. Further, for those ≥50 years, the risk in 2013 was almost equal to the risk in 1973 whereas the risk for those <50 years of age was 16% higher (exp(0.15) = 1.16). With this information, the estimates suggested that the risk for those <50 years of age was first greater than the risk for those ≥50 years in 2007.

Figure 2:

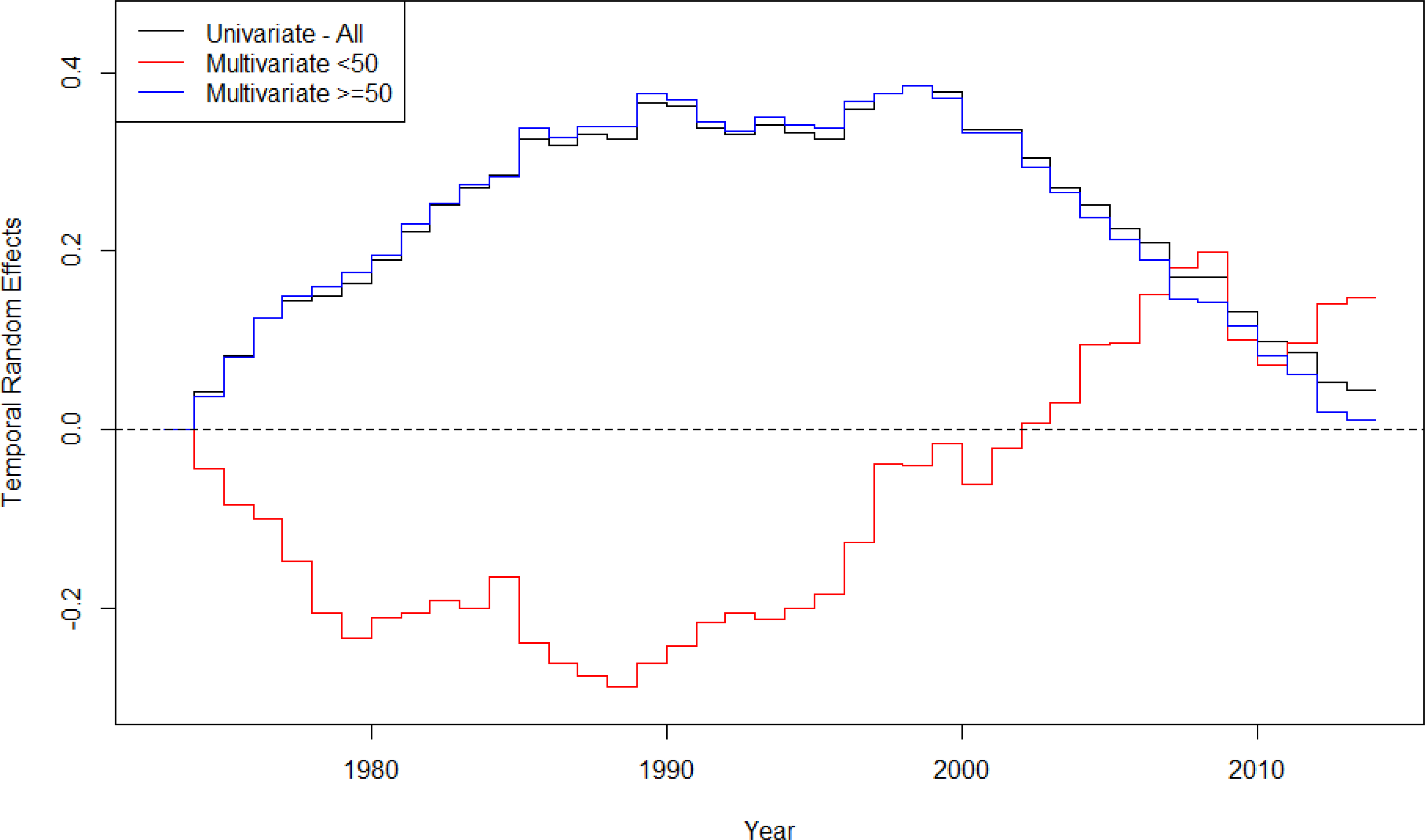
Temporal random effects estimates from the univariate and multivariate models for all patients and patients in separate age groups, examining CRC incidence in Iowa SEER data.

Supplemental Table 2 shows the relative risk for the different age groups comparing different years according to the associated temporal random effect estimate. As an example to illustrate interpretation, the relative risk of CRC in 1980 was 0.81, relative to 1973, for those <50-years-old. As such, the risk was less for younger-onset CRC in 1981 as compared to the risk in 1973. Thus, we see the same trends here as in Figure 2 where the <50 model suggested reduced risk until the 1990s and then began increasing, while the ≥50 model first had increasing risk and later decreasing risk.

Estimates for the other model parameters: fixed effect parameters and spatial terms are included in Supplemental Figures 1 and 2. The fixed effect results indicated association with incidence of CRC in Iowa for 5-year periods across the study time. From these, it was clear that the estimates differed in trend and value across many of the covariates for the two age-specific subgroup models. The estimates that were most different were for median home value and percent urban population and showed similarities between those produced from the “all” and the “≥50” models. However, the trends between these two models and the the “<50” model were nearly opposite. An example interpretation is as follows: Positive estimates indicate higher incidence of CRC for counties with higher percent white population. This relationship is the case for most years with respect to the “all” model that considers all age groups together and the “≥50” model. The 5-year intervals for which this relationship was not true were 1985–1990 and 2000–2005. The estimates in the “<50” model suggested an opposite relationship, more incidence in counties with less percent white population, for all but the first 10 years of the study time. The spatial estimates were similar between the “all” and both age-specific subgroup models, where this effect was shared between the two outcomes. The darker areas, which indicate more risk appear to be nearby the state capital, Des Moines, and in general, in the western part of the state. There was an additional cluster of increased risk in the east within counties through which Interstate 380 runs from Iowa City to Cedar Rapids then to Waterloo. The spatio-temporal estimates (data not shown) did show variation across counties and years as well as similarities between the univariate and multivariate models; however, there was no clear pattern.

3.2. Survival following CRC results

Table 1 displays descriptive statistics of the individual covariates adjusted for in the AFT “all,” “≥50,” and “<50” models. These indicated that there was a difference in these risk factors of interest between the two survival outcome groups. Further, when comparing to the tables broken down by age-specific subgroup, there does not appear to be a difference in survival outcome for young onset CRC with respect to age and death (p-value: 0.56) nor sex (p-value: 0.42) while older onset CRC survival status remains statistically different for all risk factors of interest.

Table 1:

Descriptive statistics for the individual-level risk factors from the Iowa SEER data used in the AFT model this is for all age groups, the younger onset age group, and the older onset age group separately. The data in this table are labeled as follows: N – number of individuals per category, Col % - column percentage per category, Mean (SD) – the mean and standard deviation of of the continuous variable, and P value – the P value from either a two-sample t-test (continuous) or a chi-squared test (categorical)

	No CRC Death			CRC Death
Risk Factor	N	Col %	Mean (SD)	N	Col %	Mean (SD)	P value
All age groups
Age at diagnosis			71.0 (12.4)			72.0 (12.8)	<0.001
% Urban Population			57.5 (23.3)			57.5 (23.4)	0.93
Marital status							<0.001
Single	3502	6.7		2600	8.2
Married	31076	59.6		17335	55.0
Previous	17546	33.7		11605	36.8
Sex							0.02
Male	25323	48.9		15062	47.8
Female	26801	51.4		16478	52.2
High grade							<0.001
No	43087	82.7		23380	74.1
Yes	9037	17.3		8160	25.9
Previous tumors							<0.001
No	32601	62.5		23828	75.5
Yes	19523	37.5		7712	24.5
Radiation therapy							<0.001
No	48452	93.0		28358	89.9
Yes	3672	7.0		3182	10.1
CRC surgery							<0.001
No	3365	6.5		7683	24.4
Yes	48759	93.5		23857	75.6
Less that 50 years old
Age at diagnosis			42.3 (6.4)			42.2 (6.5)	0.56
% Urban Population			57.5 (28.3)			57.5 (28.3)	1.00
Marital status							0.06
Single	442	15.1		291	17.7
Married	2092	71.3		1130	68.9
Previous	399	13.6		219	13.3
Sex							0.42
Male	1534	52.3		879	53.6
Female	1399	47.7		761	46.4
High grade							<0.001
No	2385	81.3		1072	65.4
Yes	548	18.7		568	34.6
Previous tumors							<0.001
No	2245	76.5		1432	87.3
Yes	688	23.5		208	12.7
Radiation therapy							0.007
No	2444	83.3		1314	80.1
Yes	489	16.7		326	19.9
CRC surgery							<0.001
No	141	4.5		259	15.8
Yes	2802	95.5		1381	84.2
Greater than 50 years old
Age at diagnosis			72.7 (10.5)			73.6 (10.9)	<0.001
% Urban Population			57.5 (28.3)			57.5 (28.4)	1.00
Marital status							<0.001
Single	3060	6.2		2309	7.7
Married	28984	58.9		16205	54.2
Previous	17147	34.9		11386	38.1
Sex							0.01
Male	23789	48.4		14183	47.4
Female	25402	51.6		15717	52.6
High grade							<0.001
No	40702	82.7		22308	74.6
Yes	8489	17.3		7592	25.4
Previous tumors							<0.001
No	30356	61.7		22396	74.9
Yes	18835	38.3		7504	25.1
Radiation therapy							<0.001
No	46008	93.5		27044	90.4
Yes	3183	6.5		2856	9.6
CRC surgery							<0.001
No	3234	6.6		7424	24.8
Yes	45957	93.4		22476	75.2

Figure 3 displays the temporal trends in the Iowa SEER data with respect to individual-level survival time. The temporal frailty estimates were in relation to survival time in months after CRC diagnosis. Thus, a higher number indicated longer, improved survival time. These results indicated that both age-specific subgroups have improved survival over the study time. Further, the “<50” model indicated that the younger age group had a longer survival time following diagnosis on average. The overall rate of change for the different age groups (“all,” ”<50,” ”≥50”) was as follows: 0.04, 0.05, and 0.04, respectively. These rates of change estimates translated to an average of a 4% or 5% increase in survival time per year across the study time for these age groups in the state of Iowa.

Figure 3:

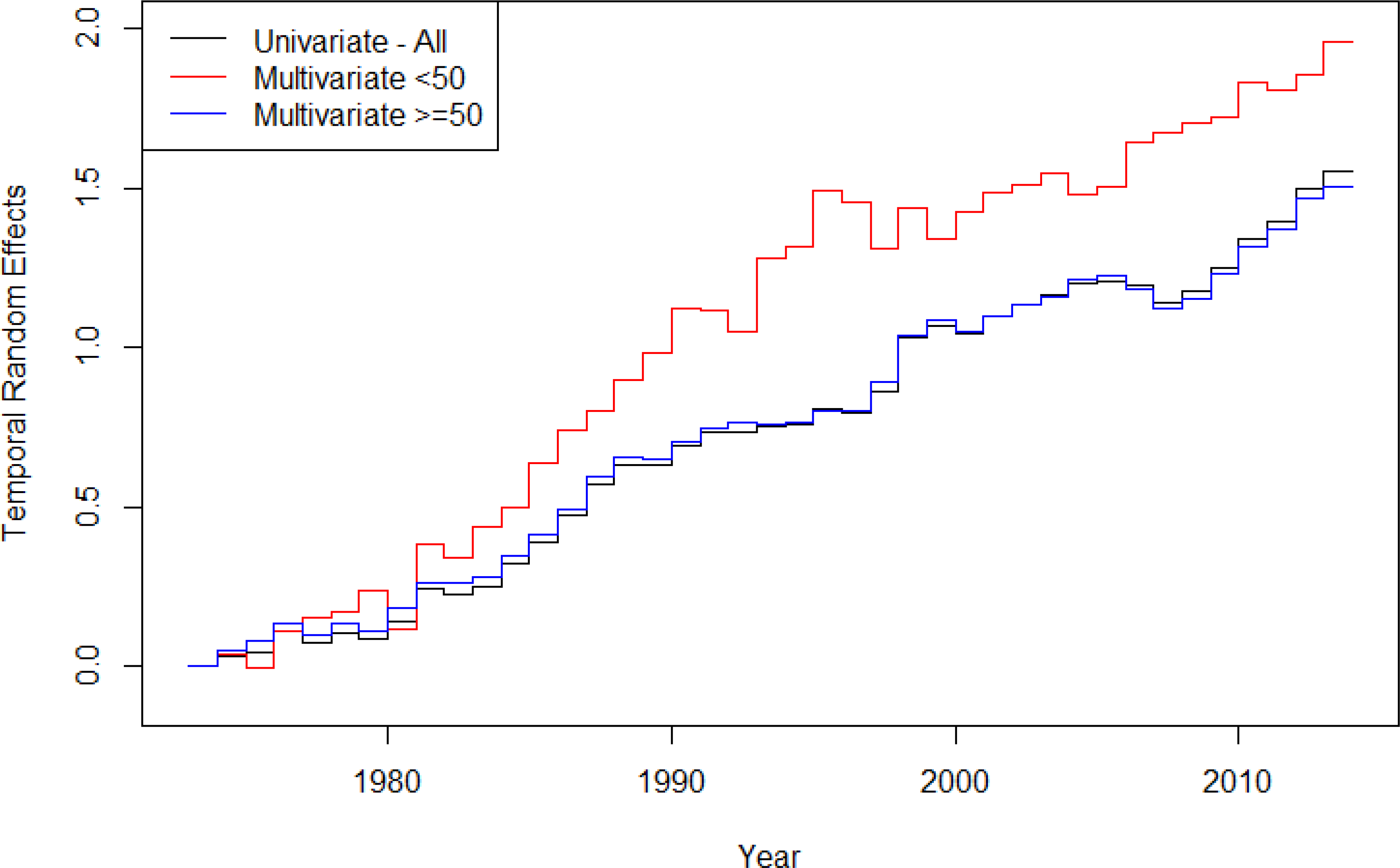
Temporal variation estimates for the AFT model assessing age-specific survival following CRC diagnosis for CRC underlying cause of death in Iowa.

Estimates for the other model parameters: fixed effect parameters and spatial terms are included in Supplemental Table 3 and Figure 3. These suggested that several of the individual covariates were associated with longer CRC survival time for the “all” model and the “≥50” model including: being married at the time of diagnosis, being female, not having a high grade of cancer, having a previous tumor, not having radiation therapy, having surgery, and being younger at the time of diagnosis. The estimates from the “<50” model suggested similar relationships to those listed above except being married at the time of diagnosis; here the estimate suggested that this lead to worse survival compared to being single at the time of diagnosis. The spatial random effect was very similar for all three models, and some secondary testing (25) (Supplemental Tables 4 and 5) suggested that this effect could be representing socio-demographic status, population health, and EPA emissions from several sources. The population health characteristics indicated longer survival for individuals in counties with higher prevalence of obesity, diabetes rates, percentage of excessive drinkers, and percentage of excess smokers. After adjusting the secondary assessment for percent urban population, many of these socio-demographic and population health associations were reduced and the county EPA emissions found to have negative associations, indicating shorter survival times, were carbon monoxide from light duty gas vehicles and motorcycles sources and ammonia from agriculture and forestry sourses. Similarly to the incidence model estimates, the spatio-temporal estimates did show variation across counties and years as well as similarities between the univariate and multivariate models; however, there was no clear pattern (data not shown).

4. Discussion

Previous work has suggested that there were differences in both incidence and survival related to CRC by age group and that those younger than the age of 50 were worse off with respect to both evaluations of risk (3). The results here agreed with respect to young onset incidence of CRC in Iowa. However, results with respect to survival indicated that younger individuals tended to survive longer following a CRC diagnosis.

The results related to fixed effect estimates and secondary assessments of the spatial random effect in the survival models were interesting. For these, we saw improved survival in Iowa for those with previous tumors and with no radiation (not for the young onset age group). These results could be related to more frequent screenings among those with history of previous tumors and radiation therapy could cause more harm than good for older onset CRC. Then, the secondary assessment results suggested some conflicting results. For the socio-demographic status and population health risk factors, we saw improved survival for individuals in counties with higher median home values, percent Medicaid eligible, percent with no insurance, percent persons living in poverty, percent high education, obesity prevalence, diabetes rate, percent excessive drinkers, and percent current smokers. Many of these could also be indicators of urbanicity since larger cities tend to have these socio-demographic and population health characteristics; to confirm this, we performed the secondary assessment while adjusting for percent urban population as a fixed effect estimate (Supplemental Table 5). After adjusting for this risk factor, many of the conflicting results became null. Further, a negative association for ammonia from agriculture and forestry sources surfaced after adjustment. Individual-level socio-demographic information could be an important measure that is unavailable with this data set.

Another important aspect of trend over time is change points due to significant events. We attempted to detect change points in both incidence and survival as in Carroll et al. (11, 12). However, the addition of this parameter did not indicate an improvement in model fit over fitting a yearly trend as in the results presented here. Previous work suggested that the decrease in incidence for older onset CRC and the rise in incidence for young onset CRC both began in the mid-1980s (3). However, our results suggested that both changes were later with the change for decrease in older onset at around diagnosis year 2000 and the change for young onset at around diagnosis year 1989. Our finding related to the change in incidence of older onset CRC at 2000 could be related to the implemented screening recommendation in 1996, assuming an approximately four year lag. All these statements are made with the caveat that this is specific to the Iowa SEER data.

For temporal trend in survival, previous studies have suggested that observed data on young onset colorectal cancer also indicated worse survival for this age group (26), but they did not suggest any changes in trend. This data from Iowa indicated that survival was better and the same as older onset for those diagnosed prior to their 50^th birthday until 1998. Another study suggested that survival for young-onset cases could be significantly worse for non-Hispanic blacks (27) and our population was largely white (99%, n=82,434); thus, the results here might not illustrate the full decline of young onset survival. Race was not adjusted for in our models as there were very few non-whites and the percentage of missing failure time (1% for each race category) and CRC-specific death (36% of non-whites and 38% for whites) for whites and non-whites was nearly identical.

The most recent change in CRC screening recommendations occurred in May 2018 as a result of recent research (6). This recommendation suggested that regular screenings should begin at age 45 rather than at age 50. This will likely help the risk associated with incidence of young onset CRC as 47% of individuals in the young-onset group used in this study were diagnosed between ages 45 and 50. However, 53% of individuals classified as having young onset CRC would remain uncaptured by the newly recommended screenings. Alternatively, a decrease to screenings beginning at 40 years old would encompass another 27% of the individuals considered here. The cost and burden of further lowering the recommended screening age should be considered.

This study was not without limitations. First, the data involved here was exclusively from the Iowa SEER registry; thus, interpretations are with respect to that specific population. Moreover, this population is largely white, and there are differences in CRC among race groups. In fact, there were so few non-white individuals in this registry that adjustment for race at the individual level was not feasible. Another data limitation involved the anatomic and histologic information that was not available for the entirety the SEER data. The only variable associated with severity of disease that was also available across all years of interest was grade, and while this does indicate severity, other variables could be more appropriate. The final limitation of the data involved lack of demographic information. From these results, we believe that disparities play a role in CRC incidence and survival; however, SEER data only offers: age, race, and sex.

5. Conclusion

The results of this project suggested that, based on the population in Iowa, there are age-group-specific differences in CRC incidence and survival. We found that timing for changes in incidence of young and older onset CRC were slightly later than what had previously been suggested and that the revised estimated inflection year appeared to be more consistent with the 1996 change in recommended screenings for older individuals. For CRC survival, we found that all age-group definitions tested indicated positive trend, e.g. toward ever-improving survival times, with the highest rate of change in the younger onset group. These results suggest that improved screening for people over 50 decreased the incidence of older-onset CRC, but did not benefit the younger population. This analysis underscores the importance of the revised recommendation that screening should instead begin at 45. The finding that survival following a CRC diagnosis continues to improve across the study time further underscores the importance of early detection for CRC.