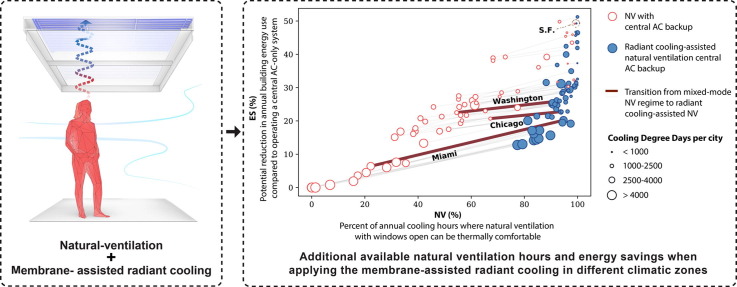
Graphical abstract
Keywords: Natural ventilation, COVID-19, Radiant systems, Thermal comfort, Air quality, Energy cost
Abstract
Radiant cooling-assisted natural ventilation is an innovative technical approach that combines new radiant cooling technology with natural ventilation to increase fresh air delivery into buildings year-round with minimal energy cost and improvment of air quality. Currently, the standard paradigm for HVAC (heating, ventilation and air conditioning) is based on central air systems that tie the delivery of heating and cooling to the delivery of fresh air. To prevent heat loss, the delivery of fresh air must be tightly controlled and is often limited through recirculation of already heated or cooled air. Buildings are designed with airtight envelopes, which do not allow for natural ventilation, and depend on energy-intensive central-air systems. As closed environments, buildings have become sites of rapid COVID-19 transmission. In this research, we demonstrate the energy cost of increasing outdoor air supply with standard systems per COVID-19 recommendations and introduce an alternative HVAC paradigm that maximizes the decoupling of ventilation and thermal control. We first consider a novel analysis of the energy costs of increasing the amount of conditioned fresh air using standard HVAC systems to address COVID-19 concerns. We then present an alternative that includes a novel membrane-assisted radiant system we have studied for cooling in humid climates, in place of an air conditioning system. The proposed system can work in conjunction with natural ventilation and thus decreases the risk of indoor spread of infectious diseases and significantly lowers energy consumption in buildings. Our results for modeling HVAC energy in different climates show that increasing outdoor air in standard systems can double cooling costs, while increasing natural ventilation with radiant systems can halve costs. More specifically, it is possible to add up to 100 days’ worth of natural ventilation while saving energy when coupling natural ventilation and radiant systems. This combination decreases energy costs by 10–45% in 60 major cities globally, while increasing fresh air intake.
Nomenclature
Specific energy of outdoor air (J/kg)
Specific energy for return air (J/kg)
Heat capacity of air (J/kg)
Wind speed coefficient
Buoyancy coefficient (ms−2 K−1)
Turbulence coefficient (m2 s−2)
Coefficient of performance (Jcooling/Jelec)
Electrical demand of the air conditioning system (J)
Energy savings (%)
Global energy savings (%)
Additional energy savings achieved by radiant-cooling assisted NV (%)
View factors between point p and all the surrounding surfaces
Heat of condensation (J/kg)
Annual number of natural ventilation-applicable hours as a fraction of 8760 h
Annual number of hours where it is too hot outside for natural ventilation; fraction out of 8760 h
Annual number of hours where either natural ventilation alone or radiant cooling-assisted natural ventilation can be thermally comfortable; fraction of 8760 h
Annual number of hours where it is too hot outside for either natural ventilation or radiant cooling-assisted natural ventilation; fraction out of 8760 h
Ratio of building latent cooling load to total cooling load
Mass of air (kg)
Mass of outdoor air (kg)
Mass of return air (kg)
Mean Radiant Temperature of of a cuboid surface (°C)
Available natural ventilation hours as percentage of all hours in the year
A prediction drawn from the quantile regression model of Chen et al.’s correlation between and
Total annual number of hours in which natural ventilation is permissible per the adaptive thermal comfort model
Outdoor air ratio - Mass of outside air / mass of total supplied air
Cooling demand (J)
Outdoor air specific humidity (kg/kg)
Return air specific humidity (kg/kg)
Supply specific humidity (kg/kg)
Specific humidity change (kg/kg)
Sensible heat ratio
Mean outdoor temperature (oC)
Width of the temperature band (oC).
Air temperature (oC)
Band of operative temperatures that an occupant can feel comfortable (oC)
- Tcmfrange,lwr,i
Lower threshold of the acceptable comfort range (oC)
- Tcmfrange,upr,i
Upper threshold of the acceptable comfort range (oC)
Dewpoint temperature (oC)
Temperature of surface i (K)
Mean outdoor temperature (oC)
Width of the temperature band (oC).
Temperature of return air (oC)
Temperature of supply air (oC)
- Top,i,RV
Operative temperature of a particular hour, i, in a year (oC)
Water supply temperature (oC)
Outdoor air temperature minus supplied air temperature (°C)
Maximum temperature difference between indoor and outdoor (oC).
Maximum indoor air velocity (m/s)
Outdoor air velocity (m/s)
1. Introduction
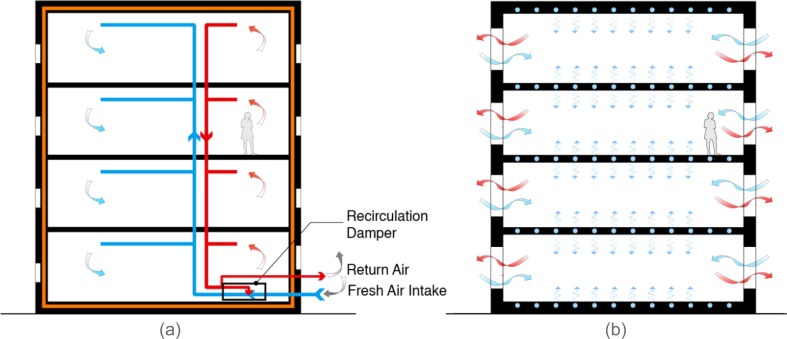
In the fallout of the COVID-19 (novel coronavirus disease 2019) pandemic, it has become clear that our reliance on conventional building Heating, Ventilation and Air Conditioning (HVAC) systems needs to be rethought. It has been established that enclosed areas with limited ventilation increase the risk of transmission [1]. Because of this, we must rethink the current HVAC paradigm in buildings. Currently, the primary mechanism used to save energy in centrally ventilated buildings is to mix return air with fresh air intake, but this puts fresh air and energy efficiency at odds. In the face of today’s health and environmental crises, if we aim to provide building environments that are both healthy and energy efficient, ventilation and air exchange must be decoupled from heating and cooling (Fig. 1 ). Air should be primarily used for breathing, not for heating and cooling.
Fig. 1.
(a) Current paradigm: airtight building with a centrally controlled air-based heating and cooling system with recirculation damper for energy savings; (b) Proposed paradigm: naturally ventilated building with radiant system for thermal comfort provision.
This study addresses the energy consequences of COVID-19 and building ventilation through two analyses: the first demonstrates a challenge, and the second demonstrates an opportunity. First, we analyze the energy consequences of increasing the fresh air delivered through typical commercial building recirculating ventilation systems caused by the significant air-conditioning costs in the latent and sensible cooling derived from a real system model. Second, we analyze the potential of alternative radiant and convective systems to provide thermal comfort, using models combined with global weather data. The output is the added natural ventilation potential and is correlated to previous work to estimate the energy savings. The first analysis relates directly to the challenge of COVID-19 ventilation energy costs for commercial buildings. The second analysis demonstrates how strict setpoints can be relaxed and shows an alternative pathway to energy savings for commercial buildings, as well as critical potential for residential buildings (that often have no mechanical ventilation) to increase natural ventilation while decreasing energy consumption.
The alternative systems considered in this analysis are convective fans, radiant systems and novel sub-dewpoint membrane radiant systems combined with natural ventilation to augment thermal comfort in lieu of air conditioning. To put this research in context, we will first provide a review of studies that have encouraged natural ventilation in buildings and recent developments in buildings’ radiant systems that allow for the use of natural ventilation while maintaining thermal comfort. Based on the review, we will discuss the applicability of radiant systems in a naturally ventilated space through an analysis of climates around the world. This research will inform the design of naturally ventilated environments that maintain consistent thermal comfort using advanced radiant systems. The COVID-19 crisis has exposed and amplified the flaws of the current HVAC design paradigm, while at the same time, has provided us an opportunity and the motivation to improve the health of our indoor environment.
2. Background
2.1. The energy/air-quality nexus in the context of COVID-19
The building sector’s share of the U.S. annual electricity consumption has grown dramatically in the past five decades from 25% of in the 1950s, to 40% in the early 1970s [2]. By 2012, its share increased to 76% with a significant fraction dedicated to heating and cooling systems. As a result of the oil crisis in 1973, energy conservation in buildings became an important priority. To conserve energy, buildings were designed to be tighter and less ventilated. Airtight spaces resulted in poor ventilation, and indoor environments ailed with “sick building syndrome” [3], [4], [5]. It has been clearly shown that inadequate outdoor air supply rates significantly impact indoor air quality and cause the “sick building syndrome” [6]. Consequently, ASHRAE and other entities recommended increasing the outdoor air ratio (OAR: the amount of fresh clean outdoor air mixed with the return air from rooms) in the design of HVAC systems [7]. Past reviews have demonstrated the many ways by which design for increased thermal comfort and ventilation rates has directly led to increased energy demand [8].
The COVID-19 pandemic has shown that current ventilation design standards for most commercial and residential buildings may be insufficient in providing the necessary ventilation rates to avoid indoor contagion [9]. Past studies have shown that recirculated air in buildings can be a source for indoor disease transmission [10]. In order to avoid indoor SARS-Cov-2 transmission, REHVA guidelines published in April 2020 [11] recommended an increase in air supply with a higher air exchange rate, and to avoid recirculated air if possible. ASHRAE has also recently published independent peer reviewed articles with guidelines that recommend systems “open minimum outdoor air dampers, as high as 100%, thus eliminating recirculation (in the mild weather season, this need not affect thermal comfort or humidity, but clearly becomes more difficult in extreme weather)” [12]. This recommendation recognizes the challenge of the large energy demand in extreme weather. More recently, the ASHRAE Journal published that “researchers concluded that there is now sufficient evidence of airborne transmission of COVID-19 to justify improving ventilation and filtration where this would reduce SARS-CoV-2 exposure, and ASHRAE has adopted that position” [13].
If we continue to conform to the current building HVAC paradigm, increasing ventilation rates would result in a huge energy expenditure to support the heating or cooling of incoming air to achieve comfort levels. This is especially true in humid climates, where often up to half of the cooling ventilation load is due to dehumidification, which can result in significant overcooling of supply air [14]. This begs the question: how can we provide healthy indoor environments without a significant increase in energy consumption?
One option is to simply open the windows. The use of natural ventilation in buildings has the potential for providing indoor air quality without expending energy on mechanical ventilation. Furthermore, certain studies have shown that the use of natural ventilation in buildings can provide the means for prevention of airborne transmission, especially in tropical climates [15], [16]. However, when an air-based mechanical system is used, the infiltration of unconditioned outdoor air can compromise the system’s efficiency. Moreover, when the outdoor air is outside of the comfort zone, most models assume that the windows would be closed. We investigate a scenario in which comfort is maintained by a radiant system independent of the air conditions. In this scenario, the windows can be kept open for longer periods of time to maximize outdoor air to meet the recommended COVID-19 ventilation guidelines. Thanks to the use of surface-based radiant systems in lieu of air-based heating and cooling, we can increase the range of allowable outdoor air temperatures for open windows and thus provide fresh air through additional natural ventilation hours.
2.2. Natural ventilation
Natural ventilation is as old as the human dwelling, but our buildings have evolved into complex thermal machines. Currently, we have many technical solutions that offer far more control over fresh air and thermal comfort than a simple facade opening, but what natural ventilation lacks in control, it makes up for in simplicity and efficiency. Previous studies have shown the significant energy saving potential of natural ventilation, especially in hot climates [17], [18], [19]. The limits to natural ventilation’s delivery of thermal comfort are primarily dependent on the conditions of outdoor air. These limits are often narrowly defined as 20–26 °C air temperature [20].
Natural ventilation has been superseded by HVAC systems because they can deliver controlled and predictable amounts of air at specific setpoints for temperature and humidity. But this control has resulted in significant increases in energy demand. Because of this, new strategies to design with natural ventilation and mixed-mode systems have gained importance.[21], [22]. Still, recent work continues to focus on mitigating losses from infiltration and lack of air-tightness of facades [23], which leads to complex ventilation systems and discounts the potential of natural ventilation.
Early thermal comfort models had fixed comfort zones that explicitly excluded many outdoor conditions. The Adaptive Comfort model allows for the zone to adapt to outdoor conditions, allowing warmer indoor temperatures in a naturally ventilated space during the summer and cooler temperatures in the winter, expanding the potential of natural ventilation [24], [25]. We propose to further consider other mechanisms to expand the potential of natural ventilation through adaptive thermal comfort. Radiant heat transfer and higher air velocity can significantly alter the net heat exchange of occupants independently of air temperature and humidity. These impact the adaptive thermal comfort calculations. We have demonstrated tools in previous work that can illustrate those potentials [26].
In order to increase the yearly hours during which natural ventilation can be utilized, we propose a strategy that uses fans and radiant systems for added thermal control while maintaining natural ventilation through porous enclosures. Previous work has demonstrated how natural ventilation hours can be determined by using comfort models combined with weather data available for different regions. These studies have gone from using standard comfort ranges [20] to using adaptive thermal comfort models in four US cities, recognizing variations in climate and occupant expectations [27]. Another study has been carried out globally [28] using a large weather file dataset, but using comfort limits of a 17 °C dewpoint for cooling and assuming internal heating gains of buildings to compensate for temperatures as low as 12.8 °C. This proposal builds on this recent global analysis by adding the potential of radiant systems as a comfort mitigation strategy for an even wider range of conditions.
It is important to note that local outdoor air quality is another major challenge to natural ventilation [29]. Outdoor pollution in many places makes natural ventilation not just challenging, but unhealthy, and has been shown to affect energy savings potential [44]. Yet, we also see the potential for centralized government policies and actions to mitigate causes of poor outdoor air quality at rates faster than similar efforts to reduce carbon emissions and energy consumption [30], [31]. The circumstances of the pandemic itself have had a significant impact on reducing air pollution in certain locations [32], so this variable is subject to relatively rapid change. However, it is also possible to use state-of-the-art technologies for window-based solutions for filtering particulate matter from the air, [33], [34] thus still allowing for large quantities of air to enter the indoor space. The air velocity loss due to the filter can be overcome by using low-energy fans in the interior as we describe in the Methods section. When assessing the suitability of a location for natural ventilation, we limited our assessment to climatic variables, as we believe it is viable to consider the theoretical potential of natural ventilation. The premise of this paper is to support discussions on the co-benefits of improving outdoor air quality while simultaneously reducing global carbon emissions.
2.3. Radiant systems
Radiant heating and cooling systems rely on the infrared radiation exchange between occupants and surrounding surfaces. This is a low-energy alternative to energy-intensive air-based systems for thermal comfort delivery [35]. Under room conditions with similar air and surface temperatures, the heat transfer exchanged by radiation to surfaces and convection to air is roughly equivalent [36]. That is, half of one’s thermal perception is driven by surface temperatures. Therefore, by manipulating surface temperatures to be colder or hotter, comfort can be maintained at a greater range of air temperatures. It is by this mechanism that the potential for increased natural ventilation hours can be achieved. In addition, for commercial buildings using radiant systems, the setpoints for air supply systems can be shifted to enable higher fractions of outdoor air and to allow 100% outdoor air (equivalent to enabled natural ventilation) for a larger number of hours during the year.
There are two main challenges to radiant systems that successfully enable more natural ventilation and reduce energy use as a consequence of increased outdoor air. First, for natural ventilation in hot humid climates, the dew point temperature is often higher than the necessary surface temperatures for radiant cooling, which means condensation would create water problems indoors. Second, when using radiant systems, large surface areas are generally needed for adequate view factors to occupants. Therefore, the convective exchange with indoor air is significant, so even if setbacks to warmer air temperatures in the summer or cooler in the winter are desirable, the air temperatures will tend to follow the radiant panel temperature [37], [38]. For natural ventilation cases, this also implies a larger fraction of losses as the high amount of air exchange would cost more convective losses.
Still, radiant systems offer an alternative path to maintaining comfort through a wider range of air temperature conditions, and thus environmental conditions, for natural ventilation. We will consider the potential of a typical radiant system to increase natural ventilation hours and review the limitations of operation in excessively humid conditions. We will also leverage our recent development of membrane-assisted radiant panels that mitigate condensation and convective loss risk to further expand potential natural ventilation hours.
2.4. Membrane assisted radiant cooling: Cold Tube
We have developed a radiant panel with a membrane transparent to infrared emissions. This protects it from condensation and minimizes the convective exchange with the surroundings [39]. We built a pavilion in Singapore that demonstrated its operation under hot and humid conditions without condensation. Our thermal comfort study on the pavilion validated that people could be made to feel “cool” with panels operating below the dew point without condensation [40].
The infrared-transparent membrane allows water to be supplied below the ambient dewpoint without condensation, increasing the potential for radiant cooling to augment cooling in naturally ventilated spaces. The membrane convectively gains heat from the ambient air to remain warmer than the dewpoint, a relationship characterized in the Teitelbaum et al. study [28]. The allowable water supply temperature (Twater in Eq. (1)) depends on the ambient air and dewpoint temperatures and is given in Eq. (1). By inspection, as the air temperature increases, cooler water can be supplied to the panel, an elegant feature that allows more cooling to be supplied when more cooling is demanded.
| (1) |
The system operated successfully without condensation in Singapore with supply temperatures between 13 and 17 °C, despite an outdoor dewpoint of 23 °C. The study described in Teitelbaum et al. [40] was limited to outdoor thermal comfort. However, this study demonstrates that the operation and control parameters from that study can be directly implemented in an indoor environment. This paper will refer to the combination of membrane-assisted radiant cooling panels with natural ventilation as ‘radiant cooling-assisted natural ventilation’.
2.5. Scope of paper
The scope of this study includes the following:
-
●
Analysis of the energy cost of increasing outdoor air intake to maximum with a conventional HVAC system
-
●
Analysis of an alternative HVAC solution which couples a membrane-assisted novel radiant system we developed with natural ventilation for ensuring increased fresh air intake while maintaining thermal comfort indoors without an energy uptick
-
●
Regression applied to the results of global natural ventilation potential study by Chen et al. [28] in order to generate a predictive relationship model between natural ventilation hours and energy savings
-
●
Estimates of the energy savings that can be achieved in 60 major cities globally through the use of radiant cooling-assisted natural ventilation
-
●
Comparison of the cooling energy consumption of three cooling scenarios in 4 major US cities situated in different climatic zones
-
●
Analysis of the potential additional hours per climate zone globally that would be comfortable with radiant cooling-assisted natural ventilation using the adaptive comfort model
3. Methods
3.1. Energy costs of increased outdoor air supply in typical commercial building cooling
We have developed a method that calculates and illustrates how much additional energy would be consumed by conventional air conditioning systems to meet increased fresh (outdoor) air recommendations for COVID-19. Conventional HVAC systems are reconfigured to introduce additional outdoor air, thereby increasing the system’s outdoor air ratio (OAR). OAR is the ratio of outdoor air supplied into a recirculating central air conditioning system as it relates to the total air supplied to the building. A window air conditioner has 0% outdoor air and a dedicated outdoor air system (DOAS) has 100% outdoor air. However, the majority of commercial buildings have ventilation systems with air handlers that use dampers to adjust the amount of outdoor air brought into the supply stream to be conditioned by heating or cooling coils. The OAR is thus adjusted for the needed ventilation. This is the control variable that facilities operators are being asked to increase due to COVID-19.
We analyzed the increase in cooling energy as it has both sensible and latent components with varying influence on system performance and energy demand. For the heating case, the load is generally proportional to the increased OAR because it is dependent only on the sensible heat based on the dry bulb temperature differences. The cooling sensible and latent energy depend on both the outdoor temperature and humidity relative to the supply conditions, as well as the return air conditions that are influenced by internal gains of both heat and humidity. The relative amount of sensible cooling to the total cooling (sensible + latent) is called the sensible heat ratio (SHR), and it is determined by a combination of the aforementioned temperatures and humidities along with the OAR. The cooling loads and SHR are critical factors in estimating the energy consumption for a typical chiller used to cool a building. We aimed to demonstrate how OAR influences cooling loads and SHR and the subsequent performance across a series of typical cities.
To calculate cooling loads, we first needed to determine the annual cooling demand generated by a reference building envelope. We selected the standard small office building provided by the Department of Energy for use in EnergyPlus simulations [41]. The building is 511 m2 (5,500 ft2), and a single climate case for this building was selected. The building was simulated in EnergyPlus to generate a generic envelope load with an indoor thermostat setpoint of 24 °C (75°F) during occupied hours (6am-7 pm) with 10% OAR and no internal gains. This output is a baseline hourly envelope heat gain and cooling demand.
The hourly envelope loads were inputted into the system model that was built in Engineering Equation Solver (EES). In this model, additional parameters were tuned, which allowed for more flexible analysis and sizing of the unit for latent and sensible loads. The overall governing energy balance is shown in Eq. (2), relating the energy change in the air to the change in sensible temperature (cooling) and the change in specific humidity (dehumidification). A 12.5-ton Lennox air conditioner was modeled using the compressor performance curves from the manufacturer. These performance curves relate system COP (coefficient of performance = cooling/electricity) to the hourly SHR, airflow rate, setpoints, and load. The load was a combination of the envelope gains, internal gains calculated in EES using daily occupancy for 80 individuals, and the air condition gains based on the EES model of outdoor air, return air influenced by envelope and internal gains, and supply setpoint that was aimed at 50% OAR and 24 °C (75°F). The supply setpoint and gains determined return air conditions, from which the impact of OAR was determined and was fed back to the SHR for system performance. This feedback was why EES interactive solving was ideal for the problem. From this we were able to determine the hourly energy consumption of the chiller and thus the cumulative cooling demand for the season as seen in Eq. (3),
| (2) |
| (3) |
where Qair is the cooling demand (J), m is mass (kg), cp is heat capacity of air (J/kg/K), Δhcond is the heat of condensation (kg/J), Δq is the specific humidity change due to dehumidification(kg/kg), the COP is the coefficient of performance (Jcooling/Jelec), is the temperature difference between the outdoor air and the supplied air, and Echiller is the electrical demand of the air conditioning system.
This simulation was carried out using weather data files for Miami, Phoenix, Duluth, Chicago, Washington D.C., and San Francisco with a baseline OAR of 10% for each city, and then increasing the OAR to 25%, 50%, 75% and 100% for each city. When the OAR was increased, there was an additional step to check if the 12.5-ton unit was sufficiently-sized to meet the peak demand as increasing OAR increased peak demand. This was done based on the EnergyPlus envelope peak load along with the design day conditions for 0.4% max sensible and coincident dew point temperatures, meaning that 99.6% of the time it would be able to achieve the setpoint. The performance curves of the reference 12.5-ton system were scaled proportionally to meet the demand. We also noted where the 12.5-ton system failed as OAR is increased.
We also developed a simple analytical solution for the linear relationship between raw air conditioning cooling energy and OAR based on outdoor air (OA) conditions, return air (RA) conditions, and supply air (SA) setpoints, expanding Eq. (2) for outdoor and return air energy fractions.
| (4) |
Rearrange and substitute for :
| (5) |
Recognize the components of outdoor air and indoor air:
| (6) |
| (7) |
Where A is the specific energy (J/kg) of outdoor air and B is the specific energy of return air, giving the following linear relationship between OAR and air cooling energy:
| (8) |
Therefore, the energy to condition the supply air per unit supply air linearly increases with OAR at a rate determined by the difference between the specific energy of outdoor air and return air and has an intercept at zero OAR defined by the specific energy of the return air when no outside air is supplied. As this is normalized by the total air supply, it is clear that both the air supply amount and the amount of fresh air directly increase the energy needed to condition that air for indoor use. We can also observe how the slope of the linear relationship describes the rate of energy increase per increase in %OAR:
| (9) |
Finally, based on the definition of SHR we can again use substitution for OAR for the mass of outdoor air, return air, and supply air to develop the relationship:
| (10) |
3.2. Energy savings of increased natural ventilation in typical commercial buildings cooling
We built a surrogate regression model of the energy savings calculated by Chen et al. [28]. They provided estimates of the percent global energy savings, , of widespread adoption of natural ventilation in the form of mixed-mode natural ventilation (MMNV) systems. Their savings compared the annual energy use of a mixed-mode system versus a 100% mechanically-ventilated central air-conditioning (central AC) system. Energy use estimates were generated using a standard Department of Energy commercial building model, using the EnergyPlus simulation software, of an archetypal three-story office building. They simulated the performance of this archetypal building across 60 different cities around the globe.
Chen et al. also developed a methodology for estimating the number of occupied hours for which natural ventilation is permissible (NV%) which could be calculated from the outputs of the energy simulation process. In their study, they defined the comfort zone for acceptable natural ventilation as having:
-
A.
A fixed lower temperature threshold of 12.8 °C and the 80% acceptability upper temperature threshold of the adaptive comfort model (Eq. (11)).
-
B.
Dew point temperature below 17 °C.
The adaptive comfort model is described in Eq. (11).
| (11) |
where Tcmfrange is the band of operative temperatures at which an occupant can feel comfortable (oC), Ta,out is the mean outdoor temperature (oC), and Taccept is the width of the temperature band (oC). Taccept is 2.5 °C and 3.5 °C for 90% and 80% thermal acceptability respectively. The upper threshold can be further widened through elevated air movement. An elevated air velocity of 0.6–0.9 m/s, 0.9–1.2 m/s and above 1.2 m/s will increase the upper threshold by 1.2 °C, 1.8 °C and 2.2 °C respectively.
We generated a surrogate regression model, , of Chen et al.’s analysis to forecast the energy savings of radiant cooling-assisted natural ventilation, specifically establishing a relationship between ES% and applicable natural ventilation hours:
| (12) |
| (13) |
Where: = Annual number of natural ventilation-applicable hours as a fraction of 8760 h.
= Annual number of hours where it is too hot outside for natural ventilation as a fraction of 8760 h.
Figure 2 provides a plot of vs as per Chen et al, along with the established regression model. Though the model is probabilistic, with illustrated confidence bounds on the prediction, for the purposes of this study, we will only use a deterministic model of the median, which can estimate within a standard error of 10% of its unit value. This deterministic model is represented by a quadratic equation (14) (see Fig. 2 plot).
| (14) |
Fig. 2.
Comparison of predictions drawn from median regression model and original forecasts of ES (%) from Chen et al.’s study; 95% prediction interval shown in red band.
3.2.1. Energy savings from extending natural ventilation using a novel radiant cooling panel system
We model the potential extension of natural ventilation using membrane-assisted radiant cooling panels [40] along with increased air movement [54]. For the case of predicting energy savings of radiant cooling-assisted natural ventilation, we apply the following method:
| (15) |
| (16) |
Where:
= Annual number of hours where either natural ventilation alone or radiant cooling-assisted natural ventilation can be thermally comfortable as a fraction of 8760 h.
= Annual number of hours where it is too hot outside for either natural ventilation or radiant cooling-assisted natural ventilation as a fraction of 8760 h.
= Ratio of building latent cooling load to total cooling load.
Whereas values for and can be found in Chen et al., here we must provide a different approach to estimating and .
The adaptive comfort model is only applicable to conditions having Ta,out (running average outdoor air temperature) between 10 °C and 33.5 °C and an internal operative temperature between 17 °C and 32 °C. When relying on a radiant system for comfort as proposed in this paper, the acceptable air temperature range expands to as high as 40 °C. The adaptive comfort model is not shifted, only the approach for creating acceptable operative temperatures through radiant-only systems [26], [40].
For the radiant cooling natural ventilation hours, the Mean Radiant Temperature (MRT) is determined for each climate scenario by considering potential surface temperatures achieved by the novel membrane-assisted radiant system [40]. Fig. 3a illustrates the scene we use to calculate MRT. For this analysis of cooling demand, we use typical ceiling cooling at an effective panel temperature of 18 °C (Fig. 3b), whereas for heating we could use typical ceiling panels up to 35 °C and a floor slab heating of 25 °C (Fig. 3c). The membrane-assisted radiant scenario allows operation even when the dew point is above 18 °C (Fig. 3b). The effective panel temperature is determined using Eq. (1).
Fig. 3.
(a) Scene for MRT calculation (b) ceiling panels are assumed for the cooling scenario (c) ceiling panels and slab heating are assumed for heating scenario.
The MRT experienced by the occupant is determined by the view factor of the occupant to the panels and the surrounding surfaces. MRT (oC) is calculated using equation the following:
| (17) |
where are the surface view factors between a point in the room and all the surrounding surfaces, used to weigh the surface temperatures (K) at each surface. The MRT is scaled for a standing person [43].
The MRT is then used with the air temperature and air velocity to determine operative temperature and the comfort of an occupant in the adaptive comfort model. The radiant cooling NV hours, hRCNV, and the too hot hours, h2H,RCNV, are calculated using the adaptive comfort ranges described in the equations below:
| (18) |
| (19) |
| (20) |
where Tcmfrange,lwr,i and Tcmfrange,upr,i are lower and upper thresholds of the acceptable comfort range of the adaptive comfort model as calculated in Eq. (11) for a particular hour, i, in a year. Top,i,RV is the operative temperature of a particular hour, i, in a year. The Top,i,RV is calculated based on Eq. (20) with MRT calculated using Eq. (17). v is the indoor air velocity (m/s).
Once we have calculated the additional hours of natural ventilation, we can apply the quartile regression model, , to estimate the additional energy savings. But we must also incorporate the energy cost of running the membrane-assisted radiant panels, which we have shown operate only with sensible cooling and no latent cooling demand [40]. In order to estimate the energy savings, , we considered several precedents to estimate the energy required to operate the panel system. In a study by Niu et al. [50], conducted in a hot and humid climate, the comparison between an all-air system and a radiant ceiling system yielded a major reduction in the cooling load in the radiant system case, thereby halving overall energy demand when dehumidification is excluded. We reviewed climate data and found that the SHR (sensible heat ratio) varies from 50% to 90%. While the local climate is not the only factor that affects latent cooling ratios, latent cooling demand is found to be in the order of 20% to 50% of total building end-use cooling loads [51], [52], [53]. We adopt an estimate of 35%, i.e. the energy savings of using the radiant panel with natural ventilation in comparison with a central A/C system, equals 35% of the savings of using natural ventilation alone. It is important to note that while the elimination of latent load can lead up to 50% savings based on precedents, there are significant additional savings on the efficiency of the sensible delivery. By eliminating the Chen et al [28] dew point limit, the new comfort hours also occur most prevalently in high latent cooling hours. Therefore a conservative 35% reduction provides a reasonable lower bound to the savings.
3.3. Evaluating the sensitivity of methods used for estimating natural ventilation hours and mapping potential global natural ventilation hours with alternative baseline
While re-evaluating the natural ventilation hours for radiant panels, we adjusted the boundary conditions used for Chen et al. [28], thus eliminating the dew point limit, which is based on typical building system limits, not actual thermal comfort. We also recognized that much of the natural ventilation hours analysis in their study was influenced by building properties such as internal gains and thermal mass that generate the assumption that 12.8 °C air temperature is warm enough for natural ventilation (which is below the adaptive comfort range). Likewise, it is building air conditioning system properties that generate the assumption that there can’t be natural ventilation above a 17 °C dew point.
For a global analysis of NV hours, it is difficult to systematically aggregate diverse building properties. Therefore, we re-analyzed the global natural ventilation hours using the adaptive comfort model assuming no building influence by simply letting indoor conditions follow outdoor conditions without any assumed building influence. This would only be valid for an infinitely low-mass building, or one that is indicative of current common outdoor heating and cooling strategies. Our analysis used the typical meteorological year data of 2590 locations obtained from the EnergyPlus website, which are derived from 20 weather data sources [42]. The analysis is used to determine the number of potential naturally ventilated hours for these scenarios:
-
1.
Base case scenario with no installation of mechanical systems. The indoor air velocity due to natural ventilation is calculated based on Eq. (21).
| (21) |
where uin,max is the maximum indoor air velocity, C1 is the wind speed coefficient, uout is the outdoor air velocity, C2 is the buoyancy coefficient (ms-2K−1), h is the vertical height of the opening (m), △Tmax is the maximum temperature difference between indoor and outdoor, and C3 is the turbulence coefficient (m2s−2). The values of C1, C2, and C3 are 0.001, 0.0035 ms-2K−1 and 0.01 m2s−2 respectively [28]. The 90% acceptability temperature range of 5 °C is used for △Tmax. The vertical variation of air velocity due to height is not considered, so h is assumed to be 1.5 m.
-
2.
Fan-assisted scenario where the air velocity is increased to 0.8 m/s to provide extra cooling.
-
3.
Radiant scenario where the Mean Radiant Temperature (MRT) is lowered or elevated for cooling/heating, as explained in Section 3.2.1 Eq. (17) and Fig. 3.
-
4.
Membrane-assisted radiant scenario uses the membrane-assisted radiant panels for cooling. This scenario is similar to the third scenario with the exception that radiant cooling is allowed even when the dew point is above 18 °C (Fig. 3b). The effective panel temperature is determined using Eq. (1). The effective panel temperature is 3 °C higher than Twater.
4. Results
4.1. Building increased outdoor air supply energy costs
Our analysis demonstrated that there is an increase in cooling energy demand with increasing OAR (Fig. 4 ). The baseline OAR for a central air system is 10%, which is the minimum allowable OAR intake per ASHRAE standards (10 L/s/person outdoor air for 20 people) for the office building with a 2,000 L/s AHU modeled. At 25% OAR, the energy demand increases range from 6% to 26%, and at 80–100% OAR they diverge further, ranging from 29% to greater than 215%. The largest increase occurs in Miami in both percentage and absolute values. Washington, DC has the next largest absolute increase in cooling energy. The percentage increase allows us to compare the OAR-energy relationship across all cities, dictated by their climate. As expected, San Francisco, with its moderate climate and low cooling demand, experienced the least cooling energy increase even with 100% outdoor air. The Miami and Washington DC simulations were capped at less than a 100% OAR since high outdoor air humidity made further increases require impractical physical changes to the HVAC control algorithms.
Fig. 4.
(a) The percent increase in annual cooling energy for 6 cities for increasing OAR from 10% to 100%; (b) the absolute cooling energy increase.
We considered the analytical OAR and SHR relationships to interpret the potential influences on the form of the modeling results shown in Fig. 4. Fig. 5 shows a linear relationship between percentage energy increase and OAR and explains how SHR relates to OAR for fixed supply conditions with two different outdoor air and return air conditions that are representative of a warm humid-climate and of a hot-dry climate. We have observed that the rate of energy increase per percentage increase in OAR (the slope in Eq. (9)) is 25% when going to a more humid condition. This appears to be the case for the drier San Francisco having a lower slope than the other cities, as shown in Fig. 4. Despite being in the desert, Phoenix actually has some relatively high latent loads to contend with and both high sensible and high latent loads contribute to increasing the slope.
Fig. 5.
Plot of the algebraic relationship between OAR and cooling energy quantity in the air (left) and with the SHR (right). These plots are independent of system performance and represent only the relationship of thermal energy in the air based on constant air specific heat and the heat of condensation for latent phase change.
The OAR-SHR relationship, analytically plotted in Fig. 5, shows how a higher OAR ratio significantly decreases SHR in a warm, humid climate, while drier conditions are not as sensitive to OAR. It also shows how completely dry conditions, where dehumidification is not necessary, will be solely dependent on managing internal humidity gains, and thus SHR will increase with higher OAR. This is important to note as the EES model of the compressor in the reference air conditioner is dependent on SHR at each dry bulb and wet bulb air condition. Therefore, the cooling energy increase for Miami at the high OAR shown in Fig. 4 is likely due to the less efficient system performance at lower SHR.
For Miami, we plotted the range of air conditioning electricity output from the hourly model. Our analysis examined each month across the year for 25%, 50%, and 75% OAR (Fig. 6 ). It is clear how the values diverge in the summer months during peak cooling. The significant increase in demand is also clearly depicted.
Fig. 6.
The monthly breakdown of hourly compressor power for 3 OAR simulation conditions in Miami.
Even with a larger chiller, the inescapable coupling of dehumidification with air conditioning equipment will greatly overcool the air supplied to a room, as it will bring in fresh air but create uncomfortable conditions. This is particularly true when the SHR is low because high capacity dehumidification is needed to cause excess sensible cooling. This is is epecially pertinentin high-humidity climates during lower sensible temperature times when high OARs are deployed. Fig. 7 shows that at a thermostat setpoint of 24 °C (75°F) air and with 50% OAR, there are hundreds of summer hours in the reference office building in Miami that have air that is well below this setpoint due to the need to adequately dehumidify the air, which results in overcooling.
Fig. 7.
A histogram plot showing the resulting room air temperature from the annual model of Miami with a 24 °C thermostat setpoint at 50% OAR caused by excess sensible cooling delivered with low SHR.
4.2. Extended natural ventilation hours
Our analysis estimated the potential impact of using the membrane-assisted radiant panels that enable increased natural ventilation for a building. Table 1 shows results of the 60 locations examined in this study, the same cities as studied by Chen et al. [28]. The description of each column is as follows:
-
●
City: Name of the location.
-
●
Natural ventilation comfort hours: Number of hours comfortable without the operation of any mechanical systems, calculated as per Chen et al. [28], and defined as hMMNV in Section 3.2.1
-
●
Number of hours too hot for NV: Annual number of hours deemed by Chen et al. [28] to be too hot for natural ventilation; defined as h2H in Section 3.2.1
-
●
Number of hours too cold for NV: Annual number of hours deemed by Chen et al. [28] to be too cold for natural ventilation
-
●
Number of additional hours that can be satisfied with RCNV: Annual number of hours, in excess of hMMNV, under which radiant cooling-assisted natural ventilation can be comfortable; defined as hRCNV in Section 3.2.1
-
●
Cooling Season Natural Ventilation %: Percentage of cooling season hours in a year where natural ventilation is permissible; defined as NV in Section 3.2.1
-
●
Cooling Season RC Natural Ventilation%: Percentage of cooling season hours in a year where radiant cooling-assisted natural ventilation is permissible; defined as NVRCNV in Section 3.2.1
Table 1.
Analysis results of 60 cities globally.
| City | Natural ventilation comfort hours | Number of hours too hot for NV | Number of hours too cold for NV | Number of additional hours that can be satisfied with RCNV | Cooling season Natural Ventilation% | Cooling season RC Natural Ventilation % |
|---|---|---|---|---|---|---|
| Singapore | 0 | 8760 | 0 | 7865 | 0 | 89.8 |
| Kuala Lumpur | 0 | 8760 | 0 | 7317 | 0 | 83.5 |
| Manila | 7 | 8753 | 0 | 7398 | 0.1 | 84.5 |
| Rio De Janeiro | 1518 | 7241 | 1 | 7013 | 17.3 | 97.4 |
| Miami | 1906 | 6675 | 179 | 6221 | 22.2 | 94.7 |
| Mumbai | 606 | 8154 | 0 | 6172 | 6.9 | 77.4 |
| Bangkok | 120 | 8640 | 0 | 6823 | 1.4 | 79.3 |
| Chennai | 1373 | 7387 | 0 | 6108 | 15.7 | 85.4 |
| Hyderabad | 2840 | 5671 | 249 | 5414 | 33.4 | 97.0 |
| Dhaka | 2240 | 6428 | 92 | 5260 | 25.8 | 86.5 |
| Hong Kong | 1785 | 6928 | 47 | 5494 | 20.5 | 83.5 |
| Kolkata | 2471 | 6283 | 6 | 5031 | 28.2 | 85.7 |
| Karachi | 2701 | 5799 | 260 | 4344 | 31.8 | 82.9 |
| Bangalore | 2434 | 5358 | 968 | 4612 | 31.2 | 90.4 |
| Guangzhou | 3100 | 5660 | 0 | 5159 | 35.4 | 94.3 |
| Houston | 2927 | 4595 | 1238 | 3934 | 38.9 | 91.2 |
| Delhi | 3331 | 4572 | 857 | 3092 | 42.1 | 81.3 |
| Cairo | 4886 | 3187 | 687 | 2233 | 60.5 | 88.2 |
| Sao Paulo | 2302 | 3325 | 3133 | 3072 | 40.9 | 95.5 |
| Shanghai | 8435 | 179 | 146 | 168 | 97.9 | 99.9 |
| Nairobi | 2193 | 3428 | 3139 | 2976 | 39 | 92.0 |
| Lima | 5164 | 3215 | 381 | 3014 | 61.6 | 97.6 |
| Dallas | 2938 | 3174 | 2648 | 2236 | 48.1 | 84.7 |
| Hangzhou | 2122 | 3433 | 3205 | 2815 | 38.2 | 88.9 |
| Tehran | 2969 | 2381 | 3410 | 2070 | 55.5 | 94.2 |
| Wuhan | 7161 | 104 | 1495 | 102 | 98.6 | 100.0 |
| Osaka | 2246 | 3015 | 3499 | 2521 | 42.7 | 90.6 |
| Atlanta | 3031 | 2241 | 3488 | 1955 | 57.5 | 94.6 |
| Mexico City | 2660 | 3153 | 2947 | 2918 | 45.8 | 96.0 |
| Nanjing | 5974 | 2784 | 2 | 2783 | 68.2 | 100.0 |
| Chengdu | 4253 | 1240 | 3267 | 713 | 77.4 | 90.4 |
| Nagoya | 2674 | 2798 | 3288 | 2330 | 48.9 | 92.1 |
| Riyadh | 2643 | 2076 | 4041 | 1781 | 56 | 93.7 |
| Tianjin | 3803 | 1776 | 3181 | 1771 | 68.2 | 99.9 |
| Buenos Aires | 2553 | 2404 | 3803 | 1926 | 51.5 | 90.4 |
| Zhengzhou | 2423 | 1967 | 4370 | 1924 | 55.2 | 99.0 |
| Johannes-burg | 6105 | 219 | 2436 | 201 | 96.5 | 99.7 |
| Barcelona | 3577 | 1436 | 3747 | 1409 | 71.4 | 99.5 |
| Istanbul | 2651 | 1907 | 4202 | 1569 | 58.2 | 92.6 |
| Beijing | 4916 | 3110 | 734 | 2610 | 61.3 | 93.8 |
| Xian | 4514 | 1690 | 2556 | 1422 | 72.8 | 95.7 |
| Seoul | 2735 | 2145 | 3880 | 1729 | 56 | 91.5 |
| Washing-ton | 2966 | 1573 | 4221 | 1378 | 65.3 | 95.5 |
| New York | 2601 | 2169 | 3990 | 1593 | 54.5 | 93.2 |
| Philadel-phia | 2883 | 1775 | 4102 | 1518 | 61.9 | 94.5 |
| Chicago | 2808 | 1368 | 4584 | 1088 | 67.2 | 94.0 |
| Santiago | 2182 | 1682 | 4896 | 1535 | 56.5 | 96.2 |
| Los Angeles | 2633 | 2131 | 3996 | 1972 | 55.3 | 96.7 |
| Tokyo | 3221 | 934 | 4605 | 880 | 77.5 | 98.7 |
| Shenyang | 4297 | 565 | 3898 | 356 | 88.4 | 95.7 |
| Milan | 4074 | 703 | 3983 | 336 | 85.3 | 92.3 |
| Madrid | 2745 | 1136 | 4879 | 1002 | 70.7 | 96.5 |
| Boston | 7197 | 526 | 1037 | 522 | 93.2 | 99.9 |
| Toronto | 2489 | 702 | 5569 | 624 | 78 | 97.6 |
| Paris | 3451 | 161 | 5148 | 134 | 95.5 | 99.3 |
| Dusseldorf | 3294 | 136 | 5330 | 112 | 96 | 99.3 |
| San Francisco | 2378 | 193 | 6189 | 173 | 92.5 | 99.2 |
| Moscow | 5337 | 57 | 3366 | 34 | 98.9 | 99.6 |
| London | 2885 | 57 | 5818 | 50 | 98.1 | 99.8 |
| St Petersburg | 2164 | 82 | 6514 | 80 | 96.3 | 99.9 |
4.3. Estimate of energy savings by increasing natural ventilation hours
In Section 3.2.1, a method for utilizing a surrogate model derived from Chen et al. [28] was described. The method makes it possible to estimate the energy savings attributed to expanding applicable natural ventilation hours in a radiant-assisted natural ventilation regime. The results of this analysis, as applied to the 60 cities listed in Table 1, is shown in Fig. 8 .
Fig. 8.
Forecasted energy savings and achieved natural ventilation hours: mixed-mode NV versus radiant cooling-assisted NV; Energy savings are compared to use of a 100% mechanically-ventilated central AC system supplying 10 L/s/person of fresh air.
With membrane-assisted cooling, the 60 cities achieved a range of 80–100% of comfortable hours with natural ventilation. In some climate contexts, particularly the hot and humid tropics, this is a significant increase in applicable NV hours compared to natural ventilation only as per Chen et al. [28]. This increase in applicable natural ventilation hours does also provide additional energy savings, though these savings are modest. In Fig. 8, the assumed baseline, or backup, central AC system is a mixed fresh air / recirculated air system with an outdoor air ratio (OAR) of 10%, supplying 10 L/s/person of fresh air. With such a system in tropical cities like Miami, the additional energy savings offered by radiant cooling-assisted natural ventilation is on the order of 10–12% above natural ventilation only. In temperate cities, the additional energy savings are less than 5%, for we recall that radiant cooling-assisted natural ventilation reduces mainly latent cooling requirements and associated fan power costs, with smaller impact on the sensible cooling energy demand of a building. In cities of temperate or mediterranean climate, cooling needs are comparatively low, and therefore the additional energy savings of natural ventilation-assisted radiant cooling remain low as well in these cities.
The relationship between natural ventilation hours and energy savings becomes more pronounced when we consider a baseline scenario of a mechanical, central AC system that aims to provide a higher rate of fresh air supply. In Fig. 9 , we compare the four cities highlighted in Fig. 8, but against different regimes of OAR. If, for example, one compares radiant cooling-assisted natural ventilation to a baseline building that seeks to provide occupants with a 50% OAR, the estimated annual energy savings increases to between 25 and 45%, highlighting the need to address increasing outdoor air flow rates when energy use is constrained.
Fig. 9.
Ratio of change in cooling energy expended for different cooling scenarios:(left) All cooling and ventilation is provided through a central-air mechanical system; (middle) Mixed mode ventilation in which natural ventilation is allowed when outdoor air falls within the comfort zone and a mechanical system sets off otherwise; (right) A radiant system provides heating and cooling with natural ventilation providing fresh air at all times in which this combination falls within the adaptive comfort boundaries and a A/C used as backup otherwise. For all cases, the projected increase for 50% OAR is included.
4.4. Mapping potential global natural ventilation hours with alternative baseline
In 3.2, 3.3, we highlighted a difference in how Chen et al. [28] established criteria for estimating applicable natural ventilation hours, versus ours. Here, we examine the relative changes in forecasting baseline applicable natural ventilation hours when we apply the latter method.
Four maps were generated for visualizing the extended natural ventilation hours analysis (Fig. 10 ). The global map was divided into about 300 km × 300 km grids. Each grid shows the average results of the locations. The map in Fig. 10a shows the base case, i.e. the number of hours in a year that a location can achieve comfort according to the adaptive comfort model without running any mechanical system and with the windows open. We can see that due to the consistent temperatures of the tropical region, there is high potential for the region to achieve comfort without any use of a mechanical system.
Fig. 10.
(a) Baseline available natural ventilation hours based on the adaptive comfort model (b) additional number of hours during which windows could remain opened and achieve comfort with elevated air velocity of 0.8 m/s (c) elevated air velocity and radiant panels (d) elevated air velocity and membrane-assisted radiant panels.
Fig. 10b shows the improvement in the number of comfort hours by 480–960 h (5–11%) if we elevate the air velocity to 0.8 m/s using mechanical fans. This strategy is only effective for the tropical region. By coupling elevated air velocity with radiant panels, we can further increase NV hours by additional 480–960 h (5–11%) and maintain comfort (Fig. 10c). The condensation risk of radiant panels limits the increase in comfort hours for regions with high humidity. When the condensation risk is mitigated by the membrane-assisted panels, and mechanical fans are coupled with membrane-assisted radiant panels, we can achieve additional 480–1440 h (5–22%) of extra comfort according to Fig. 10d, resulting in up to 27% increase compared to the baseline.
Fig. 11 provides a summary of the extended natural ventilation hours analysis. We can see the improvement in comfort hours increased in three scenarios. In comparison with the fan-assisted scenario, the use of radiant systems increases the number of locations that have 480–960 comfort hours increased (5–11%) from 200 to 1200 locations. With the membrane-assisted radiant panels, one can increase the number of locations that have a 1440–1920 comfort hours increased (16–22%) from 100 to 200 locations, and 1920–2400 comfort hours increased (22–27%) to 70 locations. These are all achieved with open windows that enable high ventilation rates.
Fig. 11.
Histograms of additional comfort hours and locations with fan-assisted, radiant panels and membrane-assisted radiant panels.
The results of the absolute natural ventilation hours mapped correlates well with the previous studies for places that fit in the respective comfort bands: the analysis of Singapore in the tropics [48] and cities in the United States [29]. Compared to the Chen et al. natural ventilation potential [28], we find an expected shift in comfort limits for the bounds of areas with natural ventilation potential. Mapping both studies in Fig. 12 , we observe that because Chen et al.’s study uses a temperature range down to 12.8 °C independent of the adaptive comfort model, that study’s results show more NV hours for colder regions. These would be deemed too cold by the adaptive comfort threshold. One could argue that their approach fails to recognize potential cold air infiltration in lightweight buildings, while our approach neglects any potential benefit of internal gains or thermal mass. Though less prominently displayed on the map, the tropical potential is also significantly expanded in our approach in comparison to the Chen et al. study by eliminating the dewpoint limit. We made the last assumption in light of our work on the more novel membrane-radiant systems being demonstrated in a fully outdoor environment with no significant internal gains to the air condition [40]. There, we have shown that high humidity alone does not cause discomfort, so long as the necessary metabolic heat dissipation is managed via convective and radiant heat transfer without requiring additional sweating/evaporative cooling.
Fig. 12.
(a) number of natural ventilation hours with no running mechanical ventilation using author’s method (b) number of natural ventilation hours with no running mechanical ventilation using [28]’s method.
5. Discussion
In comparing our analysis of the energy use penalty of increasing outdoor air (OAR), we were unable to find a paper or other published research that explicitly analyzed its physical relationship as an energy penalty for specific system operation. Numerous papers have explored ways to increase the performance of HVAC delivery of fresh air. Several of them were reviewed based on thermal comfort setbacks [8], which show savings from 29% in Hong Kong to 69% in Las Vegas for standard systems. This confirms the sensitivity of energy demand to the difference from supply temperature to source, which was also confirmed in previous EnergyPlus modeling of setpoint setbacks [44]. Another review looked at energy conservation in ventilation strategies [45] and demonstrated systems that can reduce the penalty paid by increasing outdoor air by including energy and heat recovery as well as geothermal pre-cooling. We did not consider the role of these devices and strategies in improving performance. While these are also great options to increase fresh air, they are not yet prevalent in standard installations. Finally, we considered our analysis relative to research and analyses that consider air enthalpy instead of just sensible temperature, as is done in degree-day calculations. Degree-day analysis includes the comparison of modeling accuracy [46] that describes the significant energy cost of humidity on the air-side of cooling systems and also shows an improvement in energy prediction using enthalpy cooling degree-days. Similarly, it was shown in another study how expected climate change will increase the enthalpy gradients that buildings will have to address, thus exacerbating the energy penalty of increased outdoor air ventilation rates [47].
We can therefore confirm our results qualitatively from previous work that the intuitive nature of bringing in more unconditioned air, particularly if it is hot, humid air, has very negative impact that increases energy costs. The form of the simulation results illustrates the potential negative feedback on machine performance from changing SHR, and the fundamental analytical relationships provide a more general backdrop to directly review OAR increase penalties that should be considered in practice. Further, we have confirmed that this scenario has occurred in the field during the COVID crisis, as the facilities managers at Princeton University were instructed to open outdoor air dampers to their maximum setting to bring as much outdoor air as possible into buildings, which is the scenario that was modeled.
The energy savings assessment for natural ventilation in our analysis is dependent on the regression of the cooling analysis done by Chen et al.[28] It is important to recognize that in their paper, the energy savings assessment is still based on their EnergyPlus model of a standard system. If we consider the energy consumed by a ceiling fans, it is easily as low as 1 W/m2, and we therefore argue that it would be insignificant. But we do recognize the importance of considering the delivery of radiant cooling to the surfaces modeled. As the novel membrane-assisted radiant system does not have yet an in-depth energy model for calculating its cooling load, our analysis considers 35% savings for this system in comparison with a central A/C, based on radiant cooling precedents. We plan future analyses to more accurately model the energy savings of radiant cooling-assisted natural ventilation.
We also recognize and advocate that building performance estimates presented in this paper, as per Table 1 and Fig. 8, Fig. 9, should be considered rough approximations. There are many assumptions which underlay our analysis, along with the complementary work of Chen et al. [28]. We have not examined different building designs and typologies to judge whether natural ventilation can be freely provided with windows open in all building spaces. We have not examined outdoor air quality and the effect of noise and pollution on natural ventilation viability. We have not considered the impact of climate change on these forecasts nor the optimization of mechanical ventilation strategies. For example, the implementation of heat recovery ventilators (HRVs) can reduce central AC energy use under higher OAR configurations. Likewise, the baseline backup system for a radiant cooling-assisted natural ventilation system may be a HRV-based air handling system, such as a dedicated outdoor air system (DOAS).
Finally, we recognize there are many other factors affecting access to air and airflow in buildings.. However, we suggest that studies which show that the common “solution to pollution is dilution” cliché for increasing OAR and ACH in rooms as the best method of mitigating disease spread fail to recognize the non-uniform airflows and increased mixing that occurs in high-velocity systems [49]. For COVID-19, the spread of the virus has been shown to be caused by directional airflows as well. Still, it remains clear that the vast majority of cases are transmitted indoors, and transmission would be reduced by having more fresh air exchange.
Our analysis demonstrates significant potential for the expanded use of mixed-mode systems to allow for more naturally ventilated hours. Also, in considering the cities and places that can achieve up to 100% natural ventilation, it is implied that building design in these locations can be freed from conventional ducting and air handling systems, which significantly changes the design paradigm of walls and enclosures.
While teaching classes outdoors during the 2020 pandemic to mitigate transmission risk, heat and humidity, as well as cold temperatures, were experienced during different days in temperate climates. Both could be addressed by the alternative radiant and fan paradigms we presented here. Future work should also consider how specific times of the year, such as semesters for schools, could be prioritized for analysis, and how occupied time of commercial buildings and residential buildings could be used to more accurately consider which hours in which buildings are most valuable to have the natural ventilation potential increased. We recognize that our proposed interventions are unconventional, but with the amount of change happening in work settings and building operations, alternative paradigms need to be considered, especially those that improve the health and safety of occupants and dramatically decrease energy consumption.
6. Conclusion
In light of mounting evidence for the airborne transmission risks of the SARS-COV-2 virus, we must rethink the fundamentals of HVAC systems designed to provide adequate fresh air intake without compromising buildings’ energy performance. Natural ventilation is an affordable and sustainable method for achieving this goal, but it presents challenges for thermal comfort when the outdoor air temperature falls outside of the comfort zone. We have demonstrated that it is possible to significantly increase the potential for natural ventilation hours in buildings within multiple climatic zones by using radiant systems instead of air-based systems for temperature control. Radiant systems are proven to be more energy efficient than air-based systems, and at the same time provide a high degree of occupant satisfaction.
Our models and calculations demonstrated that increasing to 100% fresh air (OAR) in standard building HVAC can significantly increase energy costs in humid climates. Alternatively, we have demonstrated that increasing natural ventilation hours by using a radiant cooling system significantly reduces the cooling energy usage. When considering a delivery of 50% OAR scenario, 20–45% cooling load reduction can be achieved with the use of a radiant system in comparison to a central A/C system. An even higher cooling load reduction can be achieved if 100% OAR delivery is considered.
Using the adaptive comfort model, we have shown that it is possible to increase natural ventilation hours by up to 100 extra days (2400 h) per year using our proposed novel radiant system for indoor temperature control. Most of the regions with the highest potential to make this switch to natural ventilation are located in Southeast Asia and South Asia. While recognizing the need to address the challenges of air pollution and noise mitigation in many of the megacities of these regions, this research shows that the potential for natural ventilation in hot humid climates should not be overlooked as it presents significant energy savings and potential health benefits.
The most significant general finding from this study is that increasing the outdoor air intake to 100% fresh air with existing mechanical ventilation systems will result in doubling space cooling energy demand in hot and humid climates, whereas switching to a 100% radiant cooling system coupled with natural ventilation will reduce net cooling energy demand and retain thermally comfortable conditions for a significant number of hours out of the year. Under the new proposed paradigm, air is supplied to building occupants for the purpose of breathing, not for heating and cooling. Thermal comfort can be instead controlled by surface temperature manipulation. By decoupling the air supply from temperature control, it is possible to achieve both high levels of indoor air quality and energy savings in interior spaces at the same time.
CRediT authorship contribution statement
Dorit Aviv: Conceptualization, Methodology, Writing - original draft, Writing - review & editing, Investigation, Visualization, Project administration. Kian Wee Chen: Conceptualization, Methodology, Software, Writing - original draft, Writing - review & editing, Investigation, Visualization, Formal analysis, Data curation. Eric Teitelbaum: Conceptualization, Methodology, Writing - original draft, Writing - review & editing, Investigation, Formal analysis. Denon Sheppard: Resources, Formal analysis. Jovan Pantelic: Conceptualization, Methodology, Supervision. Adam Rysanek: Conceptualization, Methodology, Writing - original draft, Writing - review & editing, Investigation, Visualization, Formal analysis, Supervision. Forrest Meggers: Conceptualization, Methodology, Writing - original draft, Writing - review & editing, Investigation, Formal analysis, Supervision.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors would like to thank Miranda Mote and Alexander Kim for their help with the final proofs of this paper.
References
- 1.World Health Organization . World Health Organization; 2020. Transmission of SARS-CoV-2: implications for infection prevention precautions: scientific brief, 09 July 2020. [Google Scholar]
- 2.Energy Information Administration U. Manufacturing Energy Consumption Survey (MECS) 2013.
- 3.Murphy M. Duke University Press; 2006. Sick building syndrome and the problem of uncertainty: Environmental politics, technoscience, and women workers. [Google Scholar]
- 4.Sundell J. Reflections on the history of indoor air science, focusing on the last 50 years. Indoor Air. 2017;27:708–724. doi: 10.1111/ina.12368. [DOI] [PubMed] [Google Scholar]
- 5.Menzies R., Tamblyn R., Farant J.-P., Hanley J., Nunes F., Tamblyn R. The Effect of Varying Levels of Outdoor-Air Supply on the Symptoms of Sick Building Syndrome. N Engl J Med. 1993;328:821–827. doi: 10.1056/NEJM199303253281201. [DOI] [PubMed] [Google Scholar]
- 6.Wargocki P., Wyon D.P., Sundell J., Clausen G., Fanger P.O. The effects of outdoor air supply rate in an office on perceived air quality, sick building syndrome (SBS) symptoms and productivity. Indoor Air. 2000;10:222–236. doi: 10.1034/j.1600-0668.2000.010004222.x. [DOI] [PubMed] [Google Scholar]
- 7.American Society of Heating, Refrigerating and Air-Conditioning Engineers. 2002 [Google Scholar]
- 8.Yang L., Yan H., Lam J.C. Thermal comfort and building energy consumption implications – A review. Appl Energy. 2014;115:164–173. doi: 10.1016/j.apenergy.2013.10.062. [DOI] [Google Scholar]
- 9.Morawska L., Tang J.W., Bahnfleth W., Bluyssen P.M., Boerstra A., Buonanno G., et al. How can airborne transmission of COVID-19 indoors be minimised? Environ Int. 2020;142 doi: 10.1016/j.envint.2020.105832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Riley E.C., Murphy G., Riley R.L. Airborne spread of measles in a suburban elementary school. Am J Epidemiol. 1978;107:421–432. doi: 10.1093/oxfordjournals.aje.a112560. [DOI] [PubMed] [Google Scholar]
- 11.REHVA. guidance document, April 3, 2020 19.
- 12.Schoen L.J. Guidance for Building Operations During the COVID-19 Pandemic. ASHRAE J. 2020:73–74. [Google Scholar]
- 13.Light E., Bailey J., Lucas R. Filling the Knowledge Gaps HVAC and COVID-19. ASHRAE J. 2020:20–28. [Google Scholar]
- 14.Harriman L.G., Plager D., Kosar D. Dehumidification and Cooling Loads From Ventilation Air. Energy Eng. 1999;96:31–45. doi: 10.1080/01998595.1999.10530479. [DOI] [Google Scholar]
- 15.Escombe A.R., Oeser C.C., Gilman R.H., Navincopa M., Ticona E., Pan W., et al. Natural ventilation for the prevention of airborne contagion. PLoS Med. 2007;4 doi: 10.1371/journal.pmed.0040068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hobday R., Dancer S. Roles of sunlight and natural ventilation for controlling infection: historical and current perspectives. J Hosp Infect. 2013;84:271–282. doi: 10.1016/j.jhin.2013.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Oropeza-Perez I., Østergaard P.A. Energy saving potential of utilizing natural ventilation under warm conditions–A case study of Mexico. Appl Energy. 2014;130:20–32. [Google Scholar]
- 18.Bienvenido-Huertas D., Sánchez-García D., Rubio-Bellido C. Analysing natural ventilation to reduce the cooling energy consumption and the fuel poverty of social dwellings in coastal zones. Appl Energy. 2020;279 doi: 10.1016/j.apenergy.2020.115845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rackes A., Melo A.P., Lamberts R. Naturally comfortable and sustainable: Informed design guidance and performance labeling for passive commercial buildings in hot climates. Appl Energy. 2016;174:256–274. doi: 10.1016/j.apenergy.2016.04.081. [DOI] [Google Scholar]
- 20.Axley JW, Emmerich SJ. A Method to Assess the Suitability of a Climate for Natural Ventilation of Commercial Buildings. Proc. Indoor Air 2002, Monterey, California: 2002.
- 21.Brager G. Mixed-mode cooling. ASHRAE J. 2006;48 [Google Scholar]
- 22.Heiselberg P. Principles of Hybrid Ventilation. Aalborg, Denmark: IEA Energy Conservation in Buildings and Community Systems Programme Annex 35: Hybrid Ventilation in New and Retrofitted Office. Buildings. 2002 [Google Scholar]
- 23.Ng L.C., Ojeda Quiles N., Dols W.S., Emmerich S.J. Weather correlations to calculate infiltration rates for U. S. commercial building energy models. Build Environ. 2018;127:47–57. doi: 10.1016/j.buildenv.2017.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.de Dear R, Brager GS. Developing an adaptive model of thermal comfort and preference 1998.
- 25.Parkinson T., de Dear R., Brager G. Nudging the adaptive thermal comfort model. Energy Build. 2020;206 doi: 10.1016/j.enbuild.2019.109559. [DOI] [Google Scholar]
- 26.Teitelbaum E., Jayathissa P., Miller C., Meggers F. Design with Comfort: Expanding the psychrometric chart with radiation and convection dimensions. Energy Build. 2020;209 [Google Scholar]
- 27.Emmerich S.J., Polidoro B., Axley J.W. Impact of adaptive thermal comfort on climatic suitability of natural ventilation in office buildings. Energy Build. 2011;43:2101–2107. doi: 10.1016/j.enbuild.2011.04.016. [DOI] [Google Scholar]
- 28.Chen Y., Tong Z., Malkawi A. Investigating natural ventilation potentials across the globe: Regional and climatic variations. Build Environ. 2017;122:386–396. doi: 10.1016/j.buildenv.2017.06.026. [DOI] [Google Scholar]
- 29.Chen J., Brager G.S., Augenbroe G., Song X. Impact of outdoor air quality on the natural ventilation usage of commercial buildings in the US. Appl Energy. 2019;235:673–684. doi: 10.1016/j.apenergy.2018.11.020. [DOI] [Google Scholar]
- 30.Zeng Y., Cao Y., Qiao X., Seyler B.C., Tang Y. Air pollution reduction in China: Recent success but great challenge for the future. Sci Total Environ. 2019;663:329–337. doi: 10.1016/j.scitotenv.2019.01.262. [DOI] [PubMed] [Google Scholar]
- 31.Sullivan T.J., Driscoll C.T., Beier C.M., Burtraw D., Fernandez I.J., Galloway J.N., et al. Air pollution success stories in the United States: The value of long-term observations. Environ Sci Policy. 2018;84:69–73. [Google Scholar]
- 32.Berman J.D., Ebisu K. Changes in US air pollution during the COVID-19 pandemic. Sci Total Environ. 2020;739 doi: 10.1016/j.scitotenv.2020.139864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Khalid B., Bai X., Wei H., Huang Y., Wu H., Cui Y. Direct blow-spinning of nanofibers on a window screen for highly efficient PM2. 5 removal. Nano Lett. 2017;17:1140–1148. doi: 10.1021/acs.nanolett.6b04771. [DOI] [PubMed] [Google Scholar]
- 34.Huang W.-R., He Z., Wang J.-L., Liu J.-W., Yu S.-H. Mass production of nanowire-nylon flexible transparent smart windows for PM2. 5 capture. IScience. 2019;12:333–341. doi: 10.1016/j.isci.2019.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chowdhury A.A., Rasul M., Khan M.M.K. Thermal-comfort analysis and simulation for various low-energy cooling-technologies applied to an office building in a subtropical climate. Appl Energy. 2008;85:449–462. [Google Scholar]
- 36.McIntyre D., Griffiths I. Subjective response to radiant and convective environments. Environ Res. 1972;5:471–482. doi: 10.1016/0013-9351(72)90048-5. [DOI] [PubMed] [Google Scholar]
- 37.Dawe M., Raftery P., Woolley J., Schiavon S., Bauman F. Comparison of mean radiant and air temperatures in mechanically-conditioned commercial buildings from over 200,000 field and laboratory measurements. Energy Build. 2020;206 [Google Scholar]
- 38.Woolley J, Bauman F, Duarte C, Raftery P, Pantelic J. Optimizing Radiant Systems for Energy Efficiency and Comfort 2018.
- 39.Teitelbaum E., Rysanek A., Pantelic J., Aviv D., Obelz S., Buff A., et al. Revisiting radiant cooling: condensation-free heat rejection using infrared-transparent enclosures of chilled panels. Archit Sci Rev. 2019:1–8. doi: 10.1080/00038628.2019.1566112. [DOI] [Google Scholar]
- 40.Teitelbaum E., Chen K.W., Aviv D., Bradford K., Ruefenacht L., Sheppard D., et al. Membrane-assisted radiant cooling for expanding thermal comfort zones globally without air conditioning. Proc Natl Acad Sci. 2020;117:21162–21169. doi: 10.1073/pnas.2001678117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Deru M., Field K., Studer D., Benne K., Griffith B., Torcellini P., et al. U.S. Department of Energy Commercial Reference Building Models of the National Building Stock. National Renewable Energy Lab. (NREL), Golden, CO (United States) 2011 doi: 10.2172/1009264. [DOI] [Google Scholar]
- 42.EnergyPlus. Weather Data Sources 2020. https://energyplus.net/weather/sources (accessed September 30, 2020).
- 43.Standardization IO for. ISO7726 Ergonomics of the thermal environment. Instruments for measuring physical quantities..pdf. 2001.
- 44.Hoyt T., Arens E., Zhang H. Extending air temperature setpoints: Simulated energy savings and design considerations for new and retrofit buildings. Build Environ. 2015;88:89–96. doi: 10.1016/j.buildenv.2014.09.010. [DOI] [Google Scholar]
- 45.Liu Z., Li W., Chen Y., Luo Y., Zhang L. Review of energy conservation technologies for fresh air supply in zero energy buildings. Appl Therm Eng. 2019;148:544–556. doi: 10.1016/j.applthermaleng.2018.11.085. [DOI] [Google Scholar]
- 46.Shin M., Do S.L. Prediction of cooling energy use in buildings using an enthalpy-based cooling degree days method in a hot and humid climate. Energy Build. 2016;110:57–70. doi: 10.1016/j.enbuild.2015.10.035. [DOI] [Google Scholar]
- 47.Fonseca J., Schlueter A. Daily enthalpy gradients and the effects of climate change on the thermal energy demand of buildings in the United States. Appl Energy. 2020;262 doi: 10.1016/j.apenergy.2019.114458. [DOI] [Google Scholar]
- 48.Wang L., Wong N.H. Applying Natural Ventilation for Thermal Comfort in Residential Buildings in Singapore. Archit Sci Rev. 2007;50:224–233. doi: 10.3763/asre.2007.5028. [DOI] [Google Scholar]
- 49.Pantelic J., Tham K.W. Adequacy of air change rate as the sole indicator of an air distribution system’s effectiveness to mitigate airborne infectious disease transmission caused by a cough release in the room with overhead mixing ventilation: A case study. HVACR Res. 2013;19:947–961. doi: 10.1080/10789669.2013.842447. [DOI] [Google Scholar]
- 50.Niu J.L., Zhang L.Z., Zuo H.G. Energy Savings Potential of Chilled-Ceiling Combined with Desiccant Cooling in Hot and Humid Climates. Energy Build. 2002;34(5):487–495. [Google Scholar]
- 51.TIAX, LLC. Matching the sensible heat ratio of air conditioning equipment with the building load shr. Analysis. 2003.
- 52.Zhang Lian, Lee Wai Ling. Evaluating the use heat pipe for dedicated ventilation of office buildings in Hong Kong. Energy Convers Manage. 2011;52(4):1983–1989. [Google Scholar]
- 53.Ghali Kamel. Energy savings potential of a hybrid desiccant dehumidification air conditioning system in Beirut. Energy Convers Manage. 2008;49(11):3387–3390. [Google Scholar]
- 54.Chen K.W., Teitelbaum E., Meggers F., Pantelic J., Rysanek A. Exploring membrane-assisted radiant cooling for designing comfortable naturally ventilated spaces in the tropics. Build Res Inform. 2020:1–13. [Google Scholar]