Machine Learning Enables Selection of Epistatic Enzyme Mutants for Stability Against Unfolding and Detrimental Aggregation

Abstract

Machine learning (ML) has pervaded most areas of protein engineering, including stability and stereoselectivity. Using limonene epoxide hydrolase as the model enzyme and innov'SAR as the ML platform, comprising a digital signal process, we achieved high protein robustness that can resist unfolding with concomitant detrimental aggregation. Fourier transform (FT) allows us to take into account the order of the protein sequence and the nonlinear interactions between positions, and thus to grasp epistatic phenomena. The innov'SAR approach is interpolative, extrapolative and makes outside‐the‐box, predictions not found in other state‐of‐the‐art ML or deep learning approaches. Equally significant is the finding that our approach to ML in the present context, flanked by advanced molecular dynamics simulations, uncovers the connection between epistatic mutational interactions and protein robustness.

A quick learner: Machine learning based on the innov'SAR algorithm leads to efficient selection of highly robust limonene epoxide hydrolase mutants with enhanced unfolding stability and resistance to aggregation by recognizing epistatic mutational interactions.

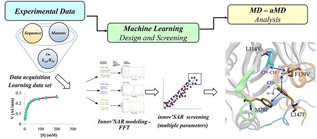
Introduction

Machine learning (ML) as a form of artificial intelligence (AI) has rapidly pervaded many realms of chemistry, including homogeneous and heterogeneous catalysis as summarized in recent reviews.[ ¹ , ² , ³ , ⁴ , ⁵ ] ML has also entered protein science,[ ⁶ , ⁷ ] likewise summarized by recent reviews.[ ⁸ , ⁹ , ¹⁰ ] A prime example concerns the utility of ML as an aid in the rational design or directed evolution of stereoselective enzymes, although possible tradeoffs in protein stability were not considered in these studies.[ ^6c , ⁷ ] Indeed, sufficient thermostability, resistance to hostile organic solvents and particularly absence of undesired aggregation following unfolding are prerequisites for real (industrial) applications in organic chemistry and biotechnology.[ ¹¹ , ¹² , ¹³ ] In our stereoselectivity study based on the ML algorithm innov'SAR (innovative sequence–activity relationship), ^[7] an epoxide hydrolase served as the model enzyme, which resulted in a set of predicted mutants with distinctly higher enantioselectivity in hydrolytic kinetic resolution than those previously evolved by state‐of‐the‐art semirational directed evolution. Innov'SAR comprises three steps: ^[7] i) encoding phase (encoding the alphabetic protein sequence into a numerical sequence using the physicochemical properties of the amino acid residues based on an index of the AA index database; ^[14] ii) modelling phase (comprising fast Fourier transformation (FFT) as a digital signal processing technique); and iii) predictive phase. An advanced innov'SAR platform was recently reported. ^[15] Accordingly, during the modelling phase, multiple encoding indices are evaluated so as to find the best combination for the construction of an appropriate model. Consequently, the descriptor of the protein sequence is different from the one used in our previous experimental application where a single index is used to generate an elementary numerical sequence. ^[7] Indeed, a concatenation of multiples indices, that is, an extended_sequence (Ext_SEQ), is evaluated as descriptor (as exemplified in Figure 1). In the most recent contribution, ^[16] we showed that the use of multiple physicochemical indices coupled with the implementation of the FFT, taking into account the interactions between residues of amino acids within the protein sequence,[ ⁷ , ¹⁷ ] leads to very significant improvement in the quality of models. The choice of the descriptor (i. e., combination of indices) with or without applying FFT, during the statistical modelling, is dependent of the couple protein/fitness, thereby improving the prediction of enzyme activity. ^[16]

Figure 1.

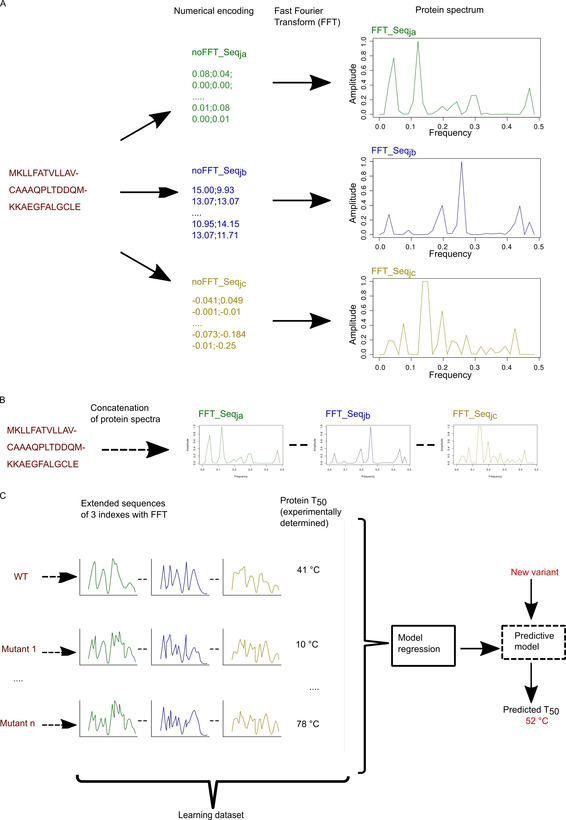
Workflow of the modelling process. A) A protein sequence is encoded in two steps: i) with numerical encoding based on an index of the AA index database, ii) FFT is applied to convert the encoded sequence into a protein spectrum. Each numerical encoding from an index will give a unique protein spectrum. Here three specific encodings give three specific protein spectra. Each protein spectrum is an elementary numerical sequence available for modelling with innov'SAR. B) Construction of a numerical extended sequence (Ext_SEQ) by concatenating the elementary numerical sequences. C) The different phases of innov'SAR: an encoding phase transforms the primary sequences of the initial dataset into protein spectra. The modelling phase uses the protein spectra and protein thermostability as a learning dataset in order to construct a regression model. Here, for the modelling of the epoxide hydrolase LEH, the construction of the model is based on a partial least‐squares regression method. Then the predictive phase uses the regression model and the protein spectra of new variants to predict their thermostability.

Undesired protein aggregation is a phenomenon prevalent in diseases such as Alzheimer and in biotechnological applications of enzymes as well. In the present ML study, we address the persisting question of how to prevent detrimental enzyme aggregation following unfolding, which causes a decrease or even shutdown in biocatalytic performance.[ ¹⁸ , ¹⁹ , ²⁰ ] Unfortunately, some protein engineers do not realize that suboptimal enzyme activity might be due to detrimental aggregation. In the present study, limonene epoxide hydrolase from Rhodococcus erythropolis (LEH), which acts via a one‐step reaction mechanism in the hydrolysis of epoxides (Scheme 1), was chosen as the model enzyme.[ ²¹ , ²² , ²³ , ²⁴ ] In nature, limonene epoxide hydrolase (LEH), as all epoxide hydrolases, catalyses the hydrolysis of epoxides to the corresponding diols.[ ²¹ , ²² , ²³ , ²⁴ ] The respective biological function varies according to the nature of the organism, for example, detoxification of epoxides, biosynthesis of natural products, and cellular signalling. LEH also attracts increasing attention due to its potential for preparing enantiomerically pure or enriched vicinal diols in organic and pharmaceutical chemistry as well as biotechnology.[ ²² , ²⁴ ] As will be seen, our results underscore the crucial role of epistatic mutational interactions, as uncovered by molecular dynamics (MD) simulations.

Scheme 1.

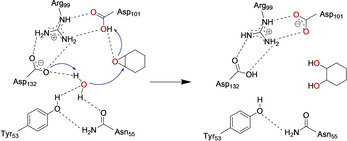
The proposed catalytic mechanism of limonene epoxide hydrolase (LEH).

In particular, our plan was to:

• Apply the innov'SAR methodology based on Ext_SEQ to LEH in the quest to enhance its resistance to unfolding and undesired aggregation;

• Generate all the possible LEH variants in silico and screen for those which are stable to unfolding and make a ranking;

• Select a subsample of stable variants and check experimentally how stable to unfolding they are;

• Evaluate experimentally their ability to suppress undesired aggregation;

• Also test the best LEH variants for stereoselectivity;

• Likewise test the best LEH variants for resistance to hostile organic solvents;

• Use molecular modelling and MD simulations in order to unravel the molecular basis behind the observed improvements. ^[25]

Results and Discussion

Machine learning design and screening

In order to predict the thermostability of LEH variants, it is necessary to build a model using the innov'SAR platform. In this study, the algorithm used is fed with a new category of descriptors termed extended sequence (Ext_SEQ). The ML procedure relies on the encoding phase, the modelling phase comprising a digital signal process (Fourier Transform), and the predictive phase. All steps from data encoding to model building with the implementation of the whole machine learning procedure, and model evaluation have been described in detail in previous papers and in experimental application case studies[ ⁷ , ¹⁵ , ¹⁶ ] including multi‐parameter optimization. ^[26] The new descriptors and the ML approach are fully described in the “Material and Methods” section of supporting information. To sum up the basic characteristic of the procedure: Only an initial dataset containing the primary sequences of enzyme variants and the respective biological properties is required. It is different from other ML approaches due to the following characteristics: i) thanks to the Fourier transform, the nonlinear aspects inside the protein sequence are captured; ii) FFT allows new mutations to be introduced at positions not previously explored or new positions of mutations; ^[15] iii) a single round, as in this case, allows the identification of high performing mutants, while avoiding iv) the need for excessively large datasets customary in other ML ^[6f] or deep learning approaches;[ ^27a , ^27b ] v) no need for alignment‐based amino acid descriptors, ^[27c] no need for protein sequences of equal length, as well as, vi) large computational resources and/or long computational times are not required.[ ^27b , ^27c ] In these two examples cited as references, a graphics processing unit (GPU) is needed for reasonable training time. The workflow is summarized in Figure 1.

In previous work ^[15] we established the ability of innov'SAR to predict accurately the experimental protein thermostability T ₅₀ (the temperature at which 50 % of enzyme activity is lost following a heat treatment). In the current study, we wondered whether it is possible, based on the predicted T ₅₀ thermostability, to switch directly to the unfolding stability (T _m, the midpoint of unfolding event) and aggregation stability (T _agg, the starting point of aggregation event). Intuitively, we understand that this would be possible if these three parameters are closely related. The advantage of such an approach is that it saves time and costs, as the experimental determination of T ₅₀ is no longer an obligatory step. The corollary of such an approach is that the system would be trained for T ₅₀, and then evaluated for T _m/T _agg. Thus, here our working hypothesis is that the unfolding stability (T _m) and aggregation stability (T _agg) are related to the thermostability (T ₅₀) of the enzyme. Our objective is also to evaluate the links between T ₅₀, T _m and T _agg.

The first step, in order to be able to verify the validity of this working hypothesis, is to obtain a high quality predictive T ₅₀ model from the available experimental data. Then, to use this model to select a few mutants likely to present the desired properties in order to test them experimentally for T _m and T _agg. Our main goal through the implementation of the ML approach is to obtain mutants presenting a high T _m. The presence among these mutants, likewise having a high T _agg, would also be desirable. In both cases, the target value, in terms of T _m or T _agg, is that of the best performing mutant known to date in the literature. As a result, based on previously determined T ₅₀ values of WT LEH and 16 variants as a starting point (Table S1), ^[28] the model for the prediction of thermostability was trained, and then used for predictions. The protein sequence numerically encoded as extended sequence of 3 indices with FFT (Ext_SEQ) is used as feature and thermostability (T ₅₀) for the target value. As we can see (Figure S1 in the Supporting information), the model appears to be of good quality since the cvR2 and cvRMSE are respectively 0.989 and 0.744. The p values associated with the calculation of cvR2 (p=4.347×10⁻¹⁶) allow us to state that for the model the predicted values are very well correlated to the measured ones. The predictive power of the model is confirmed by the method used to check the robustness of the model used during its construction: a “leave‐one‐out” cross‐validation procedure. This procedure consists in setting aside one of the n protein sequences, building the model on the remaining n−1 sequences, predicting the T ₅₀ value of the sequence and comparing it with its experimental value. This operation is repeated as many times as there are protein sequences in the learning set (n), before the cvR2 and cvRMSE are calculated. The results obtained here gives us confidence about the approach implemented and about the relevance of relying on the predicted T ₅₀ values to identify more robust mutants in terms of T _m and T _agg.

The next step is the use of this model to predict the T ₅₀ values of all the variants resulting from the combinatorics of the studied mutations. Twenty positions of mutations and 26 mutations (six positions with two mutations and 14 positions with 1 mutation) occur in the enzyme sequences. Such a large number of mutations ensure an information‐rich model. The possible mutant space for this dataset is thus 11 943 936 variants which were generated in silico and predicted using the afore‐mentioned model. This larger in silico explored sequence space allows larger jumps in the evolutionary process. Figure 2 shows the ranking of these variants. For convenience, only a subsample is exhibited in the plot. 86 090 mutants present a value equal to or greater than to the best one of the data set. We decided to randomly pick five variants inside the top 3000, under the following constraint: The number of mutations must be different for the five variants. Indeed, it is desirable to identify variants with optimal predicted properties containing as few mutations as possible. These five variants prove to have a predicted T ₅₀ values above the highest one from the train set. Seven variants (these five+the previous highly thermostable one+the wild type) were then tested in vitro in order to measure T _m and T _agg. In order to verify our working hypothesis, these predicted and experimental values of T ₅₀, T _m and T _agg are analysed, first with respect to Spearman's rank correlation and then according to a classification using a threshold, two to two ie. T ₅₀/T _m, T ₅₀/T _agg and T _agg/T _m. The Spearman's rank correlation coefficient is 0.32 between T ₅₀ and T _m (Table S2A). It reflects a low correlation between these two variables. This result is not surprising in light of the recent study published by Huang et al. ^[29] who showed that variants with extreme stability usually exhibit a similar magnitude of change in T ₅₀ and T _m results. This value is also 0.32 between T ₅₀ and T _agg (Table S2A). The p‐value indicates that the probability that the difference for the quadratic errors between T ₅₀ and T _m or the T ₅₀ and T _agg series of data corresponds at least to the obtained value, and assuming equal means, is equal to 0.49 and insignificant in both cases. This is not surprising since, first there is no linear relation between T ₅₀ and T _m or between T ₅₀ and T _agg, and second the relation does not even appear to be mathematically monotonous (e. g., indicating that they vary in the same way).

Figure 2.

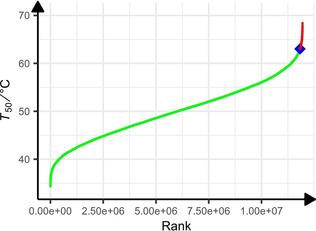
Ranking of predicted thermostability (T ₅₀ [°C]) LEH. 11 943 936 variants were considered (for convenience only a subsample is presented on this plot). In green, predictions of stabilities over the range of the dataset thermostability (from 38 to 63 °C). The blue diamond shows the thermostability of the best point from the learning dataset., Predictions of 86 090 variants with a thermostability equal to or greater than that of the previous variant are shown in red.

These values indicate that it is difficult, knowing T ₅₀, to correctly predict the ranking of T _m or T _agg. However, more interestingly, a Spearman correlation coefficient of 0.75 indicates that the relationship between the variables T _m and T _agg is almost monotonous (Table S2A). This is confirmed by the p‐value equal to 0.066 for the significance of the Spearman ranking coefficient of correlation even though the number of mutants is relatively small. This property can be favourably used, knowing T _m, for a more efficient selection of robust mutants towards aggregation upon heating. However, accurately predicting the rank of mutants in terms of T _m or T _agg is not necessarily an absolute goal. From an industrial point of view, this knowledge is not always fundamental: Indeed, the objective might be to identify mutants that present a property of interest with an improved value over that of the best performing mutant known. In this perspective, a classification of mutants as being more or less efficient than a well‐performing mutant taken as a reference is of definite interest. A classification of mutants has therefore been carried out. Temperature values (actual and predicted) were converted to binary categories by using 63 °C (T ₅₀ of the high thermostable mutant) as a threshold, in order to compute the classification performances and subsequently compare the results. All the mutants ≥63 °C will be identified as 1, otherwise as 0. Here, it is interesting to keep mutants with a T ₅₀ value equal to that of the best known mutant, that is, 63 °C because two mutants with the same T ₅₀ but different sequences, due to different mutations or combinations of mutations, will not necessarily have the same behaviour in terms of T _m and T _agg. Interestingly, the results show that accuracy, precision and recall are respectively 0.71, 0.67 and 1 for the couple T ₅₀/T _m and 0.57, 0.25 and 1 for the couple T _m/T _agg (Table S2B). These results indicate that by defining a T ₅₀ temperature target to be reached or exceeded, one can identify mutants that perform better from the T _m point of view (71 %). Nevertheless, knowing T _m, the T _agg being systematically lower than the T _m, such identification is still possible but more delicate: The accuracy falls from 71 to 57 %. On the other hand, with an accuracy value of 0.29 for the couple T ₅₀/T _agg, T ₅₀ does not tell us anything about T _agg.

To summarize these results: 1) Spearman's analysis indicates that knowing T ₅₀ it is difficult to predict the rank of the sequences in terms of T _m and T _agg, and in doing so to have an indication of their associated value. On the other hand, interestingly, the rank associated with the T _m values is rather well respected for the T _agg values, 2) the classification analysis indicates that knowing T ₅₀, the classification of the mutants into high or low performance mutants from the T _m point of view is good, but is not possible for T _agg. Also, knowing T _m, the classification of mutants into high or low performance mutants from the T _agg point of view is acceptable. Thus, with regard to our initial working hypothesis, all the results obtained allow us to highlight the following points:

• On the one hand, the knowledge of T ₅₀ does not allow us to anticipate the value of the T _agg. On this point, our working hypothesis is not validated, for the couple T ₅₀/T _agg.

• On the other hand, the knowledge of T ₅₀ allows us to classify the mutants and to distinguish between those which have a high T _m and those who do not. In this respect, our initial working hypothesis is confirmed for the couple T ₅₀/T _m. Based on this validation, we are entitled to calculate a hit rate of our approach on the basis of experimental measurements of T _m.

In the following section, we will calculate a hit rate with regard to the objective(s) we have set ourselves and to compare it with other ML approaches. The main objective was to identify, thanks to the innov'SAR approach based on extended sequences and associated T _50s, mutants with a higher T _m than the best‐known LEH mutant to date. About 1.2×10⁷ mutants were assessed computationally, and five were selected for experimental verification. Three were found to have a higher experimental T _m than the reference mutant, the hit rate is therefore 60 %. If we now take into account the secondary objective of having mutants with both higher T _m and T _agg, two of these three mutants have a higher T _agg value than the reference mutant, the hit rate is then 40 %. These hit rates are specific to the work presented in this publication: They depend on the objectives set and therefore contain a part of subjectivity. Furthermore, each research team determines what it considers to be a hit rate. Therefore, we understand that if we want to make a comparison of different approaches to ML used in the rational design or directed evolution, then we need to find an objective basis for comparison that can be applied in each case.

Church's team defined and proposed a hit rate that makes it possible to compare machine learning, including deep learning, approaches on a fairly objective basis: ^[30a] We will use this hit rate. His team has compared 12 methods, to which we have added two recently published methods, that of Wu et al. ^[27b] and that of Xu et al. ^[31] The main differences between these approaches with respect to descriptors, targets values, datasets and ML algorithms are described in detail in the corresponding publications.

One would expect the hit rate to be higher with a larger training set, so the hit rate has been normalized to the size of the training set. Figure S2 represents the hit rate value normalized to the log₁₀ number of functionally characterized mutants used for training versus log₁₀ of the search space. Application of the Church technique, ^[30a] assuming its correctness, points to the high validity of our approach (81 % success rate).

It is also interesting to compare the innov'SAR approach, which is a ML method based on signal processing coupled to a regression model, with a method based on deep learning (DL) that is gaining momentum in many areas, including protein engineering. DL approaches are of particular interest and are proving to be powerful in extracting information from protein sequences used as input to DL models. In this regard, in their recent retrospective study, Xu et al. ^[31] pointed out that the rationale for the success of their convolutional neural network (CNN) models could be found in the fact that it encodes the ordering information on the entire protein sequence in the high‐level features extracted, while other methods in their benchmark only make use of information on mutated positions. We believe that the observed performance of our approaches ^[7] is linked to the application of FFT: Applying an FFT to a protein sequence digitally encoded according to an index is not the same as simply encoding it in another way, indeed this mathematical treatment makes it possible to take into account the order of the protein sequence and all the interactions between positions within it, and thus to better identify epistatic phenomena. In this respect, the contribution of FFT in genuinely capturing the essence of epistatic phenomena has been established in our previous innov'SAR work ^[7] on the study of catalytic epoxide hydrolysis, but it did not establish the link between epistatic effects (cooperative or deleterious influences) and enzyme robustness.

It is also worth noting, as experimentally confirmed in this study, that a limited number of sequences in the training set (17 sequences here) does not hamper the possibility of obtaining mutants with superior properties, whereas Deep Learning models should ideally be fed with thousands of sequences.

It seems important to us to stress that the distinction must be made between interpolation, extrapolation and outside‐the‐box predictions. The interpolation capability consists of a model built on initial inputs, for example, mutants of a protein, to correctly predict the output (the property of interest of the protein) of new mutants not included in the training set and resulting from the combination of mutations included and learned in the training set. The extrapolation capability reflects the ability of a model to correctly predict the output of new mutants not included in the training set and obtained by modifying the nature of the input, and in particular in protein engineering, by introducing a new unseen mutation or an unlearned position in the learning set. Finally, the outside‐the‐box prediction capability expresses the ability of a model to predict an output value of the model, that is, a value of Y, a property of interest of a protein, outside the range of Y values learned during training. For example, if values of catalytic activities, Y, of an enzyme are learned for a range of Y from 10 to 100 s⁻¹ when building the predictive model, the model is able to predict outside‐the‐box if it can correctly predict values of Y of 1.5 or 150 s⁻¹, that is, values outside the learning range.

First, the interpolative nature of our approach is evidenced by the fact that the five newly constructed mutants only carry mutations presented in the multisite mutants used for the construction of the predictive model. Then, the extrapolative nature of the innov'SAR approach has already been highlighted in our previous work where both mutations and positions of mutations not included in the training set and not learned during the establishment of the predictive model did not hamper the quality of the predictions. ^[15] Finally, the ability to predict outside‐the‐box of innov'SAR has, on the one hand, been verified by Cadet et al., ^[7] and on the other hand, it is observable here from Figure S1b where the test set is made up of 20 % of the sequences of which 10 % have the lowest T ₅₀ and 10 % the highest T ₅₀, the remaining 80 % being used to learn the predictive model. The robustness of the predictive model is evaluated through a “leave‐one‐out” cross‐validation procedure: the cvR2 is 0.83, the cvRMSE 1.92. The R2 associated with the test set is 0.99 and the RMSE is 2.53. The p values associated to the calculation of cvR2 (p=1.501×10⁻⁵) and R2 (p=5.59×10⁻³) confirm that for the model (based on 80 %) the predicted values are well correlated to the measured ones.

Another major point to stress is that while Neural Networks‐based methods can give interesting results in extrapolation, they are not optimally suited for making outside‐the‐box predictions. ^[32] In this respect, the VHSE‐CNN (principal components score vectors of hydrophobic, steric, and electronic properties are used as descriptors) in the model of Xu et al. ^[31] is no exception. Indeed, the predicted values considered positive are lower, or at best the maximum value of Y of the training set. Thus, the CNN approach described allows, by screening a combinatorial, a pool of potentially interesting mutants to be identified, but it does not identify among all these mutants those which have a property superior to the best mutant of the training set. Moreover, Xu et al. rightly point out that this pool contains a large number of false positives. ^[31] Thus, the VHSE‐CNN approach remains quite useful for guiding directed evolution cycles, but is not suitable for identifying hits through outside‐the‐box predictions. This is due to the fact that a neural network and particularly a deep learning approach can map virtually any function by adjusting its parameters or hyperparameters according to the protein sequences of the training data set, but for regions of the variable space where no training data is available, the output of a neural network is not reliable.

Generally speaking, any protein engineering machine learning team will have to overcome two obstacles: i) use descriptors that best capture the totality of information and interactions within the protein sequences. This is where FFT brings added value, as we have shown previously, by highlighting small differences between highly similar variants derived from the same parent, ^[15] and ii) having an approach that works efficiently on small learning datasets. Indeed, failing to be able to experimentally generate very large datasets covering a large number of mutations, for the training dataset, it is desirable for the machine learning tool to perform on smart libraries, generated, for example, using approaches such as CASTing. ^[28] Finally, when engineering proteins, it is desirable to proceed in as few evolutionary steps as possible and as quickly as possible: In this study, the prediction of ∼12 million mutants was performed in a single round, using a model that was built in just a few seconds (38.3 s) using a personal lab computer (Intel Core(TM) i7‐6700HQ CPU 2.60 GHz). The advantage from an industrial perspective is evident.

Protein stability and possible aggregation

Protein stability generally comprises unfolding, while undesired aggregation leading to precipitation and partial loss of activity is seldomly considered.[ ¹⁸ , ¹⁹ ] Unfolding stability is an indicator of the robustness of the protein molecular structure, namely the intrinsic folding nature of a single molecule. Aggregation stability describes aggregation formation due to direct intermolecular interactions between native proteins, or between denatured proteins that have already undergone conformational changes.[ ¹⁸ , ¹⁹ , ²⁰ , ³⁴ , ³⁵ ] Increased unfolding and aggregation stability are believed to enhance overall protein stability. We therefore tested the stability of the randomly selected five variants based on UNcle stability platform and circular dichroism (CD) to confirm the prediction accuracy. For the unfolding stability, all the T _m values, except LEH‐4, measured by two different methods proved to be highly consistent (Figures S3 and S4, Tables 1 and S3). Relative to WT LEH, most of the determined T _m of predicted LEH mutants show obviously higher values (Figures S3 and S4, Tables 1 and S3). Impressively, the T _m values of LEH‐5 and LEH‐3 were enhanced by 25.9 and 27.2 K, respectively. It is commonly believed that unfolding is a precursor to protein aggregation, and many models of protein aggregation kinetics incorporate unfolding as a crucial step in the protein aggregation pathway. ^[35] Accordingly, it is expected that the predicted mutants will also display better aggregation stability. Indeed, we observed that the T _agg values of the best LEH mutants were also significantly increased relative to WT LEH (Figure S3, Table 1).

Table 1.

The determined T _m and T _agg values of WT LEH and LEH variants based on collected label‐free fluorescence, DSF and SLS.

Sample	Mutations	Predicted T 50 [°C]	Expl. T m [°C]	Expl. T agg [°C]
WT LEH		41	46.38±0.01	42.6±0.06
LEH‐1	S15P/A19K/T85V/G89C/S91C/L114V/E124D	69.14	65.95±0.36	53.4±0.02
LEH‐2	S15P/A19K/T85V/G89C/S91C/L114V/I116V/E124D	69.04	60.09±0.02	56.6±0.19
LEH‐3	I5C/S15P/A19K/L74F/T85V/G89C/S91C/L114V/I116V/E124D	66.21	73.62±0.33	63.3±0.00
LEH‐4	S15P/A19K/M78F/I80V/T85V/G89C/S91C/N92K/L114V/I116V/F139V/L147F	66.13	61.31±0.33	49.3±0.10
LEH‐5	S15P/A19K/M78F/I80V/T85V/G89C/S91C/Y96F/L114V/I116V/E124D/F139V/L147F	66.07	71.30±0.33	62.6±0.07
LEH‐F1b	I5C/S15P/A19K/T76K/E84C/T85V/G89C/S91C/N92K/Y96F/E124D	63	63.12±0.46	55.6±0.21

Resistance to hostile organic solvents, catalytic activity and stereoselectivity

Enhanced robustness to organic solvents is a highly desirable trait of enzymes to be employed for application in organic chemistry and biotechnology. To examine this aspect, we investigated the unfolding stability of WT LEH and variants in different proportions of acetonitrile or methanol (5, 10 and 20 %). Both solvents are hostile to WT LEH and in part to mutants as measured by the T _m (Figures S5 and S6, Tables S4 and S5). Relative to WT LEH, all the variants kept remarkably higher unfolding stability with ΔT _m in the range of 12–30 K in 0–20 % methanol. The results found for WT LEH and variants in 0–20 % acetonitrile are also noteworthy, with ΔT _m amounting to 12–35 K.

Although enhancing stereoselectivity was not part of the present project, in order to shed more light on the mutational effect on activity, we studied the LEH‐catalysed hydrolytic desymmetrization of cyclohexene oxide (1) with formation of (R,R)‐ and (S,S)‐2 (Scheme S1). The results show that variants LEH‐1 and LEH‐2 exhibit about a six‐ and threefold increase in activity relative to WT LEH, respectively (Table 2). The other mutants show higher enantioselectivity, but accompanied by a trade‐off in activity.

Table 2.

Activity and stereoselectivity of WT LEH and LEH mutants based on catalytic conversion of substrate 1 monitored by GC.

Enzyme	Relative activity[a]	ee [%]	Preferred enantiomer
WT LEH	100	1.4	(S,S)
LEH‐1	585.8	3.7	(S,S)
LEH‐2	298.4	1.3	(S,S)
LEH‐3	4.7	34.5	(S,S)
LEH‐4	11.8	24.9	(S,S)
LEH‐5	26.8	25.8	(S,S)
LEH‐F1b	77.2	3.6	(S,S)

[a] The relative activity was determined based on the conversion rate, and the conversion rate of WT LEH was defined as 100 %.

Molecular basis for thermostability enhancement due to epistatic interactions as revealed by molecular dynamics (MD) simulations

A computational protocol based on conventional molecular dynamics (MD) simulations followed by accelerated MD (aMD) simulations was applied to rationalize the molecular basis of the thermostability increase triggered by ML‐predicted set of mutations (see Methods section of the Supporting Information for computational details). ^[36] We applied MD and aMD simulations at a range of different temperatures to evaluate protein stability of selected LEH variants with the aim of assessing the resistance of the enzyme towards unfolding upon temperature increase. Protein folding and unfolding are complex processes that involve overcoming high energy barriers that are rarely crossed in a single conventional MD simulation. To sample the initial steps of the unfolding process, we resorted to accelerated molecular dynamics (aMD) simulations. aMD is an enhanced sampling technique that has been used before to provide unconstrained sampling of the protein folding and unfolding processes. ^[37] Although much longer aMD simulation times would be required to explore the unfolding and subsequent refolding of LEH variants at T _m temperature, local unfolding hotspots naturally arose along the aMD simulations, as we describe hereafter.

First, we analysed the root mean square fluctuations (RMSF) of the protein backbone in three selected variants (WT LEH, LEH‐1 and LEH‐5) considering their active homodimeric form at four different temperatures: 300 K (room temperature), 323 K (near WT LEH expl. T _m), 343 K (near LEH‐1 and LEH‐5 expl. T _m), and 363 K (3 replicas of 500 ns of conventional MD for each system and temperature followed by additional 500 ns of aMD). We used aMD simulations to characterize unfolding hotspots at different temperatures and to establish a relation with experimental melting temperatures. RMSF analysis along MD+aMD trajectories allowed us to evaluate the local and global flexibility of the protein and the tendency towards unfolding when temperature increases (see Figures 3 and S7 for the aMD and the conventional MD analysis, respectively).

Figure 3.

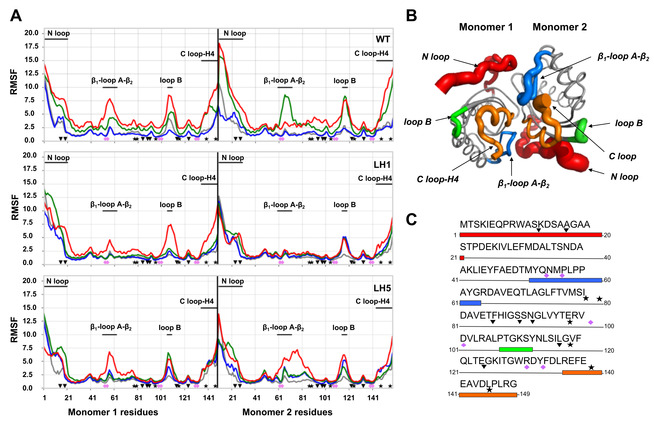
A) RMSFs of all residues computed from the aMD simulations at four different temperatures (300 K in gray, 323 K in blue, 343 K in green and 363 K in red) for the WT, LEH‐1 and LEH‐5 enzyme variants. The LEH‐1 mutations are marked as inverted triangles while the extra mutations introduced in LEH‐5 as stars and the catalytic residues as pink diamonds. The unfolding hotspots are also highlighted. B) Representation of the WT flexibility computed at 343 K by means of RMSF. The main hotpots are coloured (N loop in red, C loop‐H4 in red, β₁‐loop A‐β₂ in blue and the loop B in green). C) Enzyme sequence showing the unfolding hotspots, the LEH‐1 and LEH‐5 mutations and the positions of the catalytic residues.

For the WT LEH, aMD simulations revealed significant differences at the different temperatures studied (Figure 3A). For this case, a boost on the global flexibility of the protein is observed between 323 K (blue) and 343 K (green) temperatures, which is in line with the experimental WT T _m value of 46.4 °C (near 323 K of MD simulations), and different unfolding hotspots (RMSF peaks) were characterized. In particular, the most flexible regions in terms of RMSF correspond to the N loop (1–21 residues in Figure 3) and C loop‐H4 (135–149 residues in Figure 3) regions; β1–loop A‐β2 region (51–63 residues in Figure 3); and loop B connecting β4 and β5 (106–110 residues in Figure 3). Although these regions are spread along the protein sequence of each monomer, they are located in close proximity when considering the 3D structure of the dimeric form (Figure 3B and C). The active site catalytic residues Y53, N55, R99, D101, W130 and D132 (Figures 3 and 4A) are directly placed on these more flexible regions (Y53, and N55) or at adjacent positions in the protein sequence (R99, D101, W130 and D132).

Figure 4.

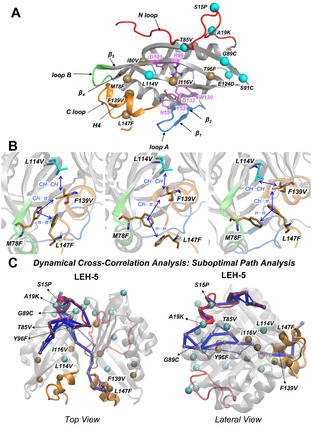
A) 3D structure of the monomeric form of LEH enzyme. The LEH‐1 mutations are highlighted by cyan spheres, the extra LEH‐5 mutations are shown as ochre spheres, and the catalytic residues are shown as violet sticks. The unfolding hotspots regions are also coloured as in Figure 4. B) Zoom view of the epistatic interactions of ML‐designed mutations observed in LEH‐5 from the MD simulations. C) Dynamical cross‐correlation analysis of the LEH‐5 variant. The suboptimal paths that connect the network of the residues are represented in blue, and the residues involved in the path are highlighted as small grey spheres. LEH‐1 mutations are highlighted as turquoise spheres; the LEH‐5 mutations are shown as ochre spheres. The terminal N loop is displayed in red and the terminal C loop in orange.

Equivalent unfolding hotspots were characterized for LEH‐1 and LEH‐5 variants in terms of RMSF analysis of aMD trajectories at different temperatures. However, these two variants display a higher resistance towards the increase of their global flexibility upon raising the temperature as compared to the WT‐LEH (Figure 3A). In these particular variants, the flexibility boost and partial unfolding upon temperature increase occurs between T=343 (green) and 363 K (red; Figure 3A), in line with the higher T _m measured for these two variants (T _m=339 and 344 K for LEH‐1 and LEH‐5, respectively).

In summary, we employed unconstrained aMD simulations to describe the ability of the enzyme to retain the native conformational ensemble with varying temperatures (300, 323, 343 and 363 K) and at a fixed simulation time. With the accumulated simulation time, this occurs up to 323 K for the WT LEH and up to 343 K for LEH‐1 and LEH‐5. As these values also correspond to the measured T _m, we found that the MD simulations confirm the thermostability trends observed experimentally. MD simulations also characterized the location of unfolding hotspots that naturally arose during the simulation. The identification of local unfolding hotspots provides meaningful information since the irreversible thermal denaturation (i. e., aggregation) is usually triggered by a partial/local unfolding. As shown in Figure 3, the mutations present in LEH‐1 and LEH‐5 variants are able to enhance the stability of some particular unfolding regions. It is, however, still unanswered how the ML‐predicted mutations collectively cooperate to stabilize LEH upon temperature increase.

Specific mutations used to create the dataset for the present work all come from previous studies,[ ² , ^23c , ³⁸ , ³⁹ ] where the specific independent role and impact of each mutation on the structure, stability, and catalytic efficiency of LEH were already described. The ML‐predicted variants, that combine mutations proposed earlier in different independent studies, display much higher thermostabilities than the ancestor ones (see above). The enhanced thermal stabilities of our new variants cannot be directly described by considering accumulative effects of single mutations, which indicates the existence of potential nonadditive but cooperative epistatic effects ^[40] between ML‐predicted mutations to thermo‐stabilize LEH. Here, we were interested in using MD simulations to unravel and describe the molecular basis of these possible epistatic interactions occurring in the mutation sets predicted by ML. As described earlier, these mutations are scattered in the protein sequence, but are usually found to be close enough in 3D space to establish non‐covalent interactions (Figure 4A).

The ML‐designed variant LEH‐1 includes a total set of seven mutations per monomer, two of which are located on the N‐terminal loop (S15P and A19K), two in internal β‐sheets β3 and β5 (T85V and L114V), two that form inter‐monomer disulfide bonds (G89C and S91C), and an additional E124D mutation which is highly solvent exposed. All the mutations included in this ML‐predicted variant are also found in the previously computationally designed LEH‐F1b variant, which also contains five additional mutations, with the exception of L114V. T_m measured for LEH‐1 variant is 66 °C, 3 K higher than the LEH‐F1b one. L114V mutation in LEH‐1 modifies the hydrophobic CH⋅⋅⋅π interactions between L114V side chain and F139 residue on the C‐terminal loop, as compared to the original L114‐F139 interaction (Figure S8). The latter helps in stabilizing this flexible terminal region, and is probably responsible for the higher thermostability of LEH‐1 as compared to LEH‐F1b. These results are in line with RMSF values collected in Figure 3A that indicate a higher stability of the C‐terminal loop in LEH‐1 compared to the WT at all range of temperatures studied. In addition, L114V backbone is H‐bonded with the backbone of the catalytic D101 residue that acts as a proton donor during the catalytic step (Figure S8). Thus, a small perturbation coming from this L114V position may directly impact the catalytic efficiency of the enzyme, as for instance the fivefold improvement in relative activity of LEH‐1 with respect to the parent WT LEH enzyme.

In contrast, pronounced epistatic interactions induced by the ML‐predicted mutations were found in the more thermostable LEH‐5 variant. This variant includes a total set of 13 mutations per monomer, the seven included in LEH‐1 plus six additional ones: two on the C‐terminal loop (F139V and L147F), two on the internal β‐sheet β3 (M78F and I80V), one on the β4 inter‐monomer region (Y96F), and one in internal β5 (I116V). Mutations in the LEH‐5C‐terminal region F139V and L147F, which are not included in LEH‐1, establish hydrophobic interactions with new mutations L114V and M78F, respectively (Figure 4B). These two pairs of mutations reshape the network of interactions between the C loop‐H4 and both β3 and β5 regions. The hydrophobic CH⋅⋅⋅π interactions between L114/L114V side chain and F139 residue in WT/LEH‐1 disappear in LEH‐5, but at the same time new hydrophobic interactions between L114V and F139V are formed. Additionally, new hydrophobic π⋅⋅⋅π interactions between ML‐predicted pair of mutations L147F and M78F are established, providing additional rigidity to the C loop‐H4 region and the core of the protein. The formation of these new hydrophobic clusters is crucial and cooperatively stabilizes the C‐terminal region. We hypothesise that local unfolding on the C loop‐H4 region might trigger protein aggregation. Thus, stabilization of the C loop‐H4 region might contribute to the higher kinetic stability (i. e., T _agg increase) of LEH‐5 respect LEH‐1 (Table 1).

Nonadditive epistatic effects can occur between residues that are in close contact directly interacting or between residues at distal positions, but connected through long‐range interactions. Other studies reporting conformational dynamics and epistasis usually focus on different protein properties, ^[41] and only few consider aggregation and unfolding phenomenon, but not machine learning. ^[42] To get further insight into the epistatic interactions ^[40] occurring between the ML‐introduced set of mutations in LEH‐5 variant, we explored the dynamic coupling of distal protein regions using dynamical cross‐correlation based tools (Figure 4C). We found that the N loop of one monomer is dynamically coupled to the C loop‐H4 region of the other monomer through a network of residues that are placed on the core region of LEH formed by the internal β‐sheets (Figure 4C). Indeed, multiple mutations are included or are in the vicinity of the principal nodes that form this communication network: T85V (next to N loop), G89C and Y96F (in the dimer interface region), L114V and I116V (both next to the catalytic residues). Particularly interesting is how L114V and I116V mutations impact the thermostability of LEH: depending on how they are combined with other mutations, they can be deleterious (Table S1, SZ348 variant) or beneficial (Table S1, B1–F12 variant) for enhanced thermostability, highlighting their degree of cooperativity (i. e., epistasis) with other amino acid substitutions found in other regions. The fact that these two residues are found next to the communication network between N and C terminal regions, indicates that the conformational dynamics of these residues is coupled with the two terminal regions. Indeed, L114V plays a direct role stabilizing the C‐terminal loop in both LEH‐1 and LEH‐5 (see above). In addition, the presence of Y96F mutation is also correlated with highly thermostable variants (Table S1). In the dynamical network, Y96F is located in the middle of the path being coupled with the conformational dynamics of both N‐ and C‐terminal regions. Mutating these positions can alter the dynamic coupling between these flexible N‐ and C‐terminal regions, tune epistatic effects, and confer an enhancement of thermostability as observed in LEH‐5 variant. All these together highlight the important long‐ and short‐range epistatic interactions between mutations predicted by ML to enhance the enzyme stability and prevent unfolding.

Conclusions

In this study, we have shown that the machine learning (ML) algorithm innov'SAR based on Ext_SEQ constitutes an efficient way to discover robust LEH variants with enhanced unfolding stability. This correlates with resistance to detrimental aggregation, as shown by the Spearman correlation coefficient between T _m and T _agg.

Although based on earlier computational design and directed evolution experiments to produce the learning dataset, our procedure nevertheless circumvents the need to generate and screen large libraries of enzyme variants, the traditional bottleneck of directed evolution.[ ²⁰ , ²¹ , ²² , ²³ , ²⁴ ] Instead, ∼1.2×10⁷ mutants were assessed computationally in one shot. Since multi‐parameter optimization in protein engineering remains a general challenge,[ ¹¹ , ¹² , ¹³ , ²⁸ , ⁴³ ] it is noteworthy that the ML‐based LEH variants predicted and verified herein also show in some cases higher stereoselectivity in a model reaction. Furthermore, the ML‐predicted variants displayed higher unfolding stability in acetonitrile and methanol, therefore highlighting organic solvent robustness.

As substantiated experimentally, the performance of the predicted mutant LEH‐5 is noteworthy, for which stability is superior to the previous most thermostable mutant LEH−F1b, predicted earlier by application of FRESCO (framework for rapid enzyme stabilization by computational libraries). ^[38] Other recent computational approaches to enzyme thermostabilization have appeared.[ ⁴⁴ , ⁴⁵ , ⁴⁶ ]

The innov'SAR approach to ML in enzyme engineering does not depend on structural or mechanistic data, yet our MD results reveal strong epistatic effects operating between mutations. Although ML‐predicted mutations are spread along the entire protein sequence, MD simulations show that they can directly interact, establishing non‐covalent interactions when they are found closer in the protein tertiary and dimer quaternary 3D structure of LEH. In addition, clusters of mutations at distal positions cooperatively interact through networks of long‐range interactions. Altogether, these cooperative direct and long‐range interactions between new introduced mutations enhance the global robustness of the enzyme preventing partial unfolding when temperature increases. Finally, we anticipate that the application of machine learning as an effective aid in solving the difficult problem of multi‐parameter enzyme optimization including the prevention of detrimental aggregation has significant potential in future work.

Conflict of interest

F.C and X.F.C are linked to Peaccel. N.F, M.N, R.P are paid employees of Peaccel. G.L, Y.Q, M.A.M‐S, F.F, M.G.‐B and M.T.R declare no competing interests.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

G. Li, Y. Qin, N. T. Fontaine, M. Ng Fuk Chong, M. A. Maria-Solano, F. Feixas, X. F. Cadet, R. Pandjaitan, M. Garcia-Borràs, F. Cadet, M. T. Reetz, ChemBioChem 2021, 22, 904.