Skip to main content
PMC home page
AIP Publishing Selective Deposit logoLink to AIP Publishing Selective Deposit
. 2021 Jan 26;33(1):011905. doi: 10.1063/5.0038180

On airborne virus transmission in elevators and confined spaces

Talib Dbouk 1,a), Dimitris Drikakis 1,b)
PMCID: PMC7984422  PMID: 33790526

Abstract

The impact of air ventilation systems on airborne virus transmission (AVT), and aerosols in general, in confined spaces is not yet understood. The recent pandemic has made it crucial to understand the limitations of ventilation systems regarding AVT. We consider an elevator as a prototypical example of a confined space and show how ventilation designs alone, regardless of cooling or heating, contribute to AVT. Air circulation effects are investigated through multiphase computational fluid dynamics, and the performance of an air purifier in an elevator for reducing AVT is assessed. We have investigated three different flow scenarios regarding the position and operation of inlets and outlets in the elevator and a fourth scenario that includes the operation of the air purifier. The position of the inlets and outlets significantly influences the flow circulation and droplet dispersion. An air purifier does not eliminate airborne transmission. The droplet dispersion is reduced when a pair of an inlet and an outlet is implemented. The overall practical conclusion is that the placement and design of the air purifier and ventilation systems significantly affect the droplet dispersion and AVT. Thus, engineering designs of such systems must take into account the flow dynamics in the confined space the systems will be installed.

I. INTRODUCTION

The COVID-19 pandemic1 is one of the most significant worldwide health and financial crises in modern history and has been causing the death of millions of people around the globe. Respiratory droplet transmission is considered as one of the most critical mechanisms responsible for the rapid spread and continued circulation of COVID-19 in humans.2 When an infected person breathes, coughs, or sneezes, thousands of contaminated saliva droplets are expelled3–5 into the surrounding environment.6 Recently, the authors7–9 developed a multiphase fluid dynamics modeling and simulation method and applied it to different airborne transmission conditions. Using new unsteady heat transfer models for the contaminated droplet evaporation, we showed that depending on environmental conditions, human saliva-disease-carrier droplets could travel unexpected considerable distances, which also depend on the environmental conditions. We also examined the effects of masks and derived new efficiency laws. Note that we use the term airborne virus transmission (AVT) in a more general context covering airborne transmission and aerosols.

Aerosol transport indoors relevant to virus transmission is an emerging topic of research. Abuhegazy et al.10 conducted a numerical investigation of aerosol transport in a classroom with relevance to COVID-19. They investigated different scenarios of the window openings and students’ configurations on the fluid physics of airborne particles. In closed spaces,11–14 the flow physics induced by ventilation systems should be expected to influence the risk of airborne virus transmission (AVT).15–17 Equally, the specific details of the virus structure are crucial.18 Bhagat et al.13 investigated the role of building ventilation on the fluid mechanics of airborne particles indoors. They indicated that indoor transmission of the virus far outstripped outdoor transmission and explained that this is possibly due to longer exposure times and less turbulence indoors. Rijn et al.19 also investigated the reduction of aerosol transmission of COVID-19 in hospital elevators experimentally.

Forced ventilation is critical in confined and relatively small indoor spaces. Many elevators are installed in buildings without air conditioning systems. Furthermore, in tropical and subtropical regions, we know that air quality can deteriorate rapidly. Smith20 showed experimentally how air quality in an elevator could be monitored during entrapment inside it. In 30 min without ventilation, air quality degraded to levels that are unhealthy according to the occupational health authorities. Hence, even a single person trapped for a short time is at significant risk. Therefore, appropriate forced ventilation is an essential tool. The influence of air circulation on airborne virus transmission is neither yet fully understood nor quantified. The recent pandemic reinforces the need to understand better the physical interaction between forced ventilation (or air circulation) and AVT in confined spaces. Some studies recently emerged linking air ventilation and indoor air purifier systems and their effect on AVT reduction.10,13,15,16,21 Elevator manufacturers have considered air purifiers22,23 as an ideal solution. However, the systems have not been designed for reducing AVT.

Air filtration has been a topic of research and development for many years in different applications.24,25 It attracted more attention recently for reducing airborne viruses, germs, and bacteria. The available air purifiers usually comprise 1.5 kg small equipment (30 × 15 × 6.6 cm3) that contains ultraviolet radiation (wholly enclosed UV photocatalyst) and an internal air intake/exhaust fan (≈60 m3/h). The contaminated air enters the purifier and leaves it as pure air free of viruses. Although a few studies dealt with fire propagation in elevators26–31 and energy consumption issues,32 studies on air purifiers in elevators concerning flow circulation in the cabin are scarce. Shao et al.33 performed a risk assessment of airborne transmission of COVID-19 by asymptomatic individuals under different practical settings such as in an elevator, a small classroom, and a supermarket. However, they studied only a single configuration of a ventilation system and, most importantly, did not consider the use of an air purifier inside the elevator.

This paper aims to deepen our understanding of the fluid dynamics of respiratory droplets in confined spaces with or without an air purifier. Mechanical air ventilation systems, e.g., intake/exhaust fans, are applied in many indoor closed spaces, such as residential buildings, schools, factories, hospitals, and car parking, among others, and at different scales, e.g., elevator cabins, cinemas and theaters, airplanes, and trains, among other applications. For the first time, we investigate the flow circulation induced by an air purifier and its effect on AVT. We focus on air ventilation systems without air conditioning, heating, or cooling34 and AVT inside an elevator (1.24 × 1 × 2.2 m3) of a maximum capacity of five persons.35,36 Without air conditioning and when an air purifier is not operational, the ventilation system alone contributes to AVT. We quantify the effect of air circulation on AVT and show that installing an air purifier (the same would apply to a sanitizer) inside an elevator alters the air circulation significantly but does not eliminate airborne transmission.

II. MODELING AND SIMULATION

We employed the Eulerian–Lagrangian multiphase modeling with a full coupling between the phases. The numerical solver is the one developed recently by the authors to account for saliva droplet dynamics in the presence of heat transfer, turbulence, and other complex phenomena such as evaporation and droplet–droplet interactions. We refer the reader to the previous papers for details,7–9 including the description of the methods for flow, heat transfer, droplet dynamics, and the associated validation.

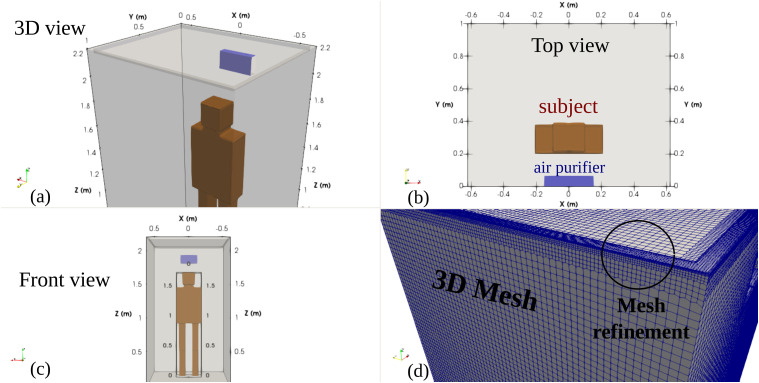
The computational domain of a human dummy (subject) inside an elevator of a maximum capacity of five persons35,36 is shown in Fig. 1. The subject’s boundary is considered as a simple geometry because the focus is given to the main flow circulation inside the cabin away from the subject’s boundary. Figure 1(a) shows a 3D view of the 2.2 m height of the cabin and an air purifier installed at z ≈ 1.9 m above the cabin ground (z = 0). Figure 1(b) shows the top view illustrating the man’s position and the air purifier. Two position scenarios (1 and 2) are considered with two respective coughing source positions: (x = 0, y = 0.41, z = 1.6) m and (x = 0, y = 0.67, z = 1.6) m. Figure 1(c) shows the front view of the computational domain, and Fig. 1(d) illustrates the adopted 3D mesh that is made of ≈6 · 105 hexahedral cells. Symmetry is imposed at the midplane x = 0.

FIG. 1.

FIG. 1.

Open in a new tab

Computational domain of a subject (human dummy) inside an elevator’s cabin of a maximum capacity of five persons.35 The subject is considered as a simple hexahedral cell geometry because the focus is on the main flow circulation inside the cabin away from the subject’s boundary. (a) 3D view showing the 2.2 m height of the cabin and an air purifier installed at z ≈ 1.9 m above the cabin’s ground (z = 0). (b) Top view illustrating the man’s position and the air purifier. (c) Front view. (d) Hexahedral 3D mesh (≈6 · 105) cells with mesh refinement near the inlets/outlets and near the subject’s boundary.

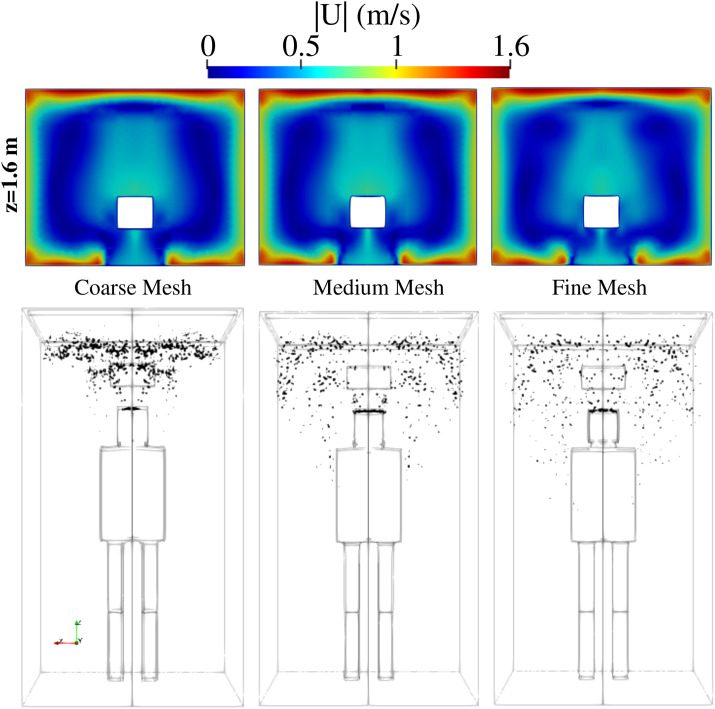
Mesh refinement is applied near the inlets and outlets and the subject’s boundary. Using the grid convergence index (GCI) by Celik et al.,37 a mesh convergence study is conducted for the fluid flow velocity U in addition to the analysis of droplets’ distribution in space and time. Three grids were generated: fine (593 268 cells), medium (388 010 cells), and coarse (284 850 cells) grids corresponding to refinement factors of r21 = 1.529 and r32 = 1.362. We adopted the fine mesh based on the results for the GCI index: GCI21 = 0.24% and GCI32 = 1.17% for the velocity. A detailed example of the results of the mesh sensitivity analysis is illustrated at t = 6 s in Fig. 2. It shows the velocity field in the plane z = 1.6 m and the spatial distribution of the saliva droplets inside the lift. The results using the medium and the fine mesh are (qualitatively) very similar. The fine mesh was used in all simulations reported below.

FIG. 2.

FIG. 2.

Open in a new tab

Scenario A—subject position 1. Mesh sensitivity analysis at t = 6 s. Top row: velocity magnitude in the plane z = 1.6 m. Bottom row: distribution of saliva droplets in space is illustrated in black after being scaled by a factor of about 250 with respect to their actual size. Fine mesh: 593 268 cells; medium mesh: 388 010 cells; coarse mesh: 284 850 cells. For the scenario A conditions, see Table I. Subject position 1 corresponds to a person who is standing in the elevator’s cabin such that her/his mouth as a coughing source is positioned at x = 0 m, y = 0.41 m, z = 1.6 m.

At the mouth position, 1000 saliva droplets (20 mg) are injected at the time step of t = 1 s at a speed of 1 m/s and over 0.25 s. This mimics a single mild cough of a person and is in the same order of magnitude as in the literature.4,5,7,9 We conducted the computations at the environmental conditions inside the elevator of 20 °C, 50% relative humidity, and atmospheric pressure.

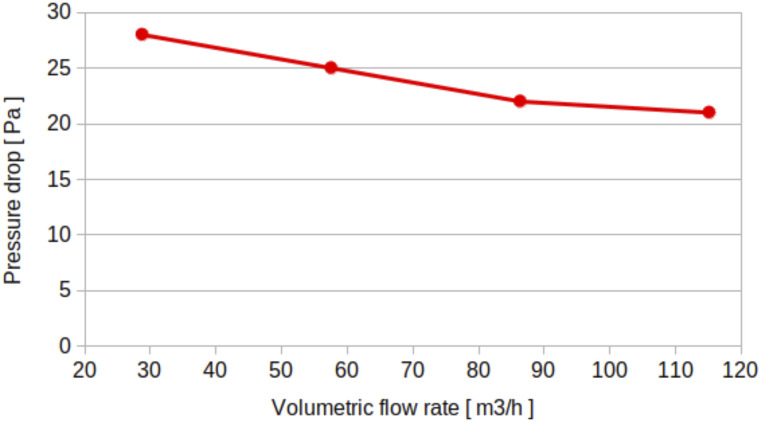
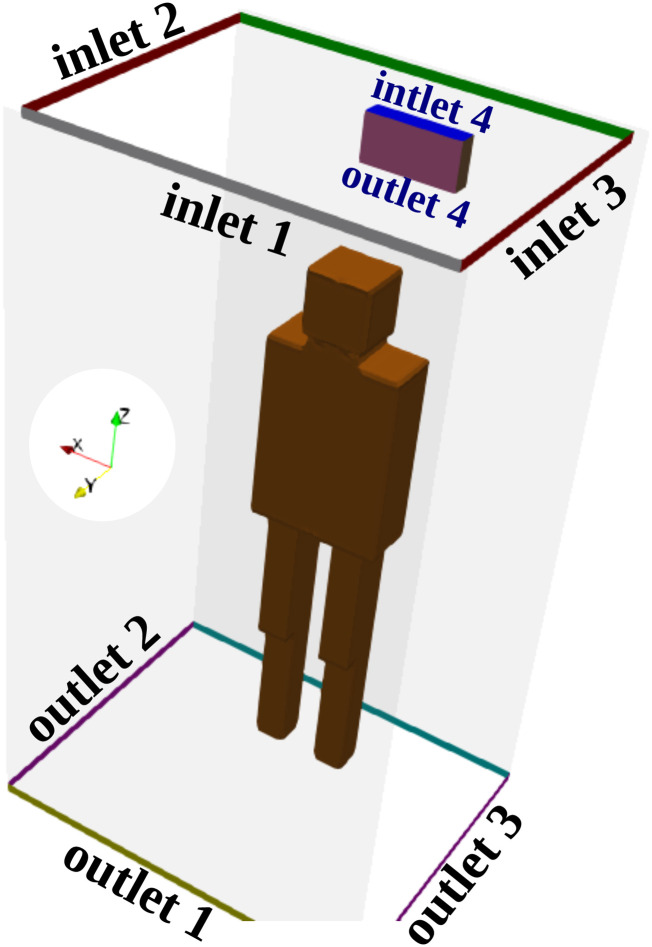
The boundary conditions for scenarios A, B, and C given in Table I correspond to a flow rate of 100 m3/h for the velocity at the inlets, the pressure condition at the outlets, and the no-slip condition on the walls. The above-mentioned conditions mimic the mechanical ventilation of a fan on top of the elevator’s ceiling. The boundary condition for scenario D given in Table I is a cyclic fan boundary condition with the flow curve illustrated in Fig. 3. We adjusted the specific flow curve to match the operating flow rate of a natural air purifier, which is in the order of 60 m3/h. This mimics the air intake at outlet 4 and the air exhaust at inlet 4, shown in Fig. 4. It is noteworthy that the patch outlet 4 of the purifier is named an outlet because at this patch, the flow leaves the computational domain, while it enters it at inlet 4, of course under scenario D given in Table I.

TABLE I.

All the applied scenarios for the operating conditions in Fig. 4.

Scenario A Inlet Outlet
On 1 1
On 2 2
On 3 3
Off 4 4
Scenario B Inlet Outlet
Off 1 1
On 2 2
On 3 3
Off 4 4
Scenario C Inlet Outlet
On 1 1
Off 2 2
Off 3 3
Off 4 4
Scenario D Inlet Outlet
Off 1 1
Off 2 2
Off 3 3
On 4 4
Open in a new tab

FIG. 3.

FIG. 3.

Open in a new tab

The flow curve of the fan integrated inside the sanitizer or air purifier.

FIG. 4.

FIG. 4.

Open in a new tab

Geometry showing the different inlets and outlets (δz = 3 cm opening) defined for the 3D computation domain. A subject is standing in the elevator’s cabin such that his mouth as a coughing source is positioned at x = 0 m, y = 0.41 m, z = 1.6 m. An air purifier (sanitizer) is attached to the wall at about 1.9 m above the ground of the elevator’s cabin. The air purifier has an air intake (outlet 4) and an air exhaust (inlet 4) for air circulation at ≈60 m3/h.

Recent studies showed how small droplets in poorly ventilated spaces could significantly contribute to SARS-CoV-2 transmission.38 Our objective in this study is to examine the fluid physics of airborne CoV contaminated saliva droplets inside an elevator at different scenarios of mechanical ventilation (Table I). Our focus is not only to study the effect of the forced ventilation design but also to investigate the effect of the integrated fan system in an air purifier on locally dispersing the droplets inside the lift. This is very important to assess the risk of AVT in confined spaces under different forced air circulation systems or designs. This will show scientists, engineers, and the wider public the significance to have an appropriate method of ventilation that could reduce the risk of AVT. Furthermore, the simulations aim to inform the regulatory authorities that they need to upgrade the safety codes of elevators and escalators (e.g., EN 81-20:2020 and EN 81-50:202039) in terms of forced ventilation to be adapted to new measures that reduce AVT in elevators.

III. RESULTS AND DISCUSSION

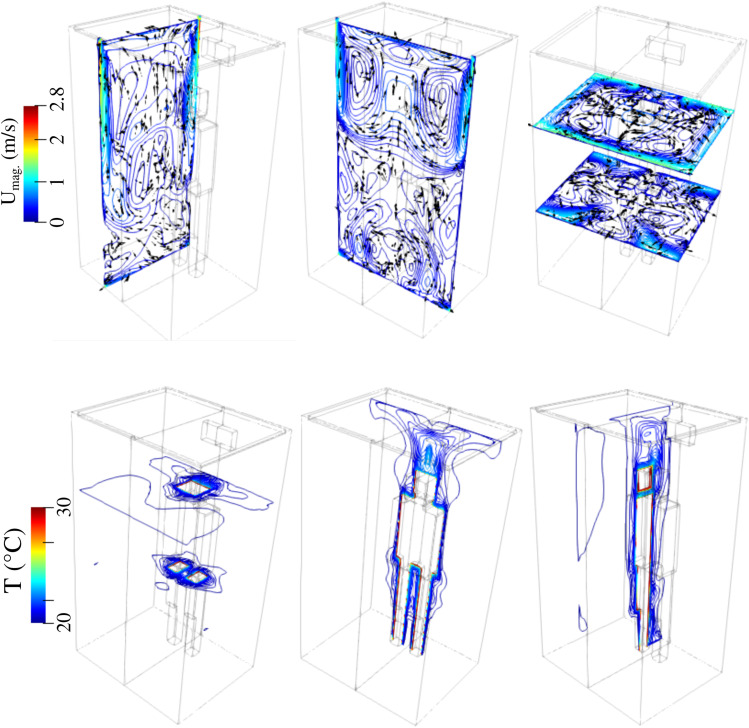
Indicatively, we present the velocity magnitude and temperature contours for scenario A (Table I) at t = 6 s in Fig. 5. Significant flow circulation occurs. The temperature is higher near the subject and tends to the ambient temperature (equilibrium) away from the subject boundary. Therefore, we should expect that different ventilation arrangements will contribute to the flow circulation and influence the droplet dynamics.

FIG. 5.

FIG. 5.

Open in a new tab

Scenario A–subject position 1. Top row: an example of the velocity magnitude at the planes x = 0.25 m, y = 0.6 m, z = 1.6 m and z = 0.8 m from left to right, respectively. Bottom row: an example of the temperature contour field at the planes x = 0.1 m, y = 0.25 m, z = 1.6 m and z = 0.8 m from left to right, respectively. The environment is at 20 °C and 50% relative humidity.

A. Qualitative analysis

1. Airborne virus transmission without an air purifier

We consider scenario A (Table I) and show the droplet dynamics in Fig. 6 at t = 2.5 s, 5 s, 7.5 s, 10 s, 12.5 s, and 14 s. The air purifier is off, and a high ventilation rate is applied with three inlets near the upper ceiling (Fig. 4). A single, mild cough from an infected person induces dispersion of the contaminated saliva droplets inside the elevator without evaporation for about 10 s. This constitutes a high risk of AVT as more people may enter the elevator during that period. The elevator speed may vary between 1 m/s, e.g., small residential buildings, and 10 m/s, e.g., towers. In a period of 10 s, an elevator may travel a total distance that can vary between 10 m (≈4 floors) and 100 m (≈45 floors).35,36 In actuality, an infected person that talks, laughs, or coughs, without a face mask, will expel a higher number of saliva droplets, compared to what we considered here for a single, mild cough case. Thus, the present scenario is the best possible scenario regarding droplet dispersion.

FIG. 6.

FIG. 6.

Open in a new tab

Scenario A—subject position 1. Top row: front view. Middle row: top view. Bottom row: side view. Contaminated saliva droplets are illustrated in black after being scaled by a factor of 250 with respect to their actual size. Subject position 1 corresponds to a person who is standing in the elevator’s cabin such that her/his mouth as a coughing source is positioned at x = 0 m, y = 0.41 m, z = 1.6 m. For the scenario A conditions, see Table I.

For a medium ventilation rate (scenario B, Table I), the droplet dispersion is still manifested in the elevator (Fig. 7). For example, at t = 12.5 s, a droplet cloud appears everywhere in front of the infected person, which increases the risk of AVT for new individuals entering the lift without wearing a face mask.9,40

FIG. 7.

FIG. 7.

Open in a new tab

Scenario B—subject position 1. Top row: front view. Middle row: top view. Bottom row: side view. Contaminated saliva droplets are illustrated in black after being scaled by a factor of about 250 with respect to their actual size. Subject position 1 corresponds to a person who is standing in the elevator’s cabin such that her/his mouth as a coughing source is positioned at x = 0 m, y = 0.41 m, z = 1.6 m. For the scenario B conditions, see Table I.

For the minimum ventilation rate—scenario C (Table I) with a single inlet being active—the AVT risk is lower than in scenarios A and B (Fig. 8). In scenario C, the dispersion of saliva droplets is limited to 3 s or 4 s only. This is due to reduced flow mixing inside the elevator when a smaller number of inlets for mechanical ventilation (or air intake) are installed. The regulatory authorities should define the minimum ventilation required depending on the type of the building.39

FIG. 8.

FIG. 8.

Open in a new tab

Scenario C—subject position 1. Top row: front view. Middle row: top view. Bottom row: side view. Contaminated saliva droplets are illustrated in black after being scaled by a factor of about 250 with respect to their actual size. Subject position 1 corresponds to a person who is standing in the elevator’s cabin such that her/his mouth as a coughing source is positioned at x = 0 m, y = 0.41 m, z = 1.6 m. For the scenario C conditions, see Table I.

Furthermore, we have investigated the influence of the position of an infected person inside the lift. The results are presented in Figs. 12Figs. 13Figs. 14 in the Appendix. The forced ventilation system can contribute significantly to AVT in confined spaces. Thus, one should take into account the above effects before designing elevator cabins, residential spaces and lobbies, restaurants, hospitals, and car parks, among others.

B. Airborne virus transmission using an air purifier

Furthermore, we consider scenario D (Table I), where an air purifier is in operation. Manufacturers have proposed the use of air purifiers to reduce the spread of COVID-19 inside elevators. Here, we do not investigate the physical mechanism inside the air purifier that deactivates viruses and/or germs, e.g., UV radiation. Instead, we are interested in the air intake/exhaust integrated system and its role in dispersing contaminated saliva droplets in the cabin. The air suction/ejection effects on AVT are usually ignored by manufacturers of air purification equipment.

For an air purifier installed and the subject experiencing a mild cough, we show (Figs. 9 and 10) the droplet transport for scenario D (Table I) for two different positions of the subject. If the person is in the middle of the elevator (Fig. 10), the air purifier induces local dispersion of the saliva droplets for at least 10 s. Moreover, positioning the subject closer to the air purifier delays the droplet spread throughout the space. We explain the mechanism by considering the flow dynamics around the subject. In position 1, the droplet source is closer to the air purifier. The space between the person and the cabin wall behind the person is smaller. Due to this, the flow circulation initially takes place at a higher position, a narrower area both ahead and behind and lateral to the person. Although we consider the least risky scenario, i.e., single, mild cough from a single person, the results show that AVT is still significant due to flow circulation. Comparing scenarios C and D, it shows that installing an air purifier may increase the droplet spread. The above effect increases when more infected persons enter the elevator. Thus, the air purifier design must be optimal for reducing flow circulation. Furthermore, we should allow a smaller number of people being in an elevator to minimize the droplet spread and its impact on each subject.

FIG. 9.

FIG. 9.

Open in a new tab

Scenario D—subject position 1. Top column: front view. Middle column: top view. Bottom column: side view. Contaminated saliva droplets are illustrated in black after being scaled by a factor of about 250 with respect to their actual size. Subject position 1 corresponds to a person who is standing in the elevator’s cabin such that her/his mouth as a coughing source is positioned at x = 0 m, y = 0.41 m, z = 1.6 m. For the scenario D conditions, see Table I.

FIG. 10.

FIG. 10.

Open in a new tab

Scenario D—subject position 2. Top column: front view. Middle column: top view. Bottom column: side view. Contaminated saliva droplets are illustrated in black after being scaled by a factor of about 250 with respect to their actual size. Subject position 2 corresponds to a person who is standing in the elevator’s cabin such that her/his mouth as a coughing source is positioned at x = 0 m, y = 0.675 m, z = 1.6 m. For the scenario D conditions, see Table I.

C. Quantitative analysis of airborne virus transmission

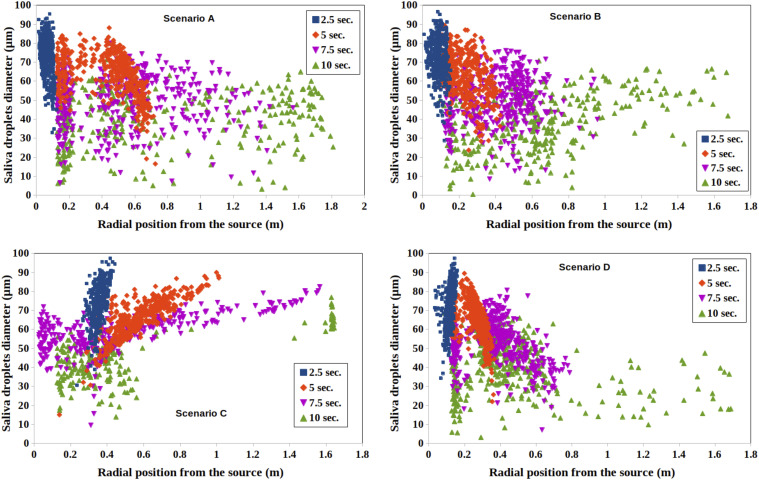
We performed a quantitative analysis of droplet dispersion resulting from mild cough of an infected person inside an elevator. Figure 11 shows the quantitative evolution of droplets and their diameter as a function of time for scenarios A, B, C, and D given in Table I. For A, at t = 2.5 s, most of the droplets lie in a radial position between 0 m and 0.15 m. Hence, they are close to the mouth of the infected individual. Their diameters vary between 30 μm and 95 μm. For t > 2.5 s, significant dispersion occurs, but the diameter of the droplets reduces with time due to evaporation.7,9

FIG. 11.

FIG. 11.

Open in a new tab

Quantitative analysis of dispersion of contaminated saliva droplets inside an elevator’s cabin resulting from a mild cough of an infected subject. The subject is at position 1 such that the source of the cough is positioned inside the lift at (x = 0, y = 0.41, z = 1.6) m (see Fig. 1). Four different ventilation scenarios A, B, C, and D are investigated according to Table I.

For scenario B (Fig. 11), the saliva droplets are less dispersed compared to scenario A, i.e., a smaller radial position from the source. The droplets’ diameter varies between 30 μm and 95 μm. For scenario C (11), at t = 10 s, two clusters of saliva droplets are observed. One is at a radial position from the source between 0.1 m and 0.8 m and another is farther away containing a small number of particles positioned radially between 1.4 m and 1.7 m. Therefore, the single inlet, per scenario C, reduces the dispersion of contaminated saliva droplets. Finally, when the air purifier is active, scenario D (Fig. 11), many contaminated saliva droplets are locally dispersed. Their radial position from the source is between 0.15 m and 1.7 m.

IV. CONCLUSIONS AND RECOMMENDATIONS

We investigated the respiratory droplet dynamics arising from a mild cough inside an elevator. The single-subject case constitutes the lowest risk scenario. We studied different ventilation configurations in conjunction with and without an air purifier inside the elevator. The computational setup is also applicable to other confined spaces.

The placement of ventilation inlets and outlets influences the flow circulation and droplet dispersion significantly. Without an air purifier, the case of a single inlet and outlet exhibits the least droplet dispersion. The subject’s position inside the cabin also influences the flow circulation and droplet spread. The air purifier reduces the droplet dispersion but will not eliminate it. The air intake integrated inside the purifier equipment induces flow circulation that can add to the transport of contaminated saliva droplets in the cabin. The time required for droplets reaching the floor of the elevator could be larger than the time necessary to deactivate the virus by other means such as UV radiation. Thus, the success of air purifiers lies in addressing the above-mentioned issue. The results of the present study are pertinent to any confined spaces, including small rooms in residential or commercial facilities, car parks, shops, as well as an aircraft cabin, submarines, and spacecraft.

The broader implications of the present findings are that health and safety authorities must revise guidelines accordingly by considering the flow circulation and droplet dispersion effects arising from air purifiers and sanitizers in confined spaces. The design of future ventilation and purification systems should aim at reducing AVT through minimization of droplet dispersion.

SUPPLEMENTARY MATERIAL

See the supplementary material (video) for the respiratory droplet dynamics inside an elevator cabin.

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request.

ACKNOWLEDGMENTS

The authors would like to thank the anonymous reviewers, the Editor-in-Chief, and Physics of Fluids staff for their assistance during the peer-review and publication of this manuscript.

APPENDIX: DIFFERENT FLOW SCENARIOS AND OPERATING CONDITIONS

Two position scenarios (1 and 2) for the subject are considered: (x = 0, y = 0.41, z = 1.6) m and (x = 0, y = 0.67, z = 1.6) m (see Fig. 1). The computational results for subject position No. 2 inside the elevator (without an air purifier) are shown in Figs. 12Figs. 13Figs. 14.

FIG. 12.

FIG. 12.

Open in a new tab

Scenario A—subject position 2. Top row: front view. Middle row: top view. Bottom row: side view. Contaminated saliva droplets are illustrated in black.

FIG. 13.

FIG. 13.

Open in a new tab

Scenario B—subject position 2. Top row: front view. Middle row: top view. Bottom row: side view. Contaminated saliva droplets are illustrated in black.

FIG. 14.

FIG. 14.

Open in a new tab

Scenario C—subject position 2. Top row: front view. Middle row: top view. Bottom row: side view. Contaminated saliva droplets are illustrated in black.

Note: This paper is part of the Special Topic, Flow and the Virus.

Contributor Information

Talib Dbouk, Email: .

Dimitris Drikakis, Email: .

REFERENCES

  • 1.WHO, Coronavirus Disease (COVID-19) (World Health Organization, 2020). [Google Scholar]
  • 2.Richard M., van den Brand J., Bestebroer T., Lexmond P., de Meulder D., Fouchier R., Lowen A., and Herfst S., “Influenza a viruses are transmitted via the air from the nasal respiratory epithelium of ferrets,” Nat. Commun. 11, 766 (2020). 10.1038/s41467-020-14626-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Yan J., Grantham M., Pantelic J., Bueno de Mesquita P. J., Albert B., Liu F., Ehrman S., Milton D. K., and Consortium E., “Infectious virus in exhaled breath of symptomatic seasonal influenza cases from a college community,” Proc. Natl. Acad. Sci. U. S. A. 115(5), 1081–1086 (2018). 10.1073/pnas.1716561115 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Xie X., Li Y., Sun H., and Liu L., “Exhaled droplets due to talking and coughing,” J. R. Soc., Interface 6, 703–714 (2009). 10.1098/rsif.2009.0388.focus [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Zhu S., Kato S., and Yang J.-H., “Study on transport characteristics of saliva droplets produced by coughing in a calm indoor environment,” Build. Environ. 41, 1691–1702 (2006). 10.1016/j.buildenv.2005.06.024 [DOI] [Google Scholar]
  • 6.To K. K.-W. et al. , “Consistent detection of 2019 novel coronavirus in saliva,” Clin. Infect. Dis. 71(15), 841 (2020). 10.1093/cid/ciaa149 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Dbouk T. and Drikakis D., “On coughing and airborne droplet transmission to humans,” Phys. Fluids 32, 053310 (2020). 10.1063/5.0011960 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Dbouk T. and Drikakis D., “On respiratory droplets and face masks,” Phys. Fluids 32, 063303 (2020). 10.1063/5.0015044 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Dbouk T. and Drikakis D., “Weather impact on airborne coronavirus survival,” Phys. Fluids 32, 093312 (2020). 10.1063/5.0024272 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Abuhegazy M., Talaat K., Anderoglu O., and Poroseva S. V., “Numerical investigation of aerosol transport in a classroom with relevance to COVID-19,” Phys. Fluids 32, 103311 (2020). 10.1063/5.0029118 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Busco G., Yang S. R., Seo J., and Hassan Y. A., “Sneezing and asymptomatic virus transmission,” Phys. Fluids 32, 073309 (2020). 10.1063/5.0019090 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Wang J.-X., Li Y.-Y., Liu X.-D., and Cao X., “Virus transmission from urinals,” Phys. Fluids 32, 081703 (2020). 10.1063/5.0021450 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Bhagat R. K., Davies Wykes M. S., Dalziel S. B., and Linden P. F., “Effects of ventilation on the indoor spread of COVID-19,” J. Fluid Mech. 903, F1 (2020). 10.1017/jfm.2020.720 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Smith S. H., Somsen G. A., van Rijn C., Kooij S., van der Hoek L., Bem R. A., and Bonn D., “Aerosol persistence in relation to possible transmission of SARS-CoV-2,” Phys. Fluids 32, 107108 (2020). 10.1063/5.0027844 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Agrawal A. and Bhardwaj R., “Reducing chances of COVID-19 infection by a cough cloud in a closed space,” Phys. Fluids 32, 101704 (2020). 10.1063/5.0029186 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Hu M., Lin H., Wang J., Xu C., Tatem A. J., Meng B., Zhang X., Liu Y., Wang P., Wu G., Xie H., and Lai S., “Risk of coronavirus disease 2019 transmission in train passengers: An epidemiological and modeling study,” Clin. Infect. Dis. ciaa1057, 1 (2020). 10.1093/cid/ciaa1057 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Lim T., Cho J., and Kim B. S., “Predictions and measurements of the stack effect on indoor airborne virus transmission in a high-rise hospital building,” Build. Environ. 46, 2413–2424 (2011). 10.1016/j.buildenv.2011.04.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Kanso M. A., Piette J. H., Hanna J. A., and Giacomin A. J., “Coronavirus rotational diffusivity,” Phys. Fluids 32, 113101 (2020). 10.1063/5.0031875 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Van Rijn C., Somsen G. A., Hofstra L., Dahhan G., Bem R. A., Kooij S., and Bonn D., “Reducing aerosol transmission of SARS-CoV-2 in hospital elevators,” Indoor Air 30(6), 1065 (2020), . 10.1111/ina.12744 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Smith R. S., “Cabin ventilation, code requirements and experimental results,” in Third Symposium on Lift and Escalator Technologies (CIBSE Lifts Group, The University of Northampton and LEIA, 2013), Vol. 3, pp. 148–156. [Google Scholar]
  • 21.Pacitto A., Amato F., Moreno T., Pandolfi M., Fonseca A., Mazaheri M., Stabile L., Buonanno G., and Querol X., “Effect of ventilation strategies and air purifiers on the children’s exposure to airborne particles and gaseous pollutants in school gyms,” Sci. Total Environ. 712, 135673 (2020). 10.1016/j.scitotenv.2019.135673 [DOI] [PubMed] [Google Scholar]
  • 22.Roy A., “A review of general and modern methods of air purification,” J. Therm. Eng. 5, 22–28 (2019). 10.18186/thermal.529054 [DOI] [Google Scholar]
  • 23.Fang J. and Zhu Z., “Material analysis and design of air purifier,” IOP Conf. Ser.: Mater. Sci. Eng. 585, 012107 (2019). 10.1088/1757-899x/585/1/012107 [DOI] [Google Scholar]
  • 24.Liu G., Xiao M., Zhang X., Gal C., Chen X., Liu L., Pan S., Wu J., Tang L., and Clements-Croome D., “A review of air filtration technologies for sustainable and healthy building ventilation,” Sustainable Cities Soc. 32, 375–396 (2017). 10.1016/j.scs.2017.04.011 [DOI] [Google Scholar]
  • 25.Tao H., Meng L., Liping P., and Jun W., “Studies on new air purification and air quality control system of airliner cabin,” Procedia Eng. 17, 343–353 (2011), part of the Special Issue: The 2nd International Symposium on Aircraft Airworthiness. 10.1016/j.proeng.2011.10.039 [DOI] [Google Scholar]
  • 26.Xia Y., “Simulation on spread of fire smoke in the elevator shaft for a high-rise building,” Theor. Appl. Mech. Lett. 4, 034007 (2014). 10.1063/2.1403407 [DOI] [Google Scholar]
  • 27.Shi L.-q., Liu Y.-z., Jin S.-y., and Cao Z.-m., “Numerical simulation of unsteady turbulent flow induced by two-dimensional elevator car and counter weight system,” J. Hydrodyn. 19, 720–725 (2007). 10.1016/s1001-6058(08)60009-8 [DOI] [Google Scholar]
  • 28.Miller R. S. and Beasley D., “On stairwell and elevator shaft pressurization for smoke control in tall buildings,” Build. Environ. 44, 1306–1317 (2009). 10.1016/j.buildenv.2008.09.015 [DOI] [Google Scholar]
  • 29.Black W. Z., “Smoke movement in elevator shafts during a high-rise structural fire,” Fire Saf. J. 44, 168–182 (2009). 10.1016/j.firesaf.2008.05.004 [DOI] [Google Scholar]
  • 30.Chen Y., Yang L., Fu Z., Chen L., and Chen J., “Gas flow behavior and flow transition in elevator shafts considering elevator motion during a building fire,” Build. Simul. 11, 765–771 (2018). 10.1007/s12273-018-0430-3 [DOI] [Google Scholar]
  • 31.Tamm G. and Jaluria Y., “Flow of hot gases in vertical shafts with natural and forced ventilation,” Int. J. Heat Mass Transfer 114, 337–353 (2017). 10.1016/j.ijheatmasstransfer.2017.06.058 [DOI] [Google Scholar]
  • 32.Zubair M. U. and Zhang X., “Explicit data-driven prediction model of annual energy consumed by elevators in residential buildings,” J. Build. Eng. 31, 101278 (2020). 10.1016/j.jobe.2020.101278 [DOI] [Google Scholar]
  • 33.Shao S., Zhou D., He R., Li J., Zou S., Mallery K., Kumar S., Yang S., and Hong J., “Risk assessment of airborne transmission of COVID-19 by asymptomatic individuals under different practical settings,” J. Aerosol Sci. 151, 105661 (2021). 10.1016/j.jaerosci.2020.105661 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Lu J., Gu J., Li K., Xu C., Su W., Lai Z., Zhou D., Yu C., Xu B., and Yang Z., “COVID-19 outbreak associated with air conditioning in restaurant, Guangzhou, China, 2020,” Emerging Infect. Dis. 26(7), 1628 (2020). 10.3201/eid2607.200764 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.CIBSE, Transportation Systems in Buildings (The Chartered Institution of Building Services Engineers, London, 1993). [Google Scholar]
  • 36.Barney G. and Al-Sharif L., Elevator Traffic Handbook: Theory and Practice (Routledge Taylor and Francis Group, London and New York, 2016). [Google Scholar]
  • 37.Celik I. B., Ghia U., Roache P. J., and Freitas C. J., “Procedure for estimation and reporting of uncertainty due to discretization in CFD applications,” J. Fluids Eng. 130, 078001 (2008). 10.1115/1.2960953 [DOI] [Google Scholar]
  • 38.Somsen G. A., van Rijn C., Kooij S., Bem R. A., and Bonn D., “Small droplet aerosols in poorly ventilated spaces and SARS-CoV-2 transmission,” Lancet Respir. Med. 8, 658–659 (2020). 10.1016/s2213-2600(20)30245-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.BSI, Safety Rules for the Construction and Installation of Lifts (BSI Standards Publication, 2020). [Google Scholar]
  • 40.Mittal R., Meneveau C., and Wu W., “A mathematical framework for estimating risk of airborne transmission of COVID-19 with application to face mask use and social distancing,” Phys. Fluids 32, 101903 (2020). 10.1063/5.0025476 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

See the supplementary material (video) for the respiratory droplet dynamics inside an elevator cabin.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Articles from Physics of Fluids are provided here courtesy of American Institute of Physics

RESOURCES