Professional musicians are a popular model for investigating experience-dependent plasticity in human large-scale brain networks. A minority of musicians possess absolute pitch, the ability to name a tone without reference. The study of absolute pitch musicians provides insights into how a very specific talent is reflected in brain networks.
Keywords: absolute pitch, connectivity, music, plasticity
Abstract
Professional musicians are a popular model for investigating experience-dependent plasticity in human large-scale brain networks. A minority of musicians possess absolute pitch, the ability to name a tone without reference. The study of absolute pitch musicians provides insights into how a very specific talent is reflected in brain networks. Previous studies of the effects of musicianship and absolute pitch on large-scale brain networks have yielded highly heterogeneous findings regarding the localization and direction of the effects. This heterogeneity was likely influenced by small samples and vastly different methodological approaches. Here, we conducted a comprehensive multimodal assessment of effects of musicianship and absolute pitch on intrinsic functional and structural connectivity using a variety of commonly used and state-of-the-art multivariate methods in the largest sample to date (n = 153 female and male human participants; 52 absolute pitch musicians, 51 non-absolute pitch musicians, and 50 non-musicians). Our results show robust effects of musicianship in interhemispheric and intrahemispheric connectivity in both structural and functional networks. Crucially, most of the effects were replicable in both musicians with and without absolute pitch compared with non-musicians. However, we did not find evidence for an effect of absolute pitch on intrinsic functional or structural connectivity in our data: The two musician groups showed strikingly similar networks across all analyses. Our results suggest that long-term musical training is associated with robust changes in large-scale brain networks. The effects of absolute pitch on neural networks might be subtle, requiring very large samples or task-based experiments to be detected.
SIGNIFICANCE STATEMENT A question that has fascinated neuroscientists, psychologists, and musicologists for a long time is how musicianship and absolute pitch, the rare talent to name a tone without reference, are reflected in large-scale networks of the human brain. Much is still unknown as previous studies have reported widely inconsistent results based on small samples. Here, we investigate the largest sample of musicians and non-musicians to date (n = 153) using a multitude of established and novel analysis methods. Results provide evidence for robust effects of musicianship on functional and structural networks that were replicable in two separate groups of musicians and independent of absolute pitch ability.
Introduction
Professional musicians are a commonly studied model for experience-dependent brain plasticity (Münte et al., 2002; Jäncke, 2009; Schlaug, 2015). Intense musical training starting early in life is thought to cause neuroplastic adaptations that are paralleled by improvements in audition, sensory-motor skills, and possibly higher-order cognitive functions (Fujioka et al., 2006; Hyde et al., 2009; Seither-Preisler et al., 2014; Habibi et al., 2018). In recent years, a major focus within the neuroscience of music has been on training-related plasticity in large-scale brain networks, which underlie most human sensory, motor, and cognitive functions (Bressler and Menon, 2010).
Previous research provides evidence that musicianship is associated with differences in both the intrinsic functional and structural networks of the human brain. However, an examination of these studies reveals inconsistencies in findings regarding the location of the effects in the brain and also the direction of these effects. For example, whereas most of the studies report hyperconnectivity in musicians compared with non-musicians (Fauvel et al., 2014; Klein et al., 2016), others have found hypoconnectivity (Imfeld et al., 2009) or both (Schmithorst and Wilke, 2002; Bengtsson et al., 2005). These studies suggest that, in musicians, connectivity between brain regions is altered across the entire brain, including sensory, motor, multisensory, and cognitive regions of the cortex (Klein et al., 2016; Palomar-García et al., 2017), subcortex (Luo et al., 2012), and the cerebellum (Abdul-Kareem et al., 2011).
The diversity of these findings could be influenced by small sample sizes and inconsistent methodology. In studies examining intrinsic functional connectivity, the number of participants in the musician groups ranged from 10 (Zamorano et al., 2017) to 25 (Luo et al., 2014); and in studies examining structural connectivity, from only 5 (Schmithorst and Wilke, 2002) to 36 (Steele et al., 2013). Studies with small samples lack the statistical power to detect small effects, and findings from small-scale studies have a higher probability of returning false positives (Button et al., 2013). With regard to methodology, many previous studies took an ROI-based approach. To our knowledge, only two functional connectivity studies exist using a data-driven, connectomic whole-brain approach (Luo et al., 2014; Klein et al., 2016). Studies on structural networks in musicians have exclusively used an ROI-based approach by focusing on separate white-matter tracts or brain regions. No previous structural connectivity study comparing musicians and non-musicians has used a whole-brain connectomic approach.
Apart from general effects of musicianship, some studies have focused on a special talent present among musicians: absolute pitch (AP), the rare ability to name a tone without reference (Deutsch, 2013). Only a few studies examined intrinsic functional networks in AP versus non-AP musicians. Again, the findings of these studies show little consistency, suggesting an effect of AP on functional connectivity of sensory, parietal, and frontal cortex (Elmer et al., 2015; Kim and Knösche, 2017; Brauchli et al., 2019). The applied methodology differed widely between studies (compare Jäncke et al., 2012; Loui et al., 2012; Wenhart et al., 2019). An effect of AP on structural connectivity has been reported in the vicinity of associative auditory areas (Loui et al., 2011; Dohn et al., 2015; Kim and Knösche, 2016; Burkhard et al., 2020). None of the previous studies investigating AP and structural connectivity used a whole-brain connectomic approach. Importantly, all of these results have yet to be replicated in an independent sample.
Together, findings from previous studies are highly inconsistent, possibly because of small samples and methodological differences. In this study, we aimed to identify robust effects of musicianship and AP on functional and structural connectivity using a multitude of previously used and novel methods on a large multimodal dataset (n = 153), consisting of 52 AP musicians, 51 non-AP musicians, and 50 non-musicians. We used ROI-based and whole-brain approaches, and a multivariate approach based on machine learning algorithms. Crucially, we determined whether effects of musicianship were replicable in both musician groups, regardless of their AP ability.
Materials and Methods
Participants
We analyzed resting-state fMRI (rsfMRI) and diffusion-weighted imaging (DWI) data of 153 female and male human participants. A portion of the rsfMRI data (Brauchli et al., 2019) and the DWI data (Burkhard et al., 2020) was previously analyzed using a different methodology. The participants consisted of three groups: AP musicians (n = 52), non-AP musicians (n = 51), and non-musicians (n = 50). The groups were comparable regarding sex, handedness, age, rsfMRI movement, and DWI movement (see Table 1). Participants of the musician groups were professional musicians, music students, or highly trained amateurs. Assignment to the musician groups (AP or non-AP) was based on self-report and confirmed by a tone-naming test (Oechslin et al., 2010a,b). During the test, participants had to name 108 pure tones presented in a pseudorandomized order. Octave errors were disregarded in the calculation of the tone-naming score. In the rare case that a potential participant had indicated to be an AP musician in the initial online application form but then performed around chance level (8.3%) in the tone-naming test, we did not invite this individual to undergo the imaging experiments in the laboratory. In contrast, we did invite individuals who had indicated to be non-AP musicians and then showed a high level of proficiency in tone-naming that was above chance level (and reiterated in the laboratory that they do not possess AP); we did not regroup these participants as AP musicians (Leipold et al., 2019a). Non-musicians had not received formal musical training in the 5 years before the study.
Table 1.
Participant characteristicsa
| AP musicians | Non-AP musicians | Non-musicians | |
|---|---|---|---|
| No. of participants | 52 | 51 | 50 |
| Sex (female/male) | 24/28 | 24/27 | 24/26 |
| Handedness (right/left/both) | 45/4/3 | 46/4/1 | 44/6/0 |
| Age | 26.37 ± 4.98 years | 25.29 ± 4.42 years | 25.86 ± 5.52 years |
| rsfMRI movementb | 8.90 ± 16.31 scans | 5.61 ± 11.77 scans | 5.26 ± 15.43 scans |
| DWI movementc | 0.47 ± 0.11 | 0.48 ± 0.11 | 0.44 ± 0.12 |
| Musical aptitude (AMMA) total | 66.04 ± 6.18 | 63.45 ± 6.96 | 52.80 ± 9.22 |
| Musical aptitude (AMMA) tonal | 32.33 ± 3.67 | 30.55 ± 4.23 | 25.34 ± 5.02 |
| Musical aptitude (AMMA) rhythm | 33.71 ± 2.78 | 32.90 ± 3.03 | 27.46 ± 4.58 |
| Tone-naming score | 76.41 ± 19.96% | 23.66 ± 19.16% | 8.41 ± 3.52% |
| Age of onset of musical training | 6.06 ± 2.40 | 6.53 ± 2.39 | — |
| Years of musical training | 20.31 ± 5.26 years | 18.76 ± 5.01 | — |
| Cumulative musical training | 16,347.68 ± 12,582.35 hours | 13,830.10 ± 9985.04 hours | — |
aContinuous measures are given as mean ± SD.
bNumber of scans with FD ≥ 0.5 (Power et al., 2012).
cMean of average scan-to-scan translational (in millimeters) and rotational motion (in degrees) (Yendiki et al., 2014).
Demographical (sex, handedness, age) and behavioral data (musical aptitude, musical experience, and tone-naming proficiency) were collected using LimeSurvey (https://www.limesurvey.org/). Self-reported handedness was confirmed using a German translation of the Annett questionnaire (Annett, 1970). Musical aptitude was assessed using the Advanced Measures of Music Audiation (AMMA) (Gordon, 1989). During the AMMA test, participants were presented with short pairs of piano sequences. The participants had to decide whether the sequences were equivalent or differed in tonality or rhythm. None of the participants reported any neurologic, audiological, or severe psychiatric disorders, substance abuse, or other contraindications for MRI. All participants provided written informed consent and were paid for their participation or received course credit. The study was approved by the local ethics committee (https://kek.zh.ch/) and conducted according to the principles defined in the Declaration of Helsinki.
Experimental design and statistical analysis
Statistical analysis of behavioral data
Participant characteristics were compared between the groups using one-way ANOVAs with a between-participant factor Group or Welch's t tests where appropriate (significance level α = 0.05). The analyses were performed in R (version 3.6.0, RRID:SCR_001905). We used the R packages ez (version 4.4-0, https://CRAN.R-project.org/package=ez) for frequentist ANOVAs and BayesFactor (version 0.9.12-4.2, https://CRAN.R-project.org/package=BayesFactor) for Bayesian ANOVAs (Rouder et al., 2012) and Bayesian t tests (Rouder et al., 2009). We used default priors as implemented in the BayesFactor package. Consequently, alongside p values, we report Bayes factors quantifying the evidence for the alternative relative to the null hypothesis (BF10) and vice versa (BF01). Bayes factors are interpreted as evidence for one hypothesis relative to the other hypothesis. A Bayes factor between 1 and 3 is considered as anecdotal evidence, between 3 and 10 as moderate evidence, between 10 and 30 as strong evidence, between 30 and 100 as very strong evidence, and larger than 100 as extreme evidence. Effect sizes of ANOVA effects are given as generalized η-squared (η2G), and effect sizes for t tests are given as Cohen's d.
MRI data acquisition
MRI data were acquired using a Philips Ingenia 3.0T MRI system (Philips Medical Systems) equipped with a commercial 15-channel head coil. For each participant, we acquired whole-brain rsfMRI and DWI data, and a whole-brain anatomic T1-weighted image to facilitate the spatial normalization of the rsfMRI and DWI data. For the musician groups, we also collected fMRI data during a pitch-processing task, which is discussed in another publication (Leipold et al., 2019a). The whole scanning session lasted ∼50 min.
rsfMRI data acquisition
For the acquisition of rsfMRI data, we used a T2*-weighted gradient echo EPI sequence with the following parameters: TR = 2300 ms; TE = 30 ms; flip angle α = 78°; slice scan order = interleaved; number of axial slices = 40; slice thickness = 3 mm; FOV = 220 × 220 × 143 mm3; acquisition voxel size = 3 × 3 × 3 mm3, reconstructed to a spatial resolution of 2.75 × 2.75 × 3.00 mm3 with a reconstruction matrix of 80 × 80; number of dummy scans = 5; total number of scans = 210; total scan duration = 8 min. Participants were instructed to relax and look at a fixation cross during the scanning.
DWI data acquisition
We acquired DWI data using a diffusion-weighted spin echo EPI sequence with the following parameters: TR = 10,022 ms, TE = 89 ms, acquisition and reconstructed voxel size = 2 × 2 × 2 mm3, reconstruction matrix = 112 × 112, flip angle α = 90°, FOV = 224 × 224 × 152 mm3, number of axial slices = 76, B = 1000 s/mm2, number of diffusion-weighted scans/directions = 64, number of non–diffusion-weighted scans = 1, total scan duration = 14 min. Additionally, we acquired six non–diffusion-weighted images (B = 0) in opposing phase-encoding directions (anterior-posterior, posterior-anterior), which were used during the preprocessing of the DWI data.
T1-weighted MRI data acquisition
The anatomic image was acquired using a T1-weighted gradient echo turbo field echo sequence with the following parameters: TR = 8.1 ms; TE = 3.7 ms; flip angle α = 8°; number of sagittal slices = 160; FOV = 240 × 240 × 160 mm3; acquisition voxel size = 1 × 1 × 1 mm3, reconstructed to a spatial resolution of 0.94 × 0.94 × 1.00 mm3 with a reconstruction matrix of 256 × 256; total scan duration = 6 min.
MRI data preprocessing
rsfMRI data preprocessing
Preprocessing of the rsfMRI data was performed in MATLAB R2016a (RRID:SCR_001622) using DPARSF (version 4.4_180801, RRID:SCR_002372), which is part of DPABI (version 4.0_190305, RRID:SCR_010501) and uses functions of SPM12 (version 6906, RRID:SCR_007037). Preprocessing included the following steps: (1) slice time correction using the middle slice as a reference; (2) realignment using a six-parameter (three translations and three rotations) rigid body transformation; (3) coregistration of rsfMRI data and the T1-weighted anatomic image; (4) segmentation of the T1-weighted anatomic image into gray matter, white matter, and cerebrospinal fluid, and estimation of deformation field for spatial normalization; (5) GLM-based removal of nuisance covariates, including (a) low-frequency trends (first degree polynomial), (b) effects of head motion estimated by the six realignment parameters and their first temporal derivatives, (c) five principle components of white matter and cerebrospinal fluid signals using CompCor (Behzadi et al., 2007), and (d) the global signal; (6) temporal filtering (0.008-0.09 Hz); (7) spatial normalization of rsfMRI data to MNI space using DARTEL (Ashburner, 2007); (8) interpolation to an isotropic voxel size of 3 mm3; (9) spatial smoothing using an 8 mm FWHM kernel; and (10) removal of scans (“scrubbing”) with framewise displacement (FD) ≥ 0.5, together with the scan immediately before, and together with the two scans immediately after the scan with FD ≥ 0.5 (Power et al., 2012). The quality of spatial normalization was manually inspected.
DWI data preprocessing
Preprocessing of the DWI data was performed in FSL (version 6.0.1, RRID:SCR_002823). First, we used topup to estimate susceptibility-induced and eddy current-induced distortions based on the non–diffusion-weighted images acquired in opposing phase encoding directions. Then, we simultaneously corrected for these distortions and for motion artifacts using eddy (Andersson and Sotiropoulos, 2016). As a quality control step, we visually checked the orientation of the principal eigenvector (V1) using DTIFIT on the preprocessed DWI data.
rsfMRI seed-to-voxel analyses
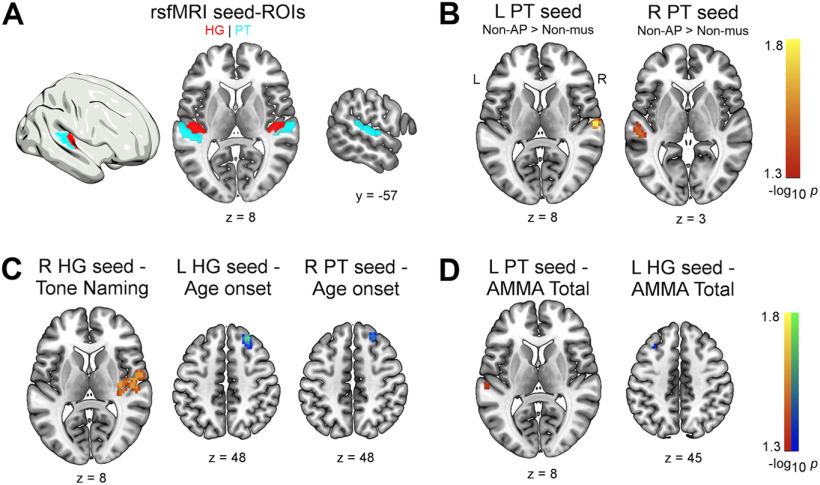
We examined intrahemispheric and interhemispheric functional connectivity between auditory ROIs and voxels in the temporal, parietal, and frontal lobe. In both hemispheres, the Heschl's gyrus (HG) and the planum temporale (PT) were selected as seed regions (Fig. 1A). For each participant, we initially computed the functional connectivity between the seed ROIs and all other voxels of the brain using DPABI. The ROIs were based on probability maps of parcels included in the Harvard-Oxford cortical atlas (probability threshold = 25%). Functional connectivity maps were built by computing the Pearson correlation coefficient between the preprocessed, spatially averaged time series within an ROI and the preprocessed time series of all voxels. To improve the normality of the resulting voxelwise correlation values, we subsequently applied a Fisher's r-to-z transformation. This resulted in four (one per ROI) z-transformed connectivity maps per participant, which were subjected to second-level analyses.
Figure 1.
A, Auditory ROIs used in the rsfMRI seed-to-voxel analyses. Red represents HG. Sky blue represents PT. Maps for ROIs were derived from the probabilistic Harvard-Oxford cortical atlas as implemented in DPABI. B, Increased intrinsic functional connectivity between left and right PT in non-AP musicians compared with non-musicians (pFWE < 0.05). C, Associations between functional connectivity and behavior in musicians and (D) across all subjects (pFWE < 0.05). L, Left; R, right.
Group comparisons of functional connectivity maps
To assess the effect of AP, we compared the functional connectivity maps between AP musicians and non-AP musicians. To assess the effect of musicianship, we compared the functional connectivity maps between non-AP musicians and non-musicians. To replicate potential effects of musicianship, we additionally compared AP musicians and non-musicians. For all group comparisons, we used nonparametric two-sample t tests (threshold-free cluster enhancement inference, 10,000 permutations) in PALM (version alpha115, RRID:SCR_017029) (Winkler et al., 2014). The significance level was set to α = 0.05, familywise error (FWE) adjusted for multiple comparisons. We restricted the search space of the group comparisons using a mask that included the following bilateral regions of the Harvard-Oxford cortical atlas thresholded at 10% probability: HG; PT; planum polare (PP); superior temporal gyrus (STG; anterior and posterior division); middle temporal gyrus (MTG; anterior and posterior division); insular cortex; supramarginal gyrus (SMG; anterior and posterior division); angular gyrus; superior parietal lobule; postcentral gyrus (postCG); precentral gyrus (preCG); inferior frontal gyrus, pars opercularis (IFG,po); inferior frontal gyrus, pars triangularis; middle frontal gyrus; and superior frontal gyrus. The selection of these regions was primarily guided by dual-stream models of auditory processing, which, in broad terms, propose that auditory information is processed in two streams: a ventral stream projecting from primary auditory areas on the supratemporal plane along anterior and middle temporal regions to inferior frontal cortex, and a dorsal stream projecting from primary areas along posterior temporal regions to parietal and superior frontal cortices (Rauschecker and Scott, 2009; Leipold et al., 2019b). We also included the insula as its functional connectivity has been previously studied as a function of musicianship (Zamorano et al., 2017; Gujing et al., 2019).
Functional connectivity-behavior associations
We used regression analysis for relating behavioral measures of musical aptitude (AMMA total scores), tone-naming proficiency, and musical experience (age of onset of musical training, years of training, cumulative training) to the functional connectivity of the auditory ROIs. Separately for each behavioral measure, we performed voxelwise regression of the functional connectivity maps with the respective behavioral measure as a single regressor using PALM (threshold-free cluster enhancement inference, 10,000 permutations, same search space as for the group comparisons). Musical aptitude can be sensibly measured in all participants (Gordon, 1989). However, tone naming requires knowledge on tone names, which non-musicians might not have, and measures of musical experience are only meaningful for musicians. Thus, we included all participants in the voxelwise regression using the AMMA total scores but only included the musician groups for the regression using the tone-naming scores, age of onset, years of training, and cumulative training. The significance level was set to α = 0.05, FWE-adjusted for multiple comparisons.
rsfMRI whole-brain graph-theoretical analysis
To assess effects of AP and musicianship on whole-brain functional connectivity, we used graph theory to characterize global differences in network topology between the groups. For each participant, we computed functional connectivity between all 96 parcels of the Harvard-Oxford cortical atlas (probability threshold = 25%) using DPABI. Functional connectivity was quantified as Fisher's r-to-z-transformed Pearson correlation coefficients between the preprocessed, spatially averaged time series of each parcel. This resulted in a 96 × 96 connectivity matrix per participant representing a whole-brain functional connectome comprising the individual parcels as nodes and the correlation coefficients as edges. Negative edges and edges from the diagonal of the connectivity matrices were set to zero.
Whole-brain functional network topology was quantified using the graph-theoretical measures of average strength, global efficiency, clustering coefficient, modularity, and (average) betweenness centrality as implemented in the Brain Connectivity Toolbox (version 2019-03-03, RRID:SCR_004841) in MATLAB R2017b (Rubinov and Sporns, 2010). Average strength characterizes how strongly the nodes are connected within a network and was defined as the mean of all node strengths. Node strength was computed by taking the sum of all edges of a node. Global efficiency, being inversely related to the characteristic path length, represents a measure of network integration and was computed as the mean inverse shortest path length in the network. The clustering coefficient is a measure of network segregation and was based on transitivity, which is the ratio of triangles to triplets in the network. Modularity describes the degree to which a network is subdivided into groups of nodes with a large number of within-module edges and a small number of between-module edges. The (average) betweenness centrality of the network was defined as the mean nodal betweenness centrality, which itself was computed based on the normalized number of all shortest paths in the network passing through a node.
For each participant, we proportionally thresholded and binarized the connectivity matrices using a wide range of thresholds from 35% to 1% retained edges in the network (in steps of 1%). We then computed the above-listed measures for each threshold resulting in 35 values per measure and participant (average strength was based on nonbinarized connectivity matrices).
Group comparisons of whole-brain functional network topology
Group comparison of the graph-theoretical measures was performed using cluster-based permutation testing in R. Cluster-based permutation testing uses the dependency of graph-theoretical measures across thresholds to control the FWE rate and circumvents the choice of a single arbitrary threshold (Langer et al., 2013; Drakesmith et al., 2015; Brauchli et al., 2020). We estimated the probability of clustered differences between the groups (i.e., across contiguous thresholds) under the null distribution. As before, we separately assessed the effects of AP (by comparing AP with non-AP musicians) and musicianship (by comparing non-AP with non-musicians). In addition, we replicated the potential effects of musicianship by comparing AP with non-musicians. In detail, we first conducted a two-sample Welch's t test at each threshold. Second, we repeated the first step 5000 times with permuted group labels. Crucially, we preserved the dependency across thresholds by keeping the random assignment of group labels identical across thresholds within one permutation. Third, we applied a (descriptive) cluster-defining threshold of p < 0.05 to build clusters of group differences. Finally, we compared the largest empirical cluster sizes k to the null distribution of cluster sizes derived from the permutations. The p value was defined as the proportion of cluster sizes under the null distribution that was larger than or equal to k (α = 0.05, FWE-adjusted across multiple thresholds).
Whole-brain functional network topology-behavior associations
We assessed associations between the graph-theoretical measures and the behavioral measures (AMMA total scores for all participants, tone-naming proficiency, age of onset, years of training, and cumulative training for the musician groups). For this, we computed the Pearson correlation coefficient (r) between the graph-theoretical measure averaged across all thresholds and the particular behavioral measure (α = 0.01, Bonferroni-adjusted across multiple graph-theoretical measures).
rsfMRI whole-brain network-based statistic (NBS) analysis
To characterize local between-group differences in the whole-brain functional networks, we identified subnetworks differing between AP and non-AP musicians, between non-AP and non-musicians, and additionally between AP and non-musicians using two-sample t tests as implemented in the NBS toolbox (version 1.2, RRID:SCR_002454) (Zalesky et al., 2010). Analogous to cluster-based permutation testing, the NBS approach estimates the probability of group differences in subnetwork sizes under the null distribution and controls the FWE rate on the level of subnetworks. We used the following parameters: 5000 permutations, test statistic = network extent, and subnetwork-defining thresholds; t = 2.8 for AP versus non-AP, and non-AP versus non-musicians; and t = 3.4 for AP versus non-musicians. Statistically significant subnetworks were visualized using BrainNet Viewer (version 1.63, RRID:SCR_009446).
rsfMRI whole-brain classification analysis
Next, using multivariate pattern analysis (MVPA), we attempted to classify the participants into the three groups based on the individual whole-brain functional connectomes. Group classification of the participants was performed with functions from scikit-learn (version 0.21.2, RRID:SCR_002577) in Python 3.7.0 (RRID:SCR_008394). We first performed a multiclass classification into the three groups (AP, non-AP, non-musicians) using a “one-against-one” approach with linear support vector machines (C = 1) as classifiers. For each participant, we extracted and flattened the upper right triangle of the connectivity matrix (excluding the diagonal) to build a 4560-dimensional feature vector representing all edges in the whole-brain functional network. These vectors were associated with their respective group labels (AP, non-AP, non-musician) and stacked to build a dataset. We then z-transformed the dataset per feature and subsequently performed the classification of the participants into the groups. Classification accuracy was estimated using a fivefold stratified cross-validation. Statistical significance of this accuracy was assessed by repeating the multiclass classification 5000 times with permuted group labels. The p value was defined as the proportion of accuracies derived from the permutations that were larger than or equal to the empirically obtained accuracy (α = 0.05). To descriptively determine whether a small number of features was sufficient for a successful classification, we used recursive feature elimination, which recursively prunes the least important feature (step = 1) to characterize accuracy as a function of the number of (informative) features (De Martino et al., 2008). The optimal number of features was determined using a fivefold stratified cross-validation. Subsequently, we performed two follow-up classifications to differentiate AP from non-AP musicians and non-AP from non-musicians. The success of these classifications was quantified by classification accuracy, precision, and recall. We used the identical algorithm, cross-validation scheme, assessment of the statistical significance of the accuracy, and recursive feature elimination as in the multiclass classification.
DWI ROI-to-ROI analysis
Based on the findings from the rsfMRI seed-to-voxel analyses, we next examined the interhemispheric structural connectivity between the left and the right PT in the three groups. First, we estimated diffusion parameters based on the preprocessed DWI data by fitting a diffusion tensor model at each voxel using DTIFIT in FSL. We specifically focused on two commonly investigated diffusion measures: fractional anisotropy (FA) and mean diffusivity (MD; computed as the mean of the three eigenvalues L1, L2, and L3). Second, we individually reconstructed the white-matter pathways between the left and right PT using probabilistic tractography in FSL (default parameters unless otherwise stated). For this, we fitted a probabilistic diffusion model at each voxel using BEDPOSTX (Behrens et al., 2003). Probabilistic tractography was performed on the output of BEDPOSTX using PROBTRACKX (10,000 samples).
As in the rsfMRI analyses, the ROIs for the probabilistic tractography were based on atlases in MNI space. The seed and target ROIs for the bilateral PT were chosen based on the Harvard-Oxford atlas (probability threshold = 25%). As a waypoint ROI, we used the midsagittal slice (3 mm thickness) of the corpus callosum map from the Jülich histological atlas (probability threshold = 10%). As exclusion ROIs, we used the preCG and postCG as included in the Harvard-Oxford atlas (probability threshold = 25%) to avoid false-positive pathways terminating in these brain regions. All ROIs were spatially dilated (5 mm spherical kernel) to increase the trackability of the pathways between them and to compensate for interindividual anatomic variability. Because probabilistic tractography was performed in participant-specific diffusion space, we computed the linear transformation from the individual diffusion space to the individual anatomic space using flirt and the nonlinear transformation from individual anatomic space to MNI space using fnirt in addition to flirt. Then, we concatenated these transformations using convertwarp and inverted the concatenated transformation using invwarp. The resulting warp fields (individual diffusion to MNI space and vice versa) were used in the tractography.
Third, we extracted FA and MD values from the DTIFIT output based on the pathways identified by the tractography, more specifically based on the sum of the connectivity distributions of pathways connecting the left PT to the right and vice versa. Before the extraction, we thresholded and binarized the connectivity distributions to retain the 3% voxels with the highest probability per participant. The extracted FA and MD values were compared between AP and non-AP musicians, and non-AP and non-musicians using Welch's t tests in R (α = 0.025, Bonferroni-adjusted for multiple diffusion measures). Again, we also compared AP and non-musicians to replicate the potential effects of musicianship. We also associated the FA and MD values with the behavioral measures (AMMA total scores for all participants; tone-naming proficiency, age of onset, years of training, and cumulative training for the musician groups) using r (α = 0.025).
DWI whole-brain graph-theoretical analysis
Analogously to the rsfMRI analyses, we assessed the effects of AP and musicianship on whole-brain structural connectivity. For this, we performed probabilistic tractography between all parcels of the Harvard-Oxford cortical atlas (probability threshold = 25%) using BEDPOSTX and PROBTRACKX (5000 samples). For each participant, this resulted in a 96 × 96 connectivity matrix representing a whole-brain structural connectome with the parcels as nodes and the connection probability (represented by the number of streamlines) between them as edges. Based on these connectivity matrices, we quantified and compared whole-brain structural network topology between AP and non-AP musicians, non-AP and non-musicians, and additionally between AP and non-musicians. All subsequent analysis steps were identical compared with the rsfMRI whole-brain graph-theoretical analysis (see above for details). We also performed the same correlations between the graph-theoretical measures and the behavioral measures as described above.
DWI whole-brain NBS analysis
We repeated the NBS analysis on the structural connectivity matrices to identify structural subnetworks differing between the groups. Apart from the subnetwork-defining threshold (here: t = 2.7 for AP vs non-AP, and non-AP vs non-musicians, and t = 2.8 for AP vs non-musicians), we used identical parameters as in the rsfMRI analysis (see above for details).
DWI whole-brain classification analysis
We also performed the classification analysis based on the whole-brain structural networks. Apart from the different connectivity matrices, all analysis steps and parameters were identical to the rsfMRI whole-brain classification (see above for details).
General methodological considerations
To comprehensively assess effects of musicianship and AP on functional and structural networks, we used a variety of methods. The acquisition techniques and analytical approaches used in this study have relative advantages and limitations, which are detailed in the following.
Validity and reliability of functional networks derived from rsfMRI
The crucial advantage of rsfMRI is its unique ability to noninvasively resolve functional connections of the human brain at a high spatial resolution. However, the relation between neuronal activity and the BOLD signal measured using rsfMRI is indirect and mediated by blood flow, volume, and oxygenation. Electrophysiological oscillations at the neuronal level are correlated with the slow oscillations in BOLD signal (<0.1 Hz) that are the basis of functional networks. This correlation is not perfect and leaves considerable variance, which can be explained by noise of (non-neuronal) biological and technical origin (Drew et al., 2020). The reliability of functional networks derived from rsfMRI varies greatly depending on factors, such as data quantity and quality, brain regions involved, preprocessing choices, time interval between scans, and the spatial level of analysis (local vs global). While individual edges can exhibit poor reliability (Noble et al., 2019), whole-brain functional networks are remarkably stable and highly sensitive to interindividual differences (Gratton et al., 2018), making them prime targets for comparing groups of different expertise (e.g., musicians and non-musicians).
Validity and reliability of structural networks derived from DWI
At present, DWI is the sole method for the noninvasive investigation of the white-matter pathways underlying structural networks of the human brain in vivo. Concerning neuroanatomical validity, it has been shown that the estimation of fiber orientations based on DWI can be reasonably high, although the measurement is indirect because it is based on water diffusion, and estimation accuracy depends on acquisition parameters (spatial resolution, number of directions), and the conformity between complexity of the studied white-matter architecture and the mathematical model to infer this architecture, among others (Jones et al., 2020). Furthermore, tractography algorithms can lack specificity in identifying white-matter tracts (Maier-Hein et al., 2017) but can also lack sensitivity for certain tracts. For example, Westerhausen et al. (2009) did not identify a tract connecting bilateral PT in >10% of participants (see below for similar findings in our study). Finally, the neurobiological interpretation of diffusion measures (e.g., FA and MD) is notoriously challenging as there are no straightforward correlates of these measures in white-matter microstructure, and DWI-based tractography cannot provide a quantitative estimate of connection strength, but only an estimate of connection probability (Jones et al., 2013). On the upside, the reliability of structural networks based on DWI is relatively high, but also dependent on many factors, for example, acquisition parameters (Wang et al., 2012), or preprocessing choices (Madhyastha et al., 2014).
Merits and shortcomings of ROI-based and whole-brain analysis approaches
Focusing on a set of brain regions in a seed-to-voxel analysis or separate tracts in an ROI-based approach is well suited to test specific hypotheses and alleviate the multiple-comparisons problem. On the other hand, whole-brain approaches are more suitable for exploration and discovery. Combining both approaches, as we have done in this study, provides a more complete picture than using each approach on its own. The same applies to the use of separate flavors of whole-brain approaches, which in turn have relative advantages and limitations. First, using graph theory has the advantage that the same approach can be applied to both functional and structural networks, providing metrics that quantify topological features of these networks in a single or a few values (Rubinov and Sporns, 2010). Graph-theoretical measures provide a bird's-eye view of networks that complements the focused perspective of ROI approaches. An issue with graph theory concerns the use of thresholding to remove spurious connections: The type of thresholding used in graph-theoretical analyses of brain networks (e.g., proportional or absolute thresholding) is subject to ongoing discussions (van Wijk et al., 2010; van den Heuvel et al., 2017). Absolute thresholding can lead to group differences in the number of edges in the networks, which in turn causes spurious group differences in topology (van Wijk et al., 2010). Proportional thresholding, as used here, equates the number of edges in the network but has been criticized for being sensitive to overall differences in functional connectivity, especially in the presence of potentially random edges (van den Heuvel et al., 2017). Nonetheless, global graph-theoretical measures show high reliability in functional (Termenon et al., 2016) and structural networks (Owen et al., 2013). Second, the application of NBS to whole-brain networks offers the opportunity to identify subnetworks differing between groups without having to test each connection separately. This allows for the localization of connectivity differences that might drive connectivity differences on the global, connectome level. On the downside, NBS is also threshold-dependent, and group differences in individual edges should not be interpreted on their own but only in the context of the whole subnetwork (Zalesky et al., 2010). Finally, seed-to-voxel, graph theory, and NBS analyses, as used here, are (mass)-univariate in nature and thus sensitive for homogeneous increases and decreases in connectivity or network topology in one group relative to another. In contrast, multivariate approaches based on machine learning algorithms show high sensitivity for group differences in patterns of connectivity characterized by simultaneous increases and decreases (Haynes, 2015).
Results
Behavioral results
Participant characteristics are given in Table 1. Group comparisons revealed no differences regarding age (F(2,150) = 0.59, p = 0.55, BF01 = 9.30, η2G = 0.008), movement during rsfMRI (F(2,150) = 0.97, p = 0.38, BF01 = 6.75, η2G = 0.01), and movement during DWI (F(2,150) = 1.44, p = 0.24, BF01 = 4.54, η2G = 0.02). Both musician groups showed substantially higher musical aptitude than non-musicians as measured by the AMMA total score: AP musicians versus non-musicians (t(85.22) = 8.48, p < 0.001, BF10 > 100, d = 1.69) and non-AP musicians versus non-musicians (t(91.17) = 6.54, p < 0.001, BF10 > 100, d = 1.30). There was a trend toward a higher musical aptitude in AP musicians than in non-AP musicians (t(99.12) = 1.99, p = 0.05, BF10 = 1.21, d = 0.39), driven by higher AMMA tonal scores in AP musicians (t(98.43) = 2.28, p = 0.02, BF10 = 2.05, d = 0.45). The musician groups were comparable in the AMMA rhythm scores (t(99.87) = 1.41, p = 0.16, BF01 = 1.98, d = 0.28). With regard to tone-naming proficiency, AP musicians showed substantially higher tone-naming scores than non-AP musicians (t(100.95) = 13.68, p < 0.001, BF10 > 100, d = 2.70), and non-AP musicians showed better tone naming than non-musicians (t(53.43) = 5.54, p < 0.001, BF10 > 100, d = 1.11). The musician groups did not differ in their age of onset of musical training (t(100.96) = −1.00, p = 0.32, BF01 = 3.08, d = 0.20), years of musical training (t(100.91) = 1.53, p = 0.13, BF01 = 1.71, d = 0.30), and lifetime cumulative musical training (t(96.81) = 1.13, p = 0.26, BF01 = 2.74, d = 0.22).
Group differences in functional connectivity of auditory ROIs
To assess the effects of AP and musicianship on the functional connectivity of the auditory ROIs, we compared the functional connectivity maps between AP and non-AP musicians, and between non-AP musicians and non-musicians (the minimal FWE-corrected p values per cluster [pFWE] and cluster sizes [k] are given in brackets). Group comparisons between AP musicians and non-AP musicians revealed no statistically significant clusters for any of the four auditory seed ROIs (all pFWE > 0.05). Comparisons between non-AP musicians and non-musicians revealed that non-AP musicians showed increased interhemispheric functional connectivity between the left PT (seed ROI) and a cluster in the right PT (pFWE = 0.02, k = 47; Fig. 1B). A subset of this cluster also survived additional correction across the four ROIs (pFWE-ROI-corr = 0.04, k = 7). We also identified differences in the symmetric functional connection between the right PT (seed ROI) and two clusters in the left PT (pFWE = 0.03, k = 51 and pFWE = 0.04, k = 8). These clusters did not survive additional correction across ROIs (minimum pFWE-ROI-corr = 0.08). Details on the clusters are given in Table 2.
Table 2.
Statistically significant group differences between non-AP musicians and non-musicians in the rsfMRI seed-to-voxel analysisa
| Contrast | Seed region | Target region | k | pFWE | x | y | z |
|---|---|---|---|---|---|---|---|
| Non-AP > Non-mus | Left PT | Right PT | 47 | 0.02 | 63 | −18 | 9 |
| Non-AP > Non-mus | Right PT | Left PT | 51 | 0.03 | −54 | −27 | 3 |
| Non-AP > Non-mus | Right PT | Left PT | 8 | 0.04 | −39 | −36 | 9 |
aCoordinates (x, y, z) of voxels with minimum p values are in MNI space. Clusters are ordered according to seed region and size. Non-mus, Non-musicians; k, cluster size in voxels; pFWE, minimal FWE-corrected p value in cluster.
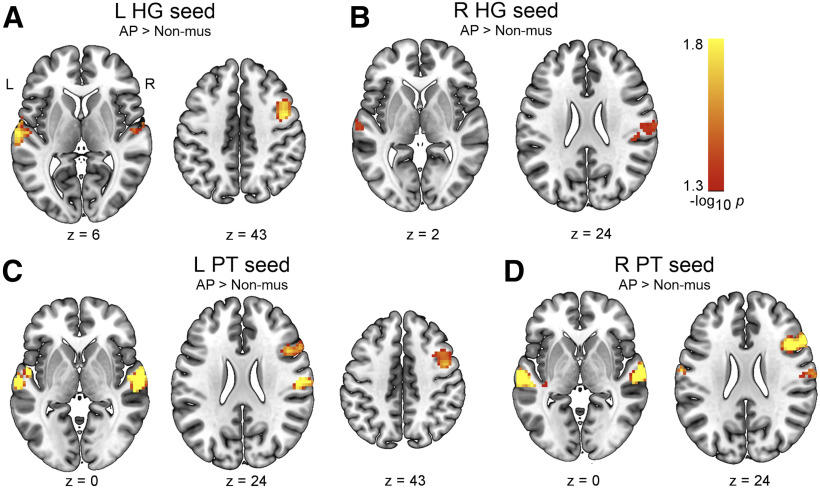
As we did not find evidence for group differences between AP and non-AP musicians in the functional connectivity of the auditory ROIs, we attempted to replicate the effects of musicianship that we identified via the comparison of non-AP and non-musicians. For this, we compared the functional connectivity maps between AP musicians and non-musicians. These comparisons revealed that AP musicians also showed increased interhemispheric functional connectivity between the left and right auditory regions (Table 3). Overall, these clusters were descriptively larger in number and size, and observable from more seed regions (Fig. 2).
Table 3.
Statistically significant group differences between AP musicians and non-musicians in the rsfMRI seed-to-voxel analysisa
| Contrast | Seed region | Target region | k | pFWE | x | y | z |
|---|---|---|---|---|---|---|---|
| AP > Non-mus | Left HG | Right PT | 357 | 0.02 | 69 | −24 | 21 |
| AP > Non-mus | Left HG | Left PT | 140 | 0.01 | −66 | −15 | 9 |
| AP > Non-mus | Left HG | Right preCG | 85 | 0.02 | 45 | 0 | 42 |
| AP > Non-mus | Left HG | Right IFG,po | 28 | 0.04 | 48 | 15 | 21 |
| AP > Non-mus | Right HG | Right aSMG | 50 | 0.04 | 69 | −15 | 27 |
| AP > Non-mus | Right HG | Left pSTG | 19 | 0.04 | −63 | −18 | 3 |
| AP > Non-mus | Left PT | Right PT | 489 | 0.005 | 63 | −24 | 12 |
| AP > Non-mus | Left PT | Left PT | 322 | 0.002 | −63 | −21 | 6 |
| AP > Non-mus | Left PT | Right IFG,po | 103 | 0.02 | 48 | 15 | 21 |
| AP > Non-mus | Left PT | Right MTG | 71 | 0.02 | 45 | 0 | 42 |
| AP > Non-mus | Right PT | Left PT | 528 | 0.001 | −60 | −18 | 0 |
| AP > Non-mus | Right PT | Right PT | 355 | 0.005 | 60 | −12 | −3 |
| AP > Non-mus | Right PT | Right IFG,po | 264 | 0.008 | 45 | 15 | 24 |
aCoordinates (x, y, z) of voxels with minimum p values are in MNI space. Clusters are ordered according to seed region and size. aSMG, anterior SMG; Non-mus, non-musicians; k, cluster size in voxels; pFWE, minimal FWE-corrected p value in cluster; pSTG, posterior STG.
Figure 2.
Increased intrinsic functional connectivity in AP musicians compared with non-musicians (pFWE < 0.05) in the seed-to-voxel analysis for the following seeds: (A) left HG, (B) right HG, (C) left PT, and (D) right PT. L, Left; R, right.
Associations between functional connectivity and behavior
Using voxelwise regression analysis, we related tone-naming proficiency, musical aptitude, and musical experience to the functional connectivity of the auditory ROIs. Within musicians, higher tone-naming proficiency was associated with increased functional connectivity between the right HG (seed ROI) and surrounding regions, including the posterior insula and associative auditory areas (pFWE = 0.02, k = 242). Most voxels of this cluster also survived additional correction across ROIs (pFWE-ROI-corr = 0.03, k = 152). Across all participants, we found that higher musical aptitude, as measured by the AMMA total scores, was associated with increased functional connectivity within the left PT (pFWE = 0.04, k = 5). Furthermore, we unexpectedly observed that higher musical aptitude was associated with lower functional connectivity between the left HG (seed ROI) and a cluster in the left MTG (pFWE = 0.04, k = 6). Both of these clusters were very small in size (k < 10) and did not survive additional correction across ROIs. Within the musician groups, lower age of onset of musical training was associated with increased functional connectivity between the right HG (seed ROI) and a cluster in the right dorsolateral prefrontal cortex (DLPFC; pFWE = 0.02, k = 46). This cluster did not survive additional correction for multiple ROIs. We further found that a lower age of onset was associated with increased functional connectivity between the right PT (seed ROI) and the right DLPFC (pFWE = 0.03, k = 23). A subset of this cluster just survived additional correction for multiple ROIs (pFWE-ROI-corr = 0.046, k = 6). Finally, we found no evidence for an association between years of training or cumulative training and the functional connectivity of the auditory ROIs (all pFWE > 0.05). Statistically significant associations within musicians are depicted in Figure 1C and across all participants in Figure 1D. Details on the clusters are given in Table 4.
Table 4.
Statistically significant voxelwise functional connectivity-behavior associationsa
| Behavior | Seed region | Target region | Sign | k | pFWE | x | y | z |
|---|---|---|---|---|---|---|---|---|
| Tone naming | Right HG | Right posterior insula, auditory association areas | + | 242 | 0.02 | 36 | −15 | 15 |
| AMMA total | Left PT | Left PT | + | 5 | 0.04 | −60 | −24 | 9 |
| AMMA total | Left HG | Left MTG | – | 6 | 0.04 | −30 | 24 | 48 |
| Age onset | Right HG | Right DLPFC | – | 46 | 0.02 | 27 | 36 | 48 |
| Age onset | Right PT | Right DLPFC | – | 23 | 0.03 | 24 | 36 | 48 |
aCoordinates (x, y, z) of voxels with minimum p values are in MNI space. Clusters are ordered according to behavioral measures and signs of the association. k, Cluster size in voxels; pFWE, minimal FWE-corrected p value in cluster; +, positive association; –, negative association.
Group differences in functional network topology
Group comparisons of whole-brain functional network topology revealed the following results (FWE-corrected p values per cluster [pFWE] and cluster size across contiguous thresholds [k] are given in brackets). We found no evidence for group differences between AP and non-AP musicians in any of the investigated graph-theoretical measures (all pFWE > 0.05). However, we observed an effect of musicianship on multiple graph-theoretical measures: We found higher average strength (pFWE = 0.01, k = 35), lower global efficiency (pFWE = 0.04, k = 11), and a higher clustering coefficient (pFWE = 0.01, k = 25) in non-AP musicians than in non-musicians (Fig. 3A). We found no evidence for an effect of musicianship on modularity, and betweenness centrality of whole-brain functional networks (both pFWE > 0.05). Strikingly similar results were obtained by comparing AP and non-musicians, replicating the effects of musicianship on functional network topology (for details, see Table 5).
Figure 3.
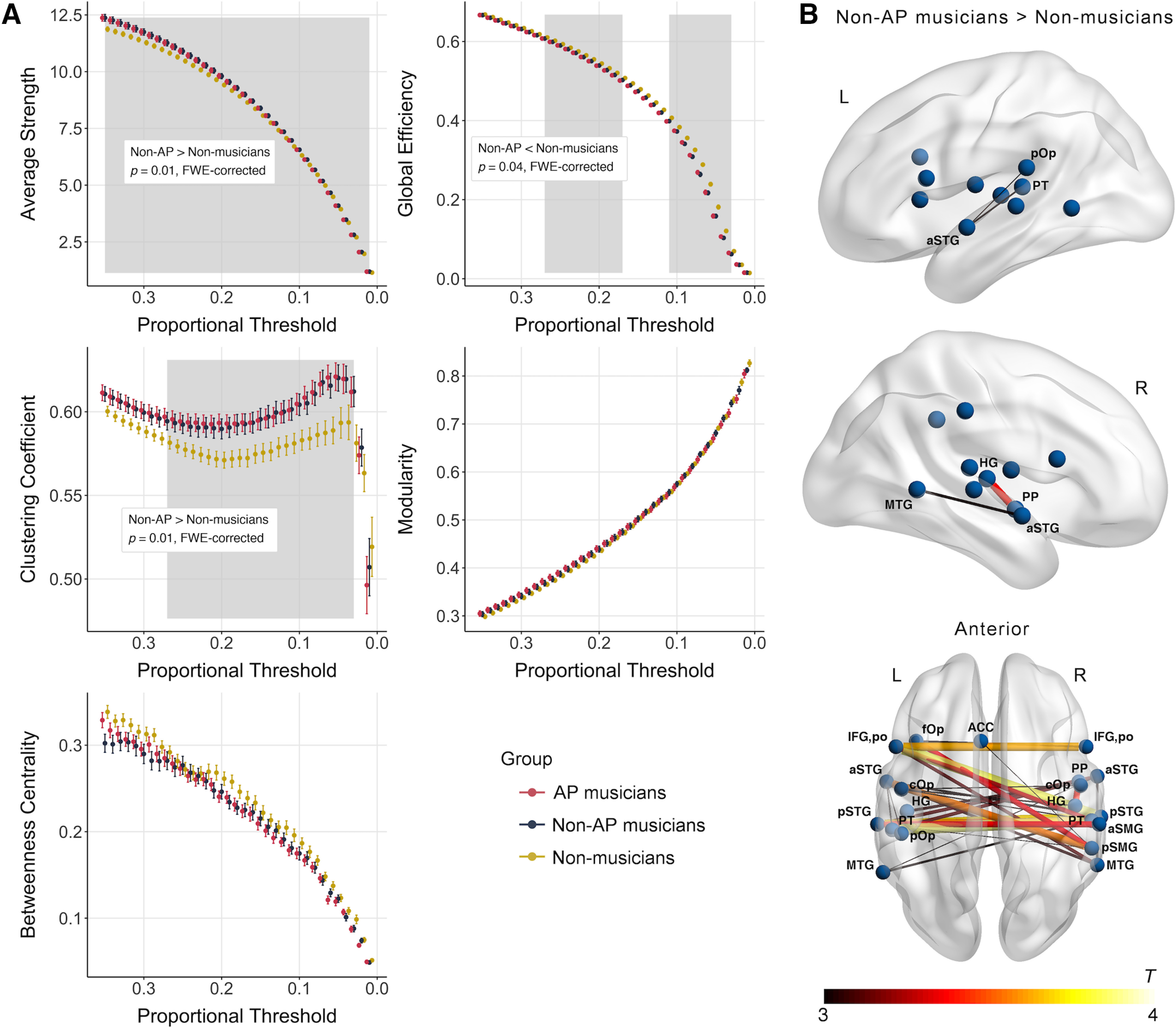
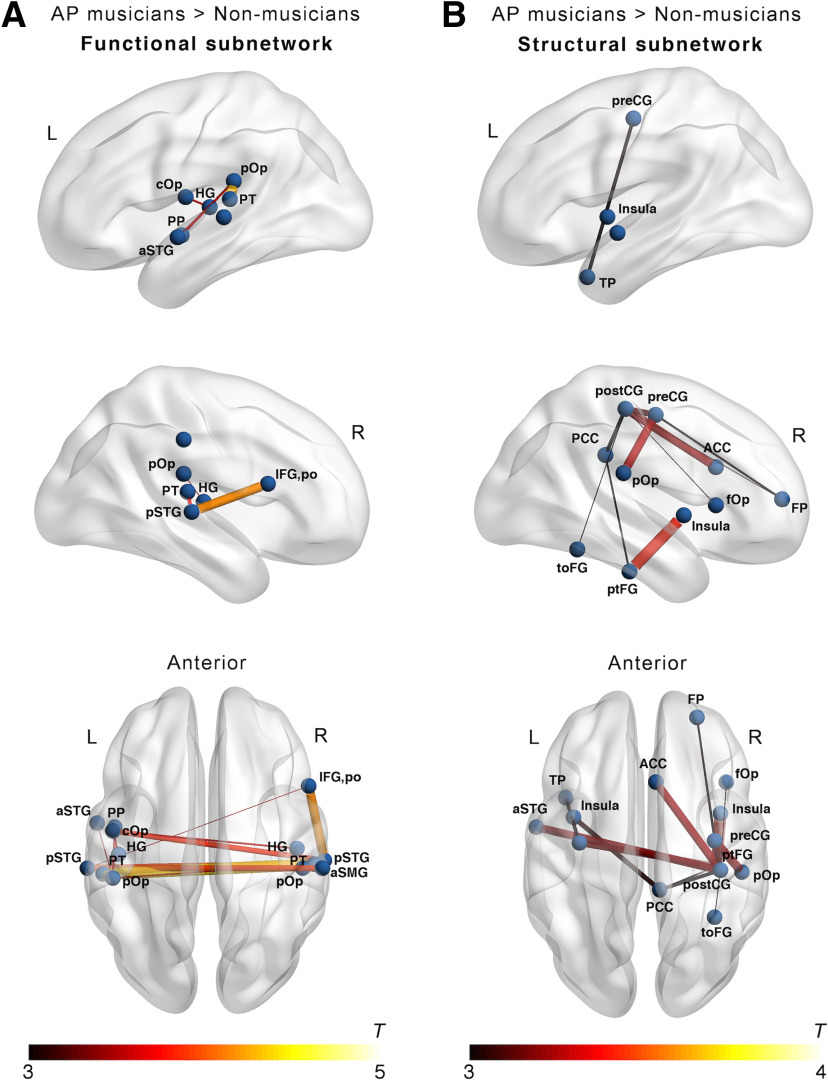
A, Group differences between non-AP musicians and non-musicians in graph-theoretical measures calculated based on whole-brain functional networks (pFWE < 0.05). Gray-shaded area represents range of thresholds belonging to statistically significant cluster. B, Subnetwork with increased functional connectivity in non-AP musicians compared with non-musicians obtained in the NBS analysis (pFWE < 0.05). ACC, anterior cingulate cortex; aSMG, anterior SMG; aSTG, anterior STG; cOp, central operculum; fOp, frontal operculum; pSMG, posterior SMG; pSTG, STG, posterior division.
Table 5.
Statistically significant group differences between AP musicians and non-musicians in whole-brain functional network topologya
| Contrast | Graph-theoretical measure | k | pFWE |
|---|---|---|---|
| AP > Non-mus | Average strength | 35 | 0.02 |
| AP < Non-mus | Global efficiency | 23 | 0.003 |
| AP > Non-mus | Clustering coefficient | 31 | 0.001 |
aNon-mus, Non-musicians; k, cluster size across contiguous thresholds; pFWE, FWE-corrected p value of cluster.
Associations between functional network topology and behavior
We found no evidence for an association between average strength, clustering coefficient, modularity, or betweenness centrality and any of the behavioral measures for musical aptitude, tone-naming proficiency, or musical experience (all p > 0.01 [α = 0.01, adjusted for multiple graph-theoretical measures]). There was a statistically significant negative correlation between global efficiency and the AMMA total scores across all participants (r = −0.23, p = 0.004). However, this correlation was likely driven by group differences in both measures as we found no evidence for a correlation within AP musicians (r = 0.01, p = 0.90), non-AP musicians (r = −0.21, p = 0.14), or non-musicians (r = −0.11, p = 0.49). For all other behavioral measures, we found no evidence for an association with global efficiency (all p > 0.01).
Group differences in whole-brain functional subnetworks
The whole-brain NBS analysis to reveal functional subnetworks differing between the groups did not show evidence for differences between AP and non-AP musicians (pFWE > 0.05). In contrast, we identified a subnetwork characterized by higher functional connectivity in non-AP musicians than in non-musicians (pFWE = 0.04). As shown in Figure 3B, the descriptively strongest group differences within this subnetwork were present in interhemispheric functional connections between the left and right PT; between the left IFG,po and the right pSTG; between left and right pSTG; and between the left and right IFG,po. Additional nodes of this functional subnetwork were located in brain regions of the temporal and parietal lobes, including HG and anterior and posterior SMG. Detailed information on all nodes and edges of the functional subnetwork differing between non-AP and non-musicians are given in Table 6. In the internal replication of these effects of musicianship, we found a strikingly similar subnetwork differing between AP musicians and non-musicians (pFWE = 0.005). This functional subnetwork is visualized in Figure 4A, and details regarding all nodes and edges are given in Table 7.
Table 6.
Edges of statistically significant functional subnetwork differing between non-AP musicians and non-musiciansa
| Contrast | Node 1 | Node 2 | t |
|---|---|---|---|
| Non-AP > Non-mus | Left PT | Right PT | 3.88 |
| Non-AP > Non-mus | Left IFG,po | Right pSTG | 3.84 |
| Non-AP > Non-mus | Left pSTG | Right pSTG | 3.68 |
| Non-AP > Non-mus | Left IFG,po | Right IFG,po | 3.63 |
| Non-AP > Non-mus | Left aSTG | Right pSMG | 3.53 |
| Non-AP > Non-mus | Left pSTG | Right PT | 3.53 |
| Non-AP > Non-mus | Right PP | Right HG | 3.39 |
| Non-AP > Non-mus | Left pSTG | Right aSMG | 3.36 |
| Non-AP > Non-mus | Right pSMG | Left fOp | 3.32 |
| Non-AP > Non-mus | Left IFG,po | Right PT | 3.23 |
| Non-AP > Non-mus | Left IFG,po | Right MTG | 3.1 |
| Non-AP > Non-mus | Right aSTG | Left PT | 3.1 |
| Non-AP > Non-mus | Right aSTG | Left pSTG | 3.09 |
| Non-AP > Non-mus | Left aSTG | Right MTG | 3.04 |
| Non-AP > Non-mus | Right PP | Left HG | 3.03 |
| Non-AP > Non-mus | Right aSTG | Right MTG | 2.98 |
| Non-AP > Non-mus | Left aSTG | Right pSTG | 2.97 |
| Non-AP > Non-mus | Right pSTG | Left MTG | 2.97 |
| Non-AP > Non-mus | Right IFG,po | Left fOp | 2.95 |
| Non-AP > Non-mus | Left cOp | Right HG | 2.9 |
| Non-AP > Non-mus | Left aSTG | Left PT | 2.89 |
| Non-AP > Non-mus | Left cOp | Right PT | 2.86 |
| Non-AP > Non-mus | Left cOp | Right cOp | 2.85 |
| Non-AP > Non-mus | Right aSTG | Left MTG | 2.83 |
| Non-AP > Non-mus | Left pSTG | Right pSMG | 2.82 |
| Non-AP > Non-mus | Left aSTG | Left pOp | 2.82 |
| Non-AP > Non-mus | Right pSMG | Left ACC | 2.81 |
aEdges are ordered according to their descriptive strength with respect to group differences. ACC, anterior cingulate cortex; aSMG, anterior SMG; aSTG, anterior STG; cOp, central operculum; fOp, frontal operculum; Non-mus, non-musicians; pSMG, posterior SMG; pSTG, posterior STG; t, t statistic describing the strength of group difference in functional connectivity between Node 1 and Node 2.
Figure 4.
Subnetworks with increased connectivity in AP musicians compared with non-musicians (pFWE < 0.05) obtained in the NBS analysis for (A) functional networks and (B) structural networks. ACC, anterior cingulate cortex; aSMG, anterior SMG; aSTG, anterior STG; cOp, central operculum; fOp, frontal operculum; pSTG, STG, posterior division; ptFG, posterior temporal fusiform gyrus; toFG, temporal occipital fusiform gyrus; TP, temporal pole.
Table 7.
Edges of statistically significant functional subnetwork differing between AP musicians and non-musiciansa
| Contrast | Node 1 | Node 2 | t |
|---|---|---|---|
| AP > Non-mus | Left PT | Right PT | 4.35 |
| AP > Non-mus | Left pOp | Left PT | 4.26 |
| AP > Non-mus | Right IFG,po | Right pSTG | 4.15 |
| AP > Non-mus | Left pSTG | Right PT | 3.94 |
| AP > Non-mus | Left pSTG | Right aSMG | 3.88 |
| AP > Non-mus | Right pSTG | Left cOp | 3.83 |
| AP > Non-mus | Right pSTG | Right PT | 3.66 |
| AP > Non-mus | Right pSTG | Left PT | 3.61 |
| AP > Non-mus | Left pOp | Left PP | 3.53 |
| AP > Non-mus | Left cOp | Left HG | 3.52 |
| AP > Non-mus | Left cOp | Right HG | 3.5 |
| AP > Non-mus | Left pOp | Right PT | 3.46 |
| AP > Non-mus | Left aSTG | Left pOp | 3.44 |
| AP > Non-mus | Right pOp | Right HG | 3.41 |
| AP > Non-mus | Right IFG,po | Left pSTG | 3.4 |
aEdges are ordered according to their descriptive strength with respect to group differences. aSMG, anterior SMG; aSTG, anterior STG; cOp, central operculum; Non-mus, non-musicians; pSTG, posterior STG; t, t statistic describing the strength of group difference in functional connectivity between Node 1 and Node 2.
Functional network-based classification
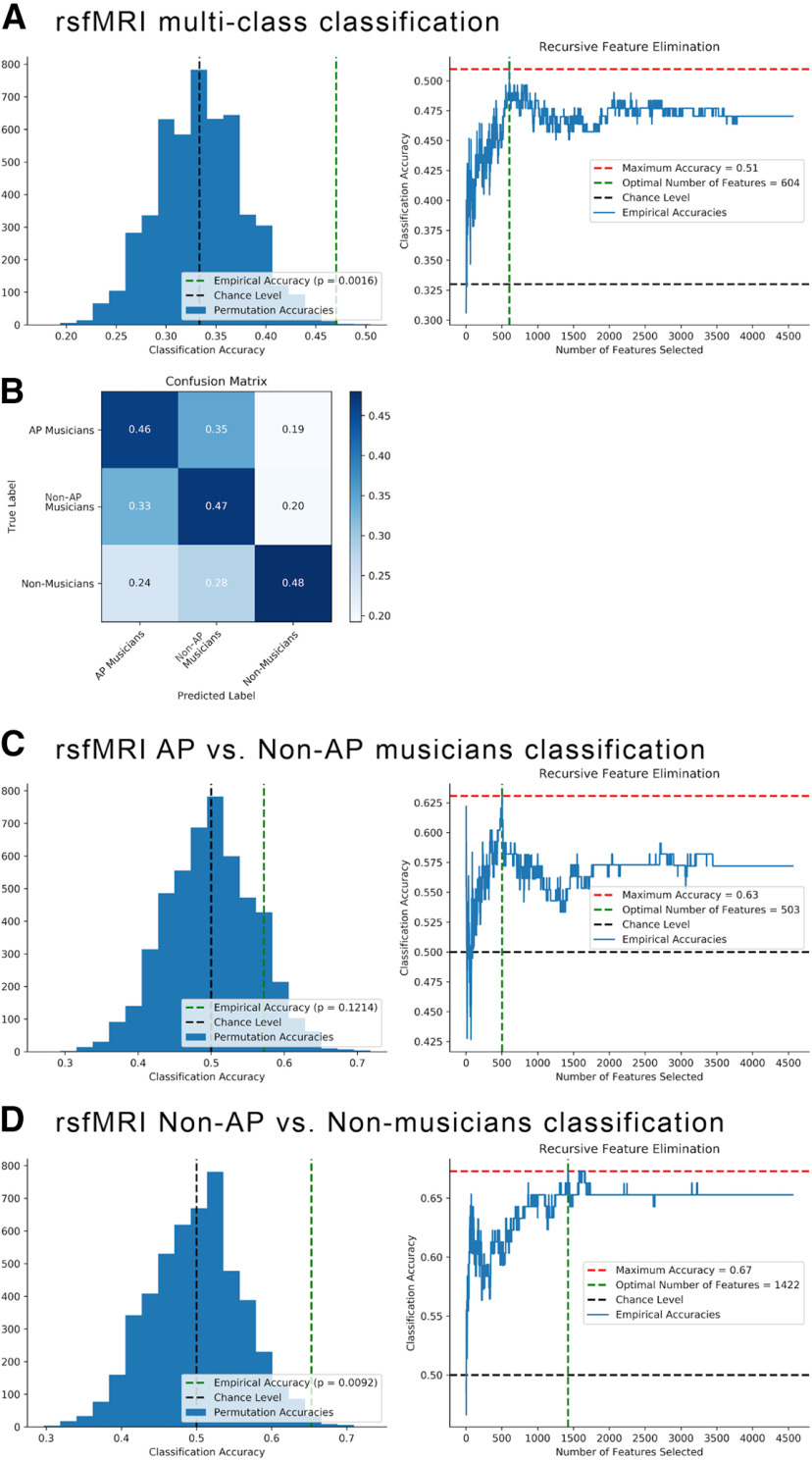
Group classification based on whole-brain functional networks using MVPA yielded the following results: The multiclass classification successfully classified the participants into the three groups with an accuracy of 47%, p = 0.002 (chance level = 33%). For a visualization of the null distribution of accuracies with permuted group labels, see Figure 5A. According to recursive feature elimination, the optimal number of features for classification was quite large (604 edges), which suggests that the connectivity patterns of a substantial part of the whole-brain functional network contained information about group membership. The confusion matrix showed that the classifier confused AP and non-AP musicians most often, but participants of the musician groups were less often classified as non-musicians and vice versa (Fig. 5B). Consistent with this pattern of results, the follow-up classification within musicians showed that AP and non-AP musicians could not be successfully differentiated (accuracy = 57%, p = 0.12 [chance level = 50%], precision = 0.56, recall = 0.6; Fig. 5C). In contrast, the classification of non-AP musicians and non-musicians was successful (accuracy = 65%, p = 0.01 [chance level = 50%], precision = 0.7, recall = 0.6; Fig. 5D). The optimal number of features necessary for successful classification was again relatively high (1422 edges).
Figure 5.
A, Multiclass classification differentiating AP, non-AP, and non-musicians based on whole-brain functional networks: Null distribution of accuracies with permuted group labels (left) and recursive feature elimination outcome (right). B, Confusion matrix of classifier performance (accuracy) for multiclass classification. C, Classification of AP versus non-AP musicians: Null distribution of accuracies with permuted group labels (left) and recursive feature elimination outcome (right). D, Classification of non-AP versus non-musicians: Null distribution of accuracies with permuted group labels (left) and recursive feature elimination outcome (right).
Group differences in transcallosal structural connectivity
In 9 AP musicians, 14 non-AP musicians, and 15 non-musicians, probabilistic tractography was not able to identify a white-matter pathway connecting left and right PT (for a visualization of the white-matter tract, see Fig. 6C). Consequently, these participants were excluded from group comparisons of transcallosal connectivity and the structural connectivity-behavior correlations. Results of the group comparisons of transcallosal structural connectivity are visualized in Figure 6A. We found no evidence for group differences in FA between AP musicians and non-AP musicians (t(68.34) = 0.81, p = 0.42, d = 0.19), and between non-AP musicians and non-musicians (t(69.17) = 0.12, p = 0.90, d = 0.03). Furthermore, there was no evidence for differences in MD between AP and non-AP musicians (t(70.02) = −1.01, p = 0.31, d = 0.23). On the contrary, we found a statistically significant difference in MD between non-AP and non-musicians, characterized by higher MD values in non-AP than in non-musicians (t(59.51) = 2.61, p = 0.01, d = 0.61). In the internal replication of this effect of musicianship, we found that AP musicians descriptively showed higher MD values than non-musicians, but this difference did not reach statistical significance (t(75.11) = 1.81, p = 0.07 [α = 0.025, adjusted for multiple diffusion measures], d = 0.40).
Figure 6.
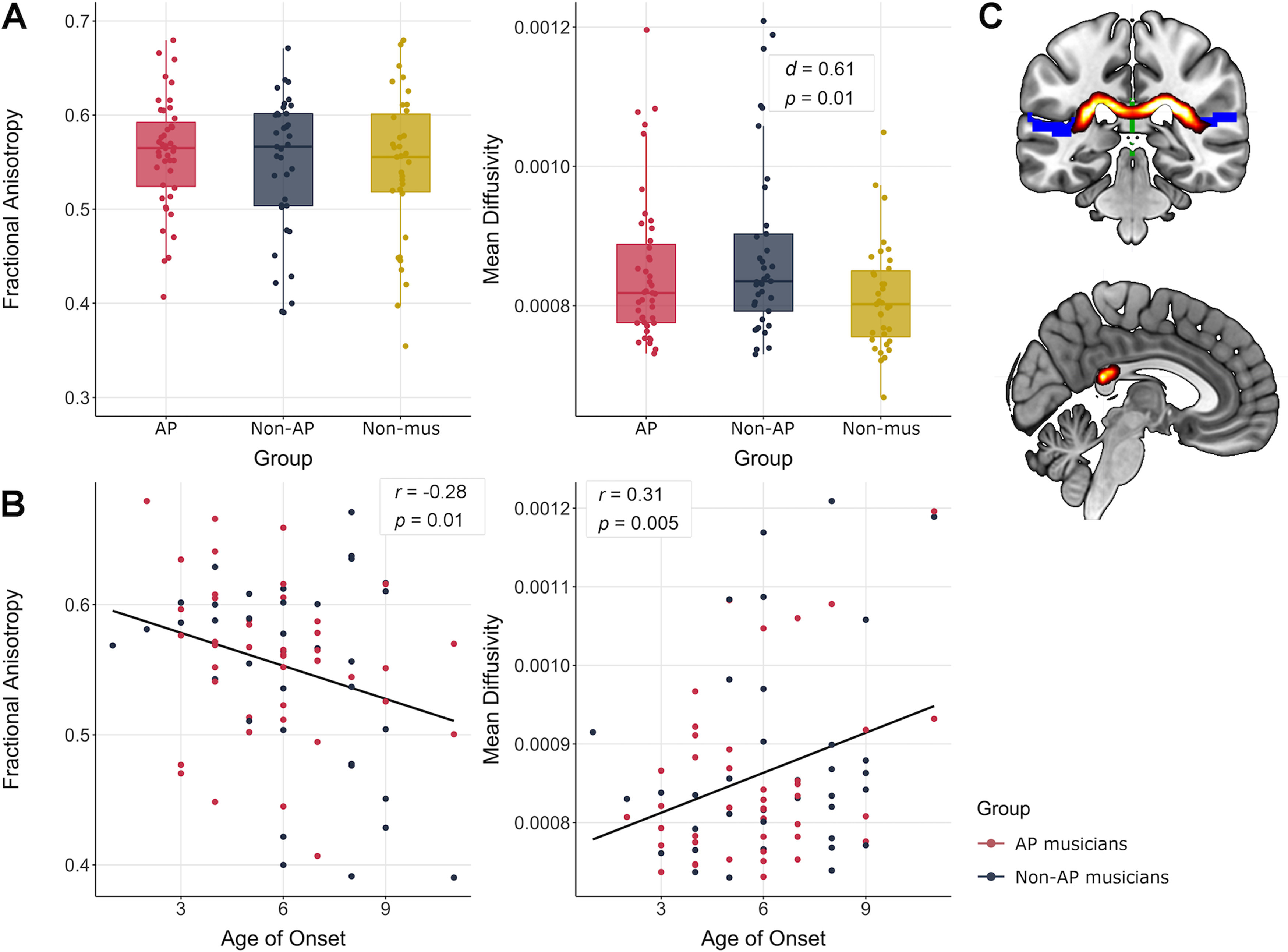
A, Group differences between AP, non-AP, and non-musicians (Non-mus) in FA and MD values (α = 0.025, adjusted for multiple diffusion measures). B, Associations between FA and MD values and age of onset of musical training. C, Coronal and sagittal view of the mean white-matter pathway between left and right PT obtained by probabilistic tractography across all subjects.
Associations between transcallosal structural connectivity and behavior
Structural connectivity-behavior associations are shown in Figure 6B. Across both musician groups, we found a statistically significant negative correlation between the age of onset of musical training and FA values within the pathway connecting left and right PT (r = −0.28, p = 0.01). We did not find evidence for an association between any of the other behavioral measures and FA (all p > 0.025). Furthermore, we found a statistically significant positive correlation between age of onset and MD values across both musician groups (r = 0.31, p = 0.005). Again, there was no evidence for an association of any of the other behavioral measures and MD (all p > 0.025).
Group differences in structural network topology
In the analysis of whole-brain structural network topology, we found no evidence for group differences between AP musicians and non-AP musicians, or between both musician groups and non-musicians in any of the investigated graph-theoretical measures (all pFWE > 0.05).
Associations between structural network topology and behavior
We found a statistically significant positive correlation between betweenness centrality and the musicians' age of onset of musical training (r = 0.27, p = 0.006). Furthermore, age of onset was also descriptively associated with average strength (r = −0.19, p = 0.049), global efficiency (r = −0.21, p = 0.04), and clustering coefficient (r = 0.22, p = 0.02; Fig. 7A). However, these correlations did not survive the adjustment of the significance level for multiple graph-theoretical measures. We found no evidence for an association of modularity and age of onset. Furthermore, there was no evidence for an association between any of the other behavioral measures (in addition to age of onset) and the graph-theoretical measures.
Figure 7.
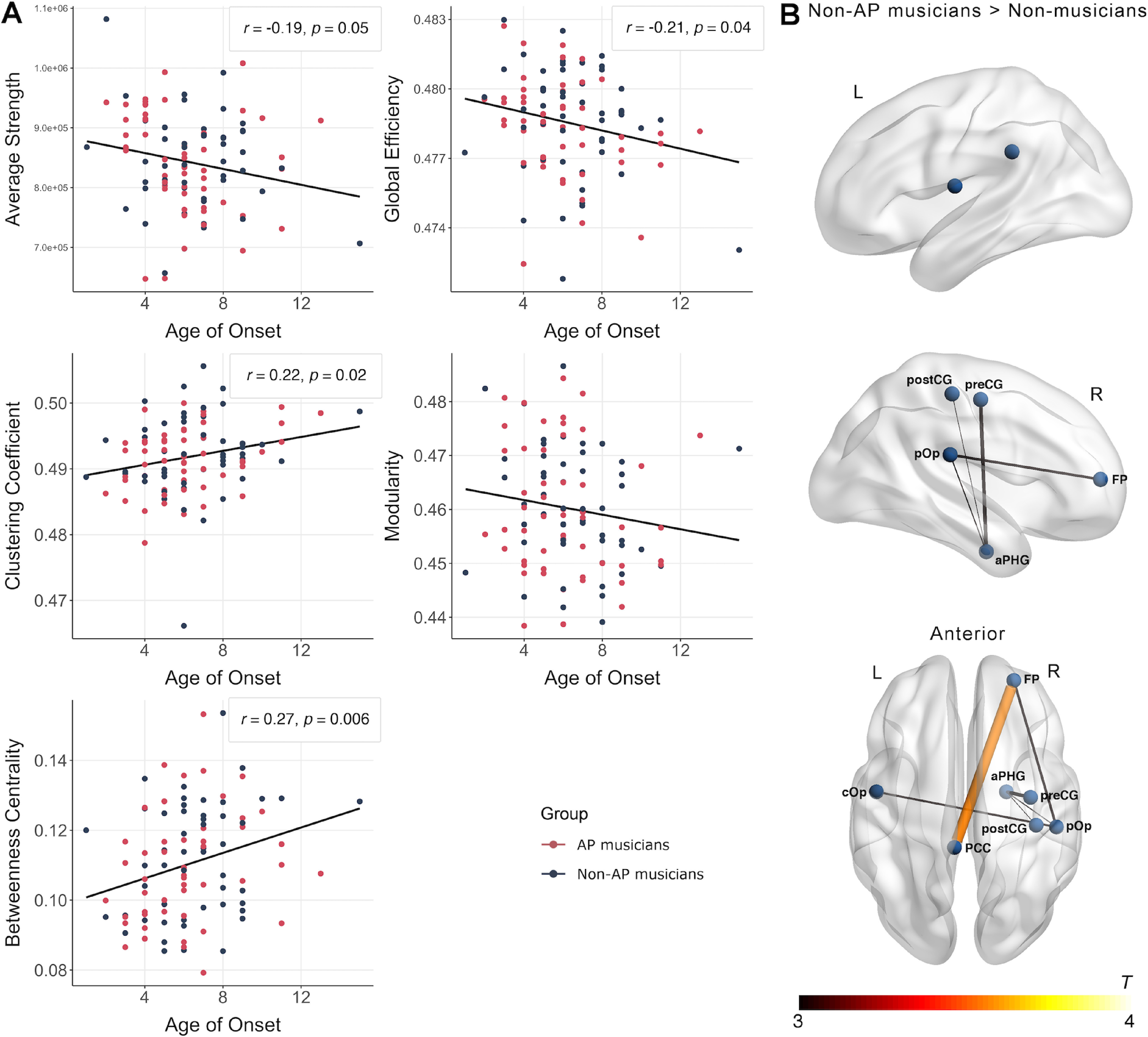
A, Associations between structural network topology and age of onset of musical training for AP- and non-AP musicians. B, Subnetwork with increased structural connectivity in non-AP musicians compared with non-musicians obtained in the NBS analysis (pFWE < 0.05). aPHG, Anterior parahippocampal gyrus; cOp, central operculum.
Group differences in whole-brain structural subnetworks
As for the functional data, the NBS analysis to identify structural subnetworks differing between the groups did not show evidence for differences between AP musicians and non-AP musicians (pFWE > 0.05). On the contrary, we again identified a subnetwork characterized by higher structural connectivity in non-AP than in non-musicians (pFWE = 0.047). As can be seen from Figure 7B, the descriptively biggest group difference in structural connectivity was between the posterior cingulate cortex (PCC) and the frontal pole (FP). Furthermore, non-AP musicians showed higher structural connectivity between right perisylvian regions, including the parietal operculum (pOp) as well as preCG and postCG. Detailed information on all nodes and edges of the structural subnetwork differing between non-AP and non-musicians are given in Table 8. A similar subnetwork was identified by comparing AP and non-musicians (pFWE = 0.003). This subnetwork had descriptively stronger group differences and was more extended than the subnetwork identified by comparing non-AP and non-musicians. This structural subnetwork is visualized in Figure 4B, and details regarding all nodes and edges are given in Table 9.
Table 8.
Edges of statistically significant structural subnetwork differing between non-AP musicians and non-musiciansa
| Contrast | Node 1 | Node 2 | t |
|---|---|---|---|
| Non-AP > Non-mus | Right FP | Left PCC | 3.56 |
| Non-AP > Non-mus | Right aPHG | Right preCG | 2.94 |
| Non-AP > Non-mus | Right FP | Right pOp | 2.86 |
| Non-AP > Non-mus | Left cOp | Right pOp | 2.83 |
| Non-AP > Non-mus | Right aPHG | Right pOp | 2.74 |
| Non-AP > Non-mus | Right aPHG | Right postCG | 2.71 |
aEdges are ordered according to their descriptive strength with respect to group differences. aPHG, Anterior parahippocampal gyrus; cOp, central operculum; Non-mus, non-musicians; t, t statistic describing the strength of group difference in structural connectivity between Node 1 and Node 2.
Table 9.
Edges of statistically significant structural subnetwork differing between AP musicians and non-musiciansa
| Contrast | Node 1 | Node 2 | t |
|---|---|---|---|
| AP > Non-mus | Right insula | Right ptFG | 3.39 |
| AP > Non-mus | Right pOp | Right preCG | 3.23 |
| AP > Non-mus | Right ACC | Right postCG | 3.2 |
| AP > Non-mus | Left aSTG | Right postCG | 3.2 |
| AP > Non-mus | Left preCG | Right ptFG | 3.12 |
| AP > Non-mus | Right postCG | Right preCG | 3.09 |
| AP > Non-mus | Left insula | Right PCC | 3.03 |
| AP > Non-mus | Right PCC | Right postCG | 2.97 |
| AP > Non-mus | Left preCG | Left TP | 2.95 |
| AP > Non-mus | Right FP | Right preCG | 2.88 |
| AP > Non-mus | Right PCC | Right ptFG | 2.87 |
| AP > Non-mus | Right fOp | Right postCG | 2.81 |
| AP > Non-mus | Right postCG | Right toFG | 2.81 |
| AP > Non-mus | Right FP | Right postCG | 2.8 |
aEdges are ordered according to their descriptive strength with respect to group differences. ACC, anterior cingulate cortex; aSTG, Anterior STG; fOp, frontal operculum; Non-mus, non-musicians; ptFG, posterior temporal fusiform gyrus; t, t statistic describing the strength of group difference in structural connectivity between Node 1 and Node 2; toFG, temporal occipital fusiform gyrus; TP, temporal pole.
Structural network-based classification
Group classification based on whole-brain structural networks using MVPA yielded no successful classifications. The three groups could not be successfully differentiated in the multiclass classification (accuracy = 35%, p = 0.33 [chance level = 33%]). Furthermore, the follow-up classifications showed that neither non-AP and AP musicians (accuracy = 43%, p = 0.90 [chance level = 50%], precision = 0.41, recall = 0.49), nor non-AP and non-musicians (accuracy = 52%, p = 0.35 [chance level = 50%], precision = 0.53, recall = 0.52) could be successfully differentiated.
Discussion
In this study, we assessed the effects of musicianship and AP on brain networks. Our main results are summarized in Table 10. We found robust effects of musicianship across various methodological approaches, which were largely replicable in AP and non-AP musicians. Both musician groups showed stronger interhemispheric functional connectivity between left and right PT, enhanced connectivity in temporal-parietal-frontal functional subnetworks, and globally altered functional network topology, compared with non-musicians. Furthermore, non-AP musicians and non-musicians could be successfully classified using MVPA based on functional connectomes. Musicians also showed altered transcallosal structural connectivity in the white-matter tract connecting bilateral PT. We detected several brain-behavior associations between connectivity and behavioral measures of musicianship, most prominently between structural network features and the age of onset of musical training. Finally, we found no evidence for group differences between non-AP and AP musicians across all analyses: the two musician groups showed striking similarities in both functional and structural networks.
Table 10.
Summary of main findings for group comparisons, classifications, and brain-behavior associationsa
| Non-AP vs Non-mus | AP vs Non-mus | AP vs Non-AP | |
|---|---|---|---|
| Functional connectivity of auditory ROIs | Non-AP musicians show increased interhemispheric functional connectivity between the left and right PT | AP musicians show increased interhemispheric functional connectivity between the left and right auditory cortex (PT and HG), and between bilateral auditory cortex and right inferior frontal regions | No statistical evidence for group differences |
| Associations between functional connectivity of auditory ROIs and behavior | Positive association between tone-naming proficiency and functional connectivity of the right HG and associative auditory areas within musicians; negative association between age of onset and functional connectivity between right PT and right DLPFC within musicians | ||
| Functional network topology | Non-AP musicians show higher average strength and cluster coefficient, and a lower global efficiency | AP musicians show higher average strength and cluster coefficient, and a lower global efficiency | No statistical evidence for group differences |
| Functional subnetworks | Non-AP musicians show increased functional connectivity within subnetwork consisting of bilateral auditory cortex, bilateral inferior frontal cortex, anterior and middle temporal cortex, and inferior parietal cortex | AP musicians show increased functional connectivity within subnetwork consisting of bilateral auditory cortex, right inferior frontal cortex, left anterior temporal cortex, and inferior parietal cortex | No statistical evidence for group differences |
| Functional network-based classification | Statistically significant classification | — | No statistical evidence for successful classification |
| Structural connectivity of auditory ROIs | Non-AP musicians show increased MD in transcallosal white-matter tract connecting left and right PT | AP musicians descriptively show a trend toward increased MD in transcallosal white-matter tract connecting left and right PT | No statistical evidence for group differences |
| Association between structural connectivity of auditory ROIs and behavior | Negative association between age of onset of musical training and FA values and positive association with MD values of white-matter tract between left and right PT within musician groups | ||
| Structural network topology | No statistical evidence for group differences | No statistical evidence for group differences | No statistical evidence for group differences |
| Association between structural network topology and behavior | Positive association between age of onset and betweenness centrality in musicians | ||
| Structural subnetworks | Non-AP musicians show increased structural connectivity within a subnetwork consisting of right-hemispheric sensorimotor (preCG, postCG), medial temporal, and frontal cortex as well as bilateral perisylvian regions | AP musicians show increased structural connectivity within a subnetwork consisting of right-hemispheric sensorimotor (preCG, postCG), inferior temporal, and frontal cortex, as well as bilateral insular cortex and bilateral perisylvian regions | No statistical evidence for group differences |
| Structural network-based classification | No statistical evidence for successful classification | — | No statistical evidence for successful classification |
aNon-mus, Non-musicians.
Results showed altered connectivity between left and right PT in both musician groups compared with non-musicians. Left and right PT are structurally connected via the isthmus and splenium of the corpus callosum (Hofer and Frahm, 2006). Whereas effects of musicianship on (more anterior) parts of the corpus callosum have been frequently observed (Schlaug et al., 1995; Bengtsson et al., 2005; Vollmann et al., 2014), only one previous study has reported microstructural differences between musicians and non-musicians in the callosal fibers connecting bilateral PT (Elmer et al., 2016). Here, we showed that altered microstructural connectivity is accompanied by increased intrinsic functional connectivity in musicians, an observation that substantiates earlier reports of increased functional connectivity between bilateral auditory areas using EEG (Klein et al., 2016). The PT's role in auditory processing is well documented (Griffiths and Warren, 2002). Increased interhemispheric functional connectivity in musicians might reflect increased information transfer between the homotopic areas. It is conceivable that enhanced auditory information coordination is the basis for the superior auditory skills frequently noted in musically trained individuals (Schneider et al., 2002; Kraus and Chandrasekaran, 2010).
The effects of musicianship on functional networks were not restricted to interhemispheric auditory-to-auditory connections: We identified widespread subnetworks showing enhanced connectivity in musicians, mostly encompassing bilateral superior and middle temporal, inferior frontal, and inferior parietal regions. These regions can be well situated within the frameworks of dual-stream models for auditory processing (Rauschecker and Scott, 2009). In particular, our data suggest that communication between regions of the bilateral ventral stream is shaped by musicianship more strongly than that between regions of the dorsal stream (Fig. 3B). However, most altered connections in the subnetwork were of interhemispheric nature. It has been shown that interhemispheric information transfer causally modulates expansive auditory and motor networks during rest (Andoh et al., 2015). Thus, experience-dependent plasticity in interhemispheric connections could have a prime role in modulating network interactions between auditory areas and cortical regions in the temporal, parietal, and frontal lobes. As we were able to replicate virtually the same enhanced subnetworks in both non-AP and AP musicians compared with non-musicians, the identified subnetworks of the current study seem to robustly reflect general characteristics of musical expertise.
A notable feature of the DWI results is the consistent and highly specific association between the age of onset of music training and structural network measures. Importantly, these network measures were not associated with other behavioral measures, such as cumulative training hours and years of training. Age of onset of musical training was correlated with diffusion measures in the transcallosal white-matter tract connecting left and right PT. This result complements previous reports of associations between age of onset and diffusion measures in parts of the corpus callosum connecting bilateral sensorimotor brain regions (Steele et al., 2013). An earlier study also showed an association of age of onset with diffusion measures of both the anterior and the posterior part of the corpus callosum (Imfeld et al., 2009). These findings suggest that microstructural properties of the corpus callosum are sensitive for changes when musical training starts at a young age, possibly during a sensitive period when the potential for plasticity is especially high (Schlaug et al., 1995). Additionally, for the first time, we observed associations between age of onset and whole-brain structural network topology. Thus, musical training during early childhood not only has local effects on microstructure, but also has global effects on the topology of the structural connectome, and these effects are stronger the earlier musical training begins.
This is the first study to analyze effects of musicianship on both structural and functional connectivity. In this context, we found a surprisingly low correspondence between effects on functional versus structural networks. Evidence suggests that rsfMRI-based functional connectivity and DWI-based structural connectivity are, to some extent, related (Hermundstad et al., 2013). However, because of indirect structural connections, functional connectivity between regions can also be observed without direct structural links (Honey et al., 2009). We found that effects of musicianship on connectivity were particularly strong in the functional domain, and less so in the structural domain. Therefore, based on our data, one might speculate that musical training more strongly shapes functional networks, and does so mostly independently of structural networks. An important exception to this general hypothesis concerns the observed differences in transcallosal connectivity between bilateral PT. However, this selective correspondence is highly consistent with the finding that interhemispheric functional connectivity causally depends on structural connectivity provided via the corpus callosum (Jäncke and Steinmetz, 1994, 1998; Roland et al., 2017).
Concerning reproducibility, the effects of musicianship were not as widespread as one might have expected from previous evidence on brain function and structure in musicians (e.g., Schlaug, 2015). This divergence could be attributable to a number of reasons: First, some previously reported findings might not be reproducible because of inadequate sample sizes (Button et al., 2013). Second, as outlined above (see General methodological considerations), the methodology applied in this and previous studies may lack the reliability for the effects to be consistently observed in different studies. Also, stereotactic normalization might diminish group differences in anatomy (e.g., asymmetries), which could have downstream consequences on connectivity. Future studies will benefit from approaches that consider interindividual anatomic variance (Dalboni da Rocha et al., 2020). Third, the investigation of intrinsic functional and structural networks could be less sensitive compared with activation or connectivity in task-based experiments (e.g., during auditory or motor tasks) (Bangert et al., 2006). One possibility to disentangle these potential causes are well-powered replication studies in a collaborative setting, making data acquisition from large samples of musicians feasible. Future studies could also benefit from a hypothesis-driven framework, where brain regions and tracts putatively involved in music production (e.g., the hand area in motor cortex or the arcuate fasciculus) are investigated more closely (Halwani et al., 2011; Rüber et al., 2015).
Across analyses, we found remarkable similarity of networks for the two musician groups, which seems surprising, given that previous studies have reported effects of AP on connectivity. There are multiple reasons potentially contributing to this discrepancy. First, previous evidence for the effects of AP on connectivity is sparse: the number of studies reporting differences in intrinsic functional and structural connectivity is relatively small, none of the effects has been replicated to date, and the effects reported were very subtle in size (Greber et al., 2020). Second, most of the studies investigated small to very small samples, making them prone to false-positive results (Button et al., 2013). Third, methodology varied widely, both between previous studies and compared with the current study. As outlined above (see General methodological considerations), current methodology might lack the sensitivity and reliability to robustly detect subtle differences. Fourth, there is no agreement on defining AP; it might represent a distinct population (Athos et al., 2007) or lie on the upper end of a continuum of tone-naming abilities (Bermudez and Zatorre, 2009). We defined AP based on self-report, and the tone-naming proficiency of our AP and non-AP musicians strongly differed (d > 2). Thus, we are confident that the similarities of AP and non-AP musicians are valid. It is important to note that our results should not be regarded as evidence that there are no effects of AP on the brain in general. For example, we found a correlation between tone naming and functional connectivity of right HG and surrounding areas. This is consistent with previous reports of AP-specific alterations in right-hemispheric auditory regions (Leipold et al., 2019a), and underlines the importance of right-hemispheric HG in AP (Wengenroth et al., 2014). Furthermore, task-based studies investigating tone labeling in action have shown considerable promise for uncovering the neural peculiarities of the AP phenomenon (Schulze et al., 2013; Greber et al., 2018; Leipold et al., 2019c,d; McKetton et al., 2019).
In conclusion, we identified robust and replicable effects of musical expertise on intrinsic functional and structural brain networks. As effects were stronger in the functional domain, we hypothesize that musical training particularly affects functional compared with structural networks. The effects of AP on large-scale brain networks might be subtle, requiring very large samples or task-based experiments to be detected.
Footnotes
This work was supported by Swiss National Science Foundation Grant 320030_163149 to L.J. We thank Désirée Yamada for invaluable help in data acquisition and research administration; Silvano Sele for support with the statistical analyses; Marielle Greber and Lisa-Katrin Kaufmann for helpful comments on the manuscript; and Chantal Oderbolz for proofreading the manuscript.
The authors declare no competing financial interests.
References
- Abdul-Kareem IA, Stancak A, Parkes LM, Al-Ameen M, AlGhamdi J, Aldhafeeri FM, Embleton K, Morris D, Sluming V (2011) Plasticity of the superior and middle cerebellar peduncles in musicians revealed by quantitative analysis of volume and number of streamlines based on diffusion tensor tractography. Cerebellum 10:611–623. 10.1007/s12311-011-0274-1 [DOI] [PubMed] [Google Scholar]
- Andersson JL, Sotiropoulos SN (2016) An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 125:1063–1078. 10.1016/j.neuroimage.2015.10.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andoh J, Matsushita R, Zatorre RJ (2015) Asymmetric interhemispheric transfer in the auditory network: evidence from TMS, resting-state fMRI, and diffusion imaging. J Neurosci 35:14602–14611. 10.1523/JNEUROSCI.2333-15.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Annett M (1970) A classification of hand preference by association analysis. Br J Psychol 61:303–321. 10.1111/j.2044-8295.1970.tb01248.x [DOI] [PubMed] [Google Scholar]
- Ashburner J (2007) A fast diffeomorphic image registration algorithm. Neuroimage 38:95–113. 10.1016/j.neuroimage.2007.07.007 [DOI] [PubMed] [Google Scholar]
- Athos EA, Levinson B, Kistler A, Zemansky J, Bostrom A, Freimer NB, Gitschier J (2007) Dichotomy and perceptual distortions in absolute pitch ability. Proc Natl Acad Sci USA 104:14795–14800. 10.1073/pnas.0703868104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bangert M, Peschel T, Schlaug G, Rotte M, Drescher D, Hinrichs H, Heinze HJ, Altenmüller E (2006) Shared networks for auditory and motor processing in professional pianists: evidence from fMRI conjunction. Neuroimage 30:917–926. 10.1016/j.neuroimage.2005.10.044 [DOI] [PubMed] [Google Scholar]
- Behrens TE, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, Matthews PM, Brady JM, Smith SM (2003) Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn Reson Med 50:1077–1088. 10.1002/mrm.10609 [DOI] [PubMed] [Google Scholar]
- Behzadi Y, Restom K, Liau J, Liu TT (2007) A component based noise correction method (CompCor) for BOLD and perfusion based fMRI. Neuroimage 37:90–101. 10.1016/j.neuroimage.2007.04.042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bengtsson SL, Nagy Z, Skare S, Forsman L, Forssberg H, Ullén F (2005) Extensive piano practicing has regionally specific effects on white matter development. Nat Neurosci 8:1148–1150. 10.1038/nn1516 [DOI] [PubMed] [Google Scholar]
- Bermudez P, Zatorre RJ (2009) A distribution of absolute pitch ability as revealed by computerized testing. Music Percept Interdiscip J 27:89–101. 10.1525/mp.2009.27.2.89 [DOI] [Google Scholar]
- Brauchli C, Leipold S, Jäncke L (2019) Univariate and multivariate analyses of functional networks in absolute pitch. Neuroimage 189:241–247. 10.1016/j.neuroimage.2019.01.021 [DOI] [PubMed] [Google Scholar]
- Brauchli C, Leipold S, Jäncke L (2020) Diminished large-scale functional brain networks in absolute pitch during the perception of naturalistic music and audiobooks. Neuroimage 216:116513. 10.1016/j.neuroimage.2019.116513 [DOI] [PubMed] [Google Scholar]
- Bressler SL, Menon V (2010) Large-scale brain networks in cognition: emerging methods and principles. Trends Cogn Sci 14:277–290. 10.1016/j.tics.2010.04.004 [DOI] [PubMed] [Google Scholar]
- Burkhard A, Hänggi J, Elmer S, Jäncke L (2020) The importance of the fibre tracts connecting the planum temporale in absolute pitch possessors. Neuroimage 211:116590. 10.1016/j.neuroimage.2020.116590 [DOI] [PubMed] [Google Scholar]
- Button KS, Ioannidis JP, Mokrysz C, Nosek BA, Flint J, Robinson ES, Munafò MR (2013) Power failure: why small sample size undermines the reliability of neuroscience. Nat Rev Neurosci 14:365–376. 10.1038/nrn3475 [DOI] [PubMed] [Google Scholar]
- Dalboni da Rocha JL, Schneider P, Benner J, Santoro R, Atanasova T, Van De Ville D, Golestani N (2020) TASH: toolbox for the automated segmentation of Heschl's gyrus. Sci Rep 10:3887. 10.1038/s41598-020-60609-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Martino F, Valente G, Staeren N, Ashburner J, Goebel R, Formisano E (2008) Combining multivariate voxel selection and support vector machines for mapping and classification of fMRI spatial patterns. Neuroimage 43:44–58. 10.1016/j.neuroimage.2008.06.037 [DOI] [PubMed] [Google Scholar]
- Deutsch D (2013) Absolute pitch. In: The psychology of music, pp 141–182. Cambridge, MA: Academic. [Google Scholar]
- Dohn A, Garza-Villarreal EA, Chakravarty MM, Hansen M, Lerch JP, Vuust P (2015) Gray- and white-matter anatomy of absolute pitch possessors. Cereb Cortex 25:1379–1388. 10.1093/cercor/bht334 [DOI] [PubMed] [Google Scholar]
- Drakesmith M, Caeyenberghs K, Dutt A, Lewis G, David AS, Jones DK (2015) Overcoming the effects of false positives and threshold bias in graph theoretical analyses of neuroimaging data. Neuroimage 118:313–333. 10.1016/j.neuroimage.2015.05.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drew PJ, Mateo C, Turner KL, Yu X, Kleinfeld D (2020) Ultra-slow oscillations in fMRI and resting-state connectivity: neuronal and vascular contributions and technical confounds. Neuron 107:782–804. 10.1016/j.neuron.2020.07.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elmer S, Rogenmoser L, Kühnis J, Jäncke L (2015) Bridging the gap between perceptual and cognitive perspectives on absolute pitch. J Neurosci 35:366–371. 10.1523/JNEUROSCI.3009-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elmer S, Hänggi J, Jäncke L (2016) Interhemispheric transcallosal connectivity between the left and right planum temporale predicts musicianship, performance in temporal speech processing, and functional specialization. Brain Struct Funct 221:331–344. 10.1007/s00429-014-0910-x [DOI] [PubMed] [Google Scholar]
- Fauvel B, Groussard M, Chételat G, Fouquet M, Landeau B, Eustache F, Desgranges B, Platel H (2014) Morphological brain plasticity induced by musical expertise is accompanied by modulation of functional connectivity at rest. Neuroimage 90:179–188. 10.1016/j.neuroimage.2013.12.065 [DOI] [PubMed] [Google Scholar]
- Fujioka T, Ross B, Kakigi R, Pantev C, Trainor LJ (2006) One year of musical training affects development of auditory cortical-evoked fields in young children. Brain 129:2593–2608. 10.1093/brain/awl247 [DOI] [PubMed] [Google Scholar]
- Gordon EE (1989) Advanced measures of music audiation. Chicago: GIA. [Google Scholar]
- Gratton C, Laumann TO, Nielsen AN, Greene DJ, Gordon EM, Gilmore AW, Nelson SM, Coalson RS, Snyder AZ, Schlaggar BL, Dosenbach NU, Petersen SE (2018) Functional brain networks are dominated by stable group and individual factors, not cognitive or daily variation. Neuron 98:439–452.e5. 10.1016/j.neuron.2018.03.035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greber M, Rogenmoser L, Elmer S, Jäncke L (2018) Electrophysiological correlates of absolute pitch in a passive auditory oddball paradigm: a direct replication attempt. eNeuro 5:ENEURO.0333-18.2018. 10.1523/ENEURO.0333-18.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greber M, Klein C, Leipold S, Sele S, Jäncke L (2020) Heterogeneity of EEG resting-state brain networks in absolute pitch. Int J Psychophysiol 157:11–22. 10.1016/j.ijpsycho.2020.07.007 [DOI] [PubMed] [Google Scholar]
- Griffiths TD, Warren JD (2002) The planum temporale as a computational hub. Trends Neurosci 25:348–353. 10.1016/s0166-2236(02)02191-4 [DOI] [PubMed] [Google Scholar]
- Gujing L, Hui H, Xin L, Lirong Z, Yutong Y, Guofeng Y, Jing L, Shulin Z, Lei Y, Cheng L, Dezhong Y (2019) Increased insular connectivity and enhanced empathic ability associated with dance/music training. Neural Plast 2019:9693109. 10.1155/2019/9693109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habibi A, Damasio A, Ilari B, Veiga R, Joshi AA, Leahy RM, Haldar JP, Varadarajan D, Bhushan C, Damasio H (2018) Childhood music training induces change in micro and macroscopic brain structure: results from a longitudinal study. Cereb Cortex 28:4336–4347. 10.1093/cercor/bhx286 [DOI] [PubMed] [Google Scholar]
- Halwani GF, Loui P, Rüber T, Schlaug G (2011) Effects of practice and experience on the arcuate fasciculus: comparing singers, instrumentalists, and non-musicians. Front Psychol 2:156. 10.3389/fpsyg.2011.00156 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haynes JD (2015) A primer on pattern-based approaches to fMRI: principles, pitfalls, and perspectives. Neuron 87:257–270. 10.1016/j.neuron.2015.05.025 [DOI] [PubMed] [Google Scholar]
- Hermundstad AM, Bassett DS, Brown KS, Aminoff EM, Clewett D, Freeman S, Frithsen A, Johnson A, Tipper CM, Miller MB, Grafton ST, Carlson JM (2013) Structural foundations of resting-state and task-based functional connectivity in the human brain. Proc Natl Acad Sci USA 110:6169–6174. 10.1073/pnas.1219562110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofer S, Frahm J (2006) Topography of the human corpus callosum revisited: comprehensive fiber tractography using diffusion tensor magnetic resonance imaging. Neuroimage 32:989–994. 10.1016/j.neuroimage.2006.05.044 [DOI] [PubMed] [Google Scholar]
- Honey CJ, Sporns O, Cammoun L, Gigandet X, Thiran JP, Meuli R, Hagmann P (2009) Predicting human resting-state functional connectivity from structural connectivity. Proc Natl Acad Sci USA 106:2035–2040. 10.1073/pnas.0811168106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyde KL, Lerch J, Norton A, Forgeard M, Winner E, Evans AC, Schlaug G (2009) Musical training shapes structural brain development. J Neurosci 29:3019–3025. 10.1523/JNEUROSCI.5118-08.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imfeld A, Oechslin MS, Meyer M, Loenneker T, Jäncke L (2009) White matter plasticity in the corticospinal tract of musicians: a diffusion tensor imaging study. Neuroimage 46:600–607. 10.1016/j.neuroimage.2009.02.025 [DOI] [PubMed] [Google Scholar]
- Jäncke L (2009) The plastic human brain. Restor Neurol Neurosci 27:521–538. 10.3233/RNN-2009-0519 [DOI] [PubMed] [Google Scholar]
- Jäncke L, Steinmetz H (1994) Interhemispheric transfer time and corpus callosum size. Neuroreport 5:2385–2388. 10.1097/00001756-199411000-00043 [DOI] [PubMed] [Google Scholar]
- Jäncke L, Steinmetz H (1998) Brain size: a possible source of interindividual variability in corpus callosum morphology. In: The role of the human corpus callosum in sensory motor integration: anatomy, physiology, and behavior; individual differences and clinical applications. (Zaidel E, Iacoboni M, Pascual-Leone AP, eds). New York: Plenum. [Google Scholar]
- Jäncke L, Langer N, Hänggi J (2012) Diminished whole-brain but enhanced peri-sylvian connectivity in absolute pitch musicians. J Cogn Neurosci 24:1447–1461. 10.1162/jocn_a_00227 [DOI] [PubMed] [Google Scholar]
- Jones R, Grisot G, Augustinack J, Magnain C, Boas DA, Fischl B, Wang H, Yendiki A (2020) Insight into the fundamental trade-offs of diffusion MRI from polarization-sensitive optical coherence tomography in ex vivo human brain. Neuroimage 214:116704. 10.1016/j.neuroimage.2020.116704 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DK, Knösche TR, Turner R (2013) White matter integrity, fiber count, and other fallacies: the do's and don'ts of diffusion MRI. Neuroimage 73:239–254. 10.1016/j.neuroimage.2012.06.081 [DOI] [PubMed] [Google Scholar]
- Kim SG, Knösche TR (2016) Intracortical myelination in musicians with absolute pitch: quantitative morphometry using 7-T MRI. Hum Brain Mapp 37:3486–3501. 10.1002/hbm.23254 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SG, Knösche TR (2017) Resting state functional connectivity of the ventral auditory pathway in musicians with absolute pitch. Hum Brain Mapp 38:3899–3916. 10.1002/hbm.23637 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein C, Liem F, Hänggi J, Elmer S, Jäncke L (2016) The “silent” imprint of musical training. Hum Brain Mapp 37:536–546. 10.1002/hbm.23045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraus N, Chandrasekaran B (2010) Music training for the development of auditory skills. Nat Rev Neurosci 11:599–605. 10.1038/nrn2882 [DOI] [PubMed] [Google Scholar]
- Langer N, Pedroni A, Jäncke L (2013) The problem of thresholding in small-world network analysis. PLoS One 8:e53199. 10.1371/journal.pone.0053199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leipold S, Brauchli C, Greber M, Jäncke L (2019a) Absolute and relative pitch processing in the human brain: neural and behavioral evidence. Brain Struct Funct 224:1723–1738. 10.1007/s00429-019-01872-2 [DOI] [PubMed] [Google Scholar]
- Leipold S, Greber M, Elmer S (2019b) Perception and cognition in absolute pitch: distinct yet inseparable. J Neurosci 39:5839–5841. 10.1523/JNEUROSCI.0653-19.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leipold S, Greber M, Sele S, Jäncke L (2019c) Neural patterns reveal single-trial information on absolute pitch and relative pitch perception. Neuroimage 200:132–141. 10.1016/j.neuroimage.2019.06.030 [DOI] [PubMed] [Google Scholar]
- Leipold S, Oderbolz C, Greber M, Jäncke L (2019d) A reevaluation of the electrophysiological correlates of absolute pitch and relative pitch: no evidence for an absolute pitch-specific negativity. Int J Psychophysiol 137:21–31. 10.1016/j.ijpsycho.2018.12.016 [DOI] [PubMed] [Google Scholar]
- Loui P, Li HC, Hohmann A, Schlaug G (2011) Enhanced cortical connectivity in absolute pitch musicians: a model for local hyperconnectivity. J Cogn Neurosci 23:1015–1026. 10.1162/jocn.2010.21500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loui P, Zamm A, Schlaug G (2012) Enhanced functional networks in absolute pitch. Neuroimage 63:632–640. 10.1016/j.neuroimage.2012.07.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo C, Guo Z, Lai Y, Liao W, Liu Q, Kendrick KM, Yao D, Li H (2012) Musical training induces functional plasticity in perceptual and motor networks: insights from resting-state fMRI. PLoS One 7:e36568. 10.1371/journal.pone.0036568 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo C, Tu S, Peng Y, Gao S, Li J, Dong L, Li G, Lai Y, Li H, Yao D (2014) Long-term effects of musical training and functional plasticity in salience system. Neural Plast 2014:180138. 10.1155/2014/180138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madhyastha T, Mérillat S, Hirsiger S, Bezzola L, Liem F, Grabowski T, Jäncke L (2014) Longitudinal reliability of tract-based spatial statistics in diffusion tensor imaging. Hum Brain Mapp 35:4544–4555. 10.1002/hbm.22493 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maier-Hein KH, Neher PF, Houde JC, Côté MA, Garyfallidis E, Zhong J, Chamberland M, Yeh FC, Lin YC, Ji Q, Reddick WE, Glass JO, Chen DQ, Feng Y, Gao C, Wu Y, Ma J, He R, Li Q, Westin CF, et al. (2017) The challenge of mapping the human connectome based on diffusion tractography. Nat Commun 8:1349. 10.1038/s41467-017-01285-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKetton L, DeSimone K, Schneider KA (2019) Larger auditory cortical area and broader frequency tuning underlie absolute pitch. J Neurosci 39:2930–2937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Münte TF, Altenmüller E, Jäncke L (2002) The musician's brain as a model of neuroplasticity. Nat Rev Neurosci 3:473–478. 10.1038/nrn843 [DOI] [PubMed] [Google Scholar]
- Noble S, Scheinost D, Constable RT (2019) A decade of test-retest reliability of functional connectivity: a systematic review and meta-analysis. Neuroimage 203:116157. 10.1016/j.neuroimage.2019.116157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oechslin MS, Imfeld A, Loenneker T, Meyer M, Jäncke L (2010a) The plasticity of the superior longitudinal fasciculus as a function of musical expertise: a diffusion tensor imaging study. Front Hum Neurosci 3:76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oechslin MS, Meyer M, Jäncke L (2010b) Absolute pitch: functional evidence of speech-relevant auditory acuity. Cereb Cortex 20:447–455. 10.1093/cercor/bhp113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Owen JP, Ziv E, Bukshpun P, Pojman N, Wakahiro M, Berman JI, Roberts TP, Friedman EJ, Sherr EH, Mukherjee P (2013) Test–retest reliability of computational network measurements derived from the structural connectome of the human brain. Brain Connect 3:160–176. 10.1089/brain.2012.0121 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palomar-García MÁ, Zatorre RJ, Ventura-Campos N, Bueichekú E, Ávila C (2017) Modulation of functional connectivity in auditory-motor networks in musicians compared with non-musicians. Cereb Cortex 27:2768–2778. 10.1093/cercor/bhw120 [DOI] [PubMed] [Google Scholar]
- Power JD, Barnes KA, Snyder AZ, Schlaggar BL, Petersen SE (2012) Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage 59:2142–2154. 10.1016/j.neuroimage.2011.10.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rauschecker JP, Scott SK (2009) Maps and streams in the auditory cortex: nonhuman primates illuminate human speech processing. Nat Neurosci 12:718–724. 10.1038/nn.2331 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roland JL, Snyder AZ, Hacker CD, Mitra A, Shimony JS, Limbrick DD, Raichle ME, Smyth MD, Leuthardt EC (2017) On the role of the corpus callosum in interhemispheric functional connectivity in humans. Proc Natl Acad Sci USA 114:13278–13283. 10.1073/pnas.1707050114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouder JN, Speckman PL, Sun D, Morey RD, Iverson G (2009) Bayesian t tests for accepting and rejecting the null hypothesis. Psychon Bull Rev 16:225–237. 10.3758/PBR.16.2.225 [DOI] [PubMed] [Google Scholar]
- Rouder JN, Morey RD, Speckman PL, Province JM (2012) Default Bayes factors for ANOVA designs. J Math Psychol 56:356–374. 10.1016/j.jmp.2012.08.001 [DOI] [Google Scholar]
- Rüber T, Lindenberg R, Schlaug G (2015) Differential adaptation of descending motor tracts in musicians. Cereb Cortex 25:1490–1498. 10.1093/cercor/bht331 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M, Sporns O (2010) Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52:1059–1069. 10.1016/j.neuroimage.2009.10.003 [DOI] [PubMed] [Google Scholar]
- Schlaug G (2015) Musicians and music making as a model for the study of brain plasticity. In: Progress in brain research. Music, neurology, and neuroscience: evolution, the musical brain, medical conditions, and therapies (Altenmüller E, Finger S, Boller F, eds), pp 37–55. Amsterdam: Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlaug G, Jäncke L, Huang Y, Staiger JF, Steinmetz H (1995) Increased corpus callosum size in musicians. Neuropsychologia 33:1047–1055. 10.1016/0028-3932(95)00045-5 [DOI] [PubMed] [Google Scholar]
- Schmithorst VJ, Wilke M (2002) Differences in white matter architecture between musicians and non-musicians: a diffusion tensor imaging study. Neurosci Lett 321:57–60. 10.1016/s0304-3940(02)00054-x [DOI] [PubMed] [Google Scholar]
- Schneider P, Scherg M, Dosch HG, Specht HJ, Gutschalk A, Rupp A (2002) Morphology of Heschl's gyrus reflects enhanced activation in the auditory cortex of musicians. Nat Neurosci 5:688–694. 10.1038/nn871 [DOI] [PubMed] [Google Scholar]
- Schulze K, Mueller K, Koelsch S (2013) Auditory Stroop and absolute pitch: an fMRI study. Hum Brain Mapp 34:1579–1590. 10.1002/hbm.22010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seither-Preisler A, Parncutt R, Schneider P (2014) Size and synchronization of auditory cortex promotes musical, literacy, and attentional skills in children. J Neurosci 34:10937–10949. 10.1523/JNEUROSCI.5315-13.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steele CJ, Bailey JA, Zatorre RJ, Penhune VB (2013) Early musical training and white-matter plasticity in the corpus callosum: evidence for a sensitive period. J Neurosci 33:1282–1290. 10.1523/JNEUROSCI.3578-12.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Termenon M, Jaillard A, Delon-Martin C, Achard S (2016) Reliability of graph analysis of resting state fMRI using test-retest dataset from the Human Connectome Project. Neuroimage 142:172–187. 10.1016/j.neuroimage.2016.05.062 [DOI] [PubMed] [Google Scholar]
- van den Heuvel MP, de Lange SC, Zalesky A, Seguin C, Yeo BT, Schmidt R (2017) Proportional thresholding in resting-state fMRI functional connectivity networks and consequences for patient-control connectome studies: issues and recommendations. Neuroimage 152:437–449. 10.1016/j.neuroimage.2017.02.005 [DOI] [PubMed] [Google Scholar]
- van Wijk BC, Stam CJ, Daffertshofer A (2010) Comparing brain networks of different size and connectivity density using graph theory. PLoS One 5:e13701. 10.1371/journal.pone.0013701 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vollmann H, Ragert P, Conde V, Villringer A, Classen J, Witte OW, Steele CJ (2014) Instrument specific use-dependent plasticity shapes the anatomical properties of the corpus callosum: a comparison between musicians and non-musicians. Front Behav Neurosci 8:245. 10.3389/fnbeh.2014.00245 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang JY, Abdi H, Bakhadirov K, Diaz-Arrastia R, Devous MD (2012) A comprehensive reliability assessment of quantitative diffusion tensor tractography. Neuroimage 60:1127–1138. 10.1016/j.neuroimage.2011.12.062 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wengenroth M, Blatow M, Heinecke A, Reinhardt J, Stippich C, Hofmann E, Schneider P (2014) Increased volume and function of right auditory cortex as a marker for absolute pitch. Cereb Cortex 24:1127–1137. 10.1093/cercor/bhs391 [DOI] [PubMed] [Google Scholar]
- Wenhart T, Bethlehem RA, Baron-Cohen S, Altenmüller E (2019) Autistic traits, resting-state connectivity, and absolute pitch in professional musicians: shared and distinct neural features. Mol Autism 10:20–20. 10.1186/s13229-019-0272-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westerhausen R, Grüner R, Specht K, Hugdahl K (2009) Functional relevance of interindividual differences in temporal lobe callosal pathways: a DTI tractography study. Cereb Cortex 19:1322–1329. 10.1093/cercor/bhn173 [DOI] [PubMed] [Google Scholar]
- Winkler AM, Ridgway GR, Webster MA, Smith SM, Nichols TE (2014) Permutation inference for the general linear model. Neuroimage 92:381–397. 10.1016/j.neuroimage.2014.01.060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yendiki A, Koldewyn K, Kakunoori S, Kanwisher N, Fischl B (2014) Spurious group differences due to head motion in a diffusion MRI study. Neuroimage 88:79–90. 10.1016/j.neuroimage.2013.11.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zalesky A, Fornito A, Bullmore ET (2010) Network-based statistic: identifying differences in brain networks. Neuroimage 53:1197–1207. 10.1016/j.neuroimage.2010.06.041 [DOI] [PubMed] [Google Scholar]
- Zamorano AM, Cifre I, Montoya P, Riquelme I, Kleber B (2017) Insula-based networks in professional musicians: evidence for increased functional connectivity during resting state fMRI. Hum Brain Mapp 38:4834–4849. 10.1002/hbm.23682 [DOI] [PMC free article] [PubMed] [Google Scholar]