Limiting mobility during COVID-19, when and to what level? An international comparative study using change point analysis

Abstract

The year 2020 saw a rapid global spread of the highly contagious novel coronavirus COVID-19. To halt the spread of the disease, decision makers and governments across the world have been forced to limit mobility and human interaction, which led to a complete lockdown and the closure of nonessential businesses and public places in many cities and countries. Although effective in curbing the spread of the disease, such measures have had major social and economic impacts, particularly at locations where a complete lockdown was required. In such unprecedented circumstances, decision makers were faced with the dilemma of deciding on how and when to limit mobility to curb the spread of the disease, while being considerate of the significant economic impacts of enforcing such a lockdown. Limited research in this area meant that decision makers were forced to experiment different courses of action without fully understanding the consequences of those actions. To address this critical gap and to provide decision makers with more insights on how to manage mobility during a global pandemic, this paper conducts statistical change point analysis of mobility data from 10 different countries with the aims of establishing links between mobility trends, COVID-19 infections, and COVID-19 mortality rates across different countries where different policies were adopted. Among other findings, the analysis revealed that slow responders experienced significantly higher mortality rates per 100,000 people and were forced to implement stricter lockdown strategies when compared to early responders. The analysis also shows that operating at 40% level of mobility is achievable if appropriate action is taken early enough. The findings of this study are extremely valuable in helping nations better manage a, highly anticipated, second wave of COVID-19 or any other highly contagious global pandemic.

1. Introduction

Restrictions on mobility, mass gatherings, and public interaction are the most common measures adopted by governments to contain the spread of the highly contagious severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), more commonly known as COVID-19 (McCloskey et al., 2020). Although containment measures have been effective in limiting the spread of the disease and have had positive environmental impacts (Berman and Ebisu, 2020; Chowdhuri et al., 2020; Pal et al., 2020), they are also associated with devastating economic and social impacts (Elliott, 2020; Musselwhite et al., 2020).

During the early stages of the COVID-19 outbreak, epidemiologists in different countries were exploring different policies that could help limit the spread of the virus. The virus’ high basic reproduction number, R₀ (i.e. the number of people who acquire the disease from an infected person) and the high effective reproductive number, R₁, (i.e. the number of people that can be infected by an individual at any given time) caused significant panic amongst officials in different countries and meant that swift action had to be taken. Although most countries ended up introducing restrictions on mobility and social interaction, some countries explored other options including allowing a significant portion of the population to contract the virus with the aims of creating what is known as “herd immunity” amongst the people (i.e. the majority of the population getting vaccinated after contracting the virus) (Boseley, 2020). In fact, some countries such as Sweden, did indeed adopt an approach where very limited restrictions on mobility and public interaction were implemented.

Even amongst countries where mobility restrictions were introduced, there were significant differences between the levels of those restrictions and the time at which they were introduced. Some countries went into a complete lockdown while others simply closed non-essential businesses. The difference in response was driven by governments trying to restrict mobility and limit the spread of the disease, without causing major disruptions to the economy. Governments attempted finding a new “optimum level” of mobility and social interaction, whereby a country is able to maintain certain levels of movement and economic activity while limiting the spread of the disease (i.e. keeping the disease under control).

Although multiple publications, including those reviewed in the Ongoing Research section of this paper, have studied the spread of the virus over time, limited work has focused on studying the relationship between imposing a lockdown (i.e. limiting mobility) and the reduction infection and mortality rates. It is unclear how the level and the timing of introducing restrictions could impact the spread of the virus and its associated mortality rate. In other words, it is not entirely clear whether timely and less strict restrictions on mobility are more effective than late and more severe restrictions or vice versa. Similarly, it is not clear whether restricting mobility to a certain level might be sufficient in curbing the deadliness of the disease.

The lack of research in this area has left decision makers with a dilemma of deciding how and when they could implement or lift mobility restrictions without sacrificing public health. Decision makers also lacked information required to identify an optimal level of mobility at which a nation can operate without severe impacts on public health. In fact, a comment recently published in The Lancet calls for research conducting a “Comparative analysis of different quarantine strategies and contexts for their effectiveness and social acceptability”, which could help control the COVID-19 pandemic (Bedford et al., 2020).

To address such a critical gap, this paper explores links between trends in mobility and the number of COVID-19 infections and the associated mortality rate in several different countries around the world where different containment measures were adopted. The paper aims to develop an improved understanding of the most effective method and strategies to manage public mobility in such a pandemic in terms of the urgency of the response and its strictness. To achieve the aforementioned objective, the paper performs statistical change point analysis of time series mobility data collected over a period of over four months to identify the time at which changes in the level of mobility in different countries were observed. The timing and the level of mobility due to the containment were then analysed to identify links between those factors and the number of COVID-19 cases and the mortality rates in the different countries. The assessment was conducted using data from 10 countries in three different continents that responded differently to the outbreak of the disease and that saw different infection and mortality rates. This provides important insights into the most effective course of action.

2. Ongoing Research

There is general consensus among epidemiologists that the SARS-CoV-2 is more contagious than other recent viral outbreaks. Wilder-Smith et al. (2020) recently reported that community spread is more prominent in COVID-19 when compared to the 2003 SARS outbreak. The reason here is that viral shedding is expected in COVID-19 patients even before the patients develop any symptoms. The high transmissibility of SARS-CoV-2 compared to other viruses is also evident in its basic reproduction number (R₀). R₀ for SARS-CoV-2 (estimated at 2.2) is significantly higher than the 1.4 that was estimated for the H1N1 (the virus that caused the 2009 swine flu pandemic) (Dawood et al., 2012). These findings have led many decision makers to opt for the adoption of complete lockdown where all non-essential businesses and public places must be closed.

Unlike the agreement on the contagiousness of the virus and the need for containment measures, there is lots of debate and speculation in the literature on what the most appropriate time to introduce the measures is and at what level (Remuzzi and Remuzzi, 2020).

Recent work assessing the effectiveness of the German intervention found statistical links between three major governmental interventions and a reduction in rate at which COVID-19 cases grew. The legislative changes found effective included (i) the cancellation of large events with more than 1000 participants, (ii) the closing of schools, childcare centers and the majority of stores, and (iii) the contact ban and closing of all non-essential stores. Lee et al. (2020) suggest that early response and efficient tracking in Singapore might have been one reason why the rate of increase in cases in the country did not follow the exponential trend observed elsewhere.

Other work has focused on augmenting deterministic epidemiological models, including the Susceptible-Infected-Removed (SIR), with information about the policy choice and the level of economic activity to help predict the impacts of the level of lockdown chosen on the spread of the disease (Alvarez et al., 2020; Atkeson, 2020; Eichenbaum et al., 2020; Stock, 2020). For instance, Gonzalez-Eiras and Niepelt (2020)predicted that economic activity is optimally reduced by two thirds of normal conditions, for around 50 days to best manage the outbreak. Piguillem and Shi (2020) likened the challenge of identifying an optimal level for the lockdown to a simple welfare maximization problem. Based on the modelling results the authors recommend implementing an early and complete lockdown for roughly two weeks. The paper reports that such practice is expected to reduce the number of total cases from 41% (in case of no lockdown) to 0.01% of the population, reducing also the total number of casualties from 1% (in case of no lockdown) to 0.0002% of the population.

These studies are extremely valuable in helping understand how contagious the SARS-CoV-2 virus strain and in helping predict the spread of the disease under different scenarios. Nevertheless, due to the lack of data, the models remain speculative models that were developed based on several different assumptions that are difficult to verify or validate. To overcome such limitations and provide more insight on the effectiveness of different containment strategies, this paper conducts change point analysis of time series data collected on the ground in 10 different countries during a period of over four months to explore the impacts of implementing different restrictive measures on a nation’s ability to contain the disease.

It is worth mentioning here that a number of recent studies have used change point analysis to analyse the spread of COVID-19. Dehning et al. (2020) used change point analysis of COVID-19 cases from Germany and used Bayesian methodology to model the spread of the disease. (Jiang et al., 2020), used a SN-NOT change point analysis to compare the epidemic’s growth rate across different countries. In Gregori et al. (2020), the authors used a Bayesian Change Point Detection Method (BCPDM) to identify the changing speed of the epidemic curve. One significant difference between all those studies and this paper is that this paper focuses on analysing the impacts of changes in mobility on the spread of the virus (i.e. we approach the problem from a transport health perspective). To that end, change point analysis is performed using mobility data (as opposed to COVID-19 cases or infections). The novelty of this work lies in the fact that it aims to help understand how restrictions that limit mobility could be most effective in limiting the spread of COVID-19 or any other highly contagious disease.

3. Methodology

Change-point and trend analysis are statistical tools that are commonly used to model and monitor the behavior of time series data (i.e. observations collected overtime). A change-point is usually related to an abrupt or structural change in the distributional properties of time series data.

In this paper, change point analysis was used to model time series data representing public mobility in 10 different countries with the aims of understanding the relationship between changes in mobility and the spread of COVID-19. Mobility data was used as a surrogate measure of the timing and the severity of the restrictions that were implemented by governments in response to COVID-19. It is worthy to mention here that actual legislative changes varied from one country to another. In fact, the date of implementing different restrictions in a single country also varied (eg: working from home, closing schools, closing entertainment businesses … etc). Using mobility data instead of government intervention dates, helps (i) integrate the impacts of all legislative changes into one variable, and (ii) eliminate the need for modelling and understanding the level of compliance to legislative changes.

3.1. Change point detection

As already noted, change point analysis works on detecting abrupt changes in the statistical distributional properties of time series data. The points in time when drastic variation in the properties of the statistical distribution of the time series data are referred to as change points. There are many algorithms available for identifying the single or multiple change points in a given dataset.

In this study, a multiple change point detection algorithm was used since more than one change point was expected in the data (a drop in mobility due to the introduction of the legislative changes and a recovery point at which the changes were lifted). The change point detection algorithm works on estimating the timing of all change points and the properties of the time series data before and after the change (i.e. the magnitude of the change observed).

Let $x_1,x_2,\dots ,x_n$ be a set of time series observations in a dataset where the subscript of each observation x denotes the time at which the observation was recorded. If we assume that $p\left(x_1\right),p\left(x_2\right),\dots p\left(x_n\right)$ represent the probability density functions of the time series observations $x_1,x_2,\dots ,x_n$ , the multiple change point model can be defined as follows

$$x_t=\{\begin{array}{c}{p}_1(x_1|{\theta }_1)1\le |t<t_1\\ p_2(x_2|{\theta }_2)t_1\le |t<t_2\\ ⋮\\ p_n(x_n|{\theta }_n)t_{n-1}\le |t<t_n\end{array}$$ (1)

where ${\theta }_t$ denotes the unknown parameter (e.g., mean or variance) of the probability model for segment t. The parameters ${\theta }_1,{\theta }_2,\dots .,{\theta }_n$ and the changepoints $t_1$ , $t_2$ , …, $t_{n-1}$ are unknown.

The series can be divided into n homogenous groups called segments if locations of change points are detected. In this study we consider change points as points in the series where there was a significant change in both the mean and variance of the mobility data. The following equation is used to test for the existence of such changes by comparing statistical properties of data among consecutive segments:

$$x_t=\{\begin{array}{c}{\mu }_1+{\epsilon }_t,{\epsilon }_t~N\left(0,{\sigma }_1^2\right),t=\mathrm{1,2},\dots ,k\\ {\mu }_2+{\epsilon }_t,{\epsilon }_t~N\left(0,{\sigma }_2^2\right),t=k+1,\dots ,T\end{array}$$ (2)

3.2. Binary segmentation

Given m segments of the data, the change point detection is achieved minimizing the following function:

$$\sum _{i=1}^{m+1}\left[C\left(x_{(t_{i-1}+1):t_i}\right)\right]+\beta f\left(m\right)$$ (3)

where C is a cost function (negative log-likelihood) for a segment and $\beta f\left(m\right)$ is a penalty to guard against overfitting.

The Binary Segmentation technique proposed in (Edwards and Cavalli-Sforza, 1965; Scott and Knott, 1974) was used to estimate an approximate minimum of the Equation (3). The algorithm first works on detecting a single changepoint in the entire data set (mobility data in this case). Once the first change point is detected the data is split into two sub-segments at the change point location and the single change point procedure is repeated on the two data sets. If further change points are identified the data is split into further sub-segments. The detection process continues until no change points are found in the data sub-segments.

The changepoint package in statistical software R version 3.6.3 was used to estimate the change points in this study (Killick and Eckley, 2014).

Upon detection of the change points in the mobility data, relationships between the trends in mobility and COVID-19 cases and fatalities were explored to identify the impacts of different limiting mobility on the spread and the deadliness of the disease.

4. Data description

Two different types of data collected from 10 different countries was considered in this study. The first dataset consisted of time series data of confirmed COVID-19 cases and deaths and the second dataset consisted of time series transit usage data collected in 10 different countries.

Data on the number confirmed COVID-19 cases and deaths were sourced from COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University(University and Medicine, 2020). This data was sourced by the John Hopkins CSSE team from multiple reliable resources including the World Health Organization (WHO), the European Center for Disease Prevention and Control (ECDC), and the US Center for Disease Control (CDC).

Mobility was tracked using the surrogate measure of the percentage of requests for transit trips (public transportation) recorded and stored by Apple Maps. The data was recorded by Apple Maps for multiple countries/regions, sub-regions, and cities as a percentage relative to the baseline number of trips conducted on January 13th, 2020 (Maps, 2020). Mobility data is publicly available on the Apple website under Mobility Trend Reports.

It is worth noting here that using data in Google’s Community Mobility Report was considered, however, this report only provides data starting the 15^th of February, which is less than a month before countries started implementing lockdown measure. This leaves us with only 25 observations in the pre-intervention period, which is not enough for the model to filter seasonal trends. In contrast, Apple Maps is provides 49 observations in the pre-intervention period and a total of 127 observations. Previous research recommends that, as a rule of thumb, no less than 50 and preferably 100 observations are obtained before analyzing intervention in timeseries data (Box and Tiao, 1975; Lehmann and Casella, 2006). This ensures that the models are more robust, and the results are more reliable.

Data for both COVID-19 infections and mobility was considered between the 22^nd of Jan 2020 and 29^th of May 2020 (data past that date was not considered due to the mass protests that took place as a results of the death of George Floyd). The data was sourced from 10 different countries where there was some variation in the response to the pandemic and the restrictions that were implemented. Some of those countries are believed to be highly impacted by the virus while others were believed to be less impacted. The countries considered were Canada, France, Germany, Italy, New Zealand, Norway, Spain, Sweden, UK, and the US.

5. Change point analysis results

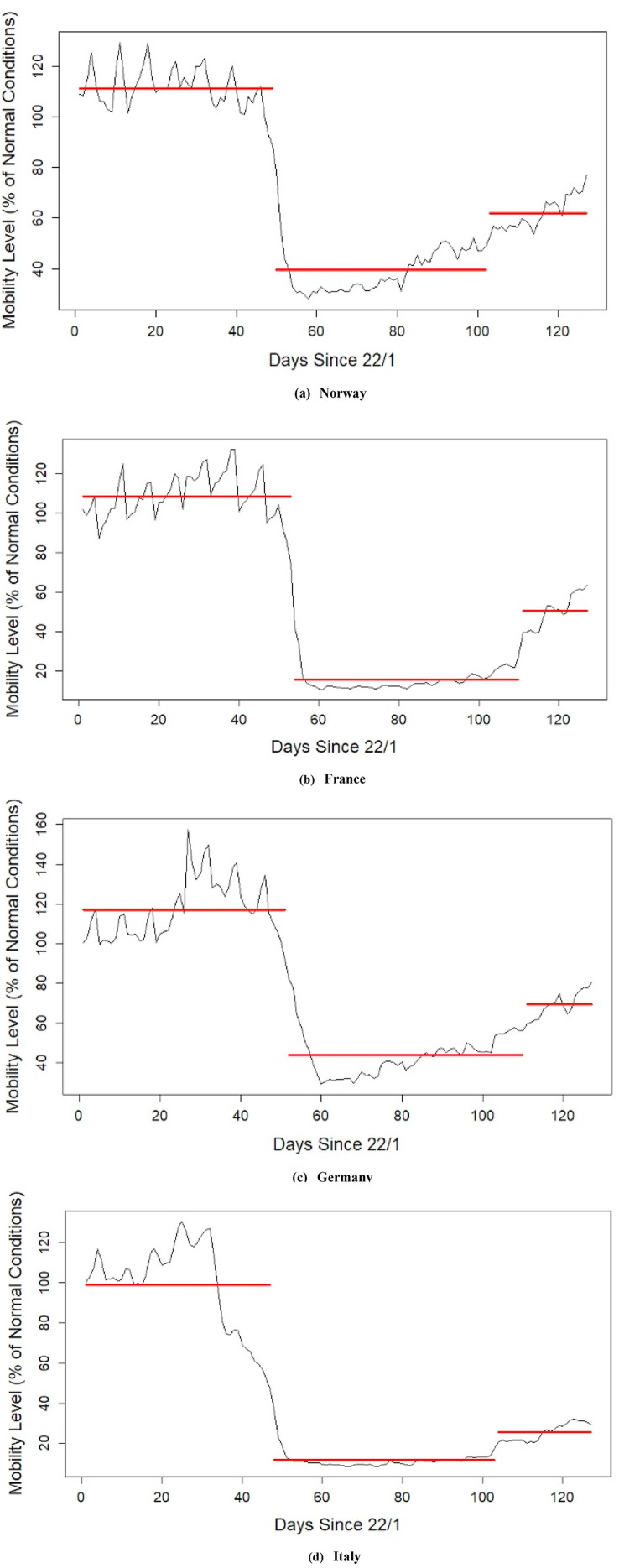
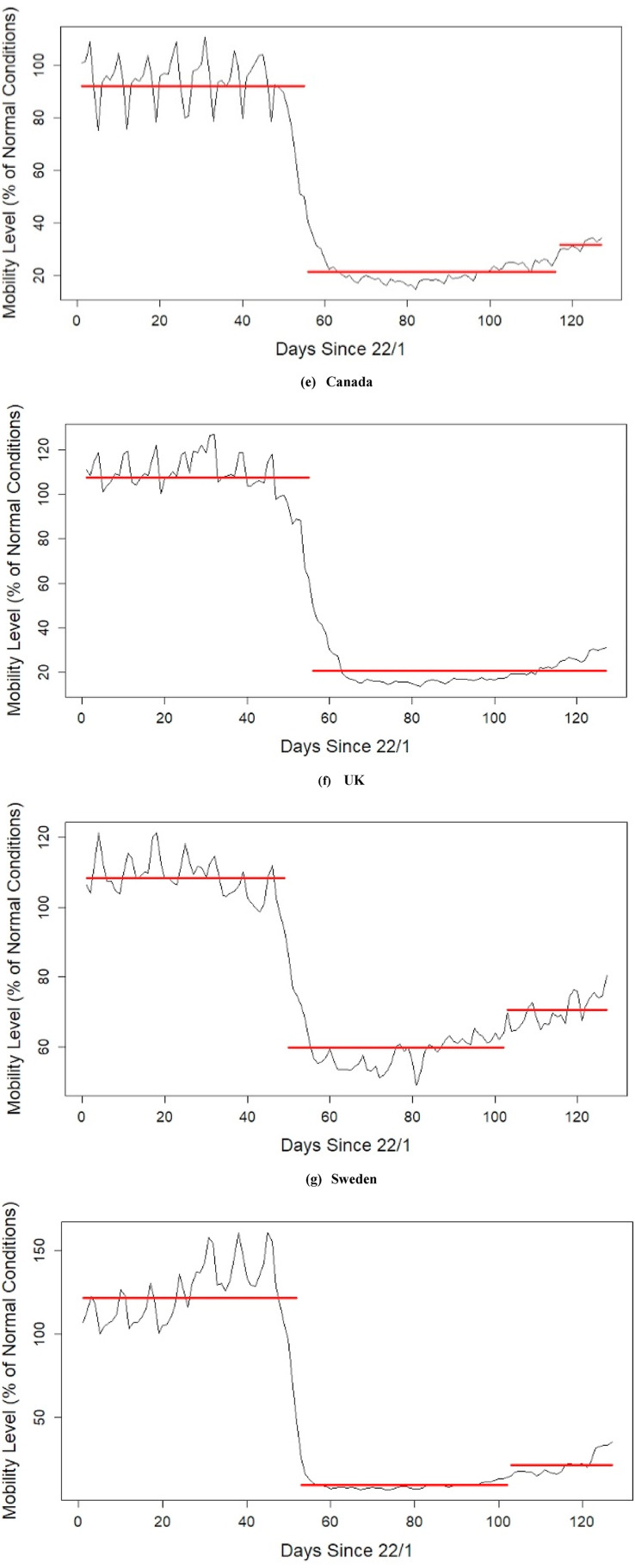
As already noted, the first part of the analysis involved using binary segmentation to detect change points in the mobility time series data. The plots shown in Fig. 1 a to j illustrate the results of the change point analysis conducted using mobility data from each of the 10 countries considered in this study. As evident in the plots, the majority (80%) of the countries considered in the study had already experienced two change points in mobility data at the time of this study (i.e. there were two points where the statistical properties of the mobility trends changed).

Fig. 1.

Trends in mobility before and after the detected change points.

The first change point, which was observed in all 10 countries, represents a statistically significant drop in mobility that can be attributed to the restrictions that were introduced by governments. This includes school closure, closure of nonessential businesses (defined as recreational businesses such as theaters and shopping malls that people do not normally rely on in everyday life (Jiang, 2020)), bans on public events and nonessential travel, and limits on public gatherings. It is worth noting here that the drop in demand for mobility could also be attributed to the public being warry of the potential risks of the contracting the disease. This is particularly true for countries where limited restrictions were implemented.

The second change point, which was observed in eight of the 10 countries represents the point of recovery in mobility data. This is the point at which restrictions started getting lifted and where it was presumed safe to travel again by the general public. It is important to note here that the UK and the US were the only two countries that had not seen such recover by the 29th of May 2020 (the last record of data considered in this study).

6. Discussion of implications

6.1. Onset of the lockdown

The second part of the analysis conducted in this study involved understanding links between changes in mobility and COVID-19 cases and fatalities. Table 1 , Row 5 shows the number of days between a country surpassing 100 cases and the time at which that country experienced its first mobility change point (MCP). The table also shows the number of confirmed cases (Row 6), the number of deaths (Row 7), the mortality rate (deaths/cases) (Row 8), and the number of deaths per 100,000 people (Row 12) at the first mobility change point in each of the 10 countries.

Table 1.

COVID-19 cases and fatalities in different countries relative to mobility change points

Variable	NZ	Norway	Germany	Canada	US	Sweden	France	Italy	UK	Spain
(1) Number of change points	2	2	2	2	1	2	2	2	1	2
(2) Date of 1st MCP	13/03	10/03	12/03	16/03	14/03	08/03	14/03	08/03	16/03	13/03
(3) Date of 2nd MCP	10/05	02/05	10/05	16/05	NA	02/05	10/05	03/05	NA	02/05
(4) Days between the change points	58	53	59	61	NA	55	57	56	NA	50
(5) Days between 100 cases and MCP 1	0	4	11	5	10	2	13	14	9	11
(6) Number of cases at MCP 1	5	400	2080	415	2859	203	4469	7375	1543	5232
(7) Number of deaths at MCP 1	0	0	3	4	60	0	91	366	65	133
(8) Mortality rate (Deaths/Cases) at MCP 1	0.000	0.000	0.001	0.010	0.021	0.000	0.020	0.050	0.042	0.025
(9) Population (million people)	4.94	5.37	83.15	36.6	329.22	10.33	67.08	60.32	67.89	47.10
(10) Population Density (people/km2)	18.44	13.93	232.65	3.67	34.18	22.95	104.19	200.16	279.95	93.09
(11) Cases per 100,000 of pop at MCP 1	0.10	7.45	2.50	1.13	0.87	1.96	6.66	12.23	2.27	11.11
(12) Deaths per 100,000 of pop at MCP 1	0	0	0.00	0.01	0.02	0	0.14	0.61	0.10	0.28
(13) Ave mobility level after MCP 1 (%)	33.80	40.28	44.48	21.95	29.31	61.64	16.13	12.18	22.88	10.50
(14) Ave mobility level after MCP 2 (%)	73.90	61.40	68.50	30.48	NA	70.16	49.02	25.18	NA	21.60
(15) Deaths on 29/5	22	236	8504	7062	102809	4350	28663	33229	38161	27121
(16) Cases on 29/5	1,504	8,422	182,922	90,908	1,746,019	36,476	183,816	232,248	271,222	238,564
(17) Mortality rate on 29/5	0.01	0.03	0.05	0.08	0.06	0.12	0.16	0.14	0.14	0.11
(18) Deaths per 100,000 of pop. on 29/5	0.45	4.40	10.23	19.30	31.23	42.10	42.73	55.09	56.21	57.58
(19) Cases per 100,000 of pop. on 29/5	30.43	156.90	219.99	248.38	530.34	352.99	274.04	385.04	399.53	506.50

MCP: Mobility Change Point.

NZ: New Zealand.

From the table we see that for Canada, Germany, Sweden, Norway, and New Zealand all had a mortality rate of less than 1% at the first mobility change point (MCP). In fact, the latter three countries had zero deaths at the point of change in mobility. In contrast, the US, UK, Italy, France, and Spain all hit a mortality rate greater that 2.1% before seeing a significant change in mobility. Italy and the UK, in particular, recorded mortality rates of 5% and 4.2%, respectively, before seeing a significant drop in mobility, which is a sign of a relatively late response.

When looking at the number of deaths per 100,000 people we note that Canada, Germany, Sweden, Norway, and New Zealand all had less than 0.01 deaths per 100,000 people when the significant drop in mobility happened. On the other end, we see that the UK, Italy, Spain and France had over 0.1 deaths per 100,000 at their mobility change points. The US stood at 0.02 deaths per 100,000 when it observed its change point.

Mortality rates (deaths/cases) and the deaths per 100,000 at the first change point indicate that Germany, Canada, New Zealand and Norway all acted earlier (and, as a result, saw earlier drops in mobility) than France, Spain, Italy, UK, and US.

When focusing on cases instead of deaths, we see that Canada, Norway, New Zealand, and Sweden all observed their first change point when the number of confirmed cases was relatively low. In Germany, the number of cases was relatively high and close to that of Italy, Spain, France, the UK, and the US. Despite that, the Germany was able to maintain a significantly lower number of deaths than those countries. In fact, when observing the number of cases per 100,000 at the first MCP in Germany and Norway we note that it is higher than that of the UK. These findings indicate the importance of placing more weight on the mortality rate when governments are deciding when to take action, particularly, in countries where the medical system is capable of handling a high number of cases. In other words, even if a country is experiencing a low number of cases, a high number of fatalities per 100,000 or a high mortality rate are signs that should be considered a red flag and a potential trigger to the introduction of legislative changes to limit mobility.

6.2. Severity of the lockdown

Table 1 also shows the mean level of mobility after the first and second change points (rows 13 and 14, respectively). Here we note that in Italy, Spain, and France the average level of mobility dropped to 12.2%, 10.5%, 16.1% of the original level of mobility before COVID-19. These three countries were forced to introduce a complete lockdown and severely drop mobility levels. In contrast, we see that countries like Germany, Norway, and New Zealand were able to operate at 44.5%, 40.3%, and 33.8% of their original level of mobility prior to COVID-19.

These results indicate taking early action could help nations operate at a higher level of mobility during the lockdown without sacrificing public health. This finding is supported by the fact that, despite operating at relatively high levels of mobility during the lockdown, Germany, Norway, and New Zealand had 10.2, 4.4, and 0.45 deaths per 100,000 people on the 29th of May 2020 (the last day considered in the assessment). These numbers are significantly lower than the 55.1, 42.7, 57.6, 31.23, and 56.21 deaths per 100,000 observed in Italy, France, Spain, the UK, and the US respectively. In fact, the German example, in particular, becomes slightly more impressive when considering the country’s population density of 233 people/km², which is significantly higher than the US (34.2), France (104.2), and Spain (93.09).

In Sweden, the average level of mobility after the first MCP was 61.6% of normal conditions. This finding is in line with expectation considering that Sweden chose to adopt, what is known as, the herd immunity approach where limited restrictions on the operation of businesses and public and private entities were enforced. To that end, the 38.4% drop could be attributed to the drop public awareness or the closure of borders in other countries. What is interesting in case of Sweden is that the mortality statistics on the 29th of May 2020 indicate a relatively poor performance. The number of deaths per 100,000 on that date stood at 42.1. This is close to the numbers seen in Italy, France, Spain, and the UK. These findings show that, despite seeing an early drop in mobility, the drop did not seem significant enough to help curb the impacts of the disease.

Besides helping countries sustain a slightly higher level of mobility during the lockdown, early action also seems to help countries recover to a higher level of mobility earlier than others. We see here that the average level of mobility in Germany, Norway, and New Zealand between the second MCP and the end of the analysis period ranged between 61.4 and 73.9% of normal conditions. This was not the case in Italy, France and Spain where the average level of mobility was 25.2, 49, and 21.6% of normal conditions.

7. Summary and conclusion

This paper analyses the relationships between changes in mobility data and the COVID-19 cases and fatalities across 10 different countries. A statistical change point detection algorithm was first employed to identify critical points in time where the effects of legislative changes were seen in different countries. This information was then used to understand the value of taking early action to halt the spread of COVID-19. The impacts of taking early action on the level of the lockdown required was also analysed. The results shown that from the countries considered in the assessment, Germany, Norway, New Zealand, and Canada took early action compared to other nations. This helped three of those nations (Germany, Norway, and New Zealand) operate at a higher level of mobility during the lockdown (approximately 40% of normal activity) without sacrificing public health. The results also show that a relatively slow response to the Italy, Spain, France, the UK, and the US forced those nations to operate at lower level of mobility during the lockdown (i.e. implement stricter measures) and resulted in a mortality rate per 100,000 people that was, on average, 82% higher than early responders. In Sweden, the analysis shows that a drop in mobility (despite happening relatively early) did not seem significant enough to limit the impacts of the virus. The mortality rate in the country was similar to that of countries that were slow in taking action, which demonstrates how critical it is to take early action.

In conclusion, unlike the majority of existing research where the focus has been on modeling the spread of the virus using information about cumulative cases, the findings of this paper help understand the relationship between restricting mobility and curbing the spread of the disease. The results demonstrate the existence of a potential relationship between (i) taking early action and lower mortality rates (i.e minimizing the consequences of the viral spread) (ii) taking early action and being able to maintain a higher level of mobility (i.e. imposing a less strict lockdown), and (iii) taking early action and the potential of seeing an early recovery onset. These findings are extremely valuable to nations looking to improve their response to the highly anticipated second wave of COVID-19 or any other contagious global health pandemic. The research helps governments and decision makers around the world develop an improved understanding of when to best enforce and/or lift mobility restrictions, and the severity of the mobility restrictions required to limit the spread of the disease. Such an understanding will help officials intelligently adopt restrictions that help preserve public health by reducing mobility and social interaction without significantly impacting the economy and social well-being. As more data becomes available, findings presented in this study could be used to develop intervention models that could help governments identify the optimal level of lockdown. One limitation of the study is the inability to relate changes in mobility to specific legislative change. This could be explored in future research and could help understand which legislative changes are more effective than others.

Author statement

SG participated in study conception, statistical data analysis, results interpretation, manuscript draft preparation and review of final version of the manuscript, and preparing the response to reviewers. AG participated in study conception, statistical data analysis, results interpretation, manuscript draft preparation and review of final version of the manuscript.

Financial disclosure

The authors did not receive any funding to conduct this study. Data sources have been acknowledged in the paper.