Carbo[n]helicenes Restricted to Enantiomerize: An Insight into the Design Process of Configurationally Stable Functional Chiral PAHs

Abstract

The most important stereodynamic feature of carbo[n]helicenes is the interconversion of their enantiomers. The Gibbs activation energy (ΔG ^≠(T)) of this process, which determines the rate of enantiomerization, dictates the configurational stability of [n]helicenes. High values of ΔG ^≠(T) are required for applications of functional chiral molecules incorporating [n]helicenes or helicene substructures. This minireview provides an overview of the mechanism, recent developments, and factors affecting the enantiomerization of [n]helicenes, which will accelerate the design process of configurationally stable functional chiral molecules based on helicene substructures. Additionally, this minireview addresses the misconception and irregularities in the recent literature on how the terms “racemization” and “enantiomerization” are used as well as how the activation parameters are calculated for [n]helicenes and related compounds.

Enantiomerization of [n]helicenes: This minireview provides the insights into the mechanism, recent developments, and factors affecting the enantiomerization barrier of [n]helicenes and related compounds with the aim to facilitate the design process of configurationally stable functional chiral molecules.

1. Introduction

Polycyclic aromatic hydrocarbons ^[1] (PAHs) have played a key role in the recent developments of the organic electronic devices owing to their exemplary optical, conducting, and magnetic properties. ^[2] These compounds are synthesized in an atomically precise and structurally well‐defined manner utilizing well‐established synthetic organic chemistry tools.[ ³ , ⁴ ] Owing to their structural diversity, common PAHs (Figure 1) can be categorized ^[5] in a simplified manner as acenes ^[6] (meta‐fused benzene rings in one dimension), nanographenes ^[4] (benzene rings fused in two dimensions to give large nanometer‐sized flakes or nanoribbons), and carbo[n]helicenes[ ⁷ , ⁸ ] (ortho‐fused benzene rings in three dimensions).

Figure 1.

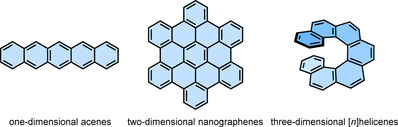
Representative structures of different classes of PAHs.

Among the various classes of PAHs, carbo[n]helicenes and related compounds are of special interest as they offer an additional element of functionality, namely, chirality, stemming from their nonplanar screw‐shaped geometry. ^[9] When compared with the linear analogs, acenes, carbo[n]helicenes exhibit distinct chemical and physical properties. ^[10] Whereas the former are excellent semiconductors and highly reactive, ^[6] the latter exhibit exceptional chiroptical properties and are very stable. Acenes with five or more meta‐fused benzene rings are reactive towards light and oxygen and therefore cannot be isolated under ambient conditions. On the other hand, carbo[n]helicene as large as [16]helicene ^[11] with sixteen ortho‐fused benzene rings was resolved into enantiomers and showed excellent chemical stability even at elevated temperatures. This difference of stabilities can be explained by the count of Clar's sextets.[ ¹² , ¹³ ] Owing to their high thermodynamic stability and chiroptical properties,[ ¹⁴ , ¹⁵ , ¹⁶ , ¹⁷ ] [n]helicenes have been applied in a variety of applications, for example, as chiral auxiliaries in asymmetric synthesis, circularly polarized light (CPL)‐responsive organic field‐effect transistors (OFETs), CPL‐emitting OLEDs, and enantioselective fluorescent sensors.[ ¹⁸ , ¹⁹ ] Moreover, the flexible and compressible structures of this class of molecules facilitate their applicability as molecular spring materials and inductors. ^[20] The latest addition to their application portfolio is their use as spin filters, a technology based on the chirality‐induced spin selectivity effect. ^[21]

Helicenes have intrigued researchers not only because of their application potential but also for their unusual physical and stereodynamic properties. One of the most important stereodynamic features of helicenes and related compounds is configurational stability, which can be quantified in terms of the Gibbs activation energy (ΔG ^≠(T)) of enantiomerization. The value of ΔG ^≠(T) determines if the compound can or cannot be resolved into enantiomers under ambient conditions and gives the first information regarding the configurational stability of the compound under study. Therefore, to access chiral functional materials based on [n]helicenes, it is necessary to design molecules with high ΔG ^≠(T). Although the chemistry and physics of carbo[n]helicenes have matured, their applications are still limited to the laboratory scale. To transform the proof‐of‐concept results into real‐world applications, there is a need for new functional chiral molecules with high charge‐carrier mobility and fluorescence quantum yield, which are stable against enantiomerization. This minireview addresses the latter issue intending to facilitate the design process of such molecules, by giving an overview of the general understanding of the mechanism and the theory behind the helicene inversion and the factors affecting configurational stability. At the beginning of the review, the physical meaning of the terms “enantiomerization” and “racemization” is briefly discussed, as there are irregularities and misconception in the recent literature on how these terms are used, and it is shown how the kinetic parameters for these processes are calculated for [n]helicenes and related compounds. In the following part, a comprehensive overview of the inversion mechanism and the factors affecting the configurational stability of carbo[n]helicenes and related compounds are described. The discussion is limited to carbo[n]helicenes—composed of only carbon atoms in the skeleton—as the hetero‐helicenes ^[22] —possessing at least one hetero‐atom—themselves are a distinct class of molecules and a general comparison cannot be made among the two types. As a large number of carbo[n]helicenes is known, here the most relevant and recent examples are chosen, especially those for which the values of ΔG ^≠(T) were calculated or experimentally determined.

2. Revisiting the Enantiomerization and Racemization Processes and their Activation Barriers

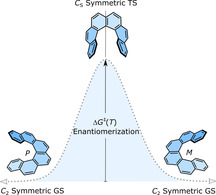
Although Hughes et al. distinguished ^[23] between racemization and enantiomerization in 1935, misconceptions still appear in the literature and often both terms are used loosely without paying attention to their physical meaning. The racemization and enantiomerization can be differentiated as the macroscopic and microscopic processes, respectively (Figure 2). In the first process at equilibrium an equal mixture of enantiomers is formed, whereas in the second process one enantiomer interconverts to another one. Reist and co‐workers described ^[24] (i) racemization as a macroscopic and statistical process, in which transformation of an enantiopure sample into a racemate occurs irreversibly, and (ii) enantiomerization as a microscopic and molecular process, in which enantiomers transform into each other reversibly. According to IUPAC, racemization is defined as “the production of a racemate from a chiral starting material, in which one enantiomer is present in excess” and enantiomerization is defined as “interconversion of enantiomers”. ^[25] Therefore, when the configurational stability of a chiral compound is quantified, it is important to know if the reported thermodynamic and kinetic parameters refer to the interconversion of two stereoisomers or the formation of a racemic mixture. As the racemization is a statistical process of irreversible transformation of the enantiopure (or enantioenriched) sample into an optically inactive racemic mixture, the rate constant for the racemization can be obtained by a variety of spectroscopic and chromatographic techniques.[ ²⁶ , ²⁷ ] While the rate constant of racemization (k _r) describes the rate of formation of a racemic mixture, the rate constant of enantiomerization (k _e) refers to the rate of interconversion of enantiomers. When one molecule transforms into the other enantiomer, the enantiomeric excess is reduced by two molecules. Hence, the rate constant of enantiomerization is half of that for racemization, k _e=1/2 k _r. On the one hand, the half‐life of racemization corresponds to the time at which the enantiopurity of a chiral compound is reduced to 50 %. On the other hand, the half‐life of enantiomerization refers to the time required for 50 % interconversion of an enantiomer, which leads to a change of enantiomeric excess from 100 % to 0 %. Considering enantiomerization as a first‐order single‐step process, the thermodynamic parameters are calculated by using the Eyring Equations 1 and 2. When k _e is measured only at one temperature, ΔG ^≠(T) is calculated by using Equation 3.

$${\displaystyle \ln (k{}_{\mathrm{e}}/T)=\ln (\kappa k{}_{\mathrm{B}}/h)+\Delta S{}^{\ne }/R-(\Delta H{}^{\ne }/R)(1/T)}$$ (1)

$${\displaystyle \Delta G{}^{\ne }\left(T\right)=\Delta H{}^{\ne }-T\Delta S{}^{\ne }}$$ (2)

$${\displaystyle \Delta G{}^{\ne }\left(T\right)=-RT\ln (k{}_{\mathrm{e}}h/\kappa k{}_{\mathrm{B}}T)}$$ (3)

Figure 2.

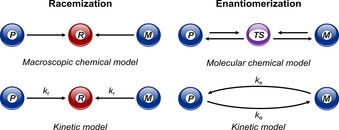
Chemical and kinetic models for the racemization and enantiomerization processes described by Reist et al. P: enantiomer with right‐handed helicity, M: enantiomer with left‐handed helicity, R: racemate, TS: transition‐state structure, k _r: rate constant for racemization, k _e: rate constant for enantiomerization.

The transmission coefficient κ=0.5 should be used in the Eyring equation because the enantiomerization process is defined as a reversible first‐order reaction and there is an equal probability of transformation of the transition state (TS) to either of the enantiomers. ^[28] There are, however, inconstancies and discrepancies in the literature whether k _r or k _e, as well as κ=1 or κ=0.5 should be used in the Eyring equation.[ ²⁶ , ²⁹ , ³⁰ ] Therefore, in the following sections, whenever the original data are available ΔG ^≠(T) was recalculated with k _e and κ=0.5 in the Eyring equation to make comparisons between the ΔG ^≠(T) values as accurate as possible. Typically for [n]helicenes, the ΔG ^≠(T) values do not change more than 1–2 kcal mol⁻¹ within the temperature range of 200 K. Therefore, ΔG ^≠(T) values reported within this temperature range can be reasonably compared and conclusions can be derived.

3. Geometrical Features of [n]Helicenes

Before investigating the mechanism of enantiomerization and the factors affecting ΔG ^≠(T), the key geometrical features ^[31] of [n]helicenes are first summarized to aid further discussion (see below). (i) All carbon atoms in the helicene skeleton are partitioned into three helices (Figure 3): inner helix comprising n+1 carbon atoms (green), middle helix with n+1 carbon atoms (red), and outer helix containing 2n carbon atoms (blue), where n is the number of fused rings. (ii) In the inner and middle helix, there are in each case only two possible positions to introduce substituents (R¹/R^1′ and R²/R^2′, respectively), whereas the outer helix can be substituted at any position. (iii) Compared with the C−C bond length in benzene (mean: 1.39 Å), the C−C bond lengths of the inner helix are larger (mean: 1.41 Å) and those of the outer helix are shorter (mean: 1.36 Å). (iv) [n]Helicenes with n=6–11 display several intriguing common geometrical features. X‐ray analysis showed that they possess nearly constant pitch (3.21±0.5 Å) for the inner helix. On the one hand, the pitch length increases from the inner to the outer helix. On the other hand, the pitches for the middle and the outer helix decreases with n (n=6–11). The helical pitch can be defined as the distance between two ends when the helix completes a 360° spiral.

Figure 3.

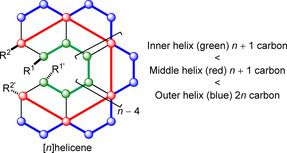
Structural and geometrical characteristic of [n]helicenes.

4. Activation Energy Barrier for the Enantiomerization of [n]Helicenes

The name “helicene” was introduced by Newman in 1955 to describe a benzo analog of phenanthrene with ortho‐fused rings forming an ultimately cylindrical helical structure. Phenanthrene (three ortho‐fused rings), although not helical, is formally the first member of the [n]helicene family, although according to IUPAC only structures with n>4 are helicenes. ^[32] Although unsubstituted phenanthrene with C _2v symmetry deviates only slightly from planarity (torsion angle 1.9°), 4,5‐disubstituted phenanthrene is nonplanar (torsion angle 31.5°) and chiral—it could be resolved into enantiomers. ^[33] The unsubstituted [4]helicene has not been resolved into enantiomers owing to its poor configurational stability at room temperature. ^[34] [n]Helicenes (n≥6) are configurationally stable at room temperature and ΔG ^≠(T) increases with the increasing number of ortho‐fused rings. [5]Helicene is the borderline case, which displays partial configurational stability. It can be resolved into enantiomers, but an enantioenriched sample racemizes within a couple of days at room temperature. In 1956, Lednicer et al. achieved the optical resolution of [6]helicene by fractional crystallization with optically active (−)‐2‐(2,4,5,7‐tetranitro‐9‐fluorenylideneaminooxy)‐propionic acid ((−)‐TAPA). ^[35] This was the first time that the partial thermal racemization of [6]helicene was observed during the melting point determination. Several years later in 1970, Stegemeyer et al. obtained ^[36] enantioenriched [5]helicene by using the same method and firstly determined the racemization rate constants, following the change in circular dichroism signal in isooctane solution, at different temperatures between 304 and 320 K. The estimated value of ΔG ^≠(298)=24.1 kcal mol⁻¹ indicates the half‐life of racemization (t _1/2) to be 29 h in solution at 298 K. Two years later, Martin et al. reported the thermal racemization of [6]‐, [7]‐, [8]‐, and [9]helicene dissolved in naphthalene (6 % w/w) when heated above their melting points.[ ³⁰ , ³⁷ ] The racemization rate constants were estimated by observing the change in optical rotation with time at different temperatures. The ΔG ^≠(298) values are plotted against n for [n]helicenes (n=4–9) in Figure 4. From the plot, it is apparent that the ΔG ^≠(T) increases exponentially with an increasing n with an upper limit of 43.1 kcal mol⁻¹ at 298 K for [9]helicene. Although for [n]helicenes (n=4–7) the ΔG ^≠(T) values increase sharply, a plateau is observed for n=7–9 (Table 1). The enantiomerization barrier for [n]helicenes (n≥10) has not yet been determined experimentally, but the theoretical calculations predict a sharp increase. ^[38]

Figure 4.

Exponential increase of ΔG ^≠(298) values for [n]helicenes (n=4–9). ΔG ^≠ for [4]helicene is a calculated value ^[38] using DFT.

Table 1.

Activation parameters for enantiomerization of [n]helicenes (n=4–9).

[n]Helicene	ΔH ≠ [kcal mol−1]	ΔS ≠ [cal K−1 mol−1]	ΔG ≠ [kcal mol−1] at 298 K[a,b]	t 1/2 [min] at 298 K
4	–	–	(4.0)	–
5	22.9	−4.1	24.1 (24.4)	1.74×103[c]
6	33.8	−5.3	35.4 (36.9)	3.40×1011[d]
7	40.4	−2.8	41.2 (42.0)	6.10×1015[e]
8	40.9	−3.4	41.9 (42.7)	1.99×1016[e]
9	41.6	−5.0	43.1 (44.2)	1.51×1017[e]

[a] ΔG ^≠ in parenthesis are calculated values using DFT, see ref. [38]. [b] All the experimental activation parameters are calculated by re‐plotting (ln(k _e/T) against 1/T) using the equation ln(k _e/T)=ln(κk _B/h)+ΔS ^≠/R−(ΔH ^≠/R)(1/T) with κ=0.5, see ref. [39]. [c] See ref. [36]. [d] See ref. [30]. [e] See ref. [37].

5. Mechanistic Insights into the Enantiomerization Process of [n]Helicenes

The first mechanistic insight into the interconversion of enantiomers also comes from Stegemeyer et al. They proposed a closed intermediate 1 involved in the enantiomerization process of [5]helicene (Scheme 1). ^[36] The proposed hypothesis was supported by the fact that [5]helicene undergoes thermal as well as photochemical cyclodehydrogenation in the presence of oxidant to yield 1,12‐benzoperylene. During this process, the involvement of the valance tautomerism between [5]helicene and the intermediate 1 was assumed. Moreover, it was suggested that because this intermediate is chiral, the enantiomerization occurs during the change of the conformation of the hydrogen atoms at the two stereogenic centers (compounds 1 and 2). This proposed mechanism sounds reasonable, given the limited knowledge of this class of compounds and spectroscopic techniques available when the mechanism was proposed. This mechanism, however, has several shortcomings: (i) it does not explain the enantiomerization process of lower or higher helicenes; (ii) the “closed” intermediate has never been isolated and the spectroscopic detection ^[40] was only possible by photoexcitation at 4.2 K, indicating the equilibrium is largely shifted towards helicene in the absence of an oxidant. Therefore, the enantiomerization mechanism involving cyclic intermediates is not generally considered.

Scheme 1.

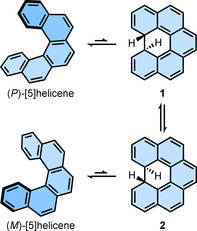
Mechanism of enantiomerization of [5]helicene proposed by Stegemeyer et al.

Later, Martin et al. hypothesized three possible pathways ^[37] for the interconversion of enantiomers of helicenes: (i) bond‐breaking, (ii) intramolecular double Diels–Alder reaction, and (iii) conformational pathway.

(i) The bond‐breaking at the inner helix would lead to reactive diradical species. Hence, a mechanism involving bond‐breaking was eliminated considering the obtained experimental kinetics data and clean transformation of enantiomers into each other without forming any side products.

(ii) The second hypothesis, involving intramolecular double Diels–Alder reaction, was experimentally verified. For example, the double Diels–Alder reaction of (M)‐1,2,3,4‐d₄‐[6]helicene after equilibration should give a 1:1 mixture of the starting material and (P)‐1,2,13,14‐d₄‐[6]helicene (Scheme 2). However, when (M)‐1,2,3,4‐d₄‐[6]helicene in naphthalene (10 % w/w) was heated under reduced pressure at 286 °C for 70 min, the NMR spectrum of the crude mixture was identical to that of the initial material. This experiment proved that during the thermal racemization of [6]helicene the Diels–Alder intermediates are not involved. A similar experiment was also performed by using 6‐methyl[7]helicene. Among the [n]helicene family, [7]helicene is the first homolog that makes a complete helical turn. Hypothetically, the double Diels–Alder reaction would, therefore, occur between rings 1 and 6, as the reaction between two terminal rings is very unlikely, which would lead to a highly strained intermediate. Such double Diels–Alder reaction would relocate the methyl substituent possibly in the positions 3, 4, 5, 13, 14, 15, or 16, yielding at least seven different products. To verify this hypothesis, a solution of 6‐methyl[7]helicene was heated at 305 °C for 1 h. The NMR spectrum of the isolated product was same as that of the initial material, indicating no shift of the methyl group. This experiment again ruled out the formation of the Diels–Alder intermediate during the enantiomerization process of 6‐methyl[7]helicene. Therefore, it was concluded that the thermal racemization of [6]‐ and [7]helicene does not follow the reaction path involving intramolecular double Diels–Alder reaction. Considering the similarities between the kinetic data for [6]‐, [7]‐, [8]‐, and [9]helicenes, Martin et al. extrapolated the aforementioned conclusion to [8]‐ and [9]helicene.

Scheme 2.

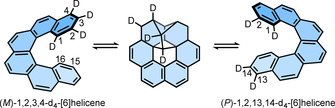
Proposed reversible double Diels–Alder reaction of (M)‐1,2,3,4‐d₄‐[6]helicene.

(iii) The last hypothesis suggested by Martin et al. was the interconversion of enantiomers via the conformational pathway. It was the most reasonable possibility and they emphasized that the hydrocarbons are much more flexible than generally believed. It is very impressive that the proposed involvement of an achiral conformation in the transition state (TS; Figure 5) by Martin et al. was later well corroborated by several theoretical calculations. The involvement of the conformational pathway also justifies the low energy barrier for smaller helicenes as the steric demand increases with the added number of benzene rings. In recent years, there have been great theoretical developments ^[38] in explaining and supporting the conformational pathway for the enantiomerization process of [n]helicenes.

Figure 5.

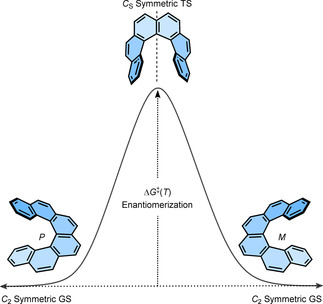
Conformational pathway for the interconversion of enantiomers of [n]helicenes. TS of [n]helicenes, n=3–4 and n≥5 are C _2v and C_S symmetric, respectively.

The ground state (GS) of [n]helicenes (n≥4) and 4,5‐disubstituted phenanthrene is C ₂ symmetric. Earlier theoretical studies by Lindner using the self‐consistent field method suggested the TS of [5]helicene adopts a planar C _2v symmetrical structure and that of [6]‐ and [7]helicene is nonplanar achiral C_S symmetric. ^[41] A few years later, Grimme et al. and Janke et al. reproduced the computed energy barrier for [n]helicenes (n=4–9) very close to the experimental trend with a plateau for n=7–9. ^[34] The calculated TS were planar C _2v symmetric for [4]helicene and achiral nonplanar C_S symmetric for [n]helicenes (n≥5). Additionally, Janke et al. found local minima close to the TS of [9]helicene indicating the possibility of a multistep enantiomerization process. The increasing barrier of enantiomerization with n was attributed to the steric interaction between two terminal rings in the TS structure. These steric interactions are largely dominated by close H⋅⋅⋅H contacts for smaller helicenes (n=3–6) and π⋅⋅⋅π interactions in larger helicenes (n=7–9). The observed plateau for n=7–9 is because the added aromatic rings in these molecules do not increase the steric effects in the C_S symmetric TS (Figure 6). Recently, Merino et al. revisited the enantiomerization mechanism ^[38] of [n]helicenes and discovered that, although enantiomerization of n=4–7 follows a single‐step mechanism, that of n≥8 is a multistep process involving 2n−14 intermediates. Moreover, they calculated that the initial plateau observed for [n]helicenes (n=7–9) was overcome by ΔG ^≠(T) of [10]helicene, which then increases linearly until another two new plateaus around 65 kcal mol⁻¹ for n=12–14 and around 71 kcal mol⁻¹ for n=18–24 are reached. These interesting theoretical findings further support Martin's argument about the flexibility of helicenes.

Figure 6.

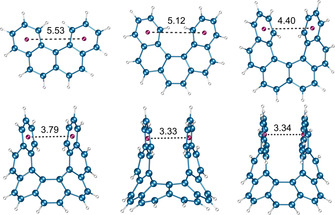
Distance (in Å) between centroids of the terminal rings of [n]helicenes (n=4–9) in TS. The optimized geometries are obtained from ref. [38].

It can be concluded that [n]helicenes follow the conformational pathway for the interconversion of enantiomers and ΔG ^≠(T) for this process increases with each additional ortho‐fused ring. However, it has been observed that there are several other factors that severely affect the enantiomerization barrier and hence the configurational resilience of [n]helicenes. In the following sections, the key factors affecting the configurational stability of [n]helicenes and related compounds are discussed: (1) substituents at the inner helix, (2) substituents at the middle and outer helix, (3) ring defects, and (4) radius of the helix.

6. Factors Affecting the Enantiomerization Barrier of [n]Helicenes

6.1. Substituents at the inner helix

Considering the conformational pathway of the enantiomerization process, the substituents at the inner helix are expected to have a large influence on the energy barrier owing to the additional steric hindrance in the TS. The effect of the substituent on the enantiomerization barrier was studied as early as in 1963 by Newman et al. ^[42] They synthesized 1‐fluoro‐12‐methyl[4]helicene and partly resolved it into enantiomers by co‐crystallization with (−)‐TAPA. The enantioenriched sample was subjected to kinetic studies and ΔG ^≠(T) was estimated to be 30.7 kcal mol⁻¹. From this first study of the substituent effect on the enantiomerization barrier of helicenes, it is apparent that the configurational stability can be dramatically enhanced by introducing substituents at the inner helix. Even the mono‐substituted [4]helicenes could be isolated as enantiomers, although the configurational stability strongly depends on the bulkiness of the substituents (Table 2). Newman et al. also proposed that introduction of substituents at positions 4 and 5 of phenanthrene would lead to distortion of the aromatic plane as a consequence of steric hindrance between methyl groups, which was later confirmed experimentally as well as theoretically.[ ³³ , ⁴³ , ⁴⁴ ] A methyl and a tert‐butyl group at the inner helix of phenanthrene increases ΔG ^≠(T)=26.6 kcal mol⁻¹, even higher than that of naked [5]helicene. ^[44]

Table 2.

Gibbs activation energy for enantiomerization of [n]helicenes (n=3–6) substituted at the inner helix.

[n]Helicene	R1 (A values)	R1′ (A values)	ΔG ≠ [kcal mol−1] at (T [K])
3	OCH2Ph	Br (0.38)	11.3 (224)[a,b]
3	OCH2Ph	tBu (>4)	19.3 (376)[a,b]
3	Me (1.7)	tBu (>4)	26.6 (353)[a,b]
3	CH2OAc	CH2OAc	18.1(298)[a,c]
3	Me (1.7)	Me (1.7)	16.1(298)[a,c]
4	OCH2Ph	H (0)	14.4 (259)[a,b]
4	Me (1.7)	H (0)	21.2 (298)[d]
4	tBu (>4)	H (0)	28.2 (353)[a,b]
4	Me (1.7)	F (0.15)	30.7 (298)[e,f]
4	Me (1.7)	Me (0.15)	41.4 (298)[d]
5	OMe (0.60)	H (0)	32.3 (423)[e,g]
5	Me (1.7)	H (0)	39.1 (473)[e,g]
5	F (0.15)	F (0.15)	36.8 (466)[e,h]
5	OMe (0.60)	OMe (0.60)	41.0 (483)[e,h]
5	Me (1.7)	Me (1.7)	44.2 (503)[e,h]
6	Me (1.7)	H (0)	41.4 (298)[e,i]
6	Me (1.7)	Me (1.7)	43.8 (543)[e,i]

[a] Originally reported values, the recalculation was not possible because values for the rate constant were not available. [b] See ref. [44]. [c] See ref. [33]. [d] DFT‐calculated values, see ref. [45]. [e] Gibbs activation energy (re)calculated by using the equation ΔG ^≠(T)=−RT ln(k _e h/κk _B T) with κ=0.5. [f] See ref. [42]. [g] See ref. [46]. [h] See ref. [39]. [i] See ref. [47].

Inspired by the potential applications of [5]helicenes and related compounds as functional materials, Juríček et al. and Usui et al. recently investigated the substituent effect[ ³⁹ , ⁴⁶ ] on [5]helicene to see if a general relationship can be established between the “bulkiness” of the substituent (quantified as the A values) and ΔG ^≠(T). The mono‐ and disubstituted [5]helicenes show a similar tendency towards enantiomerization as the substituted [3]‐ and [4]helicenes, however, a more systematic trend could be established in this case. The steric bulk of mono‐ and disubstituted helicenes was quantified in terms of the distance between the carbon atoms at positions 1 and 14, as well as the torsional twist in the inner helix of [5]helicene. As shown in Figure 7 a and b, ΔG ^≠(T) values were plotted against the torsional twist and the distance between C1 and C14. These plots showed an exponential trend with an upper limit of ΔG ^≠(T)=44.2 kcal mol⁻¹ reached by dimethyl[5]helicene, which is close to that of [9]helicene. Additionally, mono‐ and dimethyl[n]helicenes (n=3–6) also displayed an exponential increase of ΔG ^≠(T) values against n (Figure 7 c). It is important to note that the shorter [n]helicenes (n=3–5), in which steric effects are dominated by H⋅⋅⋅H interactions in the inner helix, showed a much larger improvement in ΔG ^≠(T) values compared with [6]helicene. ^[47] This can be rationalized from the TS structures: the distance between two protons (which are replaced by substituents) in the inner helix of [n]helicenes (n=3–5) increases with n. Therefore, the TS is relatively more destabilized by the substituents on the shorter [n]helicenes (n=3–5). Dimethyl[6]helicene does not overtake the upper limit of ΔG ^≠(T) values reached by dimethyl[5]helicene and monomethyl[6]helicene. It can be generalized that the introduction of substituents at the inner helix is a more efficient way to increase configurational stability than the extension of the helical core at least up to [6]helicene.

Figure 7.

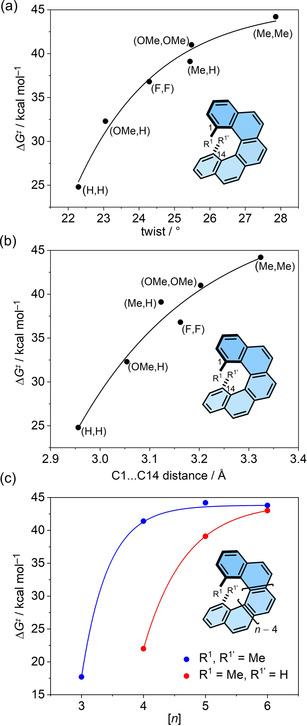
Plot of ΔG ^≠(T) values against (a) torsional twist and (b) distance between C1 and C14 of substituted [5]helicene. (c) Plot of ΔG ^≠(T) values against [n] for mono‐ (red) and di‐ (blue) methyl‐substituted helicenes.

6.2. Substituents at the middle and outer helix

Substituents at the outer helix generally show no effect on the enantiomerization barrier. This is clear from the conformational pathway, which involves only inner and middle helixes in the TS. However, the substituents R² and R^2′ at the middle helix often offer additional configurational stability by a buttressing effect, ^[48] especially for helicenes with C _2v planar TS. Laarhoven et al. studied the influence of methyl substituents at different positions of [6]helicene. ^[47] As discussed in the above section, substituents at positions C1 and C16 (inner helix) of [6]helicene largely increase the ΔG ^≠(T), however, substituents at the outer helix—positions C3, C4, C13, and C14—which do not alter the conformation have no effect on ΔG ^≠(T). Interestingly, the methyl substituents at the middle helix at positions C2 and C15 considerably increase ΔG ^≠(T) (Table 3). This influence of the methyl substituent at positions C2 and C15 can be attributed to (i) the steric effect on the helical conformation and (ii) the buttressing effect on protons at C1 and C16. The entropic effects of substituents cannot be thoroughly discussed as the experimental ΔS ^≠ values are not reported for many of the substituted helicenes and semiempirical calculations did not provide any conclusive answer. Nonetheless, for a couple of examples of methyl‐substituted [6]helicene, a larger value of ΔS ^≠ for the enantiomerization process was observed compared with unsubstituted [6]helicene.

Table 3.

Activation parameters for enantiomerization of [n]helicenes (n=3 and 6) substituted at the inner, middle, and outer helix.

	Position of methyl group(s)	ΔH ≠ [kcal mol−1]	ΔS ≠ [cal K−1 mol−1]	ΔG ≠ [kcal mol−1] at (T [K])
	1	38.5	−9.8	43.0 (542)[a]
	1,14	–	–	43.1 (543)[a]
	1,16	–	–	43.8 (543)[a]
	1,3,14,16	37.7	−12.9	43.8 (543)[a]
	2,15	–	–	40.6 (513)[a]
	4,13	–	–	36.3 (469)[a]
	4,5	13.9	−7.9	16.1 (298)[b]
	3,4,5,6	21.9	−3.9	23.1 (298)[b]

[a] Gibbs activation energy recalculated by using the equation ΔG ^≠(T)=−RT ln(k _e h/κk _B T) with κ=0.5, see ref. [47]. [b] Originally reported values, the recalculation was not possible because values of the rate constant were not available, see ref. [33].

Armstrong et al. investigated the configurational stability of phenanthrene derivatives substituted with methyl groups at the inner, middle, and outer helix. ^[33] In the previous section, we have seen that the introduction of methyl groups at the C4 and C5 positions of phenanthrene leads to the distortion of the planar aromatic system and provides a racemization barrier high enough to resolve enantiomers. When two additional methyl groups are introduced at the C3 and C6 positions at the middle helix of phenanthrene, the buttressing effect of additional methyl groups in 3,4,5,6‐tetramethylphenanthrene can be seen in its GS and TS structures when compared with 4,5‐dimethylphenanthrene (Figure 8). In the C ₂ symmetric GS structure, the torsion angle of the inner helix increased from 31.5° to 33.0°, whereas the C _2v symmetric planar TS exhibits a shorter distance between methyl groups at C4 and C5. Kinetics studies showed that the ΔG ^≠(T) value for 3,4,5,6‐tetramethylphenanthrene was increased to 23.1 kcal mol⁻¹. From the activation parameters, the buttressing effect was estimated to be 7.0 kcal mol⁻¹ (the difference between the ΔG ^≠(T) values for di‐ and tetramethylphenanthrene, Table 3). The installation of methyl groups or other substituents at the outer helix of phenanthrene did not affect the enantiomerization barrier.

Figure 8.

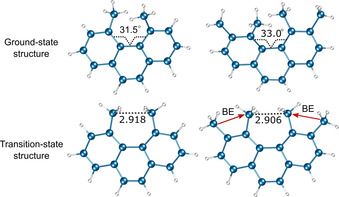
GS and TS structures of 4,5,‐dimethylphenanthrene and 3,4,5,6‐tetramethylphenanthrene. Buttressing effect (BE) of methyl substituents at the middle helix of 3,4,5,6‐tetramethylphenanthrene.

6.3. Ring defects

Helicene‐type compounds with five‐ or seven‐membered rings are of special interest for their improved photophysical and chiroptical properties. These compounds exhibit much higher fluorescence quantum yields compared with typical [n]helicenes. ^[49] Moreover, the introduction of five‐ and seven‐membered rings allow the study of the chiroptical properties of these compounds in oxidized and reduced forms. The benzo‐fused helicenes display enantiomerization barriers comparable to naked helicenes, ^[50] hence, ΔG ^≠(T) of naked [5]‐ and [7]helicenes can be compared with that of compound 5 and 6. The replacement of the middle six‐membered ring by a five‐membered ring in [5]‐ and [7]helicenes not only breaks the aromatic conjugation but also significantly decreases the enantiomerization barrier (Figure 9).[ ⁴⁹ , ⁵¹ ] The X‐ray structure analysis of compound 5 revealed that although the torsion angle (16.2°) of the inner helix is much smaller than that of [5]helicene, the distance (3.018 Å) between two terminal carbon atoms of the inner helix is slightly increased. This means that there is less steric hindrance between the protons of the terminal carbon atoms of the inner helix, which leads to a decrease in energy of the anticipated C_S‐symmetric TS and hence a decrease in ΔG ^≠(T) values. The length of the alkyl chains attached to the five‐membered ring (R=methyl to hexyl) does not affect the configurational stability of the parent compound. The configurational stability of 1,14‐dimethyl[5]helicene can be compared with that of compound 7, in which two terminal rings on both ends of helicene are replaced by seven‐ and five‐membered rings. ^[52] Compound 7 showed a decrease in configurational stability by 10 kcal mol⁻¹. Also in this molecule, although the torsion angle (22.4°) of the inner helix is much smaller, the distance (3.706 Å) between the two terminal carbon atoms of the inner helix considerably increased compared with that of 1,14‐dimethyl[5]helicene. Therefore, the earlier argument—the higher stability of the TS is responsible for the decreased ΔG ^≠(T)—can also be applied here.

Figure 9.

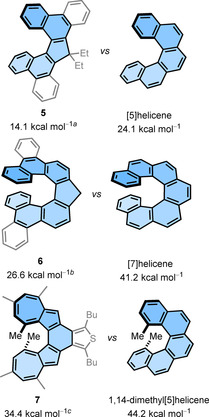
Comparison of the ΔG ^≠(T) values of [n]helicene analogs possessing five‐ or seven‐membered ring(s) with parent [n]helicenes. [a] Originally reported value from VT‐NMR experiments, see ref. [49]. [b] Recalculated by using equation ΔG ^≠(T)=−RT ln(k _e h/κk _B T) with κ=0.5, see ref. [51]. [c] DFT‐calculated value, see ref. [52].

6.4. The diameter of the helix

[n]Helicenes composed of ortho‐fused benzene rings possess a constant diameter of the inner and the outer helix unless the ortho‐ and meta‐fused ring systems are combined or alternate six‐membered rings are replaced by four‐, five‐, or seven‐membered rings. The [n]heliphenes[ ⁵³ , ⁵⁴ ] (or [n]phenylenes) are composed of alternating n benzene units fused to n−1 cyclobutadiene rings in an angular manner, forming a helical structure similar to [n]helicenes. The apparent difference among [n]helicenes and [n]heliphenes is the diameter of the helix. In the latter class of compounds, the diameter of the helix increased significantly owing to the added cyclobutadiene ring between the ortho‐fused benzene rings. Both classes of the molecules complete their first helical turn with seven benzene rings, therefore, it should be fair to compare the configurational stability of [7]helicene and [7]heliphene. The methoxymethyl‐substituted [7]heliphene showed decoalescence of methylene protons in the ¹H NMR spectrum at 246 K corresponding to ΔG ^≠(T)=12.6 kcal mol⁻¹. The extremely low value of the ΔG ^≠(T) for [7]heliphene compared with [7]helicene was attributed to: (i) the flexible molecular skeleton and (ii) the distorted bond length patterns in heliphenes. Inspired by the much higher configurational stability of methyl‐substituted [n]helicenes, Vollhardt et al. synthesized several [7]heliphene derivatives with methyl groups at the terminal rings and a methoxymethyl group at the outer helix. ^[54] Surprisingly, NMR spectroscopy of these compounds showed no apparent changes in methylene protons at temperatures as low as 203 K, indicating an even lower barrier of enantiomerization. It was rationalized that the repulsion between the methyl groups raises the energy of the GS structure more than that of the TS along the path of enantiomerization because of the larger radius of the helix. Later, the higher homologs of [n]heliphene (n=8 and 9) were synthesized, expecting that the configurational stability might be improved, however, again the obtained results were contrary. ^[53] The methoxymethyl‐substituted [8]heliphene showed decoalescence of the methylene protons in the ¹H NMR spectrum upon cooling to 268.5 K. The estimated ΔG ^≠(T)=13.4 kcal mol⁻¹ is 0.8 kcal mol⁻¹ higher than that of [7]heliphene. Interestingly, [9]heliphene did not show any change in the shape of the methylene singlet when cooled to 228 K, indicating the enantiomerization barrier was lower than 12 kcal mol⁻¹. The observed dynamic behavior of ΔG ^≠(T) for [n]heliphenes was attributed to the steric activation of helical GS towards the unwinding helix and the lower energy of TS.

Recently, Matsuda et al. and Tilley et al. reported[ ⁵⁵ , ⁵⁶ ] helical analogs of kekulene, namely, π‐expanded helicene‐like compounds composed of ortho‐ and meta‐fused benzene rings (Figure 10, compounds 8 and 9). The apparent feature of expanded helicenes 8 and 9 is the helix diameter. Although both compounds possess the same number of benzene rings, the diameter of the helix depends on the order and the number of ortho‐ and meta‐fused rings. Matsuda et al. calculated (DFT) the ΔG ^≠(T) of 13.0 kcal mol⁻¹ for 8, which is even smaller than that of [7]heliphene (calculated value 17.7 kcal mol⁻¹). Tilley et al. determined the experimental value of ΔG ^≠(T)=10.7 kcal mol⁻¹ for 9, which possesses the largest helix diameter. The very low barrier of helix inversion in the π‐expanded helicenes in comparison with [n]helicenes was attributed to the fact that the distortion required for the conformational change of these compounds is spread over a larger number of bonds and angles. To date, it remains a challenge to synthesize helicene‐type compounds with a large radius, which have an enantiomerization barrier high enough to be resolved into enantiomers.

Figure 10.

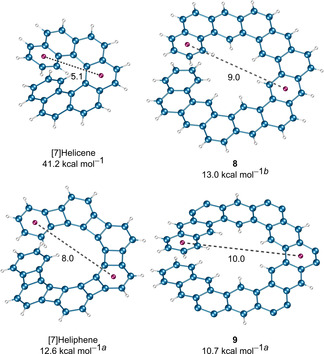
Helical compounds with different diameters (in Å) of the helix and their ΔG ^≠(T) values. The substituents on the outer helix of compound 9 are removed for clarity. [a] Originally reported value from VT‐NMR experiments, see ref. [53] and ref. [55]. [b] DFT‐calculated value, see ref. [56].

7. Summary and Outlook

Employing the insights obtained from the discussion of mechanism and the factors affecting ΔG ^≠(T) of enantiomerization of [n]helicenes, the following conclusions could be derived:

(1) [n]Helicenes pursue the conformational pathway for the interconversion of enantiomers. The enantiomerization of n=3–7 follows a single‐step mechanism, whereas that of n≥8 is a multistep process involving 2n−14 intermediates.

(2) ΔG ^≠(T) of enantiomerization of [n]helicenes increases with the added number of ortho‐fused rings, however, installation of the substituents at the inner helix is the most efficient way to improve the configurational stability of smaller helicenes (n=3–6).

(3) Although the substituents at the outer helix do not affect ΔG ^≠(T), the buttressing effect of substituents at the middle helix considerably increases ΔG ^≠(T).

(4) The replacement of one or more six‐membered ring(s) with four‐, five‐, or seven‐membered ring(s) in the helical skeleton significantly decreases the configurational stability.

(5) Helicene‐type compounds with a larger radius suffer from very low configurational stability and it remains a synthetic challenge to obtain such compounds configurationally stable enough to be resolved into enantiomers.

Often promising functional chiral molecules are synthesized, however, they cannot be resolved into enantiomers because of low configurational stability, which inhibits further investigation of their properties related to the chiral structure. I hope that this minireview will serve as a guidebook for designing configurationally robust functional chiral molecules based on helicene substructures. ^[57] Moreover, it will bring consensus among the community for the appropriate use of the terms “enantiomerization” and “racemization” as well as highlighting the fact that there are significant irregularities, even in the recent literature, for the calculation of ΔG ^≠(T) of [n]helicenes.

Conflict of interest

The authors declare no conflict of interest.

Biographical Information

Prince Ravat obtained his PhD in 2014 from the Max Planck Institute for Polymer Research, Mainz, Germany, followed by a postdoctoral stay at the University of Basel, Switzerland. Thereafter, he moved to the University of Tokyo, Japan, to work as a JSPS postdoctoral fellow. In 2018, he started his independent research group at the University of Würzburg within the “Excellent Ideas” program. His current research focuses on molecular engineering of functional chiral molecules for applications in organic electronics.

P. Ravat, Chem. Eur. J. 2021, 27, 3957.