Repeatability of IVIM biomarkers from diffusion‐weighted MRI in head and neck: Bayesian probability versus neural network

Thomas Koopman; Roland Martens; Oliver J Gurney‐Champion; Maqsood Yaqub; Cristina Lavini; Pim de Graaf; Jonas Castelijns; Ronald Boellaard; J Tim Marcus

doi:10.1002/mrm.28671

. 2021 Jan 26;85(6):3394–3402. doi: 10.1002/mrm.28671

Repeatability of IVIM biomarkers from diffusion‐weighted MRI in head and neck: Bayesian probability versus neural network

Thomas Koopman ^1,^✉, Roland Martens ¹, Oliver J Gurney‐Champion ², Maqsood Yaqub ¹, Cristina Lavini ², Pim de Graaf ¹, Jonas Castelijns ^1,³, Ronald Boellaard ^1,⁴, J Tim Marcus ¹

PMCID: PMC7986193 PMID: 33501657

Abstract

Purpose

The intravoxel incoherent motion (IVIM) model for DWI might provide useful biomarkers for disease management in head and neck cancer. This study compared the repeatability of three IVIM fitting methods to the conventional nonlinear least‐squares regression: Bayesian probability estimation, a recently introduced neural network approach, IVIM‐NET, and a version of the neural network modified to increase consistency, IVIM‐NET_mod.

Methods

Ten healthy volunteers underwent two imaging sessions of the neck, two weeks apart, with two DWI acquisitions per session. Model parameters (ADC, diffusion coefficient $D_{t}$ , perfusion fraction $f_{p}$ , and pseudo‐diffusion coefficient $D_{p}$ ) from each fit method were determined in the tonsils and in the pterygoid muscles. Within‐subject coefficients of variation (wCV) were calculated to assess repeatability. Training of the neural network was repeated 100 times with random initialization to investigate consistency, quantified by the coefficient of variance.

Results

The Bayesian and neural network approaches outperformed nonlinear regression in terms of wCV. Intersession wCV of $D_{t}$ in the tonsils was 23.4% for nonlinear regression, 9.7% for Bayesian estimation, 9.4% for IVIM‐NET, and 11.2% for IVIM‐NET_mod. However, results from repeated training of the neural network on the same data set showed differences in parameter estimates: The coefficient of variances over the 100 repetitions for IVIM‐NET were 15% for both $D_{t}$ and $f_{p}$ , and 94% for $D_{p}$ ; for IVIM‐NET_mod, these values improved to 5%, 9%, and 62%, respectively.

Conclusion

Repeatabilities from the Bayesian and neural network approaches are superior to that of nonlinear regression for estimating IVIM parameters in the head and neck.

Keywords: diffusion magnetic resonance imaging, head and neck neoplasms, repeatability

1. INTRODUCTION

Magnetic resonance DWI is used for diagnostic and prognostic purposes in head and neck cancer. ¹ , ² , ³ , ⁴ In DWI, signal decreases with diffusion weighting as result of Brownian motion of water molecules and other intravoxel incoherent motions (IVIMs) (ie, “microscopic translational motions that occur in each image voxel”). ⁵ , ⁶ By fitting the DWI signal from different diffusion weightings to an exponential model, its parameters can be estimated. A mono‐exponential can be used to estimate the ADC. A bi‐exponential model (the IVIM model ⁶ ) can be used to additionally model pseudo‐diffusion component ( $D_{p}$ ) and perfusion fraction ( $f_{p}$ )—both related to the microcirculation of blood—resulting in the corrected or “true” diffusion coefficient ( $D_{t}$ ). Because the restriction of diffusion is related to the microstructure of tissue (eg, cellular density), this can characterize tumors and provide early information on changes due to (or despite) treatment occurring before detectable tumor growth or shrinkage. ⁷

The IVIM model is appealing, as it allows the assessment of the additional biomarkers $D_{p}$ and $f_{p}$ . However, IVIM parameter estimation tends to be very sensitive to noise. As a result, parametric maps are often noisy and show poor repeatability. ⁸ Poor repeatability limits the use of IVIM in practice, because precision is required for patient‐specific clinical use of IVIM.

Recently, novel fitting methods with a Bayesian probability approach ⁹ , ¹⁰ , ¹¹ and a neural network ¹² have shown promising results in terms of reduced noise in the parameter maps based on simulations, and they reduced interobserver variability in vivo. If these techniques also help improve test–retest repeatability in vivo, they could help introduce IVIM into clinical workflows.

Therefore, in this study we investigate these new methods in terms of test–retest repeatability. We compare the intrasession and intersession repeatability of the least‐squares fitting method, the Bayesian inference fitting method, and two neural network–based fitting methods for in vivo IVIM data in the head and neck region in healthy volunteers. We hypothesize that the new Bayesian and neural network approaches will outperform the conventional least‐squares fitting approach.

2. METHODS

This study was approved by the local medical ethics committee, and written informed consent was obtained from all subjects. Ten healthy volunteers were included: 7 males, 3 females, mean age 33 years (range 22‐50 years). Each volunteer underwent two MRI sessions (at least 2 weeks apart) with two examinations per session. The subject was taken out of the MR scanner between examinations. Sequences were acquired on a 3T Ingenuity TF PET/MR scanner (Philips Healthcare, Best, the Netherlands) equipped with a 16‐channel neurovascular coil. Each examination consisted of an axial stack of 29 T₁‐weighted turbo spin‐echo images followed by a stack of DWI acquisitions in the same 29 imaging planes, covering the neck from the larynx until the base of the skull. Diffusion‐weighted imaging was acquired with a single‐shot spin‐echo EPI sequence with 12 b‐values (0, 2, 5, 25, 50, 75, 100, 150, 300, 500, 700, and 1000 s/mm²). Only the DWI images with b = 1000 s/mm² were averaged over two acquisitions. Diffusion weighting was performed in three orthogonal directions with bipolar gradients, TE = 57 ms, TR = 3242 ms, gradient time interval = 28 ms, and gradient duration = 18 ms. Further scan parameters were as follows: acquired matrix size = 128 × 111 × 29, acquired voxel size = 1.88 × 1.95 × 4 mm³, reconstructed voxel size = 1 × 1 × 4 mm³, and short TI inversion recovery used for fat suppression with a 230‐ms TI. The DWI scan duration was 6 minutes. Motion correction of the DWI images was applied by image registration, as provided by the scanner software.

The DWI data were processed voxelwise to generate parametric maps of the ADC and IVIM parameters. Parameter estimates were extracted for two tissues: tonsil and medial pterygoid muscle. Volumes of interest (VOIs) were defined on the images without diffusion weighting ( $b = 0$ s/mm²) while using the T₁‐weighted image for anatomical reference. The T₁ images were not co‐registered to the diffusion‐weighted images. Delineation was performed using in‐house‐developed software by a single observer in one session. Spherical VOIs of 5‐mm radius were placed in each tonsil, and spherical VOIs of 6‐mm radius were placed in the medial pterygoid muscle on each side. These VOIs were small enough to always fit inside the tissues of interest. The VOIs were projected onto the parametric maps, all voxels with (partial) overlap were extracted, and the median values of the parameters were then calculated.

The signal at $b = 0$ s/mm² was excluded (except for calculating fit boundary of $S_{0}$ [see subsequently] and for normalization purposes in the neural network) for the parameter estimations described subsequently, reducing the number of b‐values to 11. The reason for this is to reduce attenuation effects of macroscopic flow at small b‐values. ¹³ , ¹⁴ This additional accelerated decay between $b = 0$ s/mm² and the first nonzero b‐value is not accounted for in the conventional IVIM and ADC models. ¹⁵ , ¹⁶

The mono‐exponential model used to estimate the ADC is given by

S (b) = S_{0} \cdot e^{‐ b \cdot A D C},

(1)

where $S_{0}$ is the signal intensity without diffusion weighting ( $b = 0$ s/mm²), and $ADC$ and $S_{0}$ are estimated by performing a linear least‐squares fit on the log‐transformed data, as implemented by the scanner manufacturer.

The IVIM model extends the ADC model with a second exponential. The bi‐exponential equation of the model is given by

S (b) = S_{0} (f_{p} e^{‐ b D_{p}} + (1 ‐ f_{p}) e^{‐ b D_{t}}),

(2)

where $f_{p}$ is the perfusion fraction; $D_{p}$ the pseudo‐diffusion coefficient; $D_{t}$ is the diffusion coefficient; and $S_{0}$ is the fitted signal intensity for $b = 0$ s/mm². The IVIM model parameters were estimated using four different approaches: a nonlinear least‐squares fit, a Bayesian approach, ⁹ and two neural network‐based fitting approaches. ¹² The two neural network approaches consisted of a network nearly identical to the original publication (IVIM‐NET) ¹² and a modified network (IVIM‐NET_mod), as detailed later.

2.1. Nonlinear least squares

The nonlinear least‐squares fit was performed using the trust‐region reflective algorithm as implemented in MATLAB R2019a (MathWorks, Natick, MA), with the following fit boundaries: $0 < f_{p} < 1$ , $0 < D_{t} < 0.005$ mm²/s, $0.005 < D_{p} < 1$ mm²/s, and $0 < S_{0} < 5 \cdot max S (b)$ . Starting values were selected randomly in the range within the fit boundaries as provided by MATLAB functionality.

2.2. Bayesian probability

The Bayesian approach was also performed in MATLAB R2019a and was based on a previous publication. ⁹ In short, the method gives a maximum a posteriori estimate of each parameter by maximizing the marginal posterior probability density functions, which are acquired by means of slice‐sampling ¹⁷ the joint posterior probability. ⁹ , ¹⁷ , ¹⁸ The following multiparametric Gaussian likelihood function was used:

P (S | D_{t}, D_{p}, f_{p}, S_{0}) \propto {(\frac{1}{2} \sum_{\{b\}} {(S (b) ‐ S_{0} (f_{p} e^{‐ b D_{p}} + (1 ‐ f_{p}) e^{‐ b D_{t}}))}^{2})}^{‐ n / 2},

(3)

where $n$ is the number of b‐values. The constraint $D_{t} < D_{p}$ was implemented in the joint prior distribution. ¹⁹ Lognormal distribution priors were used for $D_{p}$ and $D_{t}$ ; a beta distribution prior was used for $f_{p}$ ; and a uniform distribution prior was used for $S_{0}$ . The priors for $D_{p}$ , $D_{t}$ , and $f_{p}$ were estimated by fitting these distributions to results of a prerun of the same Bayesian approach using bounded uniform priors ( $0 < f_{p} < 1$ , $0 < D_{t} < 1$ mm²/s, $0 < D_{p} < 1$ mm²/s, and $0 < S_{0}$ ).

2.3. Neural network

The IVIM‐NET approach was carried out in Python 3.7.4 and PyTorch 1.3.0 using the open access code from the original publication ¹² , ²⁰ and code obtained from the repository of co‐author OGC (currently shared on request; will be made public in the near future and maintained as IVIM‐NET evolves). Our source code with the network definitions and training methods is available on GitHub.

The network, depicted in Figure 1, consists of an input layer with a number of neurons equal to the number of b‐values used to analyze the data, three fully connected hidden layers (each with the same number of neurons, each using the exponential linear unit activation function), and an output layer with a neuron for each parameter. Background voxels were excluded by manually thresholding the $b = 0$ mm²/s images. Training was performed on the entire data set for each epoch, combining and shuffling the voxels from all patients. Data normalization, which is standard for neural networks, was performed using S(0). This signal measured at $b = 0$ s/mm² was only used for normalization, not as input for the network. The mean squared error between the fitted and actual, normalized, signal $(S (b) / S (0))$ was used as loss function. An early stopping criterium (patience) of 10 bad epochs was used, so training was stopped when no improvement was found during the last 10 epochs. Different from the original publication, we included an output neuron for $S_{0} / S (0)$ , where $S_{0}$ and $S (0)$ are the estimated and measured signal intensity at $b = 0$ s/mm², respectively.

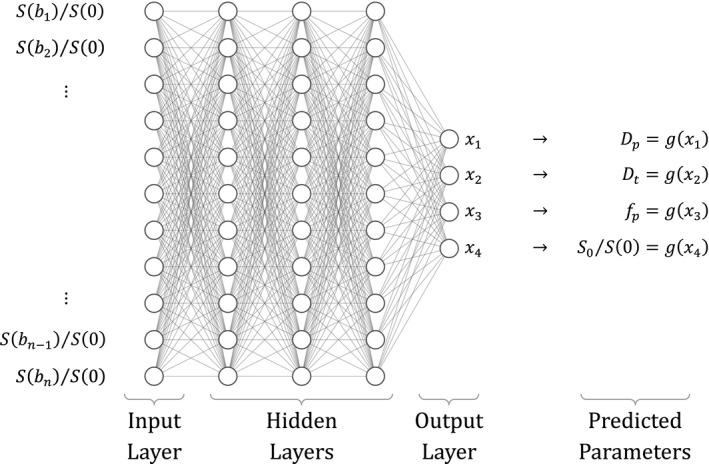
Neural network architecture, created with NN‐SVG. ²¹ The network predicts x₁ to x₄, which are converted to the intravoxel incoherent motion (IVIM) parameters by the constrain function g(x) using Equations 4 (original network) and 5 (modified network), to add parameter constraints

In addition to this implementation, we made a few modifications in a new implementation, IVIM‐NET_mod. The IVIM parameters were constrained by g(x). In the original network, the predicted IVIM parameters were constraint by taking the following absolute:

g (x) = |x| .

(4)

In the presented modified network, a sigmoid function was applied to the output as constraint instead:

g (x) = min + \frac{1}{1 + e^{x}} (max ‐ min),

(5)

which rescaled the output between the following fit boundaries (min < parameter < max): $0 < f_{p} < 0.7$ , $0 < D_{t} < 0.005$ mm²/s, $0.005 < D_{p} < 0.5$ mm²/s, and $0.8 < S_{0} / S (0) < 1.2$ . Second, with the aim of preventing overfitting, we split the data set into two parts: one for training (80%) and one for validation (20%). For the same reason, we reduced the patience (early stopping criterion, see previously) from 10 to 4. Furthermore, as we had a substantially larger data set than Barbieri et al, we limited the number of iterations during each training epoch to 1024, such that we regularly validate how well the network is performing even for large data sets. Because the batch size of an iteration is fixed (128 voxels), each epoch no longer processes the entire data set but a random selection of the training set (in our case, approximately 1.5%). Each epoch evaluates the entire validation set.

2.3.1. Network consistency

To investigate the consistency of the IVIM‐NET approaches as a whole (ie, whether the network converges to consistent estimates), we repeated the complete process of training 100 times. Each time, the network was initialized with new random weights and shuffling (and splitting in the case of IVIM‐NET_mod) of the data set. We compared the runs qualitatively by visual inspection of the parametric maps. We investigated consistency by calculating the average parameter values for both tissues over all subjects and sessions in each run, and then calculated the coefficient of variance (CoV) over the 100 runs.

2.4. Statistics

The intrasession repeatability was calculated by considering the two measurements within a session as paired measurements. Conversely, the intersession repeatability was calculated by considering the first measurements in each session as one pair, and the second measurements in each session as another pair. Moreover, the left and right measured values were considered measurements for the same tissue of interest (ie, tonsil and pterygoid muscle). Thus, each subject had four pairs of observations for the calculation of repeatability, and pairs were either between sessions or within sessions.

We used 95% confidence intervals of the mean difference between paired measurements over all subjects (for both intrasession and intersession pairing) to verify that the repeated measurements were not systematically different. ²² We then calculated the within‐subject coefficient of variation (wCV), which is a relative measure of repeatability. ²³ An overview of the concepts repeatability and consistency can be found in Table 1.

TABLE 1.

Explanation of analysis concepts used in this study

Concept	Description	Quantification	Application
Repeatability	Variation between repeated measurements	wCV	All methods
Consistency	Variation between training runs of IVIM‐NET on same measurements	CoV	IVIM‐NET

Open in a new tab

We compared the repeatability of the four methods with paired Wilcoxon signed‐rank tests of the wCV estimates. For the IVIM‐NET methods, we calculated the median wCV of the 100 runs for each subject, and used these wCV estimates in the paired tests among the four methods. A P‐value below .05 was considered significant.

3. RESULTS

Figure 2 shows examples of the parametric maps calculated with the different methods. Parametric maps calculated by nonlinear regression were most noisy, followed by the Bayesian probability approach. The IVIM‐NET method showed the least noise and most anatomical detail, and was in these terms comparable to the ADC map. The $f_{p}$ maps estimated with nonlinear regression showed systematically higher values than the other methods, as shown in Figure 2. The $D_{p}$ maps of nonlinear regression and IVIM‐NET_mod showed many regions with very high values.

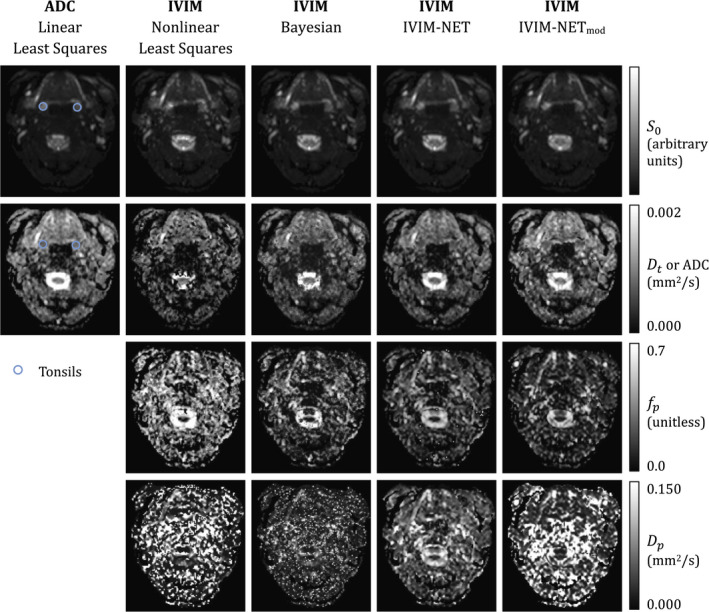
Typical parametric maps of the estimated S₀, ADC, true diffusion coefficient *D_t*. pseudo diffusion coefficient *D_p*, and perfusion fraction *f_p*. Regions of interest delineating the tonsils are shown in the ADC map. The pterygoids are not situated at this level; examples of regions of interest can be found in the Supporting Information. Parametric maps of other IVIM network (IVIM‐NET) instances can also be found in the Supporting Information. Abbreviation: IVIM‐NET_mod, modified IVIM‐NET

None of the methods showed a systematic difference between the repeated measurements for any of the parameters. The calculated wCV estimates are shown in Figure 3. Notably, intrasession and intersession wCV was comparable and both VOIs show the same patterns when comparing the IVIM methods. The methods differ in terms of repeatability and, in general, wCV was highest (worst) when parameters were estimated using nonlinear least squares (except for $f_{p}$ in the pterygoid).

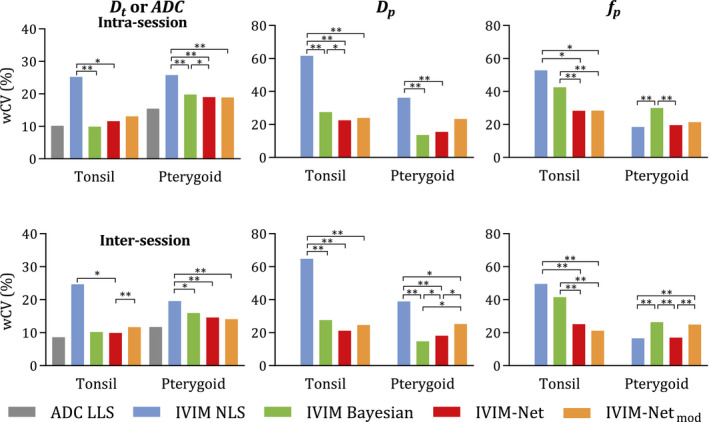
Within‐subject coefficient of variation (wCV) of the parameters for each method. The median value of 100 training runs is displayed for the neural network methods (*P ≤ 0.05, **P ≤ 0.01). Abbreviations: LLS, linear least squares; NLS, nonlinear least squares

This difference was often significant, especially for $D_{p}$ . Significance is indicated in Figure 3, comparing the wCV values of each of the methods for each of the parameters. Tables of the p‐values are available in Supporting Information Tables S1‐S3. The median repeatability results of IVIM‐NET and IVIM‐NET_mod were mostly comparable to the repeatability of the Bayesian approach, except for $f_{p}$ , in which the wCV of IVIM‐NET was significantly better; IVIM‐NET_mod was only significantly better for $f_{p}$ in the tonsils. The median repeatability of IVIM‐NET was better than for IVIM‐NET_mod, although the difference was rarely significant.

3.1. Network consistency

Visual comparison of the parametric maps of the repeated network instances showed inconsistencies for both IVIM‐NET and IVIM‐NET_mod; examples of this can be found in Supporting Information Figures S2‐S4. One hundred figures of the maps of each method are included in the Supporting Information. The network instances generally produced $D_{t}$ maps with a similar distribution but different offset/scaling values. Comparing the average parameter values for IVIM‐NET, the instances showed a CoV of 15% for $D_{t}$ and $f_{p}$ , and 94% for $D_{p}$ . The CoV for the pterygoids and tonsils were equal. The $D_{p}$ maps sometimes showed a visually different distribution. The wCV values for the IVIM‐NET instances were also inconsistent, as shown by the box plots in Figure 4. For IVIM‐NET_mod, the average parameter values were more consistent, with CoVs of 5%, 9%, and 62% for $D_{t}$ , $f_{p}$ , and $D_{p}$ , respectively (again equal for pterygoids and tonsils). The wCV values for $D_{t}$ and $D_{p}$ were also more stable for IVIM‐NET_mod, as reflected by the smaller intervals of the box plots in Figure 4.

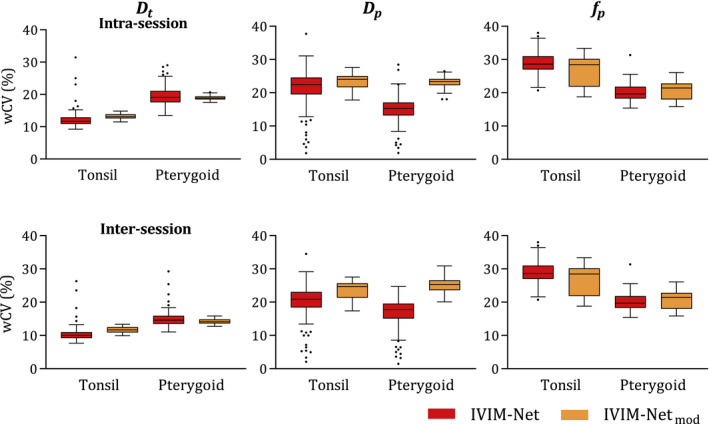
Box plots (with Tukey‐type whiskers) of wCV values for 100 runs of the neural networks

4. DISCUSSION

In this study, we quantified the test–retest repeatability of nonlinear regression, neural network–based, and Bayesian IVIM in the head and neck region. Our results show that these latter two fit approaches substantially outperform the conventional nonlinear regression approaches commonly used for IVIM fitting. Furthermore, although IVIM‐NET has an improved test–retest repeatability, it has an additional uncertainty in that repeated training of networks gives inconsistent results on identical data.

Repeatability estimates of ADC in the tonsils using linear regression fit reported in this study are similar to those reported by Kang et al ²⁴ (also in the tonsils). Two other studies focused primarily on the primary lymph nodes, which makes it hard to compare results directly. Hoang et al report a repeatability coefficient in percentages (15%), which is equivalent to a wCV of 5.3%. ²⁵ The wCV reported by Paudyal et al is 2.38% and much lower than repeatability values found in this study. ²⁶ The generally larger volumes of metastatic lymph nodes might partly explain why the reported estimates are lower. In the case of the study of Paudyal et al, no repositioning of the subject in the magnet appears to have occurred between scans, which could be a major source of measurement variability. This might also explain the difference in reported wCV between the two studies. In our present study, the subject was taken out of the scanner between scans for the intrasession repeatability estimates. No differences were seen between intrasession and intersession repeatability. This indicates that long‐term (order of weeks) physiological variability over time was secondary to the measurement error and short‐term (~30 minutes) physiological variability.

The neural network approach for calculating IVIM maps was introduced only recently. Visual interpretation of the images suggests that more realistic parametric maps are produced by both neural networks compared with the other methods; these maps do not show isolated high or low pixels, and therefore appear to be least affected by noise in the acquisitions. This is in line with earlier observations from Barbieri et al. ¹² Our study has quantified the test–retest repeatability and shows that the network also outperforms linear regression regarding this aspect.

Network training for the entire data set took up to 1 hour for IVIM‐NET and up to 5 minutes for IVIM‐NET_mod. Application of the network took only a couple of seconds for the entire data set. Barbieri et al had substantially less training data, and hence had training times of 5 minutes using the unmodified network. The large difference in training time in our data was primarily the result of decreasing the amount of data seen each epoch in the IVIM‐NET_mod. This major advantage of analysis speed, compared with the other methods investigated in this study (around half an hour per scan with nonlinear regression, and multiple hours per scan using Bayesian probability fitting), makes it viable for use in clinical practice.

Although IVIM‐NET showed promising test–retest repeatability, consistency of the neural network approach is currently still an issue. Our results show that, after renewed training, the parameter values and repeatability estimates vary. The IVIM‐NET_mod method showed more consistent results, although the method is still unstable for $D_{p}$ . Consistency of the approach might be improved by optimizing the starting point of the network, such as by choosing different weight initialization or by training on a set of simulated data first. Avoiding to fit $D_{p}$ (ie, fixing it instead to an a priori estimate) has been shown to improve repeatability ⁸ , ¹⁰ and might also improve network consistency.

A challenge for further research is to identify an acceptable neural network that does not only give estimates with good repeatability, but is also consistent after retraining. Until such consistency is achieved, it is imperative that a single network instance is used for comparative applications, such as in longitudinal studies. Use of separately trained networks will otherwise lead to biased results.

Although other DWI models ²⁷ , ²⁸ , ²⁹ are available, this study has been limited to the ADC and the IVIM model. Another limitation of our study is that we could not compare the methods in terms of accuracy, because a ground truth was unavailable in our study. We hope, therefore, that these methods will be included in future phantom studies. Finally, the choice of b‐values was probably not optimal; b‐value optimization may improve IVIM estimates. ³⁰ , ³¹

5. CONCLUSIONS

The processing speed of the neural network makes it viable for use in clinical practice. However, the inconsistency of training results is challenging. Our presented modifications in the neural network make this approach more consistent, although the output still shows some inconsistency between different training runs on the same data set. Thus, the neural network approach needs to be further improved to identify neural networks that are both consistent and precise. Nonetheless, repeatability from the Bayesian and neural network approaches are superior to that of nonlinear regression for estimating IVIM model parameters.

Supporting information

FIGURE S1 The ADC maps with examples of the regions of interest indicated

FIGURE S2 Example of D_t maps from three instances of intravoxel incoherent motion network (IVIM‐NET) with similar distribution but different absolute values

FIGURE S3 Example of D_p maps from four instances of IVIM‐NET: two with similar distribution but different values (instances 1 and 2) and two with a different distribution (instances 5 and 11)

FIGURE S4 Example of D_p maps from three instances of a modified IVIM‐NET (IVIM‐NET_mod) with different values

TABLE S1 Wilcoxon signed‐rank test p‐values, comparing paired within‐subject coefficient of variation (wCoV) values of the methods for D_t

TABLE S2 Wilcoxon signed‐rank test p‐values, comparing paired wCoV values of the methods for D_p

TABLE S3 Wilcoxon signed‐rank test p‐values, comparing paired wCoV values of the methods for f_p

Click here for additional data file.^{(22.2MB, pdf)}

ACKNOWLEDGMENT

The authors thank Dr. S. Barbieri for sharing his code for implementation of the Bayesian probability approach and for making the code of the neural network approach publicly available.

Koopman T, Martens R, Gurney‐Champion OJ, et al. Repeatability of IVIM biomarkers from diffusion‐weighted MRI in head and neck: Bayesian probability versus neural network. Magn Reson Med. 2021;85:3394–3402. 10.1002/mrm.28671

Thomas Koopman and Roland Martens contributed equally to this work.

Funding information

The Netherlands Organization for Health Research and Development (Grant/Award No. 10‐10400‐98‐14002) and KWF UVA 2014‐7197

DATA AVAILABILITY STATEMENT

The source code that supports the findings of this study is openly available at GitHub: IVIM‐NET and IVIM‐NET_mod: https://github.com/koopmant/ivim‐net, reference number 8943f073; IVIM Bayesian probability: https://github.com/koopmant/ivim‐bp, reference number a6d8f94a; IVIM‐NET main repository: https://github.com/oliverchampion/IVIMNET currently shared on request, will be public in near future and maintained as IVIM‐NET evolves.

REFERENCES

1. Wong KH, Panek R, Welsh L, et al. The predictive value of early assessment after 1 cycle of induction chemotherapy with 18F‐FDG PET/CT and diffusion‐weighted MRI for response to radical chemoradiotherapy in head and neck squamous cell carcinoma. J Nucl Med. 2016;57:1843‐1850. [DOI] [PubMed] [Google Scholar]
2. Wong KH, Panek R, Dunlop A, et al. Changes in multimodality functional imaging parameters early during chemoradiation predict treatment response in patients with locally advanced head and neck cancer. Eur J Nucl Med Mol Imaging. 2018;45:759‐767. [DOI] [PMC free article] [PubMed] [Google Scholar]
3. Hauser T, Essig M, Jensen A, et al. Prediction of treatment response in head and neck carcinomas using IVIM‐DWI: evaluation of lymph node metastasis. Eur J Radiol. 2014;83:783‐787. [DOI] [PubMed] [Google Scholar]
4. Noij DP, Martens RM, Marcus JT, et al. Intravoxel incoherent motion magnetic resonance imaging in head and neck cancer: a systematic review of the diagnostic and prognostic value. Oral Oncol. 2017;68:81‐91. [DOI] [PubMed] [Google Scholar]
5. Le Bihan D, Breton E, Lallemand D, et al. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology. 1986;161:401‐407. [DOI] [PubMed] [Google Scholar]
6. Le Bihan D, Breton E, Lallemand D, et al. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988;168:497‐505. [DOI] [PubMed] [Google Scholar]
7. Vandecaveye V, Dirix P, De Keyzer F, et al. Diffusion‐weighted magnetic resonance imaging early after chemoradiotherapy to monitor treatment response in head‐and‐neck squamous cell carcinoma. Int J Radiat Oncol. 2012;82:1098‐1107. [DOI] [PubMed] [Google Scholar]
8. Gurney‐Champion OJ, Froeling M, Klaassen R, et al. Minimizing the acquisition time for intravoxel incoherent motion magnetic resonance imaging acquisitions in the liver and pancreas. Invest Radiol. 2016;51:211‐220. [DOI] [PubMed] [Google Scholar]
9. Barbieri S, Donati OF, Froehlich JM, et al. Impact of the calculation algorithm on biexponential fitting of diffusion‐weighted MRI in upper abdominal organs: impact of the calculation algorithm on IVIM parameters in upper abdominal organs. Magn Reson Med. 2016;75:2175‐2184. [DOI] [PubMed] [Google Scholar]
10. Gurney‐Champion OJ, Klaassen R, Froeling M, et al. Comparison of six fit algorithms for the intra‐voxel incoherent motion model of diffusion‐weighted magnetic resonance imaging data of pancreatic cancer patients. PLoS One. 2018;13:e0194590. [DOI] [PMC free article] [PubMed] [Google Scholar]
11. Orton MR, Collins DJ, Koh D‐M, et al. Improved intravoxel incoherent motion analysis of diffusion weighted imaging by data driven Bayesian modeling: improved IVIM analysis with Bayesian modelling. Magn Reson Med. 2014;71:411‐420. [DOI] [PubMed] [Google Scholar]
12. Barbieri S, Gurney‐Champion OJ, Klaassen R, et al. Deep learning how to fit an intravoxel incoherent motion model to diffusion‐weighted MRI. Magn Reson Med. 2020;83:312‐321. [DOI] [PubMed] [Google Scholar]
13. Wetscherek A, Stieltjes B, Laun FB. Flow‐compensated intravoxel incoherent motion diffusion imaging: flow‐compensated IVIM diffusion imaging. Magn Reson Med. 2015;74:410‐419. [DOI] [PubMed] [Google Scholar]
14. Wáng YXJ. Living tissue intravoxel incoherent motion (IVIM) diffusion MR analysis without b = 0 image: an example for liver fibrosis evaluation. Quant Imaging Med Surg. 2019;9:127‐133. [DOI] [PMC free article] [PubMed] [Google Scholar]
15. Xiao B‐H, Huang H, Wang L‐F, et al. Diffusion MRI derived per area vessel density as a surrogate biomarker for detecting viral hepatitis B‐induced liver fibrosis: a proof‐of‐concept study. SLAS Technol Transl Life Sci Innov. 2020;25:474‐483. [DOI] [PubMed] [Google Scholar]
16. van der Bel R, Gurney‐Champion OJ, Froeling M, et al. A tri‐exponential model for intravoxel incoherent motion analysis of the human kidney: in silico and during pharmacological renal perfusion modulation. Eur J Radiol. 2017;91:168‐174. [DOI] [PubMed] [Google Scholar]
17. Neal RM. Slice sampling. Ann Stat. 2003;31:705‐767. [Google Scholar]
18. Bretthorst GL, Hutton WC, Garbow JR, et al. Exponential parameter estimation (in NMR) using Bayesian probability theory. Concepts Magn Reson Part A. 2005;27A:55‐63. [Google Scholar]
19. Gustafsson O, Montelius M, Starck G, et al. Impact of prior distributions and central tendency measures on Bayesian intravoxel incoherent motion model fitting: impact of prior and central tendency measure on Bayesian IVIM model fitting. Magn Reson Med. 2018;79:1674‐1683. [DOI] [PubMed] [Google Scholar]
20. Barbieri S. GitHub repository deep IVIM. GitHub. 2019. https://github.com/sebbarb/deep_ivim/commit/4aa19e77. Accessed September 30, 2019. [Google Scholar]
21. LeNail A. NN‐SVG: publication‐ready neural network architecture schematics. J Open Source Softw. 2019;4:747. [Google Scholar]
22. Bland JM, Altman DG. Measuring agreement in method comparison studies. Stat Methods Med Res. 1999;8:135‐160. [DOI] [PubMed] [Google Scholar]
23. Bland M. How should I calculate a within‐subject coefficient of variation? 2006. https://www‐users.york.ac.uk/~mb55/meas/cv.htm. Accessed August 12, 2019.
24. Kang KM, Choi SH, Kim DE, et al. Application of cardiac gating to improve the reproducibility of intravoxel incoherent motion measurements in the head and neck. Magn Reson Med Sci. 2017;16:190‐202. [DOI] [PMC free article] [PubMed] [Google Scholar]
25. Hoang JK, Choudhury KR, Chang J, et al. Diffusion‐weighted imaging for head and neck squamous cell carcinoma: quantifying repeatability to understand early treatment‐induced change. Am J Roentgenol. 2014;203:1104‐1108. [DOI] [PubMed] [Google Scholar]
26. Paudyal R, Konar AS, Obuchowski NA, et al. Repeatability of quantitative diffusion‐weighted imaging metrics in phantoms, head‐and‐neck and thyroid cancers: preliminary findings. Tomogr Ann Arbor Mich. 2019;5:15‐25. [DOI] [PMC free article] [PubMed] [Google Scholar]
27. Jensen JH, Helpern JA, Ramani A, et al. Diffusional kurtosis imaging: the quantification of non‐gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. 2005;53:1432‐1440. [DOI] [PubMed] [Google Scholar]
28. Lu Y, Jansen JFA, Mazaheri Y, et al. Extension of the intravoxel incoherent motion model to non‐Gaussian diffusion in head and neck cancer. J Magn Reson Imaging. 2012;36:1088‐1096. [DOI] [PMC free article] [PubMed] [Google Scholar]
29. Bennett KM, Schmainda KM, Bennett (Tong) R, et al. Characterization of continuously distributed cortical water diffusion rates with a stretched‐exponential model. Magn Reson Med. 2003;50:727‐734. [DOI] [PubMed] [Google Scholar]
30. Perucho JAU, Chang HCC, Vardhanabhuti V, et al. B‐value optimization in the estimation of intravoxel incoherent motion parameters in patients with cervical cancer. Korean J Radiol. 2020;21:218. [DOI] [PMC free article] [PubMed] [Google Scholar]
31. Sijtsema ND, Petit SF, Poot DHJ, et al. An optimal acquisition and post‐processing pipeline for hybrid IVIM‐DKI in head and neck. Magn Reson Med. 2021;85:777‐789. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

FIGURE S1 The ADC maps with examples of the regions of interest indicated

FIGURE S2 Example of D_t maps from three instances of intravoxel incoherent motion network (IVIM‐NET) with similar distribution but different absolute values

FIGURE S4 Example of D_p maps from three instances of a modified IVIM‐NET (IVIM‐NET_mod) with different values

TABLE S1 Wilcoxon signed‐rank test p‐values, comparing paired within‐subject coefficient of variation (wCoV) values of the methods for D_t

TABLE S2 Wilcoxon signed‐rank test p‐values, comparing paired wCoV values of the methods for D_p

TABLE S3 Wilcoxon signed‐rank test p‐values, comparing paired wCoV values of the methods for f_p

Click here for additional data file.^{(22.2MB, pdf)}

Data Availability Statement

[mrm28671-bib-0001] 1. Wong KH, Panek R, Welsh L, et al. The predictive value of early assessment after 1 cycle of induction chemotherapy with 18F‐FDG PET/CT and diffusion‐weighted MRI for response to radical chemoradiotherapy in head and neck squamous cell carcinoma. J Nucl Med. 2016;57:1843‐1850. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0002] 2. Wong KH, Panek R, Dunlop A, et al. Changes in multimodality functional imaging parameters early during chemoradiation predict treatment response in patients with locally advanced head and neck cancer. Eur J Nucl Med Mol Imaging. 2018;45:759‐767. [DOI] [PMC free article] [PubMed] [Google Scholar]

[mrm28671-bib-0003] 3. Hauser T, Essig M, Jensen A, et al. Prediction of treatment response in head and neck carcinomas using IVIM‐DWI: evaluation of lymph node metastasis. Eur J Radiol. 2014;83:783‐787. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0004] 4. Noij DP, Martens RM, Marcus JT, et al. Intravoxel incoherent motion magnetic resonance imaging in head and neck cancer: a systematic review of the diagnostic and prognostic value. Oral Oncol. 2017;68:81‐91. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0005] 5. Le Bihan D, Breton E, Lallemand D, et al. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology. 1986;161:401‐407. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0006] 6. Le Bihan D, Breton E, Lallemand D, et al. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988;168:497‐505. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0007] 7. Vandecaveye V, Dirix P, De Keyzer F, et al. Diffusion‐weighted magnetic resonance imaging early after chemoradiotherapy to monitor treatment response in head‐and‐neck squamous cell carcinoma. Int J Radiat Oncol. 2012;82:1098‐1107. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0008] 8. Gurney‐Champion OJ, Froeling M, Klaassen R, et al. Minimizing the acquisition time for intravoxel incoherent motion magnetic resonance imaging acquisitions in the liver and pancreas. Invest Radiol. 2016;51:211‐220. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0009] 9. Barbieri S, Donati OF, Froehlich JM, et al. Impact of the calculation algorithm on biexponential fitting of diffusion‐weighted MRI in upper abdominal organs: impact of the calculation algorithm on IVIM parameters in upper abdominal organs. Magn Reson Med. 2016;75:2175‐2184. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0010] 10. Gurney‐Champion OJ, Klaassen R, Froeling M, et al. Comparison of six fit algorithms for the intra‐voxel incoherent motion model of diffusion‐weighted magnetic resonance imaging data of pancreatic cancer patients. PLoS One. 2018;13:e0194590. [DOI] [PMC free article] [PubMed] [Google Scholar]

[mrm28671-bib-0011] 11. Orton MR, Collins DJ, Koh D‐M, et al. Improved intravoxel incoherent motion analysis of diffusion weighted imaging by data driven Bayesian modeling: improved IVIM analysis with Bayesian modelling. Magn Reson Med. 2014;71:411‐420. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0012] 12. Barbieri S, Gurney‐Champion OJ, Klaassen R, et al. Deep learning how to fit an intravoxel incoherent motion model to diffusion‐weighted MRI. Magn Reson Med. 2020;83:312‐321. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0013] 13. Wetscherek A, Stieltjes B, Laun FB. Flow‐compensated intravoxel incoherent motion diffusion imaging: flow‐compensated IVIM diffusion imaging. Magn Reson Med. 2015;74:410‐419. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0014] 14. Wáng YXJ. Living tissue intravoxel incoherent motion (IVIM) diffusion MR analysis without b = 0 image: an example for liver fibrosis evaluation. Quant Imaging Med Surg. 2019;9:127‐133. [DOI] [PMC free article] [PubMed] [Google Scholar]

[mrm28671-bib-0015] 15. Xiao B‐H, Huang H, Wang L‐F, et al. Diffusion MRI derived per area vessel density as a surrogate biomarker for detecting viral hepatitis B‐induced liver fibrosis: a proof‐of‐concept study. SLAS Technol Transl Life Sci Innov. 2020;25:474‐483. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0016] 16. van der Bel R, Gurney‐Champion OJ, Froeling M, et al. A tri‐exponential model for intravoxel incoherent motion analysis of the human kidney: in silico and during pharmacological renal perfusion modulation. Eur J Radiol. 2017;91:168‐174. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0017] 17. Neal RM. Slice sampling. Ann Stat. 2003;31:705‐767. [Google Scholar]

[mrm28671-bib-0018] 18. Bretthorst GL, Hutton WC, Garbow JR, et al. Exponential parameter estimation (in NMR) using Bayesian probability theory. Concepts Magn Reson Part A. 2005;27A:55‐63. [Google Scholar]

[mrm28671-bib-0019] 19. Gustafsson O, Montelius M, Starck G, et al. Impact of prior distributions and central tendency measures on Bayesian intravoxel incoherent motion model fitting: impact of prior and central tendency measure on Bayesian IVIM model fitting. Magn Reson Med. 2018;79:1674‐1683. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0020] 20. Barbieri S. GitHub repository deep IVIM. GitHub. 2019. https://github.com/sebbarb/deep_ivim/commit/4aa19e77. Accessed September 30, 2019. [Google Scholar]

[mrm28671-bib-0021] 21. LeNail A. NN‐SVG: publication‐ready neural network architecture schematics. J Open Source Softw. 2019;4:747. [Google Scholar]

[mrm28671-bib-0022] 22. Bland JM, Altman DG. Measuring agreement in method comparison studies. Stat Methods Med Res. 1999;8:135‐160. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0023] 23. Bland M. How should I calculate a within‐subject coefficient of variation? 2006. https://www‐users.york.ac.uk/~mb55/meas/cv.htm. Accessed August 12, 2019.

[mrm28671-bib-0024] 24. Kang KM, Choi SH, Kim DE, et al. Application of cardiac gating to improve the reproducibility of intravoxel incoherent motion measurements in the head and neck. Magn Reson Med Sci. 2017;16:190‐202. [DOI] [PMC free article] [PubMed] [Google Scholar]

[mrm28671-bib-0025] 25. Hoang JK, Choudhury KR, Chang J, et al. Diffusion‐weighted imaging for head and neck squamous cell carcinoma: quantifying repeatability to understand early treatment‐induced change. Am J Roentgenol. 2014;203:1104‐1108. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0026] 26. Paudyal R, Konar AS, Obuchowski NA, et al. Repeatability of quantitative diffusion‐weighted imaging metrics in phantoms, head‐and‐neck and thyroid cancers: preliminary findings. Tomogr Ann Arbor Mich. 2019;5:15‐25. [DOI] [PMC free article] [PubMed] [Google Scholar]

[mrm28671-bib-0027] 27. Jensen JH, Helpern JA, Ramani A, et al. Diffusional kurtosis imaging: the quantification of non‐gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. 2005;53:1432‐1440. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0028] 28. Lu Y, Jansen JFA, Mazaheri Y, et al. Extension of the intravoxel incoherent motion model to non‐Gaussian diffusion in head and neck cancer. J Magn Reson Imaging. 2012;36:1088‐1096. [DOI] [PMC free article] [PubMed] [Google Scholar]

[mrm28671-bib-0029] 29. Bennett KM, Schmainda KM, Bennett (Tong) R, et al. Characterization of continuously distributed cortical water diffusion rates with a stretched‐exponential model. Magn Reson Med. 2003;50:727‐734. [DOI] [PubMed] [Google Scholar]

[mrm28671-bib-0030] 30. Perucho JAU, Chang HCC, Vardhanabhuti V, et al. B‐value optimization in the estimation of intravoxel incoherent motion parameters in patients with cervical cancer. Korean J Radiol. 2020;21:218. [DOI] [PMC free article] [PubMed] [Google Scholar]

[mrm28671-bib-0031] 31. Sijtsema ND, Petit SF, Poot DHJ, et al. An optimal acquisition and post‐processing pipeline for hybrid IVIM‐DKI in head and neck. Magn Reson Med. 2021;85:777‐789. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Repeatability of IVIM biomarkers from diffusion‐weighted MRI in head and neck: Bayesian probability versus neural network

Thomas Koopman

Roland Martens

Oliver J Gurney‐Champion

Maqsood Yaqub

Cristina Lavini

Pim de Graaf

Jonas Castelijns

Ronald Boellaard

J Tim Marcus

Abstract

Purpose

Methods

Results

Conclusion

1. INTRODUCTION

2. METHODS

2.1. Nonlinear least squares

2.2. Bayesian probability

2.3. Neural network

FIGURE 1.

2.3.1. Network consistency

2.4. Statistics

TABLE 1.

3. RESULTS

FIGURE 2.

FIGURE 3.

3.1. Network consistency

FIGURE 4.

4. DISCUSSION

5. CONCLUSIONS

Supporting information

ACKNOWLEDGMENT

DATA AVAILABILITY STATEMENT

REFERENCES

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases