Summary
Interpreting phloem carbohydrate or xylem tissue carbon isotopic composition as measures of water‐use efficiency or past tree productivity requires in‐depth knowledge of the factors altering the isotopic composition within the pathway from ambient air to phloem contents and tree ring. One of least understood of these factors is mesophyll conductance (g m).
We formulated a dynamic model describing the leaf photosynthetic pathway including seven alternative g m descriptions and a simple transport of sugars from foliage down the trunk. We parameterised the model for a boreal Scots pine stand and compared simulated g m responses with weather variations. We further compared the simulated δ13C of new photosynthates among the different g m descriptions and against measured phloem sugar δ13C.
Simulated g m estimates of the seven descriptions varied according to weather conditions, resulting in varying estimates of phloem δ13C during cold/moist and warm/dry periods. The model succeeded in predicting a drought response and a postdrought release in phloem sugar δ13C indicating suitability of the model for inverse prediction of leaf processes from phloem isotopic composition.
We suggest short‐interval phloem sampling during and after extreme weather conditions to distinguish between mesophyll conductance drivers for future model development.
Keywords: 13C discrimination, dynamic model, mesophyll conductance, photosynthesis, Pinus sylvestris, stable carbon isotopes
Introduction
Stable carbon isotopic composition (δ13C) of tree rings has been used to inform us about past climate in paleo‐ecological records since the 1970s (Libby et al., 1976; Wilson & Grinsted, 1977; Zeng et al., 2017). After working out how wood isotopic composition is related to variation in the intrinsic water‐use efficiency of photosynthesis, many papers have been published describing variation in iWUE (e.g. Francey & Farquhar, 1982; McCarroll & Loader, 2004; Voelker et al., 2019) and with the objective of quantifying past tree productivity (Rascher et al., 2010; Schollaen et al., 2013). The basis for these analyses was laid down by the steady‐state model of photosynthetic carbon isotope fractionation by Farquhar et al. (1980, 1989) and its further developments (e.g. Lloyd & Farguhar, 1994). A straightforward application of these models provides a simple ‘inverse’ method for estimating leaf processes from xylem isotopic ratios (McCarroll & Loader, 2004). Although the simple model is often sufficient, there are instances in which more detailed descriptions are needed (Cernusak et al., 2013). Of particular interest in the last decade has been the influence of mesophyll conductance (g m) (Flexas et al., 2012) and a set of postphotosynthetic isotopic fractionation processes (Francey et al., 1985; Gessler et al., 2014; Rinne et al., 2015). A mechanistic understanding of these processes would lead to much more complex models than the early ‘inverse’ isotope models (Danis et al., 2012). An important step towards that is to quantify the additional influences on the isotopic signal (Danis et al., 2012; Cernusak et al., 2013) after which these more comprehensive models could be solved by means of modern data‐model assimilation methods, such as Bayesian analysis (Van Oijen, 2017).
The first step of the isotopic path occurs when carbon dioxide enters the intercellular airspaces (Lloyd & Farguhar, 1994) controlled by stomatal conductance (g s). From the intercellular airspaces to chloroplasts, CO2 encounters a series of resistances that aggregate to mesophyll resistance or, inversely, mesophyll conductance (Evans et al., 2009; Pons et al., 2009). g m was for a long time not explicitly considered in photosynthesis models. Recent evidence shows, however, that mesophyll conductance may strongly limit the carbon flux to chloroplasts (Pons et al., 2009; Flexas et al., 2012; Sun et al., 2014; Ogée et al., 2018) and affect the isotopic signal. Many studies have demonstrated a response of g m to environmental and internal controls (Stangl et al., 2019; Knauer et al., 2020), such as light (Campany et al., 2016), temperature (Evans & von Caemmerer, 2013), nutrients (Bown et al., 2009) and CO2 concentration in intercellular airspaces (C i) or chloroplast (C c) (Flexas et al., 2007; Tazoe et al., 2011). However, few models using dynamic g m have been presented (Sun et al., 2014; Dewar et al., 2018). Instead, mesophyll conductance has mostly been expressed either as a constant or as a constant ratio to g s (Flexas et al., 2008). At the same time, g m has been identified as one of the most important missing factors from terrestrial biosphere models and land surface models (Rogers et al., 2017; Knauer et al., 2020). Estimates of g m vary between tree species (Warren, 2008; Flexas et al., 2012). Our analysis was conducted on Scots pine (Pinus sylvestris). For Pinus species g m values 0.04–0.4 mol m−2 s−1 have been reported (De Lucia et al., 2003; Flexas et al., 2008; Maseyk et al., 2011; Veromann‐Jürgenson et al., 2017; Stangl et al., 2019).
In the chloroplasts, carboxylation produces sugars in reactions with specific isotopic fractionation characteristics (Farquhar et al., 1982; McNevin et al., 2006). A part of these sugars is loaded to the phloem and transported to other tree organs (Desalme et al., 2017). Rascher et al. (2010) observed that phloem sap δ13C of mature maritime pines correlated with environmental factors with a 4‐d time lag. This implies that phloem sap δ13C would follow the δ13C of whole canopy assimilates (Ubierna & Marshall, 2011), except for a time lag caused by a finite phloem transport rate, and thus could be used as an indicator of leaf processes. After photosynthesis, however, the isotopic signal may be weakened by the mixing of the newly synthesised sugars with those stored earlier (Offermann et al., 2011) or additional postphotosynthetic fractionation for example in sugar compound conversions, structural growth or respiration (Tcherkez et al., 2004; Badeck et al., 2005; Priault et al., 2009; Merchant et al., 2011; Rinne et al., 2015). These fractionation effects may need to be quantified if phloem sap or xylem tissue δ13C is used for precise estimates of photosynthate δ13C.
Under the steady‐state assumption of the seminal modelling work of Farquhar et al. (1980, 1989), carbon flux into the leaf equals net photosynthesis (A net) (von Caemmerer, 2013) and the δ13C of new photosynthates can be derived from the δ13C of the CO2 flux into the leaf. During high‐flux conditions, when the ratio of photosynthetic rate to respiratory rate is large, this derivation of δ13C of new photosynthates is most probably accurate. However, misinterpretation of the results is possible during mornings and evenings when the photosynthetic rate is low compared with the respiratory rate (Busch et al., 2020). High‐resolution measurements of photosynthesis and discrimination would be required to test the effects of different model assumptions on the accuracy of the 13C discrimination prediction. Such data are rarely available, as these measurements are technically challenging under field conditions (Stangl et al., 2019). However, model inspection can help to quantify the conditions in which neglecting the effects of these factors is significant.
This study was carried out with the ultimate objective of developing a tool to estimate tree WUE from a relevant set of weather input variables. For this, we evaluated different hypotheses on mesophyll conductance that could be used as a component of an inverse model for estimating leaf fluxes from phloem isotopic composition. We first formulated a dynamic model of isotopic fractionation in the leaf, then combined this with a simple description of transport of sugars down the phloem. The leaf model is essentially a dynamic version of the steady‐state model presented by Farquhar et al. (1982, 1989). It describes the photosynthesis of 12C and 13C, taking into account fractionation in fluxes through stomata and mesophyll, RuBisCo activity, as well as mitochondrial respiration and photorespiration. We formulated and compared seven mesophyll conductance descriptions that are based on published models of g m (Sun et al., 2014; Dewar et al., 2018) and recent data from our measurement site (Stangl et al., 2019). We used continuous gas‐exchange measurements conducted at Rosinedal experimental forest in northern Sweden in 2017 to parameterise the model and concurrent carbon isotope measurements to compare modelled g m with measurement‐based estimates of g m. Furthermore, the temporal pattern of phloem δ13C was measured at the site in 2018. On the basis of the results we discuss the potential of using the approach as a tool for inverse modelling of gas‐exchange or water‐use efficiency from phloem sap δ13C and environmental conditions, as well as to consider the possible benefits of the dynamic approach taken in the leaf model.
The main aims were:
To compare the seven different g m descriptions, and to analyse their implications for the predicted δ13C of photosynthesised sugars.
To study the environmental sensitivity of δ13C of phloem sugars under the different g m descriptions, and to test the respective predictions against phloem δ13C data during the summer drought of 2018.
To study the diurnal patterns of δ13C within the photosynthetic pathway.
Materials and Methods
Study site
Rosinedalsheden is a 100‐yr‐old Scots pine experimental forest located in northern Sweden (64°10′N, 19°45′E) with a cool boreal climate. The mean temperature of the summer months was 12.4°C and mean monthly precipitation 67.9 mm (average of years 2003–2017). The site had low‐fertile fine sandy soil with a 2–5 cm organic layer on top (Hasselquist et al., 2012). The average tree height was 18.6 m and leaf area index 2.7 m2 m−2 (Lim et al., 2015).
Gas‐exchange and δ13C measurements
CO2 and H2O exchange was continuously measured during the 2017 growing season on 1‐yr‐old attached shoots in the upper canopy of four pine trees. The tree canopies were accessed with 16 m high scaffolding towers built inside the stand. Shoots were enclosed in 330 ml transparent cuvettes tracking the ambient temperature by means of Peltier heat exchangers (Tarvainen et al, 2016). The difference between cuvette and ambient temperature was on average + 0.1°C and < ± 0.5°C for 97% of the time. Photosynthetic photon flux density (PPFD) was measured next to each cuvette with a leveled and cosine‐corrected quantum sensor (PAR‐1(M); PP Systems, Hitchin, Herts, UK). During the measurements ambient air was continuously drawn into the shoot cuvettes and adjacent empty reference cuvettes of the same volume. From there, heated and insulated polyethene tubing connected the cuvettes to a multichannel gas‐exchange system equipped with infrared gas analysers (IRGA, CIRAS‐1, PP systems) running in open mode (Wallin et al., 2001). The airflow through the entire system was generated using diaphragm pumps. Vapour pressure deficit was calculated according to Buck (1981). Ambient VPD was, on average, 0.2 kPa higher than inside the cuvettes. In addition, δ13C in the shoot cuvettes was measured using a cavity ring‐down spectrophotometer (CRDS; G2131‐i, Picarro Inc., CA, USA) connected to the gas‐exchange system. The CRDS analyser was calibrated once per week with two reference gases (411 µmol mol−1 CO2, δ13C = −32.4‰ and 1606 µmol mol−1 CO2, δ13C = −4.1‰).
Net photosynthesis and stomatal conductance were calculated for a sequence of days with high data quality from the gas‐exchange data following Farquhar et al. (1980) and the δ13C of net photosynthesis was determined during the summer 2017. More details of the measurement system and calculations are presented in Stangl et al. (2019).
Phloem sugar isotopes
Phloem contents were collected from three trees within the same stand at 2–4‐wk intervals between late‐June and early‐October in 2018. Samples were taken with a hole punch (∅ =10 mm) at 1.3 m height. The phloem discs were put into 1.5 ml de‐ionised water for 12–17 h at 10°C to extract the phloem contents. The tissue was removed and the samples were dried in a centrifuge connected to a cold‐trap. The isotopic composition of the phloem content was analysed by GB‐IRMS (Gasbench II – Isotope Ratio Mass Spectrometer; Thermo Fisher Scientific, Bremen, Germany) calibrated against IAEA‐co‐9 and NBS 19 standards (SLU Stable Isotope Laboratory, Umeå, Sweden).
Environmental variables
Half‐hourly air temperature and relative humidity were measured at 1.5 m height with a HC2‐S3 probe (Rotronic AG, Bassersdorf, Switzerland) installed in a ventilated radiation shield (In Situ, Ockelbo, Sweden). Half‐hourly above‐canopy PPFD was measured with a Li‐190SA PPFD‐sensor (Li‐Cor Biosciences, Lincoln, NE, USA) (Fig. 1).
Fig. 1.
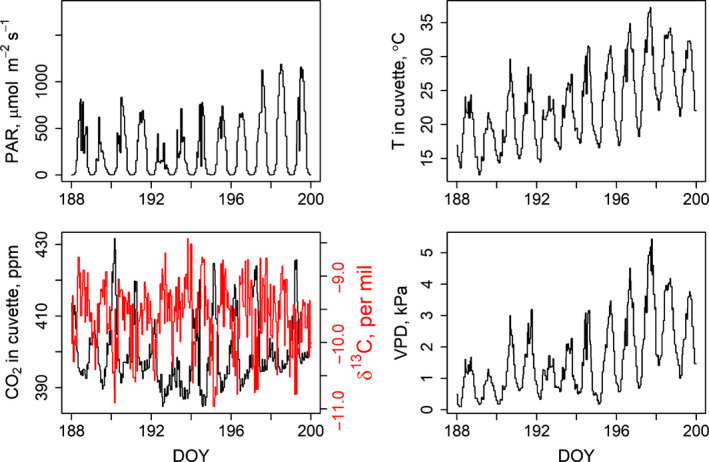
(a) Photosynthetically active radiation, (b) temperature, (c) CO2 concentration (black) and its isotopic composition (red) in the cuvette and (d) vapour pressure deficit during the study period. DOY, day of year.
The model
Leaf carbon pools and fluxes
The state variables of the model are pools of carbon in leaf intercellular airspaces () in chloroplasts () and leaf sugar pool (), expressed per leaf area (mol m−2) (Fig. 2). j denotes isotopes 12C or 13C and ‘sugar pool’ refers to total nonstructural carbohydrates. The pools can be converted to CO2 concentrations, (mol mol−1):
| (Eqn 1) |
where V I is the volume of the intercellular airspaces (V i) or chloroplasts (V c) per leaf area (m3 m−2).
Fig. 2.
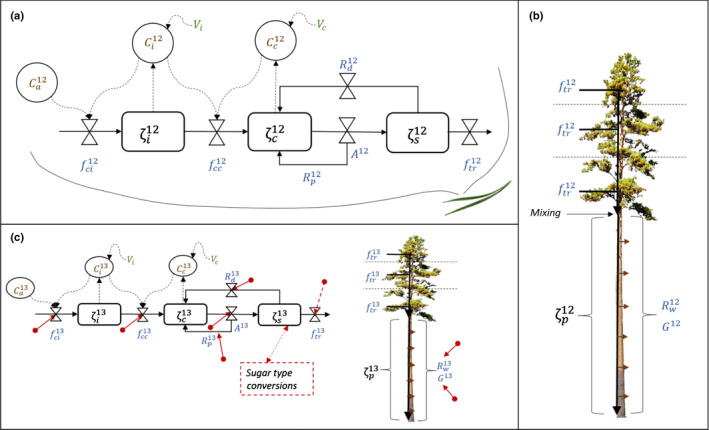
Model structure. Panels (a, b) represent the leaf model and the following transport of carbon downwards via phloem, respectively, for 12C whereas (c) shows the same for 13C with red arrows indicating processes that include isotopic discrimination, that is the processes in which the isotopic signal is altered. Dashed red arrows show processes with potential additional discrimination. ζI are the pools of 12C and 13C, that is the state variables of the model and they are expressed as carbon per leaf area (mol m−2) in intercellular airspaces, chloroplasts or leaf nonstructural sugar pool (I = i, c, s, respectively, leaf model) or nonstructural carbon in phloem per metre trunk (mol m‐1, I = p, trunk model). CI (brown colour) denotes the carbon concentrations in the corresponding pools that can be calculated with pool size ζI and pool volume VI. Ca is carbon concentration in ambient air. Blue colours indicate fluxes into the pools, between the pools or out of the pools (mol m−2 s−1). f ci and f cc are the fluxes to intercellular airspaces and chloroplasts, respectively, A is photosynthetic rate, Rd and Rp mitochondrial and photorespiration, respectively, ftr is export of sugar from leaf to phloem and Rw and G trunk respiration and growth, respectively.
The rates of change of the state variables (mol m−2 s−1), are:
| (Eqn 2) |
| (Eqn 3) |
| (Eqn 4) |
where is the carbon flux into the leaf through stomata, the carbon flux into the chloroplasts through the mesophyll, Aj carboxylation rate, and the rates of mitochondrial respiration and photorespiration, respectively and f tr is the rate of carbon transport from the leaves. Here, respired CO2 is released into . In reality CO2 is released in between ζ c and ζ i (Tholen et al., 2012; Ubierna et al., 2019). Thus, we tested the effect of the contrary assumption of CO2 being released into (see Section ‘Deriving δ13C of photosynthates from CO2 concentration inside a cuvette’).
Following Farquhar et al. (1989), the fluxes (mol m−2 s−1) are:
| (Eqn 5) |
| (Eqn 6) |
| (Eqn 7) |
| (Eqn 8) |
where g s and g m (mol m−2 s−1) are stomatal conductance to CO2 and mesophyll conductance, respectively, a s and a m are 13C/12C fractionation related to g s and g m, respectively, and C a, C i and C c are the mole fractions of CO2 in ambient air, leaf cellular airspaces and chloroplasts, respectively.
The rate at which carbon is taken to Calvin cycle is determined by a ‘bisubstrate model’ (Thornley & Johnson, 1990; Dewar et al., 2018) amended with a seasonality effect (Hari & Mäkelä, 2003; Mäkelä et al., 2004):
| (Eqn 9) |
where is direct temperature effect on photosynthetic rate, a delayed temperature effect describing seasonal acclimation, I(t) PAR (mol m−2 s−1), the light compensation point of photosynthesis, α maximum quantum yield and rx0 carboxylation resistance coefficient:
| (Eqn 10) |
where R c is the isotopic ratio of carbon in chloroplasts () and b discrimination related to RuBisCo activity (Farquhar et al., 1989). During this process, part of the carbon is released via photorespiration back inside the leaf (Busch, 2013):
| (Eqn 11) |
| (Eqn 12) |
where f is a discrimination parameter (Lloyd & Farguhar, 1994). Thus, final carbon bound in photosynthesis (mol m−2 s−1) to new sugars is:
| (Eqn 13) |
Aj enters the pool of photosynthesised carbon that is either stored in leaves, transported to other tree parts or released in mitochondrial respiration. The retention time of sugars in is described with time constant (τ R) with its inverse describing the rate of sugar export from the leaf:
| (Eqn 14) |
| (Eqn 15) |
where h tr is 13C discrimination parameter related to sugar conversion and transport.
Mesophyll conductance
Following previously suggested equations or hypotheses about factors determining mesophyll conductance, we formulated seven descriptions of g m (mol m−2 s−1) (Table 1); assuming a connection between g m and photosynthetic rate (descriptions 1, 2, and 5), estimating g m solely from environmental parameters (descriptions 3 and 4), or assuming constant g m (descriptions 6 and 7).
Table 1.
Mesophyll conductance (mol m−2 s−1) equations.
| Description | Equation | Affecting factors | References | |
|---|---|---|---|---|
| 1 |
|
Photosynthetic rate, C c, water stress | Dewar et al. (2018) | |
| 2 |
|
Photosynthetic rate, C c | Dewar et al. (2018) | |
| 3 |
|
Temperature, light environment | Sun et al. (2014) | |
| 4 |
|
Temperature, light environment, water stress | Sun et al. (2014) | |
| 5 |
|
Photosynthetic rate, C c, temperature | Dewar et al. (2018), Sun et al. (2014) | |
| 6 |
|
Constant g m | Stangl et al. (2019) | |
| 7 |
|
Constant g m | Approximating infinite g m |
is the minimum mesophyll conductance, a 2 is a parameter, A 12 is photosynthetic rate (mol m−2 s−1), C c is the CO2 concentration in chloroplasts, is mesophyll conductance at 25°C, r W, r T and r I represent the effects of water, temperature and light environment (ϵ[0, 1], unitless), respectively (Supporting Information Eqns S1.9, S1.13 and S1.14). The value of r I varies over canopy layers but is constant over time.
Other variables
g s was described with Ball–Berry–Leuning function (Leuning, 1995). R d was calculated following Launiainen et al. (2015) and its isotopic discrimination with the δ13C of leaf sugar pool and a discrimination parameter e. Equations related to these variables as well as light compensation point of photosynthesis, direct and lagged effect of temperature on photosynthetic rate and effects of water stress and temperature on mesophyll conductance are presented in Supporting Information Methods S1.
Tree canopy structure
The tree canopy was vertically divided into three parts. Previous observations show that PAR decreases by 41% and 65% to the middle and lowest layers, respectively (Tarvainen et al., 2016). According to the observation of declining stomatal conductance with canopy depth (G. Wallin, unpublished data), we reduced the value of parameter a 1 by 15% to the second and 30% to the lowest canopy layer to produce the observed increase in the C i : C a ratio. This parameterisation can be adjusted according to data availability in future applications of the model.
Transport of sugars from leaves to phloem
We assumed that in the middle canopy layer, on average, 60% of the photosynthates were transported to the stem and roots and 40% used for branch maintenance and growth (Schiestl‐Aalto et al., 2019). We further assumed that the proportions of transported sugars from the other layers were related to the ratios of photosynthetic rates between the layers. Transport and storage of recent assimilates require conversion of glucose to other soluble sugars or starch. The isotopic effect of these conversions can be expressed in analogy to other fluxes (see e.g. Eqn 12). In this first model version we, however, assumed no discrimination related to conversion.
The recent assimilates were mixed with the sugar pool of leaves and at the canopy bottom, the sugar transported from the canopy layers was mixed with the existing pool of phloem sugars. The sizes of the sugar pools were set to 6.7 gC m−2 leaf and 27 gC m−1 trunk for leaves and phloem, respectively, based on the measurements by Schiestl‐Aalto et al. (2019) conducted in a boreal Scots pine stand.
When carbon is drawn out of the phloem for use, there may be discrimination related to either respiration or structural growth, causing the rest of the phloem sugars to be either depleted or enriched. Thus, a vertical gradient would form in the δ13C of the phloem sugars. Rascher et al. (2010) observed a depletion of δ13C of −0.8 ‰ from canopy to the trunk for Pinus pinaster. By contrast, Gessler et al. (2009) found a 1.5‰ enrichment from leaf soluble matter to phloem content in the trunk in Scots pine trees. We set the discrimination parameter related to trunk maintenance respiration to −6‰ (Ghashghaie et al., 2003) and assumed that , where T(t) is ambient temperature, of the transported carbon was respired, which led to a reasonable yearly proportion of stem respiration (Schiestl‐Aalto et al., 2015). Lacking sufficient knowledge, we set the discrimination parameter related to structural growth to zero. Furthermore, we ignored the possible effects of corticular photosynthesis in the stem tissues (Tarvainen et al., 2018) on the trunk δ13C but were able to include that in future model versions.
The rate of phloem transport was assumed constant 15 cm h−1 (Högberg et al., 2008). This caused a time lag between the δ13C of new photosynthates and trunk phloem sugars. A more detailed phloem transport submodel can be adopted in further versions of the model.
Simulations
was set to 300 µmol mol−1 and to 200 µmol mol−1. We assumed that the initial δ13C of ζ i and ζ c equal the δ13C of ambient air. Initial pool was set to equal the later average pool size and isotopic composition set to −26‰ to produce reasonable respiration values right from the beginning of the simulation.
Environmental data measured with 15–30 min interval were linearly interpolated to form an input data series with a 15 min time step. The model simulation used variable time steps. As the changes of rates of carbon fluxes were caused by changes in environmental variables, the essential dynamic of the model occurred at the time of change of the drivers and then settled down to a steady state. In the beginning of each 15 min time step with possible changes in the drivers, the simulation used a time step of 1/250 to 1/4 s, depending on the rates of A c, R d and R p until the system reached steady state, that is when the rates of change of the state variables ζ i and ζ c dropped below threshold r ss (1 × 10−20 mol mol−1). After reaching the steady state, the simulation moved to the end of the ongoing 15‐min period.
Parameter estimation
The most important parameters related to photosynthesis and g s, the slope of the Ball–Berry–Leuning function (a 1), quantum yield (α) and carboxylation resistance (rx0), were estimated separately for each g m description by fitting the simulated leaf carbon influx (f ci) and stomatal conductance (g s) to cuvette measurements with R‐software nonlinear least squares function (R Core Team, 2017). The fitting was carried out for days of the year 172–193 of 2017 with high quality A net and g s measurements. Measurements were conducted on upper canopy shoots. As the vertical variation in the photosynthetic parameters in the studied trees is small (Tarvainen et al., 2016), we used the estimated parameters for all canopy layers. Other parameters were taken from previous measurements conducted at the site or from the published literature (Table 2).
Table 2.
Model parameters.
| Parameter | Value | Unit | Equation | Parameter explanation | |
|---|---|---|---|---|---|
| p norm | 1013 | hPa | Atmospheric pressure | ||
| a 1 | 4.2 | – | S1.1 | g s parameter | |
| a 2 | 6.0 | – | Table 1 | g m parameter | |
| am | 1.8 × 10−3 | – | 8 | Discrimination parameter | |
| as | 4.4 × 10−3 | – | 6 | Discrimination parameter | |
| b | 29 × 10−3 | – | 10 | Discrimination parameter | |
| C i0 | 300 × 10−6 | mol mol−1 | Initial CO2 concentration | ||
| C c0 | 200 × 10−6 | mol mol−1 | Initial CO2 concentration | ||
| D 0 | 2 | kPa | S1.1 | Threshold VPD | |
| d 1 | 0.08 | C−1 | S1.6 | Parameter of direct temperature effect | |
| d 2 | −5.0 | C | S1.6 | Parameter of direct temperature effect | |
| e | −6 | – | S1.3 | Discrimination parameter | |
| f | 11 × 10−3 | – | 12 | Discrimination parameter | |
|
|
36.9 × 10−6 | – | S1.5 | Light compensation point parameter | |
|
|
1.88 × 10−6 | K−1 | S1.5 | Light compensation point parameter | |
|
|
0.036 × 10−6 | K−1 | S1.5 | Light compensation point parameter | |
|
|
0.003 | mol m−2 s−1 | S1.1 | Minimum g s | |
|
|
0.003 | mol m−2 s−1 | Table 1 | Minimum g m | |
|
|
0.5 | mol m−2 s−1 | Table 1 | g m at 25°C | |
|
|
0.4 | mol m−2 s−1 | Table 1 | constant g m | |
|
|
0.9 | mol m−2 s−1 | Table 1 | constant g m | |
| h tr | 0 | – | 15 | Discrimination parameter | |
|
|
0.96 | – | S1.14 | Parameter of light effect on g m | |
|
|
0.89 | – | S1.14 | Parameter of light effect on g m | |
|
|
0.83 | – | S1.14 | Parameter of light effect on g m | |
| I RT | 50 × 10−6 | mol m−2 s−1 | 19 | Threshold PAR | |
| LAI | 2.7 | m2 m−2 | Leaf area index | ||
| M CO2 | 44 | g mol−1 | CO2 molar mass | ||
| M C | 12 | g mol−1 | C molar mass | ||
| p 1 | 20 | – | S1.13 | Parameter of T effect on g m | |
| p 2 | 49.6 × 103 | Pa m3 mol−1 | S1.13 | Parameter of T effect on g m | |
| p 3 | 1.4 × 103 | Pa m3 mol−1 K−1 | S1.13 | Parameter of T effect on g m | |
| p 4 | 437.4 × 103 | Pa m3 mol−1 | S1.13 | Parameter of T effect on g m | |
| p D | 5.0 | kPa−1 | S1.10 | Parameter of VPD effect on g m | |
| p S | 2.5 | – | S1.11 | Parameter of soil moisture effect on g m | |
| R | 8.314 | Pa m3 mol−1 K−1 | 1, S1.2 | Gas constant | |
| r 1 | 32 500 | K−1 | S1.2 | Mitochondrial respiration parameter | |
| r 2 | 298 | mol Pa−1 m−3 | S1.2 | Mitochondrial respiration parameter | |
| Rd , 25 | 9 × 10−6 | mol m−2 s−1 | S1.2 | Mitochondrial respiration at 25 °C | |
| r ss | 1 × 10−20 | mol mol−1 | 2.5.6 | Steady‐state threshold | |
| rx0 | 5.9 | mol−1 m2 s | 9 | Carboxylation resistance | |
| S max | 17.3 | C | S1.7 | Parameter of lagged temperature effect | |
| T N25 | 298.15 | K | S1.2, S1.5 | Temperature, 25 °C | |
| Vi | 1 × 10−4 | m3 m−2 | 1 | Intercellular airspace volume | |
| Vc | 3 × 10−4 | m3 m−2 | 1 | Mesophyll volume | |
| α | 0.14 | mol mol−1 | 9 | Maximum quantum yield | |
| θ WP | 0.059 | m3 m−3 | S1.12 | Wilting point | |
| θ FC | 0.222 | m3 m−3 | S1.12 | Field capacity | |
| τ R | 1 | Days | 14, 15 | Time constant of respiration substrate | |
| τ S | 16.1 | Day | S1.8 | Time constant of lagged temperature effect |
In g m descriptions 2, 3, 5 and 6 we set parameters a 2 and so that modelled average midday g m corresponded with the measurements conducted at the site (Stangl et al., 2019). Values of a 2 and of descriptions 2 and 3 were the adopted to descriptions 1 and 4, that further included water‐stress reduction (Table 1).
We tested the sensitivity of the model to parameters that were most uncertain and yet important for interpreting the results: e, f, τR, d 1 and d 2. Furthermore, we tested the sensitivity of the model results on varying parameter α while keeping other parameters as estimated. Parameter estimation is explained in detail in Methods S2.
Analyses
Effect of different g m models on predicted g m and the isotopic composition of assimilated sugars
We studied the effect of different mesophyll conductance descriptions on the within‐day and among‐days variations of predicted mesophyll conductance. Furthermore, we studied how these differences were reflected in the isotopic composition of assimilated sugars.
Effect of different g m models on predicted phloem sugar δ13C
We simulated the isotopic composition of phloem sugars at breast height for year 2018 with the seven g m descriptions using photosynthetic parameters estimated for year 2017 and compared the simulated phloem δ13C values with the measured values. We tested the environmental sensitivity of the isotopic signature of phloem sugars under different g m descriptions by running the model under hypothetical weather inputs, including temperature, RH and light (Fig. S1). The objective was to identify the input combinations that could tease out critical differences in the output phloem isotopes and thus best inform us about the drivers of mesophyll conductance.
Deriving δ13C of photosynthates from CO2 concentration inside a cuvette
In the cuvette measurements, the difference between CO2 concentration inside and outside the cuvette implies the rate of carbon flux from the cuvette into, or out of, the leaf, that is f ci (Fig. 2; Eqns 5, 6) and, following the steady‐state assumption, is interpreted as net photosynthesis (). When photosynthetic rate (A) is high, A is the dominating flux over R d and R p and thus roughly equals f ci and f cc, the fluxes of CO2 through stomata and mesophyll, respectively. Therefore, also δ13C of f ci roughly equals δ13C of A. However, when A is low (e.g. mornings and evenings) the interpretation of the measured δ13C of f ci becomes more difficult because of three factors:
(1) Changes in the carbon pools ζ i and ζ c (CO2 in intercellular airspaces and chloroplasts) break the equality between the fluxes of the steady‐state assumption ().
(2) Deriving δ13C of A from the measured δ13C of f ci requires accurate estimates of the rates and isotopic composition of R d and R p. The significance of the accuracy of these estimates increases as the ratio increases.
(3) CO2 released in respiration enters some point within the path between ambient air and chloroplasts and thus, faces further discrimination on its way either to chloroplasts for refixation or to atmosphere, depending on the ratios between C a, C i and C c.
The nonsteady‐state structure of the model allows us to evaluate the importance of these three factors for deriving δ13C of A from δ13C of f ci. To do that, we simulated the model with five assumptions (Table 3). We calculated the difference between the simulated δ13C of A and f ci, (i.e. ). In addition, for f ci and δ13C f ci we calculated the difference between the steady‐state value (i.e. value after the system reached steady state during the 15 min period) and the average value of the whole 15 min period.
Table 3.
Tests for comparing parameterisation or model structure on the difference between of A and f ci.
| Case | Test | Changed parameter or formula |
|---|---|---|
| a | Standard | |
| b | The effect of pool volume on δ13C A and f ci | Vi: 2e−4, Vc: 6e−4, Fig. 2 and Eqn 1 |
| c, d | The effect of respiration discrimination on δ13C A and f ci |
‘high e and f’: e = −1, f = 16, ‘low e and f’: e = −11, f = 6 Ratios and in Fig. 2; Eqns 12, Supporting Information Eqn S1.3 |
| e | The effect of the release location of respired carbon on δ13C A and f ci |
and to ζi instead of ζc in Fig. 2 (Eqn 2) (Eqn 3) |
Results
Modelled and measured fluxes
Measured daily maxima in the carbon flux into the leaves (f ci) varied between 10 and 18 µmol m−2 s−1. Stomatal conductance to CO2 was close to zero during the night and 75–180 mmol m−2 s−1 at midday. The model was able to capture the measured variation in the carbon flux and g s even though midday values were slightly underestimated (on average 4%) and some days showed clearly higher measured than simulated peak values (Fig. 3).
Fig. 3.

Measured (green) and modelled (black) f ci (upper panel) and stomatal conductance (lower panel) of Pinus sylvestris during the days used for parameter estimation. Mesophyll conductance was modelled with description 1 (Table 1). DOY, day of year.
Mesophyll conductance
Different hypotheses regarding the driving factors of mesophyll conductance (descriptions 1–7; Table 1) resulted in varying daily patterns of g m. The average daytime maximum values of descriptions 2, 3, 5 and 6 were parameterised to give c. 0.4 mol m−2 s−1 (Stangl et al., 2019) but the values varied among days depending on weather (Fig. 4a). Descriptions 1, 2 and 5 in which gm was driven by photosynthesis, showed night‐time values close to zero, whereas the temperature‐driven descriptions (3 and 4) showed a weaker diurnal cycle. The values of g m with descriptions including a water‐stress reduction (1 and 4) were slightly lower than those of descriptions without a water‐stress effect (2 and 3, respectively).
Fig. 4.
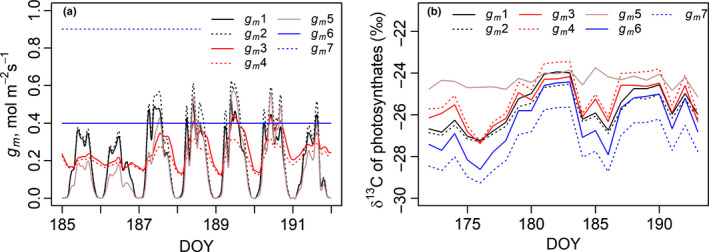
(a) Mesophyll conductance (mol m−2 s−1) of Pinus sylvestris during 7 d and (b) daily average isotopic composition of assimilated sugars during 22 d, modelled with gm descriptions 1–7 (Table 1). The driving factor of gm is A/Cc in descriptions 1 and 2, temperature in descriptions 3 and 4 and A/Cc and temperature in description 5. A further reduction related to water stress is added to descriptions 1 and 4. Descriptions 6 and 7 are constant g m. A shorter period is shown in (a) to more clearly visualise the within‐day patterns. DOY, day of year.
g m had a positive relationship with gs and net photosynthesis with descriptions 1, 2, 3 and 5 either in a saturating (1), linear (2 and 3) or exponential (5) manner (Fig. S2a–d). The form of the relationship between net photosynthesis and g m/g s resembled the positive saturating response found in the measurements of Stangl et al. (2019) in descriptions 1 and 2 whereas the other descriptions led to an opposite form (Fig. S2e,f).
Differences in g m resulted in differences in the daily average δ13C of the photosynthates (Fig. 4b). The differences in δ13C among descriptions 1–6 (excluding description 7, infinite g m) ranged from c. 1 per million to c. 3.5 per million, being largest between descriptions 5 (photosynthetic rate and temperature as driving factors) and 6 (constant g m) under cold, cloudy conditions.
Effect of different gm descriptions on phloem sugars
The model was able to reproduce the strong drought‐related peak in the isotopic composition of phloem sugars detected during the summer in 2018, especially with g m descriptions 1, 2, 6 and 7 (Fig. 5a). Also the effect of precipitation in the end of July (DOYs 210 and 211) was visible in both the measured and modelled phloem δ13C. The overall level of phloem δ13C was the closest to the measured with descriptions 1, 2 and 6.
Fig. 5.
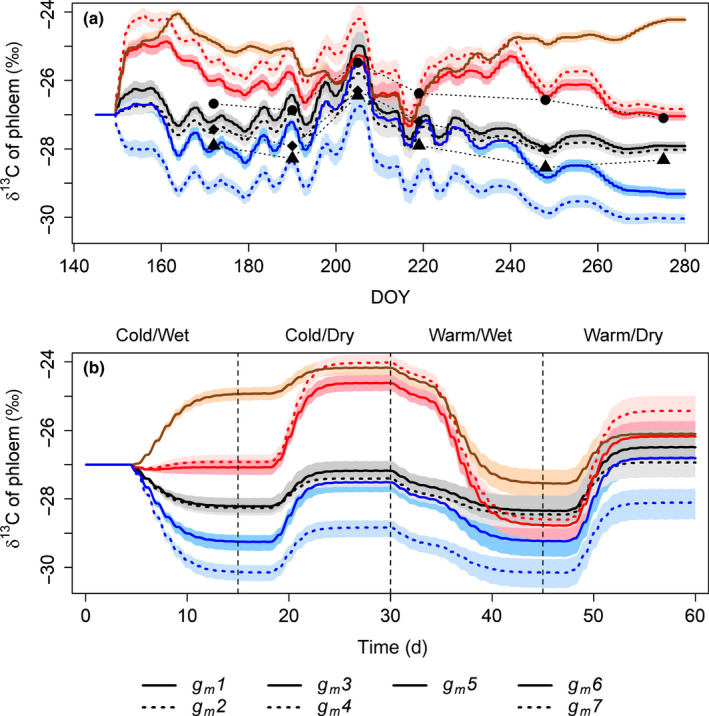
Simulated and measured isotopic composition of phloem sugars of Pinus sylvestris at breast height for: (a) year 2018 and (b) hypothetical, 60 d climate conditions with different mesophyll conductance descriptions (Table 1). The lines represent simulated values with ‘middle’ discrimination parameters e and f (e = −6, f = 11) whereas the shaded areas cover the ranges of ‘low’ and ‘high’ scenarios of parameters e and f, that is e = −11, f = 6 and e = −1, f = 16. Black symbols in (a) indicate measured phloem sugar δ13C values of three different trees. Vertical, dashed lines in (b) represent the timings of change in simulated hypothetical climate conditions.
With hypothetical environmental conditions (Fig. S1) cold days led to substantially larger discrepancies between the phloem δ13C among gm descriptions than warm days (before and after day 30, respectively, Fig. 5b). Conversely, the differences between g m descriptions 1 and 2 vs low constant gm (description 6) were more pronounced during moist, low light conditions than during dry conditions. The time lag between environmental changes and the phloem δ13C reflected the rate of sugar transport from the foliage to the lower stem, whereas the small, direct temperature response (day 30) was caused by enhanced stem respiration.
Varying the values of e and f, that is discrimination in mitochondrial respiration and photorespiration, increased or decreased the δ13C of the photosynthates and thus phloem sugars (Fig. 5). The higher end of the range was reached during warm days with both mitochondrial and photorespiration being high.
Within‐day variation of δ13C of assimilated sugars and parameter sensitivity
We used g m description 1 to study within‐day variation of the δ13C of assimilated sugars as it produced the closest correspondence with the measured pattern of g m/g s vs A net (Fig. S2) and with the measured pattern of phloem sugars in 2018 (Fig. 5a). The daily pattern of the simulated δ13C of the new photosynthates resembled the measured pattern (Stangl et al., 2019) between 05:00 and 20:00 h (Fig. 6a,b) being highest at noon and early afternoon. Modelled values decreased towards −40‰ close to midnight, while the measured values are inaccurate at low flux rates, that is early in the morning and late in the evening. δ13C in the pools ζ I and ζ C follow the same daily pattern with δ13C of ζ C being on average 2.1‰ higher than δ13C of ζ I (Fig. 6c).
Fig. 6.
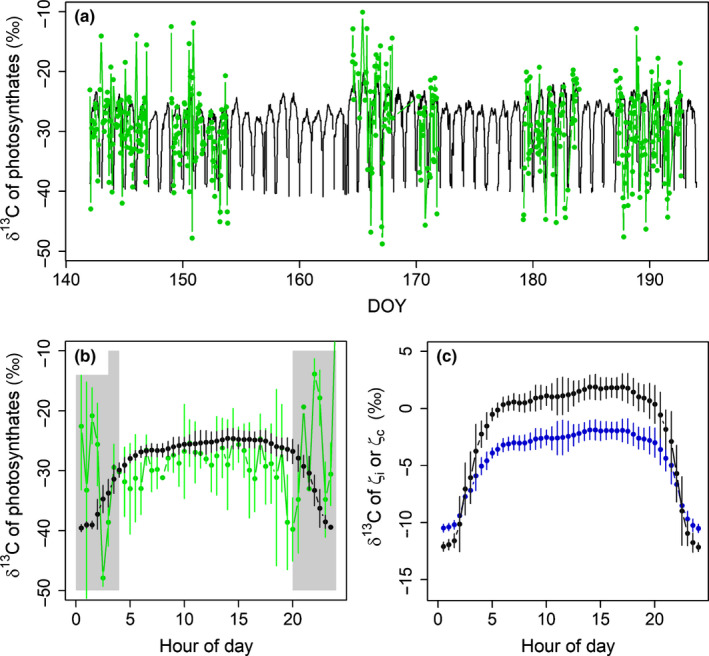
(a) Measured (green) and simulated (black) δ13C of the new photosynthates of Pinus sylvestris (b) Measured daily pattern of δ13C of A net (green) and simulated daily pattern of δ13C of the new photosynthates (black). Both measured and simulated values are averaged over the measurement days. Standard deviation of measurements and model are shown with bars. The time periods at which uncertainty of the measurements is increased due to low light availability leading to low flux rates are indicated with grey panels. (c) Daily pattern of the simulated δ13C of the pools ζ I (blue) and ζ C (black) during the same days as in (a, b).
Decreasing the value of τ R, the age of the mitochondrial respiration source carbon from 24 h to 5 h strengthened the diurnal pattern of the respiration δ13C (Fig. S3a). Changes in the direct temperature effect parameters only caused minor variation in the δ13C of photosynthates, at least during this mid‐summer period (Fig. S3b).
Increasing or decreasing the value of photosynthesis parameter α by 5 or 10%, while keeping the other parameters as estimated, resulted in a maximum 5 or 10% difference in photosynthesis, 5 or 11% difference in g m and 0.09 or 0.18‰ difference in the δ13C of new photosynthates, depending on the gm description used (Fig. S4).
Significance of nonsteady‐state assumption and respiration assumptions for deriving δ13C of photosynthates
The δ13C of carbon flux into the leaf (f ci) was very close to δ13C of new photosynthates (A) when fci > 3 µmol m−2 s−1 (Fig. 7a,b). However, when f ci was small, that is A was close to R d + P R, the simulated δ13C of A was enriched compared with δ13C of f ci. The difference was larger with the assumption of ‘low e and f’, (e = −11, f = 6) but smaller with ‘high e and f’ (e = −1, f = 16). These effects were dominated by mitochondrial respiration discrimination. Changing the release location of respiratory CO2 only had a minor effect on the difference between δ13C of A and δ13C of f ci compared with standard parameters (Fig. 7b), but led to an increase of δ13C of c. 0.4 per mil in the photosynthates.
Fig. 7.
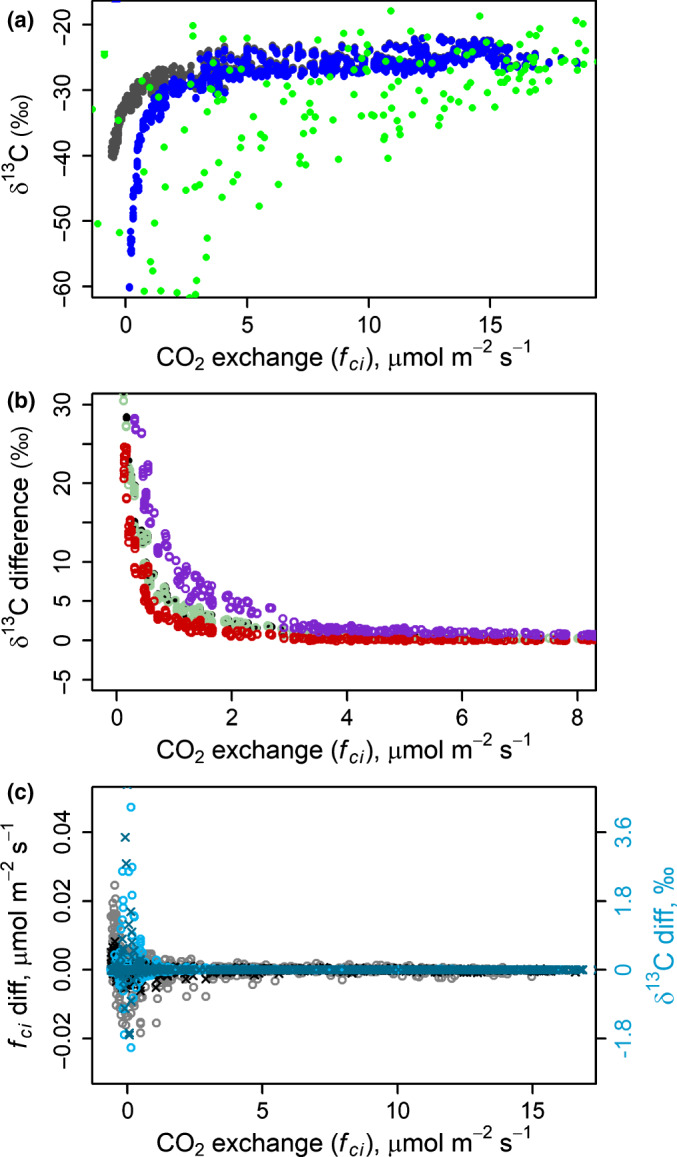
(a) δ13C of simulated photosynthesised sugars (A, black) and CO2 flux through stomata (f ci, blue) of Pinus sylvestris, average during each 15 min period. Green colour indicates δ13C of new photosynthates, estimated from cuvette measurements. (b) Difference between simulated δ13C of A and f ci (black and blue dots in (a)). Black indicates results with standard parameterisation, green results with the assumption of respired carbon being released into the pool of ζi instead of ζc, purple results with respiration discriminations e = −11, f = 6 and red results with respiration discriminations e = −1, f = 16. (c) Difference between fluxes in the steady‐state situation (end of each 15 min simulation period) and average flux during the 15 min period, including the nonsteady‐state and the steady‐state period. Grey colours indicate CO2 flux (f ci) and blue colours δ13C of f ci. Crosses denote standard case parameters and circles denote results with increased Vi and Vc.
The nonsteady‐state structure of the model was insignificant with fci > 1 µmol m−2 s−1 (Fig. 7c). When fci < 1 µmol m−2 s−1 both f ci and δ13C f ci calculated at the steady state (end of each 15 min simulation period) differed from the average value of the 15 min period. The effect was larger with larger volumes V i and V c. The system reached steady state within 0–4 min with the standard parameterisation. The time for reaching steady state increased as flux decreased.
Discussion
Mesophyll conductance
We tested seven equations for describing g m, each based on previous published literature (Table 1). Descriptions 1–5 connected g m to photosynthetic rate, temperature and water stress whereas descriptions 6 and 7 considered constant g m. Even though we set the average midday g m in descriptions 2,3,5 and 6 to correspond with the measured values reported by Stangl et al. (2019) the daily gm patterns, as well as daily average δ13C of photosynthates, varied due to differences in how the descriptions accounted for environmental variation (Fig. 4). Temperature affects gm through its physical effect on diffusion rate but also through processes requiring enzymes or other proteins (Bernacchi et al., 2002). g m descriptions with a direct temperature dependence (descriptions 3, 4 and 5) and those without (descriptions 1, 2, 6 and 7) led to different behaviours for gm and δ13C estimates between warm, sunny days and cold days (DOYs 190 and 186, respectively in Fig. 4). In addition, because temperature affects A it is included indirectly in all nonconstant g m descriptions even though indirectly. Leaf water potential is suggested to affect gm either directly or by altering its temperature response (Li et al., 2020). Conversely, Shrestha et al. (2019) found no clear effect of water stress on the response of g m to PPFD in chickpea. The water effect of our descriptions 1 and 4 reduced gm in conditions of high VPD or low soil moisture (DOYs 188–190 in Fig. 4a).
In descriptions 1 and 2, adopted from Dewar et al (2018), g m was proportional to A/C c and thus, if A remained constant, g m decreased when C c increased. The equation was based on the optimisation of leaf photosynthesis under the assumption of nonstomatal constraints depending on leaf water status (Dewar et al, 2018). The nonstomatal constraints can be interpreted as g m even though they do not provide a real mechanistic explanation. Interestingly, descriptions 1 and 2 were the only ones that produced a similar pattern between net photosynthetic rate and g m/g s measured by Stangl et al (2019). In fact, the other descriptions led to quite opposite patterns (Fig. S2). In accordance, Knauer et al. (2020) noted that most studies found a negative response of gm to Ci and a positive response to light. While descriptions 1 and 2 led to the closest correspondence with the measured g m/g s vs A net ratio, it must be borne in mind that these measurements only covered a few days with limited environmental variation. To provide a more stringent test between possible environmental responses of g m, the present method could be used in data sets covering a wider variety of weather conditions. In future model versions, it will also be possible to represent g m in greater detail by including specific equations for diffusion through cell walls, plasmalemma, cytosol and chloroplast envelopes as for example Warren (2008) and Ubierna et al. (2019) suggested.
Predicting phloem sugar isotopic composition from weather data
When phloem or tree ring isotopic data were used for backtracking past photosynthesis or water‐use efficiency, any explicit g m estimate improves the obtained photosynthesis or WUE estimates compared with ignoring g m (Sun et al., 2014). However, as discussed, g m estimates may substantially differ under different weather conditions and different types of growing seasons (warm/dry vs cold/wet) may lead to substantially different average g m depending on the description used. Thus, accurate inverse modelling requires an in‐depth understanding of the environmental effects on 13C discrimination. The present model was able to predict the drought‐related peak in phloem δ13C during summer 2018, especially with g m descriptions 1, 2 and 6 (Fig. 5a), suggesting that the model was applicable to inverse modelling. Combining phloem δ13C data with weather and photosynthesis data allowed the quantification of the dependence of g m on weather conditions (Ubierna & Marshall, 2011). Extreme weather events followed by a rapid change, provide the clearest signal for such analyses (Fig. 5). Here, the discrepancies of predicted phloem δ13C among g m descriptions were largest during cold periods (Fig. 5b). Thus, at least for boreal Scots pines, we recommend short‐interval phloem sampling during and immediately after such periods, taking also into account the transportation time lag. Conversely, dry conditions that decrease photosynthesis seem to be suitable for distinguishing between the descriptions based on Dewar et al (2018) (descriptions 1 and 2) and constant gm, such as description 6 (Fig. 5b) and thus choosing between the descriptions would benefit from frequent sampling during dry periods followed by rains. The model structure is applicable for other species as well, but species‐specific process parameters should obviously be changed. With other tree species, vertical transport of CO2 in the xylem is a potential process to be considered, even though it seems negligible in Scots pine (Tarvainen et al., 2020).
Studies reporting clear climate signals in δ13C of phloem sugars or tree rings indicated that the isotopic composition of photosynthates largely remains constant as they are transported from leaves to the sink tissues (Högberg et al., 2008; Rascher et al., 2010). However, it is also well known that isotopic discrimination related to postphotosynthetic processes, as well as mixing of newly assimilated carbon with older carbon pools, dampen the connection between δ13C of photosynthesised sugars and either nonstructural or structural carbon measured in sink tissues (Badeck et al., 2005; Gessler et al., 2009; Ogée et al., 2009; Rinne et al., 2015). Specifically, Tcherkez et al. (2004) found an effect of starch synthesis/breakdown on the isotopic composition of leaf sugars, and a 13C labelling experiment by Desalme et al. (2017) suggested that the mean residence time of newly assimilated carbon in pine needles was 1–3 d depending on the season. Such processes possibly altering the signal have to be accounted for to achieve correct predictions (Ogée et al., 2009; Zeng et al., 2017). Wingate et al. (2010) observed a 2–10 d delay and a dampening of the short‐term variation in the respiration δ13C signal when comparing photosynthetic isotope discrimination of Pinus pinaster with subsequent measurements of isotopic compositions of stem, soil and ecosystem respiration. Furthermore, significant variation in the δ13C among different sugar compounds of leaves and phloem sap has been reported (Merchant et al, 2011; Rinne et al., 2015). The present model only accounts for discrimination related to respiration along the pathway from leaves towards roots. Respired CO2 is usually enriched compared with the substrate (Duranceau et al., 2001; Ghashghaie et al., 2001). Werner & Gessler (2011) and Lehmann et al. (2016) observed respired carbon to be heaviest during early afternoon and was in agreement with our model results, although the daily variation (up to 6‰, Werner & Gessler, 2011) in the previous observations is more pronounced than in our simulation (up to 3‰; Fig. S3a). Discrimination related to transport, growth and conversion processes can easily be adopted into the model when knowledge about these processes accumulates. In the current state of the model, the assumptions related to for example proportions of sugars transported downwards from different canopy layers are very simplified. Although we think these assumptions are reasonable and thus do not expect a very large impact on model results for this analysis, it would be possible to replace the simple description of sugar transport with a mechanistic transportation and growth carbon sink model, such as presented by Hölttä et al. (2017), and/or modify the canopy model by increasing the number of canopy layers, separating sun and shade leaves or considering light attenuation within the canopy. These changes would probably make the model more accurate in predicting variations in δ13C at a finer scale than the extreme drought release effect in 2018. Verifying the whole tree model would also benefit from more detailed δ13C measurements along the transport path, including at least some of the following compartments: leaf nonstructural and structural carbon as well as branch and stem phloem and xylem nonstructural and structural carbon.
δ13C of recent photosynthates: within‐day variation and the significance of nonsteady‐state respiration assumptions
The simulated photosynthates were most enriched during midday (Fig. 6). The simulated pattern followed the measurements between 04:00 and 20:00 h, but the connection broke down outside this period as the measured δ13C increased, whereas the simulated values decreased (Fig. 6b). Uncertainties in the measured δ13C of fci increased as CO2 flux decreased (Pons et al., 2009; Stangl et al., 2019). Furthermore, the inference of δ13C of new sugars includes assumptions about the values of parameters e and f and about refixation of respired CO2. This was also noted by Bickford et al. (2010) who did not succeed in predicting diurnal variation in larch 13C discrimination. They interpreted this to emphasise the effect of unaccountable factors related to, for example, gm or fractionation of respiration. Indeed, determining the correct early morning and late evening δ13C remains challenging. The responses of the δ13C of recent photosynthates to varying respiration parameters or assumptions are however able to be studied by modelling.
The validity of the original isotopic discrimination model by Farquhar et al. (1982), at low photosynthetic rates, was recently challenged by Busch et al. (2020). They modified the model assumptions related to mitochondrial respiration, compared the new model with measured gm values and found that the new model performed better than the original when R/A was large. Following those results, we evaluated here at which flux rates the discrepancy between the δ13C of f ci and photosynthates, or the discrepancy between steady‐state and nonsteady‐state f ci or δ13C f ci, increased. With all our tests, δ13C of A equalled δ13C of f ci when f ci > 3 µmol m−2 s−1 and steady‐state f ci and δ13C f ci equalled their nonsteady‐state values when f ci > 1 µmol m−2 s−1 (Fig. 7), that is A >> R. Obviously, most of the photosynthates were produced during high A and under such conditions assumptions related to: (1) carbon pool sizes, (2) respiration parameters, or (3) the release location of respired carbon did not have an effect on the inference of δ13C of A from the δ13C of f ci. However, understanding the within‐day variation of δ13C requires quantification of the responses of the system to these assumptions at low flux. In line also with the results of Ubierna et al. (2019), the assumptions began to play a role with f ci = 0.5–3 µmol m−2 s−1 and their effect rapidly increased as fci approached zero, that is A/R approached one, especially with strong mitochondrial respiration discrimination. The volumes V i and V c affected the results after changes in the weather, when the changes in the pool sizes acted as a buffer between fluxes (Fig. 7c). Real environmental variability, especially light, is much faster than 15 min and this may lead to somewhat different mean values than assuming a mean environment for example of 15 min. The larger the volumes, the slower the steady state is reached and the larger is the effect. Thus, thick leaves and high‐frequency environmental input increased the relevance of the nonsteady‐state assumption, especially when studying phenomena related to morning or evening times.
Conclusions
We developed a dynamic model to predict isotopic signatures of photosynthates and phloem sugars based on different assumptions of g m responses to environment, and compared the results with measured data. The model resulted in different δ13C of new photosynthates with different g m descriptions. Our results showed that g m description 1 determined by the photosynthetic rate, CO2 concentration in chloroplasts and water availability yielded the closest agreement with observations during the studied mid‐summer period. We note, however, that this result remains to be confirmed with data sets collected under more varying environmental conditions. The model succeeded in predicting the drought responses of year 2018 phloem sugars, which indicates the possibility of using the model for backtracking g m with tree ring isotopic and weather data.
Author contributions
PS‐A, AM, ZRS and JM planned the study. PS‐A and AM constructed the model. ZRS, LT and GW conducted the measurements. PS‐A conducted model analysis, all authors contributed to planning the analyses. ZRS conducted the measurement data analysis. PS‐A was responsible for writing the manuscript. All authors contributed to the writing of the manuscript at various stages.
Supporting information
Fig. S1 Hypothetical environmental conditions used in analysis.
Fig. S2 The relationships between g m and g s, g m and A net, and g m /g s and A net based on seven different g m descriptions.
Fig. S3 The effects of τ R and direct temperature response parameters on model results.
Fig. S4 Sensitivity of model results to photosynthesis parameter α.
Methods S1 Other model variables.
Methods S2 Parameter sensitivity.
Please note: Wiley Blackwell are not responsible for the content or functionality of any Supporting Information supplied by the authors. Any queries (other than missing material) should be directed to the New Phytologist Central Office.
Acknowledgements
SLU stable isotope laboratory, Svartberget station for the weather and soil data, Knut and Alice Wallenberg Foundation (#2015.0047), the Strategic Research Area ‘Biodiversity and Ecosystem Services in a Changing Climate’ (BECC).
Data availability
Data are available on request from the authors.
References
- Badeck F‐W, Tcherkez G, Nogués S, Piel C, Ghashghaie J. 2005. Post‐photosynthetic fractionation of stable carbon isotopes between plant organs—a widespread phenomenon. Rapid Communications in Mass Spectrometry 19: 1381–1391. [DOI] [PubMed] [Google Scholar]
- Bernacchi CJ, Portis AR, Nakano H, von Caemmerer S, Long SP. 2002. Temperature response of mesophyll conductance. Implications for the determination of rubisco enzyme kinetics and for limitations to photosynthesis in vivo . Plant Physiology 130: 1992–1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bickford CP, Hanson DT, McDowell NG. 2010. Influence of diurnal variation in mesophyll conductance on modelled 13C discrimination: results from a field study. Journal of Experimental Botany 61: 3223–3233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bown HE, Watt MS, Mason EG, Clinton PW, Whitehead D. 2009. The influence of nitrogen and phosphorus supply and genotype on mesophyll conductance limitations to photosynthesis in Pinus radiata . Tree Physiology 29: 1143–1151. [DOI] [PubMed] [Google Scholar]
- Buck AL. 1981. New equations for computing vapor pressure. Journal of Applied Meteorology 20: 1527–32. [Google Scholar]
- Busch FA. 2013. Current methods for estimating the rate of photorespiration in leaves. Plant Biology 15: 648–655. [DOI] [PubMed] [Google Scholar]
- Busch FA, Holloway‐Phillips M, Stuart‐Williams H, Farquhar GD. 2020. Revisiting carbon isotope discrimination in C3 plants shows respiration rules when photosynthesis is low. Nature Plants 6: 245–258. [DOI] [PubMed] [Google Scholar]
- Campany CE, Tjoelker MG, von Caemmerer S, Duursma RA. 2016. Coupled response of stomatal and mesophyll conductance to light enhances photosynthesis of shade leaves under sunflecks. Plant, Cell & Environment 39: 2762–2773. [DOI] [PubMed] [Google Scholar]
- Cernusak LA, Ubierna N, Winter K, Holtum JAM, Marshall JD, Farquhar GD. 2013. Environmental and physiological determinants of carbon isotope discrimination in terrestrial plants. New Phytologist 200: 950–965. [DOI] [PubMed] [Google Scholar]
- Danis PA, Hatté C, Misson L, Guiot J. 2012. MAIDENiso: a multiproxy biophysical model of tree‐ring width and oxygen and carbon isotopes. Canadian Journal of Forest Research 42: 1697–1713. [Google Scholar]
- De Lucia EH, Whitehead D, Clearwater MJ. 2003. The relative limitation of photosynthesis by mesophyll conductance in co‐occurring species in a temperate rainforest dominated by the conifer Dacrydium cupressinum . Functional Plant Biology 30: 1197–1204. [DOI] [PubMed] [Google Scholar]
- Desalme D, Priault P, Gérant D, Dannoura M, Maillard P, Plain C, Epron D. 2017. Seasonal variations drive short‐term dynamics and partitioning of recently assimilated carbon in the foliage of adult beech and pine. New Phytologist 213: 140–153. [DOI] [PubMed] [Google Scholar]
- Dewar R, Mauranen A, Mäkelä A, Hölttä T, Medlyn B, Vesala T. 2018. New insights into the covariation of stomatal, mesophyll and hydraulic conductances from optimization models incorporating nonstomatal limitations to photosynthesis. New Phytologist 217: 571–585. [DOI] [PubMed] [Google Scholar]
- Duranceau M, Ghashghaie J, Brugnoli E. 2001. Carbon isotope discrimination during photosynthesis and dark respiration in intact leaves of Nicotiana sylvestris: comparisons between wild type and mitochondrial mutant plants. Australian Journal of Plant Physiology 28: 65–71. [Google Scholar]
- Evans JR, Kaldenhoff R, Genty B, Terashima I. 2009. Resistances along the CO2 diffusion pathway inside leaves. Journal of Experimental Botany 60: 2235–2248. [DOI] [PubMed] [Google Scholar]
- Evans JR, von Caemmerer S. 2013. Temperature response of carbon isotope discrimination and mesophyll conductance in tobacco. Plant, Cell & Environment 36: 745–756. [DOI] [PubMed] [Google Scholar]
- Farquhar GD, Ehleringer R, Hubic KT. 1989. Carbon isotope discrimination and photosynthesis. Annual Review of Plant Physiology and Plant Molecular Biology 40: 503–37. [Google Scholar]
- Farquhar GD, O'Leary MH, Berry JA. 1982. On the relationship between carbon isotope discrimination and the intercellular carbon dioxide concentration in leaves. Australian Journal of Plant Physiology 9: 121–137. [Google Scholar]
- Farquhar GD, von Caemmerer S, Berry JA. 1980. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149: 78–90. [DOI] [PubMed] [Google Scholar]
- Flexas J, Barbour MM, Brendel O, Cabrera HM, Carriquí M, Díaz‐Espejo A, Douthe C, Dreyer E, Ferrio JP, Gago J et al. 2012. Mesophyll diffusion conductance to CO2: An unappreciated central player in photosynthesis. Plant Science 193: 70–84. [DOI] [PubMed] [Google Scholar]
- Flexas J, Diaz‐Espejo A, Galmés J, Kaldenhoff R, Medrano H, Ris‐Carbo M. 2007. Rapid variations of mesophyll conductance in response to changes in CO2 concentration around leaves. Plant, Cell & Environment 30: 1284–1298. [DOI] [PubMed] [Google Scholar]
- Flexas J, Ris‐Carbo M, Diaz‐Espejo A, Galmés J, Medrano H. 2008. Mesophyll conductance to CO2: current knowledge and future prospects. Plant, Cell & Environment 31: 602–621. [DOI] [PubMed] [Google Scholar]
- Francey RJ, Farquhar GD. 1982. An explanation for the 12C/13C variations in tree rings. Nature 297: 28–31. [Google Scholar]
- Francey RJ, Gifford RM, Sharkey TD, Weir B. 1985. Physiological influences on carbon isotope discrimination in huon pine (Lagarostrobos franklinii). Oecologia 66: 211–218. [DOI] [PubMed] [Google Scholar]
- Gessler A, Brandes E, Buchmann N, Helle G, Rennenberg H, Barnard RL. 2009. Tracing carbon and oxygen isotope signals from newly assimilated sugars in the leaves to the tree‐ring archive. Plant, Cell & Environment 32: 780–795. [DOI] [PubMed] [Google Scholar]
- Gessler A, Ferrio JP, Hommel R, Treydte K, Werner RA, Monson RK. 2014. Stable isotopes in tree rings: towards a mechanistic understanding of isotope fractionation and mixing processes from the leaves to the wood. Tree Physiology 34: 796–818. [DOI] [PubMed] [Google Scholar]
- Ghashghaie J, Badeck FW, Lanigan G, Nogués S, Tcherkez G, Deléens E, Cornic G, Griffiths H. 2003. Carbon isotope fractionation during dark respiration and photorespiration in C3 plants. Phytochemistry Reviews 2: 145–161. [Google Scholar]
- Ghashghaie J, Duranceau M, Badeck FW, Cornic G, Adeline MT, Deleens E. 2001. δ13C of CO2 respired in the dark in relation to δ13C of leaf metabolites: comparison between Nicotiana sylvestris and Helianthus annuus under drought. Plant, Cell & Environment 24: 505–515. [Google Scholar]
- Hari P, Mäkelä A. 2003. Annual pattern of photosynthesis of Scots pine in the boreal zone. Tree Physiology 23: 145–155. [DOI] [PubMed] [Google Scholar]
- Hasselquist NJ, Metcalfe DB, Högberg P. 2012. Contrasting effects of low and high nitrogen additions on soil CO2 flux components and ectomycorrhizal fungal sporocarp production in a boreal forest. Global Change Biology 18: 3596–3605. [Google Scholar]
- Högberg P, Högberg MN, Göttlicher SG, Betson NR, Keel SG, Metcalfe DB, Campbell C, Schindlbacher A, Hurry V, Lundmark T et al. 2008. High temporal resolution tracing of photosynthate carbon from the tree canopy to forest soil microorganisms. New Phytologist 177: 220–228. [DOI] [PubMed] [Google Scholar]
- Hölttä T, Lintunen A, Chan T, Mäkelä A, Nikinmaa E. 2017. A steady‐state stomatal model of balanced leaf gas exchange, hydraulics and maximal source–sink flux. Tree Physiology 37: 851–868. [DOI] [PubMed] [Google Scholar]
- Knauer J, Zaehle S, De Kauwe MG, Haverd V, Reichstein M, Sun Y. 2020. Mesophyll conductance in land surface models: effects on photosynthesis and transpiration. The Plant Journal 101: 858–873. [DOI] [PubMed] [Google Scholar]
- Launiainen S, Katul GG, Lauren A, Kolari P. 2015. Coupling boreal forest CO2, H2O and energy flows by a vertically structured forest canopy – soil model with separate bryophyte layer. Ecological modelling 312: 385–405. [Google Scholar]
- Lehmann MM, Wegener F, Werner RA, Werner C. 2016. Diel variations in carbon isotopic composition and concentration of organic acids and their impact on plant dark respiration in different species. Plant Biology Journal 18: 776–784. [DOI] [PubMed] [Google Scholar]
- Leuning R. 1995. A critical appraisal of a combined stomatal‐photosynthesis model for C3 plants. Plant, Cell & Environment 18: 339–355. [Google Scholar]
- Li Y, Song X, Li S, Salter WT, Barbour MM. 2020. The role of leaf water potential in the temperature response of mesophyll conductance. New Phytologist 225: 1193–1205. [DOI] [PubMed] [Google Scholar]
- Libby LM, Pandolfi LJ, Payton PH, Marshall J, Becker B, Giertzsienbenlist V. 1976. Isotopic tree thermometers. Nature 261: 284–288. [Google Scholar]
- Lim H, Oren R, Palmroth S, Tor‐ngern P, Mörling T, Näsholm T, Lundmark T, Helmisaari HS, Leppälammi‐Kujansuu J, Linder S. 2015. Inter‐annual variability of precipitation constrains the production response of boreal Pinus sylvestris to nitrogen fertilization. Forest Ecology and Management 348: 31–45. [Google Scholar]
- Lloyd J, Farguhar GD. 1994. 13C discrimination during CO2 assimilation by the terrestrial biosphere. Oecologia 99: 201–215. [DOI] [PubMed] [Google Scholar]
- Mäkelä A, Hari P, Berninger F, Hänninen H, Nikinmaa E. 2004. Acclimation of photosynthetic capacity in Scots pine to the annual cycle of temperature. Tree Physiology 24: 369–376. [DOI] [PubMed] [Google Scholar]
- Maseyk K, Hemming D, Angert A, Leavitt SW, Yakir D. 2011. Increase in water‐use efficiency and underlying processes in pine forests across a precipitation gradient in the dry Mediterranean region over the past 30 years. Oecologia 167: 573–585. [DOI] [PubMed] [Google Scholar]
- McCarroll D, Loader NJ. 2004. Stable isotopes in tree rings. Quaternary Science Reviews 23: 771–801. [Google Scholar]
- McNevin DB, Badger MR, Kane HJ, Farquhar GD. 2006. Measurement of (carbon) kinetic isotope effect by Rayleigh fractionation using membrane inlet mass spectrometry for CO2‐consuming reactions. Functional Plant Biology 33: 1115–1128. [DOI] [PubMed] [Google Scholar]
- Merchant A, Wild B, Richter A, Bellot S, Adams MA, Dreyer E. 2011. Compound‐specific differences in 13C of soluble carbohydrates in leaves and phloem of 6‐month‐old Eucalyptus globulus (Labill). Plant, Cell & Environment 34: 1599–1608. [DOI] [PubMed] [Google Scholar]
- Offermann C, Ferrio JP, Holst J, Grote R, Siegwolf R, Kayler Z, Gessler A. 2011. The long way down—are carbon and oxygen isotope signals in the tree ring uncoupled from canopy physiological processes? Tree Physiology 31: 1088–1102. [DOI] [PubMed] [Google Scholar]
- Ogée J, Barbour MM, Wingate L, Bert D, Bosc A, Stievenard M, Lambrot C, Pierre M, Bariac T, Loustau D et al. 2009. A single‐substrate model to interpret intra‐annual stable isotope signals in tree‐ring cellulose. Plant, Cell & Environment 32: 1071–1090. [DOI] [PubMed] [Google Scholar]
- Ogée J, Wingate L, Genty B. 2018. Estimating mesophyll conductance from measurements of C18OO photosynthetic discrimination and carbonic anhydrase activity. Plant Physiology 178: 728–752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pons TL, Flexas J, von Caemmerer S, Evans JR, Genty B, Ribas‐Carbo M, Brugnoli E. 2009. Estimating mesophyll conductance to CO2: methodology, potential errors, and recommendations. Journal of Experimental Botany 60: 2217–2234. [DOI] [PubMed] [Google Scholar]
- Priault P, Wegener F, Werner C. 2009. Pronounced differences in diurnal variation of carbon isotope composition of leaf respired CO2 among functional groups. New Phytologist 181: 400–412. [DOI] [PubMed] [Google Scholar]
- R Core Team . 2017. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. [WWW document] URL https://www.R‐project.org/. [Google Scholar]
- Rascher KG, Máguas C, Werner C. 2010. On the use of phloem sap δ 13C as an indicator of canopy carbon discrimination. Tree Physiology 30: 1499–1514. [DOI] [PubMed] [Google Scholar]
- Rinne KT, Saurer M, Kirdyanov AV, Loader NJ, Bryukhanova MV, Werner RA, Siegwolf RTW. 2015. The relationship between needle sugar carbon isotope ratios and tree rings of larch in Siberia. Tree Physiology 35: 1192–1205. [DOI] [PubMed] [Google Scholar]
- Rogers A, Medlyn BE, Dukes JS, Bonan G, von Caemmerer S, Dietze MC, Kattge J, Leakey ADB, Mercado LM, Niinemets Ü et al. 2017. A roadmap for improving the representation of photosynthesis in Earth system models. New Phytologist 213: 22–42. [DOI] [PubMed] [Google Scholar]
- Schiestl‐Aalto P, Kulmala L, Mäkinen H, Nikinmaa E, Mäkelä A. 2015. CASSIA – a dynamic model for predicting intra‐annual sink demand and interannual growth variation in Scots pine. New Phytologist 206: 647–659. [DOI] [PubMed] [Google Scholar]
- Schiestl‐Aalto P, Ryhti K, Mäkelä A, Peltoniemi M, Bäck J, Kulmala L. 2019. Analysis of the NSC storage dynamics in tree organs reveals the allocation to belowground symbionts in the framework of whole tree carbon balance. Frontiers in Forests and Global Change 2: 17. [Google Scholar]
- Schollaen K, Heinrich I, Neuwirth B, Krusic PJ, D'Arrigo RD, Karyanto O, Helle G. 2013. Multiple tree‐ring chronologies (ring width, δ13C and δ18O) reveal dry and rainy season signals of rainfall in Indonesia. Quaternary Science Reviews 73: 170–181. [Google Scholar]
- Shrestha A, Buckley TN, Lockhart EL, Barbour MM. 2019. The response of mesophyll conductance to short‐ and long‐term environmental conditions in chickpea genotypes. AoB Plants 10: ply073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stangl ZR, Tarvainen L, Wallin G, Ubierna N, Räntfors M, Marshall JD. 2019. Diurnal variation in mesophyll conductance and its influence on modelled water‐use efficiency in a mature boreal Pinus sylvestris stand. Photosynthesis Research 141: 53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Y, Gu L, Dickinson RE, Norby RJ, Pallardy SG, Hoffman FM. 2014. Impact of mesophyll diffusion on estimated global land CO2 fertilization. Proceedings of the National Academy of Sciences, USA 111: 15774–15779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarvainen L, Lutz M, Räntfors M, Näsholm T, Wallin G. 2016. Increased needle nitrogen contents did not improve shoot photosynthetic performance of mature nitrogen‐poor Scots pine trees. Frontiers in Plant Science 7: 1051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarvainen L, Wallin G, Linder S, Näsholm T, Oren R, Ottosson Löfvenius M, Räntfors M, Tor‐Ngern P, Marshall JD. 2020. Limited vertical CO2 transport in stems of mature boreal Pinus sylvestris trees. Tree Physiology, tpaa113. doi: 10.1093/treephys/tpaa113. [DOI] [PubMed] [Google Scholar]
- Tarvainen L, Wallin G, Hyungwoo L, Linder S, Oren R, Ottosson Löfvenius M, Räntfors M, Tor‐ngern P, Marshall J. 2018. Photosynthetic refixation varies along the stem and reduces CO2 efflux in mature boreal Pinus sylvestris trees. Tree Physiology 38: 558–569. [DOI] [PubMed] [Google Scholar]
- Tazoe Y, von Caemmerer S, Estavillo GM, Evans JR. 2011. Using tunable diode laser spectroscopy to measure carbon isotope discrimination and mesophyll conductance to CO2 diffusion dynamically at different CO2 concentrations. Plant, Cell & Environment 34: 580–591. [DOI] [PubMed] [Google Scholar]
- Tcherkez G, Farquhar G, Badeck F, Ghashgahaie J. 2004. Theoretical considerations about carbon isotope distribution in glucose of C3 plants. Functional Plant Biology 31: 857–877. [DOI] [PubMed] [Google Scholar]
- Tholen D, Ethier G, Genty B, Pepin S, Zhu XG. 2012. Variable mesophyll conductance revisited: theoretical background and experimental implications. Plant, Cell & Environment 35: 2087–2103. [DOI] [PubMed] [Google Scholar]
- Thornley JHM, Johnson IR. 1990. Plant and crop modelling. Oxford, UK: Oxford University Press. [Google Scholar]
- Ubierna N, Cernusak LA, Holloway‐Phillips M, Busch FA, Cousins AB, Farquhar GD. 2019. Critical review: incorporating the arrangement of mitochondria and chloroplasts into models of photosynthesis and carbon isotope discrimination. Photosynthesis Research 141: 5–31. [DOI] [PubMed] [Google Scholar]
- Ubierna N, Marshall JD. 2011. Estimation of canopy average mesophyll conductance using δ13C of phloem contents. Plant, Cell & Environment 34: 1521–1535. [DOI] [PubMed] [Google Scholar]
- Van Oijen M. 2017. Bayesian methods for quantifying and reducing uncertainty and error in forest models. Current Forestry Reports 3: 269–280. [Google Scholar]
- Veromann‐Jürgenson LL, Tosens T, Laanisto L, Niinemets Ü. 2017. Extremely thick cell walls and low mesophyll conductance: welcome to the world of ancient living! Journal of Experimental Botany 68: 1639–1653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voelker SL, Wang SS, Dawson TE, Roden JS, Still CJ, Longstaffe FJ, Ayalon A. 2019. Tree‐ring isotopes adjacent to Lake Superior reveal cold winter anomalies for the Great Lakes region of North America. Scientific Reports 9: 4412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Von Caemmerer S. 2013. Steady‐state models of photosynthesis. Plant, Cell & Environment 36: 1617–1630. [DOI] [PubMed] [Google Scholar]
- Wallin G, Linder S, Lindroth A, Räntfors M, Flemberg S, Grelle A. 2001. Carbon dioxide exchange in Norway spruce at the shoot, tree and ecosystem scale. Tree Physiology 21: 969–976. [DOI] [PubMed] [Google Scholar]
- Warren CR. 2008. Stand aside stomata, another actor deserves centre stage: the forgotten role of the internal conductance to CO2 transfer. Journal of Experimental Botany 59: 1475–1487. [DOI] [PubMed] [Google Scholar]
- Werner C, Gessler A. 2011. Diel variations in the carbon isotope composition of respired CO2 and associated carbon sources: a review of dynamics and mechanisms. Biogeosciences 8: 2437–2459. [Google Scholar]
- Wilson A, Grinsted M. 1977. 12C/13C in cellulose and lignin as palaeothermometers. Nature 265: 133–135. [Google Scholar]
- Wingate L, Ogée J, Burlett R, Bosc A, Devaux M, Grace J, Loustau D, Gessler A. 2010. Photosynthetic carbon isotope discrimination and its relationship to the carbon isotope signals of stem, soil and ecosystem respiration. New Phytologist 188: 576–589. [DOI] [PubMed] [Google Scholar]
- Zeng X, Liu X, Treydte K, Evans MN, Wang W, An W, Sun W, Xu G, Wu G, Zhang X. 2017. Climate signals in tree‐ring δ18O and δ13C from southeastern Tibet: insights from observations and forward modelling of intra‐ to interdecadal variability. New Phytologist 216: 1104–1118. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig. S1 Hypothetical environmental conditions used in analysis.
Fig. S2 The relationships between g m and g s, g m and A net, and g m /g s and A net based on seven different g m descriptions.
Fig. S3 The effects of τ R and direct temperature response parameters on model results.
Fig. S4 Sensitivity of model results to photosynthesis parameter α.
Methods S1 Other model variables.
Methods S2 Parameter sensitivity.
Please note: Wiley Blackwell are not responsible for the content or functionality of any Supporting Information supplied by the authors. Any queries (other than missing material) should be directed to the New Phytologist Central Office.
Data Availability Statement
Data are available on request from the authors.


