Validation of mathematical models for the prediction of organs-at-risk dosimetric metrics in high-dose-rate gynecologic interstitial brachytherapy

Abstract

Purpose:

Given the complicated nature of an interstitial gynecologic brachytherapy treatment plan, the use of a quantitative tool to evaluate the quality of the achieved metrics compared to clinical practice would be advantageous. For this purpose, predictive mathematical models to predict the D_2cc of rectum and bladder in interstitial gynecologic brachytherapy are discussed and validated.

Methods:

Previous plans were used to establish the relationship between D2cc and the overlapping volume of the organ at risk with the targeted area (C0) or a 1-cm expansion of the target area (C1). Three mathematical models were evaluated: D_2cc = α*C₁ + β (LIN); D_2cc = α – exp(–β*C₀) (EXP); and a mixed approach (MIX), where both C₀ and C₁ were inputs of the model. The parameters of the models were optimized on a training set of patient data, and the predictive error of each model (predicted D_2cc − real D_2cc) was calculated on a validation set of patient data. The data of 20 patients were used to perform a K-fold cross validation analysis, with K = 2, 4, 6, 8, 10, and 20.

Results:

MIX was associated with the smallest mean prediction error <6.4% for an 18-patient training set; LIN had an error <8.5%; EXP had an error <8.3%. Best case scenario analysis shows that an error ≤5% can be achieved for a ten-patient training set with MIX, an error ≤7.4% for LIN, and an error ≤6.9% for EXP. The error decreases with the increase in training set size, with the most marked decrease observed for MIX.

Conclusions:

The MIX model can predict the D_2cc of the organs at risk with an error lower than 5% with a training set of ten patients or greater. The model can be used in the development of quality assurance tools to identify treatment plans with suboptimal sparing of the organs at risk. It can also be used to improve preplanning and in the development of real-time intraoperative planning tools.

I. INTRODUCTION

Dosimetric planning of interstitial brachytherapy has historically been performed through the use of specified source distribution rules, such as the Paterson-Parker system and the Quimby system. In recent years, gynecologic brachytherapy has gradually embraced the use of 3D imaging with Computed Tomography (CT) (Refs. ¹ and ²) or Magnetic Resonance Imaging (MR) (3 and 4) for insertions and for planning, thus shifting the focus from ICRU point doses⁵ to volume doses. In particular, the D_2cc metric has become popular for the assessment of the dose to the rectum and bladder;^6–9 D_0.1cc, D_1cc, and D_5cc have also been used for reporting and for planning in some cases.^6,7

A predictive mathematical model offers prediction of an outcome (e.g., the dose metrics of a treatment), given a number of input parameters, after optimization on prior data called a training set. In this work, we investigate the prediction error of models aimed at predicting the D_2cc for rectum and bladder in gynecologic interstitial brachytherapy based on the geometric relation between the organs at risk and targeted area, without using dose calculation tools and source position information. Predictive models for the dosimetry of organs at risk have been validated for intensity modulated external beam treatment planning,¹⁰ but to our knowledge have not been investigated for brachytherapy applications. These models can find applications as quality assurance tools and can be used for time-efficient preplanning and intraoperative dosimetric guidance. The methods described in this work may be transferrable to other brachytherapy techniques, such as intracavitary gynecologic brachytherapy and prostate brachytherapy.

II. METHODS AND MATERIALS

The CT scans and dosimetric data of 20 patients with gynecologic malignancies extending in the vagina (ten recurrent endometrial, five cervical, four recurrent vulvar, and one vaginal cancer) treated in our clinic with interstitial brachytherapy between March 2011 and March 2012 were retrospectively used in this study with IRB approval. Geometric information was obtained from the contours drawn by a single radiation oncologist contoured on CT. Dosimetric information was obtained from the dose-volume histograms of the clinical plan calculated on the same contour set.

Two data sets, one for rectum and one for bladder, were thus obtained. Each data point in a set is composed of the following information:

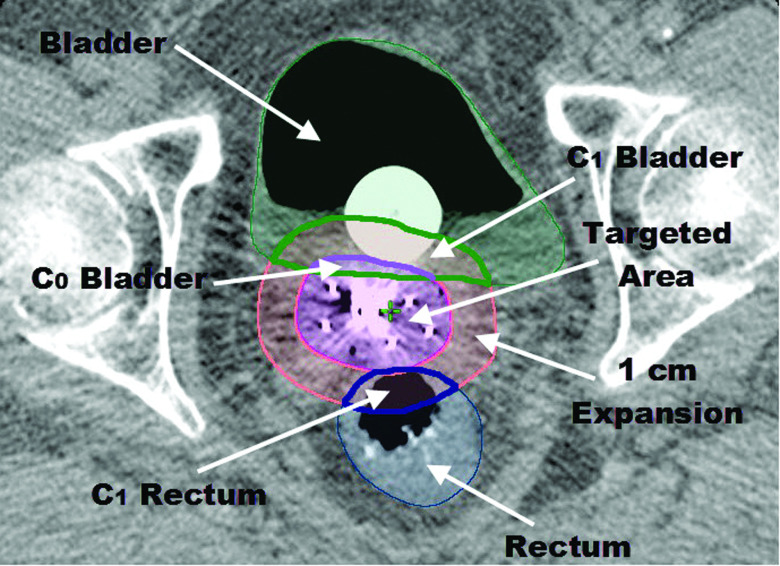
• •C₀: the volume, in cm³, of the overlap between the 100% isodose line and the organ at risk (Fig. 1);
• •C₁: the volume, in cm³, of the overlap between a 1 cm isotropic expansion of the 100% isodose line and the organ at risk (Fig. 1);
• •D_2cc: minimum dose received by the volume of 2 cm³ that receives the highest dose within the organ at risk. The D_2cc is expressed as a percentage of the prescription dose.

FIG. 1.

Example of geometrical input parameters. C₀ for the rectum is equal to zero since there is no overlap between rectum and targeted area (volume within the 100% isodose line).

C₀ and C₁ are the inputs for the models that will be discussed in this work; D_2cc is the output. Plots of the D_2cc versus C₀ and C₁ are shown in Fig. 2.

FIG. 2.

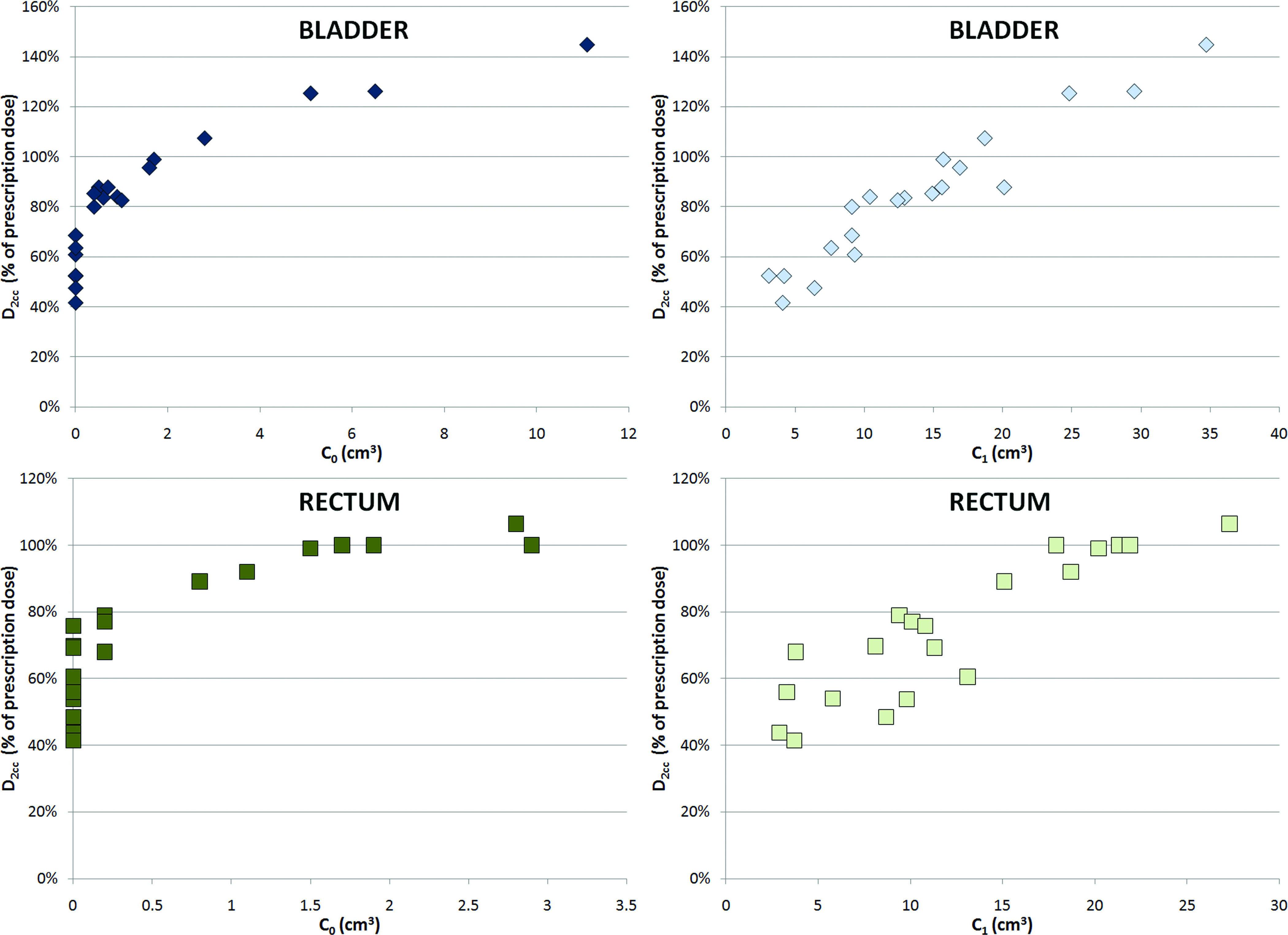
D2cc as a function of C₀ and C₁ for the bladder and rectum data sets.

A data set can be divided in two subsets: ${\{...\}}_{C_0=0}$ composed of all data points with C₀ = 0 and ${\left\{...\right\}}_{C_0>0}$, composed of all data points with C₀ > 0. The size of ${\{...\}}_{C_0=0}$ indicates the degeneracy of a data set, that is, the fact that multiple values of D_2cc are associated with the same value of C₀ across the data points in the data set.

A degeneracy of the data at C₀ = 0 was to be expected: the data points in the subset C₀ = 0 are associated with patients with no overlap between targeted area and organs at risk, which is desirable. In this study, 10 out of 20 rectum data points and 13 out of 20 bladder data points that were used for model validation belonged to their respective ${\{...\}}_{C_0>0}$, that is, had an overlap between the area receiving prescription dose and the organs at risk.

Although a degeneracy of the data at C₁ = 0 is theoretically possible, in our data set this was not observed. The 1-cm expansion of the targeted area resulted in an overlap with organs at risk in all cases.

II.A. Predictive models

Three models are proposed to predict the D_2cc of a set of validation data points (called validation set {…}_Val), of which only C₀ and C₁ are provided to the model. The models are trained based on the C₀, C₁, and D_2cc of a set of training data points (called training set {…}_Trn). In this work we will refer to the relationship between the calculated D_2cc and the input parameters C₀ and C₁ with the generic name MODEL(C₀, C₁). The index j refers to a data point in a validation set, the index i refers to a data point in a training set.

The first model is a linear model (LIN) of D_2cc as a function of C₁, that is:

$$D_{{2cc}_{LIN}}^j={\alpha }_L{C}_1^j+{\beta }_L,$$ (1)

where j ∈ {…}_Val.

The second model is an exponential model (EXP) of D_2cc as a function of C₀, that is:

$$D_{{2cc}_{EXP}}^j=1+{\alpha }_E\left(e^{-{\beta }_E·2}-e^{-{\beta }_E{C}_0^j}\right),$$ (2)

where j ∈ {…}_Val. The term $e^{-{\beta }_E·2}$ forces Eq. (2) to the trivial result that if the overlap between organ at risk and the prescription dose is equal to 2 cm³, then D_2cc must be 100%.

The parameters α and β are solutions of the following least-square optimization problem:

$$\underset{\alpha ,\beta }{\arg \min }\sum _i{\left|D_{2cc}^i-\mathrm{MODEL}\left(C_0^i,C_1^i\right)\right|}^2,$$ (3)

where i ∈ {…}_Trn.

Given the expected degeneracy of the data at C₀ = 0, we also investigated a model that is a combination of the LIN and the EXP models (MIX). Since EXP depends only on C₀, it cannot predict the differences between two data points belonging to ${\{...\}}_{C_0=0}$. Therefore, the following output was proposed:

$$\begin{array}{c}\hfill D_{{2cc}_{MIX}}^j=\left\{\begin{array}{cc}\hfill {\alpha }_L{C}_1^j+{\beta }_L& \hfill if{C}_0^j=0\\ \hfill 1+{\alpha }_E\left(e^{-{\beta }_E·2}-e^{-{\beta }_E{C}_0^j}\right)& \hfill if{C}_0^j>0\end{array},\right.\end{array}$$ (4)

where j ∈ {…}_Val. α_L, β_L and α_E, β_E are the solutions of two distinct optimization problems each optimized independently on the same {…}_Trn.

While α_L, and β_L, are solutions to the optimization problem in Eq. (3), α_E, β_E are the solutions of the following modified optimization problem:

$$\underset{{\alpha }_E,{\beta }_E}{\arg \min }\sum _i{w}_E^i·|D_{2cc}^i-1-{\alpha }_E\left(e^{-{\beta }_E·2}-e^{-{\beta }_E{C}_0^i}\right){|}^2,$$ (5a)

where i ∈ {…}_Trn. Since the EXP model depends only on C₀, it was assumed that it cannot efficiently train on ${\{...\}}_{C_0=0}$. The optimization problem presented in Eq. (3) was therefore modified by the introduction of a weight factor that decreases the importance of the training data points belonging to the degenerate set ${\{...\}}_{C_0=0}$. The weight factor was expressed as

$$w_E^i=\left\{\begin{array}{cc}\hfill w& \hfill \mathrm{if}{C}_0^i=0\\ \hfill 1& \hfill \mathrm{if}{C}_0^i>0\end{array}.\right.$$ (5b)

A different value of w was associated with each training set and was found by the following two-step optimization problem:

$$\begin{array}{ccc}& & \underset{w}{\arg \min }\sum _i|D_{2cc}^i-1-\alpha \left(w\right)\hfill \\ & & ·\left(e^{-\beta \left(w\right)·2}-e^{-\beta \left(w\right)C_0^i}\right)|:i\in \left({\{...\}}_{Trn}\cap {\{...\}}_{C_0>0}\right),\hfill \\ \\ & & \underset{\alpha \left(w\right),\beta \left(w\right)}{\arg \min }\sum _i{w}_E^i·|D_{2cc}^i-1-\alpha \left(w\right)\hfill \\ & & ·\left(e^{-\beta \left(w\right)·2}-e^{-\beta \left(w\right)C_0^i}\right){|}^2:i\in {\{...\}}_{Trn}.\hfill \end{array}$$ (5c)

Equation (5c) states that w, with (0 < w ≤ 1), is the weight needed to generate the parameters α and β (optimized over the entire training set) that provide the best linear fit to the points of the training set with C₀ > 0, given the relationship between D_2cc and C₀ described by the EXP model [Eq. (2)]. The problem in Eq. (5c) was divided in two steps because different subsets of the training set are used for the evaluation of each step: the entire training set for the evaluation of α and β (for each w), and only the patients with C₀ > 0 for the evaluation of w.

II.B. K-fold Cross-Validation

A K-Fold Cross-Validation analysis¹¹ was performed on the 20-patient data set for the validation of the predictive power of the models.

Given a subdivision λ of {…}_All into K disjointed subsets, that is ${\{...\}}_{\lambda }=\{{\left\{...\right\}}_{\lambda }^1,...,{\left\{...\right\}}_{\lambda }^{\kappa },...,{\left\{...\right\}}_{\lambda }^K\}$, of equal (if n/K is an integer number, where n = 20 is the number of data points in a set) or near-equal size, the prediction error of a model is evaluated as $p_{\lambda }^{\kappa }=\left(1/{\Sigma }_j\right){\sum }_j\left|D_{2cc}^j-\mathrm{MODEL}(C_0^j,C_1^j)\right|$, where ${\{...\}}_{Val}={\{...\}}_{\lambda }^{\kappa }$ and ${\{...\}}_{Trn}={\{...\}}_{\lambda }-{\{...\}}_{\lambda }^{\kappa }$. Repeating this calculation for every κ in {…}_λ, the prediction error p_λ of each model for a given subdivision λ is the average of $p_{\lambda }^{\kappa }$ across all K. For each subdivision λ, the relative prediction error of each model Δp_λ(MODEL₁, MODEL₂) = p_λ(MODEL₂) − p_λ(MODEL₁) is also calculated for the purpose of comparing the predictive power of the model. A negative value of Δp_λ is associated with MODEL₂ being more predictive than MODEL₁; a positive value of Δp_λ is associated with MODEL₂ being less predictive than MODEL₁.

The mean prediction error p of each model and their mean relative prediction error Δp are calculated as averages of p_λ and Δp_λ over a large number of randomly selected subdivisions λ. The lower the value of p, the more predictive is the model. The value of p is greater than or equal to 0.

A K-fold Cross-Validation provides an indicator of the prediction error of a model on a validation set of size n/K, given a training set of size n · (K − 1)/k, with n = 20. This analysis was performed for all even numbers of K from 2 to 10, and for K = 20.

The number of randomly selected subdivisions λ was 100 000. An exhaustive evaluation of all the 92 378 combinations of the twofold Cross Validation was carried out. The 20-fold Cross-Validation is equivalent to a leave-one-out analysis, with only one possible subdivision λ.

II.C. Leave-one-out restricted analysis

Results of the 20-fold Cross-Validation, which is equivalent in this work to a leave-one-out, were analyzed to evaluate the prediction error associated with data points belonging to ${\{...\}}_{C_0=0}$ and to ${\{...\}}_{C_0>0}$. Given the single possible subdivision {{1}, {2}, …, {j}, {20}}, the two quantities $R_0^j=\left|D_{2cc}^{j_0}-\mathrm{MODEL}(C_0^{j_0},C_1^{j_0})\right|$ and ${R_{+}}^j=\left|D_{2cc}^{j_{+}}-\mathrm{MODEL}(C_0^{j_{+}},C_1^{j_{+}})\right|$ were calculated, where $j_0\in ({\{...\}}_{Val}\cap {\{...\}}_{C_0=0})$ and $j_{+}\in ({\{...\}}_{Val}\cap {\{...\}}_{C_0>0})$, and their averages are called R₀ and R₊. The standard deviations of R₀^j and R₊^j are also reported.

II.D. Worst and best case scenarios

The best subdivision λ_best of the twofold Cross-Validation analysis is the subdivision associated with the lowest p; the worst subdivision λ_worst is the subdivision associated with the highest p. This information is reported to assess what the possible mean prediction error is when there is selection of the data points in {…}_Trn, and to give guidance on the possible selection of a {…}_Trn.

II.E. Programming environment

All routines were written and run in MATLAB (MathWorks, Natick, Massachusetts).

All optimization problems were solved using the trust-region-reflective algorithm in the nonlinear least-square solver provided in the Optimization Toolbox, with Jacobians of the models provided to the solver. K-fold Cross-Validation analysis was carried out using the tools provided in the Statistics Toolbox.

III. RESULTS

III.A. K-fold Cross-Validation

All mean prediction errors p are shown in Fig. 3 as a function of the average size of the training set of the K-fold, 20 · (K − 1)/K, and summarized in Table I.

FIG. 3.

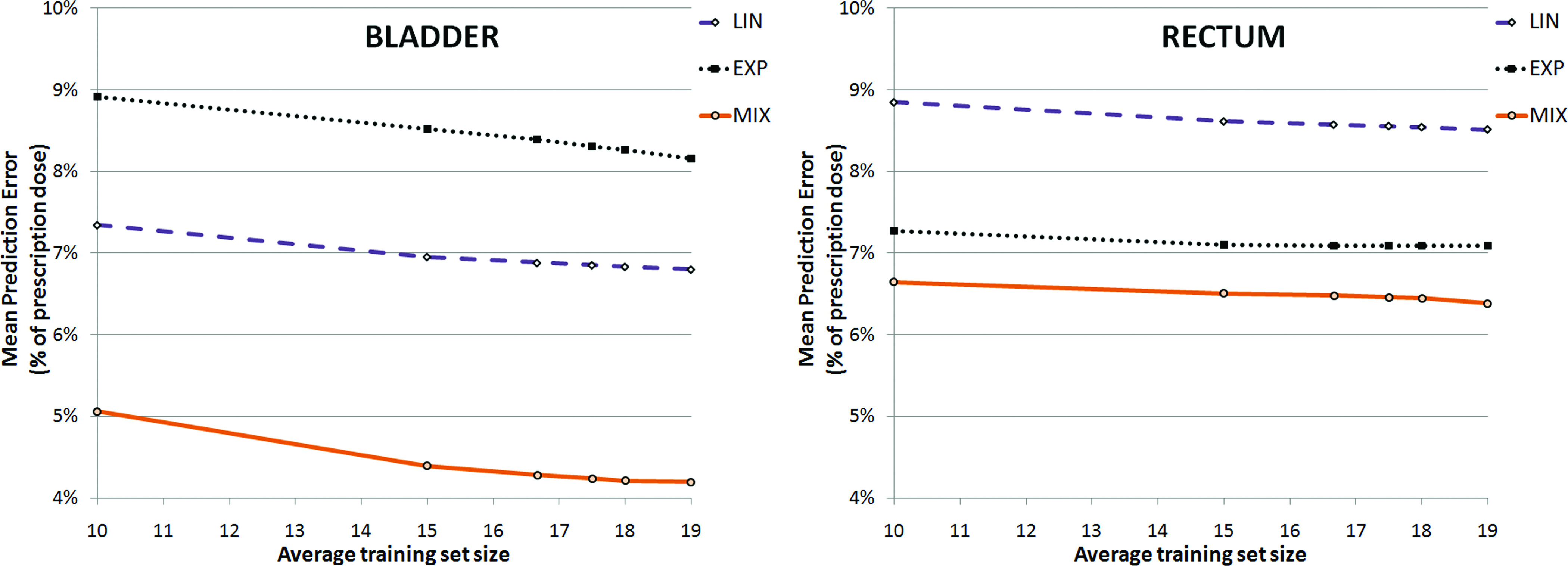
Mean prediction error of the models as a function of the average training set size, derived from K-fold Cross-Validation analysis, where the average training set size is (20·(K − 1))/K.

TABLE I.

Mean prediction error and standard deviation associated with the K-fold Cross-Validation. The standard deviation associated with the 20-fold Cross-Validation is 0, given the existence of only one partition of the total set of 20 patients into 20 folds.

K	LIN (%)	EXP (%)	MIX (%)
Bladder
2	7.3 ± 1.1	8.9 ± 1.5	5.1 ± 1.2
4	7.0 ± 0.5	8.5 ± 0.9	4.4 ± 0.5
6	6.9 ± 0.4	8.4 ± 0.6	4.3 ± 0.3
8	6.9 ± 0.4	8.3 ± 0.5	4.2 ± 0.3
10	6.8 ± 0.2	8.3 ± 0.4	4.2 ± 0.1
20	6.8 ± 0	8.2 ± 0	4.2 ± 0
Rectum
2	8.8 ± 1.0	7.3 ± 1.0	6.6 ± 0.8
4	8.6 ± 0.5	7.1 ± 0.5	6.5 ± 0.4
6	8.6 ± 0.4	7.1 ± 0.4	6.5 ± 0.4
8	8.6 ± 0.4	7.4 ± 0.7	6.5 ± 0.4
10	8.5 ± 0.2	7.1 ± 0.2	6.4 ± 0.2
20	8.5 ± 0	7.1 ± 0	6.4 ± 0

A p < 10% was observed for all models when a training set of size 10 or greater was used. Our methodology does not allow for an analysis of the prediction error for training sets of size lower than 10, given a minimum K = 2 for the K-fold Cross-Validation.

MIX was associated with the smallest mean prediction error: for the tenfold (18 size training set), p = 4.2% for bladder and p = 6.4% for rectum.

The mean relative prediction error Δp for the tenfold, between MIX and LIN, was −2.6% ± 0.3% for bladder and −2.1% ± 0.2% for rectum; between MIX and EXP, it was −4.1% ± 0.3% for bladder and −0.6% ± 0.3% for rectum. These results are consistent with the results shown in Fig. 3.

The different behavior of the MIX model between data sets, and the different relative performance of the LIN and EXP models, may be explained by two factors:

• (i)the different degeneracy of the sets at C₀ = 0, where the rectum data set has 10 of 20 data points in ${\{...\}}_{C_0=0}$ and the bladder data set has 7 of 20 data points in ${\{...\}}_{C_0=0}$;
• (ii)the different range of C₀ values in the data sets. Excluding the data points in ${\{...\}}_{C_0=0}$, the C₀ values for the rectum data set range between 0.2 and 2.9 cm³, with a mean of 1.3 ± 1.0 cm³. Excluding the data points in ${\{...\}}_{C_0=0}$, the C₀ values for the bladder data set range between 0.4 and 11.1 cm³, with a mean of 2.6 ± 3.2 cm³.

III.B. Leave-one-out restricted analysis

The leave-one-out results and the restricted analysis to ${\{...\}}_{C_0=0}$ (R₀) and to ${\{...\}}_{C_0>0}$ (R₊) are reported in Table II. The MIX model provided equal or lower prediction errors than the other models for all subgroups of patients.

TABLE II.

Leave-one-out results and restricted results to the patients with C₀ = 0 (R₀) and C₀ > 0 (R₊). Results are reported as mean prediction error for the leave-one-out analysis ± the standard deviation of the patient-by-patient leave-one-out calculation. The standard deviation associated with the 20-fold Cross-Validation is 0, given the existence of only one partition of the total set of 20 patients into 20 folds.

	Leave-one-out	R0	R+
Bladder
LIN (%)	6.8 ± 5.1	5.7 ± 6.0	7.4 ± 4.7
EXP (%)	8.2 ± 6.4	9.6 ± 7.0	7.4 ± 6.3
MIX (%)	4.2 ± 5.1	5.7 ± 6.0	3.4 ± 2.4
Rectum
LIN (%)	8.5 ± 5.7	9.3 ± 5.6	7.7 ± 5.9
EXP (%)	7.1 ± 6.1	10.4 ± 6.6	3.8 ± 3.2
MIX (%)	6.4 ± 5.3	9.3 ± 5.6	3.4 ± 3.0

One trivial result of the restricted analysis is that LIN and MIX have identical R₀ (MIX output is identical to LIN for ${\{...\}}_{C_0=0}$). LIN provided lower prediction errors than EXP for ${\{...\}}_{C_0=0}$ in both the rectum and the bladder data sets.

The weighted approach of MIX described in Eq. (5c) resulted in a lower prediction error than LIN and EXP for ${\{...\}}_{C_0>0}$ in both the rectum and the bladder data sets.

III.C. Worst and best case scenario analysis

The worst and best pair (each member of the pair called subset A and subset B) of ten-size subsets analyzed with an exhaustive twofold Cross-Validation analysis for MIX are presented in Fig. 4.

FIG. 4.

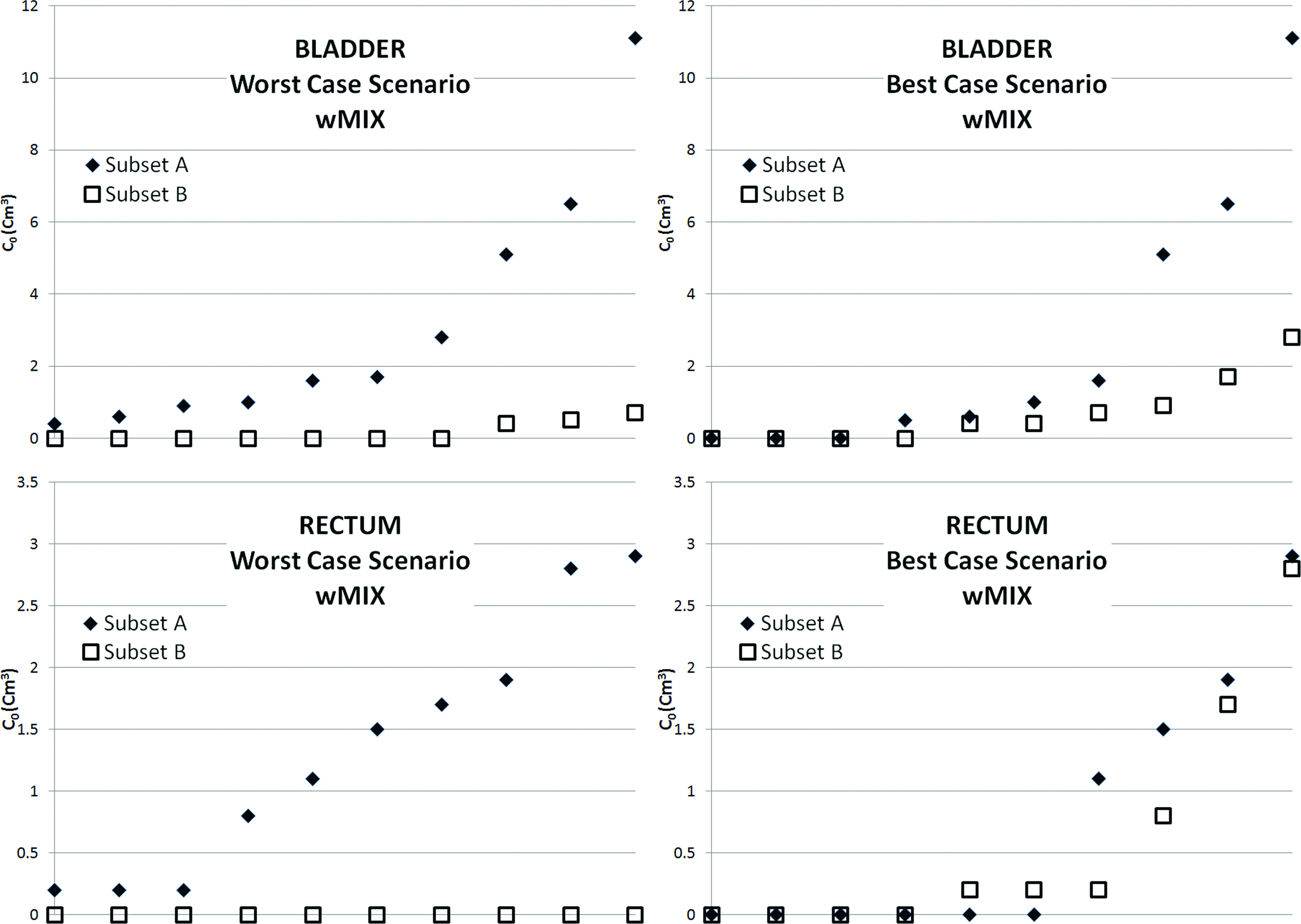
Graphical representation of the worst and best case scenarios: distribution per C₀ of the 20 data points in two sets of 10 data points. In the worst case scenarios, the points belonging to the two sets have different C₀ values. In the best case scenarios, the points belonging to the two sets have similar C₀ values.

The worst case scenario prediction error for MIX is 13.3% for the bladder data set and 12.4% for the rectum data set; for LIN it is 14.6% for the bladder data set and 20.1% for the rectum data set; for EXP it is 16.1% for the bladder data set and 13.3% for the rectum data set. This case gives an indication of the most conservative estimate of the mean prediction error if only ten patients were available to build a training set, and all ten patients are being used. Figure 4 shows that this worst case scenario is associated with training sets with very different distributions of patients between ${\{...\}}_{C_0=0}$ and ${\{...\}}_{C_0>0}$ than the data set the model needs to predict.

The best case scenario prediction error for MIX is 3.4% for the bladder data set and 5.0% for the rectum data set; for LIN it is 5.9% for the bladder data set and 7.4% for the rectum data set; for EXP it is 6.9% for the bladder data set and 5.9% for the rectum data set. This case gives an indication of the mean prediction error if ten patients were selected among a larger database of patients to form a training set specifically tailored toward the value of C₀ and C₁ in the validation set.

IV. DISCUSSION AND CONCLUSION

The results of the validation outlined in this work shows that the proposed mathematical model MIX can predict D_2cc metrics of bladder and rectum for interstitial gynecologic brachytherapy with a prediction error of less than 7% on a training set of ten patients. Proper selection of a training set may reduce the prediction error to less than 5%, and we have shown that further error reduction is possible using a training set of larger size.

These errors are below the interobserver variability errors, which have been reported to be 10% in intracavitary brachytherapy.¹² Those errors are also well below the expected interpatient variability: D_2cc ranging from 30 to 120 Gy for bladder and between 20 and 80 Gy for rectum have been reported among gynecologic interstitial brachytherapy patients.¹³

The models discussed in this work provide the D_2cc of rectum and bladder based on the overlap C₀ between the organ at risk and the area targeted by the prescription dose, and based on the overlap C₁ between the organ at risk and a 1 cm expansion of the area targeted by the prescription dose. The use of the input C₀ has the advantage of using, in the mathematical model, the trivial relationship that if exactly 2 cm³ of an organ at risk overlaps with the area covered by the prescription dose, then the D_2cc is equal to 100% of the prescription dose. However, since in clinical practice it is not in general desirable to target a portion of an organ at risk with the prescription dose, the value C₀ may be equal to 0 in many patients, resulting in a degeneracy of the data set. The targeted area expansion selected to asses C1 (1 cm) was deemed large enough to avoid a degeneracy of data at C₁ = 0, yet small enough to provide meaningful information on the geometric relationship between the organs at risk and the targeted area.

In this work we show that with proper weighting of the data in the training set for which C₀ = 0, a model based on C₀ can predict the D_2cc of patients for which C₀ > 0 with an error <3.5%. Such a model is not able to distinguish between patients for which C₀ = 0 and would result in prediction errors exceeding 10% in this subgroup. A model based on C₁ is in general able to capture the difference between patients for which C₀ = 0. The prediction error of a model based on C₁ for the patients for which C₀ = 0 is <10%. C₀ and C₁ are both input parameters in MIX, and the output will depend on C₀ if the model is predicting a patient for which C₀ > 0, and on C₁ if the model is predicting a patient for which C₀ = 0.

For the prediction of patients for which C₀ = 0, no differential weighting between training patients depending on their value of C₀ or C₁ was proposed in this work. It is possible that further reduction of the prediction error is possible with such an approach. Another possible avenue for future development is the development of models weighting the training sets based on subsets C > C_th and C < C_th, where C is C₀ or C₁, and C_th is a given threshold (in cc). The value of C_th would need to be dynamically assessed for each training set, and it is likely that a set of data larger than the one currently available will be needed for validation. A similar limitation would likely apply to the development of a model which does not separate the dependency on C₀ and C₁ but is a pure two-parameter model. We are increasing the size of our data sets and will address these different options in future work.

Depending on the application, the targeted area used for the calculation of the overlaps can be changed to the area receiving a lower percentage of the prescription dose. This can be done in an effort to reduce the degeneracy of the data at C₀ = 0. In this use, the models would provide the D_2cc as a percentage of the isodose line used to calculate the overlapping areas. This approach can be considered only in applications where the knowledge of the full dose matrix is assumed, as in the quality assurance of treatment plans.¹⁰ This approach cannot be used in applications such as dosimetric guidance during the implantation, where the targeted area would likely be delineated by the radiation oncologist and the behavior of the dose fall-off would not be known.

The model described in this work can be used as a component of a quality assurance tool to detect suboptimal treatment plans in the sparing of the organs at risk. Given the area that is targeted by the prescription dose, or a lower isodose line, a properly trained model will provide an estimate of the dose to the organs at risk that is expected with proper planning and will detect outliers that need further review. A similar quality assurance tool has been described for IMRT planning.¹⁰ Care should be taken in building a training set formed by patient data that is considered a “gold-standard.” This can be achieved through a mechanism to automatically detect and remove outlier data from a database of patient data,¹⁰ or through manual selection of patient data based on the expertise of an experienced radiation oncologist and physicist, or through a mix of the two approaches. Training sets provided by large academic institutions, or resulting from the pooling of multiple institutions, can be made available for the quality assurance of small institutions that do not routinely perform interstitial gynecologic brachytherapy or for institutions that are just starting the practice.

The scope of the quality assurance/quality control provided by the mathematical models discussed in this work is confined to organs-at-risk dosimetry compared with a clinic practice given a 100% isodose line. Compliance with clinically acceptable thresholds for rectum and bladder D_2cc should be independently verified. Moreover, differences between CTV and the area included in the 100% isodose line should also be independently checked. Methodologies such as careful visual inspection of the isodose lines and analysis of CTV D₉₀, D₉₈, V₁₀₀, and conformity index may be considered.

Another possible application of the mathematical models discussed in this work is as a part of a preplanning tool. Preplanning is the practice of simulating an interstitial or intracavitary insertion on an available image set of a patient, before the day of the insertion. This practice is used both in gynecologic brachytherapy⁸ and in prostate brachytherapy.¹⁴ The models proposed can provide an indication of the dosimetry of the organs at risk without a need to recreate a full clinical plan. This will have the advantage of saving clinical resources, as it will reduce the time for planning to only the coverage of the targeted area, without proceeding to a fine tuning of the doses to the organs at risk. If a clinic-specific training set is used, the dosimetry predicted by the model may better predict the dosimetry that will be generated under clinical conditions (e.g., under time pressure) than a preplan dosimetry.

Real-time dosimetric guidance, or real-time intraoperative planning, refers to the practice of providing information on the expected dosimetry resulting from an implantation as the procedure is occurring, therefore allowing for corrections or additions to ensure correct coverage of the target and sparing of the organs at risk. Software systems allowing intraoperative planning are commercially available for ultra-sound guided prostate brachytherapy insertion and systems based on MR guidance have also been described.¹⁵ Those techniques have not been widely implemented in gynecologic HDR brachytherapy due to the difficulty of developing and adjusting a treatment plan without greatly increasing the procedure time. The models proposed in this work can be used as one of the building blocks to obtain dosimetric guidance without the need for recreating a real-time plan, thus enabling real-time dosimetric guidance during the insertion by eliminating the need for online planning.

Preplanning or real-time guidance would likely be performed by using the clinical target volume as the targeted area. In this work, we assumed that the training sets are composed of the actual targeted area contained in the 100% isodose line. Depending on a clinic's practice, there may be situations where the clinical target volume has areas of overlap with the organs at risk that are larger than any data point in the training set. Although the results of the models may in this situation be less accurate, the general result of organs at risk exceeding tolerance previously accepted in the clinic would still be provided. We envision that in these cases, the radiation oncologist may iteratively provide to the model an adjusted targeted area, until a compromise between coverage of the clinical target volume and organs-at-risk dosimetry is found.

The application of these models for the prediction of D_5cc, D_1cc, D_0.5cc, and D_0.1cc is possible but necessitates an independent validation to establish the associated prediction error. The mathematical models discussed in this work may find application beyond interstitial gynecologic brachytherapy. Applications of these models to intracavitary and hybrid intracavitary-interstitial gynecologic brachytherapy, as well as low-dose-rate and high-dose-rate prostate brachytherapy can be considered after proper validation.