Abstract
Predicting the interactions between drugs and targets plays an important role in the process of new drug discovery, drug repurposing (also known as drug repositioning). There is a need to develop novel and efficient prediction approaches in order to avoid the costly and laborious process of determining drug–target interactions (DTIs) based on experiments alone. These computational prediction approaches should be capable of identifying the potential DTIs in a timely manner. Matrix factorization methods have been proven to be the most reliable group of methods. Here, we first propose a matrix factorization-based method termed ‘Coupled Matrix–Matrix Completion’ (CMMC). Next, in order to utilize more comprehensive information provided in different databases and incorporate multiple types of scores for drug–drug similarities and target–target relationship, we then extend CMMC to ‘Coupled Tensor–Matrix Completion’ (CTMC) by considering drug–drug and target–target similarity/interaction tensors. Results: Evaluation on two benchmark datasets, DrugBank and TTD, shows that CTMC outperforms the matrix-factorization-based methods: GRMF, 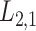 -GRMF, NRLMF and NRLMF
-GRMF, NRLMF and NRLMF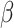 . Based on the evaluation, CMMC and CTMC outperform the above three methods in term of area under the curve, F1 score, sensitivity and specificity in a considerably shorter run time.
. Based on the evaluation, CMMC and CTMC outperform the above three methods in term of area under the curve, F1 score, sensitivity and specificity in a considerably shorter run time.
Keywords: drug–target interaction, matrix factorization, matrix completion, coupled matrix–matrix, coupled matrix–tensor
1 Introduction
One major class of in silico drug–target interaction (DTI) prediction methods is machine learning methods that compensate for the lack of 3D structures of drugs and targets in order to identify any potential binding events. Although in vitro experiments are the ultimate step in the drug discovery process, computational predictions are essential to avoid expensive and laborious lab experiments early in the process. To this end, machine learning and other prediction methods have been developed since the early pharmacological DTI predictions [3].
Many DTI prediction methods incorporate drug–drug or target–target structural relationships via ‘Similarity/Distance-Based Methods’. The main disadvantages of this approach are that they are sensitive to the fact that only a small percent of drugs have known interactions and some data sets are of binary nature, even though drug–target binding affinities are continuous in nature. Another family of solutions are the ‘Network-Based Methods’ that utilize graph-based techniques to perform DTI prediction. Although some methods use three networks of protein–protein similarity, drug–drug similarity and known DTIs in a heterogeneous network, they tend to perform poorly in DTI discovery; this may be due to the fact that the properties of DTI networks are not favorable for such methods [6, 13]. ‘Feature-Based Methods’ have recently been used in DTI prediction tasks; these include support vector machines, tree-based methods and other kernel based methods used with 3D protein structures. Any drug–target pair can be represented in terms of a feature vector, often with binary labels, and a machine learning method used to classify the pair vectors into positive or negative interacting proteins prevents extracting the main features disadvantaging performance. To deal with high-dimensional and noisy data in DTI predictions, several ‘Deep Learning Methods’ have been proposed (e.g. [27, 33]). The main disadvantages of these methods are that a great deal of training data and high computational power are required to train the complex model. Additionally, they lack the transparency in interpreting results and performance issues. The ‘Matrix Factorization Methods’, as another family of methods used in DTI, aim to find two matrices,  and
and 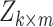 , whose multiplication gives the interaction matrix
, whose multiplication gives the interaction matrix 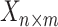 with
with 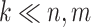 . It is assumed that the drugs and targets lie in the same distance space such that the distance among drugs and targets can be used to measure the strength of their interactions. Therefore, drugs and targets can be embedded in a common low-dimensional subspace (see [16, 28]). Matrix factorization and matrix completion have been reported to be the most reliable methods among all the other methods based on their performance ([1, 8]); however, they are not able to incorporate all the available information about the drugs and targets.
. It is assumed that the drugs and targets lie in the same distance space such that the distance among drugs and targets can be used to measure the strength of their interactions. Therefore, drugs and targets can be embedded in a common low-dimensional subspace (see [16, 28]). Matrix factorization and matrix completion have been reported to be the most reliable methods among all the other methods based on their performance ([1, 8]); however, they are not able to incorporate all the available information about the drugs and targets.
In the current Big Data era, there exist numerous examples of the ‘matrix completion problem’: impute/predict the missing values of a matrix, given an incomplete matrix with values that are noisy and potentially corrupt [5]. A common application is for ‘recommender systems’ such as the ‘Netflix Prize’ [21]. Prediction of the missing values has been an active area of research, resulting in methods such as ‘Singular Value Thresholding’ [4], ‘Fixed Point Continuation’ [18] and ‘Matrix Factorization’ [30]. However, these methods ignore supporting data that could be integrated with the main matrix.
A main challenge in DTI prediction using matrix-based method is to perform the completion task of the sparse matrices of drugs, 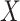 , targets,
, targets, 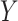 , along with their interactions,
, along with their interactions, 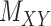 , (shown in Fig. 1) that are central to the field of drug repositioning (a.k.a. drug repurposing). To address the true structure of many real applications, the proposed matrix completion method has been expanded using the following steps: (1) ‘Coupled Matrix–Matrix Completion’ (CMMC): The matrix completion problem is expanded to cases where the matrix
, (shown in Fig. 1) that are central to the field of drug repositioning (a.k.a. drug repurposing). To address the true structure of many real applications, the proposed matrix completion method has been expanded using the following steps: (1) ‘Coupled Matrix–Matrix Completion’ (CMMC): The matrix completion problem is expanded to cases where the matrix  is coupled with additional structural information on the attributes X and Y involved in the matrix, such as a matrix
is coupled with additional structural information on the attributes X and Y involved in the matrix, such as a matrix  expressing functional similarities of different drugs, and a matrix
expressing functional similarities of different drugs, and a matrix  expressing relations among the targets. It is highly desirable to directly integrate the drug–drug similarity and target–target relation matrices (which may also be sparse themselves) in completion of the sparse DTIs (see Figure 1).
expressing relations among the targets. It is highly desirable to directly integrate the drug–drug similarity and target–target relation matrices (which may also be sparse themselves) in completion of the sparse DTIs (see Figure 1).
Figure 1 .
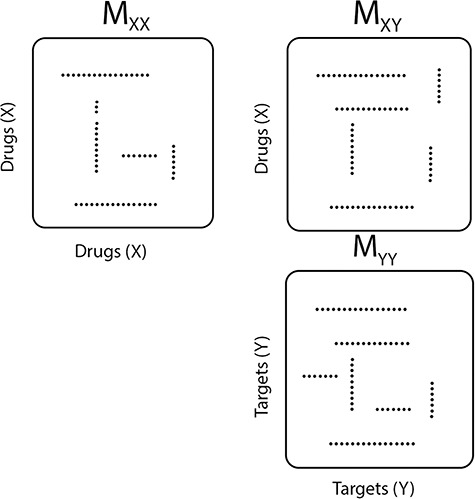
An illustration of a sparse coupled drug–drug, 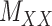 , drug–target,
, drug–target, 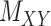 and targettarget,
and targettarget, 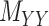 , matrices representing the interactions.
, matrices representing the interactions.
(2) ‘Coupled Tensor–Matrix Completion’ (CTMC): The similarity matrices 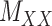 and
and 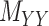 can often be calculated in complementary ways based on different criteria, resulting in multiple
can often be calculated in complementary ways based on different criteria, resulting in multiple 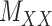 ’s and
’s and 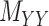 ’s (see Figure 2). For instance, the drug–drug similarities can be assessed using different structural and functional characteristics and in different chemical environments. When completing the matrix
’s (see Figure 2). For instance, the drug–drug similarities can be assessed using different structural and functional characteristics and in different chemical environments. When completing the matrix 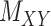 in these situations, instead of matrices
in these situations, instead of matrices 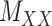 and
and 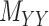 , one must deal with tensors (in this case 3-dimensional arrays)
, one must deal with tensors (in this case 3-dimensional arrays) 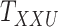 and
and 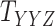 where
where 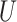 and
and 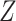 represent the number of different contexts for
represent the number of different contexts for 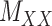 and
and 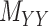 , respectively. A major current challenge in data science is that existing algorithms fail to use the highly important structural correlations within tensors. Therefore, prediction/estimation of the missing values in
, respectively. A major current challenge in data science is that existing algorithms fail to use the highly important structural correlations within tensors. Therefore, prediction/estimation of the missing values in 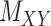 or
or 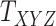 while considering all structural relations is a much more practically important problem and can be termed as CTMC. To evaluate the proposed methods, we use cross-validation to compare them with three other state-of-the-art methods, namely GRMF [9], NRLMF
while considering all structural relations is a much more practically important problem and can be termed as CTMC. To evaluate the proposed methods, we use cross-validation to compare them with three other state-of-the-art methods, namely GRMF [9], NRLMF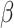 [2] and
[2] and 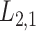 -GRMF [7].
-GRMF [7].
Figure 2 .
An illustration of a sparse coupled drug–drug tensor,  , drug–target matrix,
, drug–target matrix,  and target–target tensor,
and target–target tensor,  , matrices representing the interactions.
, matrices representing the interactions.
The rest of the manuscript is organized as follows: brief descriptions of the three competing state-of-the-art methods are provided in Section 2. Section 3 describes information about the datasets used in our work, followed by Section 4, which explains our proposed methods. We then present the experimental results of our work and provide relevant discussion in Section 5 and conclude in Section 6.
2 Related work
In Big Data applications it is common that data are sparse (mostly zeros) and partially missing. Missing data imputation, especially in the context of sparse noisy data, is therefore a central problem. A common situation is a matrix with missing entries under the assumption that the completed matrix has low rank. The low-rank matrix completion problem is NP hard and highly non-convex [11], but there are various algorithms that work under certain assumptions on the data; for instance, one approach to low-rank matrix completion is to use the nuclear norm as a convex relaxation of the matrix rank and use semi-definite programming to find a completion that minimizes the nuclear norm (see [5, 10]). Other approaches use matrix factorization with non-convex optimization such as alternating minimization ([14]) or gradient descent ([24]).
Here, we have considered four methods, two of which are based on graph regularization that are generally used in order to fully consider the internal structure of the drug–drug and target–target similarity matrices while keeping them unchanged; another two use specific probability, in particular distribution, functions in order to perform the task of DTI prediction. Moreover, a preprocessing step has been employed in order to deal with the sparsity of the interaction matrices.
2.1 GRMF
GRMF is a two-step method proposed in [9] using weighted 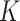 nearest known neighbors (WKNKN) as a preprocessing step and graph regularized matrix factorization (GRMF) for predicting DTIs. WKNKN is used to transform the binary into interaction likelihood values in the given drug–target matrix. Given the drug–target matrix
nearest known neighbors (WKNKN) as a preprocessing step and graph regularized matrix factorization (GRMF) for predicting DTIs. WKNKN is used to transform the binary into interaction likelihood values in the given drug–target matrix. Given the drug–target matrix 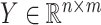 , where
, where 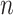 and
and 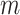 denote the number of drugs and targets, respectively, the algorithm returns the
denote the number of drugs and targets, respectively, the algorithm returns the 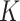 nearest known neighbor in descending order based on their similarities to the
nearest known neighbor in descending order based on their similarities to the 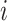 th drug,
th drug, 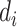 , or the
, or the 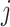 th target,
th target, 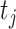 . Next, the authors derived a
. Next, the authors derived a 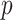 -nearest neighbor graph from the drug similarity matrix,
-nearest neighbor graph from the drug similarity matrix, 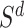 , and target similarity matrix,
, and target similarity matrix, 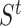 . Based on the given
. Based on the given 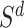 , a
, a 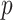 -nearest neighbor graph
-nearest neighbor graph 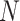 is then generated in the form:
is then generated in the form:
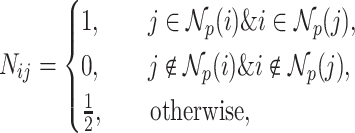 |
(1) |
for any 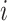 and
and 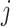 , where
, where 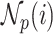 denotes the set of
denotes the set of 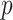 nearest neighbor to drug
nearest neighbor to drug 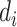 . GRMF minimizes the objective function
. GRMF minimizes the objective function
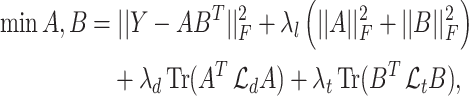 |
(2) |
where 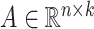 and
and 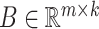 are two low-rank latent features matrices for drugs and targets, respectively, which approximates the decomposition matrix
are two low-rank latent features matrices for drugs and targets, respectively, which approximates the decomposition matrix 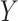 . For more explanation of the method, we refer the reader to [9]. It follows by a regularization step to prevent overfitting and a normalization step to enhance the performance.
. For more explanation of the method, we refer the reader to [9]. It follows by a regularization step to prevent overfitting and a normalization step to enhance the performance.
2.2 L2,1-GRMF
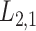 -GRMF is an improved GRMF method to address the issue that the datasets are often located at or near a low-dimensional nonlinear manifold, in combination with the previous matrix-decomposition method. To this end, authors in [7] use the Euclidean distance,
-GRMF is an improved GRMF method to address the issue that the datasets are often located at or near a low-dimensional nonlinear manifold, in combination with the previous matrix-decomposition method. To this end, authors in [7] use the Euclidean distance, 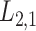 , to calculate the nearest neighbor. Next, the interaction matrix
, to calculate the nearest neighbor. Next, the interaction matrix 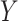 is decomposed into two low-rank latent feature matrices
is decomposed into two low-rank latent feature matrices 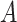 and
and 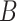 such that
such that 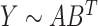 and the objective function is written as follows:
and the objective function is written as follows:
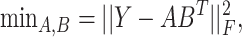 |
(3) |
where 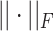 denotes the Frobenius norm with the
denotes the Frobenius norm with the 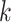 number of potential features of
number of potential features of 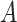 and
and 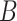 .
.
2.3 NRLMF
NRLMF [17] is one of the drug–target prediction methods based on a matrix factorization technique and is one of the state-of-the-art method. NRLMF method focuses on predicting the probability that a drug would interact with a target. Specifically, the properties of a drug and a target are represented by two latent vectors in the shared low-dimensional latent space, respectively. As such, the properties of a drug 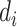 and a target
and a target 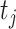 are described via two latent vectors
are described via two latent vectors 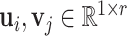 where
where 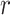 represents the dimension of the shared latent space to which both drugs and targets are mapped. The authors in [17] model the interaction probability
represents the dimension of the shared latent space to which both drugs and targets are mapped. The authors in [17] model the interaction probability 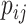 of the drug–target pair,
of the drug–target pair, 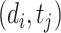 using the following logistic function:
using the following logistic function:
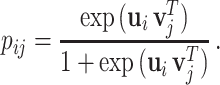 |
(4) |
The final DTI prediction model then is formulated by considering the DTIs as well as the neighborhood of drugs and targets.
2.4 NRLMF β
NRLMF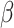 [2] is an algorithm that assigns to any score of NRLMF (see Section 2.3) a new score, based on the expected value of the beta distribution defined by
[2] is an algorithm that assigns to any score of NRLMF (see Section 2.3) a new score, based on the expected value of the beta distribution defined by
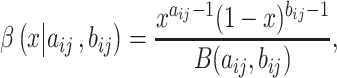 |
(5) |
where 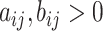 denote the shape parameters of the beta distribution, and
denote the shape parameters of the beta distribution, and 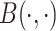 represents the beta function [31]. The beta distribution is determined based on interaction information and current NRLMF score and is also known as the conjugative prior for the Bernoulli distribution [31] used in NRLMF and can reflect the amount of interaction information for the NRLMF
represents the beta function [31]. The beta distribution is determined based on interaction information and current NRLMF score and is also known as the conjugative prior for the Bernoulli distribution [31] used in NRLMF and can reflect the amount of interaction information for the NRLMF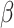 score. Likewise, GRMF and
score. Likewise, GRMF and 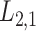 -GRMF, given the interaction matrix
-GRMF, given the interaction matrix 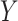 , new scores are utilized to calculate
, new scores are utilized to calculate 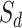 , and
, and 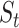 , drug similarity and target similarity matrices.
, drug similarity and target similarity matrices.
3 Data
For evaluation of our proposed methods, we used two benchmark datasets: 1) Data extracted from DrugBank [32], one of the most popular databases that is widely used as a drug reference resource. This database was first released in 2006, and a database both in bioinformatics and cheminformatics, DrugBank contains detailed drug data with comprehensive drug–target information. The DTI relationships in DrugBank are originally collected from textbooks, published articles and other electronic databases. All data can be freely downloaded from DrugBank. 2) Data extracted from Therapeutic Target Database (TTD) [29], which provides therapeutic proteins, nucleic acid targets and corresponding drug information. This database was first described in 2002 and data in TTD were mainly collected from the literature.
3.1 DrugBank
In order to establish the DTI matrix, a total of six matrices were created. In doing so, a total of 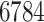 drugs with at least one polypeptide target and
drugs with at least one polypeptide target and 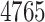 polypeptide targets that are targeted by those drugs were extracted. They form a matrix of size
polypeptide targets that are targeted by those drugs were extracted. They form a matrix of size 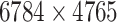 whose density is
whose density is 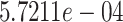 . This represents a sparsity of
. This represents a sparsity of 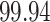 %.
%.
As it is thoroughly discussed in Section 4, multidimensional arrays (tensors) are used to evaluate the performance of the proposed methods. In order to create higher order arrays in the form of drug–drug tensors, the following slices were created:
Drug–drug interaction of every pair of the
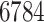 drugs, as available in the DrugBank Database,
drugs, as available in the DrugBank Database,Drug–drug similarity as calculated by the ‘Morgan Fingerprint’ score [25] provided by the RDKit Python package [15],
Drug–drug similarity as calculated by the topological torsion score [22] also provided by the RDKit Python package.
The information for the target–target interaction are obtained based upon the assumption that the interactions between targets are transitive; i.e. if protein 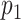 is similar to protein
is similar to protein 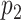 , which interacts with protein
, which interacts with protein 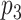 , then protein
, then protein 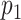 may also interact with protein
may also interact with protein 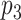 . The following matrices are used in order to create the target–target tensor array:
. The following matrices are used in order to create the target–target tensor array:
The binary target–target interaction information of every pair of the
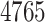 polypeptide targets, as provided by BioGrid
polypeptide targets, as provided by BioGrid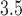 [26],
[26],The target–target similarity score of every pair of the
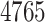 polypeptides, as defined by the inverse of ‘Jukes–Cantor’ distance [12].
polypeptides, as defined by the inverse of ‘Jukes–Cantor’ distance [12].
Jukes–Cantor distance computes the maximum likelihood estimate of the number of substitutions between two sequences with the method 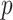 -distance, which is proportion of sites at which the two sequences are different.
-distance, which is proportion of sites at which the two sequences are different. 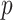 is close to 1 for poorly related sequences and is close to 0 for similar sequences. The similarity score was taken as an inverse of Jukes–Cantor distance [12].
is close to 1 for poorly related sequences and is close to 0 for similar sequences. The similarity score was taken as an inverse of Jukes–Cantor distance [12].
The entries of all the matrices are min–max normalized to 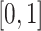 . All the matrices are symmetric with respect to the main diagonal. Therefore, each entry of the main diagonal of each matrix is 1. Table 1 summarizes the characteristics of the dataset created and all the information pertaining to the dataset are made available in supplementary materials (see Section 7).
. All the matrices are symmetric with respect to the main diagonal. Therefore, each entry of the main diagonal of each matrix is 1. Table 1 summarizes the characteristics of the dataset created and all the information pertaining to the dataset are made available in supplementary materials (see Section 7).
Table 1 .
Summary of datasets
| Matrices | Notation | Dimension | Source |
|---|---|---|---|
| Drug–Target Interaction |
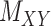
|
|
DrugBank [32] |
| Drug–Drug Interaction |
|
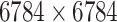
|
DrugBank [32] |
| Drug–Drug Similarity: Morgan fingerprint |
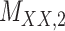
|
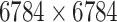
|
Structure: DrugBank [32] Score: [25] |
| Drug–Drug Similarity: topological torsion |
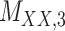
|
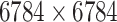
|
Structure: DrugBank [32] Score: [22] |
| Target–Target Interaction |
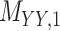
|
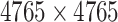
|
Biogrid [26] |
| Target–Target Similarity |
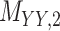
|
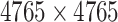
|
Sequence: DrugBank [32] Score: Inverse of Jukes–Cantor [12] |
| Drug–Target Interaction |
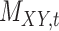
|
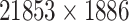
|
TTD [29] |
| Drug–Drug Similarity: Morgan fingerprint |
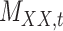
|
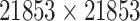
|
Structure: TTD [29] Score: [25] |
| Target–Target Similarity |
|
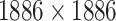
|
TTD [29] Score: Inverse of Jukes–Cantor [12] |
3.2 TTD
We also evaluated our proposed CMMC method on TTD [29]. A total of 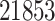 drugs were selected, along with
drugs were selected, along with 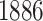 protein targets, with
protein targets, with 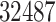 DTIs and from a matrix of density
DTIs and from a matrix of density 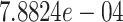 . Similar to those for DrugBank dataset, we calculated drug–drug similarity score using the Morgan Fingerprint score [25] and the target–target similarity score using inverse of Jukes–Cantor distance [12].
. Similar to those for DrugBank dataset, we calculated drug–drug similarity score using the Morgan Fingerprint score [25] and the target–target similarity score using inverse of Jukes–Cantor distance [12].
4 Methods
In the proposed method, we develop the theoretical framework necessary to create scalable algorithms for coupled matrix–matrix and tensor–matrix completion. These algorithms are applicable to the general case in which the coupled matrices/tensors are sparse themselves. The algorithms are tested against DTI databases for which the details are provided in Section 3. It is noteworthy that the performance of these algorithms in the task of drug repositioning should be evaluated by expert clinicians and their reliability of the results should be confirmed. To this end, we start by introducing the representation theory of reductive groups [20], which provides the basis for the proposed completion algorithms, as well as providing theoretical guarantees on the optimality of our solutions.
A reductive group in general is a linear algebraic group over a field satisfying certain conditions. Let 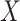 be a real or complex vector space, then the general linear group,
be a real or complex vector space, then the general linear group, 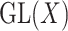 , and special linear group,
, and special linear group, 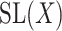 , are reductive groups and so are the products of reductive groups. In general,
, are reductive groups and so are the products of reductive groups. In general, 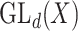 is the set of
is the set of 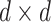 invertible matrices over
invertible matrices over 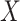 , together with the ‘matrix multiplication’ operation and
, together with the ‘matrix multiplication’ operation and 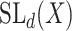 is a subset of
is a subset of 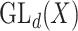 consisting of those elements whose determinants are 1. An
consisting of those elements whose determinants are 1. An 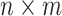 real matrix can be thought of as an element in
real matrix can be thought of as an element in
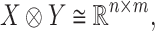 |
where 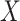 and
and 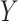 are vector spaces of dimension
are vector spaces of dimension 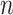 and
and 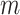 , respectively. The group
, respectively. The group 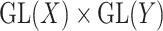 acts on the space
acts on the space 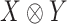 by
by
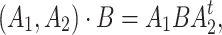 |
where 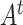 is the transpose of matrix
is the transpose of matrix 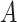 . The group
. The group 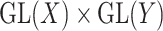 acts by linear transformations, meaning that
acts by linear transformations, meaning that 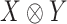 is a ‘representation’ of the reductive group
is a ‘representation’ of the reductive group 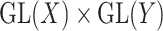 . The space of symmetric
. The space of symmetric 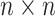 matrices can be identified with the space of symmetric tensors
matrices can be identified with the space of symmetric tensors 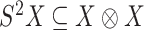 . The group
. The group 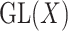 acts on a symmetric matrix
acts on a symmetric matrix 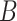 by
by
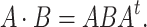 |
An 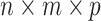 tensor (i.e. a multi-dimensional array) is an element in the representation
tensor (i.e. a multi-dimensional array) is an element in the representation 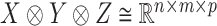 of the reductive group
of the reductive group 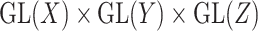 , where
, where 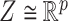 . For a coupled matrix–tensor, we get the representation
. For a coupled matrix–tensor, we get the representation
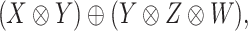 |
of the group 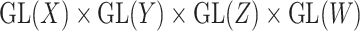 . Using the above framework, the CMMC problem depicted in Figure 1 can be identified with the representation
. Using the above framework, the CMMC problem depicted in Figure 1 can be identified with the representation
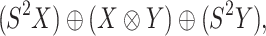 |
whereas the CTMC problem depicted in Figure 2 can be represented by
 |
of the group 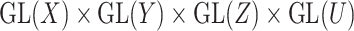 . These reformulation of the problem induces metrics with which the sparse matrices could be optimally completed. For the remainder of the section, we assume that the data under consideration lie in a representation
. These reformulation of the problem induces metrics with which the sparse matrices could be optimally completed. For the remainder of the section, we assume that the data under consideration lie in a representation 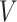 of a reductive group
of a reductive group 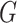 .
.
4.1 Determining optimal metrics for CMMC and CTMC
Most methods for matrix and tensor completion rely upon the choice of a fixed metric, such as the Euclidean or nuclear norm. If there is a high correlation between the rows/columns in a matrix, or between different tensor slices, then a different metric given by the data itself could be adopted. For a machine learning problem including data points in 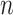 -dimensional space,
-dimensional space, 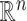 , ‘Mahalanobis distance’ [19], which is computed from the covariance matrix of the data, could also be utilized. Equivalent to the Mahalanobis distance is using the Euclidean metric ‘after’ a linear change of coordinates that normalizes the covariance matrix of the data to the identity. A proper action on group
, ‘Mahalanobis distance’ [19], which is computed from the covariance matrix of the data, could also be utilized. Equivalent to the Mahalanobis distance is using the Euclidean metric ‘after’ a linear change of coordinates that normalizes the covariance matrix of the data to the identity. A proper action on group 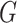 could perform the change of coordinates in the vector space
could perform the change of coordinates in the vector space 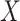 such that it preserves the mathematical structure of the data. The ‘Kempf–Ness’ theorem (see below, [23]) shows that there is essentially a unique change of coordinates that is optimal in a certain sense. It is known that the group
such that it preserves the mathematical structure of the data. The ‘Kempf–Ness’ theorem (see below, [23]) shows that there is essentially a unique change of coordinates that is optimal in a certain sense. It is known that the group 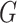 has a unique maximal compact subgroup
has a unique maximal compact subgroup 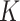 . The space
. The space 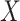 has some Euclidean metric and without loss of generality one may assume that
has some Euclidean metric and without loss of generality one may assume that 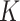 is contained in the orthogonal group
is contained in the orthogonal group 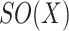 .
.
Theorem 1.
Consider the map
given by
, then either
does not have a critical point, or every critical point is a minimum and the set of critical points is a coset,
, for some
.
The theorem implies that there is a unique optimal metric, which is the Euclidean metric after the change of coordinates given by 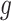 . The action of
. The action of 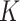 does not change the metric. To avoid a degenerated case, in the absence of any critical point, one may choose a slightly smaller reductive group
does not change the metric. To avoid a degenerated case, in the absence of any critical point, one may choose a slightly smaller reductive group 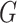 instead (e.g.
instead (e.g. 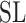 instead of
instead of 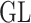 ) or utilize a regularization that is compatible with the representation theory setup. Thus, the choice of
) or utilize a regularization that is compatible with the representation theory setup. Thus, the choice of  determines the optimal metric that can be used to solve the CMMC and CTMC problems.
determines the optimal metric that can be used to solve the CMMC and CTMC problems.
The next step is to determine the optimal metric for CMMC and CTMC. Assuming  data points
data points 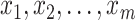 in
in 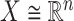 with respective mean
with respective mean 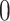 and an invertible covariance matrix
and an invertible covariance matrix 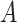 , then
, then 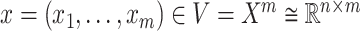 and the function
and the function 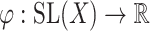 , defined by
, defined by 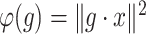 , has a critical point, namely
, has a critical point, namely 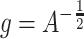 . The optimal metric is exactly the Mahalanobis distance. However, if the data points
. The optimal metric is exactly the Mahalanobis distance. However, if the data points 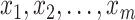 are not thus distributed, then a better choice of
are not thus distributed, then a better choice of 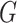 yields a more optimal metric. Determining an optimal choice of
yields a more optimal metric. Determining an optimal choice of 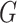 for CMMC induces a metric and regularization terms that are directly used in the algorithm. Given a tensor
for CMMC induces a metric and regularization terms that are directly used in the algorithm. Given a tensor 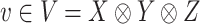 , one can optimize
, one can optimize
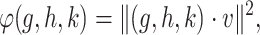 |
(6) |
for 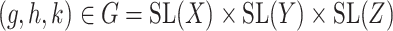 , using alternating optimization: first optimizing for
, using alternating optimization: first optimizing for 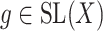 while fixing
while fixing 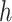 and
and 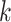 followed by optimizing
followed by optimizing 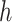 having
having 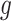 and
and 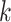 fixed and lastly, optimizing
fixed and lastly, optimizing 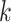 while fixing
while fixing 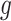 and
and 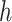 , until the desired convergence. Each optimization step reduces to the case of
, until the desired convergence. Each optimization step reduces to the case of 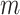 data points
data points 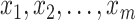 in
in 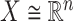 with mean
with mean 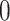 and an invertible covariance matrix
and an invertible covariance matrix 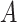 , which was discussed above. It can be shown that this procedure converges to an optimal solution and in practice only a few iterations are needed.
, which was discussed above. It can be shown that this procedure converges to an optimal solution and in practice only a few iterations are needed.
In the CTMC case, there are more potential choices for 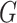 that may yield a more optimal metric. For example
that may yield a more optimal metric. For example  or
or 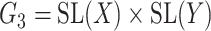 .
.
4.2 Developing the CMMC and CTMC algorithms
Assuming the actual data for 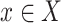 are not known yet
are not known yet 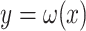 , where
, where 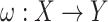 is a projection map, is given. In order to estimate the missing data,
is a projection map, is given. In order to estimate the missing data, 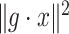 is minimized over all
is minimized over all 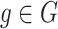 and
and 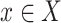 with the constraint
with the constraint 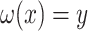 . However, a unique optimal solution is no longer guaranteed for this optimization, because even the low-rank matrix completion problem does not always have a unique optimal solution. An approach to finding an optimal
. However, a unique optimal solution is no longer guaranteed for this optimization, because even the low-rank matrix completion problem does not always have a unique optimal solution. An approach to finding an optimal 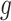 and
and 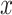 is to use alternating optimization. Starting with the element
is to use alternating optimization. Starting with the element 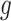 as the identity, one can find
as the identity, one can find 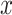 with
with 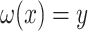 , such that
, such that 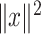 is minimal. An optimal
is minimal. An optimal 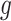 can be now found such that
can be now found such that 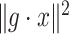 is minimal, and this procedure is repeated until a desired convergence is obtained. In some cases, such as for the CTMC case, finding an optimal
is minimal, and this procedure is repeated until a desired convergence is obtained. In some cases, such as for the CTMC case, finding an optimal 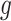 is in itself an iterative procedure. In that case one can alternate a fixed number of iteration steps for
is in itself an iterative procedure. In that case one can alternate a fixed number of iteration steps for 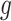 with an optimization step for
with an optimization step for 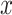 .
.
In order to improve the algorithms for CMMC and CTMC, we start by assuming that two symmetric matrices 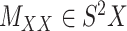 and
and 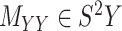 are given in a way that they are coupled with an incomplete matrix
are given in a way that they are coupled with an incomplete matrix 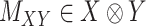 , where
, where 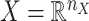 and
and 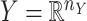 . Without loss of generality, one may assume that
. Without loss of generality, one may assume that 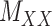 and
and 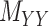 are nonnegative definite. Suppose that the only known entries of
are nonnegative definite. Suppose that the only known entries of 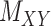 are at positions
are at positions 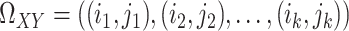 . This constraint can be written as
. This constraint can be written as 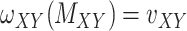 where
where 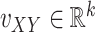 is some fixed vector, and
is some fixed vector, and 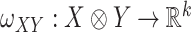 maps a matrix
maps a matrix 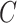 to
to 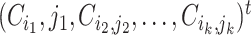 . One may use the matrices
. One may use the matrices 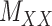 and
and 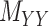 as regularization of the matrix completion problem of
as regularization of the matrix completion problem of 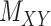 . For some fixed regularization parameters
. For some fixed regularization parameters 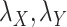 , the objective function to minimize is defined by
, the objective function to minimize is defined by
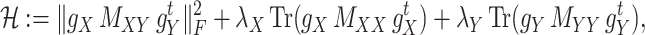 |
(7) |
over all triples 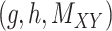 with
with 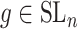 ,
, 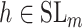 and
and 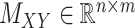 with the constraint
with the constraint
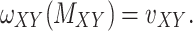 |
Here 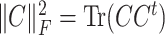 is the square of the Frobenius norm. for some arbitrary matrix
is the square of the Frobenius norm. for some arbitrary matrix 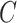 .
.
The drug–drug and target–target interaction matrices, 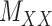 and
and 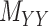 , respectively, may be incomplete as well, which in that case the following constraints are imposed
, respectively, may be incomplete as well, which in that case the following constraints are imposed
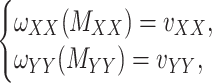 |
as well as the convex constraints that implied 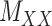 and
and 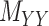 being nonnegative definite. As a result, besides
being nonnegative definite. As a result, besides 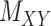 , both drug–drug and target–target matrices,
, both drug–drug and target–target matrices, 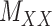 and
and 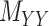 , are updated and hence the problem narrows down to a quadratic programming with convex constraints.
, are updated and hence the problem narrows down to a quadratic programming with convex constraints.
For the CTMC method, the drug–drug and target–target interactions/similarities tensors, which are obtained from several sources, are given by matrices 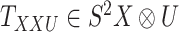 of size
of size 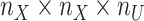 and
and 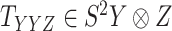 of size
of size 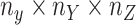 . In that case, there exist two additional transformations
. In that case, there exist two additional transformations 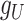 and
and 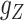 , which are diagonal matrices with determinant
, which are diagonal matrices with determinant 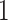 and positive entries on the diagonal. For some fixed regularization parameters
and positive entries on the diagonal. For some fixed regularization parameters 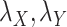 , the objective function to minimize hence becomes
, the objective function to minimize hence becomes
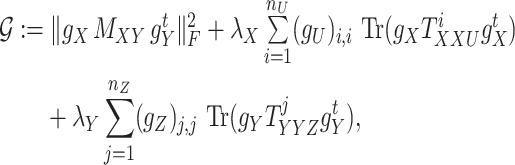 |
(8) |
over all triples 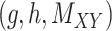 with
with 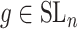 ,
, 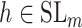 and
and 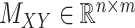 . Moreover, the objective function
. Moreover, the objective function 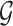 also minimizes all the number of layers added to
also minimizes all the number of layers added to 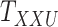 , denoted as
, denoted as 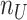 , and number of layers added to
, and number of layers added to 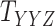 , denoted as
, denoted as 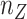 . Here
. Here 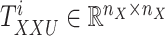 denotes the
denotes the 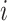 -th slice of the tensor
-th slice of the tensor 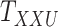 .
.
The transformations are used to balance the various sources of drug–drug and target–target interactions, and just like 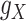 and
and 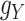 ,
, 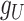 and
and 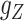 are updated iteratively. If entries of the tensors
are updated iteratively. If entries of the tensors 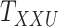 and
and 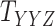 have missing entries, certain constraints are adopted in addition to the one which assumes that all the slices are nonnegative definite.
have missing entries, certain constraints are adopted in addition to the one which assumes that all the slices are nonnegative definite.
To further explain the CMMC and CTMC methods, we consider the matrix 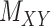 representing the interaction between drugs
representing the interaction between drugs 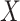 and targets
and targets 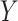 . Entries are typically within the interval
. Entries are typically within the interval 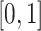 . Only a small percent of the entries of matrix
. Only a small percent of the entries of matrix 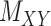 are non-zero and many are unknown. Without loss of generality one may assume the interaction matrix
are non-zero and many are unknown. Without loss of generality one may assume the interaction matrix 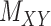 is symmetric and is considered together with two other matrices: drug–drug similarity/interaction (
is symmetric and is considered together with two other matrices: drug–drug similarity/interaction (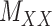 ) and target–target similarity/interaction (
) and target–target similarity/interaction (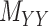 ) matrices. It is noteworthy that both rows and columns of matrix
) matrices. It is noteworthy that both rows and columns of matrix 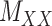 have the same labels as the rows of
have the same labels as the rows of 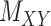 and both rows and columns of matrix
and both rows and columns of matrix 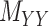 have the same labels as the columns of
have the same labels as the columns of 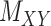 .
.
After forming the coupled structures, the next step is to determine the optimal metric for CMMC/CTMC methods as most methods for matrix (tensor) completion rely upon the choice of a fixed metric, such as the Euclidean metric (nuclear norm). Here, the optimal metric will be determined using Algorithm 1.
|
|
Intuitively, minimizing the objective function given in Eq. (7) (and same for Eq. (8)) results in finding an optimal metric under which the distance between interaction matrix 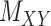 and the matrix
and the matrix 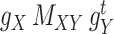 is minimal. This also applies to two other matrices,
is minimal. This also applies to two other matrices, 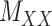 and
and 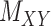 , as well. It is worth mentioning again that
, as well. It is worth mentioning again that 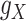 and
and 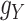 are symmetric invertible matrices whose determinants equal to 1. To this end and to help better understanding the methods, the self-contained executable codes for the two proposed methods, CMMC and CTMC, have made publicly available (see Section 7).
are symmetric invertible matrices whose determinants equal to 1. To this end and to help better understanding the methods, the self-contained executable codes for the two proposed methods, CMMC and CTMC, have made publicly available (see Section 7).
4.3 Scalable algorithms for CMMC and CTMC
A main challenge to the prediction of DT interaction lies in the fact that only a small fraction of the entries in the tensors and matrices are known [1]. It appears that the output, i.e. the completed data, is many times larger then the input of the known entries. In fact, dealing with the large sized tensors may become intractable due to the lack of memory or computational power. It seems possible, however, that the output and the intermediate results can be compressed because of the following observation in a special case. Suppose that 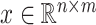 is a matrix with missing entries and
is a matrix with missing entries and 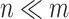 . Assuming that only the entries in the positions
. Assuming that only the entries in the positions 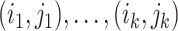 are known with
are known with 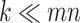 , evaluation of
, evaluation of 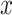 at the positions
at the positions 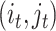
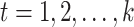 defines a map
defines a map 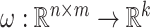 where only
where only 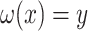 is known. The optimal solution to minimizing
is known. The optimal solution to minimizing 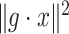 where
where 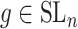 and
and 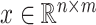 satisfying
satisfying 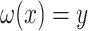 has a very special form, namely
has a very special form, namely 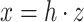 with
with 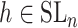 and
and 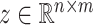 with the property that the only nonzero entries of
with the property that the only nonzero entries of 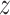 are
are 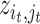 ,
, 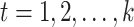 . Therefore, instead of storing the matrix
. Therefore, instead of storing the matrix 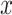 with
with 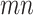 entries, it is only needed to remember the matrix
entries, it is only needed to remember the matrix 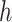 and the nonzero entries of
and the nonzero entries of 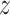 , a total of
, a total of 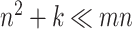 numbers.
numbers.
5 Results
For the demonstration of all the methods except CTMC, three matrices are created. For the first step, three matrices consisting of drug–drug interaction, DTI and target–target interaction are created (see Section 3). Next, all the methods are evaluated using drug–drug similarity, DTI and target–target similarity matrices. For the demonstration of CTMC, which is capable of handling multiple sources of information in a preserved tensor form, additional layers in the form of similarity scores and/or interaction information are added. Detailed information about different layers and similarity information are provided in Table 1.
5.1 CMMC performance evaluations using DrugBank
For performance evaluations, we consider the CMMC algorithm along with three other algorithms outlined in Section 2. For every iteration, a subset of the interaction matrix, 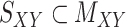 , is created by randomly selecting approximately 10% of the rows and columns of
, is created by randomly selecting approximately 10% of the rows and columns of 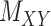 . This results in a matrix,
. This results in a matrix, 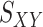 , of size
, of size 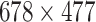 , which corresponds to 1% of the total number of elements of
, which corresponds to 1% of the total number of elements of 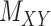 . Next, 10% of the entries are randomly selected and replaced by 0.5, as a surrogate for a value that is neither 0 nor 1, and all four algorithms are used to predict those values. We then average the performance of all algorithms over 100 iterations.
. Next, 10% of the entries are randomly selected and replaced by 0.5, as a surrogate for a value that is neither 0 nor 1, and all four algorithms are used to predict those values. We then average the performance of all algorithms over 100 iterations.
The comparison is divided into two parts; first, we consider drug–drug and target–target interaction matrices coupled with the interaction matrix 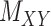 for which Table 2 represents the results. Next, the methods are compared using the coupled drug–drug and target–target similarity matrices,
for which Table 2 represents the results. Next, the methods are compared using the coupled drug–drug and target–target similarity matrices, 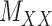 and
and 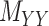 respectively, coupled with the interaction matrix
respectively, coupled with the interaction matrix 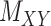 . The results are shown in Table 3. The methods are compared based on the total runtime, area under the curve (AUC), F1 score, sensitivity, specificity and accuracy. The threshold columns represent the most appropriate threshold for calling a predicted value either positive or negative to optimize the F1 score calculated over the 100 iterations.
. The results are shown in Table 3. The methods are compared based on the total runtime, area under the curve (AUC), F1 score, sensitivity, specificity and accuracy. The threshold columns represent the most appropriate threshold for calling a predicted value either positive or negative to optimize the F1 score calculated over the 100 iterations.
Table 2 .
Metrics of results produced by the algorithms using binary interaction matrices obtained from DrugBank.
| CMMC | WKNKN + CMMC | |||
|---|---|---|---|---|
| Mean | SD | Mean | SD | |
| Runtime (s) | 0.337 | 0.026 | 0.551 | 0.033 |
| AUC | 0.664 | 0.072 | 0.664 | 0.072 |
| F1 | 0.184 | 0.110 | 0.184 | 0.110 |
| Sensitivity | 0.164 | 0.085 | 0.164 | 0.085 |
| Specificity | 0.997 | 0.011 | 0.997 | 0.011 |
| GRMF | WKNKN + GRMF | |||
| Mean | SD | Mean | SD | |
| Runtime (s) | 1302.294 | 251.657 | 1299.383 | 252.889 |
| AUC | 0.629 | 0.078 | 0.645 | 0.083 |
| F1 | 0.061 | 0.068 | 0.072 | 0.078 |
| Sensitivity | 0.120 | 0.085 | 0.114 | 0.076 |
| Specificity | 0.986 | 0.025 | 0.988 | 0.031 |
L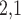 -GRMF -GRMF
|
WKNKN + L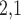 -GRMF -GRMF
|
|||
| Mean | SD | Mean | SD | |
| Runtime (s) | 1288.877 | 261.152 | 1279.952 | 254.770 |
| AUC | 0.636 | 0.078 | 0.648 | 0.076 |
| F1 | 0.062 | 0.071 | 0.074 | 0.078 |
| Sensitivity | 0.117 | 0.076 | 0.104 | 0.063 |
| Specificity | 0.986 | 0.026 | 0.990 | 0.027 |
| NRLMF | WKNKN + NRLMF | |||
| Mean | SD | Mean | SD | |
| Runtime (s) | 1.551 | 0.086 | 1.546 | 0.076 |
| AUC | 0.597 | 0.077 | 0.602 | 0.080 |
| F1 | 0.050 | 0.062 | 0.051 | 0.063 |
| Sensitivity | 0.116 | 0.079 | 0.115 | 0.090 |
| Specificity | 0.976 | 0.047 | 0.980 | 0.062 |
NRLMF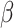
|
WKNKN + NRLMF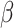
|
|||
| Mean | SD | Mean | SD | |
| Runtime (s) | 37.938 | 0.570 | 37.883 | 0.665 |
| AUC | 0.596 | 0.077 | 0.602 | 0.081 |
| F1 | 0.050 | 0.062 | 0.051 | 0.063 |
| Sensitivity | 0.116 | 0.079 | 0.116 | 0.090 |
| Specificity | 0.976 | 0.047 | 0.980 | 0.063 |
Table 3 .
Metrics of results produced by the algorithms using similarity matrices obtained from DrugBank.
| Algorithm | Runtime (s) | AUC | F1 | Sensitivity | Specificity | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | |
| CMMC | 0.374 | 0.088 | 0.761 | 0.078 | 0.078 | 0.060 | 0.167 | 0.101 | 0.994 | 0.014 |
| GRMF | 1289.686 | 145.483 | 0.631 | 0.079 | 0.062 | 0.069 | 0.115 | 0.079 | 0.987 | 0.023 |
| WKNKN + GRMF | 1292.219 | 142.135 | 0.650 | 0.076 | 0.075 | 0.071 | 0.116 | 0.105 | 0.985 | 0.071 |
| L21GRMF | 1290.000 | 136.695 | 0.637 | 0.078 | 0.064 | 0.072 | 0.115 | 0.073 | 0.987 | 0.026 |
| WKNKN + L21GRMF | 1289.366 | 143.215 | 0.648 | 0.081 | 0.076 | 0.076 | 0.111 | 0.078 | 0.988 | 0.040 |
| NRLMF | 1.593 | 1.106 | 0.601 | 0.079 | 0.053 | 0.061 | 0.119 | 0.096 | 0.974 | 0.072 |
| WKNKN + NRLMF | 1.582 | 0.079 | 0.615 | 0.091 | 0.062 | 0.070 | 0.127 | 0.128 | 0.973 | 0.085 |
NRLMF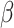
|
38.537 | 1.468 | 0.600 | 0.079 | 0.053 | 0.061 | 0.119 | 0.096 | 0.974 | 0.072 |
WKNKN + NRLMF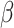
|
39.080 | 2.036 | 0.615 | 0.615 | 0.062 | 0.070 | 0.127 | 0.130 | 0.973 | 0.085 |
All the methods have been tested over the same dataset with and without the pre-processing step, called WKNKN [8] (see Section 2.1). This allows us to replace a given binary values with an interaction likelihood value in any of the matrices. Authors in [8] reported notable improvement in their method using the so called pre-processing step. However, as it is shown in Tables 2 and 3, although WKNKN improves the average value for AUC, F1 score, sensitivity and specificity as well as accuracy, it results in higher standard deviation (SD) values as well. Therefore, the pre-processing step WKNKN may also affect the robustness of the methods. On the other hand, it is noteworthy that the results under the proposed methods, CMMC and CTMC, are not affected by WKNKN and it shows the proposed methods do not necessarily require any pre-processing step. The reason lies in the fact that these methods only use the known interactions given in the original DTI matrix 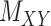 to iterate whereas drug–drug and target–target similarity/interaction matrices,
to iterate whereas drug–drug and target–target similarity/interaction matrices, 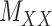 and
and 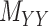 , respectively, to converge to the completed
, respectively, to converge to the completed 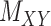 matrix; moreover, WKNKN only affects the values that are marked 0.5 as a surrogate for the ‘missing’ values, hence it does not affect the results for CMMC. As a result, it also shows the robustness of the CMMC algorithm.
matrix; moreover, WKNKN only affects the values that are marked 0.5 as a surrogate for the ‘missing’ values, hence it does not affect the results for CMMC. As a result, it also shows the robustness of the CMMC algorithm.
The best performances in terms of AUC, F1 score, sensitivity, specificity and accuracy across different algorithms are highlighted in Tables 2 and 3, based upon which, one may observe the following: Performance based on AUC: The average value of AUC was calculated for each method with and without employing the pre-processing step, WKNKN. The AUCs for CMMC are reportedly higher than all the other methods. The highest average values of AUC was calculated for the three methods outlined in Section 2 based on similarity and interaction matrices are 0.637 and 0.636, respectively. These values are remarkably smaller than those of CMMC, which are 0.761 and 0.664, respectively. The reason that using similarity matrices for both drug–drug and target–target yields a higher AUC lies in the fact that similarity matrices contain more useful information as oppose to interaction matrices that are binary and often times sparse.
Performance based on F1 scores: In terms of F1 scores, although the average scores reported for CMMC method, using similarity and interaction matrices, correspond to small numbers, 0.078 and 0.062, respectively, they still represent higher values than those of other methods.
Performance based on sensitivity and specificity: As shown in Table 3, reported average sensitivity and specificity values for CMMC are recorded as 0.167 and 0.994, respectively, using similarity information, and 0.164 and 0.997 while utilizing interaction information based on Table 2. These values are higher compared to other methods even after using the pre-processing step, WKNKN.
Performance based on runtime: The main advantage of CMMC algorithm over the others methods described in Section 2 is the total time that it takes to perform the method over the dataset. The runtime is obtained by averaging the total running time over each iteration. As shown in Tables 2 and 3 recorded runtime for CMMC algorithm is notably smaller than those of other methods, which represents a faster process.
5.2 CMMC performance evaluations using TTD dataset
To further evaluate the performance of the proposed method CMMC algorithm, we consider another database TTD as described in Section 3.2. Based on the results provided in Section 5.1, since the CMMC algorithm performed better using similarity scores given in Table 3 than interaction information shown in Table 2, we consider using similarity scores in order to evaluate the performance of CMMC algorithm over the TTD dataset. Specifically, the drug–drug similarity matrix, 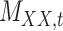 , and target–target similarity,
, and target–target similarity,  , along with the interaction matrix,
, along with the interaction matrix, 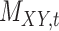 (see Table 1). The performance of CMMC method along with four other methods, GRMF,
(see Table 1). The performance of CMMC method along with four other methods, GRMF, 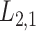 -GRMF, NRLMF and NRLMF
-GRMF, NRLMF and NRLMF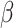 , based on the average AUC, F1 score, sensitivity and specificity over TTD dataset are shown in Table 4. Best results are marked bold. CMMC method obtains the best results in terms of average AUC, F1 score, sensitivity and specificity compared to the other method during a shorter period of time.
, based on the average AUC, F1 score, sensitivity and specificity over TTD dataset are shown in Table 4. Best results are marked bold. CMMC method obtains the best results in terms of average AUC, F1 score, sensitivity and specificity compared to the other method during a shorter period of time.
Table 4 .
Metrics of results produced by the algorithms using similarity matrices obtained from TTD.
| Algorithm | Runtime (s) | AUC | F1 | Sensitivity | Specificity | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | |
| CMMC | 3.378 | 0.307 | 0.846 | 0.037 | 0.084 | 0.070 | 0.122 | 0.093 | 0.996 | 0.008 |
| GRMF | 4176.739 | 136.152 | 0.701 | 0.064 | 0.031 | 0.029 | 0.095 | 0.067 | 0.990 | 0.013 |
| WKNKN + GRMF | 4143.534 | 120.312 | 0.683 | 0.057 | 0.083 | 0.074 | 0.091 | 0.086 | 0.991 | 0.036 |
| L21GRMF | 4148.855 | 121.843 | 0.699 | 0.064 | 0.030 | 0.031 | 0.095 | 0.071 | 0.989 | 0.018 |
| WKNKN + L21GRMF | 4156.066 | 111.406 | 0.690 | 0.057 | 0.083 | 0.076 | 0.087 | 0.071 | 0.993 | 0.025 |
| NRLMF | 4.228 | 0.639 | 0.621 | 0.066 | 0.030 | 0.025 | 0.072 | 0.057 | 0.990 | 0.019 |
| WKNKN + NRLMF | 4.579 | 0.351 | 0.651 | 0.063 | 0.054 | 0.052 | 0.077 | 0.051 | 0.996 | 0.009 |
NRLMF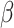
|
65.611 | 3.659 | 0.621 | 0.066 | 0.030 | 0.025 | 0.072 | 0.057 | 0.990 | 0.019 |
WKNKN + NRLMF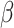
|
67.278 | 3.810 | 0.651 | 0.063 | 0.054 | 0.052 | 0.077 | 0.051 | 0.996 | 0.009 |
5.3 CTMC performance evaluations
In order to evaluate the performance of the CTMC algorithm, multidimensional arrays of drug–drug and target–target similarity/interaction were created using the information provided in Table 1. The results are shown in Table 6. In order to perform the evaluation, we incorporate both similarity and interaction information between drugs and targets in order to form the drug–drug and target–target tensors, 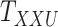 and
and 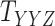 , respectively. As shown in Table 6, CTMC outperforms all the methods including CMMC in terms of average AUC and sensitivity. The results in terms of F1 score, specificity and accuracy remain the same as CMMC while using similarity information, as shown in Table 3. As stated before, the difference is more remarkable when the similarity scores are used for coupling, most likely because the similarity matrices are rather complete, whereas the interaction matrices are sparse.
, respectively. As shown in Table 6, CTMC outperforms all the methods including CMMC in terms of average AUC and sensitivity. The results in terms of F1 score, specificity and accuracy remain the same as CMMC while using similarity information, as shown in Table 3. As stated before, the difference is more remarkable when the similarity scores are used for coupling, most likely because the similarity matrices are rather complete, whereas the interaction matrices are sparse.
Table 6 .
Metrics of results produced by CTMC using data from DrugBank.
| CTMC Method | |||||
| Runtime (s) | AUC | F1 | |||
| Mean | SD | Mean | SD | Mean | SD |
| 0.513 | 0.045 | 0.775 | 0.080 | 0.169 | 0.110 |
| Sensitivity | Specificity | Accuracy | |||
| Mean | SD | Mean | SD | Mean | SD |
| 0.169 | 0.082 | 0.997 | 0.011 | 0.997 | 0.011 |
Comparing the performance of the two proposed methods CMMC (coupled with similarity matrices) and CTMC, shown in Table 3 and Table 6, respectively, it is notable that CTMC slightly outperforms CMMC in terms of average values of AUC, F1 score, sensitivity, specificity and accuracy.
Table 7 demonstrates the improvement of performance as more layers are added. Initially, the interaction matrices are coupled for CTMC. This specific case is equivalent to CMMC as one could consider matrices as a two-way tensors. The evaluation results in comparable, albeit better, AUCs. As another layer is added in the drug–drug tensor, 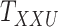 , namely the drug–drug similarity scores from Morgan Fingerprint, the AUC improves by approximately 10% as it is shown in Table 7. Similarly, adding another layer to the target–target tensor, the AUC improves by approximately 5%. Adding the third layer to drug–drug tensor, however, does not improve the performance. It is likely due to the fact that the similarity information, calculated by different algorithms from the same database (DrugBank [25]), does not provide any new information hence does not improve the results.
, namely the drug–drug similarity scores from Morgan Fingerprint, the AUC improves by approximately 10% as it is shown in Table 7. Similarly, adding another layer to the target–target tensor, the AUC improves by approximately 5%. Adding the third layer to drug–drug tensor, however, does not improve the performance. It is likely due to the fact that the similarity information, calculated by different algorithms from the same database (DrugBank [25]), does not provide any new information hence does not improve the results.
Table 7 .
Performance of the CTMC algorithm adding slices obtained from DrugBank.
|
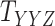
|
# of Slices | Runtime (s) | AUC | F1 | Sensitivity | Specificity | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | |||
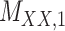
|
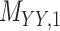
|
2 | 0.154 | 0.013 | 0.664 | 0.072 | 0.184 | 0.110 | 0.164 | 0.085 | 0.997 | 0.011 |
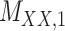 ,
, 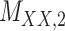
|
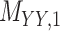
|
3 | 0.171 | 0.016 | 0.723 | 0.076 | 0.179 | 0.109 | 0.168 | 0.080 | 0.995 | 0.029 |
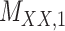 ,
, 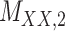
|
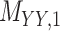 ,
, 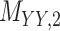
|
4 | 0.180 | 0.014 | 0.778 | 0.078 | 0.180 | 0.107 | 0.164 | 0.071 | 0.998 | 0.005 |
Metrics of results produced by the CTMC algorithm, stratified by the number of slices used in each coupled tensor. Here, 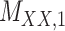 denotes binary drug–drug interaction matrix, and
denotes binary drug–drug interaction matrix, and 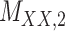 represents drug–drug similarity matrix with Morgan fingerprint scores. As for the targets,
represents drug–drug similarity matrix with Morgan fingerprint scores. As for the targets, 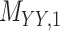 denotes binary target–target interaction matrix and
denotes binary target–target interaction matrix and 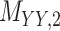 represents target–target similarity matrix as an inverse of Jukes–Cantor distance of amino acid sequences [12] (see Table 1 for more details on matrices
represents target–target similarity matrix as an inverse of Jukes–Cantor distance of amino acid sequences [12] (see Table 1 for more details on matrices 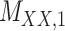 ,
, 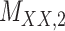 ,
, 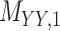 and
and 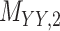 ).
).
Lastly, the recorded runtime for the CTMC algorithm, which incorporates more information and carries out more calculations, is nonetheless faster than the other algorithms.
5.4 Sensitivity analysis
The optimal regularization parameters for 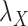 and
and 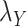 included in Eqs. (7) and (8) are chosen based on the performance of the algorithm during the execution of CMMC and CTMC methods. In order to determine how sensitive the proposed methods are based on the changes of the arbitrary-then-fixed parameters
included in Eqs. (7) and (8) are chosen based on the performance of the algorithm during the execution of CMMC and CTMC methods. In order to determine how sensitive the proposed methods are based on the changes of the arbitrary-then-fixed parameters 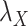 and
and 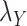 , as well as studying the roles of these parameters, the results under CMMC method have been compared from Tables 2, 3 and 4 against different variants of
, as well as studying the roles of these parameters, the results under CMMC method have been compared from Tables 2, 3 and 4 against different variants of 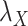 and
and 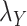 . The results are shown in Table 5. As setting either parameters
. The results are shown in Table 5. As setting either parameters 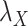 or
or 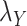 to zero simply means to ignore the role of one of the drug–drug or target–target matrices, it negatively impacts the performance. We have set
to zero simply means to ignore the role of one of the drug–drug or target–target matrices, it negatively impacts the performance. We have set 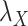 and
and 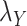 to zero and the results are shown in Table 5.
to zero and the results are shown in Table 5.
Table 5 .
AUC Results for different 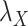 and
and 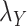 .
.
| CMMC | DrugBank | TTD |
|---|---|---|
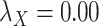 ;
; 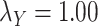
|
0.6300 | 0.4902 |
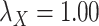 ;
; 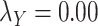
|
0.7005 | 0.8372 |
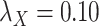 ;
; 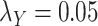
|
0.7545 | 0.8445 |
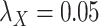 ;
; 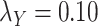
|
0.7580 | 0.8464 |
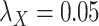 ;
; 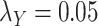
|
0.7610 | 0.8460 |
While mainly depending on the nature of the database in use, specifically the drug–drug and target–target similarity/interaction matrices, 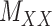 and
and 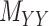 , it was found that the smaller the values of
, it was found that the smaller the values of 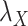 and
and 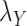 , the better the prediction performance.
, the better the prediction performance.
6 Conclusion
In this manuscript, two methods, CMMC and CTMC, for prediction of DT interactions inspired by matrix-factorization methods are presented. The experiments were performed with and without considering the preprocessing step WKNKN. The algorithm was first used to help with the sparsity of the similarity/interaction matrices. Using this, certain unknown interactions, i.e. 0’s values, were replaced by the likelihood values using 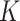 nearest neighbor method. Next, experiments were performed over coupled drug–drug, drug–target and target–target matrices, considering drug–drug similarity scores and target–target interactions. In order to test the CMMC method, we considered three matrices consisting of drug–drug similarity (calculated using Extended–Connectivity Fingerprint), drug–target and target–target interactions. For the CTMC method, in addition to the matrices, extra layers for drug–drug tensors were assigned to drug–drug interaction. In forming the target–target tensor, we included target–target similarity scores in addition to their interactions. Ten percent of the entire profile of the known DTI was intentionally left out and the two methods were run and tested in terms of predicting the known interactions. CMMC and CTMC showed strong ability in order to predict new DTI.
nearest neighbor method. Next, experiments were performed over coupled drug–drug, drug–target and target–target matrices, considering drug–drug similarity scores and target–target interactions. In order to test the CMMC method, we considered three matrices consisting of drug–drug similarity (calculated using Extended–Connectivity Fingerprint), drug–target and target–target interactions. For the CTMC method, in addition to the matrices, extra layers for drug–drug tensors were assigned to drug–drug interaction. In forming the target–target tensor, we included target–target similarity scores in addition to their interactions. Ten percent of the entire profile of the known DTI was intentionally left out and the two methods were run and tested in terms of predicting the known interactions. CMMC and CTMC showed strong ability in order to predict new DTI.
As future work, one may incorporate additional interaction and similarity information as well as different similarity scores utilizing different datasets. For instance, in order to form the drug–drug tensor, in addition to considering any possible interaction between drugs, various similarity scores could be calculated using different databases and based on distinct ways of calculating similarity scores, namely, Morgan fingerprint and ‘Avalon fingerprint’ while using different databases. Additionally, a pre-processing step to perform tensor completion ahead of applying CTMC would likely further improve the performance.
Key points
Matrix-Factorization Methods: A group of machine-learning-based methods that is used to help predict missing data using matrix factorization and matrix completion.
CMMC: A novel matrix-factorization-based method, Coupled Matrix–Matrix Completion, which outperforms several methods in the same category in a shorter runtime.
CTMC: A novel tensor-based method, Coupled Tensor–Matrix Completion, which is capable to incorporate more information in terms of different similarity scores as well as interaction details from various sources.
Supplementary Material
Maryam Bagherian is a postdoctoral research fellow at the Department of Computational Medicine and Bioinformatics. Her PhD degree is in applied mathematics and her research includes mathematical physics and mathematical biology.
Renaid B. Kim is an MD/PhD student in the Medical Scientist Training Program at Medical School, University of Michigan, Ann Arbor, pursuing a PhD in Bioinformatics.
Cheng Jiang is a master’s student in the College of Engineering, University of Michigan, Ann Arbor.
Maureen A. Sartor is an associate professor at the Department of Department of Biostatistics, School of Public Health, University of Michigan, Ann Arbor.
Harm Derksen is a professor at the Department of Mathematics, University of Michigan, Ann arbor.
Kayvan Najarian is a professor at the Department of Computational Medicine and Bioinformatics, University of Michigan, Ann Arbor. His research focuses on signal/image processing and machine learning methods for medical applications.
References
- 1. Bagherian M, Sabeti E, Wang K, et al. Machine learning approaches and databases for prediction of drug–target interaction: a survey paper. Brief Bioinform, (1477-4054), 01 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
2.
Ban T, Ohue M, Akiyama Y. Nrlmf
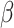 : beta-distribution-rescored neighborhood regularized logistic matrix factorization for improving the performance of drug–target interaction prediction. Biochem Biophys Rep 2019; 18: 100615. [DOI] [PMC free article] [PubMed] [Google Scholar]
: beta-distribution-rescored neighborhood regularized logistic matrix factorization for improving the performance of drug–target interaction prediction. Biochem Biophys Rep 2019; 18: 100615. [DOI] [PMC free article] [PubMed] [Google Scholar] - 3. Bock JR, Gough DA. Virtual screen for ligands of orphan g protein-coupled receptors. J Chem Inf Model 2005; 45(5): 1402–14. [DOI] [PubMed] [Google Scholar]
- 4. Cai JF, Candès EJ, Shen Z. A singular value thresholding algorithm for matrix completion. SIAM J Optim 2010; 20(4): 1956–82. [Google Scholar]
- 5. Candes EJ, Recht B. Exact matrix completion via convex optimization. Found Comput Math 9(6): 717–72. [Google Scholar]
- 6. Chen X, Liu M-X, Yan G-Y. Drug–target interaction prediction by random walk on the heterogeneous network. Mol Biosyst 2012; 8(7): 1970–8. [DOI] [PubMed] [Google Scholar]
- 7. Cui Z, Gao Y-L, Liu J-X, et al. L 2, 1-grmf: an improved graph regularized matrix factorization method to predict drug–target interactions. BMC Bioinform 2019; 20(8): 287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Ezzat A, Wu M, Li X-L, et al. Computational prediction of drug–target interactions using chemogenomic approaches: an empirical survey. Brief Bioinform 2018; 8. [DOI] [PubMed] [Google Scholar]
- 9.Ezzat A, Zhao P, Wu M, et al. Drug–target interaction prediction with graph regularized matrix factorization. IEEE/ACM Trans Comput Biol Bioinform, 14(3): 646–56, 2017. [DOI] [PubMed] [Google Scholar]
- 10. Fazel M. Matrix rank minimization with applications. PhD thesis, Stanford University, 2002. [Google Scholar]
- 11. Friedland S, Lim L-H. Nuclear norm of higher-order tensors. Math Comput 2018; 87(311): 1255–81. [Google Scholar]
- 12. Jukes TH, Cantor CR. Evolution of protein molecules. Mammal Protein Metab 1969; 3(21): 132. [Google Scholar]
- 13. Köhler S, Bauer S, Horn D, et al. Walking the interactome for prioritization of candidate disease genes. Am J Hum Genet 2008; 82(4): 949–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Koren Y. The bellkor solution to the Netflix grand prize. Netflix prize documentation 81. [Google Scholar]
- 15. Landrum G. Rdkit: Open-Source Cheminformatics.
- 16. Li L, Cai M. Drug target prediction by multi-view low rank embedding. IEEE/ACM Trans Comput Biol Bioinform 2017. [DOI] [PubMed] [Google Scholar]
- 17. Liu Y, Wu M, Miao C, et al. Neighborhood regularized logistic matrix factorization for drug–target interaction prediction. PLoS Comput Biol 2016; 12(2): e1004760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Ma S, Goldfarb D, Chen L. Fixed point and Bregman iterative methods for matrix rank minimization. Math Programming 2011; 128(1–2): 321–53. [Google Scholar]
- 19. Mahalanobis PC. On the Generalized Distance in Statistics. National Institute of Science of India, 1936. [Google Scholar]
- 20. Milne JS. Algebraic Groups: The Theory of Group Schemes of Finite Type Over a Field, Vol. 170. Cambridge University Press, 2017. [Google Scholar]
- 21. Netflix . The Netflix prize. http://www.netflixprize.com, 2009. (29 August 2019, date last accessed).
- 22. Nilakantan R, Bauman N, Dixon JS, et al. Topological torsion: a new molecular descriptor for Sar applications. Comparison with other descriptors. J Chem Inf Comput Sci 1987; 27(2): 82–5. [Google Scholar]
- 23. Olver PJ, Olver PJ. Classical Invariant Theory, Vol. 44. Cambridge University Press, 1999. [Google Scholar]
- 24. Rennie JDM, Srebro N. Fast maximum margin matrix factorization for collaborative prediction. 2332–41.
- 25. Rogers D, Hahn M. Extended-connectivity fingerprints. J Chem Inf Model 2010; 50(5): 742–54. [DOI] [PubMed] [Google Scholar]
- 26. Stark C, Breitkreutz B-J, Reguly T, et al. Biogrid: a general repository for interaction datasets. Nucleic Acids Res 2006; 34(suppl_1): D535–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Wang L, You Z-H, Chen X, et al. A computational-based method for predicting drug–target interactions by using stacked autoencoder deep neural network. J Comput Biol 2018; 25(3): 361–73. [DOI] [PubMed] [Google Scholar]
- 28. Wang M, Tang C, Chen J. Drug–target interaction prediction via dual Laplacian graph regularized matrix completion. Biomed Res Int 2018; 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Wang Y, Zhang S, Li F, et al. Therapeutic target database 2020: enriched resource for facilitating research and early development of targeted therapeutics. Nucleic Acids Res 2019; 48(D1): D1031–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Wen Z, Yin W, Zhang Y. Solving a low rank factorization model for matrix completion by a nonlinear successive over-relaxation algorithm. Math Programming Comput 2012; 4(4): 333–61. [Google Scholar]
- 31. Wimp J. Special functions and their applications (nn lebedev). SIAM Rev 1965; 7(4): 577–80. [Google Scholar]
- 32. Wishart DS, Feunang YD, Guo AC, et al. Drugbank 5.0: a major update to the drugbank database for 2018. Nucleic Acids Res 2017; 46(D1): D1074–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Zong N, Kim H, Ngo V, et al. Deep mining heterogeneous networks of biomedical linked data to predict novel drug–target associations. Bioinformatics 2017; 33(15): 2337–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



