The Crucial Role of Local Excess Charges in Dendrite Growth on Lithium Electrodes

Abstract

Much theoretical effort has been spent on the causes of dendrite formation in lithium metal batteries, but a decisive factor has been overlooked: Lithium is deposited on an electrode which carries a sizable negative charge, and this charge is not distributed homogeneously on the surface. We show by explicit model calculations that the excess charge accumulates on small protrusions and creates a strong electric field, which attracts the Li⁺ ions and induces further growth on the tip and finally the formation of dendrites. Even a small tip consisting of a few atoms will carry an excess charge of a tenth of a unit charge or more. In addition, the negative charge on the tips locally reduces the surface tension, which further fosters dendrite growth. The same principles can also explain dendrite formation on other metals with deposition potentials below the potential of zero charge.

Batteries based on Li metal promise a much higher energy density than the Li ion batteries common today, where the ions are stored in graphite. However, Li metal batteries are plagued by the formation of dendrites, which can short‐circuit the battery. As shown by calculations, excess charge accumulates on small protrusions and creates a strong electric field, which attracts Li⁺ and induces further growth on the tip and finally the formation of dendrites.

Introduction

The formation of dendrites is a severe problem for the development of rechargeable metal batteries. ^[1] They lead to the loss of active material, they can short‐circuit the two electrodes, and even set the whole battery on fire—corresponding videos on Youtube are quite popular. Although they are a disaster in battery research, they do have a certain esthetic appeal, and a few decades ago beautiful dendrites were grown because they served as models for fractal growth. ^[2]

Because of its great importance, the literature on dendritic growth, both on its experimental and its theoretical aspects, is enormous. ^[3] But in spite of these efforts, certain aspects concerning the nature of the metal are little understood. Why do dendrites form spontaneously during lithium deposition, while one has to use brute force, an overpotential of several volts, to form dendrites on copper? In a very recent paper Hagopian et al. ^[4] proposed that dendrites form when the electrode becomes thermodynamically unstable at very negative charge densities. While we agree that negative charge densities play an important role, we suggest that dendrite formation is triggered by local surface fluctuations in which the excess charge is localized on protrusions and attracts metal ions from the solution. This happens at potentials where the electrode is still thermodynamically stable. We shall return to the role of thermodynamics below.

In the following, we first review the consequences that a negative charge density has on the properties of a metal electrode, and then we present model calculations for lithium deposition focusing on the effect of small protrusions. We consider only dendrite formation in electrochemical systems—localized charges should not play a role in metal melts or in the formation of snowflakes.

Effects of an Excess Charge Density on the Properties of an Electrode

Metal deposition takes place on a cathode, so one would expect the electrode to be negatively charged. However, a quick survey of deposition potentials and the potential of zero charge (pzc) as collected in Table 1 shows that this is not necessarily so. Thus, the deposition potentials φ ₀ for six metals in aqueous solutions, including copper and silver, lie well above their pzcs. None of these metals show dendrite growth at low overpotentials. In contrast, the five other metals in the lower part of the table have a deposition potential below their pzc, and in the case of Li by more than 1 V. All these metals are prone to dendrite formation—in some solutions this may be obscured by the formation of an insulating passive film. The case of magnesium is controversial, but a very recent study ^[8] shows that there is always a rough, unwanted surface structure that forms during deposition, which at high current densities takes the shape of dendrites. We shall argue below that the relation between the pzc and the deposition potential is a crucial factor for dendritic growth.

Table 1.

Potentials of zero charge φ _pzc and deposition potentials φ ₀ for a few metals in aqueous solutions.^[a]

	Metal	φ pzc [V]	φ 0 [V]
	Cu/Cu++	−0.73	0.34
	Ag/Ag+	−0.7	0.80
	Pb/Pb++	−0.84*	−0.126
	Cd/Cd++	−0.72	−0.402
	Ni/Ni++	−0.29*	−0.228
	Tl/Tl+	−1.02*	−0.440
	Mg/Mg++	−1.36*	−2.356
	Zn/Zn++	−0.63	−0.763
	Li/Li+	−1.91	−3.045
	Na/Na+	−2.3*	−2.71
	K/K+	−2.7*	−2.925

[a] The values for φ ₀ are from Bard et al., ^[5] the pzcs are from Trasatti, ^[6] except for the pzc of copper, which is from Lukomska and Sobkowski; ^[7] values marked with an asterisk have been estimated from the work function by the formula proposed by Trasatti. ^[6] The values of the pzc are for polycrystalline surfaces. All values are given with respect to NHE.

The deposition of lithium, on which we focus in the following, in aqueous solutions is not a realistic example. Unfortunately, values for other solvents are not readily available, and there is the problem of relating potential scales in different solvents. ^[9] However, a reasonable estimate can be made by resorting to the absolute, or vacuum, scale of potentials.[ ¹⁰ , ¹¹ ] The pzc is mainly determined by the work function ^[6] and therefore its value, on the absolute scale, should not vary much with the solvent. The equilibrium potential for the deposition of a metal can be obtained from a Born cycle, which involves the free energy of sublimation of the metal, its energy of ionization, and its real free energy of solvation.[ ⁵ , ¹¹ ] The first two quantities are obviously independent of the solvent. The real free energy of solvation is the free energy gained when the ion is transferred from the vacuum to the solution, and involves a surface term. We know of no values for non‐aqueous solvents, but an estimate can be made by using conventional energies of solvation, which do not involve the surface term. The hydration energy of Li⁺ has been estimated as −5.54 eV, its solvation energy in dimethyl sulfoxide (DMSO) as about −5.9 eV. ^[12] More negative solvation energies mean lower deposition potentials, so in DMSO lithium should be deposited on an even more negatively charged electrode. In a recent detailed study of lithium deposition, Li and Qi ^[13] and Qi et al. ^[14] have reached the same conclusion using essentially the same arguments.

If we also consider that, in practice, the deposition takes place at potentials below the equilibrium value, we may safely conclude that in systems relevant for batteries lithium is deposited on an electrode with a negative charge density.

Let us look at some of the consequences that an excess charge density has on the properties of a metal electrode, bearing in mind that the electrode potential is constant on the surface of a metal, while other properties such as the surface charge density, the interfacial capacity, and the surface tension may vary locally.

The surface tension γ reaches its maximum at the potential of zero charge, φ _pzc. The change with the electrode potential φ is given by Equation 1, where σ is the surface charge density, and C the interfacial capacitance per area. To gain an idea of the order of magnitude of the dependence, we consider a flat electrode with a capacitance of 0.2 F m⁻² and a change of the electrode potential by 1 V, which gives rise to a surface charge density of 0.2 C m⁻² and a change in surface tension by 0.1 J m⁻². This is a sizable fraction of the surface tension of uncharged Li, which is about 0.5 J m⁻². At sufficiently large deviations from the pzc, the surface tension becomes negative, and the electrode dissolves, as has been noted by Hagopian et al. ^[4] Using the same values for the capacitance, this would happen at a deviation of about 2.23 V from the pzc, or about 1 V below the deposition potential. A low surface tension enhances surface fluctuations, which may initiate dendrite formation; note that the energy of activation for the formation of a nucleus scales with γ ³. Indeed, in a simple model in which a nucleus is assumed to keep its geometrical shape as it grows, ^[11] this activation energy is: 4(γa)³/27(ze ₀ η)², where η is the overpotential, z is the valence of the metal atom, and a is a geometrical factor. Note that γ varies with the potential and hence with η, as discussed above. Once a protrusion has formed on a surface with a low surface tension, there is only a small driving force for its disappearance. This matter is well discussed in the article by Wang et al. ^[15]

$${\displaystyle \gamma \left(\varphi \right)-\gamma \left({\varphi }_{\mathrm{pzc}}\right)=-\underset{{\varphi }_{\mathrm{pzc}}}{\overset{\varphi }{\int }}\sigma \left(\varphi {}^{\text{'}}\right)d\varphi {}^{\text{'}}=-\underset{{\varphi }_{\mathrm{pzc}}}{\overset{\varphi }{\int }}C\left(\varphi {}^{\text{'}}\right)\varphi {}^{\text{'}}d\varphi {}^{\text{'}}}$$ (1)

In a conductor any excess charge resides on the surface, and especially at tips or protrusions. This is the basis of the well‐known field emission microscope. This implies that the charge density on tips is much larger than that on a plane surface, and hence the surface tension is much lower. In the next section we shall illustrate this point by model calculations. If the charge on a tip is negative, it attracts metal cations and induces dendrite formation. In contrast, if the charge is positive, it favors deposition on terraces.

The local capacitance is also larger at a tip than on a terrace. In essence this can be seen by looking at the capacitance of a metal sphere of radius R embedded in a medium which is described by the linear version of the Gouy–Chapman theory. The capacitance per unit area for this case is: C=ϵϵ ₀(1/L _d+1/R), where ϵ is the dielectric constant of the medium, L _D its Debye length, and ϵ ₀ the permittivity of space.

A negative surface charge implies a greater concentration of electrons at the surface, which enhances the electronic polarizability of the surface. ^[16] Therefore, the contribution of the metal to the capacitance, and with it the overall capacitance, increases as the potential is lowered.

Because of the Smoluchowski effect ^[17] metal adatoms on terraces or on steps usually carry a positive dipole moment pointing away from the surface, which interacts with the field generated by surface charges. ^[19] As a consequence, adatom mobility is higher at positive potentials. This effect has recently been confirmed for diffusion of lithium atoms on lithium. ^[18] This increasing mobility with increasing potential is the basis of electrochemical annealing, ^[19] where the surface is smoothed by scanning the potential to higher values. Conversely, sweeping in the negative direction freezes the surface roughness.

With these considerations in mind we turn towards explicit model calculations for lithium.

Model Calculations for Lithium Tips

We have performed model calculations for lithium tips focusing on the charge distribution.We chose DFTB, a tight binding scheme based on density functional theory (DFT), as our method. This method is much faster than DFT, allows calculations for charged systems, and is of comparable accuracy in simple cases like Li clusters.[ ¹³ , ²⁰ ] Technical details are given in the Technical Information at the end.

We chose a lithium slab of six layers with 5×5 atoms each, topped by a pyramid with four layers containing, from bottom to top, 4×4, 3×3, and 2×2 atoms, and finally one top atom, as our standard model for a tip (Figure 1). Cyclic boundary conditions apply in the x and y direction parallel to the bottom layer of the slab. From DFTB we calculated the Mulliken charges on the atoms, along with the electrostatic field near the tip. Figure 1 shows the case of an uncharged system. In accordance with the Smoluchowski effect the top atom has a positive excess charge, which is balanced by the negative charge below. Atoms at the boundary of the system tend to have a small negative excess charge because of electron spill‐over, but the effect is small.

Figure 1.

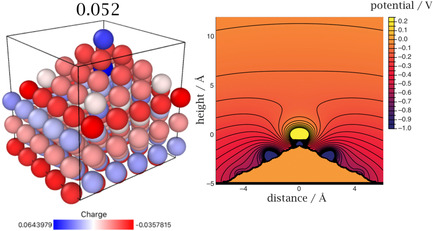
Charge distribution on a pyramidal tip for an uncharged Li electrode (left), and electrostatic potential contours (right) when the tip is in contact with a medium obeying the linear Poisson–Boltzmann equation with a Debey length of about 10 Å; the plot shows a cross section along the diagonal of the tip.

When such a tip is immersed in an electrolyte solution, the local excess charge is screened. In order to explore this effect, we treated the solution with the linear Gouy–Chapman theory and solved the corresponding Poisson–Boltzmann equation choosing a value of about 10 Å for the Debye length. The corresponding potential is plotted on the right hand side of Figure 1, which shows a cross section along the diagonal of the pyramid. The tip atom generates a positive potential, which decays to zero in the solution. A cation approaching from the solution is repelled from the tip and steered towards the side, so that further growth of the tip is inhibited.

As we have pointed out in the previous section, the electrode should carry a negative charge when lithium is being deposited. We therefore added one extra electron to our system, which results in an average surface charge density of −2.9×10⁻² C m⁻², which is very small by electrochemical standards—remember our estimate of −0.2 C m⁻² in the previous section. As expected, the excess charge accumulates on the surfaces of our system, and especially on the tip atom, which carries −0.13 of a unit charge. But also the second layer from the top carries a sizable negative charge, and all the other surface atoms are negatively charged, but less so. A brief note on the positively charged blue atom in the third layer of the pyramid, which is also conspicuous in Figure 1. This is the only bulk atom within the first three layers, all of its four nearest neighbors lie on the surface, as do most of its second neighbors. So whenever the surface atoms require extra negative charge to form a surface dipole, they take some from this atom.

Again, we solved the linear Poisson–Boltzmann equation to estimate the screening of the charge in the solution; the corresponding potential contours are shown on the right‐hand side of Figure 2. The field, which is the gradient of the potential, is strongly directed towards the tip, thus favoring its further growth.

Figure 2.

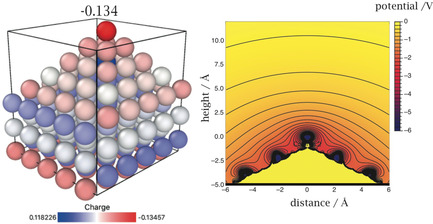
Charge distribution on a pyramidal tip for a Li electrode with an excess charge of σ=−2.9×10⁻² C m⁻² (left) and electrostatic potential contours (right) when the tip is in contact with a medium obeying the linear Poisson–Boltzmann equation with a Debey length of 10 Å; the plot shows a cross section along the diagonal of the tip.

Our standard tip comprises 30 atoms, and is perhaps too large to arise from a spontaneous fluctuation. We therefore also investigated a small tip consisting of five atoms on the same basis, again with an excess of one electron. As shown on the left‐hand side of Figure 3, the top atom of the cluster obtains a charge of −0.11 e₀, with an absolute value only a little smaller than that of our large tip, and sufficiently high to induce further tip growth.

Figure 3.

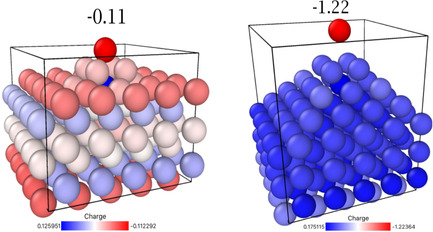
Charge distribution on a 5 atom tip for a Li electrode with an excess charge σ=−2.9×10⁻² C m⁻² (left). Detachment of the top atom for a charge of 5 electrons corresponding to an average σ=−14.5×10⁻² C m⁻² (right).

We have performed simulations for higher charges on our model system and found that the charge at the tip increases stronger than linearly. Also, the tip extends vertically as it is charged. For an excess charge of 1 e₀ it is already stretched by 0.13 Å. This leads us to the question raised in the second section: Will the system become unstable at sufficiently high surface charges? The answer is shown on the right‐hand side of Figure 3. For an excess of 5 e₀ the atom at the top becomes unstable and leaves the tip. So, locally, right at the tip, the surface tension has become negative. This suggests a mechanism of how a small section of a dendrite can become unstable and dissolve, converting the dangling part into non‐active lithium.

Conclusion

From our investigations, the following scenario for the growth of dendrites arises: Lithium deposition takes place on a negatively charged electrode, at potentials well below the potential of zero charge. This reduces the surface tension of the electrode, and enhances fluctuations of the surface and the probability to form small protrusions. Once such a protrusion has formed—and five atoms should be enough—a negative excess charge concentrates on the tip and generates an electric field, which attracts the metal cations from the solution, leading to dendrite formation. This model is compatible with views in the literature (see for example, ref. [15]). The new and essential feature is the role of the local charge density to initiate dendrite growth. Our model also suggests that non‐active lithium forms when the charge density at a part of a dendrite becomes so high that the surface energy locally becomes negative, and the dendrite breaks apart.

Given the hugh volume of literature on dendrite growth, we can only note the essential feature of our work in comparison to that of others. Much of the contemporary work considers the surface at the mesoscopic scale—see for example, ref. [23, 24, 25]—while the fluctuations which we consider occur on an atomic scale. Concerning the relation of our work with that of Hagopian et al.: ^[4] The latter work examines correctly the thermodynamic limits when the electrode becomes unstable. We suggest that dendrite formation already takes place at smaller deviations from the pzc and is caused by fluctuations.

We have performed our calculations for lithium, but our arguments should apply to the deposition of other metals, though there may be complications from other effects such as the formation of ion pairs or of insulating films. From our brief survey in the second section we can immediately understand why the other alkali metals form dendrites, and why copper does not, unless a negative overpotential of the order of 3–4 V is applied. ^[2]

Can our model give hints for the construction of batteries with lithium and similar metals as cathode? As is discussed by Hagopian et al., ^[4] there are two important potentials: the deposition potential and the potential of zero charge. The deposition potential can be varied by choosing a solvent. A low deposition potential means a low surface tension and hence a tendency to dendrite formation. Raising the deposition potential by choosing a solvent with a smaller absolute value of the solvation energy may reduce dendrite growth, but this would probably reduce the solubility as well. Indeed, if one wants to raise the deposition potential above the potential of zero charge, one would lose at least 1 V in voltage. The potential of zero charge is mainly given by the work function; this could be lowered by alloying, but again this would reduce the efficiency. So from our model we have determined the cause, but can suggest no remedies.

Technical Information

The calculations have been performed by the DFTB+ method developed by Aradi et al. ^[20] The code can be obtained from https://dftbplus.org/. The Slater‐Koster parameters for lithium have been calculated by Li and Qi ^[21] and are optimized for application to battery research. The system was built up in stages: First we prepared a 5×5 slab with 6 layers with surfaces in the (100) orientations. Subsequently we kept the bottom three layers fixed and let the rest of the slab relax. Then we placed the tip on top and let again everything but the bottom three layers relax. In subsequent calculations with charges only the tip was allowed to relax. The DFTB program calculates the charges on the atoms self‐consistently; the corresponding maximum allowed error was set to 10⁻⁶ a.u. The corresponding accuracy for geometry optimization was set to 10⁻⁵ a.u. A k‐point mesh of 4×4×4 in the Monkhorst–Pack Scheme ^[22] was used.

The linear Gouy–Chapman theory was solved by using the Green's function for the linear Poisson–Boltzmann equation [Eq. 2], where κ is the inverse Debye length, and the condition that the potential vanishes at infinity has been imposed.

$${\displaystyle G(\overrightarrow{r}-\overrightarrow{r}{}^{\text{'}})=\frac{exp-\left(\kappa \right(|\overrightarrow{r}-\overrightarrow{r}{}^{\text{'}}\left|\right)}{|\overrightarrow{r}-\overrightarrow{r}{}^{\text{'}}|}}$$ (2)

Conflict of interest

The authors declare no conflict of interest.

E. Santos, W. Schmickler, Angew. Chem. Int. Ed. 2021, 60, 5876.