PCA denoising and Wiener deconvolution of ³¹P 3D CSI data to enhance effective SNR and improve point spread function

Abstract

Purpose

This study evaluates the performance of 2 processing methods, that is, principal component analysis‐based denoising and Wiener deconvolution, to enhance the quality of phosphorus 3D chemical shift imaging data.

Methods

Principal component analysis‐based denoising increases the SNR while maintaining spectral information. Wiener deconvolution reduces the FWHM of the voxel point spread function, which is increased by Hamming filtering or Hamming‐weighted acquisition. The proposed methods are evaluated using simulated and in vivo 3D phosphorus chemical shift imaging data by 1) visual inspection of the spatial signal distribution; 2) SNR calculation of the PCr peak; and 3) fitting of metabolite basis functions.

Results

With the optimal order of processing steps, we show that the effective SNR of in vivo phosphorus 3D chemical shift imaging data can be increased. In simulations, we show we can preserve phosphorus‐containing metabolite peaks that had an SNR < 1 before denoising. Furthermore, using Wiener deconvolution, we were able to reduce the FWHM of the voxel point spread function with only partially reintroducing Gibb‐ringing artifacts while maintaining the SNR. After data processing, fitting of the phosphorus‐containing metabolite signals improved.

Conclusion

In this study, we have shown that principal component analysis‐based denoising in combination with regularized Wiener deconvolution allows increasing the effective spectral SNR of in vivo phosphorus 3D chemical shift imaging data, with reduction of the FWHM of the voxel point spread function. Processing increased the effective SNR by at least threefold compared to Hamming weighted acquired data and minimized voxel bleeding. With these methods, fitting of metabolite amplitudes became more robust with decreased fitting residuals.

1. INTRODUCTION

Phosphorus (³¹P) MRS allows to noninvasively measure phosphorus‐containing metabolites and membrane phospholipid metabolites and derivatives. ¹ , ² In recent years, ³¹P chemical shift imaging (CSI) has been shown useful in a variety of applications and organs such as the brain, ³ , ⁴ , ⁵ heart, ⁶ , ⁷ liver, ⁸ , ⁹ muscle, ¹⁰ , ¹¹ and lung. ¹² However, in vivo concentrations of observable phosphorus‐containing metabolites are in the millimolar range, and ³¹P has a low gyromagnetic ratio and thus low intrinsic sensitivity. This can make it challenging to obtain an adequate SNR in clinically feasible scan times. ¹³ Higher field strengths (7T) can be used to mitigate the low SNR in ³¹P MRS acquisitions. ¹⁴ , ¹⁵ In combination with an integrated ³¹P bore coil, ⁸ , ¹⁶ , ¹⁷ providing a homogeneous ${\mathrm{B}}_1^{+}$ field, and multi‐channel phased array receive coils, ⁸ , ¹⁷ this allows optimal sensitivity throughout the organ(s) of interest. Moreover, short TRs and Ernst‐angle excitation can be used to maximize the number of samples for a given acquisition time and thus also enabling acquisitions with a large FOV. ¹³

Despite these improvements, scan times generally are still long, typically between 10 min and 20 min, with typical nominal voxels sizes of 2 to 4 cm. Long scan times reduce patient comfort, increase motion artifacts, and limit clinical translation. Furthermore, low‐resolution acquisitions cause Gibbs‐ringing or so‐called signal bleeding. This is typically mitigated using a Hamming filter or performing Hamming‐weighted acquisition of k‐space. ¹⁸ However, Hamming filters cause an increase of the FWHM of the voxel point spread function (PSF), thereby extending the PSF beyond the nominal voxel size. This results in blurring; as such, not all signal originates from the desired or intended spatial location.

Furthermore, fitting spectra, similar to many inverse problems in MRI and MRS, is an ill‐posed problem with many degrees of freedom. ¹⁹ This means that small perturbations of the signal can have a large effect on the fitting results. Therefore, both spectral‐ and time‐domain fitting methods are often strongly regularized ²⁰ or need user‐defined prior knowledge. ²¹ Despite regularization and prior knowledge, the accuracy and precision of fitted metabolite concentrations are influenced by noise in ¹H ²² , ²³ , ²⁴ and ³¹P ²⁵ MRS for metabolite SNR levels below 30. Therefore, low SNR is seen as a challenge and pitfall for the quantification of many ³¹P metabolites. ²⁶ To overcome this, various denoising methods have been proposed, that is, spectral apodization ²⁷ or signal decomposition. ²⁸ , ²⁹ , ³⁰ However, none of such methods take advantage of the abundance of spectral information of CSI data.

Although a variety of methods for optimal ³¹P CSI acquisition exist, ¹³ only a few methods have been proposed for optimizing ³¹P CSI data processing. ¹ , ³¹ Most are aimed to optimize coil combinations in the absence of reliable coil sensitivity. ³² , ³³ For CSI datasets with a large number of voxels, such as 3D ³¹P CSI with a high spatial resolution and/or a large FOV, commonly used MRI processing techniques, for example, from Diffusion tensor imaging or fMRI, that are aimed to enhance data quality, may be applicable.

In this study, we propose 2 methods new to CSI data processing to enhance data quality after acquisition and coil combination. First, the use of principal component analysis (PCA)‐based denoising, ³⁴ , ³⁵ a technique commonly used in diffusion imaging, ³⁶ to enhance the effective SNR. Second, the use of regularized Wiener deconvolution, proposed in fMRI processing, ³⁷ , ³⁸ to reduce the increased FWHM of the voxel PSF caused by the Hamming filter without introducing Gibbs ringing. ³⁹ , ⁴⁰ The denoising and deconvolution methods are applied both to simulated and in vivo acquired 3D ³¹P CSI data to evaluate the effects of denoising and deconvolution on data quality and metabolite amplitude‐fitting performance.

2. METHODS

For this study, all simulations, processing, and fitting are performed using the open‐source toolbox QMRITools for Mathematica. ⁴¹ , ⁴² , ⁴³ The proposed processing pipeline for 3D CSI data comprises 2, for MRS, novel processing steps, that is, PCA denoising and deconvolution, which are explained below. To evaluate the processing steps, we used simulated and in vivo 3D CSI data.

2.1. Processing pipeline

The proposed processing pipeline comprises 3 steps—Hamming filter (HA), deconvolution (DC), and denoising (DN)—that can be applied in any order, although HA always precedes DC. Hamming‐filtering can be done either in the acquisition using a Hamming‐weighted k‐space acquisition (H) or by applying a Hamming‐kernel to an equally weighted k‐space acquisition (E). This operation is done in k‐space for each FID sample. The PCA‐denoising ³⁴ , ³⁵ removes noise from the spectra while maintaining the signal even if this signal is below the noise floor. Although the underlying SNR of the acquired k‐space points cannot be changed and thus remain constant, the effective SNR of the reconstructed spectra can be increased because the noise part of the signal is removed. This operation is performed in image space on a spatial patch of spectra, as is explained later. Finally, regularized Wiener deconvolution ³⁹ , ⁴⁰ is applied to reduce the FWHM of the PSF, which is increased by the Hamming filter while minimizing the reintroduction of the Gibbs‐ringing artifacts. This operation is performed in image space for each spectral point and is also explained later.

2.2. PCA denoising

The PCA denoising algorithm is shown schematically in Figure 1 and is based on the work by Veraart et al. ³⁴ , ³⁵ This method uses principal component analysis to remove noise components from the signal, which can be automatically be identified using the Marchenco‐Pastur distribution. The algorithm convolves the data with a box kernel of at least 5 × 5 × 5 voxels (see Figure 1A), but larger kernels can be used. For each voxel location, this local 5 × 5 × 5 patch is transformed into a matrix M, for which each row represents a voxel location and each column represents a location along the spectral domain. The spectra contain both a real and imaginary part, which are concatenated in the columns of M (see Figure 1A). For a spectrum with 256 samples, this local data matrix M of the 5 × 5 × 5 patch thus has dimensions 125 × 512. For optimal performance, the matrix M needs to be large; therefore, it works best on 3D CSI data for which a 3D patch is used. However, the method can also work in 2D using a larger patch (eg, 9 × 9) or for dynamic single voxel spectra for which ample dynamics are acquired.

FIGURE 1.

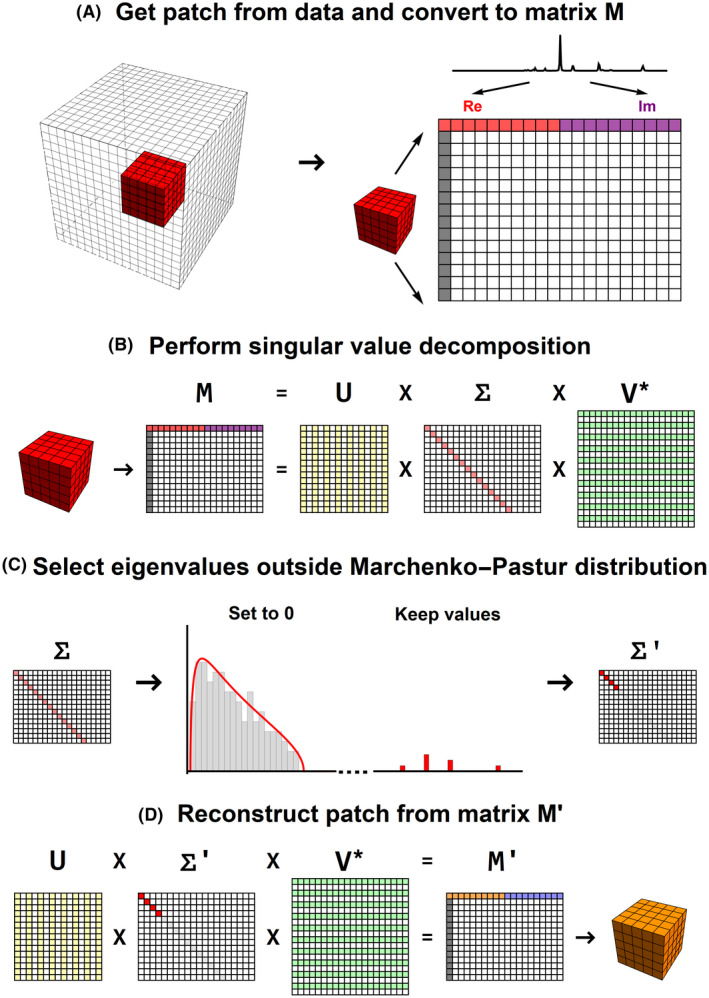
Schematic representation of the PCA denoising algorithm. (A) Conversion of an image patch to a signal matrix M. (B) SVD of the signal matrix M. (C) Finding the eigenvalues that lie within the Marchenco‐Pastur distribution and set those to 0. (D) Reconstruction of the image patch using the denoised signal matrix M′. PCA, principal component analysis; SVD, singular value decomposition

Next, a singular value decomposition of the matrix M is performed, as is shown in Figure 1B. If the noise level is constant among all elements of M and the matrix would only contain noise values, the eigenvalues of the SVD are described by the Marchenko‐Pastur Distribution. ⁴⁴ However, when the matrix also contains signal, the eigenvalues will contain both noise‐ and signal‐carrying eigenvalues (see Figure 1C). For denoising, all eigenvalues that fall within the Marchenko‐Pastur are set to 0, and the “noise‐free” signal matrix M′ can be reconstructed. The key advantage of this method is that there is no need for prior information about the signal or noise value. A detailed explanation of how to estimate the threshold for the relevant signal carrying eigenvalues is given in the original work by Veraart et al. ³⁵

In the final stage, the full denoised data are reconstructed from all the denoised patches. In the original methods by Veraart et al, only the center voxel of the reconstructed patch is the noise‐free data at that location. However, except for the border and corner voxels, each voxel is visited 125 times by the kernel; therefore, the final voxel value here is the average of each of the maximal 125 denoised patches.

2.3. Deconvolution

Image or data deconvolution can be used to restore the original signal from distorted data. ³⁹ , ⁴⁰ Deconvolution of 3D CSI data can be used to revert the increase of the FWHM of the voxel PSF caused by the Hamming filter. However, when data are deconvolved using a kernel that matches the blurring, all noise and Gibbs ringing artifacts are also restored. Therefore, we proposed to use regularized Wiener deconvolution of the absolute signal to decrease the FWHM of voxel PSF while minimizing the reintroduction artifacts and noise, as is schematically shown in Figure 2.

FIGURE 2.

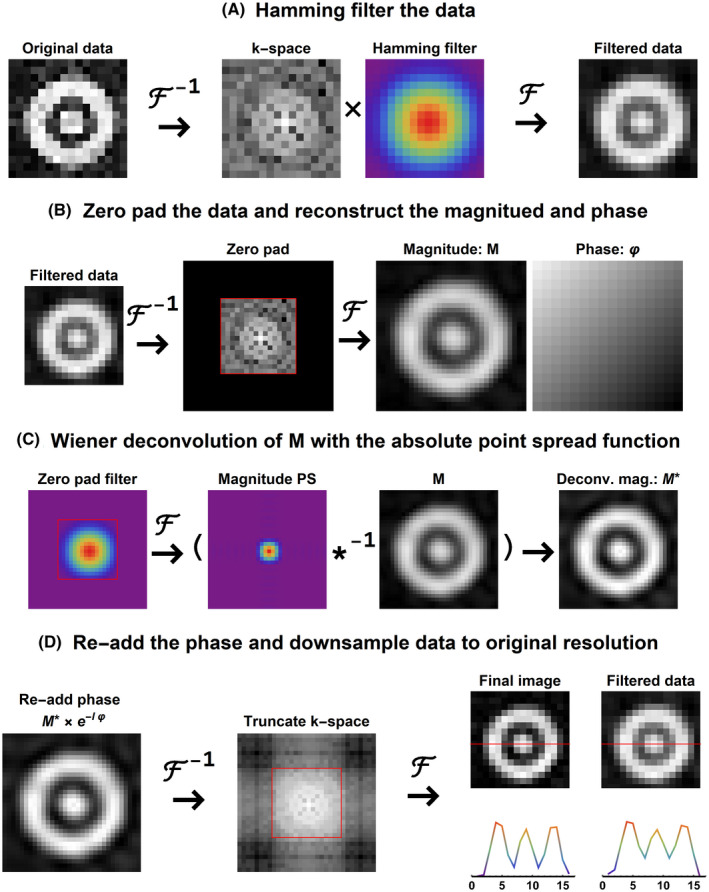
Schematic representation of the deconvolution algorithm. (A) Applying the Hamming filter to the data to reduce Gibbs‐ringing artifacts but increasing the voxel PSF. (B) Zero‐padding of data to increase the spatial resolution by a factor 2. (C) Obtaining the absolute PSF from a zero‐padded Hamming filter for regularized Wiener deconvolution of the magnitude data. (D) Reapplying the phase to the deconvolved magnitude data and truncation of k‐space to obtain the final deconvolved images in the original resolution. PSF, point spread function

The deconvolution is a spatial operation and thus has to be performed on each spectral point in the spectral domain; that is, for 3D CSI data that contains spectra with 256 samples, 256 individual 3D deconvolutions are performed. The increase of the FWHM of the PSF as a result of the Hamming‐filtering is shown in Figure 2A. To revert this operation, for each 3D volume at every point of the spectral domain the following steps are performed: First, the 3D CSI data are zero‐padded to double the spatial resolution (see Figure 2B). Next, the magnitude and phase data are reconstructed. Because we want to maintain the phase of the spectra and assume the phase of each spectral point is spatially smooth, we do not have to deconvolve the phase but only the magnitude data. To obtain the PSF with which the magnitude data are blurred, the applied Hamming filter (or k‐space weighting) is zero‐padded and converted to the image domain (see Figure 2C). Then, the blurred magnitude data are restored with the magnitude of this PSF using a regularized Wiener deconvolution. To obtain the restored complex data, the phase of the data is added back to the deconvolved magnitude data. Finally, the k‐space is truncated such that the data retains its original resolution, as is shown in Figure 2D.

2.4. Simulation

To evaluate the best order of the proposed processing steps, we simulated 2 datasets: the first consists of a spherical phantom with a hole and a rod that is rotated over 3 axes to avoid x, y, and z symmetry (as shown in Figure 3A); and the second only has signal in a 2 × 2 × 2 cm³ region. The data were simulated with a FOV of 240 × 320 × 320 mm³, which would be similar to a normal in vivo ³¹P CSI FOV for body and extremities applications yet assumes high resolution (2 × 2 × 2 mm³) isotropic voxels resulting in a matrix size of 120 × 160 × 160. For each voxel within the phantom, spectra were simulated based on typical muscle metabolite concentrations. The spectra were simulated using scalar coupling (J‐coupling) simulations of basis spectra for each metabolite based on methods presented in FID‐A. ⁴⁵

FIGURE 3.

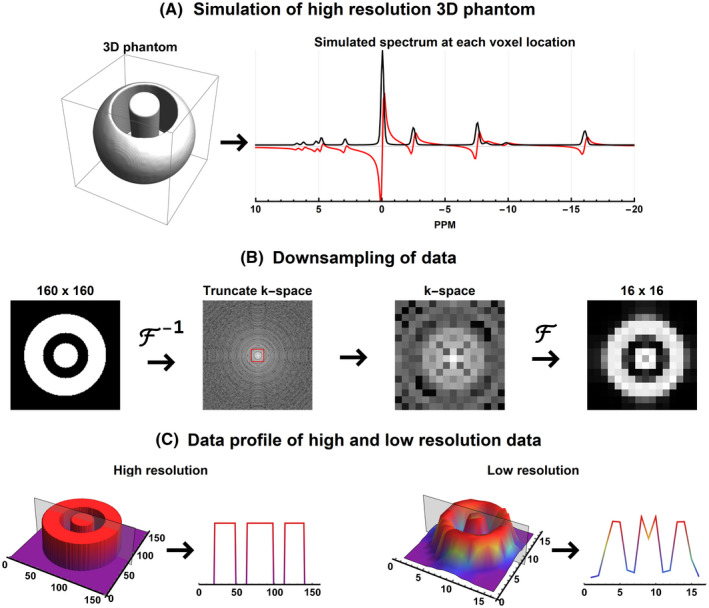
Schematic overview of the data simulation. (A) High resolution (120 × 160 × 160 voxels) spherical 3D phantom and the simulated spectrum that is used for each voxel. Supporting Information Table S1 lists the absolute peak amplitudes and effective SNR of each metabolite. (B) Downsampling of the high‐resolution phantom to typical ³¹P CSI resolution of 12 × 16 × 16 voxels. (C) The signal profile of the center slice of the simulated phantom at the original and downsampled resolution. ³¹P, phosphorus; CSI, chemical shift imaging

The simulated metabolites and their concentrations used for the spectra in every voxel are listed in Supporting Information Table S1. The spectra were simulated with the following parameters— sequence: pulse acquire; number of samples: 256; bandwidth: 5000 Hz; TE: 0 ms; field strength: 7 Tesla; linewidth: 50 Hz; line‐shape: Voigt. Next, complex normally distributed noise was added to the data such that the PCr peak would have an absolute SNR of 20 if 6 NSA would be used (ie, PCr magnitude = 1000; noise σ = 122.5, SNR of PCr for a single spectrum: 8.16).

To mimic signal averaging, 35 individual datasets were created with unique noise realization. After the noisy high‐resolution phantom was created in image space, it was transformed to k‐space and truncated to a resolution of 12 × 16 × 16 voxels with a resolution of 2 × 2 × 2 cm³ (see Figure 3B). In Figure 3C, it can be seen that the low‐resolution dataset contains the typical Gibbs‐ringing artifacts that are expected in low‐resolution 3D data. Two datasets were then generated: the first with equal k‐space weighting (Sim‐E) using 6 signal averages and the second using 35 signal averages but with Hamming k‐space weighting (Sim‐H). Thus, for the latter dataset, only the center k‐pace point has 35 averages. These numbers were chosen such that both datasets contain a similar amount of sampled k‐space points (~18500). To obtain a Hamming‐weighted k‐space, the acquisitions were added in k‐space and not averaged. An example spectrum for each of the 2 datasets is shown in Supporting Information Figure S1.

2.5. MRS experiments

To evaluate the proposed processing pipeline, 2 separate in vivo 3D CSI datasets of the upper legs (male subject, 39 years of age) were acquired during 1 scan session: the first with an equally weighted k‐space and the other with a Hamming weighted k‐space. Data acquisition was according to the institutional guidelines and with approval from the local ethics committee. For this, we used a 7 Tesla Philips scanner equipped with a ³¹P bore coil for transmitting and a 16‐channel ³¹P receive array ⁸ , ¹⁶ , ¹⁷ with 8 ¹H Tx/Rx antennas for proton imaging. ⁴⁶ On top of the middle of the left leg, a falcon tube containing polyphosphoric acid (20 ppm, 0.97 M) was placed. Data were acquired with a 3D pulse acquire CSI acquisition with the following imaging parameters: FOV: 400 × 240 × 240 mm³; voxel size 2 × 2 × 2 cm³; flip angle 15°; number of samples 256; bandwidth 5000 Hz; TE: 0.48 ms; TR: 60 ms. B₀ shimming was done using image‐based shimming using an acquired proton B₀ map. ⁴⁷ To allow for optimal B₀ shimming, the phases of the transmit elements were calibrated using image‐based B₁ shimming. ⁴⁸ , ⁴⁹ For the first dataset, an equal‐weighted k‐space was acquired with 4 signal averages (Data‐E); and for the second dataset, a Hamming‐weighted k‐space was acquired with 24 signal averages for the center k‐space point (Data‐H). The scan times were 11 min 51 s (11520 k‐space points) and 12 min 27 s (12370 k‐space points), respectively. Data analysis was performed on both datasets; therefore, all results are labeled with either Data‐E or Data‐H, indicating the use of either the equally weighted or Hamming weighted data.

The 16‐channel data were reconstructed using Roemer equal noise reconstruction ⁵⁰ , ⁵¹ in which the coil sensitivity data were estimated by dividing the complex coil data by the sum of squares reconstruction of the coil data. Additionally, the data were also reconstructed using whitened singular‐value decomposition (WSVD) reconstruction, ³² , ³³ the results for which are shown in the Supporting Information.

2.6. Data processing

To evaluate the optimal order of the processing steps explained earlier, different processing pipelines for each of the 2 different types of datasets, that is, equally and Hamming weighted k‐space, were evaluated. For the equally weighted k‐space data (Sim/Data‐E), 3 pipelines were investigated: 1) Hamming filtering followed by deconvolution and denoising (HA+DC+DN), 2) Hamming filtering followed by denoising and deconvolution (HA+DN+DC), and 3) denoising followed by Hamming filtering and deconvolution (DN+HA+DC). For the Hamming‐weighted k‐space data (Sim/Data‐H), 2 pipelines were investigated as the Hamming filtering can be omitted because it is part of the acquisition: 1) deconvolution followed by denoising (DC+DN), and 2) denoising followed by deconvolution (DN+DC).

2.7. Spectral fitting and visualization

To evaluate the performance of the proposed processing, we fit the simulated and acquired MRS spectra to evaluate the magnitudes of the individual metabolites. The spectral fitting was done by fitting basis‐spectra generated by J‐coupling simulations without considering relaxation parameters—similar to FID‐A (version 1.2) ⁴⁵ —to the spectra analogous to other software tools such as LCModel, Tarquin (version 4.3.10), and Osprey. ²⁰ , ⁵² , ⁵³ , ⁵⁴ The fitting procedure is done simultaneously in the time and frequency domain. This means that we obtain the fitting error in the spectral domain using apodized and zero‐filled spectra ²⁷ as well as in the time domain using the raw FID signal. The summed fitting error is then minimized during the fitting procedure. During fitting, the amplitude, line shape, linewidth, and peak shift of each metabolite, as well as a common value for the zeroth and first order phases, were optimized. The fitting error was defined as the sum of real and imaginary RMS error in both the spectral (range 10 to −20 ppm) and time domain. The used basis‐spectra are polyphosphoric acid (which was used in the phantom), polyphosphoric acid, phosphoethanolamine, phosphocholine (PC), intra‐ and extracellular free phosphate (Piex, Piin), glycerophosphoethanolamine, glycerophosphocholine, PCr, adenosine triphosphate (ATP‐γ, ATP‐α, ATP‐β), nicotinamide adenine dinucleotide phosphate, and uridine diphosphate.

For visualization of the fitted spectra, the spectra were corrected for the zeroth and first order phase based on fitted values, and the missing FID points due to the TE delay were extrapolated using a Hankel matrix SVD algorithm. ⁵⁵ All spectra shown in this manuscript were apodized using a Hanning window and zero‐padded by a factor 2.

2.8. Evaluation of processing

To evaluate the performance of each pipeline on the simulated and in vivo data, we performed 3 analyses: 1) visual inspection of the spatial signal distribution; 2) SNR calculation of the absolute PCr peak; and 3) fitting error of metabolite basis functions. Visual inspection was performed by looking at the spatial signal distribution of the absolute integrated spectral signal and by looking at the spectra quality (all authors performed the evaluation; experience varies from little to over 10 years). To evaluate the effective SNR and fitting of metabolites, 500 voxels with the highest absolute signal amplitude over all datasets were selected from each processed dataset. For the effective SNR calculation, the noise SD σ was estimated from the complex first and last 20 samples of each spectrum, which are assumed to only contain noise. The signal S was defined as the mean maximal absolute signal of the 500 selected voxels, and thus the effective SNR was defined as SNR = √2 S/ σ. For these same 500 voxels, the metabolite basis‐spectra were fitted to the spectra and normalized to the PCr amplitude. For the simulations, these fitted relative magnitudes were then compared to the known simulated values. For each metabolite, the relative error was calculated. Ideally the relative error has zero mean, meaning high accuracy, and a low SD, meaning high precision. Additionally, for all metabolites combined the mean, median, maximum, and minimum absolute error were computed, for which low values indicate a good overall accuracy and low SD a good overall precision. Here, we use the absolute error overall to reveal best and worst cases, for which a negative and positive bias is equally bad. For the in vivo data, fitted metabolite maps relative to the mean amplitude of the ATP peaks were created relative to the mean ATP amplitude per voxel, expressed as a percentage.

3. RESULTS

The current implementation of the proposed processing steps resulted in an average computation time of approximately 5 s and 15 s for the deconvolution and PCA denoising, respectively. These times were obtained for a 20 × 12 × 12 voxel dataset, with 256 spectral samples using a single core of an Intel Core i7 6820HQ 2.70GHz processor (Intel, Santa Clara, CA, USA).

3.1. Simulations

Using simulations each step of the processing was evaluated by visual inspection, evaluation of the point spread function, SNR calculation, and fitting. For the visual inspection of the spherical phantom, we selected 2 voxels, 1 voxel in the middle of the phantom containing signal and 1 voxel in between the rod and the outer sphere of the phantom, which should not contain signal.

3.2. Visual inspection

The effect of the processing order of the simulated spectra is shown in Figure 4 and Supporting Information Figure S2. Applying a Hamming filter or using Hamming‐weighted k‐space acquisition increases the effective SNR but blurs the image (see Supporting Information Figure S2B, and F). All processing pipeline orders provide similar results; however, Sim‐E DN+HA+DC (see Figure 4C) and Sim‐H DN+DC give the best SNR. After deconvolution, one can appreciate that the blurring is almost completely reverted. The maximal absolute amplitudes of PCr peaks in the green spectrum in Figure 4C is only 12% of the PCr peak shown in the red spectrum.

FIGURE 4.

Results of the evaluated processing pipelines on the Sim‐E weighted data. Each subfigure shows magnitude images of the mean spectral signal and the signal profile of the center slice of the simulated data. Below, it shows 2 example spectra all scaled relative to the same maximum amplitude. In red a spectrum is shown of the center voxel that should contain maximal signal and in green a voxel located in between 2 signal regions, which should show little to no signal. Abbreviations: Sim‐E, Simulated equal

3.3. Point spread function

The effect of processing on the PSF of the single voxel phantom is shown in Figure 5. The simulated voxel size, defined as the volume at the half maximum of the signal, was 8 cm³ for the high‐resolution data, which increased to 10.0 cm³ after downscaling, that is, an increase of 250%. Before and after denoising, the characteristic Gibbs ringing due to the low spatial resolution can be seen. After applying a Hamming filter (similar to Hamming weighted k‐space acquisition), the Gibbs ringing was removed; however, the effective voxel size was increased to 30.5 cm³, that is, an increase of 281%. After deconvolution, the effective voxel size was reduced to 18.9 cm³, resulting in an increase of the voxel size of only 136% compared to the original data. Compared to the raw data without the addition of noise, Hamming filtering (HA) reduced the maximum amplitude of Gibbs ringing by 98% and 78% for the real and imaginary part of the signal, respectively. Consecutively applying hamming filtering and deconvolution (HA+DC) reduces the maximum amplitude of Gibbs by 55% and 72% for the real and imaginary part of the signal, respectively. The regularization factor for the Wiener deconvolution was set to 0.01, which was the optimal balance between reducing the PSF and minimizing voxel bleeding (See Supporting Information Figure S3).

FIGURE 5.

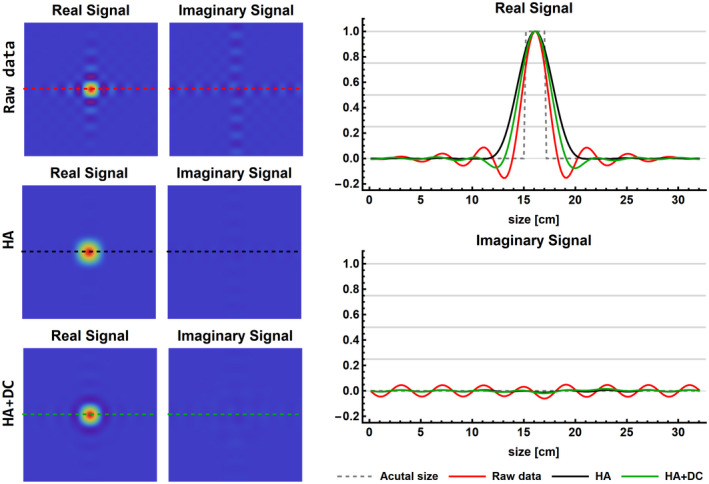
Results of the single voxel simulation to illustrate the effects of processing on the FWHM of the PSF and the Gibbs ringing. The signals are shown as a cross‐section through the voxel of the 3D CSI data at the spectral location of the PCr peak. The real and imaginary signals of the Raw, HA, and HA+DC data are shown in 2D (left column) and 1D (right column). DC, deconvolution; HA, Hamming filter

3.4. SNR evaluation

The mean effective SNR of the PCr peak for the 500 voxels with the maximal signal is reported in Table 1, and SNR maps are shown in Supporting Information Figure S4. Hamming filtering of the equal‐weighted k‐space data increases the effective SNR of the PCr peak from 21 to 66, whereas the Hamming‐weighted k‐space resulted in an SNR of 97. For both the equal and Hamming‐weighted k‐space acquisition, the largest SNR gain was obtained when first applying the PCA denoising, resulting in an effective SNR of 301 and 303, respectively. For the PCA, denoised equal‐weighted k‐space acquisition followed by the Hamming filter, an effective SNR of 463 was obtained. After deconvolution, the effective SNR for the PCA denoised equal k‐space weighting was 440 and for the Hamming‐weighted k‐space 297. This is an approximate SNR gain of four‐ and threefold compared to the raw Hamming‐weighted k‐space data, respectively. The additional effects of apodization on SNR before and after using the proposed pipeline are shown in the Supporting Information Table S2.

TABLE 1.

Effective spectral SNR of the PCr peak after each processing step for simulated and in vivo data

Data Equal k‐space (NSA = 6; k‐space points = 18432)				Data Hamming k‐space (NSA = 35; k‐space points = 18592)
Raw	1 Step	2 Steps	3 Steps	Raw	1 Step	2 Steps
A. Simulated data
Raw: 21	HA: 66	HA+DC: 52	HA+DC+DN: 118	Raw: 97	DC: 91	DC+DN: 226
		HA+DN: 403	HA+DN+DC: 94		DN: 303	DN+DC: 297
	DN: 301	DN+HA: 463	DN+HA+DC: 440

Data Equal k‐space (NSA = 4; k‐space points = 11520)				Data Hamming k‐space (NSA = 24; k‐space points = 12370)
Raw	1 step	2 steps	3 steps	Raw	1 step	2 steps
B. In vivo data Roemer coil combination
Raw: 23	HA: 57	HA+DC: 45	HA+DC+DN: 83	Raw: 76	DC: 83	DC+DN: 216
		HA+DN: 81	HA+DN+DC: 71		DN: 218	DN+DC: 206
	DN: 181	DN+HA: 226	DN+HA+DC: 209

DC, Wiener deconvolution; DN, PCA denoising; HA, Hamming filter of k‐space; NSA, q number of signal averages; PCr, phosphocreatine.

3.5. Spectra fitting

For each of the simulated datasets, 500 spectra were fitted, and the relative error compared to the defined metabolite amplitudes are reported in Table 2 and Supporting Information Table S3. The lowest mean error per metabolite is mostly present in Sim‐H DN+DC and Sim‐H. However, for Sim‐H we have seen that the data are blurred. The mean, median, minimum, and maximal absolute errors for all metabolites are also listed in Table 2 and Supporting Information Table S3. For each of these measures, Sim‐H DN +DC shows the best fitting results. However, these results were only marginally better than the results obtained with Sim‐E DN+HA+DC. As expected, the metabolites with the smallest simulated amplitudes showed the highest fitting errors but are considerably improved after processing; that is, the fitting error of phosphoethanolamine goes from 131% in Sim‐E to 0.1% in Sim‐E DN+HA+DC. Furthermore, when evaluating the relative errors per metabolite Sim‐H and Sim‐H, DC+DC are very similar, whereas Sim‐E has slightly better accuracy but overall lower precision compared to Sim‐H: DC+DC. This is even more apparent when looking at the mean, median, maximum, and minimum absolute errors, which are lower after processing. Furthermore, in Table 2 it can be seen that adding denoising to Hamming filtering or Hamming weighted acquisition decreases the fitting error compared to only using Hamming filtering or Hamming weighted acquisition. By adding the Wiener deconvolution, the fitting error slightly increases; however, this considerably reduces the voxel PSF, resulting in better signal localization.

TABLE 2.

Relative errors of fitting results of spectra from simulated data

	Defined Magnitude	Relative Error Equal‐Weighted Data				Relative Error Hamming‐Weighted Data
		Sim‐E [%]	Sim‐E HA [%]	Sim‐E DN+HA [%]	Sim‐E DN+HA+DC[%]	Sim‐H [%]	Sim‐H DN [%]	Sim‐H DN+DC [%]
PE	17	131.0 ± 234.7	15.3 ± 82.6	4.0 ± 18.3	4.3 ± 19.8	9.1 ± 59.1	1.1 ± 14.7	−3.0 ± 19.4
PC	30	63.0 ± 134.3	16.0 ± 44.4	12.5 ± 8.3	12.5 ± 9.6	3.6 ± 30.8	−0.2 ± 10.3	−3.3 ± 13.5
Piex	39	41.8 ± 109.9	3.5 ± 39.7	−4.9 ± 14.9	−4.8 ± 15.6	2.1 ± 26.7	−1.0 ± 10.2	−2.8 ± 12.6
Piin	78	10.4 ± 53.5	1.4 ± 17.1	0.4 ± 4.3	0.5 ± 4.9	0.5 ± 12.8	0.4 ± 4.4	−1.2 ± 5.9
GPE	0	‐	‐	‐	‐	‐	‐	‐
GPC	64	17.4 ± 65.0	2.2 ± 21.4	−0.7 ± 5.7	−0.5 ± 6.3	0.3 ± 14.5	−0.7 ± 5.0	−2.4 ± 6.7
PCr	1000	‐	‐	‐	‐	‐	‐	‐
ATP‐γ	231	1.9 ± 21.9	−0.5 ± 6.7	−0.6 ± 1.4	−0.6 ± 1.7	−0.3 ± 4.8	−0.4 ± 1.6	−0.7 ± 2.2
ATP‐α	290	−2.1 ± 19.6	−1.1 ± 7.3	−0.8 ± 1.9	−0.7 ± 2.0	−0.2 ± 4.9	0.2 ± 1.5	−0.3 ± 1.9
ATP‐β	210	5.7 ± 25.1	1.1 ± 8.2	1.0 ± 2.3	1.0 ± 2.5	0.4 ± 5.6	0.2 ± 2.0	−0.3 ± 2.7
NAD	18	92.7 ± 167.1	20.7 ± 59.3	8.2 ± 14.8	8.5 ± 15.7	9.6 ± 39.2	2.1 ± 11.6	−0.1 ± 14.6
UDPG	20	61.0 ± 126.5	6.9 ± 45.5	−0.1 ± 8.8	0.1 ± 10.1	3.9 ± 29.0	−0.6 ± 9.3	−4.3 ± 12.8
Mean abs error		82.4 ± 30.1	26.4 ± 9.5	7.7 ± 2.0	8.2 ± 2.2	17.7 ± 6.7	5.5 ± 1.9	7.3 ± 3.0
Median abs error		55.2 ± 23.7	15.6 ± 7.4	4.9 ± 2.0	5.1 ± 2.2	10.8 ± 5.2	3.5 ± 1.6	4.8 ± 2.4
Max abs error		285.0 ± 162.5	91.6 ± 47.6	23.7 ± 7.2	25.4 ± 8.0	62.1 ± 34.5	18.1 ± 7.9	23.0 ± 11.3
Min abs error		5.2 ± 5.0	1.7 ± 1.5	0.5 ± 0.4	0.6 ± 0.5	1.1 ± 1.0	0.4 ± 0.4	0.5 ± 0.5

The simulated amplitudes of the metabolites are listed in the second column. For each processing pipeline, the relative error of each metabolite amplitude after fitting is reported in the consecutive columns. In the bottom 4 rows, the mean, median, maximum, and minimum absolute errors overall metabolites are reported.

Abbreviations: ATP‐β, ATP‐γ, ATP‐α, adenosine triphosphate; GPC, glycerophosphocholine; GPE, glycerophosphoethanolamine; NAD, nicotinamide adenine dinucleotide phosphate; PC, phosphocholine; PE, phosphoethanolamine; Piex, extracellular free phosphate; Piin, intracellular free phosphate; sim‐E, simulated‐equal; sim‐H, simulated‐hamming; UDPG, uridine diphosphate.

3.6. MRS experiments

All results shown here are for data reconstructed with Roemer coil combination. Each of these results was also obtained for data with WSVD coil combination and is presented in Supporting Information. For the visual inspection, we selected 2 example voxels, 1 in the muscle tissue at the back of the leg where a high signal is expected and 1 in the bone where no well‐resolved phosphorus‐containing metabolite peaks are expected.

3.7. Visual inspection

The effect of processing of the acquired data are shown in Figure 6 and Supporting Information Figure S5. Similar to the results of the simulated data processing increased the SNR of the spectra. Furthermore, from Supporting Information Figure S5B and S5F, it is clear that Hamming weighting of the k‐space increases the FWHM of the voxel PSF. This can especially be appreciated in the bone regions, where no well‐resolved phosphorus‐containing metabolite peaks are expected. For both the equal and Hamming‐weighted data, deconvolution can restore part of this blurring, as can be seen in the green spectra in Figure 6. Although the results are not as pronounced as for the simulated data, the deconvolution step does increase the sharpness of the images, as is shown in Figure 6C. When using the WSVD coil combination, similar results were obtained compared with using the Roemer coil combination (see Supporting Information Figure S6).

FIGURE 6.

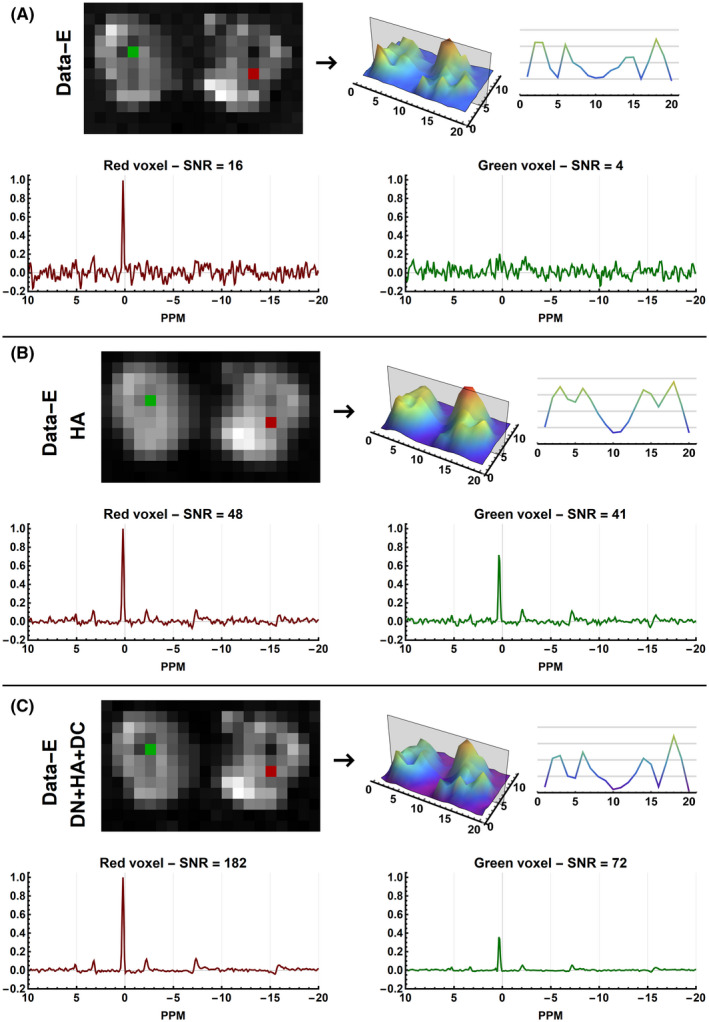
Results of the evaluated processing pipelines on the equal (Data‐E) weighted in vivo CSI data of the upper legs using Roemer coil combination. Each subfigure shows magnitude images of the mean spectral signal and the signal profile of the center slice of the acquired data. Below, it shows two example spectra all scaled relative to the same maximum amplitude. In red a spectrum is shown of muscle data that should contain maximal signal and in green a voxel located in the bone, which should show little to no signal. The reported SNR values are those of the PCr peak

3.8. SNR evaluation

After processing the acquired data, the effective SNR increased, similarly to what was shown in the simulations (see Table 1 and Supporting Information Figure S4). However, the SNR gain was not as large even though the in vivo data had similar SNR values as the simulated data. Hamming filtering and Hamming‐weighted acquisition increased the SNR of the PCr peak from 23 to 57 and 76, respectively. Hamming weighted k‐space acquisition results in a slightly higher effective SNR compared to equal‐weighted k‐space acquisition with Hamming filtering, but both have similar effective SNR after processing. The highest SNR value was obtained for Data‐E DN+HA+DC with an SNR value of 209, whereas Data‐H DN+DC resulted in an SNR of 206, both an approximate threefold SNR increase compared to the unprocessed Hamming‐weighted k‐space data. In the Supporting Information Table S4, the same results are presented for the WSVD coil combination. Here the initial SNR was 41, and the relative gain of SNR using the various processing steps was similar to those obtained using the Roemer coil combination. The maximal SNR obtained with the WSVD coil combination was 369 for Data‐H DN+DC. Spectral apodization is used during the fitting procedure, therefore, the effects of apodization on the effective SNR before and after using the proposed pipeline are shown in the Supporting Information Table S5.

3.9. Spectral fitting

Fitting results of a single measured spectrum before and after processing are shown in Figure 7. It is clear that the lowest SNR data (Data‐E) also results in the least convincing fitting results with a residual error of −0.6% ± 6.7% relative to the maximal signal of the PCr peak. Hamming‐weighting of the k‐space increases the SNR and as a result also allows for more robust spectra fitting, reducing the residual error to −0.0% ± 2.3% and −0.2% ± 1.8% for Data‐E HA and Data‐H, respectively. After full processing, the residual error is decreased even further to 0.0% ± 1.1% and −0.1% ± 1.1% for Data‐E DN+HA+DC and Data‐H DN+DC, respectively. Improved fitting is especially clear for metabolites with low concentrations, as is shown in insets shown in Figure 7.

FIGURE 7.

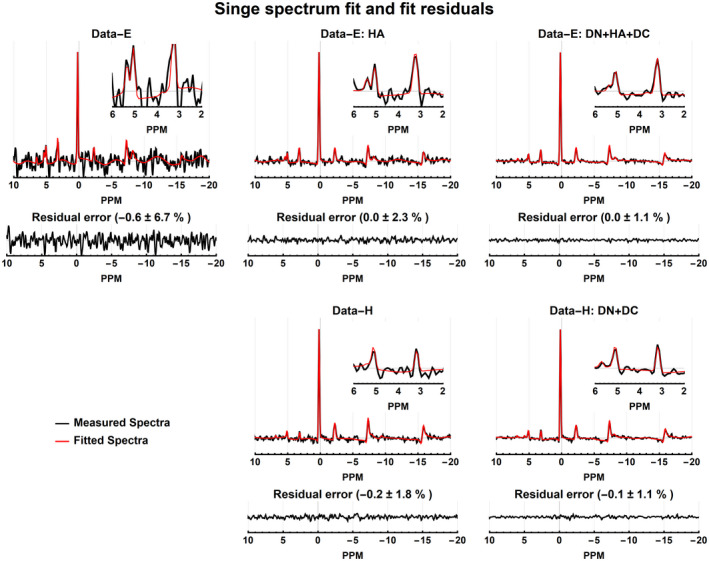
Fits of a single voxel (red voxel of Figure 6) spectrum before and after processing. The panels show the real measured and fitted spectra, and real residual errors. The mean and SD of the residual errors are reported in the percentage of the PCr amplitude

Figure 8 shows the fitted metabolite amplitudes relative to the mean fitted ATP amplitudes. Due to the relatively low SNR of Data‐E, it can be seen that the fitting results are poorest because the metabolite maps are very inhomogeneous and noisy. Especially for the low‐concentration metabolites such as PC, nicotinamide adenine dinucleotide phosphate, and Pi, the processing improved the homogeneity of the metabolite maps. After full processing, the fitted metabolite maps of Data‐E and Data‐H are comparable. For example, the PC/ATP ratio for Data‐H is 8.5 (2.0 ‐ 18.6)%, but after processing (Data‐H DN+DC) the ratio is 5.6 (1.3 ‐ 11)%, which is comparable to DataE DN+HA+DC for which the ratio is 7.2 (1.3 ‐ 16)%.

FIGURE 8.

Fitting results of the equal and Hamming weighted data using Roemer coil combination before and after processing represented as metabolite maps. The metabolite maps are calculated relative to the ATP amplitude in the respective voxel and expressed as a percentage. The metabolites shown are PE, PC, the sum of the intra‐ and extracellular free Pi, GPC, PCr, NAD, and UDPG. Above each panel, the mean amplitude and its range relative to the ATP amplitude (as a percentage) is reported for the entire muscle volume. ATP, adenosine triphosphate; GPC, glycerophosphocholine; NAD, nicotinamide adenine dinucleotide phosphate; PC, phosphocholine; PCr, phosphocreatine; PE, phosphoethanolamine; Pi, phosphate; UDPG, uridine diphosphate

Although the maximal SNR for the WSVD coil combination was higher than the Roemer coil combination, the fitting results were similar with slightly lower residual errors for the Roemer coil combination (see Supporting Information Figure S7). The metabolite maps and distribution maps are also very similar between both coil combination methods (see Supporting Information Figure S8).

4. DISCUSSION

In this study, we implemented 2 methods for enhancing SNR and reverting the increase of the FWHM of the voxel PSF caused by Hamming‐filtering of the spatial k‐space and applied these to simulated and in vivo acquired 3D ³¹P CSI data. Hamming filtering increases the effective SNR and reduces voxel bleeding but also substantially increases the FWHM of the voxel PSF. We have shown that the PCA denoising algorithm enhances the SNR in the spectral domain threefold for in vivo data of the upper leg muscles compared to Hamming‐weighted CSI data. Furthermore, regularized Wiener deconvolution decreased the FWHM of the voxel PSF while maintaining the SNR and still minimizing Gibbs ringing artifacts.

4.1. PCA denoising

PCA‐based denoising was previously developed for diffusion data of the brain ³⁴ , ³⁵ and has since found its way to other applications such as muscle diffusion data. ⁴¹ Here, we have shown the ability to enhance the SNR of 3D ³¹P CSI data. However, the method is not limited to 3D data. The only requirement is that a large matrix, with spatially relatively homogeneous noise and signal, can be constructed. As such, it can also be applied to 2D CSI data, for example, using a kernel of 7 × 7 or 9 × 9, as long as the matrix is large. It can even be extended to dynamically acquired single voxel data if the number of dynamics is large. An example of dynamic single voxel denoising using 150 dynamics is shown in the Supporting Information Figure S9.

In the PCA denoising algorithm, only the eigenvalues of the PCA decomposition which describe random noise that fall within the Marchenco‐Pastur distribution are eliminated. This means that constant signals below the noise floor are maintained after denoising. This is shown in the simulations presented in this study in which some of the simulated metabolites had SNR values smaller than 1 but could still be resolved and fitted after denoising. This affirms that the method does not eliminate small signals from the data due to denoising. Another advantage is that no prior information about the signal or the noise variance is needed. The PCA denoising method has similarities to other methods that use signal decomposition to separate desired signals from the noise, for example, WSVD for optimal coil combination ³³ ; Tensor Rank truncation‐Image enhancement ³¹ ; or stable, linear, time‐frequency denoising. ⁵⁶

Denoising performed better on simulated data than on in vivo measured data, with an approximate SNR gain of 5 and 3 compared to Hamming weighted k‐space data, respectively. This is probably because the simulated data contained identical spectra for all voxels with no spatial phase variations, no peak shifting, or changing line shapes. For the in vivo data, WSVD reconstruction of Hamming‐weighted k‐space with DN+DC resulted in the highest absolute SNR of 369. But overall we found a similar performance of the denoising algorithm for equal‐ and Hamming‐weighted acquisitions and for Roemer and WSVD coil combinations. In practice, a Hamming‐weighted acquisition provides the highest flexibility for optimizing the scan time, and for our data, Roemer coil combination resulted in the most homogeneous signal reconstruction. Furthermore, equal‐weighted k‐space data with Hamming filtering has around 30% less effective SNR compared to the Hamming weighted k‐space data; however, after processing both have the same effective SNR.

4.2. Deconvolution

Spatial Hamming‐filters are commonly applied to CSI k‐space data to reduce voxel bleeding and enhance SNR, but they increase the FWHM of the voxel PSF. Here, we proposed to use regularized Wiener deconvolution to revert the enlargement of the voxel PSF induced by the Hamming filter, without introducing Gibbs ringing or decreasing the SNR. Wiener deconvolution is widely used to enhance signals from recorded data and has been used for fMRI processing ³⁷ , ³⁸ and MRI image enhancement. ³⁹ , ⁴⁰

Because we can assume that the spatial phase of an MR image or CSI data set is smooth, we proposed to perform the deconvolution in the spatial domain for each absolute spectral point. Before we performed the deconvolution, data were up‐sampled by a factor 2 in the spatial domain. This allowed for a better definition of the voxel PSF and to better prevent the reintroduction of Gibbs‐ringing artifacts. A similar up‐sampling approach was used in the work by Haupt et al, in which the used iterative k‐space extrapolation to reduce lipid artifacts. ⁵⁷ The regularization of the Wiener deconvolution is used to prevent noise enhancement and Gibbs ringing enhancement after deconvolution. Without regularization, noise is enhanced and Gibbs‐ringing is restored. However, if there is too much regularization, the FWHM of the PSF is not reduced. The regularization was optimized empirically (0.01) using the simulated data using various regularization factors at different SNR and by evaluating at which regularization factor there was a correct balance between reduction of the FWHM of the PSF and minimization of Gibbs ringing. Because the deconvolution only takes seconds, this optimization can be done quickly. With this optimal factor, for both the simulated and in vivo data, deconvolution slightly decreased the SNR while still reducing the effective voxel size.

The effect of deconvolution is best appreciated in the SNR shown in Supporting Information Figure S4. From these maps, it is clear that Hamming‐filtering or Hamming‐weighted acquisition enhances the SNR. However, the definition of the bone is less clear. This is resolved by deconvolution, after which the anatomical structures are better distinguished without reducing the SNR.

4.3. Spectral apodization and fitting

In spectral processing, commonly, spectra are apodized and zero‐padded in the time domain for better visualization and to enhance fitting performance in the spectral domain. ²⁷ This was also done in this study, as stated in the method section. Similar to the spatial Hamming‐filter, spectral apodization increases SNR. As expected, spectral apodization increased the SNR; but in general, the relative SNR gains were similar with and without spectral apodization. However, in some cases, apodization even slightly decreased the SNR. This is most likely due to the increased linewidth of the PCr peak because we used the maximal absolute signal intensity for the SNR calculations. The effect of processing of fitting performance depends on the method used ²⁷ , ⁵⁸ and whether the fitting is done in the time or frequency domain or a combination of both. ⁵⁹ However, for signal fitting a higher effective SNR is generally beneficial. ²⁷ , ⁵⁸

4.4. Study implications

Exciting developments in CSI acquisition ¹³ and hardware ⁸ , ¹⁶ , ¹⁷ on ultrahigh field MRI scanners ¹⁴ , ¹⁵ are enabling faster CSI measurements with an increasing FOV and higher spatial resolution. Therefore, CSI is getting closer to conventional MR imaging methods and processing methods used in the imaging field also become applicable to CSI, as was demonstrated in this study. Although in this study, we used ³¹P CSI data, the methods presented are not limited to ³¹P and can be used for other nuclei such as ¹H, ²H, and ¹³C. Of course, the feasibility of other applications needs to be investigated.

5. CONCLUSION

In this study, we have shown that PCA‐based denoising in combination with regularized Wiener deconvolution allows increasing the effective spectral SNR of in vivo ³¹P 3D CSI data, with a reduction of the FWHM of the voxel PSF. Processing increased the effective SNR by at least threefold compared to Hamming weighted acquired data and minimized voxel bleeding. With these methods, fitting of metabolite amplitudes became more robust with decreased fitting residuals.

Supporting information

FIGURE S1 Simulation of the equal and Hamming‐weighted k‐space data using 6 and 35 signal averages, respectively, together with example spectra

FIGURE S2 Results of the evaluated processing pipelines on the simulated equal (data‐E) and Hamming (data‐H) weighted data. The left column shows magnitude images of the mean spectral signal and the signal profile of the center slice of the simulated data. On the right, it shows two example spectra all scaled relative to the same maximum amplitude. In red a spectrum is shown of the center voxel that should contain maximal signal and in green a voxel located in between two signal regions which should show little to no signal. The reported SNR values are those of the PCr peak

FIGURE S3 The effect of the regularization factor of the Wiener deconvolution on the voxel point spread function and Gibbs ringing. Increasing the regularization increases the voxel PSF and decreases the Gibbs ringing. The choice for regularization was made such that the voxel point spread function was reduced by half while only 50% of the Gibbs ringing was reintroduced

FIGURE S4 SNR maps of the simulated (Sim) and in‐vivo data (Data) before and after processing for the equal (E) and Hamming (H) weighted k‐space data. The SNR values per voxel are those of the largest spectral peak of each voxel. Note that the SNR scales for the Sim/Data E and H are lower than the scales of the processed data DN+HA+DC and DN+DC

FIGURE S5 Results of the evaluated processing pipelines on the equal (data‐E) and Hamming weighted (data‐H) in vivo CSI data of the upper legs using Roemer equal noise coil combination. The left column shows magnitude images of the mean spectral signal and the signal profile of the center slice of the acquired data. On the right, it shows two example spectra all scaled relative to the same maximum amplitude. In red a spectrum is shown of muscle data that should contain maximal signal and in green a voxel located in the bone which should show little to no signal. The reported SNR values are those of the PCr peak

FIGURE S6 Results of the evaluated processing pipelines on the in vivo CSI data of the upper legs using WSVD coil combination. The left column shows magnitude images of the mean spectral signal and the signal profile of the center slice of the acquired data. On the right, it shows two example spectra all scaled relative to the same maximum amplitude. In red a spectrum is shown of muscle data that should contain maximal signal and in green a voxel located in the bone which should show little to no signal. The reported SNR values are those of the PCr peak

FIGURE S7 Fits of a single voxel (red voxel of Supporting Information Figure S6) spectrum before and after processing using data reconstructed with WSVD coil combination. The panels show the real measured and fitted spectra, and real residual errors. The mean and standard deviation of the residual errors are reported in the percentage of the PCr amplitude

FIGURE S8 Fitting results of the equal and Hamming weighted data using WSVD coil combination before and after processing represented as metabolite maps. The metabolite maps are calculated relative to the ATP amplitude in the respective voxel and expressed as a percentage. The metabolites shown are phosphoethanolamine (PE), phosphocholine (PC), the sum of the intra‐ and extracellular free phosphate (Pi), glycerophosphocholine (GPC), phosphocreatine (PCr), nicotinamide adenine dinucleotide phosphate (NAD), and uridine diphosphate (UDPG). Above each panel, the mean relative amplitude and its range in percent relative to the ATP amplitude are reported for the entire muscle volume

FIGURE S9 Denoising of dynamic single voxel data. Spectra were acquired using a single coil loop during a biceps exercise protocol (30 s rest, 360 s incremental exercise, 410 s recovery) without localization. The acquisition parameters were: FA = 28 degrees; TR = 0.5 s; TE = 0.3 ms; NSA = 1; 1600 dynamics; bandwidth= 5000 Hz; Number of samples = 512

TABLE S1 Simulated metabolite concentrations and their respective SNR values

TABLE S2 Effective spectral SNR of the PCr peak after each processing step after spectral apodization and zero padding for simulated data

TABLE S3 Relative errors of fitting results of spectra from simulated data. The simulated amplitudes of the metabolites are listed in the second column. For each processing pipeline, the relative error of each metabolite amplitude after fitting is reported in the consecutive columns. In the bottom 4 rows, the mean, median, maximum, and minimum absolute errors overall metabolites are reported

TABLE S4 Effective spectral SNR of the PCr peak after each processing step for in‐vivo data using WSVD reconstruction

TABLE S5 Effective spectral SNR of the PCr peak after each processing step after spectral apodization and zero padding for simulated and in‐vivo data

NOTEBOOK 1. Mathematica notebook with simulations and data processing scripts

NOTEBOOK 2. Mathematica notebook that generates all figures for this manuscript

Froeling M, Prompers JJ, Klomp DWJ, van der Velden TA. PCA denoising and Wiener deconvolution of ³¹P 3D CSI data to enhance effective SNR and improve point spread function. Magn Reson Med. 2021;85:2992–3009. 10.1002/mrm.28654

DATA AVAILABILITY STATEMENT

All code used is part of the open‐source toolbox QMRITools for Mathematica, which is available via GitHub (https://mfroeling.github.io/QMRITools/). The toolbox is also listed on MRSHub (https://mrshub.org/software/) and MRHub (https://ismrm.github.io/mrhub/). All functions used in this study are part of the QMRITools toolbox, and all notebooks used for the simulation, evaluation, and figure generation are in the supporting information. The PCA denoise algorithm is available in QMRITools/ReconstructionTools as DenoiseCSIData. For the deconvolution, we used the build‐in Mathematica function ListDeconvolve. The deconvolution method is available in the QMRITools/ReconstructionTools toolbox as DeconvolveCSIdata. The spectra and basis functions were simulated using scalar coupling (J‐coupling) simulations and implemented in QMRTools/JcouplingTools. The spectra fitting and basis function generation algorithms are available in the QMRITools/SpectroTools toolbox as FitSpectra and GetSpectraBasisFunctions, respectively.