Electronic Point Spread Function Rotation Using a Three-row Transducer for ARFI-Based Elastic Anisotropy Assessment: In Silico and Experimental Demonstration

Abstract

Degree of anisotropy (DoA) of mechanical properties has been assessed as the ratio of Acoustic Radiation Force Impulse (ARFI) induced peak displacements (PDs) achieved using spatially asymmetric point spread functions (PSFs) that are rotated 90° to each other. Such PSF rotation has been achieved by manually rotating a linear array transducer, but manual rotation is cumbersome and prone to misalignment errors and higher variability in measurements. The purpose of this work is to evaluate the feasibility of electronic PSF rotation using a three-row transducer, which will reduce variability in DoA assessment. A Siemens 9L4, with 3×192 elements, was simulated in Field II to generate spatially asymmetric ARFI PSFs that were electronically rotated 63° from each other. Then, using the finite element method (FEM), peak displacements (PD) due to the ARFI excitation PSFs in 42 elastic, incompressible, transversely isotropic (TI) materials with shear moduli ratios of 1.0 to 6.0 were modeled. Finally, the ratio of PDs achieved using the two rotated PSFs was evaluated to assess elastic DoA. DoA increased with increasing shear moduli ratios and distinguished materials with 17% or greater difference in shear moduli ratios (Wilcoxon, p < 0.05). Experimentally, the ratio of PDs achieved using ARFI PSF rotated 63° from each other distinguished the biceps femoris muscle from two pigs, which had median shear moduli ratios of 4.25 and 3.15 as assessed by Shear Wave Elasticity Imaging (SWEI). These results suggest that ARFI-based DoA assessment can be achieved without manual transducer rotation using a three-row transducer capable of electronically rotating PSFs by 63°. It is expected that electronic PSF rotation will facilitate data acquisitions and improve the reproducibility of elastic anisotropy assessments.

I. INTRODUCTION

The mechanical properties of biological tissues relate to their underlying structures and compositions. Thus, interrogating the mechanical properties of tissue is relevant to detecting alterations in tissue structure and composition associated with disease [1]. For example, ultrasonic methods derived mechanical properties of tissue have been applied to diagnose diseases in liver [2]–[4], breast [5]–[8], thyroid [9], [10], prostate [11], kidney [12]–[14], muscles [15]–[19], carotid artery [20]–[22], and lymph nodes [23], [24]. All these methods assumed tissues as isotropic materials.

When evaluating the mechanical properties of tissue, and deciphering how they relate to underlying pathologies, it is important to consider that many biological tissues are mechanically anisotropic [25]–[30], meaning that their mechanical properties vary with orientation. If improperly considered, anisotropy may introduce error into the assessment of mechanical properties. However, if properly exploited, the degree of anisotropy (DoA) in mechanical properties has diagnostic significance. For example, Magnetic Resonance Elastography (MRE) derived mechanical DoA has been applied to differentiate healthy versus dystrophic muscles [31], breast masses [30], healthy versus amyotrophic lateral sclerosis patients [32], and pediatric versus adult brain tissues [33].

Rather than MRE, which is expensive and difficult to access, ultrasound methods have been developed for estimating mechanical DoA by considering tissue as transversely isotropic (TI) materials. TI materials are defined by a plane of isotropy perpendicular to an axis of symmetry (AoS) [34], [35]. The mechanical properties differ along versus across the AoS. The ratio of mechanical properties measured along versus across the AoS is evaluated to estimate mechanical DoA. For example, acoustic radiation force (ARF)-induced shear wave-based mechanical DoA assessments have been applied to distinguish malignant versus aggressive breasts cancers [36], [37]; differentiate skeletal muscle of healthy versus GNE-related myopathy patients [38]; investigate the effect of blood modulation on renal medulla and cortex [39] and to study anisotropy of cardiac tissues [40], [41], lymph nodes [42], skeletal muscles [25], [43], [44] and phantoms [44], [45].

The above-described ultrasound methods for interrogating mechanical DoA require observation of shear wave propagation and are thus subjected to artifacts from shear wave reflections and distortions in the finite, heterogeneous media. Moreover, to overcome challenges associated with displacement estimation error, shear wave measurement is averaged over a 2–5 mm lateral window, leading to reductions in spatial resolution of mechanical property. Finally, as the displacement reduces outside of the ARF-region of excitation (ROE) due to shear waves diffraction and dispersion, applications in deeper organs, obese patients, and stiffer tissues may be limited.

Rather than exploiting shear wave propagation, Hossain et al. demonstrated that mechanical DoA can be assessed by interrogating “on-axis” displacements induced in the ARF-ROE [34], [46]. Specifically, the ratio of peak displacements (PDs) achieved when the long-axis of a spatially asymmetric ARF excitation point spread function (PSF) in the coronal plane was aligned along versus across TI materials’ AOS reflected the material’s true DoA, in silico [34], [46]. Experimentally, the method was validated in pig kidney ex vivo and in vivo [29], demonstrated for differentiating inflammation and fibrosis in pig kidney following ischemia-reperfusion injury in vivo [47], [48], and translated to monitoring renal transplant status in humans, in vivo [29]. The method has also been extended to evaluating mechanical DoA using Viscoelastic Response (VisR) [49]–[51] derived relative elasticity (RE) and relative viscosity (RV) [47], [48], [52]. Moore et al. showed that elastic and viscous DoA expressed as the ratios of RE and RV measured along versus across muscle fibers, respectively, differentiated the lower limb skeletal muscles of boys with Duchenne muscular dystrophy from those of age-matched boys with no know neuromuscular disorders [52].

While the evaluation of mechanical DoA is beneficial, the assessments of DoA using ARFI PD or VisR RE and RV or shear wave-based measurements suffer from a potentially impactful disadvantage: the need to rotate the PSF by 90°. When imaging with a conventional 1-D linear array transducer, this rotation cannot be achieved electronically, so cumbersome physical rotation of the transducer is required, which is prone to misalignment errors and higher intra- and inter-observer variability. Alternatively, a fully-sampled 2D matrix transducer [53], [54] could be implemented for 90° rotation of the PSF, but such a transducer is difficult and expensive to fabricate and address. A second option is to use a specialized row-column transducer [55], but these are not currently commercially available. Rather than a 2D matrix or specialized row-column transducer, an array with only three rows in elevation may be implemented to achieve electronic PSF rotation, albeit to an extent that is less than 90° [56], [57].

The primary focus of this manuscript is the theoretical proof of the concept of electronic PSF rotation by a three-row array to support mechanical DoA assessment by ARFI PD. Toward this goal, first, the manuscript implements controlled and verifiable in silico experiments to demonstrate the electronic beam rotation using the element and array dimensions that are consistent with those that are currently commercially available to support shear elastic DoA assessment. Second, the impacts of noise, compressive modulus, and acoustic attenuation on DoA outcomes are considered. Third, this manuscript demonstrates that an electronic PSF rotation angle smaller than 90° supports DoA assessment, with a comprehensive review of the associated minor loss in DoA sensitivity. Finally, the smaller PSF rotation angle is demonstrated in excised pig biceps femoris muscle by physically rotating a one-row array to evaluate the experimental feasibility of electronic beam rotation for ARFI DoA assessment.

II. MATERIALS AND METHODS

A. In Silico Model

An in silico framework was adapted from the methods described in [34], [58] to simulate ARF excitation of elastic, TI solid materials. The framework utilized the LS-DYNA3D (Livermore Software Technology Corp. Livermore, CA) finite element method (FEM) solver to predict material responses to ARF impulses, which were modeled using the Field II ultrasound simulation package [59], [60]. Field II was also used to simulate radio frequency (RF) data resulting from the scatterer translations predicted by the FEM displacements.

1). Finite element method mesh configuration:

The dimension of the FE mesh was 35 mm, 16 mm, and 16 mm in axial, lateral, and elevational directions, respectively. The FE mesh consisted of homogeneous elements, each with dimensions of 0.2 × 0.2 × 0.2 mm³. The axial, lateral, and elevational dimensions spanned 7 to 42 mm, −8 to 8 mm, and −8 to 8 mm, respectively.

2). Acoustic radiation force impulse simulation:

The ARF field was simulated by computing the Field II derived 3-D acoustic intensity at each nodal location of the FE mesh. To generate the 3D acoustic intensity, a 3×192 (elevational x lateral) array transducer was simulated by mimicking the Siemens 9L4 transducer specifications (Siemens Healthineers, Ultrasound Division, Issaquah, WA, USA). The width of each lateral element was 0.176 mm, and the heights of first, second, and third elevational elements were 2.5, 4.0, and 2.5 mm, respectively. Note that the height of the center-row elevational elements was greater than that of the outer-rows. The transmitting frequency was set to 4.00 MHz with axial focal depth of 30 mm. The function “xdc_focused_multirow” in Field II was used to model a fixed acoustic lens axial focus at 40 mm in the elevational direction.

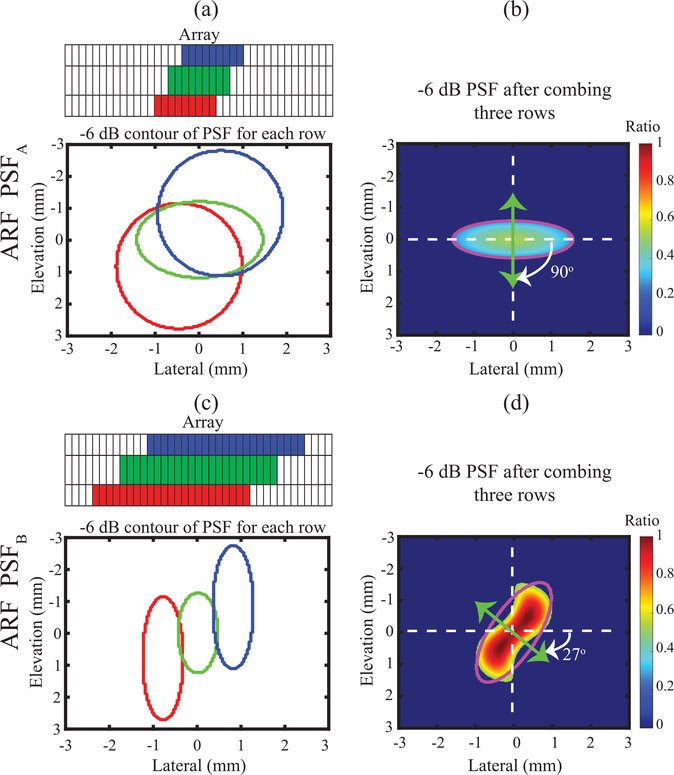
All elements in the simulated transducer could be uniquely addressed. Subapertures within each of the three elevational rows were executed to achieve spatially asymmetric point spread functions (PSFs) in the coronal (lateral x elevational) plane at the focal depth, as illustrated in Fig. 2. One set of sub-apertures (panel (a)) was implemented by selecting 31 elements (i.e., F/# 5.6) on each row and time delay of active elements were calculated based on the spatial positions (elevational, lateral, axial) of (0, −0.55, 30) mm for the first row, of (0, 0, 30) mm for the second row, and of (0, 0.55, 30) mm for the third row. This achieved a combined ARF PSF with its short-axis oriented across the lateral dimension of the simulated transducer (panel (b)). This PSF will henceforth be referred to as “ARF PSF_A”. The other set of sub-apertures (panel (c)) was implemented by selecting 68 elements (i.e., F/# 2.5) on each row and time delay of active elements were calculated based on the spatial positions (elevational, lateral, axial) of (0.95, −0.65, 30) mm for the first row, of (0, 0, 30) mm for the second row, and of (−0.95, 0.65, 30) mm for the third row. This created an ARF PSF with its short-axis oriented diagonally across both lateral and elevational dimensions of the simulated transducer (panel (d)). This ARF PSF was rotated 63° from the ARF PSF_A in panel (b), and it is henceforth referred to ARF PSF_B.

Fig. 2.

Spatial distribution of ARF excitation PSF in the lateral-elevation plane at the focal depth for orientation angles of 90°(a-b) and 27° (c-d). For each orientation, −6 dB contour plot of individual PSF for each row (a and c) and integrated −6 dB PSF (b and d) of all rows are shown. The magenta contours represent the fitted ellipse for assessing the degree of asymmetry and orientation of the PSF. The color bar indicates normalized nodal force for FEM, with normalization relative to the maximum nodal force of PSF_B.

ARF magnitude was calculated using Field II-derived intensity values and the following expression [61]:

$$F=\frac{2\alpha I}{c}$$ (1)

where, α is the absorption coefficient of the medium, I is the temporal-average beam intensity over a volume, and c is the speed of sound through the medium. Values of 0.5 or 1.0 dBcm⁻¹MHz⁻¹ were implemented for α, and c was set to 1540 ms⁻¹. The point load forces were calculated by spatially sampling the volumetric ARF. Point forces were then superimposed on the FE mesh.

For all FEM simulations, the ARFI excitation was kept constant for 70 μs, and induced displacements were modeled for 2.5 ms. Data were sampled every 0.1 ms, approximating a conventional ARFI ensemble with a 10 kHz pulse repetition frequency (PRF).

It is important to consider that, due to a difference in the number of active elements used to generate ARF and overlap of PSF of each row (panel (a) versus (c) in Fig. 1), the ARF magnitude of PSF_A versus PSF_B differed. This difference in ARF magnitudes would complicate the interpretation of the ratio of PDs as a metric for elastic anisotropy if the difference was not properly compensated. Therefore, a compensation term was developed, as described in A.3 and A.6 below.

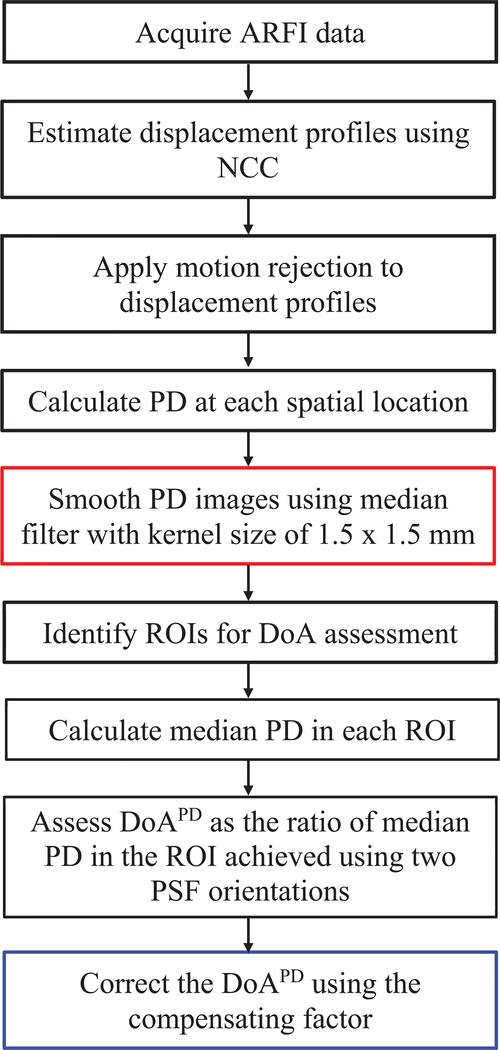
Fig. 1.

Diagram of steps for assessing peak displacement (PD)-derived degree of anisotropy (DoA^PD). Steps in red and blue boxes are unique in assessing DoA^PD in experimental and in silico data, respectively. NCC = normalized cross correlation, ROI = region of interest, PSF = point spread function.

3). Finite element material model:

To develop a term that compensated for the difference in ARF PSF_A and ARF PSF_B magnitudes, four homogeneous, linearly elastic, isotropic materials were simulated using “MAT_ELASTIC”, a built-in material model in LS-DYNA3D. All four materials had a density of ρ = 1 gcm⁻³, and the simulated shear modulus varied from 5 to 35 kPa in steps of 10 kPa. The Poisson ratio was fixed to 0.499 to approach incompressibility. For each material, a five-element-thick perfect matching layer (PML) was implemented around the mesh using the built-in material model, “MAT_PML_ELASTIC”. The mechanical properties of the PML layer were matched to the elastic constants used in the associated “MAT_ELASTIC” material model. As a requirement of the PML, all nodes on outer faces were fully constrained. The purpose of the PML was to simulate an infinite medium and remove spurious wave reflections from the boundaries of the mesh. To demonstrate DoA assessment using electronic PSF rotation, 42 different homogeneous, linearly elastic, incompressible, TI materials with biologically relevant properties [34] were simulated using “MAT_ORTHOTROPIC_ELASTIC” model. As for the simulated isotropic materials, the density of all TI materials was fixed to ρ = 1 gcm⁻³, and a five-element-thick PML was implemented around the mesh using the built-in material model, MAT_PML_ORTHOTROPIC_ELASTIC”. The ranges of elastic constants were: E_T = 12.2 – 24.4 kPa; E_L = 12.8 – 60 kPa; μ_T = 4 – 8 kPa; μ_L = 0.8 – 48 kPa; ν_LT = 0.505 – 0.875; ν_TT = 0.499, where E_L and E_T are the longitudinal and the transverse Young’s moduli, μ_L and μ_T are the longitudinal and the transverse shear moduli, and ν_LT and ν_TT are Poisson’s ratios in the plane of isotropy and the plane perpendicular to the plane of isotropy, respectively. Longitudinal (L) and transverse (T) directions were defined relative to the AoS, such that the longitudinal direction was parallel to the AoS, and the transverse direction was perpendicular to it.

4). Transversely Isotropic Material-PSF Orientation:

To investigate the effect of TI materials’ AoS – PSF orientation on PDs, ARF PSF_A was manually rotated through 360°. The AoS of 4 representative TI materials were oriented from 0° to 360° in steps of 10° relative to the ARF PSF_A short-axis. Note that an AoS-PSF short-axis orientation of 0° interrogated primarily the longitudinal shear elastic modulus, while an AoS-PSF short-axis orientation of 90° interrogated primarily the transverse shear elastic modulus [34].

To compare the DoA^PD assessment using electronic versus manual rotation of 63°, the AoS of 21 TI materials were manually oriented at 90° and 27° relative to the ARF PSF_A short-axis and to simulate the TI materials’ response to electronically rotated ARF PSFs, the TI materials were excited by both ARF PSF_A and ARF PSF_B. Note that, the AoS of the materials were oriented at 90° and 27° with respect to the short axis of the ARF PSF_A and PSF_B, respectively.

Finally, to compare the reduction in sensitivity of distinguishing mechanical DoA due to rotation smaller than 90°, the AoS of 21 TI materials were manually oriented at 90° and 0° relative to the ARF PSF_A short-axis.

5). Acoustic tracking of simulated FEM displacements and displacement estimation:

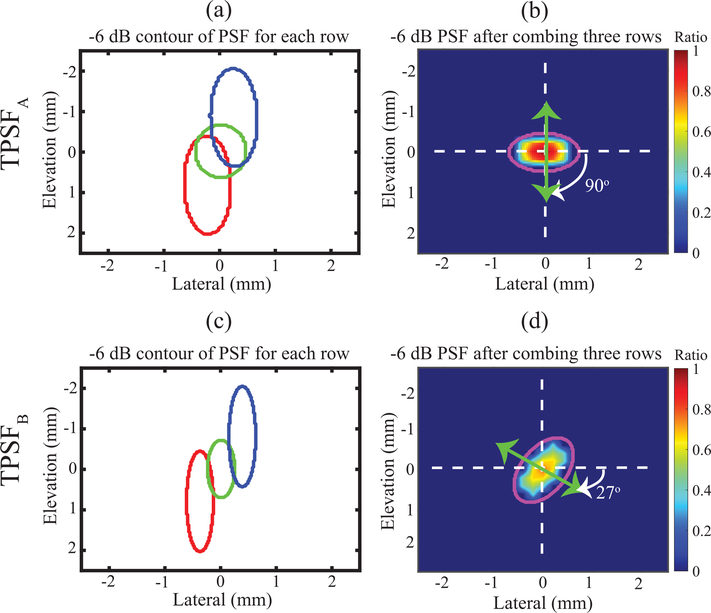
Acoustic tracking of the simulated FEM displacements was performed using Field II after adapting the methods described in [34], [62]. The acoustic attenuation and sound speed were matched to that used to generate the corresponding ARF PSF (0.5 or 1.0 dBcm⁻¹MHz⁻¹) and 1540 ms⁻¹, respectively. Fifteen independent scatterer realizations, each with 15 scatterers per resolution cell, were used to generate the simulated acoustic phantoms. Scatterer displacements were interrogated using simulated tracking pulses with PSFs TPSF_A and TPSF_B that were aligned to match the orientations of ARF PSF_A and ARF PSF_B, respectively (Fig. 3). However, unlike excitation pulses, tracking pulses were generated using a 6.0 MHz center frequency and 61 elements (i.e., F/2.5) or 100 elements (i.e., F/1.8) of each row for the 90° or 27° orientation, respectively. This gave the tracking pulses smaller beamwidths than the corresponding excitation pulses to minimize displacement underestimation [62], [63]. The time delays for active elements in the outer elevational rows were calculated based on the spatial positions (elevation, lateral, axial) of (0, −0.25, 30) and (0, 0.25, 30) mm for TPSF_A and of (0.55, −0.35, 30) and (−0.55, 0.35, 30) mm for TPSF_B. In both orientations, the time delays for elements in the center row were calculated based on the spatial position (elevation, lateral, axial) of (0, 0, 30) mm.

Fig. 3.

Spatial distribution of ARF tracking PSF in the lateral-elevation plane at the focal depth for orientation angles of 90°(a-b) and 27° (c-d). For each orientation, −6 dB contour plot of individual PSF for each row (a and c) and integrated −6 dB PSF (b and d) of all rows are shown. The magenta contours represent the fitted ellipse for assessing the degree of asymmetry and orientation of the PSF. The color bar indicates normalized acoustic intensity, with normalization relative to the maximum intensity of TPSF_A.

White Gaussian noise was added to each RF line using the awgn function in MATLAB (Mathworks Inc., Natick, MA, USA) to simulate a system SNR of 40 dB. Motion tracking was performed using one-dimensional normalized cross-correlation (NCC) [64] with the parameters listed in Table 1. After displacement tracking, a dataset describing axial displacements over time and space was generated for each simulated isotropic and TI material and each ARF PSF-material orientation.

TABLE I:

ARF EXCITATION AND TRACKING PARAMETERS USED IN THE ARFI AND SWEI EXPERIMENTS WITH NORMALIZED CROSS CORRELATION PARAMETERS FOR DISPLACEMENT ESTIMATION. METHOD IS NOT INDICATED FOR COMMON PARAMETERS.

Name	Value
Beam sequence parameters
Transducer	VF73
Bandwidth	53%
Sampling freq.	40 MHz
Acoustic lens axial focus	38 mm
ARF excitation duration	300 cycle
ARF excitation center frequency	4.21 MHz
ARF excitation F/#	1.5
ARF axial focus	20 mm
Tracking center frequency	6.15 MHz
Tracking transmit F/#	1.0
Tracking receive F/#*	0.75
Tracking transmit axial focus	20 mm
Tracking PRF	10 KHz
Tracking pulse number (ARFI)	40
Tracking pulse number (SWEI)	70
Normalized cross correlation parameter
Interpolation factor	4
Kemel length	500 μm
Search region	80 μm

^*Aperture growth and dynamic Rx focusing enabled

6). Degree of Anisotropy Assessment:

Median PD over an axial range of 29 – 31 mm was measured, and elastic DoA was assessed as the ratio of median PDs measured with the ARF PSF short-axis aligned at 90° versus 27° $\left(Do{A}_{63}^{PD}\right)$ and at 90° versus 0° $\left(Do{A}_{90}^{PD}\right)$ with respect to the material AoS. However, as described in A.2 because different numbers of elements with the difference in the overlapping area of PSF of each row were used to generate ARF PSF_A and ARF PSF_B, the ARF magnitudes produced by the two PSFs differed (Fig. 2). Similarly, the acoustic intensity of TPSF_A and TPSF_B was different which impacts the ultrasonic tracking of displacement (Fig. 3). These differences in excitation and tracking PSFs at 90° and 27° would confound anisotropy assessment by electronic PSF rotation if left uncompensated. A compensation term was developed by considering that in homogenous, isotropic, elastic materials, there are no directional differences in elastic modulus, so the PDs achieved with the ARF excitation and tracking PSF aligned at 90° and 27° should be equivalent, yielding a $Do{A}_{63}^{PD}$ of one. Deviations from a $Do{A}_{63}^{PD}$ of one were attributed to differences ARF magnitude and acoustic intensity at 90° and 27°. More specifically, the mean $Do{A}_{63}^{PD}$ measured in the four simulated homogeneous, isotropic elastic materials were used as a scaling factor for $Do{A}_{63}^{PD}$ measured in TI materials by electronic PSF rotation. Fig. 1 summarizes the steps in assessing DoA using PD.

The compensation factor was derived using simulated materials with an acoustic attenuation of 0.5 dBcm⁻¹MHz⁻¹. In practice, the acoustic attenuation of tissue is variable and often unknown. To evaluate the robustness of the derived compensation term to differences in acoustic attenuation, the factor was applied to correct electronic DoA measures made in materials simulated to have acoustic attenuation of 1.0 dBcm⁻¹MHz⁻¹. Similarly, the robustness of the compensation factor to differences in the mechanical properties of TI materials was investigated. An incompressible TI elastic material is defined by three mechanical parameters: μ_T, μ_L, and E_L/E_T [18], [35], which are generally unknown at the time of imaging. Therefore, compensated DoA^PD-derived by electronic PSF rotation was compared across eleven simulated TI materials with 2 fixed μ_T values (4.0 versus 8.0 kPa), 2 Young’s moduli ratios (1.05 versus 4.0), and 2 attenuation values (0.5 versus 1.0 dBcm⁻¹MHz⁻¹).

B. Experimental Demonstration

1). Experimental setup for imaging excised muscles:

To experimentally investigate the feasibility of assessing elastic anisotropy using ARF PSFs offset by 63°, such as the simulated electronically rotated ARF PSF_A and ARF PSF_B, ARFI imaging was performed in the excised biceps femoris muscles of two pigs. The same muscles were also interrogated by SWEI as a comparison standard.

The legs of two female pigs, each approximately three months old and weighing 14.8 (Id #1) and 19.1 (Id #2) Kg, were disarticulated at the acetabulofemoral joint after sacrificing the animals. Both pigs were part of a different study with a terminal protocol and had diabetes mellitus. The legs were kept refrigerated for 24 hours and then held at room temperature for two hours before imaging in a room-temperature water bath.

2). Acoustic Radiation Force Impulse (ARFI) and Shear Wave Elasticity Imaging (SWEI) data acquisition and processing:

Although simulations were performed using a three-row array with dimensions like those of the 9L4, the elements in the first and third rows of the physical 9L4 cannot be uniquely addressed to achieve actual electronic PSF rotation. Therefore, rather than the 9L4, the Siemens VF7–3 linear array transducer was used to produce ARF PSFs with dimensions comparable to the simulated ARF PSFs, and PSF rotation was achieved using a computerized translation stage (model: CONEX-NSR1, Newport, Irvine, California, USA) equipped with a custom transducer holder. Experiments were conducted on a motion isolation table (Newport, Irvine, California, USA).

ARFI imaging was performed using a Siemens Acuson Antares imaging system. The scanner’s Axius Direct Ultrasound Research Interface (URI) allowed customizable beam sequencing and access to raw radio frequency (RF) data. ARFI beam sequences consisted of two reference pulses, one ARF impulse, and 40 tracking lines in the ARF region of excitation, with a 10 kHz PRF. A tracking ensemble was collected in each of 40 lateral locations equally spaced across a 20 mm lateral field of view. One spatially matched B-Mode image, with 220 lateral lines spanning 40 mm laterally, was acquired immediately before each ARFI acquisition for anatomical reference. For both B-mode and ARFI acquisitions, the axial field of view was 40 mm. A summary of the employed imaging parameters is listed in Table 1.

Using the same imaging equipment as was employed for ARFI and B-mode imaging, SWEI data were collected immediately after each ARFI data acquisition using a beam sequence consisting of two reference pulses, one ARF impulse, and 70 tracking lines that were offset from the ARF region of excitation (Table 1). The ARF location was kept constant at −5.4 mm laterally, and the tracking location was shifted to 40 evenly spaced lateral locations within the ARFI lateral FOV.

Raw RF data were saved to the hard drive of the scanner and transferred to a computational workstation for custom analysis. Using the parameters listed in Table 1, ARFI displacements were measured using one-dimensional axial NCC [64] to yield a 3-D data matrix (axial x lateral x time). Then, for each axial x lateral pixel, a linear filter was applied to the associated displacement versus time profile to reduce motion artifacts [65]. Finally, from each filtered displacement profile, the peak displacement over time was identified and rendered into a 2D parametric image.

SWEI displacements were also measured using NCC [64], with the parameters listed in Table 1, and were filtered using a linear motion filter [65]. To increase the SNR of the displacement data, a built-in moving-average filter (movmean function) in MATLAB was used in the axial direction with a window size of 0.5 mm. Then, directional filtering [66] was applied to remove shear wave reflections by keeping only left-to-right propagating shear waves. Next, for each axial location, time to peak (TTP) displacement was calculated, and SWV was estimated by fitting a straight line to lateral location versus TTP in lateral sliding windows of 4.0 mm length. The estimated SWV with R² value less than 0.8 was discarded. Finally, the shear modulus (μ) was estimated from the SWV (V) as, μ = ρV², where ρ is the density, assumed to be 1 gcm⁻³. Raw RF data were used to generate B-mode images, which were calculated as the log-compressed, absolute value of the Hilbert-transformed RF data.

In the biceps femoris muscle of pig #1, ARFI data were acquired at 27° and 0° to 180° in steps of 5°, and SWEI data were collected at 0°, 27°, and 90° angles. In the biceps femoris muscle of pig #2, both ARFI and SWEI data were collected at 0°, 27°, and 90°. Note that 0° indicates the orientation whereby the short axis of the ARF PSF was aligned along the muscle fibers, such that the longitudinal shear elastic modulus was primarily interrogated, while in the 90° orientation, the ARF short axis was aligned across the muscle fibers, such that the transverse shear elastic modulus was primarily evaluated. There was an approximately 1-minute time interval between each measurement. Six repeated acquisitions of ARFI and SWEI were collected at each orientation. To collect the repeated acquisitions, the transducer was rotated from 0° to 90° and then brought back to 0° before repeating the rotation five more times.

3). Region of interest selection and degree of anisotropy assessment:

To evaluate the DoA from each ARFI and SWEI data set, rectangular ROIs with dimensions 2.0 × 3.0 mm (axial x lateral) were selected. The axial ROI size was determined by the axial range over which the asymmetric ARF excitation PSF asymmetry ratio was expected to be consistent. The lateral ROI size was selected as the expected region of overlap for the rotated PSFs [18], [29], [52]. The ROIs were centered at the ARF focal depth axially and at the center of the field of view (FOV) laterally. Within each ROI, median ARFI PD and SWEI μ values were calculated. From these measures, DoA was evaluated as the median ratios of PD₉₀ over PD₀ (for 90° rotation angels, yielding $Do{A}_{90}^{PD}$), PD₉₀ over PD₂₇ (for 63° rotation angels, yielding $Do{A}_{63}^{PD}$), μ₀ over μ₉₀(for 90° rotation angels, yielding $Do{A}_{90}^{SWEI}$) and μ₂₇ over μ₉₀ (for 63° rotation angels, yielding $Do{A}_{63}^{SWEI}$). Note that the orientation angle of the numerators and denominators for DoA^PD and DoA^SWEI assessments were inverted due to the inverse relationship between PD and μ [29]. Steps for assessing DoA^PD are diagrammed in Fig. 1.

C. Statistical Methods

All statistical analyses were carried out using MATLAB. One-way analysis of variance (ANOVA) test (anova1 function) was used to statistically compare $Do{A}_{63}^{PD}$ of four simulated isotropic materials. Note that, $Do{A}_{63}^{PD}$ was achieved with electronic rotation in these materials. Further, $Do{A}_{90}^{PD}$ achieved with manual rotation and $Do{A}_{63}^{PD}$ achieved with electronic rotation were compared between two TI materials with different shear moduli ratios using two-sample Wilcoxon ranksum tests (ranksum function). Three separate two-sample Wilcoxon ranksum tests were carried out to compare $Do{A}_{63}^{PD}$ between TI materials with μ_T = 4 versus 8 kPa, with E_L/E_T = 1.0 versus 4.0, and with α = 0.5 versus 1.0 dBcm⁻¹MHz⁻¹ for each fixed shear moduli ratio. Experimentally, $Do{A}_{90}^{PD}$, $Do{A}_{63}^{PD}$, $Do{A}_{63}^{SWEI}$, and $Do{A}_{90}^{SWEI}$ were compared between pig #1 and #2 using two-sample Wilcoxon rank-sum tests. Statistical significance was based on p < 0.05.

III. RESULTS

Fig. 2 shows the spatial distributions of ARF PSF_A and ARF PSF_B in the lateral-elevational plane at the focal depth (30 mm). The left column (panels a and c) shows the −6 dB contours of the PSFs when each row was excited separately, with a schematic drawing of the arrays at the top of each panel. Active elements are color-coded in red, green, and blue for the first, second, and third rows, respectively. The right column (panels b and d) shows the −6 dB contours of PSF_A and PSF_B when all three transducer rows were excited simultaneously. An ellipse (magenta contour) was fit to each −6 dB PSF contour to derive the PSF’s orientation and asymmetry ratio (AR) (i.e., major over minor axis length). The (major, minor) axes lengths were (3.1, 1.2) mm for PSF_A in panel (b) and (3.4, 1.3) mm for PSF_B in panel (d), with corresponding ARs of 2.62 and 2.58, respectively. The minor (i.e., short) axes of the ellipses fit to PSF_A and PSF_B were oriented at 90° and 27° with respect to the lateral direction. The color bar indicates normalized nodal force for FEM, with normalization relative to the maximum nodal force of PSF_B. Note that, the ratio of maximum force of PSF_A versus PSF_B was 0.523.

Fig. 3 similarly illustrates the spatial distribution of TPSF_A and TPSF_B with −6 dB contours of the PSFs when each row was excited separately (left column) and −6 dB contours of TPSF_A and TPSF_B when all three rows were excited simultaneously (right column). The positioning of active elements in each row was similar to Fig. 2 but with the different number of active elements (section A.5). The (major, minor) axes lengths were (1.4, 0.9) mm for TPSP_A and (1.7, 1.0) mm for TPSF_B, for corresponding ARs of 1.55 for TPSF_A and 1.7 for TPSF_B. The minor axes of the fitted ellipses in panels (b) and (d) were oriented at 90° and 27° with respect to the lateral dimension. The color bar indicates normalized acoustic intensity, with normalization relative to the maximum intensity of TPSF_A. The ratio of the maximum acoustic intensity of TPSF_B versus TPSF_A was 0.77. Note that tracking pulses were narrower than ARFI excitation pulses to reduce displacement underestimation, as described in [58].

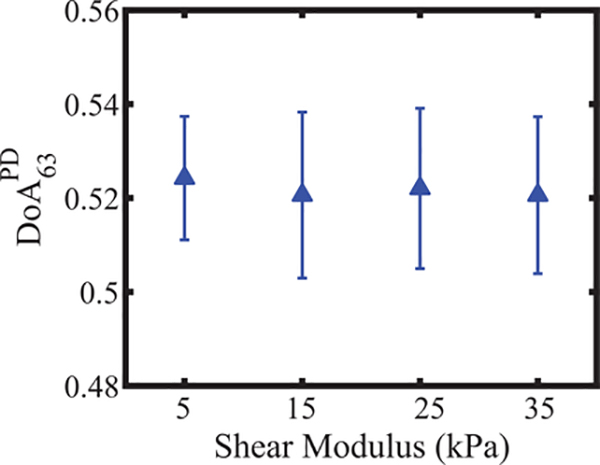
Fig. 4 depicts $Do{A}_{63}^{PD}$ in the four simulated isotropic materials. The F-statistic and p-value of the one-way ANOVA analysis were 0.11 and 0.95, respectively. The median $Do{A}_{63}^{PD}$ was 0.52. Recall that this value was used to compensate for differences in ARF magnitude at 90° versus 27° orientation by evaluating the corrected PD₂₇ as 0.52 times the measured PD₂₇. All PD₂₇ and $Do{A}_{63}^{PD}$ assessed with electronic rotation are reported using the corrected PD₂₇.

Fig. 4.

Peak displacement (PD) – derived degree of anisotropy (DoA) with 63° rotation angle $\left(Do{A}_{63}^{PD}\right)$ versus shear modulus of isotropic materials. $Do{A}_{63}^{PD}$ is shown as a median ±0.5∗ inter quartile range over 15 independent speckle realizations. One-way ANOVA indicates that there is no statistical difference between $Do{A}_{63}^{PD}$ of the materials.

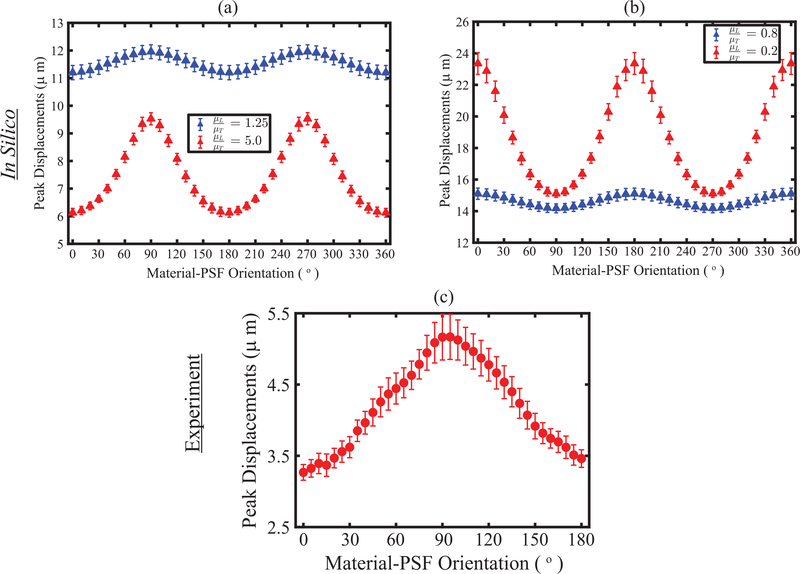
Fig. 5 shows PD as a function of material-PSF orientation in simulated TI materials (panels (a) and (b)) and in excised biceps femoris muscle from pig #1 (panel (c)). The simulated materials had shear moduli ratios (μ_L / μ_T) greater than one in panel (a) and had shear moduli ratios less than one in panel (b). In both panels, the material with the higher DoA is shown in red. The rate of change in PD with orientation was higher around 90° or 0° when the shear moduli ratios were greater or less than 1, respectively. These results suggest that the assessment of DoA at a smaller rotation angle could be exploited by using electronic PSF rotation from 90° or 0° for μ_L / μ_T >1 or < 1. For brevity, all analyses were performed with μ_L / μ_T > 1 from here to onward.

Fig. 5.

(a) Errorbar plot of peak displacement as a function of material-PSF orientation for four representative TI materials with shear moduli ratios (μ_L/μ_T) > 1 (a) and < 1 (b). All materials have fixed longitudinal Young’s modulus, transverse Young’s modulus, and transverse shear modulus (μ_T) of 21.0, 21.0, and 7.0 kPa, respectively, but have variables longitudinal shear modulus (μ_L) of 8.0 and 35.0 kPa (blue versus red in panel (a)) and 5.6 and 1.4 kPa (blue versus red in panel (b)). Errorbar plot is shown as a median ± 0.5∗ inter quartile range over 15 independent speckle realizations. (c) Experimentally, peak displacements as a function of material-PSF orientation in an ex vivo biceps femoris muscle of a pig. PD is shown as median ± 0.5∗ inter quartile range over region of interest.

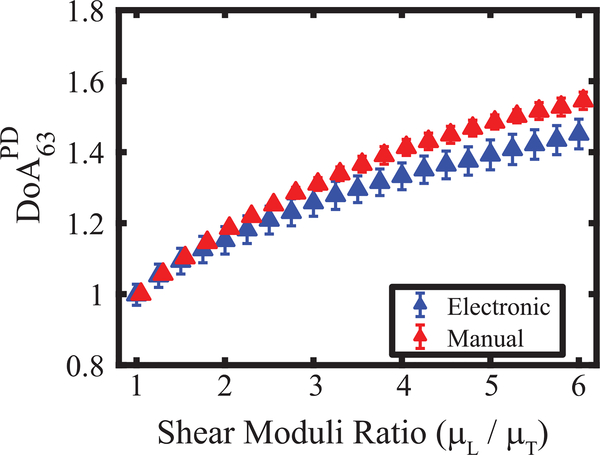
Fig. 6 shows $Do{A}_{63}^{PD}$ versus shear moduli ratios in the simulated TI materials. $Do{A}_{63}^{PD}$ achieved using only ARF PSF_A with 63° material rotation (red markers) versus using ARF PSF_A and ARF PSF_B with no material rotation (blue markers). In both cases, $Do{A}_{63}^{PD}$ increased with increasing shear moduli ratios. The percent absolute difference in median $Do{A}_{63}^{PD}$ between simulated manual versus electronic PSF rotation increased from 0.1% to 6.4% when the shear moduli ratios increased from 1.0 to 6.0, respectively.

Fig. 6.

Peak displacement (PD) – derived degree of anisotropy (DoA) with 63° electronic (blue) and manual (red) rotation angle $\left(\mathrm{D}\mathrm{o}{\mathrm{A}}_{63}^{\mathrm{P}\mathrm{D}}\right)$ versus shear moduli ratios of transverse isotropic materials. $\mathrm{D}\mathrm{o}{\mathrm{A}}_{63}^{\mathrm{P}\mathrm{D}}$ are shown as a median ±0.5∗ inter quartile range over 15 independent speckle realizations. All materials had fixed longitudinal Young’s modulus, transverse Young’s modulus, transverse shear modulus (μ_T), and acoustic attenuation of 25.6, 24.38, 4.0 kPa, and 0.5 dBcm⁻¹MHz⁻¹, respectively. Longitudinal shear modulus (μ_L) was varied from 4.0 to 24.0 kPa in steps of 1.0 kPa.

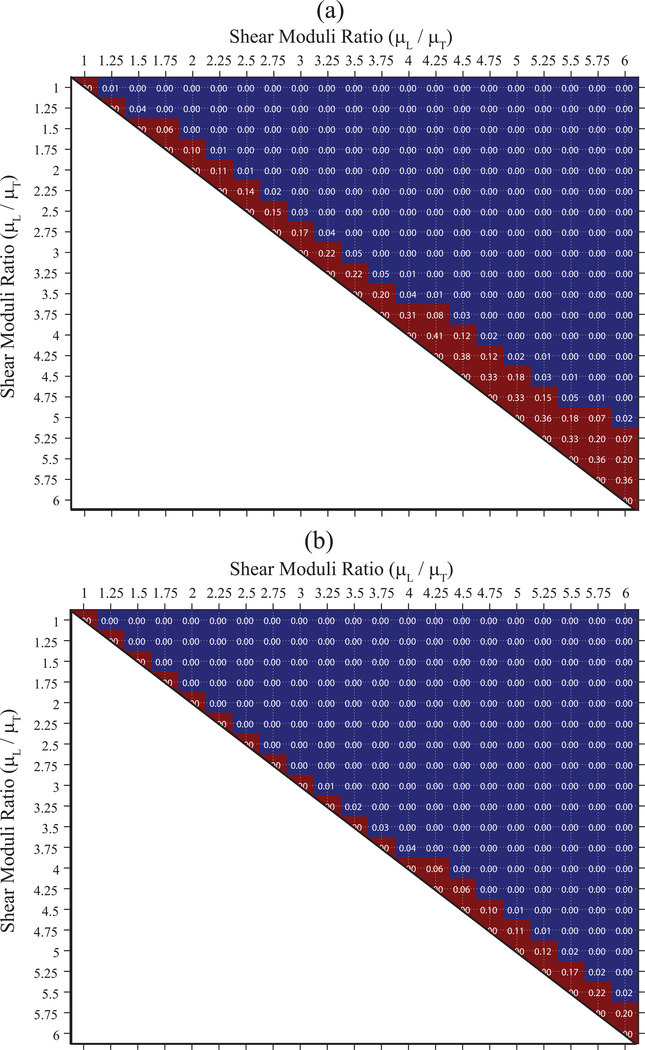
Fig. 7(a) shows p-values testing the null hypothesis that $Do{A}_{63}^{PD}$ achieved with electronic PSF rotation does not differ between all possible pairings of the 21 simulated TI elastic materials. For comparison, panel (b) shows the corresponding p-values for $Do{A}_{90}^{PD}$ with manual PSF-material rotation. The blue areas indicate p<0.05, suggesting that the DoAs were statistically different between the associated paired materials, whereas the red area indicates p ≥ 0.05, suggesting that the DoAs were not statistically different between the associated paired materials. For example, in panel (a), the $Do{A}_{63}^{PD}$ of materials with shear moduli ratios of 1.50 and 1.75 were not statistically different (p = 0.06), but the $Do{A}_{63}^{PD}$ of materials with shear moduli ratios of 1.5 and 2.0 were statistically different (p < 0.05). Overall, $Do{A}_{63}^{PD}$ distinguished materials with greater than 17% difference in shear moduli ratios (panel (a)), while $Do{A}_{90}^{PD}$ differentiated materials with greater than 6 % difference in shear moduli ratio (panel (b)).

Fig. 7.

p-values for comparisons between DoA^PD of materials with different shear moduli ratios derived using electronic PSF rotation of 63°(a) and using manual PSF rotation of 90° (b). Blue and red area indicate p<0.05 and p ≥ 0.05, respectively. All materials had transverse shear modulus (μ_T), Young’s moduli ratio and acoustic attenuation of 4 kPa, 1.05, and 0.5 dBcm⁻¹MHz⁻¹, respectively. Longitudinal shear modulus (μ_L) is varied from 4.0 to 24.0 kPa in steps of 1.0 kPa.

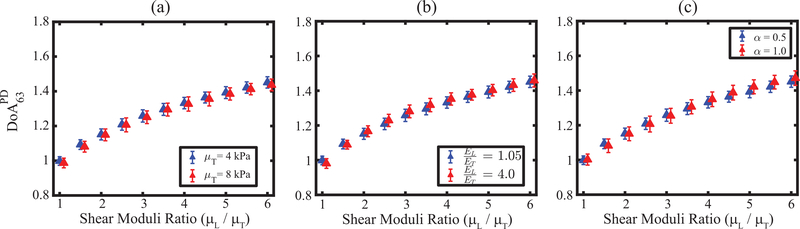
Fig. 8 depicts the impact of transverse shear modulus (μ_T) (panel a), Young’s moduli ratio (E_L / E_T) (panel b), and acoustic attenuation (panel c) on $Do{A}_{63}^{PD}$ assessed using electronic PSF rotation. In panel (a), μ_T was 4 or 8 kPa with E_L / E_T fixed at 1.05. In panel (b), E_L / E_T was 1.05 or 4.0 with an E_L of 25.6 or 60 kPa. Both materials had a μ_T of 4 kPa. In panel (c), E_L / E_T was 1.05 with E_L = 25.6 kPa and μ_T = 4.0 kPa; the attenuation coefficient was 0.5 or 1.0 dBcm⁻¹MHz⁻¹. Despite large differences in μ_T (100% difference, panel (a)), E_L / E_T (280% difference, panel (b)), and acoustic attenuation (100% difference, panel (c)), $Do{A}_{63}^{PD}$ was not statistically different (p>0.05, Wilcoxon ranksum test) between red versus blue data points for a specific shear moduli ratio. The median absolute percent difference in the PD ratios (blue versus red data points) was 0.6%, 1.2 %, and 1.0% in panels (a), (b), and (c), respectively.

Fig. 8.

Peak displacement (PD) – derived degree of anisotropy (DoA) with 63° rotation angle $\left(Do{A}_{63}^{PD}\right)$ versus shear moduli ratios with two different transverse shear moduli (μ_T) (a), Young’s moduli ratios (E_L / E_T) (b), and attenuations (α) (c). Data are plotted as median ± 0.5× interquartile range over 15 independent speckle realizations. For a specific shear moduli ratio, $Do{A}_{63}^{PD}$ were not statistically different between transverse shear moduli, between young’s moduli ratios, and between attenuations (p>0.05, Wilcoxon ranksum test).

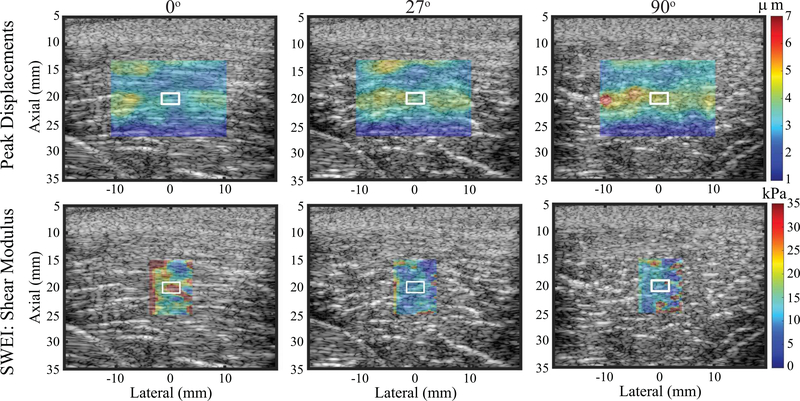
Fig. 9 shows, in a representative pig biceps femoris muscle, imaged ex vivo, ARFI PD images (top row) and SWEI-derived shear modulus (μ, bottom row) for transducer orientations of 0° (left column), 27° (middle column), and 90° (right column). Recall that because PD and shear modulus are inversely related, PD values were highest in the 90° (transverse) orientation while shear modulus was highest in the 0° (longitudinal) orientation.

Fig. 9.

ARFI peak displacement images (top row) and SWEI derived shear modulus (μ) images (bottom row) of an excised pig biceps femoris muscle for the material-PSF orientation of 0° (left column), 27°(middle column), and 90°(right column). Peak displacement and shear modulus images are overlaid with transparency on the matched B-modes. White contours indicate measurement regions of interest. Note that the color bar units and ranges differ between rows.

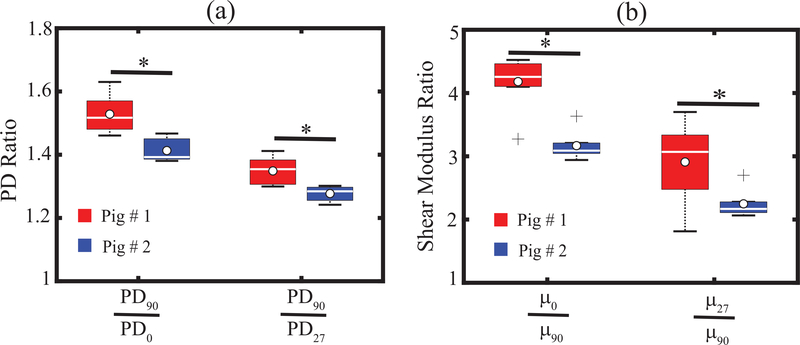
Fig. 10 shows $Do{A}_{90}^{PD}$, $Do{A}_{63}^{PD}$, $Do{A}_{63}^{SWEI}$, and $Do{A}_{90}^{SWEI}$ measured in the bicep femoris muscles of two pigs. All four DoA measures were statistically different (p<0.05, Wilcoxon ranksum test) between the two pigs.

Fig. 10.

Box plot of PD ratios (a) and SWEI-derived shear moduli ratios (b) measured in two pigs using rotation angles of 90° and 63°. PD ratios and shear moduli ratios were statistically different between pigs (p < 0.05, Wilcoxon ranksum test). White circles, white lines inside boxes, top box edges, bottom box edges, and ‘+’ marker represent mean, median, 25^th percentile values, 75^th percentile values, and outliers, respectively of repeated acquisition.

IV. DISCUSSION

Previous work has demonstrated that the degree of elastic anisotropy in transversely isotropic materials is reflected by the ratio of peak displacements achieved using two ARFI excitations that are asymmetrically shaped and orthogonally oriented [34]. Relative to methods that require observation of shear wave propagation, there are several benefits to the “on-axis” evaluation of PD ratio as a method for interrogating mechanical DoA. First, because PDs are observed immediately following the ARF excitation without waiting for shear wave propagation, interference from reflected or distorted shear waves is less likely. Second, PD measurements are made on a pixel-by-pixel basis without the need for a lateral measurement window, so the finer spatial resolution of mechanical features is supported. Third, PD is evaluated directly in the ROE where displacements are greatest, so for a given ARF excitation, DoA^PD can be assessed in deeper organs, obese patients, and stiffer tissues.

The work herein establishes the feasibility of evaluating elastic anisotropy using asymmetric ARFI excitations that are oriented less than 90° apart. Smaller rotation angles are beneficial because, as shown in Figs. 2 and 3, they are electronically achievable using a conventional three-row array. Thus, mechanical DoA can be assessed by ARFI without cumbersome manual 90° rotation of a linear array or the substantial overhead of electronic 90° rotation using a full 2-D matrix transducer.

While electronic rotation of an asymmetrical ARFI PSF is possible using a three-row transducer, it is necessary to compensate for differences in the ARF magnitude of the rotated PSF. Fig. 4 shows that, by evaluating the ratio of PDs achieved in isotropic elastic materials, a compensation factor of 0.52 was derived for PD₂₇, which corresponds to the approximately twice as large aperture size that used to generate PSF_B versus PSF_A and the approximately twice as large acoustic intensity of PSF_B versus PSF_A. After compensation, PD ratios measured using ARF PSF_A manually rotated 63° and those measured using electronically rotated ARF PSF_A and ARF PSF_B were comparable in TI materials with μ_L/μ_T ranging from one to six (Fig. 6).

Although comparable, Fig. 6 shows a slight underestimation of $Do{A}_{63}^{PD}$ assessed by electronic versus the manual rotation validation standard. This underestimation is related to the nonlinear relationship between PD ratio and shear moduli ratio. The nonlinear relationship arises because, although PSF_A predominantly interrogates the transverse and PSF_B the longitudinal shear elastic modulus, both moduli contribute to PD to a degree that depends on the asymmetry ratio of the ARF PSF [34]. The more asymmetric PSF_A and PSF_B, the more the transverse and longitudinal shear elastic moduli dominate the corresponding PD outcomes, and the more linear the relationship between PD ratio and shear moduli ratio [34]. Given this nonlinear relationship between PD ratio and shear moduli ratio, linearly applying the derived compensation factor to raw PD ratio outcomes has the effect of underestimating shear moduli ratios. This underestimation is higher for higher anisotropic materials and likely impacts the minimum detectable difference in shear moduli ratios (17%) achieved using $Do{A}_{63}^{PD}$(Fig. 7(a)).

In addition to the ARF excitation PSFs, the tracking PSFs could also be impactful to DoA assessment because they determine the degree to which PD is underestimated due to shearing artifacts under the tracking PSF [62], [63], [67]. Considering that these shearing artifacts will be directionally dependent (because shear waves will travel at different speeds at different interrogation angles in elastically anisotropic materials), changing the tracking PSFs could result in a need for a different compensation factor. However, the impact of the tracking PSFs on the correction factor is expected to be minor relative to that of the excitation PSFs. Nonetheless, future investigations evaluating the impact of the tracking PSFs on the correction factor value are warranted.

In addition to correcting for differences in excitation and tracking PSFs, optimizing PSF positioning with respect to the material AOS enhances electronically rotated small-angle anisotropy assessment in highly anisotropic materials. As shown in Fig. 5(a), for the material with μ_L / μ_{T =} 5.0, the rate of change in PD versus orientation angle was faster when the change was centered around the interrogation of transverse modulus (90° and 270°) than when the change was centered around the interrogation of longitudinal modulus (0° and 180°). Thus, greater differences between PD₉₀ and PD₂₇ will be observed when the short-axis of ARF PSF_A is aligned across verses along the material AoS, leading to higher $Do{A}_{63}^{PD}$.

Similarly in Fig. 5(b), for the material with μ_L / μ_T = 0.2, the rate of change in PD versus orientation angle is faster when the change was centered around the interrogation of longitudinal modulus (0° and 180°) than when the change was centered around the interrogation of transverse modulus (90° and 270°). Thus, higher DoA was observed when the short-axis of ARF PSF_A was aligned along versus across the material AoS. Notably, in less anisotropic materials, the rates of change in peak displacement versus orientation angle were comparable whether the change was centered around the interrogation of longitudinal or transverse modulus (blue marks in panels (a) and (b)). For brevity, only TI materials with μ_L / μ_T > 1 are shown in the presented analyses; however, discrimination of shear elastic anisotropy by the described methods was similar between μ_L / μ_T > 1 or < 1.

The above-described phenomena suggest that, for highly anisotropic materials, knowing the AoS orientation and whether elasticity is greater in the longitudinal or transverse direction enables ARF PSF positioning that improves the discrimination of DoA by small-angle anisotropy assessment. However, in reality, the AoS orientation and the dominant elastic axis may be unknown. In such a case, the detectable percent difference in elastic DoA, as reported in Fig. 7, may go above 17% for $Do{A}_{63}^{PD}$ and 6% for $Do{A}_{90}^{PD}$. Note that discrimination between simulated materials may improve if a shear moduli ratio step size smaller than the employed 0.25 is used.

When considering Fig. 7(a) and (b), it is apparent that a 90° versus a 63° PSF rotation angle supports finer discrimination of materials with different elastic DoAs. This result is predicted. When the ARF excitation PSF is rotated by 63°, rather than 90°, the PSF is oriented diagonally across the material AoS, which causes the transverse modulus to contribute to the PDs achieved by it. This makes the PDs measured by PSF_A and PSF_B more similar to each other, and their ratio smaller, than would be the case if PSF_B were rotated by 90°. This reduction in PD ratio decreases the sensitivity of the measurement technique to differences in shear elastic DoA. However, it is important to consider that the data displayed in panel (b) were generated using a perfect 90° PSF rotation. Such precise rotation is unlikely to consistently be achieved manually. It is reasonable to expect a 10–20° error in free-hand transducer rotation, with smaller errors expected in tissue, such as skeletal muscle, in which anisotropic structure is readily visible by B-Mode. In a tissue with a shear moduli ratio of 5, a 20° rotation error from 90° would result in a derived DoA estimate with an 8% error (Fig. 5(a)). This analysis does not take into account the impact of transducer translation with free-hand rotation, which is also expected. Such translation would cause different parts of the tissue to be interrogated in different rotation angles, which could result in higher DoA error, especially in heterogeneous tissue environments. In this sense, despite the larger difference in elastic DoA required for material discrimination by the 63° versus 90° PSF rotation, the precise 63° electronic rotation enabled by the three-row transducer may achieve superior material discrimination in practice. This is especially likely considering that more advanced methods for deriving and applying the compensation factor could reduce DoA underestimation by 63° electronic rotation and improve material discrimination. Further, automating active element and time delay selections to enable ARF PSFs with higher asymmetry ratios could further improve material discrimination by the 63° electronic rotation. Systematically comparing DoA assessment by free-hand 90° PSF rotation versus electronic 63° rotation is a topic of future investigation.

It has previously been reported that a material’s Young’s moduli ratio does not substantially impact shear elastic anisotropy estimated as the ratio of ARFI PDs achieved using a spatially asymmetric PSF with 90° manual rotation [34]. This previous finding translated to $Do{A}_{63}^{PD}$ assessed by electronic PSF rotation, which was also demonstrated to be robust to variations in transverse shear elastic modulus value and acoustic attenuation, as shown in Fig. 8. Notably, the employed correction factor was derived in homogeneous, isotropic materials (with α = 0.5 dBcm⁻¹MHz⁻¹), which did not account for the potential impact of the excitation and tracking PSF sizes and shapes in anisotropic media. Despite this limitation, corrected PD ratios were not statistically different in materials with the same shear moduli ratios but different transverse shear moduli, Young’s moduli ratios, and acoustic attenuations, suggesting the robustness of the correction.

Experimental translation of in silico findings is demonstrated in Figs. 9 and 10, which show that ARFI PD- and SWEI-derived elastic DoA values statistically differentiate two biceps femoris muscles excised from two pigs. Though biceps femoris muscle was imaged for both pigs, the difference in shear moduli ratios may be due to the difference in their body weight, diabetes mellitus pathology, and/or elapsed time after pigs were sacrificed. In Fig. 10, while both 90° and 63° PSF rotations differentiate the DoAs of the two muscles, the DoA₆₃ values are smaller than the DoA₉₀ values. This points to the importance of maintaining consistent PSF rotation angles when comparing DoA values between tissues, subjects, and/or time points and further highlights the benefits of precisely controlling rotation via electronic steering such as that which could be achieved conveniently using a fully addressable three-row transducer. Further, it is reasonable to consider that $Do{A}_{63}^{PD}$ measures could be quantitatively related to true shear moduli ratios through an inverse relationship, which is a topic on the future study [68].

A meaningful limitation to the study design was the inability to individually address every element in the 9L4 transducer experimentally. This limitation is due to the outer rows in the transducer being electronically connected. Thus, the electronic PSF rotation achieved in the simulation could not be realized in practice. To compensate for this limitation, a computational rotation stage was used to achieve the desired rotations experimentally using a VF73 linear array transducer. While the 9L4 with electronic PSF rotation created ARF excitation PSFs with asymmetry ratios of roughly 2.6, the VF73 generated an ARF PSF with an asymmetry ratio of 4.0. The higher asymmetry ratio resulted in less influence from the off-axis modulus in the associated PD measurement. Specifically, relative to the 9L4, PDs induced by the VF73 when the ARF PSF short axis was aligned across the AoS more strongly reflect the longitudinal shear elastic modulus with less influence from the transverse shear elastic modulus, and vice versa when the PSF was rotated 63°. As a result, the experimental measurements made using the VF73 may have a higher sensitivity to differences in shear elastic DoA than the 9L4 could have achieved if electronic ARF excitation PSF rotation were experimentally possible. Despite this limitation, the experimental work yielded outcomes that were consistent with in silico results. Specifically, the biceps femoris muscles of the two pigs, which were shown by SWEI imaging with a 90° rotation angle to have shear elastic moduli ratios of roughly 4.3 and 3.0, were statistically distinguished by $Do{A}_{63}^{PD}$. This outcome suggests the feasibility of electronic beam rotation using a three-row array and informs future transducer development for ARFI DoA assessment. A three-row array design with individually addressable elements is beneficial because it is easier to manufacture and address relative to a full 2D matrix and enables multiple rotation angles, unlike a row-column array (which is limited to 0° and 90° rotations and is not yet commercially available). Moreover, the simulated three-row array has already been developed and optimized for conventional ultrasound imaging purposes, so extending its utility to DoA assessment would enable seamless clinical integration.

A second limitation of the study design was the slight mismatch in the asymmetry ratios of PSF_A versus PSF_B and TPSF_A versus TPSF_B. The asymmetry ratio of excitation PSF impacts DoA assessment by weighing the influence of the longitudinal and the transverse modulus on the overall PD achieved. For more asymmetric PSFs, one modulus is weighed more strongly than the other. The asymmetry ratio of the tracking PSF impacts DoA assessment by averaging scatterer displacements under the PSF. The slight mismatch in excitation and tracking PSFs’ asymmetry ratios is likely a cause for the subtle discrepancies in $Do{A}_{63}^{PD}$ achieved by manual versus electronic PSF rotation, as shown in Fig. 6. Importantly, these differences were not very large.

The mismatch is PSF asymmetry ratio could be eradicated by implementing a more sophisticated approach to active element and time delay selection. In the presented work, active elements and time delays were chosen empirically to achieve electronically rotated ARF PSFs with 1) asymmetry ratios that were consistent with each other and greater than 2, and 2) at least 50° of rotation from each other. While these design criteria were exceeded by the empirically determined active elements and time delays (the ARF PSF asymmetry ratio was roughly 2.6 and rotation angle was 63°), performance could have been enhanced by more optimal ARF PSFs. In the future, active element and time delay selection could be implemented in an automated fashion to systematically generate the best possible electronically rotated PSFs for ARFI DoA assessment.

Finally, this study evaluated the ability to discriminate elastic anisotropy in purely elastic media and did not consider the impact of viscosity or the ability to detect viscous anisotropy. A comprehensive and systematic evaluation of viscosity is a topic of future work.

V. CONCLUSION

The primary innovation advanced by this work is electronic PSF rotation to support ARF DoA assessment using a three-row array with individually addressable elements. The electronically achieved rotation angle of 63° was smaller than the manually rotated 90° angle previously demonstrated, and, as a result, DoA resolution diminished from 6% to 17% in silico. However, in practice, manual rotation is cumbersome and prone to misalignment error, so the gains in convenience and precision afforded by electronic PSF rotation may outweigh the loss in DoA resolution. Further, improvements to the electronic PSF rotation, including refinement of the compensation factor and optimization of active element and time delay selection, are possible, which could lessen the gap between 63° and 90° PSF rotation performance. Application in excised pig biceps femoris muscle with comparison to SWEI demonstrated the potential for clinical translation. Overall, these results provide a theoretical proof of concept for a three-row transducer enabling ARFI-based elastic DoA assessment without manual transducer rotation. With this theoretical proof established, future work in corresponding transducer development will be more informed. Specifically, rather than a full 2D matrix or a row-column structure, three-row arrays could be considered to enable electronic PSF rotation ready integration with the design of conventional imaging probes.

Biography

Md Murad Hossain earned his B.Sc and M. Sc degree in electrical engineering from the Islamic University of Technology, Bangladesh and George Mason University, USA in 2009 and 2014, respectively. He completed his Ph.D. degree in biomedical engineering at the joint Department of Biomedical Engineering at the University of North Carolina – Chapel Hill and North Carolina State University in 2019 with a focus on ultrasound elastography. He is now a post-doctoral research scientist in the Biomedical Engineering department at Columbia University. His research interests include acoustic radiation force imaging, shear wave elastography, viscoelasticity, and medical signal processing.

Caterina M. Gallippi earned a B.S.E. degree in electrical engineering and a certificate in engineering biology from Princeton University in 1998. She completed her Ph.D. degree in biomedical engineering at Duke University in 2003 with a focus on ultrasonic imaging. She is currently an associate professor in the joint Department of Biomedical Engineering at the University of North Carolina - Chapel Hill and North Carolina State University. Her research interests include radiation force imaging, adaptive signal filtering, multidimensional motion tracking, and magneto-motive ultrasound.