Utilizing tandem mass spectrometry for metabolic flux analysis

Abstract

Metabolic flux analysis (MFA) aims at revealing the metabolic reaction rates in a complex biochemical network. To do so, MFA uses the input of stable isotope labeling patterns of the intracellular metabolites. Elementary metabolic unit (EMU) is the computational framework to simulate the metabolite labeling patterns in a network, which was originally designed for simulating mass isotopomer distributions (MIDs) at the MS1 level. Recently, the EMU framework is expanded to simulate tandem mass spectrometry data. Tandem mass spectrometry has emerged as a new experimental approach to provide information on the positional isotope labeling of metabolites and therefore greatly improves the precision of MFA. In this review, we will discuss the new EMU framework that can accommodate the tandem mass isotopomer distributions (TMIDs) data. We will also analyze the improvement on the MFA precision by using TMID. Our analysis shows that combining the MIDs of the parent and daughter ions and the TMID for the MFA is more powerful than using TMID alone.

Introduction

The function of a cellular metabolic network is to convert nutrient molecules into biochemical energy and biomass. Metabolomics which focuses on measuring the concentrations of metabolite can offer a panoramic snapshot of the metabolic network [1]. However, such a still-image characterization offers no information on how metabolites interconvert [2]. A common analogy is the car traffic. High density of cars can either be a smooth traffic having large flux, or a complete stop and no traffic flux. Simply counting cars on the road from a picture cannot tell us about the traffic. Therefore, it is important to investigate the metabolic fluxes which are rates at which metabolites are converted to their enzymatic products. For cultured cells, simple metabolic fluxes such as glucose uptake rate or lactate production rate can be calculated by measuring the decrease of glucose concentration or increase of lactate concentration in the medium over time. The intracellular fluxes, however, are impossible to measure by this method because the intracellular metabolite concentrations are constant at steady state [3]. To observe and infer the intracellular metabolic fluxes, we can use stable isotope labeled tracers. In such an experiment, a ¹³C-labeled nutrient tracer is fed to the biological system. The labeled carbon atoms are then distributed over the metabolic network [4, 5]. When the isotope labeling steady state is reached, the labeling patterns of intracellular metabolites are uniquely determined by only two factors: the metabolic fluxes in the network and the labeling pattern of the isotope tracer [6, 7]. The metabolite labeling patterns are measurable on the mass spectrometers, and can be used to infer the metabolic fluxes in a procedure referred to as the metabolic flux analysis (MFA).

MFA has been widely applied in the fields of metabolic engineering and mammalian physiology to study metabolic networks [8–10]. MFA aims at solving metabolic fluxes when given the metabolite isotope labeling patterns. The forward problem, which is to calculate the labeling patterns when given fluxes, is a deterministic problem and can be solved very efficiently using the elementary metabolic unit (EMU) framework [11, 12]. MFA is the reverse to this problem and it usually has no analytical solution. We are looking for a set of fluxes that can generate the metabolite labeling patterns that fit the measurements the best. Therefore, the fluxes are determined by an optimization process. The residual that measures the differences between simulated and measured labeling patterns should be minimized.

For mass spectrometry based labeling measurements, the conventional MFA uses metabolite mass isotopomer distributions (MIDs) as the input information. Moreover, multiple parallel experiments using different tracers can be combined to achieve better flux determination. In such parallel labeling experiments, each tracer alone may not be sufficient to determine all the fluxes in the network. However, the combined MID information can provide a comprehensive profiling of the fluxes. Crown and Antoniewicz have shown that the use of parallel labeling can dramatically improve the precision of MFA [13, 14]. It is noteworthy that the MID does not account for the positional isotope labeling. For example, 1,2-¹³C-lactate and 2,3-¹³C-lactate are both described as lactate M + 2 (or M2). Tandem mass spectrometry, which breaks specific C–C bonds in the metabolite molecules, can generate information on positional isotope labeling. Recently, new computational approaches were developed to accommodate tandem mass spectrometry data to improve the performance of MFA. Tandem MS MFA may show unique advantages when compared to the parallel labeling strategy, especially in animal studies. Parallel labeling would require more animals in the study, and unlike culture cells, the animals may not be perfectly parallel in their metabolism. The best strategy is probably to combine the use of parallel labeling and tandem MS for MFA. In this review paper, we will focus on discussing what tandem mass spectrometry data can be used for MFA. We will also analyze the flux constraints provided by the tandem mass spectrometry data. Our results show that combining the MIDs of the parent and daughter ion and the tandem MID for the MFA is more powerful than using tandem MID alone.

Tandem mass spectrometry

In tandem mass spectrometry, a parent ion is first selected on a quadrupole mass filter. The parent ion is then fragmented to give daughter ions which are detected on the mass analyzer. In the example shown in Fig. 1a, a mixture of metabolite A consists of equal amount of four isotopomers. The parent MID is 25% M0, 25% M1, 25% M2, and 25% M3. This molecule of four carbon atoms can be fragmented to a daughter ion composed of the last two carbon atoms (denoted $A_{1234}^{34}$). Based on the fragmentation pattern, the M1 parent will only generate m1 daughter ions. The M2 parent will only generate m0 daughter ions and the M3 parent will only generate m2 daughter ions. The M0 parent will always generate m0 daughter ions. Such information of the tandem mass isotopomer distribution (TMID) can be expressed in a matrix form (Fig. 1b) [15, 16]. TMID is more informative than the parent and daughter MIDs combined because the parent–daughter relationship is also revealed. From the TMID matrix, we can easily calculate the MIDs for the parent and daughter ions which are the column-wise and row-wise sums respectively (Fig. 1b). Experimentally, the measurement of TMID depends on the type of instrument. On the triple quadrupole (QQQ) instruments, each scan event covers a parent–daughter pair and provides a single number in the TMID matrix (e.g., M2-m0). On hybrid mass spectrometers such as Q-TOF or Q-Orbitrap instruments, all the daughter ions from a parent can be measured simultaneously. Therefore, each scan event on the hybrid instruments provides a whole column in the TMID matrix [17]. Note that the lower-left corner of the TMID matrix (Fig. 1b) is blank because the number of labeled atoms in the daughter ion cannot exceed the number of labeled atoms in the parent ion. Similarly, the upper-right corner of the TMID matrix is blank because the number of unlabeled atoms in the daughter ion cannot exceed the number of unlabeled atoms in the parent ion. Choi and Antoniewicz [18] proposed to use the compact tandem MS matrix in which each row is shifted to the left to remove the blank corners. Alternatively, the tandem MS data can be expressed in a vector form which is generated by concatenate the rows of the compact tandem MS matrix (Fig. 1b). The vector form is more convenient when simulating the EMU labeling patterns [19].

Fig. 1. Tandem mass spectrometry data.

a Metabolite A is ¹³C-labeled (green circles). There are 25% unlabeled A, 25% 4-¹³C₁-A, 25% 1,2-¹³C₂-A, and 25% 2,3,4-¹³C₃-A. The MS/MS of A generate a fragment of C3–C4. b The TMID of $A_{1234}^{34}$ in matrix form, compact matrix form, and vector form. c The flux confidence intervals with and without the use of tandem MS data. The model is from Anotoniewicz et al. [11] and the true flux combination is f₂ = 150, f₄ = 30. The MID of F was used for flux determination. The labeling of F on C-3 was used as the tandem MS data.

The main motivation for introducing tandem MS data to MFA is to improve the precision of flux determination. Figure 1c shows an example using the metabolic network from by Anotoniewicz et al. [11]. When using only the MID of the metabolite F in the network, the flux f₂ can take any value above 100. However, if we use the tandem MS data which measures the labeling of F at C-3 position, the f₂ is confined in the interval of (138, 164). A well-designed MFA study should have tight confident intervals on all the important fluxes. This can be achieved by utilizing measurements from tandem MS, and/or using parallel labeling technique.

A TMID is used to describe the conditional MIDs of the daughter ions generated from the same fragmentation reaction. However, a metabolite ion may fragment by breaking different bonds and generate multiple daughter fragments at the same time [20]. Kappelmann et al. [21] reported a comprehensive investigation of fragmentation patterns of central metabolism intermediates. Key information from this paper is that some daughter ions may have mixed identities. Malate, for example, may lose a water molecule and become fumarate (Fig. 2). Fumarate is a symmetric molecule and can decarboxylate at either C1 or C4 position. Both reactions generate C₃H₂O₂⁻ (m/z 71.0139). Therefore, this daughter ion represents a mixture of $Ma{l}_{1234}^{234}$ and $Ma{l}_{1234}^{134}$ at 1:1 ratio. Alternatively, malate may decarboxylate at C4 first and lost a water to become C₃H₂O₂⁻ which is exclusively $Ma{l}_{1234}^{123}$ (Fig. 2). Because the probabilities of these two fragmentation routes are unknown, the C₃H₂O₂⁻ represents the mixture of $Ma{l}_{1234}^{234}$ and $Ma{l}_{1234}^{123}$ at unknown ratio. Therefore, this daughter ion should not be used for MFA. Only the daughter ions having unambiguous identity such as $Ma{l}_{1234}^{34}$ and $Ma{l}_{1234}^{12}$ should be used for MFA. Tables 1, 2 summarize the results from Kappelmann et al. [21] and show MS fragments in TCA cycle that can and cannot be used for ¹³C-MFA.

Fig. 2. Fragmentation pathways of malate.

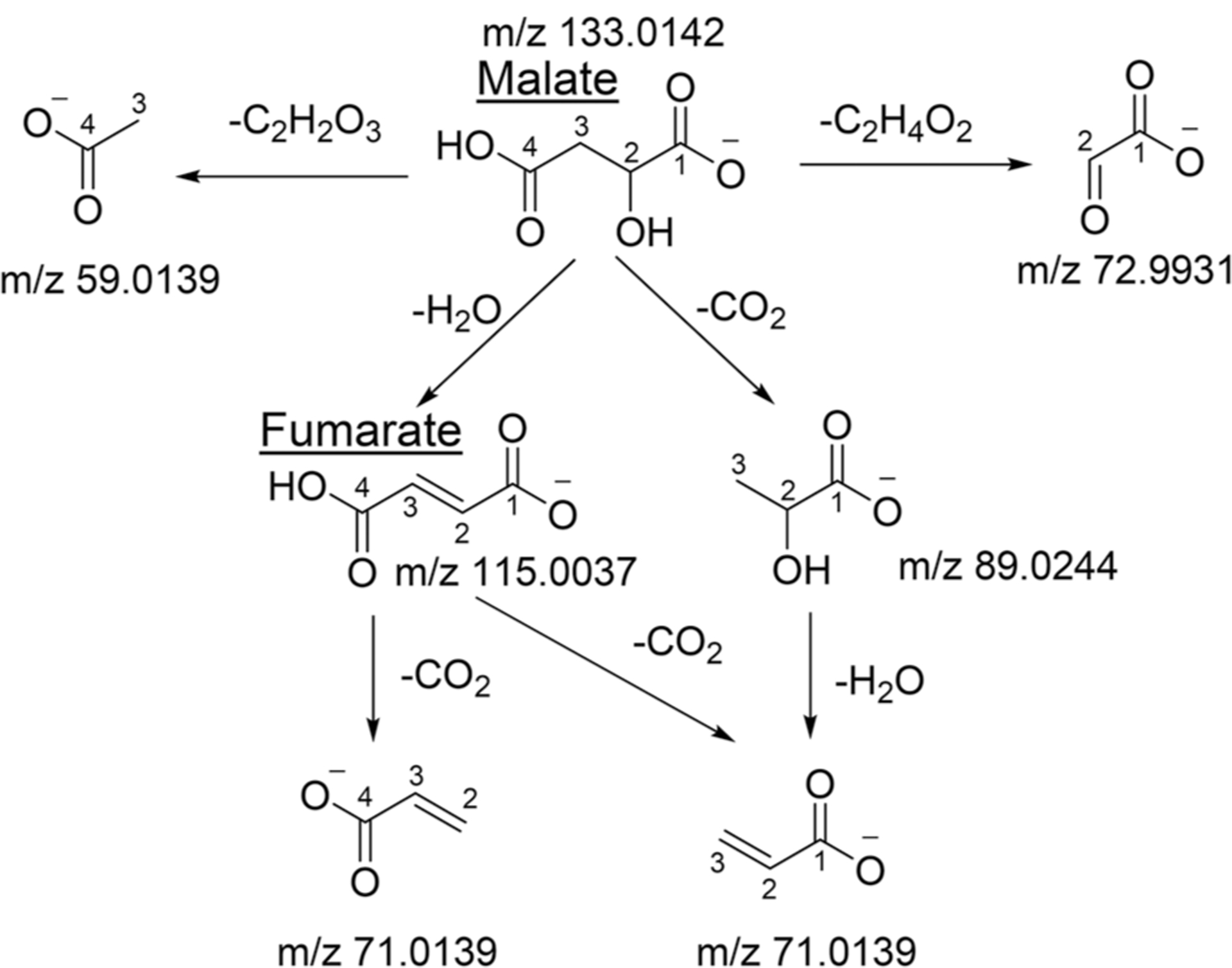
Malate can generate 2 different daughter ions with the same m/z but in unknown ratio. Consequently, these daughter ions should be used for ¹³C-MFA.

Table 1.

Summary of unambiguous fragment ions for TCA cycle metabolites.

Parent EMU	Unambiguous fragment ions	Fragment formula	m/z
Pyruvate[123]	Pyruvate[23]	C2H3O2−	59.0139
	Pyruvate[23]	C2H2O2·−	58.006
	Pyruvate[2]	CO3·−	59.9853
Malate[1234]	Malate[123]	C3H5O3−	89.0244
	Malate[234]	C3H3O3−	87.0088
	Malate[12]	C2HO3−	72.9931
	Malate[34]	C2H3O2−	59.0139
Aspartate[1234]	Aspartate[123]	C3H4NO−	70.0298
	Aspartate[12]	C2H2NO2−	72.0091
	Aspartate[34]	C2H3O2−	59.0139
	Aspartate[4]	CH2NO2−	60.0091
α-ketoglutarate (α-KG)[12345]	α-KG[2345]	C4H3O2−	83.0139
	α-KG[234]	C3H5O−	57.0346
Oxaloacetate[1234]	Oxaloacetate[123]	C3H3O3−	87.0088
	Oxaloacetate[34]	C2H3O2−	59.0139
cis-aconitate [123456]	cis-aconitate[12346]	C5H3O3−	111.0088
	cis-aconitate[1234]	C4H3O−	67.0189
trans-aconitate [123456]	trans-aconitate[2346]	C4H5O2−	85.0295
Citrate[123456]	50% citrate[12346] + 50% citrate[23456]	C5H7O5−	147.0299
	50% citrate[12346] + 50% citrate[23456]	C5H5O4−	129.0193
	50% citrate[12346] + 50% citrate[23456]	C5H3O3−	111.0088
	50% citrate[1236] + 50% citrate[3456]	C4H3O5−	130.9986
	Citrate[2346]	C4H7O3−	103.0401
	50% citrate[1234] + 50% citrate[2345]	C4H5O3−	101.0244
	50% citrate[1234] + 50% citrate[2345]	C4H3O−	67.0189
	50% citrate[236] + 50% citrate[346]	C3H3O3−	87.0088
	Citrate[234]	C3H5O−	57.0346
	50% citrate[12] + 50% citrate[45]	C2H3O2−	59.0139

We are only showing fragment ions with m/z > 50, due to the consideration of instrument limitations. All m/z values are calculated based on the unlabeled form.

Table 2.

Summary of ambiguous fragment ions for TCA cycle metabolites.

Parent EMU	Ambiguous fragment ions (cannot be used for MFA)	Fragment formula	m/z
Malate[1234]	Malate[123] and [234]	C3H3O2−	71.0139
Aspartate[1234]	Aspartate[123] and [234]	C3H6NO2−	88.0404
	Aspartate[123] and [234]	C3H4NO2−	86.0248
	Aspartate[123] and [234]	C3H3O2−	71.0139
α-ketoglutarate (α-KG)[12345]	α-KG[1234] and [2345]	C4H5O3−	101.0244
	α-KG[234] and [345]	C3H5O2−	73.0295
	α-KG[234] and [345]	C3H3O2−	55.0189
cis-aconitate[123456]	cis-aconitate[12346] and [23456]	C5H5O4−	129.0193
	cis-aconitate[1234] and [2346]	C4H5O2−	85.0295
trans-aconitate[123456]	trans-aconitate[12346] and [23456]	C5H5O4−	129.0193
Citrate[l23456]	Citrate[1234] and [2345] and [2346]	C4H5O2−	85.0295

These ions should NOT be used for tandem MS MFA. We are only showing fragment ions with m/z > 50, due to the consideration of instrument limitations. All m/z values are calculated based on the unlabeled form.

Simulating TMID using EMU

EMU is currently the most widely used mathematical framework for MFA. EMU is an algorithm that simulates metabolite MIDs when given the tracer labeling pattern and all the fluxes in the network. The concept of EMU and MID calculation was described by Anotoniewicz et al. [11]. We wish to highlight the fact that the tandem MS data are naturally simulated when calculating the MID of observable metabolites using the EMU approach. To illustrate this idea, we use the example of gluconeogenesis network shown in Choi’s paper (Fig. 3) [16]. There are 12 metabolic fluxes in this network. The tracer input to this metabolic network is asparate (Asp) that has 25% 4-¹³C₁, 25% 1,2-¹³C₂, 25% 2,3,4-¹³C₃ labeling, and 25% unlabeled. The only measurable metabolite is oxaloacetate (OAC). To calculate the MID of the whole OAC molecule (denoted OAC[1234]), we need to know the labeling pattern of Fum[1234] which makes OAC[1234] through f₆. Fum[1234] will be traced back to other size four EMUs. Additionally, we need to know the labeling patterns of AcCoA and Glyox which make OAC through f₉. AcCoA is an unlabeled input to the metabolic network. Glyox is made from Cit[45] through f₈, and Cit[45] is made from OAC[34] through f₁. Therefore, in order to calculate OAC[1234], we need to know the OAC [34] first. OAC[34] is a hypothetical EMU when calculating the MID of OAC. However, OAC[34] is also the MID of the C3C4 fragment of OAC, which is measurable using tandem MS. Therefore, from the TMID of $OA{C}_{1234}^{34}$, we can calculate the MIDs of OAC[1234] and OAC[34] and use these values as the constraints for flux optimization. This method is essentially utilizing the existing EMU framework that was designed for MS1 data measurements. To fully utilize the data from tandem MS, we need to expand the EMU to simulate TMID.

Fig. 3. Gluconeogenesis network model including TCA cycle and glyoxylate shunt.

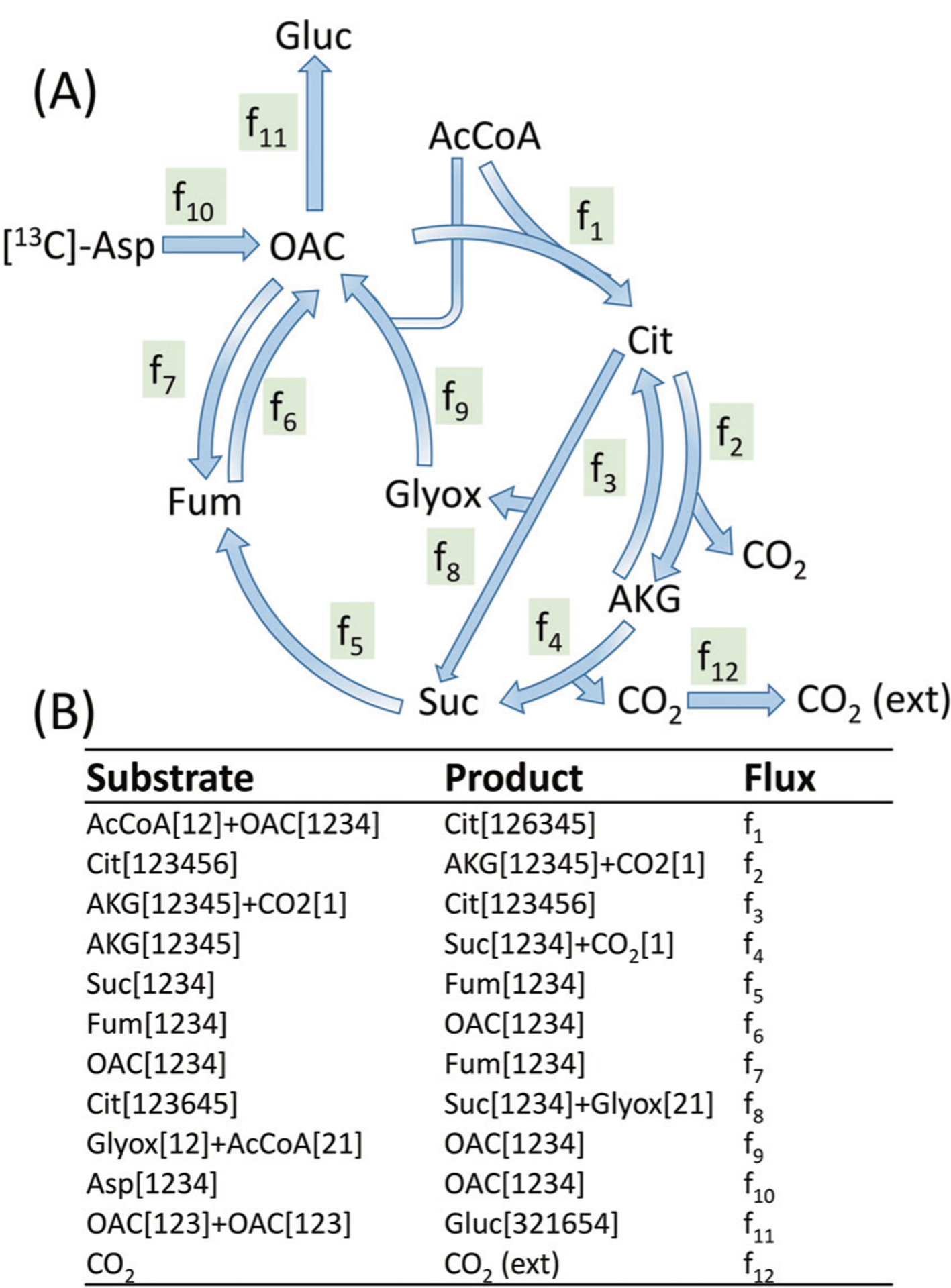
The abbreviations of the metabolites are the following: Asp aspartate, OAC oxaloacetate, AcCoA acetyl coenzyme A, Cit citrate, AKG alpha-ketoglutarate, Fum fumarate, Suc succinate, and Glyox glyoxylate. The network uses the assumed fluxes (arbitrary units): f₁ = 100, f₂ = 220, f₃ = 150, f₄ = 70, f₅ = 100, f₆ = 140, f₇ = 40, f₈ = 30, f₉ = 30, f₁₀ = 60, f₁₁ = 90, and f₁₂ = 140. A hypothetical flux f₁₃ = 1e7 is added to Suc[1234]->Suc[4321] and Fum[1234]->Fum[4321] to account for the molecular symmetry.

Tepper and Shlomi proposed the extended EMU framework to simulate TMID, which is termed tandemer [18, 19]. The tandemer EMU network decomposition is very similar to the normal EMU network decomposition process. For MS1 level measurements, the EMU network decomposition starts from OAC[1234]. For the MS2 level measurements, the tandemer EMU network decomposition starts from OAC[1234]-[34]. The tandemer EMU network decomposition may generate more EMUs than the original method because the tandem MS breaks the molecular symmetry. For example, Fum[1234] and Fum[4321] are two identical EMUs and are treated as one in the calculation. However, the Fum[1234]-[34] and Fum[1234]-[12] are two EMUs that are numerically the same but conceptually different. When the EMU network decomposition is completed, the tandem EMU calculation is the same as normal EMU, except the use of TMID vectors instead of the MID vectors.

Evaluating the power of TMID for MFA

When performing MFA, it is important to find the optimal flux solution that fits the observations. It is also important to evaluate the uncertainty of the fluxes given the measured data. Many papers report the flux uncertainty as the confidence intervals of individual fluxes [22]. Such results are often erroneously interpreted as the confidence interval of each flux is independent from others. An alternative approach to illustrate the flux uncertainty is to plot the feasible region of the fluxes [23]. This approach provides excellent visualization of the dependency of flux confidence intervals. However, it is difficult to plot for more than two free fluxes. This limitation is obvious for large metabolic networks. As a work around, we can show conditional confidence regions by plotting for two free fluxes with greatest uncertainty while leaving other fluxes unchanged. Here, we focus on the flux feasible region for the gluconeogenesis network that has four free fluxes, f₃, f₇, f₉, and f₁₀. Since the TMID is less sensitive to the two exchange fluxes f₃ and f₇, we will plot the combination of these two fluxes and leave the other two free fluxes unchanged. In Fig. 4a, we show the 95% confidence region of flux combinations determined from OAC[1234] MID. The optimal solution is f₃ = 150, f₇ = 40, which is the red center. The plot shows that both fluxes have a broad feasible region which indicates big uncertainty in the flux estimations. In this case, using only the MID of OAC[1234] is clearly not sufficient to determine the f₃ and f₇ to a high degree of precision. When both the MIDs of the parent ion OAC [1234] and the daughter ion OAC[34] are used, the feasible region of the fluxes is narrowed (Fig. 4b). Furthermore, when the complete TMID of OAC[1234]-[34] ($OA{C}_{1234}^{34}$, fragment of C3–C4 generated from OAC[1234]) is used, the flux feasible region becomes even smaller (Fig. 4c). The feasible region is very narrow in the f₇ dimension, suggesting the TMID provides strong constraint on this exchange flux. However, the f₃ estimation still has a large uncertainty. In fact, the uncertainty of f₃ calculated from TMID OAC[1234]-[34] is even larger than the one calculated from OAC[1234] and OAC[34]. This result is counterintuitive because the TMID has more information than the combination of parent and the daughter ion MIDs, yet the constraint provided by the TMID is weaker on f₃. This paradoxical result comes from the way the residual between simulated and measured MIDs is calculated. When the value of f₃ deviates from the optimal solution of 150 to the less optimal value of 350, the TMID OAC[1234]-[34] has increases of 0.27 and 0.24% in M1-m0 and M1-m1 fractions respectively. Since the assumed standard deviation of each fraction is 0.2% [16], these two fractions contribute 3.2 to the χ² statistic. Meanwhile, in the MID OAC[1234], these two fractions adds up to a deviation of 0.51% in the M1 fraction, which contributes 6.38 to the χ² statistic. This larger increase in the χ² statistic suggests f₃ = 350 makes the MID of OAC[1234] deviate more from the measurements than the TMID OAC[1234]-[34] would do. Therefore, we can conclude that although TMID provides more information than MIDs, it does not necessarily provide stronger constraints on every flux. When both the TMID and the MIDs are used, the precision of the flux estimation can be further improved (Fig. 4d). Therefore, we recommend using both TMID and the parent and daughter MIDs to constrain the fluxes.

Fig. 4. Comparison of flux uncertainty.

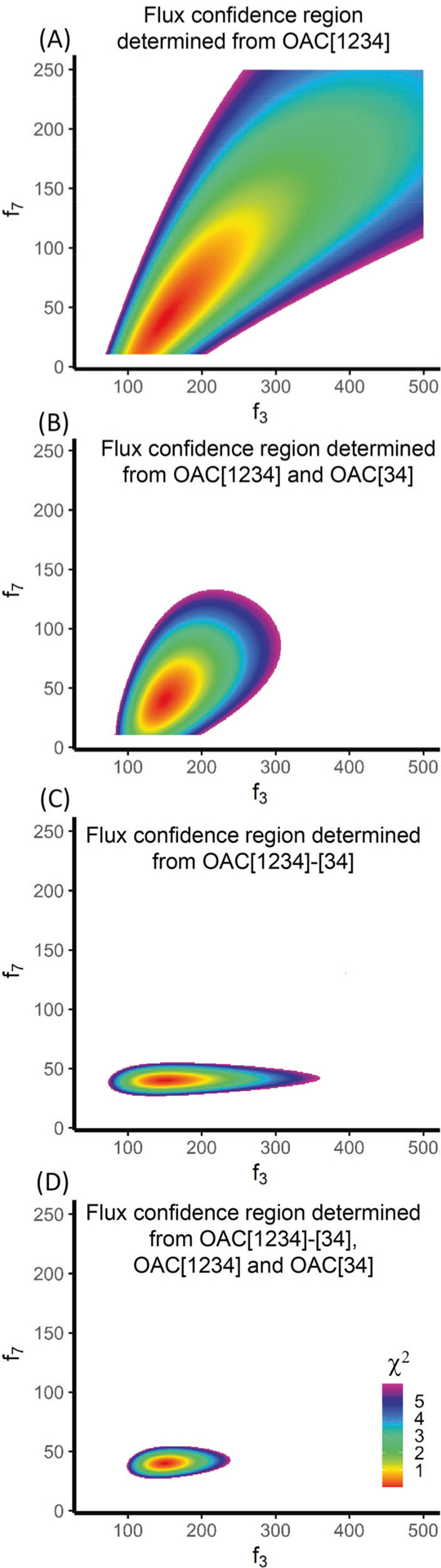
The plots evaluate the uncertainty of f₃ and f₇ which are two free fluxes. Other fluxes were left unchanged. The colored regions are showing the 95% confidence regions of the flux combinations.

Conclusion

Tandem mass spectrometry can reveal metabolite positional labeling and provide more information for improving the performance of MFA. To utilize the tandem mass spectrometry for MFA, the identity of the daughter ions must be carefully inspected. Daughter ions of mixed origins should not be used. The EMU framework has been extended to accommodate the tandem mass spectrometry data. When calculating the fluxes, the TMID as well as the MIDs of parent and daughter ions should all be used to constrain the fluxes in order to achieve the best performance.