The present and the future of microstructure MRI: From a paradigm shift to normal science

Abstract

The aspiration of imaging tissue microstructure with MRI is to uncover micrometer-scale tissue features within millimeter-scale imaging voxels, in vivo. This kind of super-resolution has fueled a paradigm shift within the biomedical imaging community. However, what feels like an ongoing revolution in MRI, has been conceptually experienced in physics decades ago; from this point of view, our current developments can be seen as Thomas Kuhn’s “normal science” stage of progress. While the concept of model-based quantification below the nominal imaging resolution is not new, its possibilities in neuroscience and neuroradiology are only beginning to be widely appreciated. This disconnect calls for communicating the progress of tissue microstructure MR imaging to its potential users. Here, a number of recent research developments are outlined in terms of the overarching concept of coarse-graining the tissue structure over an increasing diffusion length. A variety of diffusion models and phenomena are summarized on the phase diagram of diffusion MRI, with the unresolved problems and future directions corresponding to its unexplored domains.

1. Tissue microstructure imaging with MRI

Water diffusion is a ubiquitous physical phenomenon that gives rise to the sensitivity of NMR / MRI signal to the structure at the micrometer scale, i.e., to tissue microstructure. Such sensitivity is remarkable: it decouples the physiologically relevant cellular scale of ~1–10 μm from the size of a macroscopic sample or an imaging voxel, and is practically about 2–3 orders of magnitude finer than human MRI voxels.

To put the microstructure scale into a broader context, let us recognize that MRI itself is a super-resolution imaging technique, as its voxel size does not depend on radiofrequency wavelength (λ ≈ 20 cm at B₀ = 3 T), breaking the Abbe ~ λ/2 diffraction limit (Abbe, 1873) by about two orders of magnitude. This “first” super-resolution is based on encoding the positions of nuclear spins via their precession phases, avoiding the limitation nominally imposed by the wavelength in, e.g., optical microscopy. As usual with super-resolution techniques (Betzig, 2015), the MRI resolution is fundamentally limited by the signal-to-noise ratio (SNR) (Roemer et al., 1990; Wiesinger et al., 2004). As we know, SNR is not limitless, and the best we can achieve in humans at B₀ of a few tesla is about ~1 mm voxels, with the modern MRI hardware reaching ≈90% of the Ultimate Intrinsic SNR (Ocali and Atalar, 1998), as verified in simulations (Lattanzi and Sodickson, 2012) and observed experimentally (Fan et al., 2016).

To reach an even finer resolution, we rely on the “second” super-resolution principle — now based on the proportionality relation

$$\langle x^2(t)\rangle =2dD\cdot t$$ (1)

between the mean-square displacement ⟨x²⟩ of water molecules and the diffusion time t in d spatial dimensions, with D being the diffusion coefficient. Note that there is no mention of spins, NMR, MRI, SNR or wavelength in Eq. (1), which nonetheless determines a spatial scale from a temporal scale.

Basic principles of measuring the diffusion coefficient with NMR were laid out in the 1950s–1960s by Hahn (1950), Torrey (1956) and Stejskal and Tanner (1965), who measured diffusion in simple liquids. The value D = 3 μm²/ms for water at 37 °C, as well as the NMR time range t ~ 1–1000 ms (broad due to fairly long water T₁), together comprise a gift from nature, yielding the diffusion length $\sqrt{\langle x^2(t)\rangle }\sim 1-100$ μm, over which the water molecules can realistically spread, depending on the imaging protocol and the tissue. The scale L(t) fortuitously matches that of cell morphology, which means that there is hope to capture physiological and pathological changes of tissues at the cellular level in development, aging and disease. Hence, we can say that tissue microstructure imaging with diffusion MRI (dMRI) is a (super)²-resolution technique, based on the two distinct physical principles, allowing us to overcome naive hardware limitations, and to see the invisible, in vivo.

How can one practically realize the sensitivity and specificity to the microstructure? Recall that in simple liquids, the unit “packet” of molecules placed at the origin at t = 0 spreads as a Gaussian distribution $G_{t,x}^{(0)}\sim e^{-x^2∕2{\sigma }^2}$, with variance σ² = L²(t)/d = 2Dt along each dimension linearly growing with time, Eq. (1). The cellular structure makes the evolution ${\mathcal{G}}_{t;x_t,x_0}$ of the packet non-Gaussian with respect to the displacement x = x_t − x₀ as well as dependent on the initial point x₀ within a voxel; one such Brownian path, from x₀ to x_t, is highlighted in the top-left panel of Fig. 1. The local propagator ${\mathcal{G}}_{t;x_t,x_0}$ (a probability density of landing at x_t when starting at x₀ over time t) in principle “knows” a lot about the cellular structure within distance ~L(t) around x₀, as it is formally an inverse of the local diffusion operator with all the specified positions and boundary conditions for cell membranes, their permeability values, local diffusivity profiles D(x) in different tissue regions, and so on.

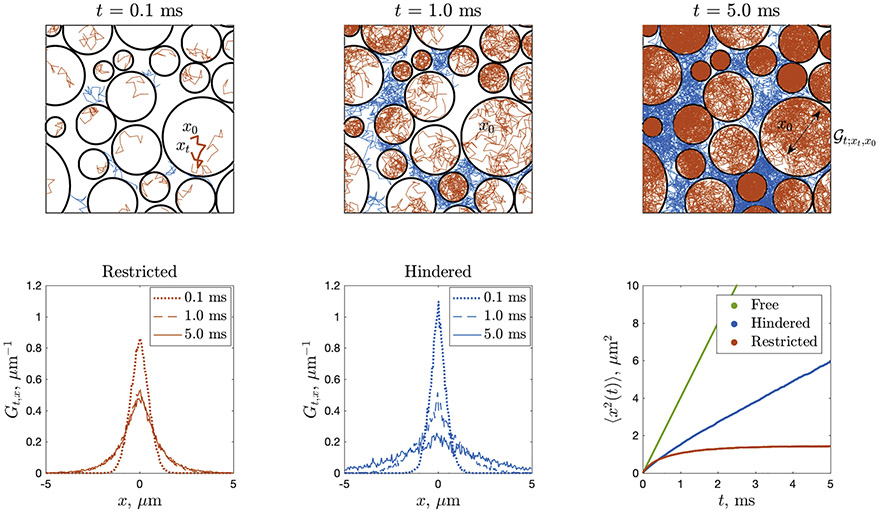
Fig. 1.

dMRI propagator G_t,x, Eq. (2), as an ensemble-average of the local diffusion propagator ${\mathcal{G}}_{t;x_t,x_0}$ (see text), here sampled using Monte Carlo (MC) simulations in the geometry of non-overlapping impermeable circular “cells” of diameters 0.35–6.25 μm. The intra-cellular (restricted) ${\mathcal{G}}_{t;x_t,x_0}$, sampled by red MC paths, for long enough t fills up each cell, such that the net restricted contribution G_t,x averaged over all red paths remains non-Gaussian, as shown in bottom-left panel (G_t,x is bounded in x, and it becomes t-independent practically after t ≳ 1ms, with a bounded variance (1) plotted in bottom-right panel). The extra-cellular (hindered) ${\mathcal{G}}_{t;x_t,x_0}$, sampled by blue MC paths, is allowed to spread infinitely far, hence its ensemble-average G_t;x asymptotically spreads as a Gaussian with variance growing asymptotically linearly with t, Eq. (1), with the slope D(t)∣_t→∞ = D_∞ < D₀. Bottom-left and middle panels show the ensemble-averaged propagator projected onto the x-axis, by integrating the displacements along the y-axis. Bottom-right panel also shows Eq. (1) for the free diffusion, with D = D₀, as a reference. Most of the information about cell sizes, shapes and their packing is washed out after the ensemble averaging. Figure courtesy of Lee (2019).

Unfortunately, we do not access ${\mathcal{G}}_{t;x_t,x_0}$ directly (and neither can we model it exactly since we do not know tissue properties with such precision anyway). Instead, an ideal narrow-pulse diffusion NMR/MRI measurement accesses the Fourier transform

$$G_{t,q}=\int \mathrm{d}x{e}^{-iqx}{G}_{t,x},G_{t,x}\equiv \langle {\mathcal{G}}_{t;x_0+x,x_0}{\rangle }_{x_0}$$ (2)

of the propagator G_t,x that is an ensemble-average of the local ${\mathcal{G}}_{t;x_t,x_0}$ over all positions x₀ within an NMR sample / MRI voxel, as illustrated in Fig. 1, and discussed in detail by Callaghan (1991), Grebenkov (2007), Kiselev (2017), and Novikov et al. (2019). The 3-dimensional wave vector q = gδ is created by a Larmor frequency gradient g applied over a short duration δ.

The key observation here is that at this averaging step, $\mathcal{G}\to G$, most of the valuable local information about different cellular environments within a voxel gets washed out. The good news is that the voxel-averaged propagator G_t,x remains non-Gaussian, and thus potentially informative. Roughly speaking, the functional form of G_t,x tells just how non-uniform and restrictive an average local environment of size ~L(t) is in a given voxel. Hence, intuitively, one can “probe” tissue microstructure by studying how distinct the object G_t,q is from a simple Gaussian $G_{t,q}^{(0)}=e^{-D{q}^{2}t}$ for t > 0.¹ Of course, the devil is in the details of how one defines a very loaded term “to probe”, as discussed in what follows.

The above few paragraphs describe in a nutshell the basis of tissue microstructure imaging with dMRI. Two things are remarkable about this field: Its foundational paradigm is over 40 years old, formulated in groundbreaking works of Tanner (1979) and Callaghan et al. (1979); yet I believe its major fundamental achievements are happening right now or about to happen in the (hopefully) near future. That is not to say that nothing significant occurred between 1970s and today in dMRI, — it is just that, strictly speaking, most developments had less to do with quantifying actual μm-level tissue structure, and more with solving important engineering and experimental challenges, developing image-processing tools, and observing empirical changes in diffusion tensor eigenvalues in different pathological and physiological settings (Jones, 2010). That it took so long to get to the forefront of tissue microstructure per se, tells just how many moving parts one has to control in an in vivo dMRI experiment, and how much sustained focus the community has demonstrated to reach today’s technical level, which finally enables us to begin performing rigorous model-based quantification of tissue microstructure. Let me give a brief outline of the past 40 years, to provide context for the future developments.

2. From Tanner and Callaghan to today

Tanner (1979) was first to formulate the paradigm of model-based quantification of micrometer-level tissue properties with a macroscopic NMR measurement. In a single paper, he applied three different diffusion-weighed sequences (oscillating gradient, pulse-gradient, and stimulated-echo diffusion), to measure the time-dependent D(t) = ⟨x²(t)⟩/2d (cf. Eq. (1)) transverse to a frog muscle over 4 orders of magnitude in diffusion time, t = 0.3–2400 ms. He then estimated the muscle fiber diameter and membrane permeability by comparing the measured D(t) to his solution for the diffusion propagator in a 1-dimensional array of periodically spaced permeable barriers (Tanner, 1978). While I hope that the neuroscience readers forgive the historical anomaly of the pioneering development happening away from the neuronal tissue, they will surely appreciate just how ahead of its time this work turned out to be: It had all the ingredients of a modern-day tissue microstructure imaging study — theory, a theory-informed experiment on an actual tissue sample with carefully chosen sequences and timings, parameter estimation and interpretation — albeit in a single NMR “voxel” (test tube).

In the same issue of the Biophysical Journal, Callaghan et al. (1979) quantified the microstructure of endosperm tissue of wheat grains, showing that the signal attenuation as function of the “k-value” (identical to modern-day b-value) was most consistent with diffusion along randomly-oriented one-dimensional channels, or narrow tubes (with negligible transverse dimensions ~0.1 μm as compared with the diffusion length L(t) in the experiment). Remarkably, decades later this work inspired the 21st century in vivo findings of similar narrow one-dimensional channels for water and metabolite diffusion in the brain, attributed in this case to axons, as well as possibly dendrites and glial cell processes (Behrens et al., 2003; Kroenke et al., 2004; Jespersen et al., 2007; McKinnon et al., 2016; Veraart et al., 2019, 2020), which will be discussed below.

The development of all the necessary tools to go from NMR test tube to human in vivo quantitative dMRI took decades: implementing basic dMRI in the 1980s by Le Bihan et al. (1986) and observing first diffusion-weighted brain images in health and disease at then-available b ~ 0.1–0.2 ms/μm²; separating the diffusion and IVIM (perfusion) effects (Henkelman, 1990; Le Bihan, 1990; Le Bihan and Turner, 1992); the two seminal 1990 discoveries — of the diffusion coefficient drop in acute stroke by almost 50% (Moseley et al., 1990) and of the diffusion anisotropy in white matter tracts (Moseley et al., 1990a); parameter estimation framework for the diffusion tensor, widely known today as diffusion tensor imaging (DTI) (Basser et al., 1994); and the anisotropy-based fiber tractography (Conturo et al., 1999; Mori et al., 1999; Basser et al., 2000). Diffusion-weighted spectroscopy enabled studying separately intra- and extra-cellular metabolites (Ackerman and Neil, 2010), whereas MRI microscopy (Callaghan, 1991), that originated within the porous media community, allowed to image individual neuronal cells and their activity (Flint et al., 2009, 2012).

The first microstructure model of diffusion in a white matter tract, suggested by Stanisz et al. (1997), was soon followed by representing intra-axonal space by impermeable cylinders for the purpose of their diameter quantification (Assaf et al., 2004, 2008). Quite naturally, these early dMRI modeling developments occurred in parallel to early microstructure models of the transverse NMR relaxation (Yablonskiy and Haacke, 1994; Kiselev and Posse, 1998, 1999), aimed at providing the quantitative foundations (Weisskoff et al., 1994; Kennan et al., 1994) of BOLD fMRI, perfusion measurements (Østergaard et al., 1996b; Østergaard et al., 1996a; Kiselev, 2001; Turner, 2002), and vessel size imaging (Dennie et al., 1998; Troprès et al., 2001; Kiselev et al., 2005). Not surprisingly, the relevant physics for quantifying the length scale of “magnetic microstructure” (Kiselev and Posse, 1998; Jensen and Chandra, 2000a,b; Kiselev and Novikov, 2002; Sukstanskii and Yablonskiy, 2003, 2004; Jensen et al., 2006; Novikov and Kiselev, 2008) is given by the same Eq. (1), as reviewed recently by Kiselev and Novikov (2018).

Progress in computer vision at the turn of the 21st century spurred representing the dMRI signal G_t,q sampled in the 3-dimensional q-space in a variety of reasonably chosen bases: spherical harmonics (Frank, 2002; Tournier et al., 2004; Anderson, 2005); Q-ball imaging (Tuch, 2004); via successive terms of the cumulant expansion (Kiselev and Il’yasov, 2007; Kiselev, 2010), such as the diffusion kurtosis imaging (Jensen et al., 2005); multiexponential (Laplace transform) (Yablonskiy et al., 2003); the harmonic oscillator eigenbasis (Özarslan et al., 2013), and so on. These “signal representations” can be useful for compression or storage of our multi-dimensional experimental data, and for empirical comparisons of the basis coefficients with physiological or pathological changes.

Often times, however, such convenient mathematical expressions have been conflated with modeling, which has resulted in a certain intellectual relativism (each group could seemingly have their own favorite “model” of the same thing, since there are infinitely many complete basis sets in the space of functions). A common ground is reached by defining a model as a simplified picture of a physical process, and drawing a distinction between many equivalent mathematical signal representations, and the unique biophysical model of diffusion in a given tissue type, characterized by its specific assumptions about the microstructure that must be validated (Novikov et al., 2018a, 2019) — i.e., by going back to our scientific roots, when the notion of a physical model was undisputed (Tanner, 1979; Callaghan et al., 1979).

Following the necessary detours to build in vivo dMRI capabilities and an ecosystem of measurement and processing tools, as well as having reaffirmed the notion of biophysical modeling, in the “modern era” (the past decade or so) rigorous modeling and validation methods adapted from the physical sciences have been employed in dMRI in a consistent and highly productive way. This progress has been recently reviewed by a number of authors actively pushing the boundaries of modeling and validation (Kiselev, 2017; Jelescu and Budde, 2017; Reynaud, 2017; Jespersen, 2018; Jones et al., 2018; Valette et al., 2018; Novikov et al., 2018a, 2019; Alexander et al., 2019), including in the present Special Issue (Afzali et al., 2020; Jelescu et al., 2020; Kiselev, 2020; Neto-Henriques et al., 2020).

3. A scientific revolution or normal science?

Following Kuhn (1962), it became customary to formulate progress in any field in terms of paradigm shifts — watershed events that radically change our thinking, followed by the periods of normal science until a new crisis demands changing the paradigm yet again. After a revolution, scientists, in the field that has been changed, “… work in a different world.”

A default clinical and neuroscience protocol, DTI, provides a representation of a signal, but it is not enough for modeling tissue microstructure (Novikov et al., 2018a). Hence, relative to DTI, any genuine microstructure metric can revolutionize our understanding of physiology or pathology. Risking abusing a cliché, an applications-oriented researcher is probably justified in touting noninvasive tissue microstructure imaging as a paradigm shift for neuroscience research or clinical practice.

But is the nascent microstructure MRI really a paradigm shift for the likes of Tanner or Callaghan? Physicists have routinely faced a setup where they study macroscopic phenomena (e.g., conductivity, heat capacity) and aim to deduce the relevant microscopic degrees of freedom (e.g., atomic or molecular interactions, electron dynamics) governing the observed behavior. Both classical and quantum transport phenomena (Altshuler and Aronov, 1985; Bouchaud and Georges, 1990; Kamenev, 2011) are used for model-based quantification of “micro”--structure (which, depending on the system, can happen at a nanometer or a micrometer or at any other scale sufficiently below macroscopic sample size). In the post-war period, physicists uncovered the remarkable universality governing the way microscopic interactions give rise to collective, or hydrodynamic modes describing their normal macroscopic behavior and critical dynamics around phase transitions (Anderson, 1972; Hohenberg and Halperin, 1977; Wilson, 1983; Cardy, 1996). Another line of progress was to realize how the effect of structural disorder at the micro-scale can radically change macroscopic transport (Anderson, 1958; Altshuler and Aronov, 1985; Kamenev, 2011). From this standpoint, all we are doing in dMRI modeling, is developing models of classical diffusive transport in structurally heterogeneous media.

For a physicist, therefore, modern-day modeling and validation of tissue microstructure looks like Kuhn’s normal science, which means “research firmly based upon one or more past scientific achievements, achievements that some particular scientific community acknowledges for a time as supplying the foundation for its further practice” (Kuhn, 1962, Chap. II).

It seems that the difference between 1962 — when the scientific community was still relatively small and nimble — and today, that Kuhn could not appreciate, is the chasm between the ways of thinking in different scientific disciplines due to an increased specialization. Perhaps today, communicating an already understood fundamental concept to an impactful applied field feels nontrivial and “paradigmatic” by itself. Indeed, it is often surprising how long it takes to formulate an applications-relevant context for a concept brought from a more basic field. In my experience, learning the language of colleagues on the frontlines of radiology and neuroscience, to formulate relevant questions and to translate from physics the theoretical concepts needed to answer them, has itself taken years of work.

However, the fact that applying a known paradigm is nontrivial, does not make this paradigm any more novel. What if we were to accept that the overarching paradigm for quantifying microstructure has long been established? This is surely not the end of science, much like nonrelativistic quantum mechanics did not end with the Schrödinger’s equation — in fact, its major impacts occurred long after 1926. A clear acceptance of a paradigm can have a refreshing effect: We become liberated from the need to claim each new model or acquisition as revolutionary. The realization of our place in the historical context, together with the recently increased level of rigor, encourage us to proceed along the path of normal science collectively chartered by the founders of diffusion NMR and of transport in disordered media. This is good news, as the absolute majority of scientific activity is of this, most productive kind: “… during the period when the paradigm is successful, the profession will have solved problems that its members could scarcely have imagined and would never have undertaken without commitment to the paradigm. And at least part of that achievement always proves to be permanent” (Kuhn, 1962, Chap. III).

The period of “normalcy” requires establishing common values and approaches. In what follows, I outline the modern-physics language for systematizing and uncovering microstructure models (Sections 4 and 5); the tool we use to chart our progress (Section 6); and discuss future directions (Section 7).

4. Language: coarse-graining and effective theory

Coarse-graining is a process of homogenizing, or averaging, the system’s dynamics and related properties over a given scale, to deduce an effective dynamics on a coarser scale. Iterated across scales from the shortest to the longest, coarse-graining gives rise to the renormalization group transformation, a central concept of statistical physics of the past half-century (Wilson, 1983; Cardy, 1996) aimed at describing how the complex interactions on a finer scale give rise to emergent phenomena on a coarser scale. An example of this concept is how the complex dynamics of myriads of atoms or molecules gives rise to hydrodynamics, where we describe a macroscopic flow, not resolving individual molecules anymore. After such gradual averaging over microscopic degrees of freedom, the effective theory on the large scale may look quite different (Anderson, 1972) from the microscopic one (the Navier–Stokes equation of hydrodynamics does not look anything like the Schrödinger’s equation), and depends on only a few effective parameters — the remnants of all the microscopic complexity that we averaged over. Thus a theoretical description of any physical system at a given scale involves deriving the effective theory describing its relevant degrees of freedom and identifying its effective parameters, while discarding myriads of other, so-called irrelevant degrees of freedom.

In this way, coarse-graining over molecular interactions in liquids gives rise to effective theories represented by the Navier–Stokes and diffusion equations, governed by just a couple effective parameters: viscosity and diffusion coefficient. These effective theories, describing the relaxation of momentum and density, correspondingly, become valid at the scale of a few nm. In a homogeneous liquid, that’s the end of the story.

Tissue microstructure adds a new layer of structural complexity at the scale of cells, ~1–10 μm. The goal of modeling is to adequately average the diffusive dynamics of spin-carrying (e.g., water) molecules over this layer of complexity, and derive the effective theory of the dMRI signal acquired over a macroscopic voxel, as schematically shown in Fig. 2. Such theory will tell which microstructure-sensitive parameters are contained in the macroscopic signal and hence can be mapped.

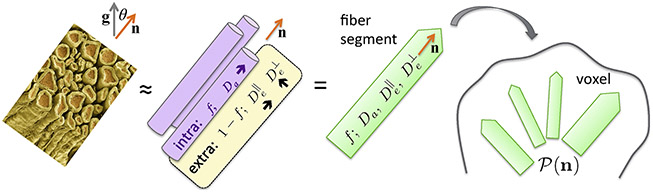
Fig. 2.

A hierarchy of effective theories relevant for tissue microstructure (bottom to top): From the atomic scale (many-body Schrödinger’s equation governing the dynamics of atoms and of their electronic orbitals); to a simple diffusion equation within any small domain of cytoplasm or extra-cellular space, with classical particle density ψ emerging after coarse-graining ∣Ψ∣² and integrating out the environment coordinates (Feynman and Vernon, 1963; Caldeira and Leggett, 1981; Kamenev, 2011); to the diffusion equation with heterogeneous local diffusivity D(x) describing the microstructural complexity at the cellular level; to the dynamics of the diffusion-weighted signal, Eq. (2), acquired over an MRI voxel, with ${\partial }_x^2\to -q^2$, ${\partial }_x^4\to q^4$, …, corresponding to the cumulant expansion in the powers of diffusion wave vector q after the Fourier transform. The effective-medium retarded response functions $\mathcal{D}(t)$, W(t), … give rise to the time-dependent diffusivity D(t), time-dependent kurtosis K(t), and so on (Novikov and Kiselev, 2010), (Novikov et al., 2019, Sec. 2).

Technically, averaging over the microstructure-level complexity involves performing a double average:

1. The average over the Brownian paths initiated from each point x₀, yielding the local propagator ${\mathcal{G}}_{t;x_t,x_0}$ introduced in Section 1. This is the coarse-graining step. It qualitatively makes each local environment homogenized over a domain of the size of the diffusion length L(t), with the envelope ${\mathcal{G}}_{t;x_t,x_0}$ playing a role of a low-pass filter over the microstructure, Fig. 3.

2. The ensemble average over all initial positions x₀ in a voxel, as in Eq. (2). This step selects typical local contributions to the overall signal for a given voxel, and swipes rare atypical ones under the experimental noise floor.

Fig. 3.

Coarse-graining of axonal fiber microstructure as an (almost) Gaussian filter with an increasing width L(t), relevant for the hindered diffusion in the extra-axonal space. With increasing t, spins “see” gradually more averaged extra-axonal space properties, with the t → ∞ limit corresponding to a perfectly homogeneous extra-axonal compartment characterized by Gaussian diffusion (Novikov et al., 2019, Sec. 1.3). For illustration purposes, a cutout of electron micrograph of axons in sector 2 of the corpus callosum in an adult rhesus monkey (Fig. 6A from the histology work by LaMantia and Rakic (1990)) was taken, and a Gaussian filter was applied to it, with a filter window ~L(t) progressively increasing from L = 0 up to L ≃ 10 μm, corresponding to the diffusion time range t ≃ 0–100 ms.

The path-averaging step (i) is naturally performed by the diffusing water molecules (or by Monte Carlo simulated paths) in a given structural arrangement, as the “packet” of molecules spreads from the initial point x₀ according to its envelope ${\mathcal{G}}_{t;x_t,x_0}$.² This envelope is determined by the particular arrangement of cells around x₀; following Eq. (1), its variance defines the local time-dependent diffusion coefficient

$$D(t;x_0)\equiv \frac{\langle (x_t-x_0{)}^2\rangle }{2d\cdot t},\langle (x_t-x_0{)}^2\rangle =\int \mathrm{d}{x}_t(x_t-x_0{)}^2{\mathcal{G}}_{t;x_t,x_0}$$ (3)

at the point x₀. If we were to start anywhere else within the range of the diffusion length L(t) from x₀, the diffusing molecules would “see” roughly the same structure, and have a similarly behaving mean-squared displacement in Eq. (3). Thus we realize that the local diffusion coefficient D(t; x), with x in the domain of size ~L(t) around x₀, is roughly uniform in space. This is why the diffusion length L(t) can be seen as a smoothing filter window over the structure, Fig. 3. Of course, the vicinity of another point $x_0^{\prime }$ far away from x₀ would have its own structure, and its own $D(t;x_0^{\prime })$, possibly quite different from D(t; x₀). By the same token, the whole local propagator ${\mathcal{G}}_{t;x_t,x_0}$ does not strongly depend on x₀ if we move x₀ by less than L(t), and can notably change if we explore a different local environment, moving $x_0\to x_0^{\prime }$ such that $\mid x_0^{\prime }-x_0\mid \gg L(t)$.

The ensemble-averaging step (ii) makes the resulting propagator (2) translation-invariant, i.e., dependent on the displacement x = x_t − x₀ rather than on the points x_t and x₀ separately.

The coarse-graining way of thinking tells us that, depending on the diffusion time, the tissue as effectively “seen” by the diffusing spins looks qualitatively different, Fig. 3. To classify these differences, let us introduce the structural length and time scales

$${\ell }_s=\{\rho \text{or}{\ell }_c\},\text{and}{t}_s=\frac{{\ell }_s^2}{D},$$ (4)

where ℓ_s can either be the size ρ of cells (for the restricted diffusion, e.g., axon or soma diameter), or the correlation length ℓ_c of their packing, which is usually of the order of the distance between their centers (Burcaw et al., 2015).

Depending on the relation between the diffusion length L(t) (the coarse-graining window) and ℓ_s, one considers the three regimes (Novikov et al., 2019, Sec. 1.5):

1. No coarse-graining, L(t) ≪ ℓ_s. Diffusion time is short, t ≪ t_s, and each spin senses its immediate vicinity characterized by its own intrinsic diffusion coefficient D(x₀) — e.g., cytoplasmic diffusivity, diffusivity inside cell nucleus, diffusivity of water in the extra-cellular space. An example is the first panel of Fig. 3. Restrictions provide a small $\sim \sqrt{t}$ correction to the overall measured diffusion coefficient (Mitra et al., 1993). This regime was recently used to determine cancer cell size using oscillating gradients in a glioma model (Reynaud et al., 2016b,a).

2. Coarse-graining over the structure, L(t) ≳ ℓ_s, when the diffusion time t ≳ t_s is such that the diffusion length matches the characteristic scale of tissue microstructure. Here, the transient (time-dependent) effects lead to the possibility to quantify ℓ_s. The coarse-graining in this regime is schematically shown in the remaining panels of Fig. 3. For the hindered diffusion, this regime is characterized by the asymptotic power-law decay (Novikov et al., 2014)

   $$D_{\text{inst}}(t)\equiv \frac{\partial }{\partial t}\frac{\langle x^2(t)\rangle }{2d}\simeq D_{\infty }+\text{const}\cdot t^{-\vartheta },t\gg t_s$$ (5)

   of the instantaneous diffusion coefficient D_inst(t), which yields the corresponding power-law tails in the conventional pulse-gradient diffusion coefficient $D(t)=\frac{1}{t}{\int }_0^t\mathrm{d}{t}^{\prime }{D}_{\text{inst}}(t^{\prime })$, and in the higher-order cumulants such as kurtosis (Burcaw et al., 2015; Dhital et al., 2019; Lee et al., 2020d). From this approach, the disorder correlation length ℓ_c of beads (Novikov et al., 2014; Fieremans et al., 2016; Jespersen et al., 2018; Lee et al., 2020c) along neurites (axons and dendrites), and packing correlation length of axonal fibers in the fiber cross-section (Burcaw et al., 2015; Fieremans et al., 2016; Lee et al., 2018b) were recently estimated to be ℓ_c ~ 1 μm, in accord with histology (Shepherd et al., 2002; Lee et al., 2019).
   For the restricted diffusion, the coarse-graining eventually stops, and the compartment gets effectively shrunk to a point when its size ρ ≪ L(t). The corresponding diffusivity scaling

   $$D(t)\sim \frac{{\rho }^2}{t}$$ (6)

   enables mapping the compartment size ρ, e.g., cancer cell size (Jiang et al., 2017), as well as axonal diameter mapping discussed below.

3. Complete coarse-graining, L(t) → ∞: Gaussian compartment(s). At times t ≫ t_s, spins have sampled large enough domains, such that their statistical properties have become similar — in other words, the local diffusivities (3) around different x₀ are practically the same. Physicists say that the diffusion process becomes self-averaging, i.e., each domain well represents the whole macroscopic tissue compartment. When t → ∞, the compartment effectively looks completely homogeneous, characterized by the long-time (“tortuosity”) limit $D_{\infty }=D(t){\mid }_{t\to \infty }$ of the diffusion coefficient, and the diffusion becomes Gaussian. The picture of multiple Gaussian compartments (Fig. 4) — for intra- and extra-axonal spaces, and possibly also for the cerebrospinal fluid (CSF) — is behind many diffusion models (Jespersen et al., 2007, 2010; Fieremans et al., 2010, 2011; Zhang et al., 2012; Sotiropoulos et al., 2012; Jelescu et al., 2016; Jensen et al., 2016; Reisert et al., 2017; Lampinen et al., 2017; Novikov et al., 2018c; Veraart et al., 2018), which fall under the overarching umbrella of the “Standard Model” for diffusion in white matter (Novikov et al., 2019, Sec. 3).

Fig. 4.

Standard Model of diffusion in neuronal tissue (Novikov et al., 2019, Sec. 3). In the long time limit (iii), elementary fiber segments (fascicles), consisting of intra- and extra-neurite compartments, are described by at least 4 independent parameters: f, D_a, $D_e^{\parallel }$ and $D_e^{\perp }$, with a possible addition of the isotropic CSF compartment. Within a macroscopic imaging voxel, such segments contribute to the directional dMRI signal according to their orientational dispersion $\mathcal{P}(\mathrm{n})$.

The role of the diffusion wave vector q is in providing a snapshot of the coarse-graining process at the length scale ∣x∣ ≲ 1/q — technically, these x define the main contribution to the Fourier integral in Eq. (2), as the exponential e^−iqx does not strongly oscillate. Applying large q, one can access the structure (size, shape) even at long times t ≫ t_s — i.e., from “under” the blurring window L(t).³ This is the diffusion-diffraction regime of Callaghan et al. (1991), where, for instance, the signal

$$G_{t,q}{\mid }_{t\gg t_s}\propto \Gamma (q),\Gamma (q)=\mid v(q){\mid }^2$$ (7)

from the intra-cellular space is given by the power-spectrum Γ(q) of the closed pore shape v(x) for t ≫ t_s. Likewise, a power-spectrum Γ(q) of the connected pore space (e.g., extra-cellular space) can be probed when the diffusion time exceeds the correlation length of the packing of the “grains” (e.g., impermeable cells) (Mitra et al., 1992). Employing the diffusion gradient makes the phase diagram of the microstructure dMRI multi-dimensional, as it will be discussed in Sections 6 and 7 below, with the regimes (i)—(iii) characterizing the temporal dimension. Technical details on quantifying the length scales (4) are further discussed by Kiselev (2020) in this issue.

5. Applying the language: coarse-graining over an axon

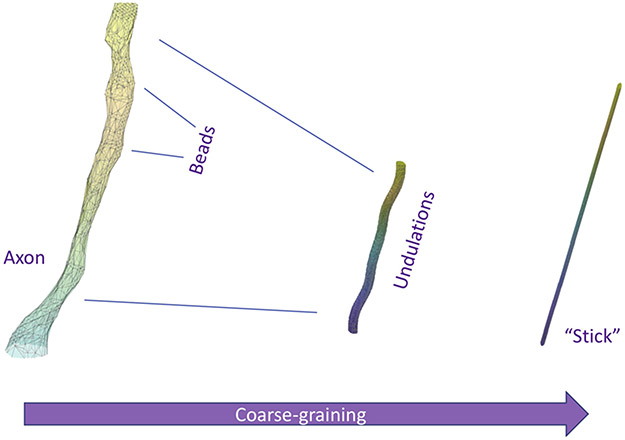
To illustrate how coarse-graining helps to think of an effective theory, consider diffusion inside a myelinated axon, assuming no exchange with the myelin or extra-cellular compartment at the relevant time scales, Fig. 5. Axon has a complicated shape (Abdollahzadeh et al., 2019; Lee et al., 2019). If we were to successively blur the structural details at an increasing diffusion length scale L(t) in the spirit of Fig. 3, we can distinguish (at least) the following structural hierarchy: cross-section of an irregular shape (ρ ~ 1 μm — Section 5.1); undulation (λ_u ~ 30 μm (Lee et al., 2020b) — Section 5.2); and a featureless one-dimensional channel (“stick”), if we were to look at an axon from afar (Section 5.3).

Fig. 5.

Which geometric features of axons are we potentially sensitive to with dMRI? Starting from a realistic axon shape segmented from 3-dimensional electron microscopy (Lee et al., 2019), coarse-graining over the increasing diffusion length L(t) first highlights the caliber variations (beads or varicosities) at the ρ ~ 1 μm scale, followed by the undulations with wavelength of the order λ_u ~ 30 μm. The fully coarse-grained “stick” compartment of negligible radius is characterized by one-dimensional Gaussian diffusion.

5.1. Axon caliber scale

At the scale L(t) below the axonal caliber ρ ~ 1 μm, intra-axonal diffusion is fully 3-dimensional. Diffusion (along and transverse) is in principle sensitive to the axon’s cross-sectional shape, its local caliber (a measure of its cross-sectional size), and caliber variations along its length, as we now outline.

Sensitivity to axon caliber (transverse).

The contribution G_t,x from the restricted compartment of Fig. 1 is sensitive to the size ρ of the cells (circles). Ideally, to measure axon caliber, one should achieve the diffusion-diffraction regime, where the wave vector q = gδ matches the inverse axon caliber, q ~ 1/ρ, such that b = q²t and D(t) given by Eq. (6) together yield − lnS ~ (qρ)², to estimate ρ. However, this regime is very difficult to access even on animal systems, as it also implies gradient pulses shorter than the diffusion time across the axon, δ ≪ t_s ≲ 1 ms (for the notion of q to be well-defined). Practically, experiments fall into the opposite, diffusion-narrowing regime (Robertson, 1966; Murday and Cotts, 1968; Neuman, 1974), where δ ≫ t_s, and the signal attenuation

$$-\text{ln}S\sim \frac{g^2{\rho }^4\delta }{D_0}\sim (g\delta \cdot \rho {)}^2\cdot \frac{t_s}{\delta }\ll (q\rho {)}^2$$ (8)

is parametrically weaker than in the diffusion-diffraction regime, by the factor of the small parameter t_s/δ ≪ 1.⁴ Here D₀ is the intrinsic axoplasmic diffusion coefficient.

The weak diffusion-narrowing attenuation (8) makes calibers ρ ≲ 1 μm of typical axons in the human brain invisible even to scanners with Connectome gradients; on clinical systems, signal attenuation (8) for such axons is about 10⁻⁶ – 10⁻⁵ (Burcaw et al., 2015; Nilsson et al., 2017)⁵. Volume-weighting the ρ⁴ dependence in Eq. (8) means that the technique, when applicable (as discussed in Section 5.4 below), measures the effective axonal radius (Burcaw et al., 2015)

$$r_{\text{eff}}={\left(\langle r^6\rangle ∕\langle r^2\rangle \right)}^{1∕4}$$ (9)

dominated by the sixth moment of axonal radius distribution, and hence, is heavily skewed by its tail (Veraart et al., 2020).

The effective radius (9) can be viewed as a result of the double average (Section 4): (i) averaging over the Brownian paths within each axon yields the attenuation (8); (ii) the ensemble average over all axons for − ln S ≪ 1 collapses a complicated distribution of axonal radii onto the ratio (9) of its moments, which can be thought of as an effective theory parameter.

Sensitivity to axon caliber variations (along).

Axon caliber and cross-sectional shape vary along its length, giving rise to caliber variations, such as varicosities or beads (Shepherd et al., 2002; Budde and Frank, 2010). Lee et al. (2020c) showed that the placements of axonal beads has a finite correlation length (short-range disorder). Such randomness results in the power-law tail (5) for the along-axon diffusivity and kurtosis with the exponent ϑ = 1/2 predicted by Novikov et al. (2014), confirmed in simulations of artificial (Palombo et al., 2018) and electron microscopy-derived axonal geometry (Lee et al., 2020c), and observed in rat (Does et al., 2003; Novikov et al., 2014), human white matter (Fieremans et al., 2016; Arbabi et al., 2020; Lee et al., 2020c), and fixed spinal cord (Jespersen et al., 2018).

The ~t^−1/2 tail (5) is a result of coarse-graining the 3-dimensional axon down to a 1-dimensional effective medium, where the transverse-to-axon degrees of freedom map onto the along-axon structural disorder (Novikov et al., 2014). The amplitude of the ~t^−1/2 tail (5) is related to the parameters of the structural disorder, such as the correlation length of the bead placements (Fieremans et al., 2016; Lee et al., 2020c). Achieving shorter diffusion times, to observe the crossover between the limits (i) and (ii) of the coarse-graining (Section 4), may in the future lead to a more robust quantification of the caliber variations — e.g., by mapping the narrow shafts between beads onto permeable barriers and applying the random permeable-barrier model (Novikov et al., 2011) in one dimension (d = 1).

5.2. Undulation scale

When L(t) reaches an order-of-magnitude larger scale λ_u ~ 30 μm, the caliber can be effectively shrunk to a point, such that we can focus on the wavy shape of an axonal “skeleton”. This wave is referred to as an undulation (Nilsson et al., 2012), and contributes to the time-dependent diffusion along and transverse to the axon (Brabec et al., 2020; Lee et al., 2020b).

In particular, undulations can strongly contribute to apparent axonal caliber (even if we were to neglect the actual axon thickness ρ). Naively, one would imagine that coarse-graining the wavy skeleton of an amplitude w₀ and period λ_u over L(t) ≳ λ_u should make it look as a tube of thickness ~ w₀, such that the attenuation − ln S ~ (qw₀)², yielding the effective caliber ~ w₀. This intuition is correct for narrow pulses, when δ is much shorter than the time $t_u\sim {\lambda }_u^2∕D_0$ to diffuse along the undulation. For wide pulses, δ ≫ t_u, the transverse-relaxation argument leading to Eq. (8) (Footnote⁴) applies instead, albeit the correlation time scale t_s, over which the successive random phase contributions become independent, is now t_u. Signal attenuation corresponds to summing N ~ δ/t_u ≫ 1 independent spin phase variances,

$$-\text{ln}S\sim (g{w}_0\cdot t_u{)}^2\cdot N\sim \frac{g^2{w}_0^2{\lambda }_u^2\delta }{D_0}\equiv \frac{g^2{r}_{\text{und}}^4\delta }{D_0}$$ (10)

defining the effective axon radius ${\mathit{r}}_{\text{und}}\sim \sqrt{w_0{\lambda }_u}$ due to the undulations (Lee et al., 2020b, Eq. (26)).

Since the undulation wavelength greatly exceeds axon caliber, λ_u ≫ ρ, whereas its amplitude w₀ ~ 1 μm is of the order of axon caliber (Lee et al., 2019; Abdollahzadeh et al., 2019), in realistic experimental settings we are more sensitive to undulations than to the actual axonal caliber, r_und ≫ r_eff. Hence, undulations strongly bias the estimation of axon diameter at moderate diffusion weighting (Lee et al., 2020b). On the other hand, the undulation effect on the along-axon diffusion is less significant (Lee et al., 2020b, Appendix E).

5.3. Axon as a “stick”

Finally, for a longer diffusion length, L(t) ≫ λ_u, and for diffusion weighting not enough to resolve ρ and w₀, the caliber- and undulation-effects can be neglected, and an axon can be simplified down to a featureless narrow “stick” (zero-radius cylinder, with effective diffusion constant D_a < D₀), Fig. 4. The signal from such sticks was studied by Kroenke et al. (2004) for NAA diffusion in rat brain, followed by water diffusion study of Jespersen et al. (2007). The dMRI signal from any collection of sticks, averaged over all gradient directions in a b-shell, becomes equivalent (Jespersen et al., 2013; Kaden et al., 2016b) to the Callaghan et al. (1979) model of isotropically distributed sticks (Section 2 above), yielding the universal b^−1/2 scaling

$${\int }_0^{\pi ∕2}\mathrm{d}\theta \sin \theta e^{-b{D}_a{\cos }^2\theta }\simeq \sqrt{\frac{\pi }{4b{D}_a}},b{D}_a\gg 1.$$ (11)

Here θ is the angle between the stick and the applied gradient. The nontrivial b^−1/2 ~ q⁻¹ functional form, coming from the intra-stick compartment, was observed only recently in vivo (McKinnon et al., 2016; Veraart et al., 2019, 2020), validating the picture of sticks for axons (and perhaps, for glia processes) in white matter. Its counterpart for the planar tensor encoding is the b⁻¹ ~ q⁻² decay (Afzali et al., 2020).

Going back to the way we obtained Eq. (11), all we really needed was to assume that diffusion over the diffusion time t was happening along a locally straight one-dimensional segment. Hence, the scaling (11) will also apply for short t, such that L(t) ≲ λ_u, i.e., the undulations are longer than the diffusion length, during which a large b-value is accumulated by applying strong gradients. In this case, the axon is effectively split into locally straight segments of size ~L(t); the contribution from each such segment, averaged over all gradient directions, yields Eq. (11) — albeit with D_a corresponding to an effective diffusion coefficient coarse-grained at the scale L(t). Therefore, angular averaging over each b-shell gives a way to factor out not just the axonal orientation dispersion $\mathcal{P}(n)$ (Fig. 4), but also the effect of the undulations (Section 5.2), which becomes instrumental in mapping axonal caliber, as we will discuss in Section 5.4.

The most remarkable property of the high-b intra-axonal signal (11) is that it decays much slower than the extra-axonal signal,⁶ and hence it was found to persist for very large 6 ≲ b ≤ 10 ms/μm² on a clinical scanner (Veraart et al., 2019), as well as for b ≤ 25 ms/μm² on the human Connectom scanner and for b ≤ 100 ms/μm² on an animal system (Veraart et al., 2020). In other words, the slow scaling (11) tells that practically all we see at such strong diffusion weightings in white matter is the intra-axonal contribution! This is an example of a “spectroscopic” property of dMRI signal, where understanding distinct functional forms allows us to separate contributions from distinct tissue building blocks (Novikov et al., 2018a).

5.4. Axon caliber mapping

Armed with the understanding of different physical phenomena, let us reexamine the feasibility and meaning of the (inner) axon caliber mapping. This concept was first put forth by representing axons as ideal straight impermeable cylinders (Assaf et al., 2008; Barazany et al., 2009) with a certain diameter distribution, or using a single diameter (Alexander et al., 2010). However, these simplified models yield axon calibers about 5–10 times greater than the typical axons in human brain known from histology (Alexander et al., 2010; Horowitz et al., 2015; Innocenti et al., 2015). What are we then really measuring, and under which conditions?

Undulations (Section 5.2) are the obvious confounding factor (Brabec et al., 2020; Lee et al., 2020b). The inner caliber is then biased by the square root of the undulation wavelength.

Another confounding factor is the non-Gaussian, time-dependent diffusion in the extra-axonal space. Burcaw et al. (2015) predicted, and Fieremans et al. (2016), Lee et al. (2018b), Tétreault et al. (2020) demonstrated the dependence of the extra-axonal diffusion coefficient $D_e^{\perp }(t)$ on diffusion time, due to the incomplete coarse-graining [regime (ii) of Section 4]. This leads to the dependence of the extra-axonal signal on the sequence timings, that turns out to be stronger than the weak intra-axonal attenuation (8). In this case, the dMRI signal transverse to axons measures the packing correlation length ℓ_c of fibers in a bundle — a parameter of the extra-axonal space geometry, typically of the order of the outer axonal diameter (Burcaw et al., 2015; Ginsburger et al., 2018; Tétreault et al., 2020).

Both undulations and extra-axonal time-dependent diffusion are relevant at low to moderate b, typical of clinical systems. Together, they can rationalize the discrepancy between dMRI and histology at moderate b. Such measurements then have little to do with inner diameters of brain axons. (In spinal cord, where axons are 5–10 times thicker than in the brain, the conditions for inner axon caliber mapping are much more favorable (Drobnjak et al., 2010; Shemesh et al., 2013; Duval et al., 2015; Benjamini et al., 2016).)

The way to eliminate the above confounds is to employ such strong b-values that the extra-axonal signal is suppressed, and the effects of undulations are factored out due to subsequent angular averaging. The sensitivity to the inner diameters can be revealed via the deviation of the angular-averaged signal from the zero-radius stick scaling (11). Such sensitivity was observed recently by Veraart et al. (2020). There, the effective radius (9) in rat corpus callosum was found to agree fairly well with that calculated from histology in the same animals; moreover, the effective radius in humans on a Connecome scanner had the right range based on the known human axon radius distributions (Aboitiz et al., 1992; Caminiti et al., 2009). The effect of undulations was assumed to be completely factored out by the angular averaging at relatively short t.

Note that, since the effective radius (9) is weighted by the tail of the distribution, there is an inherent discrepancy between dMRI and histology even when the above confounding factors are eliminated. Histology most reliably quantifies typical axons (of radius ρ ~ 0.5 μm) sampled within a relatively small field of view, whereas dMRI is sensitive only to the thickest ones, with radius ρ ≳ 1.5–3 μm (Veraart et al., 2020). By increasing the diffusion weighting from moderate to high, the effective radius (9) can be eventually uncovered on a Connecome scanner (Huang et al., 2015; Veraart et al., 2020). It may be a biomarker for pathologies where the thickest axons get altered first.

The residual effect of undulations, and of the spatially varying coarse-grained D_a along the axon, on apparent axon caliber, is an object of further investigation (Lee et al., 2020b). The deviations from the scaling (11) can also originate due to cell bodies (soma) (Palombo et al., 2020).

5.5. Axons: what have we learned thus far?

While the idea of becoming sensitive to axonal caliber is decades-old, the structural complexity of real axons has opened a plethora of effects at different scales, accessible under different experimental conditions. It is quite remarkable, that such a relatively “simple” and well-defined tissue compartment as intra-axonal space, keeps giving us unending puzzles. Only within the past few years, the effects of realistic shape (deviations from an ideal cylinder) have been studied, and elucidating the dMRI sensitivity to axonal geometry remains a very active area of research.

More generally, the coarse-graining way of thinking shows that the microstructure may look quite different to the diffusing spins, depending on the allowable spatio-temporal scales, set by our experimental design by varying gradient strength and timing, g(t). Parsimonious thinking about the microstructural complexity should always match the level of coarse-graining. It is pointless to ask, what is relevant about axonal (or any other) microgeometry, without specifying the scale at which we will perform our experiments, set by g(t).

Naturally, at this point one wishes to know, what are the qualitatively distinct regimes, or behaviors, of the dMRI signal, depending on available g(t) — and this is where we go now.

6. Charting our progress: phase diagram

In physics, multiple possible behaviors of a complex system are depicted on the phase diagram, which is a sketch of different phases (kinds of behavior) as a function of experimental parameters. These phases can be separated by sharp boundaries (phase transitions, such as water freezing into ice at a given temperature and pressure), or fuzzy boundaries (cross-overs between different regimes).

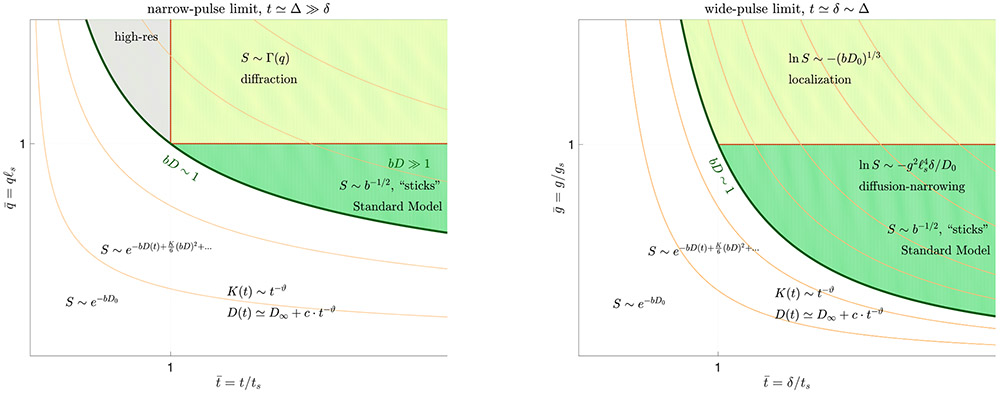
For dMRI, the natural parameters are the gradient strength g of the Larmor precession frequency, and the diffusion sequence timings; in the most often used Stejskal and Tanner (1965) pulse-gradient sequence, those are the pulse duration δ and the “diffusion time” Δ (interval between the front ends of the gradient pulses). The corresponding phase diagram sketch is shown in Figs. 6 and 7. In dMRI, the phase boundaries are fuzzy (the ridges between them are outlined as order-of-magnitude relations between parameters) — intuitively, the nature of diffusion and the form of the signal does not suddenly jump when we vary time or a diffusion gradient smoothly.⁷

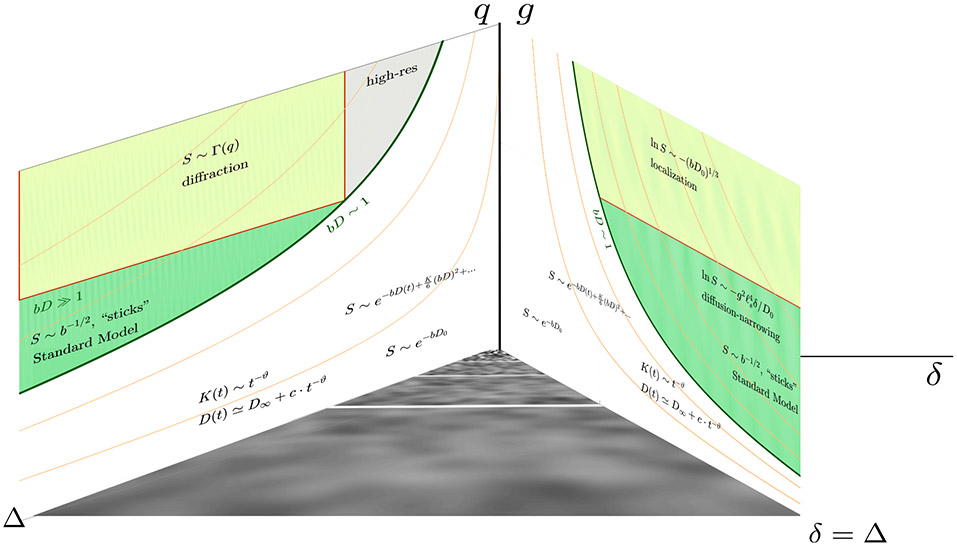
Fig. 6.

The phase diagram of dMRI, assuming the standard pulsed-gradient sequence of Stejskal and Tanner (1965), where δ is the pulse duration and Δ is the interval between pulses. The planes (Δ, q) and (δ, g) are shown separately in Fig. 7 for clarity. The bottom plane represent the sequence timings δ ≤ Δ, with the narrow-pulse limit corresponding to the Δ axis and the widest possible pulses correspond to the diagonal δ = Δ. The coarse-graining, Fig. 3, occurs in this plane: it is a property of the diffusion process, irrespective of the diffusion gradients that define the vertical axis. For convenience, the units on the vertical axis are different for different limits, representing the relevant parameters, q = gδ and g, correspondingly.

Fig. 7.

The narrow-pulse (left) and wide-pulse (right) limits of the dMRI phase diagram from Fig. 6. For convenience, the narrow-pulse plane from Fig. 6 is reflected here so that t = Δ grows from left to right; q = gδ. The units on the axes are made dimensionless using the structural length and time scales (4). The contour lines of constant b = (gδ)²(Δ−δ/3) are drawn in beige. The borderlines in the phase diagram are meant to represent smooth crossovers between regions (they are not sharp), hence their scaling, as well as that of the signal, are given only by order-of-magnitude relations. The coarse-graining regimes (i)—(iii) of Section 4 are $\overline{t}\ll 1$, $\overline{t}\gtrsim 1$, and $\overline{t}\gg 1$, correspondingly, whereas applying the diffusion gradients (vertical axes) helps one to separate between distinct compartments and to quantify the shapes and sizes (4) by taking a snapshot of the coarse-graining at the scale 1/q or ℓ_g. See Section 6 and (Kiselev, 2020) for further details.

In the narrow-pulse limit, the diffusion wave vector q = gδ is well defined; q and t ≃ Δ can be made dimensionless using the characteristic structural (restriction) size ℓ_s and the corresponding time t_s, Eq. (4), and introducing the reduced variables $\overline{q}=q{\ell }_s$ and $\overline{t}=t∕t_s$, cf. the left panel of Fig. 7.

In the wide-pulse limit, the phase factor $e^{-iqx}\to e^{-i{\int }_0^t\mathrm{d}\tau g(\tau )x(\tau )}$ in Eq. (2) becomes a functional of the gradient waveform g(t). Hence, here one studies the dependence on the applied Larmor frequency gradient g and the pulse width δ separately, cf. the right panel of Fig. 7. The scale ℓ_s, together with the free diffusion coefficient D₀, define the dimensionless Larmor frequency gradient $\overline{g}=g∕g_s$, where

$$g_s=\frac{D_0}{{\ell }_s^{{}^3}}$$ (12)

provides a natural scale for the applied gradient (Stoller et al., 1991; Hürlimann et al., 1995; Grebenkov, 2014).

We can now map different behaviors (some already described above) onto domains in the phase diagram.

The open regions bD ≲ 1 are routinely explored in clinical studies at fixed t. This is where the cumulant expansion (Kiselev, 2010) approximates the signal well. Varying the diffusion time at low b enables probing the structural disorder correlation length of axonal packing in a fiber, and the correlation length of structural heterogeneities (e.g., beads) along axons and dendrites, as discussed in Section 5.1, as well as possibly the parameters of axonal undulations, Section 5.2.

The green-shaded regions are explored in advanced research scans for, e.g., validating the picture of sticks for the axons (generally, neurites) at long t and high b, Section 5.3, and for estimating the parameters of the Standard Model corresponding to anisotropic Gaussian compartments (complete coarse-graining regime (iii) of Section 4). The deviations from the axon-as-a-stick picture provides the sensitivity needed for axonal diameter mapping (Section 5.4) practically based on signal attenuation in the diffusion-narrowing regime, Eq. (8).

For even stronger gradients g ≳ g_s, different microstructure features — sharp boundaries (e.g., cell membranes), closed/open pores (e.g., cells / extra-cellular space), and regions of smooth spatial diffusivity variations D(x) — give rise to specific and discernible functional forms of the signal. These regimes have largely not been investigated for the neuronal tissue yet, since the typical scales ℓ_s ~ 1 μm are so small, that the Larmor frequency gradient g_s ~ 1 (μm ·ms)⁻¹ corresponds to the field gradient of a few T/m. For the cell bodies, however, ℓ_s ~ 10 μm, and the interesting range of gradients becomes feasible.

Consider first the slowly varying D(x) in space, with a correlation length ℓ_s. In the high-resolution limit (Novikov and Kiselev, 2010), q ℓ_s ≫ 1 and t/t_s ≪ 1, each spin packet is “frozen” to a region of a nearly constant local diffusivity D(x) ≈ const, justifying the statistical model of Yablonskiy et al. (2003), where the signal $\mathcal{S}=\int \mathrm{d}D\mathcal{P}(D)e^{-bD}$ is given by the Laplace transform of the histogram $\mathcal{P}(D)$ of the local diffusivity values. It is not yet clear if this picture applies for the neuronal tissue, but it may apply to tissues in the body in some limiting cases, or to other heterogeneous media.

Next, we focus on the effect of confinement or restriction by the cell walls. The signal in the narrow-pulse limit from a vicinity of a wall exhibits the Debye–Porod scaling

$$S\sim q^{-(1+d)}\sim b^{-(1+d)∕2}$$ (13)

in d spatial dimensions (Sen et al., 1995; Frøhlich et al., 2006). This residual non-exponential signal decay may be relevant for the extra-cellular space (cf. Section 5.3).

The diffusion-diffraction regime of Callaghan et al. (1991), Eq. (7) in Section 4, occurs within closed pores (e.g., cells), for times longer than the characteristic t_s = ρ²/D₀. For open pores (extra-cellular space), and times t ≫ t_s longer than the time to travel across the packing correlation length ℓ_c of the “grains” (cells), the signal

$$S\sim {\left[\frac{{\ell }_c}{L(t)}\right]}^d\Gamma (q),L(t)\gg {\ell }_c$$ (14)

effectively measures the density correlation function (power spectrum) Γ(q) of the pore space (Mitra et al., 1992). The attenuation factor [ℓ_c/L(t)]^d ≪1 arises due to the unbounded spreading of the diffusing molecules.

By applying wide gradient pulses, δ ≃ Δ and strong gradients g ≫ g_s, one can sense the presence of cell walls. This happens because for such large diffusion weightings, the signal in the bulk fluid gets completely attenuated, and only the magnetization near cell walls (partially restricted by their presence, within the localization length ℓ_g = (D₀/g)^1/3 from the wall), gives an appreciable contribution

$$\text{ln}S\sim -(b{D}_0{)}^{1∕3}$$ (15)

to the overall signal. This is the localization regime of Stoller et al. (1991), so far only observed in simulations (de Swiet and Sen, 1994; Moutal et al., 2019) and in porous media (Hürlimann et al., 1995; Moutal et al., 2019). Its signature is the non-analytic in b signal attenuation, that is slower than e^−bD.

For a more technical overview of probing microstructure-level scales and a discussion of the phase diagram, see the paper by Kiselev (2020) in this issue.

7. Unresolved questions and future directions

The phase diagram, Figs. 6 and 7, much like a geographical map with regions of terra incognita, fosters the discussion about the future. Reflecting the interdisciplinary nature of our field, this discussion splits into the modeling challenges, and biology-driven questions.

While building models sharpens our thinking, their practical value lies in mapping their parameters and relating them to physiology and pathology. Attempting to define the vague and often over-used term “modeling”, Novikov et al. (2018a, 2019) formulated that

$$\text{modeling}=\text{theory}+\text{parameter estimation}.$$ (16)

Theoretical and parameter-estimation challenges will be considered respectively in Sections 7.1 and 7.2, followed by the neuroscience-driven questions (Section 7.3), and a discussion about how to bring together physics and biology (Section 7.4).

7.1. Theory

7.1.1. Modeling water exchange

Water exchange between compartments is not explicitly present on the phase diagram. Partly, this is because we do not understand it sufficiently well to plot it adequately.

So far, the accepted paradigm to model water exchange between cells and extra-cellular space is based on simple n-site exchange models (Zimmerman and Brittin, 1957; Kärger, 1985; Fieremans et al., 2010). They imply the “barrier-limited” (slow) nature of the exchange: each compartment gets fully coarse-grained much faster than the time τ_ex to exchange between compartments (Fieremans et al., 2010).

When exchange is not barrier-limited (e.g., for the possibly leaky walls of astrocytes, dendrites or unmyelinated axons), and for a general structurally-disordered placement of membranes, one has to explicitly perform the double average of Section 4: Solve for the propagator ${\mathcal{G}}_{t;x_t,x_0}$ for a given disorder realization of permeable membranes, and average the solution over the ensemble of disorder realizations, yielding G_t,x, Eq. (2). This program has so far been fulfilled only for the randomly placed and oriented flat permeable barriers in any dimension, by treating permeation across a membrane as a scattering problem, and using real-space renormalization group (a set of iterative infinitesimal coarse-graining procedures) to sum over scattering events off multiple membranes (Novikov et al., 2011). The model has found its applications in quantifying myofiber diameter and membrane permeability (Fieremans et al., 2017), an improvement over the periodic one-dimensional solution by Tanner (1978) mentioned in Section 2. However, this model geometry is too simplistic (especially for the brain), as it has no effect of curved boundaries, and does not make a distinction between intra- and extra-cellular spaces. A technical challenge remains to extend the scattering formalism onto more realistic permeable cellular geometries.

7.1.2. The effect of cell walls at strong gradients

In Section 6, we briefly touched upon the localization regime, which so far has been considered for impermeable flat walls (Stoller et al., 1991; de Swiet and Sen, 1994), permeable flat walls (Grebenkov, 2014), as well as recently for an impermeable sphere or a circle (Moutal et al., 2019). However, a general theory of the localization regime around curved boundaries, in random geometries, and also for finite permeability, is lacking.

Technically, the localization regime is challenging because the corresponding Bloch-Torrey operator is non-Hermitian, its spectrum is complex-valued, and its eigenfunctions may not in general form a complete basis in the Hilbert space. Investigating the statistics of eigenfunctions of such a random operator may benefit from drawing parallels with statistics of eigenfunctions for the Anderson localization (Anderson, 1958).

7.1.3. What information is contained in S[q(t)] for all q(t)?

The phase diagram above is reasonably well understood in the two planes of Fig. 7, but neither we know the exact system’s behavior in the bulk of the 3-dimensional Fig. 6, nor we understand its true dimensionality and information content for arbitrary q(t). Deriving the general relation S[q(t)] given a distribution of local diffusivity D(x) is a challenging problem; an ultimate prize is to invert this relationship to get to as much information about D(x) as possible from the functional S[q(t)]. The first step towards this goal, namely getting S(q) term-by-term, as a functional of the successive correlation functions Γ_n(x₁, …, x_n) = ⟨δD(x₁) … δD(x_n)⟩ of the local diffusivity variation δD(x) = D(x) − ⟨D(x)⟩ order-by-order, was done recently by Jespersen et al. (2019). Inverting this relationship is a much more difficult problem, and it so far remains unsolved.

7.1.4. Effect of micro-scale susceptibility and relaxivity variations on apparent diffusion metrics

Looking at the fundamental Eq. (2), one realizes that dMRI does not measure diffusion per se. Rather, dMRI measures the relaxation of the transverse spin magnetization in the presence of an externally applied pulsed Larmor frequency gradient. In the absence of magnetic structure, and for the short gradient pulses, this signal relaxation happens to coincide with the Fourier transform G_t,q of the ensemble-averaged diffusion propagator. In general, the spin precession phase e^−iqx → e^−iφ(t), where

$$\phi (t)={\int }_0^t\mathrm{d}\tau g(\tau )\cdot x_{\tau }+{\int }_0^t\mathrm{d}\tau \Omega (x_{\tau }),$$ (17)

gets altered by the locally varying Larmor frequency offset Ω(x) accumulated on the Brownian path x_τ = x(τ). This latter “internal” phase contribution is usually induced by the susceptibility χ(x) spatially varying on the microscopic scale, e.g., due to blood or myelin. The internal and external contributions interfere, and can produce the deviations of the apparent diffusion coefficient (and other parameters of the dMRI signal) from Eq. (2) (Zhong et al., 1991; Does et al., 1999; Kiselev, 2004; Cho et al., 2009; Álvarez et al., 2017; Novikov et al., 2018b). This effect was shown to be sequence-dependent (Pampel et al., 2010; Novikov et al., 2018b), as well as diffusion-time dependent, with the susceptibility-induced correction to the apparent diffusion coefficient increasing as a power-law function of time, and with the sign of the correction depending on the sequence (Novikov et al., 2018b).

The analytical effective-medium theory of this effect was only outlined for an ideal narrow-pulse sequence without refocussing. The theory for realistic sequences, in the presence of susceptibility-induced Ω(x), as well as the locally varying rate R₂(x), still needs to be developed.

7.2. Parameter estimation

Parameter estimation, the second component of modeling (16), has become a field in itself, recently propelled by “big data” and modern machine learning approaches. Yet the fundamental challenge of parameter estimation — the degeneracy limiting the information content — is century-old. It cannot be cured simply with better computers or more data; one often needs very specific kinds of data.

7.2.1. Understanding fit degeneracies

Fit degeneracy is the existence of multiple equivalent solutions to parameter estimation problem. It reflects the lack of sensitivity of the measurement to the model parameters.

The first empirical investigation of dMRI model degeneracies, based on a regular cumulant expansion in the powers of b around b = 0 within the model convergence radius, was performed by Kiselev and Il’yasov (2007). Recently, the degeneracies were analyzed in the context of the widely-studied Standard Model, Fig. 4. In particular, the “fit landscape” (the profile of the objective function to be minimized during fitting), its discrete and continuous degeneracies (i.e., distinct minima and flat directions), and the associated issues of accuracy and precision were pointed out numerically by Jelescu et al. (2016). The topology of this landscape was then derived analytically via the low-b expansion by Novikov et al. (2018c). The widely-adopted constraints (Zhang et al., 2012; Kaden et al., 2016a), that help stabilize the fit, were shown to fail (Lampinen et al., 2017; Novikov et al., 2018c); this has further provoked a discussion about what we can and cannot claim (Novikov et al., 2018a; Lampinen et al., 2019).

In the view of this recent experience of reassessing already published trends, statements such as “Give me a model, I will build a library and estimate all your parameters” come across as dangerously naive every time. The library (or its interpolation by any set of functions) is just a way of performing a fit, and if the model is unphysical or the fit landscape is degenerate, neither a powerful computer nor a library search/interpolation procedure will recover the nonexisting information. Numerical noise propagation with SNR mimicking that of the measurement should be a requirement for each new candidate model or measurement protocol.

7.2.2. Resolving degeneracies via complementary measurements

Fit degeneracies can be cured by acquiring sufficiently “orthogonal” (complementary) information, that helps increase the curvature of the fit landscape along the most uninformative (flat) directions.

With pure diffusion acquisitions, the freedom of choosing the gradient wave form g(t) in 3 dimensions, and hence, the shape of q(t) and of the corresponding b-tensor (generalizing the b-value) (Westin et al., 2016; Topgaard, 2017), significantly helps in resolving fit degeneracies. For the Standard Model, Fig. 4, Skinner et al. (2017) used double diffusion encoding to suppress extra-axonal compartment and then measure the diffusivity inside axons in rat spinal cord; Jensen and Helpern (2018) and Dhital et al. (2019) combined planar and linear encodings into different flavors of triple diffusion encoding, which together with orientational averaging enabled accessing the intra-axonal diffusivity. Coelho et al. (2019b) empirically found that the Standard Model fit landscape becomes notably less degenerate by including the planar tensor encoding, whereas Reisert et al. (2019) proved this statement analytically using an expansion at low b, and Fieremans et al. (2018) showed that employing the spherical tensor encoding has in practice a similar effect, making use of the earlier observation (Szczepankiewicz et al., 2015) that spherical tensor encoding provides a sufficiently complementary contrast. For this problem, Coelho et al. (2019a) and Lampinen et al. (2020) optimized the experiment design based on the Cramér-Rao bound, by optimizing b-tensor shapes for all diffusion and covariance tensor parameters, and by optimizing the q(t) wave forms for the Standard Model parameters, correspondingly. Finally, Jespersen et al. (2018) and Lee et al. (2018a) used the diffusion time dependence to break the compartment degeneracy of a time-dependent extension of the Standard Model, corresponding to the incomplete coarse-graining regime (ii) of Section 4.

Employing multiple NMR contrasts, beyond diffusion, helps achieve even greater complementarity. Multimodal examples in the brain include varying the inversion time (De Santis et al., 2016) to resolve fiber crossings; varying the echo time (Veraart et al., 2018; Lampinen et al., 2019) to alleviate fit degeneracies for the Standard Model, based on the distinct T₂ values in the intra- and extra-cellular spaces (Dortch et al., 2013); altering compartment relaxation properties by intracerebroventricular injection of contrast agent (Silva et al., 2002; Kunz et al., 2018) to measure compartment diffusivities independently, and thereby establish prior knowledge for breaking the Standard Model degeneracy; and employing the $T_{{}_2}^{{}^{\ast }}$ contrast together with strong diffusion weighting enabling the separation between intra- and extra-axonal compartments (Kleban et al., 2020).

7.2.3. Beyond dMRI: multi-modal microstructure MRI (μMRI)

While the dMRI community has been a major driving force behind quantifying tissue microstructure with MRI, it certainly does not hold a monopoly power on the concept. In fact, the earliest microstructure works in MRI were related to magnetic microstructure origins of the BOLD $R_{{}_2}^{{}^{\ast }}$ effect, as discussed in Section 2. The same cellular-level microstructure often gives rise to distinct MRI contrasts; e.g., myelin provides restrictions to diffusion, but it is also a major contribution to T₁ and T₂ relaxation (Laule et al., 2006; Dortch et al., 2013; Does, 2018), to magnetization transfer (Schmierer et al., 2007), as well as to the phase contrast (Duyn, 2018; Yablonskiy and Sukstanskii, 2018), the basis of the quantitative susceptibility mapping.

Without invoking any new paradigms, it is quite evident that one has to employ as many complementary contrasts as possible to resolve fit degeneracies, as discussed in Section 7.2. What is less trivial is to ensure that our models correct for the interference between different microstructure-related contrasts, as discussed in Section 7.1.4. Developing the corresponding effective medium theory of diffusion, relaxation and their cross-terms, would serve as a foundation for a truly multi-modal tissue μMRI, encompassing diffusion, relaxometry, magnetization transfer and quantitative susceptibility mapping.

7.3. Neuronal tissue structure and function

7.3.1. Free water elimination

This is a conceptually simple yet still practically unresolved problem: How to separate the partial volume contribution of the CSF or edema from the tissue signal? Attempts to eliminate free water are often based on the two-compartment model (Pierpaoli and Jones, 2014; Pasternak et al., 2009; Metzler-Baddeley et al., 2012)

$$S=S_0\left[f_0{e}^{-b{D}_{\text{fw}}}+(1-f_0)e^{-b\sum _{ij}\widehat{g_i}{D}_{ij}\widehat{g_j}}\right],$$ (18)

with free water fraction f₀ and fixed isotropic diffusivity D_fw = 3 μm²/ms, where the tissue signal is approximated by the diffusion tensor D_ij, and $\widehat{g}$ are the unit gradient directions.

Strictly speaking, representing the signal in the form (18) is inconsistent. At low b, at the $\mathcal{O}(b)$ level where the DTI representation of the second (tissue) term is justified, the signal $\mathcal{S}\simeq {\mathcal{S}}_0{e}^{-b{\sum }_{ij}\widehat{g_i}{D}_{ij}^{\text{tot}}\widehat{g_j}}$ is equivalently described by the overall diffusion tensor $D_{ij}^{\text{tot}}=f_0{D}_{\text{fw}}{\delta }_{ij}+(1-f_0)D_{ij}$. This leads to the one-dimensional, fully-degenerate fit manifold corresponding to the overall mean diffusivity $\overline{D^{\text{tot}}}=f_0{D}_{\text{fw}}+(1-f_0)\overline{D}=\text{const}$, such that different values of f₀ and of the tissue mean diffusivity $\overline{D}$, corresponding to the same $\overline{D^{\text{tot}}}$, describe the signal equally well. This is perhaps the simplest example of how a continuous fit degeneracy emerges (cf. Section 7.2), illustrating that no matter how much we oversample the low-b signal, the physics of diffusion does not allow us to separate between the two contributions. In other words, here we cannot just rely on more data; we need a different kind of data. (Likewise, the low-b expansion yields a nontrivial degeneracy manifold for the Standard Model mentioned earlier in Section 7.2.1.)

Employing higher b would break the above fit degeneracy — but at this point, the deviation of the overall signal (18) from a monoexponential also comes from the higher-order (e.g., kurtosis and beyond) terms in the tissue compartment. Hence, we need to represent the tissue signal with many more parameters, using multiple shells, — at which point we may just as well model it using, e.g., the Standard Model with added CSF compartment, Fig. 4. Of course, then we must also cure all the associated fit degeneracies discussed in Section 7.2. Regularized fits such as that by Pasternak et al. (2009), claiming to eliminate free water based on a single-shell DTI, employ priors or regularization terms to break the above inherent degeneracy, and hence cannot be considered reliable. Employing complementary modalities, e.g. varying inversion time (Kwong et al., 1991) or echo time (Collier et al., 2017; Veraart et al., 2018), can provide a much more reliable separation between CSF and tissue based on the difference in their relaxation properties.

7.3.2. Intra-axonal geometry

While the intra-axonal geometry and the dMRI modeling is understood better than any other brain compartment (cf. Section 5), questions still remain: What are the best realistic experimental regimes to separate the contributions of axonal beading and undulations? How wide is the range of scales for both beading and undulations, depending on the brain region? Are there any other significant signal contributions from other geometric features (e.g., branchings (Palombo et al., 2016), or the nodes of Ranvier, or glial cell bodies)? Is there a qualitative difference between the geometric features, such as caliber variations, of myelinated and unmyelinated axons?

7.3.3. Extra-axonal space geometry

Modeling the extra-axonal, and more generally, extra-cellular geometry presents greater challenges than the intra-axonal compartment. Technically, the difficulty for modeling diffusion is the structural disorder in the packing arrangement of axons, enabled by their irregular shapes and a broad diameter distribution (LaMantia and Rakic, 1990; Aboitiz et al., 1992; Caminiti et al., 2009; Liewald et al., 2014). Modeling diffusion in disordered geometries (Novikov and Kiselev, 2010; Novikov and Fieremans, 2012; Novikov et al., 2014) involves an added difficulty of performing the double average described in Section 4, usually with no hope of an exact solution. This is where the methods of modern physics, such as scattering theory, as well as renormalization group family of methods, may become particularly valuable.

The practical unresolved questions can be framed in terms of parsimonioulsy parametrizing the extra-cellular space geometry, and relating the compartment parameters, such as extra-cellular volume fraction and the (generally time-dependent) diffusion tensor eigenvalues, to the packing geometry. Initial steps have been performed in (Novikov and Fieremans, 2012; Kinney et al., 2013; Burcaw et al., 2015; Fieremans et al., 2016; Ginsburger et al., 2018; Tétreault et al., 2020), but the geometry involved in such structural models remains fairly idealized.

7.3.4. Gray matter

Gray matter is a real terra incognita of dMRI, both due to difficulties in acquisition (especially in the narrow cortical areas), and in modeling. There are at least two major extra modeling challenges that the gray matter presents relative to the white matter: water exchange (cf. also Section 7.3.5 below), and the soma compartment. Water exchange may occur both between the intra-cellular space (neurites and soma) and extra-cellular water, as well as between the neurites and soma (Palombo et al., 2020; Veraart et al., 2020; Jelescu and Novikov, 2020). Currently, we are not sure which exchange mechanism is dominant.

As for the soma compartment, the quantification of its size and volume fraction presents both theory and parameter estimation challenges. Parameter estimation requires the signal from the soma compartment to be sufficiently distinct by its functional form from the stick compartment (neurites) and the extra-cellular space, — otherwise the fit remains rather degenerate (Palombo et al., 2020). This degeneracy can be in principle cured by applying stronger gradients, using the recently found $\mathcal{O}(g^4)$ correction to the Gaussian phase approximation (8) for wide pulses (Lee et al., 2020b). Practically, this compartment is likely to be in the cross-over regime between the diffusion narrowing and localization regimes, cf. Fig. 7, right panel. The theory for such a cross-over does not yet exist; Monte Carlo simulations so far remain the prime method of investigation.

7.3.5. Measuring water exchange

A standard dMRI method to measure exchange time is based on the compartment-exchange models (Kärger, 1985), as outlined in Section 7.1.1. Such modeling may be too simplistic (compartments are usually assumed isotropic and exchange is supposed to be barrier-limited), as well as prone to fit degeneracies (the two compartment model can fit almost any signal even with zero exchange, and is rather insensitive to the exchange rate).

The compartment exchange measurements in glia or in neuronal tissue give the exchange time of the order of 10ms for isotropic compartments (Pfeuffer et al., 1998), and more recently of the same order of magnitude in the anisotropic case (Veraart et al., 2020; Jelescu and Novikov, 2020). A model-independent diffusion exchange spectroscopy (DEXSY) (Callaghan and Furó, 2004) yields about the same result in neonatal mouse spinal cord (Williamson et al., 2019).⁸ On the other hand, an order of magnitude longer exchange times τ_ex ~ 100 ms in astrocyte and neuronal cultures were found by Yang et al. (2018) using perfused magnetic resonance spectroscopy, without any diffusion contrast. Overall, this large discrepancy between the methods, as well as the overall range of exchange times commensurate with MRI-relevant time scales, make estimating exchange rate a pressing issue for adequate brain microstructure modeling in gray matter. Note that for the white matter, at least in myelinated tracts, filter-exchange dMRI measurements yield exchange time ~1 s (Nilsson et al., 2013a,b), which justifies the non-exchanging Standard Model compartments. However, the exchange time in unmyelinated axons is not well known, and such axons may as well fall into fast exchange regime.

Finally, there is a fundamental question about whether some water can be transported across cytolemma via the ATP-driven Na⁺/K⁺ channels; recently, it was suggested that about half of exchange is due to this active mechanism (Bai et al., 2018), complementing passive transmission through aquaporins. Hence, potentially, measurement of exchange rate can provide vital information about cellular function.

7.3.6. Achieving compartment specificity: dMRI + spectroscopy

Separating contributions of water from intra- and extra-cellular spaces has been a permanent complication for estimating microstructure parameters, causing fit degeneracies and the associated poor precision. While still not part of clinical protocols due to SNR issues, the diffusion-weighted spectroscopy is becoming an essential research tool for establishing the fundamental modeling building blocks, based on the fact that certain metabolites are present inside distinct cellular populations, as recently reviewed by Valette et al. (2018). The past few years saw a full-scale integration of dMRI spectroscopy with microstructure modeling (Ronen et al., 2014; Palombo et al., 2016; Ligneul and Valette, 2017; Ligneul et al., 2019), making it a highly impactful future avenue for model validation.

7.3.7. Diffusion fMRI

The observation (Darquié et al., 2001; Le Bihan et al., 2006) of subtle, at about 1% level, dMRI signal changes in neuronal activation, called diffusion fMRI (dfMRI), has been a controversial topic for a while. However, as the early concerns (Miller et al., 2007) about dfMRI being just an artifact of regular BOLD fMRI got resolved, further independent measurements gradually established this effect (Tsurugizawa et al., 2013; Spees et al., 2013, 2018; Bai et al., 2015, 2016; Nunes et al., 2019). The excitement about dfMRI is quite understandable: this may be the first neuroscience-relevant phenomenon, of the morphological neuronal tissue changes due to neuronal activation, that has been discovered solely using dMRI tools. The microstructure origins of dfMRI remain obscure, due to small contrast-to-noise ratio. However, an interesting scenario in white matter, of sub-myelinic vacuoles appearing after sufficiently long activation, was put forward by Spees et al. (2018).

7.3.8. Mapping neuroplasticity

The representation of learning and memory has long fascinated neuroscientists. While fMRI can assess active memory representations during encoding and retrieval (Kuhl et al., 2011; Brown et al., 2016), it cannot convincingly identify the permanent location of the memory trace (engram) (Brodt et al., 2018).

Microstructure MRI would be an ideal candidate to map structural plasticity. Remarkably, mean diffusivity decrease of about ~1% was observed within hours of performing corresponding tasks: in rats performing spatial naviation task (in cingulate cortex, corpus callosum and dentate gyrus) (Blumenfeld-Katzir et al., 2011), and in human hippocampus after 2 h of spatial learning and memory task based on a computer-race game (Sagi et al., 2012). Learning-specific memory engram (mean diffusivity drop of ~0.5%) was detected in humans after just 1 hour of an object-location memory task, and it was found that memory activity occurs in posterior parietal cortex, rather than in hippocampus; furthermore, this engram overlapped with the related functional activity (Brodt et al., 2018).

While mean diffusivity is not specific to tissue microstructure, histological staining revealed morphometric changes in astrocytes (Blumenfeld-Katzir et al., 2011; Sagi et al., 2012). The premise of microstructure MRI is to become specific to cellular-level changes. Of course, detecting such minute compartment-specific changes based on adequate models would be a daunting task, given the overall small signal change. However, this avenue of research seems highly impactful, with the microstructure community providing a potentially indispensable tool to study most fundamental neuroscience problems.

7.4. Looking for synergies and building bridges

The main challenge for the field of microstructure mapping, and the most impactful point of synergy, is the validation of our models using the ground truth. Conceptually, the simplest validation methods rely on building microstructure-inspired phantoms (recently reviewed by Fieremans and Lee (2018)) that can be used to calibrate our measurements. However, ultimately bridging the gap from the neuroscience side relies on obtaining the precise and intact ground truth of neuronal structure in two-dimensional histology (Chklovskii et al., 2002; Caminiti et al., 2009; Liewald et al., 2014) and more recently, in three dimensions with sequential-slice electron microscopy (Lichtman and Denk, 2011; Mikula et al., 2012; Motta et al., 2019), expansion microscopy (Chen et al., 2015), and expansion/lattice light-sheet microscopy (Gao et al., 2019). Such in vivo ground truth is nontrivial to obtain (especially to preserve the extra-cellular space from shrinkage), to segment and to analyze.

Furthermore, while ex vivo measurements are easier to compare with histology, they may not generally reflect the in vivo morphology; Shepherd et al. (2009) uncovered a strong effect of a fixative on the diffusion properties. Hence, it is key to preserve tissue morphology as intact as possible while fixing and reconstructing it in two and three dimensions.

Combining machine-learning methods for segmenting the structure (Tian et al., 2020) with Monte Carlo simulations in realistic microstructure in 2 dimensions (Xu et al., 2014) and in 3 dimensions (Lee et al., 2020c,e,a) could provide ultimate quantitative tests of the theoretical concepts outlined above, as well as bridge them with further experimental validation. This kind of interdisciplinary research is only just starting, and is bound to bring important breakthroughs. Becoming specific to distinct parts of neuronal microgeometry in vivo offers a tantalizing prospect to quantify microstructure changes, such as demyelination, axonal loss and inflammation in white matter, or functional changes such as water exchange rate in gray matter, in disease, aging and development.

Complementary to the neuroscience input into our models, the microstructure community is ready to be challenged by the pointed requests from the neuroscientists — what effects are most relevant for us to try to become sensitive to by modeling, experimental design and validation? Can we make the field of tissue microstructure imaging bigger than the sum of its parts?

8. Outlook

To recap, model-based tissue microstructure imaging rests on the foundation developed within condensed-matter and statistical physics over the past half-century, naturally embracing concepts of coarse-graining and effective medium. Arguing about convergence of integrals and model assumptions, summing up Feynman diagrams and implementing the coarse-graining as part of renormalization-group approach, all acquire a whole new dimension when performed in the building where patients are being diagnosed. Such an experience can be extremely stimulating and inspiring for a physicist, otherwise used to dealing with soulless elementary particles or electrons in a piece of a semiconductor. Establishing ties with the neuroscience community to apply modern physics methods to study brain microstructure and function may prove equally rewarding, and I hope this overview can stimulate such a dialogue at a time when our field has reached a new level of rigor.

Because an overall framework — from theory (model) to measurement to image processing to parameter estimation — performs as well as its weakest link, microstructure imaging places unusual demands on each step. It forces us to calibrate our measurements, be as precise as possible in identifying and removing noise and artifacts, and develop open-source image processing pipelines. In fact, the whole logic of microstructure imaging development, as that of a fundamental scientific field within an applications-driven MRI community, dictates setting the highest bar on understanding everything we do. In this aspect, microstructure imaging is akin to any other fundamental, curiosity-driven research field, where the lack of an immediate “killer application” shifts the emphasis onto the intellectual standards, striving for the deepest possible understanding of the phenomena we are modeling and measuring.

While maintaining this unusually high bar on the depth-above-else may seem excessive from the purely applied standpoint, history of science tells that uncompromising rigor eventually harbors the greatest dividends. It is in this way, through taking no shortcuts and excuses, that physicists were able to reinvent the world by delivering a transistor, a laser, a communications satellite, the field of NMR (which led to MRI), and the whole ecosystem of far-reaching applications of the fundamental quantum-mechanical concepts they discovered largely driven by their curiosity. Likewise, within MRI research today, the microstructure imaging community is setting the bar on the rigor in modeling, on the experimental design, image processing, accuracy and precision, calibration and validation, — thus making us better at what we do even in routine acquisitions. This may as well be the most tangible contribution of tissue microstructure imaging so far, even if its actual quantitative markers have not widely percolated into neuroscience research and clinical practice. And yet, in due course, they inevitably will.

I would like to end this review article by recalling a conversation with a manager at a major scanner manufacturer. When I expressed a wish that MRI sequences be calibrated using standardized phantoms, and the resulting precision metrics included in device specifications, I was told “Scanners are not sold as measurement devices, but rather as imaging devices.” To make progress, all of us — the community of MRI researchers, as well as radiologists and neuroscientists, and ultimately the manufacturers — better change our thinking. An MRI scanner is already a highly advanced physical measurement apparatus. We ought to treat it as such if we are to transform it into a genuine in vivo tissue microscope, especially now that the multi-decade project of bridging between the relevant fundamental physics and biology enters its most consequential stage.