Effects of intrinsic environmental predictability on intra-individual and intra-population variability of plant reproductive traits and eco-evolutionary consequences

Abstract

Background and Aims

It is widely accepted that changes in the environment affect mean trait expression, but little is known about how the environment shapes intra-individual and intra-population variance. Theory suggests that intra-individual variance might be plastic and under natural selection, rather than reflecting developmental noise, but evidence for this hypothesis is scarce. Here, we experimentally tested whether differences in intrinsic environmental predictability affect intra-individual and intra-population variability of different reproductive traits, and whether intra-individual variability is under selection.

Methods

Under field conditions, we subjected Onobrychis viciifolia to more and less predictable precipitation over 4 generations and 4 years. We analysed effects on the coefficient of intra-individual variation (CV_i-i) and the coefficient of intra-population variation (CV_i-p), assessed whether the coefficients of intra-individual variation (CsV_i-i) are under natural selection and tested for transgenerational responses (ancestor environmental effects on offspring).

Key Results

Less predictable precipitation led to higher CsV_i-i and CsV_i-p, consistent with plastic responses. The CsV_i-i of all studied traits were under consistent stabilizing selection, and precipitation predictability affected the strength of selection and the location of the optimal CV_i-i of a single trait. All CsV_i-i differed from the optimal CV_i-i and the maternal and offspring CsV_i-i were positively correlated, showing that there was scope for change. Nevertheless, no consistent transgenerational effects were found in any of the three descendant generations, which contrasts with recent studies that detected rapid transgenerational responses in the trait means of different plant species. This suggests that changes in intra-individual variability take longer to evolve than changes in trait means, which may explain why high intra-individual variability is maintained, despite the stabilizing selection.

Conclusions

The results indicate that plastic changes of intra-individual variability are an important determinant of whether plants will be able to cope with changes in environmental predictability induced by the currently observed climatic change.

INTRODUCTION

Current climate change alters averages, variability and the temporal predictability of weather events (the degree of the temporal autocorrelation; Stocker et al., 2013). Averages, variability and intrinsic predictability describe different properties of a particular measurement (e.g. of daily measures of precipitation), which can be independent statistical measures (e.g. Burgess and Marshall, 2014; Marshall and Burgess, 2015; Tonkin et al., 2017). While averages and variability are frequently investigated parameters, research regarding the ecological consequences of environmental predictability for plant trait expression is rare (Tonkin et al., 2017). Predictability can refer to whether or not an individual can predict a future environmental state (e.g. Reed et al., 2010), or it can refer to whether successive environmental states are statistically predictable, without the need for an individual to sense cues that allow them to anticipate future states. The latter case is referred to as ‘intrinsic predictability’, which is an absolute measure that represents the highest achievable predictability of a system (Garland and Bradley, 2015; Pennekamp et al., 2019). While the former assumes that individuals are able to sense a cue that reliably predicts the future state of the environment and that individuals can alter their phenotype to fit the forecasted environment, under intrinsic predictability individuals will simply react to a given sequence of environmental states by altering their phenotype.

Theoretical studies suggest that lower intrinsic predictability may increase phenotypic variance (Pigliucci, 1996; Matesanz et al., 2010; Nicotra et al., 2010; Valladares et al., 2014). Phenotypic variance (V_P) refers to the sum of genetic (V_G) and environmental variance (V_E), and all components are classically measured among individuals within a given population (Falconer and Mackay, 1996; Lynch and Walsh, 1998). However, many organisms exhibit intra-individual variability (e.g. Herrera, 2009; Diggle, 2014; Harder et al., 2019), and different studies suggest that phenotypic differences between homologous organs produced by the same individual are mainly environmentally determined (Niinemets et al., 2003; Mal and Lovett-Doust, 2005). Thus, phenotypic variance and intra-individual variability may similarly respond to differences in intrinsic environmental predictability, which can occur at different temporal dimensions. Intrinsic environmental predictability can refer to regularity in the timing and magnitude of environmental fluctuations over a short time scale (e.g. autocorrelation among daily or weekly measures), or it can refer to fluctuations over longer time scales (e.g. autocorrelation among seasonal or annual measures; Christensen et al., 2013).

Independent of the temporal scale, in more predictable environments the selective pressure is predicted to be stronger and more directional, potentially depleting phenotypic variance and intra-individual variability (Ashander et al., 2016). In contrast, less predictable environments may lead to higher phenotypic variance and intra-individual variability, given that, under lower predictability, differences in phenology, morphology and reproductive traits may bear fitness advantages (Tolle and Wagner, 2011). A number of studies have detected strong evidence for phenotypic variance to be under natural selection (Bull, 1987; Sztepanacz and Blows, 2017; Harder et al., 2019), while evidence for intra-individual variability is controversial. It has been suggested that intra-individual variability simply reflects phenotypic noise (Primack, 1979; Sultan, 1987; Peters et al., 1988), but also that intra-individual variability may have a genetic basis and be under selection (Preston and Ackerly, 2004; Dai et al., 2016; Hamel et al., 2018; Nater et al., 2018). Under the phenotypic noise hypothesis, it might be expected that only environmental conditions during the development of intra-individual variability affect its development, while under the selection hypothesis, it might be expected that rapid adaptive responses to changes in the intrinsic predictability of environmental conditions may exist in order to maintain individual performance (Liu and van Kleunen, 2017). However, such responses may depend on the time scale of intrinsic predictability (e.g. daily, weekly, seasonal or annual predictability), the constancy of the selective regime among generations, the strength of the selection and the adaptive potential of the traits under selection (Lynch and Walsh, 1998).

Most studies suggest that environmental parameters directly affect phenotypic variance (Fox et al., 2019) and thus intra-population variability (i.e. inter-individual variability at the population level), rather than intra-individual variability. In contrast, the environment may simply affect intra-individual variability without modifying average trait expression, reproductive success (Gonzalez-Jimena and Fitze, 2012) and phenotypic variance (i.e. intra-population variability). This is because microhabitat, spatial position and local effects, such as different proportions of a plant being exposed to shade, may affect intra-individual variability (e.g. Gratani et al., 2006), without altering an individual’s average. This suggests that climate change-induced decreases in intrinsic climatic predictability (Stocker et al., 2013) may affect ecological and evolutionary patterns and processes of different biological levels differently, including populations and individuals (Vázquez et al., 2017). However, experimental evidence for that is lacking and the effects of intrinsic predictability on intra-population and intra-individual variability are unclear. Consequently, experimental studies are needed to determine how intrinsic environmental predictability (the degree of statistical predictability among successive environmental states) affects trait variation across levels of biological organization and time scales.

Here we experimentally test (1) whether intra-individual variability in plant reproductive traits depends on intrinsic environmental predictability; (2) whether it is under selection; (3) whether it is determined by early and/or late growth conditions; (4) whether intra-individual variability of offspring is related to intra-individual variability of their mothers; and (5) whether the observed effects are congruent among years. Moreover, we examine whether effects of intrinsic environmental predictability on intra-individual and intra-population variability are congruent or whether they differ among hierarchical levels. We used plants because they are ideal organisms to test these hypotheses and because they are modular organisms that exhibit intra-individual variability in many traits (De Kroon et al., 2005; Herrera, 2009). Given that plants are sessile organisms with limited migration abilities, acclimation to different environmental states requires rapid changes in phenotypic expression, including shifts in allocation strategies (Adler et al., 2014), which may be facilitated by high phenotypic plasticity (Reed et al., 2010). Intra-individual variation might therefore exist in response to environmental changes, potentially reducing competition (e.g. for pollinators, for light, for resources, etc.) and affecting Darwinian fitness. We used the common sainfoin Onobrychis viciifolia Scop. (Fabaceae) as a model species, since it is widely distributed across Eurasia, and exhibits high intra-individual variability in the number, phenology and size of inflorescences and produced seeds.

We manipulated intrinsic daily and seasonal precipitation predictability during four consecutive years in outdoor plots exposed to natural conditions (e.g. March-Salas and Fitze, 2019a; March-Salas et al., 2019). Each year, seeds were sown in 16 independent plots, which were exposed to more or less predictable daily precipitation during early and late growth using a two-factorial design. For each individual, we measured reproductive traits (time to flowering per inflorescence, inflorescence length, number of seeds per inflorescence and individual seed mass), and calculated the coefficient of intra-individual variation for each trait. Moreover, offspring seeds (hereafter referred to as descendants) were planted in the subsequent year in order to investigate transgenerational responses in intra-individual variability, i.e. effects of the ancestor environment on offspring (Yin et al., 2019). Based on this experimental design, we evaluated four sets of hypotheses. Hypothesis 1: environments exhibiting lower intrinsic predictability promote greater intra-individual and intra-population variability than those exhibiting higher intrinsic predictability, intrinsic environmental predictability during early and late growth may differently affect intra-individual variability, and differences in intrinsic predictability consistently affect intra-individual and intra-population variability. Hypothesis 2: intra-individual variability in reproductive traits is under selection, and selection depends on intrinsic precipitation predictability. Hypothesis 3: intra-individual variability of the offspring is related to intra-individual variability of the mothers, and this relationship depends on intrinsic precipitation predictability. Hypothesis 4: lower intrinsic predictability promotes rapid transgenerational responses that increase the intra-individual variability of descendants. Therefore, this study will be fundamental to the understanding of how the current climatic change affects plant responses in intra-individual and intra-population variability and selective regimes.

MATERIALS AND METHODS

Experimental system, study organism and sowing procedures

Seeds of Onobrychis viciifolia Scop. (common sainfoin; Fabaceae; for details concerning the species’ ecology and life history, see the Supplementary data) were sown during four consecutive years (2012–2015) in experimental field plots located at the experimental field station ‘El Boalar’ (42°33'N, 0°37'W, 705 m a.s.l.; IPE-CSIC, Jaca, Huesca, Spain). ‘El Boalar’ exhibits no seasonality in precipitation, and wild O. viciifolia grow there (March-Salas et al., 2019). Seeds were obtained in 2011 from a farm located in Castillo de Lerés (23 km from the field site), where annual precipitation is higher than at ‘El Boalar’ (on average, approx. 340 mm more per year) and the other climatic conditions are similar (see March-Salas et al., 2019). These seeds are hereafter referred to as the ancestral generation (G₀), while generations produced at ‘El Boalar’ are referred to as descendants (G_1–3; see below).

In 2012, 16 experimental open-air plots of 1.2 × 6.0 m were established in 16 enclosures. Enclosures were delimited by metal walls that were 1 m high and extended 1 m below ground and they were covered by a mesh, protecting plants against large herbivores and birds. The mesh width used (1.6 × 1.6 cm) allowed access for pollinators. In each plot, 28 planting positions were marked, aligned in a quadratic grid and separated by >40 cm. In early April 2012, randomly selected ancestral seeds were sown at a depth of 2 cm in each planting position, and in 2013 to 2015 in seven planting positions per plot. Each year, the top 30 cm of the soil of each plot was loosened and homogenized before sowing. All weeds, roots and visible seeds were removed to avoid competition with non-experimental plants, and the ground was smoothed. Before sowing, statistical analyses were conducted to ensure that no significant differences in average and variance of seed mass existed between the sample and the sub-samples, between years, plots and experimental treatments (P ≥0.1 in all cases).

Precipitation treatment

Intra- and inter-seasonal intrinsic precipitation predictability (i.e. the degree of temporal correlation among precipitation events) was manipulated by supplementing eight experimental plots at regular intervals and another eight plots at random intervals with supplemental precipitation. Supplemental precipitation was provided by an automatic irrigation system consisting of four sprinklers per enclosure, one in each corner, which provided homogenous precipitation in the whole enclosure (e.g. San-Jose et al., 2014). M-plots were irrigated 14 times per week for 5 min at regular intervals (twice a day) and L-plots were irrigated 14 times per week for 5 min at randomly chosen time points. Together with the natural precipitation, these treatments resulted in more (M; higher autocorrelation among days) and less (L; lower autocorrelation among days) predictable daily precipitation (natural + supplemental precipitation). The timing of daily precipitation (natural + supplemental precipitation) differed between treatments, as confirmed by differences in its permutation entropy (a measure of the predictability of a time series that is negatively correlated with a system’s predictability, Pennekamp et al. 2019; see below), while the number of precipitation events and the total amount of precipitation (natural + supplemental) were identical (for more information, the see next paragraph).

Irrigation occurred from sowing to the drying up of the last inflorescence in late summer (for approx. 4.25 months), and each irrigation event provided 1.3 mm of supplemental precipitation, with a total of 330.2 mm of supplemental precipitation per year. The simulated total annual precipitation (natural + supplemental) thus corresponds to the amount of precipitation under which the G₀ seeds developed (see above). At the field site, the average annual precipitation was 916 mm (2012–2015), natural precipitation exhibited no seasonality and the maximum annual precipitation registered in the last 10 years was 1265 mm. The minimum daily precipitation at the study site was identical to the minimum total precipitation in the plots, and the daily maximum total precipitation and precipitation variance did not differ significantly from the amount and variance of the natural daily precipitation prevailing at the study site during the growing season (F_1,62 ≤0.0003, P ≥0.98). Thus, the simulated precipitation (natural + supplemental) was within the natural range of the precipitation registered at the study site and the locality from where the seeds originated. The intrinsic predictability of the total daily precipitation (natural + supplemental) estimated by permutation entropy (Pennekamp et al., 2019) was 0.77 in M-plots, which was equal to the intrinsic predictability of the natural precipitation observed at the study site (permutation entropy = 0.77). In L-plots, it was 0.86, and thus daily precipitation predictability was 11.2 % lower than that of the M-plots. This experimental design allowed us to test how differences in the intrinsic precipitation predictability feed back on reproductive components, and it avoided the drying up of the plants in late spring/early summer due to high ambient temperatures (high evapotranspiration; March-Salas et al., 2019). The experimental design thus represents a conservative measure of the effects of intrinsic precipitation predictability, since the experimental plants were able to complete their life cycle.

A two-factorial precipitation design was applied. Treatments applied from early spring to late spring (spring season; during early plant growth) are hereafter referred to as ‘early treatment’, and treatments applied from early to late summer (summer season; during late plant growth) as ‘late treatment’ (e.g. March-Salas and Fitze, 2019a, b). Intrinsic inter-seasonal predictability (i.e. the level of autocorrelation between spring and summer) was manipulated by exposing half of the plots to the same or to different predictability regimes during early and late growth, resulting in a two-factorial design with four combinations (March-Salas and Fitze, 2019a, b): MM, more predictable during early growth and more predictable during late growth; LL, less predictable in both periods; ML, more predictable during early and less predictable during late growth; and LM, less predictable during early and more predictable during late growth. Thus, plants were exposed to higher inter-seasonal predictability (MM, LL) or lower inter-seasonal (ML, LM) predictability, or, in other words, to a higher or a lower autocorrelation of precipitation between early (spring) and late growth (summer).

Multi-generation experiment

All descendant seeds were collected, dried and stored over the winter. Seeds produced by G₀ mothers in 2012 are hereafter referred to as G₁, those produced by G₁ mothers (in 2013) as G₂, and seeds produced by G₂ mothers (in 2014) as G₃. In each of the 3 years (2013–2015), and for each of the four treatment combinations, a randomly selected sub-sample of seeds of a selected sub-sample of mothers was selected to be sown. Within each treatment level, mothers were randomly selected to be used for the multi-generation experiment among the mothers that produced at least 16 seeds and that belonged to the same treatment level (e.g. within G₀ mothers originating from LL). Thereafter, we tested (within the treatment level) that there were no differences among selected and not selected mothers in mean and variance of the mothers’ emergence time (d), maximum height (mm), maximum diameter (mm), number of produced seeds, average seed mass (g), start of flowering period and above-ground and root biomass (g) (all P ≥0.2). Moreover, we also tested within each year that no significant interaction between treatments and type of mothers (i.e. selected vs. not selected mothers) existed, to make sure that we did not differentially select mothers in a given treatment level or level of the treatment combinations. Additionally, we tested for each treatment combination that no significant interactions between year and selected vs. not selected mothers and year × mother enclosure existed to make sure that mothers were not differentially selected among years within a given treatment combination. For each selected mother, we then randomly selected seeds to be used and tested (within the seeds of this mother) for differences in mean and variance of seed mass (g) between used and not used seeds. Once seeds were selected in all treatment combinations, we also tested that there was no significant interaction between seed type (selected vs. not selected) and the treatment combinations (i.e. LL, LM, ML and MM), and, as in mother, that there existed no significant seed type × year interaction. All interactions were non-significant (all P ≥0.1). For the subsequent generation (G₂), we randomly selected G₁ mothers and, additional to the above explained criteria, we made sure that G₁ mothers of all selected grandmothers (G₀) were selected. Descendants were planted in the same treatment combinations as their mother, but not in the plot where the mother was growing, to avoid local adaptation to specific conditions of a particular plot (March-Salas et al., 2019). Consequently, the mother (G₂), grandmother (G₁) and great-grandmother (G₀) of the G₃ seeds selected to be planted in a given treatment combination were all living in the same treatment combination as the G₃ seeds. To control for differences among years and plots, ancestral seeds were planted in all plots, allowing for a precise estimate of transgenerational responses, thanks to intra-plot comparisons between descendants and ancestors.

Measured traits

The beginning of the flowering period was determined for each plant, by daily checking the opening of the first flower. Thereafter, for each inflorescence, the appearance of the first open flower was determined (Fig. 1A) by weekly surveys, in order to quantify the intra-individual variability in flowering time and the duration of flowering. The length (mm) and number of produced seeds were measured for each inflorescence when all fruits of the inflorescence were ripe. Ripe fruits were collected, fruits of the same inflorescence were stored in the same paper bag, and all paper bags were maintained in a cold and dry laboratory environment. The mass of each fruit was measured with a Mettler Toledo balance (precision: 0.01 mg) and is hereafter referred to as seed mass.

Fig. 1.

Seeds and inflorescences of O. viciifolia. (A) Appearance of the first flower of an inflorescence, (B) fruits consisting of a single-seeded pod and (C) inflorescences belonging to the same plant. To follow up the development of each inflorescence, inflorescences were individually marked (see attached number). All photos stem from experimental plants growing at ‘El Boalar’ (Jaca, Huesca, Spain). Photographer: Martí March-Salas.

Data analyses

As a standardized measure of variability, a plant’s coefficient of intra-individual (i-i) variation (CV_i-i = standard deviation of the measures of the same trait belonging to the same individual/average of this trait) was calculated for four different reproductive traits: individual seed mass, week of an inflorescence’s flowering start (hereafter referred to as ‘flowering start’), number of seeds per inflorescence and inflorescence length. For each individual and reproductive trait, the trait mean was calculated. Based on these means, the intra-plot (i-p) variability (CV_i-p = standard deviation of the mean trait of all individuals belonging to the same plot divided by the average of the plot’s trait means) was calculated for each plot and year. All coefficients of variation (CsV) were standardized and log transformed prior to statistical analyses to fit the assumptions of statistical models based on Gaussian error distributions.

First, we tested whether the CsV_i-i (a) and the CsV_i-p (b) differ among predictability treatments, assessed the importance of early and late treatment and tested whether the treatment effect is consistent among years (Hypothesis 1). To this end, linear mixed-effect models (LMMs) with Gaussian error distribution were run with the (a) CsV_i-i or (b) the CsV_i-p of G₀ plants as dependent variables. Early and late predictability treatments (factor levels: less vs. more predictable), year and their interactions were modelled as fixed parameters. Plot was modelled as a random factor. Consistency of the treatment effects was evaluated by the significance of the year × treatment interactions. Non-significance indicates that the direction of the treatment effect did not significantly differ among years and, thus, that its effect was consistent.

Secondly, we tested whether the CsV_i-i of G₀ plants is under selection and whether the selective regime depends on precipitation predictability (Hypothesis 2). Selection analysis were based on fecundity selection (i.e. reproductive success measured by the number of seeds produced), and other selection agents such as competition, ecological interactions or herbivory were controlled by experimental design. For each trait, LMMs were run with seed number as dependent variable. Linear and quadratic CsV_i-i were modelled as covariates, and early treatment, late treatment and year as fixed factors. All possible interactions between treatment and covariates were included. Plot was modelled as a random factor.

Thirdly, we tested whether the CV_i-i of the mothers was correlated with the CV_i-i of the descendants and whether this varied by treatment (Hypothesis 3). The CsV_i-i were calculated for all descendants (G₁, G₂ and G₃) and for their mothers. LMMs were run with the CsV_i-i of the descendants as dependent variable, the CV_i-i of their mother as a covariate, early and late treatment as fixed factors, and all possible two- and three-way interactions. Plot, year and matriline were modelled as random factors.

Fourthly, we tested for transgenerational responses in the CV_i-i and whether potential responses were affected by the experimental treatments (Hypothesis 4). Transgenerational responses were tested in 2013, 2014 and 2015, by comparing the CsV_i-i of descendants (G₁, G₂ and G₃) and ancestors (G₀) grown in the same plot and year. For each trait, LMMs were run including generation (ancestral vs descendant), early and late treatment, and year as fixed factors, as well as their two-, three- and four-way interactions. Plot and matriline were modelled as random factors. Significant interactions between treatments, or treatment combinations and generation, would indicate the existence of transgenerational responses.

All statistical analyses were conducted with R (version 3.5.0; R Development Core Team, 2017). The lmer function from the lme4 package was used to fit mixed-effects models (Bates et al., 2015). Function sjp.lmer and tab_model from the sjPlot package (Lüdecke, 2017) were used to check the model assumptions (e.g. for the LMMs; linear relationship of the response and the explanatory variables, homoscedasticity and normality of the residuals) and to calculate the marginal and conditional R² statistics, based on Nakagawa et al. (2017). We applied stepwise backward selection using the drop1 function to select the minimum adequate model. Post-hoc tests (lsmeans package) were applied using Tukey’s HSD test, whenever significant factors (main effects or main effects in interactions) consisted of more than two levels.

RESULTS

Across all years and treatments, 724 individuals successfully reproduced. A total of 8205 inflorescences (average = 11.33 inflorescences ± 0.39 s.e. per plant) of an average length of 130.39 ± 0.64 s.e. mm, and 95 946 seeds were produced. The average number of seeds per inflorescence was 11.69 ± 0.12 s.e., and average seed mass was 21.07 ± 0.003 mg s.e.

Effects of intrinsic precipitation predictability on intra-individual (CV  _i-i  ) and intra-plot variability (CV  _i-p)

There was a significant two-way interaction between early and late treatment on intra-individual variability (CV_i-i) of seed number per inflorescence of G₀ (χ ₁² = 8.155, P = 0.004). The CV_i-i of seed number per inflorescence tended to be higher in LL (mean ± s.e. 0.649 ± 0.014) than in ML (0.586 ± 0.017, t = 2.530, P = 0.059), was significantly higher in LL than in LM (0.585 ± 0.018, t = 3.134, P = 0.011) and did not significantly differ from MM (0.657 ± 0.028, t ≤ |1.596|, P ≥ 0.394). Less predictable (L) late precipitation led to significantly higher CsV_i-i of flowering start (L, 0.044 ± 0.002; M, 0.039 ± 0.002, χ ₁² = 6.979, P = 0.008). Early predictability treatment did not significantly affect any of the CsV_i-i (χ ₁² ≤ 0.82, P ≥ 0.37), and none of the treatments affected the CV_i-i of seed mass (mean ± s.e. 0.340 ± 0.005) and inflorescence length (0.318 ± 0.005, χ ₁² ≤ 6.17, P ≥ 0.10). No significant interactions containing year existed in the models on the CsV_i-i (all χ ₃² ≤ 3.719, P ≥ 0. 240).

The late treatment significantly affected the intra-plot variability (CV_i-p) of seed number per inflorescence and flowering start, both being significantly higher in the less predictable compared with the more predictable treatment (seed number per inflorescence χ ₁² = 4.307, P = 0.038; flowering start χ ₁² = 7.016, P = 0.008). The CV_i-p of inflorescence length tended to be higher in the less predictable late treatment (χ ₁² = 3.501, P = 0.061), and the CV_i-p of seed mass was not significantly affected by the treatments (χ ₁² ≤ 0.758, P ≥ 0.384). In contrast to the late treatment, the early treatment tended to affect the CV_i-p of flowering start, which tended to be higher in the less predictable early treatment (χ ₁² = 3.351, P = 0.067). The CsV_i-p of the other traits were not significantly affected by the treatments (χ ₁² ≤ 1.983, P ≥ 0.159). In none of the models on the CsV_i-p did significant interactions exist (χ ₃² ≤ 6.059, P ≥ 0.108).

Effects of intrinsic precipitation predictability on selection acting on intra-individual variability (CV  _i-i)

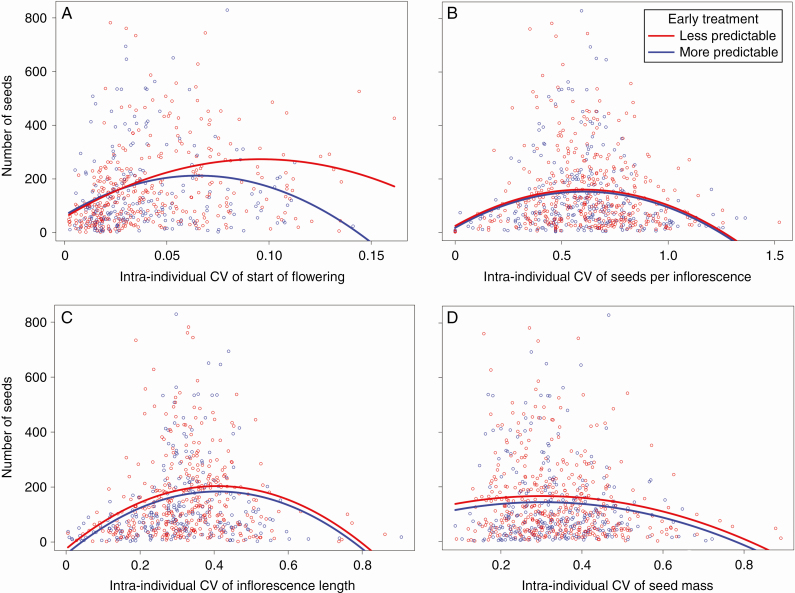
Significant stabilizing selection existed on the CV_i-i of all analysed traits (Table 1, significant quadratic terms; Fig. 2; Supplementary data Fig. S1). Selection on flowering start, and its strength, significantly depended on the treatments (Fig. 2A: early treatment × CV_i-i²; Supplementary data Fig. S1A: late treatment × CV_i-i²; Table 1). The optimal CV_i-i of flowering start was reached at a higher CsV_i-i in the less compared with the more predictable early treatment (L, 0.10; M, 0.07; Fig. 2A) and in the less compared with the more predictable late treatment (L, 0.10; M, 0.08; Supplementary data Fig. S1A). The optimal CV_i-i of flowering start was associated with a 27.31 % higher reproduction in the less compared with the more predictable early treatment and a 21.54 % higher reproduction in the less predictable late treatment. Moreover, selection was stronger under more predictable conditions in both the early and the late treatment (i.e. faster decreases in the number of seeds with increasing distance from the optima; Fig. 2A; Supplementary data Fig. S1A). Optimal CsV_i-i in the less predictable early compared with the late treatment of the other traits (number of seeds per inflorescence, inflorescence length and seed mass) led to significantly higher reproductive output, but neither the shape, the location of the optimum (optimal CV_i-i of seeds per inflorescence = 0.06, inflorescence length = 0.41, seed mass = 0.30) nor the intensity of selection differed between treatment levels (Fig. 2B–D; Table 1 – only a significant main effect of early treatment existed). Optimal CsV_i-i of seeds per inflorescence, inflorescence length and seed mass led to 2.14, 10.73 and 15.50 % higher reproduction in the less compared with the more predictable early treatment. Late treatment affected the selection acting on the CV_i-i of seed mass (Supplementary data Fig. S1B; Table 1 – main effect). Optimal CV_i-i of seed mass was associated with higher reproductive success (+28.34 %) in the less predictable compared with the more predictable late treatment, but neither the shape, the location of the optimum nor the strength of selection differed among treatments (Supplementary data Fig. S1B). In all models of Table 1, the CV_i-i × treatment × year interactions were not significant (all χ ₃² ≤ 6.471, P ≥ 0.1).

Table 1.

Effects of predictability treatment on selection acting on the coefficient of intra-individual variation (CV_i-i) of four reproductive traits

	Coefficient of intra-individual variation (CVi-i)
	Flowering start			Inflorescence length			No. of seeds per inflorescence			Seed mass
Predictors	Estimate ± s.e.	t-value	P	Estimate ± s.e.	t-value	P	Estimate ± s.e.	t-value	P	Estimate ± s.e.	t-value	P
CVi-i	0.51 ± 0.04	11.952	<0.001	0.17 ± 0.04	5.317	<0.001	–0.03 ± 0.03	–0.791	0.429	0.07 ± 0.04	1.678	0.094
Early[L]	0.03 ± 0.04	0.682	0.498	0.09 ± 0.04	2.139	0.041	0.08 ± 0.04	2.101	0.039	0.12 ± 0.04	2.662	0.012
Late[L]	–0.00 ± 0.04	–0.079	0.938							–0.10 ± 0.04	2.439	0.021
CVi-i2	–0.24 ± 0.03	–7.721	<0.001	–0.19 ± 0.02	–10.001	<0.001	–0.19 ± 0.02	–9.545	<0.001	–0.18 ± 0.02	–8.002	<0.001
Early[L] × CVi-i2	0.05 ± 0.02	2.298	0.022
Late[L] × CVi-i2	0.05 ± 0.02	2.221	0.027
Early[L] × CVi-i
Late[L] × CVi-i
Early[L] × Late[L]
Early[L] × Late[L] × CVi-i
Early[L] × Late[L] × CVi-i2
Marginal R2/conditional R2	0.200 / 0.294			0.178 / 0.217			0.126 / 0.183			0.095/ 0.200

The full model consisted of seed number as dependent variable, linear and quadratic terms of the CV_i-i (represented as CV_i-i and CV_i-i², respectively) as covariates, early and late predictability as fixed factors, and all possible two- and three-way interactions. Minimum adequate models were derived using sequential backward elimination, and results of these models are shown. Estimates ± s.e., Student’s t-statistics and P-values are given. ‘L’ in square brackets indicates that the estimate corresponds to the less predictable treatment. No significant interactions with year existed in any of the models (χ ₃² ≤ 4.360, P ≥ 0.113), and thus these parameters are not shown. The sample size was 211.

Fig. 2.

Effect of precipitation predictability during early growth on the relationship between the number of produced seeds and the CsV_i-i of flowering start (A), seed number per inflorescence (B), inflorescence length (C) and seed mass (D). Differences between the less (red) and the more (blue) predictable early treatment are shown. All quadratic relationships were significant (all P < 0.001, Table 1), and significant differences between early treatment levels existed in flowering start (P = 0.022, Table 1). Dots represent raw data, and lines indicate retransformed predictions.

Effects of intrinsic precipitation predictability on the relationship between intra-individual variability of mothers and descendants

The CsV_i-i of flowering start and seed mass of the descendants were significantly and positively correlated with the CsV_i-i of flowering start and seed mass of their mothers (hereafter referred to as ‘maternal CV_i-i’; Supplementary data Table S1), and no significant correlation existed in seed number per inflorescence and inflorescence length (Supplementary data Table S1). Less predictable precipitation of the early and late treatment significantly increased the descendants’ CV_i-i of flowering start, and the less predictable precipitation of the late treatment significantly increased the CsV_i-i of seed number per inflorescence and inflorescence length (Supplementary data Table S1). The correlation between the CsV_i-i of the descendants and the maternal CV_i-i of the number of seeds per inflorescence and inflorescence length were not significantly affected by the treatments (all P > 0.1; see Supplementary data Table S1), nor were the interactions among treatments significant (Supplementary data Table S1). In all these models, the CV_i-i × treatment × year interactions were not significant (all χ ₂² ≤ 3.186, P ≥ 0.2).

Transgenerational responses

There were no significant differences between ancestors and descendants in the CsV_i-i of seed number per inflorescence and flowering start (main effect and all interactions including generation and treatment: χ ² ≤ 4.25; P ≥ 0.12; Supplementary data Table S2), and thus no evidence for transgenerational responses existed in these traits. The CV_i-i of seed mass was affected by a significant three-way interaction between generation, year and late treatment (Supplementary data Table S2; Fig. 3). In 2013, descendants (G₁) of the more predictable late treatment exhibited a lower CsV_i-i in seed mass than ancestors of the same treatment (t = 3.528, P = 0.027), and in the less predictable late treatment descendants exhibited higher but not significantly higher CsV_i-i. In 2014, descendants (G₂) exhibited higher CsV_i-i in seed mass than ancestors of both levels of the late treatment, but only in the less predictable late treatment were they significant (t = 3.415, P = 0.038). In 2015, descendants of the more predictable late treatment exhibited slightly higher but not significantly different CsV_i-i than ancestors, while in the less predictable late treatment ancestors exhibited slightly higher but not significantly different CsV_i-i. The significant three-way interaction thus shows that the direction of the differences between ancestors and descendants significantly differed among years and levels of late treatment (Fig. 3). The CV_i-i of inflorescence length was affected by a significant two-way interaction between generation and late treatment (Supplementary data Table S2). The CsV_i-i of inflorescence length were slightly higher in descendants in the more predictable late treatment and slightly lower in the less predictable late treatment, but no significant differences existed between descendants and ancestors either in the less or in the more predictable treatment (t ≤ 1.96, P ≥ 0.21; Supplementary data Fig. S2).

Fig. 3.

Transgenerational response in intra-individual variability (CV_i-i) of seed mass. Significant late treatment × year × generation interaction on the CV_i-i of seed mass. Means ± s.e. for each level of the interaction are given. Dashed and red lines correspond to differences between ancestors and descendants in the less predictable, and solid and blue lines to the differences between ancestors and descendants in the more predictable late treatment. Significant post-hoc contrasts between ancestors and descendants within years and treatment levels are given by thick lines and non-significant contrasts with thin lines. Asterisks denote significant contrasts (*P < 0.05).

DISCUSSION

This experimental study shows that intra-individual (CV_i-i) and intra-population variability (CV_i-p) are significantly affected by intrinsic precipitation predictability, and it experimentally shows that intra-individual variability of reproductive traits is under selection. The results on CV_i-i and CV_i-p were congruent, since both were greater when precipitation was less predictable, in line with the claims that climatic changes affect intra-specific variability (Starrfelt and Kokko, 2012; Lawson et al., 2015; Hamel et al., 2018; Vasseur et al., 2018). All CsV_i-i were under stabilizing selection, and precipitation predictability additively affected Darwinian fitness. Moreover, it affected the location of the optima and the strength of selection on variance in flowering phenology. The descendants’ CsV_i-i were positively related to their mother’s CV_i-i in flowering start and seed mass, and intrinsic precipitation predictability did not significantly affect this correlation in any of the traits (no significant interactions between treatment and maternal CV_i-i). Transgenerational responses existed in two (CsV_i-i of seed mass and inflorescence length) of the four studied traits, and their effect depended mainly on late treatment and the year. The direction of the transgenerational responses on the CsV_i-i differed among years (for seed mass, see Fig. 3), which contrasts with the transgenerational responses on means of fitness-related traits, which exhibited the same direction among all study years (March-Salas et al., 2019).

Effects of intrinsic environmental predictability on intra-individual and intra-population variability

In agreement with ‘Hypothesis 1’ (i.e. that lower intrinsic predictability compared with higher intrinsic predictability promotes greater intra-individual and intra-population variability), the CsV_i-p and the CsV_i-i of flowering start and seed number per inflorescence were significantly higher in the less predictable compared with the more predictable treatment. The directions of the precipitation predictability’s effect at the intra-population and intra-individual levels were identical (i.e. at both levels, the less predictable compared with the more predictable treatment led to higher variability, CsV) and precipitation predictability affected the same traits in both hierarchical levels, which contrasts with observations that climatic effects depend on the level of biological organization (Vázquez et al., 2017). This indicates that intrinsic environmental predictability affects reproductive allocation strategies of individuals (e.g. Gonzalez-Jimena and Fitze, 2012) and phenotypic variance simultaneously, suggesting that the former may feed back on the latter, which points to scaling up from within-individual to among-individual variation, and thus from lower to higher levels of biological organization. This finding is thus congruent with a high proportion of population-wide variance contributed by intra-individual variability (Herrera, 2017), and with bottom up forces that may scale up to population variance or alter community composition under changing climatic conditions or other indirect interactions (Jeltsch et al., 2008; Des Roches et al., 2018).

There existed no significant year × precipitation predictability interactions in any of the coefficients of variation, despite the observed differences in natural monthly precipitation among the study years at the field site (March-Salas et al., 2019). The absence of significant year × precipitation predictability interactions on the coefficients of variation contrasts with significant year × precipitation predictability interactions observed on the means of reproductive traits and survival of O. viciifolia (March-Salas and Fitze, 2019a; March-Salas et al., 2019). This shows that the effects of intrinsic climatic predictability on variance – CsV – were more consistent than those on trait averages and it suggests that differences in intrinsic predictability may be more likely to induce plastic responses in trait variance rather than in the mean trait expression (note that both analyses were based on the same sample size). These results also indicate that effects of climate change on the intrinsic predictability of the weather, rather than changes on weather means, may entail greater shifts in trait variation, in line with studies suggesting that differences in environmental predictability may have greater effects on plant performance than differences in environmental averages (Katz and Brown, 1992; Ashander et al., 2016; March-Salas and Pertierra, 2020). The absence of significant year × precipitation predictability interactions may potentially have been the consequence of lower sample size in the last three experimental years, but sample sizes were equal in the analyses presented here to those on trait averages (March-Salas et al., 2019), where year × precipitation predictability interactions were found, suggesting that potential treatment interactions with year on the coefficients of variation were not of great importance.

Intrinsic precipitation predictability mainly affected the CsV_i-i and the CsV_i-p during late growth (i.e. effects of late treatment). First, lower daily precipitation predictability significantly increased the CV_i-i and the CV_i-p of flowering start and the CV_i-p of seed number per inflorescence during late growth. Secondly, there was a significant early × late treatment interaction on the CV_i-i of seed number per inflorescence, which was mainly caused by late precipitation predictability (i.e. significantly higher CsV in LL compared with LM), and not by differences in inter-seasonal precipitation predictability [the post-hoc contrast between higher (MM, LL) and lower (ML, LM) inter-seasonal predictability was not significant, P = 0.110], and evidence for early precipitation predictability effects is only based on a non-significant trend (LL vs. ML: P = 0.059). Thirdly, daily precipitation predictability during early growth only tended to affect the CV_i-p of flowering start. This shows that mainly the intrinsic environmental predictability during late growth affected the studied CsV and it suggests that early life conditions may not be very important for the studied CsV. Consequently, the importance of differences in intrinsic environmental predictability depends on when these differences manifest, suggesting that not all climate change-induced changes in intrinsic climatic predictability will affect intra-individual variation (Burton et al., 2019).

The flowering start of each inflorescence was measured during the entire growth of the plant and for each plant. CsV_i-i of the flowering start was greater in the less predictable late treatment. Given that in the less predictable late treatment the plant’s first flower appeared earlier than in the more predictable treatment (March-Salas et al., 2019), flowering in plants exposed to less predictable precipitation lasted for longer, and thus greater CsV_i-i is most probably the consequence of a longer flowering period (effect of late treatment on the duration of flowering: χ ₂² = 6.231, P = 0.012; effect of early treatment: χ ₂² = 0.135, P = 0.714), which may also explain the observed higher reproductive success (Franks et al., 2014; March-Salas et al., 2019). Moreover, flowering over longer time periods may also reduce the competition for resources and pollinators (Elzinga et al., 2007), and it may increase the chance that flowering falls within optimal climatic conditions (Cleland et al., 2007; Elzinga et al., 2007; Anderson et al., 2012).

Effects of intrinsic environmental predictability on selection acting on intra-individual variability

In agreement with ‘Hypothesis 2’ (i.e. that intra-individual variability in reproductive traits is under selection, and selection depends on intrinsic precipitation predictability), intra-individual variability of all reproductive traits was under stabilizing selection (Elzinga et al., 2007), in line with the definition of functional traits, referring to any morphological, physiological or phenological trait, measurable at the individual level, which impacts fitness indirectly via its effects on growth, reproduction and/or survival (i.e. individual performance; Violle et al., 2007). In all measured coefficients of variation, differences in precipitation predictability affected the reproductive success at the optimal CV_i-i (in Table 1 early treatment had significant effects in the four CsV_i-i), the location of the optimal CV_i-i and the strength of selection acting on the CV_i-i of flowering start, while the selection acting on CV_i-i of the other traits was unaffected. Differences in precipitation predictability did not change the type of selection (e.g. stabilizing vs. directional selection) in any of the measured reproductive traits. This shows experimentally that intrinsic environmental predictability affects the selection acting on the variance of flowering start, and thus, of a plant’s phenology, while selection acting on the variance of seed mass and inflorescence length, which are measures of reproductive success (Elzinga et al., 2007), were unaffected. This shows that intra-individual variability in reproductive traits is under consistently strong stabilizing selection and that it does not reflect phenotypic noise, which differs from the hypotheses stated in several studies (e.g. De Kroon et al., 2005; Elzinga et al., 2007; Sobral et al., 2018). These findings also indicate that intra-individual variability is a functional trait, and thus intra-individual variability should be considered in eco-evolutionary studies.

Evolutionary implications of intra-individual variability

In line with ‘Hypothesis 3’ (i.e. that intra-individual variability of the offspring is related to intra-individual variability of the mothers, and that this relationship depends on intrinsic precipitation predictability), the maternal CsV_i-i of seed mass and flowering start were positively correlated with the CV_i-i of their offspring, but intrinsic precipitation predictability and year did not significantly affect the mother–offspring correlations (Supplementary data Table S1). This is in line with heritability of intra-individual variability (Winn 1996), and it suggests that genotype × environment interactions (Tolle and Wagner 2011) may be of low importance in determining intra-individual variability (Supplementary data Table S1: lack of significant maternal CV_i-i × treatment effects).

The selection acting on the CsV_i-i indicates that rapid adaptive evolution may occur given the consistency of the selective pressure (since selection did not differ among experimental years), and given that fitness may be increased (in most of the treatment levels the observed average CsV_i-i was not close to the optimal CsV_i-i, Fig. 2; Supplementary data Table S3). Moreover, in the CsV_i-i of the number of seeds per inflorescence, the benefits of transgenerational effects would have been highest in the LL and MM treatment combination, given that in both groups the averages were further away from the optima than those of the ML and LM combination (distance from optima: in LL, 0.049; MM, 0.057; ML, 0.015; and LM, 0.014) and given that the average ± s.e. of ML and LM included the optima, but this was not the case in LL and MM (Supplementary data Table S3). This suggests that intra-individual variability could be improved in most traits and treatment levels. Nevertheless, there were no significant transgenerational effects in the CV_i-i of the number of seeds per inflorescence and flowering start, and there were no consistent transgenerational effects in the CV_i-i of seed mass and inflorescence length. This clearly contrasts with ‘Hypothesis 4’ (i.e. that lower intrinsic predictability promotes rapid transgenerational responses that increase the intra-individual variability of descendants) and with results on trait means where transgenerational responses within one or two generations occurred in many traits of O. viciifolia (March-Salas et al., 2019). This indicates that rapid transgenerational responses may mainly exist with respect to mean trait expression, but not with respect to the variance of those traits. This finding may be explained by the climatic unpredictability prevailing in most parts of the natural distribution of O. viciifolia, under which maintaining intra-individual variability may be highly beneficial and rapid responses may lead to important fitness costs (DeWitt et al. 1998).

Conclusion

This study experimentally demonstrates that intrinsic precipitation predictability (the degree of statistical predictability among successive environmental states) significantly affects intra-population and intra-individual variability of reproductive traits of O. viciifolia. Lower intrinsic precipitation predictability enhanced intra-individual and intra-population variance, suggesting that effects of reduced predictability can be generalized to several intra-specific hierarchical levels. Our results further show that intra-individual variability is a plastic trait that is under stabilizing selection, suggesting that changes in intra-individual variability may allow plants to rapidly react to environmental changes, in line with the modular nature of plants. This finding and the significant mother–offspring regression are in line with genetic and plastic determination of intra-individual variability, and it suggests that it might be important for coping with rapid changes in intrinsic environmental predictability, and, more specifically, with increases in environmental uncertainty. Consistent directional transgenerational effects were absent, which is in line with the importance of maintaining intra-individual variability in order to cope with changing conditions, at least as long as no extreme events occur. Our findings thus suggest that plastic changes of intra-population and intra-individual variability may be highly relevant for species persistence and performance under climate change.

SUPPLEMENTARY DATA

Supplementary data are available online at https://academic.oup.com/aob and consist of the following. Table S1: treatment effects on the relationship between the mothers’ coefficient of intra-individual variation and the CV_i-i of their descendants for four reproductive traits. Table S2: transgenerational responses in the CV_i-i of four reproductive traits. Table S3: scope for transgenerational responses and adaptive selection. Average CV_i-i ± s.e. of each studied trait and retransformed location of the optimal CV_i-i in the detected stabilizing selection are given. Figure S1: effects of precipitation predictability during late growth on the relationship between the number of produced seeds and the coefficient of intra-individual variation of flowering start and seed mass. Figure S2: transgenerational response in intra-individual variability of inflorescence length.

FUNDING

Funding was provided by the Swiss National Foundation (PPOOP3_128375, PP00P3_152929/1 to P.S.F.) and the Spanish Ministry of Economy and Competitiveness, the latter co-financed by the European Fund for Regional Development, (CGL2012-32459, CGL2016-76918 AEI/FEDER, UE to PSF). M.M.S. was supported by a PhD grant (BES-2013–062910) financed by the Spanish Ministry of Economy and Competitiveness.