Soft X‐ray and ENA Imaging of the Earth's Dayside Magnetosphere

Abstract

The LEXI and SMILE missions will provide soft X‐ray images of the Earth's magnetosheath and cusps after their anticipated launch in 2023 and 2024, respectively. The IBEX mission showed the potential of an Energetic Neutral Atom (ENA) instrument to image dayside magnetosheath and cusps, albeit over the long hours required to raster an image with a single pixel imager. Thus, it is timely to discuss the two imaging techniques and relevant science topics. We simulate soft X‐ray and low‐ENA images that might be observed by a virtual spacecraft during two interesting solar wind scenarios: a southward turning of the interplanetary magnetic field and a sudden enhancement of the solar wind dynamic pressure. We employ the OpenGGCM global magnetohydrodynamics model and a simple exospheric neutral density model for these calculations. Both the magnetosheath and the cusps generate strong soft X‐rays and ENA signals that can be used to extract the locations and motions of the bow shock and magnetopause. Magnetopause erosion corresponds closely to the enhancement of dayside reconnection rate obtained from the OpenGGCM model, indicating that images can be used to understand global‐scale magnetopause reconnection. When dayside imagers are installed with high‐ENA inner‐magnetosphere and FUV/UV aurora imagers, we can trace the solar wind energy flow from the bow shock to the magnetosphere and then to the ionosphere in a self‐standing manner without relying upon other observatories. Soft X‐ray and/or ENA imagers can also unveil the dayside exosphere density structure and its response to space weather.

Key Points

• Soft X‐ray and Energetic Neutral Atom (ENA) imaging instruments provide an innovative way to visualize the global solar wind‐magnetosphere interaction

• High‐cadence, wide field‐of‐view soft X‐ray, and ENA images can capture the motion of the bow shock and magnetopause

• The magnetopause motion can reveal the magnetopause reconnection mode on a global scale

1. Introduction

Impressive images from the Hubble Space Telescope not only help scientists understand our universe, but also enhance public interest in science, becoming a gateway for the youngest generation to enter Science, Technology, Engineering, and Mathematics (STEM) fields. Heliophysics observatories can also provide dramatic images of our space environment. The Solar and Heliospheric Observatory (SOHO; Domingo et al., 1995) images the dynamic activities of our Sun and its solar corona. Solar Terrestrial Relation Observatory (STEREO; Kaiser et al., 2008) monitors solar wind features propagating through interplanetary space. Imager for Magnetopause‐to‐Aurora Global Exploration (IMAGE; Burch, 2000) and Two Wide‐Angle Imaging Neutral‐Atom Spectrometers (TWINS; Goldstein & McComas, 2018) display the activities of the Earth's inner‐magnetosphere in response to varying solar wind conditions. Time History of Events and Macroscale Interactions during Substorms (THEMIS) All Sky Imagers (ASI) distributed over the northern portions of North America (Mende et al., 2008) image aurora precipitation resulting from magnetospheric activities. The one missing image is the dayside magnetosphere, the starting point for the solar wind‐magnetosphere interaction.

Two imaging techniques are currently available to visualize the Earth's dayside plasma structures (namely, the bow shock, magnetosheath, magnetopause, and cusps): one using Energetic Neutral Atoms (ENAs) and another using soft X‐rays. ENAs are produced when solar wind protons exchange electrons with the Earth's exospheric atoms (typically hydrogen atoms) (Gruntman, 1997; Williams et al., 1992). The newly generated ENAs depart with the velocities of the incident solar wind ions. They move quickly through near‐Earth space unobstructed by magnetic fields. Soft X‐rays are emitted when a highly charged solar wind particle, such as O⁷⁺ or O⁸⁺, acquires an electron from an Earth's exospheric hydrogen atom. The electron that moved to solar wind ions first stays in an excited state but soon relaxes to a rest state with the emission of a soft X‐ray photon (Carter et al., 2010, 2011; Cravens et al., 2001; Snowden et al., 2004). The magnetosheath and cusps are strong ENA and soft X‐ray emitters due to abundant source populations (i.e., solar wind plasma and exospheric neutral hydrogen densities) (Fujimoto et al., 2007; Snowden et al., 2004). By observing these signals, we can extract global motion of the bow shock, magnetopause, and cusps in response to the solar wind and interplanetary magnetic field (IMF) conditions, and thus advance our knowledge of solar wind interaction with the Earth's magnetosphere. For example, ENA or soft X‐ray images of magnetopause erosion can reveal the magnetopause reconnection mode. Fast or slow, gradual or abrupt, and global or local erosion suggest high or low, continuous or impulsive, and global or localized reconnection on the magnetopause, respectively (Branduardi‐Raymont et al., 2018; Sibeck et al., 2018).

ENA imaging has been an important technique since ENAs from Saturn (Kirsch, Krimigis, Ip, et al., 1981) and Jupiter (Kirsch, Krimigis, Kohl, et al., 1981), and from the Earth's ring current (Roelof et al., 1985) were observed by Voyager 1 (Stone, 1977) and International Sun‐Earth Explorer 1 (Ogilvie et al., 1977), respectively. The ENA instruments on IMAGE and TWINS have provided wide field‐of‐view images of the Earth's inner magnetosphere, advancing our understanding of ring current dynamics (Goldstein & McComas, 2018; Moore et al., 2000) and supporting subsequent model development (Buzulukova et al., 2010, 2018; Fok et al., 2003, 2014). Global ENA imaging of the dayside magnetosheath became available soon after the launch of Interstellar Boundary Explorer (IBEX; McComas et al., 2009) whose primary goal is to image the heliosphere. Fuselier et al. (2010) and Petrinec et al. (2011) generated images of the entire dayside system by integrating more than 9 h of line‐of‐sight ENA observations during relatively constant solar wind conditions. However, these dayside images are limited due to the constraints of IBEX orbit, the look direction of its ENA instrument, and the long observation time required for a dayside image that consequently mandates prolonged steady solar wind conditions. A wide field‐of‐view, high‐cadence, ENA imager dedicated to dayside observations would greatly benefit investigations into the solar wind‐dayside magnetosphere interaction and improve global magnetosphere models.

Unlike ENA imaging, soft X‐ray imaging is a relatively new tool to the space plasma community. Soft X‐rays from solar wind charge exchange (SWCX) in geospace were discovered by the astrophysics X‐ray mission, ROentgen SATellite (ROSAT; Trümper, 1982) in the 1990s (Cravens et al., 2001) and subsequently observed by other missions such as the X‐ray Multi‐Mirror Mission‐Newton (XMM‐Newton; Jansen et al., 2001) (Carter et al., 2010, 2011; Snowden et al., 2004). These missions have X‐ray instruments with relatively narrow fields of view, but both observed a strong, variable background signal well correlated with solar wind activity and, in the case of XMM‐Newton, spectral signatures consistent with charge exchange line emission. Carter et al. (2010, 2011) reported that XMM‐Newton observes strong near‐Earth soft X‐rays while it looks through the dayside region, indicating the magnetosheath is a strong source of soft X‐rays. These near‐Earth soft X‐ray observations provided considerable additional motivation to formulate future space missions that visualize the interaction between solar wind and the Earth's dayside system in soft X‐rays. As a result, three space missions, the Cusp Plasma Imaging Detector (CuPID) Cubesat Observatory (http://sites.bu.edu/cupid/), the Lunar Environment heliospheric X‐ray Imager (LEXI; http://sites.bu.edu/lexi/), and the Solar wind‐Magnetosphere‐Ionosphere Link Explorer (SMILE; Branduardi‐Raymont et al., 2018), are scheduled to launch in 2021, 2023, and 2024, respectively.

This study provides predictions and analysis for the scheduled satellite missions and other upcoming mission opportunities. Section 2 introduces the models used in this study and explains the methods to generate the soft X‐ray and ENA images. Section 3 presents the modeled images obtained during a southward IMF turning and a solar wind pressure enhancement, and discusses how these images can be used to study dayside reconnection. Section 4 identifies other science topics that can be addressed by these images themselves and in collaboration with other observations. Section 5 summarizes our study.

2. Calculation of Soft X‐ray and ENA Emission

2.1. Models

We use the Open Geospace Global Circulation Model (OpenGGCM) global magnetosphere‐ionosphere magnetohydrodynamics (MHD) model to produce soft X‐ray and ENA images. OpenGGCM solves resistive MHD equations in non‐uniform Cartesian grids, assuming current‐driven instabilities. Its simulation domain ranges from 20 to 30 Earth Radii (R _E) upstream to several hundreds of R _E downstream. Its Y _gse and Z _gse domains range from −45 to 45 R _E. The inner boundary of OpenGGCM is set at 2.0–3.5 R _E geocentric distance. It uses solar wind and IMF conditions as input and provides plasma density, velocity, temperature, and electromagnetic field parameters throughout the simulation domain. OpenGGCM can be coupled with Rice Convection Model (Cramer et al., 2017) and/or Coupled Ionosphere‐Thermosphere Model (Connor et al., 2016; Raeder et al., 2001b) to investigate interaction of the outer magnetosphere with the inner magnetosphere and with the upper atmosphere, respectively. In this paper, we used the stand‐alone OpenGGCM model. Details of OpenGGCM and its applications to the geospace environment can be found in Raeder et al. (2001a, 2008), Connor et al. (2012, 2014, 2015, 2016), Oliveira and Raeder (2015), Ferdousi and Raeder (2016), Cramer et al. (2017), Jensen et al. (2017), Shi et al. (2017), and Kavosi et al. (2018).

A simple exospheric density model from Cravens et al. (2001) is used to obtain the neutral hydrogen density (N _N):

$$N_{\mathrm{N}}=25{\left(\frac{10R_E}{R}\right)}^3\left[{\text{cm}}^{-3}\right]$$ (1)

where R is a radial distance from the Earth's center measured in R _E. A neutral density (N _N) inversely proportional to the cube of radial distance is a good approximation to more sophisticated empirical neutral density models (Bailey & Gruntman, 2011; Østgaard et al., 2003; Zoennchen et al., 2011, 2013, 2015).

This study considers two interesting solar wind‐magnetosphere interaction scenarios: (1) a southward IMF turning and (2) a sudden increase in the solar wind dynamic pressure (P _sw). The following solar wind and IMF conditions are introduced for the two simulations. For the IMF turning event, IMF B _z changes from 5 to −5 nT while the solar wind plasma parameters remain constant. The solar wind density, velocity, and temperature are set at 10 cm⁻³, 400 km/s, and 200,025 K, respectively. IMF B _x and B _y are zero. For the P _sw increase event, the solar wind density changes from 6 to 30 cm⁻³, while the IMF and other solar wind parameters stay the same. Solar wind velocity and temperature are 450 km/s and 120,715 K. IMF B _z is −3 nT with B _x = B _y = 0. The dipole tilt angle is set at zero for both simulations.

2.2. Soft X‐ray

We calculate the soft X‐ray intensity (R _Xray) by taking the line integral of the product of the plasma density (N _p), neutral density (N _H), plasma effective speed (v _eff), and effective scale factor ($\alpha$):

$$R_{\text{Xray}}=\frac{\alpha }{4\pi }\int N_p{N}_H{v}_{\text{eff}}ds\left[{\text{eVcm}}^{-2}{\mathrm{s}}^{-1}{\text{sr}}^{-1}\right]$$ (2)

$$v_{\text{eff}}=\sqrt{v_p^2+v_{\text{th}}^2}=\sqrt{v_p^2+\frac{3k_{B}T}{m}}$$ (3)

where v _p and v _th are the plasma bulk and thermal speeds, T is the plasma temperature, k _B is the Boltzmann constant, m is the proton mass, and ds is an infinitesimal length along the line‐of‐sight of a soft X‐ray instrument (Cravens et al., 2001; Kuntz et al., 2015, 2019; Robertson et al., 2006, 2012; Sibeck et al., 2018). The effective scale factor ($\alpha$) includes the charge‐exchange cross‐sections, soft X‐ray emission line energies, and the abundances of the soft X‐ray source plasmas in the solar wind (Whittaker & Sembay, 2016). In this study, we are interested in the 100 eV–1 keV energy band, which is densely populated by SWCX emission lines (Sibeck et al., 2018), and thus take $\alpha =6\times {10}^{-16}{\text{eVcm}}^2$ per Cravens et al. (2001) who studied soft X‐rays in a similar energy band. The OpenGGCM MHD model provides the plasma parameters (N _p and v _eff), and the simple neutral density model provides N _H.

2.3. ENA

We calculate the differential ENA intensity (J _ENA) by taking the line integral of the product of the differential proton flux ($J_{{\mathrm{H}}^{+}}$), neutral density (N _H), and H−H⁺ charge exchange cross section ($\sigma$) (Fuselier et al., 2010; Goldstein & McComas, 2018; Roelof et al., 1985):

$$J_{\text{ENA}}=\int J_{{\mathrm{H}}^{+}}{N}_{\mathrm{H}}\sigma ds.$$ (4)

where ds is an infinitesimal length along the line‐of‐sight of an ENA instrument. The differential proton flux along a line of sight is obtained from the OpenGGCM global MHD model, assuming Maxwellian distributions for the magnetosheath plasma:

$$J_{{\mathrm{H}}^{+}}=f_{\text{MB}}\frac{v^2}{m},$$ (5)

$$f_{\text{MB}}=n{\left(\frac{m}{2\pi k_{B}T}\right)}^{\frac{3}{2}}\exp \left(-\frac{m{\left(\stackrel{\rightharpoonup }{v}-{\stackrel{\rightharpoonup }{V}}_d\right)}^2}{2k_{B}T}\right)$$ (6)

where f _MB is the phase space density, m is the proton mass, k _B is the Boltzmann constant, $\stackrel{\rightharpoonup }{\mathit{v}}$ is the proton velocity of interest, and ${\stackrel{\rightharpoonup }{\mathit{V}}}_{\mathit{d}}$ is the plasma drift velocity. OpenGGCM provides proton density (n), velocity (${\stackrel{\rightharpoonup }{\mathit{V}}}_{\mathit{d}}$), and temperature (T). The magnitude of $\stackrel{\rightharpoonup }{\mathit{v}}$ is calculated from the ENA energy of interest (i.e., $v=\sqrt{2E/m}$), and the direction of $\stackrel{\rightharpoonup }{\mathit{v}}$ is toward the ENA instrument along its line‐of‐sight. Here, we focus on 1 and 10 keV protons moving toward a virtual spacecraft location that eventually become ENAs via charge exchange with hydrogen atoms. The cross sections between 1 keV protons and hydrogen atoms and between 10 keV protons and hydrogen atoms are 1.5 × 10⁻¹⁵  cm² and 0.8 × 10⁻¹⁵ cm², respectively, taken from Figure 3 of Gruntman et al. (2001). We use the neutral density model of Cravens et al. (2001), that is, Equation 1, for the ENA calculation.

3. Model Results and Discussion

3.1. Modeling of Soft X‐ray and ENA Images

Figure 1 presents the modeled soft X‐ray and ENA images during the southward IMF turning event. The top panel shows solar wind condition input into the OpenGGCM model. The bottom panel shows, from left to right, the plasma density on the noon‐midnight meridian plane, a soft X‐ray image observed from a virtual spacecraft at (X _gse, Y _gse, Z _gse)=(0, 30, 0)R _E, and the 1 keV hydrogen ENA image that a spacecraft would observe at the same location. The X‐ray and ENA images cover the same region of the plasma density plot, and the angular resolution of each image is set at 1° by 1°. The 1° angular resolution is chosen considering the capability of soft X‐ray and ENA imaging technologies that is discussed in Section 3.3. The vertical black bar in the top panel indicates the time when the bottom plots are taken. Note that the units of soft X‐ray and ENA signals are not same. The two signals result from different physical phenomena and thus have their own units widely used in the soft X‐ray and ENA communities. We adopted the typically used units in this paper.

Figure 1.

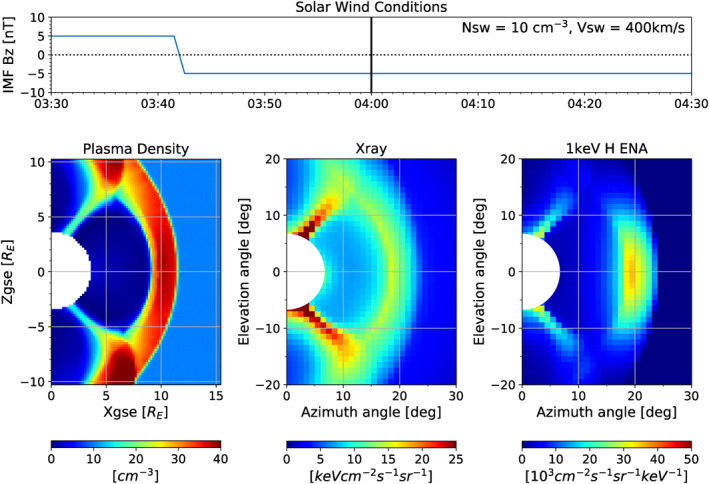
Model input and results for the southward IMF turning event, (top) solar wind and IMF conditions versus simulation time, (bottom left) plasma density on the XZ plane, (bottom middle) soft X‐ray emission rate observed by a virtual spacecraft at (X _gse, Y _gse, Z _gse)=(0, 30R _E, 0), (bottom right) 1 keV hydrogen ENA differential flux observed by the same spacecraft. The vertical bar in the top panel indicates the time of the bottom figures. Both X‐ray and ENA images use 1° × 1° angular resolution. ENA, Energetic Neutral Atom; IMF, interplanetary magnetic field.

The modeled images match our expectations. The X‐ray image resembles that predicted by previous studies (Cravens et al., 2001; Sibeck et al., 2018; Walsh et al., 2016). The ENA image resembles that constructed by Fuselier et al. (2010) from 11‐h of IBEX ENA observations during steady solar wind and IMF conditions. The magnetosheath and cusps are strong emitters of X‐rays and ENAs. Although the mid‐altitude cusp has a low solar wind plasma density, it has a very high neutral density, resulting in bright soft X‐ray and ENA emissions. The dayside magnetosheath has a lower neutral density than the cusp but a high solar wind plasma density, producing strong X‐ray and ENA signals.

Soft X‐ray and ENA images vary as the Earth's magnetosphere responds to the time‐dependent solar wind and IMF input. Figures 2 and 3 present examples at several times during the southward IMF turning and during the sudden P _sw increase, respectively. From top to bottom, each figure shows solar wind condition shifted to the bow shock nose, modeled soft X‐ray images, and modeled ENA images at the three times indicated by the vertical red lines in the top panel. The first red lines in Figures 2 and 3 represent the times before the solar wind changes, the middle red lines represent when the dayside magnetosphere is still adjusting to the new solar wind conditions, and the last red lines represent when the dayside magnetosphere is fully adjusted. The bow shock and magnetopause locations on the XZ plane are calculated from the MHD models and then projected on the X‐ray and ENA images of the bottom two panels using white and black curves. We obtain the two dayside boundaries by selecting the points where the plasma density gradient maximizes and minimizes along lines parallel to the x‐axis. Then, we calculate the azimuthal and elevation angles of these boundaries seen from the spacecraft location and plot them on the soft X‐ray and ENA images. To show more details of the image changes, we add two supplementary Movie S1 and Movie S2 for the two solar wind scenarios.

Figure 2.

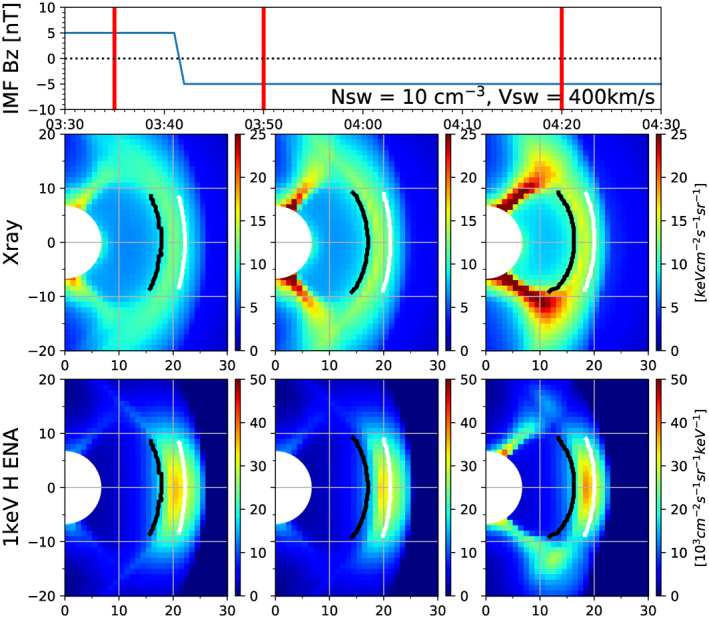
Comparison of soft X‐ray and ENA images during the southward IMF turning event. (top) Solar wind/IMF conditions versus simulation time, (middle) soft X‐ray images at three times as indicated by the red vertical bars in the top panel, (bottom) 1 keV H ENA images at the same time incidents. White and black curves in the bottom two panels indicate the locations of bow shock and magnetopause, respectively, calculated from the OpenGGCM MHD model. X and Y axes of the bottom two panels represent azimuth and elevation angles in degree, respectively. ENA, Energetic Neutral Atom.

Figure 3.

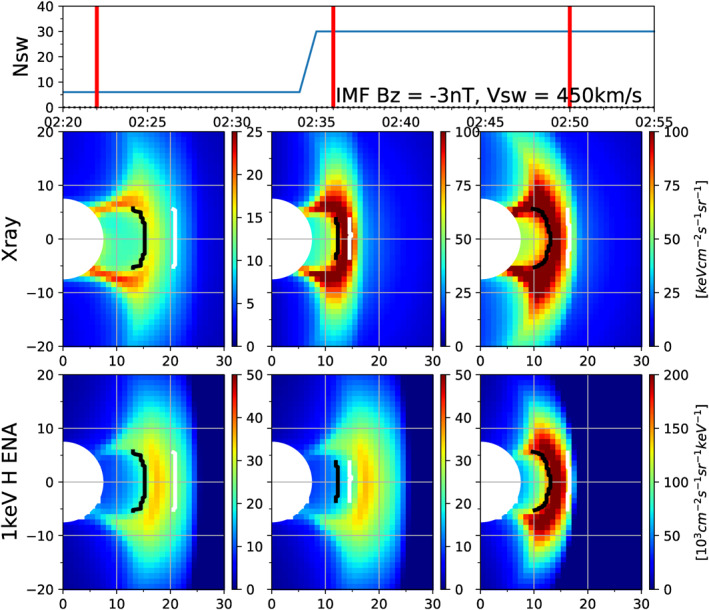
Comparison of soft X‐ray and ENA images during the sudden P _sw enhancement event in the same format as Figure 2. ENA, Energetic Neutral Atom.

The magnetosheath region seen in the soft X‐ray and ENA images (i.e., the bright emission regions in Figures 2 and 3) does not exactly match with the magnetosheath region on the noon‐midnight meridional plane (i.e., the region between the black and white lines in Figures 2 and 3) due to a geometry of an instrument's line‐of‐sight in a three‐dimensional magnetosheath. Even if an instrument looks outside of the magnetosheath on the noon‐midnight meridian plane, soft X‐ray and ENA signals can still be observed as long as a portion of the instrument's line‐of‐sight lies in the magnetosheath. In spite of this mismatch between the imaged magnetosheath and the magnetosheath on the noon‐midnight plane, Figures 2 and 3 demonstrate that soft X‐ray and ENA images catch the magnetosheath motion under the varying solar wind conditions.

As expected, the bow shock and magnetopause move Earthward after the southward IMF turning and the pressure enhancement as seen in the white and black curves in Figures 2 and 3. The Earthward motion in Figure 2 is a bit difficult to catch by eye but is clearly seen in the quantitative analysis shown later in this study. The bright soft X‐ray and ENA regions, that is, the magnetosheath, also follow the Earthward motion as seen in the first and last columns of soft X‐ray and ENA images, suggesting that the motion of the bow shock and magnetopause can be extracted from those images. However, as can be seen in the middle columns of Figures 2 and 3, the ENA images do not initially catch the Earthward magnetosheath motion due to the finite time of flight required for ENAs to reach the observing spacecraft. This delayed response of ENA images is more clearly seen for the P _sw enhancement event. The middle ENA image of Figure 3 shows that the region emitting high ENA intensities appears to remain unchanged although the bow shock (white curve) and magnetopause (black curve) have already moved Earthward. By contrast, the soft X‐ray images immediately catch the magnetosheath relocation because of the fact that soft X‐rays travel at the speed of light.

Another strength of soft X‐ray imaging over ENA imaging is that the photons are emitted in an isotropic manner while ENAs move in the direction they are going prior to charge exchange. The angle between the instrument line of sight and any plasma bulk flow velocity is of no importance for soft X‐ray detection, but can be an important factor for the detection of ENAs. The best scenario for ENA detectors occurs when the bulk flow velocity is toward the observer, the worst when it is away, but the angle remains an issue even when the flow is perpendicular to the line of sight.

Soft X‐ray and ENA images can be used to track the motion of the dayside boundaries, as speculated by Collier et al. (2005) that relates the enhancement of IMAGE low‐ENA signals to the magnetopause erosion during southward IMF turning. Figure 4 demonstrates a simple algorithm that extracts look angles tangent to the bow shock and the magnetopause from the soft X‐ray and ENA images. The left panel shows from top to bottom, the soft X‐ray emission (R _xray) along the sun‐earth line versus an azimuth angle $\varphi$ (the red angle on the right panel of Figure 4), its second derivative ($\frac{d^2{R}_{\text{xray}}}{d{\varphi }^2}$) versus $\varphi$, the differential flux of 1 keV hydrogen ENAs (J _ENA) along the sun‐earth line versus $\varphi$, and its second derivative $\left(\frac{d^2{J}_{\text{ENA}}}{d{\varphi }^2}\right)$ versus $\varphi$. The cyan line indicates the angle at which R _xray and J _ENA peak. The magenta line indicates the angle sunward from the cyan line where $\frac{d^2{R}_{\text{xray}}}{d{\varphi }^2}$ and $\frac{d^2{J}_{\text{ENA}}}{d{\varphi }^2}$ peak. At this specific time (i.e., 5:10 UT in the IMF turning simulation), both soft X‐ray and ENA images found the same peak angles for R _xray and J _ENA and for $\frac{d^2{R}_{\text{xray}}}{d{\varphi }^2}$ and $\frac{d^2{J}_{\text{ENA}}}{d{\varphi }^2}$, thus providing one cyan line and one magenta line in Figure 4, although this is not the case at other times (e.g., the transition time from old to new solar wind conditions due to the time of flight effect of ENAs). The right panel of Figure 4 displays plasma density on the equatorial plane as a color contour. Our virtual spacecraft is located at (X _gse, Y _gse, Z _gse)=(0, 30, 0)R _E. The cyan line shows the line‐of‐sight corresponding to peak signals in soft X‐ray and ENA, and the magenta line shows the line‐of‐sight corresponding to the second derivative peaks.

Figure 4.

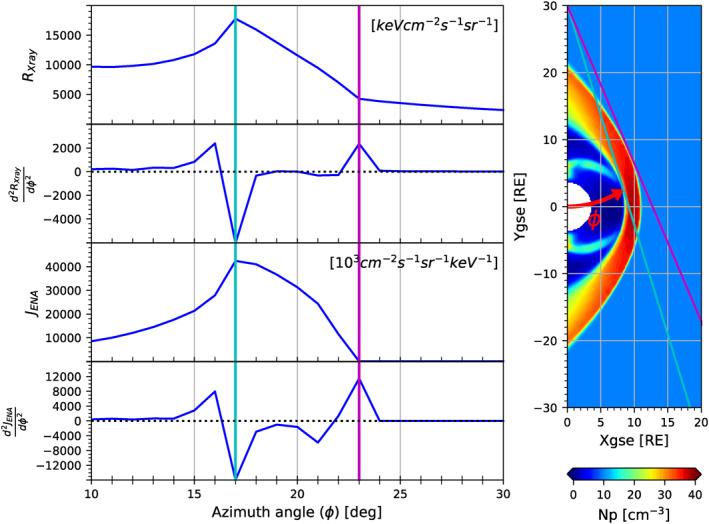
(left) Variation of soft X‐ray and ENA signals along the sun‐earth line obtained at 05:10 UT from the IMF turning simulation. The azimuth angle ($\varphi$) is defined on the righthand graph. A cyan line indicates the angle where both soft X‐ray and ENA signals (i.e., R _xray and J _ENA) peak, and a magenta line indicates the angle sunward from the cyan line at which the second derivatives of the two signals with respect to an azimuth angle $\left(\text{i.e.},,,,\frac{d^2{R}_{\text{xray}}}{d{\varphi }^2}\right.$ and $\left.\frac{d^2{J}_{\text{ENA}}}{d{\varphi }^2}\right)$ peak. At this time, both soft X‐ray and ENA images found the same peak angles for R _xray and J _ENA and for $\frac{d^2{R}_{\text{xray}}}{d{\varphi }^2}$ and $\frac{d^2{J}_{\text{ENA}}}{d{\varphi }^2}$, thus providing one cyan line and one magenta line. (right) Plasma density on the equatorial plane. The cyan line shows the line‐of‐sight corresponding to peak signals in soft X‐ray and ENA, and is tangent to the magnetopause. The magenta line shows the line‐of‐sight corresponding to the second derivative peaks, and is tangent to the bow shock. ENA, Energetic Neutral Atom; IMF, interplanetary magnetic field.

The look direction that gives peak signals (cyan line) is tangent to the magnetopause as suggested by Collier and Connor (2018). This line‐of‐sight provides the longest path inside the magnetosheath, and thus more X‐ray and ENA emissions are accumulated along the look direction. As a line‐of‐sight moves away from the magnetopause to the bow shock, its path in the magnetosheath shortens and fewer emissions are accumulated along the line‐of‐sight. As a result, R _xray and J _ENA decrease as $\varphi$ increases beyond the value for the peak emission (i.e., the cyan line), as seen in the left panel of Figure 4. As a line‐of‐sight leaves from the bow shock to the upstream solar wind, the look direction no longer passes through the magnetosheath and little accumulation of the signal occurs due to the low plasma and neutral densities in the upstream region. As a result, the slopes of R _xray and J _ENA suddenly flatten at the look angle that grazes the bow shock (i.e., magenta line). Consequently, the second derivatives $\left(\frac{d^2{R}_{\text{xray}}}{d{\varphi }^2}\right.$ and $\left.\frac{d^2{J}_{\text{ENA}}}{d{\varphi }^2}\right)$ peak at this angle.

This study traces the motions of the magnetopause and bow shock during the two solar wind scenarios by tracking the angles corresponding to peaks in the signal and its second derivative, respectively. We take note that there are more sophisticate techniques (Collier & Connor, 2018; Jorgensen et al., 2019; Jorgensen et al., 2019; Sun et al., 2020) that trace 3‐dimensional dayside boundaries from the soft X‐ray images and that are equally applicable to the ENA images. However, this paper employs the aforementioned simple approach to prove the traceability of the boundaries in soft X‐ray and ENA images.

Figure 5 shows changes of soft X‐ray (top) and ENA (bottom) emission from line‐of‐sight look directions that pass through various points along the Sun‐Earth line during the southward IMF turning (left) and the sudden P _sw enhancement (right). The upper right corner of each plot shows when each line is taken. The peak emission angle that points to the subsolar magnetopause moves to lower azimuth angle as the magnetosheath erodes Earthward. At the same time, the intensity of the peak emission also increases. For the IMF turning event, peak intensities of X‐ray and ENA increase by up to 45% and 24%, respectively (see Figures 5a and 5b) because the magnetosheath moves into a higher exospheric density region, subsequently producing more charge exchange. For the P _sw enhancement event, the peak intensities of soft X‐ray and ENA increases by up to 671% and 612%, respectively (see Figures 5c and 5d), due to the combination of 400% increase in solar wind flux and the sudden Earthward magnetosheath motion into a denser exosphere. Our modeling studies indicate that soft X‐ray and ENA imagers can expect stronger signals during a magnetopause erosion event, enabling easier magnetopause tracing for dayside reconnection studies.

Figure 5.

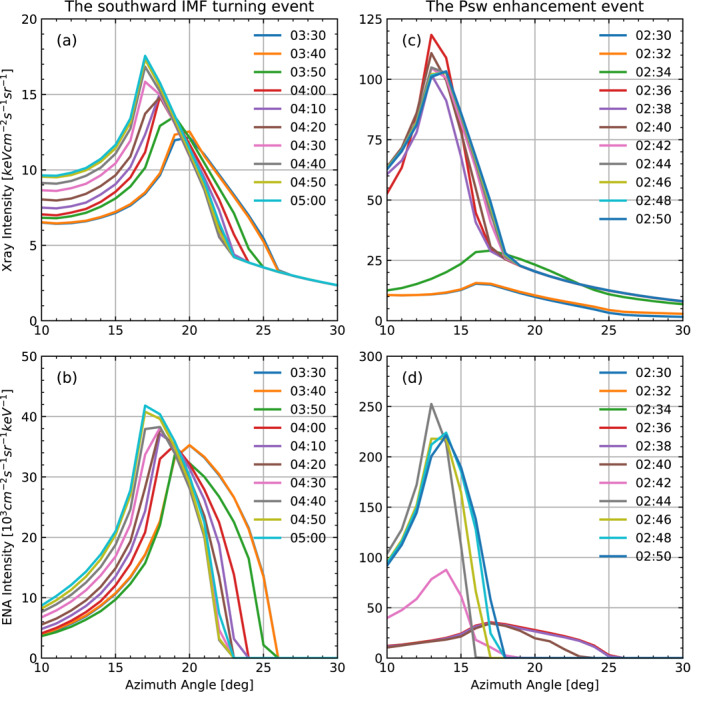
Soft X‐ray intensity (top) and ENA intensity (bottom) profiles for lines of sight that intercept the Sun‐Earth line during the southward IMF turning (left) and the sudden P _sw enhancement (right). The azimuth angle ($\varphi$) is defined on the right panel of Figure 4. The upper right corner shows when each line is taken. ENA, Energetic Neutral Atom.

We note that the modeled ENA intensity shows nearly zero signal in the upstream region (e.g., $\varphi$  = 26°–30° in Figures 5b and 5d). This is partly because the upstream region has tenuous ENA source population (i.e., exospheric neutrals and solar wind protons) and partly because combination of the purely anti‐sunward solar wind velocity and the cold solar wind temperature produces almost purely anti‐sunward ENAs, causing little ENAs moving toward our virtual spacecraft location. In reality, a virtual spacecraft at the given location expects to see weak ENA signals in the upstream region because solar wind has non‐zero velocity components perpendicular to the sun‐earth line (i.e., $V_y=V_z\ne 0)$ and because interplanetary background and instrumental noises also contribute to the ENA signals.

3.2. Magnetopause Motion and Dayside Reconnection

The location and motion of the magnetopause can provide important information concerning dayside reconnection (Sibeck et al., 2018). How quickly the magnetopause erodes Earthward is directly related to the reconnection rate. Abrupt Earthward jumps in the magnetopause location may indicate bursty reconnection (Raeder, 2006; Russell & Elphic, 1978; Scholer, 1988). Global or local erosion events may indicate global or local reconnection. Using the OpenGGCM MHD simulation, we can show that there is a close relationship between the magnetopause motion and the global dayside reconnection rate.

Figures 6 and 7 display the dayside boundary motion and reconnection rates during the southward IMF turning and the abrupt pressure enhancement, respectively. From top to bottom are the solar wind conditions for each simulation (6a and 7a), the subsolar magnetopause location obtained from OpenGGCM (6b and 7b), the tangential magnetopause location obtained along the Sun‐Earth line from the X‐ray and ENA images (6c and 7c), the subsolar bow shock location obtained from OpenGGCM (6d and 7d), the tangential bow shock location obtained along the Sun‐Earth line from the X‐ray and ENA images (6e and 7e), and the reconnection rates of the dayside and nightside magnetosphere (6f and 7f). Blue and green lines in Figures 6c, 6e, 7c, and 7e represent the boundaries extracted from the X‐ray and ENA images, respectively, using the techniques mentioned in Section 3.1. Note that the modeled images have a 1° × 1° angular resolution that limits the boundary resolutions to angles no finer than 1°. Red and blue lines in Figures 6f and 7f indicate dayside and nightside reconnection rates, respectively.

Figure 6.

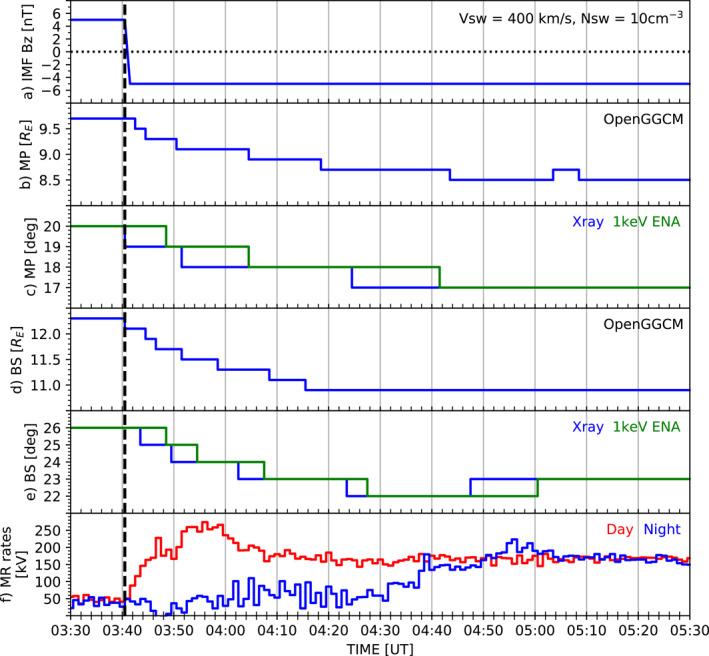
Dayside boundary motion and reconnection rates during the southward IMF turning event. (a) Solar wind and IMF conditions, (b) subsolar magnetopause location obtained from the OpenGGCM, (c) look angle tangent to the magnetopause location, obtained along the sun‐earth line from the soft X‐ray images (blue) and ENA images (green), (d) subsolar bow shock location from OpenGGCM, (e) look angle tangent to the bow shock location, obtained along the sun‐earth line from the soft X‐ray images (blue) and the ENA images (green), and (f) dayside (red) and nightside (blue) reconnection rates obtained from the OpenGGCM. ENA, Energetic Neutral Atom; IMF, interplanetary magnetic field.

Figure 7.

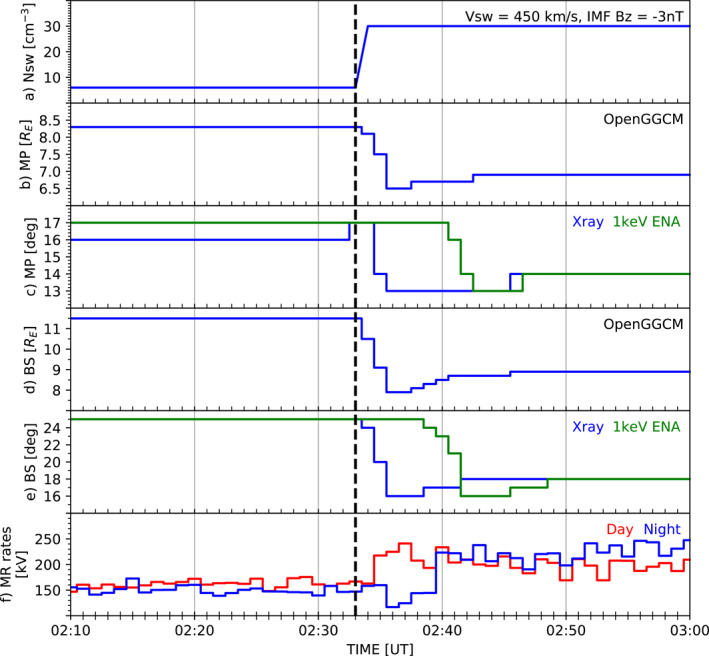
Dayside boundary motion and reconnection rates during the sudden solar wind pressure enhancement. The same format is used as in Figure 6.

To obtain positions of the subsolar magnetopause and the subsolar bow shock in the OpenGGCM model, we choose the locations of maximum and minimum plasma density gradients along the Sun‐Earth line, respectively (Collier & Connor, 2018; García & Hughes, 2007). There are other boundary selection methods used in the MHD modeling community, for example, tracking solar wind plasma streamlines (Palmroth et al., 2003) and taking maximum current densities (Samsonov et al., 2016). As discussed in Sections 2.2 and 2.3, soft X‐ray and ENA signals are closely related to the solar wind plasma density. Thus, the boundaries traced from the plasma density gradients are more reliable estimators of the boundaries traced from the soft X‐ray and ENA images.

To obtain dayside and nightside reconnection rates from the MHD model, we follow the method of Connor et al. (2014). We first obtain the net ionospheric plasma flows across the open‐closed field line boundary (OCB) in the moving reference frame of the OCB. Then, we calculate the dayside and nightside reconnection rates by taking the total electric potentials along the dayside and nightside portions of the OCB. This technique has been widely used by previous studies (e.g., Blanchard et al., 1997; de La Beaujardiere et al., 1991; Hubert et al., 2006) that employed observations of ionospheric plasma convection and auroral oval images. Connor et al. (2014) explain details of how to apply the technique to the MHD simulation.

During the southward IMF turning event, the Earthward motion of the magnetopause and bow shock in Figures 6b and 6d are clearly captured by the soft X‐ray and ENA imagers as seen in Figures 6c and 6e although the ENA images show a delayed response due to time‐of‐flight effects. The modeled dayside and nightside reconnection rates in Figure 6f match well with our general understanding of solar wind‐magnetosphere interaction during southward IMF turning (Milan et al., 2017 and references therein). Before the IMF turning, the dayside reconnection rate is comparable to the nightside one, indicating a steady‐state magnetosphere. After the southward IMF turning, the potential associated with dayside reconnection increases from ∼45 kV at ∼3:40 UT up to 275 kV at ∼3:56 UT within ∼16 min following the IMF change. The potential associated with nightside reconnection responds later around 4:30 UT and reaches ∼225 kV around 4:56 UT. After 5:05 UT, both dayside and nightside reconnection reach equilibrium, indicating that the magnetosphere enters a new steady state. The steady‐state reconnection rates are ∼170 kV during southward IMF, greater than ∼45 kV during northward IMF, indicating more active day‐night reconnection and stronger magnetospheric convection during southward IMF. Figures 6b, 6c, and 6f show a close relation between the magnetopause motion and the global‐scale dayside reconnection rate. The subsolar magnetopause rapidly erodes Earthward from 03:40 to 03:55 UT when the dayside reconnection rate quickly increases. The erosion slows down until 04:50 UT as the dayside reconnection rate slowly diminishes to ∼175 kV but is still higher than the nightside reconnection rate. The subsolar magnetopause location remains almost stationary after 04:50 UT when both dayside and nightside rates stay almost constant at ∼170 kV.

During the sudden P _sw enhancement event, the dayside boundaries in the OpenGGCM model move abruptly Earthward right after the pressure jump and then rebound slightly sunward (see Figures 7b and 7d) as reported in previous studies of P _sw impact on the magnetosphere (Němeček et al., 2011; Ridley et al., 2006; Samsonov et al., 2007, 2015). Both the model X‐ray and ENA imagers track this boundary motion (see Figures 7c and 7e) with a delayed response in the ENA results. Figure 7f shows intensification of both dayside and nightside reconnection rates after the P _sw jump, agreeing well with the observations (Boudouridis et al., 2003, 2004, 2007, 2011; Boudouridis, Lyons, et al., 2008; Boudouridis, Zesta, et al., 2008; Hubert et al., 2006, 2009; Lyons et al., 2000; Zesta et al., 2000) and other modeling results (Connor et al., 2014; Ober et al., 2006, 2007). The solar wind pressure in Figure 7a increases abruptly at ∼2:33 UT due to the density increase from 6 to 30 cm⁻³. Before the P _sw impact, both dayside and nightside reconnection rates are comparable at ∼160 kV, indicating a steady‐state magnetosphere. The dayside magnetosphere responds quickly to the P _sw jump. The dayside reconnection rate sharply increases from 160 kV at 2:33 UT to ∼240 kV at 02:37 UT, that is, within 4 min after the pressure impact. The nightside magnetosphere reacts to the P _sw jump a few minutes later at ∼02:40 UT with an abrupt enhancement in the nightside reconnection rate from ∼140 to ∼220 kV. The nightside rate remains elevated and exceeds the dayside reconnection rate after 2:40 UT. This simulation ends before the magnetosphere reaches a new steady state. The sudden Earthward motion of the subsolar magnetopause occurs with the rapidly increasing reconnection rate during 02:33–02:37 UT (see Figures 7b and 7f). Although the ENA imager has difficulty catching the exact timing, both soft X‐ray and ENA imagers trace this rapid magnetopause motion (see Figure 7c) and suggest a rapid increase in dayside reconnection. Note that pressure balance between solar wind and magnetosphere is another factor that determines magnetopause location (e.g., Gonzalez & Parker, 2015; Kivelson and Russell, 1995). The magnetopause motion observed from the soft X‐ray and ENA imagers can shed light on the relative importance of pressure variations and reconnection on the magnetopause location.

Our modeling analysis shows a close relation between the magnetopause erosion and dayside reconnection as suggested by previous studies (e.g., Dungey, 1961; Holzer & Slavin, 1978; Pudovkin et al., 1998; Semenov et al., 2002; Tsyganenko & Sibeck, 1994). In spite of the low angular resolution tested in this study, the fast and slow magnetopause motion is captured by the soft X‐ray images almost immediately after the IMF and P _sw impacts and by the ENA images with 5–16 min of delay due to the time‐of‐flight effect, as seen in Figures 6c and 7c. With good image resolution and an advanced magnetopause tracking tool (e.g., Collier & Connor, 2018; Jorgensen, Sun, Wang, Dai, Sembay, Wei, et al., 2019; Jorgensen, Sun, Wang, Dai, Sembay, Zheng, et al., 2019; Sun et al., 2020), both soft X‐ray and ENA imagers can track the magnetopause motion under various solar wind conditions and thus reveal the global dayside reconnection mode. However, for the ENA imager, a sophisticated time‐of‐flight analysis is needed to examine the exact timing of solar wind‐magnetopause interaction.

3.3. Current Technologies and Background Signals

In the previous sections, the soft X‐ray and ENA imagers have been assumed to provide 1° angular resolution with 1 min cadence. Additionally, no other sources of soft X‐ray and ENAs were considered except the near‐Earth charge exchange signals. This section discusses the status of current technologies and background signals that may complicate the image analysis.

X‐ray instruments on previous Astrophysics missions have shown a very fine angular resolution, much less than 1°. The ROSAT mission provides ∼5″ angular resolution (i.e., 0.001°) for the 0.1–2 keV X‐ray energy band (Trümper, 1982). The XMM‐Newton mirrors have an ∼8″ angular resolution (i.e., 0.002°) for the 0.1–12 keV X‐ray band (Jansen et al., 2001). However, these X‐ray instruments were designed to provide a narrow field of view which is ideal for observing astronomical objects but not appropriate for imaging the entire magnetosheath. For a wide field‐of‐view, the Soft X‐ray Imager (SXI) on SMILE uses lightweight micropore optics that provide 8–9′ angular resolution (i.e., ∼0.1°) for the 0.15–2.5 keV energy band (Branduardi‐Raymont et al., 2018). However, due to the low abundance of highly charged ions in the solar wind, soft X‐ray signals may not be strong enough to achieve this high angular resolution on a routine basis. It is likely that X‐ray counts from multiple pixels will be combined and/or those counts will be accumulated for longer time intervals to obtain good signal‐to‐noise ratios. SMILE SXI is expected to achieve at least 1.5° angular resolution near the dayside magnetopause during solar wind flux of 4.9 × 10⁸  cm⁻²s⁻¹ with 5 min cadence (requirement) and 0.4° angular resolution near the dayside magnetopause during solar wind flux of 1.6 × 10⁹  cm⁻²s⁻¹ with 1 min cadence (goal). The 1° angular resolution and 1 min cadence used in our modeling are within the range of SMILE SXI capability.

The magnetosheath is not the only region that emits soft X‐rays. Planets, stars, galaxies, and diffuse astronomical backgrounds (e.g., unresolvable faint stars and galaxies, and the interplanetary and interstellar medium) also contribute to soft X‐rays. In addition to these unwanted signals, light diffraction occurs in an instrument and blurs soft X‐ray images in a certain pattern represented by an instrument‐unique point spread function. Finally, the instrument's own glow, referred to as particle background, and Poisson noise also appear in raw soft X‐ray images. Sibeck et al. (2018) showed that even after taking into account these factors, the magnetosheath is readily distinguishable in soft X‐rays. The clean magnetosheath images in our paper can be considered as calibrated images after the removal of well‐known astronomical background (e.g., Snowden et al., 1995, 1997), removal of particle background estimated during telescope closure periods (e.g., Carter & Read, 2007), and if needed, deconvolution of images using an instrument's point spread function.

ENA instruments on previous Heliophysics missions have shown a larger angular resolution than 1°. The three ENA cameras on IMAGE provide 4°–8° angular resolution, measuring low ENAs (0.01–1 keV), medium ENAs (1–50 keV), and high ENAs (20–500 keV) (Burch, 2000). TWINS ENA instruments provide 4° angular resolution for 10–100 keV and coarser angular resolution for 1–10 keV (Goldstein & McComas, 2018), while the post‐processing image technique (e.g., the statistical smoothing technique of Valek et al., 2014) can provide 1° × 1 ° resolution. The two ENA cameras on IBEX have 3.5°–7° angular resolution, measuring low ENAs (0.01–2 keV) and high ENAs (0.54–6 keV) (Funsten et al., 2009; Fuselier et al., 2009). Recently, Westlake et al. (2016) suggested a new concept for a low‐ENA instrument that provides less than 2° angular resolution for the 0.5–20 keV energy range with high sensitivity ($\ge {10}^{-3}{\text{cm}}^2\text{sr/pixcel}$) and high energy resolution $\left(\frac{\mathrm{\Delta }E}{E}=0.2\text{at}1\text{keV}\right)$. Its cadence depends on multiple factors (e.g., the spacecraft spin period, its field of view, number of energy channels, and signal strength) and can be adjusted to meet science requirements during a mission concept study. For example, the IBEX Hi‐ENA camera covers all six energy channels every 3 min by switching an energy channel every two 15‐s spacecraft spins (Funsten et al., 2009). The magnetosheath ENA count rates are several 1,000 cm⁻²s⁻¹sr⁻¹  keV⁻¹ for the 0.9–1.5 keV energy band of IBEX Hi‐ENA camera (Petrinec et al., 2011), suggesting that signals are strong enough to provide 1 min cadence. With the technological advancement of Westlake et al. (2016) and well‐thought‐out mission planning, the 1° angular resolution and 1 min cadence used in our study may be achieved in the near future.

The Earth's magnetosheath and inner magnetosphere are the strongest ENA sources in the sky. Other sky sources that produce considerable ENAs at ∼1 keV include the heliosphere, local interstellar medium (LISM), and ubiquitous local background (Gali et al., 2014). Previous studies (Fuselier et al., 2010; Petrinec et al., 2011) reported magnetosheath ENA signals of 10³–10⁴  cm⁻²s⁻¹sr⁻¹  keV⁻¹ at ∼1 keV. By contrast, ENA signals from the heliosphere (McComas et al., 2009) and LISM (Gali et al., 2014) can be as large as a few 100 cm⁻²s⁻¹sr⁻¹  keV⁻¹, that is, 1–2 orders of magnitude weaker than the magnetosheath ENA signals. Additionally, their ENA distributions on the sky are relatively well known (e.g.,Gali et al., 2014; McComas et al., 2009), and thus can be easily removed from the raw ENA images. Ubiquitous background is local, and its origin is unclear. Its average count rate is nearly zero at 1 keV and, at lower energies, can be comparable to the average heliospheric signal, that is, much lower than the magnetosheath signal (Gali et al., 2014). Due to the strong magnetosheath ENA signals, our modeled images are expected to be very close to the raw ENA images obtained from a spacecraft.

It is worth mentioning that the time‐of‐flight effect of ENAs can complicate image analysis when dayside boundary motions are complex and/or when the energy bandwidth of an ENA camera is broad. Our study considers simple solar wind conditions and a perfect ENA instrument that observes only 1 keV ENAs. Even for these idealized cases, ENA images show 5–16 min of delay in tracking the dayside boundaries. The delayed response time is not fixed although only 1 keV ENAs are considered, because they can be created anywhere along a line‐of‐sight, traveling different distances before arriving at the virtual spacecraft. In reality, solar wind and IMF conditions vary, and the ENA instrument observes a range of ENA energies, for example, 0.9–1.5 keV for the IBEX Hi‐ENA energy channel #3. This may add complexity in the ENA imaging analysis, which needs more rigorous future study.

Overall, the 1° angular resolution and 1 min cadence used in our modeling studies are achievable with the current soft X‐ray technologies and are soon to be achievable with a recent development of a new low‐ENA imager concept. Sophisticated image processing techniques (e.g., Petrinec et al., 2011; Valek et al., 2014) can also compensate the instrumental limitation, further improving temporal and spatial resolution of images. Near‐Earth Soft X‐ray and ENA signals are strong and distinguishable from the other celestial sources. Thus, the dayside reconnection study suggested in this paper would be feasible with the soft X‐ray and ENA images of the magnetosheath. However, the impact of delayed ENA response on the reconnection analysis needs to be carefully investigated when planning a future ENA mission.

4. Other Science Topics

The model results show that both soft X‐ray and ENA images readily track earthward dayside boundary motion and thus reveal the enhancement of global‐scale magnetopause reconnection rate. In addition to reconnection studies, both imagers can be used to estimate the exosphere's density far from the Earth and, in combination of other observations, investigate global solar wind‐magnetosphere‐ionosphere interaction. This section describes how soft X‐ray and ENA images of dayside geospace advance our knowledge on these science topics.

4.1. Dayside Outer Exosphere

The Earth's exosphere is the outermost layer of our atmosphere that ranges from the exobase at ∼500 km altitude up to the distance exceeding even the lunar orbit, ∼60 R _E from Earth (Baliukin et al., 2019). Atomic hydrogen becomes the dominant species above an altitude of ∼1,500 km. The exosphere gains and loses hydrogen atoms as a result of the Sun‐solar wind‐magnetosphere‐upper atmosphere interaction via physical processes like atmospheric upwelling, photoionization, and charge‐exchange between neutrals and plasmas (Hodges, 1994 and references therein). For example, exospheric neutrals play an important role in storm‐time magnetospheric dynamics because charge exchange with exospheric neutrals represents a major energy loss mechanism for ring current ions in our magnetosphere (Ilie et al., 2013). Study of the hydrogen density distribution and its variation is key to understanding the past, present, and future of the Earth's exosphere, its role in Sun‐Earth interactions, and the relevance of its physical drivers to atmospheric escape and evolution at other planets.

Due to the lack of in situ exospheric density measurements, scientists have studied the exosphere using geocoronal observations, the remote sensing observations of solar Lyman‐alpha photons that are resonantly scattered by the Earth's exospheric hydrogen atoms. Several spacecraft missions like IMAGE and TWINS provide extensive geocorona observations from various vantage points, covering the exosphere up to ∼8R _E geocentric distance (Bailey & Gruntman et al., 2011; Østgaard et al., 2003; Zoennchen et al., 2011, 2013, 2015, 2017). However, there are only a few dayside geocoronal observations that go beyond 8 R _E (e.g.,Baliukin et al., 2019; Kameda et al., 2017) because the interplanetary Lyman‐alpha background dominates at great distances, and because views sunward from an observing spacecraft are often contaminated by the Lyman‐alpha photons coming directly from the Sun, that is, not the ones scattered by exospheric neutrals, due to the close proximity of instrument's look direction to the Sun.

The soft X‐ray and ENA images of the magnetosheath enable us to infer neutral densities within the dayside exosphere. Charge exchange between neutrals and plasmas produces soft X‐rays and ENAs, indicating that the neutral density is a parameter controlling both the soft X‐ray and ENA signals as indicated by Equations 2 and 4. Higher neutral densities lead to stronger X‐ray and ENA signals. If plasma parameters are known from either an empirical magnetosheath model, a global MHD model, or in‐situ spacecraft observations, we can extract dayside exospheric densities by removing the plasma contribution to the X‐ray and ENA observations. Fuselier et al. (2010, 2020) and Connor and Carter (2019) presented good examples of these inversion techniques using IBEX ENA observations and XMM‐Newton soft X‐ray observations, respectively.

Long hours of wide‐field‐of‐view imaging of the dayside magnetosheath will enable researchers to extract spatial and temporal variations of dayside neutral density, improving current empirical exosphere density models (e.g., Zoennchen et al., 2011, 2013, 2015) that were based primarily on global Lyman‐alpha observations with a severe lack of dayside data. If enough data are accumulated, researchers can also investigate how the dayside outer atmosphere responds to space weather. Several studies report diverse exospheric density variations below 8 R _E geocentric distance for differing solar irradiance conditions (e.g., Waldrop & Paxton, 2013; Zoenncheon et al., 2015), and during the course of geomagnetic storms (e.g., Cucho‐Padin & Waldrop, 2019; Qin et al., 2017; Zoennchen et al., 2017). However, the exospheric density behavior above 8 R _E remains unclear mainly due to a lack of observations. Soft X‐ray and ENA imaging missions can provide an invaluable data source for the dayside, outer exosphere studies.

Figure 8 compares the dayside exospheric neutral densities along the Sun ‐ Earth line, obtained from the previous literatures. Green, blue, and black lines are obtained from the exosphere density models based on the geocorona observations of TWINS (Zoennchen et al., 2015), SOHO (Baliukin et al., 2019), and Proximate Object Close Flyby with Optical Navigation (PROCYON; Furnase et al., 2015) (Kameda et al., 2017), respectively. Red and magenta lines show the ranges of exospheric neutral densities at 10R _E subsolar location, estimated from the XMM‐Newton soft X‐ray data (Connor & Carter, 2019) and the IBEX ENA data (Fuselier et al., 2009, 2020). The cyan line is obtained from Equation 1 in this study. Green solid and dashed lines show the dayside neutral densities during solar minimum and maximum, suggesting strong impact of solar activity on the exosphere density. Quite a large density discrepancy appears among the previous literatures. For example, the neutral density at 10R _E subsolar location ranges from 4 to 59 cm⁻³, showing over 1300% relative difference. However, the datasets used in these papers cover different dayside exosphere regions under various solar irradiance and solar wind conditions. Additionally, their data are only several hours to several days long. Long‐term observations of global dayside exosphere are crucial for accurate neutral density estimates.

Figure 8.

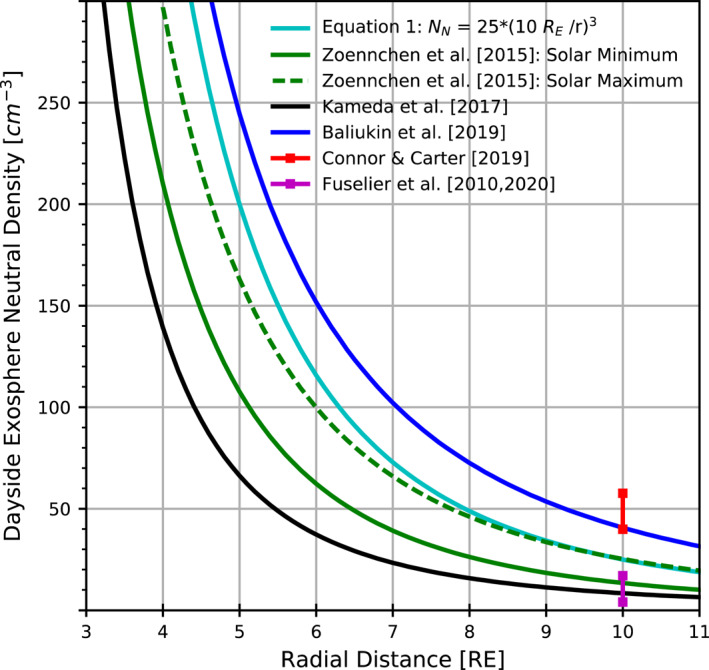
Comparison of the dayside exospheric neutral densities along the Sun‐Earth line, obtained from the previous literatures and Equation 1 in this study.

The SMILE and LEXI missions will be exemplary observers for studies of the Earth's outer exosphere. SMILE will provide wide field‐of‐view soft X‐ray images of the dayside magnetosheath continuously, more than 40 h per orbit for 3 years of its mission period. LEXI will also send continuous, wide‐FOV soft X‐ray images of the Earth's magnetosheath from the lunar surface for its two‐week mission period. Using the inversion techniques introduced in Fuselier et al. (2010) and Connor and Carter (2019), we can estimate the time dependence of the outer exospheric density near the dayside magnetosheath from the soft X‐ray images. Previous literatures have been reported various time scales of exospheric density changes, ranging from solar cycle (Baliukin et al., 2019; Waldrop & Paxton, 2013; Zoenncheon et al., 2015) to 28‐days solar rotation period (Zoenncheon et al., 2015), both of which are related to solar irradiation, and then down to 4–24 h during a geomagnetic storm (Bailey & Gruntzmann, 2013; Cucho‐Padin & Waldrop, 2019; Zoenncheon et al., 2017). Analysis of LEXI and SMILE images can improve our understanding of the outer exosphere and its spatiotemporal response to solar irradiance and geomagnetic storms.

4.2. Global Solar Wind‐Magnetosphere‐Ionosphere Interaction

As discussed above, a stand‐alone soft X‐ray or ENA imager can advance our understanding of magnetopause reconnection and the dayside exosphere. The availability of dayside images can also create great synergy in collaboration with other imagers on board the same spacecraft and with ground observatories. A high‐ENA imager like those on IMAGE and TWINS can observe ring current dynamics by capturing neutrals up to several hundred keV that are produced from charge exchange between ring current ions and exospheric neutrals. By placing the high‐ENA imager and the dayside soft X‐ray or low‐ENA imager on the same spacecraft, we can trace the energy flow from the bow shock to the inner magnetosphere. A Far Ultra Violet (FUV) or Ultra Violet (UV) imager, such as the Polar UVI instrument (Brittnacher et al., 1997) and the SMILE UVI instrument (Branduardi‐Raymont et al., 2018), can capture spatiotemporal variations of auroral precipitation over the entire high‐latitude region, and if installed with the soft X‐ray/low‐ENA imager and the high‐ENA imager, can provide important information about magnetosphere‐ionosphere coupling. Additionally, a global aurora map obtained from the FUV/UV imager can be used as an input for upper atmospheric models such as CTIPe, TIEGCM, and GTIM, helping us to investigate the magnetosphere‐ionosphere‐thermosphere as a whole system. Finally, ground observatories like the SuperDARN radars are a natural partner. They can measure fast ionospheric plasma flows resulting from the magnetic reconnection and, in conjunction with the open/closed field line boundaries obtained from auroral imagers, can extract the dayside and nightside reconnection rates as presented in Figures 6 and 7.

Figures 9 and 10 show the modeled images taken by a sample spacecraft mission with multiple imagers on board during the southward IMF turning event. We explore two vantage points by locating the spacecraft at (X _gse, Y _gse, Z _gse)=(0, 30, 0)R _E for Figure 9 and at (0, 0, 30)R _E for Figure 10, providing side‐ and polar‐views of the Earth's magnetosphere‐ionosphere system. From top to bottom are solar wind conditions, dayside plasma densities, nightside plasma velocities, dayside soft X‐ray images, dayside low‐ENA images, nightside high‐ENA images, and global auroral images. The plasma density and velocity plots show the noon‐midnight plane for Figure 9 and the equatorial plane for Figure 10, covering the same dayside and nightside regions seen in the soft X‐ray and ENA images. The four sets of images correspond to the times indicated by the vertical red lines in the top panels. We select 1  and 10 keV hydrogen atoms for the dayside and nightside ENA images, respectively, using the method described in Section 2.3. The auroral precipitation is obtained from the OpenGGCM MHD model using the empirical relations of diffuse electron aurora (Connor et al., 2016). A Movie S3 is added to show details of the side and polar view images during the southward IMF turning.

Figure 9.

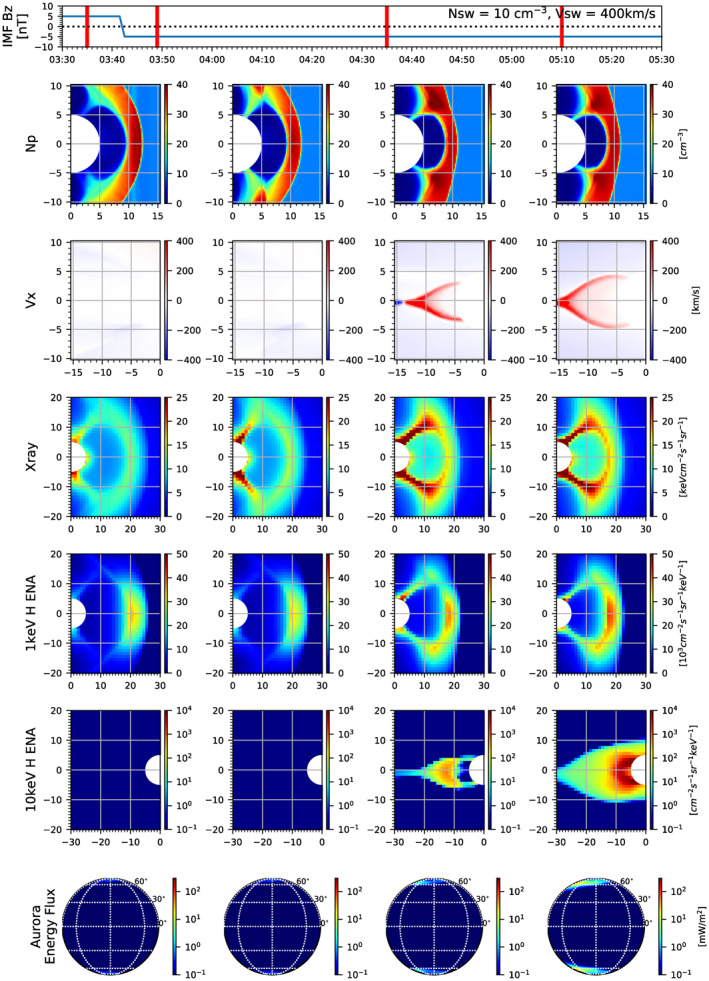
Side‐view images during the southward IMF turning event, obtained from a virtual spacecraft at (X _gse, Y _gse, Z _gse)=(0, 30R _E, 0). (top row) solar wind/IMF conditions versus time, (2nd row) dayside plasma density, (3rd row) nightside plasma velocity, (4th row) dayside soft X‐ray images, (5th row) dayside 1 keV ENA images, (6th row) nightside 10 keV ENA images, (last row) global aurora images. The red vertical bars on the top panel indicate times when the images are taken. The dayside and nightside images in 4‐6th rows cover the same regions of the dayside plasma density plot and nightside plasma velocity plot, respectively. The X and Y axes in the 2nd–3rd rows are X _gse and Z _gse in R _E, while the X and Y axes in the 4–6th rows are azimuth and elevation angles in degree, respectively. The bottom row shows the Earth's ionosphere with magnetic longitude and latitude lines (white dotted lines).

Figure 10.

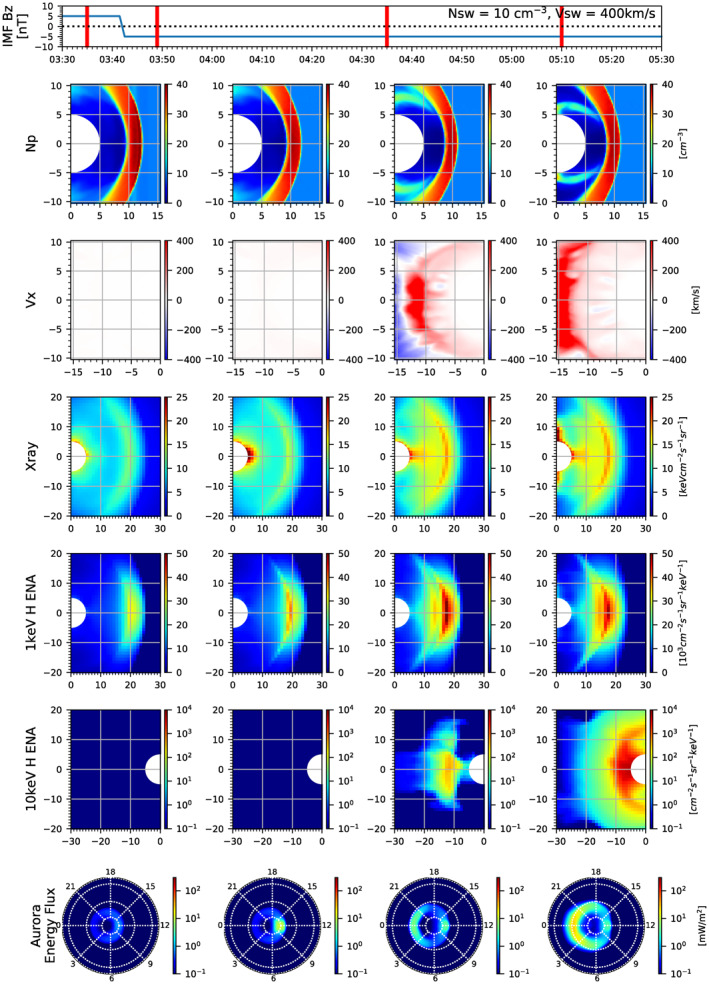
Polar‐view images during the southward IMF turning event, obtained from a virtual spacecraft at (X _gse, Y _gse, Z _gse)=(0, 0, 30R _E) in a similar format to Figure 9. The X and Y axes in the 2nd–3rd rows are X _gse and Y _gse in R _E, while the X and Y axes in the 4–6th rows are elevation and azimuth angles in degree. The bottom row shows the Earth's ionosphere with white dotted lines of magnetic local time (MLT) and magnetic latitude (MLAT). The latitudinal lines from pole to equator represents 80°, 60°, 30°, and 0° MLAT.

Figures 9 and 10 demonstrate that this virtual spacecraft mission can provide global views of the solar wind‐magnetosphere‐ionosphere interaction. As discussed in Section 3.1, the side‐view images of soft X‐ray and 1 keV ENA in Figure 9 show the Earthward motion of the bow shock and the magnetopause as observed in the plasma density plot after the IMF turning. The polar‐view images in Figure 10 also catch this inward motion of the magnetopause by showing that the locations of maximum signals along the Sun‐Earth line move Earthward. The mid‐altitude cusp also appears as a bright region near (X, Y) = (−3–3°, 5–10°) in the polar‐view images of soft X‐ray and 1 keV ENA. Unlike the soft X‐ray signals, the cusp ENA signals are weak probably because most of the ENAs produced at the mid‐altitude cusp head toward the ionosphere (the same direction as the incident solar wind plasma) and thus less ENAs reach the spacecraft location far above the north pole.

Once the prolonged southward IMF conditions trigger nightside reconnection, fast sunward plasma flows occur in the magnetotail and fill the inner magnetosphere with energetic particles, as seen in the plots of plasma velocity and 10 keV H ENAs in Figures 9 and 10. The 10 keV ENA images catch not only the sunward plasma flow but also the population of energetic ions deep in the inner magnetosphere. Although not shown in this figure, the high‐ENA imager is also possible to detect substorm‐related bursty bulk flows as reported in Keesee et al. (2012) with the TWINS ENA observations. Using multi‐channel energy bins of the high‐ENA imager, we can explore energy dependent plasma behavior as a result of nightside reconnection. Note that the stand‐alone OpenGGCM model used in this study does not fully address ring current dynamics. The global magnetosphere MHD model coupled with a ring current model (e.g., OpenGGCM‐RCM in Cramer et al., 2017) is more appropriate for the analysis of multi‐channel high ENA images, which is left for future work.

The auroral images project global magnetospheric activities on the ionosphere through particle precipitation. The aurora brightens near local noon soon after the IMF turning and then later, throughout the nightside region, revealing dynamic activity in the day‐night magnetosphere. As expected, the polar views provide optimal images of the global aurora precipitation. Although missing the dayside auroral enhancements, side views still catch southward expansions of the nightside aurora oval.

5. Summary and Concluding Remarks

We introduced two innovative imaging techniques that use soft X‐rays and ENAs to visualize the Earth's dayside magnetosphere, and discussed their utility in investigating the global solar wind‐magnetosphere‐upper atmosphere interactions. We simulated the soft X‐ray and ENA images that might be observed by a virtual spacecraft at optimal vantage points using the OpenGGCM global MHD model and a simple exospheric neutral density model. Two interesting solar wind events were explored: (1) a southward IMF turning and (2) a step function enhancement in the solar wind dynamic pressure. The magnetosheath and cusps emit strong soft X‐ray and ENA signals, revealing the bow shock and magnetopause locations. Using a simple boundary tracing algorithm, we extracted the Earthward motion of the bow shock and the magnetopause directly from the dayside images as observed in the MHD model after the southward IMF turning and the P _sw increase. We also compared the dayside and nightside reconnection rates obtained from the OpenGGCM model with the magnetopause motion. The rapid increase of dayside reconnection rate corresponds to fast magnetopause erosion, while the balance between dayside and nightside rates corresponds to almost no magnetopause motion. This indicates that the soft X‐ray and ENA images can be used to understand global‐scale magnetopause reconnection modes. However, due to the time‐of‐flight effect, the ENA images need sophisticated data analysis techniques to understand the exact timing of solar wind‐dayside magnetosphere interaction.

We also discussed other science topics that can be addressed with the soft X‐ray and ENA images. Wide‐field‐of‐view images of the dayside magnetosheath can reveal the distribution of dayside outer exosphere densities and its response to space weather events. This will help to understand how space environments affect the whole evolutionary history of the terrestrial atmosphere. Additionally, we demonstrated that a virtual spacecraft mission with multiple imagers on board can provide a complete picture of the solar wind energy flow from the bow shock to the magnetosphere and to the ionosphere. A dayside imager (either soft X‐ray or low‐ENA) catches the Earthward magnetopause motion caused by the dayside reconnection. A high‐ENA imager catches the fast‐sunward plasma flow in the magnetotail and subsequent filling of high‐energy plasmas in the inner magnetosphere, both of which result from nightside reconnection. An FUV or UV auroral imager observes both dayside and nightside aurora brightening, revealing the connection between the magnetosphere and the ionosphere.

We note that recent spacecraft missions like Cluster, THEMIS, and MMS have addressed micro‐scale phenomena. The imaging mission suggested in this study, on the other hand, addresses global‐scale dynamics. The upcoming SMILE and LEXI spacecraft will be exemplary missions to reveal physics of global dayside interaction through the wide field‐of‐view soft X‐ray images of the Earth's magnetosheath. In addition to a soft X‐ray imager, SMILE will have a light ion analyzer, a magnetometer, and an UV auroral imager. It will not only measure the plasma and magnetic field conditions in near‐Earth space environment but also observe the magnetosphere‐ionosphere interaction. When SMILE is in the upstream region, we can obtain more accurate solar wind conditions without depending on the solar wind monitors at the Lagrangian‐1 point. In collaboration with concurrent spacecraft missions and ground observatories, SMILE and LEXI can investigate global and local dynamics of our geospace system.

Supporting information

Supporting Information S1

Connor, H. K. , Sibeck, D. G. , Collier, M. R. , Baliukin, I. I. , Branduardi‐Raymont, G. , Brandt, P. C. , et al. (2021). Soft X‐ray and ENA imaging of the Earth's dayside magnetosphere. Journal of Geophysical Research: Space Physics, 126, e2020JA028816. 10.1029/2020JA028816

Data Availability Statement

Model results used in this study can be downloaded from the following website: https://sites.google.com/a/alaska.edu/hkconnor/research/data