Abstract
COVID-19, which emerged in December 2019, has affected the entire world. Therefore, COVID-19 has been a subject of research in various disciplines, especially in the field of health. One of these studies was the report made by the Deep Knowledge Group (DKG) consortium in which safe regions for COVID-19 were determined. In the report, the main criteria of quarantine efficiency, government efficiency of risk management, monitoring and detection, health readiness, regional resilience, and emergency preparedness are used in the evaluation of countries and regions (alternatives). As the data and research structure used in this report are based on multi-criteria, the purpose of this study is to evaluate and analyse the safety levels of 100 regions in the world in terms of COVID-19 using Technique for Order Performance by Similarity to Ideal Solution (TOPSIS), Vise Kriterijumsa Optimizacija I Kompromisno Resenje (VIKOR) and Complex Proportional Assessment (COPRAS) methods. The data and information required in the methods were obtained from a report prepared by the DKG. The results of the methods were compared with the ranking results presented in a report of the DKG. Accordingly, it has been observed that the method that provides the closest results to the results of the report is the COPRAS method, and the method that gives the most distant results is the VIKOR method.
Keywords: COVID-19, Regional safety, Multi-criteria decision making, TOPSIS, VIKOR, COPRAS
Introduction
Coronavirus, or “COVID-19”, emerged on 1 December 2019 in Wuhan, the capital of the Hubei region in China. This virus started to spread rapidly to China and other parts of the world at the beginning of 2020 [1], and the number of infected patients has increased exponentially [2]. Because the virus is highly contagious [3], effective treatment is urgently needed [4]. The effects of the novel coronavirus or the possible social consequences of this threat remain uncertain, and there is no vaccine yet [5]. As of 7 November 2020, 48,786,440 people have been diagnosed with COVID-19 in 219 regions worldwide, and 1,204,028 deaths have been reported [6]. The virus, which is spreading rapidly and affecting countries deeply, is the subject of numerous studies and is discussed in different disciplines.
One of the studies on COVID-19 was conducted by the DKG. The results of the research were presented in the “COVID-19 Regional Safety Assessment: Big Data Analysis of 200 Countries and Regions COVID-19 Safety Ranking and Risk Assessment” report [7]. The DKG report serves as a resource for governments to optimise security and stability during and after the pandemic. The DKG report enables governments to determine the best possible action plans to promote the health and economic well-being of the people in each region and reverse the damage indirectly caused by COVID-19 [7]. Accordingly, the report ranks 200 countries and regions using six main criteria. It was observed that multi-criteria decision-making (MCDM) methods can be applied to rank these countries and regions, and analyse these rankings, using the data presented in the DKG report. It is noted here that in the context of this study, the word “region” is used instead of “country”.
MCDM is a technique designed to investigate several alternatives within multiple criteria and conflicting goals [8] and is used to solve complex problems [9] using different methods. These methods enable decision-makers to make a more logical and scientifically defensible decision by using a technical methodology employing technical knowledge [10]. Each method may produce equivalent results or different results. In this way, MCDM methods aid in solving a decision problem that often requires considering different perspectives [11].
This study has two main aims. The first is to show that 100 regions presented in the DKG report can be solved using different MCDM methods. The second is to present different perspectives by diversifying the results about the rankings of the regions according to safety levels presented in the DKG report. In this study, region rankings were made using TOPSIS, VIKOR, and COPRAS methods to evaluate safe regions during the COVID-19 process. To the best of our knowledge, there have been no previous studies on the utilisation of MCDM techniques to determine safe regions within the scope of COVID-19.
The contributions of the study can be summarised as follows:
-
•
Using the same data, multiple ranking alternatives within the same level are obtained, and these ranking alternatives will allow decision-makers to make different evaluations in terms of COVID-19.
-
•
The measures taken by the upper-ranked regions in the fight against COVID-19 will guide the lower-ranked regions.
-
•
The ranking results presented in this study will serve as a helpful resource to ensure stability and safety during and post-pandemic times.
Information about the research conducted by the DKG is provided in the second section of the paper. The third section presents the research methodology and information about the MCDM techniques to be used in this context. In the fourth section, we examine and evaluate the analyses. Finally, a general conclusion and further study suggestions are provided.
COVID-19 Regional Safety Assessment report
DKG is an organisation that includes commercial enterprises and companies together with non-governmental organisations. It works in the fields of artificial intelligence, investment technologies, financial technologies, and pharmaceuticals. In the report, published by the DKG on 3 June 2020, comprehensive research on COVID-19 in 200 countries and regions was conducted, and the regions were ranked under the title of “COVID-19 Regional Safety Assessment: Big Data Analysis of 200 Countries and Regions COVID-19 Safety Ranking and Risk Assessment” [7]. In the relevant research, 130 qualitative (exit strategy plan, state of emergency readiness, local vaccine development attempts, export-oriented region and other parameters) and quantitative (population density, number of cases, length of quarantine, literacy rate, number of hospital beds, number of doctors, and other parameters) parameters were used, and 200 regions were grouped into four different levels (Levels 1 to 4) according to the score value in terms of safe region. Level 1 consists of 20 regions with extremely high regional safety levels. Level 2 consists of 20 regions that do not have the same levels of security as the regions in Level 1 but score well in terms of regional safety. Level 3 consisted of 60 regions with fewer positive scores. The 100 regions with the least number of points constituted Level 4. The relevant levels and regions are listed in Table 1 .
Table 1.
Regions by level [7].
| Level type | Regions |
|---|---|
| Level 1 | Australia, Austria, Canada, China, Denmark, Germany, Hong Kong, Hungary, Israel, Japan, New Zealand, Norway, Saudi Arabia, Singapore, South Korea, Switzerland, Taiwan, The Netherlands, United Arab Emirates, Vietnam. |
| Level 2 | Bahrain, Croatia, Cyprus, Estonia, Finland, Georgia, Greece, Iceland, Ireland, Kuwait, Latvia, Liechtenstein, Lithuania, Luxembourg, Malaysia, Oman, Poland, Qatar, Slovenia, Turkey. |
| Level 3 | Albania, Algeria, Andorra, Argentina, Armenia, Azerbaijan, Bahamas, Bangladesh, Belarus, Belgium, Bosnia and Herzegovina, Brazil, Bulgaria, Cambodia, Cayman Islands, Chile, Czech Republic, Ecuador, Egypt, France, Gibraltar, Greenland, Honduras, India, Indonesia, Iran, Italy, Jordan, Kazakhstan, Laos, Lebanon, Malta, Mexico, Moldova, Monaco, Mongolia, Montenegro, Morocco, Myanmar, Panama, Paraguay, Peru, Philippines, Portugal, Romania, Russia, San Marino, Serbia, Slovak Republic, South Africa, Spain, Sri Lanka, Sweden, Thailand, Tunisia, Ukraine, United Kingdom, United States, Uruguay, Vatican City. |
| Level 4 | Afghanistan, Angola, Antigua and Barbuda, Aruba, Barbados, Belize, Benin, Bermuda, Bermuda, Bhutan, Bolivia, Botswana, British Virgin Islands, Burkina Faso, Burundi, Cabo Verde, Cameroon, Central African Republic, Chad, Colombia, Comoros, Congo Rep., Costa Rica, Côte d’Ivoire, Cuba, Curaçao, Djibouti, Dominica, Dominican Republic, El Salvador, Equatorial Guinea, Eritrea, Ethiopia, Fiji, French Polynesia, Gabon, Gambia, Ghana, Grenada, Guam, Guatemala, Guinea, Guinea-Bissau, Guyana, Haiti, Iraq, Isle of Man, Jamaica, Kenya, Kyrgyzstan, Lesotho, Liberia, Libya, Madagascar, Malawi, Maldives, Mali, Mauritania, Mauritius, Micronesia Fed. Sts., Mozambique, Namibia, Nepal, New Caledonia, Nicaragua, Niger, Nigeria, North Korea, North Macedonia, Pakistan, Palau, Papua New Guinea, Rwanda, São Tomé and Principe, Senegal, Seychelles, Sierra Leone, Sint Maarten (Dutch part), Solomon Islands, Somalia, South Sudan, St. Kitts and Nevis, St. Lucia, St. Martin (French part), St. Vincent and Grenadines, Sudan, Suriname, Syrian Arab Republic, Tajikistan, Tanzania, Timor-Leste, Togo, Trinidad and Tobago, Turkmenistan, Uganda, Uzbekistan, Vanuatu, Venezuela RB, Yemen Rep., Zambia, Zimbabwe. |
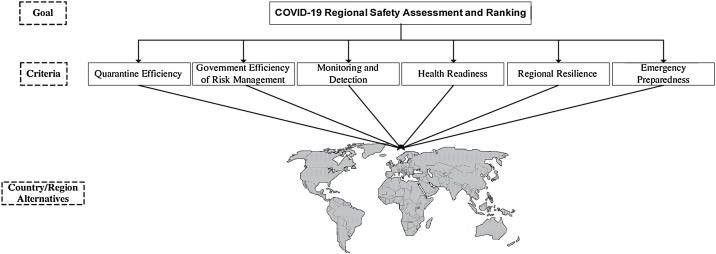
The 130 parameters used in the pre-analysis were classified under six main criteria: quarantine efficiency, government efficiency of risk management, monitoring and detection, health readiness, regional resilience, and emergency preparedness. Quarantine efficiency includes elements such as quarantine scale, quarantine timeline, and travel restriction. The government efficiency of risk management includes elements such as economic sustainability, the efficiency of the government structure, and preparedness for a pandemic. Monitoring and detection consist of elements such as monitoring systems and disaster management, the scope of diagnostic methods, and test efficiency. Healthcare readiness consists of elements such as COVID-19 equipment availability, mobilisation of new healthcare services, and the quantity and quality of medical staff. Regional resilience consists of factors such as the risk of infection spread, cultural characteristics and social discipline, and chronic diseases. Emergency preparedness consists of elements such as societal emergency resilience and emergency military mobilisation experience. The COVID-19 regional safety ranking hierarchy of the report is shown in Fig. 1 .
Fig. 1.
COVID-19 regional safety ranking hierarchy.
As the report presents many criteria for decision-making, MCDM techniques can aid in making the rank list, considering the structure of the report and the determining criteria. Therefore, in this study, rankings were made using the data from the report [7] and MCDM techniques to determine the safe regions.
Methodologies
In this section, information about TOPSIS, VIKOR, and COPRAS methods are provided, which are MCDM techniques used in ranking the safe regions. Deterministic MCDM techniques are preferred because the data presented in the DKG report are deterministic. When the problem includes uncertainty, popular fuzzy MCDM methods [12], [13], [14], [15], [16], [17], [18], [19], [20], [21] should be used to come with the imprecise data.
TOPSIS (Technique for Order Performance by Similarity to Ideal Solution)
Among the various MCDM techniques, the TOPSIS method has gained popularity because of its simple computational steps, solid mathematical foundations, and easy-to-understand method [22]. This method ranks the alternatives according to the distance between the positive and negative ideal solutions [23]. However, an alternative chosen while making a decision is expected to be close to the ideal solution and far from the non-ideal (negative ideal) solution [24]. The alternative that is closest to the positive ideal solution is also considered as the alternative that is the furthest from the negative ideal solution. The alternative closest to the positive ideal solution with the TOPSIS method is the best alternative [25]. The TOPSIS method can be used to evaluate decision-making units (DMUs). If m indicates the number of alternatives and n indicates the number of evaluation criteria, f ij indicates the value of the jth alternative according to the ith criterion. The TOPSIS method consists of the following steps [23]:
Step 1. Decision matrix is normalised.
is defined as the normalised decision matrix, and the normalised criterion value h ij is calculated using Eq. (1).
| (1) |
Step 2. The weighted normalised decision matrix is determined.
is defined as the normalised weighted decision matrix of . When is the weight of the ith criterion, the normalised weighted value is calculated using Eq. (2).
| (2) |
Step 3. Positive-ideal and negative-ideal solutions are determined.
Positive-ideal and negative-ideal solutions were determined using Eqs. (3) and (4), respectively. Ω b and Ω c represent the sets of benefit type and cost type criteria, respectively.
| (3) |
| (4) |
Step 4. Euclidean distance is calculated from positive- and negative-ideal solutions.
The Euclidean distances of each alternative solution to the positive ideal and negative ideal solutions are calculated using Eqs. (5) and (6).
| (5) |
| (6) |
Step 5. Closeness to the ideal solution is calculated.
The closeness to the ideal solution formulated with can be defined as shown in Eq. (7).
| (7) |
Step 6. The order of all alternatives is determined based on their relative closeness to the ideal solution. A larger indicates a better A j alternative. The best alternative is the one with the largest closeness to the ideal solutions.
The TOPSIS method can be applied with different evaluation criteria and is frequently used in practice. At this point, when the literature is examined, it is seen that the TOPSIS method is used in many areas such as the automotive sector [26], tourism [27], textiles [28], banking [29], the health sector [30], and the education sector [31].
VIKOR (Vise Kriterijumsa Optimizacija I Kompromisno Resenje)
The VIKOR method was developed for the multi-criteria optimisation of complex systems. It determines the compromise order list, the compromise solution, and the weight stability ranges for the preferred stability in the obtained compromise solution with the initial (given) weights. This method focuses on ordering and selecting a range of alternatives in the presence of conflicting criteria. It offers a multi-criteria ranking index based on the measure of “closeness” to the “ideal” solution [32]. This method is an effective tool used in MCDM, especially when the decision-maker cannot express their preferences at the beginning of the system design [33]. At the same time, this method focuses on ordering and choosing from a range of alternatives. It determines a compromise solution for problems with conflicting criteria that can help decision-makers reach a final solution [34]. The development of the VIKOR method starts with the criterion form given by Eq. (8) [32]
| (8) |
In the VIKOR method, (S j in Eq. (11)) and (R j in Eq. (12)) ordering measurements were used by formulating. The aim is to obtain with maximum group utility (“majority” rule) and with minimal individual regret of the “opponent.” The compromise solution F c is the result closest to the ideal F*. Compromise means an agreement with mutual concessions by and as shown in Fig. 2. The compromise ordering steps of VIKOR are as follows [32]:
Fig. 2.
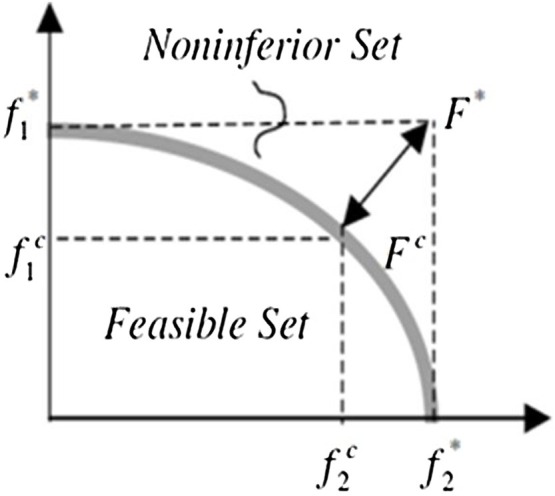
Ideal and compromise solutions [32].
Step 1. The best and worst values of all the criteria functions were determined.
where i = 1, 2, …, n, and the ith function represents a benefit. and are calculated using Eqs. (9) and (10), respectively, as follows:
| (9) |
| (10) |
Step 2. S j and R j values are calculated using Eqs. (11) and (12), respectively .
| (11) |
| (12) |
where is the criterion weight, whose relative significance is expressed.
Step 3. The Q j value is calculated using Eqs. (13), (14), (15) (j = 1, 2, …, m):
| (13) |
| (14) |
| (15) |
where x represents the strategic weight of the majority of criteria (or maximum group utility). In this study, x = 0.5.
Step 4. Three ordering lists are created by arranging the S, R, and Q values of the alternatives in ascending order.
Step 5. If the two conditions stated below are met, alternative (a′), which ranks according to the best Q (minimum) values, is recommended as a compromise solution.
Condition 1. “Acceptable advantage”
a″ is the second alternative in the ranking list. Eqs. (16) and (17) need to be satisfied to fulfil Condition 1.
| (16) |
| (17) |
where m is the number of alternatives.
Condition 2. “Acceptable stability in decision making”
Alternative a′is the best alternative and must also be ranked according to the S and/or R values. This compromise solution is stable during the decision-making process. v is the weight of the decision-making strategy. If one of these conditions is not satisfied, a compromise set of solutions is suggested. This set of solutions includes the following:
-
•
Alternative a′and a″ only if Condition 2 is not met.
-
•
Alternatives if Condition 1 is not satisfied and is determined for the maximum M with relation (closeness to the positions of these alternatives).
The best alternative, ranked according to Q values, is the alternative with a minimum Q value. The main ranking result is a compromise solution with a compromise ranking list of alternatives and an “advantage ratio”.
VIKOR is effective in a situation when the decision-maker is not aware of the design of the system. The compromise solution obtained is accepted by the decision-maker for the maximum group benefit of the majority (denoted by Eq. (11)) and the minimisation of the individual regrets of the opponents (denoted by Eq. (12)).
According to the literature, the VIKOR method is used in decision-making analyses in many studies in different disciplines, such as the automotive sector [35], the health sector [36], the banking sector [37], the textile sector [38], education sector [39], evaluation of countries in various ways [40], tourism sector [41], and evaluation of research and development performance [42].
COPRAS (Complex Proportional Assessment)
The “Complex Proportional Assessment” or COPRAS method was introduced by Zavadskas and Kaklauskas [43] and was used to evaluate the superiority of one alternative over another and makes it possible to compare alternatives [44]. This method can be applied to maximise or minimise criteria in an assessment where more than one criterion should be considered [45]. The COPRAS method ranks and evaluates alternatives step-by-step for their importance and utility degree [46]. The steps of the COPRAS method are as follows [47]:
Step 1. Decision matrix is normalised using Eq. (18).
The normalised decision matrix is denoted by . The purpose of normalisation is to obtain different dimensionless values to compare all criteria.
| (18) |
Step 2. The weighted normalised decision matrix was determined using Eq. (19).
| (19) |
Where g ij is the normalised value of jth alternative according to ith criterion.
Step 3. The sums of the weighted normalised values were calculated for both the beneficial and non-beneficial criteria. These sums were calculated using Eqs. (20) and (21).
| (20) |
| (21) |
where and are the weighted normalised values of the beneficial and non-beneficial criteria, respectively. The larger the value and the lower the value, the better the alternative. The values of and indicate the degree of goals reached by each alternative.
Step 4. The significance of the alternatives is determined by defining the characteristics of the positive alternatives and negative alternatives .
Step 5. The relative significance or priorities of the alternatives were determined. The priorities of the candidate alternatives were calculated based on C j. The higher the C j value, the higher is the priority of the alternative. The relative significance of an alternative shows the degree to which it fulfils the demand provided by that alternative. The alternative with the highest relative significance value (C_max) is the best choice among the candidate alternatives. The relative significance value of the jth alternative, C j, was calculated using Eq. (22).
| (22) |
where is the minimum value of .
Step 6. The quantitative utility (U j) was calculated for the j th alternative. The utility level of an alternative is causally related to its relative significance value (C j). The degree of utility of an alternative, determining the rank of the alternative, is determined by comparing the priorities of all alternatives for efficiency. It is calculated using Eq. (23).
| (23) |
where C max is the maximum relative significance value. As the relative significance value increases or decreases for an alternative, its utility value also increases or decreases. The utility value ranges from 0 to 100%. For this reason, this approach allows the evaluation of direct and proportional significance and utility degrees of weight and performance values according to all criteria in a decision-making problem where more than one criterion is involved [47].
COPRAS is used in decision making analyses in various fields and subjects such as the construction sector [48], investment projects [49], prototyping system selection [50], supplier selection [51], material selection problem [52].
MCDM techniques can be used to solve problems related to the COVID-19 pandemic in health [53], [54], [55], [56], education [57], and various fields [58], [59]. The purpose and the methods used for some of these studies are summarised and presented in the subsequent paragraphs.
Albahri et al. [55] present a systematic approach to evaluate and compare various artificial intelligence techniques used to detect and classify medical images of the novel coronavirus. VIKOR methods were used for the process. Further, the analytic hierarchy process (AHP) was used in weighting.
In the study by Vinodhini [58], MCDM techniques such as Weighted Sum Model (WSM), Weighted Product Model (WPM), Weighted Aggregated Sum Product Assessment (WASPAS), and TOPSIS were used, and regions were listed according to control measures implemented to stop the spread of COVID-19.
Korzeb and Niedziółka [59] used the Hellwig and TOPSIS method to evaluate the preventive measure taken by Polish commercial banks to avoid the potential negative impact caused by the COVID-19 pandemic.
Sayan et al. [54] compared the existing SARS-CoV-2 diagnostic tests and determined the most effective test among them through enrichment evaluation (fuzzy PROMETHEE) and fuzzy TOPSIS methods.
Majumder et al. [53] used MCDM techniques to determine the most important risk factor in COVID-19 and continuously monitor deaths caused by the virus. The new TOPSIS method and group method of data handling (GMDH) were used in the study.
Alqahtani and Rajkhan [57] carried out their study to identify critical success factors for e-learning during COVID-19 using multi-criteria AHP and TOPSIS techniques to improve the education process.
Shirazi et al. [56] used the fuzzy AHP-PROMETHEE hybrid approach to evaluate hospitals for patient satisfaction during the COVID-19 pandemic in one of the cities in Iran. For this study, patient satisfaction factors were determined primarily under normal conditions. Patient satisfaction factors were then determined during the COVID-19 pandemic. Hospitals were ranked for patient satisfaction under normal conditions and the COVID-19 pandemic situation using the FAHP-PROMETHEE approach.
Based on the literature review, TOPSIS, VIKOR, and COPRAS methods, which are popular MCDM techniques, were chosen to determine the safety levels of 100 regions for COVID-19. Further, the results obtained were evaluated by comparing them with the report used to obtain the data. This study is unique as a limited number of studies have used MCDM techniques to determine safe regions study for COVID-19 pandemic. This study would be a significant contribution to the literature.
Application of methodologies
This section consists of three subsections. In the first sub-section, brief information is provided regarding the alternatives considered. In the second subsection, information regarding the criteria and weights used in this study is presented in detail. In the concluding section, the results are presented.
Study region
A total of 100 regions in Level 1 (20 regions), Level 2 (20 regions), and Level 3 (60 regions), which are explained in detail in the second part, constitute the alternatives of the study. Regions in Level 4 (100 regions) are not considered because the data needed for the TOPSIS, VIKOR, and COPRAS methods are insufficient.
Evaluation criteria and data
The evaluation criteria used for the study were based on the six categories mentioned in the DKG report (2020). The values of each alternative for Level 1, Level 2, and Level 3 are presented in Table A1, Table A2, and Table A3, respectively, and the details are given in the Appendix.
Two different prioritizations are considered in this study. In the first prioritisation, the criterion weights suggested by the DKG are normalised, and in the second prioritisation, analyses are carried out with the assumption that all criteria weights are equal. In the applied methods, the criteria should be specified according to their orientation for benefit or cost. The criterion with the smallest (least cost) value in cost-oriented criteria and the criterion with the highest (the most benefit) value in benefit-oriented criteria should be determined as the best criterion. The six criteria used in this study are benefit-oriented in achieving the objective of the study (ensuring regional safety in terms of COVID-19). In other words, the high values of these criteria aid in determining the best alternative. The criteria used in this study and their weights are listed in Table 2.
Table 2.
The weights of criteria.
| Criteria | Normalised weight (NW) | Equal weight (EW) |
|---|---|---|
| Quarantine Efficiency | 0.22 | 0.16 |
| Government Efficiency of Risk Management | 0.22 | 0.16 |
| Monitoring and Detection | 0.15 | 0.16 |
| Emergency Preparedness | 0.15 | 0.16 |
| Healthcare Readiness | 0.13 | 0.16 |
| Regional Resiliency | 0.13 | 0.16 |
Findings
In this section, the TOPSIS, VIKOR, and COPRAS methods are applied to compare and rank the alternatives. The ranking results obtained were analysed for methods used and compared with the ranking results given in the report presented by DKG [7].
Six applications (TOPSIS_NW, TOPSIS_EW, VIKOR_NW, VIKOR_EW, COPRAS_NW, and COPRAS_EW) were applied because each method considers two prioritizations. Each application is applied by considering three levels (Level 1, Level 2, and Level 3) independent of each other. The results obtained for Level 1, Level 2, and Level 3 are given in Table 3, Table 4, Table 5, respectively. Each of the three tables consists of 14 columns in which the ranking results of the DKG report [7] are given in the first 2 columns. Normalised results obtained by applying equal weights are presented for the TOPSIS method in the third, fourth, and fifth columns, for the VIKOR method in the next four columns, and the COPRAS method in the last four columns. In the rows, the alternatives included in Level 1 are given in Table 3, Level 2 is given in Table 4, and Level 3 is given in Table 5.
Table 3.
Ranking of regions of Level 1 based on TOPSIS, VIKOR and COPRAS.
| DKG report [7] |
TOPSIS |
VIKOR |
COPRAS |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rn | Alternatives | NW |
EW |
NW |
EW |
NW |
EW |
||||||
| Rn | Rn | Qj | Rn | Qj | Rn | Uj | Rn | Uj | Rn | ||||
| 1 | Switzerland | 0.626 | 1 | 0.623 | 1 | 0.013 | 1 | 0.029 | 1 | 1.000 | 1 | 1.000 | 1 |
| 2 | Germany | 0.566 | 5 | 0.581 | 5 | 0.196 | 3 | 0.376 | 7 | 0.992 | 2 | 0.999 | 2 |
| 3 | Israel | 0.602 | 2 | 0.600 | 2 | 0.312 | 4 | 0.146 | 3 | 0.985 | 4 | 0.986 | 3 |
| 4 | Singapore | 0.560 | 7 | 0.555 | 8 | 0.036 | 2 | 0.088 | 2 | 0.985 | 3 | 0.986 | 4 |
| 5 | Japan | 0.568 | 4 | 0.593 | 3 | 0.386 | 6 | 0.220 | 4 | 0.975 | 5 | 0.984 | 5 |
| 6 | Austria | 0.570 | 3 | 0.590 | 4 | 0.590 | 11 | 0.510 | 9 | 0.961 | 6 | 0.966 | 6 |
| 7 | China | 0.549 | 8 | 0.560 | 6 | 0.712 | 14 | 0.663 | 11 | 0.945 | 9 | 0.949 | 8 |
| 8 | Australia | 0.560 | 6 | 0.555 | 7 | 0.431 | 8 | 0.736 | 15 | 0.951 | 8 | 0.949 | 9 |
| 9 | New Zealand | 0.521 | 9 | 0.510 | 11 | 0.406 | 7 | 0.260 | 6 | 0.953 | 7 | 0.950 | 7 |
| 10 | South Korea | 0.513 | 10 | 0.542 | 9 | 0.749 | 15 | 0.721 | 14 | 0.938 | 10 | 0.945 | 10 |
| 11 | United Arab Emirates | 0.464 | 12 | 0.511 | 10 | 0.777 | 16 | 0.693 | 13 | 0.923 | 12 | 0.940 | 11 |
| 12 | Canada | 0.445 | 13 | 0.444 | 13 | 0.440 | 9 | 0.236 | 5 | 0.923 | 11 | 0.922 | 12 |
| 13 | Hong Kong | 0.467 | 11 | 0.446 | 12 | 0.325 | 5 | 0.426 | 8 | 0.922 | 13 | 0.916 | 13 |
| 14 | Norway | 0.416 | 14 | 0.415 | 14 | 0.541 | 10 | 0.657 | 10 | 0.906 | 14 | 0.903 | 14 |
| 15 | Denmark | 0.370 | 17 | 0.390 | 17 | 0.640 | 12 | 0.678 | 12 | 0.891 | 15 | 0.892 | 15 |
| 16 | Taiwan | 0.389 | 15 | 0.373 | 18 | 0.910 | 18 | 0.922 | 19 | 0.877 | 16 | 0.869 | 18 |
| 17 | Saudi Arabia | 0.370 | 18 | 0.393 | 15 | 0.945 | 20 | 0.903 | 18 | 0.869 | 17 | 0.875 | 16 |
| 18 | Hungary | 0.379 | 16 | 0.392 | 16 | 0.914 | 19 | 0.856 | 16 | 0.868 | 18 | 0.869 | 17 |
| 19 | Netherlands | 0.333 | 19 | 0.361 | 19 | 0.689 | 13 | 0.922 | 20 | 0.863 | 19 | 0.862 | 19 |
| 20 | Vietnam | 0.275 | 20 | 0.274 | 20 | 0.886 | 17 | 0.859 | 17 | 0.844 | 20 | 0.837 | 20 |
*Rn: Rank.
Table 4.
Ranking of regions of Level 2 based on TOPSIS, VIKOR and COPRAS.
| DKG report [7] |
TOPSIS |
VIKOR |
COPRAS |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rn | Alternatives | NW |
EW |
NW |
EW |
NW |
EW |
||||||
| Rn | Rn | Qj | Rn | Qj | Rn | Uj | Rn | Uj | Rn | ||||
| 1 | Kuwait | 0.722 | 1 | 0.712 | 1 | 0.004 | 1 | 0.000 | 1 | 1.000 | 1 | 1.000 | 1 |
| 2 | Iceland | 0.500 | 3 | 0.492 | 3 | 0.139 | 2 | 0.489 | 3 | 0.936 | 2 | 0.934 | 3 |
| 3 | Bahrain | 0.579 | 2 | 0.607 | 2 | 0.504 | 12 | 0.467 | 2 | 0.932 | 3 | 0.939 | 2 |
| 4 | Finland | 0.450 | 7 | 0.480 | 4 | 0.244 | 3 | 0.559 | 5 | 0.908 | 4 | 0.914 | 4 |
| 5 | Luxembourg | 0.408 | 10 | 0.432 | 6 | 0.271 | 4 | 0.577 | 6 | 0.896 | 6 | 0.900 | 5 |
| 6 | Qatar | 0.454 | 6 | 0.431 | 7 | 0.326 | 6 | 0.523 | 4 | 0.899 | 5 | 0.890 | 6 |
| 7 | Liechtenstein | 0.423 | 8 | 0.402 | 9 | 0.329 | 7 | 0.706 | 7 | 0.892 | 7 | 0.885 | 8 |
| 8 | Poland | 0.399 | 11 | 0.337 | 18 | 0.274 | 5 | 0.764 | 11 | 0.885 | 10 | 0.867 | 14 |
| 9 | Lithuania | 0.376 | 12 | 0.388 | 10 | 0.787 | 18 | 0.772 | 12 | 0.875 | 11 | 0.877 | 9 |
| 10 | Malaysia | 0.463 | 5 | 0.402 | 8 | 0.481 | 11 | 0.837 | 16 | 0.890 | 8 | 0.875 | 10 |
| 11 | Latvia | 0.367 | 13 | 0.325 | 19 | 0.335 | 8 | 0.720 | 8 | 0.874 | 13 | 0.861 | 17 |
| 12 | Slovenia | 0.359 | 16 | 0.379 | 11 | 0.735 | 17 | 0.744 | 10 | 0.872 | 14 | 0.874 | 11 |
| 13 | Oman | 0.464 | 4 | 0.469 | 5 | 0.626 | 14 | 0.848 | 18 | 0.886 | 9 | 0.885 | 7 |
| 14 | Greece | 0.365 | 14 | 0.362 | 14 | 0.455 | 10 | 0.843 | 17 | 0.870 | 15 | 0.865 | 15 |
| 15 | Estonia | 0.344 | 18 | 0.342 | 16 | 0.420 | 9 | 0.794 | 13 | 0.868 | 16 | 0.864 | 16 |
| 16 | Croatia | 0.342 | 19 | 0.377 | 12 | 0.790 | 19 | 0.826 | 14 | 0.862 | 17 | 0.867 | 12 |
| 17 | Turkey | 0.410 | 9 | 0.377 | 13 | 0.707 | 15 | 0.738 | 9 | 0.875 | 12 | 0.867 | 13 |
| 18 | Ireland | 0.328 | 20 | 0.345 | 15 | 0.526 | 13 | 0.894 | 19 | 0.856 | 19 | 0.856 | 18 |
| 19 | Georgia | 0.364 | 15 | 0.340 | 17 | 1.000 | 20 | 1.000 | 20 | 0.848 | 20 | 0.840 | 20 |
| 20 | Cyprus | 0.346 | 17 | 0.317 | 20 | 0.720 | 16 | 0.831 | 15 | 0.857 | 18 | 0.849 | 19 |
Table 5.
Ranking of regions of Level 3 based on TOPSIS, VIKOR and COPRAS.
| DKG report [7] |
TOPSIS |
VIKOR |
COPRAS |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rn | Alternatives | NW |
EW |
NW |
EW |
NW |
EW |
||||||
| Rn | Rn | Qj | Rn | Qj | Rn | Uj | Rn | Uj | Rn | ||||
| 1 | Chile | 0.538 | 9 | 0.532 | 19 | 0.114 | 3 | 0.187 | 3 | 0.940 | 4 | 0.915 | 11 |
| 2 | Montenegro | 0.556 | 3 | 0.575 | 7 | 0.312 | 13 | 0.219 | 5 | 0.946 | 2 | 0.936 | 2 |
| 3 | Czech Republic | 0.548 | 5 | 0.585 | 6 | 0.181 | 6 | 0.227 | 7 | 0.941 | 3 | 0.936 | 4 |
| 4 | Malta | 0.538 | 10 | 0.538 | 16 | 0.249 | 7 | 0.553 | 29 | 0.936 | 5 | 0.912 | 13 |
| 5 | Spain | 0.548 | 6 | 0.598 | 5 | 0.267 | 9 | 0.129 | 2 | 0.933 | 7 | 0.934 | 6 |
| 6 | Portugal | 0.554 | 4 | 0.560 | 12 | 0.117 | 4 | 0.271 | 11 | 0.936 | 6 | 0.918 | 10 |
| 7 | Thailand | 0.500 | 19 | 0.527 | 22 | 0.292 | 12 | 0.265 | 9 | 0.923 | 10 | 0.911 | 14 |
| 8 | Bulgaria | 0.527 | 13 | 0.567 | 8 | 0.288 | 10 | 0.317 | 16 | 0.929 | 8 | 0.924 | 8 |
| 9 | Greenland | 0.545 | 7 | 0.616 | 2 | 0.575 | 31 | 0.487 | 23 | 0.924 | 9 | 0.936 | 3 |
| 10 | Mexico | 0.490 | 22 | 0.488 | 31 | 0.081 | 1 | 0.225 | 6 | 0.915 | 16 | 0.896 | 21 |
| 11 | Uruguay | 0.523 | 15 | 0.514 | 25 | 0.113 | 2 | 0.255 | 8 | 0.918 | 14 | 0.896 | 22 |
| 12 | Vatican City | 0.503 | 18 | 0.518 | 23 | 0.377 | 21 | 0.293 | 12 | 0.919 | 13 | 0.907 | 16 |
| 13 | Italy | 0.527 | 14 | 0.564 | 10 | 0.265 | 8 | 0.120 | 1 | 0.920 | 11 | 0.914 | 12 |
| 14 | Serbia | 0.490 | 21 | 0.557 | 13 | 0.375 | 20 | 0.335 | 17 | 0.911 | 18 | 0.918 | 9 |
| 15 | Philippines | 0.529 | 11 | 0.532 | 18 | 0.361 | 18 | 0.268 | 10 | 0.915 | 15 | 0.909 | 15 |
| 16 | India | 0.562 | 2 | 0.529 | 21 | 0.338 | 15 | 0.687 | 40 | 0.919 | 12 | 0.899 | 20 |
| 17 | Romania | 0.491 | 20 | 0.489 | 30 | 0.147 | 5 | 0.314 | 15 | 0.907 | 21 | 0.887 | 26 |
| 18 | Slovakia | 0.483 | 25 | 0.490 | 29 | 0.290 | 11 | 0.309 | 13 | 0.909 | 20 | 0.889 | 25 |
| 19 | United States | 0.542 | 8 | 0.615 | 3 | 0.731 | 48 | 0.680 | 39 | 0.911 | 19 | 0.931 | 7 |
| 20 | France | 0.655 | 1 | 0.691 | 1 | 0.500 | 26 | 0.500 | 26 | 1.000 | 1 | 1.000 | 1 |
| 21 | Russia | 0.528 | 12 | 0.613 | 4 | 0.697 | 44 | 0.636 | 36 | 0.912 | 17 | 0.936 | 5 |
| 22 | Argentina | 0.479 | 27 | 0.540 | 15 | 0.369 | 19 | 0.368 | 19 | 0.899 | 22 | 0.901 | 18 |
| 23 | Belarus | 0.484 | 24 | 0.530 | 20 | 0.436 | 24 | 0.337 | 18 | 0.899 | 23 | 0.893 | 23 |
| 24 | Monaco | 0.481 | 26 | 0.500 | 27 | 0.410 | 22 | 0.311 | 14 | 0.897 | 25 | 0.886 | 28 |
| 25 | Sweden | 0.476 | 29 | 0.555 | 14 | 0.589 | 32 | 0.490 | 25 | 0.892 | 27 | 0.904 | 17 |
| 26 | Ukraine | 0.477 | 28 | 0.518 | 24 | 0.332 | 14 | 0.435 | 22 | 0.894 | 26 | 0.886 | 27 |
| 27 | Gibraltar | 0.509 | 16 | 0.561 | 11 | 0.731 | 47 | 0.696 | 41 | 0.898 | 24 | 0.900 | 19 |
| 28 | United Kingdom | 0.508 | 17 | 0.566 | 9 | 0.749 | 50 | 0.698 | 42 | 0.888 | 28 | 0.892 | 24 |
| 29 | South Africa | 0.439 | 33 | 0.451 | 39 | 0.345 | 16 | 0.215 | 4 | 0.879 | 29 | 0.867 | 32 |
| 30 | San Marino | 0.455 | 31 | 0.465 | 36 | 0.361 | 17 | 0.371 | 20 | 0.879 | 30 | 0.861 | 33 |
| 31 | Kazakhstan | 0.465 | 30 | 0.514 | 26 | 0.597 | 34 | 0.506 | 27 | 0.872 | 32 | 0.874 | 30 |
| 32 | Bosnia and Herzegovina | 0.453 | 32 | 0.491 | 28 | 0.650 | 40 | 0.590 | 32 | 0.876 | 31 | 0.870 | 31 |
| 33 | Iran | 0.488 | 23 | 0.534 | 17 | 0.649 | 39 | 0.779 | 49 | 0.871 | 33 | 0.877 | 29 |
| 34 | Ecuador | 0.419 | 36 | 0.442 | 41 | 0.538 | 29 | 0.513 | 28 | 0.861 | 34 | 0.849 | 38 |
| 35 | Azerbaijan | 0.424 | 35 | 0.486 | 32 | 0.531 | 28 | 0.404 | 21 | 0.859 | 36 | 0.860 | 34 |
| 36 | Mongolia | 0.404 | 39 | 0.462 | 37 | 0.697 | 45 | 0.641 | 37 | 0.853 | 38 | 0.852 | 37 |
| 37 | Lebanon | 0.408 | 37 | 0.467 | 34 | 0.658 | 41 | 0.568 | 30 | 0.853 | 37 | 0.853 | 36 |
| 38 | Belgium | 0.435 | 34 | 0.484 | 33 | 0.645 | 38 | 0.701 | 43 | 0.860 | 35 | 0.855 | 35 |
| 39 | Andorra | 0.390 | 40 | 0.443 | 40 | 0.572 | 30 | 0.489 | 24 | 0.848 | 39 | 0.845 | 39 |
| 40 | Cayman Islands | 0.407 | 38 | 0.457 | 38 | 0.733 | 49 | 0.704 | 44 | 0.843 | 40 | 0.838 | 41 |
| 41 | Armenia | 0.383 | 41 | 0.466 | 35 | 0.821 | 54 | 0.737 | 47 | 0.827 | 43 | 0.838 | 40 |
| 42 | Moldova | 0.375 | 44 | 0.420 | 45 | 0.636 | 35 | 0.576 | 31 | 0.832 | 41 | 0.823 | 43 |
| 43 | Myanmar | 0.349 | 48 | 0.320 | 54 | 0.431 | 23 | 0.618 | 34 | 0.821 | 45 | 0.795 | 51 |
| 44 | Bangladesh | 0.380 | 43 | 0.370 | 49 | 0.516 | 27 | 0.628 | 35 | 0.830 | 42 | 0.808 | 46 |
| 45 | Sri Lanka | 0.352 | 47 | 0.339 | 51 | 0.471 | 25 | 0.653 | 38 | 0.823 | 44 | 0.796 | 50 |
| 46 | Egypt | 0.320 | 53 | 0.350 | 50 | 0.591 | 33 | 0.592 | 33 | 0.810 | 49 | 0.799 | 48 |
| 47 | Tunisia | 0.367 | 46 | 0.438 | 42 | 0.804 | 52 | 0.709 | 46 | 0.817 | 46 | 0.823 | 42 |
| 48 | Albania | 0.382 | 42 | 0.428 | 43 | 0.889 | 57 | 0.889 | 53 | 0.817 | 47 | 0.811 | 44 |
| 49 | Jordan | 0.330 | 51 | 0.392 | 47 | 0.857 | 55 | 0.802 | 50 | 0.807 | 50 | 0.809 | 45 |
| 50 | Panama | 0.344 | 49 | 0.391 | 48 | 0.721 | 46 | 0.897 | 54 | 0.805 | 51 | 0.796 | 49 |
| 51 | Brazil | 0.375 | 45 | 0.421 | 44 | 0.929 | 59 | 0.884 | 52 | 0.812 | 48 | 0.806 | 47 |
| 52 | Morocco | 0.315 | 55 | 0.292 | 55 | 0.690 | 43 | 0.706 | 45 | 0.797 | 52 | 0.771 | 53 |
| 53 | Algeria | 0.338 | 50 | 0.403 | 46 | 0.864 | 56 | 0.931 | 56 | 0.789 | 53 | 0.789 | 52 |
| 54 | Honduras | 0.298 | 56 | 0.284 | 56 | 0.812 | 53 | 0.765 | 48 | 0.785 | 54 | 0.762 | 55 |
| 55 | Paraguay | 0.316 | 54 | 0.332 | 52 | 0.986 | 60 | 0.953 | 58 | 0.780 | 55 | 0.765 | 54 |
| 56 | Peru | 0.298 | 57 | 0.328 | 53 | 0.919 | 58 | 0.966 | 59 | 0.774 | 56 | 0.761 | 56 |
| 57 | Indonesia | 0.252 | 59 | 0.262 | 58 | 0.777 | 51 | 0.810 | 51 | 0.768 | 57 | 0.749 | 57 |
| 58 | Cambodia | 0.273 | 58 | 0.270 | 57 | 0.640 | 36 | 0.920 | 55 | 0.767 | 58 | 0.739 | 58 |
| 59 | Laos | 0.246 | 60 | 0.205 | 60 | 0.642 | 37 | 0.934 | 57 | 0.752 | 60 | 0.713 | 60 |
| 60 | Bahamas | 0.326 | 52 | 0.248 | 59 | 0.683 | 42 | 1.000 | 60 | 0.765 | 59 | 0.717 | 59 |
According to Table 3,
-
•
As in the DKG report, Switzerland ranked first in all methods and prioritisation.
-
•
The ranking of the six regions for normalised weights (Netherlands, Switzerland, New Zealand, South Korea, Republic of Korea, Norway, Vietnam) and four regions for equal weights (Switzerland, Norway, Denmark, Netherlands, Vietnam) using TOPSIS method, the ranking of the two regions for normalised weights (Switzerland, Australia) and two regions for equal weights using (Switzerland, Israel) the VIKOR method, and ranking of 14 regions for normalised weights (Switzerland, Germany, Japan, Austria, Australia, South Korea Republic of Korea, Hong Kong, Norway, Denmark, Taiwan, Saudi Arabia, Hungary, Netherlands, Vietnam) and 14 regions for equal weights (Switzerland, Germany, Israel, Singapore, Japan, Austria, South Korea Republic of Korea, United Arab Emirates, Canada, Hong Kong, Norway, Denmark, Netherlands, Vietnam) using the COPRAS method are the same as those in the DKG report.
-
•
The ranking of 13 regions (South Korea, Republic of Korea, Norway, the Netherlands, Vietnam, Germany, Japan, Austria, Australia, Hong Kong, Denmark, Taiwan, Saudi Arabia, and Hungary) is the same as the DKG report ranking in at least three methods.
According to Table 4,
-
•
Kuwait, which ranks first in the report, maintains its place in all the methods.
-
•
The ranking of the three regions for normalised weights (Kuwait, Qatar, Greece) and the two regions for equal weights (Kuwait, Finland, Greece, Estonia, and Cyprus) using the TOPSIS method, the ranking of four regions for normalised weights (Kuwait, Iceland, Qatar, Liechtenstein) and two regions for equal weights (Kuwait, Liechtenstein) using the VIKOR method, and the ranking of eight regions for normalised weights (Kuwait, Iceland, Bahrain, Finland, Liechtenstein, Greece, Estonia, Croatia) and nine regions for equal weights (Kuwait, Finland, Luxembourg, Qatar, Lithuania, Malaysia, Greece, Estonia, Ireland) using the COPRAS method are the same as the ranking in the report.
-
•
The ranking of six regions (Kuwait, Finland, Qatar, Liechtenstein, Greece, and Estonia) is the same as the ranking in at least three methods.
According to Table 5,
-
•
The ranking of four regions (Bosnia and Herzegovina, Azerbaijan, Lebanon, Armenia) for normalised weights and one region for equal weights (Spain) using the TOPSIS method, the ranking of one region for normalised weights (Belgium) and three regions for equal weights (Vatican City, Sweden, Bosnia and Herzegovina, Portugal, Bulgaria) using the VIKOR method, and the ranking of 22 regions for normalised weights (Montenegro, Czech Republic, Greenland, Philippines, Argentina, Belarus, Ukraine, United Kingdom, South Africa, San Marino, Iran, Ecuador, Lebanon, Andorra, Cayman Islands, Morocco, Algeria, Honduras, Paraguay, Peru, Indonesia, Cambodia) and eight regions for equal weights (Montenegro, Bulgaria, Philippines, Belarus, Andorra, Peru, Indonesia, Cambodia) using the COPRAS method are the same as the ranking of the report.
-
•
The ranking of 31 regions (Montenegro, Czech Republic, Spain, Portugal, Bulgaria, Greenland, Vatican City, Philippines, Argentina, Belarus, Sweden, Ukraine, United Kingdom, South Africa, San Marino, Bosnia and Herzegovina, Iran, Ecuador, Azerbaijan, Lebanon, Belgium, Andorra, Cayman Islands, Armenia, Morocco, Algeria, Honduras, Paraguay, Peru, Indonesia, Cambodia) are the same as those in at least one application.
-
•
While Chile takes first place in the report, France takes first place in six applications.
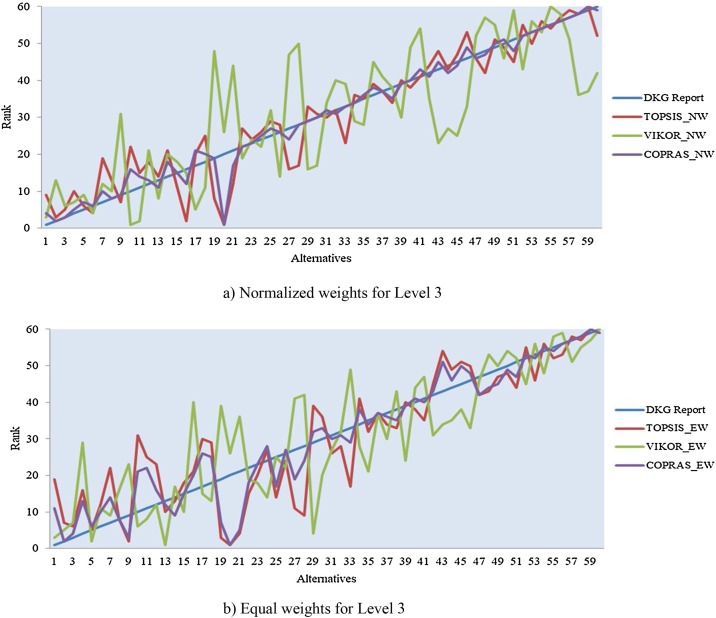
It can be seen that the success of the compromise solutions with reports provided by all three methods decreased from Level 1 to Level 3. When the methods are evaluated individually, it is observed that the ranking results are not exactly the same. Because the steps followed by each method after the weighting process are quite different, the success of the compromise solutions gradually decreases, and the ranking results are different.
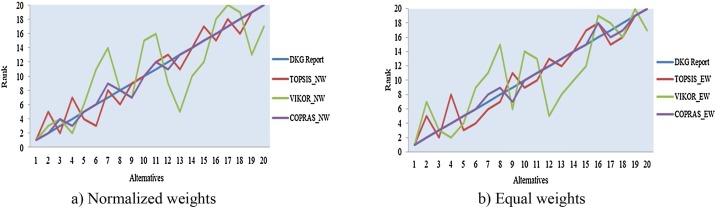
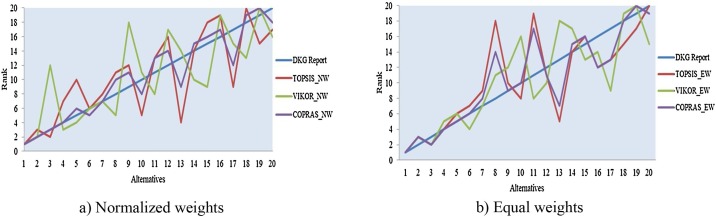
The normalised and equal weights comparison graphs of Level 1, Level 2, Level 3 are presented in Fig. 3, Fig. 4, Fig. 5. From Fig. 3, Fig. 4, Fig. 5, it is seen that the criterion weights in all methods have a significant effect on the ranking. When the data in Fig. 3, Fig. 4, Fig. 5 are compared with Table 3, Table 4, Table 5, it is found that for some regions, the ranking remains the same for the same method irrespective of the weight change. However, the ranking of many regions varies within the same method with weight change. For example, in the TOPSIS method, Switzerland, Germany, and Israel maintain their rankings, while Singapore ranks seventh in the results obtained by applying normalised weights and eighth in the results obtained by applying equal weights, respectively, as shown in Fig. 3 and Table 3.
Fig. 3.
Evaluation of methods in terms of normalised and equal weights for Level 1.
Fig. 4.
Evaluation of methods in terms of normalised and equal weights for Level 2.
Fig. 5.
Evaluation of methods in terms of normalised and equal weights for Level 3.
The evaluation of the results reveals that Switzerland ranks first for all methods and prioritisation. Similarly, Kuwait, which ranks first in the report in Level 2, maintains its ranking position in all methods and prioritizations. For Levels 1 and 2, it is determined that similarities and differences occur in rankings according to normalised and equal weights. In Level 3, while Chile ranked first in the report, France ranked first in six applications.
Conclusion and future directions
In this study, 100 regions of the world were analysed using TOPSIS, VIKOR, and COPRAS methods to determine their regional safety levels for COVID-19. The data used within the scope of the analysis were taken from the report [7] presented by the DKG, and evaluation was made by comparing the results obtained in this study with the report.
The regions Level 1, Level 2, and Level 3 constitute the alternatives. Unlike the DKG report used to obtain the data, Level 4 is not considered because the data required by the methods are insufficient. The six criteria used in this study were evaluated as benefit-oriented with the purpose of the study, which was determined to ensure regional safety in terms of COVID-19. Each region (Level 1, Level 2, and Level 3) is analysed comparatively with TOPSIS, VIKOR, and COPRAS methods, and the results are presented.
It was concluded that the COPRAS method obtained the most compatible results with the DKG report. The TOPSIS method gives a compromised result related to the report. It is observed that the VIKOR method provide the least compatible result. It has been observed that regions with an above-average score generally according to the government efficiency of risk management and quarantine efficiency criteria, which have the highest weight value, ranked high in the rankings.
Considering that MCDM techniques are auxiliary instruments for decision-makers, they are more appropriate to evaluate all methods than to suggest a single method. Decision-makers primarily evaluate the results of COPRAS. However, they should also consider the results of TOPSIS and VIKOR. In future studies, MCDM techniques that are different from the ones used in this study could be considered. By examining the procedures followed by the regions in their struggle against COVID-19 and their status, new criteria or sub-criteria presented in the DKG report [7] can be added to the criteria presented in this study, or MCDM methods can be applied by removing some criteria from the existing criteria. Further, fuzzy data that reflect the uncertainty of the real-life situation can be utilised. Therefore, fuzzy MCDM techniques can be used to solve the problem.
Funding
No funding sources.
Conflict of interest
None declared.
Ethical approval
Not required.
Appendix A
Table A1.
The values of alternatives of Level 1 used in the study.
| Region | Quarantine efficiency | Government efficiency | Monitoring and detection | Healthcare readiness | Regional resiliency | Emergency preparedness |
|---|---|---|---|---|---|---|
| Australia | 59.59 | 82.21 | 77.03 | 62.18 | 68.70 | 78.83 |
| Austria | 55.62 | 85.52 | 81.16 | 68.26 | 73.50 | 73.17 |
| Canada | 58.92 | 78.02 | 88.96 | 57.58 | 69.25 | 66.42 |
| China | 54.63 | 78.02 | 88.33 | 61.53 | 56.68 | 92.33 |
| Denmark | 62.41 | 69.53 | 85.91 | 61.35 | 71.09 | 52.92 |
| Germany | 59.45 | 88.13 | 91.97 | 78.82 | 81.10 | 52.92 |
| Hong Kong | 61.61 | 75.40 | 88.84 | 53.45 | 59.06 | 77.92 |
| Hungary | 57.01 | 66.31 | 81.33 | 50.42 | 59.14 | 79.83 |
| Israel | 57.98 | 86.66 | 95.38 | 65.38 | 68.46 | 75.43 |
| Japan | 57.62 | 83.76 | 94.70 | 83.31 | 65.62 | 60.58 |
| Netherlands | 57.96 | 71.98 | 84.58 | 65.98 | 60.70 | 49.08 |
| New Zealand | 69.72 | 70.75 | 85.43 | 57.86 | 72.56 | 72.08 |
| Norway | 58.07 | 82.20 | 81.33 | 61.26 | 73.47 | 52.92 |
| Saudi Arabia | 56.66 | 64.84 | 80.50 | 39.91 | 81.39 | 74.08 |
| Singapore | 65.92 | 80.14 | 96.41 | 66.00 | 78.21 | 60.58 |
| South Korea | 53.82 | 79.88 | 88.85 | 64.92 | 68.28 | 74.08 |
| Switzerland | 65.26 | 85.56 | 87.67 | 77.75 | 71.66 | 63.04 |
| Taiwan | 53.90 | 78.97 | 83.85 | 52.44 | 52.98 | 74.08 |
| United Arab Emirates | 54.59 | 65.22 | 95.10 | 53.88 | 78.83 | 80.83 |
| Vietnam | 58.32 | 67.71 | 82.35 | 48.79 | 55.56 | 67.33 |
Table A2.
The values of alternatives of Level 2 used in the study.
| Region | Quarantine efficiency | Government efficiency | Monitoring and detection | Healthcare readiness | Regional resiliency | Emergency preparedness |
|---|---|---|---|---|---|---|
| Bahrain | 49 | 58 | 61 | 59 | 66 | 68 |
| Croatia | 41 | 64 | 63 | 66 | 65 | 41 |
| Cyprus | 51 | 57 | 65 | 46 | 66 | 45 |
| Estonia | 47 | 63 | 62 | 59 | 64 | 42 |
| Finland | 47 | 63 | 62 | 74 | 65 | 45 |
| Georgia | 52 | 55 | 61 | 61 | 50 | 45 |
| Greece | 48 | 63 | 57 | 61 | 65 | 43 |
| Iceland | 53 | 63 | 69 | 68 | 67 | 44 |
| Ireland | 46 | 60 | 57 | 59 | 65 | 46 |
| Kuwait | 55 | 61 | 75 | 57 | 63 | 73 |
| Latvia | 50 | 64 | 67 | 47 | 65 | 43 |
| Liechtenstein | 52 | 63 | 58 | 62 | 66 | 43 |
| Lithuania | 40 | 70 | 62 | 64 | 66 | 42 |
| Luxembourg | 47 | 61 | 66 | 65 | 67 | 45 |
| Malaysia | 57 | 59 | 57 | 48 | 64 | 52 |
| Oman | 47 | 58 | 59 | 45 | 67 | 65 |
| Poland | 51 | 68 | 68 | 45 | 63 | 43 |
| Qatar | 46 | 68 | 61 | 51 | 62 | 57 |
| Slovenia | 41 | 67 | 63 | 63 | 67 | 42 |
| Turkey | 52 | 57 | 62 | 48 | 63 | 53 |
Table A3.
The values of alternatives of Level 3 used in the study.
| Region | Quarantine efficiency | Government efficiency | Monitoring and detection | Healthcare readiness | Regional resiliency | Emergency preparedness |
|---|---|---|---|---|---|---|
| Albania | 44 | 46 | 53 | 51 | 59 | 36 |
| Algeria | 37 | 48 | 53 | 52 | 57 | 35 |
| Andorra | 41 | 50 | 63 | 47 | 65 | 38 |
| Argentina | 42 | 53 | 63 | 63 | 62 | 39 |
| Armenia | 34 | 48 | 62 | 58 | 61 | 38 |
| Azerbaijan | 40 | 51 | 62 | 55 | 55 | 43 |
| Bahamas | 52 | 52 | 53 | 20 | 44 | 34 |
| Bangladesh | 46 | 52 | 63 | 39 | 42 | 44 |
| Belarus | 40 | 60 | 60 | 61 | 56 | 41 |
| Belgium | 45 | 49 | 57 | 58 | 64 | 33 |
| Bosnia and Herzegovina | 48 | 47 | 63 | 53 | 62 | 38 |
| Brazil | 44 | 45 | 55 | 52 | 59 | 33 |
| Bulgaria | 48 | 53 | 64 | 65 | 60 | 39 |
| Cambodia | 42 | 52 | 63 | 38 | 37 | 32 |
| Cayman | 44 | 47 | 62 | 57 | 57 | 33 |
| Chile | 45 | 69 | 61 | 49 | 61 | 42 |
| Czech Republic | 48 | 55 | 63 | 64 | 62 | 41 |
| Ecuador | 47 | 50 | 63 | 46 | 61 | 37 |
| Egypt | 40 | 51 | 62 | 32 | 67 | 37 |
| France | 61 | 45 | 61 | 50 | 67 | 66 |
| Gibraltar | 49 | 45 | 60 | 59 | 58 | 47 |
| Greenland | 46 | 48 | 55 | 55 | 75 | 53 |
| Honduras | 46 | 47 | 62 | 29 | 55 | 35 |
| India | 50 | 60 | 53 | 28 | 58 | 66 |
| Indonesia | 41 | 49 | 61 | 34 | 50 | 34 |
| Iran | 42 | 49 | 53 | 40 | 60 | 64 |
| Italy | 47 | 54 | 62 | 54 | 62 | 46 |
| Jordan | 33 | 52 | 62 | 43 | 67 | 36 |
| Kazakhstan | 43 | 49 | 60 | 45 | 57 | 55 |
| Laos | 41 | 57 | 61 | 19 | 49 | 31 |
| Lebanon | 42 | 48 | 63 | 53 | 63 | 37 |
| Malta | 51 | 62 | 58 | 61 | 60 | 33 |
| Mexico | 48 | 58 | 67 | 41 | 67 | 41 |
| Moldova | 38 | 55 | 62 | 52 | 50 | 37 |
| Monaco | 49 | 51 | 65 | 47 | 61 | 43 |
| Mongolia | 35 | 57 | 61 | 50 | 59 | 43 |
| Montenegro | 54 | 51 | 65 | 55 | 68 | 41 |
| Morocco | 47 | 49 | 63 | 29 | 54 | 35 |
| Myanmar | 43 | 57 | 63 | 25 | 51 | 45 |
| Panama | 39 | 52 | 53 | 47 | 59 | 35 |
| Paraguay | 45 | 45 | 53 | 37 | 60 | 34 |
| Peru | 42 | 47 | 53 | 41 | 55 | 34 |
| Philippines | 49 | 51 | 65 | 32 | 64 | 61 |
| Portugal | 50 | 60 | 58 | 56 | 61 | 41 |
| Romania | 48 | 59 | 63 | 46 | 61 | 40 |
| Russia | 41 | 45 | 61 | 50 | 67 | 66 |
| San Marino | 48 | 53 | 66 | 51 | 48 | 40 |
| Serbia | 42 | 52 | 63 | 63 | 70 | 39 |
| Slovakia | 42 | 66 | 61 | 46 | 64 | 40 |
| South Africa | 46 | 53 | 65 | 37 | 66 | 44 |
| Spain | 46 | 53 | 64 | 51 | 66 | 52 |
| Sri Lanka | 43 | 58 | 58 | 37 | 53 | 36 |
| Sweden | 41 | 48 | 64 | 62 | 62 | 45 |
| Thailand | 41 | 65 | 63 | 52 | 66 | 40 |
| Tunisia | 36 | 49 | 55 | 47 | 63 | 44 |
| UK United Kingdom | 47 | 46 | 54 | 54 | 60 | 53 |
| Ukraine | 45 | 54 | 61 | 59 | 59 | 38 |
| United States | 43 | 45 | 57 | 50 | 62 | 69 |
| Uruguay | 49 | 61 | 59 | 47 | 61 | 42 |
| Vatican City | 52 | 50 | 69 | 49 | 66 | 39 |
References
- 1.Ozili P.K. COVID-19 in Africa: socioeconomic impact, policy response and opportunities. International Journal of Sociology and Social Policy. 2020 doi: 10.1108/IJSSP-05-2020-0171. [DOI] [Google Scholar]
- 2.Huang G., Pan Q., Zhao S., Gao Y., Gao X. Prediction of COVID-19 outbreak in china and optimal return date for university students based on propagation dynamics. J Shanghai Jiaotong Univ (Sci) 2020;25:140–146. doi: 10.1007/s12204-020-2167-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yang W., Cao Q., Qin L., Wang X., Cheng Z., Pan A. Clinical characteristics and imaging manifestations of the 2019 novel coronavirus disease (COVID-19): a multi-center study in Wenzhou city, Zhejiang, China. J Infect. 2020;80:388–393. doi: 10.1016/j.jinf.2020.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mehta P., McAuley D.F., Brown M., Sanchez E., Tattersall R.S., Manson J.J. COVID-19: consider cytokine storm syndromes and immunosuppression. Lancet (London, England) 2020;395(10229):1033–1034. doi: 10.1016/S0140-6736(20)30628-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wen J., Kozak M., Yang S., Liu F. COVID-19: potential effects on Chinese citizens’ lifestyle and travel. Tour Rev. 2020 doi: 10.1108/TR-03-2020-0110. [DOI] [Google Scholar]
- 6.World Health Organization (WHO). Coronavirus disease (COVID-19) outbreak situation. https://www.who.int/emergencies/diseases/novel-coronavirus-2019 [accessed 03.11.20].
- 7.DKG. 2020. http://analytics.dkv.global/covid-regional-assessment-200-regions/full-report.pdf [accessed 23.06.20].
- 8.Gomes C.F.S., Costa H.G., De Barros A.P. Sensibility analysis of MCDA using prospective in Brazilian energy sector. J Model Manag. 2017;12(3):475–497. doi: 10.1108/JM2-01-2016-0005. [DOI] [Google Scholar]
- 9.Liu P. Multi-attribute decision-making method research based on interval vague set and TOPSIS method. Technol Econ Dev Econ. 2009;15(3):453–463. doi: 10.3846/1392-8619.2009.15.453-463. [DOI] [Google Scholar]
- 10.Linkov I., Moberg E. CRS Press; USA: 2012. Multi-criteria decision analysis environmental applications and case studies. [Google Scholar]
- 11.Kiritsis D., Bufardi A., Xirouchakis P. Multi-criteria decision aid for product end of life options selection. IEEE international symposium on electronics and the environment; IEEE; 2003. pp. 48–53. [DOI] [Google Scholar]
- 12.Zadeh L.A. Fuzzy set. Inf Control. 1965;8:338–353. doi: 10.1016/S0019-9958(65)90241-X. [DOI] [Google Scholar]
- 13.Atanassov K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986;20(1):87–96. doi: 10.1016/S0165-0114(86)80034-3. [DOI] [Google Scholar]
- 14.Chen C.T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000;114(1):1–9. doi: 10.1016/S0165-0114(97)00377-1. [DOI] [Google Scholar]
- 15.Mendel J.M., John R.I., Liu F. Interval type-2 fuzzy logic systems made simple. IEEE Trans Fuzzy Syst. 2006;14(6):808–821. doi: 10.1109/TFUZZ.2006.879986. [DOI] [Google Scholar]
- 16.Chen S.M., Lee L.W. Fuzzy multiple attributes group decision-making based on the interval type-2 TOPSIS method. Expert Syst Appl. 2010;37(4):2790–2798. doi: 10.1016/j.eswa.2009.09.012. [DOI] [Google Scholar]
- 17.Özceylan E., Paksoy T. Fuzzy multi-objective linear programming approach for optimising a closed-loop supply chain network. Int J Prod Res. 2013;51(8):2443–2461. doi: 10.1080/00207543.2012.740579. [DOI] [Google Scholar]
- 18.Ghorabaee M.K., Zavadskas E.K., Amiri M., Esmaeili A. Multi-criteria evaluation of green suppliers using an extended WASPAS method with interval type-2 fuzzy sets. J Clean Prod. 2016;137:213–229. doi: 10.1016/j.jclepro.2016.07.031. [DOI] [Google Scholar]
- 19.Gnanavelbabu A., Arunagiri P. Ranking of MUDA using AHP and Fuzzy AHP algorithm. Mater Today: Proc. 2018;5(5):13406–13412. doi: 10.1016/j.matpr.2018.02.334. [DOI] [Google Scholar]
- 20.Liu Y., Eckert C.M., Earl C. A review of fuzzy AHP methods for decision-making with subjective judgements. Expert Syst Appl. 2020:113738. doi: 10.1016/j.eswa.2020.113738. [DOI] [Google Scholar]
- 21.Wang L., Li N. Pythagorean fuzzy interaction power Bonferroni mean aggregation operators in multiple attribute decision making. Int J Intell Syst. 2020;35(1):150–183. doi: 10.1002/int.22204. [DOI] [Google Scholar]
- 22.Chakraborty S., Chatterjee P., Das P.P. A DoE-TOPSIS method-based meta-model for parametric optimization of non-traditional machining processes. J Model Manag. 2019;14(2):430–455. doi: 10.1108/JM2-08-2018-0110. [DOI] [Google Scholar]
- 23.Wu J., Sun J., Zha Y., Liang L. Ranking approach of cross-efficiency based on improved TOPSIS technique. J Syst Eng Electron. 2011;22(4):604–608. doi: 10.3969/j.issn.1004-4132.2011.04.008. [DOI] [Google Scholar]
- 24.Lai Y.J., Liu T.Y., Hwang C.L. TOPSIS for MODM. Eur J Oper Res. 1994;76(3):486–500. doi: 10.1016/0377-2217(94)90282-8. [DOI] [Google Scholar]
- 25.Cheng S., Chan C.W., Huang G.H. Using multiple criteria decision analysis for supporting decisions of solid waste management. J Environ Sci Health Part A. 2002;37(6):975–990. doi: 10.1081/ESE-120004517. [DOI] [PubMed] [Google Scholar]
- 26.Sadeghzadeh K., Salehi M.B. Mathematical analysis of fuel cell strategic technologies development solutions in the automotive industry by the TOPSIS multi-criteria decision making method. Int J Hydrogen Energy. 2011;36(20):13272–13280. doi: 10.1016/j.ijhydene.2010.07.064. [DOI] [Google Scholar]
- 27.Hashemabadi A.G., Razmi M.J. Studying Iran's tourism industry position in Middle-East using tourism development indicators and TOPSIS method. Adv Manag Appl Econ. 2014;4(5):85–97. [Google Scholar]
- 28.Bathrinath S., Bhalaji R.K.A., Saravanasankar S. Risk analysis in textile industries using AHP-TOPSIS. Mater Today: Proc. 2020 doi: 10.1016/j.matpr.2020.04.722. [DOI] [Google Scholar]
- 29.Chmielarz W., Zborowski M. Analysis of e-banking websites’ quality with the application of the TOPSIS method-a practical study. Proc Comput Sci. 2018;126:1964–1976. doi: 10.1016/j.procs.2018.07.238. [DOI] [Google Scholar]
- 30.Barrios M.A.O., De Felice F., Negrete K.P., Romero B.A., Arenas A.Y., Petrillo A. An AHP-TOPSIS integrated model for selecting the most appropriate tomography equipment. Int J Inf Technol Decis Mak. 2016;15(04):861–885. doi: 10.1142/S021962201640006X. [DOI] [Google Scholar]
- 31.Jati H. Comparison of university webometrics ranking using multicriteria decision analysis: topsis and vikor method. World Acad Sci Eng Technol. 2012;71:1663–1669. [Google Scholar]
- 32.Opricovic S., Tzeng G.H. Compromise solution by MCDM methods: a comparative analysis of VIKOR and TOPSIS. Eur J Oper Res. 2004;156(2):445–455. doi: 10.1016/S0377-2217(03)00020-1. [DOI] [Google Scholar]
- 33.Opricovic S., Tzeng G.H. Extended VIKOR method in comparison with outranking methods. Eur J Oper Res. 2007;178(2):514–529. doi: 10.1016/j.ejor.2006.01.020. [DOI] [Google Scholar]
- 34.Sayadi M.K., Heydari M., Shahanaghi K. Extension of VIKOR method for decision making problem with interval numbers. Appl Math Model. 2009;33(5):2257–2262. doi: 10.1016/j.apm.2008.06.002. [DOI] [Google Scholar]
- 35.Luthra S., Govindan K., Kannan D., Mangla S.K., Garg C.P. An integrated framework for sustainable supplier selection and evaluation in supply chains. J Clean Prod. 2017;140:1686–1698. doi: 10.1016/j.jclepro.2016.09.078. [DOI] [Google Scholar]
- 36.Zeng Q.L., Li D.D., Yang Y.B. VIKOR method with enhanced accuracy for multiple criteria decision making in healthcare management. J Med Syst. 2013;37(2):9908. doi: 10.1007/s10916-012-9908-1. [DOI] [PubMed] [Google Scholar]
- 37.Toloie-Eshlaghy A., Bayanati M. Ranking information system success factors in mobile banking systems with VIKOR. Am J Sci Res. 2012;59:42–54. [Google Scholar]
- 38.Hassanpour M. Evaluation of Iranian textile and leather industries. J Appl Res Ind Eng. 2019;6(1):33–51. doi: 10.22105/jarie.2019.167432.1072. [DOI] [Google Scholar]
- 39.Mančev M. Service quality management in the libraries at the University of Niš Faculties using the VIKOR method. J INFO Theca. 2013;14(1):15–25. [Google Scholar]
- 40.Dang W.V., Dang W.V.T. Multi-criteria decision-making in the evaluation of environmental quality of OECD countries: the entropy weight and VIKOR methods. Int J Ethics Syst. 2020;36(1):119–130. doi: 10.1108/IJOES-06-2019-0101. [DOI] [Google Scholar]
- 41.Bagheri M., Shojaei P., Khorami M. A comparative survey of the condition of tourism infrastructure in Iranian provinces using VIKOR and TOPSIS. Decis Sci Lett. 2018;7(1):87–102. doi: 10.5267/j.dsl.2017.4.001. [DOI] [Google Scholar]
- 42.Özkan B., Özceylan E., Çetinkaya C. A GIS-based DANP-VIKOR approach to evaluate R&D performance of Turkish cities. Kybernetes. 2019;48(10):2266–2306. doi: 10.1108/K-09-2018-0456. [DOI] [Google Scholar]
- 43.Zavadskas E.K., Kaklauskas A. Deutsch-Litauisch-Polnisches Kolloquim zum Baubetriebswesen. Hochschule fur Technik. Wirtschaft und Kultur in Leipzig. 3 Jahrgang. Sonderheft. 1996. The new method of multicriteria evaluation of projects; pp. 3–8. [Google Scholar]
- 44.Zavadskas E.K., Kaklauskas A., Vilutiene T. Multicriteria evaluation of apartment blocks maintenance contractors: Lithuanian case study. Int J Strateg Prop Manag. 2009;13(4):319–338. doi: 10.3846/1648-715X.2009.13.319-338. [DOI] [Google Scholar]
- 45.Podvezko V. The comparative analysis of MCDA methods SAW and COPRAS. Eng Econ. 2011;22(2):134–146. doi: 10.5755/j01.ee.22.2.310. [DOI] [Google Scholar]
- 46.Kaklauskas A., Zavadskas E.K., Naimavicienė J., Krutinis M., Plakys V., Venskus D. Model for a complex analysis of intelligent built environment. Autom Constr. 2010;19(3):326–340. doi: 10.1016/j.autcon.2009.12.006. [DOI] [Google Scholar]
- 47.Chatterjee P., Athawale V.M., Chakraborty S. Materials selection using complex proportional assessment and evaluation of mixed data methods. Mater Des. 2011;32(2):851–860. doi: 10.1016/j.matdes.2010.07.010. [DOI] [Google Scholar]
- 48.Kildienė S., Kaklauskas A., Zavadskas E.K. COPRAS based comparative analysis of the European country management capabilities within the construction sector in the time of crisis. J Bus Econ Manag. 2011;12(2):417–434. doi: 10.3846/16111699.2011.575190. [DOI] [Google Scholar]
- 49.Popović G., Stanujkic D., Stojanovic S. Investment project selection by applying COPRAS method and imprecise data. Serb J Manag. 2012;7(2):257–269. doi: 10.5937/sjm7-2268. [DOI] [Google Scholar]
- 50.Makhesana M.A. Application of improved complex proportional assessment (COPRAS) method for rapid prototyping system selection. Rapid Prototyp J. 2015;21(6):671–674. doi: 10.1108/RPJ-03-2014-0027. [DOI] [Google Scholar]
- 51.Madić M., Marković D., Petrović G., Radovanović M. Application of COPRAS method for supplier selection. In the Fifth International Conference Transport and Logistics-TIL 2014, Proceedings. 2014:47–50. [Google Scholar]
- 52.Mousavi-Nasab S.H., Sotoudeh-Anvari A. A comprehensive MCDM-based approach using TOPSIS, COPRAS and DEA as an auxiliary tool for material selection problems. Mater Des. 2017;121:237–253. doi: 10.1016/j.matdes.2017.02.041. [DOI] [Google Scholar]
- 53.Majumder P., Biswas P., Majumder S. Application of new TOPSIS approach to identify the most significant risk factor and continuous monitoring of death of COVID-19. Electron J Gen Med. 2020;17(6):em234. doi: 10.29333/ejgm/7904. [DOI] [Google Scholar]
- 54.Sayan M., Sarigul Yildirim F., Sanlidag T., Uzun B., Uzun Ozsahin D., Ozsahin I. Capacity evaluation of diagnostic tests for COVID-19 using multicriteria decision-making techniques. Comput Math Methods Med. 2020:560250. doi: 10.1155/2020/1560250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Albahri O.S., Zaidan A.A., Albahri A.S., Zaidan B.B., Abdulkareem K.H., Al-Qaysi Z.T. Systematic review of artificial intelligence techniques in the detection and classification of COVID-19 medical images in terms of evaluation and benchmarking: taxonomy analysis, challenges, future solutions and methodological aspects. J Infect Public Health. 2020;13:1381–1396. doi: 10.1016/j.jiph.2020.06.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Shirazi H., Kia R., Ghasemi P. Ranking of hospitals in the case of COVID-19 outbreak: a new integrated approach using patient satisfaction criteria. Int J Healthc Manag. 2020 doi: 10.1080/20479700.2020.1803622. [DOI] [Google Scholar]
- 57.Alqahtani A.Y., Rajkhan A.A. E-Learning critical success factors during the COVID-19 pandemic: a comprehensive analysis of e-learning managerial perspectives. Educ Sci. 2020;10(9) doi: 10.3390/educsci10090216. [DOI] [Google Scholar]
- 58.Vinodhini G.A.F. Country ranking of COVID 19 using MCDM methods. J Crit Rev. 2020;7(5):1333–1338. doi: 10.31838/jcr.07.05.244. [DOI] [Google Scholar]
- 59.Korzeb Z., Niedziółka P. Resistance of commercial banks to the crisis caused by the COVID-19 pandemic: the case of Poland. Equilib Q J Econ Econ Policy. 2020;15(2):205–234. doi: 10.24136/eq.2020.010. [DOI] [Google Scholar]