Feasibility of Laboratory-Based EXAFS Spectroscopy with Cryogenic Detectors

Abstract

Extended X-ray Absorption Fine Structure (EXAFS) spectroscopy is a powerful technique that gives element-specific information about the structure of molecules. The development of a laboratory EXAFS spectrometer capable of measuring transmission spectra would be a significant advance as the technique is currently only available at synchrotron radiation lightsources. Here, we explore the potential of cryogenic detectors as the energy resolving component of a laboratory transmission EXAFS instrument. We examine the energy resolution, count-rate, and detector stability needed for good EXAFS spectra and compare these to the properties of cryogenic detectors and conventional X-ray optics. We find that superconducting tunnel junction (STJ) detectors are well-suited for this application.

1. Introduction

In this paper, we explore whether a practical laboratory spectrometer for extended X-ray absorption fine structure (EXAFS) can be built using a cryogenic detector as the energy resolving component. EXAFS spectroscopy gives element-specific structural information about molecules [1–3]. The term “EXAFS” describes the oscillations that extend over 1000 eV above an X-ray edge in an X-ray absorption spectroscopy (XAS) measurement (Fig. 1 left). These oscillations arise from interference between the emitted photoelectron waves from X-ray absorption and those backscattered from nearby atoms, and they can be analyzed to give the number, distances and element-type of atoms within approximately 7 Å of the absorbing atom. The extraction of EXAFS data from an XAS spectrum is illustrated in Fig. 1. Note that EXAFS spectra are typically plotted against the photoelectron wave vector k (in Å⁻¹) and since the intensity of the EXAFS oscillations reduce substantially with increasing k, spectra are typically multiplied by k³ for clarity (Fig. 1 center). The Fourier transform of an EXAFS spectrum (Fig. 1 right) is a plot of magnitude against distance from the absorbing atom, with peaks corresponding to neighboring atoms. Detailed analyses of EXAFS data use specialized curve-fitting software such as EXAFSPAK [4] and FEFF [5].

Fig. 1.

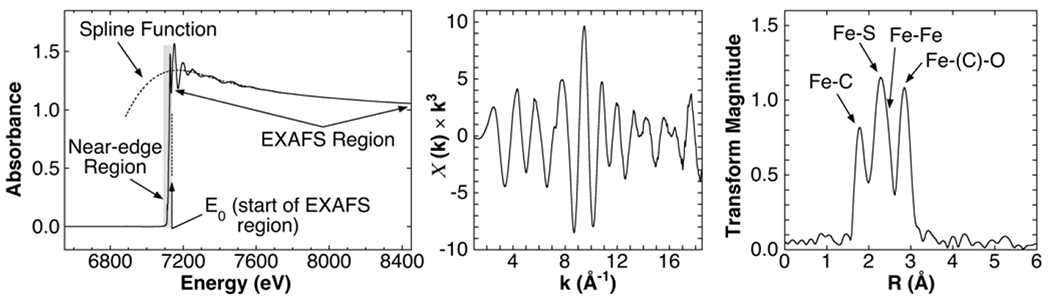
EXAFS data extraction illustrated using experimental Fe K-edge data from Fe₂(adt)(CO)₆ (adt = the azadithiolate ⁻SCH₂NHCH₂S⁻) [6] (Fig. 2 left). Left: The XAS absorption spectrum. A spline function is fitted to the X-ray edge to extract the post-edge oscillations. Center: The EXAFS spectrum is transformed into k-space and re-scaled by k³. Right: The EXAFS Fourier transform shows atoms as a function of distance from the absorbing element.

Fig. 2.

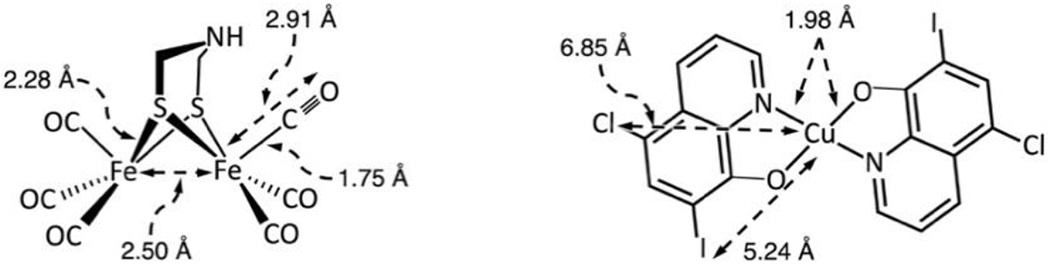
Structures and relevant distances used in this work. Left: Fe₂(adt)(CO)₆ [6]. Right: Cu(CQ)₂; (CQ = clioquinol) [7].

EXAFS has the significant advantage that it does not need a specialized sample form such as a crystal, and thus can be readily used with amorphous or heterogeneous materials such as solutions, biological tissues and complex mixtures. Consequently, it has been applied with great success to a wide range of problems in the physical, chemical, environmental and biomedical sciences [1–3]. Indeed, searching the term “EXAFS” on Google Scholar, reveals over 20,000 articles citing the technique in the title or abstract between 2014–2018.

A major limitation of EXAFS is that it is only available at synchrotron lightsources so the development of a laboratory EXAFS instrument would be a significant advance. Laboratory XAS spectrometers have been built using both traditional X-ray optics (Fig. 3 left) [8] and cryogenic X-ray detectors (Fig. 3 right) [9,10] as their energy-resolving components. While these have been used to measure good near-edge spectra, they so far lack the signal-to-noise needed to measure EXAFS spectra with k > 8 Å⁻¹ on routine samples. This is not surprising, as EXAFS oscillations at high k can be orders of magnitude weaker than near-edge XAS structure (Fig. 1). A practical EXAFS instrument needs to measure up to at least k = 12 Å⁻¹ and preferably k ≥ 17 Å⁻¹, as this allows the analyses to have good spatial resolution and to observe long-distance interactions. For example, EXAFS measurements to k = 8 Å⁻¹ give a poor resolution of ~ 0.25 Å and are limited to distances ~ 3 Å, while k = 17 Å⁻¹ data allows a resolution of ~ 0.10 Å and observation of distances up to ~ 7 Å.

Fig. 3.

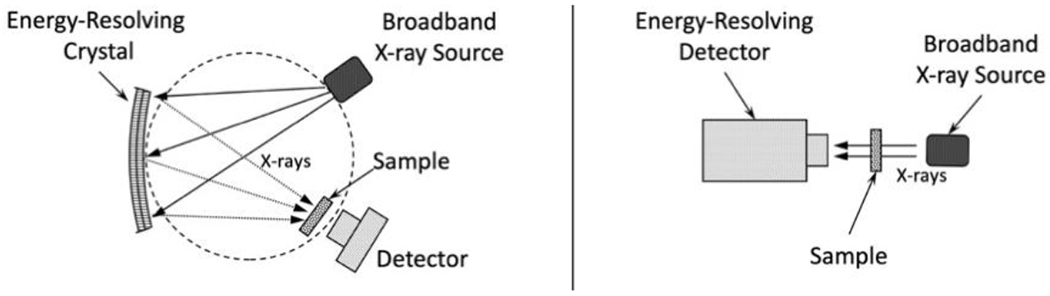
Approaches to laboratory transmission EXAFS. Left: Using an energy-resolving crystal optic. A spectrum is collected one energy point at a time through a combined movement of the crystal, X-ray source and detector [8]. Right: Using an energy-resolving cryogenic detector. The entire spectrum is collected in a single X-ray exposure with no moving parts [9,10].

In this paper, we present a series of computational experiments on the energy resolution, count-rate, and stability needed for good EXAFS to high k. We then use the results to assess the feasibility of using a cryogenic detector as the energy-resolving component of a laboratory EXAFS spectrometer.

2. Methods

Our computational experiments used custom software and EXAFSPAK [4]. We used experimental data from two organometallic complexes with different structural characteristics: Fe₂(adt)(CO)₆ (Fig. 2 left) [6] comprises four groups of atoms at similar distances between 1.75 Å and 2.91 Å, while Cu(CQ)₂, (Fig. 2 right) [7] contains three groups of well-separated and long-distance interactions. Increasing energy resolution was simulated by convolving XAS spectra with appropriate Gaussian functions before extracting the EXAFS. To assess the required statistics, we (1) calculated the transmission without EXAFS, (2) added measured EXAFS, (3) added Poissonian noise for a given detector count rate, and (4) extracted the EXAFS, binning with k = 0.05 Å⁻¹.

3. Results

3.1. Energy Resolution Requirements

The energy resolution of a synchrotron EXAFS facility is typically ~0.5 eV. Broadening this value will tend to attenuate the shorter period components of the EXAFS oscillations in terms of energy. This is expected to both quench oscillations at low k and disproportionally attenuate longer distance interactions. We found that convolving a 5 eV FWHM Gaussian has very little effect on the EXAFS of Cu(CQ)₂, while further broadening attenuates the Fourier peaks, as expected disproportionally impacting the longer interactions (Fig. 4). A similar, but less pronounced effect is seen in the Fe₂(adt)(CO)₆ EXAFS (not shown). In both cases, it is clear that a good EXAFS spectrum can be measured at 15 eV and a satisfactory spectrum at 20 eV.

Fig. 4.

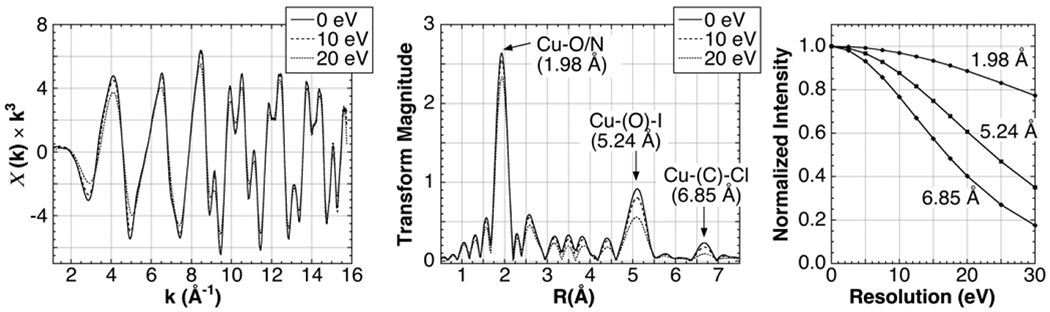
Simulated effect of energy resolution on the Cu K-edge EXAFS of Cu(CQ)₂. Left: EXAFS spectrum convolved with Gaussian functions with increasing FWHM linewidths. Center: The corresponding Fourier transform with key interactions indicated. Elements in parentheses are multiple scattering intermediate atoms. Right: Plot of the intensity of the main peaks in the Fourier Transform as a function of simulated energy resolution.

3.2. Statistics and Stability Requirements

The k-range and thus the spatial resolution of EXAFS measurements are limited by the signal-to-noise ratio at high energies. This is because EXAFS intensity drops ~1/k³, so from 1 to 17 Å⁻¹ the intensity is reduced by ~5000, with a concomitant need for low noise at the high-energy end of the spectrum.

To assess these statistical requirements, we assumed a total count rate of 400,000 s⁻¹ of incident light at the detector over a bandwidth of 4,000 eV (100 s⁻¹ per eV), an intensity well within the capability of laboratory X-ray sources [11]. We found that under these conditions, samples of pure, undiluted Fe₂(adt)(CO)₆ and Cu(CQ)₂ with optimized pathlengths yield good simulated data to k ~ 17 Å⁻¹ in about an hour (not shown). A more challenging case is presented in Fig. 5, with data simulated for a relatively dilute Fe₂(adt)(CO)₆ solution in acetonitrile (0.4% Fe). Such a sample is typical of the more demanding transmission measurements performed at a synchrotron EXAFS facility. Here a recognizable spectrum was obtained to k ~ 17 Å⁻¹ in about 3 hours, and a curve-fitting analysis revealed the major structural features. The spectrum after 10-20 hours is clearly of high quality.

Fig. 5.

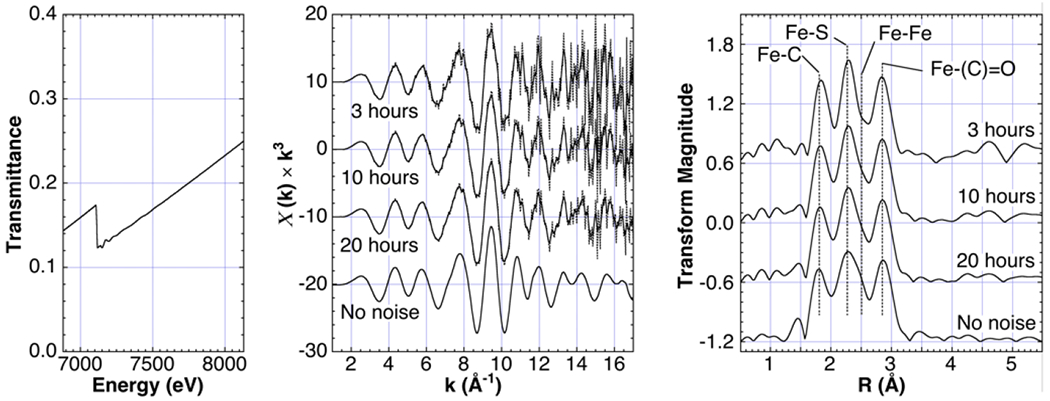
Effect of adding Poissonian noise to the Fe EXAFS of 25 mM Fe₂(adt)(CO)₆ in acetonitrile (0.4% Fe). Left: Transmission. Center: EXAFS at different acquisition times. Right: Corresponding Fourier transform spectra.

Finally, because an EXAFS spectrum is a sum of modified sine waves, non-systematic noise, such as steps, crystal glitches and other discontinuities can substantially disrupt both the spline fit and curve fitting. Indeed, these often limit the experiment at synchrotron lightsources. We note that such noise should be essentially absent from our proposed spectrometer as it collects an entire spectrum in a single exposure with no moving parts. This, of course, requires the detector to have a mostly linear response and to be stable over the hours necessary for the EXAFS measurement.

4. Discussion

Our calculations show that a high quality EXAFS spectrum to k = 17 Å⁻¹ can be measured on dilute (~ 50 mM) samples in a few hours, given an energy-resolving detector with an energy resolution of 15 eV or better, and an overall count rate of around 400,000 s⁻¹ for a 4,000 eV incident energy bandwidth. Table 1 compares the characteristics of current detector technologies. While Ge and Si semiconductor detectors have more than sufficient speed, their resolution is insufficient for EXAFS. By contrast, cryogenic transition edge sensors (TES) [9,10,12] and metallic magnetic calorimeters (MMC) [13] have more than sufficient resolution but their slower speeds would require long data acquisition times for comparable statistics. Finally, scanning instruments based on spherical bent crystal analyzers (SBCAs) do not have sufficient throughput and may well be susceptible to crystal glitch discontinuities.

Table 1.

Comparison of detector technologies.

Detector	Resolution	Speed/Pixel	Stability	Energy Range
Ge, Si	~100-200 eV	~100,000 s−1	Good	~MeV
SBCA [8]	~1 eV	Scanning	Difficult	~100 keV
TES [9,10,12]	~2 eV	~100 s−1	Good	~100 keV
MMC [13]	~2 eV	~10 s−1	Good	~100 keV
STJ [14–16]	~15 eV	~5000 s−1	Good	~1 keV

Superconducting tunnel junction (STJ) detectors [14,15] are well-suited for transmission EXAFS, as their energy resolution is still sufficient, and their relatively high speed enables short data acquisition time. A 100-pixel STJ array meets our criteria for measuring EXAFS spectra to k = 17 Å⁻¹ within hours. Unfortunately, while most EXAFS measurements use energies between 4–14 keV, our current Ta-based STJ detectors lose resolution and suffer from a line-splitting artifact above ~1 keV. However, Pb-STJs with a resolution of 11 eV at 6 keV and without line-splitting artifacts have been demonstrated [16]. An STJ array capable of operating in the typical EXAFS energy range of 3-12 keV would be a novel device, and we are exploring development paths based on STAR Cryoelectronics’ existing commercial STJ platform.