Simultaneous cross-evaluation of heterogeneous E. coli datasets via mechanistic simulation

Abstract

The extensive heterogeneity of biological data poses challenges to analysis and interpretation. Construction of a large-scale mechanistic model of Escherichia coli enabled us to integrate and cross-evaluate a massive, heterogeneous dataset based on measurements reported by various labs over decades. We identified inconsistencies with functional consequences across the data, including: that the total output of the ribosomes and RNA polymerases described by data is not sufficient for a cell to reproduce measured doubling times; that measured metabolic parameters are neither fully compatible with each other nor with overall growth; and that essential proteins are absent during the cell cycle - and the cell is robust to this absence. Finally, considering these data as a whole leads to successful predictions of new experimental outcomes, in this case protein half-lives.

The generation of biological data is rapidly presenting us with one of the most demanding data analysis challenges the world has ever faced (1) - not only in terms of storage and accessibility, but perhaps more critically in terms of its extensive heterogeneity and variability (2). With respect to heterogeneity, study of a biological system of interest typically involves many diverse measurements, from lower-throughput blotting techniques to high-throughput sequence and spectrometry-based technologies, and beyond. In terms of variability, it is often the case that studies produced independently from each other report results that seem to be at odds with one another. This is most readily apparent when studies of the same system perform the same measurements, but obtain different results – an issue that has led high-profile journals to question the reproducibility of results in multiple scientific fields (3,4).

Although issues associated with heterogeneity and variability each represent major analysis problems on their own, the challenges posed by both in combination are still more difficult - but also present greater opportunities for discovery. The problems arise because assessing the data’s veracity means not only determining whether the data are reproducible (i.e., does a repeated study produce the same measured outcomes), but also, and perhaps more deeply, whether they are cross-consistent - meaning that the interpretation of multiple heterogeneous datasets all points to the same conclusion. The opportunities emerge as seemingly discrepant results across multiple studies and measurement modalities may be not only due to the error associated with a technique or the human hands performing it, but also because of the complex, non-linear and highly interconnected nature of biology. In such cases, the identification of data discrepancy would be a strong indicator for future insight and discovery.

To this end, the goal of this project is to cross-evaluate a massive, heterogeneous set of measurements that have been reported in model organism Escherichia coli in thousands of papers and by hundreds of labs over the past several decades. Determining the cross-consistency between these various measurements requires an understanding of the known or presumed biological relationships which connect them. Thus, we adopt a mathematical approach that can represent these relationships mechanistically while simultaneously accommodating many millions of heterogeneous data points. Efforts to model cell behavior at the cell scale span several decades (5–12). We reported a modeling approach which was capable of integrating all of the known functions in the simplest culturable bacterium, Mycoplasma genitalium (13).

A major advantage of this “whole-cell” modeling approach is that heterogeneous data are linked mechanistically through the simulated interaction of cellular processes, providing the most natural, intuitive interpretation of an integrated dataset (14). The Mycoplasma model successfully reproduced many measured data, and even predicted previously unmeasured parameters which were subsequently verified experimentally (15). Construction of this model also enabled us to cross-evaluate data and identify discrepancies: as a relatively simple but illustrative example, the DNA concentration per cell measured in M. genitalium was only a fraction of the DNA mass required to make up the genome sequence (13). This led us to favor the genome sequence data in determining the parameters governing DNA concentration.

E. coli has nearly ten times more genes than M. genitalium, comprises roughly 50 times as many molecules, can readily grow in a wide variety of environmental conditions, and exhibits extensive self-regulation and control, all of which pose significant challenges to whole-cell modeling – and the model described in this report only accounts for a subset of these genes, environments and functions. However, one of the most exciting aspects of modeling E. coli on a large scale is the enormous effort in data generation that has already been performed. Thus, whereas only 27.5% of the parameter values in our M. genitalium model were actually derived from measurements using that organism, 100% of the values incorporated into the model we describe here were derived directly from E. coli. This provided us with an unprecedented opportunity to assess the literature against itself.

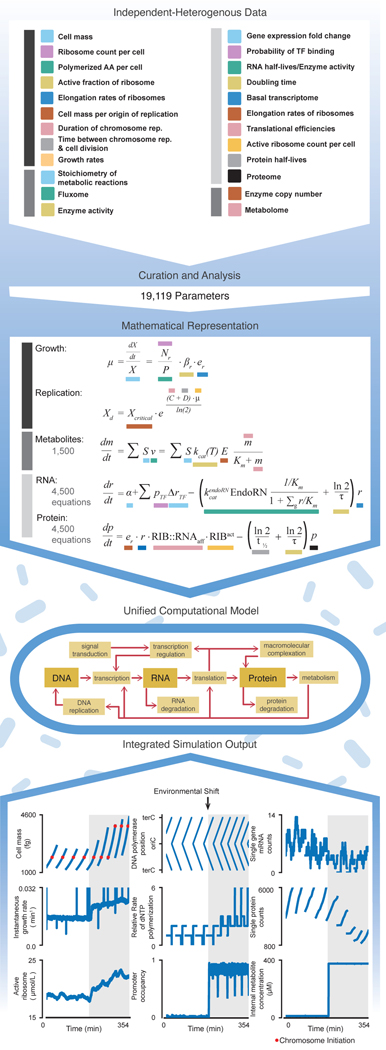
Our overall approach is depicted in Fig. 1 and Movie S1. We compiled an extensive set of high- and low-throughput measurements from databases and published reports, to identify datasets that characterize mRNA and protein expression under a variety of environmental conditions (some of which we generated for this study, see Online Methods), mRNA and protein half-lives, ribonuclease kinetics, gene locations, transcription factor binding sites, dissociation constants for proteins bound to DNA binding sites or other cellular and environmental ligands, translational efficiencies of mRNA transcripts, chemical reaction stoichiometry, enzyme kinetic and substrate transport rates, internal metabolite concentrations, ribosome and RNA polymerase concentrations and elongation rates, the rate of DNA initiation and other cell cycle parameters, and other physiological properties (e.g., growth rates, chemical composition of the cell) (see the Supplement for a complete description of included data).

Fig. 1. A large-scale, integrated modeling approach to simultaneously cross-evaluate millions of heterogeneous data.

The data were collected from the primary literature and key databases, and in some cases were also generated as part of this study. Subsequent data curation and analysis led to the determination of 19,119 parameter values. We then incorporated these data into a large-scale computational model of E. coli gene expression, metabolism and growth, based on a foundation of > 10,000 interdependent mathematical equations that are then transformed into appropriate computational representations of biological processes. Color coding is used to connect terms in these equations to the data that produced their parameter values. This unified model was then used to produce fully integrated simulations, with output as shown at bottom. See Fig. S1, Movies S1 and S2, and the Supplement for more detail. Full details of the analysis required to generate this figure, as well as a pointer to the generating code, can be found in the Supplement, Section 1.2.

Curation of these data led to the identification of over 19,000 parameter values, listed by category in Table S1, and given in detail in the GitHub repository for our model. To compile these values, we created a computational model that brings RNA and protein expression together with carbon and energy metabolism, in the context of balanced growth. These datasets are integrated mathematically, beginning with a system of over 10,000 mathematical equations which are schematically illustrated in Fig. 1 (we use ordinary differential equations here as a reduced representation of the actual model, whose implementation is more complex - details can be found in the Supplement). Functionally, 1,214 genes (or 43% of the well-annotated genes) were included to represent these processes, which required several major improvements over our previous work in M. genitalium, not only in terms of modeling but also software improvements in runtime and accessibility (see Supplement for details). For this study, the model-data comparisons were examined under the conditions of exponential growth in three experimentally-characterized environments: minimal (M9 salts plus glucose under aerobic conditions), rich (minimal plus all amino acids), and minimal-anaerobic media.

We assessed the cross-consistency of the parameter set as a whole and identified areas of inconsistency by populating our model with these literature-derived parameters and running detailed simulations of cellular life cycles. In the analysis of these simulations, we identified several critical areas in which the data contributing to these models were not cross-consistent. These inconsistencies led to readily observable consequences. Moreover, by incorporating these findings, we constructed a functional and predictive model which produced simulation output as shown in Fig. 1, Fig. S1 and Movie S2.

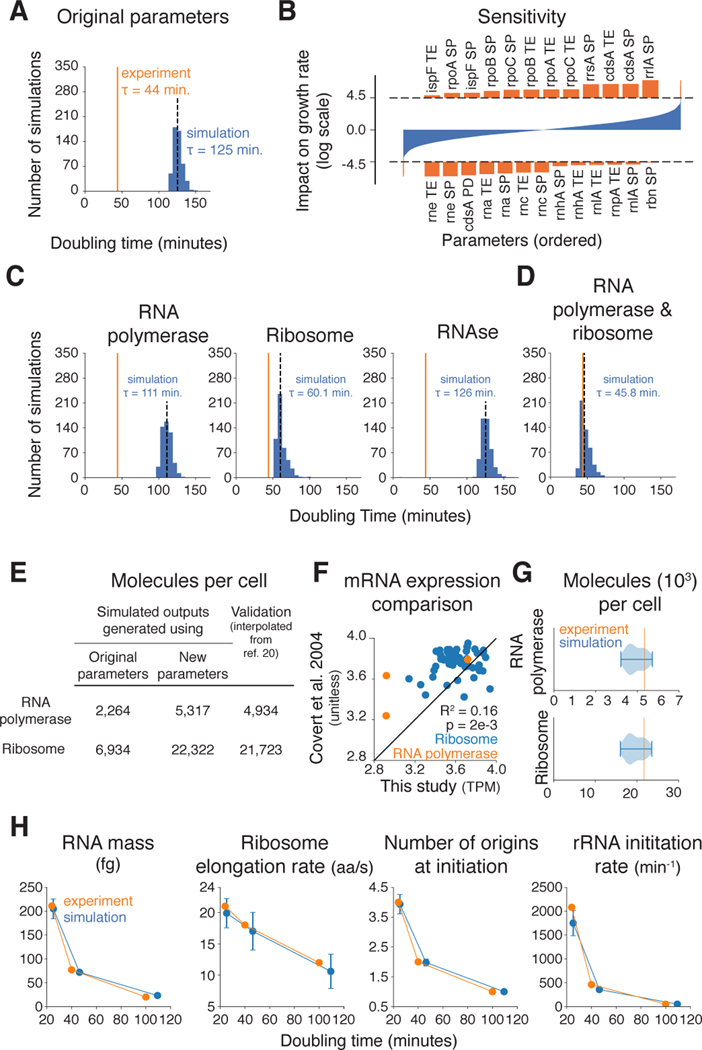
The first inconsistency we identified was that the total output of the ribosomes and RNA polymerases – as derived from the integrated data sets – was not sufficient for the simulated cell to reproduce measured growth rates. The overall growth of the cell depends on the production of protein, which in turn is largely governed by these two major complexes, the cell’s mRNA and protein synthesis machinery. The ribosomal content of the cell has been measured or estimated for different growth rates, as have the expression and half-lives of the ribosomal RNA and protein components (11,16,17), their associated translational efficiencies (18), and the stoichiometry of the functional complex (19). The expression and half-lives of the RNA polymerase subunits has also been measured or estimated (11,16). When these measurements were integrated into our simulation, the resulting median doubling time for our simulations was 125 minutes, in comparison to the 44 minutes measured experimentally for cells growing on glucose minimal media (Fig. 2A). Thus the doubling time measurements and the measurements related to ribosomal and/or RNA polymerase output appeared to be inconsistent.

Fig. 2. Ribosomal and RNA polymerase output must be increased to support measured doubling times.

(A) Histogram comparing simulated doubling times (blue) to the experimentally determined doubling time for aerobic growth on glucose minimal media (orange line) with the model’s original parameter values taken directly from the literature. Median simulated doubling time is 125 minutes (dashed black line). (B) Sensitivity analysis outcome reported as the z-score (log-scale) of the difference in growth rate for all simulations where a given parameter was adjusted higher and all simulations where a given parameter was adjusted lower. Horizontal dashed lines represent a z-score cutoff for a p-value below 0.05 that has been adjusted for multiple hypothesis testing of each of the parameters that were adjusted (93% of the total parameters, see supplement for more details). Parameters are ordered by their impact on the simulated cells’ growth rate along the x-axis with those having a significant z-score highlighted in orange and shown in more detail above and below the plot of all parameters. Parameters with the largest positive correlation with model growth are listed across the top, and parameters with the largest negative correlation are listed across the bottom. Parameter abbreviations are: translational efficiency (TE), RNA synthesis probability (SP) and protein degradation rate (PD). (C and D) Histograms comparing simulated doubling times (blue) to the experimentally determined doubling time for aerobic growth on glucose minimal media (orange line), with RNA polymerase, ribosome, and RNAse expression calculated from the known doubling time as independent experiments (C), and with both RNA polymerase and ribosome expression calculated from the known doubling time (D). Median simulated doubling times are shown as dashed black lines. (E) RNA polymerase and ribosome abundances per cell as generated by the model in this study using the original (Fig. 2A) and new transcript synthesis probabilities (Fig. 2D), as compared to experimental data that was withheld from the model’s original parameterization from (20). (F) Comparison of mRNA expression as measured by RNA-sequencing in this study (TPM, transcripts per million) and from a previous microarray study (51). (G) Violin plots showing distributions of RNA polymerase and ribosome cellular abundances from the simulations shown in Fig. 2D, compared with expected values determined experimentally (orange lines) (20). (H) Cellular properties calculated from the simulations for three different environmental conditions compared with their counterpart measurements reported in the literature (21). Error bars report standard deviations of each property calculated over the 1,024 cells that were simulated for each medium. Full details of the analysis required to generate this figure, as well as a pointer to the generating code, can be found in the Supplement, Section 1.2.

To further dissect this inconsistency, we performed a sensitivity analysis to determine which parameters were most likely to have an impact on the doubling time. We ran 20,000 simulations, each for 10 seconds of simulation time, in which 10% of the parameter values were randomly chosen and their value increased or decreased by five-fold (also chosen at random). In order to cause an observable impact, it was necessary to vary many parameter values at once because there are so many interaction effects between parameters. After the growth rate was determined at the end of each simulation, the effect of a particular parameter on growth rate was determined by finding the average growth difference between the cases in which the parameter was raised and when it was lowered, and then assessing each parameter’s individual effect in the context of the total distribution of parameter effects. The top hits from our analysis involved parameters related to ribosomal and RNA polymerases, RNAses, and a metabolic enzyme encoded by the cdsA gene (Fig. 2B).

Based on these findings, we first considered changing parameters related to the expression of ribosomes, RNA polymerases, and RNAses (the enzyme cdsA is considered in more detail below). When increasing the expression of one protein, the expression of all other genes must be decreased in order to maintain the total amount of mRNA and protein per cell at their experimentally measured values. Thus, we used an iterative parameter estimation approach based on ODEs that calculates the amount of protein produced from the ribosomal and RNA polymerase content at a given growth rate (see Supplemental Methods). Our results showed that increasing the RNA polymerase, ribosomal, or RNAse expression alone was not sufficient to lower the doubling time to measured values (Fig. 2C). However, an increase in the expression for both RNA polymerases and ribosomes did enable us to simulate an accurate doubling time (Fig. 2D). The new polymerase and ribosome calculations matched well with estimates of expression [compiled in (20)] that were not used to create our model (Fig. 2E).

Although these results supported the hypothesis that the expression of RNA polymerases and ribosomes were not adequately captured by the initial parameters fed into the model, it was not clear which parameters were most likely to be problematic. Thus, we evaluated each parameter contained in our RNA polymerase and ribosomal expression equations, grading them on three criteria: (1) literature reproducibility, meaning that the parameter value could be supported by independent measurements; (2) whether changing the parameters would lead to an adequate change in the simulated doubling time; and (3) whether the simulations performed in (2) also matched the abundances of ribosomes and RNA polymerases from Fig. 2E (20). This analysis (detailed in Fig. S2A and S2B) revealed that the transcript synthesis probabilities of genes that produce subunits of RNA polymerases and ribosomes were the most favorable parameters to change, since they were relatively variable between experiments (Fig. 2F) and had a strong enough effect on the doubling time (Fig. 2D) and protein abundances (Fig. 2G). Thus, we calculated new gene transcription probabilities for RNA polymerase and ribosomal subunits based on the measured doubling time instead of from global mRNA measurements; these new transcription probabilities are the only changes to the data that continue to the rest of this study (Table S2A). In total, production of all RNA polymerase genes had to be increased by roughly twofold to recapitulate measured growth rates (see Table S2B for all changes to expression parameters). Ribosomal gene expression was more complex: although some genes required an increase in the production rate greater than threefold, the expression of other subunits was actually decreased. Accommodating these changes further required a global decrease in production rate (for all other non-ribosome and non-RNA polymerase genes) to roughly 89% of their original values to maintain the overall RNA mass in the cell. These adjustments led to simulated doubling times that were consistent with measurements on the glucose minimal aerobic medium (Fig. 2D). Similar analyses were performed for the other two environments; the final simulations in all three simulated environments were consistent not only with doubling times (Fig. S2C), but also with other measurements including RNA mass per cell, ribosome elongation rates, stable RNA synthesis rates, and the average number of DNA replication origins per cell at the time of replication initiation (Fig. 2H) (21). The final simulations could also reproduce the linear relationship, between the RNA/protein mass ratio and the growth rate, that was previously observed for cells growing in different environments (22) (Fig. S2D). Finally, the simulation output also showed that in fast-growing cells, the cell mass added over the life cycle is uncorrelated with the initial cell mass (a phenomenon referred to as “adder” behavior), whereas for slower growing cells, the added and initial cell masses are correlated (“sizer” behavior) (Fig. S2E), in agreement with recent reports (23–26). We concluded that modifying the parameters related to the expression of certain ribosomal subunits, together with a global increase in RNA polymerase expression, caused our simulations to better reflect multiple physiological observations.

The second major discrepancy we found concerned the parameter values that determine the activity and output of E. coli’s metabolic network. These are the kinetic parameters of each biochemical reaction, as well as the parameters related to gene expression for each metabolic enzyme. Taken as a whole, these parameter values must be consistent with each other such that the metabolic network can support mass and energy demands without unstable pooling or depletion of intermediate metabolites. In practical terms, this means that the chemical composition of a cell, or the metabolic demand on the cell, has to be balanced with the supply provided by the metabolic network.

Metabolism is probably the most thoroughly characterized network in E. coli (8,27,28). In our model, a metabolic network model derived from the EcoCyc database (29) is represented using an expansion of flux balance analysis (FBA), which uses an optimization strategy to predict metabolic network behavior even when few parameters are known (30). To add kinetic information to this model, we searched through this literature – thousands of papers in all – and identified 639 relevant kinetic parameters governing the activity of 404 biochemical reactions in the metabolic network. Whereas traditional FBA is based on an objective function that serves to maximize biomass concentration in fixed relative proportions, our method uses an objective function that is both more flexible [and thus better suited to dynamic simulations (31)] and explicitly incorporates kinetic parameters, as well as metabolite and enzyme concentrations. Specifically, we implemented a two-term objective which penalizes unbalanced growth or depletion of intermediate metabolite concentrations (the metabolic cost function) while also encouraging the flux through the network to match that predicted using the kinetic parameters described above (the kinetic cost function). These two terms are related by a weighting factor, which we set to optimize a trade-off between including kinetic data in the model while not compromising cell growth (see Fig. S3A–F and Supplemental Text for complete details).

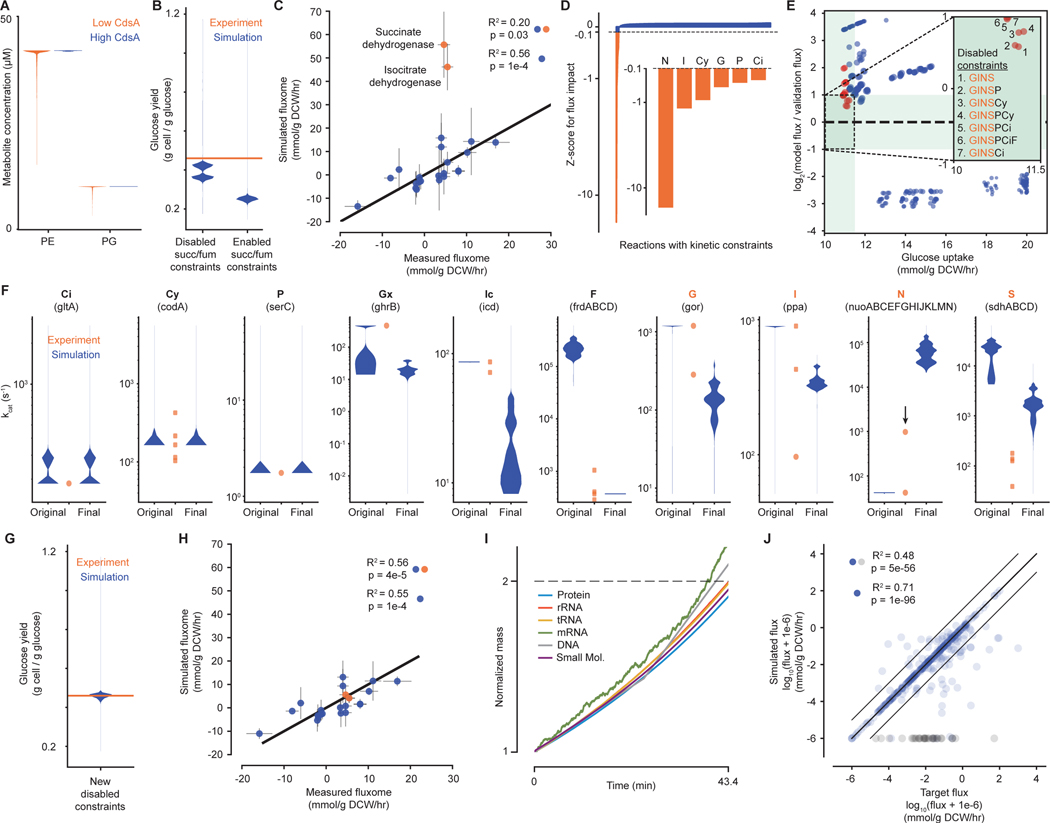
During this process, we noticed three areas of inconsistency with regard to metabolism. First, low expression of enzyme-encoding genes could overconstrain the biochemical capacity of the metabolic network. The only example of this we found concerned the cdsA gene product; in particular, we found that a significant fraction of simulations would not produce an adequate amount of phospholipids unless cdsA expression was artificially increased in the model (Fig. 3A). We investigated the low expression of this gene further in the context of RNA-Seq (18), proteomics (32) and gene essentiality datasets (33) – the latter two of which were not used in the construction of the model. This comparison confirmed that mRNA expression of cdsA was indeed low (further confirmed via qPCR in Fig. S3G), but was detectable at the protein level, and also that it was an essential gene. That this essential protein – identified in Fig. 2B as one of the most important effectors of simulation doubling time - was so lowly expressed that its count dropped to zero in the simulations was a puzzling contradiction within our data (investigated further below).

Fig. 3. Evaluating metabolic parameter values against each other and in the context of cellular growth.

(A) Violin plot of concentrations at each simulation time point for downstream metabolites of the reaction catalyzed by CdsA – phosphatidylethanolamine (PE) and phosphatidylglycerol (PG) – when the concentration of CdsA is low (orange – original, short protein half-life) or high (blue – new, longer protein half-life, see main text). (B) Violin plot for glucose yield at each simulation time point for simulations with succinate dehydrogenase and fumarate reductase kinetics constraints disabled or enabled. Experimental value is 0.46 g cell / g glucose at μ=0.900 hr⁻¹ (52). (C) Comparison of the average fluxes from simulations with succinate dehydrogenase and fumarate reductase constraints disabled for a set of reactions in central carbon metabolism with experimental measurements (34). Orange points indicate outlier fluxes, which are discussed in more detail in the text. Correlation is shown for all data points (blue and orange) and when excluding outliers (blue). (D) Impact of individually disabling each kinetic reaction constraint on the succinate dehydrogenase flux in simulations, shown as a z-score representing the average change in flux for removing one constraint compared to the distribution of the average change in flux for removing each constraint. Constraints that have a z-score of <−0.1 are highlighted in orange and shown in more detail. Highlighted reaction constraints are part of the reactions that are further explored in E (abbreviations are listed below in F). (E) Comparison of average metrics for simulations from a two-level full factorial design to test the effects of removing up to eight kinetic constraints of interest. Inset shows the target region where the simulated glucose uptake rate is close to the expected glucose uptake rate and simulation succinate dehydrogenase flux is within a factor of 2 of the experimental flux (green region). Disabled constraint combinations are enumerated for each point in the target region. Orange points indicate simulations run with combinations of disabled constraints that included G, I, N and S; blue points indicate simulations run with at least one of these constraints enabled. (F) Distributions of predicted k_cat value at each simulation time step (blue) and curated kinetic parameters (orange) for each reaction identified – citrate synthase (Ci), cytosine deaminase (Cy), phosphoserine aminotransaminase (P), glyoxylate reductase (Gx), isocitrate dehydrogenase (Ic), fumarate reductase (F), glutathione reductase (G), inorganic pyrophosphatase (I), NADH dehydrogenase (N),and succinate dehydrogenase (S). Original is from simulations without constraints for S and F; final is from simulations without constraints for Gx, Ic, G, I, N, and S. The black arrow for N indicates a newly curated k_cat parameter that was not used in the model. (G and H) Similar to (B and C), but based on data from simulations with the new set of disabled constraints. (I) Representative output from simulations with the new set of disabled constraints, showing the increase in mass (normalized to initial mass and over a single life cycle) of six key cellular mass fractions. (J) Comparison between the metabolic fluxes calculated directly from the kinetic parameters (target) and the fluxes computed by simulations with the new set of disabled constraints, as summarized by the R² value. Gray points correspond to reactions with no simulated flux despite having a target flux. Correlations are shown for all data points (blue and gray) and with gray points excluded (blue only). Full details of the analysis required to generate this figure, as well as a pointer to the generating code, can be found in the Supplement, Section 1.2.

Having considered the constraints that low cdsA expression imposed on the metabolic network, we then turned to the constraints imposed by kinetics, and found that the kinetic parameter set in its initial form was also inconsistent with (i.e., unable to produce) known cellular growth rates. Preliminary comparisons between the simulations with and without kinetics specifically identified the constraints on succinate dehydrogenase and fumarate reductase as preventing cell growth due to inefficient carbon source utilization (Fig. 3B). The constraints imposed on these enzymes by their parameter values were therefore initially removed from the model. However, when comparing our simulated metabolic flux outputs to a metabolic flux validation dataset (34) which was not originally used to create or parameterize the model, we found the simulation and data were highly correlated, with the exception of two fluxes in the TCA cycle: those mediated by succinate and isocitrate dehydrogenase (Fig. 3C). The identification of succinate dehydrogenase as problematic in both analyses – even with its kinetic constraint removed – indicated that the kinetic parameters for other reactions might also be responsible for our observations. Thus, we performed a global analysis in which every kinetic constraint was tested individually to see whether perturbing its value impacted the flux pathways through either succinate or isocitrate dehydrogenase. This analysis identified six additional reactions as having potentially problematic kinetic parameter values, for a total of nine: NADH dehydrogenase, inorganic pyrophosphatase, cytosine deaminase, glutathione reductase, phosphoserine aminotransaminase, citrate synthase (Fig. 3D), in addition to succinate dehydrogenase, fumarate reductase (Fig. 2B) and isocitrate dehydrogenase (Fig S3H). A deeper review of the literature revealed that isocitrate dehydrogenase is part of a more complex control circuit, also involving glyoxylate reductase (35), which has not been completely specified. Because the full behavior of this circuit cannot be described, the isolated kinetic constraints for these reactions were removed from the final model, leaving us with eight reactions to consider in more depth.

To determine the main and interaction effects between the eight remaining kinetic constraints, we performed a full factorial, two level experimental design, with 256 (2⁸) sets of simulation runs. These runs simulated the result of removing or including all of our identified kinetic constraints in every possible combination. The combinations of constraints that produced simulation outputs with strong agreement with the fluxome (34), as well as with the growth yield on glucose, were always missing at least succinate dehydrogenase, NADH dehydrogenase, inorganic pyrophosphatase, and glutathione reductase (Fig. 3E) indicated that the values for these kinetic constraints are inconsistent with the rest of the data. We therefore removed the constraints associated with these final four reactions for a new round of simulations, and used the simulated fluxes and enzyme expression data to calculate a new estimated distribution for each kcat. Fig. 3F shows the kcat distributions for all ten of the reactions mentioned above, in both our original and final model, together with kinetic parameters identified from the literature. In the cases of citrate synthase, cytosine deaminase, and phosphoserine transaminase, the distributions were similar in the original and final model, and were acceptably close to measured values. The remaining cases showed stronger differences between the original and final model. We expected these differences in the cases of glyoxylate reductase and isocitrate dehydrogenase, due to the complexity of these enzymes’ regulation. In contrast, for the cases of fumarate reductase, glutathione reductase, and inorganic pyrophosphatase, the new kcat distributions were a better reflection of the measured values. Finally, NADH dehydrogenase and succinate dehydrogenase are both membrane proteins, which are notoriously difficult to characterize kinetically. For NADH dehydrogenase in particular, a new kinetic measurement, not used in the construction of the model, was derived from a recent and more sensitive technology (36). The resulting kcat (highlighted with an arrow in Fig. 3F) was roughly 23-fold higher than previous measurements, and was closer to our new model kcat value distribution. This supports others’ assertions that the effective kcats for membrane-bound enzymes may be much higher in vivo than measurements have reported (37), and may therefore explain the discrepancies between experimental measurements and our model distributions for these enzymes. In total, we found that our new version of the model was better at matching the measured kcats (Fig. 3F), as well as the growth yield (Fig. 3G) and fluxome (Fig. 3H), and also was able to reproducibly simulate balanced growth (Fig. 3I).

Finally, beyond our growth and fluxome comparisons we also wanted to test the global cross-consistency of all kinetic parameters governing the activity of metabolic pathways in the overall network. One way to achieve this is by comparing the target flux values included in the kinetic component of the objective function (calculated from both the curated kinetic parameter values and the simulation’s enzyme and metabolite concentrations) with the simulation output flux values. As shown in Fig. 3J, 215 out of 380 fluxes were within 5% of the target flux. However, there were also 33 fluxes whose values are zero in the simulations but have non-zero target values; these values reflect the fact that the model is not yet functionally complete and so the resulting metabolites would be left unused. We found that we could obtain higher – never perfect – consistency between the flux values by increasing the weight on the kinetic component of the objective function – but this resulted in slower and less steady growth (Fig. S3B). Barring the above exceptions, the strong agreement between these two sets of flux values indicates a high level of cross-consistency between the kinetic parameter values themselves.

Our third finding was that the production of cellular protein can only be met by the overall capacities of the cell (in terms of building block resources as well as cell size and mass) if most of the genes are transcribed less than once per cell cycle - including a number of essential genes. This observation was preceded by a comparison between our model simulations of protein expression with a validation dataset (>2,000 points) that was also withheld from the creation and parameterization of the model (32). We found a strong correlation between the predicted and observed protein abundances at higher expression levels; at lower levels, we did not see a correlation – which can be explained by the detection limits of high-throughput mRNA and protein measurement technologies (Fig. 4A) (38). The overall correlation for protein abundances ≥30, although significant, has an interesting consequence at the level of individual genes: we found that although many genes are transcribed multiple times as a typical cell grows and divides under these conditions (aerobic glucose minimal media), a clear majority of the genes in E. coli are transcribed at a rate of less than once per cell cycle (Fig. 4 B and C). Such sub-generational gene expression has been observed, both theoretically (39,40) and experimentally (41–43), but our model led us to two insights: first, that sub-generational transcription impacts over 50% of the genes in E. coli – and second, that 72 essential genes are among those that are sub-generationally transcribed (Fig. 4D) (see Supplement for essentiality criteria).

Fig. 4. A large fraction of E. coli genes are transcribed less than once per cell cycle.

(A) A comparison of simulation and experimental results (32) with regard to the number of proteins expressed per cell for each gene. The proteins are grouped as being highly abundant if the measured count per cell is greater than or equal to 30, and otherwise low-abundant. The R-squared statistic is computed separately for each group on the log-transformed data. (B) Simulations of mRNA and protein expression over multiple generations for genes that are expressed at high (left, in red) and low levels (right, in blue; note that colors are conserved to preserve meaning throughout the figure) of transcriptional frequencies. Counts are shown for a representative six-generation long window, with an arbitrarily chosen zeroth starting generation. (C) Frequency of observing at least one gene transcript per generation over a 32-generation simulation. Histograms show that 1,547 genes are transcribed at least once per cell cycle (red), 203 genes are essentially never expressed in this environment (yellow), and the remaining 2,603 genes are transcribed with a frequency between zero and one (blue). (D) Expression frequency analysis of known essential genes. (E) Division of the sub-generationally transcribed genes into those for which at least one protein is present at all times during the simulations, and those for which the protein is absent for at least one time step (gray bars). Protein products of essential genes are indicated by the blue bars. Distinct protein units represent sub-generationally expressed monomers and protein complexes composed of sub-generationally expressed monomers. (F) Transcription, translation, complexation and metabolic activity of the PabAB heterodimer, which catalyzes a reaction responsible for producing folates. Each new generation is indicated with a tick mark along the x-axis; the gray area highlights a period of time in which the heterodimer is not present in the cell. All y-axes are linearly scaled except the [10^-3, 0.44] region of the reaction flux plot which is log-scaled for better readability. Full details of the analysis required to generate this figure, as well as a pointer to the generating code, can be found in the Supplement, Section 1.2.

How might cells survive and grow when some of its essential genetic content is not transcribed at all during a typical division cycle? One possibility is that, although the mRNAs may be rarely present in the cell, the corresponding proteins and protein complexes produced are numerous and stable enough that the cell never experiences their functional absence (i.e., a period of time in which the protein is completely absent from the cell). In fact, this accounted for roughly one thousand of the functional protein units (including complexes and functional monomers) of sub-generationally transcribed genes in our simulations – leaving just over 1,400 protein products which are completely absent from the cell at least part of the time, including 23 proteins which are considered products of essential genes (Fig. 4E) (Table S4).

This suggests that certain proteins believed to be required for cell viability are likely to be absent from single cells for periods of time. In the case of an essential protein, how does the cell compensate for its temporary loss due to very low expression rates? To answer this question, we turned to our integrative modeling framework, which uniquely enables us to investigate the loss of these proteins as part as a unified system. A representative example is 4-amino-4-deoxychorismate synthase, a heterodimeric enzyme involved in folate biosynthesis. The genes encoding this enzyme, pabA and pabB, are each transcribed with a frequency of 0.94 and 0.66 times per cell cycle, respectively (Fig. 4F), producing an average of 34 PabA proteins and 101 PabB proteins per generation. The enzyme is only active as a heterodimer (PabAB) in our model, for which the average count of active complex in our simulations is 43.8, with a standard deviation of 35.3 – and we readily observed periods of time in which no heterodimer existed (Fig. 4F, gray region). During the periods in which the PabAB dimer is completely absent, the internal pool of 5,10-dimethylene tetrahydrofolate (methylene-THF) was reduced over time; however, following a new round of pabA or pabB expression, methylene-THF was rapidly resynthesized. We further confirmed that the parameter value for the synthesis probability of pabB mRNA is causal for PabAB and methylene-THF depletion, as lowering the value exacerbated it (Fig. S4). Supporting this proposed mechanism, others have shown that bacterial metabolite pools display a much wider dynamic range than protein concentrations, and can change by 50- to 170-fold over time, including by almost complete depletion of certain metabolites (44). We conclude that internal metabolite pools, replenished by rapid enzyme kinetics, can provide a literal buffer to make cell growth robust to intermittent loss of key enzymes.

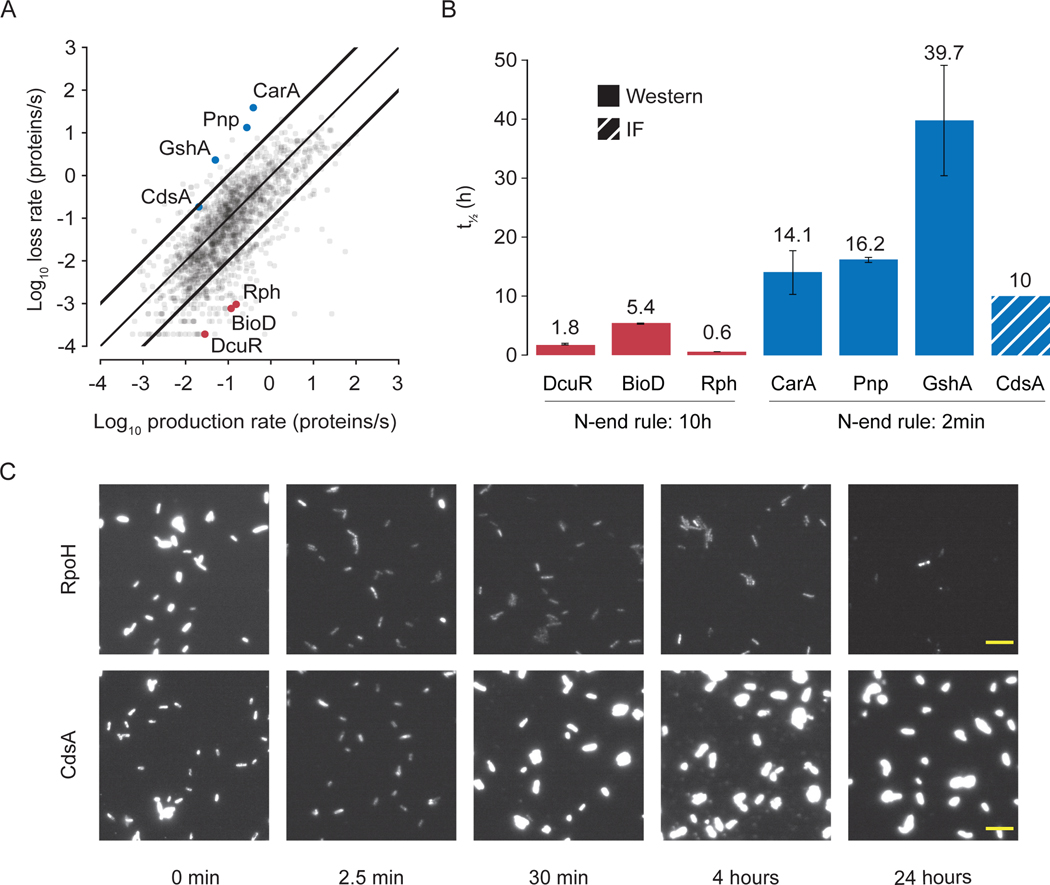
The fourth finding of this study was that the data we compiled, when considered as a unified whole, can lead to successful predictions in vitro – in this case protein half-lives. As shown in Fig. 1, the equations that govern mRNA and protein expression incorporate many types of available data, and once populated in our model, were able to successfully predict protein abundance measurements which were previously withheld from the model (Fig. 4A). Not all proteins display such consistency, however, and so we performed further analysis in which the previously-withheld proteomics data (32) was also taken into account, to identify and understand the causes of discrepancy for these proteins. We first noted that cells whose entire division cycle occurs in the log or exponential phase of growth may be considered to be operating at a steady state in terms of maintaining mRNA and protein concentrations. This can be represented mathematically by setting the derivative terms in Fig. 1 to zero, and substituting the solution for the mRNA concentration into the equation governing protein concentration. If the experimental data which populate these equations are consistent, then the average rate of protein production should equal the average rate of protein loss (where the loss rate includes loss by dilution as well as by degradation). This proved to largely be the case, with 85% of the production rates within an order of magnitude of the corresponding loss rate (Fig. 5A).

Fig. 5. Integrated model-data comparison leads to improved prediction of protein half-lives.

(A) A comparison of calculated protein production rates against protein loss rates for each gene. Bold lines indicate areas where the production rate and loss rate differs by more than one order of magnitude. (B) Comparison of the N-end rule to new measurements of protein half-lives for the genes highlighted in (A). The three points highlighted in red were predicted to be outliers in the steady-state analysis because their corresponding protein half-lives were much shorter than the N-end rule’s prediction of 10 hours. Similarly, the proteins highlighted in blue were were predicted to have much longer half-lives than the N-end rule’s prediction of 2 minutes. Solid bars indicate half-lives that were determined by intensities on a western blot and the striped bar indicates an estimate (assumed from higher N-end rule value) from intensity measurements using immunofluorescence. In all seven cases, these predictions were correct. The results of control experiments (testing our protein half-life measurements against previous reports) can be found in Fig. S5. (C) Images of E. coli MG1655 cells with either a His-tagged RpoH or CdsA plasmid that were induced for 1 hour using IPTG followed by the addition of tetracycline to inhibit translation. At the indicated timepoints, aliquots of the culture were harvested, and immunofluorescence was carried out using an anti-His antibody. His-RpoH protein signal decreased within minutes, while His-CdsA protein signal was maintained or increased over the timecourse. All images shown are scaled between 50–1000 AU. Scale bar (yellow) = 10 μm. A detailed look at the localization of RpoH and CdsA is shown in Fig. S5B. Replicates are shown in Figs. S5C and D. Full details of the analysis required to generate this figure, as well as a pointer to the generating code, can be found in the Supplement, Section 1.2.

However, the flip side of this result is that roughly 15% of the protein production rates differ from the loss rates by more than an order of magnitude. In considering the cases where the production and loss rates were discrepant, we considered that one likely source of discrepancy is due to the “N-end” rule, which uses the amino acid sequence of a protein to predict its half-life (16). The N-end rule is usually accurate, but in the discrepant cases we noted, we wondered whether the rest of the data populating the model could provide a better estimate of protein half-life. To test this hypothesis, we identified six outlier proteins from this analysis, three of which were predicted by our analysis to have longer half-lives and three more predicted to have shorter half-lives. Measurement of the actual half-lives of these proteins experimentally confirmed our predictions were correct (Fig. 5B). We then replaced the N-end rule-based parameter values with these new measurements (which also preserved the proteomics data as a validation data set). This result caused us to revisit our analysis of cdsA expression (Fig. 2B, 3A), because the N-end rule assigns the CdsA protein a short half-life, which if incorrect could cause the simulation to have an enormously low CdsA concentration. Our steady-state analysis supported the idea that the CdsA protein may have a longer half-life (Fig. 5A). CdsA is a membrane protein, which makes protein extraction and traditional Western blotting difficult (45). As a result, we used immunofluorescence of over-expressed CdsA to measure the presence of protein over time, and found abundant expression of CdsA, but not RpoH (which has a short half-life, see Fig. S5A) after 24 hours (Fig. 5C, Fig S5 C and D). This is consistent with a half-life on the order of 10 hours for CdsA (Fig. 5B), which was included in the finalized model. The resulting simulations (i.e., the simulations shown in Figs. 1–4) had a higher protein count and predicted normal growth – resolving our questions regarding cdsA. Our steady-state analysis thus confirmed that the N-end rule holds in most cases, but also identified the points which were most likely to be discrepant and even calculated estimates of protein decay rates that were predictive of new experimental data.

In sum, construction of a highly integrative and mechanistic mathematical model provided us with a unique opportunity to integrate and cross-validate a vast and heterogeneous set of data in E. coli – a process we now call “deep curation” to reflect the multiple layers of curation we perform (analogous to “deep learning” and “deep sequencing”) (Fig. 1). These layers include: (1) a data layer; (2) a layer of parameters derived from the data; (3) a layer of equations that encapsulate the parameters, and also describe the underlying biological mechanisms (which notably must also be curated from the literature); (4) a layer which contains the unified model; and (5) a layer of the simulation output, which is executable and can be used for automated comparison to any future data that are generated. By highlighting those areas in which studies contradict each other, our work suggests lines of fruitful experimental inquiry for the future that may help resolve discrepancies – leading to both new biological insights and a more coherent understanding of this critical model organism.

We found that most of the data is in fact cross-consistent with itself. This means that the data generated by this scientific community is reliable on the whole, and may be particularly interesting given how many of these measurements were performed in vitro rather than in vivo. Moreover, the model that holds these data is capable of validatable predictions – not only on previously withheld data (Figs. S2E, 3G, and 4A) but also of experimental results obtained later (Fig. 5B). This strongly suggests that the model is a good representation of the overall dataset, and a starting point from which we can build towards a whole-cell model that includes many more functionalities, such as mechanisms of DNA replication initiation (46), response to nitric oxide stress (47), the formation of colonies (48), the dynamics of division-site selection (49), and many more – all of which will in turn enable us to encapsulate many more environments and data types.

Our synthesis of heterogeneous data, along with the deep curation approach we described, provides a way of encapsulating and interpreting such a synthesis as a unified whole. We hope that this work, by demonstrating the value of a large-scale integrative approach with regard to understanding, interpreting and cross-validating large datasets, will inspire further efforts to comprehensively characterize not only E. coli (as originally suggested by Francis Crick and Sydney Brenner (50)), but also other organisms of interest.