Patient-Specific bicuspid aortic valve biomechanics: a magnetic resonance imaging integrated fluid-structure interaction approach

Abstract

Congenital bicuspid aortic valve (BAV) consists of two fused cusps and represents a major risk factor for calcific valvular stenosis. Herein, a fully coupled fluid-structure interaction (FSI) BAV model was developed from patient-specific magnetic resonance imaging (MRI) and compared against in vivo 4-dimensional flow MRI (4D Flow). FSI simulation compared well with 4D Flow, confirming direction and magnitude of the flow jet impinging onto the aortic wall as well as location and extension of secondary flows and vortices developing at systole: the systolic flow jet originating from an elliptical 1.6 cm² orifice reached a peak velocity of 252.2 cm/s, 0.6% lower than 4D Flow, progressively impinging on the ascending aorta convexity. The FSI model predicted a peak flow rate of 22.4 l/min, 6.7% higher than 4D Flow, and provided BAV leaflets mechanical and flow-induced shear stresses, not directly attainable from MRI.

At systole, the ventricular side of the non-fused leaflet revealed the highest wall shear stress (WSS) average magnitude, up to 14.6 Pa along the free margin, with WSS progressively decreasing towards the belly. During diastole, the aortic side of the fused leaflet exhibited the highest diastolic maximum principal stress, up to 322 kPa within the attachment region. Systematic comparison with ground-truth non-invasive MRI can improve the computational model ability to reproduce native BAV hemodynamics and biomechanical response more realistically, and shed light on their role in BAV patients’ risk for developing complications; this approach may further contribute to the validation of advanced FSI simulations designed to assess BAV biomechanics.

INTRODUCTION

Bicuspid aortic valve (BAV) is the most common congenital cardiac disease with an estimated worldwide incidence of 1–2%⁴⁴. It occurs when two of the three leaflets that constitute the healthy tricuspid aortic valve are fused together; a fibrous thickening, called raphe, can appear along the fusion. Three main BAV types can be identified with type 1, characterized by a fusion of the left (L) and right (R) coronary cusp, being the most frequent phenotype identified⁴³. At least one third of BAV patients develops secondary pathologies affecting the valve, e.g., calcific aortic valve disease (CAVD) such as valve stenosis or regurgitation, or the aorta, e.g., aortic dilation or dissection⁵⁰. The largest population-based follow-up study ³⁴ revealed that aortic valve replacement (AVR) occurs in more than 50% cases within 25 years from initial BAV diagnosis, while about 25% cases required aortic surgery. Of note, AVR is required about 18 years earlier in BAV patients as compared to trileaflet aortic valve (TAV) individuals, confirming that the process of leaflets degeneration and calcification is accelerated in BAVs.

BAV-induced biomechanical and hemodynamic alterations, such as increased mechanical stress and abnormal wall shear stress (WSS), have been speculated to play a role in CAVD pathogenesis and progression along with genetic factors ^{7, 11, 47, 48}. The understanding of the combined effects of genetic, atherogenic and biomechanical factors has been just postulated and still need to be systematically investigated. However, the lack of patient-specific data represents the major limiting factor to thoroughly characterize and monitor biomechanical alterations affecting BAV cusps. To this purpose, different strategies have been proposed to quantify BAV-related derangements exploiting numerical models^{7, 12, 22, 30, 32}, in vitro experiments^41,52 and in vivo studies, which are mainly based on 3D time-resolved phase-contrast magnetic resonance imaging (PC-MRI) pulse sequences with three-directional velocity encoding, i.e., 4D Flow^{4, 24, 38, 39}. All these studies confirmed the compresence of common BAV features: an elliptical orifice with an eccentric systolic flow jet impinging onto the aortic wall, blood recirculation zones with abnormal helical flow pattern evolution in the ascending aorta, and WSS overloads on both aortic wall and valvular cusps. To overcome the spatiotemporal 4D Flow limitations,^{10, 18, 39} FSI methods, e.g., Arbitrary Lagrangian-Eulerian⁷, Immersed Boundary²² and Cut-Cell^{30, 32}, have been designed to capture BAV dynamics and compute the mechanical stress transferred between the deforming leaflets and the blood flow. However, these FSI-based studies are still far from a robust patient-tailored reproduction of the BAV-related aortic bulk flow since they employed parametric or paradigmatic anatomical models, thus neglecting the patient-specific realism of BAV anatomy. Accordingly, a deeper integration of the FSI modeling strategy with in vivo patient-specific imaging is advocated.

In the present study, we sought to overcome these limitations in order to achieve a patient-tailored characterization of the BAV-related flow pattern and quantify the regional WSS distribution on BAV cusps. To this aim, a patient-specific FSI model was reconstructed from MRI, and BAV-related fluid dynamics simulated and compared with volumetric 4D Flow acquisitions. We exploited a boundary conforming Cut-Cell method, called Sub-Grid Geometry Resolution (SGGR)^{21, 45} to reproduce in vivo BAV-related hemodynamics and enable the quantification of mechanical stress and flow-induced WSS acting on BAV leaflets.

MATERIALS AND METHODS

Geometry reconstruction

Cardiac MRI acquisition of a 26-year-old female patient, presenting with type-1 BAV fusion⁴³, was performed on a MAGNETOM Aera 1.5 T clinical scanner (Siemens Healthcare, Erlangen, Germany). The study was approved by the local Ethical Review Board of IRCCS San Raffaele (Milan, Italy) and informed written consent was provided by the study subject prior to MRI. The study was performed in accordance to the principles of the Declaration of Helsinki.

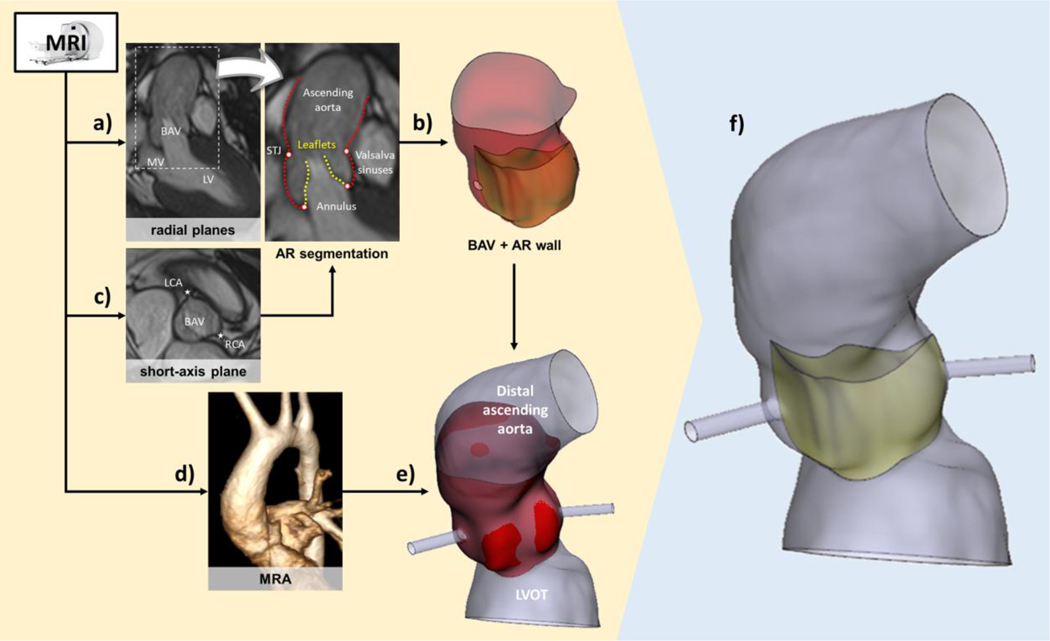
The patient-specific aortic root (AR, Fig. 1) geometry was reconstructed from a T1-weighted cine MRI sequence through a semi-automated in-house Matlab graphical user interface (The Mathworks, Inc, Natick, Massachusetts)⁵¹; we acquired 18 long-axis planes evenly rotated, i.e., one every 10°, around the axis passing through the aortic annulus center and the center of the sino-tubular junction (STJ). Thirty frames per cardiac cycle were collected using R‐wave triggering with in‐plane spatial resolution and slice thickness equal to 1.5 and 8.0 mm, respectively.

Figure 1.

MRI-derived reconstruction of the anatomical 3D model: a) tracing of AR sub-structures from cine MRI radial planes, b) generation of aortic wall and BAV leaflets surfaces, and (c) inclusion of coronary artery insertions through landmarks from a short-axis plane; d) MRA elaboration to complement the anatomical AR model (e) with LVOT and distal ascending aorta; f) final structural 3D patient-specific model.

The AR geometry was reconstructed at early systole, identified as the first MRI frame characterized by the open configuration of the aortic valve (AV)¹³. Subsequently, AR substructures were traced by manually selecting on each radial MRI plane (Fig 1a): 2 annular points, 2 STJ points and multiple points lying on the Valsalva sinuses, the ascending aorta and the AV leaflets, respectively. Traced points on the profiles of the ascending aorta, of the sinuses and of the leaflets were interpolated by cubic splines and then resampled. Approximating 4^th-order Fourier functions were employed to filter the coordinates of these points, which were directly imported in the CAD software Gambit (Ansys, Fluent Inc., Canonsburg, Pennsylvania) to define the corresponding vertices. These vertices were automatically interpolated with non-uniform rational cubic splines (NURBS) along the axial and circumferential directions of the AR geometry. AR commissures were automatically defined, at the level located halfway between the annulus and the STJ profiles, as the three filtered points with the least distance from the longitudinal AR axis. As inferable from CMR imaging, the interleaflet triangle (ILT) height within the fusion region was considered negligible and the corresponding commissure removed, accordingly. The NURBSs were then interpolated by bicubic surfaces, defined in Gambit as Net Surfaces, thus obtaining 3 regions that shared their boundaries and formed the whole aortic wall (Fig 1b).

Similarly, the coordinates of the points obtained by leaflets tracing were filtered as for AR wall points, though adopting 2^nd-order Fourier functions to face the noise affecting raw data. A net of NURBS was generated interpolating filtered points, running in the leaflet basis‐to‐free edge direction and in the commissure‐to‐commissure direction, respectively; leaflet surface was obtained by bicubic interpolation of the corresponding NURBS.

No physical connection was required between each leaflet and the AR wall surface though removal of gaps between each leaflet attachment edge and the surrounding AR wall was mandatory to enable FSI simulation. An additional cine MRI short-axis plane (pixel spacing=1.29×1.29 mm, slice thickness=8 mm) was used to identify the position of both right and left coronary ostia (Fig. 1c), whose projections were determined on the reconstructed AR surface.

To include a larger portion of the distal ascending aorta and the left ventricular outflow tract (LVOT) in the patient-specific geometry, a magnetic resonance angiography (MRA) sequence with isotropic voxel resolution of 1.1×1.1×1.1 mm³ was used (Fig. 1d): MRA semi-automated segmentation through Mimics Medical v20.0 (Materialise, Leuven, Belgium) yielded the 3D inner-wall of the distal ascending aorta and LVOT, which were merged to the proximal portion of the AR geometry (Fig. 1e) using Mimics 3-Matic v.12 (Materialise, Leuven, Belgium). Each coronary artery (CA) was assumed circular with a diameter of 3.0 and 3.6 mm for the right and left CA, respectively ¹⁶; an overall CA length of 15 mm was prescribed.

FSI numerical simulation

We herein performed a 2-way partitioned FSI simulation, based on the boundary-fitted SGGR method^{21, 45}. Fluid (native BAV and proximal ascending aorta) and structural (BAV leaflets) domains were subtracted from an initial Cartesian grid; to ensure a body-fitted mesh during the FSI simulation, fluid cells automatically conformed based on the solid domain motion.

Geometry discretization -

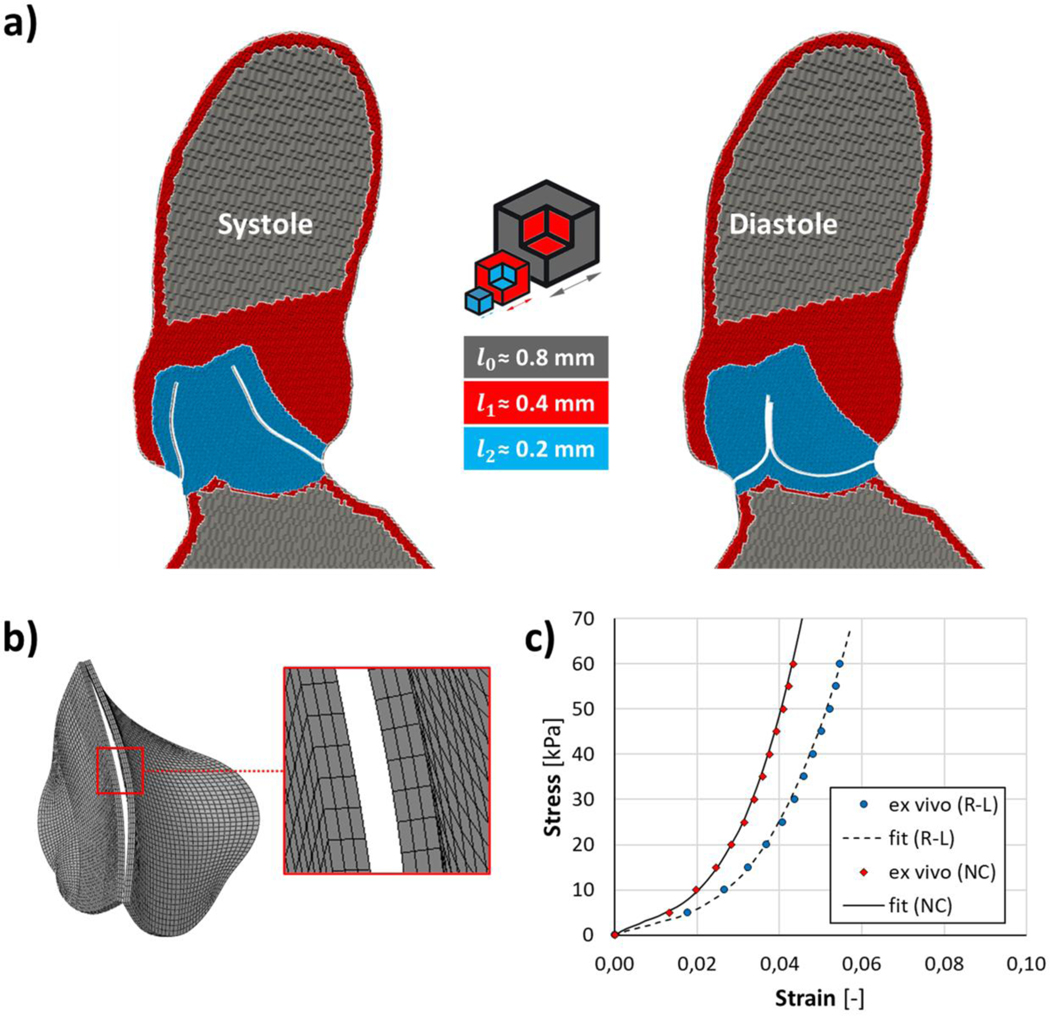
The fluid domain was discretized through a two-stage process in FlowVision (Capvidia NV, Leuven, Belgium). A user defined initial cartesian grid was implemented with a characteristic dimension (l₀) of 0.8 mm (Fig. 2a); subsequently, the computational grid was further refined in proximity of AR wall and BAV leaflets, prescribing different mesh adaptation levels. Specifically, in Flow Vision, mesh adaptation by one level means division of a hexahedral cell into 8 equal cells: herein, adaptation by one level was prescribed close to the AR wall boundaries (l₁ around 0.4 mm) while adaptation by two levels (l₂ equal to 0.2 mm) was specified within the fluid region where BAV leaflets kinematics is expected to occur. The entire aortic surface was discretized with triangular shell elements (S3 Abaqus element library) with a characteristic dimension of 0.5 mm. Aortic leaflets were discretized with a quadrilateral structured mesh, adopting a mesh characteristic size of 0.5 mm; the surface grid was then locally extruded, along the outward nodal normals, to obtain 3 layers of hexahedral elements (C3D8R Abaqus element library) (Fig. 2b) across the leaflet thickness, assumed uniform and equal to 0.6 mm²³.

Figure 2.

Fluid domain discretization (a) with two levels of mesh adaptation to progressively refine grid characteristic dimension (l) within the aortic root; b) BAV leaflets were discretized into 3 layers of hexahedral elements along their thickness; c) fitting of the isotropic and hyperelastic Ogden strain energy function on ex vivo experimental data for non-fused (NC, R²=0.9996) and fused (R-L, R²=0.9986) AV leaflet, averaging biaxial test data between circumferential and radial tested directions.

A preliminary mesh convergence analysis was accomplished to achieve a reasonable trade-off between numerical accuracy and computational expense. To this aim, three different mesh refinements were investigated (Table 1) and the grid convergence index (GCI)¹⁴, indicating how much the calculated variable of interest would change with a further grid refinement, was calculated for the fine-to-medium and medium-to-coarse grid refinements. The solution computed with the fine grid refinement (1.45×10⁶ cells) was herein chosen since relatively insensitive to further mesh refinement, reporting a GCI of 1.6% for AV geometric orifice area (GOA), 1.1% for mean velocity magnitude at the STJ cross-section, and GCI values below 2.2% and 1.2% for mechanical stress and strain on BAV leaflets. Further details available in the supplementary material (section A).

Table 1.

Summary of grid independence study

Grid	Total no. of cells (× 106)	GOAMAXa	Vmeanb	GCI σI,MAXc	εI,MAXd
Fine	1.45	1.6 %	1.1 %	2.2 % (R-L) 1.2 % (NC)	1.2 % (R-L) 0.4 % (NC)
Medium	0.75	8.6 %	9.8 %	9.3 % (R-L) 5.7 % (NC)	5.1 % (R-L) 2.3 % (NC)
Coarse	0.40	-	-	-	-

^aGrid convergence index (GCI) evaluated for the maximum AV geometric orifice area (GOA_MAX);

^bGCI for mean velocity magnitude (V_mean) on the STJ aortic cross-section;

^cGCI for maximum principal stress peak (σ_I,MAX) computed at diastolic peak of transvalvular pressure on both fused (R-L) and non-coronary (NC) leaflet, respectively;

^dGCI for maximum principal strain peak (ε_I,MAX) computed at diastolic peak of transvalvular pressure on both fused (R-L) and non-coronary (NC) leaflet, respectively.

Tissues mechanical properties -

As previously described^{7, 21}, we employed an hyperelastic isotropic model to characterize the mechanical response of the AV leaflets, assumed incompressible. Specifically, we employed a 3^rd-order Ogden strain energy function W:

$$W\left({\overline{\lambda }}_1,{\overline{\lambda }}_2,{\overline{\lambda }}_3\right)={\displaystyle \sum }_{i=1}^N\frac{2{\mu }_i}{{\alpha }_i^2}\left({\overline{\lambda }}_1^{{\alpha }_i}+{\overline{\lambda }}_2^{{\alpha }_i}+{\overline{\lambda }}_3^{-{\alpha }_i}-3\right)$$ (1)

where ${\overline{\lambda }}_1$, ${\overline{\lambda }}_2$ and ${\overline{\lambda }}_3$ are the deviatoric principal stretch ratios, N is the order of the Ogden potential (i.e., N = 3), and μ_i and α_i are the constitutive parameters (Table 2), which were identified by fitting data from ex vivo biaxial mechanical tests on human TAV cusps specimens³³, averaging the biaxial data between circumferential and radial directions (Fig. 2c). Specifically, to mimic the mechanical properties for a type-I fusion, mechanical data from the right and left coronary AV leaflets were averaged to fit the mechanical response of the fused leaflet; accordingly, data from the non-coronary leaflet were adopted for the non-fused BAV leaflet. A density of 1100 Kg/m³ was assumed for all the BAV leaflets¹² while the aortic wall surface was assumed as a rigid body.

Table 2.

Constitutive parameters of the 3^rd Ogden model to describe the mechanical response of the non-coronary and the fused aortic leaflet, respectively.

Leaflet	μ1	α1	μ2	α2	μ3	α3
Non-coronary (NC)	−47.75	2.00	33.23	4.00	14.60	−2.00
Fused (R-L)	−24.50	2.00	17.16	4.00	7.39	−2.00

Numerical FSI set-up -

The structural problem was solved through the commercial explicit finite element (FE) solver ABAQUS 6.14 (SIMULIA, Dassault Systèmes, Providence, RI, USA), while FlowVision 3.10 (Capvidia NV, Leuven, Belgium) was used for the transient laminar flow simulation. Blood was treated as a Newtonian incompressible fluid with a density of 1060 Kg/m³ and a dynamic viscosity equal to 0.0035 Pa·s. FlowVision Multi-Physics Manager (Capvidia NV, Leuven, Belgium) was exploited to couple both the solvers on an Intel Xeon workstation (2.0 GHz), with the 2-way coupling procedure exchanging information between Abaqus and FlowVision every 5 × 10⁻⁴s ²¹. On the one hand, moving boundaries are provided by the structural response to the flow domain and, on the other hand, pressure loads are directly applied by the flow domain on the structural one⁴⁵. The minimum structural explicit time step was equal to 1 × 10⁻⁶s; the fluid solver adopted a spatially 2^nd order upwind scheme with a maximum of 2000 iterations allowed for solving the equation. All the simulations were computed on 56 processors of Stony Brook University SeaWulf cluster with a computational expense of about 45 hours per cardiac cycle. Aiming at exploiting the FSI capability to effectively capture BAV transient dynamics, we considered the 2-way FSI approach to be worth the substantial computational cost; FSI advantages with respect to a simpler “dry” model are detailed in the supplementary material (section B).

The Abaqus/Explicit general contact algorithm was used to model contact between leaflets: a scale penalty frictionless method was used to prevent penetrations in the direction normal to the contacting surfaces ³².

Loading and boundary conditions -

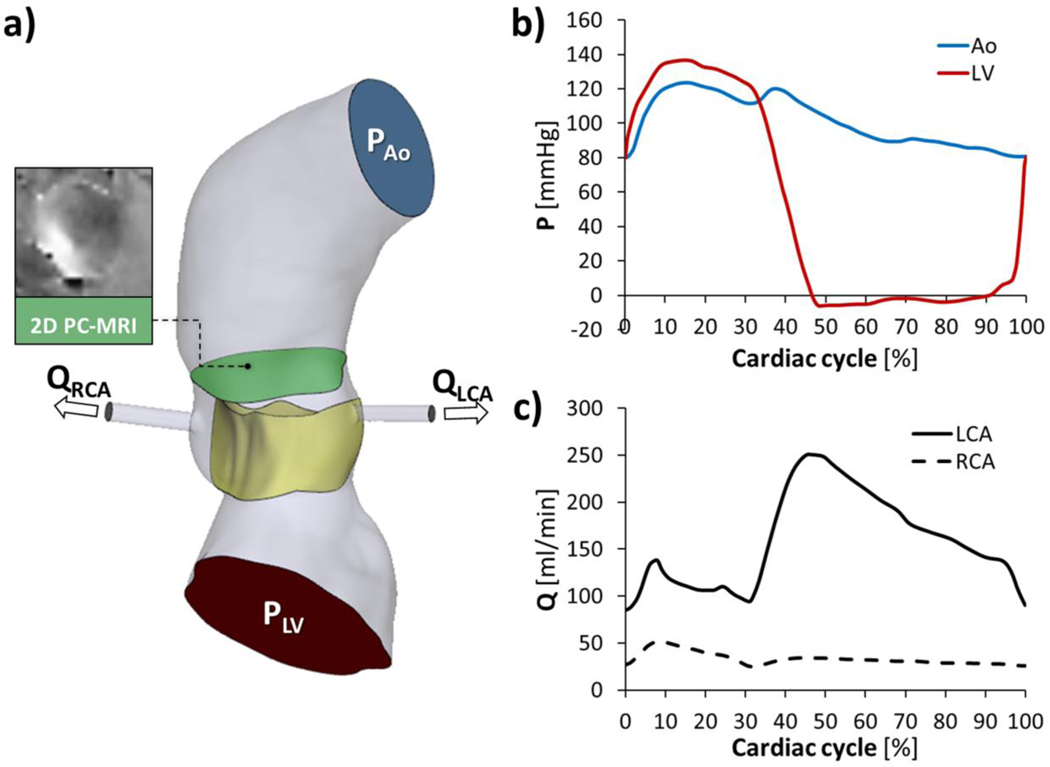
Ventricular and aortic physiological time‐dependent pressures were retrieved ⁵¹ and adapted to the patient-specific heart rate (i.e., HR = 93 bpm, Fig. 3a). Furthermore, the ventricular pressure curve was adjusted with a 8% increase in its magnitude, so to set the peak flow rate of the FSI model on a level comparable with 2D time-resolved PC-MRI sequences with velocity encoded in the through-plane direction, as generally accomplished in the clinical routine to quantify blood flow and peak flow velocities⁵. To do so, a through-plane velocity-encoded PC-MRI sequence (in-plane resolution=1.98×1.98 mm, slice thickness=6 mm) was available on a plane located on the STJ (Fig. 3a), which is an universally accepted landmark, generally uniform in structure, facilitating consistent clinical measurements¹⁹. An expert clinical user processed PC-MRI data in Medis Suite MR PC flow (Medis, Leiden, The Netherlands); the FSI model well approximated in vivo data from 2D PC-MRI overestimating of 0.9% the peak flow rate (22.4 vs. 22.2 l/min) and of 1.7% the peak of velocity (238.6 vs. 234.5 cm/s). Ventricular and aortic curves (Fig. 3b) were finally imposed at the inlet and the outlet of the fluid domain, respectively.

Figure 3.

Loading conditions (a)consisting of ventricular (LV) and aortic (Ao) pressure waveforms (b), imposed respectively at the inlet and at the outlet of the fluid domain, right and left coronary artery (i.e., RCA and LCA) flow rate curves (c).

Paradigmatic flow rate curves of the right and left coronary arteries ²⁸, adapted to the patient-specific HR, were specified at the coronaries outlets (Fig. 3c). No-slip fluid boundary conditions were imposed at each fluid-structure interface as well as along the aortic inner-wall. Four cardiac cycles were simulated and FSI results were extracted from the last cycle.

FSI comparison with 4D Flow imaging

For the sake of comparison, FSI results were compared against in vivo hemodynamics, exploiting a prototype 4D Flow sequence acquired in the same patient with prospective ECG-gating and respiratory navigation. The 4D volume of acquisition was oriented along an oblique-sagittal plane encompassing the ascending aorta, the aortic arch, and the thoracic aorta. The following parameters were employed: in-plane resolution=1.9 mm; slice thickness=2.0 mm; repetition time=37 ms; echo time=2.3 ms; flip angle=8°. The velocity-encoding range (VENC) was set to 280 cm/s to avoid aliasing. 4D Flow manual segmentation and post-processing was accomplished through ad hoc Matlab codes³⁸; data visualization was performed in ParaView (Sandia Corporation, Kitware Inc., Albuquerque, NM, USA).

RESULTS

We herein present the results of the FSI simulation and the comparison of the FSI-derived BAV hemodynamics against 4D Flow in vivo evidences.

3D BAV-related flow pattern

Aortic bulk flow was qualitatively assessed in terms of velocity streamlines (Fig. 4), in particular during systole, to highlight the velocity ejection jet across the BAV and the flow rotational evolution downstream of it.

Figure 4.

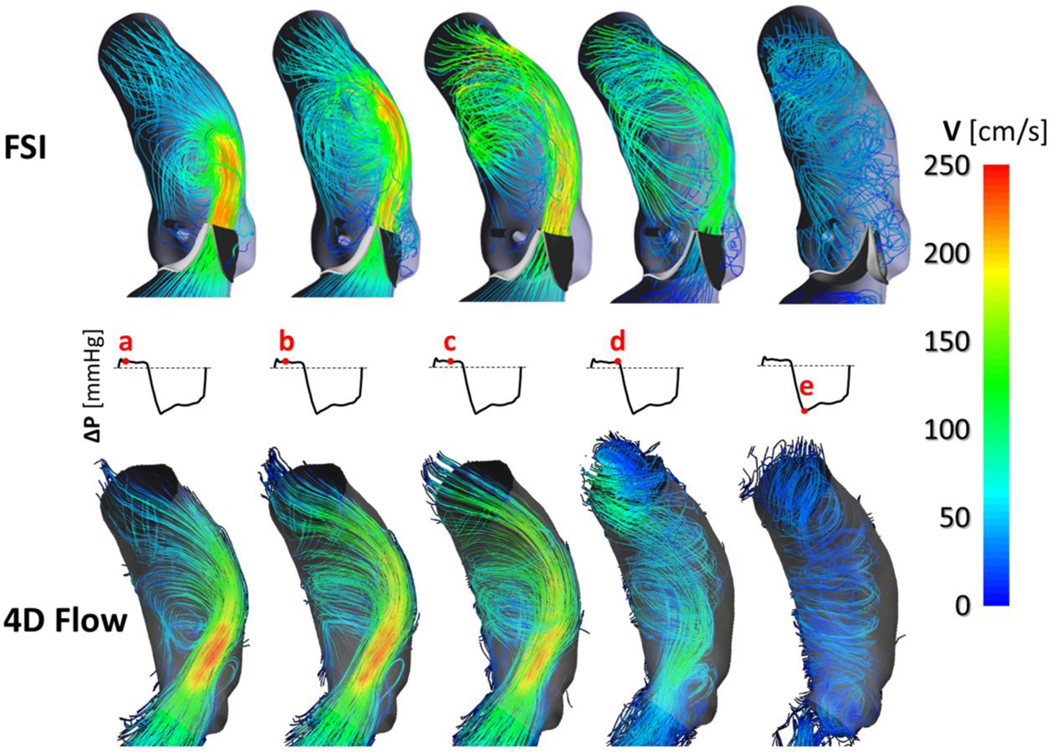
Velocity streamlines extracted at different frames over the cardiac cycle from the FSI model (upper panel) and from the 4D Flow sequence (lower panel), respectively; complete BAV closure is visible during diastole.

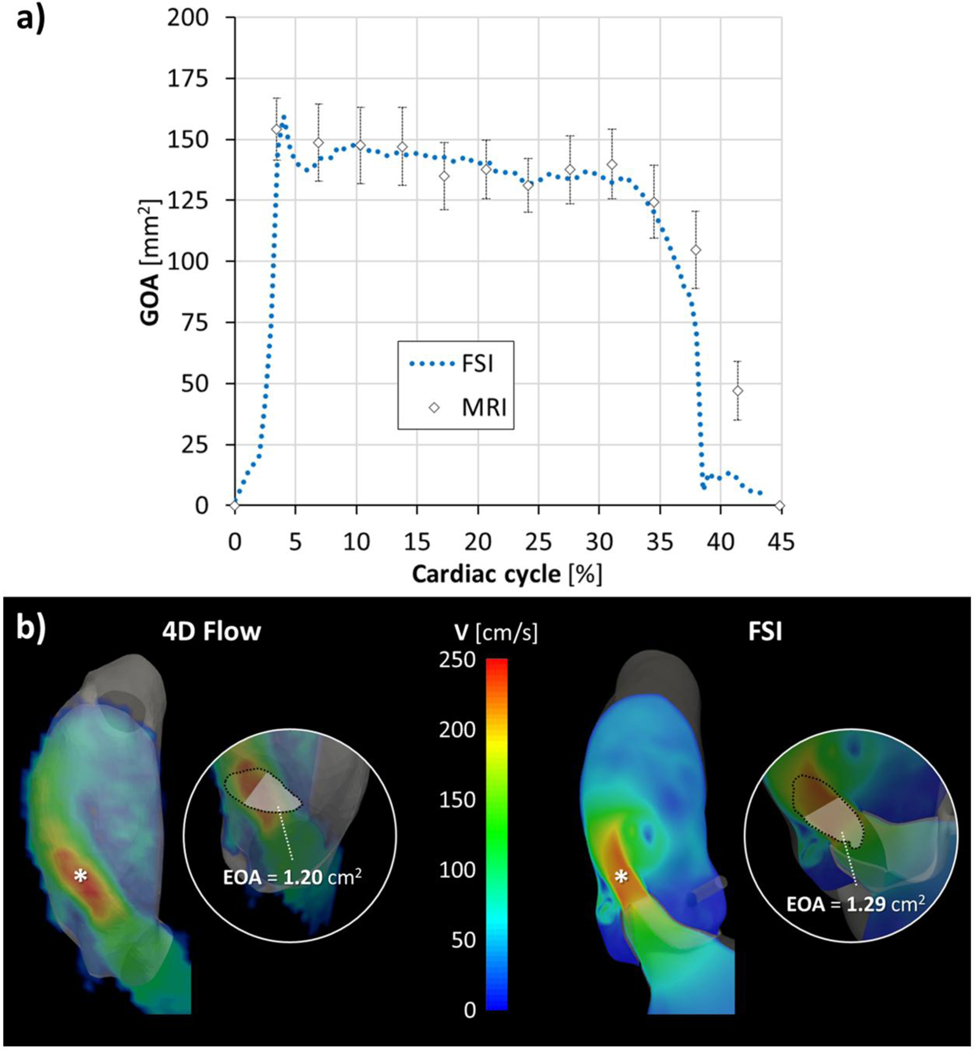
BAV leaflets generated an oval-shaped orifice and an eccentric systolic flow jet skewed toward the non-coronary leaflet (Fig. 4a), reaching a peak of velocity magnitude equal to 252.5 cm/s. Geometric orifice area (GOA), computed as the bi-dimensional projection of AV leaflets’ free edge on the AR cross‐sectional area ⁵¹, reported a maximum value of 160 mm² at peak systole, well comparing with the maximum GOA of 154 ± 13 mm² calculated in Medis by an expert user, averaging 10 measurements on a cine short-axis MRI plane intersecting the leaflets’ free margin (Fig. 5a). Both velocity and GOA peak values, agreed in grading as mild the severity of AV stenosis ³. Complete BAV leaflets coaptation was visible at peak diastolic transvalvular pressure.

Figure 5.

Systolic GOA comparison (a) between the FSI model and MRI-derived measurements; b) location of vena contracta (highlighted with an asterisk) and EOA calculation, at peak systole, in the FSI model and 4D Flow, respectively. At the level of the vena contracta cross-section, EOA was estimated as the area enclosed by the 3D isosurface velocity characterized by the same velocity magnitude corresponding to the 65^th percentile of velocity peak²⁰.

During the systolic acceleration phase, secondary flows originated in proximity of leaflets’ free edge (Fig. 4b); of note, a vortex progressively enlarged downstream of the fused leaflets and propagated to the ascending aorta throughout systole while a smaller vortex continued persisting within the non-coronary sinus (Fig. 4c). The jet flow impinging on the aortic wall resulted, at end systole, in helical flow (Fig. 4d) rotating along the ascending aorta during the deceleration phase; complete BAV closure was visible during diastole (Fig. 4e) with low-velocity rotating flow throughout the ascending aorta.

Comparison vs. 4D Flow -

FSI-derived aortic bulk flow well compared with in vivo blood flow pattern (Fig. 4); 4D Flow analysis confirmed both direction and magnitude of the velocity flow jet impinging onto the aortic wall as well as both location and extension of the secondary flows and vortices developing during systolic ejection. At peak systole, the 4D Flow velocity magnitude reached a peak value of 253.9 cm/s, i.e., 0.6% higher than the corresponding FSI value computed; the FSI peak flow rate resulted 6.7% higher than 4D Flow, i.e., 22.4 vs. 21.0 l/min. During diastole, at peak of transvalvular pressure, 4D analysis confirmed the absence of BAV regurgitation with no evidence of leakage.

In addition, the FSI model matched very well the 4D Flow analysis in terms of the location of aortic peak velocity within the 3D velocity field, i.e., vena contracta, and the corresponding effective orifice area (EOA), representing the cross-sectional area of the compressed bloodstream at the level of vena contracta (Fig. 5b)²⁰.

Mechanical and flow-induced shear stresses on BAV leaflets

Regional analysis of mechanical and flow-induced stresses acting on the BAV leaflets was accomplished subdividing each leaflet into each characteristic regions²³: free margin, attachment edge, belly region and coaptation area (Fig. S1).

Continuous variables, not-normally distributed as verified with Shapiro-Wilk test, are expressed with median and interquartile range (IQR). Wilcoxon matched-pairs signed-rank test was used to compare stresses on fused vs. non-fused leaflet and on ventricularis vs. fibrosa leaflet surface, respectively. Regional stress differences on BAV leaflets were analyzed using Friedman test. Statistical significance was indicated by a probability value of P < 0.05.

Mechanical stress -

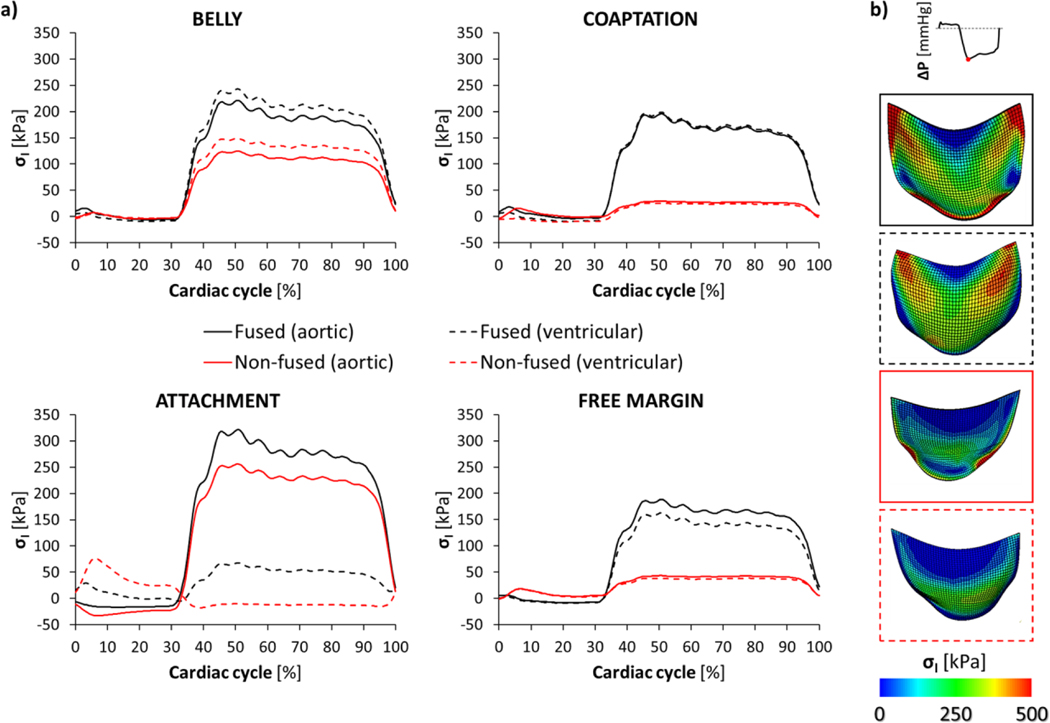
We assessed the mechanical response of the BAV leaflets in terms of the maximum principal stress (σ_I), which was extracted throughout a cardiac cycle from the aortic (fibrosa) and ventricular (ventricularis) surface of each leaflet (Fig. 6a).

Figure 6.

Maximum principal stress (σ_I) averaged throughout the cardiac cycle (a) on each region of the fused (black lines) and non-fused (red lines) BAV leaflets, reported for both the aortic (continuous line) and the ventricular (dotted line) surface, respectively; b) contour maps of σ_I magnitude, extracted from the FSI model at peak of diastolic transvalvular pressure, on BAV leaflets.

During systole (Table S1), the regional σ_I distribution remained comparable on a large portion of both the leaflets; along the attachment edge, compression was localized on the aortic side of each leaflet and was paralleled by the increased traction of the ventricular counterpart as visible, in particular, on the non-fused leaflet.

During diastole (Table S2), the time course of σ_I, averaged within each leaflet region, revealed higher σ_I values (P<0.0001) on the fused leaflet if compared to the non-coronary one, with significant regional differences (P<0.0001) visible on both the leaflets.

At the diastolic peak of transvalvular pressure (Fig. 6b), the fused leaflet exhibited the highest σ_I values within each region, with the attachment region reporting the highest σ_I value of 322 kPa on its aortic surface; σ_I markedly differed (P=0.0038) between the two sides of the leaflet, with the leaflet attachment exhibiting the highest diastolic σ_I increase, passing from the ventricular to the aortic side.

Comparing diastolic σ_I values between the two leaflets, the coaptation region reported the highest difference with the σ_I median value passing from about 25 kPa in the non-fused leaflet to more than 150 kPa in the fused leaflet. Similarly, median σ_I values were up to 4 times higher on the free margin of the fused leaflet. Differences in σ_I values between leaflets progressively decreased on the belly (+66% on the aortic and +53% on the ventricularis side) and along the aortic surface of leaflet attachment (+19%); on the non-fused leaflet, compression persisted on its ventricularis side during the entire diastole with a median σ_I value equal to 13.2 kPa.

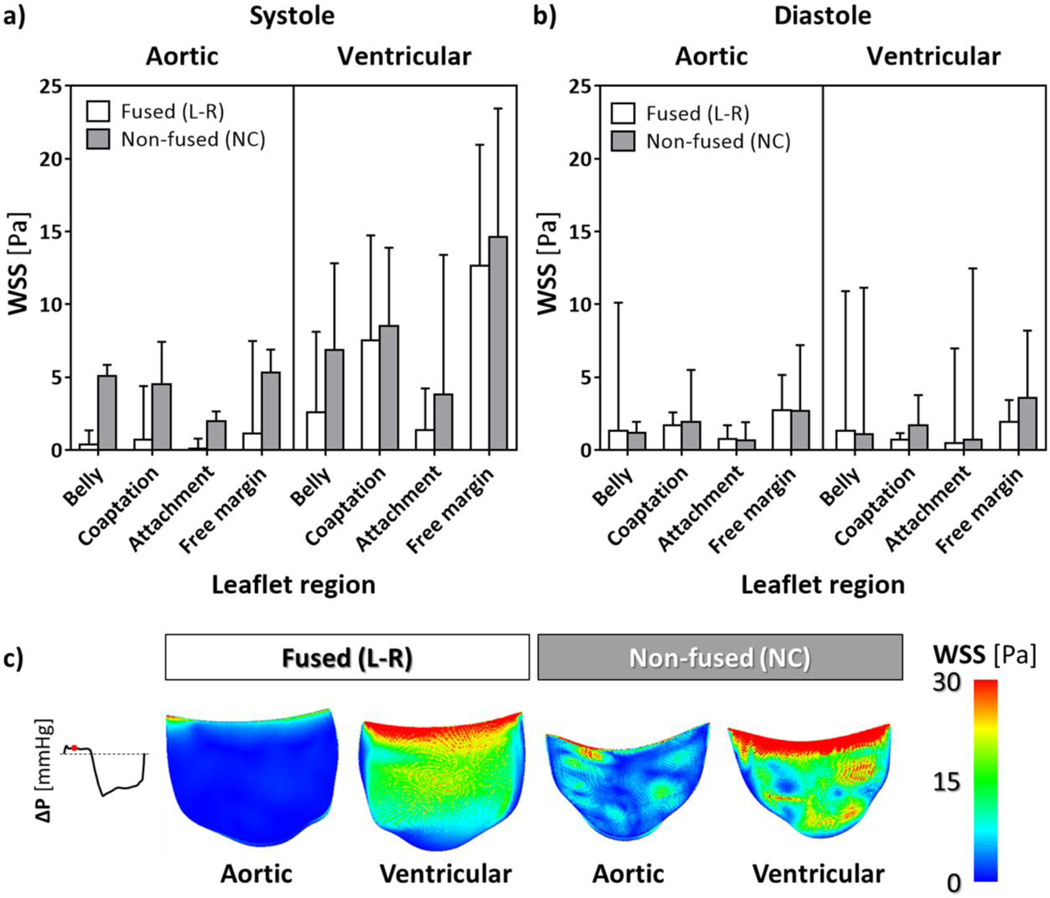
Wall shear stress -

Flow-induced stresses acting on the leaflets were quantified in terms of the wall shear stress (WSS) magnitude, whose distribution was quantified on both the ventricular and aortic surface of each leaflet and averaged over the systolic and diastolic phases, respectively.

At systole (Fig. 7a, Table S3), averaged WSSs were higher on the non-fused leaflet (P<0.0001), with the highest values concentrated on the ventricularis surface of the free margin, i.e. up to 14.6 Pa. WSS regional differences proved to be statistically significant (P<0.0001), with WSSs progressively decreasing from the free margin towards the leaflet belly and the attachment regions; WSS values computed on the aortic side of each leaflet were significantly lower (P<0.0001) if compared to the corresponding ventricular side (Fig. 7c).

Figure 7.

Median values and upper quartile (i.e., 75^th percentile) of WSS distribution on BAV leaflets, averaged during systole (a) and diastole (b) on both the aortic and ventricular surface, for each region of the fused (L-R) and non-fused (NC) leaflet; c) contour maps of mid-systolic WSS magnitude extracted from the FSI model.

Diastolic averaged WSSs (Fig. 7b, Table S4) markedly decreased with respect to systole, though revealing significant differences between the two leaflets (P<0.0011) and reporting a similar pattern of regional differences (P<0.0001); WSSs on aortic and ventricular sides of BAV leaflets remained comparable (P=0.3494).

DISCUSSION

We herein developed a patient-specific image-based FSI model, whose reliability has been tested by comparing its fluid dynamics with in vivo 4D Flow. The model has been used to quantitatively assess the temporal evolution of the BAV-related hemodynamics and its impact on the patient-specific anatomy, focusing on the mechanical and flow-induced stresses acting on BAV leaflets. Although BAV abnormality may still guarantee a normal valvular function, complications such as calcific aortic valve disease (CAVD) and aortic dilation may present within a wide age range ⁵⁰. BAV-related flow alterations, e.g., due to the existence of an eccentric high jet velocity, are increasingly pointed as potential contributors to BAV pathogenesis; in this scenario, different FSI approaches have been proposed to mimic in vivo BAV hemodynamics and quantify WSS experienced by the leaflets ^{7, 9, 22, 32}.

To the best of our knowledge, this is an innovative FSI approach fully integrating the modeling strategy with in vivo MRI data to reliably assess BAV-related biomechanics and hemodynamics, and extract velocity-derived variables potentially relevant to quantify BAV dysfunction but not otherwise attainable from a direct processing of in vivo MRI imaging due to the inherent spatiotemporal limitations of current MRI sequences.^{10, 18}

The use of the patient-specific imaging allowed to overcome previous parametric and partially idealized representations of the BAV geometry ^{7, 32}: MRI is a non-invasive imaging modality able to provide a detailed analysis of the aortic morphology and complement it with the volumetric 4D Flow assessment of aortic hemodynamics. In addition, if compared to computed tomography (CT), MRI sequences did not require ionizing radiation and provided a higher temporal resolution.

Fluidynamic results of the FSI simulation well agree with the aortic hemodynamics extracted from 4D Flow (Fig. 4), successfully capturing the peculiar features of a BAV Type I fusion⁵⁰: the high-velocity jet is skewed toward the non-coronary leaflet progressively approaching the convexity of the ascending aorta, which is a frequent region prone to dilatation in patients with a R-L fusion. Both eccentricity and skewness of the jet across the BAV orifice generate recirculation regions marked by the presence of asymmetrical vortices with larger extension above the fused leaflet^{9, 38}. Within the ascending aorta, 4D Flow data confirmed the anticlockwise fluid rotation (Online Video 1), i.e., a right-handed helical flow, which is the most common flow pattern occurring in more than 70% of BAV patients⁴. Nonetheless, it is worth noting that the use of a single VENC ability to capture the BAV-specific high jet velocity avoiding velocity aliasing, diminished the reliability of the comparison of the aortic bulk flow diastole (shown by the weaker agreement between FSI and 4D Flow at the diastolic peak of transvalvular pressure, Fig. 4e). Single VENC 4D flow MRI is apparently hampered by poor velocity resolution and noise when imaging during diastole⁶.

Distribution of mechanical σ_I stress on valvular leaflets well agree with previous numerical BAV models ^{12, 27, 30}, highlighting a remarkable diastolic σ_I concentration along the leaflet attachment and the belly regions, with σ_I increasing above 300 kPa. Though the bending stresses are generally greatest where leaflets are attached to the aortic wall ¹⁵, the region of high σ_I concentration can markedly expand on the fused leaflet when BAV fusion is characterized by a small strip of non-valvular tissue, i.e., raphe, which is clinically associated with a higher prevalence of significant aortic stenosis and regurgitation²⁹. Unequal σ_I distribution, with diastolic average σ_I higher on the fused leaflet, was paralleled by a noticeable asymmetric jet flow as observed when simulating BAV biomechanics with a small non-fused leaflet angle ³⁰, i.e., 120–140 degrees.

The WSS pattern on BAV leaflets well compared with previous FSI models^{7, 32}: the highest WSS magnitude is concentrated along the free margin of each leaflet, while lower WSSs are progressively visible moving towards the belly and the attachment region.

During systole, WSSs markedly increased with respect to diastole: the ventricular side of each leaflet directly interacts with the unidirectional high-velocity jet across the BAV orifice, while the aortic side is exposed to low-velocity flow recirculating within the Valsalva sinuses. Accordingly, on the ventricular surface of the leaflet, the systolic WSS magnitudes were systematically higher than those on the aortic side.

The average WSS magnitude we computed during systole on the ventricular side of BAV leaflets (Fig. 7a) slightly underestimates (up to 11% on the fused leaflet) the corresponding values computed by Cao and colleagues⁷. Conversely, our FSI model markedly overestimates the average WSS magnitude on the aortic surface, with values about four and six times higher on the fused and non-fused BAV leaflets, respectively.

Comparable WSS patterns were achieved, however relevant modelling factors may shed light on these differences in WSS magnitude on the aortic BAV surface indicated by our study. The use of the patient-specific geometry can effectively take anatomical dimensions and asymmetries (e.g., between the sinuses of Valsalva) into account, recreating a more faithful description of the complex BAV hemodynamics. For instance, the eccentricity of the BAV jet and the severity of stenosis can impact differently the fluid dynamics in the aortic root and ascending aorta⁴¹. Taking coronary artery perfusion into account is yet an additional factor which may influence the fluid “washout” of aortic BAV surface³⁶.

In type-I BAV, the particular vulnerability of the fused leaflet to calcification is already documented, and calcific nodules primarily occur on the aortic side of the leaflet ^{31, 40, 48}; in this scenario, accurate and comprehensive assessment of fluid-mediated stimuli is relevant to deepen the pathologic CAVD pathway of BAV leaflets, which is presumably activated and triggered not only by cardiovascular risk factors but also by biomechanical abnormalities⁴⁹. The use of non-invasive MRI data can enhance the reliability of FSI analysis and facilitate the reproduction of the native BAV hemodynamics and mechanical WSSs, the latter being currently exploited on ex vivo platforms to investigate the BAV-related mechanisms of CAVD pathogenesis⁴⁹.

Limitations

The following limitations of our FSI modeling strategy should be taken into consideration when interpreting results.

Paradigmatic pressure loading conditions were retrieved from the scientific literature. However, exhaustive patient-tailored modeling could be derived from 4D Flow through non-invasive mapping of aortic relative pressures⁴². 4D Flow estimation of aortic flow rate is also feasible, though, if compared to 2D PC-MRI, reported underestimation of net and peak aortic flow rate in part due to the relatively low 4D Flow temporal resolution¹⁸. In vivo coronary artery flow could be integrated through 2D PC-MRI sequences though several challenges are still related to the small size, tortuous path and extensive motion of the coronary vessels³⁷.

The effects exerted on the fluid flow by the aortic wall motion were excluded since a deformable aortic wall was not taken into account by our FSI model. However, wall deformability is reported to affect WSS ³⁵; in the supplementary material (section C), we report the estimated impact of aortic wall deformability, over the cardiac cycle, on the simulated BAV biomechanics of the present case. Further studies are ongoing to incorporate the effects of the aortic wall deformability and extend our analysis to BAV-induced detrimental effects on the aortic wall. To this purpose, in vivo MRI monitoring of aortic dimension and estimation of arterial stiffness surrogates,⁸ e.g., pulse wave velocity and arterial distensibility (the latter requiring a concomitant aortic pulse pressure measure), could improve the validation of the numerical results and contribute to a finer patient-tailored tuning of the FSI model.

Our FSI model neglected the anisotropic mechanical response of aortic leaflets and both fibers structure and orientation were not considered;² the hyperelastic and isotropic mechanical response of BAV leaflets was tuned to experimental data from normal tricuspid aortic valves.

Of note, previous quantifications of fiber architecture in excised TAV and BAV leaflets under polarized light reported in BAV leaflets more disorganized layers;¹ though on a coarse scale differences in the mean fiber direction were negligible, this was supposed to potentially lead to a more isotropic mechanical response, in particular in the belly region where fibers revealed to be less aligned.

Nonetheless, a larger population-averaged characterization of the anisotropic mechanical properties of BAV leaflets are required to improve the reliability of mechanical and flow-induced BAV strain and stresses. Herein, since the fibers are the load bearing structure of AV leaflets, we estimated the impact that this approximation may have on AV biomechanics (supplementary material, section D).

The FSI comparison against 4D Flow is further affected by the lower spatial MRI resolution, which may result in discrepancies, e.g., in terms of velocity magnitude and WSS ³⁵, due to the MRI spatial averaging. Furthermore, to assess in vivo aortic bulk flow, only one mask of the 3D aortic lumen geometry was manually segmented from the 4D Flow magnitude images at the time-frame representing peak systole³⁸; conversely, the aortic FSI domain was constructed from cine MRI and MRA sequences with higher spatial resolution than 4D Flow. In future studies, focusing on aortic wall biomechanics, this aspect will deserve further attention to avoid a potential source of errors, due to discrepancies in the lumen delineation, while comparing FSI results against 4D Flow measurements.

The Reynolds number of our study (Re, Re_FSI = 4881, Re_PCMRI = 4727)⁴⁶ indicates intermittent transient turbulence. We assumed aortic laminar flow. Given our main interest in comparing our patient-specific FSI analysis and the MRI flow patterns, the use of laminar flow assumption was found to be reasonable³⁰. as the Expected differences due to the adoption of a fluid turbulence model would have only a marginal effect on the current study and its relevance from a clinical standpoint²⁵.

CONCLUSIONS

We herein developed a 2-way FSI model of BAV biomechanics, the first of its kind demonstrating how patient-specific clinical imaging and FSI modeling can be effectively combined in order to improve the assessment of BAV biomechanics and enhance its realism against in vivo aortic bulk flow features extracted from MRI. This can promote a more robust validation, driven by clinical non-invasive MRI, of the advanced FSI approaches currently employed to retrieve mechanical and flow-induced stresses from valvular biomechanics. A more accurate and personalized analysis of BAV-related biomechanical alterations may elucidate the mechanisms of CAVD onset and progression and facilitate the detection of BAV anatomies more prone to valvular inflammation and progressive degeneration; advances in the understanding of CAVD mechanisms could identify novel therapeutic targets and consequently reduce the need for aggressive BAV repair surgical strategies ²⁶.

Given the emerging off-label use of transcatheter aortic valve replacement (TAVR) in young BAV patients developing CAVD, we are concurrently conducting numerical TAVR deployment of a commercially available self-expandable prosthesis in a calcified patient-specific BAV anatomy. This would help to inform clinicians whether TAVR can be considered as a safe and effective solution for BAV symptomatic patients who suffer from aortic stenosis¹⁷.