Abstract
We introduce a novel kernel low-rank algorithm to recover free-breathing and ungated dynamic MRI data from highly undersampled measurements. The image frames in the free breathing and ungated dataset are assumed to be points on a bandlimited manifold. We show that the non-linear features of these images satisfy annihilation conditions, which implies that the kernel matrix derived from the dataset is low-rank. We penalize the nuclear norm of the feature matrix to recover the images from highly undersampled measurements. The regularized optimization problem is solved using an iterative reweighted least squares (IRLS) algorithm, which alternates between the update of the Laplacian matrix of the manifold and the recovery of the signals from the noisy measurements. To improve computational efficiency, we use a two step algorithm using navigator measurements. Specifically, the Laplacian matrix is estimated from the navigators using the IRLS scheme, followed by the recovery of the images using a quadratic optimization. We show the relation of this two step algorithm with our recent SToRM approach, thus reconciling SToRM and manifold regularization methods with algorithms that rely on explicit lifting of data to a high dimensional space. The IRLS based estimation of the Laplacian matrix is a systematic and noise-robust alternative to current heuristic strategies based on exponential maps. We also approximate the Laplacian matrix using a few eigen vectors, which results in a fast and memory efficient algorithm. The proposed scheme is demonstrated on several patients with different breathing patterns and cardiac rates.
I. INTRODUCTION
The imaging of dynamically changing objects is a key application in many imaging applications, including microscopy [1], MRI, and ultrasound imaging [2]. For example, dynamic imaging of the heart in MRI allows the non-invasive assessment of structure and function. In many cases, the achievable temporal resolution is often limited by the slow nature of the acquisitions. To overcome this challenge, early work in cine MRI relied on reconstructing the images from undersampled k − t space measurements by exploiting the structure of x-f space [3]–[5], diversity of coil sensitivities [6], and the sparsity of k-space [7]. To further improve image quality, low-rank based schemes that rely on k-space navigators were introduced in [8], [9]. These schemes rely on different subspace/rank models for cardiac and non-cardiac spatial regions, which are identified manually [8], [9]. Another popular strategy is to estimate the cardiac and respiratory phases from navigators or central k-space regions, followed by the recovery of the binned phase images using compressed sensing [10], [11]. These schemes rely on a series of steps, including bandpass filtering using prior information about the cardiac and respiratory rates to estimate the phases. While the good performance of these methods have been demonstrated in several subjects, their utility in subjects with irregular respiration and cardiac motion (e.g. arrhythmia) is not clear.
We had recently introduced the SToRM [12] framework, which assumes that the images in the free-breathing MRI dataset lie on a smooth and low-dimensional manifold, parameterized by a few variables (e.g. cardiac & respiratory phases). The acquisition scheme relies on navigator radial spokes, which are used to compute the graph Laplacian matrix that captures the structure of the manifold. This implicit soft-binning strategy facilitates the simultaneous imaging of cardiac and respiratory function and eliminates the need for explicit binning of data as in [10], [11]. Since the framework does not assume periodicity of the signal, it is readily applicable to several dynamic applications, including speech imaging as shown in [12], or cardiac applications involving arrhythmia. Conceptually similar manifold models have been proposed by other groups [13]–[15]. We, as well as others [13], [15], have relied on the widely used exponential kernel to evaluate the Laplacian entries. To reduce oversmoothing, the entries were then truncated to keep the number of neighbours (degree) of each node fixed, resulting in a regular graph. Note that in practice, we do not have much control on the sampling of the manifold; some manifold neigborhoods are oversampled, while some others are not as well sampled; the use of a regular graph to capture its structure may result in a tradeoff between oversmoothing of poorly sampled regions and good performance in well-sampled regions. We observe that the image quality is quite sensitive to the choice of the node degree. Another challenge with the SToRM algorithm is the need to reconstruct and store the entire dataset (around 1000 frames), which makes the algorithm memory demanding and computationally expensive, and restricts the eventual extension to 3-D applications.
In this work, we introduce a novel kernel low-rank formulation for the recovery of dynamic imaging data from undersampled measurements. This approach reconciles SToRM and related approaches [12]–[15] with previous kernel low-rank methods [16] that rely on explicit mapping of the data to non-linear features; the explicit approach [16] is restricted to low dimensional signals such as patches or voxel time profiles because of the curse of dimensionality. We model the images as high dimensional points on a smooth surface/curve, which is represented as the zero level-set of a band-limited function. We show that under this assumption, feature maps of the images lie on a low-dimensional subspace. We note that previous methods [16] made the assumption of a low-rank kernel matrix, without specifying the underlying model on the images. Since the feature maps are low dimensional, we propose to recover the points from their missing entries using a nuclear norm penalty on their feature maps. The direct implementation of the approach would involve the lifting of the images to high dimensional feature maps, projection to lower-dimensional subspaces, followed by back-projection of the feature maps to images as in [16]; this approach, which is conceptually similar to structured low-rank methods that rely on lifting [17]–[20], is prohibitive from a computational and memory perspective when the manifold structure of large images are to be considered. In addition, analytical back-projection steps as in [16] are not available for many feature maps of practical relevance. Motivated by [21], we propose an iteratively reweighted least square (IRLS) algorithm with gradient linearization to directly solve the nuclear norm minimization scheme. This approach does not require the explicit lifting and hence is considerably more efficient. IRLS algorithms typically alternate between the estimation of a null-space matrix and a quadratic subproblem, where the penalty term is the energy of the projection to the null-space. In our setting, we alternate between the estimation of a Laplacian-like matrix from the current set of images, and a quadratic SToRM-like subproblem involving the Laplacian-like matrix.
The above link with the proposed kernel low-rank algorithm enables us to further improve the performance of SToRM. To make the recovery from undersampled data well-posed and to further reduce computational complexity, we propose to pre-estimate the Laplacian matrix from k-space navigators; this approach is motivated by similar approaches in low-rank regularizati [17], [22]–[28]. We estimate the Laplacian matrix from the navigators using an iterative reweighted algorithm. This is a more systematic approach compared to the SToRM approach of using exponential maps, followed by truncating the neighbours. To further reduce the computational complexity and memory demand of SToRM by an order of magnitude, we approximate the Laplacian matrix by a few of its eigen vectors. The eigen vectors of the Laplacian are termed as Fourier exponentials on the manifold/graph [29]. Instead of reconstructing the entire dataset, we propose to only recover the coefficients of the Laplacian basis functions. Since the framework is an improvement over SToRM using bandlimited modelling of the manifold, we refer to the proposed scheme as b-SToRM.
This approach is built upon our recent work on annihilation based image recovery [19], [20], [25], [30], [31] and the work on polynomial kernels introduced in [21]; we extend [21] to Gaussian kernels in this paper. While the eigen decomposition strategy in this paper was suggested in [12] to demonstrate the links with PSF methods [22], [23], this approach was not implemented or validated as a means to speed up the algorithm in [12]. We validate b-SToRM on nine adult congenital heart disease patients with different imaging views, as an add-on to the routine contrast enhanced cardiac MRI study. We study the impact of patient motion, reduced number of navigators, and reduced acquisition time on the algorithm. We also demonstrate that the reconstructed images can be sorted into respiratory and cardiac phases using the eigen-vectors of the estimated Laplacian matrix, facilitating the easy visualization of the data.
II. Background
A. Image recovery using smooth manifold regularization
A manifold is a topological space that locally resembles a low-dimensional Euclidean space. Many classes of natural images can be modelled as points in high-dimensional ambient space, lying on a low-dimensional manifold. The dimension of the ambient space (n) is equal to the number of pixels in the images, while the dimension of the manifold (m) depends on the degrees of freedom of the class of images. For example, each image in a real-time cardiac MRI acquisition can be parameterized by the cardiac and respiratory phases.
Many machine learning algorithms exploit the smoothness of signals on the manifold, by using the regularization prior ; for an arbitrary function f, this metric is the energy of the gradient of the function on the manifold. Most algorithms operate on discrete samples , and the metric is approximated as:
| (1) |
The widely used weight matrix is computed as:
| (2) |
Here, . is a matrix, whose columns correspond to and L = D − W is termed as the graph Laplacian. D is a diagonal matrix with elements defined as . The weight matrix (2), originally introduced in [32], is inspired by the heat kernel. This approximation is only valid for a well-sampled manifold. To improve the approximation, a common approach in practical applications is to remove graph edges that are separated by more that a specified threshold. Another approach is to use fixed number of neighbours, resulting in regular graphs. However, this approach may result in false edges or does not make full use of the redundancy in the dataset. The problem with these approaches is the need to choose σ, threshold, and/or the number of neighbours, which would impact the image quality.
B. SToRM framework
SToRM [12] relies on a navigated radial acquisition scheme where the same navigator lines (2–4 radial spokes) are played at the beginning of every 10–12 spokes. The acquisition of the ith image frame xi can be represented as:
| (3) |
Here, F is the 2-D Fourier transform matrix, Cj is a diagonal matrix corresponding to weighting by the jth coil sensitivity map and ηij is the noise. Φ is the sampling matrix corresponding to the navigators that is kept the same for all frames. Bi samples different k-space locations every frame.
The weight matrix of the image manifold is estimated from the navigator samples using (2), where . This results in high weights between images with similar cardiac and respiratory phase, while the weights between images with different phases are small. The manifold Laplacian L is computed from W.
SToRM reconstructs the images by solving:
| (4) |
where X = [x1,...,xk] is the Casorati matrix obtained by stacking the vectorized images as columns, while captures the measurement process described in (3).
A key drawback of SToRM is the sensitivity of the Laplacian matrix to noise and artifacts in the acquisition process. As discussed previously, the exponential weight choice assumes a well-sampled manifold and the specific way in which neighbours are selected. Another challenge is the large memory demand and computational complexity associated with the recovery of the large dataset, often consisting of 1000 frames. This makes it difficult to extend SToRM to 3D+time applications.
III. Theory
A. Bandlimited manifold shape model
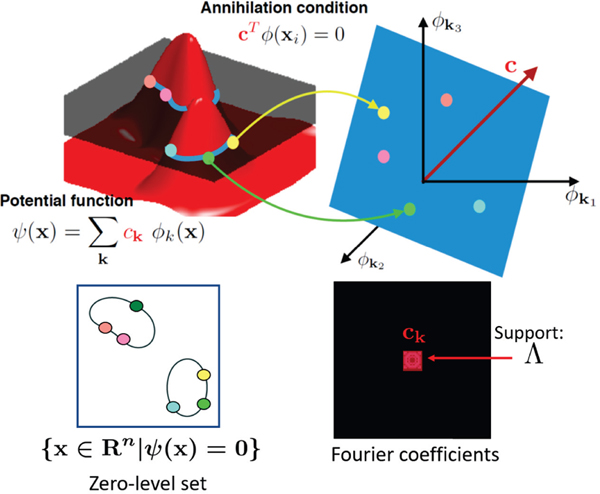
We model the manifold by a surface/curve, which is represented as the zero-level set of a bandlimited function . Specifically, we have ψ(x) = 0 for all points on the manifold. In this work, we assume that ψ is represented using a finite Fourier series expansion:
| (5) |
Here, is a set of contiguous discrete locations that indicate the support of the Fourier series co-efficients of ψ. The number of Fourier co-efficients is equal to the number of elements in the set Λ, denoted by |Λ|. For example, if Λ is a rectangular region of size n1 × n2, then |Λ| = n1n2. We assume that {ck} is the smallest set of Fourier co-efficients that satisfies (5); we term it as the minimal filter. We refer to the above representation as a bandlimited manifold. All points x on the zero-level of the surface (5) satisfy ψ(x) = 0, which implies that:
| (6) |
where c ∈ |Λ| has entries {ck, k ∈ Λ}. The entries of are non-linear transformations of x, similar to kernel approaches [33]; we term as the non-linear feature map of x (see Fig. 1). When there are multiple points x1,..,xk sampled from the manifold, we have the following annihilation relation:
| (7) |
Fig. 1:
Illustration of annihilation condition for 2D curves: The data points x are assumed to lie on a curve, which is the zero-level set of a band-limited function ψ. Each point x on the curve satisfies the relation: ψ(x) = 0. The Fourier series co-efficients c satisfy the annihilation relation (see (6)), where is a non-linear feature mapping of x. Since all the feature maps of all the points satisfy these annihilation conditions (see (8)), the feature maps lie on a subspace, and hence the feature matrix ΦΓ is low-rank. The annihilation relation implies that c (indicated in red) is orthogonal to the subspace spanned by the feature maps, as is illustrated in the figure. Under our assumption, is bandlimited, and the Fourier co-efficients {ck} are support-limited to the locations in the set Λ. The theory generalizes to arbitrary dimensions; it is illustrated in 2D for simplicity in this figure.
Since c is the unique minimal filter of ΦΛ(X), the dimension of the null-space of ΦΛ(X) is 1. Thus, by the rank-nullity theorem, rank(ΦΛ(X)) = |Λ| − 1.
B. Kernel low-rank relation
In practice, the exact support of Λ is unknown. We choose a rectangular support such that Λ ⊇ Γ; the corresponding feature matrix is denoted by ΦΓ(X). c1 obtained by zero-padding the original coefficients c will satisfy . c2 obtained by shifting c1 by an integer value will also satisfy . We denote the number of valid shifts of c such that it is still support limited in Γ by |Γ : Λ| [25]. Thus, we have:
| (8) |
See [34], [35] for details. Thus, we obtain right null-space relations ΦΓ(X) vi = 0, or equivalently, , where . These annihilation relations are similar to the ones in structured low-rank literature [17], [20], [24], [25], [36]–[38]. The rank of the feature map matrix ΦΓ or the kernel matrix can be used as a measure of the smoothness of the manifold. Specifically, if the rank is small, a low bandwidth implicit surface ψ is sufficient to annihilate all the images in the dataset. The kernel low-rank regularization thus encourages the points to lie on a smooth manifold, which is the zero level set of a bandlimited ψ.
C. Dynamic imaging using kernel low-rank regularization
We propose to use the low-rank property of the feature matrix to recover the images from the undersampled measurements:
| (9) |
where denotes the nuclear norm and Φ(X) denotes a matrix whose columns are the non-linear maps of the columns of X (corresponding to different frames), similar to (6). Note that this formulation is similar to structured low-rank methods [17], [20], [24], [25], [36]–[38], where the low-rank property of a matrix, whose entries are dependent on the original signal, is exploited. The main difference is that the lifted matrix is now dependent on X by a non-linear relation, as opposed to linear lifting operators in the classical structured low-rank settings. Note that the above formulation simplifies to low-rank recovery [39], when , which is the identity map.
This low-rank formulation has conceptual similarities to the approach in [16], where the low-rank structure of pixel intensity profiles that are considerably smaller in dimensions than the images in our setting are considered. In addition, we consider shift invariant kernels unlike the polynomial setting in [16]. Note that the dimension of the feature matrix is even higher than the dimension of the large dynamical imaging dataset X. Hence, the direct approach of lifting the signals, followed by projection to a subspace, and backprojection as in [16] is not feasible in our setting. We hence propose to use the iterative reweighted least squares (IRLS) algorithm [40].
D. Iterative reweighted least-squares algorithm
The IRLS algorithm relies on the property:
| (10) |
to realize an algorithm which alternates between the update of and the minimization of the quadratic cost function with penalty . Applying the IRLS algorithm to (10), we obtain the following iterations:
| (11) |
| (12) |
Here, the is the k × k Gram matrix of Φ(X) and is a small positive constant added to ensure invertibility. We choose , where η > 1 is a constant. Note that this matrix can be computed without explicitly evaluating the feature matrix Φ(X); the use of this property to speed up algorithms is often termed as the kernel trick [33].
The second term on the right hand side of (11) involves the non-linear map Φ. Motivated by [21], we focus on the gradient of (11) with respect to X. The gradient of the objective function with respect to the ith image Xi is given by:
When is a Gaussian kernel, we can simplify , where is the (i,j)th entry of the matrix:
| (13) |
Here, indicates the point-wise multiplication of two matrices. In matrix form, we thus have:
| (14) |
where
| (15) |
and D(n) is a diagonal matrix with elements defined as . The steepest descent update of (11) is given by:
| (16) |
E. Relation to SToRM regularization
We note that (16) can also be viewed as the steepest descent update of the quadratic cost function:
| (17) |
which is essentially the main cost function solved in SToRM [12]. Thus, the IRLS scheme can also be interpreted as an algorithm that alternates between SToRM and an update of L using (15) and (13). This result shows the link between kernel low-rank regularization and SToRM. The main difference between the methods is that the matrix W is derived from the current iterate using a fundamentally different formula as in (13), as opposed to its estimation from the navigators using (2), followed by truncation to obtain a regular graph.
The computational complexity and memory demand of the above iterative reweighted algorithm is expected to be high, especially since the data involving 500 – 1000 frames is heavily undersampled in k−t space. Two-step algorithms have been introduced by several researchers in low-rank regularization to reduce the computational complexity and memory demand of structured low-rank algorithms. These methods estimate the signal subspace (or equivalently the null-space) from fully sampled k-space sub-regions or navigator data, which is then used to solve for the signal. In our prior work in the context of structured low-rank matrix regularization, we estimated the matrix P in (10) that approximates the null-space of the matrix, which was used to solve for the signal. We now propose a similar strategy, where we estimate the L matrix in (17), to obtain a computationally feasible framework.
F. Two step recovery using k − t space navigators
We acquire multi-coil k − t space navigators Z = ΦX as described in Section II-B. Since this data is corrupted by noise and subtle subject motion, we propose to estimate L using kernel low-rank regularization. Specifically, we solve:
| (18) |
Solving the above optimization scheme using IRLS as discussed in Section III-D, we obtain the alternating algorithm
| (19) |
where
| (20) |
Here, , where . Note that the size of Z is considerably smaller than X; the computational complexity of the above algorithm to solve (18) is significantly lower than (17). When the above iterations converge, we use the final L to recover the image frames from their undersampled measurements.
Our empirical results show that the estimation of the L matrix as the by-product of the above IRLS scheme is considerably more robust than the use of (2). In addition to being more robust to noise and subject motion, this approach do not require us to artificially truncate the weight matrix or restrict the number of neighbours to obtain a regular graph. Note that we do not constrain the degree of the nodes, and hence they can be arbitrary. In our experiments, we observe that the off diagonal entries of L for any specific row are often small with few significant entries.
G. Approximation of Laplacian matrix for fast computation
We now propose to use the property of the L matrix to reduce the computational complexity and memory demand of the algorithm. Denoting the eigen decomposition of the symmetric Laplacian matrix as L = VΣVH, we rewrite the SToRM cost function in (4) as:
| (21) |
Here, the columns of V form an orthonormal temporal basis set and ui are the spatial coefficients.
We observe that the eigen values often increase rapidly, if L is the Laplacian matrix. Hence, the weighted norm in the penalty encourages signals X that are maximally concentrated along the eigen vectors vi with small eigen values; these eigen vectors correspond to smooth signals on the manifold. While this reformulation was introduced in [12] to show similarity with PSF methods, we did not make use of this property to accelerate the algorithm.
We now observe that in the optimization scheme (21) the projections of the recovered signal onto the higher singular vectors are expected to be small. We pick the r smallest eigen vectors of L to approximate the recovered matrix as:
| (22) |
where Ur is a matrix of r basis images (typically around r ≈ 30) and Vr is a matrix of r eigen vectors of L with the smallest eigen values. Thus the optimization problem (4) now reduces to:
| (23) |
The outline of our scheme is illustrated in Fig. 2. We observe r ≈ 30 is sufficient to approximate (21) with high accuracy.
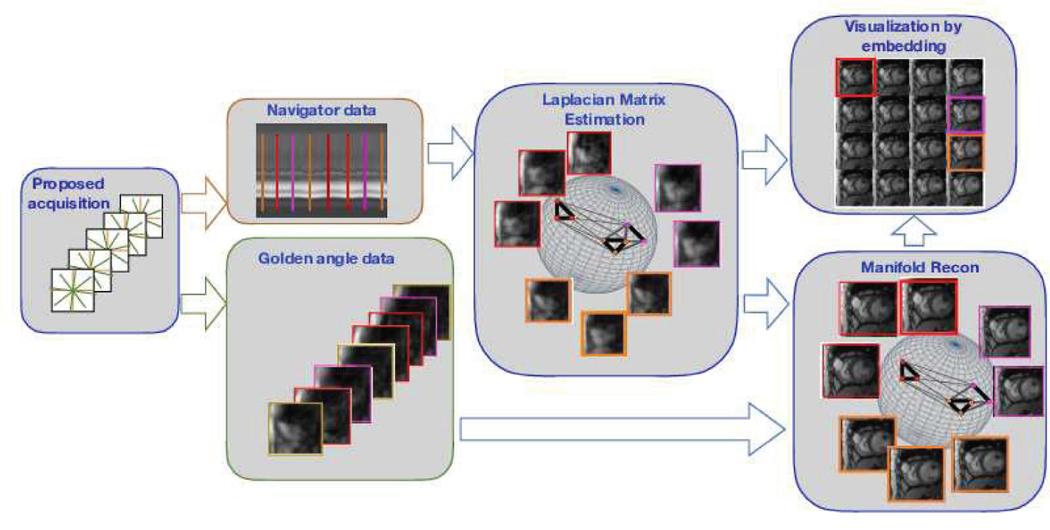
Fig. 2:
Outline of b-SToRM. The free breathing and ungated data is acquired using a navigated golden angle acquisition scheme. We estimate the Laplacian matrix from navigator data using the kernel low-rank model. The entries of the Laplacian matrix specify the connectivity of the points on the manifold, with larger weights between similar frames in the dataset. The manifold is illustrated by the sphere, while the connectivity of the points are denoted by lines whose thickness is indicative of proximity on the manifold. Note that neighbouring frames on the manifold may be well separated in acquisition time. The bandlimited manifold recovery scheme uses the Laplacian matrix to recover the images from the acquired k-space measurements. The Laplacian matrix also facilitates the easy visualization of the data.
Since we only have to recover r coefficient images from the measurements, the optimization problem is an order of magnitude more computationally efficient than (4). For both the formulations, a conjugate gradient algorithm is used to solve for the images. We compare the computational complexity of one iteration of conjugate gradient for both the formulations. Two main factors influence the computational time. The first factor is the number of 2D FFTs and IFFTs required to compute the gradient of the cost functions. In the proposed scheme, we solve for U, and hence r 2D FFTs and IFFTs are required. For the SToRM [12] scheme, we solve for k frames and hence k 2D FFTs and IFFTs are required. The second factor is the number of variables we solve for using conjugate gradient. For the proposed scheme, we solve for nr variables, while for SToRM, we solve for nk variables. Hence, for each PCG iteration, the speed-up should be .
H. Visualization using manifold embedding
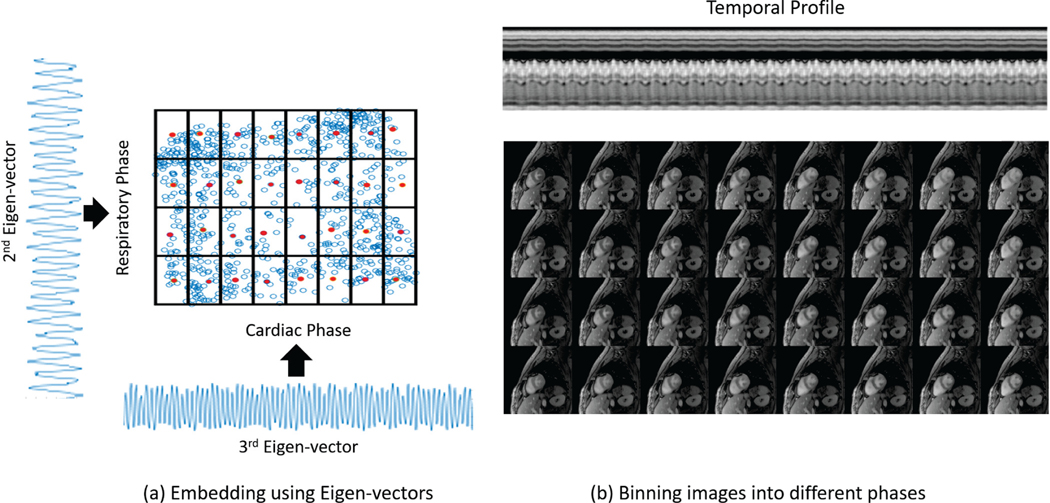
Laplacian eigen-maps rely on the eigen vectors of the Laplacian matrix to embed the manifold to a lower dimensional space. When the signal variation in the dataset is primarily due to cardiac and respiratory motion, the second and third lowest eigen vectors are often representative of the cardiac and respiratory phases. This information may be used to bin the recovered data into respiratory and cardiac phases for visualization as in Fig. 9, even though we do not use explicit binning for image recovery. This post-processing step can be thought of as a manifold embedding scheme using an improved Laplacian eigen-maps algorithm [32], where the main difference with [32] is the estimation of the Laplacian.
Fig. 9:
Binning into cardiac and respiratory phases. We demonstrate that the reconstructed ungated image series can easily be converted to a gated series of images if desired. For this purpose, the 2nd and 3rd eigen-vectors of the estimated Laplacian matrix are used as an estimate of the respiratory and cardiac phases respectively. The images can then be separated into the desired number of cardiac and respiratory bins. Here, we demonstrate this on a dataset that has been separated into 8 cardiac and 4 respiratory phases. Representative images from these bins have been shown in the figure. Similar results on an additional dataset are available in the supplementary material.
IV. EXPERIMENTS
Cardiac data was collected in the free-breathing mode from nine patients at the University of Iowa Hospitals and Clinics on a 1.5 T Siemens Aera scanner. The institutional review board at the local institution approved all the in-vivo acquisitions and written consent was obtained from all subjects. A FLASH sequence was used to acquire 10 radial lines per frame out of which 4 were uniform radial navigator lines and 6 were Golden angle lines. The sequence parameters were: TR/TE=4.3/1.92 ms, FOV=300mm, Base resolution=256, Bandwidth=574Hz/pix. 10000 spokes of k-space were collected in 43 s. Data corresponding to two views (two-chamber/short-axis and four-chamber) was collected for each patient, resulting in a total of 18 datasets. We used b-SToRM to reconstruct these datasets. A common set of parameters of the image reconstruction algorithm were manually selected for the first two datasets, and kept fixed for the rest of the datasets.
We compare the reconstructions using our technique to a few other competing methods:
PSF scheme [22]: For this method, we estimated the temporal profiles using the navigator signals. The recovery of the spatial coefficients was then posed as a least-squares optimization problem, regularized by the Frobenius norm of the spatial coefficients. The number of basis functions was fixed to 30.
SToRM [12]: The SToRM scheme was applied using our default parameter settings for both datasets. The exponential weight matrix was thresholded to retain only 2 neighbours per frame.
SToRM with few basis functions: For this method, we estimated the weight matrix as in SToRM and formed the Laplacian matrix corresponding to it. A few eigenvectors of the Laplacian matrix were retained as the temporal basis functions. The spatial co-efficients were then obtained using (23). The number of basis functions was fixed to 30.
XD-GRASP [11]: We adapted the authors’ code that is available online for contrast enhanced liver MRI, to the setting of free-breathing cardiac MRI, using [11] as a guideline. For both datasets, we assumed 10 respiratory phases and 18 cardiac phases, and manually tuned the regularization parameters for best visual quality.
Since our acquired data was prospectively under-sampled, we did not have access to the ground-truth images, and the above comparisons could only be done qualitatively on this data. In order to enable a quantitative comparison, we also applied the above reconstruction techniques on a simulated cardiac dataset with breathing motion. This was a single-coil dataset, with matrix size 300 × 300 and 424 frames spanning 16 cardiac cycles and 4 respiratory cycles. The data was under-sampled using 10 radial lines per frame, out of which 4 were navigator lines.
Since the technique in [16] is conceptually similar to ours, we also compare its performance to our method. This technique requires a fully sampled centre k-space region to form image domain training signals, which is not present in the datasets acquired using radial acquisitions. Hence we perform the comparison on the simulated dataset, where we have access to a fully sampled ground-truth. We consider two methods to form the training signals. In the first case, we do not have calibration lines, but we use a 7 × 7 centre k-space region, which is a subset of the radially undersampled dataset to form the training signals. In the second case, we use 15 fully sampled centre k-space lines to form the training signals, similar to [16]. In both cases, we use the training signals to reconstruct the radially under-sampled data. We consider 50 training signals and a polynomial kernel defined as: .
We conduct a few experiments to study the performance of our method in different datasets, and with different acquisition parameters. We study the impact of motion patterns on the reconstructions, using two of the most challenging datasets, with different breathing and cardiac patterns. We also study the effect of the number of navigator lines on the quality of the recovered images using a dataset with a large amount of breathing motion. The main goal is to determine the minimum number of navigator lines per frame to acquire in future studies. For this purpose, we compared the reconstruction using 4 navigator lines to that using only 1 or 2 navigator lines. Two experiments were conducted using 2 navigator lines per frame (corresponding to 0° and 90°) and 1 navigator line per frame (corresponding to 0°) respectively to estimate the weights. For the purpose of reconstruction, we used the full data (6 golden angle lines and 4 navigators). We also study the impact of the acquisition duration on image quality. For 2 datasets with different types of motion patterns, we compare the reconstruction using the entire data, 450 contiguous frames corresponding to 22 s, and also 300 frames corresponding to 12 s.
We demonstrate that the recovered data can be automatically binned into respiratory and cardiac phases using two eigen-vectors of the estimated Laplacian matrix. Thanks to the accurate and robust estimation of the Laplacian matrix, these eigen-vectors accurately represent the respiratory and cardiac motion of the patient over the entire acquisition. Using this information, each image frame can be assigned a bin depending on its respiratory and cardiac phase. Images from each bin can be viewed to find representative members of a particular cardiac or respiratory phase. We also compare our free-breathing ungated reconstructions to images obtained from a clinical breath-held sequence on the same patients.
V. RESULTS
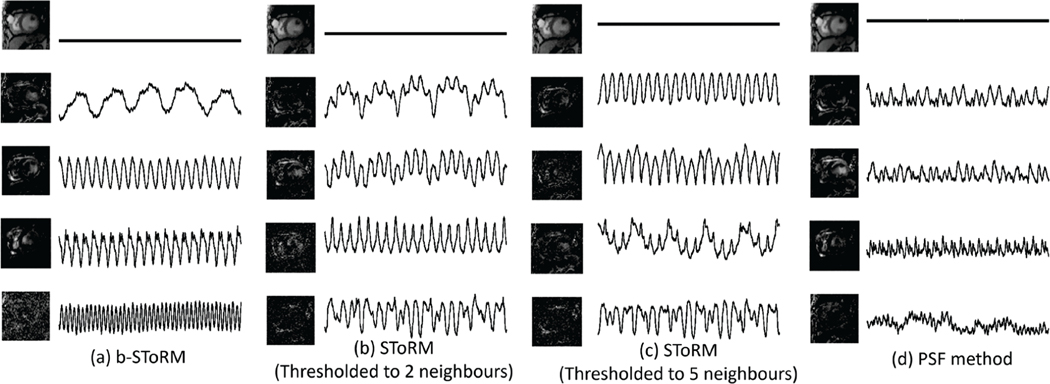
The basis images and temporal profiles obtained using different schemes that utilize the factorization of the Casorati matrix are illustrated in Fig. 3. We note that the temporal basis functions obtained with the b-SToRM scheme in (a) captures the physiological components of the motion. Specifically, we observe that the 2nd and 3rd lowest eigen vectors correspond to the respiratory and cardiac motion respectively, while the higher eigen vectors can be thought of as harmonics of the above dynamics. By contrast, the SToRM estimates show mixing of the dynamics. The comparison of (b) and (c) show the sensitivity of the estimates to the degree of the regular graph; the approximation of the manifold samples by a regular graph is poor. While the PSF scheme also relies on the factorization of the Casorati matrix, the non-linear manifold model facilitates the better representation of the non-linear dynamics in free-breathing datasets with large respiratory motion.
Fig. 3:
Visualization of the basis images and temporal functions. We compare the matrices Ur and Vr defined in (22) obtained using different methods that employ factorization of the Casorati matrix. (a) corresponds to b-SToRM, while (b) & (c) correspond to the SToRM approach (exponential weight matrix, followed by truncation) of estimating the Laplacian matrix, where 2 and 5 neighbours per node are retained. The temporal basis functions are the eigen vectors V of the estimated Laplacian matrix with the smallest eigen values. For the PSF scheme, the temporal basis functions are the eigen vectors of the navigator signal matrix with the smallest eigen values. These are shown in (d). It is observed that b-SToRM provides more accurate estimates of cardiac and respiratory motion than the other schemes, thus facilitating the recovery of smooth signals on the manifold. Moreover, by comparing (b) and (c), it is observed that the basis functions are quite sensitive to the choice of the threshold used to compute the SToRM exponential weight matrix.
The b-SToRM scheme is compared to other competing methods in Fig. 4. A few reconstructed images and temporal profiles are shown for (a) b-SToRM (b) StoRM with few basis functions (c) SToRM (d) PSF method. It is observed that the images in (a) show less artefacts as compared to the competing methods. In addition, the computational complexity of (a) is significantly lower than (c). The PSF scheme shows some streaking artefacts. In (b), we observe that there are some artefacts in the temporal profile, since the dataset has sudden gasps of breath. This could be because a few eigenvectors do not capture the physiological motion in this case, or equivalently the approximation of the SToRM Laplacian matrix using few eigen vectors is poor. More frames of this challenging dataset as reconstructed by b-SToRM are shown in Fig. 5 and Fig. 6. The temporal profiles of SToRM appear more noisy than that of PSF, while the b-SToRM scheme provides improved results. Note that this experiment is significantly more challenging than the results in [12] and Fig. S1 in the supplementary material due to motion as well as increased noise resulting from GRE acquisitions.
Fig. 4:
Comparison with other methods. Few frames and temporal profiles are shown from a dataset reconstructed using (a) b-SToRM (b) SToRM using few basis functions (c) SToRM [12] (d) PSF scheme [22]. It is observed that b-SToRM yields the best overall results, followed by SToRM that shows some degradation in image quality indicated by the red arrows. Note that b-SToRM also benefits from a speed-up due to the factorization of the Casorati matrix. It is also observed from (b) that using a few basis functions of the SToRM Laplacian matrix results in artefacts in the images and the temporal profile. Specifically, the approximation of the SToRM Laplacian matrix using few basis functions is poor, which translates to poor recovery. The PSF method also shows some image artefacts as compared to b-SToRM, which shows the benefit of the non-linear manifold modeling over subspace approximation. The red arrows in the figure point to artefacts in the images reconstructed using the competing methods. Similar results on an additional dataset are included in the supplementary material.
Fig. 5:
Comparison to XD-GRASP: Images corresponding to a few cardiac and respiratory phases reconstructed using XD-GRASP are shown in (a). Since both methods use drastically different reconstruction strategies, we rearrange the images obtained using b-SToRM into respiratory and cardiac phases in (b) for direct comparison to (a). Likewise, the recovered frames of XD-GRASP are also re-arranged to form a temporal profile. It is seen that the images and temporal profiles in (a) have more artefacts as compared to (b). The images in (a) contain speckle-like artefacts. Since the dataset included sudden gasps of breath, some respiratory phases are very poorly sampled and the artefacts are more pronounced in these phases. In comparison, b-SToRM can recover more natural-looking images and temporal profiles. Similar results on an additional dataset can be found in the supplementary material.
Fig. 6:
Sensitivity of the algorithm to high motion. We illustrate b-SToRM on datasets acquired from two patients with different types of motion. For both datasets, we show a temporal profile for the whole acquisition to give an idea of the amount of breathing and cardiac motion present. We also show a few frames from time points with varying respiratory phase. The dataset on the left has regions with abrupt breathing motion at a few time points. Since these image frames have few similar frames in the dataset (poorly sampled neighbourhood on the manifold), the algorithm results in slightly noisy reconstructions at the time points with high breathing motion (red box). The regions with low respiratory motion (blue and light blue boxes) are recovered well. The dataset on the right shows consistent, but low respiratory motion. By contrast, the heart rate in this patient was high. We observe that b-SToRM is able to produce good quality reconstructions in this case, since all neighbourhoods of the manifold are well sampled.
We show the comparison of b-SToRM with XD-GRASP in Fig. 5 (a). Only 4 respiratory and 5 cardiac phases are shown here for better visualization. The reconstructions using b-SToRM are also re-arranged in Fig. 5 (b) for a direct comparison to (a). For the purpose of re-arranging the frames of the b-SToRM dataset, we used the cardiac and respiratory signals that were estimated using XD-GRASP from the centre k-space temporal profile. It is observed that the images obtained using b-SToRM have less artefacts due to motion and noise, especially in cardiac and respiratory phases which only have a few k-space samples (bottom row). The frames reconstructed using XD-GRASP are also re-arranged to recover a temporal profile. It is observed that the temporal profile is quite noisy and motion is also suppressed, which is due to the discrete segmentation of the frames into phases.
The reconstruction techniques were only compared qualitatively in Fig 4 and Fig 5 since the data was prospectively under-sampled and the ground-truth was not available. Table I shows a quantitative comparison of the different techniques on a simulated dataset. It is observed that b-SToRM outperforms the other techniques according to the Signal-to-error ratio value. The reconstructed images and temporal profiles are available in the supplementary material. The total reconstruction time for each method is also reported. It is observed that the computational complexity of b-SToRM is comparable to the PSF scheme. The SToRM and XD-GRASP techniques are significantly more computationally intensive. Besides the total computation time, we also include a breakup of the time taken to perform some initial computations for some of the methods. This includes the total time to compute the Laplacian matrix for SToRM and the basis functions V for b-SToRM, SToRM with few basis functions and PSF. It also includes the time to pre-compute the constant terms required for the conjugate gradient step. After these initial computations, the time required to perform 40 iterations of conjugate gradient to compute the images or basis images is also reported. It is observed that there is a large speed-up in the conjugate gradient step for b-SToRM over SToRM.
TABLE I:
Quantitative comparison of reconstruction techniques R1.C2
| Method | SER (dB) | Total time (s) | Initial computation (s) | Conjugate gradient (s) |
|---|---|---|---|---|
| b-SToRM | 25.03 | 10.66 | 1.91 | 8.75 |
| SToRM with few basis functions | 16.63 | 8.8 | 0.43 | 8.37 |
| SToRM | 19.80 | 100.65 | 1.79 | 98.86 |
| PSF | 17.08 | 8.27 | 0.85 | 7.42 |
| [16] without calibration lines | 9.73 | 27.08 | ||
| [16] with calibration lines | 17.95 | 27.06 | ||
| XD-GRASP | 9.86 | 324.45 |
The performance of [16] on the simulated dataset can be seen with and without the calibration lines in Table I. The reconstructed images and temporal profiles are available in the supplementary material. It is observed that the performance of the technique is heavily dependent on the presence of a calibration region, which is absent in our acquired prospectively sampled datasets.
The datasets in Fig. 6 have a high amount of respiratory and out-of plane motion, compared to the other datasets that we have collected. The first dataset shows a normal cardiac rate (68 beats/min) accompanied by a very irregular breathing pattern, characterized by several large gasps of breath. We show a few reconstructed frames from different time points, at various states of motion. The reconstruction quality is better in presence of less respiratory motion since there are frames similar to it in the dataset; the manifold neighbourhood is well sampled in these neighbourhoods. By contrast, the images are seen to be more noisy in manifold regions that are not well-sampled (red box). The second dataset shows a high cardiac rate (107 beats/min) accompanied by heavy regular breathing (42 breaths/min). We observe that the algorithm is able to reconstruct this case satisfactorily, despite the rapid motion since the manifold is well-sampled.
We observe from Fig. 7 that for both high and low motion regions, there is no degradation in image quality when the number of navigator lines are reduced to two from four. Only using one navigator spoke induces some error, especially for the frames highlighted in green since they have more respiratory motion. This is expected since the approach will only be sensitive to the motion in one direction and not to the direction orthogonal to it. As a result of this experiment, we plan to keep only two navigator lines per frame in the future, and consequently increase the number of golden angle lines to 8 (from 6 in the current acquisition). This should improve image quality by making the sampling patterns between frames more incoherent.
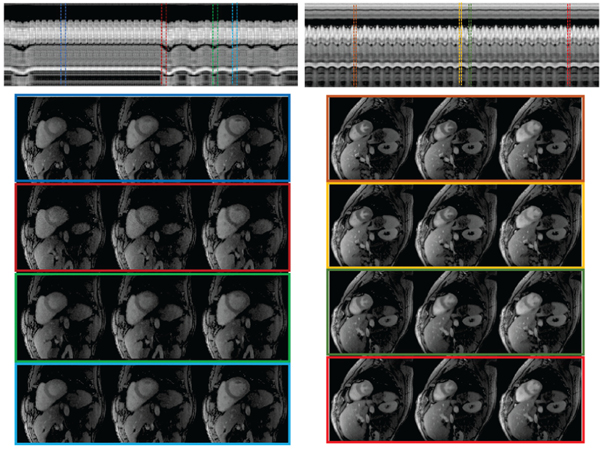
Fig. 7:
Effect of number of navigator lines on the reconstruction quality. We perform an experiment to study the effect of computing the Laplacian matrix L from different number of navigator lines. For this purpose, we use one of the acquired datasets with 4 navigator lines per frame. We compute the ground-truth L matrix using all 4 navigators. Next, we also estimate the L matrix using 2 navigator lines (keeping only the 0° and 90° lines) and 1 navigator line (keeping only the 0° line). We now reconstruct the full data using these three Laplacian matrices, as shown in the figure. We observe that two navigator lines are sufficient to compute the Laplacian matrix reliably. Using one navigator line induces some errors, especially in the frames highlighted in green which are from a time point with higher respiratory motion. As a comparison, note that the error images are in the same scale as those for Fig. 8.
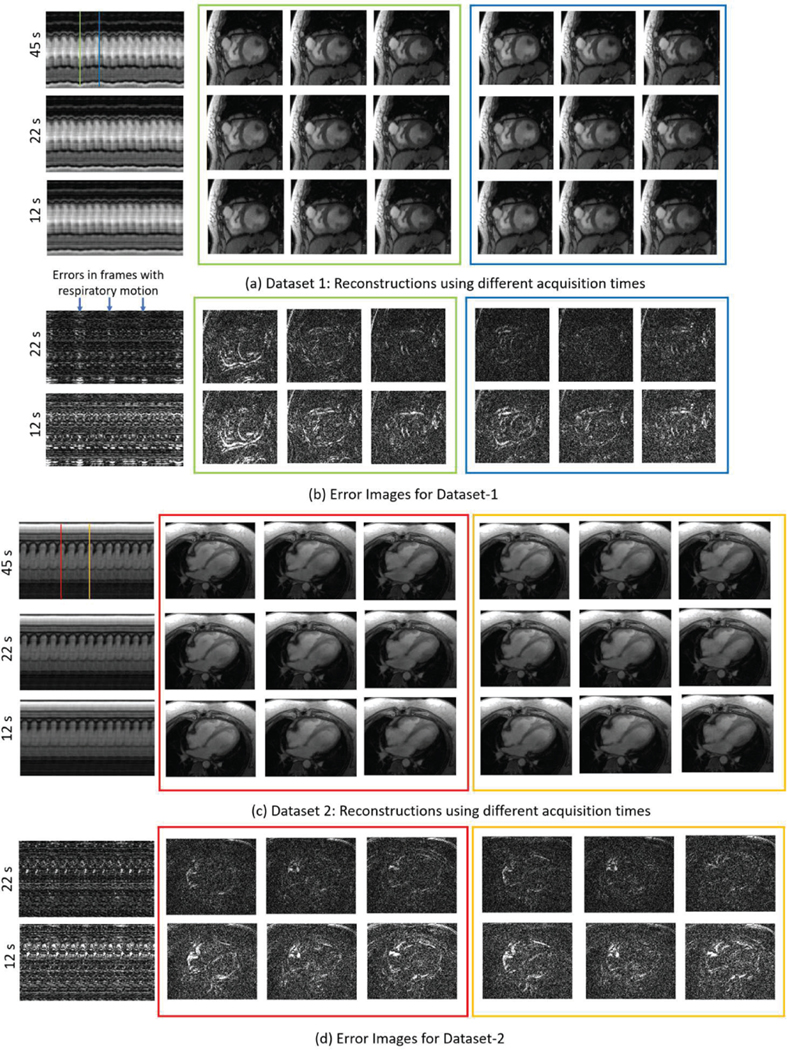
The effect of reducing acquisition time is illustrated in Fig. 8. The dataset at the top has more breathing motion as compared to the bottom one. We observe that the bottom dataset is robust to decrease in the number of frames; it can be reliably recovered even from 12 seconds of data. The top dataset is more sensitive to reduction in scan time. The green line corresponds to the lowest position of the diaphragm, which is less frequent in the dataset. By contrast, the blue line corresponds to a more frequent frame. The frames around the green line, shown in the green box are more noisy when the scan time is reduced to 12 seconds, compared to the reconstructions within the blue box. We observe negligible errors in both datasets when the acquisition time is reduced to 22s, whereas relatively noisy reconstructions are seen in high motion frames when it is reduced to 12 second acquisition windows. The error images for Fig. 7 and Fig. 8 are on the same scale, to illustrate the relative effects of changing the number of navigators and the number of frames.
Fig. 8:
Effect of number of frames on the reconstruction quality. We perform an experiment to study the effect of reconstructing the data from a fraction of the time-frames acquired. The original acquisition was 45 seconds long, resulting in 1000 frames. We compare the reconstruction of the 1st 250 frames, using (1) all 1000 frames (2) only 550 frames, i.e. 22 s of acquisition (3) only 350 frames, i.e. 12 s of acquisition. As can be seen from the temporal profiles, Dataset-1 has more respiratory motion than Dataset-2. Consequently, the performance degradation in Dataset-1 is more pronounced with decrease in the number of frames. Moreover, the errors due to decrease in the number of frames is mostly seen in frames with higher respiratory motion, as pointed out by the arrows. As a comparison, note that the error images are in the same scale as those for Fig. 7.
The results in Fig. 9 show that the improved Laplacian eigen maps approach facilitates the easy visualization of the data. In general, we observe that the eigen-vectors of the Laplacian matrix with the second and third lowest eigen values correspond to respiratory and cardiac motion. It can be appreciated from Fig. 3 that such a binning strategy is not possible when the exponential weights are used.
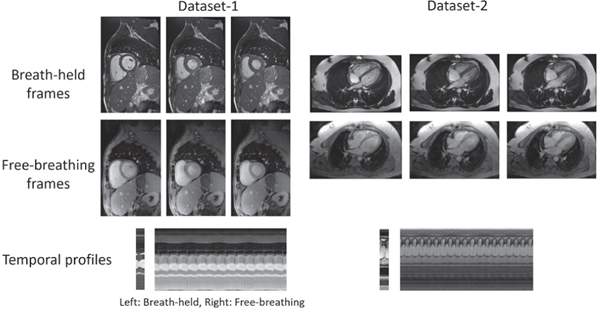
Fig. 10 demonstrates the potential of b-SToRM to replace clinical breath-held and gated techniques. There is some difference in the appearance of the breath-held and free-breathing reconstructions due to mismatch in slice position. Moreover, the breath-held acquisition was done using a TRUFI sequence, and thus shows higher contrast than the free-breathing data which was acquired using a FLASH sequence. In spite of these differences, we note that the images reconstructed using b-SToRM are of clinically acceptable quality.
Fig. 10:
Comparison to breath-held scheme. We demonstrate that b-SToRM produces images of similar quality to clinical breath-held scans, in the same acquisition time. Note that there are differences between the free-breathing and breath-held images due to variations in contrast between TRUFI and FLASH acquisitions, and also due to mismatch in slice position. However, the images we obtain are of clinically acceptable quality. Moreover, unlike the breath-held scheme we reconstruct the whole image time series (as is evident from the temporal profile). This can provide richer information, such as studying the interplay of cardiac and respiratory motion.
VI. DISCUSSION
We have introduced a new framework for the recovery of free-breathing and ungated cardiac images in a short 2-D acquisition. We assume that the images are points on a smooth manifold. We estimate the graph Laplacian from radial navigators. This framework relies on two key innovations over the SToRM algorithm: (i) A novel algorithm assuming a bandlimited manifold model is used to estimate the Laplacian matrix (ii) Using only a few eigenvectors of the Laplacian as the temporal basis functions reduces the computational complexity and memory demand of the algorithm by an order of magnitude. Due to its computational efficiency and lack of need for manual intervention, the new framework may be a good candidate for clinical scans where patients (e.g. pediatric patients, patients with COPD) are unable to hold their breath for sufficiently long periods of time, or are unable to follow breath-holding instructions.
While the framework has similarities to approaches that rely on the factorization of the Casorati matrix [23], [39], [41], [42], the key difference is the signal model and the approach in which the temporal basis functions are estimated. Moreover, we have shown in Fig. 3 that unlike other approaches, b-SToRM is able to automatically estimate the respiratory and cardiac signals from the eigen-vectors of the estimated Laplacian matrix. When the Laplacian matrix is estimated using the exponential function as in SToRM, or using the navigator signals as in the PSF method, a few eigen-vectors do not capture the physiological motion. For SToRM, it is also required to threshold the weight matrix to achieve good reconstruction results. This is equivalent to heuristically forming a regular graph by fixing the node degree. In this case, the eigenvectors are dependent on the specific thresholding function that is used. The proposed Laplacian estimation technique does not require any manual thresholding and does not constrain the graph to be a regular one. When reconstructing using a fixed number of basis functions (r = 30), it is shown that the proposed Laplacian preserves the temporal profiles better than when an exponential weight matrix is used as in SToRM. While we expect the performance of both SToRM and b-SToRM to degrade when certain cardiac and respiratory phases are not repeated frequently in the dataset, it is demonstrated in our results (for example in Fig 4) that b-SToRM is more robust to such situations. Moreover, due to the need to reconstruct only a few basis images, b-SToRM is significantly faster than SToRM. It was illustrated in [12] that an exponential weight matrix can also be used to estimate the respiratory and cardiac signals. However, this was shown for phantom data, and we have found that it does not hold true in general for many real datasets. Other conventional methods often require the binning of the k-space data to respiratory bins before reconstructions, using self gating approaches [10]. The main benefit of b-SToRM is that it does not require any explicit binning. However, we have shown in Fig. 5 and Fig. 9 that our reconstructions can easily be visualized in a binned fashion. In contrast, as shown in Fig. 5, the temporal profiles obtained by rearranging the XD-GRASP reconstructed images often have artefacts due to binning into discrete phases. Thus, when images are reconstructed using a binned approach, they might not always be rearranged to get back the original time series.
Since our acquired data was prospectively under-sampled, we were not able to perform quantitative comparisons for the various techniques used to reconstruct this data. We performed additional experiments on a retrospectively under-sampled phantom dataset for quantitative comparison. The results are summarized in Table I. It is observed that b-SToRM has the highest SER (25.03 dB) out of all the methods reported, while SToRM performs second-best (19.80 dB). The PSF scheme has the lowest reconstruction time (7.42 s), closely followed by SToRM with few basis functions (8.37 s) and b-SToRM (8.75 s). SToRM and XD-GRASP are significantly more computationally intensive. b-SToRM shows good performance in a considerably low reconstruction time, and thus outperforms the other techniques. The kernel low-rank based method in [16] performs poorly in the absence of calibration lines (7.93 dB), but improves considerably when we use calibration lines to form the training signals (17.95 dB). The reconstructed images and temporal profiles for all the techniques are illustrated in the supplementary material. The times for initial computations and conjugate gradient are also reported separately for PSF and the SToRM-based methods. 40 iterations of the conjugate gradient algorithm for b-SToRM is 11.3 times faster than for SToRM. The speed-up is of the same order as .
We demonstrate our algorithm on a number of datasets with different respiratory and cardiac patterns. We show that the technique is able to reconstruct data with irregular breathing motion, since there is no periodicity assumption in our reconstruction technique. The method only requires some repetitive motion, which need not be periodic. We also expect that the algorithm will work on datasets with arrhythmia. However, we did not have access to any patient datasets with arrhythmia, so this could not be illustrated in the paper.
There are two parameters in the reconstruction algorithm, namely the regularization parameter λ, and rank r. For a low λ value, we will get a lot of aliasing artefacts, and the reconstructions will be close to the zero-filled inverse Fourier transforms of the acquired data. For a very high λ value, we will notice a lot of motion blur. Note from (21), (22), (23) that the modification of the original SToRM cost function using the low-rank approximation is exact if the rank is appropriately high. If the rank is set to a very low value, then we would notice some motion artefacts since a few basis functions would not be able to capture the motion. If the rank is set to a very high value, the computational complexity would become higher, and comparable to the SToRM approach. Note that the use of the penalty in (23), weighted by the singular values, ensures that the recovery with larger number of basis functions is still well-posed. Specifically, the higher order eigen vectors are penalized more heavily than the ones corresponding to smoother functions on the manifold. For our first 2 datasets, we empirically selected a common regularization parameter λ and rank r which gave qualitatively good reconstructions. We then kept this parameter fixed for the rest of our datasets and did not do any manual tuning. We noticed good performance with this approach for all our 18 datasets. We expect the performance to improve if the parameter is manually tuned for each dataset. However, since this is not practically feasible for clinical practice, we suggest that the parameters be kept at their default setting.
In accordance with the results of our retrospective experiments on the impact of the number of navigator lines, we plan to collect data with only two navigator lines in the future. This would increase the incoherence of the undersampling patterns across frames, resulting in better quality reconstructions. Our experiments on reduced scan time show that we can obtain reliable data from datasets with high motion with around 22s of data/slice, while it can be pushed down to 12s for datasets with less motion. The results may be further improved by using patch based regularization [43], [44].
Our method produces a series of ungated images, enabling the user to visualize the real-time data with both respiratory and cardiac motion. This approach may be useful in studies on patients with pulmonary complications such as COPD. The data can also be automatically segmented into respiratory and cardiac phases post reconstruction for easy visualization, using the eigen-vectors of the estimated Laplacian matrix.
Since the study was an add on to the routine cardiac exam, there was no perfect control on the specific time point of acquisition following contrast administration. This explains the differing contrast between the datasets.
VII. CONCLUSION
We proposed a novel bandlimited manifold regularization framework for free-breathing and ungated cardiac MR imaging. The validation of the dataset using cardiac datasets with differing amount of cardiac and respiratory motion shows the ability of the scheme to provide good image quality. It is also demonstrated that the resulting ungated images can be easily binned into respiratory and cardiac phases and viewed as a gated dataset. The success of the method on very challenging datasets with high cardiac rate and irregular breathing patterns suggests a useful clinical application of the method on patients who have difficulty in following traditional breath-holding instructions.
Supplementary Material
Acknowledgments
This work is supported by NIH 1R01EB019961-01A1.
References
- [1].Chan KG, Streichan SJ, Trinh LA, and Liebling M, “Simultaneous temporal superresolution and denoising for cardiac fluorescence microscopy,” IEEE Transactions on Computational Imaging, vol. 2, no. 3, pp. 348–358, 2016. [Google Scholar]
- [2].Cikes M, Tong L, Sutherland GR, and D’hooge J, “Ultrafast cardiac ultrasound imaging: technical principles, applications, and clinical benefits,” JACC: Cardiovascular Imaging, vol. 7, no. 8, pp. 812–823, 2014. [DOI] [PubMed] [Google Scholar]
- [3].Liang Z-P, Jiang H, Hess CP, and Lauterbur PC, “Dynamic imaging by model estimation,” International journal of imaging systems and technology, vol. 8, no. 6, pp. 551–557, 1997. [Google Scholar]
- [4].Sharif B, Derbyshire JA, Faranesh AZ, and Bresler Y, “Patient-adaptive reconstruction and acquisition in dynamic imaging with sensitivity encoding (PARADISE),” Magnetic Resonance in Medicine, vol. 64, no. 2, pp. 501–513, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Tsao J, Boesiger P, and Pruessmann KP, “k-t BLAST and k-t SENSE: Dynamic MRI with high frame rate exploiting spatiotemporal correlations,” Magnetic resonance in medicine, vol. 50, no. 5, pp. 1031–1042, 2003. [DOI] [PubMed] [Google Scholar]
- [6].Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P et al. , “SENSE: sensitivity encoding for fast MRI,” Magnetic resonance in medicine, vol. 42, no. 5, pp. 952–962, 1999. [PubMed] [Google Scholar]
- [7].Lustig M, Santos JM, Donoho DL, and Pauly JM, “kt SPARSE: High frame rate dynamic MRI exploiting spatio-temporal sparsity,” in Proceedings of the 13th Annual Meeting of ISMRM, Seattle, vol. 2420, 2006. [Google Scholar]
- [8].Christodoulou AG, Hitchens TK, Wu YL, Ho C, and Liang Z-P, “Improved subspace estimation for low-rank model-based accelerated cardiac imaging,” IEEE Transactions on Biomedical Engineering, vol. 61, no. 9, pp. 2451–2457, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Brinegar C, Schmitter SS, Mistry NN, Johnson GA, and Liang Z-P, “Improving temporal resolution of pulmonary perfusion imaging in rats using the partially separable functions model,” Magnetic Resonance in Medicine, vol. 64, no. 4, pp. 1162–1170, 2010. [Online]. Available: 10.1002/mrm.22500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Feng L, Grimm R, Block KT, Chandarana H, Kim S, Xu J, Axel L, Sodickson DK, and Otazo R, “Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI,” Magnetic resonance in medicine, vol. 72, no. 3, pp. 707–717, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, and Otazo R, “XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing,” Magnetic resonance in medicine, vol. 75, no. 2, pp. 775–788, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Poddar S and Jacob M, “Dynamic MRI using smoothness regularization on manifolds (SToRM),” IEEE Tran. Medical Imaging, vol. 35, no. 4, pp. 1106–1115, April 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Bhatia KK, Caballero J, Price AN, Sun Y, Hajnal JV, and Rueckert D, “Fast reconstruction of accelerated dynamic MRI using manifold kernel regression,” in International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, 2015, pp. 510–518. [Google Scholar]
- [14].Chen X, Usman M, Baumgartner CF, Balfour DR, Marsden PK, Reader AJ, Prieto C, and King AP, “High-resolution self-gated dynamic abdominal MRI using manifold alignment,” IEEE transactions on medical imaging, vol. 36, no. 4, pp. 960–971, 2017. [DOI] [PubMed] [Google Scholar]
- [15].Usman M, Atkinson D, Kolbitsch C, Schaeffter T, and Prieto C, “Manifold learning based ECG-free free-breathing cardiac CINE MRI,” Journal of Magnetic Resonance Imaging, vol. 41, no. 6, pp. 1521–1527, 2015. [DOI] [PubMed] [Google Scholar]
- [16].Nakarmi U, Wang Y, Lyu J, Liang D, and Ying L, “A kernel-based low-rank (KLR) model for low-dimensional manifold recovery in highly accelerated dynamic MRI,” IEEE Transactions on Medical Imaging, vol. PP, no. 99, pp. 1–1, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Haldar JP, “Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI,” IEEE transactions on medical imaging, vol. 33, no. 3, pp. 668–681, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Jin KH, Lee D, and Ye JC, “A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank hankel matrix,” IEEE Transactions on Computational Imaging, vol. 2, no. 4, pp. 480–495, 2016. [Google Scholar]
- [19].Ongie G, Biswas S, and Jacob M, “Convex recovery of continuous domain piecewise constant images from nonuniform fourier samples,” IEEE Transactions on Signal Processing, vol. 66, no. 1, pp. 236–250, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Ongie G and Jacob M, “A fast algorithm for convolutional structured low-rank matrix recovery,” IEEE Transactions on Computational Imaging, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Ongie G, Willett R, Nowak RD, and Balzano L, “Algebraic variety models for high-rank matrix completion,” in Proceedings of the 34th International Conference on Machine Learning, ser. Proceedings of Machine Learning Research, Precup D and Teh YW, Eds., vol. 70. International Convention Centre, Sydney, Australia: PMLR, 06–11 Aug 2017, pp. 2691–2700. [Online]. Available: http://proceedings.mlr.press/v70/ongie17a.html [Google Scholar]
- [22].Liang Z-P, “Spatiotemporal imagingwith partially separable functions,” in Biomedical Imaging: From Nano to Macro, 2007. ISBI 2007. 4th IEEE International Symposium on. IEEE, 2007, pp. 988–991. [Google Scholar]
- [23].Zhao B, Haldar JP, and Liang Z-P, “PSF Model-Based Reconstruction with Sparsity Constraint: Algorithm and Application to Real-Time Cardiac MRI,” Annual International Conference of the IEEE Engineering in Medicine and Biology Society., vol. 2010, pp. 3390–3393, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Shin PJ, Larson PE, Ohliger MA, Elad M, Pauly JM, Vigneron DB, and Lustig M, “Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion,” Magnetic resonance in medicine, vol. 72, no. 4, pp. 959–970, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Ongie G and Jacob M, “Off-the-grid recovery of piecewise constant images from few fourier samples,” SIAM Journal on Imaging Sciences, vol. 9, no. 3, pp. 1004–1041, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Nguyen HM, Peng X, Do MN, and Liang Z-P, “Denoising mr spectroscopic imaging data with low-rank approximations,” IEEE Transactions on Biomedical Engineering, vol. 60, no. 1, pp. 78–89, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Qu X, Mayzel M, Cai J-F, Chen Z, and Orekhov V, “Accelerated nmr spectroscopy with low-rank reconstruction,” Angewandte Chemie, vol. 127, no. 3, pp. 866–868, 2015. [DOI] [PubMed] [Google Scholar]
- [28].Ying J, Lu H, Wei Q, Cai J-F, Guo D, Wu J, Chen Z, and Qu X, “Hankel matrix nuclear norm regularized tensor completion for n-dimensional exponential signals,” IEEE Transactions on Signal Processing, vol. 65, no. 14, pp. 3702–3717, 2017. [Google Scholar]
- [29].Ortega A, Frossard P, Kovačević J, Moura JM, and Vandergheynst P,´ “Graph signal processing,” arXiv preprint arXiv:1712.00468, 2017. [Google Scholar]
- [30].Ongie G and Jacob M, “Super-resolution mri using finite rate of innovation curves,” in Biomedical Imaging (ISBI), 2015 IEEE 12th International Symposium on ISBI, 2015, pp. 1248–1251. [Google Scholar]
- [31].Ongie G, “A fast algorithm for convolutional structured low-rank matrix recovery,” IEEE transactions on computational imaging, vol. 3, no. 4, pp. 535–550, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Belkin M and Niyogi P, “Laplacian eigenmaps and spectral techniques for embedding and clustering,” in Advances in neural information processing systems, 2002, pp. 585–591. [Google Scholar]
- [33].Scholkopf B and Smola AJ, Learning with kernels: support vector machines, regularization, optimization, and beyond. MIT press, 2002. [Google Scholar]
- [34].Poddar S and Jacob M, “Recovery of point clouds on surfaces: Application to image reconstruction,” in Biomedical Imaging (ISBI 2018), 2018 IEEE 15th International Symposium on. IEEE, 2018, pp. 1272–1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Poddar S, “Recovery of noisy points on band-limited surfaces: Kernel methods re-explained,” arXiv preprint arXiv:1801.00890, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Ongie G, Biswas S, and Jacob M, “Convex recovery of continuous domain piecewise constant images from nonuniform fourier samples,” IEEE Transactions on Signal Processing, vol. 66, no. 1, pp. 236–250, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Lee D, Jin KH, Kim EY, Park S-H, and Ye JC, “Acceleration of mr parameter mapping using annihilating filter-based low rank hankel matrix (ALOHA),” Magnetic resonance in medicine, vol. 76, no. 6, pp. 1848–1864, 2016. [DOI] [PubMed] [Google Scholar]
- [38].Haldar JP and Zhuo J, “P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data,” Magnetic resonance in medicine, vol. 75, no. 4, pp. 1499–1514, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Lingala SG, Hu Y, DiBella E, and Jacob M, “Accelerated dynamic MRI exploiting sparsity and low-rank structure: kt SLR,” IEEE transactions on medical imaging, vol. 30, no. 5, pp. 1042–1054, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Daubechies I, DeVore R, Fornasier M, and Güntürk CS, “Iteratively reweighted least squares minimization for sparse recovery,” Communications on pure and applied mathematics, vol. 63, no. 1, pp. 1–38, 2010. [Google Scholar]
- [41].Lingala SG and Jacob M, “Blind compressive sensing dynamic MRI,” IEEE transactions on medical imaging, vol. 32, no. 6, pp. 1132–1145, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Lingala SG, “A blind compressive sensing framework for accelerated dynamic mri,” in IEEE International Symposium on Biomedical Imaging, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Mohsin YQ, Ongie G, and Jacob M, “Iterative shrinkage algorithm for patch-smoothness regularized medical image recovery,” IEEE transactions on medical imaging, vol. 34, no. 12, pp. 2417–2428, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Mohsin YQ, Lingala SG, DiBella E, and Jacob M, “Accelerated dynamic mri using patch regularization for implicit motion compensation.” Magnetic Resonance in Medicine, vol. 77, no. 3, pp. 1238–1248, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.