Evaluation of the Artificial Neural Network and Naive Bayes Models Trained with Vertebra Ratios for Growth and Development Determination

Abstract

Objective

This study aimed to evaluate the success rates of the artificial neural network models (NNMs) and naive Bayes models (NBMs) trained with various cervical vertebra ratios in cephalometric radiographs for determining growth and development.

Methods

Our retrospective study was performed on 360 individuals between the ages of 8 and 17 years, whose cephalometric radiographs were taken. According to the evaluation of cephalometric radiographs, growth and development periods were divided into 6 vertebral stages. Each stage was considered as a group, each group had 30 girls and 30 boys. Twenty-eight cervical vertebral ratios were obtained by using 10 horizontal and 13 vertical measurements. These 28 vertebral ratios were combined in 4 different combinations, leading to 4 different datasets. Each dataset was split into 2 parts as training and testing. To prevent the overfitting, a 5-cross fold validation technique was also used in the training phase. The experiments were conducted on 2 different train/test ratios as 80%–20% and 70%–30% for both NNMs and NBMs.

Results

The highest determination success rate was obtained in NNM 3 (0.95) and the lowest in NBM 4 (0.50). The determination success of NBM 1 and NBM 3 was almost similar (0.60). The success of NNM 2 did not differ much from that of NNM 1 (0.94). The determination success of stage 5 was relatively lower than the others in NNM 1 and NNM 2 (0.83).

Conclusion

The NNMs were more successful than the NBMs in our developed models. It is important to determine the effective ratio and/or measurements that will be useful for differentiation.

INTRODUCTION

Growth and development (maturation) and bone age determination play an important role in shedding light on medical and legal issues in many disciplines such as anthropology, pediatrics, forensic medicine, orthopedics, endocrinology, and dentistry. In dentistry, craniofacial growth, growth-development, and bone age determination have an important place, not only in the sciences of pedodontics and orthodontics but also in determining the implantation time in surgery. Active growth in the head-neck area, the timing of treatment, and determination of remaining growth helps dentists in identifying the treatments to be applied diagnostically (1–3). In orthodontic treatment, the determination of growth and development periods is extremely important for the timely and effective resolution of functional anomalies in sagittal, transversal, and vertical planes (4, 5).

In determining bone age and growth-development, morphological, histological, and radiological methods are used; however, the radiological method is often preferred (6, 7). In orthodontics, panoramic, cephalometric, and hand-wrist radiographs are used for growth and development determination (8–13). Although hand-wrist radiographs have been proved to be valid, skeletal maturation can also be detected from the cervical vertebrae. It was first reported by Lamparski (9) that vertebrae could be used, and their reliability was evaluated by hand-wrist radiographs by many researchers (9–17). In addition to routine use in diagnosis and treatment, cephalometric radiographs provide benefits such as ease in recording and evaluating and not causing extra radiation (14–16). Although several studies have reported high levels of accuracy and reproducibility of the cervical vertebra maturation (CVM) method, Gabriel et al. (18) and Zhao et al. (19) reported moderate or low intra-observer and inter-observer agreement. Predko-Engel et al. (20) stated that experienced clinicians who use the CVM method routinely, made better diagnosis, were more consistent than the inexperienced clinicians who do not use the CVM method or use it rarely.

Computers are now indispensable in our daily lives. The ability of computers to learn and make decisions like a human being has led to their increased use in a wide array of areas. Artificial intelligence involves the use of a computer-controlled machine or when a computer performs tasks associated with higher mental activities, such as understanding past experiences, reasoning, generalization, and learning, which are generally considered to be human-specific qualities (21, 22). Artificial neural networks (ANNs) are computer programs developed as mathematical models of human cognition and neural biology by imitating human neural networks, characterized by its architecture, training or learning algorithms, and activation functions (23). Naive Bayes (NB) is one of the oldest statistical classification algorithms that calculates the probability of each state for an element and classifies it based on the highest probability value. The ANNs and NB are both developed using artificial intelligence techniques. Researchers have aimed at achieving more objective results by taking advantage of computer software and digital images. There are few studies on ANN in orthodontics. Raith et al. (24) reported that ANN could classify teeth according to geometrical features. Xie et al. (25) set up an ANN in determining whether extraction or non-extraction treatment was best for malocclusion and was effective with 80% accuracy. Larson et al. (26) studied pediatric hand radiographs with a convolutional neural network (CNN) model and reported their accuracy value similar to that of an expert radiologist (26). Wand et al. (27) used CNNs to analyze hand-wrist radiographs in which the radius classification was with 92% accuracy, and the ulna classification was with 90% accuracy. Kök et al. (28) and Amasya et al. (29) used artificial intelligence algorithms for CVM assessment. Kök et al. (28) evaluated the success of seven different algorithms on a model consisting of linear measurements. Amasya et al. (29) proposed machine learning classifier models used for the prediction of cervical vertebrae morphology.

In light of this information, the purpose of our study is to evaluate the success rates of the artificial neural network models (NNMs) and naive Bayes models (NBMs) trained with various cervical vertebra ratios in cephalometric radiographs for determining growth and development.

METHODS

Our retrospective study was performed on 360 individuals between the ages of 8 and 17 years, whose cephalometric radiographs were taken. According to the cephalometric radiographs’ evaluation, the growth and development periods were divided into 6 vertebral stages (10). The patients’ radiographs were evaluated by a senior orthodontist (HK) and divided into 6 vertebral stages. Thereafter, the radiographs of 30 girls and 30 boys were selected for each maturation level randomly. Written consent was obtained from all patients who applied to the clinic for treatment purposes, indicating that their radiographs or materials can be used in scientific articles. Ethics committee approval was received for this study from the Ethics Committee of Necmettin Erbakan University. Individuals with any disease that could prevent bone development and also who had any systemic diseases and syndromes, growth and development retardation, an anomaly that can prevent craniofacial growth, endocrine disorders, and/or malnutrition, or a long-term infectious disease, were not included in our study.

A total of 28 cervical vertebral ratios were obtained by using 10 horizontal and 13 vertical measurements on the second vertebra (C2), the third vertebra (C3), the fourth vertebra (C4), and the fifth vertebra (C5). All measurements were taken by an orthodontist (MSI), twice at 15-day intervals. These 28 vertebral ratios were combined in 4 different combinations; so, 4 different datasets that were used for training the NNM (NNM 1–4) and the NBM (NBM 1–4) were obtained (Figure 1). For example, NNM 1 and NBM 1 trained with Dataset 1, and so on.

Figure 1.

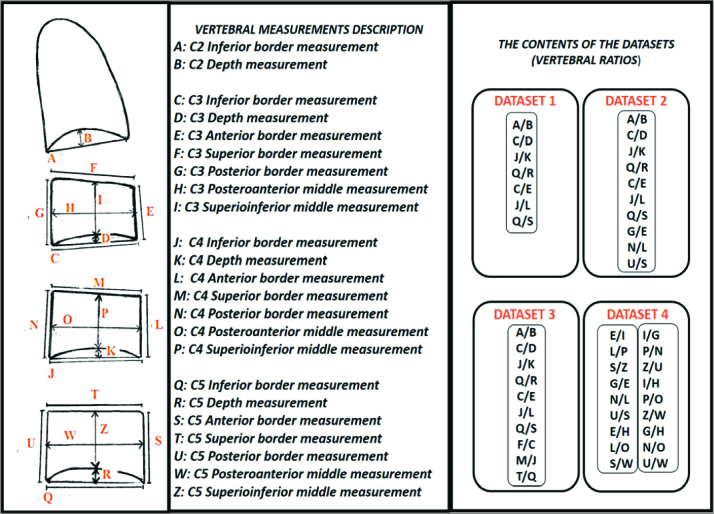
Description of the vertebral measurements and the contents of the datasets

MLP Classifier, Gaussian NB, Standard Scaler, train test split, Grid Search CV, metrics, cross val score, confusion matrix, accuracy score, classification report functions of the scikit-learn, and a machine learning library in Python 3.7, were used in this study. Multi-Layer Perceptron Classifier (MLP Classifier) library was used for training the ANN models. Logistic was used as an activation function. Alpha value, learning rate, and epoch (maximum iteration) were taken as 0.1, 0.001, and 200, respectively. One hidden layer was used, and for determining the appropriate neuron numbers in the hidden layer, experiments were conducted for each ANN model. It was explored between 5 and 30 neurons. Twenty-five for NNM 1 and NNM 2; 20 for NNM 3, and 15 for NNM 4 were found. L-BFGS solver, an optimizer based on the quasi-Newton methods, was chosen as the optimizer. As the dataset used in this study consists of continuous data, Gaussian Naive Bayes Classifier (Gaussian NB) library was used.

Statistical Analysis

The intraclass correlation coefficients (ICCs) were evaluated for all measurements. Each dataset was split into 2 parts as training and testing. To prevent the overfitting, a k-fold cross-validation technique was also used in the training phase. In this study, k was chosen as 5. First, the dataset was partitioned into training and test set. Then, 5-fold cross-validation (5-fold cv) was applied to the training set. In 5-fold cv, the training dataset is split into 5 portions. Each time, 1 of the 5 partitions is used as a validation set, and the other 4 portions compose the training set. (Figure 2) The mean accuracy of the training and validation sets are the results of 5-fold cv.

Figure 2.

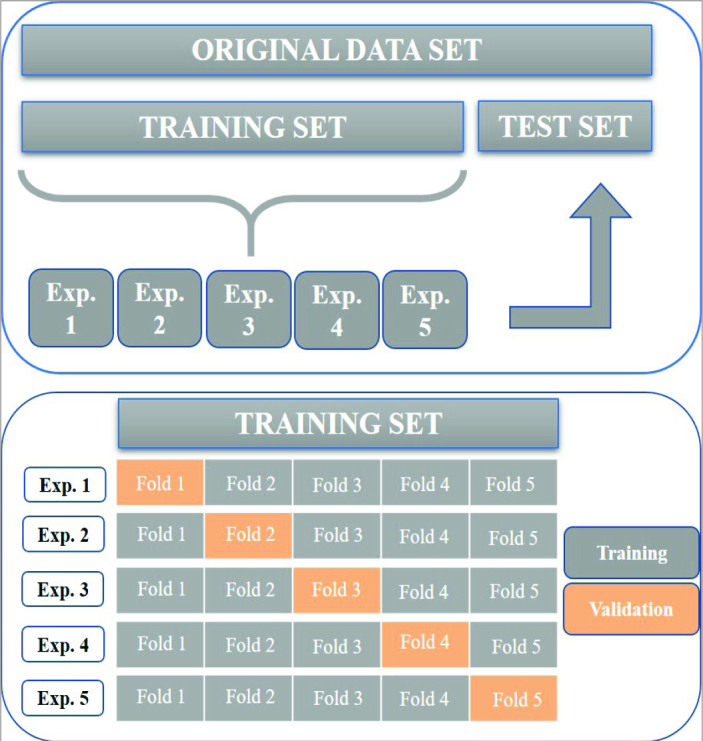
Description of the 5-fold cross-validation

The experiments were conducted on 2 different train/test ratios as 80%–20% and 70%–30% for both NNMs and NBMs. The function “train test split” was used from the scikit-learn library to split the dataset randomly. The test size was given as an input parameter to the function. 0.3 (for 70/30) and 0.2 (for 80/20) were used as test size. To be compatible with the real-life problem, random splitting was used. There is no outside intervention during the test set formation. We added this explanation to the statistical analysis part. The results of NNMs and NBMs were evaluated using the Precision, Recall (Sensitivity), Accuracy, and F1-score performance metrics, which were calculated via the confusion matrix and kappa coefficients. A confusion matrix is basically a tabular summary representation of how well the model was performed. The structure of a confusion matrix for multi-classification (in our study, there were 6 classes called Stage 1 (S1), Stage 2 (S2), Stage 3 (S3), Stage 4 (S4), Stage 5 (S5), and Stage 6 (S6), respectively) process and the graphic representations of the performance metric equations of the are given in Figure 3.

Figure 3.

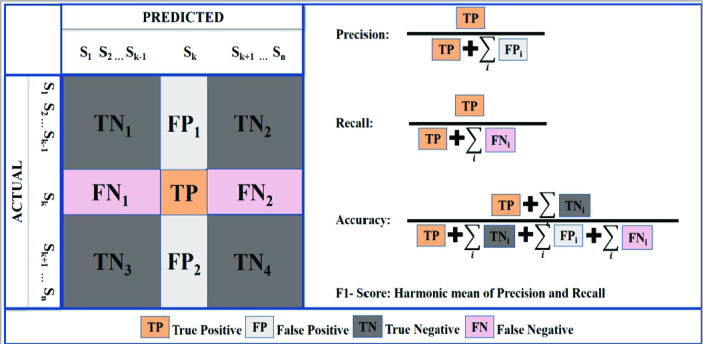
Structure of a confusion matrix for multiclass and graphic representations of the performance metrics

The performance metrics and kappa values of the models are presented in Table 1 and Table 2. Precision is the ratio of correctly predicted positive determinations to the total predicted positive determinations. Recall (sensitivity) is the ratio of correctly predicted positive determinations to all determinations in the actual class. Accuracy is the ratio of correctly predicted determination to the total determinations. The F1-score is the harmonic mean of Precision and Recall and calculated as F1 = 2 (Recall × Precision)/(Recall + Precision). In all the metrics, a higher value means a better estimation result.

Table 1.

Performance metrics of the artificial NNMs for the vertebral stage determination (70%–30% and 80%–20%)

Model no.	Vertebra stage	70%–30%			80%–20%
		Precision	Recall	F1-score	Precision	Recall	F1-score
NNM 1	Stage 1 (S1)	0.95	1.00	0.97	1.00	1.00	1.00
	Stage 2 (S2)	1.00	0.91	0.95	0.93	0.93	0.93
	Stage 3 (S3)	0.93	1.00	0.97	0.86	0.86	0.86
	Stage 4 (S4)	0.95	1.00	0.98	1.00	1.00	1.00
	Stage 5 (S5)	0.83	0.83	0.83	0.73	1.00	0.84
	Stage 6 (S6)	0.95	0.90	0.92	1.00	0.79	0.88
NNM 1 accuracy			0.94			0.93
NNM 1 kappa			0.95			0.94
NNM 2	Stage 1 (S1)	1.00	1.00	1.00	0.94	1.00	0.97
	Stage 2 (S2)	0.95	0.95	0.95	0.93	0.93	0.93
	Stage 3 (S3)	0.93	0.93	0.93	1.00	0.86	0.92
	Stage 4 (S4)	0.95	1.00	0.98	1.00	1.00	1.00
	Stage 5 (S5)	0.83	0.83	0.83	0.80	1.00	0.89
	Stage 6 (S6)	0.95	0.90	0.92	1.00	0.86	0.92
NNM 2 accuracy			0.94			0.94
NNM 2 kappa			0.94			0.93
NNM 3	Stage 1 (S1)	1.00	1.00	1.00	1.00	1.00	1.00
	Stage 2 (S2)	1.00	0.91	0.95	0.93	0.93	0.93
	Stage 3 (S3)	0.88	1.00	0.93	0.86	0.86	0.86
	Stage 4 (S4)	1.00	1.00	1.00	0.93	1.00	0.96
	Stage 5 (S5)	0.85	0.92	0.88	0.75	0.75	0.75
	Stage 6 (S6)	0.95	0.90	0.92	0.92	0.86	0.89
NNM 3 accuracy			0.95			0.92
NNM 3 kappa			0.92			0.94
NNM 4	Stage 1 (S1)	0.58	0.79	0.67	0.53	0.53	0.53
	Stage 2 (S2)	0.69	0.50	0.58	0.44	0.47	0.45
	Stage 3 (S3)	0.46	0.43	0.44	0.25	0.29	0.27
	Stage 4 (S4)	0.58	0.52	0.55	0.55	0.46	0.50
	Stage 5 (S5)	0.42	0.42	0.42	0.38	0.38	0.38
	Stage 6 (S6)	0.91	1.00	0.95	0.93	0.93	0.93
NNM 4 accuracy			0.63			0.54
NNM 4 kappa			0.44			0.50

NNM: Neural Network model

Table 2.

Performance metrics of the NBMs for the vertebral stage determination (70%–30% and 80%–20%)

Model no	Vertebra stage	70%–30%			80%–20%
		Precision	Recall	F1-score	Precision	Recall	F1-score
NBM 1	Stage 1 (S1)	0.47	1.00	0.64	0.50	1.00	0.67
	Stage 2 (S2)	0.09	0.05	0.06	0.00	0.00	0.00
	Stage 3 (S3)	0.33	0.29	0.31	0.25	0.29	0.27
	Stage 4 (S4)	1.00	0.62	0.76	1.00	0.54	0.70
	Stage 5 (S5)	0.83	0.83	0.83	0.78	0.88	0.82
	Stage 6 (S6)	0.90	0.90	0.90	0.92	0.86	0.89
NBM 1 accuracy			0.60			0.60
NBM 1 kappa			0.52			0.51
NBM 2	Stage 1 (S1)	0.47	1.00	0.64	0.50	1.00	0.67
	Stage 2 (S2)	0.25	0.05	0.08	0.00	0.00	0.00
	Stage 3 (S3)	0.61	0.79	0.69	0.55	0.86	0.67
	Stage 4 (S4)	1.00	0.67	0.80	1.00	0.62	0.76
	Stage 5 (S5)	0.83	0.83	0.83	0.78	0.88	0.82
	Stage 6 (S6)	0.90	0.90	0.90	0.92	0.86	0.89
NBM 2 accuracy			0.68			0.67
NBM 2 kappa			0.61			0.60
NBM 3	Stage 1 (S1)	0.49	1.00	0.66	0.50	1.00	0.67
	Stage 2 (S2)	0.10	0.05	0.06	0.00	0.00	0.00
	Stage 3 (S3)	0.38	0.36	0.37	0.38	0.43	0.40
	Stage 4 (S4)	0.93	0.62	0.74	1.00	0.62	0.76
	Stage 5 (S5)	0.75	0.75	0.75	0.75	0.75	0.75
	Stage 6 (S6)	0.90	0.90	0.90	0.86	0.86	0.86
NBM 3 accuracy			0.60			0.61
NBM 3 kappa			0.52			0.53
NBM 4	Stage 1 (S1)	0.48	0.63	0.55	0.53	0.60	0.56
	Stage 2 (S2)	0.00	0.00	0.00	1.00	0.07	0.12
	Stage 3 (S3)	0.26	0.57	0.36	0.15	0.43	0.22
	Stage 4 (S4)	0.59	0.62	0.60	0.53	0.62	0.57
	Stage 5 (S5)	0.50	0.08	0.14	0.50	0.12	0.20
	Stage 6 (S6)	0.80	1.00	0.89	0.82	1.00	0.90
NBM 4 accuracy			0.50			0.50
NBM 4 kappa			0.40			0.40

NBM: Naive Bayes model

RESULTS

The ICCs of all measurements provided in Table 3 indicated excellent reliability (ICC>0.9). Performance metrics of NNMs and NBMs for the determination of vertebral stages (S1–S6) on the test sets are given in Table 1 and Table 2, respectively. The confusion matrices are also given for the NNMs in Figure 4 and the NBMs in Figure 5. Mean accuracy and standard deviations of train and validation sets are provided in Table 4 to assess the overfitting situation of NNMs and NBMs.

Table 3.

The ICC values of all the measurements

Measurements	ICC	Measurements	ICC
A	0.973	M	0.999
B	0.988	N	0.998
C	0.984	O	0.999
D	0.999	P	0.999
E	0.987	Q	0.999
F	0.988	R	0.992
G	1.000	S	0.992
H	0.990	T	0.997
I	1.000	U	0.999
J	0.999	W	0.910
K	0.999	Z	0.999
L	1.000

ICC: Intraclass correlation coefficient

Figure 4.

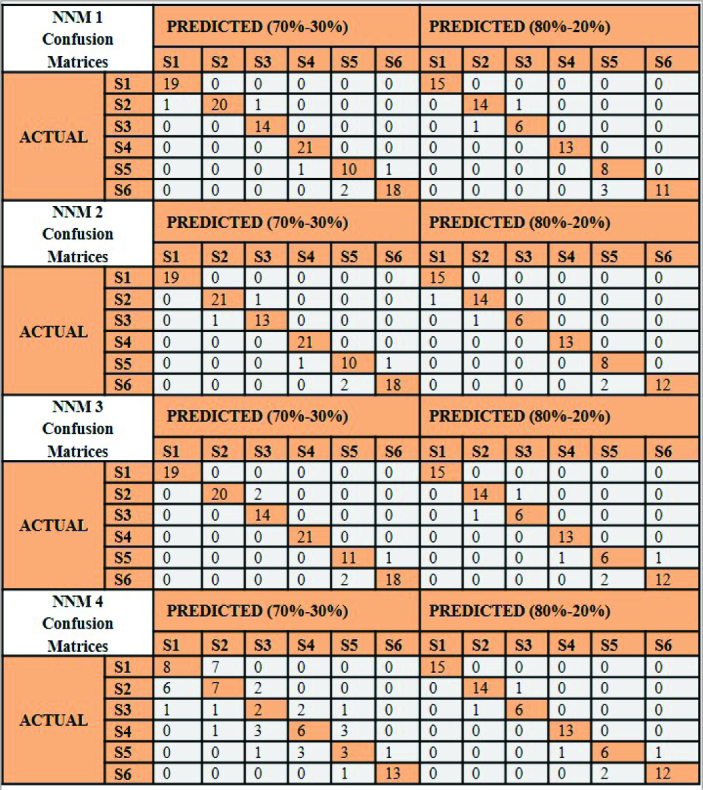
The confusion matrices of the artificial neural network models (NNMs) for vertebral stage determination (70%–30% and 80%–20%)

Figure 5.

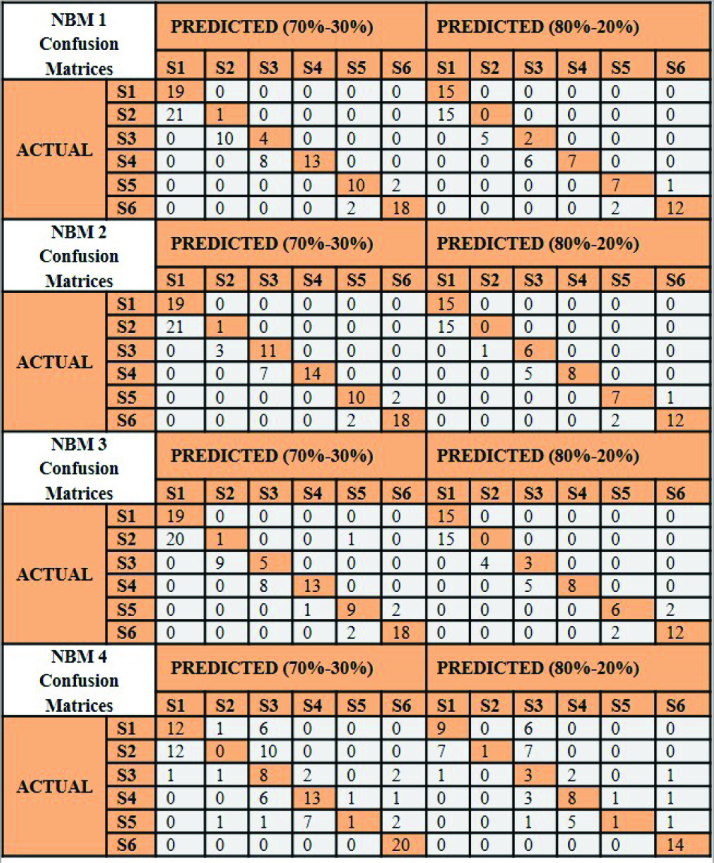
The confusion matrices of the naive Bayes models (NBMs) for vertebral stage determination (70%–30% and 80%–20%)

Table 4.

Mean and standard deviation of training and validation sets for the artificial NNMs and the NBMs

	Model no.	5-fold cv (train set ratio)	Test sets		Train sets
			Mean	Standard deviation	Mean	Standard deviation
Neural network	NNM 1	5-fold cv (70%–30%)	0.928	0.026	1	0
		5-fold cv (80%–20%)	0.930	0.028	1	0
	NNM 2	5-fold cv (70%–30%)	0.940	0.030	0.987	0.003
		5-fold cv (80%–20%)	0.944	0.029	0.993	0.003
	NNM 3	5-fold cv (70%–30%)	0.928	0.019	1	0
		5-fold cv (80%–20%)	0.934	0.036	1	0
	NNM 4	5-fold cv (70%–30%)	0.626	0.056	0.802	0.013
		5-fold cv (80%–20%)	0.642	0.063	0.792	0.017
Naive Bayes	NBM 1	5-fold cv (70%–30%)	0.686	0.097	0.720	0.085
		5-fold cv (80%–20%)	0.666	0.046	0.706	0.078
	NBM 2	5-fold cv (70%–30%)	0.714	0.085	0.758	0.064
		5-fold cv (80%–20%)	0.698	0.032	0.745	0.055
	NBM 3	5-fold cv (70%–30%)	0.694	0.116	0.726	0.078
		5-fold cv (80%–20%)	0.663	0.024	0.710	0.077
	NBM 4	5-fold cv (70%–30%)	0.606	0.045	0.665	0.021
		5-fold cv (80%–20%)	0.579	0.080	0.654	0.015

NBM: Naive Bayes model; NNM: Neural Network model

DISCUSSION

To determine skeletal age without the need for hand-wrist radiography using the cervical vertebrae on the cephalometric radiograph, which are taken for every patient in orthodontic treatment, has attracted orthodontists’ attention. Studies indicate that the evaluation of chronological age phases according to the cervical vertebrae development periods is as reliable as the periods of hand-wrist development (30–32). For this reason, our study was carried out on cephalometric radiographs. Moreover, with the digitalization of the cephalometric radiographs, which is one of the routine orthodontic recordings, we think that it will be beneficial to provide a clinician decision support or a system that can be integrated into cephalometric evaluations.

Researchers aimed to achieve more objective results by taking advantage of digital images with computer software and wanted to automate the vertebral evaluation. Mito et al. (33), Alhadlaq and Al-Maflehi (34), and Beit et al. (35) evaluated vertebral age determination with the help of vertebral ratios by regression analysis. In regression analysis, a formula was drawn, and the vertebral age of the patients was calculated. Mito et al. (33) and Alhadlaq and Al-Maflehi (34) used ratios of C3 and C4, and Beit et al. (35) preferred ratios of C2, C3, and C4. We conducted our study on C2–C5. In our study, Dataset 1 had 7 ratios, Dataset 2-Dataset 3 had 10 ratios, and Dataset 4 had 18 ratios. Baptista et al. (36) studied 7 ratios by 10 lines with the NB to evaluate the 2 examiners’ and NB’s bone age assessments using cervical vertebral maturation. The highest accuracy rate was seen at NB1 (55.85%). Considering a deviation of 1 adjacent stage, the accuracy rate of NB1 was 90.42%. The researchers stated that the NB repeated the examiner’s performance and predicted the vertebral stages. We preferred to study both NB and ANNs. Because ANNs work just like a human learning system that cannot be formulized or standardized. They learn the relationships between events from examples and then make decisions about examples they have never seen using the information they have learned before (37–39). Similar to Random Forest, NB can perform well in some classifications, despite its naive design and oversimplified assumptions. Through its essential multiclass method, NB is also well suited for medical application and allows examples to be classified into more than 2 categories without changing the parameters. When a new one is submitted, the learned classifier assigns it to the most probable stage (36, 40, 41).

According to our results, all NNMs were observed to be more successful than all NBMs. When Table 1 and Table 2 were examined, it was seen that NNM 1 had high success and consistent model for determining vertebral stages (the accuracy values were 0.94 and 0.93 for Training-Test set ratio:70%–30% and 80%–20%, respectively). NBM 1 determination success was low (0.60), and slightly increased in NBM 2 (0.68 and 0.67 for Training-Test set ratio: 70%–30% and 80%–20%, respectively). The success of NNM 2 did not differ much from NNM 1 (0.94). NNM 3 determination success was increased 0.95 for Training-Test set ratio: 70%–30%, whereas NBM 3 success decreased to 0.60 for both Training-Test set ratio: 70%–30% and 80%–%20. The determination success of S5 was relatively low than the others in NNM 1 and NNM 2 (F1-score: 0.83 for Training-Test set ratio: 70%–30%). It was observed that NNM 4 and NBM 4 determination success were quite low, although more vertebral ratios were used in Dataset 4. The accuracy value of NNM 4 was 0.63 and 0.54 for Training-Test set ratio: 70%–30% and 80%–20%, respectively. NBM 4 accuracy value was 0.50. For this reason, it was observed that the ratios in Dataset 4 were not effective and efficient in separating the stages. We could say that the vertebral superior border, anterior border, and depth measurements were important for the determination success of the NNM. Because Dataset 3 consisting of the ratios, that had been determined based on the shape changes that could be observed in the vertebrae with growth development, had the highest success in NNM. Amasya et al. (29) evaluated five different algorithms and reported that the success of ANN increased in the models for determining the presence of concavity. The success of the algorithms in determining the stages in this study is CS1 (90.91%), CS2 (90.48%), CS3 (88.89%), CS4 (83.78%), CS5 (87.5%), and CS6 (80%), respectively. The model’s average was 86.93%. Moraes et al. (42) used only C3 concavity and declared that their results were promising in the determination of bone age by the help of the ANN. They reported only one feature (C3 concavity) has a high correlation with bone age. Also, Santiago et al. (43) studied a multinomial logistic regression model for the cervical vertebral geometry assessment and its relationship to skeletal maturation. They declared that the satisfactory prediction was observed in the model that included age, gender, and four parameters of the vertebral measurements. The knowledge of age and gender were not included in our models. Although these parameters were meaningful clinically and could be increased the models’ success rate, we just focused on radiographic data (the vertebral ratios) and wanted to see their success level.

ANN is designed to generalize the relationship between input-output data. Stated in other words, it learns enough about the past to generalize to the future. At the end of the ANN training process, the perfect fit of the learned weight values to the training set is overfitting. Overfitting corresponds to a model that has learned the training data very well, so the training accuracy will be close to 100%. When this model run on the test data, the accuracy results will probably be very low compared with the training data. To prevent overfitting via choosing the proper model structure, cross-validation, a standard tool in statistics, could be used (39). According to these results, we could say that NNM 1, NNM 2, NNM 3 were acceptable models. When the results of all NBM 4 were inspected, it was seen that these models mean accuracy values lower than the others. It has been observed that the vertebral ratios used in the NBM 4 were not discriminatory in the classification.

Our study consists of individuals belonging to a specific population. It will be necessary to study different and multiracial communities. In our research, we investigated 4 models based on vertebral ratios used in the literature. The method’s performance could also be improved by increasing the number of individuals included in the study and the number of models obtained with different combinations of measurements. In addition, our research did not focus on automating the landmarks. Reviews on this subject are promising and are progressing rapidly. Obtaining measurement data fully automatically will be clinically beneficial. These are the limitations of our study, and further studies are needed on these aspects.

CONCLUSION

1. The NNMs were more successful than the NBMs in our developed models.

2. The increase in the number of ratios did not increase success.

3. The vertebral superior border, anterior border, and depth measurements affected success.

4. It is important to determine the effective ratio and/or measurements that will be useful for differentiation.

Main points.

• The neural network models are more successful than the naive Bayes models in our developed models.

• The neural network model determination success was 0.95 for training-test set ratio: 70%–30%.

• The increases in the number of ratios did not increase success.

• The vertebral superior border, anterior border, and depth measurements affected success.