Flow control in a laminate capillary-driven microfluidic device

Abstract

Capillary-driven microfluidic devices are of significant interest for on-site analysis because they do not require external pumps and can be made from inexpensive materials. Among capillary-driven devices, those made from paper and polyester film are among the most common and have been used in a wide array of applications. However, since capillary forces are the only driving force, flow is difficult to control, and passive flow control methods such as changing the geometry must be used to accomplish various analytical applications. This study presents several new flow control methods that can be utilized in a laminate capillary-driven microfluidic device to increase available functionality. First, we introduce push and burst valve systems that can stop and start flow. These valves can stop flow for > 30 min and be opened by either pressing the channel or inflowing other fluids to the valve region. Next, we propose flow control methods for Y-shaped channels that enable more functions. In one example, we demonstrate the ability to accurately control concentration to create laminar, gradient, and fully mixed flows. In a second example, flow velocity in the main channel is controlled by adjusting the length of the inlet channel. In addition, the flow velocity is constant as the inlet length increases. Finally, the flow velocity in the Y-shaped device as a function of channel height and fluid properties such as viscosity and surface tension was examined. As in previous studies on capillary-driven channels, the flow rate was affected by each parameter. The fluidic control tools presented here will enable new designs and functions for low cost point of need assays across a variety of fields.

Table of Contents entry:

We present novel flow control methods including valve, mixing control, and flow rate control applicable to the laminate capillary-driven microfluidic devices

Introduction

Capillary-driven microfluidic devices have gained popularity in the last decade as alternatives to traditional microfluidics. Instead of using an external pump to induce flow, capillary driven devices utilize the surface tension of a fluid acting on the channel wall (or fibers in the case of paper) to drive flow ^3–5. Without the need for a pump, these devices can be operated outside centralized laboratories in resource limited settings without a power source ^6–8. Pregnancy tests are an example of a capillary-driven analytical device, and their widespread use demonstrates the utility of this platform for at-home diagnostic testing ^9–11.

Capillary-driven microfluidics have been used in many applications, including the detection of bacteria, viruses, biomarkers, pesticides, and heavy metals ^12–16. In each application, accurate and precise flow control is critical to realize a reduced assay time, simplified operation, and improved analytical performance ¹⁷. Flow is most commonly controlled by valving and adjusting flow velocity ^{18, 19}. Passive control methods such as adjusting the contact angle with the channel surface ^{20, 21} and manipulating channel geometry ^{22, 23} are common ways to modify flow behavior because the capillary force is difficult to manipulate once flow begins. Capillary-driven microfluidic devices can also be made from porous materials like cellulose. Although paper-based devices have shown promise as diagnostic tools, the porous material has limitations in particle and reagent transport, low flow rate, and non-uniform flow as compared to other capillary-driven microfluidic devices. ^{24, 25}

Lamination-based methods that stack multiple layers of pre-cut paper or film to form microfluidic channels have been introduced to overcome the limitations of conventional porous-based devices. In this approach the channel geometry is defined on each layer and all layers are bonded using adhesive ^{26, 27}, plasma bonding ²⁸, or toner ²⁹. Double-sided adhesive (DSA) is a common material for the fabrication of lamination-based microfluidic channels because the hollow channel can be generated directly on the DSA layer through a cutting process ^{27, 30}. Laminate capillary-driven microfluidic devices fabricated with porous material as one or more walls have shown a large increase in flow rate compared to single-layer alternatives ^31–33. Lamination-based methods can also combine various substrate materials including paper, ³¹ transparency film, ^{30, 34, 35} glass slide ²⁸, and acrylic ³⁶. A recent laminate microfluidic device composed of transparency films and DSA showed for the first time that capillary-driven flow and rapid mixing could be achieved without porous media ³⁵. Here, non-uniform flow and flow resistance caused by cellulose fibers is reduced, and accurate and rapid flow functionality can be realized. The hollow channel in this device was also made with transparent film so direct visualization of particles and flow is possible. Therefore, laminate devices made of transparency film enabled flow and analytical applications that could not be achieved in conventional, porous-based capillary driven channels. However, previous studies of flow control in capillary-driven devices were focused on porous materials, so there is a need to investigate flow control methods in laminate capillary-driven microfluidic devices. Furthermore, although the electrode valve system has been implemented in capillary-driven microfluidic devices,²⁰ no attempts at passive valving have been reported. In this study, we present several different flow control methods for a laminate capillary-driven microfluidic device. Emphasis is placed on flow control methods that utilize geometric changes in microfluidic channels of the same untreated material without needing any additional equipment. The microfluidic channels used in this study were fabricated using DSA and transparency film layers and were composed of a multi-layered channel. First, we developed push valve and burst valve systems that can be implemented in a multi-layered channel geometry. The systems are similar to the simultaneous inflow system introduced in a previous study ³⁵, but the fluid stop time and open functions were improved. We then developed a flow control method applicable to a Y-shaped device which has two inlets and one outlet. The two fluids introduced through each inlet channel are mixed in the junction and flow through the straight main channel. The geometry of the inlet channels were modified to control the flow rate and mixing characteristics of two fluids in the main channel. Finally, we confirmed the flow rate variation due to the channel height and fluid properties such as viscosity and surface tension. Given the current lack of flow control and valving in many capillary-driven devices, we anticipate the new fluidic control systems we present will have a significant impact in field of low-cost, point-of-need diagnostics.

Experimental

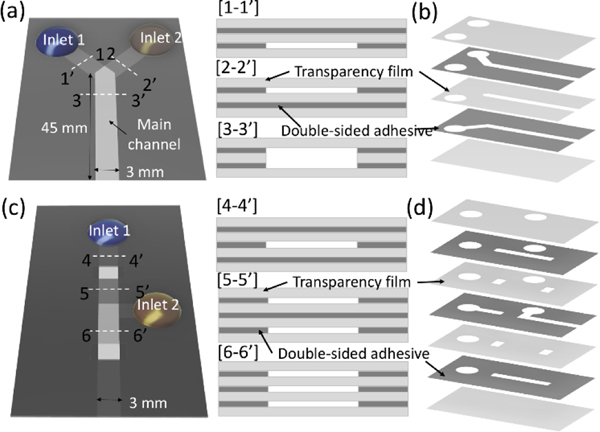
Deionized (DI) water, 10 wt% and 20 wt% glycerin aqueous solutions (Sigma Aldrich), and 2.44 and 4.80 mM concentrations of sodium dodecyl sulfate (SDS) solutions were used for the experiments to control surface tension. All solutions were dyed with tartrazine (yellow dye, 1.9 mM) and erioglaucine (blue dye, 0.800 mM). Two types of capillary-driven microfluidic devices were fabricated by laminating double-sided adhesive (467MP, 3M) and transparency film (PP2500, 3M) as shown in Figure 1. The thickness of DSA and transparency film is 50 and 100 μm, respectively. The channel geometry was designed using drawing software (CorelDRAW X4, Corel) and defined on each layer by laser cutting (Zing 10000, Epilog Laser) before assembling all layers. We applied a multi-layered inlet geometry in all devices. The Y-shaped device (Figure 1a) consisted of two inlet channels and one main channel designed with 45 mm length and 3 mm width. The width of the inlet channel is 3 mm and was fabricated in three lengths ranging from 2.5 mm to 10 mm. Each inlet channel was placed in a different vertical position, and the main channel formed between the top and bottom transparency film layers, as shown in the cross-sectional view. Three different heights of main channels were fabricated from 200 μm to 400 μm by increasing the number of double-sided adhesive (DSA) layers sandwiched between transparency film. As a result, the inlet channels heights ranged from 50 μm to 150 μm, depending on the height of the main channel. Figure 1b shows all geometries of the transparency film and DSA layers for the Y-shaped device. Details of the channel geometry are shown in the supporting information S1. The valve device (Figure 1c) was fabricated using 3 layers of DSA and 4 layers of transparency film (Figure 1d) and composed of a push valve and burst valve systems. The length and width of the main channel are 45 mm and 3 mm, respectively, and the inlet channels were formed in the middle DSA layer. For the experiments, 30 μL of blue and yellow solutions were pipetted into each inlet of the horizontally oriented device. All experiments were performed at approximately 25°C and 30% relative humidity and recorded via a portable camera (iPhone 11 Pro, Apple) under the lab lighting environment. We analyzed the distance variation of the flow front over time and the dye concentration distribution in the main channel area using MATLAB (MathWorks). The concentration was calculated based on the hue variations between blue and yellow colors, and details are described in the supporting information S2.

Figure 1.

Schematics of the y-shape and valve device. (a) The y-shape device consisted of two inlet channels placed in the different vertical positions, as shown in the cross-sectional view of [1–1’] and [2–2’], and the main channel with a larger height than inlet channels. (b) Channel geometries of the y-shape device defined on each layer. (c) The valve device with the cross-sectional views for three different locations along the channel. (d) Channel geometries of the valve device defined on each layer.

Results and discussion

Push valve and burst valve systems

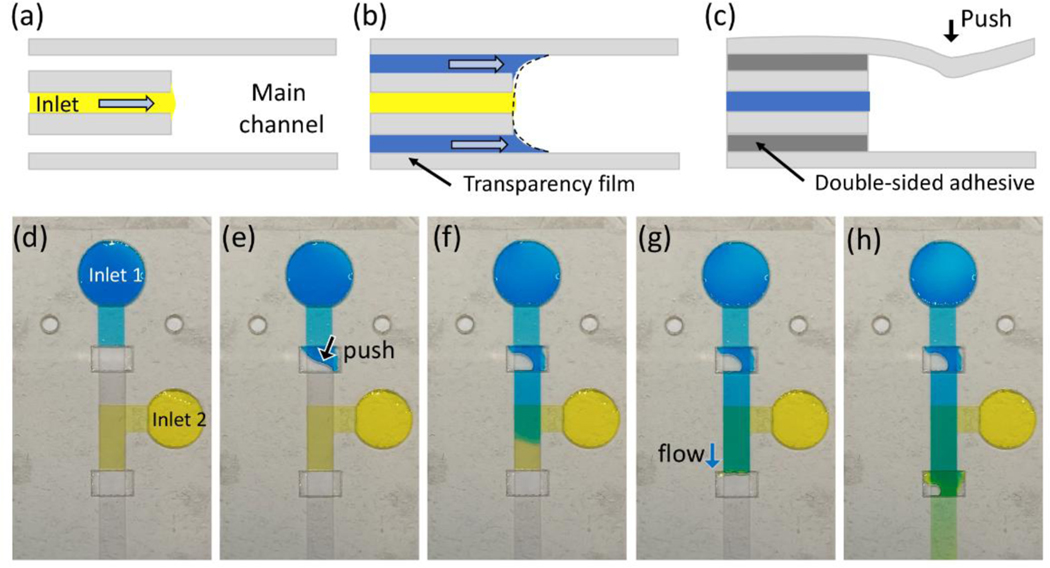
Given the critical need to control when flow is delivered, we first sought to determine if we could make simple, power-free valves for capillary-driven microfluidic devices. Systems where two flows come together at the same point in a channel, called simultaneous inflow systems, are essential in capillary-driven devices composed of multiple inlets but arrival of fluids at different times can cause air to be trapped within the channel and/or inconsistent flows ³⁷. A simultaneous inflow system in the capillary-driven microfluidic device containing a high aspect ratio (channel width over channel height) step-change feature, as introduced recently ³⁵, can address this problem. Figure 2 shows sequential images and the side-sectional schematics for the simultaneous inflow system implemented in our Y-shaped device. We injected dyed DI water at each inlet region. The Y-shaped device consists of two separate inlet channels with a 50 μm height connected to the main channel (Figure 2a). Although two fluids are pipetted at the same time, one fluid arrives at the junction first (Figure 2b), because the flow through the inlet channel is very fast (<1 s) and it was not possible to consistently synchronize fluid delivery to the inlets. However, the fluid arriving first cannot continue to flow into the main channel because of the transparency film in the middle layer at the junction. As a result, the fluid meniscus loses contact with the transparency surface on one side. When second fluid reaches the junction and creates a combined meniscus in the main channel (Figure 2c), both fluids start flowing into the main channel (Figure 2d). We refer to this form of valve as a burst valve because it bursts open when the second fluid arrives. The geometry of the stacked inlets enables simultaneous flow from two different inlets using a burst valve. However, there is a limit to achieving the valve function that stops the fluid for a long time because the fluid still contacts one side of the channel surface. The meniscus contact on one side of the channel surface decreases the burst pressure dramatically ³⁸ and the flow stop lasts for less than 30 seconds.

Figure 2.

Sequential images and side-sectional schematics of the simultaneous inflow system at the moments of (a) pipetting the solutions, (b) arriving the junction, (c) making a combined meniscus, and (d) entering into the main channel.

To implement a more stable fluidic valve, we fabricated a multilayer microfluidic device by stacking 3 layers of DSA and 4 layers of transparency film (Figure 3). The updated valve device has an inlet in the middle layer and a significant gap between both top and bottom sides of transparency film layers at the valve area as shown in Figure 3a. When the flow enters the inlet of the valve system, it stops at the valve. The principle of a fluid stop is the same as that of the simultaneous inflow system, but the fluid can be stopped longer than the Y-shaped device since the fluid loses both the top and bottom contact surfaces. The length of the fluid stop can be affected by fluid properties such as surface tension and contact angle, injected volume, and channel height. Among the several factors that affect the fluid stop, the injected volume is important because it is related to the pressure gradient in the inlet channel. Large amounts of fluid at the inlet can increase the pressure gradient, resulting in fluid stop failure. A stop function of more than 30 min can be achieved by injecting the exact amount of fluid that fills the channel upstream of the valve.

Figure 3.

Side-sectional schematics when (a) the flow stop, (b) burst valve system forming a single meniscus, and (c) push valve system. Sequential images of the valve device showing the moments of (d) flow stop, (e) push valve open, (f) push valve release, (g) form a single meniscus, and (h) burst valve release.

The valving system can be divided into two types depending on the valve opening method. The first type is a burst valve with two flow channels above and below the inlet channel (Figure 3b). The trigger principle of the burst valve is similar to the simultaneous inflow system in a Y-shaped device, but the burst valve requires fluids arriving through both channels. All fluids entering the valve area are mixed to form a single meniscus with subsequent flow downstream. The push valve is another type of valve and is opened when the transparency film layer of the valve area is pressed (Figure 3c). Since the transparency film of the top layer is flexible, it can be bent to contact fluid to initiate flow by changing the meniscus shape. Push valves were previously introduced in a microfluidic channel through a polydimethylsiloxane (PDMS) cover layer ³⁹, but this is the first demonstration in a lamination-based device. Unlike the burst valve, the push valve can be implemented for controlling a single fluid.

We designed a valve device that includes a push valve and a burst valve to demonstrate two valve systems for capillary-driven microfluidic devices (Figure 3d). The two inlets connect to the middle layer of the device and are filled with blue- and yellow-colored DI water. After initial injection, the blue flows to the push valve and the yellow flows to the burst valve and flow stops. Figure 3e shows the push valve opened by depressing the valve area. After the valve is opened, the fluid begins to fill the valve area that has a height of 350 μm. However, the fluid does not evenly fill along the channel direction because the height of the valve area is 7 times greater than the inlet channel and restricting fluid flow through the inlet channel. As a result, air is trapped in the valve area when the fluid front enters the downstream channel and blocks airflow. Even if air bubbles were in the valve region, the downstream channel shows uniform flow (Figure 3f). After the push valve is activated, the flow from the push valve channel activates the burst valve upon reaching this second zone. As shown in Figure 3g and 3h, blue dye combines with the yellow dye of the middle channel forming a single meniscus in the burst valve region and constant flow downstream. Since all layers are assembled by hand, as the number of layers increases, alignment errors can occur, resulting in unexpected fluid flows such as fluid stop failure and channel blocking. However, controlling the injected volume worked well to control the valve function, even if there is still an error in the device. These valve systems were able to stop the fluid for more than 30 min in the microfluidic channel, and the opening function could be successfully achieved by manual pressing and fluid inflow.

Flow control by changing inlet geometry

Since the main channel consisted of an untreated surface with straight geometry, flow cannot be manipulated in the middle of the main channel. Therefore, to generate the desired flow in the main channel, the flow entering the main channel should be controlled as well. We devised a method to change the mixing characteristics of two solutions and flow velocity in the Y-shaped device by changing the geometry of the inlet channels. First, we changed the geometry of the middle layer to control the concentration distribution of the dyes in the main channel. In the Y-shaped device, the middle layer of transparency film has an important role. This layer enables the simultaneous inflow into the main channel as well as fluid transport to the junction without mixing. The geometry of the middle layer in the junction area also determines how the two fluids enter the main channel. Figure 4a shows three types of Y-shaped devices that consist of five layers and have two inlet channels at different vertical locations. These devices have the same geometries for all layers except for the middle layer. Each geometry of the middle transparency film layer for three types of Y-shaped devices is shown in Figure 4b. Interestingly, each Y-shaped device generated a non-mixed, gradient, and fully mixed flows just after the junction region, all of which were formed instantly when the two fluids entered the main channel.

Figure 4.

(a) Three types of the Y-shaped device generating (i) non-mixing, (ii) a concentration gradient, (iii) fully mixing concentration profile. (b) Different geometries of the middle transparency layers. (c) Blue fraction distributions with respect to the channel width. Each value indicated in the plot calculated by averaging an enlarged image shown in Figure 4a. Error bars represent the standard deviation between experiments for each value.

To confirm the device performance, we analyzed the blue dye fractions in the rectangular area 6 mm distance from the junction area for three devices. This is because the 6mm distance is sufficient to present the mixing characteristics for a 200μm height channel.³⁵ Figure 4c shows the average blue fractions in a 6 mm distance with respect to the channel width. In this plot, 1 corresponds to all blue while 0 indicates pure yellow dye. Since the laminar flow device was designed where two fluids meet side by side as they enter the main channel, blue and yellow dyes flow without mixing, and blue and yellow dyes are clearly divided at the middle of the channel. The gradient generator has a transparency film layer in the middle of the junction area. This small change of the middle layer design made a different pressure gradient across the channel width and generated a concentration gradient within the channel. In this design, blue and yellow dyes flow through the left and right sides of the junction area, respectively, due to the distance difference of the flow path in inlet channels. As a result of the pressure gradient, a concentration gradient was formed immediately after the junction area. The concentration gradient was measured using the 1 to 0 scale and was nearly linear across the channel width as indicated by orange symbols in the Figure 4c. Finally, if the middle transparency film layer was extended downstream, the device creates a fully mixed flow of blue and yellow dyes as indicated by the uniform and an average blue fraction value of 0.50±0.03. Structurally, a slight concentration variation occurred along the channel width because the distance difference between the left and right sides in the channel from the inlet cannot be exactly equal. However, we confirmed that the mixing ratio of the two fluids was relatively constant compared with the concentration generator. Also, the symmetrical distribution of blue fraction means that the flow from two inlets was accurately controlled by geometrical change. We used a middle transparency layer with a different geometry as shown in Fig 4b to control the concentration distribution in the main channel. Variations in the channel width or inlet channel angle can lead to different pressure distributions across the channel width. Therefore, when the devices have a different geometry, the middle layer should be redesigned to form the desired concentration distribution.

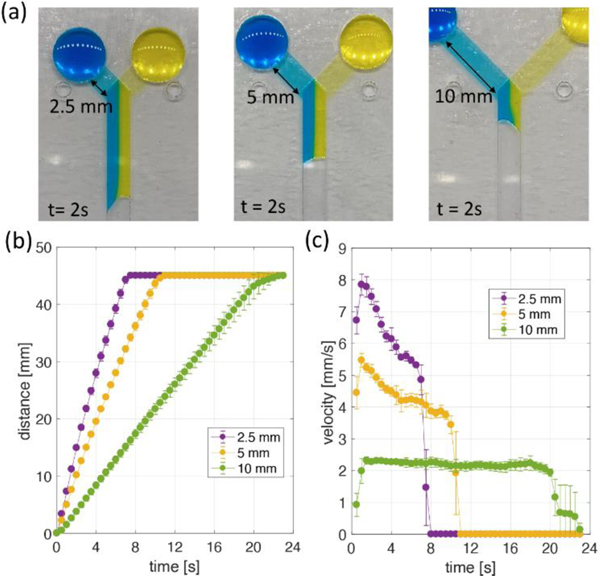
The flow rate in the main channel can also be tuned by changing the length of the inlet channels. Figure 5a shows the images of the Y-shaped device with different inlet channel lengths. Three different lengths of 2.5, 5, and 10 mm between the inlet and the junction area were tested. All images were captured 2 s after the same injected volume of blue and yellow dye entered the main channel. We then analyzed the distance (Figure 5b) and velocity (Figure 5c) variation over time in the main channel. The flow velocity in the main channel increased as the inlet channel length decreased. The 2.5 mm inlet channel device achieved a flow velocity of up to 8 mm/s, and the 10 mm inlet channel device filled all channels while maintaining a flow velocity of about 2.2 mm/s. Although the pressure drops occurring at the flow front in the main channel of all devices are the same, the short inlet channel could generate a fast flow velocity due to its lower flow resistance. Interestingly, Y-shaped devices with this configuration do not follow traditional Washburn characteristics where flow velocity decreases over time, and this characteristic was more pronounced as the inlet channel resistance increased. Constant flow velocity might be caused by the significant difference in channel height between the inlet and main channel regions, because this makes relatively high flow resistance in the inlet channel even if the flow distance of the main channel increases.

Figure 5.

(a) Y-shape devices with three different inlet length channels. All images show 2 s after blue and yellow dyes begin to flow through the main channel. (b) Flow distance in the main channel and (c) velocity variations over time for three different inlet channel devices. All data were calculated every 0.5 s and indicate the average (symbol) with the standard deviation (error bar) for three repeated experiments.

Flow rate variation due to channel height and fluid properties

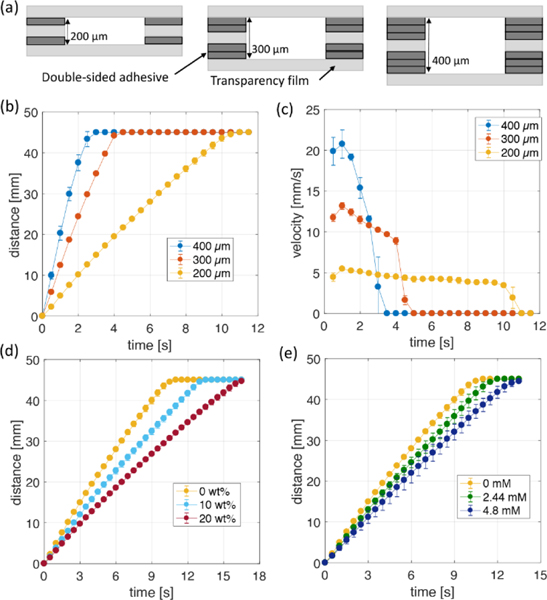
We next explored factors that affect the flow velocity in the laminar flow Y-shaped device fabricated by the lamination method. First, the velocity as a function of main channel height was examined. Several studies have shown that channel height is a key factor in determining the flow rate. ^{32, 40} The height of the channel in this system was increased by changing the number of DSA layers forming the inlet channel. As the number of DSA layers between transparency film layers increased from one to three, the height of the main channel increased from 200 to 400 μm as shown in Figure 6a. Although the height of the inlet and main channels changed, two fluids entered the main channel at the same time on all devices. Figure 6b shows the distance variation of the flow front over time in the main channel, and Figure 6c shows the flow velocity over time calculated from the distance variation result. As in previous experimental and theoretical studies, it was confirmed that the flow rate of the Y-shaped device increased as the channel height increased ^{40, 41}. The 200, 300, and 400 μm height channels caused flow to travel 45 mm in 11.6±0.6, 4.2±0.1, and 2.6±0.3 s, respectively, with maximum flow velocity of 4.9 ± 0.1, 13.3±0.3, and 21.1±1.6 mm/s. After calculating the flow rate, we confirmed that the 400 μm channel produced more than 8 times the flow rate compared to the 200 μm channel over the same time. The flow velocity varied with the channel height, but it is not affected by the channel width change because the fluid flow in the microfluidic channel, which has a small aspect ratio (height/width), can be assumed to be two-dimensional flow.⁴² Next, the flow rate as a function of fluid viscosity and surface tension was examined. We used the laminar flow Y-shaped device with a height of 200 μm and 5 mm inlet channel. As the fluid viscosity increases, the viscous drag due to friction increases and the flow rate decreases. The surface tension is another parameter affecting the capillary pressure which is the driving force for the flow. As the surface tension decreases, the capillary force decreases, resulting in a lower flow rate. To quantify the effects of viscosity and surface tension we mixed glycerin and SDS surfactant with DI-water. The viscosity and surface tension for the concentration of each added substance are shown in Table 1. For experiments, we pipetted the same solution into each inlet and measured the distance variation over time. Figure 6d shows the front distance versus time as a function of glycerin concentration. For glycerin mass fractions of 0, 10, and 20 wt%, it took 10.4±0.2, 13.2±0.2, and 16.6±0.4 s to reach 45 mm, corresponding to average flow velocities of 4.34±0.08, 3.41±0.06, and 2.71±0.06 mm/s, respectively. Compared with 0 wt% glycerin, the 10 wt% mixture velocity decreased by 22% and the 20 wt% mixture decreased by 37%. In capillary-driven flow, the flow rate is predicted to be proportional to the surface tension and inversely proportional to the viscosity ⁴³. The predicted decrease in flow velocity due to increased viscosity is 22% and 41% respectively compared to 0 wt% case, similar to the actual experimental values.

Figure 6.

(a) Cross-sectional view of the y-shape device with three different channel height. (b) Flow distance in the main channel and (c) velocity variations over time for three devices. Distance variations over time for different concentrations of (d) glycerin and (e) SDS solutions in the y-shape device with 200 μm of the main channel height. All data were calculated every 0.5 s and indicate the average (symbol) with the standard deviation (error bar) for three repeated experiments.

Table 1.

Fluid properties for different viscosity and surface tension. The viscosity and surface tension values for the concentrations of each substance were predicted by empirical formulas in the reference.^{1, 2}

	Concentration (wt%)	Viscosity (cP)		Concentration (mM)	Surface tension (mN/m)
	0	0.89		0	72
Glycerin	10	1.14	SDS	2.44	60
	20	1.52		4.8	50

Figure 6e shows the front distance over time as the SDS concentration of the mixture is varied to create surface tensions of 72, 60, and 50 mN/m; the resulting average flow velocities were 4.34 ± 0.08, 3.96 ± 0.17, and 3.43 ± 0.13 mm/s, respectively. Although the surface tension of 60 and 50 mN/m SDS solutions decrease 16.7 and 30.6 % compared with the 72 mN/m case, the flow velocity decreases 8.8 and 21.0 %, respectively. This is because the contact angle decreases as the surface tension decreases ⁴⁴, which affects the capillary action. Despite these differences, the trend of flow rate decreases due to surface tension decrease based on the Washburn equation is clearly observed. In addition to changing the surface tension and viscosity separately, we also determined the impact of simultaneously varying the viscosity and surface tension. Table 2 shows the average flow velocity to travel 45 mm for each glycerin/SDS concentration. For all cases, the standard deviation is less than 6.5%, showing good reproducibility. Here, flow rates are independently affected by viscosity and surface tension and the flow rate decreases as the viscosity increases and the surface tension decreases. Therefore, to design the capillary-driven flow device made of film and to control the flow rate, the viscosity and surface tension of the fluid used should be considered.

Table 2.

Velocity variations in the y-shape device for different concentrations of glycerin and SDS.

Velocity (mm/s)		SDS concentration (mM)
		0	2.44	4.8
Glycerin concentration (wt%)	0	4.34 ± 0.08	3.96 ± 0.17	3.43 ± 0.13
	10	3.41 ± 0.06	3.24 ± 0.18	2.99 ± 0.17
	20	2.71 ± 0.06	2.53 ± 0.10	2.34 ± 0.15

Conclusions

In this work, we present flow control methods that create flow characteristics which can be utilized in the development of laminate capillary-driven microfluidic devices for point-of-need diagnostics. All flow controls were implemented by changing channel geometries without changing the device material. The device consisted of several layers of the transparency film and double-sided adhesive and was fabricated by laminating all layers after defining the channel geometries on each layer. First, two types of valve systems able to perform fluid stop and release functions without using additional equipment were developed and tested. The valve systems can stop the fluid for up to 30 min depending on solution conditions, which is longer than the stop time of the simultaneous inflow system. It should also be noted that the stop time may vary depending on the fluid properties and inlet conditions that affect the pressure in the inlet channel. Therefore, optimization of the inlet geometry and injection volume according to the desired flow behavior is necessary. The push and burst valve systems were operated either by pressing the top layer of the valve area or through the inflow from a second channel, respectively. Next, we developed flow control methods by changing the inlet geometry to adjust concentration fields and flow rate in the Y-shaped device. The methods discussed can produced tailored solute concentration profiles such as the three demonstrated here, and specifically tune flow rates. The flow and mixing characteristics of the device were quantified by simultaneously measuring changes of fluid front location and blue dye intensity distributions over time. Finally, various factors affecting the flow rate were examined. We measured the flow rate of the Y-shaped device for changes in channel height, viscosity, and surface tension. Through the flow control methods and flow characteristics presented in this study, it was confirmed that the laminate capillary driven device can sensitively and accurately control the flow through the channel geometry. The fabrication cost of these devices is very cheap compared to conventional microfluidic devices, and the optimizing the number of device layers and alignment processes of each layer will increase productivity. In addition, since the device consists of a hollow channel unlike the paper-based device, several biofluids such as whole blood, plasma, urine, saliva could be loaded and work through the channel, even if it contains particles. We expect these features will be of great help in developing practical capillary-driven sensor applications utilizing sequential reagent delivery, electrochemical detection, and particle movement.