Jonckheere–Terpstra–Kendall-based non-parametric analysis of temporal differential gene expression

Abstract

Time-course experiments using parallel sequencers have the potential to uncover gradual changes in cells over time that cannot be observed in a two-point comparison. An essential step in time-series data analysis is the identification of temporal differentially expressed genes (TEGs) under two conditions (e.g. control versus case). Model-based approaches, which are typical TEG detection methods, often set one parameter (e.g. degree or degree of freedom) for one dataset. This approach risks modeling of linearly increasing genes with higher-order functions, or fitting of cyclic gene expression with linear functions, thereby leading to false positives/negatives. Here, we present a Jonckheere–Terpstra–Kendall (JTK)-based non-parametric algorithm for TEG detection. Benchmarks, using simulation data, show that the JTK-based approach outperforms existing methods, especially in long time-series experiments. Additionally, application of JTK in the analysis of time-series RNA-seq data from seven tissue types, across developmental stages in mouse and rat, suggested that the wave pattern contributes to the TEG identification of JTK, not the difference in expression levels. This result suggests that JTK is a suitable algorithm when focusing on expression patterns over time rather than expression levels, such as comparisons between different species. These results show that JTK is an excellent candidate for TEG detection.

INTRODUCTION

Time-course experiments using a parallel sequencer or mass spectrometry capture dynamic changes during the development or perturbation of a cellular system over time (1,2). Although specific issues in biological data, such as low sampling frequency, exist (3), recent advancements in modern high-throughput techniques have enabled description of the regulatory molecular circuits that drive differentiation processes and adaptation to the environment in greater detail (4,5).

One of the major steps in analyzing time-series omics data is the identification of genes that are differentially expressed between two groups (e.g. wild-type versus knockout strain) on a time axis (6). We defined differentially expressed genes over time as temporal differentially expressed genes (TEGs). While algorithms for general differentially expressed gene analysis (7,8) and algorithms for interpretation of time-series data in the field of circadian rhythms have been relatively well studied (9,10), the golden standard for TEG analysis has not been established.

Many tools have been implemented in the detection of TEGs in time-course experiments (11). MaSigPro (12,13) performs polynomial regressions to model time-course expression values, and a log likelihood ratio test to detect TEGs. MaSigPro consists of two steps; in the first step, dynamic (non-flat) genes are selected, and in the second step, the best model is sought, and the P-value is calculated using user-specified parameters. SplineTimeR (splineTC) (14) was originally developed for the construction of gene networks and for provision of pathway-enrichment analysis and visualization functions. SplineTC fits natural cubic spline curves to time-course data and applies empirical Bayes moderate F-statics between two groups. ImpulseDE2 (15) fits the impulse model (16,17) to time-course data, and the null model is represented by a common impulse model; therefore, the alternative model is represented by a different impulse model. LimoRhyde is designed to detect differential rhythmicity and differential expression using cosinor regression (18). These methods have shown high accuracy in comprehensive comparative studies of Spies et al., except for the recently published LimpRhyde (11). These studies are considered as good benchmarks for TEG detection algorithms.

Previous approaches for TEG analysis have mainly been performed by fitting regression models to two groups and by assessing whether the models are statistically consistent by using a hypothesis test. However, experimental data contain genes and proteins that differ in complexity, which poses the risk of modeling linearly increasing genes with higher-order functions or fitting cyclically varying genes with linear functions, thereby leading to false positives or false negatives. To tackle this issue, we need to explore the parameters to model each gene or develop a model-free and non-parametric approach.

Here, we propose a Jonckheere–Terpstra–Kendall (JTK)-based non-parametric TEG detection algorithm to characterize time-course experiments. The Jonckheere–Terpstra test (19,20) is a non-parametric test for the detection of ordering patterns between two measured quantities, with the correlation coefficient, Kendall’s τ, measuring the ordinal association between two groups. In circadian rhythm studies, the JTK algorithm, which combines these two statistical methods, has been widely used to detect oscillating molecules in omics datasets (9,21). We expanded this application of the JTK algorithm to TEG detection. To the best of our knowledge, JTK is the only non-parametric TEG detection method. Our study demonstrates the novelty of a powerful non-parametric approach in the exploration of differentially expressed genes in time-series omics datasets.

MATERIALS AND METHODS

Design

The schematic diagram of JTK and the definition of TEG in each method are shown in Figure 1. JTK calculates Kendall’s τ between two groups (e.g. control and case). For two time-series with lengths n, the replicates were averaged, x = (x₁, x₂, ..., x_n) and y = (y₁, y₂, ..., y_n), we define:

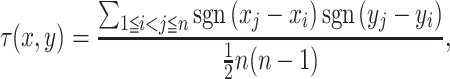(1)

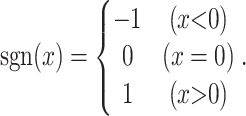(2)

The numerator in Equation (1) indicates the number of pairs with consistent behavior between the two time-series, minus the number with inconsistent behavior. All possible pairs, and not just neighboring points, are included in the calculation of τ. The denominator indicates the total number of pairs in the datasets, and τ must be in the range from −1 to 1. Two time-series are perfectly correlated if τ = 1, and are perfectly anti-correlated if τ = −1, or uncorrelated if τ = 0. Null distributions for each gene were predicted by permutation. The number of Kendall’s τ obtained by permutation, which is smaller than the τ obtained from the actual order, was counted and divided by the number of permutations (1000 times) to be considered as the P-value.

Figure 1.

(A) An illustration of the JTK algorithm. Solid arrows pointing upward, downward and sideways indicate an increase, decrease and constant, respectively, between two points. JTK compares the increase/decrease pattern of two sequences (e.g. control versus case). The relationship of all combinations between the points is summed up, and normalized by the number of combinations that are within the range of −1 to 1. The two time-series are perfectly correlated if τ = 1, are perfectly anti-correlated if τ = −1 and are uncorrelated if τ = 0. (B) The definition of the TEG in each method. (*1) MaSigPro performs a TEG test for non-flat genes only. (*2) SplineTC offers a choice to include or exclude the intercept in the test.

Data simulation

To assess the performance of each method, we generated synthetic data that mimicked read count data of RNA-seq data. The time-course of each gene was simulated using the following four functions based on the work of Wang et al. (22):

(3)

(4)

(5)

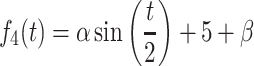(6)

where, t is the time point, and α and β set the amplitude and intercept, respectively. The α and β followed a power-law distribution, and were generated by the rplcon function (n = 1, min = 30, α = 2.5) of the powerRaw package in R. The values obtained by these functions (average expression values) were converted to read counts by a negative binomial (NB) distribution.

(7)

where ϕ indicates the magnitude of the noise, and in this study, the noise level refers to ϕ. TEGs, which had different time-series expression patterns between controls and cases, were generated from different functions for controls and cases, while non-TEGs were generated from the same function. The synthetic dataset for Figures 2 and 3 contains 200 time-series gene expression data conducted for each condition. The data in Figure 4 contains 100 time-series gene expression data for each condition. For the gene-labeled non-TEG, the time-series data for the control and cases were generated using the same function, and for the gene-labeled TEG, were generated using the two specified functions. The combination of functions in the labeled genes is constant and is shown in the figure.

Figure 2.

Example plots and ROC curves of simulated data. (A) Simulated data for different sequence lengths and (B) number of points. In the case of sine curves, the number of peaks increases as the sequence length increases. As the number of time points increases, the number of peaks remains the same, but the sampling intervals become shorter. The box on the left indicates typical examples of non-TEG genes, and the box on the right indicates typical examples of TEG genes. The noise level is 0.05, and the error bars represent the standard deviation (n = 3). The top boxes represent examples of sequence length or time points of 8, while bottom boxes represent examples of 9. Comparison of method performance with ROC curves for different (C) sequence lengths and (D) number of time points. Datasets in A were used to generate the ROC curves in (C), and datasets in (B) corresponded to (D). The numbers at the top indicate the length of the sequence or the number of time points, and the numbers on the right indicate the noise level. The degree and degree of freedom are shown using the color legend. As the degree and degree of freedom should be less than a time point, only limited conditions are illustrated in the boxes with sequence length or time points of 4.

Figure 3.

Comparison of method performance with ROC curves for different number of replicates with 16 time points. Numbers at the top indicate the number of replicates, while numbers on the right indicate the noise level. Since ImpulseDE2 requires multiple replicates to predict the NB distribution, the condition of n = 1 is not shown.

Figure 4.

Preferences of each method and function. Functions 1–4 correspond to Equations (3–6), respectively. For example, the top left box in each panel shows the results of the performance evaluation of the dataset containing only function 1 and 2. The y-axis represents the AUC, and the x-axis represents various methods. (A) 4 time points, (B) 8 time points, (C) 16 time points and (D) 32 time points, with a noise level of 0.05.

Implementation of other methods

A brief summary of each method is shown in Table 1. With maSigPro version 1.56.0 the first step was performed with the following parameters: degree = 3, 5 or 7, counts = TRUE, Q = 1, and the second step, step.method = ‘backward’, α = 1. SplineTC version 1.16.1 was performed by df = 3, 5 or 7, intercept = FALSE for simulation datasets, or intercept = TRUE for experimental data. ImpulseDE2 version 1.8.0 was performed with the following parameters: boolCaseCtrl = TRUE, scaNProc = 4, scaQThres = 1, boolIdentifyTransients = TRUE. LimoRhyde version 0.1.2 was used along with default parameters to perform the analysis. LimoRhyde is used to conduct analysis using the following three steps: (i) test for rhythmicity, (ii) test for differential rhythmicity in rhythmic genes and (iii) TEG analysis of non-differential rhythmicity genes. The first step was performed for all the genes and the second step was performed for the only significantly rhythmic genes (q < 0.15) determined in the first step. For the significantly differential rhythmic genes (q < 0.05) determined in the second step, the P-values calculated in the second step were used to draw ROC. For all genes that were not significant in the first and second steps, the P-values calculated in the third step were used to draw the ROC. All P-values were corrected using the Benjamini–Hochberg (BH) method (23). Unless otherwise noted, the significance level was set at 0.05.

Table 1.

Summary of each of the methods compared in this study

Method	Model/algorithm	Hypothesis test	Ref
maSigPro	NB model polynomial regression	Log likelihood ratio	(13)
splineTC	Spline regression	Moderate F-statics	(14)
ImpulseDE2	NB model Impulse model	Log likelihood ratio	(15)
LimoRhyde	Cosinor regression	Moderate F-statics	(18)
JTK	Jonckheere–Terpstra-Kendall’s τ	Permutation test	This work

This table is based on Spies et al.(11).

Processing of biological data

We used time-series RNA-seq data from the study recently published by Cardoso-Moreira et al. (24) for method comparison using realistic datasets. The fastq files were downloaded from ArrayExpress with the accession codes E-MTAB-6798 (mouse) and E-MTAB-6811 (rat). We used the RNA-seq data on seven tissue types (forebrain, hindbrain, heart, kidney, liver, ovary and testis) across developmental time points, from early organogenesis to adulthood, for mouse and rat. Each developmental stage was investigated in the original study (e.g. e13.5 of mouse was assigned to e15 of rat, and P63 of mouse was assigned to P112 of rat). The corresponding stages between mouse and rat are shown in Table 2. We mapped the reads against the reference genome, GRCm38 and Rnor_6.0, for mouse and rat, respectively, using STAR version 2.7.6 (25). We calculated transcripts per million (TPM) using RSEM version 1.3.0 (26). The BAM files were converted to count data by HTSeq version 0.12.4 (27) with option ‘-s reverse’ using the reference genome. Data on genes whose average expression level (in TPM) at each point in mouse and rat was less than 1 were deleted. This was done to delete data on genes with low expression, excluding data on genes that are highly expressed in mice but not in rats. The input for JTK, maSigPro, splineTC and LimoRhyde was TPM, and the input for ImpulseDE2 comprised count data. Enrichment analysis was performed by gprofiler2 with the default parameters (28).

Table 2.

Stage correspondences between mouse and rat

Organism\stage number	0	1	2	3	4	5	6	7	8	9	10	11	12
Mouse	e10.5	e11.5	e12.5	e13.5	e14.5	e15.5	e16.5	e17.5	P0	P3	P14	P28	P63
Rat	e11	e12	e14	e15	e16	e18	e19	e20	P0	P3	P14	P42	P112

Computational resource and software

All analyses, except for the RNA-seq data analysis, were performed on a MacBook Pro 2.3 GHz Intel Core i5 with 16 GB of RAM, using R version 3.6.1 (29). RNA-seq data analysis was performed using DELL PowerEdge R640 (Intel Xeon Gold 6138) and DELL PowerEdge R930 (Intel Xeon E7-8890v4). The running time was measured with a single thread.

RESULTS

Our approach is a non-parametric TEG detection algorithm based on JTK. The JTK-based approach calculates the similarity between two series (e.g. with and without stimuli) and sequentially identifies genes with temporally different expression trajectories by calculating their P-values in a permutation test. We compared this JTK-based approach with maSigPro, splineTC and ImpulseDE2 using simulated and temporal RNA-seq datasets.

JTK outperforms other methods in performance test with synthetic time-series datasets

We generated synthetic data to compare the performance of each method. The simulated datasets consisted of 200 genes, comprising 100 TEG and 100 non-TEG genes. Each gene was generated by the four functions shown in the ‘Materials and Methods’ section. Non-TEG genes were generated from the same function in the control and case, while TEG genes were generated from a different function. We sampled three replicates based on an NB distribution, and evaluated the statistical test power of each method based on the area under the receiver operator characteristic (ROC) curve. Here, the input for the ROC curves was BH-corrected P-values. In order to compare the method performance under different conditions, we generated data based on two scenarios. In the first scenario, the sequence length was varied, for example, genes based on a sine function increased in frequency with increasing sequence length (Figure 2A); the second scenario involved varying the number of time points, with the sampling interval decreasing with an increase in the number of time points (Figure 2B).

Considering the resulting ROC curves, the JTK-based approach performed the best under most conditions compared with the other methods (Figure 2C and D). In both scenarios, all methods performed poorly as the noise level increased, but JTK performed well even under high noise levels. Notably, the performance of the JTK-based approach tended to increase as the sequence length increased (Figure 2C). We found that the area under curve (AUC) values was saturated for conditions with more than 16 points, but the AUC tended to increase for conditions with 4–16 points.

In addition to sequence length and time points, we also studied the effect of the number of replicates on method accuracy (Figure 3). The results showed that the JTK-based approach also outperformed the other methods in fewer replicates. All methods performed worse with increasing noise levels, but accuracy tended to increase with increasing number of replicates. In order to clarify the preference of each method and function, we compared the performance under the condition that the combination of functions was fixed for the gene labeled as TEG (Figure 4). As a result, it was found that the performance of the methods differed depending on the combination of functions.

Comparison of TEG detection approaches using simulation data reported by Spies et al.

To impartially compare the different methods, we performed a performance test using the simulation dataset created by Spies et al. (11). This dataset contained 18 503 genes, of which 1200 were TEGs. To mimic realistic biological datasets, mean and dispersion indexes were extracted from expression datasets comprising 41 immortalized β-cell samples (30), and NB distributions were created based on the parameters. Control sequences were sampled from corresponding NB distributions, and TEGs were generated by multiplying arbitrary multiplicators by the control sequences. For example, ‘Down early slow’ was generated by multiplying each of the four data points by 0.5, 0.17, 0.17 and 0.17, respectively (Figure 5A). Similarly, ‘Mixed slow’ indicates the second, third and fourth data points multiplied by 6, 3 and 1.2, respectively. While ‘Up early slow’ indicates data points multiplied by 2, 6 and 6, respectively, ‘Down early slow’ indicates data points generated by multiplying each of the four data points by 0.5, 0.17, 0.17 and 0.17, respectively. Based on the resulting ROC curve, ImpulseDE2 exhibited the best performance, followed by splineTC, while maSigPro and JTK were less accurate than the other approaches, and roughly exhibited the same performance (Figure 5B).

Figure 5.

Performance test using the simulation data generated by Spies et al. (11). (A) Genes labeled as TEGs that had q > 0.05 in JTK, and (B) genes labeled as TEGs that had q < 0.05 in JTK. Simulation patterns are shown at the top of each plot. Error bars represent standard deviations (n = 3). (C) ROC curves using data from Spies et al. (11). The methods are represented by different colors.

Application for the transcriptomes across developmental time points for mouse and rat

To assess the methods in a practical dataset, we evaluated each method using developmental time-series RNA-seq data from mice and rats. The resulting overlap in genes in the forebrain, hindbrain, heart, kidney, liver, ovaries and testes identified as TEG by each method are shown in Figure 6A, B, C, D, E, F and G, respectively. ImpulseDE2, successively followed by splineTC, LimoRhyde, maSigPro and JTK, detected the largest number of TEGs. The time-series changes in the expression of genes identified by TEGs by each method are shown in Figure 7. Figure 7A shows a TEG, identified by all methods in the liver and Figure 7B shows a gene that were identified as TEGs only by JTK and ImpulseDE2. Figure 7C show a gene that was identified as TEGs by the three methods barring JTK. The enrichment analysis using significant genes identified by LimoRhyde, which includes an intermediate number of candidates, is shown in Supplementary Table S1.

Figure 6.

Overlap of genes identified as TEGs by each method. Venn diagrams showing the overlap of TEGs (q < 0.05) detected by each method in (A) forebrain, (B) hindbrain, (C) heart, (D) kidney, (E) liver, (F) ovary and (G) testis.

Figure 7.

Examples of genes identified as TEGs by each method. (A) A gene identified as TEGs by all methods; (B) a gene identified as TEGs by JTK and ImpulseDE2 only; (C) a gene identified by the three methods barring JTK. The x-axis indicates developmental stages, and the y-axis indicates gene expression (TPM). Error bars represent the standard deviation.

Evaluation of running time

Finally, we evaluated the computational speed of the JTK-based approach by comparing it with other methods using simulated datasets that comprised eight time points and two hundred genes (Figure 8). The permutation test for the JTK-based method was performed 1000 times. For maSigPro, a non-flat gene extraction step was included in the running time. JTK had the second-longest computation time after ImpulseDE2, followed by maSigPro, splineTC and LimoRhyde. The ranks did not depend on the degree or degree of freedom. Most of the running time of JTK was utilized in the performance of a permutation test to calculate the P-values.

Figure 8.

A comparison of the computation time of each method for eight time points and 200 genes. Error bars represent the standard deviation (n = 3).

DISCUSSION

The best approach depends on the research objectives

The primary outcome of this study suggests that the selection of an analytical method depends on its adaptability to your hypothesis and objectives because each method has a different definition of TEGs, as shown in Figure 1B. For example, whether a gene with the same waveform but with a different intercept is a TEG depends on the purpose of the analysis. Therefore, if the aim is to detect it as a TEG, you should select a method that also includes the intercept in the hypothesis test, and you should not choose a method, such as JTK, that focuses only on the correlation of magnitude between data points. Alternatively, if the aim is to explore genes with different waveform shapes rather than expression levels, JTK, which focuses on the large and small relationships between time points, is an excellent candidate.

Benchmarks

In a performance comparison using unique simulation data based on several scenarios, JTK showed an advantage over other methods (Figure 2). The performance of JTK improved as the sequence length increased, while there was barely any change in accuracy with an increase in time points. This suggests that a longer experimental period may result in a better experimental design for TEG detection with JTK, compared to a more frequent sampling period. Furthermore, data show that increasing the number of replicates as well as the sequence length, improves the accuracy of TEG detection in all methods (Figure 3). These results suggest an essential fact when considering the experimental design. Even if the noise is considerable, frequent sampling and the use of many replicates guarantee accuracy. In contrast, for experimental systems with low noise, accuracy is maintained even if the number of sampling points and replicate usage is reduced, thus decreasing the experiment’s cost. Furthermore, optimization of the sampling frequency is required to differentiate genes with similar expression patterns. It is essential to examine or estimate the phase duration by pilot experiments to optimize the sampling frequency. These results show that an appropriate experimental design that considers the cost, precision, replication and sampling frequency leads to the design of a successful time-series experiment.

Although the general workflow of maSigPro and LimoRhyde involves multiple tests for hypothesis validation, we decided to evaluate the results of the hypothesis test in the final step only. This is because the definition of TEG differs among various methods, and the P-values obtained by a single hypothesis test, and those obtained by multiple hypothesis tests have different false discovery rates. There is also a problem regarding whether the P-values obtained in the first step or the second step should be used as input of the ROC curve. LimoRhyde detects the phase change of periodic gene expression as differential rhythmicity in the second step, but the second step is skipped in determination of the comparison in this study such that the results may be different in the analysis by using the general workflow. The benchmark may be disadvantageous for LimoRhyde because the synthetic data set includes both sine and cosine curves as TEGs.

Next, the analysis with a fixed combination of functions revealed each method’s preference (Figure 4). Although the trends were generally consistent across time point lengths, the combination of functions 1 and 4 in Figure 4A (bottom left box) showed an AUC of almost 0.5 for all methods. This is because the waveforms of the first half of the sine curve and the exponentially increasing pattern are consistent under the condition with few time points. As the number of time points increased, a trough of the sine curve was formed, which could be discriminated by each method. Furthermore, the combination of functions 3 and 4 (lower right box) in JTK, that is, the sine and cosine curves, can be accurately distinguished, which indicates that JTK can also be used to detect the phase. The Limorhyde workflow may detect genes with different phases in the second step, but as we skipped that step, we could not detect the difference between sine and cosine curves. These results show that JTK exhibits no extreme bias due to specific functions and shows consistent performance for all functions.

In contrast, a comparison of the method accuracy using the simulation data reported by Spies et al. (11) showed that the performance of JTK was similar to that of maSigPro and lower than that of the other two approaches (Figure 5). This is due to the specific method used in the identification of TEGs that are generated by multiplying some control sequence points by a constant. With this method of TEG creation, the magnitude of correlation of each time point may not change; therefore, JTK cannot elucidate the change, but can only detect a change if the magnitude of correlation of each time point has changed. To accurately detect TEGs in such data, a pairwise comparison with each time point as a category may be more appropriate than the analysis in the time domain used here, as argued by Spies et al. (11). Thus, the detectable TEGs may vary between methods, and a method must be selected by considering the type of TEG intended for detection.

JTK also had the second-longest running time among the comparators in this study (Figure 8). This is because the computation cost increases linearly depending on the number of permutations, since the P-value is computed by the permutation test. This problem can be solved by using the Harding algorithm to predict the null distribution (31). However, it should be noted that because the Harding algorithm requires a long sequence (>10), the datasets that can be analyzed are limited.

In this study, we used the mean expression level rather than the median. Since outliers may influence accurate testing, the median may be more robust when analyzing samples with high variability. Appropriate statistical treatment should be applied depending on the experimental design. The JTK concept can also be applied to the clustering of time-series data. Most of the existing methods, such as DTWscore (22), are used to calculate the distance between two time series data to obtain the similarity. In contrast, as JTK only focuses on increasing or decreasing values between two points, it may be possible to cluster the data according to the waveform patterns rather than expression levels. We assessed the performance on the small simulation data, but it would be interesting to verify it on a more extensive data set, say with 20k genes. This will evaluate the robustness of the false positive rate.

Application for RNA-seq datasets

The analysis of time-series developmental RNA-seq data for mice and rats showed that method selection and threshold settings were essential for the analysis of time-series data (Figure 6). While about 0.5–1% of the genes were significant at the 5% level of significance for JTK, more than 95% of the genes in ImpulseDE2 were determined to be TEGs. This suggests that JTK is a more statistically conservative test than the other methods. These results indicate that not only the selection of the method but also the setting of the significance level is essential for TEG analysis because the distribution of P-values varies between methods. Furthermore, many genes that were not determined as TEGs by JTK but were determined as TEGs by the other four methods, had different expression baselines between mouse and rat (Figure 7C). This is because JTK is an algorithm that focuses only on the relative increase or decrease between time points, and not on absolute expression.

Limitations

The number of permutation tests must be increased to increase the number of significant digits in the P-value, and the computational cost increases linearly. Since JTK focuses only on the magnitude of correlation of each time point, it is not possible to distinguish between linear and non-linear increases. The relationship for each time point indicates an increasing pattern in both cases, even if one increases exponentially while the other increases linearly, as illustrated in the third row from the top of Figure 1B. Hence, JTK considers linear and non-linear increases as equivalent.

CONCLUSION

We proposed a JTK-based non-parametric temporal differential expressed gene detection algorithm. JTK calculates the similarity between two time-series expression datasets by comparing the increase or decrease pattern between each time point, while P-values are calculated using a permutation test. A comprehensive comparison with other methods using synthetic data shows that JTK is an excellent TEG detection algorithm, especially when the dataset has a long sequence, or high noise levels. Additionally, we identified genes that were differentially expressed between mouse and rat developmental stages by applying JTK to time-series RNA-seq data of seven organs across developmental time points. Furthermore, JTK did show a tendency to identify genes as TEGs when the genes had different baselines but similar wave patterns. These results suggest that JTK is a suitable algorithm when focusing on expression patterns over time rather than absolute expression levels, for example, comparisons between different species. Moreover, the results show that the JTK-based non-parametric TEG detection algorithm is an excellent approach for TEG detection.

DATA AVAILABILITY

Source codes and datasets are available on Github (https://github.com/hiuchi/JTK/).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Ministry of Education, Culture, Sports, Science and Technology (KAKENHI) [JP17K20032, JP16H05879, JP16H01318, JP16H02484, JP18KT0016, JP16H06279, JP20H00624 to M.H.].

Conflict of interest statement. None declared.