Effect of macro-calcification on the failure mechanics of intracranial aneurysmal wall tissue

Abstract

Background:

Calcification was recently found to be present in the majority of cerebral aneurysms, though how calcification and the presence or absence of co-localized lipid pools affect failure properties is still unknown.

Objective:

The primary objective is to quantify the biomechanical effect of a macro-calcification with surrounding Near-Calcification Region (NCR) of varying mechanical properties on tissue failure behavior.

Methods:

We utilized a structurally informed finite element model to simulate pre-failure and failure behavior of a human cerebral tissue specimen modeled as a composite containing a macro-calcification and surrounding NCR, embedded in a fiber matrix composite. Data from multiple imaging modalities was combined to quantify the collagen organization and calcification geometry. An idealized parametric model utilizing the calibrated model was used to explore the impact of NCR properties on tissue failure.

Results:

Compared to tissue without calcification, peak stress was reduced by 82% and 49% for low modulus (representing lipid pool) and high modulus (simulating increase in calcification size) of the NCR, respectively. Failure process strongly depended on NCR properties with lipid pools blunting the onset of complete failure. When the NCR was calcified, the sample was able to sustain larger overall stress, however the failure process was abrupt with nearly simultaneous failure of the loaded fibers.

Conclusions:

Failure of calcified vascular tissue is strongly influenced by the ultrastructure in the vicinity of the calcification. Computational modeling of failure in fibrous soft tissues can be used to understand how pathological changes impact the tissue failure process, with potentially important clinical implications.

1. Introduction

Intracranial aneurysms (IA), the pathological enlargement of the cerebral arterial wall, are present in about 3.2% of the adult population [1]. Spontaneous rupture of a cerebral aneurysm is fatal for approximately 45% of patients, while 50% of the survivors suffer from disabilities that prevent them from returning to work [2,3]. Currently, it is difficult for clinicians to confidently select aggressive and somewhat risky treatments over more careful observation [4,5]. Indeed, current clinical treatment protocols such as clipping, endovascular coiling, and stenting carry significant risks, including a 1-2% risk of mortality, that can be higher than the risks associated with a rupture which occurs at an average rate of 1.1% per year [6,7]. Thus, there is a pressing need for improved evidence-based methods to stratify the aneurysms at a higher risk of rupture and avoid unnecessary treatment in others. As patient specific information about the aneurysm wall is limited; most IA rupture risk assessment protocols are based on patient characteristics combined with metrics of aneurysm geometry, such as aspect ratio, diameter and surface lobulation of the aneurysm. While patient specific hemodynamics within the aneurysms also have great potential for risk assessment, due to their direct influence on the health of the aneurysm wall, controversy remains on how best to use such information to guide clinical decisionmaking [8-10].

From a biomechanics point of view, aneurysmal wall rupture is the mechanical failure of the wall tissue in the presence of wall stresses in excess of the tissue strength. Different structural pathways, such as anomalous remodeling of the wall collagen architecture, inflammation, the presence of lipid pools or calcified regions within the wall tissue, have been variously implicated as wall-weakening mechanisms leading to the IA rupture. Our group recently reported that calcification is more prevalent in human IA wall tissue than previously believed [11]. We also found that physical environment around the calcification varied. For example, calcification could exist within or even separate from lipid pools [11]. Moreover, in some cases, the collagen fibers could traverse around the calcification, while in other cases, the calcification appeared in pockets surrounded by apparently damaged collagen fibers [11,12]. Additionally, we found that for ruptured aneurysms, the calcification was never co-localized with lipid pools, suggesting the environment around the calcification is of importance. Furthermore, while calcification was found in nearly all samples, calcifications that were 1 mm or greater in dimension were only found in unruptured aneurysms. These findings suggest information as to the physical existence of either lipids and/or calcifications is insufficient to assess rupture. A physical explanation for these correlations would potentially have tremendous value, both for risk assessment in cerebral aneurysms and also for plaques in extracerebral vessels.

While the role of calcifications in altering the stress state of the tissue has received more attention in extra-cerebral vessels than for cerebral vessels [13-15,11,16,17], similarly crucial unanswered questions remain for these vessels as to the relationship between calcification and rupture risk. In addition, whether biomechanical principles operative at the calcified extra-cranial vessel wall translate to the intracranial aneurysmal tissue is not known. In the present work, we investigated the multifactorial nature of IA rupture to understand how the calcification and also its surrounding wall tissue environment influence rupture risk. We hypothesized that the material composition of the Near-Calcification Region (NCR) of the IA wall tissue influences the mechanical stress distribution within the tissue, and thus impacts the overall failure properties of the calcified IA tissue. To test this hypothesis, we undertook a combined experimental and computational approach in this paper. First, we developed a 3D embedded fiber finite element method capable of modeling discrete fibers embedded within a matrix. Second, we applied that method on a unique tissue sample in which we had multiphoton microscopy (MPM), microCT, and uniaxial extension to failure data. We used the multimodality imaging protocol and uniaxial data to fit our finite element model material parameters. To our satisfaction, we observed similar failure localization in the in-situ model as seen in the uniaxial experiment after fitting the material parameters. Lastly, we ran a parametric study to quantify the effect of calcification and NCR stiffness on failure properties. To remove the effect of local features of the calcification and edge effects we chose to run the parametric study on an “idealized” model with the material parameters extracted in the second step. We identified a non-monotonic relationship between NCR stiffness and failure properties and behavior.

2. Methods

2.1. Multimodal Bioimaging and uniaxial testing of calcified human IA specimen

2.1.1. Tissue harvest

Aneurysm tissue was harvested after surgical clipping from a patient (59 years old female) with unruptured cerebral aneurysm at the Allegheny General Hospital, Pittsburgh, USA. Informed consent was signed by the patient before surgery and all study protocols were approved by the Institutional Review Board at both the University of Pittsburgh and Allegheny General Hospital. Harvested tissue was kept in 0.9% (w/v) saline solution and transported to the University of Pittsburgh within 3 hours after surgery. As detailed below, the sample was then scanned under micro-CT and mechanically tested.

2.1.2. Micro-CT scanning and CT data reconstruction

The sample was scanned at a resolution of 6 μm using a high-resolution micro-CT scanner (Skyscan 1272, Bruker microCT, Belgium). The scanning and reconstruction protocols were detailed in our previous publications [11,12]. Briefly, the sample was placed in a 1.5 ml micro-centrifuge tube with wet gauze to prevent dehydration, and then scanned 180° around the vertical axis with an average framerate of 8 per second and a rotation step of 0.3°. After 45 minutes of scanning, a stack of 3D images was reconstructed using NRecon reconstruction software (Bruker microCT, Belgium). The 3D reconstructed images were segmented into two different masks, calcified region and normal tissue region, based on grayscale values using Simpleware ScanIP (Synopsys, Mountain View, CA). The harvested specimen had a single macrocalcification in a crescent moon shape with radius 2.22 mm and thickness 0.662 mm. A series of image processing operations, including thresholding, Gaussian smoothing, and connected components filtering, were performed to clean up the segmentation mask. Triangular surface meshes for the calcified region and the rest of the tissue were then generated from the segmentation masks.

2.1.3. Biomechanical testing

Harvested aneurysmal tissue was trimmed into a rectangular shape with a dimension of 6 mm x 2.5 mm. A part of the calcified region had to be excluded during the trimming procedure. The prepared specimen was subsequently tested in a custom designed uniaxial loading system [18,19]. The testing protocol was described in detail in a previous article [18]. Briefly, the sample was gripped by metal clamps with sandpaper attached to the grip surfaces and was subjected to uniaxial extension with a speed of 20 μm/s. Images from a camera mounted above the specimen recorded the specimen geometry at 1 fps during the testing process. Extension was terminated after the peak load and before complete failure of the tissue specimen. The sample was fixed at the stopped extension configuration with 4 % paraformaldehyde solution for 2 hours.

2.1.4. Multiphoton imaging

After fixation, the collagen fiber network within the tissue specimen was assessed using multiphoton microscopy (Olympus FV1000 MPE, Tokyo, Japan) equipped with a Coherent Chameleon Ti-sapphire laser and 1.12NA 25× MPE water immersion objective [19,20]. The excitation wavelength was set to be 870 nm and the second harmonic generation (SHG) signal from collagen was collected using a 400 nm emission filter. A stack of images with 1024 X 1024 pixels was acquired at multiple locations on the sample with a step size of 2 μm through the thickness. Projected stacks of images through the thickness were then used to measure collagen orientation using open source software, CT-fire (Laboratory for Optical and Computational Instrumentation, University of Wisconsin-Madison, WI) [21]. Areal density was calculated by applying a threshold mask in ImageJ and averaging through the thickness of the stack and at multiple locations [22]

2.2. Sub-tissue scale modeling of the tissue using fiber-reinforced finite element method

We utilized a recently developed fiber-reinforced finite element method for all simulations in this paper. Details of this model can be found in our previous publications [23,24]. Briefly, this method modeled the fibrous soft tissue microstructure as a network of discrete 1D rod elements embedded within the 3D continuum at the sub-tissue level, while the uniaxial testing procedure was simulated at the specimen level by upscaling the information gathered at the lower length scale. No slip at the fiber-continuum interface was allowed so that the deformation was affine at all material points within the domain. A master-slave approach was used to enforce this condition. Continuum components of the specimen, comprising of the calcified region and the non-fibrous matrix at the non-calcified region, were modeled with a two-parameter isotropic homogeneous nearly-incompressible neoHookean material

$$\Psi =0.5\mu \left(J^{-\frac{2}{3}}{I}_1-3\right)+0.5K(J-1{)}^2$$

with Ψ as the strain energy per unit reference volume, μ as the shear modulus, K a penalty parameter enforcing incompressibility condition [25], J=det(F) as the determinant of the deformation gradient, and I₁ = trC as the first invariant of the right Cauchy-Green deformation tensor. The collagen fibers were modeled as discrete elastic rods with linear stress-stretch relationship with elastic modulus of E_f beyond recruitment stretch λ_r, with zero load bearing capability below this stretch [24,23]. The constitutive model for the fiber was defined such that the fiber stress σ increased linearly with stretch λ up to the fiber strength σ_f with a subsequent linear decline to zero as a result of fiber damage:

$$\sigma =\{\begin{array}{cc}0\hfill & \text{if}\lambda <{\lambda }_r\hfill \\ E_f(\lambda -{\lambda }_r)S\hfill & \text{if}\lambda \ge {\lambda }_r\hfill \end{array}\phantom{\}}$$

In this equation, S ∈ [0,1] is an internal damage parameter for the fiber that imposes the decline in fiber stress to zero as the fiber stretches beyond the peak fiber stretch (λ_p) and experiences subfailure damage and eventually complete failure. In particular, S takes the value S_init = 1 up to the peak stretch of the fiber, λ_p. If the fiber stretch is monotonically increased beyond λ_p up through the failure stretch of the fiber, λ_max, S monotonically decays to zero. In the event of unloading, S for the fiber remains constant so that the fiber will follow the same loading path upon subsequent loading. At and beyond the failure stretch of λ_max, the fiber is fully failed (S = 0) and does not bear any further load, even under potential unloading. The equation describing the evolution of S is based on our previous work [26] and is given by

$$S=\text{min}\left[S_{min},\langle 1-\frac{\lambda -{\lambda }_p}{{\lambda }_{max}-{\lambda }_p}\rangle \right]$$

where S_min ≥ 0 is the minimum value of S over the course of the simulation. The operator 〈a〉 is defined as

$$\langle a\rangle =\{\begin{array}{cc}a\hfill & a>0\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$

We note that according to our discrete fiber stress-stretch relationship, fiber stress depends on the fiber recruitment stretch. In this study, we have chosen the fiber recruitment stretch to be constant.

2.3. Model calibration using uniaxial testing results

2.3.1. Finite element model of the tissue specimen

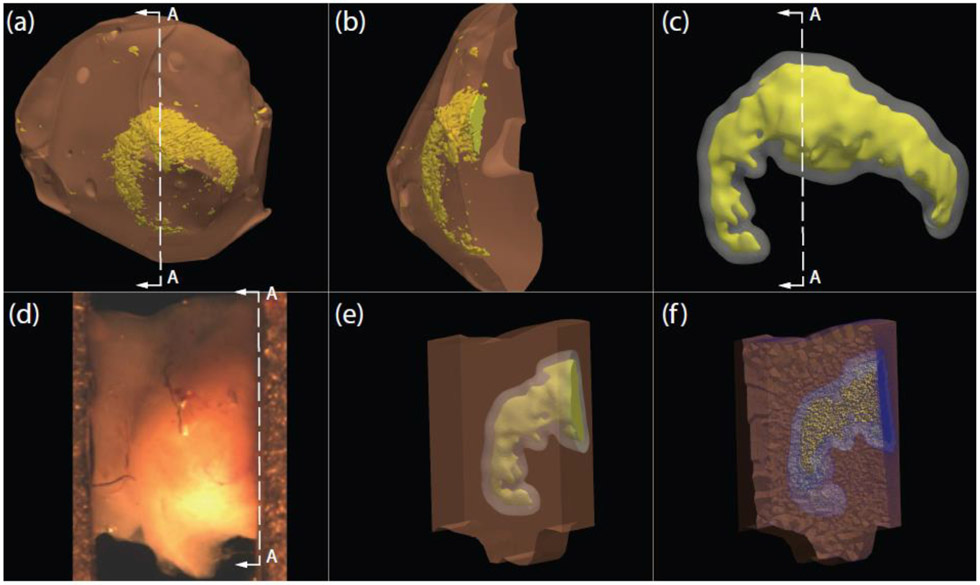
The calcification surface mesh was created using a 3D micro-CT imaging protocol (see Section 2.1.2), Figure 1(a), and smoothed, Figure 1(b), in Meshmixer (Autodesk, San Rafael, CA). The orientation and position of the calcification was approximately aligned with the uniaxial tissue specimen, Figure 1(c). The solid model of the tissue specimen with embedded calcification, Figure 1(d-e), was created in Fusion 360 (Autodesk, San Rafael, CA) after importing the calcification surface mesh. An offset surface, representing the boundary between NCR and rest of the tissue, was also created in Meshmixer. The dimensions of the solid model were approximately 1.33 mm by 2.33 mm that varied along its length to match the actual specimen geometry, as obtained from the image acquired by the overhead camera before the start of uniaxial extension. The thickness of the unloaded solid model was kept uniform at 1 mm, in the range of the specimen thickness measured by calipers. The finite element mesh was created using Trelis (csimsoft, American Fork, UT), and consisted of four-noded tetrahedral elements. The convergence criterion was taken as the change in peak stress, measured from the stress-stretch curve, to be less than 5% between successive mesh refinements. For numerical convergence, 289,000 elements and 50,000 nodes were required for modeling the uniaxial tissue specimen.

Fig. 1.

(a) Surface meshes of cerebral aneurysm dome tissue and calcification created from 3D micro-CT protocol. (b) Cross-section A-A of aneurysm dome and calcification surface meshes (c) Smoothed calcification surface mesh in yellow, and the offset surface that models the boundary of near-calcification region (NCR) in grey. (d) Experimental uniaxial tissue specimen at zero load configuration. (e) Opaque specimen solid model illustrating internal calcification in yellow and near-calcification region surrounding the calcification. (f) Cross-section image of the 3D finite element mesh of the in-situ uniaxial specimen

2.3.2. Input parameters for the finite element model

MPM image analysis of the medial layer of the cerebral arterial wall tissue revealed well aligned fibers in the circumferential direction with little dispersion [27]. However, aneurysmal tissues such as the one tested here can potentially exhibit variation in fiber dispersion between samples. Ideally, we would incorporate exact fiber orientation information measured by MPM imaging before uniaxial extension of the tissue specimen. However, in this case we only had MPM imaging after extension, which showed collagen fibers to be highly aligned in the circumferential direction. Therefore, we created the model fiber network from a normal distribution of fiber angles with the mean as the circumferential direction, and a standard deviation of 10°. Other fiber network properties, extracted from MPM image analysis, were collagen fiber bundle diameter, 20 μm, and areal density, 30%. Based on this areal density, fiber bundle diameter, and tissue dimensions, 2,242 fibers were inserted within the specimen. A large range of material properties, specifically stiffness, of vascular calcification have been reported in the literature [28-30]. As the calcification is much stiffer than the surrounding soft tissue, it effectively acts as a rigid body under physiological loads and hence the simulation results are insensitive to the precise value in this range. In the present study we chose a shear modulus of 6.9 MPa and a Poisson ratio of v = 0.3 (Cardoso et al., 2014). Shear modulus of NCR, μ_NCR, was assumed to be similar to that for the nonfibrous matrix μ_matrix for model calibration purpose. Recruitment stretch for the collagen fibers was fixed at 1.15. Maximum fiber stretch was fixed at 1.5 to ensure stability of the post-peak regime of the stress-stretch curve. Non-fibrous matrix shear modulus, and the modulus and strength of the individual collagen fibers were kept as free parameters of the model.

2.3.3. Finite element simulation procedure and model calibration

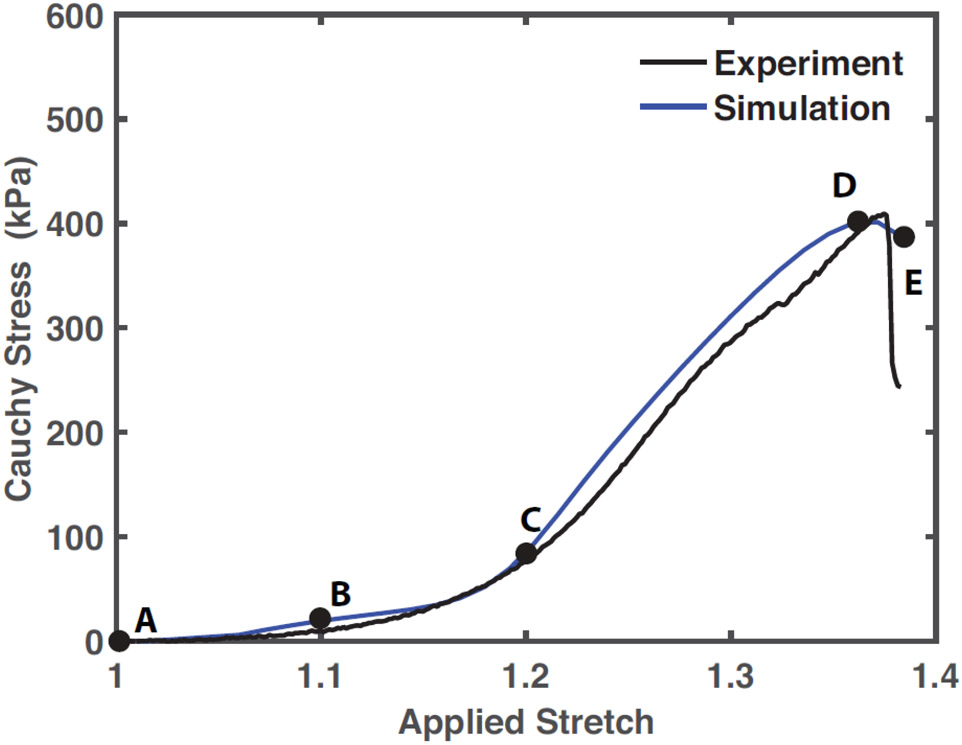
To simulate uniaxial testing, finite element mesh nodes on the left face of the specimen were fixed and nodes on the right face were prescribed a uniform displacement of 0.8 mm over 5000 load steps, which yielded temporal convergence. Reaction forces at each load step, which corresponded to the load cell recordings in physical uniaxial experiments, were recorded to compute the average Cauchy stress. Current cross-sectional area was approximated by the initial cross-sectional area mid-specimen divided by the current stretch, as was performed to process experimental data. Free parameters of the model were estimated using regression analysis between the simulated and experimental stress-stretch curve (Figure 2). The material parameters in Table 1 yielded an R² of 0.97.

Fig. 2.

Experimental stress-stretch curve in black and the simulated stress-stretch curve in blue (R² = 0.97). Material parameters input to the fiber-reinforced finite element model, employed for the simulation of tissue biomechanical behavior for the rest of the article, were regressed from the simulation case shown here. Labels A-E correspond to the loading state of the tissue from the beginning of loading to overall failure

Table 1.

Regressed parameters of solid model to fit expeirmental uniaxial extension data

Role	Parameter	Regressed Value
Non-fibrous matrix	μmatrix	33.56 kPa
Collagen Fiber	Ef	8 MPa
Bundle	σf	1.8 MPa

2.4. Model building for the parametric study

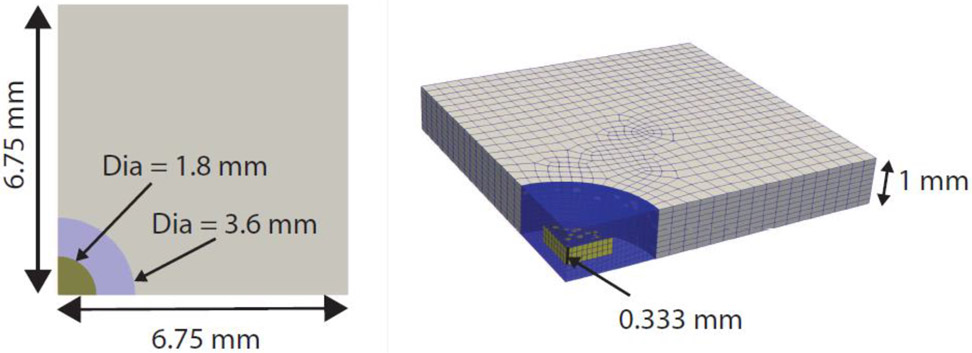
For the parametric study of the effect of NCR material properties on the overall tissue failure behavior, we constructed a simplified rectangular tissue domain with one central disk-shaped calcification of height 0.333 mm and diameter 1.8 mm embedded at the center of the specimen, see Figure 3. The simplified geometry was chosen to remove the effect of local surface topology of the calcification on the ensuing stress field so that insights gained from the parametric study are general in nature. The diameter of the calcification was motivated from the size of the calcification of the uniaxial tissue specimen shown in Figure 1. The near calcification zone was taken to be a cylinder encapsulating the disk-shaped calcification with a diameter of 3.6 mm and extending to both surfaces of the specimen in the thickness direction. Dimensions were chosen as 6.75 mm x 6.75 mm x 1 mm to minimize boundary effects on the stress field in the vicinity of the calcification. The convergence criterion was taken as the change in peak stress, measured from the stress-stretch curve, to be less than 5% between successive mesh refinements. For numerical convergence, 7,542 elements and 8,990 nodes were required for modeling the rectangular specimen. Input material parameters for the finite element model were kept similar to the actual tissue specimen as discussed in Section 2.3.3 and shown in Table 1, except for the shear modulus of NCR. This parameter was varied parametrically and defined as the shear moduli ratio (SR) of the NCR to tissue matrix ($\frac{{\mu }_{NCR}}{{\mu }_{matrix}}$). The range of the SR ratio (0.01-1000) was motivated by published mechanical properties describing soft lipid pools, μ_NCR = 0.1-1 kPa, and stiff calcification μ_NCR = 6 MPa (Cardoso 2014, Ferrara 2008). Due to the larger specimen size for the parametric model, more fibers were required to keep the area density consistent with the experimental tissue specimen. As a result, 6,446 fibers were inserted and modeled using our embedded fiber finite element model. Usually the fibers were terminated at the surface of the NCR except for one “control” case in which we modeled the tissue without either calcification or NCR. To model perfect uniaxial extension boundary conditions, the specimen was still extended in the positive x-direction in a displacement-controlled manner, but all negative x,y,z surfaces were on rollers to exploit symmetry in x,y planes and restrict out of z plane motion. All data post-processing protocols are similar to those discussed in Section 2.3.3.

Fig. 3.

Solid model used for parametric studies illustrating embedded calcification (yellow) inside NCR (blue) at the center of specimen. Computational domain exploits problem symmetry

3. Results

3.1. Microstructural events leading to the failure of the human IA tissue specimen

Stress evolution in the collagen fibers and the non-collagenous matrix of the tissue and NCR of the human IA specimen, used earlier for the model calibration purpose, is shown in Figure 4. The top row (a) demonstrates the stress evolution within the fibers at increasing applied stretch λ from left to right, while the bottom row (b) depicts the same for the non-collagenous matrix. Magnitudes of the applied stretch λ chosen for this figure are marked by letters A-E on the experimentally obtained stress-stretch curve of the specimen in Figure 2. We note that for this figure and subsequent stress map figures, we presented only maximum principal Cauchy stress. The range of stress in the matrix is approximately an order of magnitude lower than in the fibers and therefore a different scale is used for the corresponding rows in Figure 4. It can be observed that the stress evolution was highly heterogenous in all components of the tissue. Matrix stress was about 4 times amplified around the calcification in contrast to the rest of the tissue. This stress concentration is expected due to the stiffness mismatch arising from the presence of the calcified region within the tissue. The collagen fibers also exhibited a similar pattern of heterogeneous stress distribution. However, the highly stressed fibers were not confined to the vicinity of the calcification. The region of high fiber stress was more dispersed compared to the region of high matrix stress and in the loading direction away from the calcified region and NCR.

Fig. 4.

Evolution of the nominal stress in collagen fibers and maximum principal Cauchy stress in the NCR and tissue matrix. The frames were captured at applied stretches corresponding to labels A-E in Figure 2. Top (a) and bottom (b) rows illustrate the evolving stress fields in the collagen fibers and non-collagenous matrix, respectively, during the entire uniaxial testing until just beyond the peak stress (λ=1.38), labeled E in Figure 2. Note: stress scale in first and second row are different.

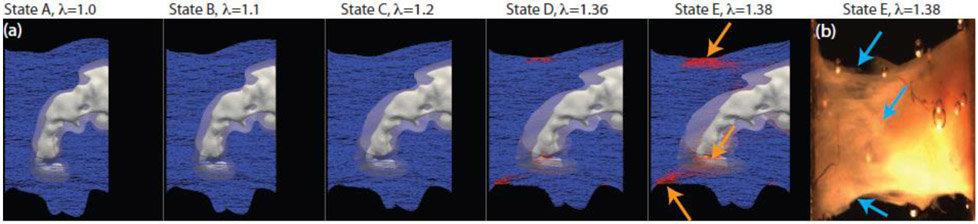
At higher applied stretch closer to the peak stretch (λ = 1.36, State D in Figure 4), the collagen fiber stress focused at the top and bottom edges of the sample, where abrupt changes in tissue geometry created stress concentration zones. Microtears appeared in these regions, which eventually propagated further into the tissue to cause failure of the entire tissue specimen. The evolution of the collagen fiber subfailure damage can be seen in Figure 5 with the undamaged blue fibers (S=S_init) evolving into failed red fibers as S tends to zero (S<S_init), for the same magnitudes of applied stretch used in Figure 4. An abrupt change in the volume fraction of the failed fibers from 5% to 13% was computed between λ = 1.36 and 1.38, the states just before and after the peak of the stress-stretch curve. A sudden increase in the number of failed fibers is also reflected in the abrupt post-peak drop of the stress-stretch curve (Figure 2). We marked the simulation predicted tissue failure regions with orange arrows in the fourth panel of Figure 5, corresponding to λ=1.38. We also included an image of the tissue, the rightmost panel in Figure 5, and marked the experimentally observed failure regions with blue arrows. It can be noted that simulation predicted locations of the tissue failure matched well with the experimental observations.

Fig. 5.

Evolution of internal damage parameter S for fiber failure shown at the same states of applied stretch as in Figure 4 for the specimen depicted in Figure 1(a). Red fibers have started to fail S<S_init and blue fibers have not yet begun to fail, S=S_init. The last panel (b) presents the actual experimental specimen in State E. Orange arrows in the State E (a) simulation frame indicate regions of fiber failure. Blue arrows on the actual tissue specimen at State E (b) indicate regions of tissue failure observed during uniaxial testing. State E with λ = 1.38 corresponds to the point just beyond the peak of the stress-stretch curve in Figure 2

3.2. Effect of near-calcification region on the pre-failure tissue mechanics

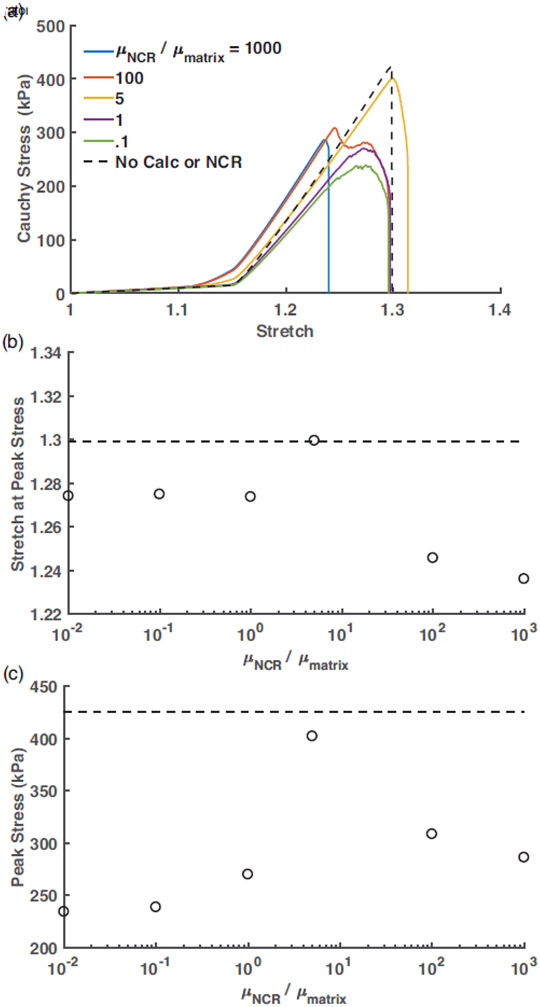
After the primary IA tissue failure mechanisms were elucidated, we wanted to determine the influence of NCR on the overall failure behavior of the diseased tissue. Towards that end, we simulated tissue biomechanics with an idealized specimen geometry, but with all essential components of the calcified tissue present (Figure 3). Uniaxial stress-stretch curves for the stiffness ratio varying from SR = 0.1 to 1000 are presented in Figure 6(a). For the reference purpose, we also simulated mechanical behavior of a rectangular tissue specimen with similar dimensions, but without any calcified or near-calcified region. The peak of the stress-stretch curve for the noncalcified tissue is marked by a dot in Figure 6(a) and by dotted lines in Figures 6(b) and (c). As expected from the rule of mixtures, incorporation of higher modulus NCR resulted in a steady increase in the pre-failure slope of these curves. Peak stress for all cases of NCR stiffness were lower than the “control” tissue, revealing adverse effects of the calcification and NCR on the tissue failure properties. Interestingly, the peak stress varied non-monotonically with the increase in SR, as plotted in Figure 6(b). The peak stress initially increased from 234 kPa (82% less than non-calcified reference case) to 400 kPa (6% less than non-calcified reference case) as the NCR shear modulus increased from 1 kPa to 500 kPa, corresponding to SR from 0.01 to 5. However, beyond SR=5, a sharp drop in the peak stress to ~300 KPa (42% less than non-calcified reference case) could be observed. Overall, a 72% increase in the peak stress could be observed between the lowest and highest peak stress cases (SR=0.01 and SR=5). We also evaluated the peak stretch, defined as the applied uniaxial stretch at which the peak stress is achieved, for all cases of SR and plotted them in Figure 6(c). The peak stretch varied in a narrow range of 1.28 to 1.3 and remained within ~2% of the peak stretch for the reference non-calcified case. However, when the stiffness ratio was further increased, the peak stretch decreased to 1.24, a value 4.8% lower than found in the non-calcified case.

Fig. 6.

(a) Uniaxial Cauchy stress vs stretch curves for in-situ specimens with varied NCR stiffness quantified by the ratio of the NCR and tissue matrix shear modulus, SR ($\frac{{\mu }_{NCR}}{{\mu }_{matrix}}$). The black curve denotes the response of an in-situ specimen with the same dimensions but with no calcification or NCR region. (b) Variation of applied uniaxial stretch at peak stress with the SR. Dashed horizontal line represents the peak stress for the rectangular tissue specimen with no calcification or NCR. (c) Variation of the peak stress, defined by the maximum stress observed from the uniaxial stress-stretch curve, with SR. Dashed horizontal line represents the peak stress for the rectangular tissue specimen with no calcification or NCR

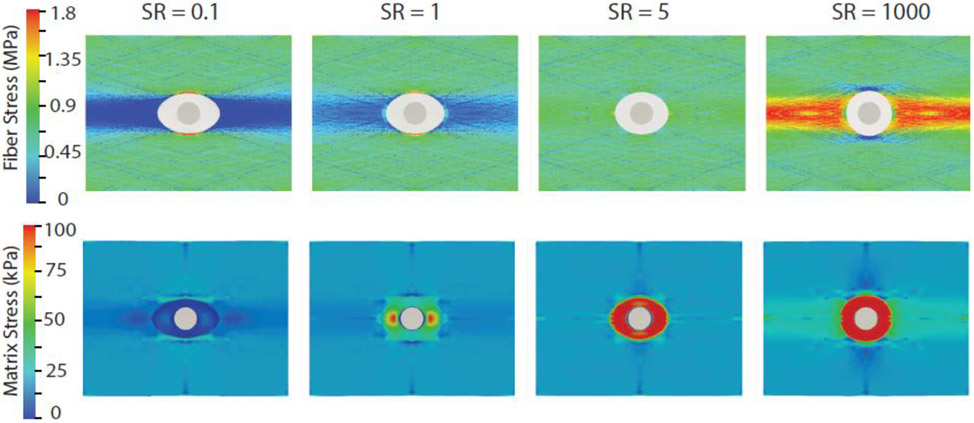
Figure 7 shows the pre-failure stress state within the fiber and the matrix for different stiffness ratios at an applied stretch of λ = 1.2 . Overall, fiber stresses were about one order of magnitude higher than the stresses within non-fibrous tissue components for all simulation cases. Interestingly, for SR≤1, stress concentrated regions for the fibers were located orthogonal to the loading axis. For SR≥ 100, stress concentration regions reappeared along the loading axis, and spanned a much larger area than those observed for SR ≤ 1 cases. In comparison to the other cases, the fiber stress concentration was mostly mitigated when the stiffness ratio was 5. The stress concentration factor (SCF) for the fibers, defined as the ratio of the fiber peak stress to the ambient fiber stress, was estimated as ~3, while that for SR=5 was reduced to ~1.6. The NCR region experienced low stresses for low values of NCR shear modulus. For example, for SR = 0.1, the peak maximum principal Cauchy stress within the NCR was 12 kPa, compared to a peak of 20 kPa for the same component within the tissue matrix. However, with the increase in stiffness ratio, the NCR region experienced higher stress with stress concentration region in the direction of the loading axis that subsequently spread through the entire NCR for SR≥5. High stress within the NCR increased monotonically in contrast to the tissue matrix region as SR was increased. For example, the ratio of stress concentration factor in the NCR and tissue matrix was 0.6, 5, 10, and 15 for SR = 0.1, 1, 5, and 1000, respectively.

Fig. 7.

Distribution of collagen fiber nominal stress (top) and Cauchy stress in non-collagenous matrix including NCR (bottom) at λ = 1.2 (pre failure) for four different cases of SR ($\frac{{\mu }_{NCR}}{{\mu }_{matrix}}$): 0.1, 1, 5, 1000. Only maximum principal Cauchy stress, which is in the loading direction, is shown

3.3. Effect of near-calcification region on failure and post-failure tissue mechanics

A distinction in the peak and post-peak regions of the stress-stretch curves corresponding to different stiffness ratios could be observed in Figure 6(a). For SR≤1, the peak region of these curves were rounded; a decrease in the slope of the stress-stretch curves could be detected starting from λ ~1.24 (SR = 0.01 and 0.1) and λ ~1.25 (SR=1), while the peak stress was achieved at an applied stretch of 1.27 (SR=0.01, SR=0.1, and SR = 1). In contrast, the SR≥5 cases dropped sharply immediately after the peak. We quantified the ratio of the area under the post-peak region to the area under the entire curve (R Factor) as a measure of severity of the post-peak drop in tissue stress [18]. The R Factor for low NCR stiffness cases, SR = 0.1 and 1, were 0.2 and 0.24 respectively. Generally, the R Factor decreased with increasing SR. In particular, the R Factor was 0.14 and 0.06 for the SR=5 and SR=1000 cases, respectively. However, it is interesting to note that SR=100 exhibited a non-monotonic decrease in the stress-stretch curve after the peak, which created a high R Factor of 0.43. Similar bi-peak curves were observed for some human basilar specimens in our uniaxial experiments reported in [18].

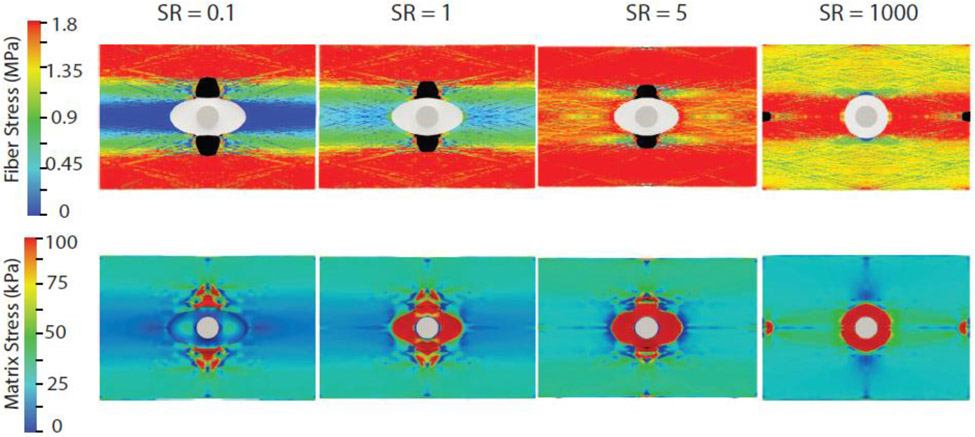
To further investigate whether this variation in the shape of the stress-stretch curve reflected altered failure behavior at the microstructure level, we examined tissue stress distribution and tear location at the peak of these curves for all simulation cases. Stress distribution in the collagen fibers and the non-collagenous matrix of the tissue and NCR at the peak of the stress-stretch curve for SR = 0.1,1,5, and 1000 is shown in Figure 8. For SR ≤ 5, the tissue tear appeared in the vicinity of the NCR orthogonal to the loading axis, but the tear mouth was highly blunted. Interestingly, the tear was already initiated for all these cases, suggesting tear onset and propagation even for sample stretches below the peak stretch (when overall uniaxial stress was increasing). The rounded appearance of the peak region was an outcome of this tear propagation while the tissue was still being loaded. In contrast, for SR>100, tear initiation corresponded to the peak of the stress-stretch curve. For the SR=1000 case shown in Figure 8, tears could be observed along the loading direction near the grip and orthogonal to the loading direction in the vicinity of NCR. Subsequently, the tear near the grips dominated, and all the fibers in that region failed simultaneously (not shown) at 0.32% additional applied stretch.

Fig. 8.

Distribution of collagen fiber nominal stress (top) and non-collagenous matrix Cauchy stress (bottom) at peak stress for four different cases of SR ($\frac{{\mu }_{NCR}}{{\mu }_{matrix}}$): 0.1, 1 5, 1000. Failed fibers are highlighted in black. Only maximum principal Cauchy stress, which is in the loading direction, is shown in the matrix (bottom)

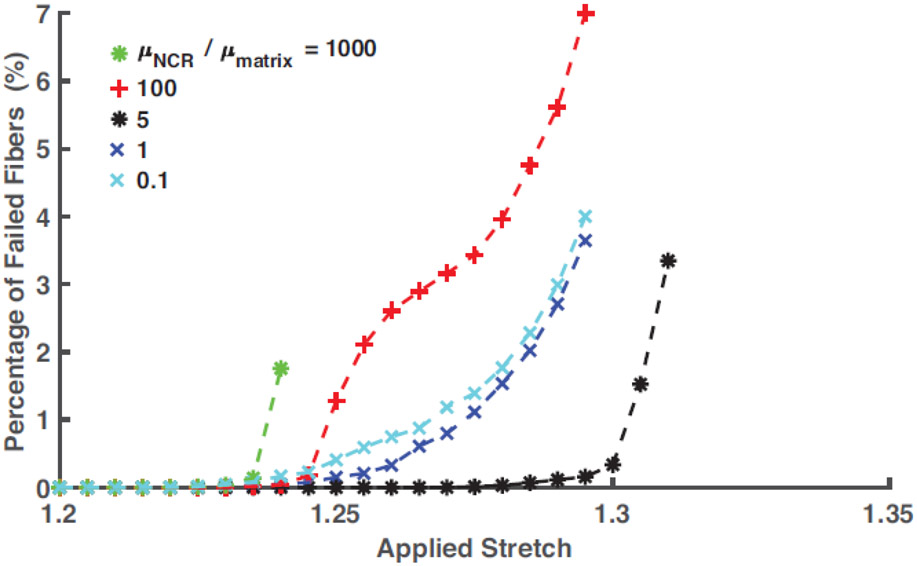
We plotted the evolution of the fraction of failed fibers with the applied stretch for the different SR cases, Figure 9, to gain insight into the effect of NCR stiffness on the post-peak region of the stress-stretch curve. It can be observed that for SR = 0.1 and 1, the fiber failure evolved gradually, and the completion of the entire fiber failure process occurred over an applied stretch range of 7%. The gradual failure of the fibers explains the extended post-peak region of corresponding stress-stretch curves, a topic studied in detail in our recent publication [27]. In contrast, for SR = 5, onset to completion of the failure process occurred within 2.5% stretch, starting from λ=1.29 suggesting an abrupt drop in stress after the peak. Non-monotonic post-peak behavior for SR = 100 is reflected in the evolution of fiber failure for this case. In this case, the initial rapid increase in the fraction of failed fibers was followed by a relatively quiescent phase, which led to the final rapid failure. An examination of the actual failure process (not shown) suggested a competition of tears propagating from grip and NCR region, giving rise to this post-peak behavior. For SR>100, evolution of the failed fibers demonstrates early onset (λ=1.24) and rapid completion of the failure process.

Fig. 9.

Evolution of the percentage of failed fibers, defined by the volume of collagen fibers failed during the uniaxial loading process, for SR ($\frac{{\mu }_{NCR}}{{\mu }_{matrix}}$) ranging from 0.1 to 1000

4. Discussion

In the current study, we demonstrated that the altered biomechanics of the near-calcification region influences overall failure behavior of the calcified cerebral aneurysm tissue. We found that while calcifications elevate the tissue stress in its vicinity, mechanical property of the near-calcification region determines how this high stress is propagated and distributed over the rest of the tissue. The stress distribution determines the location of tear initiation and its rate of propagation at the tissue microstructural level. These microstructural mechanisms, in turn, control the emergent tissue scale failure biomechanics, reflected at the experimentally obtainable uniaxial stress-stretch curve.

Softer near-calcification regions that are biomechanically equivalent to the lipid pools resulted in the tear initiation in locations orthogonal to the loading axis at a relatively low specimen level peak stress. These tears, however, propagated in a longitudinal, stable manner accompanied by a low rate of fiber failure, resulting in a gradual reduction of the post-peak tissue stress. In contrast, NCR with shear modulus higher than the tissue matrix, as may happen due to the presence of dispersed unstructured neocollagen fibrils and/or micro-calcified granules, resulted in an amplified stress distribution over a larger volume of the tissue along the loading axis. A larger number of collagen fibers within that region oriented along the loading direction were available to transmit the high stress, and thus the stress at the individual fiber level remained low. As a consequence, the tissue specimen was able to sustain larger overall stress before ultimate failure. However, the peak stress was achieved at a lower stretch compared to the soft NCR cases, and the post-peak tissue failure process was abrupt with simultaneous failure of all the loaded fibers. The case of SR = 5 was a transition between these two modes of failure. NCR and fiber-reinforced tissue mechanical properties were matched resulting in very low stress concentration. Subsequently, the specimen achieved the peak values comparable to the no-calcification case with 0.05% and 5.59% difference in peak stretch and stress, respectively. However, the post-peak response was abrupt, similar to the cases with higher NCR stiffness or SR. Taken together, these observations strongly support our overall concept that while tissue biomechanical properties are compromised in the presence of calcifications, the actual failure progression is significantly influenced by the properties of the near-calcification region.

The role of calcification on the rupture of intracranial aneurysms is not well understood yet, although our group has recently shown that prevalence of calcification in human intracranial aneurysmal tissue is high, with 24% of the examined samples also exhibiting the presence of colocalized lipid pools [11]. Interestingly, co-existence of calcification and lipid pool was not found in any of the tissue specimens harvested from ruptured aneurysms. Our results of stable tear propagation and gradual post-peak failure process indicates that softer NCR such as lipid pools can result in a more gradual failure process that may have a protective role against IA rupture. For example, the early fiber failure before the peak stretch is reached could possibly trigger vessel remodeling, thereby avoiding complete failure. Further research is required to corroborate this conjecture.

The role of calcifications in altering the stress state of the tissue in extra-cranial arteries has received more attention than for cerebral vessels. However, there similarly remain crucial unanswered questions as to the relationship between calcification and rupture risk. A two-fold increase in stress above the ultimate stress induced by the microcalcifications has been reported, implicating their role in atherosclerotic plaque rupture [31]. Size and orientation of the calcifications have been hypothesized to influence potential rupture of these plaques [32]. Kelly-Arnold et al. studied the effect of micro-calcifications on the stress distribution within the tissue and reported stress concentration factors between 1.0-7.0 [32]. We also found a similar range of stress concentration factors within the tissue caused by the macrocalcifications investigated in this work. Additionally, Vengrenyuk et al. predicted prolate spheroid shaped micro-calcifications to amplify the stress concentration in the tissue as opposed to more idealized spherical shapes [31]. In the study of abdominal aortic aneurysms, intramural calcifications were found to strongly influence the wall stress state [16] and increase rupture risk [17,14]. As a common theme, all these studies have implied calcification induced stress amplification is the sole indicator for tissue rupture. In this work, we distinctly show that while stress concentration is an important contributor for tissue tear initiation, actual tear propagation and eventual failure of the tissue critically depends on the management of this elevated stress. Biomechanics of the near-calcification region contributes towards the stress management mechanisms, and thus significantly influences the ultimate tissue rupture.

Due to the incorporation of the actual collagen fiber architecture, our IA tissue model behaved as an anisotropic heterogeneous medium. Cardoso et al. demonstrated that consideration of anisotropy can reduce the stress concentration significantly compared to that resulting from isotropic analysis [15]. Explicitly accounting for the individual fibers enabled us to model sub-tissue level fiber-matrix biomechanical interaction. We found that the collagen fibers were primarily responsible for stress transmission within the tissue and resulted in “stress paths” that dispersed the focal high stress over a large tissue region. The localized failure of these fibers resulted in micro-tears within the tissue that acted as tear initiation sites. Using collagen hybridizing peptide, Converse et al. have shown that cerebral artery tissue yielding is associated with the molecular level damage of the collagen fibers aligned in the loading direction [33]. These image-based observations are in agreement with our prediction of fiber-mediated tissue failure mechanism. Our recent experimental work on uniaxial failure behavior of cerebral tissue [18] has shown post-peak stress-stretch response of the tissue ranging from abrupt to gradual drop in the tissue stress. The current study reveals that differential rates of collagen fiber failure during tear propagation can give rise to the entire gamut of post-peak failure response. Given that post-peak response may have a profound effect on the potential of the tissue to avoid complete, catastrophic failure and also impact the tissue capacity for remodeling and healing process, quantification of the effect of micro-scale fiber failure on tissue-scale post-peak biomechanical behavior requires further attention.

The material parameters of collagen fibers bundles obtained in this work were regressed from experimental uniaxial extension data using an effective area (see Table 1) and are lower than the typical range of collagen fiber modulus and strength [34-41]. Although, the regressed values are not meant to be literally taken as values for specific collagen fibers, several points should be noted. There is a great need for additional high quality data on failure and stiffness properties for collagen fiber that accounts for factors such as type of collagen fiber (collagen I and III), animal species, type of tissue (tendon, artery), disease state and age. Gentlemen et al. noted that fiber diameter has a significant effect on fiber stiffness and strength [35]. Larger diameter fibers such as the 1-2 μm collagen fibers observed by multiphoton imaging of cerebral aneurysmal tissue [19], are more likely to contain defects, resulting in reduced stiffness and strength. This factor, in conjunction with probable degradation of fiber quality due to disease progression and age, may explain the lower magnitude of the collagen material parameters in the current study. The other structural component of the tissue, the non-collagenous matrix, was modeled with one material parameter (shear modulus). The regressed magnitude of this parameter is similar to the values reported in the cardiovascular tissue literature [39,40].

Our study has the following limitations. In our tissue microstructure model, some of the collagen fibers terminated abruptly at the edge of the NCR, as observed in only some calcified IA tissue [11]. We anticipate that incorporation of continuous fibers around the calcification will introduce additional stress paths in the vicinity of the calcification and further reinforce our overall suggestion of tissue failure cascade. We note that according to our discrete fiber linear stress-stretch relationship, fiber stress depends on the fiber recruitment stretch. In this study, we have chosen the fiber recruitment stretch to be constant. Also, our model does not incorporate any damage response for the underlying matrix components. In the future, we will introduce matrix damage in our model to investigate its effect on the overall tissue failure behavior.

5. Conclusions

We have revealed the role of the material properties of the near calcification region (NCR) on the uniaxial biomechanical failure behavior of calcified tissue from human intracranial aneurysm. We found a nonmonotonic relationship between strength reduction and modulus of the NCR. We also determined that the location of the stress concentration region, and as a consequence tissue tear initiation site, depends on the stiffness of the NCR. Although both low and high modulus of NCR resulted in a significant reduction of the peak tissue stress compared with calcification free tissue, the mode of tear propagation differed in these two limits. High modulus NCR, representing further calcification in the vicinity of the original macro-calcification, resulted in abrupt failure of the tissue. In contrast, tissue with a low modulus NCR, simulating the effect of a collocated lipid pool, resulted in a more gradual or blunted failure process, potentially enabling a biological recovery to avoid complete failure. Interestingly, our recent experimental study found that human aneurysms for which the calcified region was embedded in lipid pools were never ruptured [11].

Current knowledge of the biomechanical role of vascular calcification is primarily focused on the focal elevation of tissue stress in the vicinity of calcified regions. In this work, we demonstrated that while stress concentration within the tissue is an important factor for failure initiation, propagation of tears is influenced by the biomechanical state of the tissue surrounding the calcification. Furthermore, this influence ultimately determines how the cascade of fiber failure proceeds. Our work extends the current knowledge of the rupture biomechanics of calcified vascular tissue and demonstrates that biomechanical pathways of tissue rupture can be altered by ultrastructural remodeling in the vicinity of the calcifications. The work presented herein is an important first step towards understanding the failure propensity of the calcified IA wall tissue. Further research is required to ascertain the role of lipid pools on the rupture propensity of the calcified tissue under physiologic biaxial loading conditions. In the long term, identification of biomechanical factors governing tissue integrity will lead to better understanding of aneurysm rupture mechanisms in-vivo.