Theoretical Study on the Degree of CO₂ Activation in CO₂-Coordinated Ni(0) Complexes

Abstract

The geometrical characteristic and the degree of CO₂ activation of the CO₂-coordinated Ni(0) complexes were investigated computationally by quantum chemical means for bidentate and tridentate ligands of PP, PP^MeP, and PNP, and sometimes with co-complexing Fe(II) to differently coordinate CO₂. We show that the coordination geometry of the central metal is determined by the ligand geometry. The charge and the energy decomposition analyses show that the charge transfer energy through orbital mixing has a strong correlation with CO₂ net charge, while the binding energy cannot due to the lack of the coordination number and the deformation energy of the ligand. Among the examined ligands, PNP with negatively charged secondary amine makes Ni(0) an electron-rich atom, which results in an ∼20% higher CO₂ activation than those of PP and PP^MeP. In particular, Fe(II)-PNP in the CO₂-bridged diatomic complex enhances CO₂ activation by another ∼20%, partly through the inductive effect of Fe(II), which pulls electron density from Ni-PNP across the CO₂-bridge and partly by the backward donation from Fe(II)-PNP. Therefore, the present study encourages us to design a strongly electron-donating ligand and a CO₂-bridged diatomic complex to develop more efficient homogeneous catalyst.

I. Introduction

As human civilization has continued to develop, energy consumption has increased exponentially, especially after the industrial revolution. Because this energy demand has mostly been met by burning carbonaceous fossil fuels such as oil, coal, and natural gas, the liberated carbon has increased the CO₂ level in the air, which is believed to be responsible for global warming and the ongoing climate disaster on this planet.¹ As a result, developing renewable energies and related technologies for environmental protection has become an urgent and imminent issue. Although there are diverse approaches to mitigate the CO₂ level in the atmosphere, the most promising strategy is to reduce CO₂ to any form of a valuable material because carbon itself is also a necessary resource for energy circulation and sustaining the framework of organic substances.² By chemical reduction, depending on the reduction pathway and the degree of reduction, CO₂ is converted into an energy resource such as CO, methanol, or methane. In the full pathway of CO₂ reduction, the first reduction step of CO₂ + e^– → CO₂^– shows the highest activation barrier of 1.9 eV.³ Inevitably, this higher activation barrier necessitates the assistance of the catalyst toward decreasing the energy cost in the CO₂ reduction.

There have been many developments in finding catalysts for CO₂ activation in the areas of both homogeneous⁴ and heterogeneous catalysis.⁵ Regardless of the area, to understand the nature of CO₂ in the activated form with the characteristics of the catalysts themselves will be important in developing new strategies of activating CO₂.⁶ In the homogeneous area, the molecular catalyst is solvated in a solution, normally in water, and it takes part in a catalyzing reaction in free solution or by being bound on the electrode surface. These catalysts are conventionally composed of a central metal (M), normally a transition metal (TM), and surrounding ligands. Carbon dioxide then adds to a vacancy in a metal atom or replaces a loosely bound ligand for further reaction. Many combinations of diverse metals and ligands have been studied in detail.⁷ Among them, Ni-cyclam⁸⁻¹² (cyclam = 1,4,8,11-tetraazacyclotetradecan) and Fe- and Co-porphyrin families⁷ have shown interesting behaviors in terms of their performance and chemical mechanisms. Particularly in the cyclam series, [Ni(II)(cyclam)]Cl₂ showed superior performance to those of Co²⁺ and Fe²⁺ with a low bias of −1.05 V and higher CO selectivity.^9,10 A mechanistic study by Song et al.⁸ revealed that Ni(II)(cyclam) is first bound to the electrode surface and reduced by one electron with −1.07 V (experimentally −1.23 V),¹² Ni(I)(cyclam). This step is followed by thermoneutral CO₂ binding where CO₂ is reduced by one electron and Ni(I) is oxidized to Ni(II). In the whole catalytic reaction, the role of Ni(I) is crucial, as CO₂ is attached to Ni(cyclam)⁺. Also, the amount of charge moving from Ni(I) to CO₂ in this step would control the feasibility of the whole reduction mechanism.

The effect of the ligand was further studied experimentally by substituting H with a methyl group in the secondary amine position of the cyclam. The substitution lowered the overpotential compared to the pristine Ni(cyclam)²⁺, but it enhanced the Gibbs energy of CO₂ binding, which overall decreased the catalyst performance.⁸ The performance deterioration was ascribed to the thermodynamic stability of the CO₂ adduct and its steric hindrance. Even though important insights have been drawn from these studies, many questions remain with regard to the characteristics of ligands (e.g., steric and/or inductive effect, roles of anchor atoms such as N, P, and S) and the central metals (e.g., the shape of d- and f-orbitals, HOMO-LUMO energy gap, and the oxidation state). In the case of polydentate ligands, the coordination bond between the central metal and the coordinating atoms can be strained and affect the catalytic role.

Because the state of the central metal, Ni(I) in cyclam rather than Ni(II), is crucial for CO₂ reduction, as stated above,⁸ the study for the low-valent metal-CO₂ adducts has attracted much interest. After the characterization of (PCy₃)₂Ni(η²-CO₂)¹³ (Cy = cyclohexyl) with zero-valent Ni, referred to as Ni⁰, many Ni-CO₂ adducts with low valency were compounded.^14,15 When the metal makes a coordination bond to C of CO₂, Ni⁰ with large electron density can act as a strong nucleophile. Therefore, it is expected that the lower valent Ni will reduce CO₂ much more and make it more feasible to reduce CO₂ to other materials.

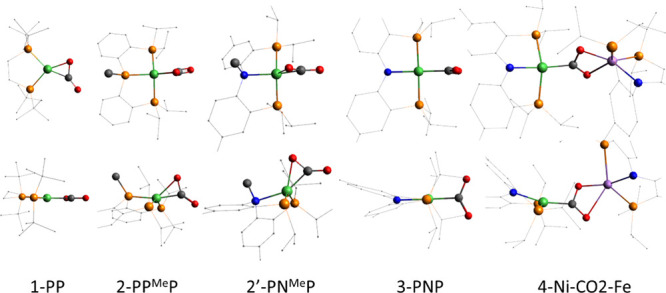
Recently, Lee’s group synthesized a series of CO₂-coordinated Ni⁰ complexes where each ligand has a denticity of two or three for each Ni⁰ atom.¹⁶⁻¹⁹ Therefore, it is very heuristic to investigate the nature of Ni⁰-CO₂ interaction systematically for this series. The models to be studied are represented in Scheme 1. The first model is (dtbpe)Ni-(η²-CO₂) (dtbpe = 1,2-bis(di-tert-butylphosphino)ethane)¹⁴ denoted by 1-PP, where dtbpe is a bidentate neutral ligand with two P’s as anchor atoms. The second one is (PP^MeP)Ni-(η²-CO₂)¹⁶ denoted by 2-PP^MeP, where PP^MeP (PMe[2-PⁱPr₂-C₆H₄]₂, PⁱPr₂ = di-iso-propylphosphino-) is the modification of PPP anion of bis(2-di-iso-propylphosphinophenyl)phosphide²⁰ as a tridentate ligand. Note that all P’s are tertiary phosphine excluding coordination to Ni. The third one is (PNP)Ni-η¹-CO₂-κC (PNP = N[2-PⁱPr₂–4-Me-C₆H₃]₂^–)^19,21 denoted by 3-PNP, where PNP is an anionic ligand of the charge of −1. Note that the middle N in PNP is a secondary amine with two lone pairs, which results in a formal charge of −1. The fourth one is (PNP)Ni-μ-CO₂–κC:κ²O,O′-Fe(PNP)¹⁸ as denoted by 4-Ni-CO2-Fe, where two metal centers are bridged by CO₂. This is a biomimetic complex of carbon monoxide dehydrogenase (CODH), which converts CO₂ and CO reversibly.^22,23 In the active site of CODH, CO₂ is bridged between two metal centers of Ni and Fe (Ni-μ-CO₂–κC:κO-Fe), as shown in Figure S1. Some calculations have been performed for a hypothetical model, as shown in Scheme S1, which replaces the middle P in 2-PP^MeP with the tertiary N, referred to as 2′-PN^MeP, to understand the difference of the effects of the anchor atom species and its valence electrons. 2′-PN^MeP resembles 2-PP^MeP with respect to the shape of valence electrons while it has the same anchor atom species as 3-PNP. We try to analyze the structural characteristics and the degree of CO₂ activation for these models based on DFT calculations. For the estimation of the degree of CO₂ activation, the electron charge density of CO₂ is analyzed because the amount of electron charges on a CO₂ molecule would facilitate the CO₂ reduction reaction.

Scheme 1. Schematic Presentation of Four Models.

The metallic oxidation number and total charge are denoted. R, R₂, and R₃ represent the methyl, isopropyl, and isobutyl groups, respectively.

II. Computational Results and Discussion

For theoretical investigation, the hybrid density functional of B3LYP/6-31G(d) with dispersion correction²⁴ equipped in Q-Chem²⁵ was applied for geometry optimization, and the triple zeta basis set of G3Large was used for energy calculation. Each model was fully optimized, and the natural bond orbital (NBO)²⁶ analysis was applied for the charge of metals (M = Ni, Fe) and CO₂. The energy decomposition analysis (EDA)²⁷ was done between the fragments of CO₂ and the metal complex for each model. The charges and spin multiplicities used in the calculation are 0, 0 for Ni(0) and +2, 5 for Fe(II), and the overall charge of ligand PNP is −1, whereas all the other ligands are neutral.

a. Analysis of Geometry

The optimized structures are shown in Figure 1, and some geometrical parameters are summarized in Table 1. In Figure 1, H was removed, and C of ligands is drawn as a point for clear view. The full geometrical presentations including H are presented in Figure S2 in the Supporting Information.

Figure 1.

The optimized structures of five models in Scheme 1 and Scheme S1 are drawn with the top view (top) and side view (bottom) using B3LYP/6-31G(d) + D. H’s are removed and some C’s in ligands are drawn as points for clarity. Color scheme: Ni, green; P, brown; C, black; O, red; N, blue; Fe, violet.

Table 1. Geometry Parameters for Models in Scheme 1 Using B3LYP/6-31G(d) + D^a.

parameters	1-PP	2-PPMeP	3-PNP	4-Ni-CO2-Fe
chg, mul	0, 1	0, 1	–1, 1	0, 5
geometry Ni	Pl (Pl)14	Td (Td)16	Pl (Pl)19	Pl (Pl)18
d(C–O) (Å)	1.289, 1.212 (1.266,1.200)	1.252, 1.224 (1.252, 1.217)	1.258, 1.257 (1.248, 1.247)	1.318, 1.255 (1.289, 1.269)
d(Ni–C)	1.811 (1.868)	1.875 (1.904)	1.880 (1.911)	1.844 (1.831)
d(Ni–O)	1.877 (1.904)	2.234 (2.191)	2.664 (2.614)	2.856, 2.575 (2.705, 2.772)
∠O–C–O(°)	137.8 (138.0)	133.4 (135.1)	129.6 (128.5)	118.4 (116.5)
d(Fe–O)				1.946, 2.503 (2.008, 2.289)
∠O–Fe–O(°)				58.0 (61.0)

^aThe values in parenthesis are given from crystallography. Pl and Td stand for planar and tetrahedral structures, respectively.

Because there are so many CO₂ adsorption modes for a single-atomic and diatomic catalyst,⁴ all the modes addressed in this work are presented in Figure S3. It is known that η²-C,O is the most stable for Ni⁰ without any ligands.²⁸ The ground state of Ni⁰ with the coordination of a ligand is a singlet state of d¹⁰ (Table S1). As presented in the previous work,²⁸1-PP and 2-PP^MeP have η²-C,O mode as shown in Figure 1. While many CO₂-adducts appear as η²-mode, it is known that some CO₂-adducts have η¹-C mode when a metal is in a relatively low oxidation state so that the energy of the d-orbital is relatively high, as well as when a central metal has a square planar or square pyramidal structure.⁴ Then, in 3-PNP, Ni⁰ has square planar-like structure without CO₂, which makes it prefer η¹-C mode, as shown in Figure 1. As for Fe(II) in model 4-Ni-CO2-Fe, it has κ²O,O′ mode with respect to CO₂. Note that the charge of PNP-Fe is +1 as it is composed of Cl^– in synthesis.¹⁷ Hereafter, Ni(0)-PNP and Fe(II)-PNP without the coordination to CO₂ are simply denoted as Ni-PNP and Fe-PNP, respectively, without any complexity in notation. The calculation shows that Fe²⁺ has a multiplicity of quintets with high spin in PNP-Fe, as shown in Table S2. All the charges and multiplicities of models in calculation are listed in Table 1.

The values with parentheses in Table 1 come from X-ray crystal structures. In this calculation regime, the coordination geometries of all the models are well reproduced except for 4-Ni-CO2-Fe, where two bulky PNP ligands are closely located and the calculation overestimates the dispersion correction, causing the ligands to become slightly twisted, as shown in Figure S4.

From 1-PP to 3-PNP, there is a systematic change of ligands. As for Ni⁰ with two coordination to P’s, there is an in-depth theoretical study with minimal monodentate ligands of two PH₃, where two ligands have no geometrical constraint.²⁹ In the 1-PP model, although two ligands are connected by the ethyl group, the geometry with Ni and CO₂ is not much different from that with the two monodentate ligands. All the atoms of CO₂ lie in the molecular plane, as shown in Figure 1, as is the case with Ni(PH₃)₂.²⁹

Moving to 2-PP^MeP, the coordination number is increased to three with the tridentate ligand of PP^MeP, where Ni has a Td-like structure with three P’s and CO₂ in η²-C,O mode. The CO₂ plane is perpendicular to the ligand plane, which is composed of the three anchor atoms of the ligand. To understand the effect of the tridentate ligands on coordination geometries, three tridentate ligands are shown in Figure 2. The optimized structure of PP^MeP is shown in Figure 2 a, where some valence orbitals are drawn with parity. Those orbitals mainly correspond to the lone pair electrons of the anchor atoms and are directed to above the ligand plane displayed with green triangle. Each MO is separately drawn in Figure S5. The directions of the lone pairs are ascribed to the sp³ structure of the tertiary P as shown with the black arrow. Therefore, Ni can be located on top of the ligand plane, which results in the tetrahedral structure of Ni, as shown in Figure 1.

Figure 2.

The optimized ligand structure of (a) PP^MeP, (b) PN^MeP, and (c) PNP, and (d) structure of [Ni(0)(PCH₃)₂NH₂]⁻¹-CO₂ calculated by B3LYP/6-31G(d) + D. In the ligand structures (a–c), H was removed for clarity. The black arrows denote the direction of the occupied molecular orbitals (MO) near the HOMO level, and the green triangle shows the ligand plane. The MOs in ligand structures are overlaid as much as the number of lone pairs. Colors scheme: Ni, green; C, gray; P, orange; N, blue; H, white; Fe, brown (drawn using Jmol).

The effect of the substitution of the tertiary N for the middle P^Me in PP^MeP, referred to as PN^MeP, is shown in Figure 2b, where MOs are almost identical to PP^MeP in Figure 2a. Therefore, the geometry of the hypothetical model of 2′-PN^MeP remains almost the same as 2-PP^MeP, but the bond length of N–Ni and the angle of Me-N-Ni were decreased by about 0.05 Å and 25°, respectively, compared to 2-PP^MeP due to the size and the electronegativity of N.

In 3-PNP, Ni-PNP makes a planar structure with η¹-C for CO₂, where all the anchor atoms and Ni locate in the same plane together with C of CO₂, as shown in Figure 1. The structure of ligand PNP and the four uppermost occupied MOs are shown in Figure 2c, where MOs are located in the ligand plane. The two lone pairs of N are completely symmetric with respect to the ligand plane as shown in Figure S6, and the ligand shows the complete C2 symmetry, as shown in Figure S7a. Therefore, Ni⁰ as well as Fe(II) is located in the ligand plane, making the Pl structure of Ni-PNP and Fe-PNP. From the ligand field theory, Ni⁰ with a strongly donating ligand makes the electronic configuration of d¹⁰,¹⁰ which leaves sp³ orbitals for M-L (metal–ligand) coordination, resulting in a Td structure. Therefore, if the PNP ligand is replaced by three monodentate ligands such as two P(CH₃)₃ and one [NH₂]⁻¹, it surely goes to a Td structure with η²-C,O mode for CO₂ coordination, as shown in Figure 2d. Therefore, although Ni⁰ prefers a Td structure in its low oxidation state, when it is enforced to have a Pl structure, for example, due to the constraint of the chelating PNP ligand, it favors the η¹-C mode in CO₂ binding.

In 4-Ni-CO2-Fe, CO₂ is bridged by Ni-PNP and Fe-PNP in the type of μ-CO₂-κC:κ²O,O′. This molecule is prepared by two different metal complexes of Ni-PNP and Fe-PNP. Note that although the coordination structure of Fe-PNP is Pl in its optimized structure, it becomes Td in 4-Ni-CO2-Fe.

b. Analysis of Electronic Structure

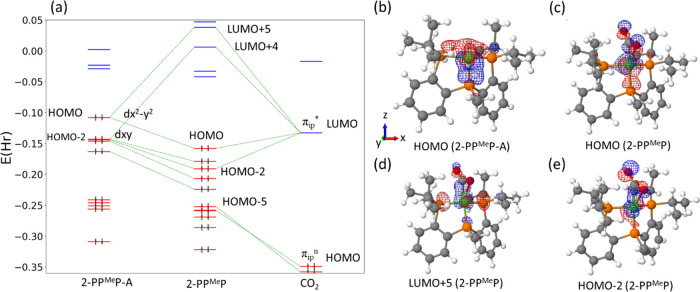
To study the electronic properties of CO₂-coordinated Ni⁰ complexes, the energy levels and the atomic basis coefficients of molecular orbitals (MOs) were analyzed. The MO energy levels of 1-PP are shown in Figure 3a with its two fragments of CO₂ (right side) and the Ni complex (left side) referred to as 1-PP-A in their fixed geometries. When a free CO₂ is bent, the doubly degenerate HOMO (π_gⁿ, nonbonding orbital with 1 node) and LUMO (π_u*, antibonding orbital with 2 nodes) levels are broken and the HOMO-LUMO gap is decreased as the HOMO level is increased and LUMO level is lowered, as shown in Figure S8. In the broken degeneracy, the MOs in the CO₂ plane, also called in-plane mode, take up LUMO (π_ip*) and HOMO (π_ipⁿ), while the MOs perpendicular to them, also called out-of-plane mode, are located at LUMO+1 (π_oop*) and HOMO-1 (π_oopⁿ). In Figure 3a, the red lines denote the occupied orbital levels, and the blue ones denote the unoccupied orbital levels. In Figure 3a, only the selected MO levels are drawn, which are related to the atomic orbitals of Ni and CO₂ for clarity. The green dashes denote the corresponding MOs between before and after CO₂ coordination, which can be just the energy shift or an orbital interaction. All the levels and the relaxed structures of both fragments are shown in Figure S9. From the relaxed geometry to the fixed geometry (1st → 2nd and 5th → 4th column in Figure S9), the occupied levels are raised and the unoccupied levels are lowered around HOMO and LUMO levels, which explains the energetically unstable structure due to geometrical deformation. In the binding of 1-PP-A and CO₂ in Figure 3a, the MO levels of Ni complex decrease while those of CO₂ increase. This large shift of the energy levels is ascribed to the charge transfer from Ni to CO₂, where the electron–electron repulsion energy is raised in CO₂ and lowered in Ni. The backward donation normally occurs through the orbital interactions between LUMO of the bent CO₂ (π_ip*) and any occupied orbitals of M complex, whereas the forward donation occurs through the orbital interactions between HOMO of the bent CO₂ (π_ipⁿ) and any unoccupied orbitals of M complex if it exists. In 1-PP, HOMO of 1-PP-A interacts with π_ip* of CO₂, which means that the backward donation occurs dominantly and is responsible for the CO₂ activation.

Figure 3.

(a) MO levels of 1-PP and its fragments of 1-PP-A and CO₂ in fixed geometries. Only selected MOs are drawn, which are related to Ni and CO₂. Representation of MOs of (b) HOMO of 1-PP-A (top view from z axis), (c) HOMO of 1-PP (side view from y axis), (d) LUMO+1 of 1-PP (slanted to view d_xy-Ni), and (e) HOMO-7 of 1-PP. Colors scheme: Ni, green; C, gray; P, orange; N, blue; H, white (drawn using Jmol).

The five occupied orbitals below HOMO in 1-PP-A mainly belong to Ni-3d orbitals but also include 4s, 4p orbitals due to the pre-existing coordination bond to P’s. HOMO of 1-PP-A is mainly composed of d_xy-Ni, as shown in Figure 3b. Note that the molecular ring is located on the xz plane. In Figure 3c, π_ip*-CO₂ is well developed in HOMO of 1-PP, which comes from HOMO of 1-PP-A. Therefore, this demonstrates that d_xy-Ni charges are moved to the empty CO₂ orbital, which confirms the backward donation of CO₂. The correspondent antibonding appears in LUMO+1 as shown in Figure 3d, where the parity of CO₂ is changed compared to Figure 3c, while the parity of d_xy-Ni remains the same. HOMO and HOMO-1 of the bent CO₂ are located at HOMO-5 and -6 in 1-PP, respectively, which are just the shift of MO levels primarily due to the electrostatic effect ascribed to the increased charge density. Some complicated interactions appear as shown in Figure 3d and Figure S10; however, no trace of the forward donation was detected through MO analysis, so the binding of CO₂ on Ni(0) occurs mainly through the backward donation.

The MO levels of 2-PP^MeP and its fragments of CO₂ and Ni complex (Ni-PP^MeP-A) in fixed geometries are shown in Figure 4a, and there is not much difference from those of 1-PP. The overall molecular orbital levels including the relaxed geometries are also presented in Figure S11. In Figure 4a, there appears backward donation of CO₂ with d_x²_–y² and d_xy in HOMO and HOMO-2 of 2-PP^MeP-A, respectively. Then, the bonding and antibonding orbitals are shown in Figure 4c,d, and another backward donation at HOMO-2 in 2-PP^MeP is detected Figure 4e.

Figure 4.

(a) MO levels of 2-PP^MeP and its fragments of 2-PP^MeP-A and CO₂ in fixed geometries. Only selected MOs are drawn, which are related to Ni, and C and O in CO₂. Representation of MOs of (b) HOMO of 2-PP^MeP-A, (c) HOMO of 2-PP^MeP, (d) LUMO+5 of 2-PP^MeP, and (e) HOMO-2 of 2-PP^MeP. Colors scheme: Ni, green; C, gray; P, orange; N, blue; H, white (drawn using Jmol).

The substitution of the tertiary P with the tertiary N for 2′-PN^MeP does not make a significant difference, as shown in Figure S12, as expected through the similar valence electron structure. However, the secondary N-substitution effect on MO levels in 3-PNP is significant as shown in Figure 5a. The HOMO level of 3-PNP-A is much higher than the level of π_ip*-CO₂. This is ascribed to the raised HOMO level of 3-PNP-A due to the negatively charged N, while the level of π_ip*-CO₂ stays at a similar energy level. The MO level difference between HOMO of 3-PNP-A and LUMO of CO₂ reaches 0.198 Hartree, which is much larger than those of 0.025–0.043 Hartree for the previous models. Therefore, this large energy difference can be a driving force for charge transfer from Ni complex to CO₂. Due to the high energy of HOMO, PNP itself has a strong tendency to donate electrons when combined with any other molecule. Therefore, any M-PNP complex is expected to have a strong tendency to donate electrons when any molecule is coordinated to the central metal. Figure 5b shows HOMO of d_x²_–y² of 3-PNP-A, which interacts with π_ip*-CO₂. The bonding and antibonding orbitals are drawn in Figure 5c,d, and another backward donation appear, as shown in Figure 5e.

Figure 5.

(a) MO levels of 3-PNP and its fragments of 3-PNP-A and CO₂ in fixed geometries. Only selected MOs are drawn, which are related to Ni and CO₂. Representation of MOs of (b) HOMO of 3-PNP-A, (c) HOMO of 3-PNP, (d) LUMO+5 of 3-PNP, and (e) HOMO-2 of 3-PNP. Colors scheme: Ni, green; C, gray; P, orange; N, blue; H, white (drawn using Jmol).

Lastly, MO levels of the CO₂-bridged bimetal complex of 4-Ni-CO2-Fe are presented in Figure 6a with those of its fragments in the fixed geometries. The green lines represent only the backward donations between metals and CO₂. As for 4-Ni-CO2-Fe-A, two separate molecules of Ni-PNP and Fe-PNP exist, so they were calculated together as a supramolecule, as shown in Figure S14. The MO splitting in Figure 6a shows that both α- and β-spin contribute to the backward donation to CO₂. In the bonding orbital of α-HOMO-11, two MOs from 4-Ni-CO2-Fe-A contribute, one from Ni (HOMO-3) and the other from Fe (HOME-5). The bonding and antibonding orbitals for α-spin are drawn in Figure 6b,c. In the α-bonding orbital, the C-p_z orbital of π_ip*-CO₂ bonds with Ni-d_x²–y² while one of two O-pz’s of π_ip*-CO₂ interacts with the Fe-d_xz orbital. Considering the parity of the Fe-d_xz orbital and π_ip*-CO₂, only one O1-p_z orbital (blue color) can overlap with the d-orbital of Fe (blue color) because the other O2-p_z (blue color) has the opposite parity to Fe (red color), as shown in Figure 6b. Therefore, we can say that some portion of the backward donation can occur through the Fe-PNP complex when co-complexing CO₂ in κ²O,O′mode. Note that the α-spin is fully occupied in high spin of Fe²⁺, even though the d-orbital is not fully occupied. As for β-spin, the considerable backward donation appears only through Ni, as shown in Figure 6d. Because Fe²⁺ has only one electron of β-spin in high spin configuration, no meaningful backward donation occurs from Fe²⁺. Resultantly, Fe(II)-PNP partly contributes to the backward donation to CO₂ in a concerted mode with Ni⁰ in its high spin configuration.

Figure 6.

(a) MO levels of 4-Ni-CO2-Fe and its fragments of 4-Ni-CO2-Fe-A and CO₂ in fixed geometries. Only selected MOs are drawn, which are related to Ni, Fe, and C and O in CO2. Representation of MOs of (b) α-HOMO-11, (c) α-HOMO-2, (d) β-HOMO-6, and (e) β-LUMO+10 of 4-Ni-CO2-Fe. Colors scheme: Ni, green; Fe, brown; C, gray; P, orange; N, blue; H, white (drawn using Jmol).

c. Charge and Energy Decomposition Analysis

Energy decomposition analysis (EDA)²⁷ was done and displayed in Figure 7a for the five models in Scheme 1 and Scheme S1. In Figure 7a, FRZ of EDA components stands for the electrostatic repulsion energy attributed to the frozen electron density when two fragments of CO₂ and the Ni complex are combined in the fixed geometries. POL is the polarization energy through intrafragment relaxation from the frozen density, and CT is due to the interfragment electronic relaxation of MOs. Note that FRZ makes the system unstable while POL and CT make the system stable, so FRZ has an opposite sign. In Figure 7a, the sign of FRZ was reversed for comparison. The total SCF energy, referred to as SCF_total in Figure 7a, is given by CT + POL – FRZ. FRZ (orange line) is increasing from 1-PP to 4-Ni-CO2-Fe, which means that the overlap interaction between two fragments is increasing. The POLs (violet line) of 1-PP and 4-Ni-CO2-Fe are higher than those of 2-PP^MeP and 3-PNP, but their differences are relatively small compared to FRZ and CT. The large differences in the total SCF (blue line) mainly come from CT (green line) so both energies show a similar trend in Figure 7a. Roughly estimated, it looks like the relative energy differences between models in FRZ and POL counterbalance each other; thus, SCF resembles CT.

Figure 7.

(a) Energy decomposition analysis (EDA). FRZ denotes frozen electron density, POL, polarization, CT, charge transfer, SCF_TOTAL, the sum of CT, POL, and -FRZ. (b) Comparison between CO₂ charges from the natural atomic orbital and CT energy from EDA.

Therefore, the SCF energy is largely affected by the CT energy, which comes from the charge delocalization. Because the CO₂ binding occurs mainly through the backward donation, CT and BE are expected to be aligned. However, by definition, BE includes the deformation energy of each fragment with reference to the fully relaxed structures of each fragment, which is different from SCF_TOTAL in EDA. BE in Figure S15a increases from 2-PP^MeP to 4-Ni-CO2-Fe smoothly. However, the abnormally high BE of 1-PP is ascribed to the lack of coordination bonds to Ni, which increased POL in Figure 7a. The difference between SCF and BE is much more for 4-Ni-CO2-Fe, where the coordination geometry of Fe-PNP changes greatly from Pl to Td. This deformation energy abruptly reduced the BE of 4-Ni-CO2-Fe, which induces the inconsistency between BE and total SCF in this model series.

The natural atomic orbital (NAO) charge in natural bond orbital (NBO)²⁶ package was applied to measure the amount of charges on CO₂, which can directly determine the degrees of CO₂ activation. The charges on CO₂ of NAO and CT of EDA show strong correlation in Figure 7b. The NAO charges on CO₂ are similar from 1-PP to 2-PP^MeP but largely increase via 3-PNP to 4-Ni-CO2-Fe. This trend is similar to CT, which is represented by the green line in Figure 7b.

To quantitatively investigate the change of charges in the model series, NAO charges are analyzed as presented in Table 2, and all the atomic charges are in Table S3. The charge of M is the partial charge of M in each model. Δ_eM and Δ_e(M,A’s) stand for the charge difference of M alone and the sum of M and its anchor atoms, respectively, between the cases before and after CO₂-coordination. Some reference charges before CO₂ coordination are presented in Figure 8a,c,e and Table S3. The amount of the negative charge of CO₂ is around −0.80e in 1-PP and 2-PP^MeP but increased to −1.04e in 3-PNP and −1.21e in 4-Ni-CO2-Fe. Note that as shown in Figure S16, the charge of CO₂ cannot be correlated with that of the central metal alone, but when it is summed with the charges of the anchor atoms, some correlation appears. Therefore, from 1-PP to 2-PP^MeP, CO₂ gets a little less charged, although Ni⁰ becomes more positive. This is ascribed to the additional anchor atom, P, which is more electronegative (EN = 2.19) than Ni (EN = 1.91). The additional electronegative anchor atom would make the central atom less active for CO₂ activation. As for the PNP ligand, N has formal charge of −1 with two lone pair electrons that can donate charges to the next metal Ni(0) and Fe(II). As shown in Figure 8c, Ni in 3-PNP is less positive compared to 2-PP^MeP in Figure 8a. Then, after CO₂ is coordinated, more electron charges on Ni can move to CO₂ by the amount of about 0.31e (3-PNP), compared to 0.21e in 2-PP^MeP, which results in CO₂ activation of about −1.04e. As for the CO₂-bridged diatomic complex of 4-Ni-CO2-Fe, the charge of CO₂ is increased to about −1.21e. First, from the Ni-PNP side, there is a positive charge increase, which means some electron charges are donated to CO₂. Before adding Fe-PNP, the remaining part of 4-Ni-CO2-Fe is exactly the same as 3-PNP. Therefore, by coordinating Fe-PNP to 3-PNP as κ²O,O′ mode, Δ_e(Ni⁰,A’s) in 4-Ni-CO2-Fe is raised by 0.15e compared to that of 3-PNP, as shown in Table 2. It is very interesting that Fe²⁺, a strong Lewis acid can draw electron density from Ni-PNP across the CO₂ bridge, which means Fe²⁺ strengthens the electron donation of Ni-PNP to CO₂. On the other side, Δ_eFe²⁺ of 4-Ni-CO2-Fe shows an increased charge of about 0.15e, as shown in Table 2, compared to the charge of Fe-PNP shown in Table S3. Considering that the sum of the charges of the anchor atoms is almost not changed, it can be interpreted like this. Fe²⁺ in Fe-PNP has relatively lower partial charge due to the PNP ligand, compared to Fe²⁺ with neutral ligands. Therefore, some extra electron charges of Fe²⁺ in Fe-PNP can be donated to CO₂ through the backward donation as was examined in MO analysis previously. Therefore, though Fe²⁺ is Lewis acidic, when it is combined with an electron-rich ligand such as PNP(−1), the backward donation from Fe²⁺ to CO₂ can occur. Accordingly, Fe-PNP coordinated to CO₂ with κ²O,O′ mode can activate CO₂ through two methods: (1) by inductively attracting the electrons from the Ni-PNP side and (2) by directly donating the electron charges from itself.

Table 2. Partial Charges from Natural Atomic Orbital Analysis^a.

		Ni0			Fe2+
models	CO2	Ni0	ΔeNi0	Δe(Ni0,A’s)	Fe2+	ΔeFe2+	Δe(Fe2+,A’s)
1-PP	–0.812	0.804	0.334	0.588	N/A
2-PPMeP	–0.793	0.862	0.215	0.556	N/A
3-PNP	–1.044	0.792	0.318	0.729	N/A
4-Ni-CO2-Fe	–1.214	0.908	0.434	0.884	1.424	0.147	0.143

^aΔ_eM and Δ_e(M,A’s) stand for the difference of atomic charges after CO₂ coordination for M and the sum of M and the anchor atoms (A’s) of the ligand, respectively. The reference charges are 0.474 for Ni⁰ and 1.277 for Fe²⁺ in M complex without CO₂.

Figure 8.

Atomic charges from natural atomic orbitals for (a) 2-PP^MeP-A, (b) 2-PP^MeP, (c) 3-PNP-A, (d) 3-PNP, (e) Fe-PNP, and (f) 4-Ni-CO2-Fe. Colors scheme: Ni, green; C, gray; P, orange; N, blue; Fe, brown.

III. Conclusions

We investigated the nature of CO₂ binding on four Ni(0) complexes: 1-PP (η²-CO₂), 2-PP^MeP (η²-CO₂), 3-PNP (η¹-CO₂), and 4-Ni-CO₂-Fe (μ-CO₂-κC:κ²O,O′). The DFT calculations in the regime of B3LYP/6-31G(d) + D accurately reproduced the coordination geometries of the central metals, where PP^MeP ligand induces the tetrahedral structure (Td) of Ni and PNP ligand induces planar structure (Pl). Although the ligand field theory predicts that Ni⁰ prefers Td, the geometry of the chelating ligand enforces the coordination geometry of metal, where PP^MeP leads to Td and PNP leads to Pl. As for CO₂ binding mode, normally CO₂ is strongly bound to the central metal in η²-mode, but planar structure of Ni⁰-PNP complex prefers η¹-C mode.

Based on the analysis of molecular orbitals, the backward donation to LUMO of the bent CO₂ is mainly responsible for the CO₂ binding, which is also responsible for the degree of CO₂ activation. However, the binding energy (BE), although it comes from backward donation, cannot precisely explain the degree of CO₂ activation because the coordination number and the deformation of ligand do affect BE. Otherwise, the charges of CO₂ show strong correlation with the charge transfer (CT) energy from the energy decomposition analysis (EDA). Compared to 1-PP and 2-PP^MeP, 3-PNP shows a largely increased CO₂ charge of about 0.2e due to the negatively charged [PNP]⁻ ligand. Ni⁰ with the coordination to PNP is already in an electron-rich state, so it can activate any adsorbate such as CO₂. In the diatomic complex of 4-Ni-CO₂-Fe, an additional charge transfer of about 0.2e occurs. Interestingly, after the coordination of Fe-PNP to 3-PNP with κ²O,O′ mode, Fe(II) pulls the electron density from Ni-PNP across the CO₂ bridge, which enhances the backward donation from Ni-PNP to CO₂. Furthermore, Fe(II) also donates some charge from itself to CO₂ through the backward donation mechanism. So, the resultant increased charge on CO₂ comes partly from the inductive effect of Fe(II) and partly from the backward donation ascribed to PNP in Fe-PNP complex. Therefore, this finding gives insight to designing a new catalyst and explains why we should aim at the diatomic catalyst for CO₂ reduction.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c06257.

• The details of the geometry of models, MO levels of Ni(0) atom, ligands, and models, multiplicity of Ni⁰ and Fe²⁺ and their complexes, BE and SCF of EDA, and NBO analysis (PDF)

The authors declare no competing financial interest.