Abstract
We recently coined the term clusteromics as a holistic approach for obtaining insight into the chemical complexity of atmospheric molecular cluster formation and at the same time providing the foundation for thermochemical databases that can be utilized for developing machine learning models. Here, we present the first paper in the series that applies state-of-the-art computational methods to study multicomponent (SA)0–2(base)0–2 clusters, with SA = sulfuric acid and base = [ammonia (A), methylamine (MA), dimethylamine (DMA), trimethylamine (TMA), and ethylenediamine (EDA)] with all combinations of the five bases. The initial cluster configurations are obtained using the ABCluster program and the number of relevant configurations are reduced based on PM7 and ωB97X-D/6-31++G(d,p) calculations. Thermochemical parameters are calculated based on the ωB97X-D/6-31++G(d,p) cluster structures and vibrational frequencies using the quasi-harmonic approximation. The single-point energies are refined with a high-level DLPNO-CCSD(T0)/aug-cc-pVTZ calculation. Using the calculated thermochemical data, we perform kinetics simulations to evaluate the potential of these small (SA)0–2(base)0–2 clusters to grow into larger cluster sizes. In all cases we find that having more than one type of base molecule present in the cluster will increase the potential for forming larger clusters primarily due to the increased available vapor concentration.
1. Introduction
The existence of nano- to microscale aerosol particles in the atmosphere has pronounced effects on our global climate. Aerosol particles affect the global radiation balance by scattering sunlight away from the surface of the Earth.1 Aerosol particles of size above roughly 50 nm can act as seeds for cloud formation and have an effect on cloud precipitation patterns2 and consequently their residence time. Aerosol–cloud interactions remain the single largest uncertainty in our current and future climate prediction.3
Up to half the number of cloud condensation nuclei (CCN) particles4 originate from new particle formation via a gas-to-particle transition. New particle formation can be initialized via the formation of strongly noncovalently bonded acid–base molecular clusters.5 In continental regions, sulfuric acid (SA) is considered the prime driver for cluster formation.6 However, SA combined with water is not capable of forming strongly bound clusters under realistic conditions in the lower atmosphere, and hence additional stabilizing vapor molecules are essential to lead to new particle formation. Especially, highly abundant bases in the atmosphere, such as ammonia,7,8 or bases with high basicity, such as alkyl-monoamines [methylamine (MA), dimethylamine (DMA), and trimethylamine (TMA)]9−159−15 and alkyl-diamines ethylenediamine (EDA),16−18 are believed to be important stabilizers of sulfuric acid-driven new particle formation. The computational work by Kurtén et al.9 and experimental work by Almeida et al.19 have demonstrated that even trace amounts (a few ppt) of DMA can enhance the new particle formation rates by several orders of magnitude compared to ammonia. This has led to the general belief that the gas-phase basicity of the base is one of the defining factors in forming the initial stable clusters with sulfuric acid.18,20−22 Several experimental studies have demonstrated that atmospheric bases show a synergistic effect on SA-driven new particle formation.15,23 A molecular-level understanding of the role of the synergistic effect between ammonia and stronger bases such as DMA in stabilizing SA clusters has been obtained using quantum chemical calculations by Temelso et al.,22 Myllys et al.,24 and Li et al.25
Measuring the initial steps in cluster formation is difficult using an experimental setup. Mass spectrometry techniques26 can measure the charged cluster compositions, but it remains dubious whether the measured cluster was the one originally formed and fragmentation is believed to take place inside the instrument.27,28 In this regard, quantum chemical calculations and kinetics modeling remain the only possible approach to obtain direct molecular-level information about the structures, thermochemistry, and formation pathways of electrically neutral clusters of atmospheric relevance. However, quantum chemical calculations are computationally expensive, and screening potentially important cluster systems up to, for instance, four acids and four bases (i.e., a 4 × 4 grid) is virtually impossible for all relevant combinations of acids and bases. Using quantum chemical methods and kinetics modeling, it has been shown that sulfuric acid–base clusters have the lowest free energy barrier along the diagonal on the acid–base grid. This implies that sulfuric acid–base clusters are most stable when there is an approximately 1:1 ratio of the acids-to-bases.20,29 This finding has been confirmed by experiments conducted in the CLOUD chamber8,30 and by electrospray ionization experiments (in both positive and negative mode) of ammonium sulfate solutions.31 Quantum chemical calculations have elucidated that the limiting steps in acid–base particle formation depend strongly on the formation of the smallest (acid)1–2(base)1–2 clusters as these provide a basis for further cluster growth.20,29 This implies that if a given cluster system does not form strongly bound electrically neutral or ionic (acid)1–2(base)1–2 clusters, they will most likely not be capable of growing into larger sizes. Thus, instead of screening the time-consuming systems up to 4 × 4 acid–base grid sizes, screening the smaller 2 × 2 systems will yield direct information about those systems that might be relevant in an atmospheric context. Such a holistic clusteromics32 approach will advance the field by giving direct insight into the chemical complexity puzzle of cluster formation, concurrently providing the foundation for the much-needed thermochemical databases that can be utilized for developing machine learning models.
This work is the first in a series of clusteromic papers that sets out to map the thermodynamics and kinetics of the initial steps in cluster formation involving potentially important cluster precursor vapors. The comprehensive mapping of the chemical space will be performed using well-established configurational sampling procedures and state-of-the-art quantum chemical methods. Here we report on the thermodynamics and cluster growth kinetics of (SA)0–2(base)0–2 clusters, with SA = sulfuric acid and base = [ammonia (A), methylamine (MA), dimethylamine (DMA), trimethylamine (TMA), and ethylenediamine (EDA)]. We study all combinations of the bases up to 2 × 2 clusters on the acid–base grid to elucidate the potential synergistic effects between the components and to evaluate which clusters can grow into larger sizes. This series of papers will provide guidance regarding which cluster systems are relevant for extending to larger sizes and will provide a systematic approach for obtaining the much-needed thermochemical data.
2. Theory
2.1. Computational Details
All density functional theory (DFT) geometry optimizations and vibrational frequency calculations were performed using the Gaussian 16 program.33 In the following, we will only briefly outline the computational tools used. For a detailed description of the applied computational methods employed in cluster formation studies, we refer to the recent comprehensive review by Elm et al.34 We used the ωB97X-D35 density functional with a 6-31++G(d,p) basis set. We applied the Gaussian 09 default convergence criteria (fine grid and a 2-electron integral accuracy of 10–10) to allow direct comparison with the existing data in the Atmospheric Cluster DataBase (ACDB).60 The functional was chosen based on its performance in yielding accurate binding energies in comparison to benchmark coupled cluster calculations.36−38 To correct for the low-lying vibrational frequencies, we applied the quasi-harmonic approximation as described by Stefan Grimme.39 In the quasi-harmonic approximation, vibrational frequencies below a certain cutoff (here 100 cm–1) are treated as due to rotation rather than vibrations when calculating the entropy. The quasi-harmonic calculations were carried out using Goodvibes.40 Domain-based local pair natural orbital DLPNO-CCSD(T0)41,42 single-point energies were calculated using TightSCF with the ORCA 4.2.1 program.43,44 We used an aug-cc-pVTZ basis set with the corresponding correlation (/C) and Coulomb/exchange (/JK) auxillary basis sets. We applied a NormalPNO criterion and the semicanonical (T0) approximation for the triples as Schmitz et al.38 recently demonstrated that there is no clear overall performance improvement by using a TightPNO criterion45 or the improved (T1) correction46 for strongly bonded clusters of atmospheric relevance when using an aug-cc-pVTZ basis set.
2.2. Cluster Configurational Sampling
The cluster structures were sampled based on several previously well-established protocols using the following workflow
For the ABCluster calculations, the settings recommended by Kubečka et al.47 were used with SN = 3000, gmax = 200, and glimit = 4, and the estimated maximum coordinate value L was scaled by system size. It should be mentioned that the approach employed by Temelso/Odbadrakh et al.22,48 using the genetic algorithm implemented in the OGOLEM program should provide a similar functionality as the ABCluster program. As proton transfer is not possible using a CHARMM forcefield, the clusters were sampled using both neutral as well as anionic and cationic monomers to mimic different protonation states. In this process, we only allowed a single proton transfer from each of the sulfuric acid molecules in the clusters. For instance, for the (SA)2(base)2 clusters we included three different protonation states: neutral, partially ionic monomers (1 proton transfer), and fully ionic monomers (2 proton transfers). In the cases where two different bases could receive a proton, the base with the highest basicity had preference. A total of 1000 local minima were saved for each cluster protonation state. When unavailable, the CHARMM force field parameters were taken from similar compounds and the Hirshfeld charges were calculated at the MP2/6-31++g(d,p) level of theory. After identifying the minima with ABCluster, each configuration was re-optimized using PM7.49 This led to ∼700–800 converged structures for each cluster protonation state. The PM7 configurations were then sorted based on root mean square deviations (RMSD) between atomic positions to identify redundant configurations. For sorting the structures, the ArbAlign method by Temelso et al.50 was applied, which employs the Kuhn–Munkers algorithm to permute the atom indices. A cutoff of 0.38 Å in the RMSD was used to identify redundant conformers based on previous experience with sulfuric acid–water clusters51 and carboxylic acid–water clusters.52 The strength of using the RMSD method lies in that redundant conformers are identified exclusively based on how similar their structures are and no arbitrary (free) energy cutoffs need to be introduced. Unfortunately, it becomes time-consuming for large systems with many configurations.
After sorting the cluster structures based on the RMSD, around 100–300 unique structures were obtained for each protonation state of the systems. The geometry of each cluster system was then optimized and vibrational frequencies were calculated at the ωB97X-D/6-31++G(d,p) level of theory. Clusters that failed to converge due to a too disadvantageous starting geometry from the PM7 calculations were restarted once. The lowest free energy cluster for each system was visually inspected and up to five manually adjusted structures were constructed based on chemical intuition. Only in a few cases did the manual inspection lead to a configuration lower in free energy and this usually corresponded to simple rotations around vacant S–OH bonds. In all cases, the manual adjustment led to a gain of less than 1 kcal mol–1. For the five cluster structures lowest in free energy, DLPNO-CCSD(T0)/aug-cc-pVTZ calculations were carried out on top of the DFT geometries.
2.3. Cluster Binding Free Energies
The standard-state binding free energies of the clusters are calculated as the free energy of the cluster relative to its binding monomers
| 1 |
Besel et al.53 recently demonstrated that it is quite important to correctly assign the rotational symmetry number (σ) of the monomers. Here we optimized the geometry of the monomers to the appropriate point groups: SA (C2, σ = 2), A (C3v, σ = 3), MA (Cs, σ = 1), DMA (Cs, σ = 1), TMA (C3v, σ = 3), and EDA (C1, σ = 1). The binding free energy can be divided into a purely electronic energy contribution (ΔEbind) and a thermal contribution to the free energy (ΔGbind,thermal)
| 2 |
Here both the zero-point vibrational energy and entropy contribution are contained in the ΔGbind,thermal term. The final binding free energy is then calculated as follows
| 3 |
Here ΔGbind,thermal,qhDFT is the thermal contribution to the free energy, calculated based on the quasi-harmonic approximation with a cutoff value of 100 cm–1. The sampling of the clusters was conducted at 298.15 K and the ΔG values at other temperatures were calculated assuming that the enthalpy and entropy change (ΔH and ΔS) remain constant under the studied temperature range.
2.4. Synergistic Effects
We define a synergistic effect between two cluster components as thermodynamics that leads to a highly non-additive behavior. To explicitly quantify the synergistic effects, we define the synergy factor Γj,k between component j and k as
| 4 |
This corresponds to the difference in free energy (in kcal mol–1) between a cluster that consists of components j, k and the average of the corresponding clusters that consist of j, j and k, k. This clearly illustrates potential synergistic effects between the components, by how much Γj,k deviates from zero, and the magnitude in kcal mol–1. From the definition in eq 4, a negative number indicates a synergistic effect, i.e., a lowering of the binding free energy, while a positive number indicates a dyssynergistic effect, i.e., an increase in the binding free energy. This formulation makes it transparent whether or not positive/negative synergistic effects are present and can unambiguously be applied to both acid/base components. Furthermore, the formulation can easily be extended to additional components if desired.
2.5. Cluster Formation Potential—Jpotential
Screening many potentially relevant cluster systems up to 4 × 4 grid sizes is very time consuming. If the clusters turn out to be weakly bound and not capable of forming particles, this leads to a massive waste of computational resources. It has been shown that the smallest (acid)1–2(base)1–2 clusters comprise the limiting steps for new particle formation in the atmosphere.20,29 Larger clusters consisting of 3–4 acids and 3–4 bases are often quite stable against evaporation. Thus, the potential for smaller (acid)1–2(base)1–2 clusters to grow into larger sizes can be estimated by simulating the flux toward the larger clusters. We will denote this value as the cluster formation potential, Jpotential, which corresponds to the flux toward relevant larger clusters at realistic atmospheric conditions and vapor concentrations. Previous studies have shown20,29 that acid–base clusters are predominantly most stable along the diagonal on the acid–base cluster grid. This implies that the (acid)n(base)n, (acid)n+1(base)n, and (acid)n(base)n+1 clusters are possible candidates to grow into larger sizes. For the (acid)0–2(base)0–2 cluster systems studied here, this means that the (acid)2(base)3, (acid)3(base)2, and (acid)3(base)3 clusters are allowed to grow out of the simulations and contribute to the potential cluster formation rate, Jpotential (see Figure 1 for illustration). However, the (acid)2(base)3 cluster is often significantly less stable than the (acid)3(base)2 and (acid)3(base)3 clusters,20 so it needs to be tested for the individual systems whether it should be allowed to grow to larger sizes or not.
Figure 1.
Clusters on the acid−base grid that are allowed to contribute to the potential cluster formation rate, Jpotential.
The (acid)0–1(base)3 and (acid)3(base)0–1 clusters are not allowed to contribute to the potential cluster formation rate as these are usually too unstable and have high evaporation rates. Diamines might stabilize more than one sulfuric acid molecule, so for ethylenediamine (EDA) it was tested to allow the (acid)3(base)1 clusters to grow out. It should be noted that the flux toward larger clusters is purely a “potential” to form larger clusters and should not be used as a measure for the actual cluster formation rate as including larger clusters will inevitably change the J-value. A recent study by Besel et al.53 demonstrated that the simulated cluster formation rate increased as the simulation system was decreased. Furthermore, this effect was found to be larger for the more weakly bound systems. Hence, the cluster formation potential is simply meant as a measure for assessing the potential importance of different compounds in cluster formation as this is very difficult to assess based solely on the calculated thermochemistry.
All the cluster distribution dynamics simulations have been performed using the Atmospheric Cluster Dynamics Code (ACDC).54 The code was supplied at the courtesy of Tinja Olenius from the ACDC repository.29,55,56 A constant coagulation sink of −1.6 × 10–3 s–1 was applied to account for scavenging by larger particles and all simulations have been performed at 278.15 K. These conditions correspond to a typical sink value and temperature during springtime in the boreal forest environment.57,58
3. Results and Discussion
3.1. Cluster Structures
We studied (SA)0–2(base)0–2 clusters, with SA = sulfuric acid and base = [ammonia (A), methylamine (MA), dimethylamine (DMA), trimethylamine (TMA), and ethylenediamine (EDA)]. The (SA)1(base)1 clusters were taken from ref (38). We studied all combinations of bases, which implies a total of 51 different cluster systems have been evaluated (including the 15 pure (base)2 clusters). Some of the cluster compositions have previously been reported in the literature. For instance, Kupiainen et al.59 studied the (SA)1–2(A)1(DMA)1 clusters and Temelso et al.22 studied the (SA)1–2(A)1(MA/DMA/TMA)1 clusters. For the sake of consistency, and to allow access to numerous new local minima as well, all of the cluster systems were re-calculated in this work. Applying the protocol outlined in Section 2.2 for screening the cluster structures led to the identification of a total of 2824 unique cluster structures. All the cluster structures and corresponding thermochemistry have been added to the Atmospheric Cluster DataBase (ACDB).60Figure 2 presents the identified, lowest-free-energy, cluster structures consisting of two sulfuric acid clusters and two different bases. The calculations are performed at the DLPNO-CCSD(T0)/aug-cc-pVTZ//ωB97X-D/6-31++G(d,p) level of theory with the quasi-harmonic approximation, at 298.15 K and 1 atm.
Figure 2.

Lowest free-energy cluster structures (298.15 K, 1 atm) calculated at the DLPNO-CCSD(T0)/aug-cc-pVTZ//ωB97X-D/6-31++G(d,p) level of theory with the quasi-harmonic approximation.
It is seen that the cluster structures do not simply adopt similar structures with just the bases exchanged, but show very distinct hydrogen-bonded interaction patterns, depending on the base combination. For instance, having weaker bases present in the cluster appears to lead to more “dangling” vacant S–OH bonds compared to the stronger bases. The identified (SA)1–2(A)1(MA/DMA/TMA)1 cluster structures are in all cases very similar to the ones identified by Temelso et al.22
3.2. Thermochemistry
Table 1 presents the calculated binding free energies at 298.15 K and 1 atm. The calculations are performed at the DLPNO-CCSD(T0)/aug-cc-pVTZ//ωB97X-D/6-31++G(d,p) level of theory using the quasi-harmonic approximation with 100 cm–1 cutoff. The clusters have been divided into different classifications depending on the combination of bases they consist of (w = weak, m = medium, and s = strong). This classification is based on the gas-phase basicity of the compounds (in kJ mol–1): A(w) = 819, MA(m) = 865, DMA(s) = 897, TMA(s) = 918, and EDA(s) = 913.61
Table 1. Calculated Binding Free Energies (at 298.15 K, 1 atm) of the Studied Clusters at the DLPNO-CCSD(T0)/aug-cc-pVTZ//ωB97X-D/6-31++G(d,p) Level of Theory Using the Quasi-Harmonic Approximationa.
| classification | (acid)0 | (SA)1 | (SA)2 | |
|---|---|---|---|---|
| (base)0 | –5.5 | |||
| (A)1 | w | –5.6 | –19.4 | |
| (MA)1 | m | –7.2 | –24.4 | |
| (DMA)1 | s | –11.5 | –29.4 | |
| (TMA)1 | s | –12.6 | –27.9 | |
| (EDA)1 | s | –10.4 | –28.1 | |
| (A)2 | w,w | 3.7 | –9.7 | –27.0 |
| (MA)2 | m,m | 6.1 | –10.7 | –36.6 |
| (DMA)2 | s,s | 5.7 | –14.9 | –44.0 |
| (TMA)2 | s,s | 6.7 | –15.3 | –41.5 |
| (EDA)2 | s,s | 5.5 | –16.3 | –41.8 |
| (A)1(MA)1 | w,m | 5.4 | –10.0 | –32.4 |
| (A)1(DMA)1 | w,s | 5.1 | –13.4 | –34.7 |
| (A)1(TMA)1 | w,s | 4.1 | –13.6 | –32.3 |
| (A)1(EDA)1 | w,s | 5.1 | –12.8 | –33.7 |
| (MA)1(DMA)1 | m,s | 5.5 | –14.2 | –40.6 |
| (MA)1(TMA)1 | m,s | 5.1 | –13.4 | –38.1 |
| (MA)1(EDA)1 | m,s | 5.7 | –13.4 | –39.1 |
| (DMA)1(TMA)1 | s,s | 5.4 | –14.8 | –42.3 |
| (DMA)1(EDA)1 | s,s | 5.7 | –17.4 | –43.4 |
| (TMA)1(EDA)1 | s,s | 5.7 | –15.1 | –42.7 |
The classifications refer to the base strength of the constituents: weak (w), medium (m), and strong (s).
Three different kinds of dimer clusters are included in the cluster test set: the (base)2, (SA)2, and (SA)1(base)1 clusters. In all cases, the pure base clusters have a positive formation free energy. For the (A)2 cluster the ΔG-value is calculated to be +3.7 kcal mol–1 and for the remaining bases (and combinations thereof) the ΔG-value lies in the range of +4.1 to +6.7 kcal mol–1. While experimental cluster reaction free energies are very scarce for atmospheric species, there exist a few studies on the (base)2 cluster systems. Du et al.62,63 studied the (DMA)1(TMA)1 and (DMA)2 clusters and identified a free energy value of 3.6 and 3.7 kcal mol–1, respectively. These values are based on a combination of gas-phase Fourier transform infrared (FTIR) spectroscopy and local-mode perturbation theory at the CCSD(T)-F12a/VDZ-F12 level. We used the updated values provided by Hansen et al.64 We identify slightly higher free energies of 5.4 and 5.7 kcal mol–1, respectively, for the two complexes. This implies that our calculated ΔG-values might be slightly too high across the board, leading to slightly unstable clusters. As the DLPNO-CCSD(T0)/aug-cc-pVTZ energies should not yield errors much larger than 1 kcal mol–1, this discrepancy might originate from the fact that the structures and vibrational frequencies are still limited to the DFT level with a small basis set. Nevertheless, our calculations can correctly confirm that the (DMA)1(TMA)1 cluster is slightly more stable than the corresponding (DMA)2 cluster, so the relative free energies are sufficiently accurate and can still yield direct insight into the studied systems.
The thermochemistry of the (SA)1(base)1 clusters is in all cases more favorable than that of the sulfuric acid dimer (ΔG-value of −5.5) and adopts the following pattern in stability (values in kcal mol–1) (SA)1(A)1(–5.6) < (SA)1(MA)1(–7.2) < (SA)1(EDA)1(–10.4) < (SA)1(DMA)1(–11.5) < (SA)1(TMA)1(–12.6). The strength of the intermolecular interactions is clearly governed by the basicity of the clustering base (w, m, or s) in these small (SA)1(base)1 clusters. Hence, the stronger the acid and base, the stronger the intermolecular interaction, and the more stable the cluster will be. While this is true for the smallest clusters, Temelso et al.22 recently suggested that this pattern cannot necessarily be directly translated to larger clusters as other effects such as hydrogen bond capacity and sterical hindrance also play a role.
The trimer clusters consisting of two acids and one base are in all cases significantly lower in free energy than the (SA)1(base)2 clusters. The (SA)2(base)1 clusters show the following pattern in stability (values in kcal mol–1) (SA)2(A)1(–19.4) < (SA)2(MA)1(–24.4) < (SA)2(TMA)1(–27.9) < (SA)2(EDA)1(–28.l) < (SA)2(DMA)1(–29.4). This pattern in stability is consistent with the experimental study by Jen et al.13 where the stabilization of the sulfuric acid dimer was observed to follow a A < MA < TMA ≲ DMA trend.
In general, the thermochemistry of the clusters quite well follows the classification of the clustering bases. For instance, the thermochemistry of having a weak and a strong base present (w,s) in the (SA)1(base)2 clusters yields ΔG values in the range of −12.8 to −13.4 kcal mol–1. Hence, the different bases do not, to a large extent, present any synergistic effects in these small clusters. This can easily be identified by calculating the cluster synergy factors. Table 2 presents the calculated synergy factors at the DLPNO-CCSD(T0)/aug-cc-pVTZ//ωB97X-D/6-31++G(d,p) level of theory using the quasi-harmonic approximation, at 298.15 K and 1 atm.
Table 2. Calculated Synergy Factors (at 298.15 K, 1 atm) of the Mixed Base Clusters at the DLPNO-CCSD(T0)/aug-cc-pVTZ//ωB97X-D/6-31++G(d,p) Level of Theory Using the Quasi-Harmonic Approximation.
| (SA)1 | (SA)2 | |
|---|---|---|
| ΓA,MA | 0.2 | –0.6 |
| ΓA,DMA | –1.1 | 0.8 |
| ΓA,TMA | –1.1 | 2.0 |
| ΓA,EDA | 0.2 | 0.7 |
| ΓMA,DMA | –1.4 | –0.4 |
| ΓMA,TMA | –0.4 | 0.9 |
| ΓMA,EDA | 0.1 | 0.1 |
| ΓDMA,TMA | 0.3 | 0.5 |
| ΓDMA,EDA | –1.8 | –0.6 |
| ΓTMA,EDA | 0.7 | –1.1 |
It is seen that the synergy factors take values in the range of −1.8 to 2.0 kcal mol–1, with most values being within ±1 kcal mol–1. The only cluster that presents a significant synergy factor is the (SA)1(DMA)1(EDA)1 cluster, which has a free energy value that is lower than that of both the (SA)1(DMA)2 or (SA)1(EDA)2 clusters, with a synergy factor of ΓDMA,EDA = −1.8 kcal mol–1. It should be noted that changing the cluster thermochemistry by up to −1.8 kcal mol–1 for important clusters in the clustering path, such as the initial (SA)1(base)1 cluster, might potentially enhance the cluster formation potential quite drastically. However, the (SA)1(base)2 clusters are most likely not very important in the cluster formation process, as these are not particularly stable. Similarly, changing the thermochemistry of the (SA)2(base)2 cluster by −2 kcal mol–1 has been shown to only yield around a factor of two increase in the cluster formation rate for the SA–MA system.20 This implies that it might be possible to simply classify the thermochemistry of the smallest (SA)1–2(base)1–2 clusters based on the base strength of the clustering bases. Hence, for unknown sulfuric acid–base cluster systems, a first approximation could be to simply use the thermochemistry presented in Table 1 depending on the base strength (w, m or s) of the clustering bases. It is worth noting that while synergistic effects between bases might not be very important for small (SA)1–2(base)1–2 clusters, it might have a pronounced effect on larger clusters, as shown in the studies by Myllys et al.24 and Temelso et al.22
3.3. Simulated Cluster Formation Potentials
The thermochemistry is not the only decisive factor when assessing whether the clusters will form or not. The actual vapor concentrations of the consisting components are also important. We study the following atmospheric relevant concentration ranges of the compounds: sulfuric acid (1 × 106 molecules cm–3), ammonia (10 ppt to 10 ppb), methylamine (1–100 ppt), dimethylamine (1–10 ppt), trimethylamine (1–10 ppt), and ethylenediamine (1–10 ppt). While atmospheric measurements of diamine concentrations are scarce, Jen et al.16 measured various diamines at three different sites (Lamont, Lewes, and Atlanta). EDA was found on average in mixing ratios of 1 ppt, with diamine peak mixing ratios as high as tens of ppt for putrescine + cadaverine. Hence, 1–10 ppt should be a reasonable concentration range for diamines. Allowing the (SA)2(base)2 clusters to grow to larger sizes by collisions with bases would lead to the formation of the (SA)2(base)3 clusters. As identified in the previous section, the clusters consisting of more bases than acids are in all cases significantly less stable. Hence, in the following, only the (SA)3(base)2 and (SA)3(base)3 clusters are allowed to grow to larger sizes. The results for allowing the (SA)2(base)3 clusters to contribute to the cluster formation potential are presented in the Supporting Information.
Table 3 presents the cluster formation potential of the SA–base clusters under the condition that only one type of base is present in the clusters. The sulfuric acid concentration was fixed at 1 × 106 molecules cm–3 and the simulations were performed at 278.15 K. The upper and lower limit concentrations of the studied bases are tabulated.
Table 3. Simulated Cluster Formation Potential (Jpotential) for Sulfuric Acid Clusters Containing a Single Type of Basea.
| sulfuric acid–base cluster | lower limit | upper limit | |
|---|---|---|---|
| ammonia | 10 ppt | ··· | 10 ppb |
| (A) | |||
| 1.26 × 10–10 cm–3 s–1 | ··· | 1.26 × 10–4 cm–3 s–1 | |
| methylamine | 1 ppt | ··· | 100 ppt |
| (MA) | |||
| 5.49 × 10–6 cm–3 s–1 | ··· | 0.0211 cm–3 s–1 | |
| dimethylamine | 1 ppt | ··· | 10 ppt |
| (DMA) | |||
| 0.503 cm–3 s–1 | ··· | 6.69 cm–3 s–1 | |
| trimethylamine | 1 ppt | ··· | 10 ppt |
| (TMA) | |||
| 0.539 cm–3 s–1 | ··· | 21.9 cm–3 s–1 | |
| ethylenediamine | 1 ppt | ··· | 10 ppt |
| (EDA) | |||
| 0.0428 cm–3 s–1 | ··· | 1.07 cm–3 s–1 |
The sulfuric acid concentration was fixed at [H2SO4] = 1 × 106 molecules cm–3. Simulations were performed at 278.15 K.
At low mixing ratios of either ammonia or methylamine, the SA–A and SA–MA clusters literally do not form, but a small amount is formed when reaching the considered upper limit. Clusters consisting of MA show a weak cluster formation potential despite MA being considered in concentrations up to ten times that of DMA, TMA, and EDA. It is worth mentioning that herein we only study electrically neutral systems, and that weakly bound systems have been shown to be significantly enhanced by including ionic pathways.29,53,65 It is clear that the SA–TMA clusters show the largest cluster formation potential compared to the other bases in the considered upper limit of 10 ppt. At the lower limit, DMA and TMA exhibit similar cluster formation potentials. The cluster formation potential of the diamine EDA is seen to be lower than that of TMA and DMA, in agreement with previous studies.16−18 It is evident that the Jpotential value is directly connected to the thermochemistry of the formation of the very initial (SA)1(base)1 cluster. Hence, the thermochemistry of the (SA)1(base)1 cluster could potentially be a direct metric for the potential of a given system to form particles.
For A, MA, and DMA, the clusters leave the system more or less exclusively via the (SA)2(base)2 cluster colliding with a sulfuric acid molecule. However, TMA binds strongly enough for the (SA)1(TMA)1 clusters to be involved in the formation process. This implies that a ΔG value of around −12.5 kcal mol–1 (298.15 K, 1 atm) is the turning point for the dimer cluster to be stable enough to contribute to the cluster growth processes. At 1 ppt of TMA the (SA)2(base)2 + 1 SA collision contributes 86% to the cluster formation potential, with a 10% contribution from the (SA)2(TMA)1 cluster colliding with the (SA)1(TMA)1 cluster. At 10 ppt of TMA, collisions with the (SA)1(TMA)1 cluster lead to 28% of cluster growth.
As diamines might be capable of stabilizing more than one sulfuric acid molecule, it was tested to allow the (SA)3(EDA)1 cluster to grow out of the simulations. For instance, allowing the (SA)3(EDA)1 to grow out of the simulations yielded a cluster formation potential of 0.113 cm–3 s–1 at 1 ppt and 1.23 cm–3 s–1 at 10 ppt. At both mixing ratios, there was found a 75% contribution to the cluster formation potential for collisions of the (SA)2(EDA)1 cluster with sulfuric acid molecules. As this has negligible effect on the high concentration limit and only corresponds to around a factor of 2 in the low concentration limit, in the following we will constrain EDA to follow the same pattern as the other bases and not allow the (SA)3(EDA)1 clusters to contribute to the Jpotential.
Considering more than one type of base molecule in the clusters will lead to a two-dimensional scan over the range of atmospheric relevant concentrations. Figure 3 presents scans of the cluster formation potential for clusters containing ammonia. For each base concentration range 100 points were simulated, leading to a total of 104 ACDC simulations in each subfigure. The sulfuric acid concentration was fixed at 1 × 106 molecules cm–3 and the simulations were performed at 278.15 K.
Figure 3.

Simulated cluster formation potential Jpotential in cm–3 s–1 as a function of the base mixing ratios. The sulfuric acid concentration was fixed at [H2SO4] = 1 × 106 molecules cm–3 and the simulations were performed at 278.15 K. Note the different scales on the plots.
The SA–A–MA clusters are dependent on both the ammonia and methylamine concentration to form clusters. For the SA–A–DMA and SA–A–TMA clusters, the stronger bases are clearly seen to dominate the cluster formation potential with very little contribution from ammonia. In the SA–A–EDA clusters, the curved cluster formation potential seen in the upper right corner indicates that even though EDA is the stronger base, a high abundance of ammonia (such as 10 ppb) will lead to a contribution to the cluster formation potential. Having a weak (w) and a medium (m) base in the cluster will lead to both bases contributing substantially to the cluster formation rate, while a weak (w) and a strong (s) base will clearly be dominated by the cluster formation potential of the strong base for these small clusters. Figure 4 presents scans of the cluster formation potential for the the remaining six combinations of the bases.
Figure 4.
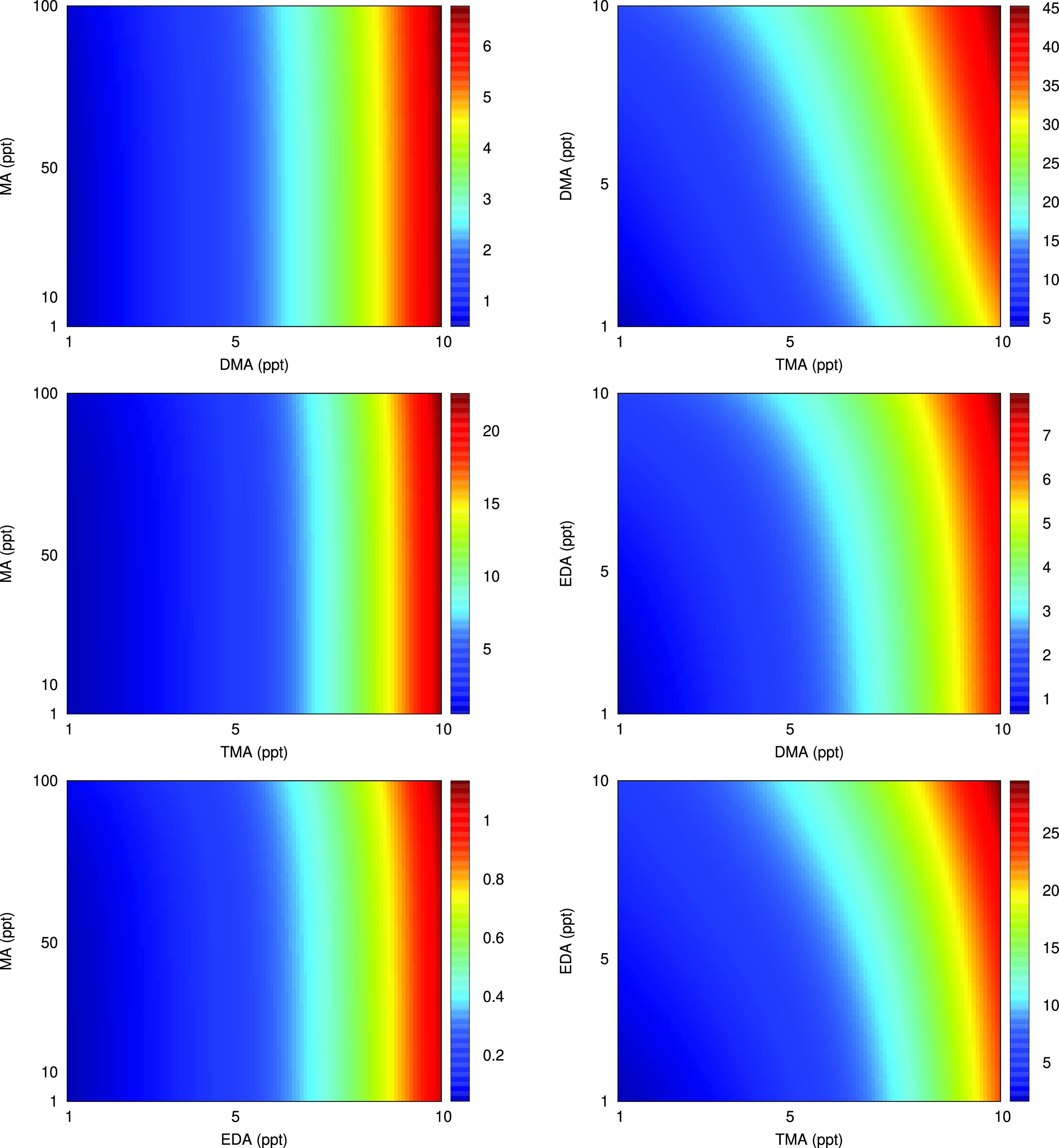
Simulated cluster formation potential Jpotential in cm–3 s–1 as a function of the base (A, MA, DMA, TMA and EDA) mixing ratios. The sulfuric acid concentration was fixed at [H2SO4] = 1 × 106 molecules cm–3 and the simulations were performed at 278.15 K. Note the different color scales on the plots.
For the SA–MA–DMA/TMA/EDA clusters, the inclusion of MA clearly has very little influence on the cluster formation potential. Hence, when there is a medium (m) and one strong (s) base present in the cluster, the cluster formation potential is predominantly governed by the strong base. When having two strong (s) bases present in the cluster, such as in the SA–DMA–TMA, SA–DMA–EDA, and SA–TMA–EDA clusters, the cluster formation potential depends on both bases. These findings clearly suggest that TMA has the highest cluster formation potential for sulfuric acid clusters compared to A, MA, DMA, and EDA, even when considering the significantly higher concentration of A and MA present in the atmosphere.
The cluster formation potential of the three-component systems is not a simple sum of the two corresponding isolated two-component systems. By inspecting the higher limit of the base mixing ratios, corresponding to the upper right corner of the plots in Figures 3 and 4, we can estimate the potential synergistic effect between the bases by comparing the cluster formation potential of the combined system with that of the sum of the isolated systems. Table 4 presents the percentage increase of the combined system compared to the sum of its parts.
Table 4. Percentage Increase in Cluster Formation Potential (Jpotential) for Clusters Consisting of Two Different Basesa.
| cluster | % increase |
|---|---|
| SA–A–MA | 806.0 |
| SA–A–DMA | 3.8 |
| SA–A–TMA | 0.0 |
| SA–A–EDA | 20.8 |
| SA–MA–DMA | 1.2 |
| SA–MA–TMA | 3.0 |
| SA–MA–EDA | 4.1 |
| SA–DMA–TMA | 58.4 |
| SA–DMA–EDA | 2.6 |
| SA–TMA–EDA | 28.7 |
The increase is calculated relative to the sum of the two isolated systems. The base concentrations are taken as the upper limit of the studied ranges (A = 10 ppb, MA = 100 ppt, DMA, TMA, EDA = 10 ppt).
In all cases (except the SA–A–TMA cluster system), there is a synergistic effect of having more than one base present in the clusters. The effect is seen to be largest for the SA–A–MA clusters, which is most likely due to the very low absolute cluster formation potential for this system. In all other cases, the increase in the cluster formation potential is between a few % and up to ∼50%. It should be noted that emissions of different bases might very well be correlated. For instance, Zheng et al.66 showed that ammonia and amine (methylamine, C2-amine, and C3-amine) emissions are to some extent correlated and most likely originate from similar sources, with high concentrations being associated with heavy industry. The increase in cluster formation potential can easily be understood from the increase in the available vapor concentration when more than one base is considered. Hence, this is a synergistic effect based on the available base concentrations and not an intrinsic synergistic effect in the thermochemistry. This might also imply that it is possible to approximate a small 2-base system with a 1-base system by increasing the vapor concentration, under the assumption that the thermochemistries are similar.
Not surprisingly, these findings show that sulfuric acid–base clusters are capable of growing into larger sizes, depending on the base strength of the clustering base. Especially, having several different bases present in the cluster can lead to an enhanced cluster formation potential. Furthermore, there is seen a clear connection between the base strength and the cluster thermochemistry, the synergy factor Γj,k, and the Jpotential for the SA–base clusters. Despite considerable work already been dedicated to SA–base clusters, we can recommend that larger sulfuric acid–base clusters with two or, potentially, more different bases will still be relevant to study in the future.
4. Conclusions
We have screened the cluster formation potential of small multicomponent (SA)0–2(base)0–2 clusters, with the bases ammonia (A), methylamine (MA), dimethylamine (DMA), trimethylamine (TMA), or ethylenediamine (EDA). We find that the thermochemistry and cluster formation potential correlate well with the base strength classification (weak, medium, strong) of the bases. We find that the presence of two bases will increase the potential for forming larger clusters due to the increased available vapor concentration. These findings prompt the further study of multicomponent clusters consisting of SA and multiple bases. We recommend that the Jpotential of a given cluster system should always be checked before extending it to larger sizes, thus eliminating the risk of calculating computationally expensive redundant clusters.
In the following papers in this series we will look into other vapor molecules that might be relevant for stabilizing the initial cluster formation. While SA–base clusters are relevant for inland new particle formation, methanesulfonic acid (MSA) has been speculated to be important over seas. Quantum chemical studies of MSA–base cluster formation has in the recent years attracted immense attention67−78 and the cluster formation potential of MSA–base clusters should be further elucidated.
Acknowledgments
J.E. thanks the Independent Research Fund Denmark grant number 9064-00001B and the Swedish Research Council Formas project number 2018-01745-COBACCA for financial support. The numerical results presented in this work were obtained at the Centre for Scientific Computing, Aarhus http://phys.au.dk/forskning/cscaa/
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c00306.
Simulated cluster formation potential when allowing the (SA)2(base)3 cluster to grow out; importance of assigning the base strength in the ACDC simulations when multiple bases are present in the cluster; energetics of the five lowest free energy clusters for each system (PDF)
Geometries of the five cluster structures lowest in free energy are available in xyz format (ZIP)
The author declares no competing financial interest.
Supplementary Material
References
- Haywood J.; Boucher O. Estimates of the Direct and Indirect Radiative Forcing due to Tropospheric Aerosols: A Review. Rev. Geophys. 2000, 38, 513–543. 10.1029/1999RG000078. [DOI] [Google Scholar]
- Boucher O.; Lohmann U. The Sulfate-CCN-cloud Albedo Effect. Tellus B 1995, 47, 281–300. 10.3402/tellusb.v47i3.16048. [DOI] [Google Scholar]
- IPCC. In Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker T. F.; Stocker T. F.; Qin D.; Plattner G.-K.; Tignor M.; Allen S. K.; Boschung J.; Nauels A.; Xia Y.; Bex V.; Midgley P. M., Eds.; Cambridge University Press: Cambridge, United Kingdom and New York, NY, USA, p 1535.
- Merikanto J.; Spracklen D. V.; Mann G. W.; Pickering S. J.; Carslaw K. S. Impact of nucleation on global CCN. Atmos. Chem. Phys. 2009, 9, 8601–8616. 10.5194/acp-9-8601-2009. [DOI] [Google Scholar]
- Kulmala M.; Kontkanen J.; Junninen H.; Lehtipalo K.; Manninen H. E.; Nieminen T.; Petäjä T.; Sipilä M.; Schobesberger S.; Rantala P.; et al. Direct Observations of Atmospheric Aerosol Nucleation. Science 2013, 339, 943–946. 10.1126/science.1227385. [DOI] [PubMed] [Google Scholar]
- Sipilä M.; Berndt T.; Petäjä T.; Brus D.; Vanhanen J.; Stratmann F.; Patokoski J.; Mauldin R. L.; Hyvärinen A.-P.; Lihavainen H.; Kulmala M. The Role of Sulfuric Acid in Atmospheric Nucleation. Science 2010, 327, 1243–1246. 10.1126/science.1180315. [DOI] [PubMed] [Google Scholar]
- Weber R. J.; Marti J. J.; McMurry P. H.; Eisele F. L.; Tanner D. J.; Jefferson A. Measured Atmospheric New Particle Formation Rates: Implications for Nucleation Mechanisms. Chem. Eng. Commun. 1996, 151, 53–64. 10.1080/00986449608936541. [DOI] [Google Scholar]
- Kirkby J.; Curtius J.; Almeida J.; Dunne E.; Duplissy J.; Ehrhart S.; Franchin A.; Gagne S.; Ickes L.; Kürten A.; Kupc A.; Metzger A.; Riccobono F.; Rondo L.; Schobesberger S.; Tsagkogeorgas G.; Wimmer D.; Amorim A.; Bianchi F.; Breitenlechner M.; David A.; Dommen J.; Downard A.; Ehn M.; Flagan R.; Haider S.; Hansel A.; Hauser D.; Jud W.; Junninen H.; Kreissl F.; Kvashin A.; Laaksonen A.; Lehtipalo K.; Lima J.; Lovejoy E.; Makhmutov V.; Mathot S.; Mikkilä J.; Minginette P.; Mogo S.; Nieminen T.; Onnela A.; Pereira P.; Petäjä T.; Schnitzhofer R.; Seinfeld J.; Sipilää M.; Stozhkov Y.; Stratmann F.; Tomé A.; Vanhanen J.; Viisanen Y.; Vrtala A.; Wagner P.; Walther H.; Weingartner E.; Wex H.; Winkler P.; Carslaw K.; Worsnop D.; Baltensperger U.; Kulmala M. Role of Sulphuric Acid, Ammonia and Galactic Cosmic Rays in Atmospheric Aerosol Nucleation. Nature 2011, 476, 429–433. 10.1038/nature10343. [DOI] [PubMed] [Google Scholar]
- Kurtén T.; Loukonen V.; Vehkamäki H.; Kulmala M. Amines are Likely to Enhance Neutral and Ion-induced Sulfuric Acid-water Nucleation in the Atmosphere More Effectively than Ammonia. Atmos. Chem. Phys. 2008, 8, 4095–4103. 10.5194/acp-8-4095-2008. [DOI] [Google Scholar]
- Loukonen V.; Kurtén T.; Ortega I. K.; Vehkamäki H.; Pádua A. A. H.; Sellegri K.; Kulmala M. Enhancing Effect of Dimethylamine in Sulfuric Acid Nucleation in the Presence of Water—A Computational Study. Atmos. Chem. Phys. 2010, 10, 4961–4974. 10.5194/acp-10-4961-2010. [DOI] [Google Scholar]
- Nadykto A. B.; Yu F.; Jakovleva M. V.; Herb J.; Xu Y. Amines in the Earth’s Atmosphere: A Density Functional Theory Study of the Thermochemistry of Pre-Nucleation Clusters. Entropy 2011, 13, 554–569. 10.3390/e13020554. [DOI] [Google Scholar]
- Nadykto A. B.; Herb J.; Yu F.; Xu Y. Enhancement in the Production of Nucleating Clusters due to Dimethylamine and Large Uncertainties in the Thermochemistry of Amine-Enhanced Nucleation. Chem. Phys. Lett. 2014, 609, 42–49. 10.1016/j.cplett.2014.03.036. [DOI] [Google Scholar]
- Jen C. N.; McMurry P. H.; Hanson D. R. Stabilization of Sulfuric acid Dimers by Ammonia, Methylamine, Dimethylamine, and Trimethylamine. J Geophys. Res. Atmos. 2014, 119, 7502–7514. 10.1002/2014JD021592. [DOI] [Google Scholar]
- Nadykto A. B.; Herb J.; Yu F.; Xu Y.; Nazarenko E. S. Estimating the Lower Limit of the Impact of Amines on Nucleation in the Earth’s Atmosphere. Entropy 2015, 17, 2764–2780. 10.3390/e17052764. [DOI] [Google Scholar]
- Glasoe W. A.; Volz K.; Panta B.; Freshour N.; Bachman R.; Hanson D. R.; McMurry P. H.; Jen C. Sulfuric Acid Nucleation: An Experimental Study of the Effect of Seven Bases. J. Geophys. Res. Atmos. 2015, 120, 1933–1950. 10.1002/2014JD022730. [DOI] [Google Scholar]
- Jen C. N.; Bachman R.; Zhao J.; McMurry P. H.; Hanson D. R. Diamine-Sulfuric Acid Reactions are a Potent Source of New Particle Formation. Geophys. Res. Lett. 2016, 43, 867–873. 10.1002/2015GL066958. [DOI] [Google Scholar]
- Elm J.; Jen C. N.; Kurtén T.; Vehkamäki H. Strong Hydrogen Bonded Molecular Interactions between Atmospheric Diamines and Sulfuric Acid. J. Phys. Chem. A 2016, 120, 3693–3700. 10.1021/acs.jpca.6b03192. [DOI] [PubMed] [Google Scholar]
- Elm J.; Passananti M.; Kurtén T.; Vehkamäki H. Diamines Can Initiate New Particle Formation in the Atmosphere. J. Phys. Chem. A 2017, 121, 6155–6164. 10.1021/acs.jpca.7b05658. [DOI] [PubMed] [Google Scholar]
- Almeida J.; Schobesberger S.; Kürten A.; Ortega I. K.; Kupiainen-Määttä O.; Praplan A. P.; Adamov A.; Amorim A.; Bianchi F.; Breitenlechner M.; et al. Molecular Understanding of Sulphuric Acid-Amine Particle Nucleation in the Atmosphere. Nature 2013, 502, 359–363. 10.1038/nature12663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elm J. Elucidating the Limiting Steps in Sulfuric Acid–Base New Particle Formation. J. Phys. Chem. A 2017, 121, 8288–8295. 10.1021/acs.jpca.7b08962. [DOI] [PubMed] [Google Scholar]
- Olenius T.; Halonen R.; Kurtén T.; Henschel H.; Kupiainen-Määttä O.; Ortega I. K.; Jen C. N.; Vehkamäki H.; Riipinen I. New Particle Formation From Sulfuric Acid and Amines: Comparison of Mono-, Di-, and Trimethylamines. J. Geophys. Res. Atmos 2017, 122, 7103–7118. 10.1002/2017JD026501. [DOI] [Google Scholar]
- Temelso B.; Morrison E. F.; Speer D. L.; Cao B. C.; Appiah-Padi N.; Kim G.; Shields G. C. Effect of Mixing Ammonia and Alkylamines on Sulfate Aerosol Formation. J. Phys. Chem. A 2018, 122, 1612–1622. 10.1021/acs.jpca.7b11236. [DOI] [PubMed] [Google Scholar]
- Yu H.; McGraw R.; Lee S.-H. Effects of Amines on Formation of Sub-3 nm Particles and Their Subsequent Growth. Geophys. Res. Lett. 2012, 39, L02807 10.1029/2011GL050099. [DOI] [Google Scholar]
- Myllys N.; Chee S.; Olenius T.; Lawler M.; Smith J. Molecular-Level Understanding of Synergistic Effects in Sulfuric Acid-Amine-Ammonia Mixed Clusters. J. Phys. Chem. A 2019, 123, 2420–2425. 10.1021/acs.jpca.9b00909. [DOI] [PubMed] [Google Scholar]
- Li H.; Ning A.; Zhong J.; Zhang H.; Liu L.; Zhang Y.; Zhang X.; Zeng X. C.; He H. Influence of Atmospheric Conditions on Sulfuric Acid-dimethylamine-ammonia-based New Particle Formation. Chemosphere 2020, 245, 125554 10.1016/j.chemosphere.2019.125554. [DOI] [PubMed] [Google Scholar]
- Jokinen T.; Sipilä M.; Junninen H.; Ehn M.; Lönn G.; Hakala J.; Petäjä T.; Mauldin R. L. III; Kulmala M.; Worsnop D. R. Atmospheric Sulphuric Acid and Neutral Cluster Measurements Using CI-APi-TOF. Atmos. Chem. Phys. 2012, 12, 4117–4125. 10.5194/acp-12-4117-2012. [DOI] [Google Scholar]
- Zapadinsky E.; Passananti M.; Myllys N.; Kurtén T.; Vehkamäki H. Modeling on fragmentation of clusters inside a mass spectrometer. J. Phys. Chem. A 2019, 123, 611–624. 10.1021/acs.jpca.8b10744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Passananti M.; Zapadinsky E.; Zanca T.; Kangasluoma J.; Myllys N.; Rissanen M. P.; Kurtén T.; Ehn M.; Attouid M.; Vehkamäki H. How well can we predict cluster fragmentation inside a mass spectrometer?. Chem. Commun. 2019, 55, 5946–5949. 10.1039/C9CC02896J. [DOI] [PubMed] [Google Scholar]
- Olenius T.; Kupiainen-Määttä O.; Ortega I. K.; Kurtén T.; Vehkamäki H. Free Energy Barrier in the Growth of Sulfuric Acid-Ammonia and Sulfuric Acid-Dimethylamine Clusters. J. Chem. Phys. 2013, 139, 084312 10.1063/1.4819024. [DOI] [PubMed] [Google Scholar]
- Kürten A.; Jokinen T.; Simon M.; Sipilä M.; Sarnela N.; Junninen H.; Adamov A.; Almeida J.; Amorim A.; Bianchi F.; Breitenlechner M.; Dommen J.; Donahue N. M.; Duplissy J.; Ehrhart S.; Flagan R. C.; Franchin A.; Hakala J.; Hansel A.; Heinritzi M.; Hutterli M.; Kangasluoma J.; Kirkby J.; Laaksonen A.; Lehtipalo K.; Leiminger M.; Makhmutov V.; Mathot S.; Onnela A.; Petäjä T.; Praplan A. P.; Riccobono F.; Rissanen M. P.; Rondo L.; Schobesberger S.; Seinfeld J. H.; Steiner G.; Tomé A.; Tröstl J.; Winkler P. M.; Williamson C.; Wimmer D.; Ye P.; Baltensperger U.; Carslaw K. S.; Kulmala M.; Worsnop D. R.; Curtius J. Neutral Molecular Cluster Formation of Sulfuric Acid-Dimethylamine Observed in Real Time under Atmospheric Conditions. Proc. Natl. Acad. Sci. U.S.A. 2014, 111, 15019–15024. 10.1073/pnas.1404853111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bzdek B. R.; DePalma J. W.; Johnston M. V. Mechanisms of Atmospherically Relevant Cluster Growth. Acc. Chem. Res. 2017, 50, 1965–1975. 10.1021/acs.accounts.7b00213. [DOI] [PubMed] [Google Scholar]
- Elm J. Towards a Holistic Understanding of the Formation and Growth of Atmospheric Molecular Clusters: A Quantum Machine Learning Perspective. J. Phys. Chem. A 2021, 895, 125 10.1021/acs.jpca.0c09762. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.. et al. Gaussian 16, revision A.03; Gaussian, Inc.: Wallingford, CT, 2016.
- Elm J.; Kubečka J.; Besel V.; Jääskeläinen M. J.; Halonen R.; Kurtén T.; et al. Modeling the Formation and Growth of Atmospheric Molecular Clusters: A Review. J. Aerosol Sci. 2020, 149, 105621 10.1016/j.jaerosci.2020.105621. [DOI] [Google Scholar]
- Chai J.; Martin H. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
- Elm J.; Bilde M.; Mikkelsen K. V. Assessment of Binding Energies of Atmopsheric Clusters. Phys. Chem. Chem. Phys. 2013, 15, 16442–16445. 10.1039/c3cp52616j. [DOI] [PubMed] [Google Scholar]
- Elm J.; Kristensen K. Basis Set Convergence of the Binding Energies of Strongly Hydrogen-Bonded Atmospheric Clusters. Phys. Chem. Chem. Phys. 2017, 19, 1122–1133. 10.1039/C6CP06851K. [DOI] [PubMed] [Google Scholar]
- Schmitz G.; Elm J. Assessment of the DLPNO binding energies of strongly non-covalent bonded atmospheric molecular clusters. ACS Omega 2020, 5, 7601–7612. 10.1021/acsomega.0c00436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimme S. Supramolecular Binding Thermodynamics by Dispersion-corrected Density Functional Theory. Chem. - Eur. J. 2012, 18, 9955–9964. 10.1002/chem.201200497. [DOI] [PubMed] [Google Scholar]
- Luchini G.; Alegre-Requena J. V.; Funes-Ardoiz I.; Paton R. S. GoodVibes: Automated Thermochemistry for Heterogeneous Computational Chemistry Data. F1000Research 2020, 9, 291 10.12688/f1000research.22758.1. [DOI] [Google Scholar]
- Riplinger C.; Neese F. An Efficient and Near Linear Scaling Pair Natural Orbital Based Local Coupled Cluster Method. J. Chem. Phys. 2013, 138, 034106 10.1063/1.4773581. [DOI] [PubMed] [Google Scholar]
- Riplinger C.; Sandhoefer B.; Hansen A.; Neese F. Natural Triple Excitations in Local Coupled Cluster Calculations with Pair Natural Orbitals. J. Chem. Phys. 2013, 139, 134101 10.1063/1.4821834. [DOI] [PubMed] [Google Scholar]
- Neese F. The ORCA program system. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 73–78. 10.1002/wcms.81. [DOI] [Google Scholar]
- Neese F. ”Software update: the ORCA program system, version 4.0”. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2017, 8, e1327 10.1002/wcms.1327. [DOI] [Google Scholar]
- Liakos D. G.; Sparta M.; Kesharwani M. K.; Martin J. M. L.; Neese F. Exploring the Accuracy Limits of Local Pair Natural Orbital Coupled-Cluster Theory. J. Chem. Theory Comput. 2015, 11, 1525–1539. 10.1021/ct501129s. [DOI] [PubMed] [Google Scholar]
- Guo Y.; Riplinger C.; Becker U.; Liakos D. G.; Minenkov Y.; Cavallo L.; Neese F. Communication: An Improved Linear Scaling Perturbative Triples Correction for the Domain Based Local Pair-natural Orbital Based Singles and Doubles Coupled Cluster Method [DLPNO-CCSD(T)]. J. Chem. Phys. 2018, 148, 011101 10.1063/1.5011798. [DOI] [PubMed] [Google Scholar]
- Kubečka J.; Besel V.; Kurtén T.; Myllys N.; Vehkamäki H. Configurational Sampling of Noncovalent (Atmospheric) Molecular Clusters: Sulfuric Acid and Guanidine. J. Phys. Chem. A 2019, 123, 6022–6033. 10.1021/acs.jpca.9b03853. [DOI] [PubMed] [Google Scholar]
- Odbadrakh T. T.; Gale A. G.; Ball B. T.; Temelso B.; Shields G. C. Computation of Atmospheric Concentrations of Molecular Clusters from ab initio Thermochemistry. J. Vis. Exp. 2020, 158, e60964 10.3791/60964. [DOI] [PubMed] [Google Scholar]
- Stewart J. J. P. Optimization of Parameters for Semiempirical Methods VI: More Modifications to the NDDO Approximations and Re-optimization of Parameters. J. Mol. Model. 2013, 19, 1–32. 10.1007/s00894-012-1667-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Temelso B.; Mabey J. M.; Kubota T.; Appiah-Padi N.; Shields G. C. ArbAlign: ATool for Optimal Alignment of Arbitrarily Ordered Isomers Using the Kuhn–Munkres Algorithm. J. Chem. Inf. Model. 2017, 57, 1045–1054. 10.1021/acs.jcim.6b00546. [DOI] [PubMed] [Google Scholar]
- Kildgaard J. V.; Mikkelsen K. V.; Bilde M.; Elm J. Hydration of atmospheric molecular clusters: A new method for systematic configurational sampling. J. Phys. Chem. A 2018, 122, 5026–5036. 10.1021/acs.jpca.8b02758. [DOI] [PubMed] [Google Scholar]
- Kildgaard J. V.; Mikkelsen K. V.; Bilde M.; Elm J. Hydration of atmospheric molecular clusters II: Organic acid-water clusters. J. Phys. Chem. A 2018, 122, 8549–8556. 10.1021/acs.jpca.8b07713. [DOI] [PubMed] [Google Scholar]
- Besel V.; Kubečka J.; Kurtén T.; Vehkamäki H. Impact of Quantum Chemistry Parameter Choices and Cluster Distribution Model Settings on Modeled Atmospheric Particle Formation Rates. J. Phys. Chem. A 2020, 124, 5931–5943. 10.1021/acs.jpca.0c03984. [DOI] [PubMed] [Google Scholar]
- McGrath M. J.; Olenius T.; Ortega I. K.; Loukonen V.; Paasonen P.; Kurtén T.; Kulmala M.; Vehkamäki H. Atmospheric Cluster Dynamics Code: A Flexible Method for Solution of the Birth-Death Equations. Atmos. Chem. Phys. 2012, 12, 2345–2355. 10.5194/acp-12-2345-2012. [DOI] [Google Scholar]
- GitHub, 2021. https://github.com/tolenius/ACDC.
- Roldin P.; Ehn M.; Kurtén T.; Olenius T.; Rissanen M. P.; Sarnela N.; Elm J.; Rantala P.; Hao L.; Hyttinen N.; et al. The Role of Highly Oxygenated Organic Molecules in the Boreal Aerosol-cloud-climate System. Nat. Commun. 2019, 10, 4370 10.1038/s41467-019-12338-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maso M. D.; Hyvrinen A.; Komppula M.; Tunved P.; Kerminen V.-M.; Lihavainen H.; Viisanen Y.; Hansson H.-C.; Kulmala M. Annual and Interannual Variation in Boreal Forest Aerosol Particle Number and Volume Concentration and their Connection to Particle Formation. Tellus B 2008, 60, 495–508. 10.1111/j.1600-0889.2008.00366.x. [DOI] [Google Scholar]
- Kontkanen J.; Lehtipalo K.; Ahonen L.; Kangasluoma J.; Manninen H. E.; Hakala J.; Rose C.; Sellegri K.; Xiao S.; Wang L.; Qi X.; Nie W.; Ding A.; Yu H.; Lee S.; Kerminen V.-M.; Petäjää T.; Kulmala M. Measurements of Sub-3 nm Particles using a Particle Size Magnifier in Different Environments: From Clean Mountain Top to Polluted Megacities. Atmos. Chem. Phys. 2017, 17, 2163–2187. 10.5194/acp-17-2163-2017. [DOI] [Google Scholar]
- Kupiainen O.; Ortega I. K.; Kurtén T.; Vehkamäki H. Amine Substitution into Sulfuric Acid—Ammonia Clusters. Atmos. Chem. Phys. 2012, 12, 3591–3599. 10.5194/acp-12-3591-2012. [DOI] [Google Scholar]
- Elm J. An Atmospheric Cluster Database Consisting of Sulfuric Acid, Bases, Organics, and Water. ACS Omega 2019, 4, 10965–10974. 10.1021/acsomega.9b00860. [DOI] [Google Scholar]
- Hunter E. P. L.; Lias S. G. Evaluated Gas Phase Basicities and Proton Affinities of Molecules: An Update. J. Phys. Chem. Ref. Data 1998, 27, 413–656. 10.1063/1.556018. [DOI] [Google Scholar]
- Du L.; Kjaergaard H. G. Fourier Transform Infrared Spectroscopy and Theoretical Study of Dimethylamine Dimer in the Gas Phase. J. Phys. Chem. A 2011, 115, 12097–12104. 10.1021/jp206762j. [DOI] [PubMed] [Google Scholar]
- Du L.; Lane J. R.; Kjaergaard H. G. Identification of the Dimethylamine-trimethylamine Complex in the Gas Phase. J. Chem. Phys. 2012, 136, 184305 10.1063/1.4707707. [DOI] [PubMed] [Google Scholar]
- Hansen A. S.; Vogt E.; Kjaergaard H. G. Gibbs Energy of Complex Formation—Combining Infrared Spectroscopy and Vibrational Theory. Int. Rev. Phys. Chem. 2019, 38, 115–148. 10.1080/0144235X.2019.1608689. [DOI] [Google Scholar]
- Myllys N.; Kubečka J.; Besel V.; Alfaouri D.; Olenius T.; Smith J. N.; Passananti M. Role of Base Strength, Cluster Structure and Charge in Sulfuric Acid-Driven Particle Formation. Atmos. Chem. Phys. 2019, 19, 9753–9768. 10.5194/acp-19-9753-2019. [DOI] [Google Scholar]
- Zheng J.; Ma Y.; Chen M.; Zhang Q.; Wang L.; Khalizov A. F.; Yao L.; Wang Z.; Wang X.; Chen L. Measurement of Atmospheric Amines and Ammonia using the High Resolution Time-of-flight Chemical Ionization Mass Spectrometry. Atmos. Environ. 2015, 102, 249–259. 10.1016/j.atmosenv.2014.12.002. [DOI] [Google Scholar]
- Dawson M. L.; Varner M. E.; Perraud V.; Ezell M. J.; Gerber R. B.; Finlayson-Pitts B. J. Simplified Mechanism for New Particle Formation from Methanesulfonic Acid, Amines, and Water Via Experiments and Ab Initio Calculations. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 18719–18724. 10.1073/pnas.1211878109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H. H.; Ezell M. J.; Arquero K. D.; Varner M. E.; Dawson M. L.; Gerber R. B.; Finlayson-Pitts B. J. New Particle Formation and Growth from Methanesulfonic Acid, Trimethylamine and Water. Phys. Chem. Chem. Phys. 2015, 17, 13699–13709. 10.1039/C5CP00838G. [DOI] [PubMed] [Google Scholar]
- Chen H. H.; Varner M. E.; Gerber R. B.; Finlayson-Pitts B. J. Reactions of Methanesulfonic Acid with Amines and Ammonia as a Source of New Particles in Air. J. Phys. Chem. B 2016, 120, 1526–1536. 10.1021/acs.jpcb.5b07433. [DOI] [PubMed] [Google Scholar]
- Chen H. H.; Finlayson-Pitts B. J. New Particle Formation from Methanesulfonic Acid and Amines/ammonia as a Function of Temperature. Environ. Sci. Technol. 2017, 51, 243–252. 10.1021/acs.est.6b04173. [DOI] [PubMed] [Google Scholar]
- Arquero K. D.; Gerber R. B.; Finlayson-Pitts B. J. The Role of Oxalic Acid in New Particle Formation from Methanesulfonic Acid, Methylamine, and Water. Environ. Sci. Technol. 2017, 51, 2124–2130. 10.1021/acs.est.6b05056. [DOI] [PubMed] [Google Scholar]
- Arquero K. D.; Xu J.; Gerber R. B.; Finlayson-Pitts B. J. Particle Formation and Growth from Oxalic Acid, Methanesulfonic Acid, Trimethylamine and Water: A Combined Experimental and Theoretical Study. Phys. Chem. Chem. Phys. 2017, 19, 28286–28301. 10.1039/C7CP04468B. [DOI] [PubMed] [Google Scholar]
- Shen J.; Xie H.; Elm J.; Ma F.; Chen J.; Vehkamäki H. Methanesulfonic Acid-driven New Particle Formation Enhanced by Monoethanolamine: A Computational Study. Environ. Sci. Technol. 2019, 14387–14397. 10.1021/acs.est.9b05306. [DOI] [PubMed] [Google Scholar]
- Perraud V.; Xu J.; Gerber R. B.; Finlayson-Pitts B. J. Integrated Experimental and Theoretical Approach to Probe the Synergistic Effect of Ammonia in Methanesulfonic Acid Reactions with Small Alkylamines. Environ. Sci.: Processes Impacts 2020, 22, 305–328. 10.1039/C9EM00431A. [DOI] [PubMed] [Google Scholar]
- Chen D.; Li D.; Wang C.; Liu F.; Wang W. Formation Mechanism of Methanesulfonic Acid and Ammonia Clusters: A Kinetics Simulation Study. Atmos. Environ. 2020, 222, 117161 10.1016/j.atmosenv.2019.117161. [DOI] [Google Scholar]
- Chen D.; Li D.; Wang C.; Luo Y.; Liu F.; Wang W. Atmospheric Implications of Hydration on the Formation of Methanesulfonic Acid and Methylamine Clusters: A Theoretical Study. Chemosphere 2020, 244, 125538 10.1016/j.chemosphere.2019.125538. [DOI] [PubMed] [Google Scholar]
- Shen J.; Elm J.; Xie H.; Chen J.; Niu J.; Vehkamäki H. Structural Effects of Amines in Enhancing Methanesulfonic Acid-Driven New Particle Formation. Environ. Sci. Technol. 2020, 13498–13508. 10.1021/acs.est.0c05358. [DOI] [PubMed] [Google Scholar]
- Chen D.; Wang W.; Li D.; Wang W. Atmospheric Implication of Synergy in Methanesulfonic Acid-base Trimers: A Theoretical Investigation. RSC Adv. 2020, 10, 5173–5182. 10.1039/C9RA08760E. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.




