Collective Dynamics of Ion Channels on Bilayer Lipid Membranes

Abstract

Ion channels self-organize on cellular and organelle membranes as clusters and mutually modulate their gating behavior. It has been reported that the efficient information transfer is achieved by cooperative clustering of ion channels. To address the origin and nature of collective dynamics in ion channel clusters, a statistical mechanical model, namely, the Zimm–Bragg-type model in two dimensions with unequal weight distribution in channel–channel interactions, has been proposed. Nearest neighbor interaction along with next-nearest neighbor interaction has been considered, assuming symmetric spatial organization. The multichannel bilayer electrophysiology recordings of the voltage-dependent anion channel (VDAC) from rat brain mitochondria have been analyzed in order to test and further extend the model. The model successfully describes the multichannel gating behavior and self-organization of the VDAC cluster.

Introduction

The importance of transport of ions and metabolites across cell and organelle membranes has been well established in cellular physiology.¹ Such exchange of ions and metabolites is facilitated by ion channels, which are mainly transmembrane proteins or peptide molecules. Over the years, biophysical properties of ion channels have been extensively studied and this helped us immensely to understand a wide variety of functions such as cellular homeostasis, cell signaling, cellular electrical properties, and so forth. Reports have shown that various kinds of ion channels like voltage-gated Na⁺ channels, voltage-gated potassium channels, Ca²⁺ channels, IP3R [IP3 (inositol 1,4,5-trisphosphate) receptor], voltage-dependent anion channel (VDAC), and connexins are present as dense groups or clusters on membranes.²⁻⁷ The clustering has also been observed in small channel-forming peptides such as S6 peptide derived from the KvAP channel in vitro conditions.⁸ The gating dynamics of a channel cluster reflect the intrinsic physico-chemical properties of ion channels such as spatial distribution pattern of ion channels, voltage sensitivity, and so forth.^9,10 It has been observed that the gating behavior of single channel is different when it is in close proximity with other ion channels.^4,11 An increasing body of literature has shown that the cluster organization of ion channels can facilitate enhanced regulation of cellular response to external stimuli.^6,8,11,12 Thus, formation of ion channel clusters acts as an intrinsic mechanism of self-regulation of cellular responses.¹³ For example, the oligomerization of VDAC is important in mitochondrial signaling and apoptosis,^12,14 and the clustering of IP3 receptors has been found to regulate Ca²⁺ puff during calcium signaling.⁴ Especially in the case of neurons, clustering of ion channels can significantly affect action potential dynamics.^2,15,16 Clustering could facilitate interaction among neighboring ion channels, thus enhancing or inhibiting the gating of its surrounding channels.^15,17−19 It has been mentioned by various authors that the capability of ion channel clusters to represent enhanced gating dynamics should be viewed as a collective phenomenon.²⁰⁻²²

A collective phenomenon has been observed in nature at different levels of organization from physical and biological systems to societies and behavior of animals and humans.²³ In ion channel clusters, the phenomena can emerge from various types of interactions, (a) direct interactions, such as formation of bonds between different ion channel subunits,¹⁴ (b) indirect interactions due to diffusion, gradient, entropy, and so forth of ion channels,^11,24 and (c) interactions among the local fields around ion channel gates.²⁵ In addition, the membrane properties such as elasticity²⁶ can also play an important role in cooperative clustering of ion channels. Opening of a channel causes sudden influx of ions across the membrane, creating a local gradient near the channel pore. Depending on the strength of this local gradient, it interacts with the neighboring channels. When ion channels are distributed randomly and spaced far apart, they hardly interact with each other.¹³ The collective gating dynamics arises when these ion channels come sufficiently close to each other and form clusters of different sizes. The size of an ion channel cluster varies with the type of ion channel and the physiological conditions. VDAC and IP3 receptors can have less than eight individual components,^4,27,28 whereas connexin can have more than 100 channels in one cluster.⁶ The distance among the channels and size of cluster determines collective gating behavior.²⁹

VDAC is a large pore-forming protein of the mitochondrial membrane. It is present in abundance on the outer mitochondrial membrane in the form of clusters, where it facilitates the transport of ions and metabolites across the mitochondrial membrane matrix and the cytosol.^5,14,27 This mitochondrial porin and permeability transition pore have been found to play an important role in mitochondrial signaling through controlling ATP supply, buffering of Ca²⁺ ions and other metabolites, and so forth.^12,30,31 High-resolution atomic force microscopy investigation has identified the pore diameter on the membrane, which is around 38 × 27 Å. VDAC is known to exist in various oligomeric forms.^5,27,32 The most frequent nearest neighbor distance reported is 53 Å, possibly allowing interactions between VDAC channels. The other frequent neighbor distance is 92 Å, which indicates rough hexagonal packing of VDAC. It was observed that VDAC is present in the hexagonal form with p2 symmetry in membrane patch of 180 Å. The clustering of VDAC on the outer mitochondrial membrane has evolved as cellular strategies for efficient transport of various ions and metabolites, such as maximizing ATP supply, and has a role to play in apoptosis.^12,14

In modeling of ion channel clusters, it is usually assumed that the spatial interaction pattern could be disregarded.^9,21 Consideration of the ion channels as present in the symmetric finite grid with only nearest neighbor interaction ignores the importance of the spatial pattern. In fact, the spatial pattern can be extremely important in shaping the activity dynamics of neighboring channels and can have strong correlations with cluster behavior.^26,29 Although the underlying mechanism of cluster gating dynamics remains mostly unclear, the significance of spatial modeling has gained attention over the years. The prime approach for studying interactions between neighbors is the Ising model and more precisely, the Zimm–Bragg model.³³⁻³⁵ Ising developed Hamiltonian for a system of particles and included mutual interaction terms. Initially applied to spin–spin interactions, this is a generalized model later applied to various collective phenomenon. More extensions of the Ising model were performed later, based on statistical mechanics in 1, 2, and 3 dimensions and applied to complex problems in physics and chemistry, for example, spin–spin interactions, superconductivity, and so forth. As these methods proved to be ubiquitous for analyzing the collective phenomenon, these were applied to biology, initially to helix–coil transition in DNA, later to other molecular and cellular events.^36,37 However, in some systems, especially biological macromolecules, the generalized Ising treatment becomes mathematically difficult, if not impossible to solve analytically and hence there is a need of other models based on the principles of the Ising. The Zimm–Bragg model belongs to one of those where the matrix method has been applied to simplify the mathematical analysis of the system based on some more assumptions specific to the macromolecular systems.³⁸

Here, a mathematical framework of ion channel clustering has been proposed in consideration of unequal interactions among channels with the possibility of long-range interactions using the Ising type model. The detailed description of the model is presented in the Modeling Ion Channel Clustering section of this paper. In order to validate our model experimentally, we have performed multichannel bilayer electrophysiological recordings of VDAC. Investigating the dynamics of VDAC clustering gives us an insight into the nature of biophysical parameters that can govern the gating behavior of VDAC clusters. On the whole, this work focuses on the collective phenomenon of ion channels with emphasis on long-range interactions in ion channel clusters.

Modeling Ion Channel Clustering

In our earlier studies of collective phenomena of ion channels, it has been demonstrated that the ion channel interaction can be modeled using the statistical mechanical approach, that is, Ising model formulation.^39,40 We extend these studies to include the importance of their spatial distribution and consider non-nearest neighbor interactions. The ion channels have been represented in the form of cluster of size n on a two-dimensional (2D) membrane, where gating of one channel affects its neighbors. It has been assumed that coupling among ion channels can be categorized into two different types of interactions based on neighbor distance, that is, type A: interaction of surrounding channels with the channel at the center represented by “k” (Figure 1) and type B: interactions among surrounding channels represented by “p” (Figure 1). Here, surrounding ion channels are represented by [p] = [i, i + 1, i + 2, ...]. The model considers variable nearest neighbor interaction strengths in the form of unequal transition probabilities of channels. As per the model, a stochastically gating channel can have four possible states with respect to its neighbors. Here, we represent the relative weight or probability of a channel “i” along with its neighboring channel (i + 1) as a 2 × 2 matrix. For details of the model, it is recommended to refer to Ghosh and Mukherjee (1993).³⁹

1.1

Here, ω₀₀ and ω₀₁ denote the weight of the closed channel with nearest neighbor channel in the closed and open state, respectively. Similarly ω₁₀ and ω₁₁ represent the weight of open channel with nearest neighbor channel in the closed and open state, respectively. The corresponding partition function can be constructed by summing over all the states, that is, it can be expressed as the product of individual weight matrices, one at each site.

Figure 1.

Model of ion channel clustering: ion channels are represented on a 2D membrane as circle and the lines represent the interaction between pair of channels (cross-sectional view). Black color lines represent the interaction between the central ion channel with the surrounding channels, and gray lines represent the interaction among surrounding channels. n = total number of ion channels in a cluster (cluster size). k = center ion channel. [p] is surrounding ion channels represented by [i, i + 1, i + 2...].

The corresponding weight matrices for type A interaction between surrounding ion channels “i” with the center channel “k”. More details of model formalism and matrix multiplication are available in the ref (38).

1.2

We assume that the interaction of surrounding ion channels with the central ion channel is the same because of symmetric arrangement. Thus, the weight matrix is written as

1.3

In the case of type B interactions, the total weight matrix can be written as multiplication of weight matrix between nearest neighbor pairs and the next to nearest neighbor pair and so on. The weight matrix, if we start from the ith channel of surrounding ion channels, is given by

1.4

Similar weight matrix can be written to define the state of each pair of surrounding ion channels. Here, the weight matrix w_i,i+1 will be the same as w_i+1,i due to double counting. We also assumed that the weight matrix between any two nearest neighbors such as i and i + 1 or i + 1 and i + 2 is the same, the possible reason could be the equal distance between nearest neighbor pairs. Thus, weight matrices w_i,i+1, w_i+1,i+2, w_i+2,i+3 and so forth are equal. The assumption holds true for the next to nearest neighbor interaction and so on. The corresponding weight matrix of type B interaction is

1.5

p designates the surrounding channel interactions. Hence, the ultimate weight factor matrix is

1.6

The weight matrix W_k can be rewritten in the form of weight factors for open–close (ξ) and open–open (η) neighbors, respectively, for type A interaction. Similar weight matrix for W_p can be written for type B interactions among the surrounding neighboring channels, where σ and s denote the weight factors for open–close and open–open neighbors, respectively, as shown below.

For channel–channel interactions of surrounding channels with the center channel

For channel–channel interactions among the surrounding channels

Thus

1.7

The largest eigenvalues of the matrices are given below.

1.8

1.9

It may be noted that the present system of the ion channel cluster is a dynamical system and not in the equilibrium state, rather the system can be considered to be in steady or quasi equilibrium state. In view of this, we have defined the partition function of the system in a manner similar to that in the equilibrium state.⁴¹

Thus, the partition function is written as

The partition function is dominated by the term containing the largest eigenvalue (λ_max) of the weight matrix W when n is large. We have divided the system (channel–channel interactions) into smaller subsystems (type A and B interactions), the individual eigenvalues correspond to weight factors of smaller subsystems. For a case where sites were arranged in an array of size N₁·N₂, the partition function of the entire system can be written as

A case where sites were arranged in an array of size

1.10

Here, n represents the total number of ion channels present in a cluster, whereas k and p represent type A and type B interactions, respectively. Sum over p is done in the case of partition function for type B interactions.

As per the Zimm–Bragg model, the mean fraction of channels in open state θ can be calculated from the expression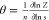

Thus

1.11

1.12

1.13

In a population of n channels, the fraction of channels open (θ) is represented by the sum of θ_p and θ_k for both kinds of interactions.

1.14

1.15

As mentioned earlier, the contribution of channel–channel interactions among the surrounding channels is different for different pairs of channels (Figure 1). Thus, θ_p needs to be summed for n – 2 ion channels, leaving one channel at the center. Due to computational complexity, we further assumed that the distribution of ion channels in a cluster is symmetric around the center such as W_i,i+1 and W_i,n–2 are same and so on. Thus, the contribution to the partition function needs to be summed for pairs. The total θ is given by the following equation.

1.16

In the above equation, s_p, σ_p, η, and ξ are functions of internal structural parameters and experimental conditions. In our analysis, we considered each of the weight factors as functions of time and voltage. We assume that the s_p, σ_p, η, and ξ can be expressed as the separable functions of time and voltage, as follows.

2.1

2.2

2.3

2.4

One formal issue with this approach is to choose suitable form of time and voltage functions. In order to gain the insight into the functional forms of s_p, σ_p, η, and ξ, we performed the multichannel electrophysiological recording of the VDAC channel and quantitatively and qualitatively analyzed the behavior of multichannel current with time and voltage. This gives us the experimental basis for choosing the function and finding the best fit values of variable parameters from the experimental results. The multichannel current recorded from VDAC was analyzed to compute the mean fraction and most-probable fraction (MPF) of the channel that remains in the open state as a function of time and voltage. In order to find the suitable function first, the fits were obtained separately as functions of time and voltage. In the next step, s_p, σ_p, η, and ξ were considered as multiplicative functions of time and voltage (eqs 2.1–2.4), where the choice of function depends on the results obtained from the individual fit. The detailed analysis is presented in the Results section of this paper.

While investigating individual interactions changing with time and voltage, we found that the number of parameters to be optimized is large. The total number of parameter depends upon the cluster size and functional form of expression s_p, σ_p, η, and ξ. In the case of cluster size 7–8, the total number of parameter can be around 12–15. We used different optimization methods such as the least square method and simulated annealing (SA) method to best fit our experimental data. The fraction of channels open (θ) will depend on eqs2.1–2.4, where dominance of s_p, σ_p, η, and ξ parameters indicate the importance of these functions in governing the gating state of clusters of VDAC channel. We assumed that the central ion channel has equal cooperative effect with its surrounding channels because of equal distance from neighbors. In the case of type B interaction, a different range of neighbor interaction was represented by R; with increase in R, the distance among a pair of neighbor increases. Thus, type B interactions are different for different range of interactions and type A interaction is uniform.

Experiments

Isolation and Purification of VDAC from Rat Brain

All the animal experiments were performed as per norms of Committee for the Purpose of Control and Supervision of Experiments on Animals (CPCSEA), India. The purification of mitochondrial VDAC was carried out as per the protocol of de Pinto et al.⁴² Briefly, 20 Wister rats weighing 150–200 g male or female were anaesthetized and their brains were removed aseptically in chilled solution A [250 mM sucrose, 1 mM K⁺–EDTA, 10 mM Tris–HCl (pH 7.4)]. Excess blood was removed from brain tissue by solution A as it causes damage at later steps of purification. To get crude mitochondrial pellets, brain pieces were homogenized and centrifuged at 2000g for 10 min followed by centrifugation of supernatant at 12,500g for 10 min. The crude mitochondrial pellet was centrifuged at 12,500g for 30 min to obtain the pure pellet. Then, mitochondrion was allowed to swell by suspending in a hypo-osmotic chilled solution B [10 mM Tris–HCl (pH 7.4) and 1 mM K⁺–EDTA]. The suspension was incubated in ice for 15 min and centrifuged at 27,000g for 10 min. Then, mitochondrial pellet was suspended in solution C [10 mM Tris–HCl, 1 mM K⁺–EDTA and 3% (v/v) Triton X-100] by gentle vortexing and incubated in ice for 30 min. Further supernatant was collected after centrifugation at 44,000g for 30 min. A hydroxyapatite/celite (2:1) column was used in the final step for 6 mL of the supernatant obtained. Elution was performed with solution C. First 20 mL of elute containing pure VDAC was collected. Identification of brain VDAC was carried out by 12% sodium dodecyl sulfate–polyacrylamide gel electrophoresis.

Bilayer Electrophysiology/Multichannel Recording

Purified VDAC was reconstituted into the black lipid membrane (BLM) as per the standard method.⁴³ Briefly, a Delrin cuvette and chamber (Warner Instrument Corp, USA) were filled with BLM buffer having 1 M KCl, 2 mM CaCl₂ along with 8 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) (pH 7.4 using Tris–Cl). The Ag/AgCl electrode was placed at the BLM setup and connected to the patch amplifier (Axopatch 200A, Molecular Devices, USA). The bilayer membrane was formed using 1,2-diphytanoyl-sn-glycero-3-phosphocholine (DPhPC) (Avanti Polar Lipids, USA). After successfully forming the bilayer membrane, VDAC was supplied to the cis side of the chamber. Multichannel bilayer recording was performed after insertion of VDAC molecules on BLM at the voltage clamp mode from −50 to +50 mV, holding potentials with difference of 10 mV. The signals were recorded at 10 kHz and filtered using a low pass filter at 2 kHz.

Computational Analysis

The experimental data were visualized by CLAMPFIT (pCLAMP 10.2, Molecular Devices, CA, U.S.A.) and analyzed using Python 3.7.1. The channel conductance of VDAC was calculated from full open state current recordings, and VDAC conductance observed in single channel recording was compared with multichannel recordings.⁸ The multichannel recordings contain ion channel cluster of different sizes from two to nine. For our analysis, only those recordings were selected where number of ion channels in a cluster was more than six. A sufficiently long duration single channel current trace was selected to draw the all point histogram. The value of the peak corresponding to full open state of the channel was identified. The single channel current value of full open state was divided by respective voltage to compute conductance. The final conductance value was then calculated from three individual recordings, and the mean and the standard error were plotted against voltage. In the case of multichannel current recordings of VDAC, one channel conductance was calculated. The one channel conductance is defined as the minimum current value of full open channel state (after two partially open state) in overall multichannel recording. Another approach in the calculation of one channel conductance was the average conductance value of each channel in a multichannel current recording. The maximum conductance of the cluster was divided by the number of channel (N) present on the membrane, where number of channel is estimated from the number of current steps in the recording. The latter method gave the approximate value of number of channel present and actively gating during recording. The value of N was verified by the calculation of number of channel computed from the total conductance divided by one channel conductance (calculated from the former approach).

Mean Fraction of Channel in Open State

In order to understand the central tendency in cluster gating, the experimental mean fraction of channel in open state (θ_e) was computed at different time scales.

Here, θ_e(t) is the experimental mean fraction of channel in open state as a function of time at each potential, n_t is the average number of channel open till time t (0 to t s), and N is the maximum number of channel active in the overall current recording. The θ_e value was calculated for a window size of 1000 data points (0.1 s recording).

MPF of Cluster in Open State

The mean fraction of channel was insufficient to capture the properties of optimal cluster size and the cluster dynamics; hence, MPF was computed. As per our definition, the MPF is the conducting fraction of the cluster of channels mostly “favored” during its gating in open state. The formal definition of MPF is as follows: in a symmetric 2D membrane consisting of N number of ion channels, the MPF is the conducting fraction of channels, most frequently attended by the cluster of channels. It is the fraction of channels open in a burst of openings, where burst opening is facilitated by cooperative gating of ion channels. In the case of VDAC which is a voltage-dependent ion channel, the size of this “cooperative cluster” is a function of time and voltage.

Steps for MPF computation as a function of time and voltage.

• 1.The VDAC multichannel current recorded were analyzed by selecting the current signal of sufficient length at each potential. In multichannel recording of approximately 2 min, VDAC shows higher activity for shorter period of time and then goes to less active or stable state. For the purpose of data analysis, we chose these shorter duration (∼18 s) signals of higher activity to calculate the MPF as a function of time at each potential.
• 2.Current signal (∼18 s) was used to plot all point histogram; the current state corresponding to the highest peak was identified as the most frequent current state of the channel.
• 3.In order to calculate the contribution of a particular current state in ion channel recording, following approach was used. The best Gaussian fitting was carried out in histogram with multiple peaks finding algorithm (Python—PeakUtils 1.3.0). The approach also facilitates counting of approximate number of channels in an open state. The best Gaussian fit was obtained by the SA method.
• 4.In the next step, the area under the Gaussian curve was calculated for the most frequent current state, which was then divided by the overall area under the curve. This gives the fractional contribution of the most frequently occurred state in the overall recording. The value obtained was noted as MPF of the channel.

2.5

The MPF is the ratio of the area under the most frequent current state at time t (A_MPF) to the total area (A_total) of the amplitude histogram. A_o,n is the area under the nth current level.⁴

• 5.Finally, the MPF was plotted as a function of time for a step size of 0.1 ms (1000 data points). This gives the idea about how the contribution of MPF changes with time. The MPF data were normalized by dividing it with the maximum MPF value.
• 6.MPF was calculated at voltage from −50 to +50 mV in a similar manner.

Fitting of Model with Experimental Data

Experimentally calculated MPF was fitted with the theoretical model followed by optimization of parameters using the SA method. We observed that the simple least square fitting does not work when number of parameter is large. SA is a method of choice for solving constrained and unconstrained optimization problems, where the number of variable parameter is large.⁴⁴ The optimization of our objective function (eq 1.16) was carried out by minimizing the cost function, that is, root-mean-square difference (RMSD). SA algorithm mimics the process of increasing temperature in a material and then slowly cooling it to lessen the defects, ultimately leading to minimization of system energy. In every iteration of optimization, a new solution of variables is generated arbitrarily. The extent of search of new minima depends on the probability of distribution and temperature. In iteration, all solutions corresponding to lower RMSD values as compared to experimental observation were accepted, including the new solutions that have higher RMSD values but with some probability. The approach allows the algorithm to cross the local minima and explore the possibility of global solutions.

Algorithm:

• 1.At first, an approximate random guess solution was provided for all the variables, the values were generated randomly in the range of −1 to 1. The random parameters were generated with the “random” function of Python. The best fit was performed for MPF of 18 s VDAC multichannel current recording.
• 2.The difference between experimental results and results of our model was calculated by RMSD and sum of standard deviation (SSD).
• 3.If the RMSD or SSD value is lower than the previous value, the new solution is accepted, otherwise it is accepted with certain probability (P) calculated as follows.

• 4.In the next step, a new solution was generated based on history of simulation.
• 5.New solutions = previous solutions + Δ deviations
• 6.This improves the efficiency of search of minima in the SA method. Furthermore, the algorithm was optimized by selectively updating few variables at a time instead of modifying all the parameters at once. This change in algorithm efficiently improves the computational cost in fitting the model as voltage and time function. The best fit parameters were then combined to get the final fit.
• 7.Over 10,000 iterations were performed to achieve the best fit of our model result with experimental findings. Detailed findings have been presented in the Results section.

Results

Figure 2 shows the representative traces of VDAC multichannel current recorded at various potentials. The conditions remain constant throughout the experiments, as mentioned in the Bilayer Electrophysiology/Multichannel Recording section. The multichannel recording was performed by allowing more than one channel to get incorporated into the bilayer membrane. In order to avoid the excess VDAC insertion on a bilayer lipid membrane, we either supplied protein (VDAC) in optimal quantity (20 μL) in BLM buffer or perfusion was performed to remove excess protein. It was observed that after certain number of VDAC insertion, the DPhPC bilayer membrane was unable to hold the proteins and breaks. The reason might be that each VDAC protein molecule is large in size (pore size ∼ 2.5 Å). It is thought that multiple VDAC molecules might cause mechanical stress on the bilayer membrane.³² The overall nature of states remains distinct from each other in multichannel recording (Figure 2). As represented in Figure 2, the steady-state current shows distinct steps of opening and closing with its sub states. In single channel recording of VDAC, the results of various conducting states coincide with the earlier reports, where VDAC exhibits one full open state, one full close state, and in between there were two partially open states. In the case of lower potential range (±25 mV), VDAC remains in full open state with higher opening probability. In general, current traces were recorded for around 1 min for each potential in the range of −50 to +50 mV; out of that the domain of higher activity was selected. The corresponding amplitude histograms were drawn for each trace. On an average, ∼18 s recording was selected for further analysis, as shown in Figure 2.

Figure 2.

Multichannel current trace recorded from VDAC at various potentials: the selected trace of multichannel current recording (18 s). DphPC bilayer membrane was formed keeping symmetric buffer solutions of 1 M KCl, 2 mM CaCl₂, and 8 mM HEPES at pH 7.4. The signals were recorded at 10 kHz and filtered using a low pass filter at 2 kHz. Base line remains near 0 pA at 0 mV applied potential. (a) Multichannel VDAC recording at −35 mV with approximately 6–7 channels in a cluster. (b) Multichannel VDAC recording at +35 mV with approximately 6–7 channels in a cluster. (c) Multichannel VDAC recording at −50 mV with approximately 6–7 channels in a cluster. (d) Multichannel VDAC recording at +50 mV with approximately 6–7 channels in a cluster. Current trace shows distinct conducting states of the cluster. Immediately after the voltage clamp, the cluster shows higher gating activity for approximately 7 s, after that the cluster gets stabilized and shows low channel activity. At least three sets of recordings for each potential were used for further analysis.

VDAC Cluster Dynamics

As per our understanding, the difference in single channel and one channel conductance is an indication of collective phenomenon. When ion channels are present in the cluster (as in multichannel recordings), they can interact with each other and modulate their conductance. The interaction could also lead to distinct gating dynamics of cluster, where gating of each VDAC can facilitate or inhibit its neighbors. This interaction would lead to the collective opening of certain number of ion channels depending on the range of interactions. The quantification of size of cooperative cluster was carried out by calculating the mean fraction of channels in open state. Due to the abovementioned cooperation, the channel remains in open state for longer duration. As shown in Figure 3, the mean fraction of channels open in multichannel recording decreases with time. It indicates that in bilayer electrophysiological experiments just after the application of voltage, all the channels present on the membrane become active and show opening but slowly the channels acquire an optimized state which is lower than the maximum number of channels present in the bilayer membrane, as indicated by a decrease in current amplitude. We observed that approximately 3–4 channels remain open after the cluster system gets stabilized, although the maximum cluster size is 6–7, thus 3–4 is the cooperative cluster size.

Figure 3.

Mean fraction of channel in open state (θ_e) of VDAC multichannel recording: the data were normalized to one. Representative figures at membrane potentials (a) +35, (b) +50, (c) −35, and (d) −50 mV. The overall behavior shows decrease in the mean fraction of channel in open state with time (18 s recording trace). We observed that at all the potentials, approximately 60–70% of channels remain open for longer duration (experimental conditions remain the same as reported earlier).

Next, we checked the contribution of each conducting state with time. We computed the MPF at each potential. Figure 4 shows the histogram of full current trace (18 s) with Gaussian fitting at various potentials as indicated in the panel. The MPF was identified as the current state contributing to highest peak. In a histogram of 18 s signal, the distinct state of opening is represented by different Gaussian peaks. For example, at +35 mV, the histogram shows 13 distinct conducting states (Figure 4a), where the highest peak or MPF is at 400 pA. Similarly, for +50, −35, and −50 mV, we observed 11 current states with the highest peak at 515 pA, 13 current states with the highest peak at −465 pA, and 13 current states with the highest peak at −560 pA, respectively. Our 18 s recording does not show complete closer of the cluster, that is, where no channel is open. In general, VDAC has four gating states consisting of one full open state, two partially open states, and one close state. Usually VDAC does not close completely with 0 conductance value, even at the close state, it allows small flux of ions to pass through. We checked how the contribution of this highest peak state or MPF varies with time at each potential. The cooperative nature in cluster can facilitate the cluster to visit the MPF state more frequently.

Figure 4.

Histogram-based analysis of VDAC multichannel recording: representative figures of all point histogram at membrane potentials (a) +35, (b) +50, (c) −35, and (d) −50 mV. Multiple peak Gaussian fittings were carried out on the histograms out of which the highest peak and area under the curve were calculated (experimental conditions remain the same as reported in the Bilayer Electrophysiology section).

Histograms were plotted incrementally for 0.1 s time step, and the area under the MPF state (previously identified from complete 18 s trace) was calculated. This area was divided by the overall area to calculate MPF. The MPF value was normalized to 1 (0–1). As represented in Figure 5, contribution of MPF increases with time. It gives the idea on the fraction of a channel opening with time. After the incorporation of ion channel into the bilayer membrane, the voltage clamp can lead to possible reorganization in cluster dynamics. We expect that the steepness of the MPF plot would depend on the rate of this cluster reorganization. As mentioned in the model, to gain the insight into VDAC cluster dynamics, we used the experimental results as the basis for choosing the functions of our model. The observed behavior of MPF as a function of time inspires the choice of function that can be used to model s_p, σ, η, and ξ. Inspired by the experimental data (MPF vs time) of VDAC, we used the exponential function to model θ with time. First, individual fitting was performed at each voltage by considering s_p, σ_p, η, and ξ as only functions of time. The following expressions were substituted in the eqs 2.1–2.4, where a, b, α, β, c, d, γ, and δ are constants and SA optimization was performed to get the best fit values.

3.1

3.2

3.3

3.4

Figure 5.

Values of MPF in VDAC multichannel recording: the contribution of MPF increases with increase in time (18 s recording trace). Figure panel shows the recording potentials and best fit SSD values. Representative subplots at (A) −35, (B) +35, (C) −50, and (D) +50 mV.

These expressions were used to calculate the weight factors of the open channel and then fraction of the open channel in the cluster. The parameter values were limited in such a way that the value of the function remains in the range of 0–1 (eqs 2.5–3.4) so that the function is bounded. The initial fitting was performed for the random solutions of the parameters using least square fitting. As our model has large number of parameters, initial optimization does not lead to proper fitting of the experimental results. The values of the parameters were optimized in the later step of computation using the SA method. In all the cases, the optimization was achieved in total number of 10,000–50,000 simulation steps. After the optimization of the parameters, best fit values of SSD and RMSD were recorded. As indicated in Figure 5, our algorithm for optimization of parameters pertained to the best fit of the model works successfully. Similar optimization was performed for all the potentials from −50 to +50 mV with a difference of 10 mV and discussed later. The results were considered best fit once the SSD value of 0.4 or lower is achieved. Our observation is that exponential function gives best results (minimizes SSD) describing the dynamics of channel clustering with change in time. Tables 1 and 2 show the values of constant parameters after the optimization at four different applied membrane potentials (±35 and ±50 mV). Data were analyzed for all other membrane potentials, as mentioned above.

Table 1. Optimized Constant Parameters for Type A Interactions.

	voltage
parameters	50.0 mV	–50.0 mV	–35.0 mV	35.0 mV
c	–0.003	0.002	0.002	0.003
d	0.029	0.035	0.035	0.036
γ	0.463	0.452	0.433	0.516
δ	0.273	0.262	0.243	0.325

Table 2. Optimized Constant Parameters for Type B Interactions^a.

	voltage = 50.0 mV		voltage = −50.0 mV		voltage = −35.0 mV		voltage = 35.0 mV
parameters	R = 1	R = 2	R = 1	R = 2	R = 1	R = 2	R = 1	R = 2
a	0.004	0.020	–0.079	0.011	0.026	–0.033	0.030	–0.014
b	0.084	0.100	–0.0001	0.091	0.105	0.047	0.110	0.066
α	0.534	0.459	1.025	0.848	0.765	0.381	0.537	0.354
β	0.391	0.317	0.882	0.706	0.622	0.238	0.394	0.210

^aHere, R = 1 represents nearest neighbor pair, whereas R = 2 represents next-nearest-neighbors pair.

Here, the constant parameters indicate the contribution of each type of interaction in the cluster reorganization or stabilization. We considered the circular organization of ion channels with one channel present at the center of cluster on 2D membrane. We selected those VDAC multichannel recordings where at least six ion channels are present in a cluster. As mentioned earlier, when number of channels inserted on the bilayer membrane cross 8 or 9, the membrane does not remain stable and it gets leaky or breaks, probably due to stress. As shown in Figure 2 multichannel recordings, the size of cluster is around six. The experiments were repeated (three times) for traces with around six ion channels in a cluster. Thus, we assumed that one channel is present at the center surrounded by five neighboring ion channels of the membrane. In the case of type “A” interactions which is interaction of central ion channel with all its surrounding neighbors, the functional form of ξ and η depends on the values of c, d, γ, and δ (eqs 2.3 and 2.4). The γ and δ determine the steepness of the exponential function, whereas c and d determine the amplitude in the plot. As per our model, the transition probability of an ion channel from non-conducting state to conducting state depends on the gating state of its neighbors. ξ and η correspond to weight factor for open–close and open–open neighbors, respectively. The optimized parameters obtained after simulations, as mentioned in Table 1, the values of c and γ are comparable to the values of d and δ, respectively, indicating that both open–close and open–open states of channels play crucial role in determining the gating dynamics of clusters. The values of γ are slightly higher than the values of δ, resulting in dominance of open–open state over open–close state; the results are consistent in all the potentials, as detailed in Table 1.

Similarly, in the case of type B interaction, the functional form of s_p and σ_p depends on the values of a, b, α, and β. Type B interactions occur among surrounding ion channels for nearest neighbor (R = 1) and next-nearest neighbor (R = 2) pairs. The values of constant parameters (a, b, α, and β) for R = 1 and R = 2 are comparable for different applied potentials (Table 2), although the values of a, b, α, and β are slightly higher for R = 1. This observation indicates a possible role of distance in determining the nature and strength of interactions at various ranges of cooperation. The results indicate that the next-nearest neighbor interaction is also important in determining the cluster gating behavior and cannot be ignored when considering the interactions among neighbors. Next, we compared the open–close state parameters with open–open state parameters. The results (Table 1) show that the values of α is higher than the values of β at each applied voltage. This observation is similar to that in the case of type A interaction. The weight factor of open–open state is higher than that of the open–close state. This means that the open state of neighboring ion channel influences more in determining the state of the cluster.

Observations:

• 1.In the case of type A interaction, the gating state of VDAC cluster is slightly dominated by weight factor of open–open state over that of open–close state.
• 2.Also in the case of type B interaction, weight factor of open–open state is slightly higher than that of open–close state.
• 3.In the case of type B interaction, the importance of nearest neighbor (R = 1) and next-nearest neighbor interaction (R = 2) depends on the applied potentials (Table 2). As observed from Table 2, the next-nearest neighbor interaction is nearly the same as the nearest neighbor interaction in determining the transition dynamics of cluster; hence, nearest neighbor interactions make a non-negligible contribution to the transition dynamics.

MPF as Function of Voltage

Having investigated MPF as a function of time, we also investigated the MPF of multichannel VDAC recording as a function of voltage. As per our understanding, the state of cooperative cluster and its dynamics can change with change in the applied potential. The analysis was carried out as described earlier. Figure 6 shows the variation of MPF with change in voltage for 18 s recording. We observed that the value of MPF is high when applied voltage is in the range of −20 to +20 mV. The MPF decreases with increase in applied voltage. The overall distribution of MPF with voltage was bell shaped in nature. We modeled each of s_p, σ_p, η, and ξ as a function of voltage only (eqs 2.1–2.5). Inspired by the experimental pattern (bell-shaped curve), the functional form is represented below. The optimization parameters are tabulated in Table 3. Here, the functional form f₁(V), f₂(V), f₃(V), and f₄(V) represent change in fraction of open channel with voltage.

4.1

4.2

4.3

4.4

Figure 6.

MPF of the channel in open state as a function of voltage: the VDAC multichannel data recorded for 18 s were analyzed and the MPF was plotted as a function of voltage (recoding at 10 kHz, sampling at 2 kHz, 1 M KCl buffer). The dots represent the experimentally calculated MPF and the blue line shows the fitting of our model eq 1.16.

Table 3. Constant Parameters When s_p, σ_p, ξ, and η Were Modeled as a Function of Voltage Only.

type A interaction		type B interaction
parameters	values	parameters	R = 1	R = 2
y	–1.124	w	1.161	0.922
z	0.709	x	1.17015	0.932
ρ	0.0004	ϵ	0.00039	0.0001
τ	0.0004	ζ	0.00039	0.0001

The parameters of the partition functions s_p, σ_p, ξ, and η are probabilities (weights) for each state. Here, the values of y, z, ρ, and τ contribute to the weights of type A interactions. Biophysically speaking, relative values of y and ρ compared with z and τ denote statistical weight of the open–open state compared with the open–close state. Similarly, in the case of type B interactions, the statistical values of w_p and ϵ_p were compared with x_p and ζ_p.

The theoretical model parameters best fit with the experimental results, calculated using the bell-shaped function as described above, are shown in Figure 6. In the case of voltage functions, the parameter values obtained from SA optimizations for the nearest neighbor (R = 1) and next-nearest neighbor (R = 2) interaction for type B interactions are nearly equal. This means that both kinds of interactions have equal contributions in our model. In the case of type A and B interactions, the weight factors for open–open state (s) and open–close state (σ) are also nearly equal displaying equal contributions in the case of voltage functions.

Model as a Function of Time and Voltage

To reduce the number of parameters in our model and give unified expression for time and voltage functions, the combined characteristics of MPF with change in time and voltage were investigated. As mentioned in eqs 2.1–2.5, s_p, σ_p, η, and ξ can be expressed as multiplicative function of time and voltage. The contributions to the partition function are as below. The fraction of channels in open state can be calculated from eq 1.16.

5.1

5.2

5.3

5.4

Here, f₁^′(V), f₂(V), f₃^′(V), and f₄(V) represent the time dependencies of the parameters. It may be mentioned here that the parameter values of the abovementioned equation have been chosen in such a way so that the values of s_p, σ_p, η, and ξ remain in the range of 0–1.

Our experimental studies lead to the following observations. (1) As a function of voltage in the range of +50 to −50 mV, the MPF shows a bell-shaped pattern. (2) MPF increases exponentially with time. In the three-dimensional (3D) plot, the multichannel current recorded from VDAC was plotted as both function of time and voltage. 3D plot gives overall characteristics of ion channels in the form of surface, where x, y, and z axes represent time, voltage, and MPF, respectively. The MPF of the channel is higher at lower potentials, indicating that the voltage plays a crucial role in deciding most frequently visited state of the channel. The results are similar to the single channel features, where opening probability is high at lower potentials and low at higher potentials. Values of the constants are tabulated in Table 4. As shown in Figure 7, our model fits well with experimental results of VDAC. In both kinds of interactions, that is, type A and type B, the values of α and γ are higher than the values of β and δ. Here, α, γ and β, δ are weight factors for open–open state (s) and open–close (σ) states, respectively. This observation is consistent with our earlier observation where weight factor for open–open state is higher than that of open–close state, indicating higher opening probability in a cluster of channel. Similarly, the values of ϵ and ρ are slightly higher than the values of ζ and τ. This observation can also be interpreted in a similar manner. When we compared the parameters for nearest neighbor interactions (R = 1) with the parameters of next-nearest neighbor interactions (R = 2), values of the former is slightly higher, indicating the change in interaction strength with distance. Thus, our model indicates the importance of collective phenomena in multichannel gating behavior of VDAC. In future studies, the 3D surface can be used to quantify the cluster behavior.

Table 4. Combined Model Parameters of MPF with Time and Voltage^a.

type A interaction		type B interaction
parameters	values	parameters	R = 1	R = 2
c	0.001	a	0.023	–0.032
d	0.034	b	0.103	0.0477
γ	0.448	α	0.797	0.368
δ	0.257	β	0.654	0.225
ρ	0.0003	ϵ	0.0003	0.0003
τ	0.0002	ζ	0.0002	0.0002

^aThe values of parameters simulated as per the eqs 2.1–2.5.

Figure 7.

3D surface of VDAC cluster dynamics: the plot indicates the change in MPF with time and voltage. The MPF surface shows that its contribution increases with time but decreases with the increase in voltage.

As mentioned earlier, the parameters of Table 4 contribute toward the probabilities (weights) as a function of time and voltage. We investigated the contribution of various factors in both types of interaction, that is, type A and type B. More details of biophysical insights of channel–channel interactions are given in the Discussion section.

Discussion

The idea of the present paper is to highlight the importance of mutual interactions of ion channels in a cluster. This work is a continuation of our previous work on modeling collective behavior of ion channels on a 2D bilayer lipid membrane.^20,39 While our previous model on the ion channel interaction on a cell or bilayer lipid membrane was limited to the nearest neighbor interaction like any model in the class of Ising models, the present model goes a step further by including next to nearest neighbor interaction. For this purpose, a symmetric cluster of ion channels was considered, as described in the Modeling Ion Channel Clustering section. The existence and importance of distance interaction have been evidenced through various experimental facts, as discussed in the Introduction section.^9,29 It may be mentioned here that while nearest neighbor interaction models, for example, Ising, Zimm–Bragg and so forth, are very useful to explain collective behavior of a system, the reality goes beyond it. Keeping this in view, we attempted here to extend our 2D model to non-nearest interactions of ion channels. The major assumptions of our model are discussed in the Modeling Ion Channel Clustering section. However, while carrying out the computation in order to investigate the nature of the solutions of the mathematical equations, we decided to choose functional expressions of the statistical weight factors of interacting ion channels inspired by experimental facts. Subsequently, we conducted bilayer electrophysiology (BLM) experiments on VDAC multichannels and used the results in our computation. We believe this makes our theoretical investigation more realistic.

In the BLM electrophysiology experiment, we investigated the behavior of the mean fraction of ion channels open as a function of time and voltage. The multichannel current recording shows that the maximum 6–7 ion channels are present in the cluster (Figure 3). The number of channels was estimated based on the maximum current value, as described in Computational Analysis section. As per our recordings, the application of voltage caused activation of larger number of ion channels on the membrane. The fraction of channels open, which represents the central tendency of multichannel VDAC current, decreased exponentially with time to an optimal conducting state lower than the initial state (Figure 3). This might be due to the fact that VDAC cluster undergoes reorganization on the bilayer membrane to reach an optimal conducting state, where the total energy of the system is minimum. Various factors such as ion channel structure and external environment can play important roles in defining the size of the abovementioned stable cluster.⁴⁵ Shuai et al. have shown that entropy could play an important role in cluster dynamics.²⁴ Also, the size of a cluster depends on the range of interactions.

As mentioned in the Computational Analysis section, mean fraction of channel was insufficient to capture the properties of optimal cluster size and the cluster dynamics. Hence, we shifted the focus of our investigation to the most favored conducting (open) state. Accordingly, the MPF of ion channels open was chosen for our studies of channel interactions. Through MPF, we are able to find the most visited open state of the channels with time and voltage (histogram count, Figure 4). The MPF gives the contribution of the dominant conducting state in overall recording, which can be studied as a function of voltage and time. With time, the contribution of MPF increases exponentially (Figure 5) up to a limit and with change in voltage MPF follows the bell-shaped pattern (Figure 6). Here, the slope in MPF curve depicts how fast a cluster of channels tries to reach an optimal state and visit this state more often as compared to other states. An optimized state could be an active state of an oligomer, for example, trimer, tetramer, pentamer, or hexamer of VDAC. We observed that our model can be best fitted to VDAC MPF (experimental) with cluster size 3–4 (Figures 2 and 4). Finally, in the 3D plot of MPF (Figure 7), the highest peak area of the surface represents the most favored region. As observed in Figure 7, the MPF values are higher around +30 to −30 mV which decrease with increase in the potentials. The lower applied potentials favor higher conduction of ions across the membrane and fast stabilization of the cluster gating state, whereas increase in the potential can cause stress on the channel cluster and favor slow rate of cluster reorganization. The observed MPF indicates critical dependence of nature of interaction among channels as a function of time and voltage.

In general, the interaction among ion channels could be positive, negative, or noncooperative. Our simulated values of the model parameters represent the probabilities (weights) of the states, which define the contribution of various types of interaction in ion channel gating. The values were compared in type A interaction with type B interaction and nearest neighbor interaction (R = 1) with next-nearest neighbor interaction. Fitting the MPF distribution with our model gave us biophysical insights into the internal mechanism of ion channel collective behavior. As predicted by our model, the contribution of weight factor for open–open state is higher than that of open–close state (Tables 1 and 2). Thus, collective opening of ion channels is preferred over isolated opening. In other words, the system shows positive cooperativity in its gating (opening–closing) dynamics. Although a considerable effort has been made to experimentally support and validate our model, further experiments are required to confirm that the system of VDAC cluster is cooperative. Nevertheless, we have proposed a general model for the ion channel cluster, which could be positive, negative, or noncooperative.

What could be the physico-chemical basis of ion channel cooperativity? In a collective system, each element of the system contributes to an interaction field or environment that affects its neighbors.²² The field created by the individual units could be strong enough to affect large number of its neighbors or it could be weak affecting only nearest neighbors. As VDAC is a large pore-forming membrane protein with definite gating charges,⁴⁶ the opening and closing of each channel create a local disturbance of electromagnetic field around it, which would affect its nearest and non-nearest neighbors. Also, opening of an ion channel leads to the sudden movement of large number of ions across the cellular membrane, which creates local charge gradient near the channel. The combined effect of all these local phenomena would lead to the activation of neighboring ion channels in response to the gating of a single channel. Depending on the strength of this fields, the range of interaction can be defined.⁴⁷ Here, the local interaction field could be a function of distance, time, and voltage (Tables 1–3). Modeling non-nearest neighbor interactions among ion channels help us to identify the parameters controlling cooperativity and also elucidate the role of spatial distribution in ion channel clustering. We observed that both nearest and non-nearest interactions contribute to cooperativity in clustered ion channels (Table 2). The coefficients of the eqs 2.1–2.5 combined with equations depend on the mutual distance of the two peripheral ion channels in a cluster (Figure 1).

There could be three possible mechanisms of ion channel cluster reorganization in the lipid membrane:⁴⁵ first, lateral diffusion of VDAC in the membrane, leading to formation of relatively small densely packed cluster; second, stabilization of membrane charge properties which could affect the lipid–protein interaction and cluster reorganization;^26,48 and third, formation of cooperative field based on the activity of channels, leading to cluster reorganization.²² To the best of our knowledge, the possible mechanism could be the last one, that is, activity-driven mechanism.

In the proposed model, various assumptions have been made, such as considering two different kinds of interactions (type A and type B interactions) and the symmetric organization of channels (W_i,i+1 = W_i–1,i). These assumptions not only simplify the equations but also reduce the number of unknown parameters, which immensely helped the computation. In addition, the weight factors of this system of ion channels on a 2D membrane in quasi-equilibrium have been expressed as separable functions of voltage and time. These have been carried out in view of simplification of mathematical and computational analyses. Given the fact that the proposed model is a general one, it needs to be revalidated for ion channels other than VDAC. In our opinion, smaller peptides or organic channels, for example, alamethicin, gramicidin, and S6 peptides of potassium channels, could be better systems for such experimental verification of the model. It is understood that the cooperative nature of these channels would vary with the system of channel, namely, its structure and physico-chemical properties. Such issues are kept for future studies.

Author Contributions

R.S.: methodology, formal analysis, investigation, validation, computer programming and analysis, contributed to manuscript writing, reviewing, and editing. S.G.: conceptualization, mathematical model, formal analysis, methodology, contributed to manuscript writing, reviewing, and editing.

The authors declare no competing financial interest.

Notes

Data available on request from the authors: the data that support the findings of this study are available from the corresponding author upon reasonable request.