Oxygen Transport Parameter in Plasma Membrane of Eye Lens Fiber Cells by Saturation Recovery EPR

Abstract

A probability distribution of rate constants contained within an exponential-like saturation recovery (SR) electron paramagnetic resonance signal can be constructed using stretched exponential function fitting parameters. Previously (Stein et al. Appl. Magn. Reson. 2019.), application of this method was limited to the case where only one relaxation process, namely spin-lattice relaxations due to the rotational diffusion of the spin labels in the intact eye-lens membranes, contributed to an exponential-like SR signal. These conditions were achieved for thoroughly deoxygenated samples. Here, the case is described where the second relaxation process, namely Heisenberg exchange between the spin label and molecular oxygen that occurs during bimolecular collisions, contributes to the decay of SR signals. We have further developed the theory for application of stretched exponential function to analyze SR signals involving these two processes. This new approach allows separation of stretched exponential parameters, namely characteristic stretched rates and heterogeneity parameters for both processes. Knowing these parameters allowed us to separately construct the probability distributions of spin-lattice relaxation rates determined by the rotational diffusion of spin labels and the distribution of relaxations induced strictly by collisions with molecular oxygen. The later distribution is determined by the distribution of oxygen diffusion concentration products within the membrane, which forms a sensitive new way to describe membrane fluidity and heterogeneity. This method was validated in silico and by fitting SR signals from spin-labeled intact nuclear fiber cell plasma membranes extracted from porcine eye lenses equilibrated with different fractions of air.

Introduction

Molecular oxygen is an effective probe molecule for studying membrane lipid packing. Molecular oxygen is small, hydrophobic, and fast diffusing; therefore, it can enter even transiently formed, small vacant pockets in a lipid bilayer membrane. Because of that, the oxygen diffusion-concentration product reflects the dynamics of gauche-trans isomerization of acyl chains and structural nonconformability of neighboring lipids [1–3]. Because lipid packing is affected by the lipid composition and the presence of membrane proteins, the solubility and diffusion of molecular oxygen are different in induced membrane domains. Due to the paramagnetic nature of molecular oxygen, a dual-probe saturation recovery (SR) electron paramagnetic resonance (EPR) method allows observation of the bimolecular collision rate between spin labels and molecular oxygen that depends on the local oxygen-diffusion-concentration product, termed oxygen transport parameter (OTP) [4].

First developed in the 1980s, this oximetry method was used to calculate the permeability coefficient for oxygen across model [1,5–7] and biological [8–11] membranes. Comparing this coefficient with the permeability coefficient of a water layer of the same thickness as the membrane allowed determination of whether the membranes form a barrier to oxygen transport. The logical conclusion of such a finding was that membrane domains of different compositions must have different OTP profiles and, thus, different oxygen permeability coefficients. Spin-label oximetry has since been used to differentiate bulk, boundary, and trapped lipids [9,12–14]; liquid ordered phase domains [15–17]; and pure cholesterol bilayer domains [16–22] within model and biological membranes.

The SR EPR spin labeling method measures the spin-lattice relaxation rate (T₁⁻¹) of nitroxide spin labels in membranes, which, in magnetically diluted samples, is determined by the rotational diffusion of the probe [23–27]. In the dual-probe SR EPR method, molecular oxygen (a fast-relaxing paramagnetic species) induces spin exchange during collisions with spin labels (a slow-relaxing paramagnetic species), which provides an additional relaxation pathway for spin labels. It provides a quantitative and the most sensitive way to measure the collision rate between a spin label and molecular oxygen [8,28].

The SR signal is recorded as an exponential-like decay and can be analyzed using mono- and multi-exponential decay functions. Due to the nonorthogonal nature of exponential function, the fitting requires previous knowledge or a strong assumption about the number of exponentials and their values. In membrane studies, it means that the number of membrane domains should be preliminary defined. Due to the practical limitation of fitting, this number is limited to two or three homogeneous domains. This is convenient for describing model membranes; however, it is problematic for describing complex biological membrane samples. These samples may consist of mixtures of membranes with different lipid and protein compositions. For example, the composition of an eye lens membrane changes gradually as cells mature [29–42]. These changes induce variability in domains and local environments.

The application of the stretched exponential function (SEF) to analyze SR EPR signals from spin-labeled biological membranes removes the requirement for a specific number of discrete exponentials. It reduces the number of fitting parameters to two: the characteristic spin-lattice relaxation rate (T_1str⁻¹) and the heterogeneity parameter β. When β is 1, the function is a single exponential and the environment is homogeneous. When β is less than one, more than one exponential is present. The fitting parameters provide the means to construct a probability distribution of rates contained within the signal.

Previously, we used the SEF to analyze SR data obtained from deoxygenated intact cortical and nuclear fiber cell plasma membranes extracted from porcine eye lenses and spin-labeled with phospholipid and cholesterol analogs [43]. The constructed probability distributions of spin-lattice relaxation rates due to the rotational diffusion provides quantitative information about the rigidity and heterogeneity of the samples. The method of separating the OTPs and spin-lattice relaxation rates due to the rotational diffusion when fitting the data to distinct exponentials was also reported previously [4]. Here, we develop a method to separate spin-lattice relaxation rates due to the rotational diffusion and oxygen collision in the complex biological samples where assumption of the numbers and values of distinct exponentials is not desirable or feasible. The term stretched oxygen transport parameters (SOTP) is defined, and two methods for its extraction from the total SR EPR signal are outlined. These methods are evaluated in silico and with real data from complex biological membranes.

Outline of theory

Stretched exponential as a sum of exponential decays

The SEF can be used to describe a distribution of decay rate constants (k) as a sum of exponential decays [44]:

$$I(t)=\Sigma I_{\text{o}(\text{n})}\exp \left(-t{k}_{(\text{n})}\right)=I_{\text{o}}\exp \left(-{\left(t{k}_{\text{str}}\right)}^{\beta }\right).$$ (1)

In this equation, I(t) is the signal amplitude at time (t), I_o(n) is a fractional contribution of each exponential term n toward the signal at time zero, I_o is a normalized signal amplitude at time zero, k_(n) is the individual decay rate constant, k_str is a characteristic or stretched rate constant, and β is the heterogeneity parameter that corresponds to k_str.

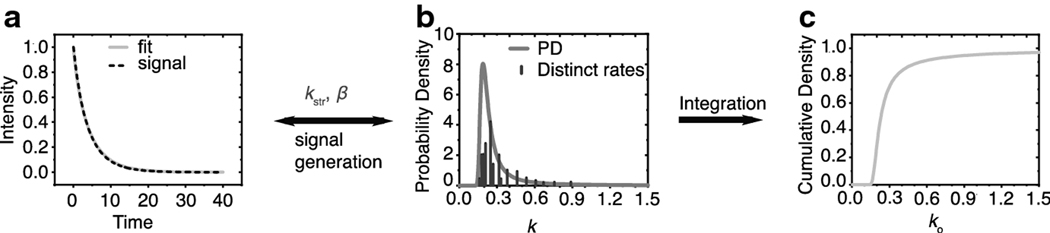
The distribution of rate constants can be generated using the two fitting parameters obtained from the fitting of the multi-exponential-like signal to the SEF, the characteristic rate constant, k_str, and the β, as shown in Fig. 1. This distribution can be used to evaluate the probability of finding a range of rate constants within the signal and, in that, the portion of the signal that may arise from the range of these constants.

Fig. 1.

Illustration of the principle of using the SEF as a sum of exponentials. In (a), the dashed line is a signal generated from the sum of 15 random exponential decay constants, which are represented as the vertical lines in (b). The relative heights of these lines reflect their fractional contribution to the signal, and the position the value of the rate constant. The solid line in (a) represents the SEF of the signal with two parameters, k_str and β. These parameters were used to construct the continuous probability distribution as described in Stein et al. [43]. This distribution covers all the rate constants within the signal. (c) The cumulative distribution function was obtained by integrating the area under the probability distribution and can be used to assess the probability of finding a range of rate constants within the signal.

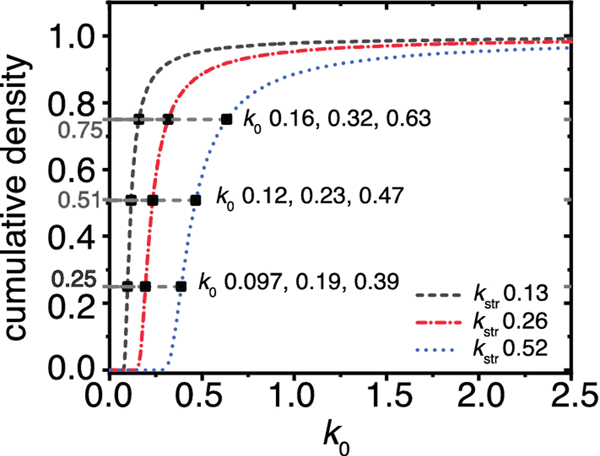
The β parameter determines the shape of the distribution; hence, it is termed heterogeneity parameter. When k_str is multiplied by a factor, all individual rates within the distribution range are multiplied by that same factor; see Fig. 2. Conversely, if all rates in a distribution range are multiplied by the same factor, as is the case in membrane oximetry, the k_str will increase by that same factor and the beta parameter will remain the same. This relationship of the SEF parameters to probability distribution is key to extracting the distribution of OTPs using data obtained by SR EPR.

Fig. 2.

Illustration of stretched rate constant properties. The cumulative density of three stretched exponential distributions that possess the same β parameter (0.90), and k_str parameters that differ by the factor of two, as indicated. Consequently, the k_os at cumulative density values of 0.25, 0.51, and 0.75 increase by the factor of two. Hence, as rates within the distribution are multiplied by a factor of two, so is the k_str.

Oxygen transport parameter

In SR EPR, the OTP, which is defined as the oxygen diffusion-concentration product, is measured as the effective oxygen collision rate with spin labels [4]. In the magnetically diluted samples (under nitrogen atmosphere), the SR signal (mainly) depends on the rotational diffusion of the spin probe. If no heterogeneity exists within the rotational diffusion of the probes, the signal can be fitted with a single exponential decay:

$$I(t)=I_{\text{o}}\exp \left(-t{T_{1\text{N}2}}^{-1}\right),$$ (2)

where T_1N2⁻¹ is the rotational diffusion spin-lattice relaxation rate.

Because molecular oxygen is paramagnetic, the collision between molecular oxygen and a spin label provides an additional relaxation pathway for the spin label. The increase in the relaxation rate of the signal can be described by the product of two exponentials:

$$I(t)=I_{\text{o}}\exp \left(-t{T_{1\text{N}2}}^{-1}\right)\exp (-tW),$$ (3)

where W is the effective oxygen collision rate with spin labels in samples saturated with air at 760 mmHg.

If no heterogeneity in W exists, then the signal can be fitted to a single exponential:

$$I(t)=I_{\text{o}}\exp (-t{T_{1\text{air}}}^{-1})=I_{\text{o}}\exp \left(-t\left({T_{1\text{N}2}}^{-1}+W\right)\right),$$ (4)

where T_1Air⁻¹ is the spin-lattice relaxation in samples saturated with air.

W is the difference between T_1Air⁻¹ and T_1N2⁻¹ [4]:

$$W={T_{1Air}}^{-1}-{T_{1\text{N}2}}^{-1}.$$ (5)

In other words, W is the slope of the straight line formed by the observed spin-lattice relaxation rates (T_1obs⁻¹s) at various air fractions:

$$I(t)=I_{\text{o}}\exp \left(-t{T_{1\text{obs}}}^{-1}\right)=I_{\text{o}}\exp \left(-t\left({T_{1\text{N}2}}^{-1}+f_{\text{Air}}W\right)\right),$$ (6)

where f_Air is the air fraction at which the sample is equilibrated before the signal is recorded.

Stretched oxygen transport parameters

Special case

When the SR EPR signal is recorded in the presence of molecular oxygen, two independent processes contribute to the spin-lattice relaxation process: rotational diffusion and oxygen collision. Therefore, in heterogenous samples, these rates can be described by two distributions of relaxation rates.

If the spin-lattice relaxation is homogeneous under nitrogen atmosphere but the oxygen transport parameter is not, the signal will consist of the sum of products of exponentials in Eq. 7a. The T_1N2⁻¹ can be readily factored out as in Eq. 7b.

$$I(t)=A_1\exp \left(-t{T_{1\text{N}2}}^{-1}\right)\exp \left(-t{f}_{\text{Air}}{W}_1\right)+A_2\exp \left(-t{T_{1\text{N}2}}^{-1}\right)\exp \left(-t{f}_{\text{Air}}{W}_2\right)+\dots A_{\text{n}}\exp \left(-t{T_{1\text{N}2}}^{-1}\right)\exp (-t{f}_{\text{Air}}{W}_{\text{n}})$$ (7a)

$$I(t)=\exp \left(-t{T_{1\text{N}2}}^{-1}\right)\left(A_1\exp \left(-t{f}_{\text{Air}}{W}_1\right)+A_2\exp \left(-t{f}_{\text{Air}}{W}_2\right)+\dots A_{\text{n}}\exp \left(-t{f}_{\text{Air}}{W}_{\text{n}}\right)\right).$$ (7b)

The multi-exponential portion can be replaced with the stretched exponential term, providing the SOTP:

$$I(t)=\exp \left(-t{T_{1\text{N}2}}^{-1}\right)\exp \left(-{\left(t{f}_{\text{Air}}{W}_{\text{str}}\right)}^{\beta }\text{W}\right),$$ (8a)

where W_str is the stretched oxygen collision rate and β_W is the heterogeneity of the W_str.

Eq. 8a represents the special case where the SOTP is fitted directly while holding the rotational diffusion parameter obtained under the nitrogen constant. W_str is extracted either from the slope of f_AirW_str versus air fraction or by fitting the W_str of a sample equilibrated in air. β_W represents the heterogeneity of the SOTP term and does not change with air fraction. In biological membranes, rotational diffusion term T_1N2⁻¹ is rarely homogeneous. The relaxation processes by the rotational diffusion or Heisenberg exchange are independent as are the distributions of the rates by which they are represented. Because of that, the special case also can be applied to instances where the rotational diffusion measured under nitrogen is heterogenous:

$$I(t)=\exp \left(-{\left(t{T_{1\text{strN2}}}^{-1}\right)}^{\beta \text{N}2}\right)\exp \left(-{\left(t{f}_{\text{Air}}{W}_{\text{str}}\right)}^{\beta \text{W}}\right),$$ (8b)

where β_N2 represents the heterogeneity of the rotational diffusion spin-lattice relaxation rates, and T_1strN2⁻¹ is the characteristic rotational diffusion spin-lattice relaxation rates. Because the addition of oxygen does not change these parameters, the SOTP can be fitted directly when holding parameters obtained under the nitrogen constant.

The special case relies on the data obtained in the absence of oxygen for fitting.

General case

We developed an alternative, “general case” to extract SOTP parameters from the total signal, which does not use the rotational diffusion spin-lattice relaxation parameter.

At any air fraction, the observed relaxation rate (T_1strobs⁻¹) represents the sum of the products of the rotational diffusion spin-lattice relaxation rate, and the OTP is multiplied by the air fraction at which the observation was recorded:

$$I(t)=A_1\exp \left(-t{{T_{\text{1N2}}}^{-1}}_1\right)\exp \left(-t{f}_{\text{Air}}{W}_1\right)+A_2\exp \left(-t{{T_{\text{1N2}}}^{-1}}_2\right)\exp \left(-t{f}_{\text{Air}}{W}_2\right)+\dots A_{\text{n}}\exp \left(-t{{T_{\text{1N2}}}^{-1}}_{\text{n}}\right)\exp \left(t{f}_{\text{Air}}{W}_{\text{n}}\right)$$ (9a)

$$I(t)=\exp \left(-{\left(t{T_{1\text{strobs}}}^{-1}\right)}^{\beta \text{obs}}\right)=\exp \left(-{\left(t{\left({T_{\text{1N2}}}^{-1}+f_{\text{Air}}W\right)}_{\text{str}}\right)}^{\text{βobs}}\right)=\exp \left(-{\left(t{T_{1\text{strN}2}}^{-1}+t{f}_{\text{Air}}{W}_{\text{str}}\right)}^{\text{βobs}}\right),$$ (9b)

where the heterogeneity of that term is β_obs. During air titration, the rate only increases when the probe collides with molecular oxygen; therefore, W_str can be extracted from the slope of the straight line formed by T_1strobs⁻¹s versus air fraction. The y-intercept of such line corresponds to T_1strN2⁻¹.

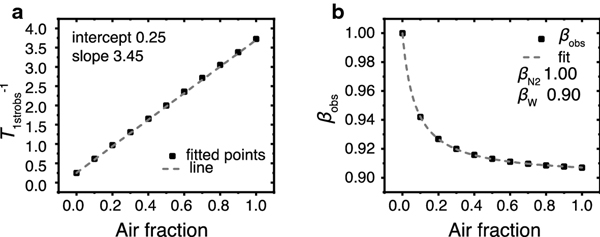
More difficult is determining the observed heterogeneity behavior. In the absence of air (i.e., when f_AirW_str is zero), the observed heterogeneity corresponds to that of the rotational diffusion spin-lattice relaxation rates. When the f_AirW_str term is sufficiently large (i.e., when tT_1strN2⁻¹ is negligible by comparison), the β_obs corresponds to the heterogeneity of the OTPs. The behavior of β_obs between the two extremes was determined empirically and can be described as the weighted sum of the heterogeneities (β parameters) contributed by the rotational diffusion and oxygen collision rates. Eq. 10, which describes this dependence, was validated in silico (see Fig. 3) and through the fitting the experimental data to Eq. 10.

Fig. 3.

Signals that were simulated using Eq. 8a with the parameters T_1N2⁻¹ 0.25, W_str 3.45, β_W 0.90, and various f_Air were fitted with Eq. 9b. The fitted parameters were then plotted versus the air fraction. (a) shows T_1strobs⁻¹ versus air fraction, and (b) shows β_obs versus air fraction. In (A), the square dots are the fitted values and the dashed line is the linear fit of the data. In (b), the square dots are the fitted values and the dashed line is the fit with Eq. 10; the W_str and T_1N2⁻¹ parameters obtained from the linear fit in (a) were held constant.

$${\beta }_{\text{obs}}=\left({\beta }_{\text{N}2}\left({T_{1\text{strN}2}}^{-1}/\left({T_{1\text{strN}2}}^{-1}+f_{\text{Air}}{W}_{\text{str}}\right)\right)\right)+\left({\beta }_{\text{W}}\left(f_{\text{Air}}{W}_{\text{str}}/\left({T_{1\text{strN}2}}^{-1}+f_{\text{Air}}{W}_{\text{str}}\right)\right)\right)$$ (10)

Materials and Methods

Materials

The spin-labeled cholesterol analog (androstane spin label [ASL]) was purchased from Molecular Probes (Eugene, OR); see the structures in Fig. 1 of Ref. [18]. Other chemicals of at least reagent grade were purchased from Sigma-Aldrich (St. Louis, MO).

Isolation of nuclear fiber cells

The following procedures were described previously [14,45]. Porcine eyes from 2-year-old animals were obtained on the day of slaughter from Johnsonville Sausage, LLC (Watertown, WI). Lenses were dissected and kept at −80°C until needed. Next, the lenses were thawed and decapsulated, and the nuclear portion of the fiber cells was separated from the cortical portion based on their consistencies [41,46] and used in experiments.

Isolation of intact fiber cell membranes

Intact nuclear membranes from 36 eye lenses were isolated from tissue, as reported previously [47–49], using the method developed in [50] with minor modifications. Special care was taken to produce a uniform suspension by repeatedly aspirating the solution through a syringe fitted with an 18-gauge needle. The final pellet was washed and resuspended in 10 mM PIPES pH 7.0, 150 mM NaCl. Half of the suspension was stored at −80°C; the other half was washed with water and lyophilized.

Isolation of total lipids

The total lipids were extracted from the lyophilized membranes using the Folch procedure [51] with minor modifications. The resultant lipid samples were soft, white solids and were stored at −20°C.

Spin labeling of intact membranes

Spin labeling was performed as described previously [45]. ASL film was prepared on the bottom of a test tube by drying the appropriate amount of spin label in chloroform (to achieve the molar ratio of spin label/total lipids of ~1/100 in each sample). Intact membrane suspensions (~0.2 mL containing 1 to 2 mg of total lipids) were added to the test tubes and shaken for about 2 h at room temperature. This incubation time was enough to incorporate all the spin-label molecules into the membranes. Finally, membrane suspensions were centrifuged for a short time, and the loose pellet was transferred to a 0.6 mm i.d. capillary made of gas-permeable methylpentene polymer (i.e., TPX) and used for EPR measurements [52].

Preparation of lens lipid membranes

Multilamellar vesicles made from the total lipids contained 1 mol% of ASL. They are referred to as “lens lipid membranes (LLMs)” and were prepared using the rapid solvent exchange method [53–55]. The final membrane dispersions (1 to 2 mg of total lipids) were centrifuged briefly (12,000 g, 15 min, 4°C), and the loose pellet was used for EPR measurements.

SR EPR measurements

The SR EPR signal for each sample was obtained on the central line of the ASL EPR spectrum by short-pulse SR EPR at X-band using a loop-gap resonator [1,56]. The signal was recorded 100 ns (dead time) after a short (300 ns duration) saturating pulse of 1 W power. All measurements of samples equilibrated with the same gas that was used for temperature control (i.e., a controlled mixture of nitrogen and dry air adjusted with flow meters [model 7631H-604; Matheson Gas Products, Irvine, TX]) were carried out at 36°C [52]. The constant temperature of the sample and the resonator was established after 30 min. After changing the gas to the new mixture of nitrogen and dry air, we waited minimum 20 min to ensure that the new equilibrium was established. The record time was at least 20 times the stretched relaxation time of the sample, and the sampling interval was approximately 1/80^th of the stretched relaxation time.

Analysis of SR signals using the SEF

All data fitting was performed using the OriginPro Version 2019 OriginLab Corporation (Northampton, MA) software package. The SR signals were fitted as appropriate with Eqs. 8a, 8b, and 9b after 220 ns of dead time using the Levenberg-Marquardt algorithm. The zero time was adjusted to 220 ns after the end of the pulse. When Eq. 8a or 8b was used, the T₁⁻¹ and β_N2 values obtained from fitting the anaerobic sample with the single exponential were held constant as T_1N2⁻¹. When Eq. 10 was used to fit β_obs versus air fraction, the T_1strN2⁻¹ and W_str values were held constant while the β_N2 and β_W values were free to vary.

The probability densities were computed in Matlab R2018a (MathWorks, Natick, MA) using the previously reported probability distribution function [44] and adjusted for either T_1strN2⁻¹ or W_str as described in [43]. Additionally, a cutoff time for high rates was implemented at 22.7 μs⁻¹. Due to our time delay, rates faster than that would have been at less than 1% of their initial amplitude.

Fitting of SR signals and evaluation of SEF parameters

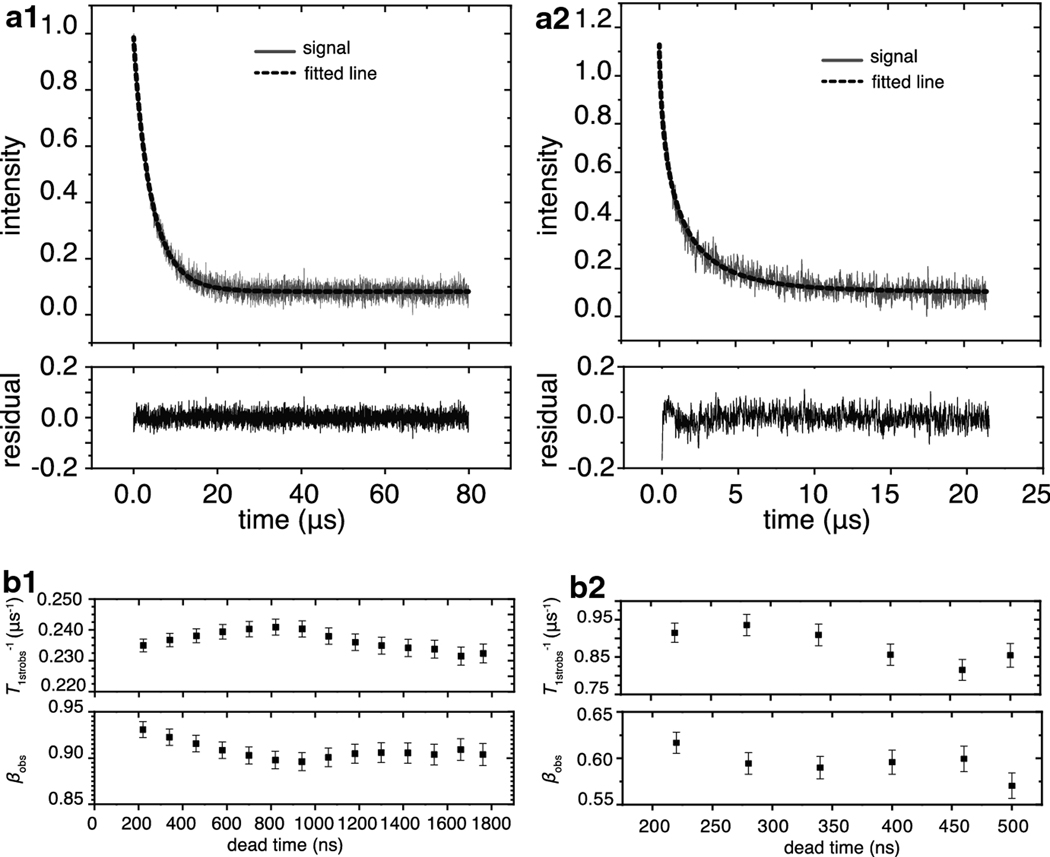
Within this section, we describe the raw data fit at various air fractions in order to evaluate the error introduced by dead time. The SR signals of intact nuclear membranes obtained under nitrogen and under 50% air were fitted with Eq. 9b after 220 ns of dead time, as presented in Figs 4a1 and 4b1. Because molecular oxygen enhances the spin-lattice relaxation rate, the observation time and sampling intervals were cut to 20 μs and 5 ns, respectively, for the signal obtained at 50% air as compared with 80 μs and 20 ns, respectively, for the signal obtained under nitrogen. Based on the residuals (the experimental signal minus the fitted curve), both signals fit well to Eq. 9b with T_1strobs⁻¹ 0.235 ± 2.1 × 10⁻³ μs⁻¹ and β_obs 0.931 ± 8.67 × 10⁻³ for the sample under nitrogen, and 0.915 ± 0.0259 μs⁻¹ and 0.617 ± 0.0115 for the sample saturated with 50% air. The values following the ± signs are the standard-error-of-parameter, which is larger for a signal obtained at 50% air than for that obtained under nitrogen. When compared in terms of the percentages, the standard-error-of-parameter for the T_1strobs⁻¹ of the signal obtained under nitrogen is 0.894%, and the signal obtained under 50% air is 2.8%. Likewise, the standard-error-of-parameter for β_obs is 0.931% for the signal under nitrogen versus 1.86% for the signal under 50% air. These percentages did not increase significantly for signals obtained under air and were found to be 3.2% for T_1strobs⁻¹ value and 1.7% for the β_obs parameter (data not shown).

Fig. 4.

Raw signal fitness to Eq. 9b and effect of the dead time on fitting parameters. (a1) The signal obtained under nitrogen (gray line) fitted to Eq. 9b (black dashed line) after 220 ns of dead time. The residual plotted in the box below indicates that no additional parameters are required to fit the signal. (a2) The fitted T_1strobs⁻¹ and β_obs parameters are plotted as a function of dead time for the signal obtained under nitrogen. The vertical bars are the standard-error-of-parameter. (b1) The signal obtained under 50% air (gray line) fitted to Eq. 9b (black dashed line) after 220 ns of dead time. The residual plotted in the box below indicates that no additional parameters are required to fit the signal. (b2) The T_1strobs⁻¹ and β_obs parameters are plotted as a function of dead time for the signal obtained under 50% air. The vertical bars indicate the standard-error-of-parameter.

As demonstrated in Figs. 4a2 and 4b2, the fitting parameters were found to be sensitive to the dead time after which signals were analyzed. For signals obtained under nitrogen, the effect of dead time from 220 ns and up to 1660 ns was evaluated. Because signals obtained under 50% air decayed faster, the effect of dead time from 220 ns and up to 500 ns was evaluated. The fitting parameters oscillate around the same values, and when the β_obs value is lowered, the T_1strobs⁻¹ parameter shifts to the faster rates. The β_obs parameters have a maximum difference of 3.8% from the mean value for signals obtained under nitrogen and 7.6% for signals obtained under 50% air. The T_1strobs⁻¹ parameters have a maximum difference of 4.16% from the mean value for signals obtained under nitrogen and 12.9% for signals obtained under 50% air. These results indicate that the introduction of air increases the standard-error-of-parameter and differences in the values obtained after various dead times.

Results and Discussion

Special and general cases: A comparison of samples with homogeneous T_1N2⁻¹s in LLMs

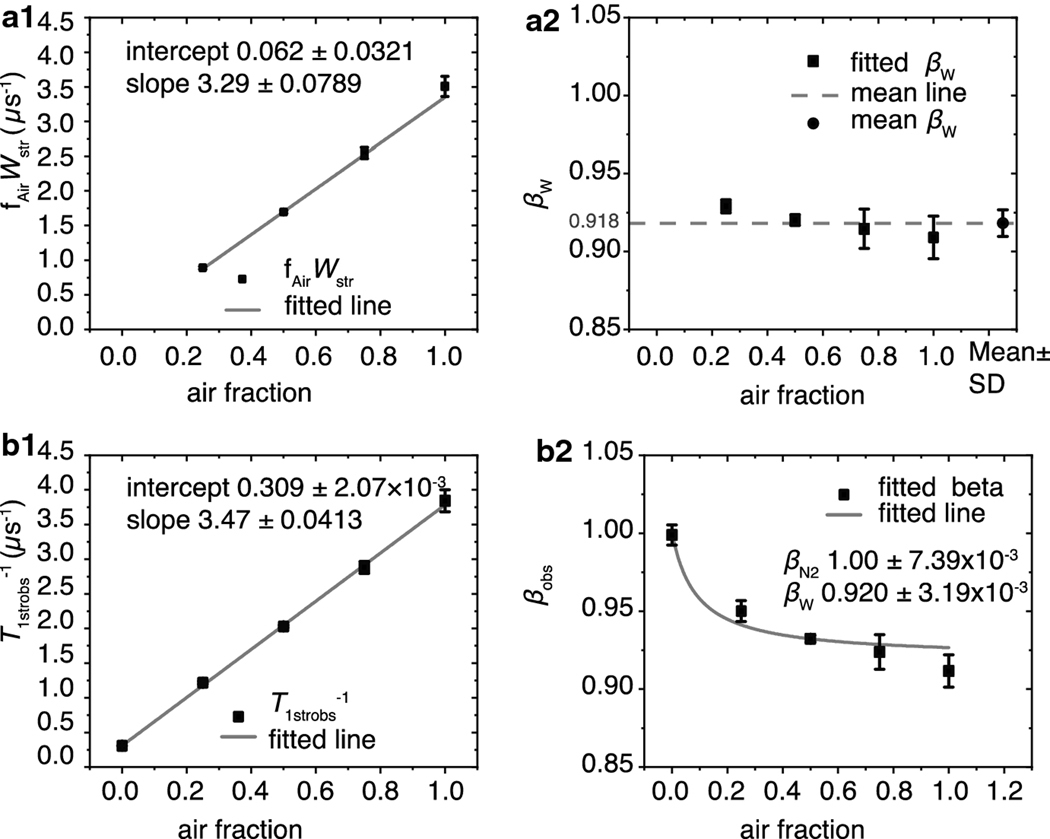
Here, we compare SOTP (W_strs and β_Ws) and rotational diffusion (T_1strN2⁻¹ and β_N2) parameters extracted using Eqs. 8a (special case) and 9b (general case) from experimentally obtained SR signals of ASL labeled LLMs. The results are summarized in Fig. 5.

Fig. 5.

The fitting parameters f_AirW_str, β_W, T_1strobs⁻¹, and β_obs obtained from fitting the SR signals of the LLM using appropriate equations and plotted versus the air fractions at which they were obtained. (a1) The average f_AirW_str values obtained from fitting at least three SR signals using Eq. 8a are indicated by black squares with vertical bars that represent the standard deviations. The gray line is the linear fit of these data points with an intercept of 0.062 ± 0.032 and a slope of 3.29 ± 0.0789 μs⁻¹_. The values following the ± sign are standard-error-of-parameter. (a2) The black squares are the average values of β_Ws obtained from fitting at least three SR signals using Eq. 8a. The vertical bars represent their standard deviations. The average of these values was found to be 0.918 ± 8.55 × 10⁻³ and is represented by a black circle; the standard deviations are represented by vertical bars, respectively. The dashed gray line indicates where the measured values fall in relation to the mean. (b1) The average T_1strobs⁻¹ values obtained from fitting at least three SR signals using Eq. 9b are indicated by black squares with vertical bars that represent the standard deviations. The gray line is the linear fit of these data points with an intercept of 0.309 ± 2.07 × 10⁻³ and a slope of 3.29 ± 0.0413 μs⁻¹. The values following the ± sign are standard-error-of-parameter. (b2) The black squares are the average values of β_obs obtained from at least three SR signals, and the vertical lines correspond to standard deviations. The fit to Eq. 10 is indicated by the gray line. The values of the intercept and slope obtained from the linear fit of the points in (b1) represent T_1strN2⁻¹ and W_str, respectively, and were held constant during fitting. The β_N2 and β_W parameters were allowed to vary and converged at 1.00 ± 7.38 × 10⁻³ and 0.920 ± 3.19 × 10⁻³, respectively. The values following the ± signs are the standard-error-of-parameter.

When fitted with Eq. 9b, the averaged T_1strobs⁻¹ and β_obs values from at least three SR signals obtained anaerobically were 0.309 ± 1.65 × 10⁻³ μs⁻¹ and 1.00 ± 6.37 × 10⁻³, respectively. The value of β_obs indicates that the spin-lattice relaxation rate is a single exponential and that rotational diffusion of the spin labels is homogeneous. However, as demonstrated in Fig. 5 (a2 and b2), the LLMs contain more than one OTP. LLMs made of the total lipid extract from the lens nucleus contain more than 50 mol% cholesterol, which ensures that these membranes are in the liquid-ordered phase [45]. Additionally, at such a high cholesterol content, pure cholesterol bilayer domains are formed within that phase. This phase is named structural liquid-ordered phase [57] (or dispersed phase [58]). In SR experiments, these domains cannot be discriminated with the use of only ASL because the spin-lattice relaxation times of ASL due to rotational diffusion in these domains are too close. Only in the presence of molecular oxygen are these domains clearly distinguished [18]. The results presented here confirm our previous results.

W_str was obtained from the slope of a straight line formed by either f_AirW_str or T_1strobs⁻¹ versus air fraction Fig.5 (a1and b1). W_str extracted from the slope of the straight line formed by the values obtained from Eq. 8a (f_AirW_str versus air fraction) was 3.29 ± 7.89 × 10⁻² μs⁻¹, and that extracted from the slope of the line formed by the values obtained from Eq. 9b (T_1strobs⁻¹ versus air fraction) was 3.47 ± 4.12 × 10⁻² μs ⁻¹. These values have an approximately 5% difference.

To check for self-consistency, the y-intercept of each graph also was analyzed. When Eq. 8a was used the obtained y-intercept, −6.22 × 10⁻² ± 3.21 × 10⁻² μs⁻¹ was close to its theoretical value of zero. When Eq. 9b was used, the y-intercept of the T_1strobs⁻¹ versus air fraction line matched the value obtained under nitrogen 0.309 ± 4.08 × 10⁻² μs⁻¹.

The β_W values obtained from Eq. 8a are plotted versus the air fraction that they were obtained at in Fig. 5a2. Their average was found to be 0.918 ± 8.55 × 10⁻³. When using Eq. 9b, the β_W of 0.920 ± 3.19 × 10⁻³ and β_N2 of 1.00 ± 7.39 × 10⁻³ were elucidated by fitting the graph of β_obs versus air fraction with Eq. 10. The corresponding T_1strN2⁻¹ and W_str values obtained from the rate graph Fig. 5b1 were held constant. Notably, the fitted β_N2 matches the β_obs obtained anaerobically of 1.00 ± 6.37 × 10⁻³ and confirms the self-consistency of the results.

Together, these analyses demonstrate that Eqs. 8a and 9b provide comparable and self-consistent rate and heterogeneity parameter values. The rate parameter variability of 5% may be due to the noise. The heterogeneity parameters display a similar pattern of being higher than the fitted value at lower air fractions and lower than the fitted value at higher air fractions.

Special and general cases: A comparison of samples with heterogenous T_1N2⁻¹s in intact membranes

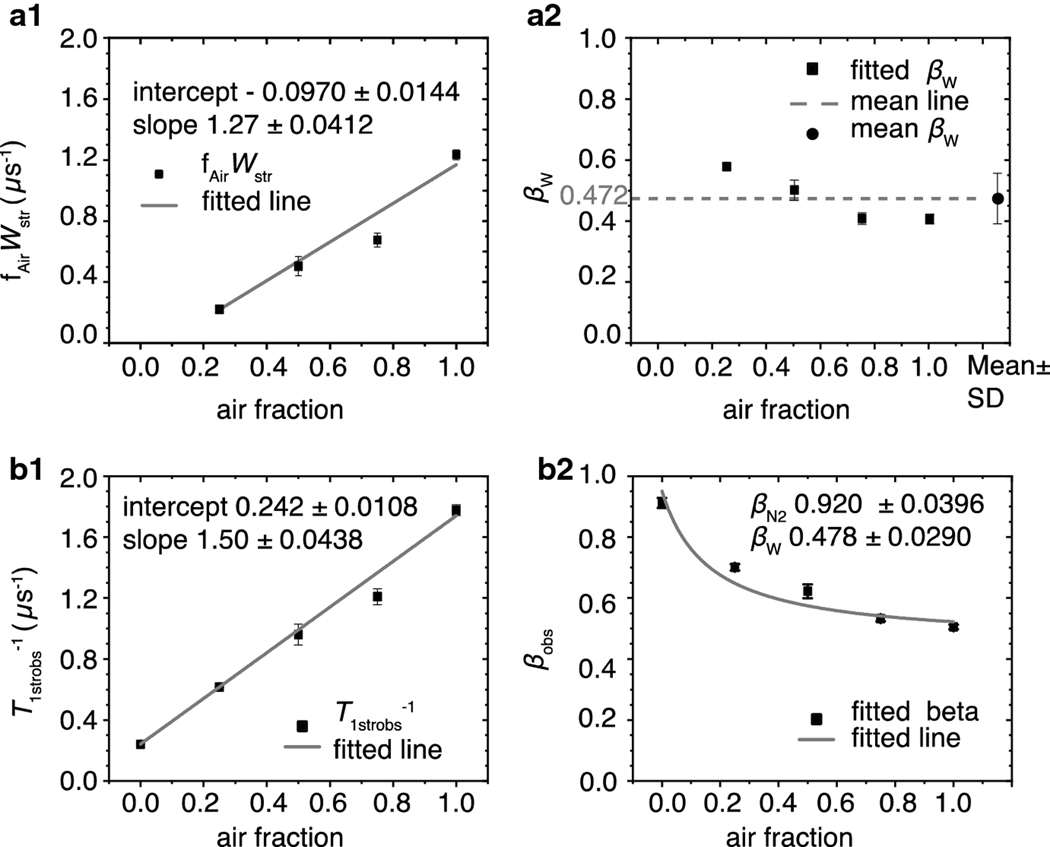
To demonstrate the application of “special” and “general” cases to analysis of the SR signals from samples that showed heterogeneity under deoxygenated conditions, we isolated intact porcine nuclear eye lens membranes and labeled them with ASL. The SR signals for samples equilibrated at different air fractions were obtained, as described in the Methods section. These signals were fitted using Eqs. 8b and 9b, and the results are summarized in Fig. 6.

Fig. 6.

The fitting parameters f_AirW_str, β_W, T_1strobs⁻¹, and β_obs obtained from air titration of intact nuclear eye lens membranes plotted versus the air fractions at which the signals were obtained. (a1) The black squares are the average f_AirW_str values obtained from fitting at least three SR signals using Eq. 8b. The vertical bars represent the corresponding standard deviations. The gray line is the linear fit of these data points with an intercept of −9.70×10⁻² ± 1.44×10⁻² and a slope of 1.27 ± 4.12 ×10⁻² μs⁻¹. The values following the ± sign are standard-error-of-parameter. (a2) The black squares are the average values of β_Ws obtained from fitting at least three SR signals using Eq. 8b. The vertical bars represent their standard deviations. The black circle represents the average of these values of 0.472, and the vertical bars indicate the standard deviation of 0.0766. The dashed gray line indicates where the measured values fall in relation to the mean. (b1) The average T_1strobs⁻¹ values obtained from fitting at least three SR recovery signals using Eq. 9b are indicated by black squares with vertical bars that represent the standard deviations. The gray line is the linear fit of these data points with an intercept 0.242 ± 1.08 × 10⁻² and a slope of 1.50 ± 4.38 × 10⁻² μs⁻¹. The values following the ± sign are standard-error-of-parameter. (b2) The black squares are the average values of β_obs obtained from at least three SR signals, and the vertical lines correspond to standard deviations. The fit to Eq. 10 is presented by the gray line. The values of the intercept and slope obtained from the linear fit of the points in (b1) represent T_1strN2⁻¹ and W_str, respectively, and were held constant during fitting. The β_N2 and β_W parameters were allowed to vary and converged at 0.920 ± 0.0396 and 0.477 ± 0.0290, respectively. The values following the ± signs are the standard-error-of-parameter.

The average T_1strN2⁻¹ and the corresponding standard deviation of at least three SR signals obtained under nitrogen was found to be 0.241 ± 6.94 × 10⁻³ μs⁻¹ with a corresponding β_N2 of 0.912 ± 0.0167. The presence of integral membrane proteins in intact nuclear fiber cell membranes induced the formation of new lipid domains, namely boundary lipids and trapped lipids [14,45]. In these domains, the motion of lipids was significantly restricted as compared with bulk lipids, which is reflected by the smaller T_1strN2⁻¹ as compared with those measured in LLMs. Additionally, the presence of these domains increased the heterogeneity of the rotational diffusion of ASL measured under nitrogen. To extract SOTP parameters, these values were held constant while the signals were fit to Eq. 8b. The fitted f_AirW_str values were plotted against the air fractions at which they were obtained in Fig. 6a1. The slope of the straight line formed by these points, which corresponds to W_str, was found to be 1.27 ± 4.12 × 10⁻² μs⁻¹. Similarly, the T_1strobs⁻¹ values obtained from fitting the same signals to Eq. 9b were plotted versus the air fractions at which they were obtained, and W_str of 1.50 ± 4.38 × 10⁻² μs⁻¹ was obtained from the slope of the straight line formed by these points. Although the errors of fitting are comparable, the resulting two values differ from one another by 15%.

We evaluated the y-intercepts of each graph to check the self-consistency of results. The “special case” rate line, which should pass through the origin, came in at −9.70 × 10⁻² ± 1.44×10⁻². The “general case” line was 0.242 ± 1.08×10⁻² μs⁻¹ and matches the T_1strN2⁻¹ obtained under nitrogen.

The heterogeneity parameter β_W for the special case was obtained directly by fitting the signals using Eq 8b. The average of these values was 0.472 ± 7.66 × 10⁻². This value is close 0.478 ± 2.90 × 10⁻², which is the value obtained by fitting the β_obs versus air fraction graph with Eq. 10, as demonstrated in Fig. 6b2. The W_str and T_1strN2⁻¹ were kept constant during the fitting. According to that fit, the β_N2 is 0.920 ± 3.99 × 10⁻² and is close to the value of 0.912 ± 1.67 × 10⁻² obtained under nitrogen (Fig. 6).

Also, in intact membranes, the β_obs parameters do not fit the idealized behavior predicted by Eq. 10. These parameters are higher than the fitted values at lower air fractions and lower than the fitted values at higher air fractions (Fig. 6b2). Similarly, when the “special case” method was used, the fitted β_Ws at lower air fractions were higher than the mean and at higher air fractions were lower than the mean (Fig. 6a2). Because the same pattern of behavior was observed for β parameters as a function of air fraction both in LLMs and in intact membranes, and because the behavior is independent of the method used (special case or general case), we do not think it is due to the method. These deviations may be due to the spectrometer noise and the higher number of averages required to obtain a signal at higher air fractions, or they may be due to problems with the spectrometer baseline. Such deviations also could be a sign that the real distributions are not ideal stretched exponentials.

The SR signals from the intact membrane are noisier than those from liposomes. The measurements may contain a larger error that is reflected in the slight inconsistency of results obtained by the “special case” and “general case.”

Distribution of spin-lattice relaxation rates of ASL in intact membranes and LLMs due to rotational diffusion

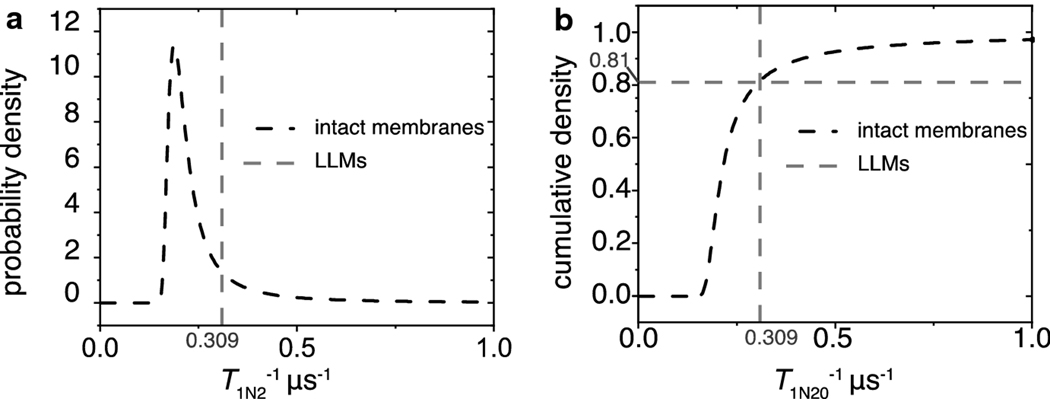
To make ultimate sense of the fitting parameters obtained by the SEF, we constructed and analyzed probability distributions [43,44]. First, as demonstrated in Fig.7, we did so for the parameters obtained for membranes equilibrated with nitrogen, when they reflected the rotational diffusion of lipid spin labels. Spin-lattice relaxation rates due to the rotational diffusion are heterogenous in intact membranes, while in LLMs the SR signal is fitted by a single exponential function with the spin-lattice relaxation rate depicted by a single line (delta function). The distribution of rates in intact membranes indicates that 81% of the signal is due to relaxation rates slower than those of the LLMs, and the remaining are faster.

Fig. 7.

The probability distribution densities of rotational diffusion spin-lattice relaxation rates and the integrals (cumulative densities) were constructed as described in the text. (a) The probability distribution density for the spin-lattice relaxation rates associated with the rotational diffusion of ASL in the intact membrane is represented by the dashed black line. The dashed gray line at 0.309 μs⁻¹ represents the rotational diffusion spin-lattice relaxation rate of ASLs in LLMs. (b) The dashed black line is the cumulative density of rotational diffusion spin-lattice relaxation rates for ASL in the intact membranes. The gray dashed line signifies the rotational diffusion spin-lattice relaxation rate of ASLs in LLMs. The crossing point between these lines indicates that 81% of the signal in the intact membranes is from ASLs that relaxed slower than those in the LLMs, and the remainder of the signal relaxed faster.

LLMs approximate bulk lipid domains in intact membranes and are expected to be the most fluid in terms of rotational diffusion. The presence of faster spin-lattice relaxation rates due to rotational diffusion in the intact membranes can be explained by the fact that the LLMs are composed of lipids from all layers in the nuclear region that are pulled together and made into multilamellar vesicles. The lipids in the intact membranes maintain their unique lipid compositions for each isolated fiber cell layer, and the SR signal is the sum of signals from membranes of each layer. Additionally, intact membranes possess integral and peripheral proteins that induce specific lipid organization and asymmetry [59–61] that may be responsible in a more fluid environments than in LLMs.

Distribution of OTPs in intact membranes and LLMs

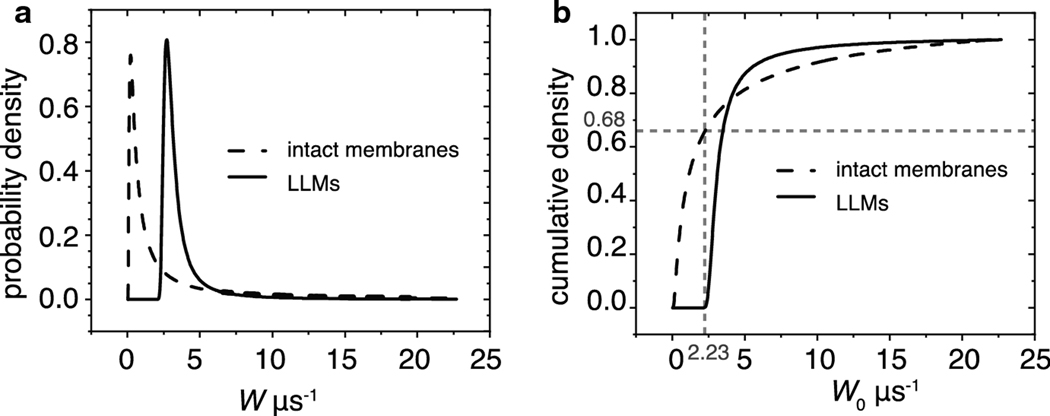
The extracted SOTP parameters were used to construct distribution of OTPs in intact membranes and in LLMs as outlined in [43]. The distributions in Fig. 8, allowed us to make the following observations. The LLMs exhibit OTP heterogeneity that indicates the presence of various domains. The heterogeneity of the OTPs in intact membranes is significantly larger than that in LLMs. In intact membranes, 66% of the collisions of oxygen with spin labels possess collision rates slower than 2.23 μs⁻¹. Fewer than 0.01% account for such slow rates in LLMs. The slow rates may be indicative of trapped lipid domains where oxygen concentration is low, or diffusion is slow. The crossing point of cumulative density curves in Fig. 8b indicates that, similar to rotational diffusion, a higher density of fast oxygen collision rates is present in the intact membranes than in LLMs. This indicates that the organization of intact membranes in the sample is considerably more heterogenous than in the LLM sample.

Fig. 8.

The probability density distributions of OTPs sensed by ASL in LLMs and intact membranes and their integrals were constructed as described in the text. (a) The probability density distributions of OTPs in intact membranes are indicated by a dashed black line, and in LLMs by a solid black line. (b) The integrals of these distributions are the cumulative densities. The dashed black lines are the cumulative densities of OTPs in intact membranes, and the solid black line is that of LLMs. The gray dashed lines indicate that 68% of the density in the intact membranes falls below 2.23 μs⁻¹, whereas less than 0.01% of the density of the LLMs can be found below that rate.

The shapes of the stretched exponential distributions are unique because the two fitting parameters can produce only a single distribution that cannot be reproduced with different T_1str⁻¹s and βs and that uniquely predicts the probability of finding a range of rate constants within the signal. The heterogeneity parameter β dictates the shape of the distribution. For instance, when β is one, the mode of the distribution and the T_1str⁻¹ value are the same, and the distribution is a delta function. When the β becomes smaller, the mode of the distribution shifts toward slower rates and away from the T_1str⁻¹ value; the distribution widens and produces a longer tail associated with a probability of faster relaxation rates that can be found within the signal.

Conclusion

SR EPR data from spin labeled lipid membranes provide membrane physical properties in terms of the rotational diffusion of lipids and oxygen-diffusion-concentration product within the membrane. In our previous publication [43], using SEF parameters, we constructed the probability distributions of spin-lattice relaxation rates due to the rotational diffusion in the biological spin-labeled membrane samples coming from porcine eye lenses. This data treatment removes the need to fit a complex sample to the distinct exponentials. Because cholesterol, phospholipid [29,34,37,46], and protein compositions [48,62] of fiber cell membranes change gradually as the cells age, and our samples are composed of many layers of such cells, the number of different environments experienced by spin labels may be difficult to estimate. The SEF method of analysis allows us to consider the minute physical property differences in membranes of cells from different layers as well as the different domains within those membranes. Our understanding of the properties of the SEF fitting parameters allowed us to take on a new level of complexity when two independent relaxation processes contribute to SR signals. The additional relaxation pathway was provided by paramagnetic molecules of oxygen that, through collisions with spin labels, contribute to the decay of the SR signals. To the best of our knowledge, we are the first to apply the SEF analysis to a system in which two relaxation processes contribute to the exponential-like decay signal. We developed theory to analyze SR signals with the SEF, which allowed us to obtain stretched exponential fitting parameters separately for each contributing process and applied it to practice.

Because any enhancement of the spin-lattice relaxation rate during air titration is due to Heisenberg exchange with oxygen, the “special” case method (Eqs. 8a and 8b) relies on accurately obtained rotational diffusion parameters. These remain constant at any oxygen partial pressure so long as other experimental conditions remain constant. Holding rotational diffusion parameters constant allows to extract SOTP parameters W_str and β_W at any known oxygen concentration.

The “general” case relies on observation that the product of two stretched exponential terms produces a relaxation curve that can be fitted to a third stretched exponential. The stretched rate of the new exponential was found to correspond to the sum of the stretched rates of the two contributing processes (Eq. 9b). Thus, analogous to the previously defined OTP [4], the rate component of SOTP is defined as:

$$W_{\text{str}}={T_{\text{1strAir}}}^{-1}–{T_{\text{1strN2}}}^{-1}.$$ (11)

A β parameter remains constant when all rates within a distribution are multiplied by the same factor. The β_obs of a product of the two stretched exponentials is the sum of the two parameters weighted by their stretched exponential rates (Eq. 10).

We demonstrated that the advanced theory for the application of the SEF to analyze SR signals for membranes saturated with molecular oxygen allowed construction of (a) probability distributions of spin-lattice relaxation rates determined by the rotational diffusion of spin labels, and (b) the distribution of relaxations induced strictly by collisions with molecular oxygen. These probability distributions were constructed for simple LLMs and intact nuclear fiber cell membranes. They show the effects of integral and peripheral membrane proteins on membrane fluidity, as well as the heterogeneity of membrane fluidity sensed by the cholesterol analog spin label alone (Fig. 7) and sensed by the movement and solubility of molecular oxygen (Fig. 8. The latter distribution is determined by the distribution of oxygen-diffusion-concentration products within the membrane, which forms a flexible new way to describe membrane fluidity and heterogeneity. Use of lipid spin labels, SR EPR, stretched exponential analysis, and discrimination by oxygen transport offer a powerful approach to analyze complex membranous samples derived from biological tissue.

Future Directions

The major goal of this paper was to advance the already established spin label SR EPR methods with the use of SEF analysis [43], while paying special attention to the effect of molecular oxygen. We developed the theory and formulated basic equations for the analysis of SR EPR signals using SEF in membranes equilibrated with air. Because this is a new methodological approach, we focused our paper on one spin label, namely the cholesterol analog, ASL. We also chose two systems on which we showed application of these new approaches, namely intact fiber cell plasma membranes of the eye lens nucleus and LLMs prepared from the total lipid extract from these intact membranes. In this section, we indicate other significant applications of the developed method.

We think that the most significant and exciting application is to use the two fitting parameters provided by the SEF for a multivariate cluster analysis of stretched-exponential data from complex intact membranes. The feasibility of the cluster separation based on the origin of lens fiber cell membranes was demonstrated in our recent paper where porcine cortical and nuclear fiber cell membranes were clearly separated into two groups [43]. These experiments were performed for deoxygenated samples; thus, only the fluidity and heterogeneity of lipid spin labels defined the separation of the data. Our preliminary data indicate that the separation of data points of these clusters increases enormously for membranes saturated with air when the SOTP parameters are used to separate the data points.

State-of-the-art EPR techniques developed at the National Biomedical EPR Center at the Medical College of Wisconsin (Milwaukee, WI) were advanced to a level that allows measurements using very small samples, i.e., volumes of 30–150 nL [63–65]. This makes performing measurements for membranes separated from a single human lens feasible and, thus, permits the data analysis to consider the health history of the donor. Thus, stretched-exponential data can be used for exploratory research where membranes from different human populations will be obtained and SR EPR SEF data compared based on health histories. We believe that these clusterings should help to elucidate predispositions for cataract formation. This is the first step to developing alternative strategies to prevent, slow the progression of, and ultimately cure cataracts.