Toward Precisely Controllable Acoustic Response of Shell-Stabilized Nanobubbles: High Yield and Narrow Dispersity

Abstract

Understanding the pressure dependence of the nonlinear behavior of ultrasonically excited phospholipid-stabilized nanobubbles (NBs) is important for optimizing ultrasound exposure parameters for implementations of contrast enhanced ultrasound, critical to molecular imaging. The viscoelastic properties of the shell can be controlled by the introduction of membrane additives, such as propylene glycol as a membrane softener or glycerol as a membrane stiffener. We report on the production of high-yield NBs with narrow dispersity and different shell properties. Through precise control over size and shell structure, we show how these shell components interact with the phospholipid membrane, change their structure, affect their viscoelastic properties, and consequently change their acoustic response. A two-photon microscopy technique through a polarity-sensitive fluorescent dye, C-laurdan, was utilized to gain insights on the effect of membrane additives to the membrane structure. We report how the shell stiffness of NBs affects the pressure threshold (P_t) for the sudden amplification in the scattered acoustic signal from NBs. For narrow size NBs with 200 nm mean size, we find P_t to be between 123 and 245 kPa for the NBs with the most flexible membrane as assessed using C-Laurdan, 465–588 kPa for the NBs with intermediate stiffness, and 588–710 kPa for the NBs with stiff membranes. Numerical simulations of the NB dynamics are in good agreement with the experimental observations, confirming the dependence of acoustic response to shell properties, thereby substantiating further the development in engineering the shell of ultrasound contrast agents. The viscoelastic-dependent threshold behavior can be utilized for significantly and selectively enhancing the diagnostic and therapeutic ultrasound applications of potent narrow size NBs.

Clinical ultrasound contrast agents (UCAs), also referred to as microbubbles (MBs), have augmented the capabilities of ultrasound (US) in areas such as cancer detection, tumor characterization, and theranostics.¹⁻⁵ There has been a substantial recent interest in the preclinical development of nanoparticle-based UCAs; these include nanobubbles (NBs), nanodroplets, and nanovesicles.⁶⁻¹⁰ One advantage of the submicron UCAs is that they have been shown to extravasate beyond leaky tumor vasculatures, unlike MBs that are confined to the blood vessels because of their large size (1–10 μm).¹¹⁻¹⁵ This extravasation is well-suited for applications such as molecular imaging and targeted drug delivery. Applications of submicron UCAs range from measuring T lymphocyte infiltration in cardiac tissue¹⁶ to detection of type 1 diabetes,¹⁸ prostate cancer,^13,17 and targeted delivery for photothermal therapy.¹⁹ Despite the recent growth of MB- and NB-based imaging applications, little work has been done thus far in understanding how the physical properties of the shell determine their interaction with US, and whether this interaction is consistent with the current theoretical and experimental understanding of models of bubble oscillation. In this work, we thus examine how changes in the NBs size distribution and shell structure affect their acoustic response.

The dynamics of MBs in an acoustic field depend strongly on US parameters (e.g., US acoustic pressure and frequency) and bubble properties (e.g., size, gas, shell elasticity, and shell viscosity) and can be mathematically described by nonlinear encapsulated bubble models such as the Marmottant model.²⁰⁻²² Numerous studies have demonstrated the strong effect of the UCA shell elasticity and size on the UCA resonance frequency^20,23,24 and acoustic pressure of maximal signal intensity with minimal MB destruction.²⁵ Experiments with various lipid shell compositions have also shown a strong dependence on nonlinear MB behavior.²⁶⁻³⁰ Thus, the rational design of the shell structure and size of the UCAs has the potential to tune their behavior to a given US frequency and pressure.

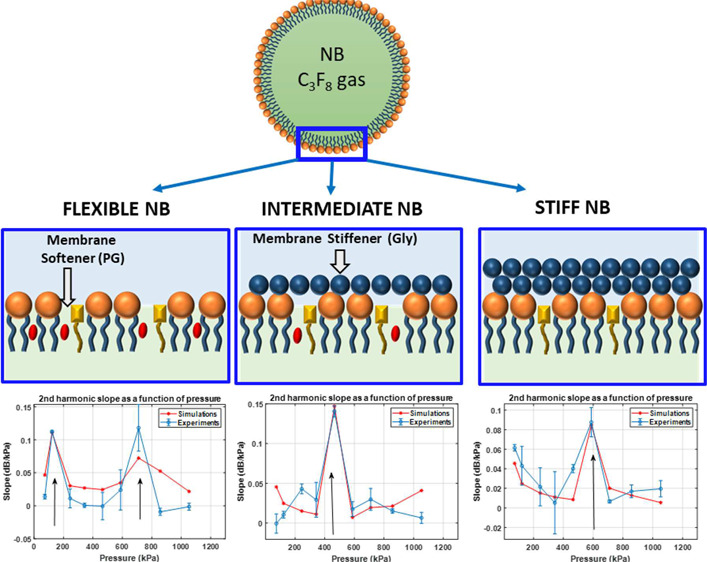
The shell properties of phospholipid (PL)-stabilized UCAs can be altered by introducing membrane additives. PL shells can be made stiffer by incorporating membrane stiffeners such as glycerol (Gly) and carbohydrates or more flexible by incorporating membrane softeners (or edge-activator) such as propylene glycol (PG) and cholesterol.³¹⁻³⁴ Gly has been shown through X-ray and neutron reflectivity measurements to preferentially interact via hydrogen bonding with the PL head, dehydrating the PL shell and increasing shell stiffness.³⁵ On the other hand, PG has been utilized as a membrane softening component in ultradeformable liposomes.^36,37 PG assembles in the PL membrane, reducing PL packing order and stiffness and imparting membrane fluidity.³⁶⁻⁴² Incorporation of either Gly or PG into a bubble shell affects its shell properties as a result of a change in the PL packing order.^{35,36,41,43−45}

In order to accurately explore the influence of shell properties on the bubble behavior, we need to make the measurements independent of the effect of the bubble size distribution. In polydisperse solutions, the acoustic response is dominated by bubble-to-bubble variations that would dominate over any effects of shell structure. In this work, we aim to investigate the effect of shell stiffness on the nonlinear behavior of NBs independent of the size effects. To achieve this, NBs with three different shell compositions were manufactured. NBs of different shell stiffness were prepared by the incorporation of different amounts of Gly as a membrane stiffener and PG as a membrane softener. The relative PL packing order in the bubble membrane was assessed by a common assay typically used to examine lipid packing in cell membranes.^32,46−48 The technique provides complementary information to the developed shell property measurement techniques. This can be done through two-photon microscopy with a polarity-sensitive fluorescent probe such as 6-lauryl-2-dimethylamino-napthalene (C-laurdan)^{32,33,46−52} by calculating the average generalized polarization (GP) value from the emitted fluorescence intensities at 450 and 500 nm after exciting C-laurdan with a 800 nm laser in a two-photon microscopy setup. This method has been used to measure lipid transfer from MBs to cell membranes and recently to measure MB shell characteristics.⁵³

We then introduce a simple but effective method to produce NBs with very narrow size distribution and high yield. Three NB populations were filtered to have similar sizes with a narrow size distribution and diluted to have similar concentration. The effect of shell characteristics on the nonlinear oscillations of NBs in an US field was then studied by exposing NB solutions to US of varying pressures and analyzing the contrast harmonic images. The dependence of pressure for substantial increase in nonlinear oscillation of PL-stabilized NB solution (200 nm diameter) on shell stiffness was studied both experimentally and numerically.

Results and Discussion

In this section, we first present the experimental results of the work. We discuss how the addition of different shell additives changes the stiffness of the NB shells. Then we report on the influence of the shell stiffness and size distribution on the acoustic behavior of the NBs. Next, we present a detailed numerical investigation of the influence of the viscoelastic behavior of the shell on the NB behavior. Using the insights gained by analyzing the numerical results, we discuss the mechanisms behind the observed experimental behavior and their possible applications.

Shell Lipid Packing Order and Stiffness

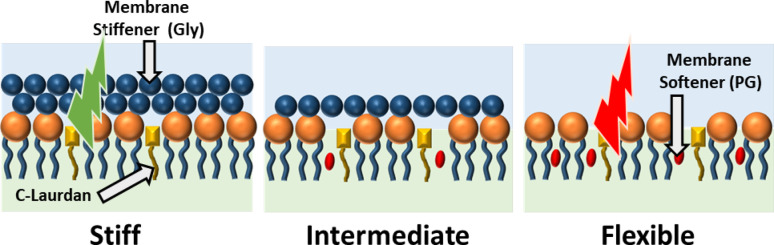
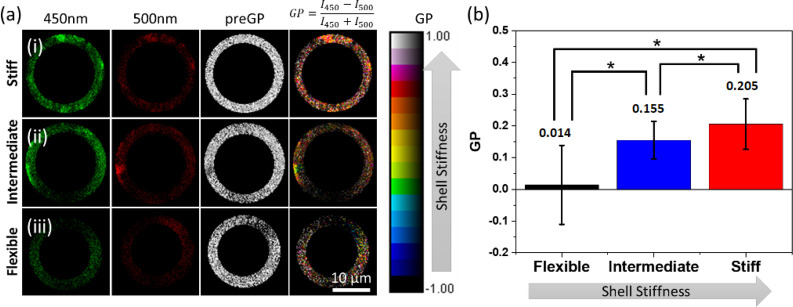
Figure 1 shows a schematic representation of the assembly of C-laurdan, PG, and Gly in the PL membrane. Incorporation of Gly (20% v/v) dehydrates the PL membrane, which increases the PL packing order as shown schematically in Figure 1. The increase in PL packing order causes the C-laurdan to emit a higher intensity light at 450 nm compared to 500 nm since it is surrounded by a less polar environment (Figure 2a). The GP value (formula indicated in Figure 2a) for each pixel was calculated and averaged throughout the whole bubble shell. The average GP value for PL membrane with Gly was determined to be 0.205 (Figure 2b). On the other hand, incorporation of PG (20% v/v) in the PL membrane increases the distance between the PL molecules, thereby letting more water surround C-laurdan (Figure 1). The emission of C-Laurdan at 450 nm has a similar intensity as compared to at 500 nm (Figure 2a,iii). The mean GP for the PL membrane with PG was calculated to be 0.014 (Figure 2b), which is less than the mean GP for PL with Gly. Therefore, incorporation of PG results in an increase in PL disorder and a consequent decrease in membrane stiffness. The measurement of GP for the PL membrane with PG or Gly provides an additional confirmation that incorporation of Gly increases the PL packing order, consistent with what Terakosolphan et al. and Pocivavsek et al. have reported.^43,64 Incorporation of both Gly (10% v/v) and PG (10% v/v) resulted in an average GP value of 0.155 (Figure 2b) that is in-between the GP values for PL with Gly and PL with PG. This suggests that the C-laurdan in the membrane is surrounded by a relatively polar environment in some areas and a relatively nonpolar environment in other areas, as schematically shown in Figure 1. The difference in PL packing order through addition of different membrane additive is expected to have a significant impact on the shell stiffness, and subsequently on how NBs interact with US.

Figure 1.

Schematic of bubble membrane showing the influence of membrane stiffener and membrane softener in the PL packing as detected by the fluorescence emission of C-laurdan. C-Laurdan in the packed membrane is expected to emit a higher intensity light at 450 nm compared to 500 nm (green). On the other hand, C-laurdan in a loosely packed membrane is expected to emit a similar intensity light at 450 and 500 nm (red).

Figure 2.

(a) Fluorescent images, pre-GP, and GP images of the shell membrane with different additives at 450 and 500 nm emission wavelength. (b) Comparison of average GP for bubbles with different shell stiffness (n = 55 for each bubble type).

Size Isolated NBs

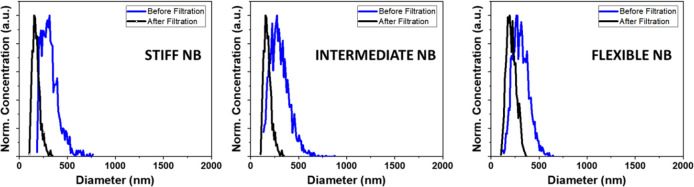
After centrifugation, the size distribution and concentration were determined using a resonant mass measurement system before and after filtration (Figure 3, Table 1) as previously described.⁶⁵ Although no bubbles larger than 1 μm can be observed in the unfiltered population, the size of NBs broadly ranged from 100 nm to about 800 nm with a mean diameter of 310 ± 10 nm for flexible NB, 301 ± 9 nm for intermediate NB, and 318 ± 11 nm for stiff NB. The broad size distribution of the population hinders the accurate study of the shell viscoelasticity on the NB dynamics. The size distribution of filtered NBs (Figure 3, black trace) shows a mean size of 213 ± 5 nm for flexible Ref 66 was not cited in your paper so a citation was placed here; please rectify.NB, 176 ± 3 nm for intermediate NB, and 178 ± 5 nm for stiff NB nm (Table 1), with no NBs larger than 400 nm observed for all groups. NB solutions were of different concentrations after filtration but were adjusted to an approximate number density of 5.0 × 10⁸ NBs/mL by addition of PBS for subsequent US studies.

Figure 3.

Size distribution and concentration of NBs, characterized by a resonant mass measurement, of each type before and after filtration through a 400 nm pore membrane filter.

Table 1. Min, Max, and Mean Size before and after Filtration of NBs with Different Additives^a.

	before			after
	min	max	mean (nm)	min	max	mean (nm)
flexible NB	125	645	310 ± 10	105	375	213 ± 5
intermediate NB	135	875	301 ± 9	105	345	176 ± 3
stiff NB	185	765	318 ± 11	105	325	178 ± 5

^aThe size distributions are shown in Figure 3. In each case, the standard deviation is for the measured mean.

Acoustic Signals from NBs

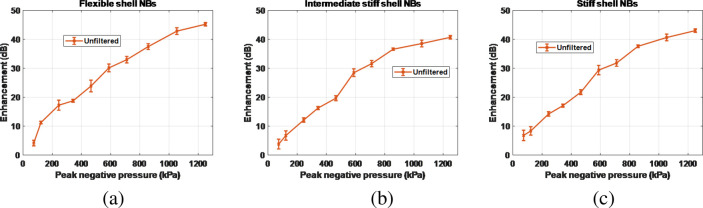
Results of the acoustic measurements of the unfiltered polydisperse populations are shown in Figure 4. To quantify the nonlinear signal from the NB solution, the raw US echo power was averaged over the region of interest (ROI), and the enhancement was calculated relative to the signal from the surrounding agarose phantom at the same depth. Figure 4 shows that there is no clear difference between the received signals from the three populations, most likely due to the polydisperse nature of the NB solutions that masks the shell effects.

Figure 4.

Contrast enhancement of polydisperse NB solution with (a) flexible, (b) intermediate, and (c) stiff shells, relative to the agarose phantom for different PNPs. Error bars are the standard deviation of three independent replicates.

Figure 5 shows the comparison between the second harmonic contrast enhanced images of the filtered monodisperse NB solutions. There is a clear difference between the echogenicity of the three NB populations. This is witnessed by a sudden increase in the contrast enhancement of the flexible NBs at 245 kPa, followed by the sudden enhancement at 465 and 588 kPa for the intermediate and stiff shell NBs, respectively. The flexible NB solution undergoes another sudden enhancement at 857 kPa, followed by loss of echogenicity at 1053 kPa (possibly due to NB destruction, and the mechanism is explored in the Supporting Information).

Figure 5.

Representative US CHI mode contrast images of solutions of filtered monodisperse: (a) flexible, (b) intermediate and (c) stiff shell NBs for PNP = 74–1250 kPa.

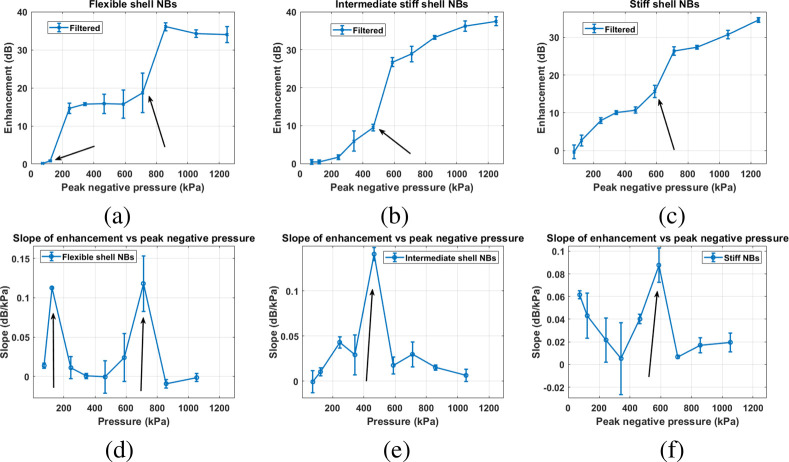
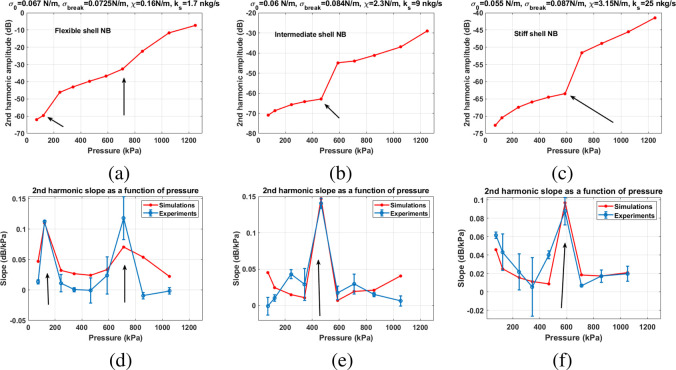
Figure 6 shows the enhancement as a function of pressure for all three filtered formulations. To better identify the pressure threshold for the signal and the sudden amplification, we also plot the slope of the contrast enhancement as a function of pressure. To plot these graphs, the raw US echo power was averaged over the ROI (white dashed square in Figure 6), and the enhancement was calculated relative to the signal from the surrounding agarose phantom at the same depth. Compared to Figure 4, a substantial difference in enhancement was observed for the US signal from NBs before and after filtration for all formulations. Narrowing of the size distribution by filtration (black traces in Figure 3) yielded clear activation pressure thresholds for all bubble types. This threshold was not detectable for the unfiltered NBs (blue traces, Figure 3).

Figure 6.

Contrast enhancement of filtered monodisperse NB solution with (a) flexible, (b) intermediate, and (c) stiff shells relative to the agarose phantom for different PNPs. The slope of the contrast enhancement with respect to peak negative pressure for (d) flexible, (e) intermediate and (f) stiff shell NBs. Arrows mark the pressure threshold (P_t) of sudden signal enhancements. Error bars are the standard deviation of three independent replicates.

For flexible NBs, the peak negative pressure (PNP) was varied between 74 and 1250 kPa, as shown in Figure 6a. There is no detectable nonlinear activity at PNP between 74 and 123 kPa (MI = 0.03–0.05). Increasing the PNP to 245 kPa results in a 14 dB increase in enhancement. A significant increase in enhancement occurred when the PNP was increased from 123 to 245 kPa, with a slope of 0.11 dB/kPa (Figure 6d). The absence of detectable signal from filtered flexible NBs at low PNP implies that these NB oscillations at this pressure are very weak, thus the signal generated is not within the detectable range of the US transducer. This behavior is unlike the polydisperse NB solution where there is no observable pressure threshold (P_t) for the unfiltered flexible NB solution. A further increase in PNP results in another sudden enhancement in pressure amplitude at 710–857 kPa with a slope of 0.12 dB/KPa.

For NBs containing both Gly and PG (intermediate NBs), the presence of the two membrane additives results in a membrane stiffness between that of the membrane with PG and membrane with Gly, as confirmed by intermediate GP value in Figure 2b.⁵⁴ Similar to the solution of the filtered flexible NB, there is a negligible detectable nonlinear activity when filtered intermediate NBs were exposed to a PNP below 343 kPa, as shown in Figure 6b,e. As soon as the PNP increases above 465 kPa, the signal is enhanced suddenly with a slope of 0.14 dB/kPa at 465 kPa (Figure 6e). A further increase in the PNP to 1250 kPa resulted in a steady increase in the enhancement.

For the filtered monodisperse stiff NBs, a steady increase in enhancement was measured between 343 and 465 kPa. Further increases in PNP to 588 kPa resulted in a substantial increase in brightness that continued to increase up to a PNP of 710 kPa. Analysis of the raw echo power and enhancement as a function of PNP reveals that a threshold pressure for a sudden amplification (P_t) exists between PNPs of 588 and 710 kPa with a slope of 0.08 dB/kPa. Such a transition region is not observed with the solution of unfiltered NBs, likely due to the effect of a broad NB size distribution on the scattering. The first P_t for the filtered flexible NB solution occurs at a lower pressure range (123–245 kPa) as compared to the intermediate NB solution (465–588 kPa) and filtered stiff NB solution (588–710 kPa). Moreover, only the flexible NB solution exhibits the second amplification P_t at 710–857 kPa.

These results suggest that there is a strong correlation between the P_t of different NB formulations and their relative shell stiffness as quantified by their average GP. Plotting the midpoint of the range of pressure values P_tvs average GP (Figure 7) reveals a linear dependence with an intercept of −0.06 ± 1.84 × 10^–4 and a slope of 0.041 ± 3.41 × 10^–5. This shows that there is a strong correspondence between NB shell stiffness and its nonlinear behavior under US.

Figure 7.

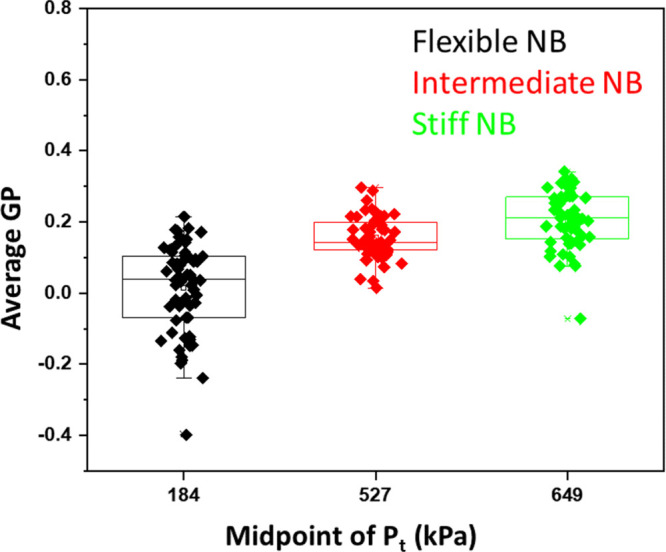
Correlation between the midpoint of the range of pressure values P_t of NB of different shell stiffness and the average GP of its shell.

Numerical Simulations

In order to investigate the mechanism behind the observed changes in the P_t for different NBs, we ran simulations over a large range of parameters and visualized the results of the second harmonic component (second SuH)⁶¹ of the scattered pressure and the slope of the second SuH as a function of excitation pressure amplitude. In this section, we show the effect of the different shell parameters (R₀), σ_rupture, χ, and k_s on the pressure threshold of the enhancement in the second SuH. Next, the shell parameters values that best fit the slope vs pressure curve in each case will be calculated. The reason the slope vs the pressure was chosen as the fitting curve is to minimize the influence of the parameters that lead to quantitative differences between the modeled second SuH and the enhancement amplitude in experiments. As the slope curve is relative to before and after the enhancement, its magnitude should be better matched between the experiments and the numerical simulations. This is because the different contributing factors may be canceled due to the relative nature of the slope curves, leaving only the enhancement difference.

Influence of the Shell Properties on the Threshold Behavior

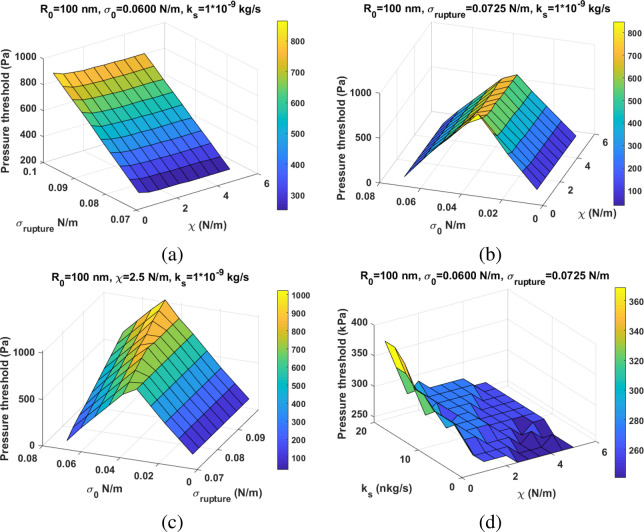
Figure 8 shows the pressure threshold for the sudden amplification of the second SuH as a function of the shell parameters. The changes in the value of shell elasticity have no (or minimal) effect on the pressure threshold (P_t) of the amplification (Figure 8a,b). However, changes in σ(R₀) and σ_rupture have a significant influence on the P_t. For a constant σ(R₀), P_t increases with increasing σ_rupture (Figure 8a). For a constant σ_rupture (using the water surface tension of 0.0725 N/m), there are two scenarios for the dependence of the P_t. P_t increases with increasing σ(R₀) until it reaches σ_rupture/2, beyond which P_t decreases with increasing σ(R₀) (Figure 8b). Figure 2c shows the P_t as a function of σ(R₀) and σ_rupture for constant k_s and χ. For σ(R₀) < σ_rupture/2, increasing σ_rupture has no effect on the P_t; however, for σ(R₀) < σ_rupture/2, increasing σ_rupture increases the P_t, with the highest rate of increase for σ(R₀) = σ_rupture/2. A higher k_s may increase the P_t (Figure 8d), however, the influence of the k_s on the P_t is orders of magnitude smaller than the influence of σ_rupture and σ(R₀). The k_s has a stronger effect on the P_t for a NB with smaller χ.

Figure 8.

Pressure threshold of the sudden enhancement in the second SuH (Z-axis) of a NB with R₀ = 100 nm as a function of: (a) χ – σ_rupture, (b) χ – σ(R₀), (c) σ_rupture – σ(R₀), and (d) χ – k_s.

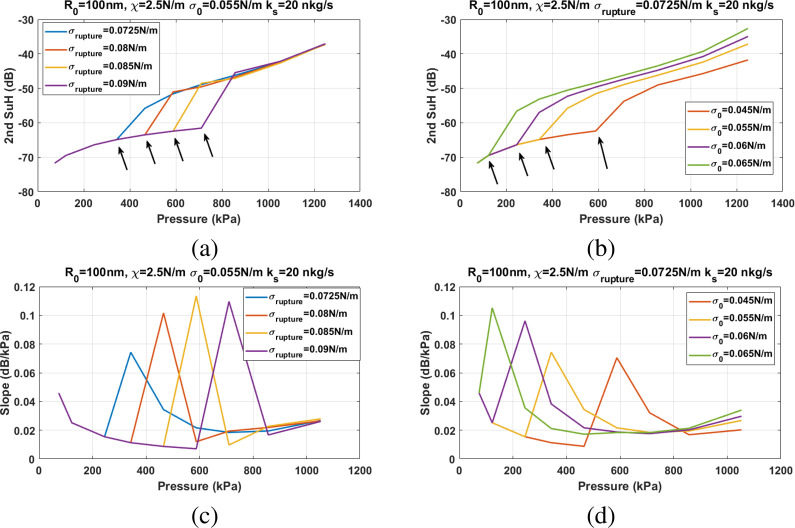
Figure 9 shows the influence of the σ_rupture and σ(R₀) on the P_t and the slope of the second SuH enhancement. For a given initial surface tension above 0.036 N/m, P_t (Figure 9a) increases with increasing σ_rupture with no apparent relation between the slope of enhancement (in dB/kPa) and σ_rupture (Figure 9c). For a given σ_rupture and for σ(R₀) > 0.036 N/m, the P_t (Figure 9b) and slope of enhancement (Figure 9d) decrease with increasing σ(R₀).

Figure 9.

Second SuH amplitude of the scattered pressure as a function of excitation pressure for a NB with R₀ = 100 nm, k_s = 20 nkg/s, and χ = 2.5 N/m: (a) for different σ_rupture when σ(R₀) = 0.055 N/m and (b) for different σ(R₀) when σ_rupture = 0.0725 N/m. (c and d) The corresponding slope of the second SuH enhancement as a function of the excitation pressure.

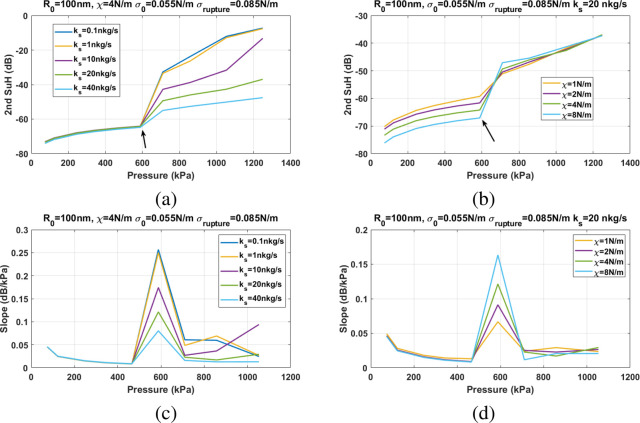
Figure 10 shows the influence of χ and k_s on the P_t and the slope of second SuH enhancement. Changes in χ and k_s do not have any effect on the P_t (Figure 10a,b). However, the slope of second SuH enhancement decreases with increasing k_s (Figure 10c) and increases with increasing χ (Figure 10d).

Figure 10.

Second SuH amplitude of the scattered pressure as a function of excitation pressure for a NB with R₀ = 100 nm, σ(R₀) = 0.055 N/m, and σ_rupture = 0.085 N/m: (a) for different k_s when χ = 4 N/m and (b) for different χ when k_s = 20 nkg/s. (c and d) The corresponding slope of the second SuH enhancement as a function of the excitation pressure.

Using the information gained by analyzing Figures 8–10, numerical simulations were performed for different values of the σ_rupture, σ(R₀), χ, and k_s (see the Methods section), and the results of the best fit to the experimental slope curves are presented in Figure 11. The shell parameters combinations for the best fit were chosen as ones that minimized the least mean-square error of the difference between the experimental and numerical values of all the data points in the slope curves. There is an excellent agreement between the numerical simulations and the experiments for (a) the pressure threshold of enhancement and (b) the slope of the enhancements. Numerical simulations predict the two experimentally observed pressure thresholds for the enhancement of the signal from the flexible NB solutions at 125 and 857 kPa (Figure 11a). There is also a very good agreement between the numerical and experimental slope curves (Figure 11d). In agreement with experiments, the simulations predict the P_t of 465 kPa (Figure 11b) and 588 kPa (Figure 11c) for the intermediate and the stiff shell NBs. The corresponding numerically calculated slope curves have qualitative and quantitative agreement with experimentally measured curves (Figures 11e,f). In agreement with the GP measurements, numerical results predict the smallest shell elasticity for the flexible NBs (χ = 0.16 N/m) and medium elasticity of χ = 2.3 N/m for the intermediate NBs and the highest elasticity of χ = 3.15 N/m for the stiff NBs. Moreover, it is numerically predicted that the addition of Gly increases the surface tension for rupture from 0.0725 N/m for the flexible NBs to 0.084 N/m for the intermediate NBs and 0.087 N/m for the stiff NBs. Addition of Gly is also accompanied by a reduction in the initial surface tension from 0.067 N/m for flexible NBs to 0.06 N/m for the intermediate NBs to 0.055 N/m for the stiff NBs. As expected, due to a higher viscosity of Gly, addition of Gly also increases the viscosity of the shell from 1.7 nkg/s for the flexible NBs to 9 nkg/s for the intermediate NBs and 25 nkg/s for the stiff NBs.

Figure 11.

Second SuH frequency component of the numerically calculated scattered pressure of a NB with R₀ = 100 nm with (a) flexible, (b) intermediate, and (c) stiff shells. Comparison between the slope of the contrast enhancement with respect to the excitation pressure amplitude between numerical simulations and experiments for: (d) flexible, (e) intermediate, and (f) stiff shell NBs. Arrows mark the pressure thresholds (P_t) of the sudden signal enhancement. Error bars are standard deviation of the three independent replicates.

To gain a better insight on the radial oscillations of the NBs and the mechanism behind the enhancement, samples of the radial oscillations of the NBs are analyzed at pressures before and at the first and second enhancements of the flexible NBs (Figure 11a,e). These results are presented in the Supporting Information.

In this study, the shell viscoelastic properties were modified by the introduction of membrane PG as a membrane softener and Gly as a membrane stiffener. A two-photon microscopy technique through a polarity-sensitive fluorescent dye, C-Laurdan, was utilized to gain insights on the effect of membrane additives to the membrane structure. PG and Gly affect the structure and properties of the membrane of PL-stabilized UCAs and therefore UCA response to an US field. The solutions were sonicated with US pulses with a 6 MHz center frequency and a PNP range of 100–857 kPa. The filtered NBs (200 nm mean diameter, narrow size distribution) exhibited a threshold behavior with increasing PNP. Above a pressure threshold, the echogenicity of the second harmonic contrast-mode contrast harmonic imaging (CHI) images of NBs increased suddenly. The pressure threshold for signal amplification increased with shell stiffness. A rapid enhancement of the second harmonic was observed for PNP ranges of 123–245 kPa for the flexible membrane, 465–588 kPa for the intermediate membrane, and 588–710 kPa for the stiff membrane. The difference in the amplitude of the excitation pressure for threshold behavior may be explained by the shell composition properties with changes in elasticity, shell rupture threshold, initial surface tension, and viscosity.

Increased Elasticity

The significant difference in measured GP (e.g., 0.205 for stiff shells, 0.155 for intermediate, and 0.014 for flexible shells) reflects how Gly and PG interact with the PL membrane. Large parameter numerical simulations showed that the changes in the elasticity and shell viscosity do not have a significant influence on the pressure threshold, however, they largely affect the slope of the second harmonic amplitude as a function of pressure. The slope curves were used to fit the numerical simulations to the experimental measurements, as they have information on both the pressure threshold and growth rate of the second harmonic as a function of the excitation pressure. Moreover, due to the relative nature of the slope curves, a good quantitative agreement between experiments and numerical simulations was achieved. According to numerical simulations, addition of Gly leads to an increase in shell elasticity from 0.15 N/m for the flexible NBs to 2.3 N/m for intermediate NBs and 3.15 N/m for the stiff NBs. Comparing the ratio of the predicted elasticities to the ratio of GP values also shows a good correlation between experiments and numerical simulations. The ratio of the predicted elasticity of the intermediate NBs to flexible NBs is 14.37, which is in the range of the ratio of the measured GP of the intermediate to flexible shells of 11.07 ± 8.85, and the ratio of the elasticity of the stiff NBs to intermediate NBs is 1.37, which correlates well with the corresponding ratio of GPs which is 1.32 ± 0.54.

The effect of Gly and PG on the properties of PL membranes for biological and biomedical applications has been extensively studied through experiments, numerical simulations, and molecular dynamics simulations.^{35,37,42−45,67} Gly is a good osmotropic agent enhancing the water–water hydrogen bonding at the PL solvation shell and thereby imparting an ordering effect on PL packing.^43,64,68 PG, on the other hand, is a synthetic molecule with lower polarity as compared to Gly.^69,70 The lower polarity of PG also implies that it can be incorporated in the PL membrane through solvation of the headgroup, partitioning of PG into the hydrophobic core, or a combination thereof as shown by Harvey et al.⁴¹ Furthermore, incorporation of PG results in a decrease in gel–liquid phase transition temperature of the acyl chains.⁴¹ The decrease in stiffness of PL membrane upon incorporation of PG has been utilized in the formulations for ultradeformable liposomes as an edge activator.⁷¹ Here, we show the addition of Gly and PG changes the shell structure and therefore the acoustic behavior of the narrow size dispersed NBs. The changes in the shell properties are quantified both experimentally and numerically.

Increased Shell Rupture Threshold

Gly stiffens the NB membrane (Figure 2c), which limits the NB oscillation amplitude. Moreover, the stiffer shells need higher pressures for rupture.²⁰ As soon as the shell ruptures, the amplitude of bubble oscillations increases significantly, resulting in the enhancement of the NB scattered pressure.²⁰ The shell resists the rupture until the applied pressure reaches a threshold at which tensile stresses on the shell exceed the rupture threshold.²⁰ The stiffer the bubble, the higher the rupture surface tension, and consequently higher pressures are required to achieve the enhancement. The stiffening effect of Gly on the PL membrane has been well-established in literature. Recently, Abou-Saleh et al., reported that Gly induces water structuring around the PL membrane of a MB through the formation of a glassy layer that increases MB stiffness. The stiffening effect of Gly on the MB membrane was determined through the compression of a MB using a tipless atomic force microscopy cantilever. The force to achieve a given compression was shown to increase with increasing Gly content up to 20% Gly.⁶⁷ Conversely, PG softens the membrane, making it more flexible and thereby requiring a lower P_t. PG has been used as an edge activator for ultradeformable liposomes for enhanced drug delivery, especially through the skin.⁷²⁻⁷⁴ Ultradeformable liposomes have been shown to squeeze through narrow openings without disruption of its vesicular structure, and this is facilitated by its flexible and strain-compliant membrane. Zhao et al. utilized drug-loaded liposomes with PG for enhanced delivery of epirubicin into breast cancer tumors.³⁹ PG was specifically chosen for this study because PG-liposomes have a higher encapsulation efficiency, better membrane flexibility, and longer stability as compared to normal liposomes.

Numerical simulations using the Marmottant model confirm that higher pressures are required for NB scattering enhancement when the NBs have stiffer shells.^20,59 The shell can withstand finite tensions only; increasing the acoustic pressure gradually shows a strong abrupt enhancement above a critical pressure. This is due to the shell rupture: In this new state, the bubble oscillates as a free bubble. This is because above a critical tension (corresponding to σ_rupture), the shell ruptures and that part of the bubble surface is uncovered.²⁰ Once this threshold has been reached, the surface tension upper bound will be the surface tension of water, allowing the bubble to expand more easily (which translates in the backscatter enhancement). The stiffer bubbles have more resistant shells, thus the rupture occurs at higher pressures. Numerical simulations predicted σ_rupture of 0.0725 N/m, 0.084 N/m, and 0.087 N/m for the flexible, intermediate, and stiff shell NBs.

Decreased Initial Surface Tension

The second reason behind the increase in the pressure threshold of the enhancement of the signal with the addition of Gly is the increased stability of the NBs with initial surface tension reduction. We have previously shown that the initial surface tension of the NBs decreases significantly (p < 0.0001) through the incorporation of Pluronic L10.⁷⁵ The initial surface tension decreased by 28% at a lipid to Pluronic ratio of 0.2.⁷⁵ Here, addition of Gly has a similar stabilizing effect to the incorporation of Pluronic by reducing the initial surface tension. Predictions of the numerical simulations validate this hypothesis, as the predicted initial surface tension decreased from 0.067 N/m for the flexible NBs to 0.055 N/m for the stiff NBs. According to the numerical simulations, the differences between the initial surface tension and the surface tension for rupture determine the pressure threshold for the sudden signal amplification; the pressure threshold increases with increasing the margin between the initial and rupture surface tension.

Increased Shell Viscosity

Incorporation of Gly increased the viscosity of the shell from 0.9 nkg/s for flexible NBs to 9 nkg/s for intermediate and 25 nkg/s for stiff NBs. This can be explained by the higher viscosity of the Gly (1.412 Pa·s)⁷⁶ compared to PG (0.042 Pa·s).⁷⁷ Viscosity of a mixture of liquids can be calculated using⁸¹

1

where x is the mass fraction, μ is the viscosity, and the sub index a and b represent fluid a and b, respectively. By neglecting the influence of lipids due to their small mass fraction and assuming the viscosity of 0.001 for PBS and densities of 1 g/mL for PBS, 1.04 g/mL for PG, and 1.26 g/mL for Gly, we can estimate the viscosity of each mixture as μ_flexible = 0.0032 Pa·s, μ_intermediate = 0.0158 Pa·s, and μ_stiff = 0.0415 Pa·s. Thus 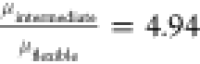and 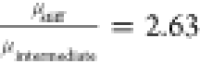, which correlates well with the ratio of the numerically fitted shell viscosities of 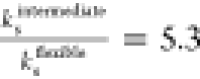and .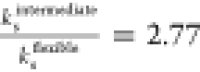

The goal of the simulations in this paper was to shed insight on the physical mechanisms of the NB behavior with different shells and elucidate the threshold behavior observed in the experiments. The simulation parameters that are presented as the best fit to each case are representative of the relative comparison between the shell parameters, but the absolute value for each parameter may not be accurate. The estimated ratios of the shell elasticity and viscosity values were roughly concordant with the ratios of the experimentally measured GP and ratios of the calculated viscosity of the solutions, respectively, thus confirming the trends observed in experiments. Accurate quantification of the physical parameters of the NBs is a challenging task and requires attenuation and scattering measurements in tandem. Nevertheless, the estimated values for the NB shell parameters here are consistent with the reported values for MBs with similar shell compositions⁸²⁻⁸⁴ (using linear estimations) and parameters that were extracted using optical measurements of radius–time curves⁵⁹ and pressure-dependent attenuation measurements.^85,86

The use of NBs with a narrow size distribution in this study significantly aided in observing the effect of the shell structure on the bubble behavior.⁵³ Such a clear difference in the behavior of various shelled bubbles has not been observed to date, likely due to the absence of size-controlled measurements. The polydispersity of MBs may be the reason behind why there was no clear difference between the acoustic behaviors of different shell MBs in ref (53) with different GP values. This shows the importance of the applications of monodisprse NBs and MBs to achieve high control over their acoustic behavior, making the therapeutic and imaging effects more potent while at the same time increasing the safety of medical procedures. These findings further confirm the results of previous studies on the importance of narrow size distributions of UCAs on their response to ultrasonic exposure.^78,79 In polydisperse populations, the intricate acoustic signatures of different shells can easily be masked by the response of the other bubbles in the polydispersion. For a given shell and using a rough analysis of the resonance frequency of the Marmattant model,²⁰ doubling the radius (for initial radii between 0.1 μm ≤ R₀ ≤ 2 μm) results in ≈64% decrease in the resonance frequency, while the shell elasticity should be changed by about 8.3 times to compensate for that effect. Thus, the changes in the size distribution can easily mask the differences in the acoustic signals due to different shell parameters. Moreover, due to the sensitive response of the lipid-coated bubbles to variations in pressure,^78,80 at each pressure a different subpopulation may become active which complicates the inference of the shell-dependent acoustic signals. In a recent in vivo study, it is shown that the sensitivity of the monodisperse MBs can be at least 10 times higher than that of the polydisperse MBs.⁷⁹ Studies related to the attenuation and scattering of mondisperse vs polydisperse populations of MBs⁷⁸ also showed that at the second harmonic, monodisperse MBs may have up to a 3 orders of magnitude increase in the sensitivity. Thus, in the narrow size filtered population, not only the pressure-dependent effects are not masked by the overall response of the polydispersion, but, consistent with recent studies of MBs, they are also significantly enhanced. As a result, when the desired subpopulation becomes active at the pressure-dependent superharmonic resonance, the enhancement can easily supersede the response of the nonactive population, consequently revealing a distinct influence of the shell parameters on the NB behavior.

Here, we show that the acoustic response of narrow-sized NBs can be controlled and altered by their shell structure. The controllable pressure threshold in this study has potential advantages for US contrast enhanced methods that rely on the nonlinear response of UCAs. One of these techniques is amplitude modulation where two pulses with different pressure amplitude are used in the imaging sequence. One pulse usually has an amplitude that is twice the other pulse. The received signals are scaled and subtracted upon receive. Due to the linear response of the tissue, the signal from tissues cancels, and the only remaining signal is from UCAs, increasing the contrast to tissue (CTR). Sending a pulse below the pressure threshold and sending one above the threshold for enhancement will significantly increase the CTR. An increase in CTR would be particularly beneficial in US molecular imaging. Sojahrood and Kolios numerically investigated the pressure-dependent superharmonic resonances of monodisperse UCAs and showed that, above a pressure threshold, a significant increase in harmonic emissions is expected.⁸⁷ This can aid in heating enhancement in treatments while reducing the undesired effects in the off-target tissue. The dynamics of size isolated UCAs which are excited by their pressure-dependent resonance frequency (PDfr) has also been numerically investigated.⁶³ Above a pressure threshold, bubble oscillations undergo an abrupt increase, resulting in the enhancement of the nondestructive scattered pressure by the bubbles. The authors concluded that the use of PDfr can used to increase the contrast in amplitude modulation imaging-based techniques. Moreover, the attenuation of the UCAs in the beam path can be suppressed to allow more US energy to reach bubbles at the target. Therefore, eliminating the effects of size disparity in bubble populations is a highly effective method, in principle, to enhance and control the outcome of the diagnostic and therapeutic procedures. In agreement with conclusions of refs (63 and 87), the reduction of prefocal beam attenuation has been experimentally shown in ref (78) where monodisperse populations of lipid-coated MBs were sonicated by their PDfr. We showed that NBs with flexible shells need smaller amplitude acoustic pressures for the nonlinear oscillations leading to the pressure-dependent scattering enhancement. This leads to a higher scattering cross section and thus better outcomes for imaging. Stiffer shells increase the pressure to higher values, thus making them more suitable for therapeutic purposes like enhanced heating applications where higher pressures are required.⁸⁸ Importantly, due to the negligible oscillation amplitude of the prefocal NBs, and taking advantage of the steep pressure gradients of focused US transducers, we may significantly decrease the attenuation of prefocal NBs in the US path. Thus, delivering energy to the resonant NBs at the target will contribute to efficiently producing enhanced heating effects. Undesired heating in the off-target region is minimized due to the off resonant bubbles.

Conclusion

NBs of narrow size distribution with three different shell compositions were manufactured. The relative shell stiffness of different NB formulations was assessed by calculating the average GP value from the relative fluorescence intensities at 450 and 500 nm using a two-photon excitation microscopy technique. NBs prepared with 20 wt % Gly show the highest GP and therefore have the highest shell stiffness, while NBs prepared with 20 wt % of PG show the lowest GP and therefore have the lowest shell stiffness. We introduced a simple and efficient method by which high concentrations of narrow-sized NBs can be prepared through filtration for its use in US imaging experiments. Acoustic measurements of signals from filtered NBs showed that the difference in shell stiffness has a pronounced effect in the pressure threshold P_t of PL-stabilized NB solutions, with the flexible membrane requiring a lower PNP and the stiffer membrane requiring a higher PNP to elicit nonlinear oscillations. Numerical simulations confirmed the experimental observations of the stiffness-dependent threshold behavior.

Methods

Experiments

Materials

The following materials were used and purchased as indicated: 1,2-Dibehenoyl-sn-glycero-3-phosphocholine (C22, Avanti Polar Lipids Inc., Pelham, AL), 1,2 dipalmitoyl-sn-glycero-3-phosphate (DPPA, Corden Pharma, Switzerland), 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine (DPPE, Corden Pharma, Switzerland), and 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy(polyethyleneglycol)-2000] (ammonium salt) (DSPE-mPEG2000, Laysan Lipids, Arab, AL), propylene glycol (PG), glycerol (Gly), phosphate buffer solution (PBS, Gibco, pH 7.4), 6-dodecanoyl-N,N-dimethyl-2-naphthylamine (C-Laurdan, Sigma-Aldrich), octafluoropropane (C₃F₈, Electronic Fluorocarbons, LLC, PA), and agarose (Sigma-Aldrich).

Preparation of Bubble Solutions

Nanobubbles (NBs) were formulated as reported previously.^54,55 Briefly, a solution for bubbles with a membrane of intermediate flexibility (10 mg/mL) was prepared by first dissolving 6.1 mg of C22, 1 mg of DPPA, 2 mg of DPPE, and 1 mg of DSPE-mPEG2000 into 0.05 mL of PG by heating and sonicating at 80 °C until all the lipids were dissolved. A mixture of 0.05 mL of Gly and 0.9 mL of PBS preheated to 80 °C was added to the lipid solution. The resulting solution was sonicated (Branson Sonicator CPX2800H) for 10 min at room temperature. The solution (1 mL) was transferred to a 3 mL headspace vial, capped with a rubber septum and aluminum seal, and sealed with a vial crimper. The solutions for bubbles with flexible and stiff membranes were prepared similarly but with 0.1 mL of PG or 0.1 mL of Gly, respectively, added to the solution instead of 0.05 mL of PG and 0.05 mL of Gly.

Quantitative Imaging of Membrane Lipid Order with C-Laurdan

The relative change in PL packing order and stiffness upon incorporation of additives was determined through quantitative two-photon fluorescence microscopy with a polarity-sensitive fluorescent probe (C-laurdan). Five μL of 5 nM C-laurdan solution in DMSO was added to each bubble solution. To form MBs, air was manually removed with a 30 mL syringe and was replaced by injecting C₃F₈ gas. After air was replaced by C₃F₈, the PL solution was activated by mechanical shaking with a VialMix shaker (Bristol-Myers Squibb Medical Imaging Inc., N. Billerica, MA) for 45 s. 0.1 mL of bubble solution was withdrawn and mixed with 1 wt % agarose solution in PBS at 30 °C. 100 μL of agarose solution with bubbles was transferred to a glass bottom dish for two-photon microscopy imaging using a Leica TCS SP2 multiphoton confocal system (Buffalo Grove, IL) equipped with a Coherent Chameleon XR IR laser (Santa Clara, CA) tuned to 800 nm. Samples were imaged using either a 63×/1.40 NA oil or a 63×/1.20 NA water immersion objective. Sixty bubbles for each bubble type were imaged with a sampled pixel size of ca. 230 nm, using 2 line averages and 2 frame averages. The two-photon microscope was precalibrated by imaging a 1:1000 dilution of 5 mM Laurdan solution in DMSO at three different laser power settings (the same setting used for imaging the sample as well as a setting 50% higher and 50% lower). Emission was collected by PMT detectors at 400–460 nm and at 470–530 nm. Detector gain and offset were held constant throughout the imaging. Analyses of the fluorescent images and determination of GP values were performed using the ImageJ macro developed previously.⁵⁶ In addition, the shell of the bubble was segmented by taking a pixel border equivalent to ≈1 μm around each bubble.⁵¹ Note that the fluorescence emission from the bubble membrane is required for calculation of membrane GP; NBs are too small for this purpose. For this reason, larger bubbles were chosen. Figure 1 shows a schematic representation of how C-laurdan, PG, and Gly are assembled in the PL membrane.

Formulation of NBs

As previously described,^54,55 air was manually removed from lipid solutions in sealed vials using a 30 mL syringe and was replaced by C₃F₈ gas, and the PL solution was activated by mechanical shaking with a VialMix shaker for 45 s. Nanobubbles were isolated from the mixture of foam and MBs by centrifugation at 50 rcf for 5 min with the headspace vial inverted, and 100 μL of NB solution was withdrawn from a fixed distance of 5 mm from the bottom with a 21G needle. To better highlight the effect of NB shell stiffness and eliminate the influence of size on the acoustic response, the size distribution was narrowed via filtration through a 400 nm pore size filter, shown schematically in Figure 12. Isolation by differential centrifugation alone is insufficient to isolate NBs of a narrower size distribution brought about by the low NB terminal velocity (i.e., calculated to be 22 nm/s for a 200 nm bubble).⁵⁷ The concentration and size distribution before and after filtration were characterized by resonant mass measurement.^54,55,58

Figure 12.

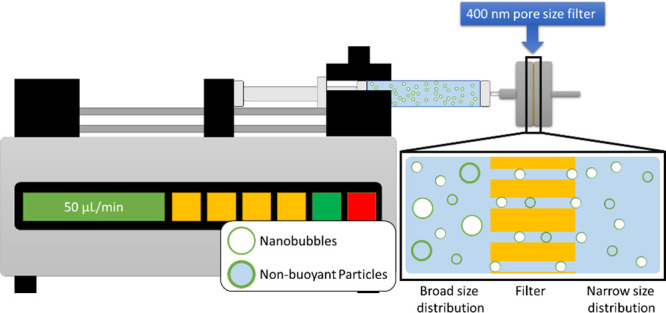
Schematic of filtration setup to narrow down the size distribution of NB.

Acoustic Measurements

One mL of NBs with a narrow size distribution (5.0 × 10⁸ NBs/mL) was placed in an agarose phantom container for nonlinear US imaging. Nonlinear US imaging was carried out on an AplioXG SSA-790A clinical US imaging system (formerly Toshiba Medical Imaging Systems, now Hitachi Healthcare) with a 12 MHz center frequency linear array transducer (PLT-1204BT). Images were acquired in CHI mode with parameters set at 65 dB dynamic range, 70 dB gain, receiving frequency 12 MHz, and peak negative pressure 74 to 857 kPa. The agarose phantom was composed of 1.5 wt % agarose in Milli-Q water (resistivity of 18 Mω·cm) heated in a microwave until the agarose is dissolved. The hot agarose solution was then poured into a mold avoiding any trapped bubbles and cooled down to obtain phantom with the desired channel dimension, as shown in Figure 13. Intensity of the backscattered nonlinear US signal was determined using a preloaded quantification software (CHI-Q) setting the ROI to be around inside the channel, as shown in Figure 5 (top left image). The experiments were replicated three times. Enhancement was calculated by normalizing the measured backscattered US intensity of the NB solution with respect to the backscattered US intensity of the agarose phantom selected from an ROI at the same depth as the solution ROI.

Figure 13.

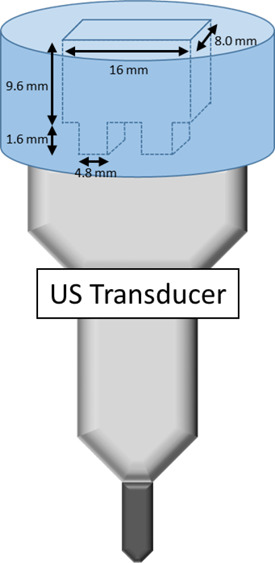
Schematic of agarose phantom used for US imaging.

Simulations

The bubble model

The influence of the viscoelastic properties of the shell on NB dynamics was investigated using the modified Marmottant model.²⁰ The Marmottant model was modified by Li et al., where the effects of shear thinning of the shell were added to the Marmottant model.^59,60 The model was recently used by Pellow et al. to investigate the NB dynamics.²² The modified Marmottant model can be presented as

2

where R is radius at time t, R₀ is the initial MB radius, Ṙ is the wall velocity of the bubble, R̈ is the wall acceleration, ρ is the liquid density (998 kg/m³), c is the sound speed (1481 m/s), P₀ is the atmospheric pressure, k is the polytropic constant (1.068 for C₃F₈), σ(R) is the surface tension at radius R, μ_L is the liquid viscosity (0.001 Pa·s), and k_s is the shell viscosity. The values in the parentheses are for pure water at 293 K. In this paper, the gas inside the MB is C₃F₈, and water is the host media. P_a(t) is the amplitude of the acoustic excitation (P_a(t) = P_a sin(2πft)), where P_a and f are the amplitude and frequency of the applied acoustic pressure.

The surface tension σ(R) is a function of radius and is given by

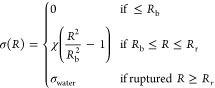3

where σ_water is the water surface tension (0.072 N/m), 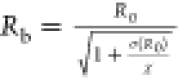is the buckling radius, 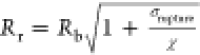is the rupture radius, and χ is the shell elasticity. Shear thinning of the shell is included in the Marmottant model using^59,60

4

where k₀ is the shell viscous parameter and α is the characteristic time constant associated with the shear rate. In this work, α = 0.75 ± 0.25 μs which is in the range examined in refs (22, 59, and 60).

The σ_rupture has been varied between 0.072 N/m for water and 1 N/m for different shells in the original work of Marmottant.²⁰ When the bubble is compressed below its buckling radius, the effective surface tension on the bubble becomes zero. Above the buckling radius and below the break up radius, the effective surface tension follows a linear elastic relationship. Above the rupture radius, the effective surface tension on the bubble becomes equal to that of water. This is because the molecules of the shell will become farther apart, leaving the bare gas exposed to water.²⁰

In this work, the frequency of the insonation is fixed at 6 MHz (the frequency used in the experiments), the excitation pressure amplitude is between 74 and 1249 kPa (pressure amplitude used in the experiments), the pulse duration is 2 cycles, and the R₀ of the NBs is 100 nm (comparable to the mean diameter of 200 nm measured in the experiments).

Scattered Pressure

Oscillations of a bubble generate a scattered pressure (P_sc) which can be calculated:⁶²

5

where d is the distance from the center of the bubble (and for simplicity is considered as 1m in this paper).⁶³ The second harmonic component of the scattered pressure (at 12 MHz consistent with experiments) was analyzed to compare the simulation results to the received signals in the experiments. In our numerical simulations, shell elasticity was varied between 0.1 and 10 N/m, and σ(R₀) was varied between 0 and 0.072 N/m. The rupture surface tension was varied between that of water (0.072 N/m) and 1 N/m, and shell viscosity was varied between 1 × 10^–10 kg/s and 6 × 10^–8 kg/s.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.0c09701.

• Examination of the radial oscillations before and after the pressure threshold of signal enhancement. Simulated radius vs time curves for the case of the flexible NB before and at the first P_t. Simulated radius vs time curves for the flexible NB before and at the second P_t (PDF)

Author Contributions

^⊥ These authors contributed equally.

Views and opinions of, and endorsements by the author(s), do not reflect those of the National Institutes of Health or the Department of Defense.

The authors declare no competing financial interest.