Assessing the predictive ability of the Suicide Crisis Inventory for near‐term suicidal behavior using machine learning approaches

Abstract

Objective

This study explores the prediction of near‐term suicidal behavior using machine learning (ML) analyses of the Suicide Crisis Inventory (SCI), which measures the Suicide Crisis Syndrome, a presuicidal mental state.

Methods

SCI data were collected from high‐risk psychiatric inpatients (N = 591) grouped based on their short‐term suicidal behavior, that is, those who attempted suicide between intake and 1‐month follow‐up dates (N = 20) and those who did not (N = 571). Data were analyzed using three predictive algorithms (logistic regression, random forest, and gradient boosting) and three sampling approaches (split sample, Synthetic minority oversampling technique, and enhanced bootstrap).

Results

The enhanced bootstrap approach considerably outperformed the other sampling approaches, with random forest (98.0% precision; 33.9% recall; 71.0% Area under the precision‐recall curve [AUPRC]; and 87.8% Area under the receiver operating characteristic [AUROC]) and gradient boosting (94.0% precision; 48.9% recall; 70.5% AUPRC; and 89.4% AUROC) algorithms performing best in predicting positive cases of near‐term suicidal behavior using this dataset.

Conclusions

ML can be useful in analyzing data from psychometric scales, such as the SCI, and for predicting near‐term suicidal behavior. However, in cases such as the current analysis where the data are highly imbalanced, the optimal method of measuring performance must be carefully considered and selected.

1. INTRODUCTION

Suicide is a widespread and devastating public health concern, albeit a potentially preventable one. Globally, an estimated 8,00,000 suicide deaths occurred in 2012. Suicide was the second leading cause of death among people aged 15–29 years (World Health Organization, 2016) and is the tenth leading cause of death in the United States (Hedegaard, Curtin, & Warner, 2018). However, despite decades of effort dedicated to researching and preventing the phenomenon, national rates of suicide have steadily risen in recent years (Hedegaard et al., 2018).

A critical component of suicide prevention is research on risk factors for suicidal behavior (SB). Numerous researchers have developed their own, often overlapping, sets of risk factors which aim to predict future SB and divide the population into high and low suicide‐risk groups (Kraemer et al., 1997). However, despite the density and variability of risk assessment literature, recent systematic reviews indicate that many suicide prediction models have poor predictive abilities and practical utility (Belsher et al., 2019; Franklin et al., 2017). These findings emphasize the complexity of SB, as well as the methodological limitations present in traditional suicide research, which ultimately result in poor clinical significance (Franklin et al., 2017).

One such limitation is that traditional statistical approaches commonly used in suicide research require researchers to guess at a small number of risk factors and their interrelatedness prior to running statistical analyses (Walsh, Ribeiro, & Franklin, 2017). This inherent limitation results in simplistic models which fail to capture the variety and complexity of suicide risk factors (Franklin et al., 2017). However, recent computational advances allow for improved suicide risk‐factor research that was not possible using traditional methodologies. One such example is the emergence of machine learning, where algorithms work to find patterns by using sets of input data, rather than explicit programming instructions.

Supervised machine learning maps input variables to predefined outcomes. In this context, an algorithm would use given data to predict whether a patient would engage in SB or not. Machine learning (ML) has already been implemented in retrospective suicide risk analysis and statistically predicted SB with seemingly greater predictive validity than did traditional methods (Walsh et al., 2017; Walsh, Ribiero, & Franklin, 2018). ML has also been used in the analysis of electronic medical records of approximately 3 million patients; here, short‐term SB following mental health specialty visits and primary care visits were retrospectively predicted with seemingly greater ability than extant suicide risk assessment tools (Simon et al., 2018). Promising results were also found by a prospective ML analysis of patients' verbal and nonverbal suicide thought markers, where SB was predicted with 85% classification accuracy (Pestian et al., 2017).

However, a deficit exists in ML studies that analyze prospective and proximal suicide prediction data. Prospective, longitudinal studies measure participants at two or more time points to see how certain factors influence specific outcomes, allowing the establishment of genuine suicide risk factors which may differ from retrospective correlates (Franklin et al., 2017). Additionally, clinicians and concerned families and friends are more often tasked with assessing proximal, rather than long‐term, suicide risk in a patient (Rudd, 2008). Therefore, a shifted focus from long‐term/trait predictors of suicide to imminent/state predictors of suicide is essential for clinical practice and significance.

One such predictor of imminent risk is the Suicide Crisis Inventory (SCI), which measures symptoms of the proposed Suicide Crisis Syndrome (SCS). The scale was previously found to be predictive of short‐term SB among psychiatric inpatients (Galynker et al., 2017). SCS appears to be a distinct mental state that may precede SB by 4–8 weeks and shows promise in assessing imminent suicide risk in clinical settings (Yaseen, Hawes, Barzilay, & Galynker, 2019). Patients exhibiting SCS experience a feeling of entrapment/frantic hopelessness which can be understood as an urgent need to escape coupled with a hopelessness of escape, in addition to one or more of the following symptoms: affective/emotional disturbance, loss of cognitive control, hyperarousal, and social withdrawal (Bloch‐Elkouby et al., 2020; Schuck, Calati, Barzilay, Bloch‐Elkouby, & Galynker, 2019). Data gathered by the SCI thus offers a prospective look into short‐term suicide risk.

In this context, the purpose of this study was to achieve three aims. The first aim was to establish whether ML analysis of the SCI would be appropriate for predictions of future SB. The second aim was to compare the predictive power of three ML algorithms (random forest, logistic regression, and gradient boosting). Finally, our third aim was to compare three sampling methods (split sample, Synthetic minority oversampling technique (SMOTE), and enhanced bootstrap) to determine which would yield the best results.

2. METHODS

2.1. Study setting

Patient participants admitted to a psychiatric inpatient unit at the Mount Sinai Health System for suicidal ideation or suicide attempt from January 10, 2016 until January 10, 2019 were recruited. The Icahn School of Medicine at Mount Sinai institutional review board approved the study (inpatients: Human Subjects: 16‐01350, Grants and Contracts Office: 16‐2484 [0001]).

2.2. Informed consent and study procedures

Inpatient clinicians referred potential participants to the study and provided diagnoses for consenting participants using the fifth edition of the Diagnostic and Statistical Manual of Mental Disorders (DSM‐5). The study's exclusion criteria were homelessness, lack of any means of contact, inability to understand the consent form, or a medical condition that may affect participation. Within 72 h of admission, eligible patients were approached by trained research assistants who explained the study, its risks and benefits, and the method of compensation. Consenting participants were given a study battery to complete, and a few measures were administered again 48 h prior to discharge. Patients were contacted 4 weeks following initial intake for a one‐month follow‐up, which was conducted over the phone or in person per their preference and convenience.

2.3. Measures

2.3.1. Suicide Crisis Inventory

The SCI is a validated self‐report instrument designed to measure the intensity of the SCS (Galynker et al., 2017). The SCI version used in this study includes 49 items measuring 5 sub‐scales on a 5‐point Likert scale, and was administered during the discharge interview. In the ML analysis, the input data for each of the 591 participants was thus a vector of 49 different integers ranking their self‐reported severity of certain feelings or symptoms associated with SB from 0 (“Not at all”) to 4 (“Extremely”).

The first and central SCI sub‐scale is Entrapment/Frantic hopelessness, which describes a feeling of being trapped and a need for escape and is measured by items such as, “Felt helpless to change.” Panic‐dissociation is the second sub‐scale, describing an altered sensorium and panic‐associated derealization (e.g., “Felt strange sensations in your body or on your skin”). The third subscale is Ruminative flooding, which is a feeling of uncontrollable, racing thoughts, and is associated with somatic symptoms such as headaches (e.g., “Felt your head could explode from too many thoughts”). The fourth and fifth subscales are Emotional pain (e.g., “Had a sense of inner pain that was too much to bear”) and Fear of dying (e.g., “Became afraid that you would die”), respectively (Galynker et al., 2017).

Items in the 49‐item SCI measure SCS Criterion A Entrapment/Frantic hopelessness, Criterion B1 Affective discontrol, and Criterion B2 Loss of cognitive control. Criterion B3 Hyperarousal and Criterion B4 Social withdrawal are directly measured in later versions of the SCI.

2.3.2. Columbia Suicide‐Severity Rating Scale

The Columbia Suicide‐Severity Rating Scale (CSSRS; Posner et al., 2011) is a semi‐structured interview that assesses the severity of current and lifetime suicidal thoughts and behaviors. The “lifetime and recent” form was administered to patients during the initial intake and the “since last assessment” form was used at the 1‐month follow‐up. SB at follow‐up is defined as any aborted, interrupted, or actual suicide attempt as categorized by the CSSRS made between intake and follow‐up sessions. Participants' lifetime suicide ideation and ideation at intake were also measured using the CSSRS, with a score of 0 indicating an absence of ideation and a score of 1 through 5 indicating the presence of ideation.

2.4. Algorithms used

Three predictive algorithms were used in this study (logistic regression, random forest, and gradient boosting) and were implemented using the sklearn and XGBoost packages available in Python v3.5.2. All code was written using Jupyter notebooks. The entire study sample (N = 591) was utilized in each algorithm and sampling combination. Therefore, the percentage of participants who attempted suicide between intake and follow‐up dates (cases 3.4%) and percentage of participants who did not (controls 96.6%) remained the same across all methods.

2.4.1. Logistic regression

Logistic regression is designed to find a link between input data and a binary outcome variable (Hosmer Jr., Lemeshow, & Sturdivant, 2013). Here, the input data are responses to the 49 items of the SCI and the output variable is whether the participants demonstrated SB between intake and follow‐up sessions.

When using logistic regression, the assumption is made that the outcome y is linked linearly to the input vector X via the logistic function

$$Pr(y=1)=f\left(x\right)=\frac{1}{1+e^{-\left({\beta }_0+{\beta }_1{x}_1+\dots +{\beta }_n{x}_n\right)}}$$

where β ₁,…,β _n represent the weights for each predictor x ₁,…,x _n (for this study, n = 49). The ideal weights of each input variable, or the relative contribution of each of the 49 SCI items in predicting the outcome, are estimated via maximum likelihood estimation, an iterative method for estimating parameters in a probability distribution that seeks coefficient weights for the input variables that best separate the classes.

2.4.2. Random forest

Random forest makes predictions by using an ensemble of decision trees. Each decision tree is composed of a subset of input variables at each node and the consensus prediction among the ensemble is the final output prediction. In this case, each tree is constructed using a subset of the 49 SCI questions as nodes and the outcome of 0 (control) or 1 (case) as the output. Each decision tree is created using bootstrapped samples, which are samples where participants are drawn from our dataset with replacement (Breiman, 1996). One hundred such trees were created in this analysis. For each bootstrap sample, a decision tree is created such that the best splits are chosen from among a random sample of inputs. Each split is determined using Gini impurity, which measures how well a potential split separates the samples of each class in that particular node (Menze et al., 2009). This algorithm takes advantage of bagging, a.k.a. bootstrap aggregating. If we draw B bootstrap samples from our original dataset $\mathcal{D}$, we get B prediction functions, ${\widehat{f}}_1,\dots ,{\widehat{f}}_B$. These can be combined to make a bagged prediction function

$${\widehat{f}}_{\text{avg}}=\text{Combine}\left({\widehat{\mathrm{f}}}_1\left(\mathbf{x}\right),\dots ,{\widehat{\mathrm{f}}}_{\mathrm{B}}\left(\mathbf{x}\right)\right)$$

which yields the final prediction. It should be noted that the bootstrap samples used to create the decision trees differ from those used in the bootstrap sampling technique described later.

2.4.3. Gradient boosting

While random forest uses an ensemble of decision trees created in parallel, gradient boosting builds decision trees sequentially. Both methods create trees from a subset of inputs. However, gradient boosting creates trees in a manner which corrects for errors made in previous trees using a process called gradient descent in which “steps” are iteratively taken toward an ideal function which minimizes the error (Friedman, 2001). In other words, a strong learner is created from an ensemble of weak learners in a process called “boosting.”

2.5. Sampling methods

2.5.1. Split sample

Here, 70% of the data was used to train models using the aforementioned algorithms and the remaining 30% was used to test their predictive capabilities. Due to the vast imbalance between the numbers of controls and cases, a stratified split approach was used where the ratio of controls/cases in the total dataset was maintained in each portion. Although this approach does not make use of the entire dataset in building the models, it is a commonly used sampling technique in ML.

2.5.2. Synthetic minority oversampling technique

SMOTE is used to create artificial data points of the minority class (cases). SMOTE was used to oversample cases to comprise 50% of the training set. The oversampling was applied after the data were split into training and testing samples to ensure that the cases in the testing set are true cases and not synthetically created.

2.5.3. Enhanced bootstrap

Here, a predictive model was created using the entire dataset, applying this model to that same dataset and gathering the apparent results. These results were intentionally overfit, meaning the resulting model fits too closely to that particular dataset and thus cannot be generalized to new data. To correct for this, bootstrap samples were drawn and predictive models were built using these samples without splitting. The created models were then applied to the same samples used to create them, which again yields results that are overfit. Each of these bootstrap models were then applied to the original dataset and the difference in performance metrics was calculated and averaged over the number of bootstrap samples drawn. This difference, called the “optimism,” quantifies the amount of overfitting. We used 500 samples, each of size 591 (equaling our N number). Adjusted results were obtained by subtracting the optimism from the apparent results to provide bias‐corrected results (Tibshirani & Efron, 1993).

2.6. Indices of predictive performance

Scores for most of the performance metrics described below range from 0 to 1, with a higher score indicating superior performance. The two exceptions are the Brier score, which also ranges from 0 to 1 but with a lower score indicating superior performance; and the net benefit, which directly measures the benefit versus harm of different approaches in terms or patients treated correctly.

2.6.1. Classification accuracy/balanced accuracy

Classification accuracy is the ratio of correct predictions (true positives and true negatives) over the total number of predictions. If we create a confusion matrix of each possible

	Actual positive	Actual negative
Predicted positive	True positive (TP)	False positive (FP)
Predicted negative	False negative (FN)	True negative (TN)

Then the classification accuracy is defined as

$$\frac{TP+TN}{TP+TN+FP+FN}$$

However, when dealing with imbalanced data, classification accuracy can be misleading. In the current analysis, there was a large difference between the number of cases (3.4%) and controls (96.6%) in the dataset, meaning a classification accuracy of 96.6% could be achieved by simply predicting that all patients will not exhibit SB.

Balanced accuracy provides an alternative which avoids the potentially inflated results seen in classification accuracy. Defining the true positive rate (TPR, or sensitivity) and true negative rate (TNR, or specificity) as follows

$$\text{TPR}=\frac{TP}{TP+FN},\text{TNR}=\frac{TN}{TN+FP}$$

then

$$\text{Balanced}\text{accuracy}=\frac{TPR+TNR}{2}$$

This metric gives us the average accuracy across each class. If the conventional classification accuracy is high solely due to an imbalance in the outcome classes, then the balanced accuracy will drop to 50% (Broderson et al., 2010).

2.6.2. Precision/recall

Precision is the fraction of true positive predictions over all positive predictions, true or false. Recall is the fraction of true positives over the sum of true positives and false negatives.

$$\text{Precision}=\frac{TP}{TP+FP},\text{Recall}=\frac{TP}{TP+FN}$$

These metrics are important because their scores rely on correctly predicting true positives (cases), which is a challenge in any dataset which contains a heavy imbalance toward the controls.

2.6.3. Brier score

The Brier score measures the mean squared difference between the predicted probability of a certain outcome for a particular instance and the actual outcome, in this case, whether a patient attempts suicide. For binary outcomes, the Brier score is defined as

$$\text{Brier}\text{score}=\frac{1}{N}{\displaystyle \sum }_{t=1}^N{\left(f_t-o_t\right)}^2$$

where f _t is the predicted probability for example t, o _t is the actual outcome of example t and N is the total number of examples in the sample. Because the Brier score measures the mean squared difference between the predicted probability of a certain outcome for a particular instance and the actual outcome, lower Brier scores indicate better performance (Fernández et al., 2018). However, for imbalanced datasets, the Brier score may appear very promising overall but poor for the rare class (cases; Wallace & Dahabreh, 2012). For this reason, the Brier score is prone to optimism similar to classification accuracy and Area under the receiver operating characteristic (AUROC; Collell, Prelec, & Patil, 2018).

2.6.4. Area under the receiver operating characteristic

AUROC is calculated by plotting the false positive rate (FPR)

$$\text{FPR}=\frac{FP}{FP+TN}$$

on the x‐axis and the true positive rate on the y‐axis across different discrimination thresholds and then measuring the area under this curve. This value represents the probability that the classifier will rank a randomly chosen case higher than a randomly chosen control (Fawcett, 2006). However, when a dataset is highly imbalanced, AUROC may fail to reflect a model's true predictive abilities. Specifically, when controls greatly outnumber cases, the FPR can be expected to be small, leading to a larger and less informative AUROC score (He & Garcia, 2009).

2.6.5. Area under the precision‐recall curve

The Area under the precision‐recall curve (AUPRC) is a scalar value of the area under a precision‐recall plot, which shows precision values for the corresponding recall values for different thresholds. As these plots focus on precision and recall, which estimate a model's ability to detect true positive cases, they are able to express less misleading interpretations of classifier performance for imbalanced datasets relative to the AUROC. For our dataset, AUPRC may be a more appropriate and informative metric than AUROC (Saito & Rehmsmeier, 2015).

2.6.6. Net benefit

Net benefit differs from the other metrics presented here because it explicitly quantifies the value of treating a TP (i.e., someone who would attempt suicide in the near‐term without treatment) and not treating a false positive. Net benefit is calculated as (Peirce, 1884; Vickers & Elkin, 2006):

$$\text{Net}\text{benefit}=\frac{\text{true}\text{positive}\text{count}}{n}-\frac{\text{false}‐\text{positive}\text{count}}{n}\left(\frac{p_t}{1-p_t}\right)$$

where p _t is the threshold probability, or the minimum probability of SB where treatment is warranted (Vickers, van Calster, & Steyerberg, 2019). In this study, net benefit is the number of cases per 100 patients who can be correctly treated for near‐term SB without unnecessarily treating controls (patients who will not exhibit near‐term SB).

When p _t is varied over a range, the different net benefits for each approach can be plotted to create a decision curve where the x‐axis and y‐axis represent p _t values and net benefit, respectively. This plot also includes net benefit results for the naïve “Treat all” and “Treat none” approaches where treatment is provided to all or none of our sample, respectively, allowing visual comparison of each approach. Their differences can be used to calculate the reduction in how many controls are incorrectly treated for near‐term SB per 100 patients without a decrease in the number of cases who are correctly treated:

$$\frac{\left(\text{net}\text{benefit}\text{of}\text{the}\text{model}\text{–}\text{net}\text{benefit}\text{of}\text{treat}\text{all}\right)}{\left(p_t/\left(1–p_t\right)\right)}\times 100.$$

The “Treat none” approach is represented in the decision curve graph as a horizontal line at y = 0, since it involves no TPs or FPs.

2.7. SCI item ranking

We used a chi square test to rank the SCI items by their weighted contribution in predicting near‐term SB.

3. RESULTS

3.1. Patient characteristics

The sample consisted of 591 participants in total, 20 of whom attempted suicide at a one‐month follow‐up and 571 of whom did not (Table 1). Participants differed significantly on the basis of ethnicity, in that a greater than expected percentage of Hispanic/Latino participants attempted suicide between intake and 1‐month follow‐up (p < 0.05). Furthermore, intake suicide ideation was present at a higher rate among participants who demonstrated SB at follow‐up when compared to those who did not (p < 0.05). Age varied between groups as well, with a Mann–Whitney U‐test indicating that participants with a follow‐up suicide attempt tended be younger (Mdn = 25) than those without (Mdn = 36) (U = 3693, p = 0.008). Lifetime SB and suicide ideation, and patients' primary diagnosis did not vary significantly between both groups.

TABLE 1.

Participant demographic and clinical characteristics

Participant variables	Whole sample N = 591 (100%)	With follow‐up SA N = 20 (3.4%)	Without follow‐up SA N = 571 (96.6%)	p
Gender—N (%)				0.307
Male	195 (33.0)	4 (20.0)	191 (33.5)	‐
Female	381 (64.5)	16 (80.0)	365 (63.9)	‐
Other	15 (2.5)	0 (0.0)	15 (2.6)	‐
Race—N (%)				0.192
American Indian	6 (1.0)	0 (0.0)	6 (1.1)	‐
Asian	47 (8.0)	3 (15.0)	44 (7.7)	‐
Black	146 (24.7)	1 (5.0)	145 (25.4)	‐
Pacific Islander	1 (0.2)	0 (0.0)	1 (0.9)	‐
White	218 (36.9)	6 (30.0)	212 (37.1)	‐
Other	166 (28.1)	9 (45.0)	157 (27.5)	‐
Ethnicity—N (%)				0.015*
Hispanic/Latino	191 (32.3)	12 (60.0)	179 (31.4)	‐
Not Hispanic/Latino	396 (67.0)	8 (40.0)	388 (67.9)	‐
Age—mean [sd]	37.61 [14.24]	29.70 [11.11]	37.89 [14.26]	0.008**
Years of Education—mean [sd]	14.38 [3.03]	14.77 [2.69]	14.36 [3.04]	0.553
Primary diagnosis—N (%)				0.696
Depressive disorder	298 (50.4)	10 (50.0)	288 (50.4)	‐
Anxiety disorder	45 (7.6)	0 (0.0)	45 (7.9)	‐
Bipolar & related disorder	80 (13.5)	3 (15.0)	77 (13.5)	‐
Schizophrenia spectrum disorder	43 (7.3)	3 (15.0)	40 (7.0)	‐
Obsessive compulsive disorder	1 (0.2)	0 (0.0)	1 (0.2)	‐
Trauma and stress‐related disorders	64 (10.8)	2 (10.0)	62 (10.9)	‐
Other	33 (5.6)	2 (10.0)	31 (5.4)	‐
Suicidal behaviors—N (%)
Lifetime actual SA	288 (48.7)	14 (70.0)	274 (47.9)	0.088
Lifetime interrupted SA	73 (12.4)	3 (15.0)	70 (12.3)	0.925
Lifetime aborted SA	102 (17.3)	4 (20.0)	98 (17.5)	0.903
Lifetime SI	539 (91.2)	20 (100.0)	519 (90.9)	0.312
Intake SI	400 (67.7)	19 (95.0)	381 (66.7)	0.016*

Abbreviations: SA, suicide attempt; SI, suicide ideation.

p*<0.05; p**<0.01.

3.2. ML analyses

3.2.1. Split sample

The split sample approach produced the poorest results of the three sampling techniques (Table 2). Across all three algorithms, precision and recall scores were 0.000 and AUPRC's were in the 0.075–0.117 range with gradient boosting producing the highest score. Gradient boosting also produced the lowest Brier score of 0.032. The classification accuracy fell within the 0.944–0.966 range, but these scores are misleading due to the highly skewed balance between cases and controls. Balanced classification accuracy was significantly lower than classification accuracy, with all three algorithms producing scores between 0.488 and 0.500. Finally, the net benefit scores of all three algorithms exceeded the net benefit of treating all patients when pt ranged from ∼4% to 25% but were lower than the net benefit for treating none of the patients once p _t exceeded 15% (Figure 1).

TABLE 2.

Results of 3 Machine Learning Approaches 70/30 train‐test split

	AUPRC	AUROC	Precision	Recall	Balanced Accuracy	Classification Accuracy	Brier Score
LR	0.075	0.759	0.000	0.000	0.488	0.944	0.050
RF	0.097	0.590	0.000	0.000	0.500	0.966	0.034
GB	0.117	0.743	0.000	0.000	0.500	0.966	0.032
SMOTE
LR	0.102	0.760	0.125	0.333	0.626	0.899	0.091
RF	0.137	0.523	0.000	0.000	0.500	0.966	0.047
GB	0.170	0.687	0.500	0.167	0.580	0.966	0.030
Enhanced bootstrap
LR	0.063	0.820	0.445	0.185	0.586	0.960	0.037
RF	0.710	0.878	0.980	0.339	0.669	0.977	0.021
GB	0.705	0.894	0.940	0.489	0.744	0.981	0.019

Abbreviations: AUROC, Area Under Receiver Operating Characteristic Curve; AUPRC, Area Under Precision Recall Curve; GB, Gradient boosting; LR, Logistic regression; RF, Random forest; SMOTE, Synthetic Minority Oversampling Technique.

FIGURE 1.

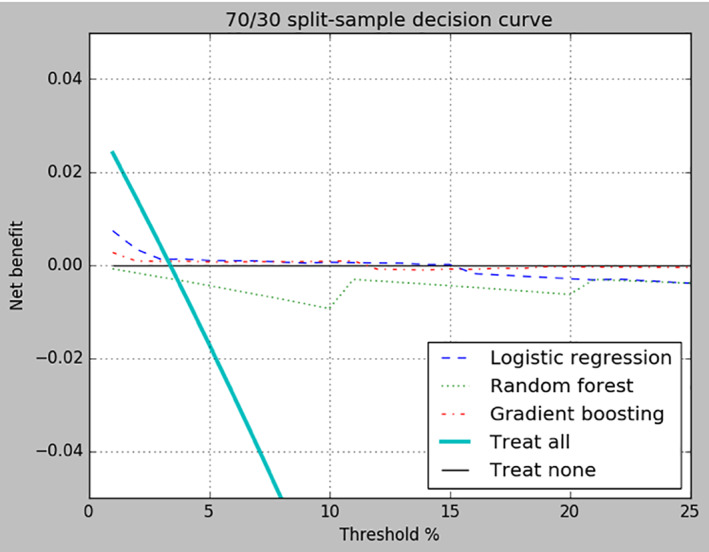
Decision curve for split‐sample. Net benefit of treating all patients, treating none of the patients, and each of the three algorithms are compared across probability threshold values ranging from 1% to 25%

3.2.2. Synthetic minority oversampling technique

When positive cases of short‐term SB were oversampled via SMOTE, logistic regression and gradient boosting showed a modest improvement in both precision and recall while random forest was unchanged at 0.000 for both metrics (Table 2). AUPRC scores fell within the 0.102–0.170 range. Brier scores for logistic regression and random forest using SMOTE were inferior to their Brier scores produced using split sampling, however, they were still low in general. Lastly, all three algorithms produced greater net benefit scores than did treating all patients when p _t ranged from ∼4% to 25% but drifted below the benefit line for “Treat none” as p _t increased (Figure 2).

FIGURE 2.

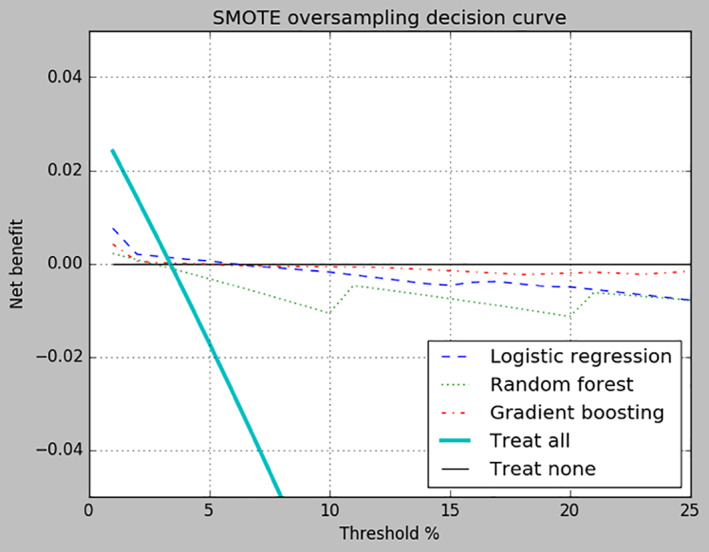
Decision curve for Synthetic minority oversampling technique (SMOTE) sampling. Net benefit of treating all patients, treating none of the patients, and each of the three algorithms are compared across probability threshold values ranging from 1%‐ to 5%

3.2.3. Enhanced bootstrap

Random forest and gradient boosting produced the highest AUPRC (random forest 0.710; gradient boosting 0.705), precision (random forest 0.980; gradient boosting 0.940), and recall (random forest 0.339; gradient boosting 0.489) scores when using the enhanced bootstrap approach (Table 2). Balanced accuracy scores for all three algorithms exceeded 0.500, with random forest (0.669) and gradient boosting (0.744) producing the highest values. The AUROC values for random forest and gradient boosting were 0.878 and 0.894, respectively. Logistic regression did not perform as well, showing decreases in AUPRC and recall, but improved precision over SMOTE.

The net benefit scores of all three algorithms exceeded the net benefits of treating all patients and treating no patients for all p _t values from 1% to 25% (Figure 3). In clinical terms, this means fewer controls will be incorrectly treated for near‐term SB, with no increase in the number of cases being untreated. This difference, relative to the “Treat all” approach, increases with p _t and can be quantified using the formula described in the Methods section. As each algorithm using enhanced bootstrap sampling was superior to the default strategies across the entire range of reasonable threshold probabilities, we can say that the use of any of these models would improve patient outcomes (Van Calster et al., 2018).

FIGURE 3.

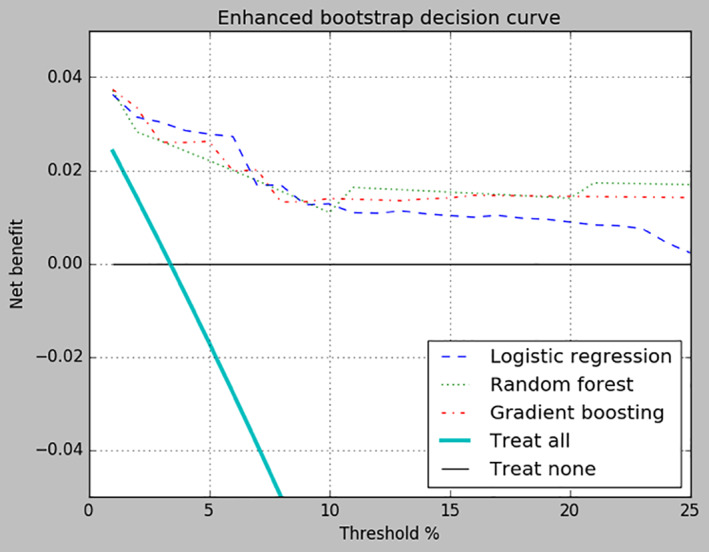
Decision curve for enhanced bootstrap sampling. Net benefit of treating all patients, treating none of the patients, and each of the three algorithms are compared across probability threshold values ranging from 1% to 25%

3.3. Chi square ranking of SCI items

The chi square ranking of the top 15 SCI items is presented in Table 3. The five highest performing items represented all five factors of the SCI (Galynker et al., 2017). The two best‐performing items, SCI‐6 “Felt unusual physical sensations that you have never felt before” and SCI‐32 “Felt the blood rushing through your veins” belonged to the Panic‐dissociation factor, followed by SCI‐8 “Felt your head could explode from too many thoughts” of the Ruminative flooding factor. The fourth‐ranking item, SCI‐48 “Felt urge to escape the pain was very hard to control,” reflected Entrapment/Frantic hopelessness and Emotional pain, and the fifth‐ranking item, SCI‐5 “Became afraid that you would die,” represented the Fear of dying factor.

TABLE 3.

Chi square ranking of SCI items

Ranking	Items	SCI Factors a	SCS Diagnostic Criteria b
1	SCI 6—Felt unusual physical sensations that you have never felt before	Panic‐dissociation	Affective discontrol
2	SCI 32—Felt the blood rushing through your veins	Panic‐dissociation	Affective discontrol
3	SCI 8—Felt your head could explode from too many thoughts	Ruminative flooding	Loss of cognitive control
4	SCI 48—Felt urge to escape the pain was very hard to control	Entrapment/Frantic hopelessness; emotional pain	Entrapment/Frantic hopelessness
5	SCI 5—Became afraid that you would die	Fear of dying	Affective discontrol
6	SCI 26—Felt bothered by thoughts that did not make sense	Ruminative flooding	Loss of cognitive control
7	SCI 22—Felt strange sensations in your body or on your skin	Panic‐dissociation	Affective discontrol
8	SCI 49—Felt there were no good solutions to your problems	Entrapment/Frantic hopelessness	Entrapment/Frantic hopelessness
9	SCI 17—Felt the world was closing in on you	Entrapment/Frantic hopelessness	Entrapment/Frantic hopelessness
10	SCI 45—Felt pressure in your head from thinking too much	Ruminative flooding	Loss of cognitive control
11	SCI 44—Felt there is no escape	Entrapment/Frantic hopelessness	Entrapment/Frantic hopelessness
12	SCI 9—Felt ordinary things looked strange or distorted	Panic‐dissociation	Affective discontrol
13	SCI 7—Had a sense of inner pain that was too much to bear	Emotional pain	Affective discontrol
14	SCI 47—Felt like you were getting a headache from too many thoughts in your head	Ruminative flooding	Loss of cognitive control
15	SCI 13—Felt there was no way out	Entrapment/Frantic hopelessness	Entrapment/Frantic hopelessness

Abbreviation: SCI, Suicide Crisis Inventory.

^a Galynker et al., 2017.

^b Schuck et al., 2019.

4. DISCUSSION

Our findings indicate that the SCI, which is a postulated measure of a putative presuicidal mental state—SCS, is predictive of short‐term SB when analyzed using machine learning. Of the sampling techniques, we found that the enhanced bootstrap approach produced the best results. Of the three algorithms, gradient boosting and random forest did not differ significantly in their respective performances and generally outperformed logistic regression. Thus, the optimal combination of algorithm and sampling technique in this context was using enhanced bootstrapping along with gradient boosting or random forest.

In a widely cited meta‐analysis, many prominent models of suicide risk assessment were found to perform barely above chance (Franklin et al., 2017). Using AUROC score as a benchmark for performance, the SCI outperforms these models when using enhanced bootstrap sampling along with random forest and gradient boosting algorithms. Furthermore, popular instruments routinely used in clinical practice, such as the Beck Hopelessness Scale, the Manchester Self Harm Rule, and the SAD PERSONS scale were shown to have low precision scores for detecting future suicide attempts (Runeson et al., 2017). Commonly used warning signs of imminent suicide risk, such as suicide ideation or stressful life events, are similarly associated with a moderate to high risk of false positive predictions of suicide attempts (Fowler, 2012). Our study yielded relatively high precision rates which suggests that, despite having no items assessing self‐reported suicide ideation, our model is able to more reliably detect true positive cases of SB than widely used suicide risk assessment methods. If administered in a clinical setting, the SCI may thus provide clinicians with an acute risk assessment tool to measure suicidality without directly inquiring about suicide, which could increase the likelihood of patient disclosure (Chu et al., 2015). The results of our best performing prediction models are especially promising, given the challenge of separating cases from controls in a high‐risk population, such as an inpatient population, where there is likely an overlap in clinical characteristics between both groups (Walsh, Ribeiro, & Franklin, 2018). However, it is important to note that because the approaches described here were trained and tested using one study sample, they are considered internal validation techniques and thus contribute to model development rather than model validation (Moons et al., 2015). The models and results in this study await replication in a different sample.

The chi‐squared test to rank the individual contributions of the SCI items in predicting the outcome, in general agreement with the original SCI analysis (Galynker et al., 2017), showed that the 15 highest performing questions of the 49‐item SCI represented all the five factors included in the SCS (Table 3). Furthermore, the number of highest performing items per factor corresponded with the order loading of the five factors, that is, the central element of the SCS (Entrapment/Frantic hopelessness) was represented by the most items (5 items), followed by Ruminative flooding (4 items) and Panic‐dissociation (4 items), Emotional pain (2 items), and Fear of dying (1 item). The finding that the two highest performing SCI items (SCI‐6 “Felt unusual physical sensations that you have never felt before” and SCI‐32 “Felt blood rushing through your veins”) belonged to the Panic‐dissociation factor does not correspond with the findings of the original paper, which observed that this factor has a relatively minor contribution to the SCS when compared to the Entrapment/Frantic hopelessness and Ruminative flooding factors (Galynker et al., 2017). However, this finding aligns with a recent network analysis of the SCS, which groups Panic‐dissociation symptoms into the same factor as Entrapment/Frantic hopelessness and Ruminative flooding (Bloch‐Elcouby et al., 2020).

The recently proposed DSM criteria for the SCS (Calati et al., 2020; Schuck et al., 2019), derived from previous analyses of the SCI and its earlier versions (named the Suicide Trigger Scale; Galynker et al., 2017; Yaseen, Gilmer, Modi, Cohen, & Galynker, 2012; Yaseen et al., 2014), also neatly corresponded with the 15 item ranking (Table 3): Criterion A Entrapment/Frantic hopelessness (5 items), Criterion B Affective discontrol (6 items), and Criterion B2 Loss of cognitive control (4 items). Criterion B3 Hyperarousal was not directly measured, however, it was indirectly reflected in items SCI‐8 and SCI‐48. Criteria B4 Social withdrawal was the single excluded criteria, as it was only included in the later versions of the SCI, along with dedicated Hyperarousal items.

4.1. Limitations

The results of this study need to be considered within its limitations. First, 3.4% of the patients in our dataset attempted suicide, which is 4.69 times higher than the annualized suicide attempt rate among discharged psychiatric inpatients as reported by Forte, Buscajoni, Fiorillo, Pompili, and Baldessarini (2019). Thus, results may vary when our approach is applied to patient data from other sources. Second, the present study only included 1‐month follow‐ups. Including longer term follow‐up periods may capture more information from patients who attempt suicide beyond the initial month post hospital discharge. The same study from Forte et al. (2019) found that while 26.4% of suicide events (attempted and completed suicides) took place within the initial month after discharge, 73.2% took place within 12 months of discharge.

Third, the current study had a low events‐per‐variable (EPV) ratio of 0.41. While some studies propose that an EPV of at least 10 is ideal (Peduzzi, Concato, Kemper, Holford, & Feinstein, 1996), there is no consensus on the importance of a high EPV. A replication study using a different dataset with a higher EPV would reduce the potential confound of data overfitting. Lastly, this current analysis was unable to attain a recall score higher than 49%, in other words, our models could at best distinguish cases out of the overall sample less than half the time. Adjustments such as hyperparameter tuning or adjusting the decision threshold may yield a higher recall.

5. CONCLUSION

Machine learning shows promise in predicting SB when using data from psychometric scales, such as the SCI, with the right combination of sampling approach and algorithm. An overarching challenge of this analysis, and one that is common in risk assessment research, was the vast imbalance between the number of cases and controls present in the cohort. Nevertheless, using the enhanced bootstrap sampling approach in combination with ensemble tree based algorithms yielded respectable results that are comparable with prior research findings. When conducting ML analyses of imbalanced data, it is important to select meaningful evaluation metrics.