Improved Simultaneous Multi-slice Cardiac MRI Using Readout Concatenated k-Space SPIRiT (ROCK-SPIRiT)

Abstract

Purpose:

To develop and evaluate a simultaneous multi-slice (SMS) reconstruction technique that provides noise reduction and leakage blocking for highly accelerated cardiac MRI.

Methods:

Readout Concatenated K-Space SPIRiT (ROCK-SPIRiT) utilizes the concept of readout concatenation in image domain to represent SMS encoding, and performs coil self-consistency as in SPIRiT-type reconstruction in an extended k-space, while allowing regularization for further denoising. The proposed method is implemented with and without regularization, and validated on retrospectively SMS-accelerated cine imaging with 3-fold SMS and 2-fold in-plane acceleration, ROCK-SPIRiT, is compared to two leakage-blocking SMS reconstruction methods, ReadOut (RO)-SENSE-GRAPPA and Split Slice-GRAPPA. Further evaluation and comparisons are performed using prospectively SMS-accelerated cine imaging.

Results:

Results on retrospectively 3-fold SMS and 2-fold in-plane accelerated cine imaging show that ROCK-SPIRiT without regularization significantly improves on existing methods in terms of PSNR (RO-SENSE-GRAPPA: 33.5±3.2, Split Slice-GRAPPA: 34.1±3.8, ROCK-SPIRiT: 35.0±3.3) and SSIM (RO-SENSE-GRAPPA: 84.4±8.9, Split Slice-GRAPPA: 85.0±8.9, ROCK-SPIRiT: 88.2±6.6 in %). Regularized ROCK-SPIRiT significantly outperforms all methods as characterized by these quantitative metrics (PSNR: 37.6±3.8, SSIM: 94.2±4.1 in %). The prospectively 5-fold SMS and 2-fold in-plane accelerated data shows that ROCK-SPIRiT and regularized ROCK-SPIRiT have visually improved image quality compared to existing methods.

Conclusion:

The proposed ROCK-SPIRiT reduces noise and inter-slice leakage in accelerated SMS cardiac cine MRI, improving on existing methods both quantitatively and qualitatively.

Introduction

Despite numerous advances in the past decade, long acquisition times remain the major challenge for cardiac MRI (CMR). Clinical CMR techniques usually require whole heart coverage at sufficient temporal and in-plane resolution (1). However, these requirements either lead to longer scan times or necessitate trade-offs (2). For a number of CMR scans, including cine imaging, breath-holding remains the dominant clinical respiratory motion compensation strategy, where increased scan times lead to longer or more breath-holds (3). In turn, this necessitates higher patient cooperation and may be challenging for patients who are suffering from dyspnea.

Although parallel imaging is the most clinically utilized accelerated MRI approach (4–6), it incurs a SNR loss related to the square root of the acceleration rate, R. Simultaneous multi-slice (SMS) imaging is an alternative approach for improving coverage without a SNR loss dependent on the acceleration factor (7). In SMS imaging, multiple slices are excited and acquired simultaneously, and the redundancy in the multi-coil receiver array is utilized to disentangle the individual slices during reconstruction. Hence, the only SNR loss is due to g-factor (7), and additional in-plane acceleration is possible due to the variations in coil sensitivities within slices. SMS imaging is typically coupled with controlled aliasing to further increase dissimilarities among the coil profiles across the slices to reduce g-factor noise amplification (8). Multiple studies have explored the use of SMS imaging in CMR for faster coverage (9–22). In particular, SMS acceleration has been used for myocardial T₁ mapping (13,18), for cine imaging (16,21), and for perfusion imaging (11,14,15,17,22) using both Cartesian and non-Cartesian acquisitions at different acceleration rates. However, due to coil geometry limitations, SMS acceleration remains limited for CMR, especially in conjunction with in-plane parallel imaging, where leakage artifacts and noise amplification are observed at high acceleration rates (23), necessitating improvements in reconstruction.

Several SMS imaging reconstruction techniques have been proposed. Early work utilized SENSE-type reconstructions (24–26). Subsequently, GRAPPA-type techniques were utilized to disentangle the SMS accelerated slices as k-space based reconstructions (27–29). GRAPPA-type reconstructions are adapted in multiple large-scale neuroimaging projects like Human Connectome Project (HCP) (30) and in CMR (13) due to their superior g-factor and inter-slice leakage reducing performance. Among the k-space based methods, Slice-GRAPPA extends GRAPPA (5) to SMS imaging, projecting SMS-accelerated data into new k-spaces for each slice using convolutional kernels (28). Split slice-GRAPPA further incorporates a leakage-blocking kernel optimization to this reconstruction approach, albeit at the cost of increased noise amplification (29,30). Recently, SPIRiT-type reconstructions (6) have also been utilized for myocardial T₁ mapping (31) and for non-Cartesian SMS imaging (15,32). Finally, ReadOut (RO)-SENSE-GRAPPA proposes the idea of readout concatenation in image domain to encode SMS acceleration (27,33), which reduces the reconstruction problem into a conventional 1D or 2D GRAPPA interpolation problem, when the acquisition is performed without or with in-plane regularization respectively. This approach has also been demonstrated to have inter-slice leakage blocking capabilities (34).

In this study, we sought to develop and evaluate a new regularized SMS reconstruction technique ReadOut Concatenated K-Space SPIRiT (ROCK-SPIRiT) that simultaneously provides leakage and noise reduction. The proposed method combines advantages of RO-SENSE-GRAPPA in leakage blocking using readout concatenation in image domain to encode SMS acceleration, and SPIRiT in enforcing coil self-consistency while allowing further noise reduction by regularization. ROCK-SPIRiT is quantitatively compared to existing leakage blocking techniques, RO-SENSE-GRAPPA and Split Slice-GRAPPA in cine imaging at 3-fold SMS and 2-fold in-plane acceleration in a retrospective study. Further qualitative evaluation is performed at higher acceleration rate (35) on a prospectively 5-fold SMS and 2-fold in-plane accelerated cine imaging. Our results showed that the proposed ROCK-SPIRiT improves upon existing methods both quantitatively and qualitatively by reducing noise and inter-slice leakage.

Methods

ReadOut Concatenated k-Space SPIRiT (ROCK-SPIRiT)

An alternative way of representing the SMS acceleration is based on readout concatenation in image domain (33). In this strategy, the slices that are simultaneously excited are viewed via concatenation along the readout direction (Supporting Information Figure S1a), and the SMS acceleration is characterized as a uniform sub-sampling in this extended readout direction (Supporting Information Figure S1b). Note that there is no actual acceleration in the readout direction during acquisition, but this approach provides a method for viewing the SMS encoding as a 1D acceleration in the extended readout direction. Further acceleration can be achieved by additional in-plane sampling which forms a 2D GRAPPA interpolation problem (Supporting Information Figure S1c). The Fourier transform of this image-domain readout-concatenated domain is referred to as the extended k-space.

ROCK-SPIRiT utilizes the extended k-space from the concatenated domain and performs SPIRiT coil self-consistency by solving the following objective function:

$$\text{arg\hspace{0.17em}}{\text{min}}_{{\kappa }_{\text{ext}}}\Vert P_{\Omega }{\kappa }_{ext}-{\kappa }_{\text{SMS}}{\Vert }_2^2+\Vert G_{\text{ROCK}}{\kappa }_{\text{ext}}-{\kappa }_{\text{ext}}{\Vert }_2^2+\sigma \Psi \left(E{\kappa }_{\text{ext}}\right),$$ [1]

where P_Ω is the sub-sampling operator that only picks the acquired data specified by the sampling mask (i.e. the index set of Ω) (Figure 1a), κ_SMS is the acquired SMS data across all coils, κ_ext is the extended k-space across all coils, Ѱ is the regularizer, E is the SENSE-1 operator and σ is a weight term. G_ROCK is the ROCK-SPIRiT self-consistency operator calibrated on reference scans (Figure 1b). Note that the weight term between data fidelity and SPIRiT self-consistency was set to 1 as in SPIRiT (6), and regularization was performed across the temporal dimensions introduced by the regularizer, Ѱ. To perform this calibration, the low-resolution reference k-space data are inverse Fourier transformed along the readout direction, and concatenation is performed along this direction as described earlier. Then this low-resolution reference data is Fourier transformed to generate the extended k-space data corresponding to the calibration data, ${\mathbf{\kappa }}_{\mathbf{e}\mathbf{x}\mathbf{t}}^{\mathbf{r}\mathbf{e}\mathbf{f}}$, on which SPIRiT calibration is performed. A schematic of the SMS encoding, data consistency (first term), and ROCK-SPIRiT coil self-consistency (second term) in Eq. [1] are depicted in Figure 1. The objective function in Eq. [1] was solved using Alternating Direction Method of Multipliers (ADMM) (36). Implementation of ROCK-SPIRiT will be provided online (https://github.com/obdemirel/ROCK_SPIRiT).

Figure 1:

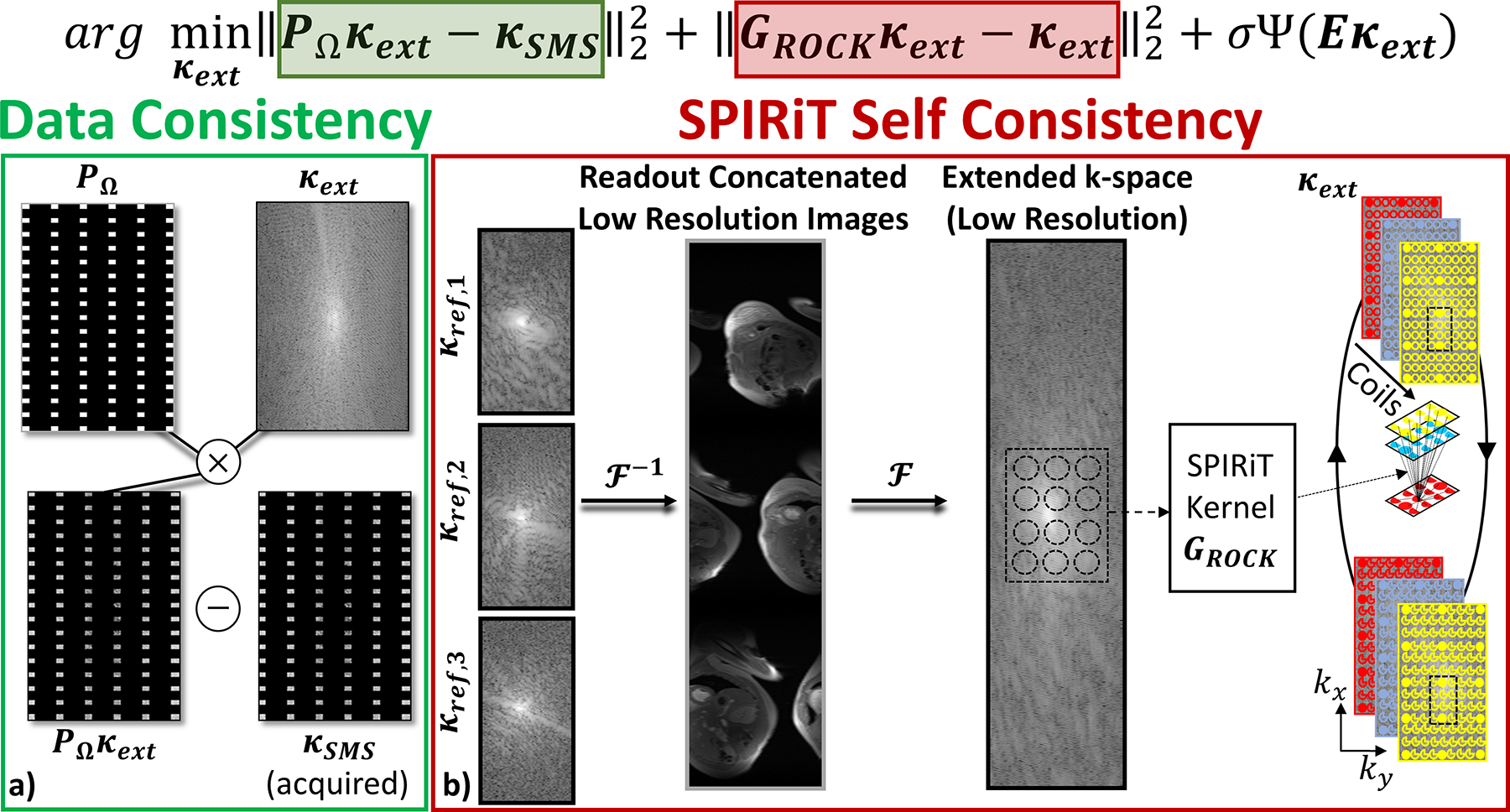
Illustration of the objective function in Equation 1 for the proposed ROCK-SPIRiT method for an example SMS acceleration rate of 3 and in-plane acceleration rate of 2. a) The data consistency term in Equation 1 enforces consistency between extended k-space (κ_ext) and acquired SMS k-space data (κ_SMS), b) Coil self-consistency is enforced using SPIRiT kernels, G_ROCK, on the extended k-space. These convolutional kernels are calibrated on the extended RO-concatenated k-space of reference low resolution slices for calibration. Regularization can also be added, although it is not depicted in the schematic.

Imaging Experiments with Retrospective SMS Acceleration

Imaging was performed on a 3T Siemens Magnetom Prisma (Siemens Healthineers, Erlangen, Germany) in 6 subjects (4 men, 2 women, mean age: 56±14 years) with no contraindications to MRI using a 30-channel body coil array. This study was approved by our institutional review board, and written informed consent was obtained before each examination.

Cine imaging was performed using FLASH readouts and retrospective ECG gating with the following parameters: Repetition time (TR)/ echo time (TE)/ flip angle (FA) = 4.3 ms/2.1 ms/12°; FOV = 320×320 mm²; spatial resolution = 1.7×1.7 mm²; slice thickness = 6 mm, slice gap = 3 mm; temporal resolution = 33–45 ms using 25 retrospectively gated cardiac phases; end-exhalation breath-hold duration = 15–17s, bandwidth = 770 Hz/pixel, 8–10 segments per heartbeat and linear k-space ordering. 10 fully-sampled individual slices, referred to as single-band reference images, covering the whole heart were acquired for each subject. A separate free-breathing scan corresponding to 64 reference lines for all ten slices was acquired over a single cardiac phase with no ECG gating, as calibration data for reconstruction with identical imaging parameters but lower spatial resolution = 1.7×4.7 mm². Reconstruction of SMS accelerated images using free-breathing did not show a difference compared to breath-held calibration scans in an earlier work (13). Therefore, all SMS reconstructions were performed using free-breathing calibration scans in order to minimize additional breath-holding and reduce overall scan time. Calibration scans lasted 275 ms per slice and were acquired without ECG gating.

To test the performance of different methods with respect to a ground-truth reference, a retrospective 3-fold SMS and 2-fold in-place acceleration, with 24 ACS lines was performed over 3 sets (Set 1: Slices 1-4-7, Set 2: Slices 2-5-8, Set 3: Slices 3-6-9) for each subject for a total of 18 SMS encodings across all subjects. CAIPIRINHA (8) was utilized with a phase increment of 2π/3 to provide 1/3 FOV shifts between adjacent SMS-encoded slices. We note that although savings in number of breath-holds is expected to scale with the SMS acceleration rate, the actual savings in scan time may be higher due to the elimination of recovery periods between a large number of breath-holds (13).

These accelerated cine images were reconstructed offline in MATLAB (MathWorks, Natick, Massachusetts, USA) on a workstation with Intel Xeon Gold 6136 CPU. Two conventional SMS reconstruction methods, RO-SENSE-GRAPPA and Split Slice-GRAPPA were compared to the proposed ROCK-SPIRiT with and without regularization for the reconstruction of SMS-accelerated data. RO-SENSE-GRAPPA kernels were calibrated using the readout-concatenated low-resolution reference data with an 8×8 kernel size (27). In Split Slice-GRAPPA, reconstruction was performed first using multi-slice unaliasing followed by in-plane GRAPPA. Split Slice-GRAPPA kernels were calibrated using the low-resolution reference data with a 7×7 kernel size for multi-slice unaliasing (29,37) and a 7×6 kernel size for in-plane unaliasing. ROCK-SPIRiT was implemented with a 9×9 kernel size. All SPIRiT kernels were calibrated on the full range of calibration data using Tikhonov regularization with a penalty of 10⁻², following the original SPIRiT implementation (6). ROCK-SPIRiT without regularization is a linear reconstruction algorithm similar to the RO-SENSE-GRAPPA and Split Slice-GRAPPA. Furthermore, regularization was incorporated into ROCK-SPIRiT using a locally low-rank (LLR) (38–41) constraint as a regularizer:

$$\Psi \left(x\right)=\sum _{\mathit{k}}{‖B_{\mathit{k}}^{\mathit{b}}\left(\mathit{x}\right)‖}_{*}$$ [2]

where a b×b block is extracted by the ${\mathbf{B}}_{\mathit{k}}^{\mathit{b}}(·)$ operator whose top-left corner is at pixel k and ‖·‖_* is the nuclear norm. These blocks are vectorized and stacked up into a b²×n_T matrix, where n_T = 25 was the number of cardiac phases in the series. In this study, b = 8 was employed as the block size (41). For solving the objective equation based on Equations [1] and [2], singular value thresholding was used in the proximal operation of ADMM. The normalized mean-square residual error threshold was set to 10⁻⁶ as a stopping criterion for the ADMM. The thresholding parameter was empirically set in an additional subject, to a value corresponding to 7.5×10⁻² times the ℓ_∞ norm of the SENSE-1 image of the SMS accelerated data in regularized ROCK-SPIRiT (Supporting Information Figure S2).

Image and Data Analysis

Reconstruction quality was evaluated based on the single-band fully sampled reference data using peak signal-to-noise ratio (PSNR) (42) and structural similarity index (SSIM) (43) across all subjects, all slices and all cardiac phases over a region of interest (ROI) covering the heart region. The error images were calculated as the difference between single band acquisitions and reconstructed slices.

In SMS reconstruction, inter-slice leakage is an important measure of image quality, and reflects residual aliasing due to cross talk between slices that may disrupt image quality (29,44,45). Leakage analysis was performed using CAIPIRINHA-shifted single band slices to match with the SMS acquisition for the linear methods. One of the slices was picked as a slice of interest and was run through the reconstruction algorithm using the same kernels used for reconstruction. Leakage was defined as the residual signal in the two non-input slices (29,46). Using the linearity of the reconstruction techniques, for each slice of interest, total leakage was calculated by summing the leakage signals from the rest of the slices. g-factor analysis was performed using Monte-Carlo based simulations (47). Gaussian distributed random synthetic complex-valued noise was added to the SMS data, and was run through all reconstruction algorithms 256 times with different random instantiations (47). Resulting g-factor maps were generated by dividing the standard deviation of the reconstructed image noise by the standard deviation of the synthetic noises and normalized by the standard deviation of the SENSE-1 images of the fully sampled reference data. Leakage and g-factor analyses were not performed with regularized ROCK-SPIRiT since it is a non-linear reconstruction technique. Statistical difference in PSNR and SSIM measures were assessed using paired t-test with a P value < 0.05 being considered significant.

Evaluation with Prospective SMS Acceleration

Additional prospectively accelerated SMS imaging was performed using an outer volume suppressed sequence with the same parameters described earlier, but with 5-fold SMS acceleration (35) and an outer volume suppression (OVS) module to suppress extra-cardiac tissues. The following parameters were used in the OVS module: BWT=8, RF peak shift =15%, 3.8 ms asymmetric sinc, saturation slab size = 150mm (each side), interleaved between every 8 imaging pulses (35). CAIPIRINHA was again utilized with a phase increment of 2π/5 to provide 1/5 FOV shifts between adjacent SMS-encoded slices. To test the reconstruction methods in a high acceleration regime, the data was further retrospectively undersampled by 2-fold in-plane acceleration while keeping ACS=24 reference lines. RO-SENSE-GRAPPA, Split Slice-GRAPPA, and ROCK-SPIRiT with and without regularization were used to reconstruct the dataset. The results were qualitatively compared. Split Slice-GRAPPA reconstruction of the acquired 5-fold SMS accelerated dataset without further in-plane undersampling was used as visual baseline.

Results

Figure 2 shows representative results from retrospectively 3-fold SMS and 2-fold in-plane accelerated images. The fully-sampled single band acquisitions, which are used as reference in this setting, are depicted in the leftmost column along with RO-SENSE-GRAPPA, Split Slice-GRAPPA, ROCK-SPIRiT and regularized ROCK-SPIRiT reconstructions. For this subject, the three slices reconstructed with RO-SENSE-GRAPPA have the lowest PSNR and SSIM (32.1±1.1, 84.6±2.9 in %, respectively). Split Slice-GRAPPA shows improved PSNR, and similar SSIM (32.7±0.8, 85.0±2.7 in %). ROCK-SPIRiT reduces the noise amplification compared to RO-SENSE-GRAPPA and Split Slice-GRAPPA, leading to higher PSNR and SSIM values (34.5±1.0, 89.4±1.9 in %). Regularized ROCK-SPIRiT shows visibly improved image quality, closely matching the single-band data, as well as the highest PSNR and SSIM values (38.5±1.1, 96.6±0.7 in %). The error images shown below the reconstructed images confirm these observations, with regularized ROCK-SPIRiT showing the least difference among all methods.

Figure 2:

Representative cine CMR results with retrospective 3-fold SMS and 2-fold in-plane acceleration. a) Single band acquisitions are shown as reference images in the leftmost column along with RO-SENSE-GRAPPA, Split Slice-GRAPPA, ROCK-SPIRiT and regularized ROCK-SPIRiT reconstructions. RO-SENSE-GRAPPA has the lowest PSNR and SSIM (32.1±1.1, 84.6±2.9 in %, respectively). Split Slice-GRAPPA improves upon RO-SENSE-GRAPPA (32.7±0.8, 85.0±2.7 in %) in terms of these metrics. ROCK-SPIRiT shows higher PSNR and SSIM (34.5±1.0, 89.4±1.9 in %) with reduced noise amplification compared to these two methods. Regularized ROCK-SPIRiT provides the highest PSNR and SSIM (38.5±1.1, 96.6±0.7 in %), closely matching reconstructed images visually compared to the reference images. b) The error images depicted under the reconstructed images are in-line with these observations, with regularized ROCK-SPIRiT showing the lowest difference.

Leakage and g-factor analyses for the same subject are depicted in Figure 3 for a single cardiac phase. Regularized ROCK-SPIRiT is not included in these analyses due to its non-linear nature. Among all three reconstruction techniques, RO-SENSE-GRAPPA and Split Slice-GRAPPA show similar leakage (up to 12.9% and 12.1% respectively). ROCK-SPIRiT shows substantial leakage improvement compared to these methods with only up to 8.1% leakage (Figure 3a). RO-SENSE-GRAPPA shows the highest g-factor values (up to 2.9), Split Slice-GRAPPA shows lower noise amplification (up to 2.5) compared to RO-SENSE-GRAPPA. ROCK-SPIRiT provides the smallest g-factor (up to 1.8) with a more spatially uniform and lower noise amplification compared to both methods (Figure 3b).

Figure 3:

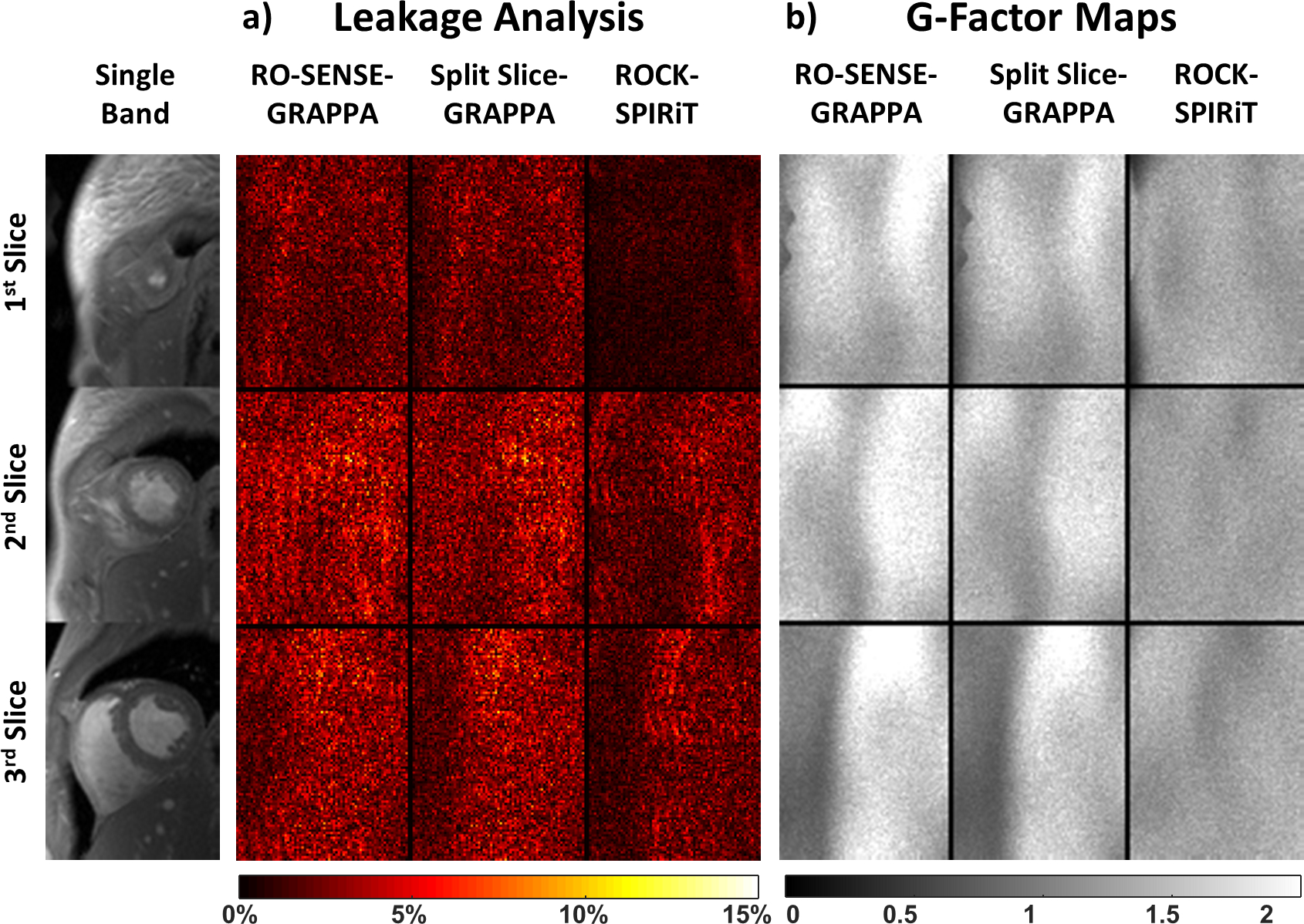
Leakage and g-factor analyses for the subject shown in Figure 2. a) RO-SENSE-GRAPPA (up to 12.9%) and Split Slice-GRAPPA (up to 12.1%) show similar leakage profiles. ROCK-SPIRiT provides the lowest leakage (up to 8.1%) among these linear reconstruction methods. Regularized ROCK-SPIRiT is not included in the g-factor analysis due its non-linear nature. b) RO-SENSE-GRAPPA has the highest g-factor (up to 2.9), with Split Slice-GRAPPA having a lower g-factor (up to 2.5). ROCK-SPIRiT improves upon all methods and has the lowest g-factors (up to 1.8). Similar to leakage analysis, g-factor quantification depends on the linearity of the image reconstruction, thus regularized ROCK-SPIRiT cannot be included in this analysis.

Spatio-temporal plots through the blood-myocardium interface are depicted in Figure 4, where the yellow dashed lines indicate the cross section of the heart for each slice. Consistent with the previous observations, RO-SENSE-GRAPPA and Split Slice-GRAPPA show similar spatio-temporal plots, both with apparent noise amplification. ROCK-SPIRiT shows lower noise amplification compared to both non-regularized methods. Regularized ROCK-SPIRiT provides the lowest noise amplification, with no degradation in temporal fidelity, closely matching the quality of the single band spatio-temporal plots. No temporal blurring was observed in any of the methods.

Figure 4:

Spatio-temporal plots of the blood-myocardium boundary for an a) apical, b) mid-ventricular and c) basal slices of the 10-slice short-axis stack of a subject. Yellow dashed lines indicate the position of the displayed cross sections of the heart. Comparable spatio-temporal plots and noise levels are observed with RO-SENSE-GRAPPA and Split Slice-GRAPPA reconstructions. ROCK-SPIRiT shows slightly lower noise amplification compared to both methods. Regularized ROCK-SPIRiT provides the lowest noise amplification and closely matches the reference spatio-temporal profiles. None of the methods show temporal blurring.

Figure 5 shows representative slices from another subject, including the single-band reference and regularized ROCK-SPIRiT reconstructions for a systolic cardiac phase, along with the regularized ROCK-SPIRiT reconstruction for every third cardiac phase throughout the cardiac cycle. The quantitative metrics of these three slices agree with previous observations, with RO-SENSE-GRAPPA (PSNR: 38.8±0.8, SSIM: 93.9±1.9 in %) and Split Slice-GRAPPA (PSNR: 39.3±0.7, SSIM: 94.3±1.9 in %) being outperformed by ROCK-SPIRiT (PSNR: 40.0±0.8, SSIM: 94.8±1.7 in %) and regularized ROCK-SPIRiT (PSNR: 43.1±0.6, SSIM: 97.9±0.6 in %). The corresponding movie of the cine images through the cardiac cycle is included in Supporting Information Video S1.

Figure 5:

a) Representative cine CMR results with retrospective 3-fold SMS and 2-fold in-plane acceleration on a different subject. Systolic cardiac phase along with reference single-band images and regularized ROCK-SPIRiT reconstructions are shown. b) Every third cardiac phase for the regularized ROCK-SPIRiT reconstruction is depicted on the right-hand side. ROCK-SPIRiT shows close agreement with the reference data with highest PSNR and SSIM measures (PSNR: 43.1±0.6, SSIM: 97.9±0.6 in %).

Figure 6 depicts the scattered box plots of PSNR and SSIM across all subjects, slices, and cardiac cycles. For both quantitative metrics, regularized ROCK-SPIRiT has the highest PSNR and SSIM values. All methods show significantly different PSNR and SSIM values (all pairwise t-tests: P < 10⁻⁴). In concordance with the previous visual assessments, RO-SENSE-GRAPPA has the lowest PSNR (33.5±3.2, 84.4±8.9 in %). Split Slice-GRAPPA has higher PSNR, but its average SSIM value is in the same range (34.1±3.8, 85.0±8.9 in %). ROCK-SPIRiT (35.0±3.3, 88.2±6.6 in %) shows PSNR and SSIM gains compared to both of these conventional methods. Finally, regularized ROCK-SPIRiT outperforms all methods with substantial gains in PSNR and SSIM (37.6±3.8, 94.2±4.1 in %). Additionally, analyses of PSNR, SSIM and leakage across all cardiac phases were performed, with results depicted in Supporting Information Figure S3, showing no significant variations across the cardiac cycle for any metric or reconstruction method based on analysis of variance. Variation across cardiac phases for all methods were below 0.4%, 0.2% and 1.7% for PSNR, SSIM and leakage, respectively.

Figure 6:

Scattered box plots of PSNR and SSIM for all four methods. Both quantitative metrics were calculated across all subjects, slices and cardiac cycles. Pairwise t-tests show that all methods are significantly different PSNR and SSIM values (P < 10⁻⁴). RO-SENSE-GRAPPA has the lowest PSNR but comparable SSIM values (33.5±3.2, 84.4±8.9 in %) compared to Split Slice-GRAPPA (34.1±3.8, 85.0±8.9 in %). ROCK-SPIRiT shows higher PSNR and SSIM values (35.0±3.3, 88.2±6.6 in %) compared to these two methods. Regularized ROCK-SPIRiT has the highest PSNR and SSIM gain compared to all methods (37.6±3.8, 94.2±4.1 in %).

Figure 7 shows the results of prospectively SMS-accelerated cine imaging on another subject using a fast imaging sequence (35). The leftmost column represents the Split Slice-GRAPPA reconstruction of the acquired 5-fold SMS accelerated data without any in-plane sampling, which serves as the qualitative baseline (35). The rest of the columns depict the reconstructions from an additional retrospective 2-fold in plane acceleration on this dataset. RO-SENSE-GRAPPA has similar image quality compared to Split Slice-GRAPPA, with both showing apparent noise amplification. ROCK-SPIRiT improves on both methods with less noise, and the regularized ROCK-SPIRiT provides the highest visual image quality among all methods. The corresponding movie of the cine images through the cardiac cycle is included in Supporting Information Video S2. Additionally, Supporting Information Figure S4 depicts the results in Figure 7 along with separate single-band acquisitions without OVS pulses.

Figure 7:

Prospectively 5-fold SMS-accelerated cine imaging using a fast imaging sequence (35). Split Slice-GRAPPA reconstruction of the acquired data without in-plane acceleration is shown on the left-most column as a qualitative baseline. Additional 2-fold in-plane acceleration is performed retrospectively, and the results from four reconstruction techniques on this data are shown in the other four columns. RO-SENSE-GRAPPA and Split Slice-GRAPPA show similar image quality, both with visible noise. ROCK-SPIRiT improves upon these methods, reducing noise amplification. Regularized ROCK-SPIRIT provides the highest image quality among all methods.

Discussion

In this study, we proposed a new regularized reconstruction method called ROCK-SPIRiT for SMS imaging and applied it to cine CMR. Non-regularized linear ROCK-SPIRiT showed better image quality, higher PSNR and SSIM values, as well as improved leakage and g-factor characteristics, compared to the existing leakage-reducing SMS reconstruction methods, RO-SENSE-GRAPPA and Split Slice-GRAPPA. Regularized ROCK-SPIRiT with an LLR constraint outperformed all methods with substantial PSNR and SSIM gains.

ROCK-SPIRiT utilizes the extended k-space formulation to calibrate SPIRiT kernels and uses these to reconstruct the missing k-space information. While kernel sizes for SPIRiT methods have been studied in the literature (6,48), these concentrate on single-band imaging, and not extended RO-concatenated k-spaces, which have a different energy spread per k-space sample in the extended RO dimension. Therefore, we performed a validation study on an additional subject for tuning this hyperparameter on an extended k-space (Supporting Information Figure S5). Although different kernel sizes led to variations in PSNR and SSIM values, there is only up to 1.4% change with respect to SSIM measures and up to 1.1% change with respect to PSNR values. The [9,9] kernel size was chosen for its high SSIM and PSNR performance. However, smaller kernels such as [9,5] and [9,7] can also be utilized since the difference in SSIM and PSNR values is minor. On the other hand, smaller kernels may have the advantage of reducing the total reconstruction time. The effect of calibration range was also investigated for the ROCK-SPIRiT kernel calibration, whose results are shown in Supporting Information Figure S6. PSNR and SSIM values decreased with decreasing calibration range, with limited savings in computational time. Thus, in this study, all calibration was performed on the full calibration of data. In terms of computational time, non-regularized ROCK-SPIRiT took approximately 18 seconds/iteration whereas regularized ROCK-SPIRiT took approximately 35 seconds/iteration to reconstruct all slices at all cardiac phases.

LLR constraint was utilized with ROCK-SPIRiT to improve image quality. LLR utilizes local redundancies across an image series, and has already been utilized in cardiac phase resolved imaging (3,39,49). Spatio-temporal constraints share information across dynamics, and carry the risk of temporal blurring. However, this was not observed in our study for the acceleration rates considered. Higher acceleration rates in MRI have recently been achieved with physics-based deep learning methods that use algorithm unrolling to solve a regularized least squares problem with a learned regularizer (50–56). The iterative process for solving ROCK-SPIRiT naturally lends itself to such algorithm unrolling, thus these approaches can be used to further improve regularization quality without manual parameter tuning, especially for higher acceleration rates. However, this was not explored since we only have a limited number of such cine volumes. These approaches warrant further investigation for SMS imaging in general, but optimization of the regularizer using deep learning is beyond the scope of our study, which focuses on using SPIRiT-type interpolation on the extended RO-concatenated k-space.

Cross talk between simultaneously excited slices or inter-slice leakage is a crucial problem in highly-accelerated SMS imaging. Therefore, Split Slice-GRAPPA (29) is the preferred choice over slice-GRAPPA (28) and SENSE-based methods in many applications (30) with improved leakage-reduction although it is prone to noise amplification. RO-SENSE-GRAPPA has also been shown to have similar properties as Split Slice-GRAPPA in terms of both g-factor and inter-slice leakage (30). In this work, ROCK-SPIRiT benefits further from employing RO-concatenated domain and provides better inter-slice leakage profiles compared to RO-SENSE-GRAPPA and Split Slice-GRAPPA. Our leakage analysis shows that ROCK-SPIRiT has 33% relative reduction of inter-slice leakage compared to the closest performing method split Slice-GRAPPA, whereas our g-factor analysis shows that ROCK-SPIRiT improved 30% relative to Split Slice-GRAPPA and 38% relative to RO-SENSE-GRAPPA. The improvement over RO-SENSE-GRAPPA, which uses the same RO-concatenation formulation, is consistent with previous studies that showed that SPIRiT-type reconstructions with coil self-consistency have better performance in terms of g-factor noise, as well as residual aliasing compared to 2D-GRAPPA problems as in the RO-SENSE-GRAPPA formulation (6).

In parallel imaging applications, ESPIRiT provides an image domain reconstruction methodology, which is intricately connected to the k-space domain SPIRiT approach (57). The coil sensitivities generated using the eigenvector decomposition of the calibration matrix in ESPIRiT are then used to reconstruct the images in an iterative SENSE-like image-domain framework. Extension of our ROCK-SPIRiT approach to the ESPIRiT framework may further bridge the gap between k-space and image domain based methods for SMS reconstruction. However, this was not explored in this study, as it is beyond the scope of our current work. Recently, the virtual slice concept has been proposed for SMS reconstruction, using a single split-slice GRAPPA-type kernel for correcting for both slice-aliasing and phase-encoding undersampling, along with a weighted data fidelity term for regularization (58). This objective function containing an SMS reconstruction kernel and a data fidelity term is reminiscent of a 2D undersampled reconstruction with ROCK-SPIRiT. However, the major difference is in the kernel term, where the virtual slice concept uses a one-time projection onto individual slices, whereas ROCK-SPIRiT uses an iterative self-consistency term. Thus, it is not straightforward to extend the former to an iterative algorithm that can incorporate low-dimensional regularizers. Nevertheless, our previous work includes approaches that can combine both one-time projection and self-consistency kernels in the same objective function, along with low-dimensional regularizers (23,31). But the application of such methods to virtual slice and the readout concatenation concepts warrant further investigation, which is beyond the scope of this work.

This study has limitations. Retrospectively 3-fold SMS and 2-fold in-plane accelerated images were utilized to test the performance of the proposed ROCK-SPiRiT and regularized ROCK-SPIRiT. Further evaluation with prospectively SMS-accelerated imaging in a larger cohort is warranted. FLASH imaging has been utilized in this study due to its resilience against off-resonance and susceptibility artifacts at higher field strength, although steady-state free precession (SSFP) cine MRI has inherent advantages in terms of contrast-to-noise ratio (CNR) and acquisition speed (49). However, SMS acceleration rates with SSFP sequences are limited for wider coverage in cardiac MRI applications (18,19,59), and were not considered in this study. We also note that in a 7T cine imaging study with retrospective gating, it was noted that in order to maintain steady state, phase encode lines per segment were chosen as a multiple of the SMS/MB factor (12). This was not observed at our 3T study with the prospectively SMS-accelerated data, where 8 phase encode lines per segment were acquired for SMS = 5. However, in our case OVS modules comprising substantial gradient spoiling moments were interleaved. Thus, more thorough gradient spoiling may be the reason for suppressing the artifacts previously observed in (12). An exploration of the relation between irregular phase-cycling patterns, applied spoiler gradient moments and steady-state artifacts warrant further investigation to ensure robustness in a variety of sequences. In this study, the prospectively accelerated data was acquired only on one subject as proof-of-concept evaluation to show the feasibility of reconstruction at highly accelerated prospectively SMS-encoded cine imaging. Additionally, quantitative analyses, similar to the retrospective acceleration study, could not be conducted on the 5-fold SMS and retrospectively 2-fold in-plane accelerated data due to the lack of reference images in this case.

Conclusion

The proposed ROCK-SPIRiT reconstruction improves image quality in SMS CMR compared to existing methods, while providing leakage reduction and allowing the use of regularization for further noise reduction.

Supplementary Material

Supplementary Material

Supporting Information Figure S1: Illustration of SMS encoding for an example SMS acceleration rate of 3. a) The readout concatenation formulation for SMS encoding represents the individual slice as concatenated along readout direction in image domain. The corresponding extended k-space is formed by taking a Fourier transform of these concatenated images. b) In this space, SMS encoding is represented as a retrospective undersampling (the sampling mask is shown by P_Ω) along the extended readout direction. c) Further acceleration by additional in-plane sampling is captured as undersampling along the phase encoding direction as in the traditional setting. The sampling mask with additional in plane masking is shown by P_Ω.

Supporting Information Figure S2: Tuning of the singular value thresholding hyperparameter for regularized ROCK-SPIRiT on an additional subject. PSNR and SSIM are calculated based on the corresponding single-band reference images. Singular value parameter thresholding was empirically tuned to 0.075 times the ℓ_∞ norm of the SENSE-1 image of the SMS encoded data, since the highest PSNR and SSIM are observed between 0.07 and 0.08.

Supporting Information Figure S3: PSNR, SSIM and leakage analyses across cardiac phases for all reconstruction methods. a) Regularized ROCK-SPIRiT has the highest PSNR values among all methods and 0.36% fluctuation across cardiac phases in terms of mean values. RO-SENSE-GRAPPA, Split Slice-GRAPPA and ROCK-SPIRiT have 0.19%, 0.16% and 0.20% fluctuation across cardiac phases, respectively. b) For SSIM, regularized ROCK-SPIRiT again has the highest SSIM values and 0.12% fluctuation across cardiac phases. RO-SENSE-GRAPA, Split Slice-GRAPPA and ROCK-SPIRiT have 0.13%, 0.14% and 0.11% fluctuations across cardiac phases, respectively. c) Leakage analysis across cardiac phases show that ROCK-SPIRiT has 1.21% fluctuations across cardiac phases, whereas. RO-SENSE-GRAPPA and Split Slice-GRAPPA have 1.59% and 1.66% fluctuation across cardiac phases, respectively. Note that leakage analysis could not be performed for regularized ROCK-SPIRiT due to the non-linear nature of this method. Based on analysis of variance across cardiac phases for each method, no significance difference was observed in either PSNR, SSIM or leakage across the different cardiac phases (P = 1).

Supporting Information Figure S4: The data from Figure 7, also including a) separate single-band acquisitions without OVS pulses, coming from 5 different breath-hold scans. The remainder of the figure depicts: b) prospectively 5-fold SMS-accelerated cine imaging using a fast imaging sequence (35), and reconstructed using Split Slice-GRAPPA reconstruction; c) RO-SENSE-GRAPPA, d) Split Slice-GRAPPA, e) ROCK-SPIRiT, f) Regularized ROCK-SPIRiT reconstructions for an additional retrospective 2-fold in-plane acceleration of this 5-fold SMS-accelerated acquisition.

Supporting Information Figure S5: Effect of kernel size on PSNR and SSIM for G_ROCK convolution kernels. This hyperparameter was tuned empirically over 20 different kernel sizes on the extended k-space of an additional subject. [9,9] kernel size was chosen to be the kernel size of the ROCK-SPIRiT method with its high PSNR and SSIM values. There are only 1.4% change SSIM difference and 1.1% PSNR difference among the different kernel sizes. Additional PSNR gain can be achieved while sacrificing SSIM values and a cost of increased computational time.

Supporting Information Figure S6: Calibration range vs. PSNR and SSIM metrics are depicted. Calibration range for ROCK-SPIRiT kernels was varied from 100% to 20%. % corresponds to the reduction of ACS region in each of the extended RO and PE directions. PSNR and SSIM values decrease with decreasing calibration range. Significant PSNR and SSIM losses observed at 20% calibration range (14.5% loss for PSNR and 4.1% loss for SSIM). At 80% calibration range, minimal PSNR and SSIM losses are observed (0.2% for PSNR and 0.2% for SSIM) compared to full calibration range (100%). Calibration time takes approximately 40 seconds for 100%, 34 seconds for 80%, 29 seconds for 60%, 25 seconds for 40% and 23 seconds for 20%. Thus, a smaller calibration region provides a mild saving in computational time, while lowering the PSNR and SSIM values. Since the computational savings were modest, this work utilized full calibration range (100%) for all subjects.

Supplemental Video S1

Supporting Information Video S1: Movie of the cine images in Figure 5 through the cardiac cycle.

Supplemental Video S2

Supporting Information Video S2: Movie of the cine images in Figure 7 through the cardiac cycle.