A hierarchical model of abdominal configuration changes extracted from golden angle radial magnetic resonance imaging

Abstract

Abdominal organs are subject to a variety of physiological forces that superimpose their effects to influence local motion and configuration. These forces not only include breathing, but can also arise from cyclic antral contractions and a range of slow configuration changes. To elucidate each individual motion pattern as well as their combined effects, a hierarchical motion model was built for characterization of these 3 motion modes (characterized as deformation maps between states) using golden angle radial MR signals. Breathing motions are characterized first. Antral contraction states are then reconstructed after breathing motion-induced deformation are corrected; slow configuration change states are further extracted from breathing motion-corrected image reconstructions. The hierarchical model is established based on these multimodal states, which can be either individually shown or combined to demonstrate any arbitrary composited motion patterns. The model was evaluated using 20 MR scans acquired from 9 subjects. Poor reproducibility of breathing motions both within as well as between scan sessions was observed, with an average intra-subject difference of 1.6 cycles min⁻¹ for average breathing frequencies of 12.0 cycles min⁻¹. Antral contraction frequency distributions were more stable than breathing, but also presented poor reproducibility between scans with an average difference of 0.3 cycles min⁻¹ for average frequencies of 3.2 cycles min⁻¹. The magnitudes of motions beyond breathing were found to be significant, with 14.4 and 33.8 mm maximal motions measured from antral contraction and slow configuration changes, respectively. Hierarchical motion models have potential in multiple applications in radiotherapy, including improving the accuracy of dose delivery estimation, providing guidance for margin creation, and supporting advanced decisions and strategies for immobilization, treatment monitoring and gating.

Introduction

The internal configuration of the abdomen is subject to continuous changes due to various physiological processes as well as voluntary motions. Respiratory motion contributes greatly to the overall motion, where a motion range of more than 20 mm (Keall et al 2006, Feng et al 2009, Mori et al 2009, Wysocka et al 2010) has been documented, with potentially significant impacts including insufficient tumor treatment and/or normal organ overdosing (Balter et al 1996).

In addition to breathing, internal organs and tumors are subject to other physiological forces including gastrointestinal (GI) periodic contraction motions and slow drifting motions of the GI tract. To fully appreciate these motions and their potential impact on precision radiation therapy, it is important to isolate and quantify the more dominant motions typically present in the abdomen. Whereas breathing motion in the abdomen has been well studied, GI contraction as well as other predominantly cyclic motions have been given little attention to date. Several preliminary studies have assessed gastrointestinal motion using various imaging methods including radiography and fluoroscopy (Watanabe et al 2008), 4D computed tomography (4DCT) (Kumagai et al 2009), cine magnetic resonance imaging (MRI) (Baba et al 2009, Wysocka et al 2014, Nonaka et al 2019) and multi-modality imaging (Mostafaei et al 2018). These investigations have shown that gastrointestinal motion has a similar magnitude to respiratory motion. Based on these observations, the joint effects of respiratory and GI motions should be sufficiently investigated to determine, and manage their impact on local radiation dose delivery.

In addition to two cyclic motions, movements of abdominal organs are influenced by other, less periodic motions, as well as spontaneous patient voluntary movements (Zachiu et al 2015). These motions and their impact on organ position have been identified by several studies to be more than 5 mm on a time scale of over 20 min, (von Siebenthal et al 2007, Langen et al 2008), and can be grouped together as slow configuration changes. These slow configuration changes have not been well characterized with respect to their impact on abdominal radiation therapy. Considering the current length of treatment session for a typical stereotactic body radiation therapy, these motions should also be taken into consideration during treatment planning.

A common way to study motion effects in radiotherapy is by constructing a motion model. A motion model takes surrogate data as input, and produces a motion estimate as output (McClelland et al 2013). Various motion models have been introduced in the past few decades to estimate the nature and the magnitude of breathing motion (McClelland et al 2011, 2013, Stemkens et al 2016, Baumgartner et al 2017, Uh et al 2017). These models have been shown to be able to predict respiration motions during image acquisition or radiotherapy.

To support the investigation of the combined effects of multiple motion sources, we have constructed a hierarchical motion model that includes various motion modes on a subject level, allowing reconstruction of combinations of breathing, cyclic GI (due to stomach contraction), and slow configuration changes. Breathing and cyclic antral contraction states are extracted and reconstructed using a previously published method that applies deformable motion correction to separate breathing from other abdominal motions (Johansson et al 2018). Slow configuration changes are characterized using a time series of image volumes after breathing motion is corrected. Following this, the multidimensional model is built by the composition of specific states from these three motion modes, to elucidate motion effects at any given time.

Methods

Sampling and reconstruction of motion states

Under an institutional review board-approved protocol, 20 min golden-angle stack-of-stars gradient-echo dynamic contrast-enhanced (DCE-) MRI scans (Block et al 2014) were acquired on a 3 T scanner (Skyra, Siemens Healthineers, Erlangen, Germany) in two consecutive 10 min blocks and used for the construction of the motion model. A total of 7000 radial stacks of spokes were acquired during each scan. Each sample of stack-of-spoke was used to define a frame of patient motion states at a temporal resolution of 0.17 s.

Motion identification

In this investigation, three assumptions were used to separate the three types of motion including breathing motion, antral contractions (a dominant source of cyclic GI motion), and slow configuration changes. First, it was assumed that breathing motion amplitude is greater than antral contractions and slow configuration changes, with respect to its impact on the liver. A second assumption was that the periodicity of breathing and antral contractions are sufficiently different to expect minimal, if any, synchronization between the two. The third assumption was that slow configuration changes were of sufficiently low temporal resolution such that images could be sampled on times that approximate or exceed the typical duration of antral contraction cycles. This precondition essentially blurs antral contraction-induced motions for any frame wherein the slow configuration changes are sampled. Using these assumptions, breathing motion was first extracted and corrected, followed by reconstruction of GI contraction states, and slow configuration changes, from images reconstructed over 17 s time intervals.

Reconstruction and modeling of respiratory motion states

Respiratory motion states for each scan were reconstructed and used to correct projections using a previously published method (Johansson et al 2018). To extract the breathing motion signal for each radial spoke, images with high temporal but low spatial resolution were reconstructed by combining neighboring spokes with a view-sharing filter. The reconstructed image volumes were rigidly aligned so that the liver position (voxels within an expert-delineated contour) matched that of a vendor-reconstructed reference (exhale) image. Breathing motion signals for each spoke were defined as the superior-inferior (SI) displacement of the transform that aligned the image centered in that spoke to the reference state. These motion signals were used to sort radial spokes from inhale to exhale states. After sorting, spokes were combined using the view-sharing filter with the motion signal as view-sharing dimension rather than time. Following the reconstruction, the end-exhale state was selected as the reference and the remaining 20 states were aligned to this state using a B-spline based deformable image registration (DIR) algorithm. The resulting 20 deformations, combined with the null transformation defining end-exhale, yielded a breathing motion transform domain consisting of 21 deformation fields.

These deformation fields were used to interpolate new deformation fields for every spoke using the motion signal as an index. Specifically, for a given spoke, a non-integer number of states between 1 and 21 was determined by the sort index of its motion signal; the interpolation based on its state was conducted linearly among its neighboring motion states, generating the deformation field for this given spoke. The resulting deformation fields were applied to their corresponding radial projections to yield their corresponding respiratory motion-induced deformations.

Cyclic antral contraction reconstruction and modeling

Antral contraction motion states were built using a previously described method (Johansson et al 2018) applied to breathing motion-corrected projections. Similar to what was done to index respiratory motion, a time series of high temporal and low spatial resolution images were reconstructed using a narrow view-sharing filter from breathing motion-corrected radial spokes. The stomach was contoured by an expert on the same vendor-reconstructed reference image, and propagated to these time-series images. Here, the reference image was manually defined as the image volume with end-exhalation, 21st antral contraction state, and last frame of slow configuration motion. A time-intensity matrix was built based on the intensity levels on all voxels inside the stomach contour from these time series images, with one dimension representing the time and another one the vectorized voxels. A Rician-distribution filter (equation (1)) was applied to this matrix, emphasizing the expected frequency window of the antral contraction cycle, followed by principal component analysis (PCA), where the 1st principal component contains the phase information of antral contraction motion. Here, we used the non-centrality parameter s = 0.05 Hz, and scale parameter σ = 0.01 Hz. I₀ is the zero-order modified Bessel function of the first kind

$$f(x\mid s,\sigma )=I_0\left(\frac{xs}{{\sigma }^2}\right)\frac{x}{{\sigma }^2}{e}^{-\left(\frac{x^2+s^2}{2{\sigma }^2}\right)}.$$ (1)

The phase angle between the 1st principal component and its derivative was calculated, which was assigned as the GI cyclic motion signal for each spoke and used for sorting. After sorting, 21 GI contraction state images were reconstructed using a view sharing filter along the GI motion signal dimension. Note that all these GI state images are at the end-exhale breathing state since they were reconstructed from breathing motion-corrected spokes. Similarly, 20 other GI contraction state images were deformably registered to the reference state image with the same algorithm described above (here the reference state was arbitrarily chosen). Together with the null deformation field for the reference state, we again have 21 deformation fields corresponding to 21 GI contraction motion states.

Slow configuration states reconstruction

Images demonstrating slow configuration changes were reconstructed via a view sharing filter with time as the sharing dimension on breathing motion-corrected projections. Due to the slow nature of change and to blur out antral contraction effects, the temporal resolution of reconstructions was set to 16.67 s, resulting in a total of 72 image volumes for a 20 min scan. Again, DIR was applied to align 71 state images with the reference image volume which was arbitrarily set to be the state at 20 min’ frame (last frame of the scan), yielding deformation fields that characterized slow abdominal configuration changes for the subject during the scan time window.

Hierarchical motion model construction

From the deformation fields representing the 21 breathing motion, 21 GI contraction states, and 72 slow configuration motion states, a hierarchical motion model was built. Any arbitrary combination of breathing, antral contraction, and slow configuration change states can be synthesized by superimposing deformation fields of assigned motion states:

$$T(i,j,k)=T_1\left(T_2\left(T_3(k),j\right),i\right),$$ (2)

where T_i,_j,_k is the combined deformation fields and T_i, T_j and T are deformations for ith state of motion mode 1 (e.g. respiratory), jth state of motion mode 2 (e.g. antral contraction), as well as kth state of motion mode 3 (e.g. slow configuration). The superimposed deformation field is then applied to the reference state image, resulting in an image volume representing the mixed motion pattern of all 3 modes. Here, the reference state was arbitrarily defined as the image volume at the 21st respiratory state (end-exhalation state), 21st antral contraction state (reference antral contraction state), and 72nd slow configuration motion state (reference slow change state).

For each stack of spokes, we also assigned a non-integer motion state value for each of the motion modes. This value was determined as the sorting index from motion signals with respect to all 21 states for each cyclic motion mode (e.g. respiration and GI contraction). The sorting index for slow configuration was simply the time of acquisition of the specific stack of spokes. Linear interpolation of the deformation field centered around each of the 7000 acquisitions for each motion mode was used to create deformations demonstrating the change in patient configuration from the reference state to that at the specific time of acquisition. In addition, a composite deformation was generated using equation (2) and used to deform the reference state image, yielding motion state images for all 7000 spokes; thus, a time series image volume, which was able to interpret mixed motion patterns with high spatial resolution as well as temporal resolution up to 0.17 s per frame was generated.

Hierarchical motion model evaluation

To demonstrate the potential for generating and using a hierarchical motion model, k-space data from 20 scans of 9 subjects acquired with institutional board approval were analyzed. Cycle frequencies of both respiratory and GI contraction motions were calculated for each scan. The time change (Δt) between each cycle peak was also calculated across the entire scan window to study intra-fraction frequency variations. Motion signals for all 7000 spokes were sorted and binned into histograms describing the motion state density functions for the two cyclic motion modes.

For illustration and measurement of gastric organ (stomach, duodenum, bowel, etc) motions from not only breathing, but also GI contraction and slow configuration sources, contours containing these organs were drawn by an expert for each of the scans on the reference state images. These contours were only used to guide the region that was used for model evaluation, and as such the actual accuracy of the contour delineation minimally impacted the reported motion. Maximum, average and standard deviation values of motion ranges for these organs were determined from the composite motion model, as well as the separate respiration-only, GI contraction-only and slow configuration motion modes. This was done by extracting the magnitudes of deformation vectors at corresponding locations within drawn contours.

Five of the 9 patients included in the study had 2 separate scans performed on different days, and 3 patients had 3 separate scans all of which were separated by at least 39 d (table 1), providing an opportunity to preliminarily study the reproducibility of abdominal motion patterns for the same subject at different times. The reproducibility was investigated in 3 aspects: frequency, motion state density, and motion magnitude. The former two were compared for 2 cyclic motions, while the latter was investigated for all 3 motion modes. The coefficient of repeatability (RC) was calculated for motion magnitudes using the following equation:

$$\text{RC}=1.96\sqrt{2*{\sigma }^2/d},$$ (3)

where σ² is the variance of repeat measurements on the same subject, d is the degree of freedom (i.e. number of repeated scans − 1). RC is the measurement which represents the value below which the absolute difference between two repeated test results may be expected to lie with a probability of 95%.

Table 1.

Subjects and number of scans involved into the study, time interval between scans and subject weight, height and BMI recorded post-treatment when available.

Subject no.	Number of scans	Time interval from the first scan (d)	Weight (kg)	Height (m)	BMI
Subject 1	2	44	85.0	1.75	27.7
Subject 2	2	44	73.8	1.55	30.8
Subject 3	2	133	N/A	N/A	N/A
Subject 4	3	50, 99	108.5	1.78	34.3
Subject 5	2	47	N/A	N/A	N/A
Subject 6	1	N/A	76.2	1.83	22.9
Subject 7	3	44, 106	96.5	1.83	28.9
Subject 8	2	48	142.7	1.83	42.7
Subject 9	3	39, 95	86.4	1.88	24.5

Results

Figure 1 displays three example motion states for each mode from one example scan. For breathing motion, we could clearly see liver motions in the SI direction, where a maximal 24.3 mm motion was observed in the case shown. For antral contraction motion, deformations of the stomach are visible, with the stomach continuously moving close to and pushing away from the edge of the liver; for this case, maximal deformations of 6.2 mm and 5.3 mm were measured at stomach surface in the AP and LR directions respectively. For slow configuration changes, motion effects are mainly observed in the bowel, with a maximal motion of 17.4 mm observed.

Figure 1.

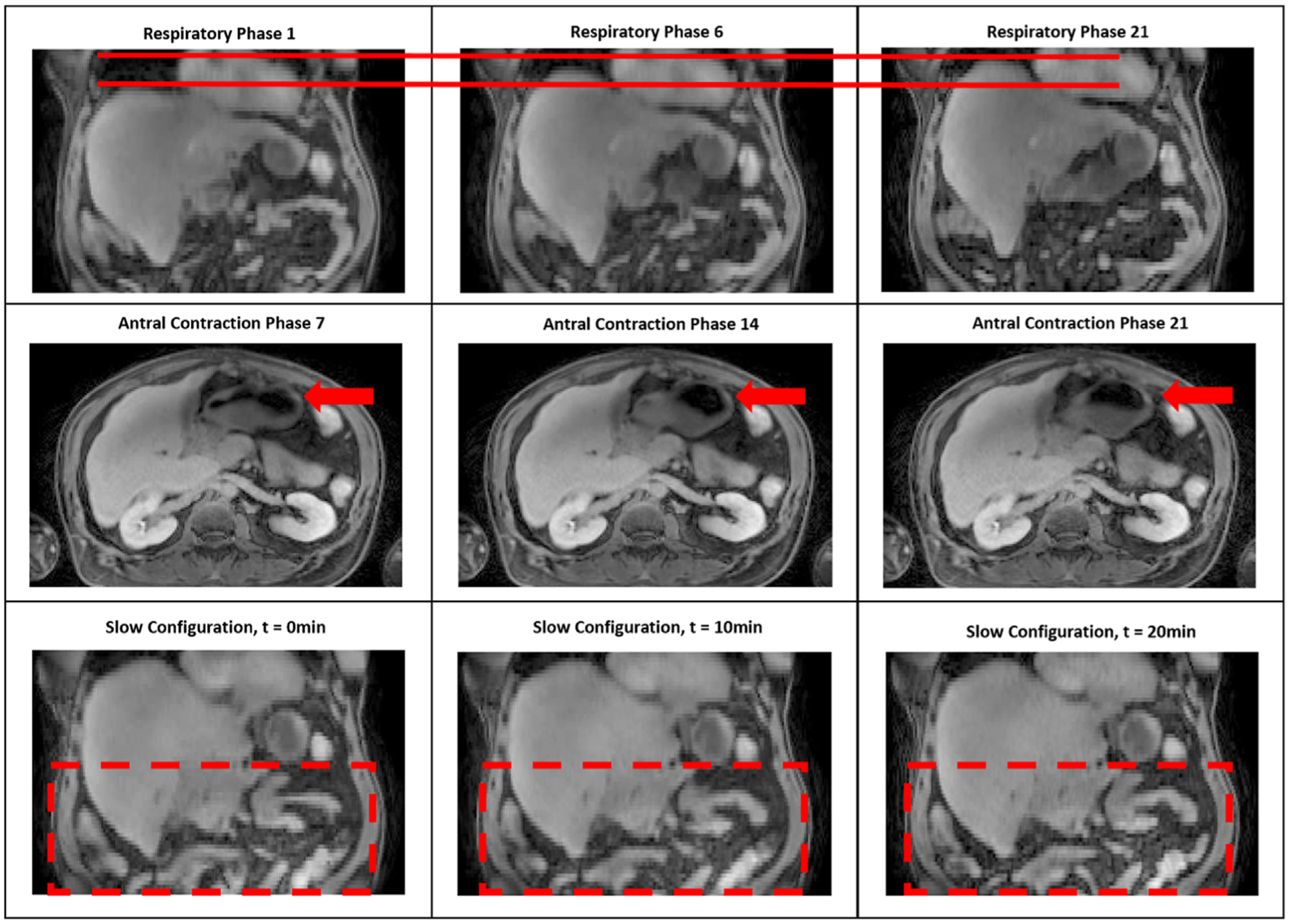
motion state images for each of three motion modes. Top row: respiration (the solid line showing different liver positions on SI direction); middle row: antral contraction deforming the stomach (arrows); bottom row: slow configuration, showing deformations of the bowel (within dashed box).

To further demonstrate the interpretability of the hierarchical motion model, figure 2 displays 9 reconstructed image volumes for the same example scan with combined motions estimated from the model. For all the image volumes at different time points, motions are composited from all 3 modes. Deformations could be easily seen at different time points due to effects from composite abdominal motions. For this example scan, a maximum of 25.7 mm movement was observed within the stomach, and maximal motion for bowel of 39.0 mm was observed.

Figure 2.

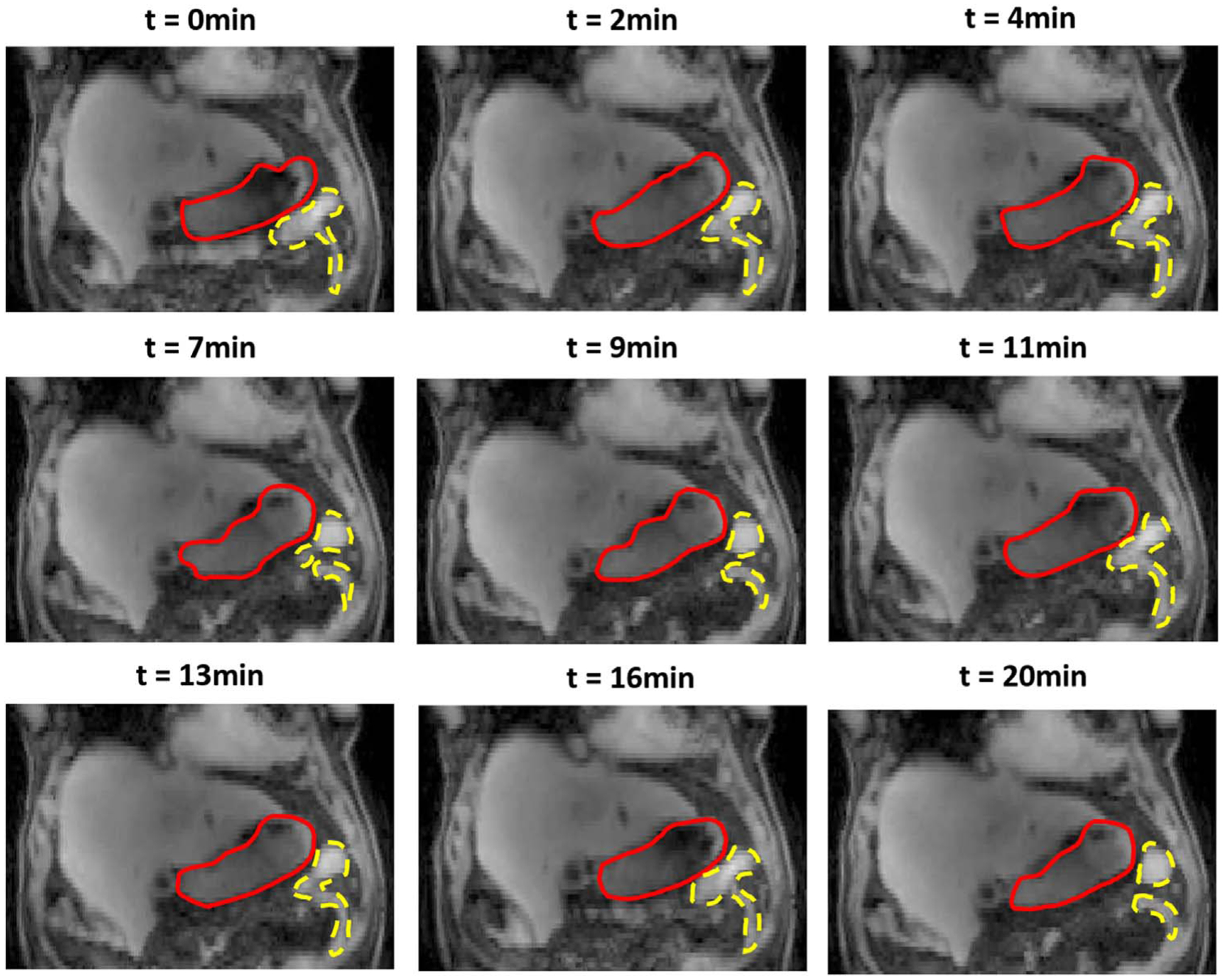
An example of reconstructed image volumes showing compositing motion patterns from all motion modes at different time points for a complete 20 min’ scan. Red solid lines contours stomachs; yellow dashed lines represent part of bowel.

Frequency and reproducibility

Frequencies of each cyclic motion mode (respiration and antral contraction) are listed in table 2. The average respiratory frequency for all scans was 12.0 cycles per minute, with a standard deviation of 3.5. Respiratory frequency varied significantly across scans with a minimum of 6.2 cycles min⁻¹ and a maximum of 18.8 cycles min⁻¹.

Table 2.

Average frequencies of respiration and gastrointestinal contraction during the whole 20 min’ scan period. Units are cycle per minute.

	Respiration motion frequency (cycles min−1)			Antral contraction frequency (cycles min−1)
Subject No.	Scan 1	Scan 2	Scan 3	Scan 1	Scan 2	Scan 3
Subject 1	12.4	13.3	N/A	3.7	3.6	N/A
Subject 2	15.6	15.8	N/A	3.1	3.0	N/A
Subject 3	10.8	14.0	N/A	3.1	3.2	N/A
Subject 4	9.3	7.1	6.2	3.4	2.4	2.8
Subject 5	9.8	9.7	N/A	2.8	3.2	N/A
Subject 6	8.8	N/A	N/A	2.9	N/A	N/A
Subject 7	18.8	13.7	10.5	4.2	3.3	4.3
Subject 8	16.4	16.8	N/A	3.4	3.6	N/A
Subject 9	9.8	10.3	10.1	3.1	3.2	2.6

Compared to respiratory motion, antral contraction motion was observed to be more stable, with a mean frequency of 3.2 cycles per minute and a standard deviation of 0.5 cycles min⁻¹. The maximum and minimum measured frequencies of antral contraction were 4.3 and 2.4 cycles min⁻¹, respectively.

Examination of peak-to-peak Δt of these 2 motion modes demonstrated that antral contraction motion is more stable than breathing motion during the 20 min’ scan period. An example distribution from a single scan (figure 3) shows respiration velocity changing significantly during the whole scan period with a Δt variation range of 1.0–5.8 s compared to an average of 4.2 s; for the antral contraction, however, the periodicity of motion remained more stable, with minimum and maximum Δt of 15.4 and 18.0 s respectively compared to an average of 16.4 s.

Figure 3.

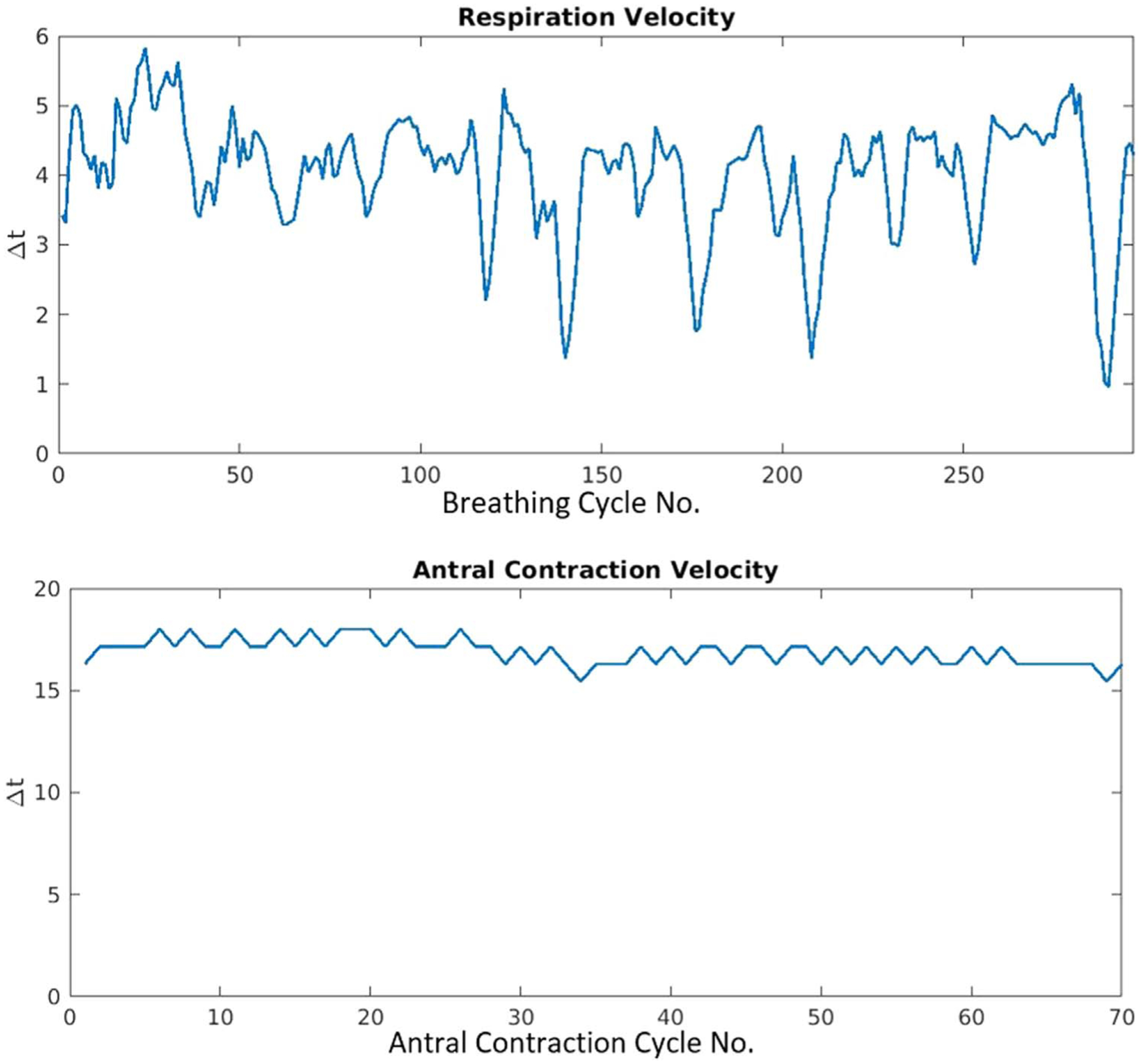
Example of respiration (top) and antral contraction (bottom) velocity variations during a 20 min’ scan presented by time interval (Δt) between each peaks of successive motion cycles (cycle number is denoted on the x axes).

Inter-scan periodicity showed subject-specific behaviors. The average intra-subject frequency difference for respiration motion is 1.6 cycles min⁻¹ across the population, while this number for contraction motion is 0.3 cycles min⁻¹. For breathing motion, 3 out of 8 subjects showed large inter-scan variations (larger than 2 cycles min⁻¹), while the rest showed variations less than 1 cycle min⁻¹. The largest detected intra-subject difference was 5.5 cycle min⁻¹. For contraction motion, four subjects had differences larger than 0.4 cycles min⁻¹, while others showed variations less than 0.2 cycles min⁻¹. The largest difference observed was 0.7 cycle min⁻¹.

Probability density and reproducibility

Figure 4 shows frequencies of occurrence for breathing motion states for all patients with at least two scans. The 21st state is the end-exhalation state, whereas the 1st state is the inhalation state, and thus progression from the left to right represents liver positions advancing from their most inferior to the most superior locations. The measured curves are typical for distributions of breathing over several minutes, with features including greater time spent towards the exhale state, as well as greater variation in the inhale positions as compared to the exhale position of the liver. Within this general trend, exact density distributions still varied across different scans. By comparison, GI contractions (figure 5) were more uniformly distributed than breathing, consistent with reasonably uniform and reproducible gastric motion cycles.

Figure 4.

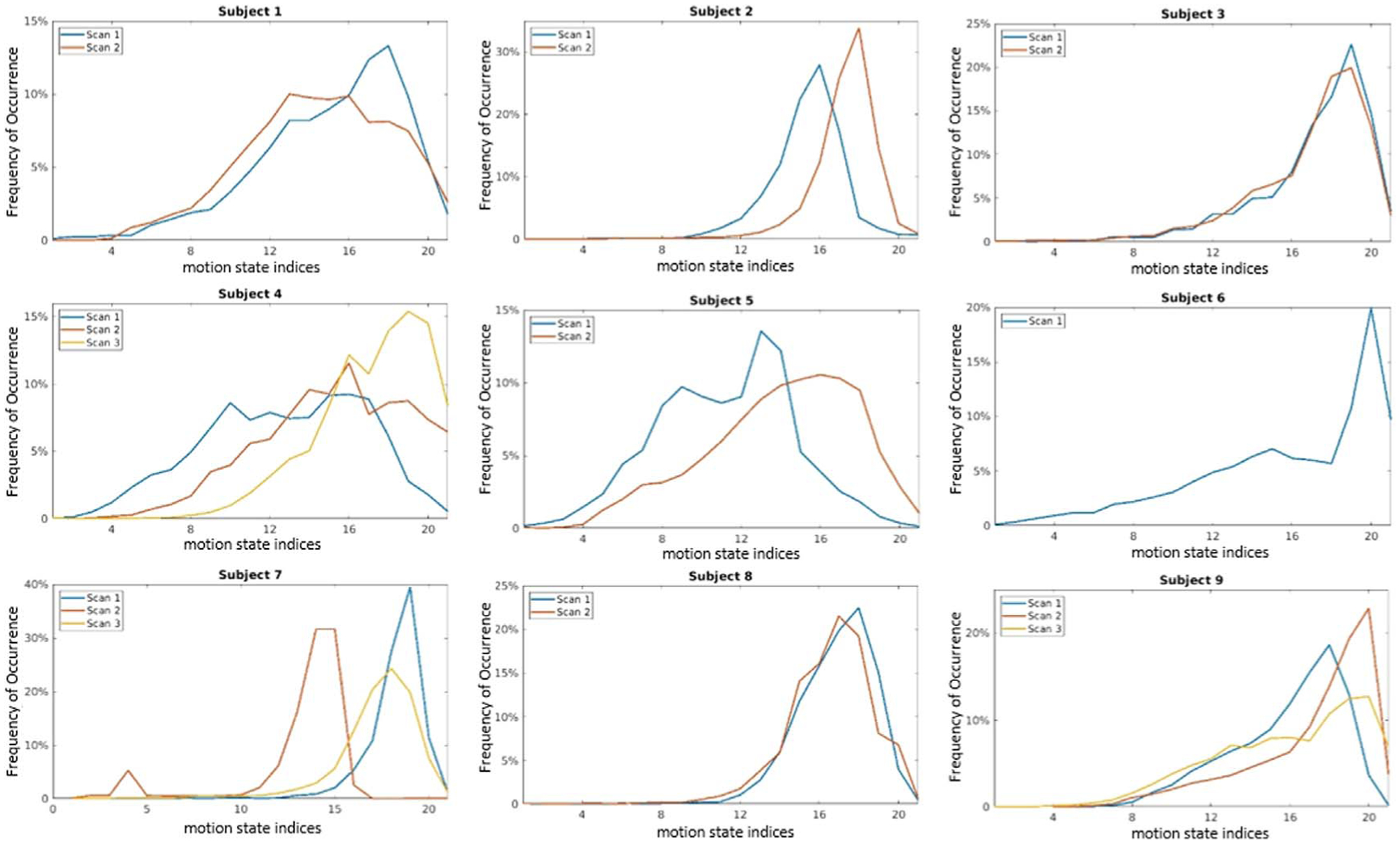
Frequency distributions of respiration motion states. X-axis represents the motion state index, with 0 representing end-inhale and 21 representing end-exhale.

Figure 5.

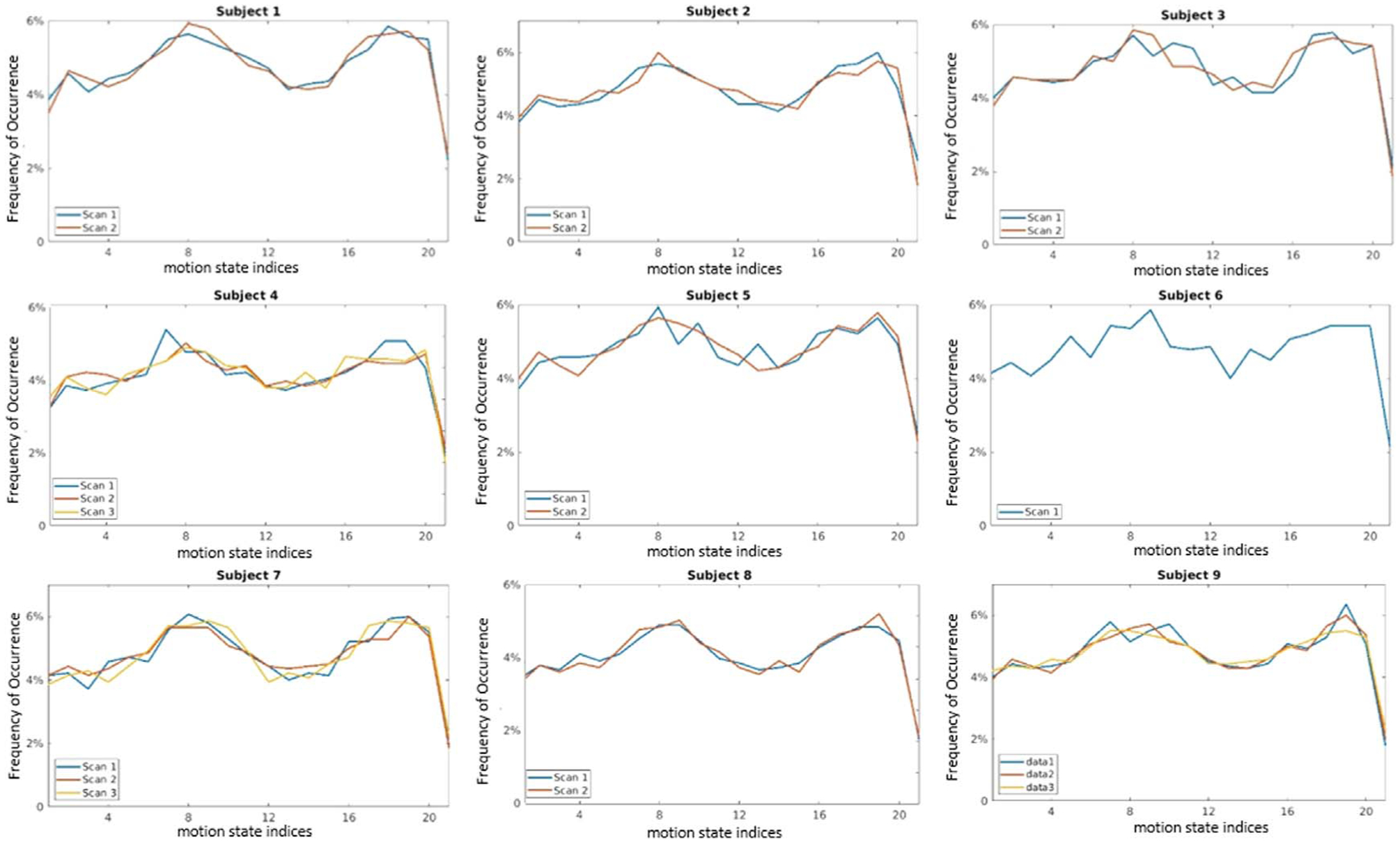
Frequency distributions of antral contraction motion states for all scans. The abscissa values are the motion state indices.

Motion range and reproducibility

Maximum motion magnitudes of points on the surfaces of 3 gastric organs (stomach, bowel and duodenum) for individual motion modes as well as their observed composites were gathered for all the 20 scans. Population range and average were calculated and evaluated. The largest combined maximal motion was detected on the bowel surface, with a population average of 33.9 mm and range of 22.4–47.6 mm; duodenum and stomach showed close average maximal motion with 26.3 mm (ranging from 20.5–37.3 mm) and 26.1 mm (ranging from 18.5 to 44.5 mm). By examining each individual motion mode, bowel was more affected by slow change motions, with an average of 24.7 mm, compared to 16.9 mm for duodenum and 13.7 mm for stomach. Exact maximal motion magnitudes for each scan were listed in table 3 while the population range and average were summarized in table 5.

Table 3.

Maximum motion magnitudes for 3 gastric organs (bowel, stomach and duodenum) from all 20 scans due to respiration, GI contraction, slow change and observed combinations of these 3 modes. Units are mm.

Structure name	Subject no.	Scan no.	Respiration (mm)	Antral contraction (mm)	Slow change (mm)	Composite motion (mm)
Bowel	Subject 1	Scan 1	23.4	8.7	29.4	34.8
		Scan 2	21.8	6.7	26.3	31.8
	Subject 2	Scan 1	24.2	9.5	22.8	29.0
		Scan 2	15.8	8.3	28.8	36.1
	Subject 3	Scan 1	21.8	8.5	26.8	31.5
		Scan 2	23.6	11.0	26.7	34.6
	Subject 4	Scan 1	26.2	11.9	31.1	33.9
		Scan 2	18.9	10.2	28.5	33.7
		Scan 3	23.1	4.4	26.7	33.2
	Subject 5	Scan 1	22.8	7.4	22.3	30.4
		Scan 2	27.9	6.9	31.8	44.7
	Subject 6	Scan 1	29.6	9.8	26.0	47.6
	Subject 7	Scan 1	19.1	6.2	14.0	31.7
		Scan 2	27.3	5.3	11.2	34.8
		Scan 3	18.6	9.3	33.8	43.5
	Subject 8	Scan 1	16.8	7.4	25.3	27.8
		Scan 2	18.1	9.8	16.3	22.2
	Subject 9	Scan 1	29.7	9.1	24.9	36.3
		Scan 2	21.5	7.4	23.8	30.9
		Scan 3	21.5	10.0	16.3	30.4
Duodenum	Subject 1	Scan 1	11.4	4.3	18.4	26.8
		Scan 2	12.3	5.8	17.2	22.9
	Subject 2	Scan 1	15.4	7.9	15.0	26.1
		Scan 2	16.3	6.2	13.4	20.6
	Subject 3	Scan 1	19.2	7.9	18.4	23.2
		Scan 2	20.5	9.7	13.7	25.1
	Subject 4	Scan 1	19.8	7.7	22.1	32.3
		Scan 2	8.6	12.1	17.7	27.2
		Scan 3	18.9	5.2	20.6	27.9
	Subject 5	Scan 1	17.2	6.3	20.1	26.8
		Scan 2	24.6	6.2	29.9	37.3
	Subject 6	Scan 1	20.4	7.4	17.5	33.6
	Subject 7	Scan 1	15.2	5.8	8.9	20.5
		Scan 2	19.5	8.5	13.6	23.1
		Scan 3	14.1	6.9	19.3	31.5
	Subject 8	Scan 1	15.5	7.9	15.3	23.1
		Scan 2	16.7	6.4	8.5	22.1
	Subject 9	Scan 1	24.1	8.7	14.9	29.1
		Scan 2	16.9	6.2	22.7	24.7
		Scan 3	18.1	8.9	10.2	22.1
Stomach	Subject 1	Scan 1	16.9	7.4	21.5	28.1
		Scan 2	20.3	5.8	16.5	23.6
	Subject 2	Scan 1	18.0	10.4	15.0	25.0
		Scan 2	18.1	7.7	11.2	22.6
	Subject 3	Scan 1	19.3	7.9	18.4	23.4
		Scan 2	17.3	14.4	12.2	25.7
	Subject 4	Scan 1	21.9	8.7	29.2	44.5
		Scan 2	11.9	12.6	13.4	21.8
		Scan 3	27.5	3.6	18.7	25.1
	Subject 5	Scan 1	16.4	7.7	12.3	25.7
		Scan 2	26.7	4.9	7.0	30.9
	Subject 6	Scan 1	24.9	8.1	19.3	33.6
	Subject 7	Scan 1	16.2	12.1	6.5	18.5
		Scan 2	19.8	8.3	9.3	22.4
		Scan 3	15.0	12.0	8.4	21.7
	Subject 8	Scan 1	17.4	6.6	10.4	22.5
		Scan 2	16.6	6.7	6.1	20.2
	Subject 9	Scan 1	25.9	12.1	9.2	33.5
		Scan 2	19.8	8.9	17.0	26.6
		Scan 3	19.1	7.6	13.1	27.0

Table 5.

Summary of population range and average of maximal motion magnitudes as well as mean and standard deviation of motion magnitudes for 3 gastric organs (bowel, stomach and duodenum) from all 20 scans due to respiration, GI contraction, slow change and observed combinations of these 3 modes.

		Maximal motion magnitude		Mean and standard deviation of motion magnitude
Structure name	Motion modes	Population range (mm)	Population average (mm)	Population range (mm)	Population average (mm)
Bowel	Respiration	15.8–29.7	22.6	4.0 ± 2.6–12.0 ± 4.5	8.0 ± 3.4
	Antral contraction	4.4–11.9	8.4	0.6 ± 0.5–2.4 ± 1.3	1.2 ± 0.7
	Slow change	11.2–33.8	24.7	2.7 ± 1.5–12.3 ± 5.0	6.3 ± 3.4
	Composite motion	22.2–47.6	33.9	6.6 ± 4.6–14.6 ± 5.2	10.8 ± 4.6
Duodenum	Respiration	8.6–24.6	17.2	3.8 ± 1.3–10.9 ± 3.1	7.5 ± 3.0
	Antral contraction	4.3–12.1	7.3	1.0 ± 0.7–2.9 ± 1.6	1.7 ± 1.2
	Slow change	8.5–29.9	16.9	2.2 ± 1.2–10.4 ± 3.4	4.9 ± 2.5
	Composite motion	20.5–37.3	26.3	6.3 ± 3.0–13.6 ± 3.9	9.3 ± 3.6
Stomach	Respiration	11.9–27.5	19.5	4.6 ± 1.9–11.8 ± 3.8	8.6 ± 3.1
	Antral contraction	3.6–14.4	8.7	0.7 ± 0.4–3.2 ± 1.8	1.6 ± 1.0
	Slow change	6.1–29.2	13.7	2.2 ± 0.9–7.3 ± 3.1	4.3 ± 2.0
	Composite motion	18.5–44.5	26.1	7.5 ± 2.8–13.7 ± 5.3	10.1 ± 3.7

Means and standard deviations of motion magnitudes of the surface of various gastric organs are summarized in table 4. Population range and average were computed and summarized in table 5. The bowel had the largest average motion magnitudes ranging from 6.6 to 14.6 mm (mean 10.8 mm), followed by stomach (mean 10.1 mm), and duodenum (mean 9.3 mm, ranging from 6.3 to 13.6 mm). Similarly, slow configuration changes had the largest influence on bowel motion, with an average of 6.3 mm compared to stomach (4.3 mm), and duodenum (4.9 mm); meanwhile, bowel was less affected by antral contraction motion compared to stomach and duodenum, with average of 1.2 mm compared to 1.6 mm and 1.7 mm respectively.

Table 4.

Means and standard deviations of motion magnitudes for 3 gastric organs (bowel, stomach and duodenum) from all 20 scans with respiration only, GI contraction only, slow change only and the combination of all 3 modes.

Structure name	Subject no.	Scan no.	Respiration (mm)	Antral contraction (mm)	Slow change (mm)	Composite motion (mm)
Bowel	Subject 1	Scan 1	6.9 ± 2.7	1.0 ± 0.6	5.2 ± 3.1	9.6 ± 4.4
		Scan 2	7.1 ± 3.7	1.1 ± 0.6	6.4 ± 3.9	10.4 ± 4.8
	Subject 2	Scan 1	6.2 ± 3.8	1.5 ± 0.8	7.0 ± 4.4	9.0 ± 4.9
		Scan 2	4.0 ± 2.6	1.2 ± 0.7	6.1 ± 4.5	6.6 ± 4.6
	Subject 3	Scan 1	8.6 ± 3.6	1.3 ± 0.8	8.9 ± 3.3	12.1 ± 3.7
		Scan 2	6.5 ± 3.5	1.4 ± 0.9	5.8 ± 3.7	9.6 ± 4.3
	Subject 4	Scan 1	8.9 ± 3.5	1.4 ± 0.9	6.9 ± 3.8	13.0 ± 4.7
		Scan 2	4.8 ± 2.5	2.4 ± 1.3	9.0 ± 4.1	11.1 ± 3.9
		Scan 3	8.5 ± 3.2	0.6 ± 0.5	12.3 ± 5.0	14.6 ± 5.2
	Subject 5	Scan 1	9.7 ± 3.3	1.2 ± 0.7	6.4 ± 2.8	12.9 ± 4.1
		Scan 2	11.6 ± 4.1	1.0 ± 0.6	6.2 ± 3.4	14.5 ± 5.8
	Subject 6	Scan 1	11.1 ± 4.7	1.3 ± 0.8	6.1 ± 3.6	14.1 ± 6.5
	Subject 7	Scan 1	9.4 ± 2.7	0.9 ± 0.5	3.4 ± 2.1	10.6 ± 3.9
		Scan 2	12.0 ± 4.5	0.7 ± 0.4	2.7 ± 1.5	12.6 ± 4.9
		Scan 3	7.5 ± 2.9	1.2 ± 0.7	7.6 ± 4.6	11.4 ± 5.4
	Subject 8	Scan 1	6.6 ± 2.6	1.3 ± 0.8	5.5 ± 3.1	8.8 ± 3.5
		Scan 2	6.8 ± 2.9	1.0 ± 0.7	3.3 ± 1.7	7.5 ± 3.7
	Subject 9	Scan 1	10.6 ± 4.5	1.3 ± 0.7	5.6 ± 2.9	11.2 ± 5.0
		Scan 2	5.4 ± 3.1	1.1 ± 0.8	6.1 ± 4.0	7.2 ± 3.9
		Scan 3	7.2 ± 3.2	1.1 ± 0.7	5.0 ± 2.1	9.5 ± 3.9
Duodenum	Subject 1	Scan 1	6.8 ± 1.8	1.3 ± 0.6	4.2 ± 2.3	9.3 ± 3.4
		Scan 2	6.7 ± 2.2	1.3 ± 0.7	4.7 ± 2.7	8.7 ± 3.2
	Subject 2	Scan 1	6.2 ± 3.0	1.5 ± 0.9	4.8 ± 2.5	7.7 ± 4.5
		Scan 2	6.3 ± 3.1	1.3 ± 0.7	5.1 ± 3.7	6.7 ± 3.2
	Subject 3	Scan 1	8.2 ± 3.5	1.4 ± 0.8	6.5 ± 2.1	8.9 ± 3.1
		Scan 2	8.8 ± 3.7	1.7 ± 1.2	3.4 ± 1.9	10.4 ± 3.9
	Subject 4	Scan 1	10.9 ± 3.1	1.8 ± 1.0	5.8 ± 3.2	12.5 ± 4.5
		Scan 2	3.8 ± 1.3	2.9 ± 1.6	7.5 ± 2.5	6.3 ± 3.0
		Scan 3	7.6 ± 3.2	1.0 ± 0.7	10.4 ± 3.4	13.6 ± 3.9
	Subject 5	Scan 1	8.0 ± 2.8	1.3 ± 0.7	4.6 ± 3.1	10.9 ± 3.7
		Scan 2	9.1 ± 3.8	1.4 ± 0.8	6.2 ± 4.9	12.7 ± 5.4
	Subject 6	Scan 1	9.9 ± 3.5	1.4 ± 0.8	4.3 ± 2.8	13.5 ± 4.5
	Subject 7	Scan 1	7.4 ± 2.2	1.2 ± 0.7	2.2 ± 1.2	7.5 ± 2.8
		Scan 2	7.7 ± 3.5	1.1 ± 0.7	2.8 ± 1.5	7.9 ± 3.4
		Scan 3	6.8 ± 2.5	1.3 ± 0.7	5.0 ± 2.3	8.8 ± 3.4
	Subject 8	Scan 1	6.8 ± 3.0	1.6 ± 1.0	4.2 ± 1.9	7.6 ± 3.9
		Scan 2	5.9 ± 3.0	1.7 ± 1.0	2.6 ± 1.2	6.3 ± 3.5
	Subject 9	Scan 1	10.4 ± 4.4	1.6 ± 0.9	4.4 ± 2.2	11.2 ± 4.4
		Scan 2	5.4 ± 3.8	1.2 ± 0.8	6.5 ± 3.4	8.2 ± 4.1
		Scan 3	6.4 ± 4.1	1.2 ± 0.9	3.2 ± 1.8	7.8 ± 4.6
Stomach	Subject 1	Scan 1	7.9 ± 2.6	1.6 ± 0.9	4.3 ± 2.2	9.3 ± 3.9
		Scan 2	8.3 ± 3.5	1.5 ± 0.9	4.2 ± 2.0	8.9 ± 4.1
	Subject 2	Scan 1	8.1 ± 3.3	1.3 ± 0.9	5.7 ± 3.3	9.0 ± 3.2
		Scan 2	5.8 ± 3.5	1.1 ± 0.6	4.8 ± 1.5	7.5 ± 3.7
	Subject 3	Scan 1	8.5 ± 3.7	1.5 ± 0.9	6.3 ± 2.4	8.8 ± 3.0
		Scan 2	7.5 ± 3.1	2.8 ± 2.0	3.6 ± 1.7	9.1 ± 3.9
	Subject 4	Scan 1	10.4 ± 3.0	1.6 ± 1.0	5.5 ± 3.4	12.8 ± 4.1
		Scan 2	4.6 ± 1.9	3.2 ± 1.8	6.1 ± 2.1	9.0 ± 3.3
		Scan 3	11.8 ± 3.8	0.7 ± 0.4	7.3 ± 3.1	13.0 ± 3.3
	Subject 5	Scan 1	8.5 ± 2.3	1.4 ± 0.8	4.1 ± 2.0	11.9 ± 3.3
		Scan 2	11.1 ± 4.3	1.1 ± 0.6	3.0 ± 1.1	12.6 ± 4.2
	Subject 6	Scan 1	8.8 ± 4.1	1.9 ± 1.1	6.2 ± 3.2	13.7 ± 5.3
	Subject 7	Scan 1	8.5 ± 2.3	2.1 ± 1.6	2.2 ± 0.9	8.4 ± 2.9
		Scan 2	9.9 ± 3.2	1.6 ± 1.2	2.2 ± 1.3	10.4 ± 3.6
		Scan 3	7.7 ± 2.3	1.8 ± 1.3	3.4 ± 1.5	8.2 ± 2.7
	Subject 8	Scan 1	8.0 ± 2.4	1.3 ± 0.7	4.0 ± 1.8	8.8 ± 2.9
		Scan 2	7.9 ± 2.4	1.7 ± 1.0	2.2 ± 1.0	7.5 ± 2.8
	Subject 9	Scan 1	10.7 ± 4.2	2.0 ± 1.2	2.9 ± 1.3	12.7 ± 4.9
		Scan 2	9.3 ± 3.4	1.5 ± 0.8	4.5 ± 2.2	9.7 ± 4.2
		Scan 3	9.1 ± 3.2	1.1 ± 0.7	3.7 ± 1.9	9.9 ± 4.2

Motion range magnitudes demonstrated poor reproducibility. Example instances elucidate this observation. For the stomach, average breathing motion magnitude varied from 4.6 to 11.8 mm. The maximum bowel motion due to breathing varied from 11.9 to 27.5 mm (subject 4). The average antral contraction-induced motion had observed differences ranging from 0.7 to 3.2 mm, with a 71.4% difference in maximum motion magnitude (3.6–12.6 mm). While slow configuration change exhibited smaller variation in average motion magnitude (5.5–7.3 mm), significantly large variations were observed (13.4–29.2 mm) in maximum magnitude. These large variations did not only happen on one single example as shown here, but were observed on motions of different gastric organs across multiple subjects. RC was also computed for maximal motion magnitudes, with 10.5 mm for bowel, 8.5 mm for duodenum, and 8.6 mm for stomach.

Discussion

A novel hierarchical motion model that includes multiple independent motion modes was developed, allowing for reconstruction of images of any arbitrary composition of motion states from different modes. To the best of our knowledge, this is the first motion model that provides a description of multiple independent motion sources at any given time point. Three motion modes, including respiration, antral contraction and slow configuration changes, are successfully implemented into the model. From the model, each motion can be individually shown, while multiple motions may also be combined to show superimposed patterns from a reference state to the actual estimated configuration at any given time. We also conducted some statistical analysis of these three motion modes including cyclic frequencies, geometric and temporal reproducibility, as well as motion magnitudes.

Probability density functions were evaluated for each of the two extracted cyclic motion modes. These density functions can help determine the dominant states for each type of motion. For breathing motion, our results show consistency with previous reports (George et al 2005, Geneser et al 2011). A higher density can be observed at the state close to the end-exhale. The very first and end states are less likely to appear according to the histogram, which is likely due in part to the reproducibility of repeated end exhale and end-inhale states. Another factor that may influence our breathing motion signal would be baseline drifts in breathing position over time, similar to those reported by prior investigators (Takao et al 2016, Jensen et al 2017).

By comparing maximal motion ranges for three separate motion modes together with their composited effects, we can evaluate how each motion mode would contribute to overall organ movements. For the contoured gastric organ surfaces, although breathing still contributes the most to observed motions, slow configuration changes also have a significant impact on these structures, especially for the bowel. Compared to these modes, contributions from antral contraction seem lower, but still have maximum magnitudes up to 12.6 mm. Current standard radiation therapy motion management typically only considers the influence of breathing motions on intra-fractional abdominal changes during treatment planning. Our results lead to the question that whether it is sufficient to only consider breathing motions in treatment planning, as other motion modes will add an expansion of motion ranges in the abdomen. Future investigations will include simulations of dose calculation under different motion patterns (breathing, antral contraction, slow configuration, and composition of all three motions).

Our preliminary results show poor reproducibility of cyclic motion patterns. This is within our expectations: respiration is actively controlled by the subject and is difficult to be well reproduced at different times. There are no general patterns of respiratory behavior that can be assumed for a particular patient prior to observation and treatment (Keall et al 2006). Antral contraction motion patterns would similarly be expected to vary during different gastric states (fasting, postprandial) (Nonaka et al 2019), and such variation was likely the cause of the observed inter-scan variations in antral contraction periodicity.

One of the benefits of this motion model is that we can reconstruct high spatial resolution images at a high temporal resolution. This is achieved by interpolating deformation fields according to motion states of each spoke. This actually exploits the sparsity of abdominal motions, which has been extensively studied (Gamper et al 2008, Otazo et al 2010). Through the model, we can reconstruct image volumes showing current motion effects at any given time point. Another benefit is that, instead of storing all image volumes, our hierarchical model allows us to only store a reference state image volume, motion signals for each spoke and deformation fields corresponding to the motion states.

One potential challenge with our model is that it relies on DIR. Prior studies have demonstrated inaccuracies arising from DIR, which may also bring uncertainties into our motion model(Brock and C Deformable Registration Accuracy 2010, Jamema et al 2015). It is also questionable whether DIR-derived deformations can fully describe local organ motion. Our current validation involves visual evaluation of the registration results to ensure sufficient accuracy for interpretation of resulting motions.

The hierarchical motion model has a number of potential applications. Conventional treatment planning typically estimates dose using a single static model of the patient from a treatment planning image volume. A number of studies have also reported using multiple breathing phases from 4DCT for dose calculation (Flampouri et al 2006, Guckenberger et al 2007, Ehrbar et al 2016). Using the motion model to incorporate the combined effects of these 3 motions can improve the accuracy of estimated delivered dose compared to current approaches, which will better inform our modeling of toxicity, improve robustness of treatment planning, and highlight the necessity of monitoring positions of various organs at risk. The motion model also allows the prediction of abdominal motions during treatment delivery on MR-Linac systems. Prediction of all 3 motion modes can allow for real-time monitoring of the target and/or normal organs to support gating or tracking during treatment delivery. Motion-corrected image reconstructions using the motion model can also improve image quality by removing blurring and artifacts caused by abdominal motions. This can potentially improve target delineation accuracy, as well as the precision of temporally analyzed pharmacokinetic models such as that used for liver functional mapping (Simeth et al 2018). By quantifying magnitudes of superimposed motions on different abdominal structures, the model can also provide guidance for determining margins for tumors to be treated with high radiation doses as well as normal organs to be avoided, potentially on a subject-specific level. Combined with the measured state density functions, the model can also be helpful in treatment immobilization decisions, as well as selecting and optimizing surrogates of anatomy and strategies for use in treatment gating.

The current model is generated for individual subjects and scan instances. As more data is accumulated, we will be able to investigate trends in the reproducibility as well as variation of motions within individual subjects, as well as motion similarities and differences across a population of different subjects. In addition to applications in precision radiation therapy treatment planning, improved knowledge of such motions can guide improved understanding of normal tissue dose tolerances, as well as providing a resource for advanced physiological assessments of the abdomen for applications beyond cancer treatment.

Conclusion

A hierarchical motion model is presented which can incorporate multidimensional motions and estimate their composite effects on the abdominal region. The model includes three different motion modes: respiration, antral contraction, and slow configuration changes. Frequencies of each motion mode were identified, and motion state density functions were shown to describe dominant states, as well as to estimate frequencies of occurrence of individual states. The current model has value in multiple applications, including dose delivery estimation and guidance for evaluation of the spaces that can be occupied by normal organs in the abdomen, thus aiding in treatment planning to minimize radiation dose to such moving structures.