Abstract

The infrared (IR) and vibrational circular dichroism (VCD) spectra of 2,3-butanediol and trans-1,2-cyclohexanediol from 900 to 7500 cm–1 (including mid-IR, fundamental CH and OH stretchings, and near-infrared regions) have been investigated by a combined experimental and computational strategy. The computational approach is rooted in density functional theory (DFT) computations of harmonic and leading anharmonic mechanical, electrical, and magnetic contributions, followed by a generalized second-order perturbative (GVPT2) evaluation of frequencies and intensities for all the above regions without introducing any ad hoc scaling factor. After proper characterization of large-amplitude motions, all resonances plaguing frequencies and intensities are taken into proper account. Comparison of experimental and simulated spectra allows unbiased assignment and interpretation of the most interesting features. The reliability of the GVPT2 approach for OH stretching fundamentals and overtones is confirmed by the remarkable agreement with a local mode model purposely tailored for the latter two regions. Together with the specific interest of the studied molecules, our results confirm that an unbiased assignment and interpretation of vibrational spectra for flexible medium-size molecules can be achieved by means of a nearly unsupervised reliable, robust, and user-friendly DFT/GVPT2 model.
1. Introduction
An accurate description of the nuclear dynamics of bound states in molecular systems is pivotal for the reproduction of molecular spectra, especially in the infrared (IR) region of the electromagnetic spectrum. Despite some remarkable achievements (see, e.g., refs (1−3)), the development of efficient yet accurate methodologies to go beyond the harmonic approximation is still a challenging issue when one or more among the following features must be taken into account: (i) high number of vibrational degrees of freedoms; (ii) presence of large-amplitude motions (LAMs); and (iii) presence of many symmetry elements. Assessment of the various strategies devised for the inclusion of anharmonic effects in the calculation of vibrational spectra can be easily found in the literature,1−9 but the comparison is usually restricted to the region of fundamental IR transitions, most often to the mid-IR. Nowadays, the advancements of the experimental techniques related to near-infrared (NIR) spectroscopy10 and the increased use of vibrational circular dichroism (VCD) spectroscopy in the mid-IR,11 but also in the NIR range,12,13 are boosting the demand of reliable and efficient computational strategies for the reproduction of more challenging experimental observables (such as dipole and rotational strengths of overtone and combination transitions, intrinsically forbidden at the harmonic level).
In this work, we provide novel experimental results on 2,3-butanediol [of which, three stereoisomers exist, two enantiomeric forms, (2R,3R) and (2S,3S), and one meso (2R,3S) form] and trans-1,2-cyclohexanediol [existing in two enantiomeric forms, (1R,2R) and (1S,2S)]. IR, NIR, VCD, and NIR–VCD spectra have been recorded and computed; the anharmonic effects in the calculation of experimental observables have been included by means of two different methodologies: the generalized vibrational second-order level of perturbation theory (GVPT2) approach implemented in the Gaussian14 suite of programs by two of the present authors15,16 and a local mode approach developed earlier by other two of us.17−19
The two enantiomeric forms of 2,3-butanediol were characterized by means of several experimental techniques:20−27 IR (in solution21,22,25 and in the gas phase23), VCD,21,22 photoelectron circular dichroism,26 and microwave24 spectra have been published. Conformer stabilities and harmonic spectra in the region of fundamental transitions have already been computed.22,24,27,28
trans-1,2-Cyclohexanediol was previously studied experimentally21,28,29 and computationally:28,29 IR21,28 and VCD21 spectra in the OH stretching region, nuclear magnetic resonance data,21 an experimental determination of the crystal structure,30 and an experimental evaluation of the gas-phase acidities29 have also been reported. For what concerns computational characterization, data on the equilibrium structures calculated with density functional theory (DFT) methods28,29 and a two-dimensional cut of the global potential energy surface (2D-PES) describing the energetic landscape associated with the rotation of two dihedral angles which determine the orientation of the two OH groups28 were published.
This article is organized as follows. In Section 2, the theoretical background of the employed computational approaches is summarized and briefly discussed. Experimental and computational methodologies are outlined in Section 3. The results of a computational characterization of LAMs for 2,3-butanediol and 1,2-cyclohexanediol molecules are reported in Section 4. Experimental IR and VCD spectra have been obtained in various spectral regions: the results are reported and discussed in Section 5. Furthermore, the computational prediction of IR and VCD spectra has been performed by means of two different methodologies: the results are compared and discussed in Section 5, focusing particularly on the role of anharmonicity and LAMs. Finally, conclusions and a discussion of possible further developments can be found in Section 6.
2. Theoretical Background
In this section, a brief account of the two approaches chosen in this work for the numerical solution of the Schrödinger nuclear equation including anharmonic terms is given.
In the customary treatment of molecular vibrations, the zero-order vibrational hamiltonian is built by adopting the double-harmonic approximation,31 with the 3Na – 6 molecular vibrations described as uncoupled harmonic oscillators (Na = number of atoms). This means that the coupling among the various internal coordinates (internuclear distances, valence, and dihedral angles) is already retained in the zero-order model, while cubic and higher-order terms of the potential energy expansion are neglected: the anharmonic effects are then included as perturbations (the GVPT2 approach follows this route). In the case of a treatment based on local mode vibrations (the harmonically coupled anharmonic oscillator, hereafter referred as HCAO,32 belongs to this class), the zero-order vibrational hamiltonian includes a relevant part of the diagonal anharmonic correction, while the coupling among the various internal coordinates is taken into account at a higher order, often in a perturbative fashion (interested readers can find more details in ref (33)).
The choice between the GVPT2 and the local mode pictures must be made at the very beginning, and the nature of the molecular vibrations under investigation can suggest the most effective option: for example, the inclusion of the harmonic couplings among the various internal coordinates excluding diagonal anharmonic effects is advantageous for the computational reproduction of the fundamental transitions in the mid-IR region (900–1600 cm–1) where vibrations are strongly delocalized. The situation changes drastically when the vibration under investigation is a high overtone of X–H stretching, whose anharmonicity is not a small perturbation and the corresponding fundamental frequency is quite different from those of other modes. Therefore, the inclusion of anharmonic effects at the zero-order level is highly desirable, and the coupling of the other internal coordinates to the internuclear X–H distances is less important.
In what follows the two approaches (GVPT2 and local mode approximation) employed in this work are concisely summarized.
2.1. GVPT2
In the framework of the VPT2 theory, the vibrational energy (relative to the zero-point energy, ZPE, and for an asymmetric top molecule) of the state |k⟩ is given by eq 1
| 1 |
In eq 1, N is the number
of normal modes
in the molecular system considered, ωi is the harmonic wavenumber associated with the i-th normal mode with nik quanta in state |nk⟩, and χij is an element of the χ matrix collecting the anharmonic
coefficients, which are explicit functions of cubic and semidiagonal
quartic force constants together with harmonic frequencies, equilibrium
rotational constants, and Coriolis couplings.4 The derivation of equations allowing the computation of intensities
with due account of mechanical, electrical, and, possibly, magnetic
anharmonicities can be performed along the same lines5 but ends up with different equations depending on the transitions
and possibly the type of property.6,7,34 Our most recent implementation8,16 (available
in the Gaussian16 code14) includes transitions
from the ground state involving up to three quanta for a large panel
of vibrational spectroscopies (IR, Raman, VCD, and ROA). As is well
known, the VPT2 calculations are plagued by different kinds of resonances.15,35−39 In our implementation,15 Fermi resonances
(FRs) and Darling–Dennison resonances (DDRs) are identified
through two-step procedures as described in refs (3, 8), and (40), and the corresponding terms are removed, leading to the
deperturbed (D) VPT2 approximation. Resonant terms, coupled with additional
interaction terms, are then treated variationally by diagonalizing
the resulting matrix, which includes up to three-quanta excitations.
The final results are referred to as generalized (G) VPT2. Similar
to frequencies, the Fermi resonances can also be present for intensities,
but here, Darling–Dennison resonances might also have a direct
impact. In fact, in the expression of transition moments for 1-quantum
transitions,40,41 possibly diverging terms 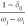 are already
present at the second order
and need to be accounted properly. For this purpose, additional tests
aimed at catching terms with negligible impact on energies, but critical
for intensities, have been developed.40,42 The eigenvectors
of the variational matrix are then used to project the resonance-free
transition moments on the final vibrational states.
are already
present at the second order
and need to be accounted properly. For this purpose, additional tests
aimed at catching terms with negligible impact on energies, but critical
for intensities, have been developed.40,42 The eigenvectors
of the variational matrix are then used to project the resonance-free
transition moments on the final vibrational states.
Another problem for a robust GVPT2 implementation is the treatment of LAMs (e.g., torsion and/or inversion motions) in flexible molecules.43,44 LAMs are not only poorly described by VPT2, but they may also contaminate the results, thus leading to large errors on those vibrations that are coupled to LAMs, even if intense and at high frequency. Therefore, a robust mean to identify and successively exclude them (together with their contribution to the anharmonic force field) from the VPT2 treatment is required to achieve reliable results. For both the diols of interest in the present work, LAMs are associated with some dihedral angles and were systematically removed (the complete list is provided in the Supporting Information).
2.2. Local Mode Approximation
The local mode approach to the interpretation of IR, NIR, VCD, and NIR–VCD spectra in the OH-stretching regions, which will be briefly reviewed here, is fully described in refs (17−19). Pure local modes are assumed without any intermode harmonic coupling. The mechanical behavior of the isolated stretching modes is forced to a Morse-type behavior to conveniently calculate the transition moments. Thus, for each one of the two OH-bond stretchings, which, for the present case of diols, are numbered l = 1, 2, the energy levels are obtained by an equation formally identical to eq 1 retaining only the diagonal term
| 2 |
The harmonic wavenumber ωl can be obtained in two ways: (i) directly from the output of harmonic computations performed by a quantum chemical program such as Gaussian (assuming that i ≈ l and ωi ≈ ωl) and (ii) by extrapolation from the quadratic force constant ϕll relative to the local stretching coordinate z corresponding to the OH stretching under investigation (see ref (45)). χll is evaluated numerically, by introducing the internuclear distance changes za between the O and H atoms, as described in refs (17−19), performing an adequate number of z positive and negative displacements and evaluating quadratic ϕll (∂2V/∂z2), cubic ϕlll (∂3V/∂z3), and quartic ϕllll (∂4V∂z4) force constants by a polynomial fitting to a Morse potential in the internal stretching coordinate z. The following expression for the mechanical anharmonicity holds33,46
| 3 |
where ℏ and c are the reduced Planck constant and the speed of light, respectively. mR is the reduced mass of the OH bond
| 4 |
The relation between χll and the cubic and quartic force constants with respect to the OH stretching coordinate zl is given in ref (46)
| 5 |
| 6 |
The O and H atomic displacements are related to the internuclear stretching z by
| 7 |
where M = mO + mH. The transition moments necessary for the transitions Δnl = 1 and Δnl = 2 for the j-th component (j = x, y, z) of the electric dipole moment μ and magnetic dipole moment m operators are
| 8 |
| 9 |
In eqs 8 and 9, Παjz0 and Aαjz denote, respectively, an element of the atomic
polar tensor
(APT) and of the atomic axial tensor (AAT), corresponding to the jz element of the α atom (O and H) when the molecule
is considered at an optimized (minimum energy) geometry. In our treatment,
only the first derivatives of APT and AAT elements with respect to
the z-stretching (∂Παjz/∂z and ∂Aαjz/∂z) at the equilibrium position are needed. These derivatives are the
so-called electrical and magnetic anharmonicity terms and are obtained
through a polynomial interpolation of the xz, yz, and zz components of the H and O APTs
and AATs versus the z-stretching coordinate: 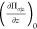 and
and 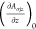 are obtained from the first-order terms.
Introducing the quantity (ωl and
χll in wavenumber units)
are obtained from the first-order terms.
Introducing the quantity (ωl and
χll in wavenumber units)
| 10 |
d having the dimension of a distance, the transition moments given in refs (17) and (18) can be rewritten in a more compact and perspicuous way: with this notation, the relevance of the ratio of the mechanical anharmonicity term with respect to the harmonic frequency χll/ωl on the given transition integrals can be readily estimated and the difference between the harmonic and the anharmonic case can be easily evaluated. The transition moments for z, z2, p, and zp are given in Table 1 for fundamental (Δnl = 1) and in Table 2 for first overtone (Δnl = 2) transitions.
Table 1. Transition Integrals for Fundamental Local Mode Transition.
| quantity | harmonic case | anharmonic case | ||
|---|---|---|---|---|
| ⟨0|z|1⟩ | d/2π | |||
| ⟨0|z2|1⟩ | 0 | |||
| ⟨0|p|1⟩ | ||||
| ⟨0|zp|1⟩ | 0 |
Table 2. Transition Integrals for First Overtone Local Mode Transition.
| quantity | harmonic case | anharmonic case | ||
|---|---|---|---|---|
| ⟨0|z|2⟩ | 0 | |||
| ⟨0|z2|2⟩ | ||||
| ⟨0|p|2⟩ | 0 | |||
| ⟨0|zp|2⟩ |
3. Experimental and Computational Methods
3.1. Experimental Methods
Optically pure chiral diastereomeric 2,3-butanediol and trans-1,2-cyclohexanediol samples were bought from Sigma-Aldrich and used without further purification.
Mid-IR, IR-fundamental CH-stretching, and OH-stretching VCD spectra were recorded with the FVS-6000 JASCO FTIR apparatus for both 2,3-butanediol and trans-1,2-cyclohexanediol. For the mid-IR region, a liquid-N2-cooled MCT detector was employed, while for the CH- and OH-stretching regions, an InSb detector was used. For the mid-IR and CH-stretching regions, 200 μm BaF2 cells were employed with 0.1 M/CCl4 and 0.1 M/CDCl3 concentrated solutions in the case of 2,3-butanediol and trans-1,2-cyclohexanediol, respectively. In the case of the fundamental OH-stretching region, infrasil 1 mm quartz cuvettes bought from Hellma were used, while concentrations and solvents were the same as mentioned above. In all cases, VCD and IR spectra of the solvents and solutions were taken in the same conditions, namely, with 5000 scans, 4 cm–1 resolution for the mid-IR, and 8 cm–1 resolution for the CH- and OH-stretching fundamental regions, respectively. IR and VCD spectra of the solvents were subtracted from those of the solutions.
The NIR and NIR–VCD spectra for the first overtone OH-stretching region were recorded with the home-built dispersive apparatus first described in ref (12); the CD and absorption baseline (ABL) spectra were recorded in the same conditions, and ABL signals were subtracted from CD signals and spectra were processed as described there. A 2 cm-thick quartz cuvette was used for trans-1,2-cyclohexanediol and a 5 cm quartz cuvette was used for 2,3-butanediol, with the solvent spectra taken in the same conditions and subtracted from the solution data. Concentrations were still 0.1 M/CDCl3 for trans-1,2-cyclohexanediol and 0.1 M/CCl4 for 2,3-butanediol. Five scans were taken for both the CD and ABL positions and the resolution was 2 nm, corresponding to ca. 10 cm–1 at 1400 nm (ca. 7140 cm –1), where the OH-stretching first overtone signals are centered (the grating monochromator of our apparatus is indeed linear in λ).
3.2. Computational Methods
Unless explicitly stated, calculations have been performed with a development version of the Gaussian suite of programs.47 Geometry optimizations were performed with tight convergence criteria (i.e., 1 × 10–5 hartree/bohr and 4 × 10–5 bohr on RMS force and displacements, respectively, with maximum values being 1.5 times larger), and minima and transition states were confirmed by Hessian evaluations.
Harmonic force fields were obtained using analytic derivatives of energy and transition moments, whereas higher-order derivatives were computed through numerical differentiation using a step of 0.01 amu1/2 Å for the displacements along the mass-weighted normal coordinates. While harmonic frequencies (as well as energies and gradients) were always computed in the presence of solvent effects represented with the polarizable continuum model (PCM),48,49 finite differences leading to cubic and quartic force constants do not include PCM contributions for XH stretchings because their motions are too fast to allow solvent equilibration.49,50
Within a composite scheme, the double-hybrid B2PLYP51 functional including empirical dispersion (D3BJ)52 in conjunction with the jun-cc-pVTZ53,54 basis set (B2) was used for the harmonic force fields, whereas the combination of B3LYP55−57 functional with empirical dispersion (D3BJ) and the jul-cc-pVDZ53,54 basis set (B3) was used for the evaluation of the anharmonic force fields. Free energies were determined by adding zero-point energy, thermal contributions, and PCM contributions evaluated in the framework of the rigid rotor/harmonic oscillator approximation to electronic energies.39,48,49
Concerning VCD spectroscopy, because the magnetic dipole transition moments are not available at the B2PLYP level of theory, the B3 level was used to compute both electric and magnetic transition dipole moments and their derivatives. Nevertheless, simulations of the IR spectra revealed that employing electric dipole transition moments computed at the B2 level has negligible impact on the simulated spectra in the systems under investigation; therefore, in all the calculations, the B3 transition dipole moments were used.
Possible LAMs were initially flagged through evaluation of the cubic and quartic force constants, and once confirmed (see Section 4), they were excluded from the VPT2 treatment. A complete list of the removed normal modes for each anharmonic calculation is provided in the Supporting Information. As recalled in Section 2, resonances can occur in both energy and property calculations, and in the DVPT2 approach, they are removed from the perturbative summations. Fermi (FRs) and Darling–Dennison (DDRs) resonance identification relies on a two-step procedure as described in refs (3, 8), and (40). Some DDRs are explicitly present in the one-quantum intensity equation3,41 and can have a massive impact on the final band shape. In the present work, identification of 1–1 DDRs, that is between fundamental states, was done considering as resonant states the ones within 50 cm–1 with interaction terms larger than 5 cm–1. All the other resonance types were identified employing the default Gaussian thresholds. In addition to the default tests, the two-step procedure to identify FRs affecting intensities introduced in ref (42) was used.
The GVPT2 approach was used to calculate anharmonic spectra in all the spectral regions, except the CH stretching in trans-1,2-cyclohexanediol, where a DVPT2 approach was preferred, because the overestimation of the coupling among those modes in a Cartesian-based description can sensibly affect the calculations. It is worth noting that for the OH stretchings, the DVPT2 and GVPT2 approaches are equivalent because these two modes are naturally decoupled from the rest of the vibrations.
To carry out the local mode calculations of IR, NIR, IR-VCD, and NIR–VCD spectra, the parameters χll, ωl, (∂Παjz/∂zl), and (∂Aαjz/∂zl) are needed: they have been evaluated numerically as described in refs (17) and (18), using Gaussian16,14 at the B3LYP/TZVP level of theory. We scanned the stretchings of the two OH bonds for each conformer of the two molecules under investigation in 50 steps, with a step size of 0.017 Å, from −0.33 to +0.454 Å with respect to the equilibrium OH bond length. The resulting functions of energy versus zl were interpolated with 8th-degree polynomials and the first three terms ϕll, ϕlll, and ϕllll were used to compute ωl and χll. From the interpolated numerical curves of Παjz and Aαjz as functions of zl, we obtained the needed first derivatives at equilibrium, which represent the electrical and magnetic anharmonicity terms.
4. Computational Characterization of LAMs
This section deals with a conformational study of 2R,3R-butanediol22−24 and 1R,2R-cyclohexanediol aimed to characterize their LAMs and relative energy minima together with transition states ruling their interconnections.
4.1. 2R,3R-Butanediol
This is a highly flexible molecule. The conformational flexibility associated with the two hydroxyl groups can be described with two dihedral rotations. Furthermore, this molecule is characterized by two LAMs associated with the internal rotations of the two methyl groups and with another internal rotation involving the O–C–C–O dihedral angle. Therefore, a complete description of the conformational flexibility of this system can be achieved with 5 degrees of freedom. In what follows, the assumption is made that the internal rotation of the two methyl groups can be treated independently from the other 3 degrees of freedom: this assumption appears reasonable because a change in the orientations of the two hydroxyl groups or a rotation of the O–C–C–O dihedral angle does not affect significantly (at least to a first approximation) the barriers to the internal rotation of the two methyl groups. A proper description of the concerted rotation of the two hydroxyl groups needs to take into account its coupling with the rotation of the O–C–C–O dihedral angle. A simplified description of the LAMs in terms of the two HOCC LAMs is sketched in Figure 1 with reference to the stable minima defined in Figure 2 through Newman projections. The two interconnection paths between these two LAMs representing the interconversion between the two Newman projections are reported in Figure S4 in the Supporting Information. The LAMs reported in Figure 1 can be described as concerted rotations of the HOCC torsions associated with the two hydroxyl groups (qualitatively, it is the same kind of motion suggested for the two enantiomers of trans-1,2-cyclohexanediol, as represented in Figure 4, vide infra) for conformers I and II in Figure 2, respectively.
Figure 1.
B3 structures and relative energies (in cm–1) for low-energy conformers (in black) of 2R,3R-butanediol and for transition states (in red) governing their interconversion. The upper panel includes structures corresponding to the Newman projection (I) of Figure 2, whereas the lower panel refers to structures corresponding to the Newman projection (II).
Figure 2.
Newman projections for the two most relevant structures of 2R,3R-butanediol.
Figure 4.
B3 structures and relative energies (in cm–1) for low-energy conformers (in black) of 1R,2R-cyclohexanediol and for transition states (in red) governing their interconversion. The broken lines connecting stationary points do not have any quantitative meaning and are drawn only for a better visualization.
Moreover, LAMs become even more complicated for conformers of I and II, which are connected by two possible paths (see the Supporting Information). There is a third Newman projection of 2R,3R-butanediol, not reported in Figure 2, where the two hydroxyl groups are not adjacent. Despite the existence (already pointed out by other authors22,24) of relative energy minima with a structure that can be represented with this third Newman projection (with an O–C–C–O dihedral angle of about 180°), the structures associated with this projection (see the Supporting Information) are not taken into account in the following because the absence of the intramolecular hydrogen bond between the two hydroxyl groups leads to quite higher energies and, therefore, a negligible contribution to IR and VCD spectra.
4.2. 1R,2R-Cyclohexanediol
This is a cyclic molecule with a six-membered central ring of carbon atoms and two adjacent hydroxyl groups in trans relative positions. The ring-puckering of the central ring can be described with three coordinates,58,59 and, similarly to 2R,3R-butanediol, the rotation of the two hydroxyl groups can be described with the two associated dihedral angles. This intuitive description of the conformational flexibility of 1R,2R-cyclohexanediol in terms of 5 degrees of freedom can be further simplified because an explicit treatment of puckering motion is not necessary because of the same ring conformation (chair conformation with both hydroxyl groups in equatorial position) shared by all the lowest energy structures. Although a series of relative energy minima encompassing chair conformations with both hydroxyl groups in axial positions can be obtained (their relative energies are reported in the Supporting Information), they are significantly less stable than the previous ones because of the absence of any hydrogen bond between the two hydroxyl groups. In what concerns the two OH-dihedral angles, the 2D-PES reported in Figure 1 of ref (28) is of particular interest: this figure suggests that the two dihedral rotations are involved in a single LAM described by a combination of the two dihedral rotations. In other words, the conformational flexibility of 1R,2R-cyclohexanediol can be described in terms of 1 (instead of 5) degree of freedom governing the concerted rotation of the two dihedral angle associated with the two hydroxyl groups.
To refine the qualitative description of the LAM given above, we have optimized its minima and transition states: energies and corresponding structures of the relevant stationary points are reported in Figure 4. One may see that, roughly speaking, the minima are connected by simple, independent HOCC rotations about the CO bonds, with little coupling to other low-frequency modes.
4.3. Low-Lying Conformers and Evaluation of Relative Stabilities
In both molecules, exploration of the PES along the LAMs associated with the two hydroxyl groups allowed identification of several low-lying conformers. This first screening was done at the B3 level of theory, and the selected conformers for both molecular systems are reported in Figure 3. In the case of more flexible 2R,3R-butanediol, the four most stable conformers were considered, whereas in the case of 1R,2R-cyclohexanediol, only the two most stable conformers were taken into account. For both molecules, these choices represent more than 95% of the total Boltzmann populations at room temperature.
Figure 3.
Structures of the four most stable conformers of 2R,3R-butanediol (left side of the figure) and structures of the two most stable conformers of 1R,2R-cyclohexanediol (right side of the figure).
The next step was to evaluate the relative stabilities of the selected conformers at higher level of theory. A reliable description of the relative stabilities is a crucial step that can substantially influence the final results because the simulated spectrum can be very sensitive to the Boltzmann population. Relying on previous investigations,42,60,61 we employed the B2 level of theory also accounting for the solvent by means of the PCM approximation,48,49 which allows to achieve accurate results at affordable computational cost. The results are collected in Table 3, and ΔG PCM values were used to compute Boltzmann population at room temperature in order to get the final simulated spectra.
Table 3. Relative Electronic Energy (ΔE), Free Energy at 298 K (ΔG), Free Energy at 298 K in Solution (ΔG PCM) Values (kJ mol–1) for 1R,2R-Cyclohexanediol, and 2R,3R-Butanediol Conformers Calculated at the B3 and B2 Levels of Theorya.
| B3 |
B2 |
||||||
|---|---|---|---|---|---|---|---|
| ΔE | ΔG | ΔG PCM | ΔE | ΔG | ΔG PCM | Pop. | |
| 2R,3R-Butanediol | |||||||
| conf.1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 47.1 |
| conf.2 | 0.53 | 0.81 | 0.53 | 0.90 | 1.14 | 0.85 | 33.5 |
| conf.3 | 3.31 | 2.82 | 3.21 | 2.91 | 2.84 | 2.84 | 11.5 |
| conf.4 | 4.33 | 4.13 | 4.09 | 4.42 | 4.46 | 4.46 | 7.9 |
| 1R,2R-Cyclohexanediol | |||||||
| conf.1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 54.7 |
| conf.2 | 0.72 | 1.03 | 0.47 | 1.11 | 1.36 | 0.80 | 45.3 |
Percent population factors (Pop., computed from the Boltzmann distribution) based on ΔG PCM.
The normal modes related to the investigated OH LAMs have been removed from the VPT2 treatment, together with low-energy modes involving methyl rotation and butane torsion angle in 2,3-butanediol and ring deformations in trans-1,2-cyclohexanediol (a complete list of all the normal modes removed in each anharmonic calculation is provided in the Supporting Information).
5. IR and VCD Spectra: Experimental and Computational Results
Experimental IR and VCD spectra are displayed in Figure 5 in four spectroscopic regions for the two optically active enantiomers of 2,3-butanediol and the two enantiomers of trans-1,2-cyclohexanediol. Very good-to-excellent mirror image spectra have been obtained in all regions for the enantiomeric species even employing the rather diluted solutions required to avoid (or at least to minimize) intermolecular hydrogen bonding.62 This gives us confidence in testing high-level calculated spectra to compare to the experimental ones.
Figure 5.
Experimental IR (left column) and VCD (right column) spectra of trans-1,2-cyclohexanediol (enantiomers 1R,2R and 1S,2S) and 2,3-butanediol (enantiomers 2R,3R and 2S,3S). From the top, mid-IR (850–1500 cm–1), CH stretchings (2750–3050 cm–1), fundamental OH stretchings (3300–3800 cm–1), and NIR (6800–7400 cm–1) spectroscopic regions are reported. The spectra have been recorded in diluted solutions, with CDCl3 (in the case of trans-1,2-cyclohexanediol) and CCl4 (in the case of 2,3-butanediol).
IR and VCD spectra of both diols (see Figure 5) show several similar features concerning both shapes and intensities, although the IR and VCD spectral features of 2,3-butanediol are more spread out and broader than their analogues in trans-1,2-cyclohexanediol.
In the mid-IR region, both compounds show a strong IR band at ca. 1050 cm–1 and a corresponding VCD band of negative sign for the (S,S) species (and of course “+” for the (R,R) species), which is particularly valuable for the configuration assignment. It is noteworthy that this characteristic VCD band is accompanied in both diols by two other bands of opposite sign at higher frequencies, leading to a “+, +, −” triplet for the (S,S) species (and of course “–, −, and +” for the (R,R) species), extending between ca. 1150 and 1050 cm–1 in the case of 2,3-butanediol and between ca. 1170 and 1070 cm–1 in the case of trans-1,2-cyclohexanediol. Such a spectral region is known to host normal mode transitions having contributions from CO-stretchings. An enantiomeric VCD triplet of quite similar shape (and opposite signs) is observed between 1000 and 850 cm–1 for 2,3-butanediol. Another VCD band common to both compounds is the broad one at ca. 1400 cm–1, which is “+” for the (S,S) species and “–” for the (R,R) species.
In the CH-stretching region, both molecules show two major IR absorption bands, at slightly different wavenumbers but with similar intensities and shapes. The lower-energy band (2870 cm–1 for 2,3-butanediol and 2850 cm–1 for trans-1,2-cyclohexanediol) is the less intense one in IR and corresponds to a broad, very intense monosignate VCD band, which is positive for the (S,S) species (and negative for the (R,R) species) in both compounds. The higher-frequency band (2965 cm–1 for 2,3-butanediol and 2945 cm–1 for trans-1,2-cyclohexanediol) is the most intense in the IR spectrum and corresponds to a triplet of alternating VCD features with equal signs but different intensities in the two compounds.
IR and VCD spectra of trans-1,2-cyclohexanediol21,28 and 2R,3R-butanediol21 in the region of fundamental OH stretchings have already been published. Our data are in agreement with previous findings: in the case of trans-1,2-cyclohexanediol, a “–, +” doublet (going from higher to lower wavenumbers) for the 1R,2R enantiomer has been observed in the VCD spectrum21 between 3500 and 3700 cm–1 and the corresponding IR spectrum exhibits a doublet in the same region.21,28 For 2R,3R-butanediol, a “–, +” doublet (with the negative feature weaker than the positive one) is observed in the VCD spectrum21 between 3500 and 3700 cm–1 and a doublet in the corresponding IR spectrum.21,25 More precisely, our spectra suggest a “–, −, +” structured feature for the VCD spectrum, with negative bands weaker than the positive one, as previously observed by Siligardi.63 In ref (28), the broad IR band below 3500 cm–1 is interpreted as the signature of aggregation of two or even three molecules promoted by the formation of intermolecular hydrogen bonds. Although it is tempting to explain the observation of a similar feature below 3500 cm–1 in the IR spectrum of 2R,3R-butanediol in terms of analogous aggregates stabilized by intermolecular hydrogen bonds, we do not push our analysis any further.
In the first-overtone region, while a NIR absorption doublet is observed in both cases, a VCD doublet with components of alternating signs is observed only for trans-1,2-cyclohexanediol; the only constant feature is indeed the high-frequency acceptor-type band, which has a “+” sign for (S,S) (and a “–” sign for (R,R)).
Wang and Polavarapu reported the IR and VCD spectra of 2R,3R-butanediol in the mid-IR region.22 Both spectra are essentially identical to those reported in Figure 5 for the spectral region under evaluation. However, to the best of our knowledge, the spectra reported for the fundamental CH stretching region and for the NIR region in Figure 5 are new.
The observed anisotropy ratio (also called g-factor) for the various signals of the spectra reported in Figure 5 is between 10–4 and 10–5 in the mid-IR region, about 10–5 in the CH stretchings region, between 10–6 and 10–5 for the fundamental OH stretchings transitions, and about 10–5 for the first OH stretchings overtones (the values for trans-1,2-cyclohexanediol and the chiral forms of 2,3-butanediol are similar).
Comparison of the experimental spectra of both enantiomeric pairs examined in this work reveals some similarities that suggest common structural motifs and normal mode behaviors. The computational simulation of the corresponding IR and VCD spectra can be extremely useful in two different ways: (i) relating statistical and quantum mechanical computed data on one side and experimental data on the other side allows one to discriminate whether the empirical correlations between the experimental spectra noted above for the two diols can be explained in terms of similar physical–chemical properties and (ii) the comparison between experimental and computational spectra is essential to evaluate the reliability of a computational approach.
In what follows, the computational simulation of the IR and VCD spectra reported in Figure 5 is presented and discussed. All the calculated spectra reported in the main text have been obtained as average spectra of the two most populated conformers (corresponding to the two lowest energy minima of the global PES) for 1R,2R-cyclohexanediol (see Figure 4 and Table 3) and of the four most populated conformers for 2R,3R-butanediol (see Figure 1 and Table 3). The influence of less-populated conformers on the final calculated spectra has also been evaluated and the results are summarized in the Supporting Information. In Figures 6–8, the experimental IR and VCD spectra of 1R,2R-cyclohexanediol and of 2R,3R-butanediol in the mid-IR, CH/OH stretching fundamental, and OH stretching first overtone regions, respectively, are compared with the anharmonic calculations of IR, NIR, VCD, NIR–VCD spectra. For the fundamental and first overtone OH stretching regions, two different approaches have been employed for the anharmonic calculation of IR and VCD spectra (see Section 2).
Figure 6.
Comparison of experimental spectra of 1R,2R-cyclohexanediol (top left and top right images) and 2R,3R-butanediol (bottom left and bottom right images) with anharmonic calculations of IR and VCD spectra in the mid region. The spectra of each conformer were weighted with their respective Boltzmann population based on B2PLYP harmonic energy.39 The spectra were simulated assigning Gaussian distribution functions of 10 cm–1 half-width at half-maximum.
Figure 8.

Comparison of experimental spectra of 1R,2R-cyclohexanediol (top images) and 2R,3R-butanediol (bottom images) with anharmonic calculations of IR and VCD spectra in the regions of fundamental OH stretching transitions (Δν = 1) in the left side of the figure and of first overtone OH stretching transitions (Δν = 2) in the right one. The spectra of each conformer were weighted with their respective Boltzmann population based on B2PLYP harmonic energy. The spectra were simulated assigning Gaussian distribution functions of 15 cm–1 half-width at half-maximum in Δν = 1 region and 40 half-width at half-maximum in Δν = 2 region.
The similarity indexes (SI and Sim_NN) between experiment and theory64−67 reported in Table 4 show that both scaled harmonic and bare anharmonic results are in good agreement with experimental spectra in the mid-IR (Figure 6), especially for 1R,2R-cyclohexanediol. Of course, at the harmonic level, a good agreement is obtained only by introducing a scaling factor (sf) of 0.988. It is interesting to note in Figure 6 that the VCD bands commented above, namely, the triplet (“–, −, +”) in decreasing order of frequency, at ca. 1100 cm–1 and the negative VCD band at ca. 1400 cm–1 receive contributions from the different conformers mostly of the same sign, even though with unequal intensity; thus, we may argue that those features are valuable for configurational assignment. We checked that in the case of the triplet at ca. 1100 cm–1, the normal modes underlying the three components of the triplet correspond to the CO stretching, the CH bending, and the COH in plane bending, all coordinates involving the stereogenic carbon C.
Table 4. 2R,3R-Butanediol and 1R,2R-Cyclohexanediol: Similarity Indices for IR and VCD Experimental and Calculated Spectraa.
| IR |
VCD |
|||
|---|---|---|---|---|
| conf. | SI | Sim_NN | SI | Sim_NN |
| 2R,3R-Butanediol | ||||
| Mid. H (sf 0.988) | 0.91 | 0.79 | 0.63 | 0.33 |
| Mid. A GVPT2 | 0.79 | 0.61 | 0.64 | 0.33 |
| CH. H (sf 0.955) | 0.53 | 0.27 | 0.46 | 0.26 |
| CH. A GVPT2 | 0.93 | 0.86 | 0.71 | 0.42 |
| OH. H (sf 0.955) | 0.69 | 0.51 | 0.71 | 0.13 |
| OH. A GVPT2 | 0.73 | 0.58 | 0.74 | 0.25 |
| 1R,2R-Cyclohexanediol | ||||
| Mid. H (sf 0.988) | 0.94 | 0.89 | 0.74 | 0.52 |
| Mid. A GVPT2 | 0.90 | 0.79 | 0.60 | 0.39 |
| CH. H (sf 0.955) | 0.96 | 0.69 | 0.78 | 0.32 |
| CH. A GVPT2 | 0.90 | 0.78 | 0.29 | 0.02 |
| CH. A DVPT2 | 0.92 | 0.82 | 0.89 | 0.41 |
| OH. H (sf 0.955) | 0.74 | 0.56 | 0.30 | 0.09 |
| OH. A GVPT2 | 0.80 | 0.61 | 0.67 | 0.27 |
H = based on harmonic calculations, A = based on anharmonic calculations. The spectra of each conformer were weighted with their respective Boltzmann population based on B2PLYP harmonic energy. The spectra were simulated assigning Gaussian distribution functions of 10 cm–1 half-width at half-maximum. In parentheses, we report the scaling factors (sf) employed in the harmonic approximation in the various spectroscopic regions.
Calculations are also in good agreement with experiment in the CH-stretching region (see Table 4), provided that the DVPT2 model is used in anharmonic computations or an sf of 0.955 (quite different from that employed for the mid-IR) is applied to harmonic frequencies.
Let us now try to give a general interpretation of the observed IR and VCD spectra. The case of 1R,2R-cyclohexanediol is more perspicuous, and thus, we focus on this molecule, even though some conclusions may be extended to 2R,3R-butanediol. The two IR features at ca. 2850 and at 2930 cm–1 are ascribed in a first approximation to axial and equatorial CH-bond stretching transitions, respectively.68,69 Two of the axial CH-stretching modes exhibit strong VCD signals, which are observed in the broad band extending from 2840 to 2880 cm–1. Such CH bonds involve the two stereogenic carbon atoms and acquire intensity because of the vicinity to the C–O–H···O ring, stabilized in this case by intramolecular hydrogen bond, as first proposed by Nafie et al. in a number of cases70 and recently confirmed in ref (71). The frequency of these two CH-stretching modes is also influenced by their relative conformation with respect to the nearby OH moieties.72 The other IR and VCD bands at higher frequencies are not so clearly interpretable and we do not insist on them here.
Figures 7 and 8 allow one to appreciate that the features in the OH stretching fundamental region, which are much weaker in IR and VCD than the bands in the CH-stretching region, are also correctly predicted without the need of any sf by the GVPT2 approach, as highlighted by the satisfactory similarity indexes. The results of harmonic calculations are not too far from the observed spectral patterns as well, provided that transition frequencies are corrected by about 200 cm–1, by means of an sf of 0.955. The “–, +” experimental VCD doublet of 1R,2R-cyclohexanediol corresponds to the “+, −, +” triplet predicted by the harmonic calculation, taking into account that the first “+” feature of the triplet is weak with respect to the other two. For the OH-stretching fundamental and overtone regions the local mode approach provides satisfactory results for the transition frequencies, even though, in general, they are of slightly lower quality than GVPT2 and experimental ones, and this also happens for the harmonic frequencies issuing from the one-dimensional interpolation. Studies are underway to better analyze this issue. The agreement between calculated and experimental intensities deserves distinct comments for the various cases. Neglecting the aggregation effects in the broad band below 3500 cm–1, the calculated IR intensities displayed in the spectra of Figure 7 are satisfactory for both compounds, although with a greater number of peaks in the computational spectra, especially in the case of 2R,3R-butanediol, because of the contributions of several conformers. The effects of intra- and intermolecular hydrogen bonding are fairly evident and are similar for trans-1,2-cyclohexanediol and the chiral forms of 2,3-butanediol: thus, the two observed features, one just below and the other just above 3600 cm–1, can be assigned to the stretching modes of the donor and acceptor OH bonds, respectively, involved in an intramolecular hydrogen bonding. Considering the VCD spectra issuing from anharmonic GVPT2 calculations, the “–, +” doublet observed for 1R,2R-cyclohexanediol is correctly reproduced with the donor OH feature at a lower frequency than the acceptor one (although the calculated absolute value of Δϵ is a bit too high); the “+, +, −” structure observed in the experimental VCD spectrum of 2R,3R-butanediol is not correctly predicted by GVPT2 and local mode calculations, even though the donor OH stretching at lower frequency has a positive VCD sign in both diols, while the acceptor one is predicted to be negative.
Figure 7.
Comparison of experimental spectra of 1R,2R-cyclohexanediol (top left and top right images) and 2R,3R-butanediol (bottom left and bottom right images) with anharmonic calculations of IR and VCD spectra in the region of fundamental OH stretching transitions (Δν = 1) and CH stretching region. The spectra of each conformer were weighted with their respective Boltzmann population based on B2PLYP harmonic energy. The spectra were simulated assigning Gaussian distribution functions of 15 cm–1 half-width at half-maximum. Dashed lines represent the contribution of each conformer to the final spectra.
The best agreement between anharmonic GVPT2, local mode calculations, and experimental data is obtained in the NIR region (see Figure 8). Despite some differences, essentially related to a larger number of peaks in the calculated IR and VCD spectra than in the experimental ones, it must be underlined that not only frequencies and relative intensities but also absolute intensities are well reproduced by the anharmonic GVPT2 calculations in this region.
The comparison of the local mode and GVPT2 approaches is further detailed in Table 5, where the calculated frequencies, dipole strengths, and rotational strengths for all Δν = 1 and Δν = 2 (and Δν = 1 + 1) transitions are compared for all conformers of 1R,2R-cyclohexanediol and 2R,3R-butanediol. The low intensity of (1 + 1) combination bands computed at the GVPT2 level confirms that a full decoupling of acceptor and donor OH-stretching modes represents a sound approximation.
Table 5. Comparison of Calculated Wavenumbers, Dipole Strengths, and Rotational Strengths in the OH Fundamental and Overtone Regions Through the GVPT2 and Local Mode Approaches for all Conformers of 2R,3R-Butanediols and 1R,2R-Cyclohexanediols.
| 2R,3R-butanediol | ||||||
|---|---|---|---|---|---|---|
| (0–1) | νLMa | νVPT2 | DLMb | DVPT2 | RLMc | RVPT2 |
| Conformer Bd-I | ||||||
| ν+ | 3664.8 | 3652.4 | 21.22 | 41.58 | 1.30 | 2.18 |
| ν– | 3555.4 | 3600.3 | 49.31 | 67.33 | 0.46 | 0.21 |
| Conformer Bd-II | ||||||
| ν+ | 3578.9 | 3603.7 | 13.52 | 27.74 | –0.50 | –5.64 |
| ν– | 3520.1 | 3571.5 | 55.59 | 80.74 | –0.95 | 2.89 |
| Conformer Bd-III | ||||||
| ν+ | 3641.8 | 3655.2 | 1.58 | 37.17 | –3.01 | 1.20 |
| ν– | 3548.7 | 3585.0 | 31.92 | 44.27 | 2.47 | 4.24 |
| Conformer Bd-IV | ||||||
| ν+ | 3647.1 | 3649.9 | 15.48 | 20.98 | –1.84 | –2.65 |
| ν– | 3515.9 | 3583.2 | 55.68 | 41.13 | –1.21 | 9.59 |
| 2R,3R-butanediol | ||||||
|---|---|---|---|---|---|---|
| (0–2) | νLM | νVPT2 | DLM | DVPT2 | RLM | RVPT2 |
| Conformer Bd-I | ||||||
| ν+ + ν– | 7252.9 | <0.01 | <0.01 | |||
| 2ν+ | 7154.2 | 7133.2 | 6.20 | 2.43 | –0.21 | –0.27 |
| 2ν– | 6932.2 | 7030.7 | 3.76 | 1.73 | 0.04 | 0.16 |
| Conformer Bd-II | ||||||
| ν+ + ν– | 7169.6 | 0.01 | 0.11 | |||
| 2ν+ | 6978.8 | 7030.0 | 4.65 | 1.97 | –0.05 | –0.14 |
| 2ν– | 6857.6 | 6961.3 | 3.48 | 1.72 | –0.09 | 0.23 |
| Conformer Bd-III | ||||||
| ν+ + ν– | 7240.1 | <0.01 | <0.01 | |||
| 2ν+ | 7107.5 | 7140.7 | 4.09 | 2.21 | 0.41 | –0.31 |
| 2ν– | 6918.7 | 6996.8 | 3.21 | 1.48 | –0.15 | –0.21 |
| Conformer Bd-IV | ||||||
| ν+ + ν– | 7232.4 | <0.01 | –0.01 | |||
| 2ν+ | 7118.2 | 7144.7 | 4.71 | 1.82 | –0.09 | 0.03 |
| 2ν– | 6849.5 | 6989.1 | 3.81 | 1.45 | 0.11 | –0.21 |
| 1R,2R-cyclohexanediol | ||||||
|---|---|---|---|---|---|---|
| (0–1) | νLM | νVPT2 | DLM | DVPT2 | RLM | RVPT2 |
| Conformer Cd-I | ||||||
| ν+ | 3660.5 | 3651.7 | 18.54 | 47.31 | 1.41 | 2.12 |
| ν– | 3620.2 | 3602.3 | 36.26 | 63.14 | 0.36 | –0.63 |
| Conformer Cd-II | ||||||
| ν+ | 3622.5 | 3602.1 | 27.57 | 36.71 | –0.25 | –7.74 |
| ν– | 3603.4 | 3580.5 | 36.66 | 76.02 | –0.27 | 6.70 |
| 1R,2R-cyclohexanediol | ||||||
|---|---|---|---|---|---|---|
| (0–2) | νLM | νVPT2 | DLM | DVPT2 | RLM | RVPT2 |
| Conformer Cd-I | ||||||
| ν+ + ν– | 7231.8 | <0.01 | <−0.01 | |||
| 2ν+ | 7146.2 | 7096.3 | 8.65 | 2.85 | –0.25 | –0.40 |
| 2ν– | 7065.8 | 7000.6 | 5.55 | 2.13 | 0.06 | 0.27 |
| Conformer Cd-II | ||||||
| ν+ + ν– | 7175.8 | 0.03 | –0.19 | |||
| 2ν+ | 7076.2 | 7025.9 | 2.56 | 2.14 | –0.11 | –0.03 |
| 2ν– | 7029.9 | 6983.2 | 5.79 | 2.11 | 0.13 | 0.37 |
cm–1.
10–40 esu2 cm2.
10–44 esu2 cm2.
Finally, we wish to comment on the influence of LAMs on the calculated anharmonic spectra in the region of fundamental and OH stretching first-overtone transitions (documented in the Supporting Information). In the region of OH stretching fundamental transitions, the inclusion or exclusion of LAMs discussed in Section 4 leads to substantial variations in the calculated anharmonic GVPT2 spectrum, especially in the case of VCD. Such variations are not observed when the effects of LAMs are evaluated in the region of first overtone OH stretching transitions. These observations suggest that the disagreement between experimental and calculated VCD spectra in the region of fundamental OH stretching transitions might be related to the unsatisfactory handling of LAMs outlined in Section 4.
6. Conclusions
In this work, the IR/NIR absorption and VCD spectra have been recorded in the 900–7500 cm–1 range for 2,3-butanediol optically active diastereomers and trans-1,2-cyclohexanediol enantiomers and have been interpreted, thanks to a thorough treatment of anharmonicity. This was made possible thanks to an adequate consideration of LAMs and a correct handling of Fermi and Darling–Dennison resonances in their frequency and intensity aspects (GVPT2 and DVPT2 approaches). Both medium-size molecules considered in the present study are quite flexible and show several low-energy conformers, so that the good performance of anharmonic calculations could not be taken for granted a priori. Yet the results are satisfactory: thus, we hope that this work may give further impulse to the increased use of anharmonic computations by a larger number of scientists to aid the interpretation of vibrational, in particular vibrational optical activity spectra. Finally, the use of the more approximate local mode approach gave fairly similar results to the GVPT2 method for the OH-stretching regions, both approaches providing calculated IR/NIR absorption and VCD spectra quite close to the experiment. In this way, we verified that OH stretchings, either acceptor-type or donor-type, behave in diols as local modes, decoupled from one another and not strongly perturbed by other vibrational modes.
Acknowledgments
Support from the Italian MIUR (PRIN 2017, project “Physico-chemical Heuristic Approaches: Nanoscale Theory Of Molecular Spectroscopy” (PHANTOMS), prot. 2017A4XRCA), is acknowledged. We are thankful for the computer resources provided by the high performance computer facilities of the SMART Laboratory (http://smart.sns.it/).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.9b11025.
Experimental half-sum and half-difference VCD spectra; 2R,3R-butanediol interconnections; conformational search results; harmonic IR and VCD spectra; anharmonic calculations and treatment of resonances and LAMS; and optimized structures in XYZ format (PDF)
The authors declare no competing financial interest.
Footnotes
For notational simplicity, we refer to either zl internal OH-stretching coordinate (l = 1, 2) as simply z. Also, the corresponding conjugated momenta pl are treated in the same way and are called p.
Supplementary Material
References
- Christiansen O. Selected New Developments in Vibrational Structure Theory: Potential Construction and Vibrational Wave Function Calculations. Phys. Chem. Chem. Phys. 2012, 14, 6672–6687. 10.1039/c2cp40090a. [DOI] [PubMed] [Google Scholar]
- Roy T. K.; Gerber R. B. Vibrational Self-Consistent Field Calculations for Spectroscopy of Biological Molecules: New Algorithmic Developments and Applications. Phys. Chem. Chem. Phys. 2013, 15, 9468–9492. 10.1039/c3cp50739d. [DOI] [PubMed] [Google Scholar]
- Barone V.; Biczysko M.; Bloino J. Fully Anharmonic IR and Raman Spectra of Medium-Size Molecular Systems: Accuracy and Interpretation. Phys. Chem. Chem. Phys. 2014, 16, 1759–1787. 10.1039/c3cp53413h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosnik A. M.; Polik W. F. VPT2+K Spectroscopic Constants and Matrix Elements of the Transformed Vibrational Hamiltonian of a Polyatomic Molecule with Resonances Using Van Vleck Perturbation Theory. Mol. Phys. 2014, 112, 261–300. 10.1080/00268976.2013.808386. [DOI] [Google Scholar]
- Willetts A.; Handy N. C.; Green W. H.; Jayatilaka D. Anharmonic Corrections to Vibrational Transition Intensities. J. Phys. Chem. 1990, 94, 5608–5616. 10.1021/j100377a038. [DOI] [Google Scholar]
- Barone V.; Bloino J.; Guido C. A.; Lipparini F. A Fully Automated Implementation of VPT2 Infrared Intensities. Chem. Phys. Lett. 2010, 496, 157–161. 10.1016/j.cplett.2010.07.012. [DOI] [Google Scholar]
- Vázquez J.; Stanton J. F. Simple(r) Algebraic Equation for Transition Moments of Fundamental Transitions in Vibrational Second-Order Perturbation Theory. Mol. Phys. 2006, 104, 377–388. 10.1080/00268970500290367. [DOI] [Google Scholar]
- Puzzarini C.; Bloino J.; Tasinato N.; Barone V. Accuracy and Interpretability: The Devil and the Holy Grail. New Routes across Old Boundaries in Computational Spectroscopy. Chem. Rev. 2019, 119, 8131–8191. 10.1021/acs.chemrev.9b00007. [DOI] [PubMed] [Google Scholar]
- Rauhut G.; Barone V.; Schwerdtfeger P. Vibrational Analyses for CHFClBr and CDFClBr Based on High Level Ab Initio Calculations. J. Chem. Phys. 2006, 125, 054308. 10.1063/1.2236112. [DOI] [PubMed] [Google Scholar]
- Czarnecki M. A.; Morisawa Y.; Futami Y.; Ozaki Y. Advances in Molecular Structure and Interaction Studies Using Near-Infrared Spectroscopy. Chem. Rev. 2015, 115, 9707–9744. 10.1021/cr500013u. [DOI] [PubMed] [Google Scholar]
- He Y.; Bo W.; Dukor R. K.; Nafie L. A. Determination of Absolute Configuration of Chiral Molecules Using Vibrational Optical Activity: A Review. Appl. Spectrosc. 2011, 65, 699–723. 10.1366/11-06321. [DOI] [PubMed] [Google Scholar]
- Castiglioni E.; Lebon F.; Longhi G.; Abbate S. Vibrational Circular Dichroism in the Near Infrared: Instrumental Developments and Applications. Enantiomer 2002, 7, 161–173. 10.1080/10242430212877. [DOI] [PubMed] [Google Scholar]
- Guo C.; Shah R. D.; Dukor R. K.; Freedman T. B.; Cao X.; Nafie L. A. Fourier Transform Vibrational Circular Dichroism from 800 to 10,000cm–1: Near-IR-VCD Spectral Standards for Terpenes and Related Molecules. Vib. Spectrosc. 2006, 42, 254–272. 10.1016/j.vibspec.2006.05.013. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford CT, 2016.
- Barone V. Anharmonic Vibrational Properties by a Fully Automated Second-Order Perturbative Approach. J. Chem. Phys. 2005, 122, 014108. 10.1063/1.1824881. [DOI] [PubMed] [Google Scholar]
- Bloino J.; Barone V. A Second-Order Perturbation Theory Route to Vibrational Averages and Transition Properties of Molecules: General Formulation and Application to Infrared and Vibrational Circular Dichroism Spectroscopies. J. Chem. Phys. 2012, 136, 124108. 10.1063/1.3695210. [DOI] [PubMed] [Google Scholar]
- Gangemi F.; Gangemi R.; Longhi G.; Abbate S. Calculations of Overtone NIR and NIR-VCD Spectra in the Local Mode Approximation: Camphor and Camphorquinone. Vib. Spectrosc. 2009, 50, 257–267. 10.1016/j.vibspec.2009.01.004. [DOI] [Google Scholar]
- Gangemi F.; Gangemi R.; Longhi G.; Abbate S. Experimental and Ab-Initio Calculated VCD Spectra of the First OH-Stretching Overtone of (1R)-(-) and (1S)-(+)-endo-Borneol. Phys. Chem. Chem. Phys. 2009, 11, 2683–2689. 10.1039/b818432a. [DOI] [PubMed] [Google Scholar]
- Abbate S.; Castiglioni E.; Gangemi F.; Gangemi R.; Longhi G. NIR-VCD, Vibrational Circular Dichroism in the Near-Infrared: Experiments, Theory and Calculations. Chirality 2009, 21, E242–E252. 10.1002/chir.20805. [DOI] [PubMed] [Google Scholar]
- Kuhn L. P. The Hydrogen Bond. III. The Effect of the Size of Substituents upon the Length of the Hydrogen Bond in Various Substituted 1,2-Diols. J. Am. Chem. Soc. 1958, 80, 5950–5954. 10.1021/ja01555a016. [DOI] [Google Scholar]
- Yamamoto K.; Nakao Y.; Kyogoku Y.; Sugeta H. Vibrational Circular Dichroism in Hydrogen Bond Systems: Part III. Vibrational Circular Dichroism of the OH Stretching Vibrations of 1,2-Diols and β-MethoxyalcoholsVibrational circular dichroism in hydrogen bond systems. J. Mol. Struct. 1991, 242, 75–86. 10.1016/0022-2860(91)87128-5. [DOI] [Google Scholar]
- Wang F.; Polavarapu P. L. Predominant Conformations of (2R,3R)-(-)-2,3-Butanediol. J. Phys. Chem. A 2001, 105, 6991–6997. 10.1021/jp010550z. [DOI] [Google Scholar]
- Lopes Jesus A. J.; Rosado M. T. S.; Reva I.; Fausto R.; Eusébio M. E.; Redinha J. S. Conformational Study of Monomeric 2,3-Butanediols by Matrix-Isolation Infrared Spectroscopy and DFT Calculations. J. Phys. Chem. A 2006, 110, 4169–4179. 10.1021/jp0572737. [DOI] [PubMed] [Google Scholar]
- Paul J.; Hearn I.; Howard B. J. Chiral Recognition in a Single Molecule: a Study of Homo and Heterochiral Butan-2,3-diol by Fourier Transform Microwave Spectroscopy. Mol. Phys. 2007, 105, 825–839. 10.1080/00268970701241649. [DOI] [Google Scholar]
- Ma X.; Wang J. Differentiating Subtle Variation of Weak Intramolecular Hydrogen Bond in Vicinal Diols by Linear Infrared Spectroscopy. J. Phys. Chem. A 2009, 113, 6070–6076. 10.1021/jp9016085. [DOI] [PubMed] [Google Scholar]
- Daly S.; Tia M.; Garcia G. A.; Nahon L.; Powis I. The Interplay Between Conformation and Absolute Configuration in Chiral Electron Dynamics of Small Diols. Angew. Chem., Int. Ed. 2016, 55, 11054–11058. 10.1002/anie.201603771. [DOI] [PubMed] [Google Scholar]
- Daly S.; Powis I.; Garcia G. A.; Tia M.; Nahon L. An Imaging Photoelectron-Photoion Coincidence Investigation of Homochiral 2R,3R-Butanediol Clusters. J. Chem. Phys. 2017, 147, 013937. 10.1063/1.4983139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jesus A. J. L.; Redinha J. S. Self-Association of 1,2-Cyclohexanediols: A Spectroscopic and Computational Study. J. Mol. Struct. 2014, 1067, 104–111. 10.1016/j.molstruc.2014.02.066. [DOI] [Google Scholar]
- Chen X.; Walthall D. A.; Brauman J. I. Acidities in Cyclohexanediols Enhanced by Intramolecular Hydrogen Bonds. J. Am. Chem. Soc. 2004, 126, 12614–12620. 10.1021/ja049780s. [DOI] [PubMed] [Google Scholar]
- Thorey P.; Bombicz P.; Szilágyi I. M.; Molnár P.; Bánsághi G.; Székely E.; Simándi B.; Párkányi L.; Pokol G.; Madarász J. Co-crystal of (R,R)-1,2-Cyclohexanediol with (R,R)-Tartaric Acid, a Key Structure in Resolution of the (±)-Trans-Diol by Supercritical Extraction, and the Related Ternary Phase System. Thermochim. Acta 2010, 497, 129–136. 10.1016/j.tca.2009.09.001. [DOI] [Google Scholar]
- Wilson E. B.; Decius J. C.; Cross P. C.. Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra; Dover Books on Chemistry; Dover Publications: New York, 1980. [Google Scholar]
- Child M. S.; Lawton R. T. Local and Normal Vibrational States: a Harmonically Coupled Anharmonic-Oscillator Model. Faraday Discuss. Chem. Soc. 1981, 71, 273–285. 10.1039/dc9817100273. [DOI] [Google Scholar]
- Jensen P. An Introduction to the Theory of Local Mode Vibrations. Mol. Phys. 2000, 98, 1253–1285. 10.1080/002689700413532. [DOI] [Google Scholar]
- Bak K. L.; Bludský O.; Jørgensen P. Ab Initio Calculations of Anharmonic Vibrational Circular Dichroism Intensities of Trans-2,3-Dideuteriooxirane. J. Chem. Phys. 1995, 103, 10548–10555. 10.1063/1.469838. [DOI] [Google Scholar]
- Fermi E. Über den Ramaneffekt des Kohlendioxyds. Z. Phys. 1931, 71, 250–259. 10.1007/bf01341712. [DOI] [Google Scholar]
- Darling B. T.; Dennison D. M. The Water Vapor Molecule. Phys. Rev. 1940, 57, 128–139. 10.1103/physrev.57.128. [DOI] [Google Scholar]
- Martin J. M. L.; Lee T. J.; Taylor P. R.; François J. P. The Anharmonic Force Field of Ethylene, C2H4, by Means of Accurate Ab Initio Calculations. J. Chem. Phys. 1995, 103, 2589–2602. 10.1063/1.469681. [DOI] [Google Scholar]
- Kuhler K. M.; Truhlar D. G.; Isaacson A. D. General Method for Removing Resonance Singularities in Quantum Mechanical Perturbation Theory. J. Chem. Phys. 1996, 104, 4664–4671. 10.1063/1.471161. [DOI] [Google Scholar]
- Bloino J.; Biczysko M.; Barone V. General Perturbative Approach for Spectroscopy, Thermodynamics, and Kinetics: Methodological Background and Benchmark Studies. J. Chem. Theory Comput. 2012, 8, 1015–1036. 10.1021/ct200814m. [DOI] [PubMed] [Google Scholar]
- Bloino J.; Biczysko M.; Barone V. Anharmonic Effects on Vibrational Spectra Intensities: Infrared, Raman, Vibrational Circular Dichroism, and Raman Optical Activity. J. Phys. Chem. A 2015, 119, 11862–11874. 10.1021/acs.jpca.5b10067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloino J.; Baiardi A.; Biczysko M. Aiming at an Accurate Prediction of Vibrational and Electronic Spectra for Medium-to-Large Molecules: An Overview. Int. J. Quantum Chem. 2016, 116, 1543–1574. 10.1002/qua.25188. [DOI] [Google Scholar]
- Fusè M.; Mazzeo G.; Longhi G.; Abbate S.; Masi M.; Evidente A.; Puzzarini C.; Barone V. Unbiased Determination of Absolute Configurations by Vis-à-Vis Comparison of Experimental and Simulated Spectra: The Challenging Case of Diplopyrone. J. Phys. Chem. B 2019, 123, 9230–9237. 10.1021/acs.jpcb.9b08375. [DOI] [PubMed] [Google Scholar]
- Császár A. G. Anharmonic Molecular Force Fields. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 273–289. 10.1002/wcms.75. [DOI] [Google Scholar]
- Njegic B.; Gordon M. S. Exploring the Effect of Anharmonicity of Molecular Vibrations on Thermodynamic Properties. J. Chem. Phys. 2006, 125, 224102. 10.1063/1.2395940. [DOI] [PubMed] [Google Scholar]
- Howard D. L.; Jørgensen P.; Kjaergaard H. G. Weak Intramolecular Interactions in Ethylene Glycol Identified by Vapor Phase OH-Stretching Overtone Spectroscopy. J. Am. Chem. Soc. 2005, 127, 17096–17103. 10.1021/ja055827d. [DOI] [PubMed] [Google Scholar]
- Mills I. M.; Robiette A. G. On the Relationship of Normal Modes to Local Modes in Molecular Vibrations. Mol. Phys. 1985, 56, 743–765. 10.1080/00268978500102691. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; et al. Gaussian Development Version, Revision J.02; Gaussian, Inc.: Wallingford CT, 2019.
- Mennucci B. Polarizable Continuum Model. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 386–404. 10.1002/wcms.1086. [DOI] [Google Scholar]
- Cappelli C.; Bloino J.; Lipparini F.; Barone V. Toward Ab Initio Anharmonic Vibrational Circular Dichroism Spectra in the Condensed Phase. J. Phys. Chem. Lett. 2012, 3, 1766–1773. 10.1021/jz3006139. [DOI] [PubMed] [Google Scholar]
- Cappelli C.; Lipparini F.; Bloino J.; Barone V. Towards an Accurate Description of Anharmonic Infrared Spectra in Solution within the Polarizable Continuum Model: Reaction Field, Cavity Field and Nonequilibrium Effects. J. Chem. Phys. 2011, 135, 104505. 10.1063/1.3630920. [DOI] [PubMed] [Google Scholar]
- Goerigk L.; Grimme S. Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals—Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2011, 7, 291–309. 10.1021/ct100466k. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Dunning T. H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron Through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
- Papajak E.; Zheng J.; Xu X.; Leverentz H. R.; Truhlar D. G. Perspectives on Basis Sets Beautiful: Seasonal Plantings of Diffuse Basis Functions. J. Chem. Theory Comput. 2011, 7, 3027–3034. 10.1021/ct200106a. [DOI] [PubMed] [Google Scholar]
- Becke A. D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- Becke A. D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
- Cremer D.; Pople J. A. General Definition of Ring Puckering Coordinates. J. Am. Chem. Soc. 1975, 97, 1354–1358. 10.1021/ja00839a011. [DOI] [Google Scholar]
- Paoloni L.; Rampino S.; Barone V. Potential-Energy Surfaces for Ring-Puckering Motions of Flexible Cyclic Molecules through Cremer–Pople Coordinates: Computation, Analysis, and Fitting. J. Chem. Theory Comput. 2019, 15, 4280–4294. 10.1021/acs.jctc.9b00363. [DOI] [PubMed] [Google Scholar]
- Barone V.; Biczysko M.; Bloino J.; Cimino P.; Penocchio E.; Puzzarini C. CC/DFT Route Toward Accurate Structures and Spectroscopic Features for Observed and Elusive Conformers of Flexible Molecules: Pyruvic Acid as a Case Study. J. Chem. Theory Comput. 2015, 11, 4342–4363. 10.1021/acs.jctc.5b00580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Spada L.; Chen J.; Gao S.; Alessandrini S.; Feng G.; Puzzarini C.; Gou Q.; Grabow J.-U.; Barone V. The Unexplored World of Cycloalkene–Water Complexes: Primary and Assisting Interactions Unraveled by Experimental and Computational Spectroscopy. Angew. Chem., Int. Ed. 2019, 58, 13935–13941. 10.1002/anie.201906977. [DOI] [PubMed] [Google Scholar]
- Devlin F. J.; Stephens P. J.; Besse P. Conformational Rigidification via Derivatization Facilitates the Determination of Absolute Configuration Using Chiroptical Spectroscopy: A Case Study of the Chiral Alcohol Endo-Borneol. J. Org. Chem. 2005, 70, 2980–2993. 10.1021/jo0478611. [DOI] [PubMed] [Google Scholar]
- Siligardi G.The Analysis of Molecular Configuration and Conformations of Biologically Important Molecules using Electronic UV an Vibrational IR Circular Dichroism Spectroscopy. Ph.D. Thesis, University of London, U.K., 1990. [Google Scholar]
- Kuppens T.; Langenaeker W.; Tollenaere J. P.; Bultinck P. Determination of the Stereochemistry of 3–Hydroxymethyl– 2, 3–dihydro–[1,4] dioxino[2,3–b] −pyridine by Vibrational Circular Dichroism and the Effect of DFT Integration Grids. J. Phys. Chem. A 2003, 107, 542–553. 10.1021/jp021822g. [DOI] [Google Scholar]
- Shen J.; Zhu C.; Reiling S.; Vaz R. A Novel Computational Method for Comparing Vibrational Circular Dichroism Spectra. Spectrochim. Acta, Part A 2010, 76, 418–422. 10.1016/j.saa.2010.04.014. [DOI] [PubMed] [Google Scholar]
- Covington C. L.; Polavarapu P. L. CDSpecTech: A Single Software Suite for Multiple Chiroptical Spectroscopic Analyses. Chirality 2017, 29, 178–192. 10.1002/chir.22691. [DOI] [PubMed] [Google Scholar]
- Mazzeo G.; Cimmino A.; Masi M.; Longhi G.; Maddau L.; Memo M.; Evidente A.; Abbate S. Importance and Difficulties in the Use of Chiroptical Methods to Assign the Absolute Configuration of Natural Products: The Case of Phytotoxic Pyrones and Furanones Produced by Diplodia Corticola. J. Nat. Prod. 2017, 80, 2406–2415. 10.1021/acs.jnatprod.7b00119. [DOI] [PubMed] [Google Scholar]
- Longhi G.; Ricard L.; Abbate S.; Zerbi G. A Comparative Study of the Fundamental and Overtone Spectra of Dioxane. J. Mol. Struct. 1986, 141, 325–330. 10.1016/0022-2860(86)80343-x. [DOI] [Google Scholar]
- Longhi G.; Zerbi G.; Ricard L.; Abbate S. Electric Dipole Moment Functions from Vibrational Absorption Intensities of Fundamental and Overtone Transitions. J. Chem. Phys. 1988, 88, 6733–6741. 10.1063/1.454417. [DOI] [Google Scholar]
- Gigante D. M. P.; Long F.; Bodack L. A.; Evans J. M.; Kallmerten J.; Nafie L. A.; Freedman T. B. Hydrogen Stretching Vibrational Circular Dichroism in Methyl Lactate and Related Molecules. J. Phys. Chem. A 1999, 103, 1523–1537. 10.1021/jp9837885. [DOI] [Google Scholar]
- Passarello M.; Abbate S.; Longhi G.; Lepri S.; Ruzziconi R.; Nicu V. P. Importance of C*–H Based Modes and Large Amplitude Motion Effects in Vibrational Circular Dichroism Spectra: The Case of the Chiral Adduct of Dimethyl Fumarate and Anthracene. J. Phys. Chem. A 2014, 118, 4339–4350. 10.1021/jp502544v. [DOI] [PubMed] [Google Scholar]
- Longhi G.; Zerbi G.; Paterlini G.; Ricard L.; Abbate S. Conformational Dependence of CH(CD)-Strechings in D-glucose and some Deuterated Derivatives as Revealed by Infrared and Raman Spectroscopy. Carbohydr. Res. 1987, 161, 1–22. 10.1016/0008-6215(87)84001-6. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.









