Lateral Heterostructure Field-Effect Transistors Based on Two-Dimensional Material Stacks with Varying Thickness and Energy Filtering Source

Abstract

The bandgap dependence on the number of atomic layers of some families of two-dimensional (2D) materials can be exploited to engineer and use lateral heterostructures (LHs) as high-performance field-effect transistors (FETs). This option can provide very good lattice matching as well as high heterointerface quality. More importantly, this bandgap modulation with layer stacking can give rise to steep transitions in the density of states (DOS) of the 2D material that can eventually be used to achieve sub-60 mV/decade subthreshold swing in LH-FETs thanks to an energy-filtering source. We have observed this effect in the case of a PdS₂ LH-FET due to the particular DOS of its bilayer configuration. Our results are based on ab initio and multiscale materials and device modeling and incite the exploration of the 2D-material design space in order to find more abrupt DOS transitions and better suitable candidates.

Semiconductor heterostructures of the III–V and II–VI materials systems have played a fundamental role in the progress of electronics and optoelectronics. First proposed by Kroemer in the 1950s,¹ they have been involved in the invention of quantum-well lasers² and high-electron-mobility transistors.³ The large number of available two-dimensional (2D) materials and the possibility to combine them even in the presence of significant lattice mismatch has led to a new wave of interest in materials engineering based on heterostructures of 2D materials. In particular, 2D materials enable the realization of vertical heterostructures, also called “van der Waals” heterostructures, consisting in the vertical stacking of layers of different 2D materials loosely coupled by van der Waals interactions,^4,5 and of lateral heterostructures (LHs), in which a single 2D layer consists of juxtaposed regions of different lattice-matched 2D materials.⁶⁻⁹

LHs have been shown to be particularly well suited as channel materials in high-performance field-effect transistors (FETs) for digital electronics.¹⁰ However, the quality of the heterojunction is one of the major obstacles toward the experimental demonstration of high-performance LH-FETs. The possibility of fabricating LHs by modulating the stacking order of a single 2D material provides the opportunity of perfect lattice matching and growth compatibility and therefore a chance to obtain high material quality.¹¹

Recently, a particular group of transition-metal dichalcogenides (TMDs) involving noble transition metals (Pt, Pd, and Ni), combined with S, Se, and Te, have been predicted¹² and demonstrated to have strong gap dependence on the number of stacked layers.¹³ The so-called “noble TMDs” are, thus, promising contenders to build 2D LHs by modulation of the number of layers of adjacent regions of the same material. Indeed, these structures based on noble TMDs, which strictly speaking could be considered homostructures instead of heterostructures, would be easier to realize than those made of different 2D materials. Ab initio calculations predict that the bandgap is reduced by more than 1 eV when these noble TMDs vary from monolayer (1L) to bilayer (2L), leading in some cases to a change of electronic phase from semiconductor to metal.^12,14 Monolayer and few-layer PtS₂ and PtSe₂ have already been synthesized,¹⁵⁻¹⁷ and devices such as Schottky barrier diodes on silicon have been fabricated.¹⁸ More recently, FETs made of few-layer PdSe₂ and PtSe₂ have been experimentally realized showing ambipolar transfer characteristics,^13,19,20 and a large dependence of PtSe₂ conductance on the number of layers has been observed.¹³

There is an additional advantage of some noble TMDs in their bilayer form: Their density of states (DOS) exhibits a steep nonmonotonic variation around the Fermi energy that can be used as an energy filtering mechanism in order to obtain a subthreshold swing (SS) of the FET smaller than the Boltzmann limit of 60 mV/decade at room temperature. Indeed, in thermionic FETs, the inverse of the maximum slope of the current–voltage characteristics is limited to SS = k_BT/q ln(10) per decade, where k_B is Boltzmann constant, q is the elementary charge, and T is the absolute temperature.²¹⁻²³ This provides a room-temperature SS value of 60 mV/decade. A lower value can only be obtained if (1) injection is energy constrained, such as in a Tunnel FET^24,25 or using impact ionization²⁶ or (2) if an effective negative capacitance is realized in the gate oxide stack, thus amplifying the surface potential at the channel.^27,28 In particular, the energy-constrained injection from a steep DOS source has been demonstrated very recently using a graphene source in combination with a CNT channel in ref (21) or a MoS₂ channel in refs (22 and 23). We show here that this effect can be achieved in a system based on a single 2D material, specifically PdS₂, where a bilayer source (injecting into a monolayer channel) can provide sufficient energy filtering to yield an SS below the Boltzmann limit.

In this work we investigate the potential of noble TMDs as channel materials for LH-FETs, showing the possibility to engineer an energy-filtering source in order to obtain sub-60 mV/dec SS at room temperature and to design devices with competitive figures of merit when compared to the predictions of the International Roadmap for Devices and Systems (IRDS).²⁹ Finally, we show that noble TMDs enable the realization of a 2D resonant tunneling diode (RTD) based on LHs obtained with modulation of the number of atomic layers.

Results and discussion

Lateral Heterostructure FETs

We have selected those noble TMDs exhibiting a sharp nonmonotonic DOS around the Fermi level and therefore potentially able to achieve SS < 60 mV/decade at room temperature. Following bandstructure calculations available in the literature,^11,14 we have opted for PdS₂ and NiS₂. Both materials are semimetal in bilayer form and semiconductors in monolayer form, so it is possible to build a FET with a lateral heterostructure formed by a bilayer source, a monolayer central channel region, and a bilayer drain. This results in two semimetal–semiconductor Schottky barriers at the source and drain ends. For the sake of clarity, a semimetal is a material with zero gap but a relatively low DOS around the Fermi energy. We have also considered PtS₂ which presents a strong modulation of the bandgap from monolayer to bilayer, still maintaining a semiconducting gap.

We have adopted a multiscale simulation approach combining different levels of physical abstraction, ranging from ab initio calculations of materials properties to full device simulations based on coherent quantum transport.³⁰ We have calculated the electronic band-structure of monolayer and bilayer PdS₂, PtS₂, and NiS₂ using density functional theory (DFT) as implemented in the Quantum Espresso suite³¹ (see Methods). The strong dependence of the electronic structure on the number of layers is highlighted in Figure 1a: When the crystal structure is varied from monolayer to bilayer, PdS₂ and NiS₂ undergo a phase change from semiconductor to semimetal, whereas PtS₂ has its energy gap reduced from 1.59 to 0.48 eV. The drastic variation of the DOS of bilayer PdS₂ and NiS₂ around the Fermi level can be exploited to inject carriers from the source with submaxwellian energy tails, leading to SS < 60 mV/decade at room temperature.

Figure 1.

(a) Electronic band structure on a highly symmetric path along the Brillouin zone (depicted aside in gray with the path marked in red), and DOS integrated in the whole Brillouin zone, as computed with DFT, for monolayer (1L) and bilayer (2L) PdS₂, NiS₂, and PtS₂. (b) Schematic representation of the construction of the lateral heterostructure Hamiltonian from the Hamiltonian of the bilayer and monolayer materials. (c) Schematic of the LH-FET, with bilayer source, monolayer channel, and bilayer-drain. (d) Illustration of the energy band edge profile of the PdS₂ and NiS₂ LH-FETs and (e) band edge profile of PtS₂ LH-FET.

The plane-wave DFT basis set has been translated into a maximally localized Wannier functions (MLWFs) basis set by means of the Wannier90 code,³² which provides us with tight-binding (TB) Hamiltonians for every material and stacking (see Methods and Figure S1 in the Supporting Information). The TB Hamiltonians are then employed to build a total Hamiltonian of the lateral heterostructure devices, following the procedure developed and validated in ref (33) (Figure 1b and Methods). In order to accurately model the Schottky barrier formed at the bilayer/monolayer interfaces, we have performed an energy analysis from first-principles taking into account the band offsets and the formation of dipoles³⁴ (see Supporting Information).

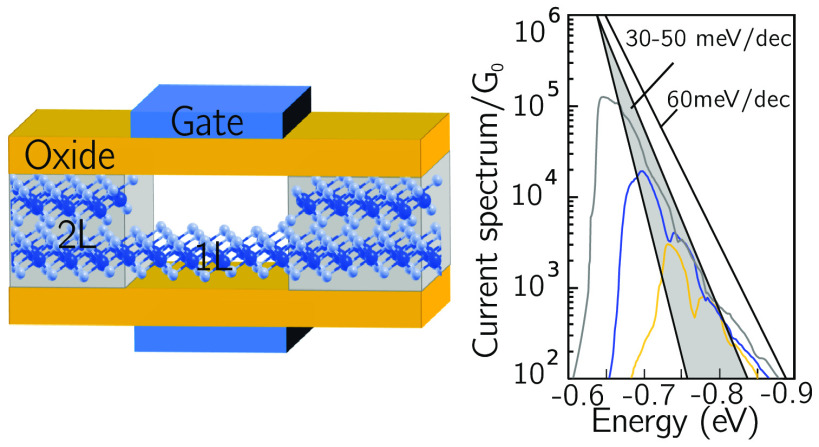
The considered LH-FETs are also illustrated in Figure 1c. The length of the bilayer source and drain regions are L_s/d = 11, 10.4, and 16.7 nm for PdS₂, NiS₂, and PtS₂ respectively. They are assumed to be ohmically contacted by the external metal leads with work functions of 5.6 and 5.8 eV for PdS₂ and NiS₂, respectively, and 5.3 eV/6.0 eV for the n-type/p-type PtS₂. The monolayer 2D channel, with length L_ch, is embedded in top and bottom SiO₂, with thickness t_ox = 0.5 nm.

Sketches of the band-edge profiles of the PdS₂ and NiS₂ LH-FETs with semimetal source and drain are shown in Figure 1d; the PtS₂ LH-FET with small gap source and drain is shown in Figure 1e. The complete MLWF Hamiltonian describing the channel including source and drain regions feeds the open-boundary Schrödinger equation, within the non-equilibrium Green’s functions (NEGF)³⁵ formalism, that is self-consistently solved with the electrostatics of the whole device (see Methods).^36,37

In order to study the potential performance of the considered LH-FETs for logic applications, we set a supply voltage V_dd = 0.5 V, and we simulate the transfer characteristics for a drain-to-source voltage V_DS = V_dd. Those are shown in Figure 2 in semilogarithmic scale for channel lengths ranging from L_ch ≃ 5 nm up to L_ch ≃ 10 nm and for the three different materials. As it can be seen, the bilayer metallic source/drain regions in PdS₂ and NiS₂ lead to an ambipolar behavior. For channel lengths longer than 10 nm, I_off is not further reduced, being the ambipolarity determined by the bandgap of the monolayer channel and the capability of the bilayer source to inject both kinds of carriers. In this regard, some improvement might be achieved following the back-gate over/underlapping strategy at the source/drain discussed in ref (38). Here we have tuned the gate workfunction in the PdS₂ and NiS₂ devices to 5.52 eV so to observe the crossover between n-type and p-type conduction at V_GS = 0 V.

Figure 2.

Transfer characteristic in semilogarithmic scale for the LH-FETs with PdS₂ (a), NiS₂ (b), and p-type/n-type PtS₂ (c)/(d) considering a channel length ranging from ≃5 nm up to ≃10 nm and drain-to-source voltage |V_DS| = 0.5 V. In the case of PdS₂ and NiS₂, an ambipolar behavior is observed due to the semimetallic source and drain. In the case of PtS₂, we consider both the nFET and the pFET. The channel is always undoped. A metal gate workfunction of 5.52 eV is assumed in the PdS₂ and NiS₂ devices to observe the crossover between n-type and p-type conduction at V_GS = 0 V. For the PtS₂ nFET and pFET, the gate workfunction is tuned to 5.28 and 6.2 eV, respectively, to set I_off = 100 nA/μm at V_GS = 0 V.

The PtS₂ LH-FET is not ambipolar since it has semiconductor source and drain. In this case we show in Figure 2c,d both the nFET and the pFET characteristics, where the gate workfunction is tuned to 5.28 and 6.2 eV, respectively, to obtain the current in the OFF state I_off = 100 nA/μm at V_GS = 0 V, as required by the IRDS²⁹ for high-performance (HP) applications where the OFF state corresponds to V_GS = 0 V and V_DS= ±V_dd. The source and drain regions have a donor doping with molar fraction N_D = 4.1 × 10^–2 in the case of nFET and acceptor molar fraction N_A = 9.5 × 10^–2 in the case of pFET. The channel is undoped for all devices.

Interestingly, the p-type branch of the PdS₂ LH-FET I_DS–V_GS curve exhibits a submaxwellian SS down to 52 mV/decade, as shown in Figure 3a. The possibility to achieve sub-60 mV/decade SS in a thermionic FET has been a subject of debate.^39,40 In particular, in ref (40) the authors argue that the 60 mV/decade limit cannot be beaten in a single barrier device, although they eventually conclude that the role of the DOS can be essential to reverse this situation, as has already been experimentally demonstrated in the case of a graphene source.²¹

Figure 3.

SS, I_on/I_off, τ, and PDP as a function of the channel length, L_ch, for the LH-FETs based on PdS₂, PtS₂, and NiS₂, evaluated according to the IRDS requirements for high-performance applications: I_off = 100 nA/μm.

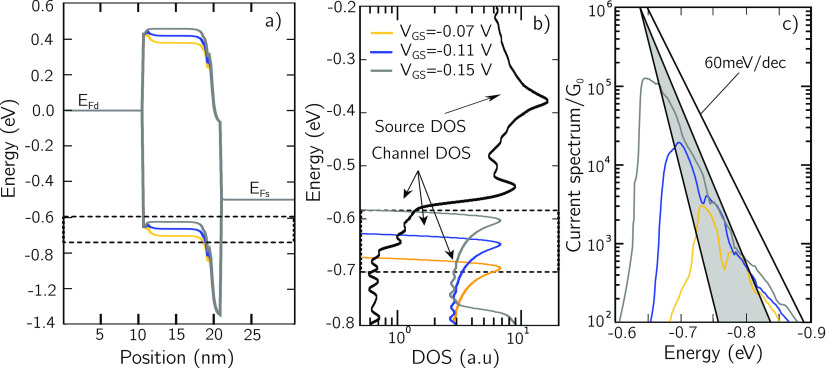
We can discuss the specific mechanism in the PdS₂ LH-FET by considering the band edge profiles shown in Figure 4a for V_DS = V_dd and for three different values of V_GS in the subthreshold region of the p-type branch. The Schottky barriers of drain–channel and source–channel junctions are calculated from first principles (see Supporting Information). A variation of V_GS modulates both the conduction and valence band edges in the channel and the transparency of the Schottky barrier between source and channel. The drop of the DOS in the source for energy below the source Fermi level (corresponding to −0.5 eV for the considered bias point) is clearly visible in Figure 4b, where the DOS is obtained from refined calculations applying, for visualization purposes, a Gaussian smoothing with σ = 10 meV (see Supporting Information), and is responsible for a sharper energy filtering than that provided by the Maxwell–Boltzmann tail of the occupation factor, and therefore for an SS lower than the so-called Boltzmann limit. This is even more apparent by considering the energy spectrum of the current, that is, the current density per unit energy, for different values of V_GS shown in Figure 4c. The slope of the logarithm of the current spectrum as a function of energy would be exactly −1/(k_BT) for a constant DOS, corresponding to one decade every 60 meV at room temperature. Due to the nonconstant DOS in the source, such a slope is however not constant, and in one decade around an energy of −0.7 eV, where the DOS is dramatically quenched, it is in the range of 30–50 meV, marked as a shaded region in Figure 4c. This more confined current spectrum is responsible for the sub-Maxwellian subthreshold swing of the p-type branch transfer characteristics of the PdS₂ LH-FET.

Figure 4.

(a) Conduction and valence band edge profiles of the PdS₂ LH-FET for V_DS = −V_dd and three different values of V_GS = −0.07, −0.11, and −0.15 V in the subthreshold region of the p-branch. (b) DOS of the source and of the channel for the corresponding values of V_GS obtained in a dense k-mesh grid, see Supporting Information, and after a Gaussian smoothing for the energy integration with σ = 10 meV. (c) Current spectrum as a function of energy. The range of slopes between 30 mV/decade and 50 mV/decade is in the shaded gray. The 60 mV/decade Boltzmann limit is also plotted.

Energy filtering is not observed in the n-branch because the DOS of the conduction band states in PdS₂ do not show a similar steep transition (see Supporting Information for more details). The effect is not observed in NiS₂ where the small gap of the monolayer semiconductor results in large interband tunneling currents and very poor SS (above 200 meV/decade and therefore not shown in Figure 3a). The PtS₂ LH-FET has a close to ideal Maxwellian SS of 60 mV/decade for HP applications due to the dominant Fermi window tail that restricts the SS.

Other transistor figures of merit for digital electronics are considered in Figure 3 following the IRDS specifications for HP applications. In particular, Figure 3b shows I_on/I_off ratio, where I_on is the drain current in the ON state, corresponding to V_GS = V_DS = ±V_dd and I_off = 100 nA/μm, is the current in the OFF state as defined by the IRDS for HP. To this purpose, the PdS₂ LH-FET exhibits the highest I_on/I_off ratio for channel length close to 10 nm thanks to the lower SS just discussed, but not for shorter channel lengths (down to 5 nm), because of the high I_off due to ambipolarity and large source-to-drain tunneling. The situation is worse for the NiS₂ LH-FET: Its smaller monolayer bandgap (0.47 eV) leads to a very poor I_on/I_off ratio. The PtS₂ LH-FET, instead, has a semiconducting bandgap and negligible source-to-drain tunneling and therefore exhibits high I_on/I_off ratio for L_ch down to 5 nm.

Relevant figures of merit for transistor performance in digital circuits are also the intrinsic delay time τ = (Q_on – Q_off)/I_on and the power delay product (PDP) = V_ddτI_on, where Q_on and Q_off are the total mobile charge in the channel in the ON and OFF states, respectively (Figure 3c,d). The nFETs based on PdS₂ and PtS₂ exhibit expected τ and PDP compliant with IRDS requirements for next technology nodes,^10,29 together with an I_on/I_off ratio close to 10⁴ for channel lengths of at least 10 nm, which implies acceptable stand-by power consumption for HP applications.²⁹ The pFETs have slightly worse PDP and τ than the nFETs, due to the smaller source DOS in the valence band, apparent in Figure 1a, which is responsible for a smaller I_on, as can be seen in the asymmetric transfer characteristics of Figure 2.

While the ambipolarity of PdS₂ and NiS₂ FETs spoils their use in low-power (LP) applications, PtS₂ FETs also satisfy the IRDS requirements to this purpose (i.e., they reach an I_off = 100 pA/μm) achieving I_on/I_off ratios above 10⁶ and 10⁵ for n-type and p-type FETs, respectively (see Supporting Information). For low stand-by power, SS is spoiled in shorter channel lengths since the tunneling current becomes comparable to the pursued I_off: For L_ch ≈ 5–8 nm it is in the range 80–100 mV/decade for nFETs and 70–90 mV/decade for pFETs, deviating considerably from the 60 mV/decade observed in longer channels. Finally, the PDP is slightly lower and the intrinsic delay time slightly higher than the values obtained for HP (see Supporting Information for details).

Resonant Tunneling Diode

Finally, we have studied the operation of a 2D resonant tunneling diode based on a PtS₂ LH (LH-RTD). We have considered bilayer PtS₂ drain and source regions with a length of 11.2 nm. Two monolayer regions act as energy barriers confining a bilayer well. The barrier length is L_b = 1.9 nm, and the length of the well L_w is varied from 1.9 nm up to 5.6 nm. The whole 2D channel is embedded in SiO₂. Figure 5a shows the I_DSvsV_DS characteristics for L_w = 1.9 nm at room temperature. The current has a clear nonmonotonic behavior exhibiting a pronounced negative differential resistance, due to resonant tunneling through quantized states in the 2D well. The local DOS in the channel is plotted in Figure 5b as a function of energy and of position along the device length (y) for V_DS = 0.25 and 0.5 V, corresponding to the main peak and to the valley of the current–voltage characteristics. Let us stress the fact that the bandstructure of different regions is fully considered in the calculation, but inelastic processes and heterojunction defects are not included.

Figure 5.

(a) I_DSvsV_DS characteristic of the LH-RTD based on PtS₂ with L_w = 1.9 nm. Inset: Schematic of the LH-RTD. (b) Local DOS as a function of the energy and the position along the device length and current-density spectrum, normalized to the conductance quantum (G₀ = 2q²/ℏ), for the RTD with a L_w = 1.9 nm, and for V_DS = 0.25 and 0.5 V. (c) Current–voltage characteristics of the LH-RTD for different well lengths.

The Fermi level at the source (μ_s) and drain (μ_d) leads are marked. We have superimposed the conduction and valence band profiles to the local DOS colormaps. The alignment of μ_s with these quantized energy levels results in resonances in the current spectrum density and is controlled by V_DS. We have also explored different well lengths: L_w = 1.9, 3.7, and 5.6 nm (Figure 5c), observing that the NDR effect is preserved, although the position of the peak varies with the well length as so does the energy quantization, while the position of the valley is not modified as it depends on the height of the barrier limiting the thermionic emission.

Conclusion

We have shown that the strong dependence of the bandgap upon the number of layers of noble TMDs can be used to devise electron devices based on transport through lateral heterostructures of TMDs, such as LH-FETs and LH-RTDs. We have used ab initio multiscale simulations to demonstrate that LH-FETs based on PdS₂ and PtS₂ can comply with IRDS performance requirements²⁹ for future integrated circuit technology for high-performance digital applications. On the other hand, LH-FETs made of NiS₂ cannot meet such requirements, due to the low gap and ambipolar behavior.

We have also predicted the steep (submaxwellian) subthreshold behavior of p-type FETs based on PdS, due to the asymmetry of the bilayer PdS₂ DOS around the Fermi level, achieving SS = 52 mV/decade. The demonstration of this effect in an intrinsic 2D material observed here can be further exploited for device design. It must be noted that in the presence of electron–electron or electron–phonon scattering, the behavior of the studied devices would be degraded with respect to the optimum ballistic condition assumed here, with direct impact on the achieved sub-Boltzmann slope. Moreover, the SS value for PdS₂ FETs is not expected to boost the device performance stunningly as compared to the conventional limit. However, and more importantly, the results presented here confirm that the 60 mV/decade limit can be beaten in 2D-based FETs, as it has been proved experimentally in graphene, encouraging the exploration of new 2D materials with sharper DOS and consequently steeper SSs.

Finally, we have also predicted the possibility of using 2D LHs to obtain a resonant tunneling diode, with a pronounced peak-to-valley ratio of the current–voltage characteristics, which is suitable for experimental observation.

Methods

Density functional theory as implemented in Quantum Espresso code has been employed to determine the electronic structure of PdS₂, NiS₂, and PtS₂. The crystal geometry of monolayer and bilayer 2D crystals is characterized by a 1T arrangement, with a layer of Pt/Pd/Ni atoms sandwiched between two atomic layers of S atoms. The atom coordinates and lattice vectors have been obtained after,¹⁴ where a structural optimization of the unitary cell was performed. We have considered 40 Å of vacuum in the direction orthogonal to the 2D layers to minimize spurious interactions between periodic repetitions of the cell. For the exchange–correlation functional, the local density approximation has been considered under the Perdew–Zunger⁴¹ parametrization within norm-conserving pseudopotentials. The energy cutoffs for charge density and wave function expansions have been set to 360 and 60 Ry, respectively. A Monkhorst–Pack 10 × 5 × 1 k-mesh has been used for the Brillouin-zone integration, and an energy convergence threshold of 10^–6 eV in the iterative solution of the Kohn–Sham equations was ensured. Additionally, an analysis of the Schottky barriers formed at the 2L/1L heterojunction has been performed (see Supporting Information).

Maximally localized Wannier functions (MLWFs) have been obtained by means of the Wannier90 code³² for every material and stacking. For the change of basis, the same k-sampling of the Brillouin zone as in the DFT simulations has been used to compute the overlap matrices required to determine the MLWFs. Twelve bands around the fundamental gap have been considered, and a threshold of 10^–10 Å has been set for the total spread change in the MLWFs in 20 consecutive iterations. The MLWFs band structures have been calculated along the same path as in DFT, showing very good agreement (see Supporting Information Figure S1). The MLWF Hamiltonians of the 1L and 2L regions have been employed to build the total Hamiltonian of the lateral heterostructure following the procedure presented in ref (33).

The device simulations consist of the self-consistent solution of the open-boundary Schrödinger equation, within the non-equilibrium Green’s functions (NEGF)³⁵ formalism, and the Poisson equation, for which we have used the open-source code NanoTCAD ViDES.^36,37 The construction of the Hamiltonian of the heterostructure from the Hamiltonians of the different regions/materials requires a careful treatment, with special attention to the mixing of the interface elements. We have followed the procedure we developed and validated in ref (33). In particular, the off-diagonal elements connecting the 1L and 2L regions and determining their coupling have been assumed to be equal to those of the monolayer region. We have tested different alternatives for the off-diagonal coupling elements at the interface (see Supporting Information) observing little variation in the device behavior. This mixing procedure provides the best results in terms of robustness in the convergence, preserving computational accuracy as compared to ab initio simulations. For all devices we have considered operation at temperature of 300 K.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.9b08489.

• Additional details on the electronic band structure of monolayer and bilayer PtS₂, PdS₂, and NiS₂ and on the Hamiltonian construction as well as the current spectrum for the PdS₂ LH-FET (PDF)

The authors declare no competing financial interest.