Abstract
With inherent orthogonality, both the spin angular momentum (SAM) and orbital angular momentum (OAM) of photons have been utilized to expand the dimensions of quantum information, optical communications, and information processing, wherein simultaneous detection of SAMs and OAMs with a single element and a single-shot measurement is highly anticipated. Here, a single azimuthal-quadratic phase metasurface-based photonic momentum transformation (PMT) is illustrated and utilized for vortex recognition. Since different vortices are converted into focusing patterns with distinct azimuthal coordinates on a transverse plane through PMT, OAMs within a large mode space can be determined through a single-shot measurement. Moreover, spin-controlled dual-functional PMTs are proposed for simultaneous SAM and OAM sorting, which is implemented by a single spin-decoupled metasurface that merges both the geometric phase and dynamic phase. Interestingly, our proposed method can detect vectorial vortices with both phase and polarization singularities, as well as superimposed vortices with a certain interval step. Experimental results obtained at several wavelengths in the visible band exhibit good agreement with the numerical modeling. With the merits of ultracompact device size, simple optical configuration, and prominent vortex recognition ability, our approach may underpin the development of integrated and high-dimensional optical and quantum systems.
Subject terms: Metamaterials, Sub-wavelength optics, Nanophotonics and plasmonics
Introduction
From the perspective of quantum mechanics, photons can carry both spin angular momentum (SAM) and orbital angular momentum (OAM). SAM is manifested as a circular polarization state with a bounded value of ±ℏ per photon1, whereas OAM is associated with the “twist” of a helical phase front of exp(ilφ) and has unbounded states denoted by lℏ (φ is the azimuth, l is the mode number and ℏ is Planck’s constant divided by 2π)2–4. With inherent orthogonality, both SAMs and OAMs of light have been utilized to expand the dimensions of quantum information5, optical communications6–8, and signal processing9–12, wherein unambiguous SAM and OAM identification is one of the significant topics.
Compared with the direct generation of OAM modes through various optical elements, such as spiral phase plates13, form-birefringent elements14,15, computer-generated holograms16, spatial light modulators (SLMs), and ultrathin and planar metasurfaces17–20, OAM identification is challenging due to the missing phase information for traditional intensity detectors. The earliest OAM diagnosis strategies were proposed based on interference with the mirror image or a reference wavefront21–24, diffraction through specific apertures25–28, and reciprocal projection through a forked diffraction grating5. Various vortices have been successfully detected, including single-photon vortices21,23, supercontinuum femtosecond vortices, noninteger vortices26, ultrabroadband vortices28, and entanglement vortices5. However, most of the aforementioned approaches require complicated optical setups or bulky devices. Furthermore, counting the number of interference fringes and multiple repeated projection measurements were inefficient for the detection of various possible OAM modes, especially for high-order OAMs29.
Recently, with the appearance of on-chip plasmonic nanostructures30 and metasurfaces17,31, compact OAM detection strategies have been proposed18,19,32, exhibiting additional merits of ease of interfacing with photodiodes30,33 and robustness to certain misalignments34,35. Multichannel or superimposed OAM recognition36,37 and simultaneous detection of SAMs and OAMs have been demonstrated35,37. Nevertheless, restricted by the wavevector-matching condition, on-chip plasmonic nanogratings operate only at a specific wavelength. On the other hand, the detectable OAM modes of dielectric metasurfaces are generally no more than ten37.
Alternatively, optical transformation systems that translate different OAMs into separated or distinct intensity patterns on a transverse plane have been investigated. Theoretically, the detectable mode space of the optical transformation methodology is not limited, and it has demonstrated mode detection up to 100 orders38. Optical transformations generally require two or more optical elements separated by specific distances with precise alignment. Typically, to perform log-polar transformation39–42, one element converts helical OAMs into a beam with a transverse phase gradient, and the other element performs a phase correction and completes the transformation. Most recently, excellent advances have been made for alleviating the mode overlap via spiral transformation43,44 and for decreasing the number of utilized optical elements via a single angular lens45. However, the above optical transformations mainly rely on bulky refractive elements or large diffractive elements and cannot simultaneously distinguish SAM and OAM. Quite recently, metasurface versions of the log-pol and spiral transformation sorters have been presented for total angular momentum sorting at 1310 and 1550 nm46,47, respectively.
In this paper, a single azimuthal-quadratic metasurface-based photonic momentum transformation (PMT) principle is illustrated with detailed mathematical deductions and theoretical analyses. Different vortices in a large mode space are converted into focusing patterns with distinct azimuthal coordinates on a transverse plane via PMT, and thus, OAMs can be determined through a single-shot measurment. Moreover, spin-controlled dual-functional PMTs are proposed for simultaneous SAM and OAM sorting, which is implemented by a single spin-decoupled metasurface that merges both the geometric phase and dynamic phase. With the simultaneous SAM and OAM sorting ability, our proposed method can detect cylindrical vortex vector beams (CVVBs) with both phase and polarization singularities, which may find potential applications in singular optics. Furthermore, our methodology can sort superimposed OAM modes with a certain interval step. For proof-of-concept demonstrations, dielectric metasurfaces have been fabricated by high-resolution electron-beam lithography (EBL) and atom-layer deposition (ALD). Experimental results obtained at several wavelengths in the visible band exhibit good agreement with the numerical modeling. Detailed discussions about the operation bandwidth, detection range, and resolving power of our proposed method are also presented.
Results
Principle of PMT
A PMT is an optical transformation that maps received OAM modes into rotational focusing patterns on a transverse plane. Through a mathematical deduction (Section 1 of the Supplementary file), we find that the PMT hinges on a single azimuthal-quadratic phase mask (termed the angular lens in ref. 45 and implemented by an SLM), which is expressed as:
| 1 |
where l0 is the quadratic phase coefficient and φ is the azimuthal coordinate defined as tan−1(y/x). For OAM with a topological charge of l, the phase accumulated when passing through the phase mask can be written as:
| 2 |
where φ′ denotes a new azimuthal coordinate. Neglecting the azimuth-independent term on the right-hand side of the equation, we find that there is only a mode-dependent rotation through the PMT:
| 3 |
A phenomenological explanation of the azimuthal rotation is illustrated in Section 2 of the Supplementary file. According to Eq. (3), opposite vortices are focused symmetric about azimuthal coordinate φ = 0. With an increase in the topologic charge from negative to positive, the focusing pattern rotates clockwise with an azimuthal interval of 1/l0. If we can record the azimuthal coordinate of the focusing pattern through such a phase mask, then the received OAM mode can be determined as:
| 4 |
From Eq. (1), it is not easy to deduce the focal distance of the azimuthal-quadratic phase mask. Fortunately, we can obtain it by drawing an analogy between the PMT illustrated here and a similar optical symmetry transformation reported previously48–50. As shown in Fig. 1, the optical symmetry transformation is performed through a single radial-quadratic phase mask (), which is mathematically expressed as48:
| 5 |
where k0 is the wavevector in free space, θ is the oblique angle of the incident light, and f is the focal length of the phase mask. The optical symmetry transformation translates off-axis plane waves into focusing spots of different transverse shifts on a focal plane and thus offers a novel design paradigm for single metalens-based extreme field-of-view (FOV) imaging48,51,52 and wide-angle beam-steering antennas49,50.
Fig. 1. Analogy of two types of optical transformations based on a single quadratic phase mask.
a Principle of the optical symmetry transformation that translates the rotational symmetry of wide FOV illumination into a transverse symmetry of focus shift, which is utilized for single thin metalens-based wide FOV imaging and wide-angle beam scanning. b Principle of the PMT that translates different OAM modes into rotating focusing patterns, which is leveraged for single-metasurface-based single-shot OAM detection
With a coordinate transformation (Section 3 of the Supplementary file), the equivalent focal distance of the azimuthal-quadratic phase mask can be determined as:
| 6 |
where r0 = (ri + ro)/2 and ri and ro denote the inner and outer radii of the ring phase mask, respectively. According to Eq. (6), the focal length is independent of the topological charge of incident OAM modes, and thus, different OAM modes can be detected on a permanent transverse plane.
Left-handed circularly polarized (LCP) OAM sorting via a single geometric metasurface
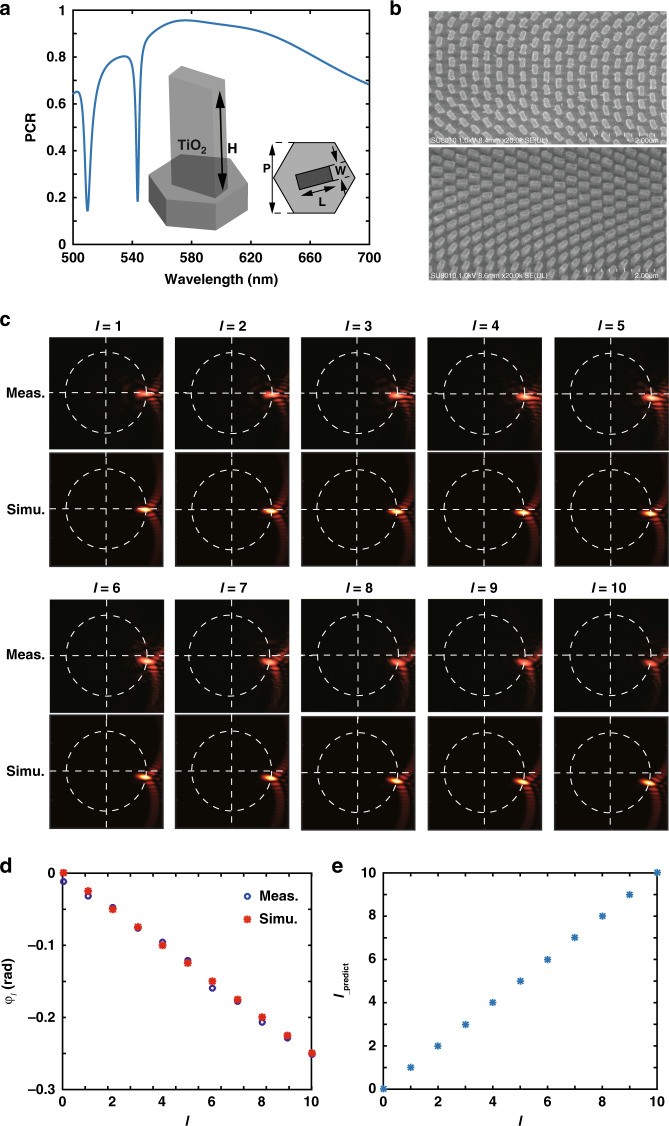
As illustrated in Fig. 1b, a typical azimuthal-quadratic phase profile changes rapidly toward the azimuthal coordinate of ±π, leading to an equivalent wavevector that is several times larger than k0. Such an azimuthal-quadratic phase mask cannot be easily realized via either refractive or diffractive optics. In contrast to the SLM-based angular lens45, a compact geometric metasurface composed of rotating titanium dioxide (TiO2) nanopillars in a hexagonal lattice (with C6 symmetry) is leveraged here. The unit cell of the geometric metasurface is shown in the inset of Fig. 2a. TiO2 is chosen as the constituent material due to its high refractive index and low loss at visible frequencies. To make the rectangular nanopillars approach an ideal half-wave plate, the geometric parameters of the unit cells are optimized as height H = 800 nm, length L = 240 nm, width W = 100 nm, and period P = 300 nm. The pixel size is one order of magnitude smaller than the current commercial SLMs, which helps approach the ideal azimuthal-quadratic phase as much as possible. As indicated in Fig. 2a, the simulated cross-polarization conversion ratio (PCR) is above 90% around 580 nm and gradually decreases away from this wavelength. Therefore, the dispersion of the PCR restricts the operation bandwidth of the geometric metasurface to a certain extent. Nevertheless, the PCR is still >50% in almost the whole visible band.
Fig. 2. Design and fabrication of geometric metasurfaces and LCP OAM sorting at a wavelength of 633 nm.
a Simulated polarization conversion ratio (PCR) of the unit cell. Inset: Schematic diagram of the unit cell, which is composed of TiO2 nanopillars on a SiO2 substrate in a hexagonal lattice. H = 800 nm, P = 300 nm, L = 240 nm, and W = 100 nm. b Top-view and perspective-view scanning electron microscopy (SEM) images of the fabricated geometric metasurfaces. c Measured and simulated focusing patterns for different OAM modes with the topological charge increasing from 1 to 10. d Theoretical and measured azimuthal coordinates of the focus peak versus the topological charge. e OAM prediction results based on the measured azimuthal coordinates in (d)
As an example for proof-of-concept demonstration, a ring-shaped geometric metasurface with ri = 50 μm and ro = 80 μm (the selection of the radii of the phase mask is discussed in Section 4 of the Supplementary file) is fabricated by etching the complementary patterns into the resist by EBL and conformal growth of high aspect-ratio nanopillars by ALD (see “Metasurface fabrication” in Materials and methods). Top-view and perspective-view scanning electron microscopy (SEM) images of fabricated metasurfaces are shown in Fig. 2b. The in-plane orientation ξ of nanopillars for left-handed OAM is determined as:
| 7 |
Here, l0 is set to 40 to obtain a large mode recognition space. An OAM sorting experiment is performed for LCP vortices at a wavelength of 633 nm with a continuous-wave He–Ne laser. The geometric phase shift generated by the spin-orbit interaction (SOI) of the geometric metasurface is picked up by the spin-reversed light, and the PMT is performed at a transverse focal plane ~1048.4 µm behind the metasurface, where the focusing pattern is amplified and imaged onto a camera through an objective lens. The experimental setup and measurement procedure are presented in Section 5 of the Supplementary file.
As indicated in Fig. 2c, when the topological charge of the OAM mode increases from 0 to 11, the shape variation of the focusing patterns can be neglected, and there is only a clockwise rotation along the white dotted circle. The results simulated via vectorial angular spectrum theory (see “Numerical modeling” in Materials and methods) are also presented in Fig. 2c and agree well with the measured results. The energy efficiency is limited for several reasons. First, owing to the fabrication defects, the measured diffraction efficiency of the fabricated metasurface is only ~30% (Section 6 of the Supplementary file), which can be further improved by optimizing the fabrication process and adopting semicontinuous metasurfaces20,53. Second, since the intensity is spread over a sort of V-shape with a cusp, the amount of energy focused on the specific spot of interest is ~16.3%. Finally, the detection efficiency is fundamentally limited by the intensity fraction in the weak cross-talk area. The detection efficiency of each mode is only ~22.2% (see Section 7 of the Supplementary file). Although it is not high enough for OAM sorting at a single-photon level, it is sufficient for many-photon cases. With careful alignment, the differences between the measured and theoretical azimuthal coordinates are no more than ±0.01 radians (see Section 8 of the Supplementary file). In this situation, the peak intensity is still located within the weak cross-talk region of each mode (the azimuthal separation between the intensity peaks of two adjacent modes is 1/40 = 0.025 radians). Therefore, the topological charge can be unambiguously predicted as:
| 8 |
where the operation [•] represents the nearest integer to cancel the deviations caused by the limited pixel size of the camera. The prediction results match the topological charge of the received vortices well, as indicated in Fig. 2e (the influences of misalignment on the detection results are analyzed in Section 9 of the Supplementary file). In addition, simulated results of the PMT for different OAMs with topological charge from 1 to 100 are given in Section 10 of the Supplementary file, demonstrating a large mode detection space of our method.
Simultaneous SAM and OAM sorting via a single spin-decoupled metasurface
Since the geometric phase is spin-dependent, i.e., the phase profile will be the opposite when the spin is reversed, the geometric metasurface-based PMT only operates under one of the spins. To simultaneously sort SAMs and OAMs, a spin-decoupled dual-functional metasurface that merges dynamic and geometric phases is developed here, which is composed of TiO2 rectangular nanopillars with various orientations and geometries. On the one hand, the dynamic phases along the main axes of the rectangular nanopillars can be adjusted by tailoring L and W. On the other hand, an arbitrary geometric phase can be realized by controlling the local orientation of the fast axes of the nanopillars between 0 and π. Owing to the introduction of the spin-independent dynamic phase, the conjugation limitation of the SOI is broken, and thus, dual-functional metasurfaces can be realized19,54–57. Distinct from multifunctional metasurfaces constructed by the aperture–division–multiplexing methodology58,59, each spin can interact with the whole aperture in spin-decoupled metasurfaces.
As shown in Fig. 3a, LCP and right-handed circularly polarized (RCP) incident light picks up spin-decoupled azimuthal-quadric phase profiles as follows:
| 9a |
| 9b |
and undergoes a pair of center-symmetric PMTs, mapping vortices of different spins into the upper and lower halves of the screen. Therefore, SAMs can be easily sorted by inspecting which half of the screen the focal spot is focused on, and OAMs can be identified by determining the azimuthal coordinate of the focusing patterns, similar to in the demonstration for geometric metasurfaces.
Fig. 3. Single spin-decoupled metasurface-based PMTs for simultaneous SAM and OAM sorting.
a Schematic of a spin-decoupled metasurface that merges the geometric phase and dynamic phase for simultaneous SAM and OAM sorting via spin-controlled PMTs. Vortex beams with different spins are transformed into focusing patterns on two separated halves of the screen on a transverse focal plane with topological charge-dependent azimuthal rotations. b Eight unit cells of the spin-decoupled metasurface and their corresponding phase modulation around a wavelength of 532 nm. c Perspective-view SEM images of the fabricated spin-decoupled metasurfaces
It has been demonstrated by our19,54,56 and other groups57,60 that to construct spin-decoupled metasurfaces, the anisotropic dynamic phase shifts (δx and δy), and orientation of nanopillars should satisfy:
| 10a |
| 10b |
| 10c |
Through parameter sweeping of L and W, eight nanostructures with the same height H = 600 nm and period P = 370 nm, including four fundamental nanopillars with different lengths and widths (L, W) and their orthogonal structures with length and width (W, L), are selected to provide eight phase levels with an equal phase step of π/4 (Fig. 3b) and a high PCR up to 85% around the wavelength of 532 nm (Section 11 of the Supplementary file). SEM images of the fabricated spin-decoupled metasurface are presented in Fig. 3c.
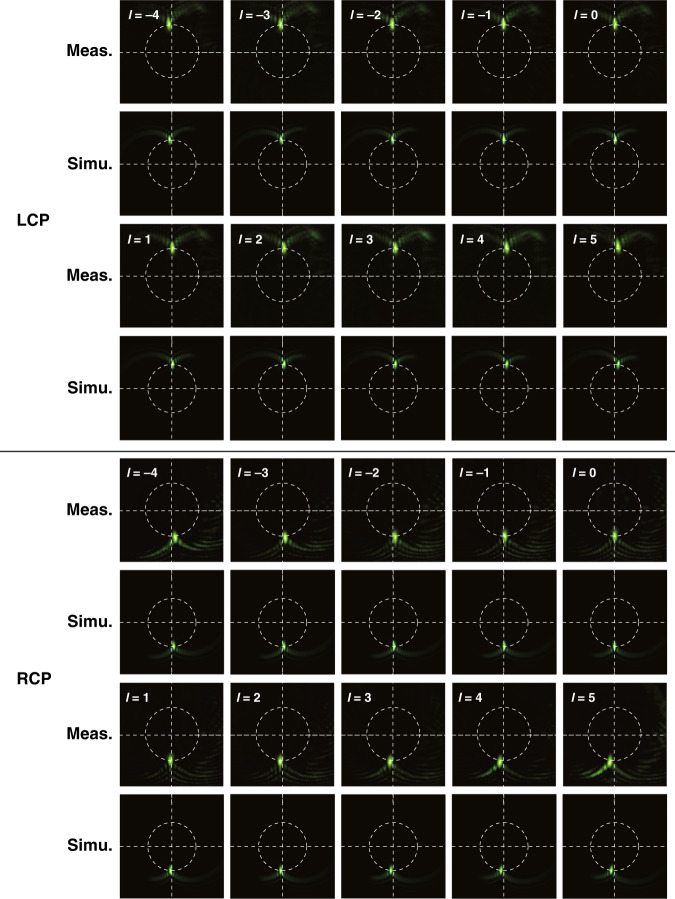
Simultaneous SAM and OAM sorting was performed at a wavelength of 532 nm with a continuous-wave diode-pumped solid-state laser. From Fig. 4, we can see that vortices with different SAMs are mapped into focusing patterns on different halves of the screen, i.e., LCP (σ = 1) vortices in the upper half of the screen and RCP (σ = −1) vortices in the lower half of the screen; thus, the SAMs can be easily determined. Specifically, for LCP and RCP plane waves (l = 0), the focusing patterns are located at φ = π/2 and φ = −π/2, respectively. Since the focusing patterns rotate clockwise with increasing topological charge, the OAMs are identified by inspecting the rotation angle relative to the referenced plane wave. The simulated results are also presented in Fig. 4, which are consistent with the measured results.
Fig. 4. SAM and OAM sorting at a wavelength of 532 nm.
Measured and simulated focusing patterns for different SAMs and OAMs with the topological charge changing from −4 to 5
Intuitively, for linearly polarized vortices that can be taken as superimpositions of LCP vortices and RCP vortices with the same topological charge, there will be two focusing patterns located at two center-symmetric positions on the white dotted circle via spin-decoupled PMTs, which has been demonstrated by the measured results shown in Section 12 of the Supplementary file. A similar sorting experiment was reported in ref. 61. The slightly unequal intensities of the two focusing patterns may be attributed to the imperfect fabrication and measurement.
Sorting of CVVBs with both phase and polarization singularities
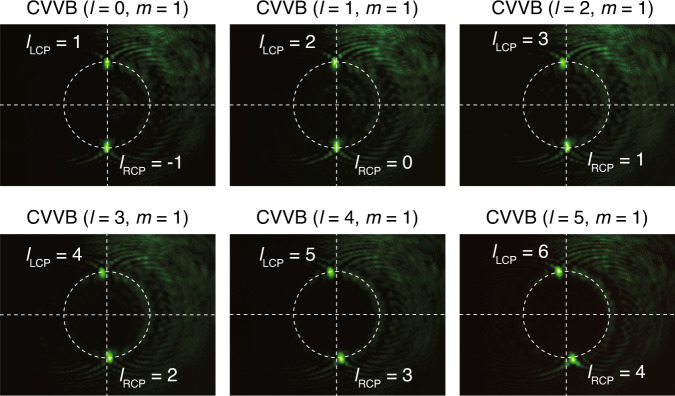
As a family of solutions of the more general vector wave equation62, CVVBs feature an inhomogeneous polarization in the dimension transverse to the propagation direction and find important applications in high-resolution imaging and nanoparticle manipulation due to the extra degree of freedom for light manipulation63. Theoretically, spin-decoupled metasurface-based dual-functional PMTs can also be utilized to identify CVVBs with phase and polarization singularities, which can be treated as a sum of an LCP vortex with topological charge (l + m) and an RCP vortex with topological charge (l – m) according to the Jones matrix of a CVVB35,64:
| 11 |
where φ0 is the initial phase, l is the topological charge, and m is the polarization order. To generate the CVVB, we added a vortex wave plate with m = 1 (Thorlabs WPV10–532) after the SLM. The measured results in Fig. 5 show that the two focusing patterns in the two halves of the screen are no longer center-symmetric due to the unequal topological charges of the LCP and RCP vortices, demonstrating that full detection of the phase and polarization singularities of the incident beam is achieved. Note that when l = 0, the CVVB degenerates into an ordinary cylindrical vector beam (CVB) with only polarization singularity. In this situation, the topological charge values of the LCP and RCP vortices are the same, and the focusing spots are center-symmetric again, which is similar to the observations reported in ref. 65.
Fig. 5. Cylindrical vortex vector beam sorting at a wavelength of 532 nm.
Measured focusing patterns for different phase singularities changing from 0 to 5 and polarization singularity m = 1
Discussion
In subsequent discussions, we take the geometric metasurface as an example, and the conclusions can be easily extended to the spin-decoupled metasurface.
Sorting of superimposed vortices
Thus far, we have demonstrated a resolving power of Δl = 1 when there is only a single isolated OAM mode received at a time, i.e., there is no cross-talk between adjacent modes. However, when multiple superimposed vortices are simultaneously received, the intensity overlap between them causes a deteriorated resolving power. The simulated and measured results presented in Section 13 of the Supplementary file (Fig. S17) indicate that one cannot resolve two superimposed vortices with a mode interval smaller than Δl = 5, which means that at most 41 superimposed vortices can be simultaneously detected (Fig. S18). Similar mode overlap and resolution limitations were also observed in the log-polar transformation39 and angular lens-based OAM sorting methods45.
To alleviate mode overlap and improve the sorting resolution, a modified azimuthal-quadratic phase mask is utilized, which is expressed as:
| 12 |
Then, the PMT in Eq. (2) can be rewritten as:
| 13 |
The azimuth of the focusing patterns can be calculated as:
| 14 |
Equation (14) indicates that the azimuth difference of adjacent OAM modes becomes n2 times the original one.
By adjusting n, an equivalent azimuthal-quadratic phase coefficient l0/n2 is realized. According to Eq. (13), the detectable mode range is proportional to l0/n2, while the resolving power is inversely proportional to l0/n2. With l0/n2 decreasing, the mode resolving power for superimposed vortices increases but at the sacrifice of decreasing the detectable mode range. As an example, for a modified phase mask with n = 3 (Fig. S19A), the resolving power increases to Δl = 2, while the detection range shrinks to within ±6 orders (Fig. S19B, C). Therefore, the coefficients l0 and n should be selected according to the requirements of the detection range and resolution in practical applications. Details are presented in Section 13 of the Supplementary file. In practical applications, we can realize a mode resolving power of Δl = 1 for a modified phase mask with n = 3 by coding the adjacent modes into opposite spins (e.g., , , , , ). In addition, our results reported here may have many important applications in not only the measurement of both the spin and angular momentum but also the detection of both phase and polarization singularities. In these scenarios, an isolated vortex mode is generally investigated.
Broadband PMTs and vortex sorting
A supercontinuum laser source (NKT Photonics, EXP-15) attached to an acoustic optical tuning filter was used to generate light beams across the visible band. Owing to the limited operation band of the SLMs (PLUTO-VIS-014, 420–650 nm) and camera (AmScope MU300, 380–650 nm), the PMTs were experimentally performed at different wavelengths in a range of 480–633 nm. The measured results (Section 14 of the Supplementary file) indicate that both the geometric metasurface and spin-decoupled metasurface can perform mode sorting at these wavelengths, although the spin-decoupled metasurface is optimized at a wavelength of 532 nm.
In addition, we have simulated the longitudinal propagation properties at five wavelengths of 480, 532, 580, 633, and 780 nm. As indicated in Fig. S23A–E, although the focal distances are wavelength-dependent, the depths of focus are sufficiently long such that we can select a transverse plane across all the focal planes. The simulated focusing patterns of 26 superimposed vortices at five different wavelengths on the transverse plane are combined and shown in Fig. S23F, and the corresponding intensity curves along the white dotted line are displayed in Fig. S23G, from which we can see that the peak and valley positions of the focusing patterns at different wavelengths well match each other. These results demonstrate that it is possible to simultaneously detect broadband vortices covering the whole visible band, although additional optical spectral filters are needed for further wavelength identification.
In summary, we have theoretically and experimentally demonstrated a single geometric TiO2 metasurface-based OAM mode discrimination method via PMT of the azimuthal-quadratic phase metasurface. Then, we showed that a single spin-decoupled TiO2 metasurface that merges the geometric phase and dynamic phase could perform simultaneous SAM and OAM mode discrimination via spin-dependent PMTs, where vortex beams of different spins were transformed into focusing patterns on two separated halves of the screen on a transverse focal plane with topological charge-dependent azimuthal rotations. Further experimental investigations have proven that the single spin-decoupled metasurface possesses the ability to detect cylindrical vortex vector beams with simultaneous phase and polarization singularities. Spin-decoupled PMTs were experimentally demonstrated at several different wavelengths in the visible band. Finally, we showed that the proposed approach could be extended to sorting of superimposed OAMs with a proper mode interval. These results reported here may have many important applications in momentum measurement of both the spin and angular momentum and singularity detection of both phase and polarization singularities.
Materials and methods
Numerical modeling
The transversely simulated area is set as 800 × 800 μm2, and the grid number N in a transverse plane is set as 1024 × 1024. For an arbitrary point (x, y) in Cartesian coordinates, the corresponding polar coordinates can be expressed as:
| 15 |
An amplitude and azimuthal-quadratic phase mask is utilized:
| 16 |
where:
| 17 |
When a light beam carrying an OAM mode is normally projected on the amplitude and phase mask, the output electric field can be expressed as:
| 18 |
Then, the electric field at an arbitrary transverse plane behind the metasurface can be calculated via vectorial angular spectrum theory66:
| 19 |
where and .
Metasurface fabrication
The fabrication process began with spin-coating a layer of 800-nm-thick electron-beam (e-beam) resist (AR-P 6200) and e-beam evaporation of 10-nm-thick chromium (Cr) onto 540-μm-thick fused silica substrates. Afterward, e-beam lithography was performed at an accelerating voltage of 125 kV and a beam current of 2 nA. The Cr layer was removed by the chromium removal solution, and the samples were developed in o-xylene for 90 s. Atomic layer deposition (ALD) at a low temperature of 100 °C was subsequently used to deposit TiO2 onto the developed resist. The overcoated TiO2 layer was then etched by reactive ion etching (RIE) with a gas mixture of SF6 (20 sccm) and CHF3 (5 sccm). Finally, the resist was removed by RIE with O2.
Supplementary information
Acknowledgements
This work was supported by the National Natural Science Funds of China under Grant Nos. 61875253 and 61975210 and the Chinese Academy of Sciences Youth Innovation Promotion Association under Grant No. 2019371.
Author contributions
Y.G. and M.P. conceived the idea and carried out the numerical simulations. S.Z. and J.J. performed the experiments. Q.H. and P.G. fabricated the devices. Y.G. and Y.Z. designed the metasurface and analyzed the measured results. Y.G. wrote the paper. X.L. supervised the project. All authors contributed to the final version of the paper.
Conflict of interest
The authors declare no competing interests.
Supplementary information
The online version contains supplementary material available at 10.1038/s41377-021-00497-7.
References
- 1.Beth RA. Mechanical detection and measurement of the angular momentum of light. Phys. Rev. 1936;50:115–125. doi: 10.1103/PhysRev.50.115. [DOI] [Google Scholar]
- 2.Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular-momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A. 1992;45:8185–8189. doi: 10.1103/PhysRevA.45.8185. [DOI] [PubMed] [Google Scholar]
- 3.Yao AM, Padgett MJ. Orbital angular momentum: origins, behavior and applications. Adv. Opt. Photon. 2011;3:161–204. doi: 10.1364/AOP.3.000161. [DOI] [Google Scholar]
- 4.Franke-Arnold S, Allen L, Padgett M. Advances in optical angular momentum. Laser Photon. Rev. 2008;2:299–313. doi: 10.1002/lpor.200810007. [DOI] [Google Scholar]
- 5.Mair A, Vaziri A, Weihs G, Zeilinger A. Entanglement of the orbital angular momentum states of photons. Nature. 2001;412:313–316. doi: 10.1038/35085529. [DOI] [PubMed] [Google Scholar]
- 6.Shen Y, et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019;8:90. doi: 10.1038/s41377-019-0194-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wang J, et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics. 2012;6:488–496. doi: 10.1038/nphoton.2012.138. [DOI] [Google Scholar]
- 8.Willner AE, et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photon. 2015;7:66–106. doi: 10.1364/AOP.7.000066. [DOI] [Google Scholar]
- 9.Fang X, Ren H, Gu M. Orbital angular momentum holography for high-security encryption. Nat. Photonics. 2020;14:102–108. doi: 10.1038/s41566-019-0560-x. [DOI] [Google Scholar]
- 10.Zhou H, et al. Polarization-encrypted orbital angular momentum multiplexed metasurface holography. ACS Nano. 2020;14:5553–5559. doi: 10.1021/acsnano.9b09814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ruffato G, Massari M, Romanato F. Multiplication and division of the orbital angular momentum of light with diffractive transformation optics. Light Sci. Appl. 2019;8:113. doi: 10.1038/s41377-019-0222-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wen Y, Chremmos I, Chen Y, Zhang Y, Yu S. Arbitrary multiplication and division of the orbital angular momentum of light. Phys. Rev. Lett. 2020;124:213901. doi: 10.1103/PhysRevLett.124.213901. [DOI] [PubMed] [Google Scholar]
- 13.Beijersbergen MW, Coerwinkel RPC, Kristensen M, Woerdman JP. Helical-wave-front laser-beams produced with a spiral phase plate. Opt. Commun. 1994;112:321–327. doi: 10.1016/0030-4018(94)90638-6. [DOI] [Google Scholar]
- 14.Biener G, Niv A, Kleiner V, Hasman E. Formation of helical beams by use of Pancharatnam-Berry phase optical elements. Opt. Lett. 2002;27:1875–1877. doi: 10.1364/OL.27.001875. [DOI] [PubMed] [Google Scholar]
- 15.Marrucci L, Manzo C, Paparo D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 2006;96:163905. doi: 10.1103/PhysRevLett.96.163905. [DOI] [PubMed] [Google Scholar]
- 16.Heckenberg NR, McDuff R, Smith CP, White AG. Generation of optical phase singularities by computer-generated holograms. Opt. Lett. 1992;17:221–223. doi: 10.1364/OL.17.000221. [DOI] [PubMed] [Google Scholar]
- 17.Yu N, et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science. 2011;334:333–337. doi: 10.1126/science.1210713. [DOI] [PubMed] [Google Scholar]
- 18.Pu M, et al. Catenary optics for achromatic generation of perfect optical angular momentum. Sci. Adv. 2015;1:e1500396. doi: 10.1126/sciadv.1500396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Guo Y, et al. Merging geometric phase and plasmon retardation phase in continuously shaped metasurfaces for arbitrary orbital angular momentum generation. ACS Photonics. 2016;3:2022–2029. doi: 10.1021/acsphotonics.6b00564. [DOI] [Google Scholar]
- 20.Luo, X. Catenary Optics (Singapore Springer, 2019).
- 21.Leach J, Padgett MJ, Barnett SM, Franke-Arnold S, Courtial J. Measuring the orbital angular momentum of a single photon. Phys. Rev. Lett. 2002;88:257901. doi: 10.1103/PhysRevLett.88.257901. [DOI] [PubMed] [Google Scholar]
- 22.Padgett M, Arlt J, Simpson N, Allen L. An experiment to observe the intensity and phase structure of Laguerre–Gaussian laser modes. Am. J. Phys. 1996;64:77–82. doi: 10.1119/1.18283. [DOI] [Google Scholar]
- 23.Leach J, et al. Interferometric methods to measure orbital and spin, or the total angular momentum of a single photon. Phys. Rev. Lett. 2004;92:013601. doi: 10.1103/PhysRevLett.92.013601. [DOI] [PubMed] [Google Scholar]
- 24.Harris M, Hill CA, Vaughan JM. Optical helices and spiral interference fringes. Opt. Commun. 1994;106:161–166. doi: 10.1016/0030-4018(94)90314-X. [DOI] [Google Scholar]
- 25.Jack B, Padgett MJ, Franke-Arnold S. Angular diffraction. N. J. Phys. 2008;10:103013. doi: 10.1088/1367-2630/10/10/103013. [DOI] [Google Scholar]
- 26.Araujo LEEde, Anderson ME. Measuring vortex charge with a triangular aperture. Opt. Lett. 2011;36:787–789. doi: 10.1364/OL.36.000787. [DOI] [PubMed] [Google Scholar]
- 27.Hickmann JM, Fonseca EJS, Soares WC, Chávez-Cerda S. Unveiling a truncated optical lattice associated with a triangular aperture using light’s orbital angular momentum. Phys. Rev. Lett. 2010;105:053904. doi: 10.1103/PhysRevLett.105.053904. [DOI] [PubMed] [Google Scholar]
- 28.Anderson ME, Bigman H, Araujo LEEde, Chaloupka JL. Measuring the topological charge of ultrabroadband, optical-vortex beams with a triangular aperture. J. Opt. Soc. Am. B. 2012;29:1968–1976. doi: 10.1364/JOSAB.29.001968. [DOI] [Google Scholar]
- 29.Liu Z, et al. Measuring high-order optical orbital angular momentum with a hyperbolic gradually changing period pure-phase grating. Opt. Lett. 2018;43:3076–3079. doi: 10.1364/OL.43.003076. [DOI] [PubMed] [Google Scholar]
- 30.Genevet P, Lin J, Kats MA, Capasso F. Holographic detection of the orbital angular momentum of light with plasmonic photodiodes. Nat. Commun. 2012;3:1278. doi: 10.1038/ncomms2293. [DOI] [PubMed] [Google Scholar]
- 31.Luo X. Principles of electromagnetic waves in metasurfaces. Sci. China.: Phys., Mech. Astron. 2015;58:594201. [Google Scholar]
- 32.Jin J, et al. Generation and detection of orbital angular momentum via metasurface. Sci. Rep. 2016;6:24286. doi: 10.1038/srep24286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ji Z, et al. Photocurrent detection of the orbital angular momentum of light. Science. 2020;368:763. doi: 10.1126/science.aba9192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chen J, Chen X, Li T, Zhu S. On-chip detection of orbital angular momentum beam by plasmonic nanogratings. Laser Photon. Rev. 2018;12:1700331. doi: 10.1002/lpor.201700331. [DOI] [Google Scholar]
- 35.Feng F, Si G, Min C, Yuan X, Somekh M. On-chip plasmonic spin-Hall nanograting for simultaneously detecting phase and polarization singularities. Light Sci. Appl. 2020;9:95. doi: 10.1038/s41377-020-0330-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Li Y, et al. Orbital angular momentum multiplexing and demultiplexing by a single metasurface. Adv. Opt. Mater. 2017;5:1600502. doi: 10.1002/adom.201600502. [DOI] [Google Scholar]
- 37.Zhang S, et al. Broadband detection of multiple spin and orbital angular momenta via dielectric metasurface. Laser Photonics Rev. 2020;14:2000062. doi: 10.1002/lpor.202000062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kotlyar VV, Kovalev AA, Porfirev AP. Astigmatic transforms of an optical vortex for measurement of its topological charge. Appl. Opt. 2017;56:4095–4104. doi: 10.1364/AO.56.004095. [DOI] [PubMed] [Google Scholar]
- 39.Berkhout GCG, Lavery MPJ, Courtial J, Beijersbergen MW, Padgett MJ. Efficient sorting of orbital angular momentum states of light. Phys. Rev. Lett. 2010;105:153601. doi: 10.1103/PhysRevLett.105.153601. [DOI] [PubMed] [Google Scholar]
- 40.Mirhosseini M, Malik M, Shi Z, Boyd RW. Efficient separation of the orbital angular momentum eigenstates of light. Nat. Commun. 2013;4:2781. doi: 10.1038/ncomms3781. [DOI] [PubMed] [Google Scholar]
- 41.O’Sullivan MN, Mirhosseini M, Malik M, Boyd RW. Near-perfect sorting of orbital angular momentum and angular position states of light. Opt. Express. 2012;20:24444–24449. doi: 10.1364/OE.20.024444. [DOI] [PubMed] [Google Scholar]
- 42.Lightman S, Hurvitz G, Gvishi R, Arie A. Miniature wide-spectrum mode sorter for vortex beams produced by 3D laser printing. Optica. 2017;4:605–610. doi: 10.1364/OPTICA.4.000605. [DOI] [Google Scholar]
- 43.Wen Y, et al. Spiral transformation for high-resolution and efficient sorting of optical vortex modes. Phys. Rev. Lett. 2018;120:193904. doi: 10.1103/PhysRevLett.120.193904. [DOI] [PubMed] [Google Scholar]
- 44.Wen Y, et al. Compact and high-performance vortex mode sorter for multi-dimensional multiplexed fiber communication systems. Optica. 2020;7:254–262. doi: 10.1364/OPTICA.385590. [DOI] [Google Scholar]
- 45.Sahu R, et al. Angular lens. Opt. Express. 2018;26:8709–8718. doi: 10.1364/OE.26.008709. [DOI] [PubMed] [Google Scholar]
- 46.Ruffato G, Capaldo P, Massari M, Mafakheri E, Romanato F. Total angular momentum sorting in the telecom infrared with silicon Pancharatnam-Berry transformation optics. Opt. Express. 2019;27:15750–15764. doi: 10.1364/OE.27.015750. [DOI] [PubMed] [Google Scholar]
- 47.Wang B, Wen Y, Zhu J, Chen Y, Yu S. Sorting full angular momentum states with Pancharatnam-Berry metasurfaces based on spiral transformation. Opt. Express. 2020;28:16342–16351. doi: 10.1364/OE.393859. [DOI] [PubMed] [Google Scholar]
- 48.Pu M, Li X, Guo Y, Ma X, Luo X. Nanoapertures with ordered rotations: symmetry transformation and wide-angle flat lensing. Opt. Express. 2017;25:31471–31477. doi: 10.1364/OE.25.031471. [DOI] [PubMed] [Google Scholar]
- 49.Guo Y, et al. High-efficiency and wide-angle beam steering based on catenary optical fields in ultrathin metalens. Adv. Opt. Mater. 2018;6:1800592. doi: 10.1002/adom.201800592. [DOI] [Google Scholar]
- 50.Guo Y, et al. Spoof plasmonic metasurfaces with catenary dispersion for two-dimensional wide-angle focusing and imaging. iScience. 2019;21:145–156. doi: 10.1016/j.isci.2019.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Martins A, et al. On metalenses with arbitrarily wide field of view. ACS Photonics. 2020;7:2073–2079. doi: 10.1021/acsphotonics.0c00479. [DOI] [Google Scholar]
- 52.Zhang, F. et al. Extreme‐Angle Silicon Infrared Optics Enabled by Streamlined Surfaces. Adv. Mater. 2008157 (2021). 10.1002/adma.202008157. [DOI] [PubMed]
- 53.Zhang F, et al. Broadband and high-efficiency accelerating beam generation by dielectric catenary metasurfaces. Nanophotonics. 2020;9:20200057. [Google Scholar]
- 54.Zhang F, Pu M, Luo J, Yu H, Luo X. Symmetry breaking of photonic spin-orbit interactions in metasurfaces. Opto-Electron. Eng. 2017;44:319–325. [Google Scholar]
- 55.Balthasar Mueller JP, Rubin NA, Devlin RC, Groever B, Capasso F. Metasurface polarization optics: independent phase control of arbitrary orthogonal states of polarization. Phys. Rev. Lett. 2017;118:113901. doi: 10.1103/PhysRevLett.118.113901. [DOI] [PubMed] [Google Scholar]
- 56.Zhang F, et al. All-dielectric metasurfaces for simultaneous giant circular asymmetric transmission and wavefront shaping based on asymmetric photonic spin–orbit interactions. Adv. Fun. Mater. 2017;27:1704295. doi: 10.1002/adfm.201704295. [DOI] [Google Scholar]
- 57.Devlin RC, Ambrosio A, Rubin NA, Mueller JPB, Capasso F. Arbitrary spin-to-orbital angular momentum conversion of light. Science. 2017;358:896–901. doi: 10.1126/science.aao5392. [DOI] [PubMed] [Google Scholar]
- 58.Khorasaninejad M, et al. Multispectral chiral imaging with a metalens. Nano Lett. 2016;16:4595–4600. doi: 10.1021/acs.nanolett.6b01897. [DOI] [PubMed] [Google Scholar]
- 59.Maguid E, et al. Photonic spin-controlled multifunctional shared-aperture antenna array. Science. 2016;352:1202. doi: 10.1126/science.aaf3417. [DOI] [PubMed] [Google Scholar]
- 60.Huo, P. et al. Photonic spin-multiplexing metasurface for switchable spiral phase contrast imaging. Nano Lett. 10.1021/acs.nanolett.0c00471 (2020). [DOI] [PMC free article] [PubMed]
- 61.Capaldo P, et al. Nano-fabrication and characterization of silicon meta-surfaces provided with Pancharatnam-Berry effect. Opt. Mater. Express. 2019;9:1015–1032. doi: 10.1364/OME.9.001015. [DOI] [Google Scholar]
- 62.Hall DG. Vector-beam solutions of Maxwell’s wave equation. Opt. Lett. 1996;21:9–11. doi: 10.1364/OL.21.000009. [DOI] [PubMed] [Google Scholar]
- 63.Zhan Q. Cylindrical vector beams: from mathematical concepts to applications. Adv. Opt. Photon. 2009;1:1–57. doi: 10.1364/AOP.1.000001. [DOI] [Google Scholar]
- 64.Ignacio Moreno, Jeffrey A. Davis, Isaac Ruiz, Cottrell DM. Decomposition of radially and azimuthally polarized beams using a circular-polarization and vortex-sensing diffraction grating. Opt. Express. 2010;18:7173–7183. doi: 10.1364/OE.18.007173. [DOI] [PubMed] [Google Scholar]
- 65.Lei T, Fan J, Xie Z, Yuan X. High-resolution cylindrical vector beams sorting based on spin-dependent fan-out optical geometric transformation. Opt. Express. 2019;27:20901–20909. doi: 10.1364/OE.27.020901. [DOI] [PubMed] [Google Scholar]
- 66.Ciattoni A, Crosignani B, Di Porto P. Vectorial free-space optical propagation: a simple approach for generating all-order nonparaxial corrections. Opt. Commun. 2000;177:9–13. doi: 10.1016/S0030-4018(00)00569-1. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.