Understanding Hypervelocity Sampling of Biosignatures in Space Missions

Abstract

The atomic-scale fragmentation processes involved in molecules undergoing hypervelocity impacts (HVIs; defined as >3 km/s) are challenging to investigate via experiments and still not well understood. This is particularly relevant for the consistency of biosignals from small-molecular-weight neutral organic molecules obtained during solar system robotic missions sampling atmospheres and plumes at hypervelocities. Experimental measurements to replicate HVI effects on neutral molecules are challenging, both in terms of accelerating uncharged species and isolating the multiple transition states over very rapid timescales (<1 ps). Nonequilibrium first-principles-based simulations extend the range of what is possible with experiments. We report on high-fidelity simulations of the fragmentation of small organic biosignature molecules over the range v = 1−12 km/s, and demonstrate that the fragmentation fraction is a sensitive function of velocity, impact angle, molecular structure, impact surface material, and the presence of surrounding ice shells. Furthermore, we generate interpretable fragmentation pathways and spectra for velocity values above the fragmentation thresholds and reveal how organic molecules encased in ice grains, as would likely be the case for those in “ocean worlds,” are preserved at even higher velocities than bare molecules. Our results place ideal spacecraft encounter velocities between 3 and 5 km/s for bare amino and fatty acids and within 4–6 km/s for the same species encased in ice grains and predict the onset of organic fragmentation in ice grains at >5 km/s, both consistent with recent experiments exploring HVI effects using impact-induced ionization and analysis via mass spectrometry and from the analysis of Enceladus organics in Cassini Data. From nanometer-sized ice Ih clusters, we establish that HVI energy is dissipated by ice casings through thermal resistance to the impact shock wave and that an upper fragmentation velocity limit exists at which ultimately any organic contents will be cleaved by the surrounding ice—this provides a fundamental path to characterize micrometer-sized ice grains. Altogether, these results provide quantifiable insights to bracket future instrument design and mission parameters.

1. Introduction

Hypervelocity refers to velocities that are typically over 3000 m/s (3 km/s, 6700 mph, 11,000 km/h or Mach 8.8). During hypervelocity impact (HVI) of organic compounds, or any other material, the strength of the chemical bonds that holds them together is lower than the inertial stresses. This results in fragmentation of the impacting molecules and, in some cases, degradation of the impacted surfaces (Jaramillo-Botero et al., 2012).

In space missions meant to study the potential for life in other planetary bodies, current sampling strategies include analysis of planetary atmospheres and plumes during hypervelocity flyby/flythrough encounters at different altitudes. This is conventionally done through the use of mass spectrometers (MSs) and other instruments capable of measuring the composition of gases, ices, and organic compounds. During collection, fragmentation of these materials can occur following their initial impact with an instrument's intake walls, or from radiolytic processes on the surface, before or during the surface sputtering process (Sephton et al., 2018). HVI can also cause postimpact chemistry, potentially confounding interpretation of the collected data. Mitigation or avoidance of these problems imposes strict constraints on mission parameters, in particular flyby velocities, as well as on instrument design choices geared to reduce fragmentation and postimpact chemical reactions from HVI (Darrach et al., 2015).

Although fragmentation upon impact with a hard surface can be mitigated by reducing the flyby speed of the spacecraft relative to the atmosphere, this compromises sampling signal intensities, collisional ionization strategies for analyzing dust, and may not be practical for certain planetary missions. Previous approaches to study these phenomena include efforts to relate organic fragmentation processes in analytical pyrolysis and ionizing fragmentation from laser or electron impacts (Wörgötter et al., 1997), dust accelerator experiments for organic particles (Goldsworthy et al., 2003; Srama et al., 2009), and more recently, by accelerating/decelerating charged aerosols and nanoparticles (Adamson et al., 2017).

Notwithstanding recent progress, the effects of HVI on the mass spectra of single impacting molecules remain only incompletely quantified.

This article provides quantitative results to address some of these unknowns, specifically for neutral molecules, to:

• 1.determine if existing space mission data obtained at hypervelocity from MSs, and other instruments, are compromised by impact-induced fragmentation, hence requiring reanalysis of the data aided by laboratory or theoretical simulations,
• 2.contribute design criteria for the optimization of spacecraft instruments meant to measure low concentrations of neutrals in low-density atmospheres during hypervelocity flybys, and
• 3.establish parameter bounds for future hypervelocity sampling missions, considering the trade-off between potential HVI-induced ionization and high encounter velocities to increase the effective mass flow and accuracy in signal resolution (especially in low-density gaseous environments).

In this work, we focus on the water-soluble biosignature molecules of amino acids and fatty acids (C ≤10), the building blocks of proteins and lipid membranes, longer water-insoluble fatty acids, and mixed aromatic and aliphatic structures that are known to be present on the surfaces of planetary satellites such as Titan, in the plume of Enceladus (Postberg et al., 2018b; Khawaja et al., 2019), and on comets and interplanetary dust particles (Kwok, 2016). The latter is used to contrast differences in fragmentation thresholds due to variations in structure, and include naphthalene, 2-octanone, and 1,3-dicyanobenzene. The water-soluble biological molecules are a necessary condition for life (as we know it), along with the existence of organics, and an energy source to drive metabolism (Sephton et al., 2018).

National Aeronautics and Space Administration's main candidates in the search for life are the so-called ocean worlds (Lunine, 2017). Within this class, three bodies can be prioritized as having multiple lines of evidence for a subsurface ocean: Saturn moons Enceladus (Spencer and Nimmo, 2013) and Titan, and Jupiter moons Europa (Kivelson et al., 2000) and Ganymede, although recent analysis by Saur et al. (2015) casts doubts about the existence of an ocean in the last of these. In the case of Enceladus, considerable information on the composition and even properties of the ocean exists. We leverage on data from recent missions to these bodies to guide the nature of our HVI simulations.

Hypervelocity sampling is challenging in any environment because materials undergoing HVI experience physical and chemical extremes: high energies (10s to 100s of eV), extreme pressures (>MPa), fast strain rates (>10¹¹/s), and local temperatures (>1000 K), leading to a large number of electronically excited states in the impacting molecule as well as complex-phase changes, all occurring over extremely fast (femto to picosecond) timescales. These conditions are challenging, if not impossible, to reproduce when using current laboratory techniques.

HVI is studied today by examining naturally occurring phenomena or via manufactured physical experiments using gas guns, magnetic accelerators, laser shock fields, linear accelerator motors, and electrostatic dust accelerators. Many of these experiments are designed to simulate micrometeoroid and orbital debris impacts on spacecraft shielding, components, and materials in various test configurations. These experimental setups and their results are not easily transferable to studying single-molecule impacts, especially for neutral molecules that are unaffected by electric or magnetic fields, which are of interest to planetary scientists and instrument developers seeking to explore the ocean worlds.

Computer simulations, however, can explore the effects of HVI on individual molecules under realistic conditions over the appropriate timescales. Simulations have their own challenges, given the inherent nonequilibrium and nonadiabatic phenomena involved in HVI (i.e., ionizing fragmentation, plasma formation, luminescence, or radiative transport, mixed-phase flows, bond-breaking, and recombination events, among others); however, the advent of high-performance computers and progress in quantum mechanics (QM) and QM-approximate methods now enable a first-principles approach capable of retaining the chemical degrees of freedom while bridging the time and length scales necessary for comparison with phenomenological evidence (including space mission data).

Prior in silico work on HVI includes atomistic simulations to show the cratering behavior for metallic projectile impacts on metal surfaces at impact velocities comparable to typical meteoroid velocities (Samela and Nordlund, 2008), the study of damage initiation during HVI on hard coatings (Branicio et al., 2008), and continuum-level models of particle impacts on different structural spacecraft materials to study their performance during perforation and fragment ejection (Hiermaier et al., 1997; Murr et al., 1998; Taylor et al., 2003; Clegg et al., 2006; Ryan et al., 2006).

Our own work on the development of novel QM-based explicit-electron dynamics methods has allowed us to study the nonadiabatic nature of materials in extreme conditions (Jaramillo-Botero et al., 2011; Xiao et al., 2015), including ionizing fragmentation, damage, and phase transformations (Jaramillo-Botero et al., 2011), while our work on adiabatic reactive molecular dynamics (RMD) has enabled prediction of fragmentation products and mixing ratios in HVI events of primary small neutrals (including water, ammonia, and carbon dioxide) in the context of the Cassini Mission's multiple encounters with the Enceladus plume and Titan atmosphere (Jaramillo-Botero et al., 2012). In that work, we confirmed and explained how changes in the sampling velocity of small neutrals at Enceladus' south pole plume caused significant variance in Cassini's ion and neutral mass spectra (INMS) data from different flybys, and the importance of structural material inertness.

In Section 2 of this article, we provide a brief introduction to the topic of HVI-induced bond dissociation, describe the general properties of the biosignature and other molecules of interest, and describe the set of simulation protocols and procedures applied here to study molecular HVI systematically. In Section 3, we discuss the main results of this study, starting from the general anatomy of molecular HVI through the prediction of instrument design variables and mission parameters that need to be considered during hypervelocity sampling of organics as a function of impact velocities, specifically fragmentation velocity thresholds, scattering dynamics, energetics of molecular collisions, fragmentation pathways and mass spectra. Section 4 summarizes the key contributions from this work and some of the persisting challenges, and justifies why addressing these is important in moving forward with the search for life elsewhere in the solar system by using hypervelocity sampling techniques (Section 4).

Additional details about the QM and QM-approximate chemical methods used in this work, along with the further results to support our conclusions, are included as part of the Supplementary Data.

2. HVI-Induced Bond Dissociation

To study molecular fragmentation processes, we must first understand the fundamental nature of the chemical bond and how to capture the corresponding physics using simulations. We discuss this in the context of dissociating bonds, and make a distinction between two levels of theory currently available to describe the dynamics of bond dissociation, namely, one in which electrons that participate in bonds can be excited to delocalize from any pairing electron/s or nuclei (nonadiabatic regime) before decaying into an antibonding state, and another in which electronic effects, as they pertain to chemical bonds, are embedded in a pseudoatom model capable of distinguishing its bonding environment (approximately). The former can result in good electronic structure accuracy, but it remains impractical for the size- and timescales involved in the models used in this study. The latter is a ground-state compromise that overcomes the multiscale limitations.

2.1. Nonadiabatic versus adiabatic interpretation of bond dissociation

During HVI of molecules, individual bonds get compressed and extended. Molecular fragmentation will occur when the impact energy is sufficiently high to overcome the 0 eV line, as given in Fig. 1. The dissociation energy barrier (D_E) corresponds to the maximum energy required to cleave the pair of atoms involved in a covalent bond, at their equilibrium distance. This figure depicts the classical bond energy curve for a C–H bond in a methane (CH₄) molecule, as the singlet ground-state curve (S0) with a D_E = 4.292 eV. It also shows a piece of the quantum bond dissociation picture, with low-laying excited electronic singlets and triplets, calculated at the QM level of generalized valence bond-restricted configuration interaction (with double excitation, see Section 4 for details on this calculation).

FIG. 1.

Potential energy curves for the ground state (S0), the first triplet (T1) and singlet (S1) excited states, the second triplet (T2) and singlet (S2) excited states, and the third triplet (T3) excited state. D_E = 4.67899 eV (or 107.9 kcal/mol), R₀ = 1.09 Å. The molecular geometry of CH₄ was optimized at M06–2X/6–311G**++ level [using Jaguar (Bochevarov et al., 2013)], followed by a rigid scan of the C–H bond at the level of GVB-RCI with cc-pVTZ basis set [using GAMESS (Gordon and Schmidt, 2005)]. The black horizontal lines within the potential well represent the rovibrational excitations caused during an HVI. For the strictly adiabatic case in our RMD simulations, bonds dissociate homolytically for interactions above the 0 eV horizontal line (i.e., one electron stays with each partner, forming radicals after dissociating). HVI, hypervelocity impact; RMD, reactive molecular dynamics; GVB, generalized valence bond; RCI, restricted configuration interaction. Color images are available online.

An HVI event may be sufficiently energetic to overcome the potential well of the S0 state (D_E), resulting in bond compression or stretching, and ultimately, bond dissociation if the energy versus bond length relationship falls above the 0 eV line. In the quantum picture, where heterolytic and homolytic cleavage is possible, sufficiently high ro-vibrational states can cause an excited electron participating in a bond to quench along an antibonding potential energy state surface (e.g., triplet first excited state, T1), leading to bond dissociation, and in extreme cases, electrons can also delocalize completely from parent nuclei, resulting in molecular ionization.

For this work, we use the semiclassical adiabatic approximation in the ReaxFF (van Duin et al., 2001) RMD simulation method. This is justified, given that the length (number of atoms and ensembles) and time scales needed to achieve statistically relevant sampling of the dynamic HVI dissociation space are well beyond the reach of current higher accuracy quantum chemistry (QC)-based methods, and because ReaxFF provides a technically sound compromise between accuracy, time, and length-scale performance. ReaxFF is a first-principles approximation trained to the many-body potential ground-state energy surface that is capable of accurately describing chemical reactions, based on the rigorous relationship between bond-orders, bond-energies, and bond-lengths in valence interactions (see Supplementary Fig. S8 in the Supplementary Data).

Given that the true bond energy between atoms is, for most cases except diatomic molecules, the average of the bond dissociation energies that can result from different molecular structures and compositions, reaxFF parameters are trained to describe the average kinetics of chemical reaction and pathways from multiple motifs. Therefore, the transferability of any particular set of force field parameters is dependent on the diversity of the training set used and the solution's closeness to a global minima, for which there is no analytical proof (especially for a complex energy expression involving multiple interatomic interactions over the entire space of possible conformations). This means the force field's transferability, performance, and accuracy are all part of the multiobjective optimization balancing act to approach a problem's solution that is otherwise intractable, computationally and experimentally (to date).

We validate the accuracy of the force field parameter set against a set of motifs characterized using QC methods, and from phenomenological results, when available. In our particular case, HVI of neutral molecules, there are no direct experimental results to compare against, and so, we rely on the QC characterizations.

Here, we use the ReaxFF parameters from Verlackt et al. (2015) for most interactions, except for the sigma C–C bonds, resulting in an ∼24 kcal/mol higher dissociation energy when compared with the experimental value expected on ethane (Branko, 2015). Given the importance of C–C pairs for the molecules of interest, we optimized the sigma bond dissociation parameter ($D_e^{\sigma }$) in the force field to 128.2 [see the Supplementary Information in Chenoweth et al. (2008) for the full ReaxFF energy expression]. This results in a sigma C–C bond dissociation energy value of 90.88 kcal/mol that is thermodynamically equivalent and almost within the experimental error bars (Table 1). All the ReaxFF bond dissociation energies of interest in this work were compared with the corresponding experimental values, for the species and reaction coordinates listed in Table 1, and to the full QC calculated bond dissociation curves using the configuration interaction (CI) method (see Supplementary Fig. S9 in the Supplementary Data). CI is a post-Hartree–Fock method for solving the nonrelativistic Schrödinger equation within the Born–Oppenheimer approximation for a quantum chemical multielectron system (see Section “Methods” in the Supplementary Data).

Table 1.

Experimental Versus ReaxFF-Predicted Bond Dissociation Energies

Bond	Reaction	ReaxFF DE(kcal/mol)	Exp DE(kcal/mol)	Method	ΔDE(ReaxFF-Exp)	ΔR0%	Year	Refs.
H–H	H2 → 2H	107.65	103.397 ± 0.001	Spectroscopic	3.713 ± 0.001	−1.351	1960	(Herzberg and Monfils, 1960)
H–O	H2O → H + OH	115.188	118.8 ± 0.002	Thermochem	3.612 ± 0.002	−1.042	2015	(Ruscic, 2015)
C–C	C2H6 → 2CH3	90.88	90.2 ± 0.2	Thermochem	−0.68 ± 0.2	−0.584	1983	(Kolesov and Papina, 1983)
C = C	C2H4 → 2CH2	154.0	170.15 ± 1.2	Thermochem	16.15 ± 1.2	1.0447	1990	(Ervin et al., 1990)
C–H	CH4 → CH3 + H	108.5	101.6 ± 2.0	Thermochem	6.9 ± 2.0	−4.954	2015	(Ruscic, 2015)
C–O	CH3OH → CH3 + OH	94.75	88.6	Thermochem	−6.15	−9.090	2015	(Ruscic, 2015)
C = O	H2CO → O + CH2	191.18	179.24 ± 0.036	Thermochem	11.95 ± 0.036	−7.500	2015	(Ruscic, 2015)
C–N	CH3NH2 → CH3 + NH	82.32	76	Thermochem	−6.32	−0.136	1967	(Wagman et al., 1967)
N–H	NH3 → H + NH2	117.64	103.96	Thermochem	13.68	−0.990	1958	(Cottrell, 1958), (Darwent, 1970), (Benson, 1965), (Kerr, 1966)

Underpredicted bond dissociation energy values have a negative ΔD_E (weaker) and overpredicted energy values have positive ΔD_E (stronger). The average ΔD_E for all reactions is 7.05 ± 3.439 kcal/mol and the standard deviation is 4.002 ± 3.1317 kcal/mol.

In ReaxFF, there are no explicit electrons, and hence, excited electronic states cannot be described and atoms move along the ground-state potential energy surface (PES). To determine a bond's state, the bond-order (aka bond-strength, for each type of bond) is computed as a function of interatomic distance, and this is then correlated to the pairwise energy. This avoids the expensive quantum calculations by casting computationally cheap analytic valence-bond interatomic potentials within the bond-order formalism, computed as a function of interatomic distances. To avoid discontinuities in the PES during bond dissociation and bond formation events, ReaxFF includes polarizable charge descriptions for all interactions. Corrections to remove spurious bond character between nonbonded neighbors, especially for highly compressed states during HVI, are included. Bond energy, and angle and torsion strains are calculated directly from the corrected bond orders and added to the nonbonded van der Waals and electrostatic terms.

This homolytic ground-state picture is a sound approximation for determining the velocity thresholds at which fragmentation occurs during HVIs, even though it is not necessarily accurate at higher impact energies in which electrons may evolve nonadiabatically. HVIs of molecules are dynamical events that can trigger many different fragmentation pathways. This means multiple variables will affect the outcome, including dynamic redistribution of molecular electronic clouds, that is, transient charge redistribution, dynamic changes to the ro-vibrational energy of the impacted molecule (i.e., “thermalization”), structural properties that condition how impact energy transfers and distributes across the different modes (translational, rotational or vibration) after impact, and changes to the bonding environment, including valency, hybridization, bond-order, caused by interactions with other molecules in the gas phase, or direct interactions with the impacting surface. This RMD method is able to describe all of the above, but not delocalizing electrons that can cause cascaded fragmentation or single bond dissociation events.

We now turn our attention to the target organic molecules of interest in this study, and how HVI can affect their integrity.

2.2. Neutral organic molecules in this study

To study the composition of Enceladus' plume as it pertains to habitability and the possibility of life in the subsurface ocean, we focus on the amino acids shown in Fig. 2. Amino acids are found in carbonaceous chondrites (Engel and Nagy, 1982; Shock and Schulte, 1990), and might be present as part of the organic inventory of outer solar system moons. The distribution of amino acids relative to glycine (Gly) has been invoked as a biosignature (McKay, 2004; McDonald and Storrie-Lombardi, 2006; Davila and McKay, 2014), due to the fact that in abiotic systems (such as carbonaceous chondrites), there is a correlation between Gibbs free energies of reaction and the observed rank in abundance of amino acids; that is, abiotic systems tend to produce the simplest amino acid (Gly) in abundances several orders of magnitude greater than others (Higgs and Pudritz, 2009), while life synthesizes a set of complex amino acids in greater abundance to utilize their diverse functional groups in proteins. Similarly, life also imposes a pattern on the building blocks of lipid membranes: fatty acids. In eukaryotes and bacteria, fatty acid synthesis proceeds via addition of carbon in units of two, producing aliphatic chains with even numbers of carbon atoms in much greater abundance than odd-numbered chains; for Archaea, aliphatic chains are produced by using isoprenoids, resulting in a five-carbon addition pattern (Berg et al., 2012; Georgiou and Deamer, 2014). Here we select a subset of fatty acids, representing a range of those commonly used by Earth-based organisms (C16–C26), including the saturated and unsaturated species shown in Fig. 3.

FIG. 2.

Selected amino acid molecular structures in this study, in their initial arbitrary orientations (in left to right and top down order, Ala, Arg, Asp, Cit, Gly, Lys, Orn, Ser, Thr, and Tyr). General properties included in the Supplementary Table S1. Carbon atoms are depicted in green, oxygen atoms in red, nitrogen atoms in blue, and hydrogen atoms in white. Color images are available online.

FIG. 3.

Selected fatty acid molecular structures in this study, in their initial arbitrary orientations (in left to right order, palmitic acid, oleic acid, and cerotic acid). General properties included in Supplementary Table S2. Color images are available online.

We explore the in silico survivability of these biosignature molecules, both as bare molecules and embedded within ice Ih clusters of different sizes, as Cassini measurements indicate that such molecules may be trapped within the ice grains of the Enceladus plume (Postberg et al., 2009, 2011, 2018b; Khawaja et al., 2019).

With the exception of Gly, which has no enantiomers, the amino acids considered in this work are the left-handed isomers given that fragmentation signatures are expected to be achiral in HVI and because of their role in biological processes associated with life as we know it. While a comprehensive in silico study of the vast inventory of ocean world molecules lies outside of the scope of this work, we include three isobaric (identical mass) species representing a cross section of possible functional groups (aromatic, ketone, and nitrile) in Titan's dense atmosphere: naphthalene, 2-octanone, and 1,3-dicyanobenzene (shown in Fig. 4). This was done to compare how structural differences with the amino and fatty acids affect fragmentation thresholds and pathways.

FIG. 4.

Titan-relevant (left to right order 1,3-dicyanobenzene, 2-octanone, and naphthalene) molecular structures in this study, in their initial arbitrary orientations. General properties included in Supplementary Table S3. Color images are available online.

In the following section, we describe the first-principles-based RMD protocols and simulations performed to determine the physicochemical phenomena that emanate from HVI of the species shown above. Details on the methods used can be found in Section 4.

2.3. Simulation protocols and procedures

We took the selected molecules presented in Figs. 2–4 and simulated the HVI dynamics described in Fig. 5.

FIG. 5.

Steps in HVI simulations of amino, fatty acids, and other molecules of interest (Gly at θ_in = 25° impact angle shown). Color images are available online.

The general procedure applied in this work involved using RMD simulations to study molecular impact dynamics phenomena over a range of velocities (v = 1−12 at 1 km/s resolution intervals) and analyzing the individual trajectory results. We note that the average translational kinetic energy for a single molecule in vacuum and at 100 K is negligible, that is, ½ m < v2> = (3/2)k_BT, where k_B corresponds to the Boltzmann constant, and T = PV/(nR) from the ideal gas law. On the contrary, the translational energy introduced by hypervelocities is not negligible. Using the kinetic energy of motion expression ½ m <V2>, or ½|p|²/m, where m is the molecular mass, p the momentum, and v the velocity, we can determine the kinetic energy difference for our velocity interval of 1 km/s and therefore confirm the dissociation energy (D_E) resolution provided by the force field. For the lightest molecule in this work, glycine (75.05 amu), this results in ½(1.247e − 25 kg)(1000 m/s)² = 6.2351e − 20 kg · m²/s², which is equivalent to 8.972 kcal/mol. For the heaviest molecule, cerotic acid (396.69 amu), this results in 3.293595925e − 19 kg m²/s² or 47.3887 kcal/mol. Our force field resolution is therefore accurate to one standard deviation of ΔD_E (4.002 ± 3.1317 kcal/mol) for capturing impact fragmentation differences at a 1 km/s velocity resolution for the molecular species in this study (Table 1).

In the process, we established the velocity threshold at which these molecules fragment on impact, v_f, and characterized the two velocity regimes, namely: (1) v < v_f, and (2) v > v_f. This approach was repeated for 17 different angles of impact (i.e., θ = 0°−85°:5°) with respect to the impacted surface normal, and in turn, for 1296 different molecular landings, orientations were evaluated per impact angle. The molecular landing orientations were defined via a movable coordinate frame ouvw with origin o fixed at the molecule's center of mass, and axes uvw initially aligned with the inertial reference frame axes xyz. The compounded rotations are given by the product R_y(φ)z(α), where R_y and R_z correspond to basic rotation matrices about y and z, respectively, φ = 0−175: 5 and α = 0−175: 5 (for a total of 36 × 36 = 1296 different landing orientations). Given that the inertial x axis corresponds to the direction of impact and that the impacted surface is atomically flat, we only sampled changes in orientation about the y and z axes starting from the initial (arbitrary) orientations shown in Figs. 2–4.

The protocol is schematically represented in Fig. 5 and involves 12 × 17 × 1296 = 108,864 different runs per molecule. All simulations were performed starting from structures equilibrated at the expected atmospheric temperature of 100 K. The gas temperature is estimated around 100 K, while it is 250 K at the instrument's vent. It then drops steeply due to supersonic expansion, and hence, our choice of 100 K. Equilibration meant obtaining atomic velocities that lead to a net zero center of mass momentum (translational and angular) and a Boltzmann distribution equivalent to the temperature setting of 100 K.

For each bare organic molecule, we study how the following conditions affect molecular fragmentation:

• •  impact velocity (v),

• •  angle of impact with respect to surface normal, and

• •  molecular landing orientation.

We discuss how these conditions lead to differences in scattering dynamics (v < v_f), input/output molecular energetics (v < v_f), fragmentation threshold velocities v = v_f, fragmentation species and pathways for v > v_f, and how ice shells around the organic molecules can lead to significant changes in v_f.

For the latter, we study HVIs of an amino acid embedded at the center of ice Ih (ice Ih) spherical clusters of different diameters (3.2, 6.4, 12.8, and 25.6 nm). This is to account for sampling of Enceladus' south polar plume, although grains in the plume go up to a few micrometers in size, and it is also highly relevant for Europa Clipper where the SUrface Dust Analyser (SUDA) instrument samples potentially organic bearing ice grains at 4−4.5 km/s. We claim that understanding the HVI in nanometer-sized grains will provide sufficient evidence to build constitutive relationship between impact velocity and grain size to extrapolate over to the larger grains.

The roughness of current metallic surfaces (e.g., TiO₂, Au, Pt) used in MS collection and detection elements is in the order of R_a = 5−20 nm (Hellwig et al., 2019). As the smoothness of surfaces improve, HVI landing orientation and impact angle effects for bare molecules will become more evident. Therefore, understanding these phenomena within an impact-surface-agnostic framework is essential to provide an unbiased benchmark for surface materials' optimization, that is, a reference point from which to optimize their surface properties by design. For this reason, we use a fixed Lennard–Jones 12-6 potential wall (see Section 4 “Reactive molecular dynamics HVI protocol” of the Supplementary Data for additional details) to characterize the HVI phenomena listed above for all the target molecules. A consequence of this simplification is that the translational kinetic energy before impact is primarily transferred into the molecules' translational, angular, and vibrational modes, that is, minor surface interactions.

Although materials exposed to HVI of molecules introduce a significantly larger number of physical and chemical degrees of freedom, their characterization and optimization are beyond the scope of this article. Suffice to say that surface roughness will affect the angular distribution of reflected molecules and their chemical interactions with the surface material will be a function of the angle of incidence and surface morphology, although this changes with fluence. We point out how impact surface material properties may lead to deviations from our results.

3. Results and Analysis

3.1. General anatomy of molecular impacts

We start by dissecting the general anatomy of molecular impacts at high velocities, using bare naphthalene to highlight key points that are addressed further across all molecules of interest.

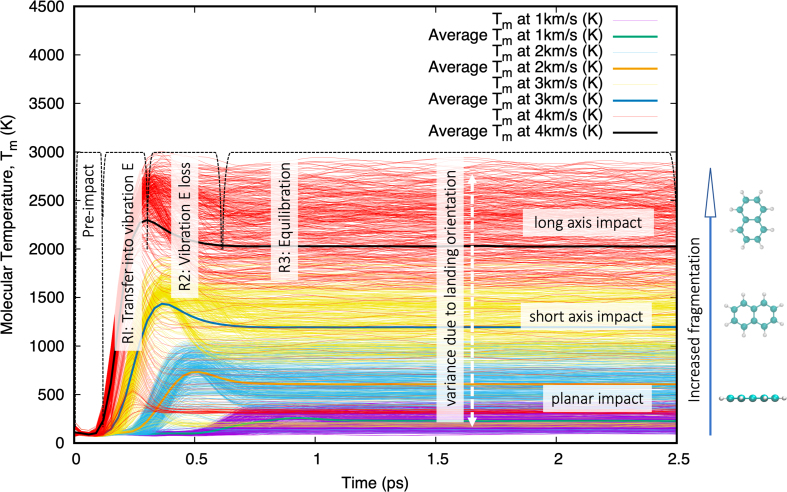
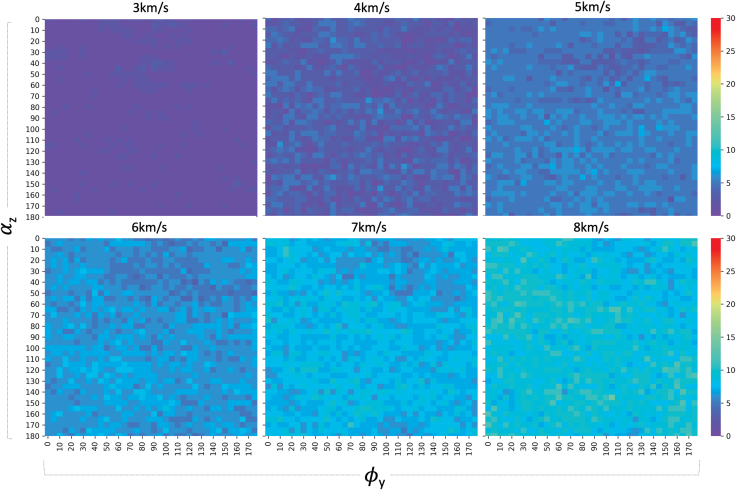
Figure 6 shows the internal molecular quasitemperature of naphthalene before, during, and after impacts at v = 1–4 km/s (v < v_f). Three identifiable regimes are observed:

FIG. 6.

HVI of naphthalene at different velocities, v = 1–4 km/s, shows how the energy transfer pathways are affected by molecular landing orientation on the impact surface. For clarity, only a subset of the impact trajectories is depicted, R_y(0:175:5) independently from R_z(0:175:5) for a total of 72 trajectories. The following different regions are identified in captions: R1: underdamped impact energy transferred into molecular vibrational modes, R2: vibrational energy loss decay into a steady state, and higher thermal equilibrium regime (i.e., faster particle velocities with respect to the molecule's center of mass). Color images are available online.

R1: Fast loss in translational kinetic energy, due to impact, quickly converted into vibrational kinetic energy (i.e., thermalization), through electronic excitations that decay in fractions of a picosecond. This is potential energy gain (+) through internal degrees of freedom.

R2: Fast covalent (dominant two-body bonds, minor three-body angles, and four-body torsions) and nonbonded energy transitions (Pauli repulsions) lead to an overdamped molecular response, characterized by fast rebound/repulsion [potential energy loss (−), i.e., binding energy recovery].

R3: Stabilization of the molecule's internal momentum, into a quasiequilibrium at higher vibrational energy states corresponding to molecular “thermalization.” In this case, v ≤ 4 km/s, no fragmentation events occur, and hence, we do not see any trajectory excursions.

No secondary, tertiary, or higher order collisions are assumed, and hence, no additional thermal energy dissipation is expected—this is a reasonable assumption considering the scattering dynamics of an expanding gas. The dynamic evolution of averaged internal energies (covalent and nonbonded) for these particular trajectories is shown in Supplementary Fig. S10.

It also follows from the depicted trajectories in Fig. 6 that:

• 1.The molecule's landing orientation affects how impact energy is absorbed into its vibrational, rotational, and translational degree modes (e.g., the vibrational energy gain order as a function of landing orientation for naphthalene is given by flat < short-axis < long-axis).
• 2.The initial atomic contact footprint of the molecule, along with the strength and number of surface-normal covalent interactions, provides an indication of the time it takes to transfer impact energy into all of the molecule's vibrational degrees of freedom and the maximum amount of impact energy that is effectively transferred to each mode/atom at any particular moment.

Naphthalene shows a ΔT_3−4km/s ≈ 750 K distributed among 18 atoms and 19 bonds, or 41.66 K/atom. This is higher that the ΔT_3−4km/s ≈ 900 K distributed among 26 atoms and 25 bonds or 39.4 7 K/atom for Arg (see equivalent Supplementary Fig. S1 in the Supplementary Data). The planar structure of naphthalene leads to three specific surface contact footprints: (1) flat or semiflat impacts with faster energy transfer yet lower “thermalization” (impact energy rapidly transferred and distributed among all degrees of freedom) without significantly affecting its equilibrium bond distances (and valence terms in general), (2) short-axis impact landings (with five sequential bonds along the surface normal direction, plus multiple three- and four-body valence interactions) with slower energy transfer and higher “thermalization,” and (3) long-axis impact landings (with six sequential bonds along the surface normal direction, plus multiple three- and four-body valence interactions). On the contrary, Arg has a longer, branched backbone topology, and hence, a larger number of impact energy transfer pathways and a low instantaneous impact footprint, meaning fewer atoms/bonds will receive the brunt of the initial impact energy. Of course, Arg has several exposed C–N bonds, which are weaker than the C–C and C = C bonds in naphthalene. All of the above lead to Arg having a lower v_f than naphthalene.

It should be clear then that molecular fragmentation thresholds depend on a number of intrinsic and extrinsic factors, besides the initial impact velocity. Some of these factors are discussed in the following sections, after establishing the velocity fragmentation thresholds (v_f) under maximum energy transfer conditions, that is, surface normal impacts.

3.2. Fragmentation velocity thresholds (v_f)

Normal impacts will cause the largest average projected stresses/strains on the bare impacting molecules, and hence, the lowest fragmentation threshold velocities v_f. We define v_f to be the velocity at which at least one covalent dissociative event persists, without recombination or subsequent reactions, for a minimum of 2 ps after a collision, over the entire set of molecular landing orientation angles.

Each molecule in Supplementary Tables S1–S3 was tested as outlined in Fig. 5 over every value of θ, φ, α, and v defined. The resulting trajectories were postprocessed by using the chemical bond-order information to determine the fragmentation velocity thresholds, the species, and number of fragments produced on every condition. The fragmentation velocity threshold results are tabulated in Table 2, based on the lowest velocity at which a single fragmentation event occurs, out of 1296 trajectories, or ≈0.772 ppt.

Table 2.

Velocity Fragmentation Thresholds, Established from Any Single Covalent Dissociative Event (of the One Thousand Two Hundred Ninety-Six Trajectories) Induced by a Collision Trajectory Lasting More than 3 ps

Name	vf(km/s)	Name	vf(km/s)
Ala	4	Palmitic acid	3
Arg	3	Stearic acid	4
Asp	3	Arachidic acid	4
Cit	3	Cerotic acid	3
Gly	3	Oleic acid	4
Lys	4	Oleic acid	4
Orn	4
Ser	3	Naphthalene	5
Thr	3	1,3-dicyanobenzene	3
Tyr	4	2-octanone	3

Velocity fragmentation thresholds increase by 1 km/s near 1% fragmentation. These results are directly from the count of fragment species produced by simulations at 1 km/s resolution intervals, and hence, no error bars are needed.

In spacecraft flythroughs of atmospheres or plumes, it is challenging to control the landing orientation of these molecules as they hit the spacecraft or its instruments; and hence, the reliance on statistical averages from multiple conformer trajectories.

The results shown in Table 2 imply that HVI-induced fragmentation cannot be interpreted solely from a bond-energy, bond enthalpy perspective, because there are multiple factors during HVI that affect how impact energy is transferred into any particular bond. By such norm, all the amino acids in this study would be expected to break at the threshold velocity required to break the weakest bond, that is, C–N, which is not the case. As a reference for comparison, Supplementary Table S4 of the Supplementary Data includes the average bond energies/enthalpies at 0 K for all the possible atomic pairwise bonds in the molecules involved in this study.

We now take a closer look at other factors that influence v_f, including angle of impact, molecular landing orientation, and fragmentation pathways.

3.3. Factors that influence v_f

We consider in this section how impact angle, molecular structure, and composition (topology and landing orientation, bonding structure, rotational and vibrational excitations, and energy transfer pathways), and enveloping ice-water structures lead to changes in v_f. The latter is of critical importance in the context of “ocean worlds,” such as Enceladus and Europa.

3.3.1. Angle of impact

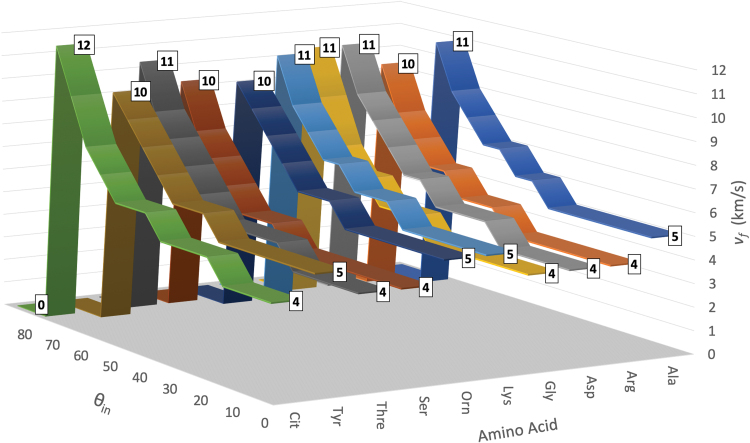
Increasing impact angles with respect to the impact surface normal reduces the net impact energy, thus increasing the velocity fragmentation thresholds v_f for all species—as shown in Fig. 7 (Supplementary Figs. S11 to S17 in the Supplementary Data provide additional results). This is important in the context of designing optimized molecular collectors in MS instruments, as described in Darrach et al. (2015), where concentric angled conical collectors enable gas molecules to specularly reflect in a single collision before exiting through the instrument's aperture.

FIG. 7.

Fragmentation velocity thresholds >1% for amino acids in this study, as a function of impact angle. Color images are available online.

It also changes how impact energy is transferred into the translational and ro-vibrational modes of the organic molecules. To analyze these effects, we explored the scattering thermodynamics for molecules with different v_fs (Arg, Ala, and naphthalene), but within v < v_f, specifically evaluating the gain in internal molecular temperature, linear and angular momentum, and torque—all quantities are expressed with respect to the molecule's center of mass.

Figure 8 (left) depicts the gain in vibrational energy, expressed as an instantaneous “molecular” temperature, that is, $T={\sum }_{i=1}^N{m}_i{v}_i^2∕k_B{N}_{dof}$, where N corresponds to the total number of atoms of the molecule, N_dof the molecule's total number of degrees of freedom (i.e., 3N), v_i is the atom velocity, m_i is the atomic mass, and k_B the Boltzmann constant. We observe that there is a larger transfer of translational to vibrational energy as the angle of impact gets closer to the surface normal. Naphthalene tends to have lowest vibrational gain, followed by Arg and Ala, respectively. This is most likely due to the fast energy dissipation through the aromatic C = C bonds. Ala has the highest average vibrational gain at 2 km/s and θ_in < 45°, despite its smaller mass. It also shows a constant rate of angular momentum loss for every θ_in > 0° at this velocity, as shown in Fig. 8 (left), while Arg and naphthalene tend to accelerate loss past θ_in = 30°. This would explain its faster ΔT loss rate at v = 2 km/s as a function of θ_in. Ala's relative topological symmetry and smaller radius of gyration reduce the length of energy dissipation pathways during near-normal impacts. Large gains in vibrational excitation during HVI can induce fragmentation before an MS's ionizing stage, and lead to altered biosignature measurements with higher intensities toward the low mass fragments.

FIG. 8.

(left) Internal temperature difference as a function of impact angle (θ_in) for Arg, Ala, and naphthalene over v = 1−2 km/s with standard deviation bars; (center) output/input momentum ratios as a function of (θ_in for the same species with standard deviation bars; and [right] angular momentum over the same) (θ_in range (errors bars removed for clarity). Color images are available online.

Momentum loss after impact is not only a function of molecular mass and body velocity. Molecular topology also plays a significant role, as evidenced from differences depicted between naphthalene (mass = 128.1705 g/mol) and Ala (mass = 89.09 g/mol) at v = 2 km/s in Fig. 8 (center), that is, naphthalene has ∼10% less momentum loss than Ala under surface normal impacts. All molecules exhibit momentum loss for increasing θ_in angles.

Figure 8 (right) shows the average angular momentum vector magnitude for the same molecules, as a function of θ_in. Angular momentum decreases almost linearly at v = 1 km/s for all species, before dropping close to 0 at θ_in = 85° for Arg and Ala. At v = 2 km/s, Arg and naphthalene exhibit a monotonically decreasing angular momentum θ_in that remains finite at θ_in = 85°, while Ala decreases linearly in the same range θ_in.

Figure 9 shows the evolution of molecular torque magnitudes as a function of θ_in for the amino acids, naphthalene, and 1,3-dicyanobenzene. Given that the torque magnitude is computed from the three directional vector components due to the forces on individual atoms of the molecule, with respect to its center-of-mass, it is directly associated with stresses imposed on its individual atoms on impact. Therefore, it provides an indication of how the molecule dissipates impact force, mainly via three- and four-body valence terms (i.e., angles and dihedrals). Initial torque magnitude at v = 1–2 km/s increases gradually for all molecules (except naphthalene) until it peaks past θ_in > 55° and then decreases rapidly thereafter. Naphthalene remains constant until θ_in = 45° and then falls off quickly. In contrast to the cases at v = 1 km/s, torque magnitudes at v = 2 km/s go down until θ_in = 45°, at which point they increase to peak and die off quickly past θ_in = 70°. The heavier and longer molecules (e.g., amino acids with more than six C atoms along the molecule's backbone, naphthalene, and 1,3-dicyanobenzene) peak in torque magnitude at high angles. This would indicate that heavier molecules could be ripped apart at high-impact angles, in some cases, easier than from a direct hit.

FIG. 9.

Torque curves for amino acids at v = 1 km/s (left), v = 2 km/s (center), and for naphthalene, and 1,3-dicyanobenzene at v = 1–2 km/s (right) as a function of θ_in. Color images are available online.

These results would favor instruments with conical capture apertures, suggesting the need to balance the angle of impact with the sampling velocities, that is, θ_in < 45° and v > 2 km/s. This would involve establishing a capture angle sweet spot that minimizes the vibrational excitation gains and the induced torque after impact, that is, the maximum angle at which torque is minimum, while avoiding multiple collisions in the funnel.

Increasing impact angles (θ_in), therefore:

• • increase v_f by reducing the surface normal kinetic energy component and overall molecular thermalization,

• • increase v_f by reducing the output/input momentum ratio (hence the kinetic energy output/input ratio), and

• • can decrease in v_f due to increased molecular torque magnitudes at high θ_in.

Of course, these effects can be exacerbated or quenched by the choice of surface morphology and material, as discussed later.

3.3.2. Molecular structure and composition

Molecular structure and composition effects on v_f can be observed through different physical quantities associated with molecular HVI events. Some are readily available to experiments, such as output/input energy ratios and scattering angles, while others are not directly accessible (e.g., landing orientation effects, energy partitions between translational, rotational, and vibrational modes). Here, we explore the former and include fragmentation pathways through heatmaps that illustrate the effect of molecular landing orientation that are beyond experimental capabilities.

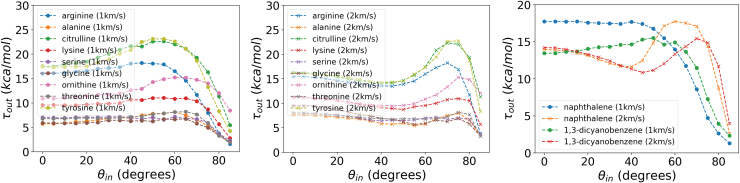
Figure 10 presents the kinetic energy output/input ratios as a function of impact angle, for v = 1−2 km/s. The order in which this ratio changes for the different structures as a function of v provides additional evidence to support how impact energy is transferred through different pathways for the same molecule, as a function of impact velocity. In general, higher impact velocities and higher impact angles lead to higher output/input energy ratios. However, the percent change toward higher velocities, shown in Fig. 11, is primarily driven by molecular mass, although with some notable exceptions such as Gly, Ser, Naph, and Tyr. This seems to imply that the role of structure and topology in momentum transfer becomes less dominant as we move toward v_f, although for an ideally flat impact surface.

FIG. 10.

Output/input kinetic energy ratios for all amino acids and naphthalene, as a function of θ_in for v = 1 km/s (left) and v = 2 km/s (right). The center inset ranks the energy ratios by descending value (i.e., a rank of 1 corresponds to the least energy lost upon impact) at θ_in = 0°, for v = 1−2 km/s. Color images are available online.

FIG. 11.

Percent change in output/input kinetic energy ratios for amino acids and naphthalene molecules between v = 1–2 km/s at θ_in = 0° shows that mass dominates the Δ%, with exceptions in Gly, Ser, Naph, and Tyr. Color images are available online.

Molecular structure differences will also induce changes to the scattering dynamics as a function of v and θ_in. Scattering angular distributions are larger for planar geometries (e.g., naphthalene) and narrower for increasing velocities.

3.3.2.1. Fragmentation patterns and pathways

Molecular structure and composition also condition fragmentation pathways/patterns. This is shown here via two-dimensional (2D) fragmentation heatmap matrices, for which each (row, column) pair represents the number of fragments at a particular impact velocity for the entire set of landing orientation angle pairs, R_y(φ) and R_z(α). Figure 12 shows maps for Arg between v = 3–8 km/s, Fig. 13 maps for Gly between v = 3–8 km/s, and Fig. 14 for Naph with matrix columns representing impact velocities v = 6−9 km/s and rows θ_in = 0°, 25, 50°. For each case, the poses that lead to initial fragmentation at the corresponding v_f are shown as numbered insets.

FIG. 12.

Arg 2D fragmentation heatmaps as a function of variations in landing orientation about y and z and v for normal impacts. This shows the number of smaller fragments from a single parent molecule. There are no fragmentation events for v = 1, 2 km/s. Heatmap colors (as shown on the right-hand side of the figure) correspond to the number of fragments, α_z to the angle change about the z axis, and $\varnothing$_y to the change about the y axis (all changes with respect to initial arbitrary positions and the coordinate frames depicted in Fig. 2). 2D, two dimensional. Color images are available online.

FIG. 13.

Gly 2D fragmentation heatmaps as a function of variations in landing orientation (about y and z) and v for normal impacts. This shows the number of smaller fragments from a single parent molecule. There are no fragmentation events for v = 1, 2 km/s, and so, these maps are not shown. Colors and axes are the same convention as those in Fig. 12. Color images are available online.

FIG. 14.

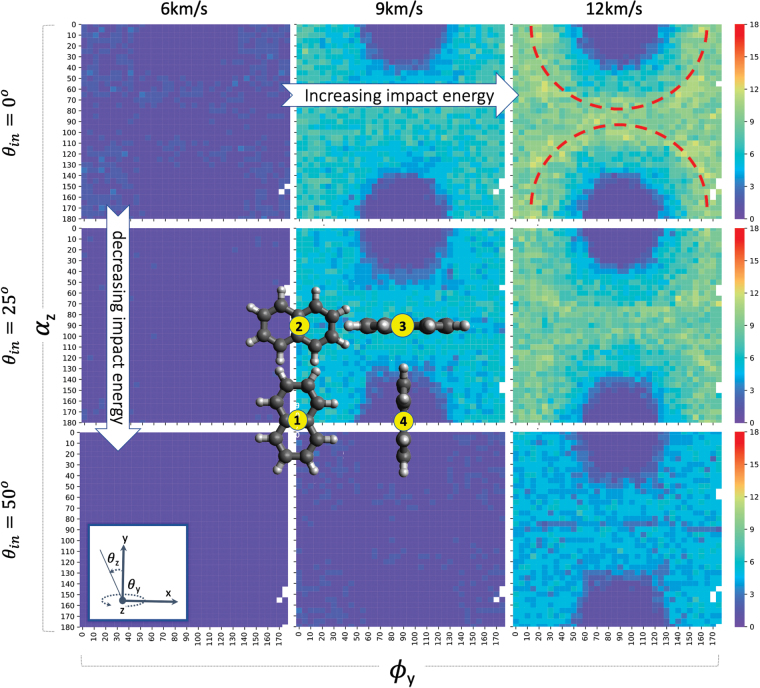
Naphthalene fragmentation patterns at v = 6, 9, 12 km/s for impact angles θ_in = 0°, 25, 50°, as a function of molecular impact landing orientation. This shows the number of smaller fragments from a single parent molecule. Inset figures correspond to different landing impact orientations of naphthalene, namely: ① R_y(0)z(0), ② R_y(0)z(90), ③ R_y(90)z(90), and ④ R_y(90)z(0). The impact direction is to the right of the page. The dotted lines in the subfigure for v = 12 km/s and θ_in = 0° show that the maximum fragmentation occurs slightly off the long and short axis of the molecule. Colors and axes are the same convention as those in Fig. 12. Color images are available online.

Two- and three-dimensional heatmaps for the other species are included for reference in the Supplementary Data.

Figure 12 shows a nearly symmetric fragmentation surface across all y and z landing orientations, with fragmentation onset at v ≈ 3 km/s. Arg has four exposed C–N bonds (weakest in our Supplementary Table S4) that will be invariably impacted from every orientation, once the fragmentation threshold velocity is reached. By contrast, Gly reveals a very asymmetric heatmap across the different orientations (Fig. 13). Gly is much shorter and has a single C–N side and a single C–O side, which have fragmentation energies that differ by ≈12 kcal/mol; the fragmentation asymmetry is most likely a function of landing orientation.

In Fig. 14, we add the effect of θ_in to show the expected increase in v_f as the impact angle increases with respect to the surface normal. There are minor but noticeable effects on the fragmentation patterns for different impact angles. Particularly noticeable is the near-zero fragmentation along R_z = 90° for all R_y and θ_in = 50°(image in row 3, column 3).

Under thermal equilibrium conditions, the equipartition theory tells us that energy is shared equally among all of its various forms (i.e., translational, rotational, vibrational). Therefore, weaker bonds are expected to break first, within a purely thermal decomposition scenario.

This no longer holds in the highly nonequilibrium conditions of HVI.

These heatmaps provide visual qualitative evidence on how fragmentation pathways vary as a function of velocity and molecular structure/composition (via changes in the molecular impact landing orientation).

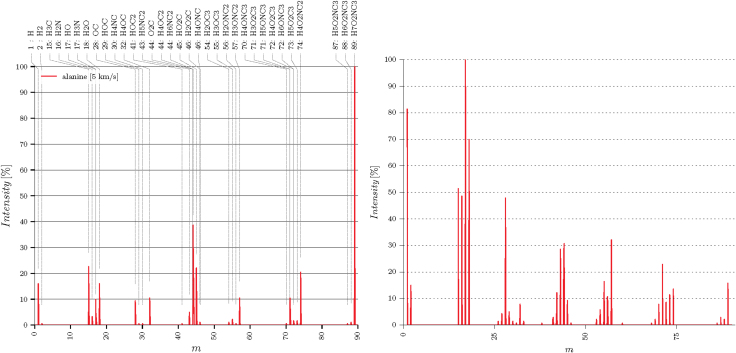
Additional quantitative details can be obtained directly from the RMD-simulated trajectories, specifically from the number and type of chemical subspecies produced after an impact. The quantitative information on the fragments produced enables determination of pseudomass spectrum plots, constructed from the statistical distribution of subspecies with intensities normalized to the parent mass over 1296 trajectories. Keep in mind that the intention here is not to reproduce the standard electron-impact ionization stage in an MS, but the effect of HVI-induced fragmentation on posterior MS results. These pseudomass spectra allow us to predict how the parent species can change due to HVI before they enter an MS detector. Figure 15 shows the pseudo-MS computed for Ala HVIs at v = 4 and 5 km/s, and how higher impacts exceeding v_f lead to an increase in the lower mass intensities.

FIG. 15.

Pseudomass spectra for Ala at (left) v = 5 km/s and (right) v = 6 km/s, obtained from HVI ensemble averages. Intensities in the latter show a shift in the lower mass fragment intensities due to increased impact energy. Color images are available online.

As observed in Fig. 8, HVI sampling of molecules will induce significant “thermalization” via vibrational excitations. Depending on the MS setup used, for example, in the absence of an accommodation and equilibration chamber after initial impact, this may also lead to significant MS data alterations. To demonstrate this, we studied the regime v < v_f and the contribution of vibrational excitations on impact for the ionization stage results of an MS. This requires capturing electronic excitations to describe single-electron impact-induced ionization, which is beyond the RMD capabilities. To overcome this, we use ab initio quantum mechanical molecular dynamics calculations and adapt the statistical approach introduced by Grimme (2013) to predict single-electron MS (SE-MS) in six steps:

• 1.Perform a dynamical conformation search of the parent molecule (M) using RMD with a canonical nVT ensemble dynamics (i.e. constant number of particles, n, constant volume, V, and controlled temperature, T) at a temperature of 500 K, to produce a randomized ensemble of neutral ground state structures.
• 2.Determine the amount of average “thermal” gain (ATG) from the RMD HVI simulations for different impact velocities (above an equivalent reference energy of 500 K).
• 3.Assign the ATG as an “excess” substrate temperature and apply an ionization excess energy (IEE) to each random initial structure of M to instantaneously ionize it (i.e., the ground state of M*⁺), assuming a Poisson distribution chosen to max IEE per atom at 0.6 eV.
• 4.Propagate each ionized structure over the M⁺ PES and compute the corresponding fragmentation pathways on the fly, using the semiempirical ab initio molecular dynamics approach from Grimme (2013).
• 5.Track secondary, tertiary, and so on fragmentation events.
• 6.Count fragments according to statistical weight, to produce a calculated single-electron impact MS.

Figure 16 (left) shows the predicted SE-MS produced for naphthalene after a direct impact at v = 1 km/s (assuming a vapor substrate temperature of 500 K within the ionizing chamber of an MS) and Fig. 16 (right) shows the SE-MS for naphthalene after a direct impact at v = 2 km/s. The 300 K difference observed from Fig. 8 between 1 and 2 km/s at θ_in = 0° for naphthalene was used as thermal gain above the 500 K reference (i.e., 800 K net temperature). Differences in the fragmentation patterns and trajectories after the initial ionization event are included for reference in the Supplementary Figs. S2–S7 of the Supplementary Data, as well as additional details on the calculations performed.

FIG. 16.

The HVI-induced increase in vibrational excitations, equivalent to a 300 K thermalization, observed in Figure 8 for naphthalene impacts between v = 1–2 km/s, causes an increase in lower mass fragment intensities (25–50) of the single-electron MS (left corresponds to v = 1 km/s and right to v = 2 km/s). Predicted MS shown in black lines, compared with experimental MS data from the National Institute of Standards and Technology (NIST) Standard Reference Database, shown in brown lines (https://webbook.nist.gov/cgi/cbook.cgi?Name=naphthalene&Units=SI). MS, mass spectrometer. Color images are available online.

The primary electron impact process leads to an excited ion state (M*⁺) that relaxes very quickly (0.5–2 ps) by internal conversion to a vibrationally hot ion ground state. Therefore, the nuclei can be propagated classically on a Born–Oppenheimer PES. The fragmentation simulation is therefore guided by the gradient of the PES on the fly without any prior knowledge of the decomposition pathways. The trajectories obtained provide energetically accessible paths through a vast chemical reaction space of unimolecular decomposition reactions of neutral molecules and radical anions.

We now turn our attention to the HVI of ice-encapsulated organic molecules.

3.3.3. Ice shells

Given the effect of ice-shells on the decomposition or racemization of organic molecules during HVI, it is essential to understand their behavior during HVI. This is particularly relevant for studying MS data collected during hypervelocity flythroughs of the plume of Enceladus and Europa, where such plumes may be sourced from subsurface liquid water oceans, as argued compellingly for Enceladus from Cassini data (Postberg et al., 2009, 2011). The Europa Clipper mission will sample ice grains ejected at hypervelocities by micrometeroid impacts from Europas' surface, even in the absence of a plume.

The ice grains analyzed by the Cosmic Dust Analyzer (CDA) instrument aboard Cassini can be classified into three types: Type I grains are almost pure water-ice, Type II grains contain either organic or silicate impurities, and Type III grains are salt-rich, comprising 0.5–2% sodium and potassium salts by mass. Type I grains likely form via homogeneous nucleation from the gas phase; the Type III salt-rich grains likely form via flash-freezing of ocean water, and therefore may be more representative of the composition of the ocean. A subset of the Type II grains (∼12%, which corresponds to this is about 3% of all grains measured by CDA) contain significant amounts of organic molecules (1% by mass); these organics appear to be unsaturated and partially aromatic, and contain both C–C and C–N double and triple bonds (Postberg et al., 2018a, 2018b).

Although the process by which ice forms around organic molecules remains poorly understood, several studies have attempted to elucidate the pathways/processes. Postberg et al. (2018b) suggested a possible formation mechanism for the formation of the Type II organic-rich grains observed in the Enceladus plume. They hypothesized that bubbles bursting from an organic-rich layer at the ice/ocean interface could entrain nonvolatile organic molecules—similar to how sea spray aerosols form on the Earth (Porco et al., 2017; Postberg et al., 2018b). These small organic droplets would then be coated with water-ice condensing from the vapor phase as they together ascended in the plume. Alternative hypotheses for the entrainment of organic molecules in ice include the proposition that the formation of large icy bodies in oceanic conditions could concentrate the building blocks of life, including amino acids, in eutectic fluids (Sanchez et al., 1966). This would suggest that they do not mix well in ice structures.

Recently, Hao et al. (2018) conducted freezing experiments that rebuke the generality of this eutectic assumption, by allowing ice Ih crystals to grow slowly from a few seeds in equilibrium with an aqueous solution analogous to seawater with certain nonpolar amino acids, and demonstrated that considerable amounts of the latter existed in the ice Ih phase. Ice Ih is also thermodynamically stable on the surface of Saturn's icy satellites (Hendrix et al., 2018).

It is unlikely that ice clathrate hydrate structures would be carriers of amino or fatty acids in these “ocean worlds”—at least not in Enceladus. The data obtained from Cassini-Huygens' INMS show that a large portion of the sampled plumes is mostly H₂O (>90.01 volume mixing ratio) (Waite et al., 2009). Most common clathrate structures [types I or sI, II or sII, and H or sH (von Stackelberg and Muller, 1954; Ripmeester et al., 1987)] would require ∼85% (mol) water and 15% gas (Sloan, 1998). Furthermore, even though abnormal incorporation of the nonpolar amino acids in the crystal lattices is possible (Sa et al., 2014), only a few amino and fatty acids would fit by size into the larger clathrate cavities—from our estimates, alanine and glycine [with van der Waals volume of 67 ų and 48 ų, respectively (Darby and Creighton, 1993)].

We therefore explore organic molecules entrained within ice Ih next.

3.3.3.1. HVI of amino acids incorporated in ice Ih nanoclusters

To determine the effect of ice shells surrounding an amino acid on the fragmentation velocity threshold of the former, we applied the procedure described in Section 2 (although limited to surface normal impacts) to spherical ice Ih NPs of different diameters (Table 3). The spherical ice structures were prepared from a supercell of the basic ice Ih unit cell structure, and cut to a spherical form for each diameter; any water subspecies or water molecules without paired hydrogen bonds were then removed. The average ice Ih density was confirmed from the periodic cell to be ρ₀ = 0.916723 g/cc, which is consistent with the experimentally reported density for ice Ih, ρ_exp = 0.917 g/cc (Atkins and de Paula, 2010). Arg was chosen as the guest molecule because of its relatively low v_f on bare impacts (Table 2); Arg has also been invoked as an indicator of active or recent production in the Enceladus ocean, as it may not persist over geologic timescales (Truong et al., 2019). We use the anionic (deprotonated carboxy group) amino acid form of Arg as the representative structure of basic saltwater system expected in “ocean worlds” (pH between 7.6 and 8.4, Enceladus is expected to have a pH >8) (Postberg et al., 2009; Glein and Waite, 2020), and assume that the solvated structures are formed via bubbles bursting followed by condensation of water-ice, without any chemical interactions with salts.

Table 3.

Ice Ih Nanoparticle Diameters and Average Number of Atoms per Nanoparticle Used in This Work

Average NP diameter (nm)	Average atoms per NP with Arg
3.2	1288
6.4	11,342
12.8	93,954
25.6	772,824

NP = nanoparticle.

The zwitterion of l-Arg was prepared separately and equilibrated at 100 K, with a single stabilizing water molecule, as shown in Fig. 17. We confirmed using our RMD simulations that this particular zwitterionic form is thermodynamically more stable than the canonical form in the gas phase at 100 K, thanks to the strongly basic guanidine side chain (Im et al., 2008), and within the expected water-solvated oceanic conditions of Enceladus or Europa. Although solvated cationized Arg zwitterionic forms are also possible, for example, sodiated, hydration of the metal ion in these clusters weakens the interactions between the metal ion and the amino acid, with little to no effect on the hydrogen-bond strengths between the amino acid and its stabilizing water environment (Bush et al., 2007).

FIG. 17.

Timed snapshot sequence during an ice Ih+arginine cluster HVI at v = 5 km/s shows (a) an Arg zwitterion with a single stabilizing water form inserted and equilibrated at the center of an ice Ih sphere at t = 0, right before impact, (b) the shock wave reaching the Arg molecule by t = 1 ps, (c) passing through the Arg molecule at t = 1.2 ps, and (d) the tension/expansion phase after t = 3 ps. It is under this last phase that fragmentation takes place. Color images are available online.

The anionic Arg with its water molecule was then inserted at the center of each ice Ih nanoparticle model, removing the excluded volume, that is, all water molecules within a van der Waals radius of the amino acid shell (2.4°Å). To determine the minimum energy conformation of the system, the Arg was rotated about each one of the principal axes of the ice Ih nanoparticles, at 15° intervals, in a roll–pitch–yaw rotational convention. The full system's geometry was then reoptimized for every case, using a conjugate gradient algorithm, with a convergence criteria set to 1e-6 RMS force or 1e-6 energy difference, and re-equilibrated at 100 K for 5 ps. The 1728 conformers were then ranked by total average energy, to select the lowest energy conformer for the HVI simulations reported next.

The full HVI simulation protocol was then executed as described in Sections 2 and in the “Methods” section of the Supplementary Data.

Figure 17 shows a sequence of snapshots that track the anatomy of ice-borne impacts.

Several distinct domains characterize the anatomy of ice-borne HVIs, as depicted in Fig. 18, but overall there is a stopping domain and a shock wave back-propagation domain. The stopping domain occurs between the moment of impact and the moment the impactor is either slowed or its direction reversed (Jaramillo-Botero et al., 2013), marked as numeral 4 in Fig. 18. The shock wave propagation domain, on the contrary, refers to the shock wave traversing through the NP while it excites the different vibrational modes of the system. The question that then arises is whether the ice shells can dissipate enough impact energy to protect embedded organic guest molecules. If so, by how much can ice extend v_f?

FIG. 18.

(Left) General anatomy of an HVI of an amino-loaded ice Ih NP. (left) Center of mass v_x component and x position with respect to the wall as a function of impact velocity shows different regimes: (1) preimpact, (2) impact onset, (3) shock wave front reducing the center of mass velocity of the embedded organic guest, (4) density behind shock transitions to maximum stopping power, (5) organic guest pushed backward at peak density and tension-phase onset, and (6) full expansion regime leading to water and organic guest fragmentation; (right) time evolution of Arg zwitterion's position and velocity during HVI at different impact velocities (magnitude quantities shown). NP, nanoparticle. Color images are available online.

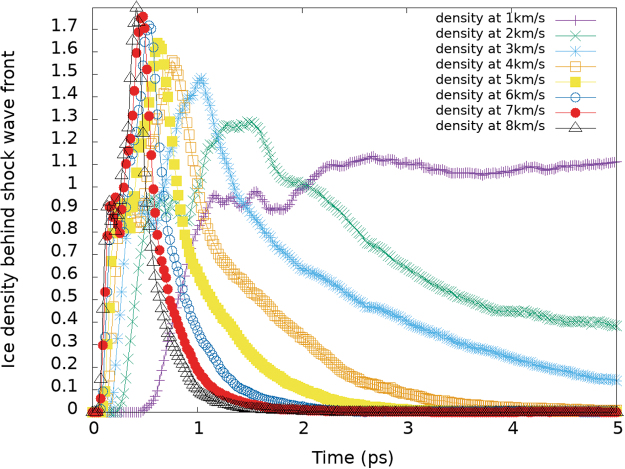
On impact, we observe a curved shock front that tracks the inverted image of the particle surface, with a shock velocity front U_s moving in the opposite direction to the preimpact particle velocity U_p. To track the density of the compressed portion during the HVI, we established a thin region of constrained volume, between x_low = wall(−10): x_high = wall(−5), y_low = −5: y_low = 5, and z_low = −5: z_low = 5, for a total volume of 500 ų (as shown in Fig. 19). Figure 20 shows the evolution of material density behind the shock wave front during 5 ps.

FIG. 19.

A color-coded (x direction) ice Ih cluster with diameter = 4 nm before and during impact, relating the physical quantities (P, V, E, and ρ) within the uncompressed and compressed regions, the shock front propagation in the opposite direction to the particle velocity. Color images are available online.

FIG. 20.

(Left) Density behind the shock wave front of a 3.2-nm-diameter ice Ih particle, with an embedded Arg guest, subjected to HVI in the range of v = 1–8 km/s. Given the spherical shape of the NP and the fixed region chosen to compute the density near the wall, the density starts at zero, rapidly increases to the material's density (small kink at around 0.92 g/cc), peaks at around 1.8 g/cc (for v = 8 km/s), and then exponentially decays as the molecules are dispersed away from the fixed volume region. Color images are available online.

When the shock wave reaches the Arg, it reduces its translational velocity (v_x) with a driving force that is proportional to the density distribution. This force maximizes at the peak of the density distribution (i.e., the shock-induced entropy change peaks when the full diameter of the nanoparticle is affected). Although this stopping domain is the main contributor to extending the molecule's v_f, as shown in Fig. 21, fragmentation at v_f does not take place during the compression phase, but rather in the tension/expansion phase. The amount of thermal (vibrational) energy transferred by the passing shock wave into the Arg will also reduce the barriers to bond dissociation, but it is ultimately the amount of tension force driving the expansion phase after impact that defines v_f. This tension force can be exacerbated by the decompressing water molecules, some of which may form radicals under sufficient impact energy.

FIG. 21.

HVI of ice Ih clusters of different diameters with an embedded Arg zwitterion molecule shows an increase in v_f compared with bare Arg impacts (v_f = 3 km/s), and an increase in the exponential prefactor to fragmentation percentage as a function of increasing impact velocities (i.e., steeper fragmentation curve after v_f). These results are in direct agreement with Klenner et al. (2020b). Color images are available online.

To summarize this section:

• • Ice water shells will dissipate HVI energy on embedded organic molecules, by adding as much as 2 km/s to v_f at 12.8 nm from the organic molecule to the outer shell.

• • Fragmentation occurs during the tension (material expansion) phase, as opposed to the compressive phase of an HVI event.

• • There is an exponential increase in fragmentation percentage (after v_f) that grows for increasing v (indicated by the inset text in Fig. 21) that is most likely due to an exponential increase in the number and magnitude of tensile forces affecting the organic molecule. Water molecules will be imposing tensile forces on the organic molecule from all directions, a phenomenon that could also be explained by the strong electric dipole of the water molecule (Wiederschein et al., 2015). This behavior is highly indicative of an impact velocity limit at which embedded organic molecules will always fragment, independently from the amount of surrounding ice (this will avoid the need to model micron-sized clusters).

• •  Although water O–H dissociation occurs at near 5 km/s, the expansion into vacuum after impact reduces the probability of secondary reactions of the embedded organic molecules with oxygen, although this will depend on the setup.

We are currently working on an approximate analogy to the single shock Hugoniot relationship to correlate U_s and U_p velocities at the peak of the density distribution, with the molecular bonding energies. We expect this will allow us to determine the mechanisms that drive the fragmentation of organic molecules embedded in ice clusters. This will be the topic of a separate publication.

3.4. On the force field's accuracy and results

Table 1 provides a measure of the accuracy of the force field and its impact on fragmentation results. As discussed in Section 3, a ΔD_E = 7.05 ± 3.439 kcal/mol with respect to experimental values is within the velocity 1 km/s resolution of our simulated experiments. In other words, fragmentation differences within this velocity interval will be captured and discriminated by the force field, for all of the species involved in this study. Furthermore, bond lengths are accurately predicted by ReaxFF (most within a 5% deviation from experimental values, except for C–O and C = O, which are within 10%). Therefore, the accuracy of the predicted dissociation energy and of the potential energy curvature (forces) near the ground state minima (bottom of the well is consistently reproduced by ReaxFF in comparison with CI) provides confidence in these results, under the HVI conditions explored by this work.

Although dissociation energy thresholds will ultimately drive the fragmentation results, atomic connectivity in ReaxFF is sensitive to the pairwise specific bond-order cutoffs used. Here, we have applied a default (de facto standard) bond order cutoff of 0.3 for all species and to avoid transient fragments from the dynamics of vibration after impact, we tallied species that remained bonded over the last 1 ps.

In terms of the specific interactions, we expect that the overpredicted binding energy for C–O and C = O could represent a lower count of product species containing these bonds, and this should be taken into account when reading the MS data produced from these simulations.

Last but not least, the standard ReaxFF engine used here is not meant to capture the nonadiabatic nature of HVIs that lead to a significant amount of ionizing fragmentation, and so, the upper range of velocities (beyond 8 km/s) should be read with a reduced degree of confidence.

4. Conclusions

We have conducted high-fidelity simulations of the fragmentation of small organic biosignature molecules and predicted the mass spectra of the parent plus fragments, using the first-principles-based approach. We find the following:

• Amino acids do not break at v_f required to break the weakest bond, that is, C–N.

• Equipartition theory no longer holds in the high nonequilibrium conditions of HVI (i.e., energy is no longer shared equally among all of its various forms during the first few picoseconds of an impact, and this could drive fragmentation.

• The fragmentation fraction is a sensitive function of impact angle for some species and not others, which highlights the importance of molecular structure on the scattering and fragmentation dynamics of neutrals.

• The heavier and longer species could be ripped apart by high torques at shallow impact angles, in some cases, easier than from a direct hit.

• In general, there is no such thing as a chemically “inert” surface, and the effect of both static and dynamic roughnesses need to be considered based on the expected chemical environment to be sampled at hypervelocity, for these may (positively or negatively) influence the amount of impact energy dissipation, scattering angle distributions, surface chemistry, and ultimately v_f.

• Minimal to no fragmentation occurs for velocities below 3 km/s for bare molecules, or below 4 km/s for ice grains above 6.4 nm in diameter encapsulating Arg, while interpretable fragmentation pathways and mass spectra are generated for values considerably higher.

• Encasing organic molecules in ice grains, as would likely be the case for those samples in the Enceladus plume and Europa's atmosphere, preserves molecules at even higher velocities, by as much as 2 km/s more for grains of 25.6 nm in diameter.

• The shock wave that results from HVI on ice Ih cluster dissipates the impact energy partially through thermalization of the guest organic molecule; it is ultimately the tensile forces caused by the expansion phase that drives the v_f in the embedded organics, that is, water molecules and atoms bouncing back from the wall and hitting the organics.

These results are consistent with a recent experimental study recommending plume encounter velocities of 4–6 km/s to sample amino and fatty acids using laser-induced ionization that simulates the impact ionization and analysis via mass spectroscopy (Klenner et al., 2020a).

Additional work is needed to evaluate the velocity limit at which water ionization could affect biosignatures through radical interactions, although secondary reactions during the expansion phase into a lower density gas are not expected to be significant. Work is underway to benchmark this study with additional laboratory experiments (Cable et al., 2012; Hörst, 2017). A second article discusses the ice-protected cases in more detail and how these results would extrapolate to micron-sized ice clusters more representative of the ice grain size distribution of the Enceladus plume, and a third article will focus on the collector or detector surface effects on v_f.

Abbreviations Used

ATG

average “thermal” gain

CDA

Cosmic Dust Analyzer

CI

configuration interaction

GVB

generalized valence bond

HVI

hypervelocity impact

IEE

ionization excess energy

INMS

ion and neutral mass spectra

MS

mass spectrometer

NP

nanoparticle

PES

potential energy surface

QC

quantum chemistry

QM

quantum mechanics

RCI

restricted configuration interaction

RMD

reactive molecular dynamics

SE-MS

single-electron MS

Author Disclosure Statement

No competing financial interests exist.

Funding Information

Jet Propulsion Laboratory Research and Technology Development Program.

Supplementary Material

Supplementary Data

Supplementary Figure S1

Supplementary Figure S2

Supplementary Figure S3

Supplementary Figure S4

Supplementary Figure S5

Supplementary Figure S6

Supplementary Figure S7

Supplementary Figure S8

Supplementary Figure S9

Supplementary Figure S10

Supplementary Figure S11

Supplementary Figure S12

Supplementary Figure S13

Supplementary Figure S14

Supplementary Figure S15

Supplementary Figure S16

Supplementary Figure S17

Supplementary Table S1

Supplementary Table S2

Supplementary Table S3

Supplementary Table S4

Associate Editor: Christopher McKay