Abstract
While facial coverings reduce the spread of SARS‐CoV‐2 by viral filtration, masks capable of viral inactivation by heating can provide a complementary method to limit transmission. Inspired by reverse‐flow chemical reactors, we introduce a new virucidal face mask concept driven by the oscillatory flow of human breath. The governing heat and mass transport equations are solved to evaluate virus and CO2 transport. Given limits imposed by the kinetics of SARS‐CoV‐2 thermal inactivation, human breath, safety, and comfort, heated masks may inactivate SARS‐CoV‐2 to medical‐grade sterility. We detail one design, with a volume of 300 ml at 90°C that achieves a 3‐log reduction in viral load with minimal impedance within the mask mesh, with partition coefficient around 2. This is the first quantitative analysis of virucidal thermal inactivation within a protective face mask, and addresses a pressing need for new approaches for personal protective equipment during a global pandemic.
Keywords: COVID, face mask, reverse‐flow reactor, thermal inactivation, virus
1. INTRODUCTION
Face masks reduce the rate of person‐to‐person transmission of coronaviruses, influenza, and other respiratory viruses from breath and coughing. 1 , 2 , 3 During the COVID‐19 pandemic, widespread adoption of effective masks has led to improved health outcomes around the world. 1 , 4 Face masks, however, are not uniformly effective in preventing person‐to‐person viral spread, and availability during the COVID‐19 pandemic has often been limited. 3 An overwhelming majority of masks that have been employed during the pandemic, including N95 respirators, reduce viral transport by mechanical filtration at ambient temperature. 5 In contrast, there has been a dearth of versions designed around thermal viral inactivation and sterilization of air flow.
As an engineering problem, the cyclic reversal of air flow associated with human inhalation and exhalation enables a particular chemical reactor design: the reverse‐flow reactor. A reverse‐flow reactor 6 , 7 , 8 , 9 periodically reverses the direction of the convective feed through a one‐dimensional reactor, typically a packed bed, to propagate a reactive zone over lengths that exceed the physical dimensions of the reactor. After the first patent filing by Frederick Cottrell in 1935, 10 reverse‐flow reactors have been used industrially for nearly a half century and are well‐studied. 6 , 8 , 11 , 12 This type of reactor offers several advantages when compared to unidirectional packed bed reactors. Depending on the frequency of flow direction switching, the reaction zone for an exothermic reaction can extend beyond the physical limits of the reactor in both directions, increasing conversion, reducing the need for heat exchange, limiting reactor fouling, 6 and improving stability to fluctuating inputs. 11 Coupling between heat and momentum transfer results in several periodic steady states. 12 While canonical reverse‐flow reactors involve exothermic reactions, reverse‐flow reactor designs can be applied to endothermic and mixed endothermic‐exothermic systems as well. 12 In the case of a heated mask, the reaction (i.e., thermal inactivation of SARS‐CoV‐2) is not appreciably endothermic or exothermic, decoupling the temperature profile from the extent of reaction. In a strict sense, this eliminates some of the advantages of a reverse‐flow reactor design. The reverse‐flow concept in a virucidal mask, however, is imposed by the oscillations of human breath, not consciously selected by the engineer. Concepts taken from reverse‐flow reactors, particularly the idea of distinct operating regimes delineated by bifurcation variables, 7 can be applied to a heated mask and yield insight to its design.
A heated mask to inactivate SARS‐CoV‐2 represents a new concept for personal protective equipment to address a critical and timely challenge. Thermal inactivation in a non‐mask context has been widely discussed as a way to sterilize surfaces and objects to prevent transmission of the coronavirus. 13 , 14 , 15 Air circulation and heating of rooms and buildings have been proposed to reduce spread of SARS‐CoV‐2 in air as well. 16 With respect to masks, mechanical filtration is the main mechanism of pathogen impedance to date. N95 respirators and other mechanical filtration masks operate by interception, inertial impaction, and diffusion of particles, resulting in rejection of a majority of particles with sizes from the sub‐micron scale to micron scale. 5 While N95 respirators are recommended for use in health care environments, 17 they are designed for single use and widespread adoption by non‐healthcare workers can lead to shorages. 18 Reusable masks, such as cloth masks, offer substantial social benefit but may not offer adequate levels of protection from coronavirus in all circumstances, 19 while efforts to reuse masks (like N95 respirators) that are designed for single use may also reduce filtration efficiency. 20 , 21 , 22 Mask shortages, the generation of waste from single‐use facemasks, and the spread of the COVID‐19 pandemic to regions of the world with weaker healthcare infrastructure present an urgent need to reconsider designs and concepts for protective face masks. 3 , 23 In response, we propose a mask that blocks SARS‐CoV‐2 by thermal inactivation rather than mechanical filtration. Such masks have not been analyzed before in detail, making this the first quantitative analysis of the temperatures, volumes, and materials that could be used for thermal inactivation of a pathogen in a protective face mask.
In this work, we present a concept for a reusable facemask, which contains a heated, porous mesh to thermally inactivate SARS‐CoV‐2. We formulate coupled mass and energy balances across a mask to create a design space that maps the operating temperature, mask volume, and air flow to viral load reduction and CO2 accumulation. We analyze the wearable heated mask as a thermochemical reverse‐flow reactor, and explore its design given three key model inputs: (1) oscillatory breath flow, (2) first‐order thermal inactivation of SARS‐CoV‐2, and (3) a maximum allowable pressure drop. We propose a 300 ml mask that operates at a temperature of 90°C, containing a copper mesh with an approximate mesh diameter of 0.1 mm. We show that this mask design can achieve a 3‐log reduction in virus concentration with moderate viral impedance, in which virus particles travel one‐third as fast as air inside the mask, or a 6‐log reduction in virus concentration with higher viral impedance. By considering adsorption and desorption mechanisms and setting an overall pressure drop constraint, we determine that these partition coefficients can likely be achieved. These results show that a heated face mask is a promising, new design to reduce person‐to‐person spread of SARS‐CoV‐2, and will inform future prototyping and more detailed 3D modeling of pathogen thermal inactivation in heated face masks.
2. PROBLEM STATEMENT
A heated mask for thermal inactivation of SARS‐CoV‐2 contains a well‐specified interior volume with a porous mesh, insulating outer layer, inlets to the bulk, and outlets to the nose and mouth, as shown in Figure 1A,B. This can be conceptualized as a 1D domain of length L, as shown in Figure 1C,D. The mask design is bounded by several constraints, including the volume and period of human breath, coronavirus inactivation kinetics, and a maximum pressure drop for safety and comfort. Within this design space, the optimal face mask is compact, achieves high viral inactivation, allows CO2 exhalation, operates within a safe temperature range, and can be battery‐powered for an extended time. These performance metrics, particularly the log reduction in viral concentration, depend on the mask volume, temperature, and a partition coefficient K p . Five aspects of problem formulation—human breath, SARS‐CoV‐2 thermal inactivation, mass transfer, heat transfer, and viral impedance—are discussed below.
FIGURE 1.
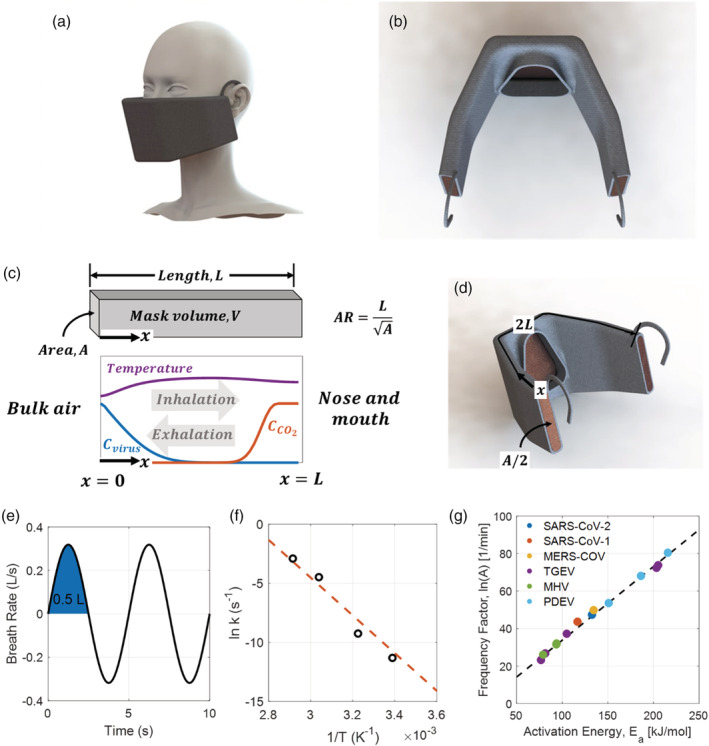
Heated mask design and problem formulation. (A) CAD drawing of a 0.3 L mask. The final proposed design is a mask with a volume of 0.3 L at an operating temperature of 90°C, which can cause thermal inactivation of SARS‐CoV‐2 and operate comfortably with insulation and cooling. (B) A second CAD drawing of a 0.3 L mask, showing a porous 0.6 mm diameter copper mesh interior, 0.3 cm thick neoprene insulation, two inlets for air on the sides of the mask, and one outlet to the nose and mouth. (C) The interior of the mask can be modeled as a 1D domain extending from bulk air at x = 0 to the nose and mouth at x = x max . The mask length, cross‐sectional area, and aspect ratio are defined. Temperature, virus concentration, and CO2 concentration vary with position and time within the domain. Neumann and Danckwerts boundary conditions are enforced at x = 0 and x = L , and switch with inhalation and exhalation. (D) CAD drawing showing the 1D coordinate system and dimensions superimposed on the 3D mask. (E) Sinusoidal approximation of human breath waveform, with a period of 5 s and a tidal volume of 0.5 L. (F) Thermal inactivation of SARS‐CoV‐2 follows first order kinetics, with a linear relationship between the natural log of the rate constant, ln k, and inverse temperature, 1/T. Data reproduced from Chin et al. 27 (G) Thermal inactivation of SARS‐CoV‐2 is well‐characterized, with first‐order rate parameters following a Meyer–Neldel rule in agreement with other coronaviruses like the first severe acute respiratory syndrome coronavirus (SARS‐CoV‐1), middle east respiratory syndrome (MERS‐CoV), transmissible gastroenteritis virus (TGEV), mouse hepatitis virus (MHV), and porcine epidemic diarrhea virus (PEDV). Data reproduced from Yap et al 28 [Color figure can be viewed at wileyonlinelibrary.com]
2.1. Human breath
The oscillations of human breath impose a periodically reversing flow through the mask, in analogy with a reverse‐flow reactor. The tidal volume, which is the volume of air displaced between inhalation and exhalation, is assumed to be 0.5 L, 24 while the period is assumed to be 5 s. 24 To ensure comfort, the pressure drop is held below 60 Pa L−1/s at maximum flow, which represents the threshold for detection of inspiratory resistance. 25 The velocity within the mask, U(t), is assumed to be sinusoidal 26 :
| (1) |
where U max is the maximum velocity and τ is the period. The assumed breath waveform is shown in Figure 1E. Positive velocities represent inhalation, and negative velocities represent exhalation.
2.2. Thermal inactivation of SARS‐CoV‐2
The thermal inactivation of a virus, including SARS‐CoV‐2, follows well‐characterized kinetics. It can be conceptualized as a first‐order chemical reaction with a rate that varies with temperature as shown below:
| (2) |
where r is the reaction rate, k is the first‐order rate constant for thermal inactivation, and C is viral concentration. The rate of thermal inactivation of SARS‐CoV‐2 was fit following an Arrhenius relationship of the following form:
| (3) |
where k is the first‐order rate constant for thermal inactivation, E a is the activation energy for inactivation, R the gas constant, T the temperature, and A the frequency factor. We fit experimental data obtained from Chin et al 27 for SARS‐CoV‐2, as shown in Figure 1F, to find an activation energy of 132.6 kJ/mol and a natural log of the frequency factor, ln(A), of 47.4. The correlation between the two fit parameters, E a and ln(A), follows a Meyer‐Neldel rule that is suggestive of protein denaturation at high temperatures, 28 and is in agreement with the kinetics of thermal inactivation of a broad range of other coronaviruses, including the first severe acute respiratory syndrome coronavirus (SARS‐CoV‐1), Middle East respiratory syndrome (MERS‐CoV), transmissible gastroenteritis virus (TGEV), mouse hepatitis virus (MHV), and porcine epidemic diarrhea virus (PEDV), as reported by Yap et al 28 and plotted in Figure 1G. While experimental data for thermal inactivation of SARS‐CoV‐2 extends only from room temperature to 70°C, data and model predictions for several coronaviruses collected by Jiang et al 29 extend to temperatures of 120°C and justify the kinetics assumed in this analysis, as shown in Figure S1.
2.3. Mass transfer
A 1D reaction‐convection‐diffusion model was used to analyze the concentration of virus and carbon dioxide inside a domain, which extends through a mask from the mouth to bulk air. The governing equation for this system is as follows 30 :
| (4) |
where x is position, t is time, and D e is the dispersion coefficient.
The dispersion coefficient for the virus traveling within the mask is estimated as 5 × 105 m2/s, taken from experimental evaluations of dispersion resulting from fluid flow through a mesh‐screen packed column. 31 Virus concentration in exhaled breath is assumed to be zero, while virus concentration in the bulk is set to an arbitrary value C0. During inhalation, Neumann boundary conditions are applied at the mouth and Danckwerts boundary conditions at the mask edge; these conditions are switched for exhalation. 32 , 33 Partial differential equations within the 1D mask domain were solved in MATLAB using function pdepe to obtain profiles of virus concentration, CO2 concentration, and temperature during inhalation and exhalation.
2.4. Heat transfer
The temperature distribution is governed by a similar equation to that of the concentration profiles. The temperature and concentration PDEs are not coupled: the temperature profile determines the concentration profiles, but the concentration profiles do not affect the temperature profile due to the negligible heat of reaction. The mask is assumed to contain a porous copper mesh, which is heated by Joule heating, causing thermal inactivation of virus as well as slowing viral transport. Rapid thermal equilibrium between the mesh packing and air is assumed, while radiative heat transfer, work done by pressure changes, and viscous dissipation are ignored. 34 Validation of thermal equilibrium approximation is included in the Supporting Information. Under these simplifications, the governing equation for the thermal distribution within a mask containing solid and fluid phases is as follows:
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
The subscripts s and f refer to a solid phase (i.e., copper mesh) and a fluid phase (i.e., virus‐laden air), respectively. c is the specific heat of copper and is taken as 400 W mK−1, c p is the specific heat at constant pressure of the fluid and is taken as 1020 J kg−1 K−1, U 0 is the superficial velocity of the fluid, k m is the effective thermal conductivity, q is the heat production per unit volume, W is the imposed electric power, A c is the mask flow area, L is the length of the mask, P m is the perimeter, T amb is the ambient temperature taken as 20°C, h eff is the effective heat‐transfer coefficient, h f is the free convection heat‐transfer coefficient for air on the outside surface of the mask and is taken as 2 W m−2 K−1, and L ins and k ins are the thickness and thermal conductivity of insulator material, which we assume for sake of comparison is neoprene and 0.3 cm thick. The porosity of the mesh, φ , is taken as a constant 0.9. During inhalation, the outflow Neumann boundary condition is applied at the mouth and the Danckwerts boundary condition at the mask edge. 32 , 33 During exhalation, the boundary conditions are flipped:
| (10) |
| (11) |
| (12) |
| (13) |
Physically speaking, heat transferred at the outer surface of the mask preheats the cold air that enters the mask when inhaling (Equation 10) when exhaling, air that is breathed out also heats up due to the heat transfer at the mask‐mouth interface (Equation 12). The temperature of the air entering the mask is taken to be 20°C, and the temperature of the exhaled air is taken to be 37°C.
2.5. Viral impedance
Virus in the mask is subject to thermal inactivation, but it is also impeded by the porous mesh as in other masks that operate purely by filtration. Numerous mathematical models have been developed to predict the particle transport and retention in porous media, using either macroscopic or microscopic approaches. 35 , 36 Macroscopic methods use the particle transport equation in a continuous media:
| (14) |
in which Λ is the filtration coefficient, which is related to many parameters, including pore structure, particle‐size distribution, and the particle‐surface interactions that govern the particle adsorption and release on/from the surface. Theoretical calculation of Λ is very difficult, so its value is usually determined experimentally. 37 , 38 , 39
On the other hand, microscopic approaches investigate the particle retention at pore scale, using direct models such as CFD‐DEM6 or, more recently, pore network modeling. 40 , 41 , 42 , 43 Pore network modeling starts with force balances on a single particle, accounting for hydrodynamic drag, body force, electrostatic, van der Waals, and inertial force and relating the particle velocity to fluid velocity:
| (15) |
in which U p is the particle velocity, F B is body force, F E is the electrostatic force, and F V is the van der Waals force. Estimates for each force term can be determined from particle and surface potentials. In addition to advection, the Brownian diffusion of virus must also be included in its microscopic transport formulation. In addition, particle retention in the porous mesh occurs via particle adsorption and binding to the mesh. Each of these steps may be explained by a combination of phenomena, including gravitation sedimentation, Brownian motion, and surface forces. Eventually, these single‐particle equations must be applied to an interconnected network of pores and throats. 44 In the absence of an experimentally measured filtration coefficient and other parameters for SARS‐CoV‐2 and to avoid the complicated pore network modeling, a simple model relating the virus velocity to bulk air velocity must be used. We introduce a simple model of viral impedance within the mask, where the virus is subject to slowing according to a partition coefficient K p as shown below:
| (16) |
In this case, U vir is the effective virus velocity and U is the bulk air velocity. Viral impedance occurs because virus particles adsorb to the copper mesh and desorb from the copper mesh in two first‐order processes. The partition coefficient K p can be defined as the ratio of these two rates:
| (17) |
where k ads is the virus adsorption rate constant, while k des is the virus desorption rate constant. Mask performance metrics, including viral inactivation and CO2 concentration, can be calculated as a function of mask volume, mean temperature, and partition coefficient K p .
3. RESULTS AND DISCUSSION
3.1. Mask design
Equations (4) and (5), which govern temperature, virus concentration, and CO2 concentration within the mask as function of position and time, were solved in MATLAB using function pdepe. Time‐variant virus, CO2, and temperature profiles for a 300 ml mask operating at a mean temperature of 90°C are shown in Figure 2, with inhalation in Figure 2A–C and exhalation in Figure 2D–F. Boundary conditions, as described above, fix the virus and CO2 concentrations at the mask‐bulk air interface ( x = 0) and mask‐mouth interface ( x = L ) during inhalation and exhalation, in accordance with the coordinate system presented in Figure 1C. The CO2 concentration of exhalation was fixed at the mask‐mouth interface at 3.8%, while the CO2 concentration in bulk air is essentially zero. During inhalation, in Figure 2A, virus is inhaled but does not reach the mask‐mouth interface due to viral impedance and thermal inactivation. A large majority of non‐inactivated virus is exhaled, as shown in Figure 2D. CO2, by contrast, is transported faster and is not subject to thermal inactivation. Air with near‐zero CO2 concentration is inhaled in Figure 2B, while air with high CO2 concentration is exhaled in Figure 2E and transported across the mask to the bulk. For this design, a mean temperature of 80°C, as shown in Figure 2C,F, is achieved with a power input of 18.89 W. Concentration and temperature profiles for candidate designs with different volumes and temperatures are similar to the profiles shown.
FIGURE 2.
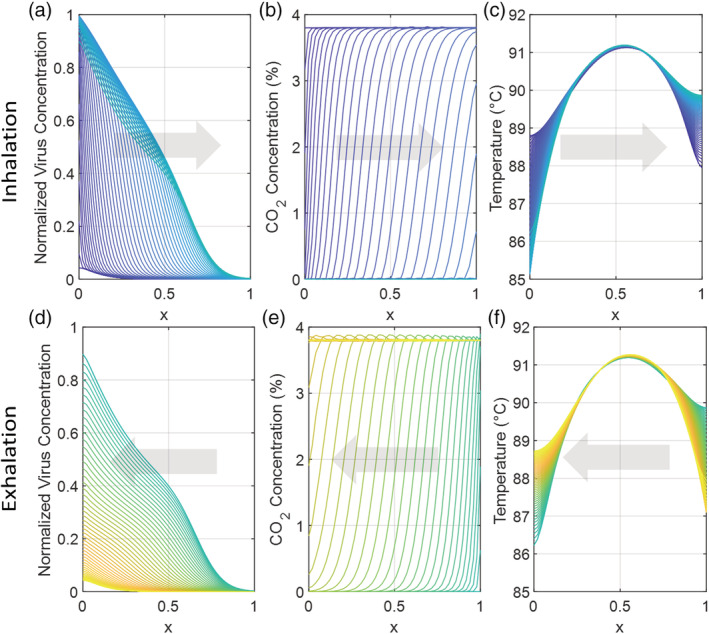
Viral concentration, CO2 concentration, and temperature vary with position and time during a single 5 s cycle of inhalation (A, B, C) and exhalation (D, E, F) in the 1D mask model. The mask extends from bulk air ( x = 0) to the mouth ( x = 1). In this case, the mask volume is 0.3 L, the aspect ratio is 3, the partition coefficient (K p) is 2, and the power is 18.89 W, generating a mean temperature of 90°C. (A) During inhalation, virus is impeded and inactivated, and is generally not transported from the bulk to the mouth. (B) During inhalation, low‐CO2 concentration air is inhaled. (C) The mean temperature during inhalation is 90°C, with slight variations. (D) During exhalation, active virus in the mask is generally transported back to the bulk. (E) During exhalation, CO2 is transported from the mouth through the mask. (F) The mean temperature during exhalation is 90°C, with slight variations [Color figure can be viewed at wileyonlinelibrary.com]
Power requirements, average inhaled CO2 concentration, and log viral inactivation are shown in Figure 3 for masks ranging from 0.1 to 1 L in volume, operating temperatures ranging from 40 to 140°C, and K p ranging from 0 to 10. Power requirements range from 3.79 W for a 0.1 L mask at 40°C to 52.96 W for a 1 L mask at 140°C. CO2 concentration, as expected, does not vary with temperature, but varies strongly with mask volume. Given the poor mixing in the mask, the mask volume must be less than the human tidal volume (500 ml) in order to achieve a non‐hazardous CO2 concentration. 45 By comparing log10 viral reduction at low temperature to that at high temperature in Figure 3, the effect of thermal inactivation can be distinguished from the effect of filtration. This is shown explicitly in Figure S2, which calculates the ratio of log10 viral reduction versus that at low temperature, as a function of mask temperature and volume. Thermal inactivation has an appreciable effect on SARS‐CoV‐2 transport at temperatures above 80°C.
FIGURE 3.
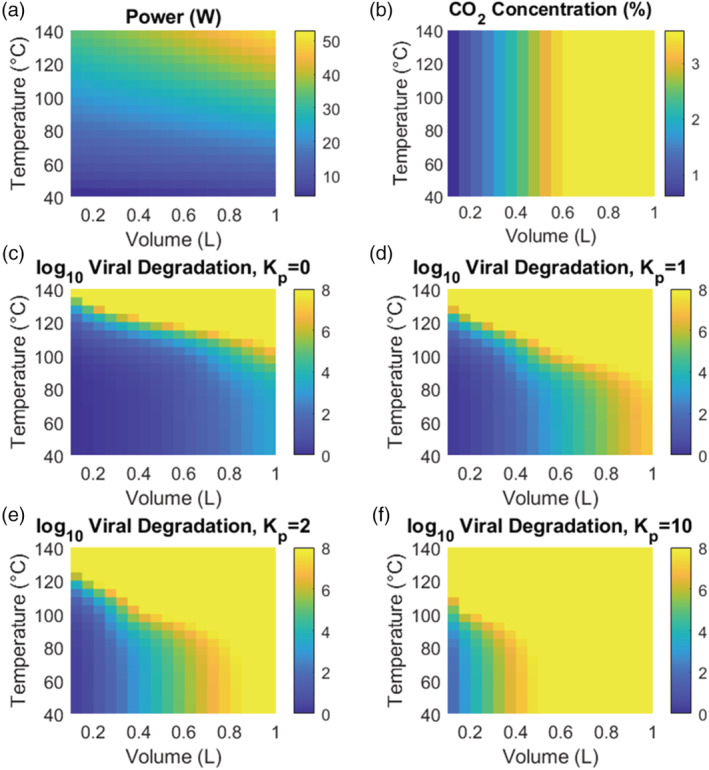
(A) Required power at steady state as a function of mask volume and operating temperature. Power requirements range from 3.79 W for a 0.1 L mask at 40°C to 52.96 W for a 1 L mask at 140°C. (B) Inhaled CO2 concentration, averaged over a breath cycle. CO2 concentration increases with increasing mask volume but is invariant with operating temperature. (C–F) log10 viral inactivation as a function of mask volume and mean operating temperature. Results are plotted for several values of the partition coefficient, K p, which captures impedance of virus in the porous mask mesh, with K p = 0 indicating that virus is transported with the same velocity as air in the mask, while K p ≫ 1 indicates substantial slowing of viral particles relative to air [Color figure can be viewed at wileyonlinelibrary.com]
Performance of heated masks in achieving specified log reductions in SARS‐CoV‐2 is presented in Figure 4. The required operating temperature to induce a specified viral load inactivation is plotted as a function of mask volume for a range of values of the partition coefficient K p . Two thresholds for viral inactivation are shown: a 3‐log, or thousand‐fold, reduction in inhaled viral concentration, and a 6‐log, or million‐fold, reduction in inhaled viral concentration. In general, 6‐log reduction is the standard for sterilization. 46 In all cases, the mask aspect ratio—defined as the ratio of mask length to the geometric mean of cross‐sectional dimensions—was set to 3.
FIGURE 4.
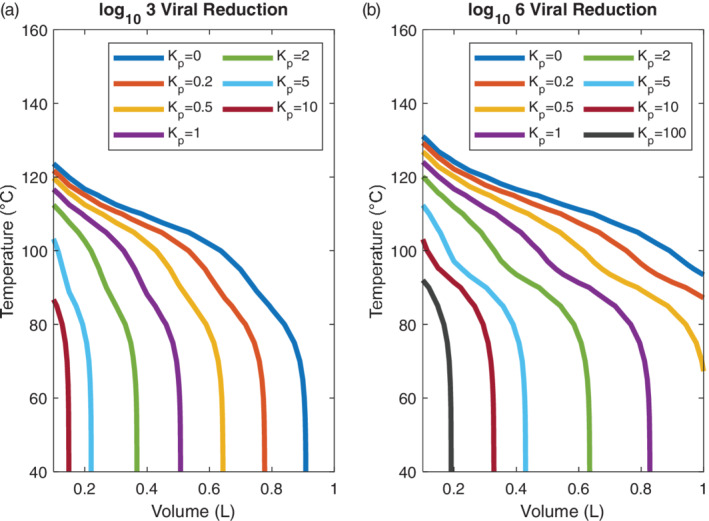
(A) Mask volume and operating temperature that is required to achieve 3‐log reduction in SARS‐CoV‐2 concentration through a heated mask. Results are plotted as a function of a partition coefficient, K p, which captures impedance of virus in the porous mask mesh, with K p = 0 indicating that virus is transported with the same velocity as air in the mask, while K p ≫ 1 indicates substantial slowing of viral particles relative to air. A 3‐log reduction in inhaled virus can be achieved in masks with volumes less than 0.4 L at temperatures below 100°C if there is slight viral impedance in the mask ( K p > 1). (B) Mask volume and operating temperature that is required to achieve 6‐log reduction, or sterilization, of SARS‐CoV‐2 concentration through a heated mask. A 6‐log reduction in inhaled virus can be achieved in masks with volumes less than 0.4 L at temperatures below 100°C with moderate viral impedance in the mask ( K p > 2) [Color figure can be viewed at wileyonlinelibrary.com]
A 3‐log viral reduction can be achieved in a compact mask (<0.5 L) at a reasonable operating temperature (<100°C) if viral transport is impeded moderately in the mask ( K p > 1), as shown in Figure 4A. A 6‐log viral reduction can be achieved within the same volume and temperature constraints with slightly higher virus impedance in the mask ( K p > 2), as shown in Figure 4B. Without viral impedance, where K p = 0, temperatures exceeding 100°C or volumes approaching 1 L are required to achieve 3‐log viral reduction, while temperatures exceeding 100°C and volumes exceeding 1 L are required to achieve 6‐log viral reduction. The case of no viral impedance represents a worst‐case scenario for mask function, as any reasonable mesh design would combine thermal inactivation with filtration and particle impedance to some degree.
Two regimes are apparent in Figure 4: At low temperatures, below 90°C, viral reduction is due largely to viral impedance. Vertical lines in this range show that there is little temperature dependence, with large differences in required volume for different levels of K p . By contrast, at high temperatures above 90°C, viral reduction is due largely or entirely to thermal inactivation. The inflection and flattening of curves in this range show that the degree of viral reduction is substantially temperature dependent above 90°C but decreasingly dependent on viral impedance, with only minor differences in required volume for different levels of K p . At high temperatures, the virus is thermally inactivated so rapidly that viral reduction obtained for lower and higher values of K p become nearly identical. While this is extremely promising for viral inactivation, operating at temperatures above 100°C presents issues for power requirements and human safety. In general, the presence of these two regions and the transition between them suggests a tradeoff between heated mask volume and heated mask temperature. A small, hot mask can achieve a similar level of viral inactivation as a larger, cooler mask. The secondary tradeoff, however, is in CO2 levels and user comfort; a small mask allows for lower CO2 levels during inhalation, while a large mask can be operated at a milder temperature.
The optimal mask design is located at the knee of the curves in Figure 4A,B. This volume and temperature will make maximum use of both thermal inactivation and traditional filtration to reduce viral transport and ensure safety for the mask wearer and those around them. The mask volume also determines the CO2 concentration: a mask volume below the tidal volume of 500 ml is necessary to allow sufficient CO2 transport for comfortable breathing. Based on these criteria, we choose a mask volume of 300 ml and an operating temperature of 90°C. Renderings of a 300 ml mask, showing a porous copper mesh interior, 0.3 cm thick neoprene insulation, two air inlets on the sides of the mask, and an outlet to the nose and mouth, are shown in Figure 1A,B. The neoprene insulation constitutes most of the mask mass of 350 g without batteries, for a total mass of 600 g with batteries. Full details of the proposed design are compiled in Table S1.
3.2. Mask performance regimes
In analogy with reverse‐flow chemical reactors, 9 the mask design space can be split into distinct regimes with qualitative differences in performance, as shown in Figure 5. These four regimes are characterized by two dimensionless groups: the dispersion number (Di) and the reduced volume (). The reduced volume is the ratio of mask volume to breath tidal volume; in the case of a reverse‐flow reactor, this is the ratio of the residence time to the switching time:
| (18) |
The dispersion number captures dispersion of reactants in a reactor. A reactor with Di ≫ 1 will behave as a stirred‐tank reactor, while a reactor with Di ≪ 1 will behave as a plug‐flow reactor:
| (19) |
In this case, the limit, as shown in Figure 5A, has a large mask volume and is poorly mixed. While this means that the virus is not transported from the bulk to the mouth, it also does not allow transport of CO2 out. We can call this the plastic bag limit, and it is not suitable for a protective facemask. There is a sharp bifurcation at , beyond which is the regime, as shown in Figure 5B. In this regime, the mask volume is small but poorly mixed, leading to near‐complete transport of CO2 out of the mask at the end of exhalation. This straw limit is promising for a heated mask, provided that thermal inactivation of virus is suitably fast. In the well‐mixed limit, with Di ≫ 1 , there is no strong qualitative difference at . These cases are shown in Figure 5C,D. In both a small mask (Figure 5C) and large mask (Figure 5D), the high level of mixing means that there are virtually no spatial gradients in virus and CO2 concentration, but there are strong temporal gradients during the breath cycle. In these cases, virus concentration is maximized after inhalation, while CO2 concentration is maximized after exhalation.
FIGURE 5.
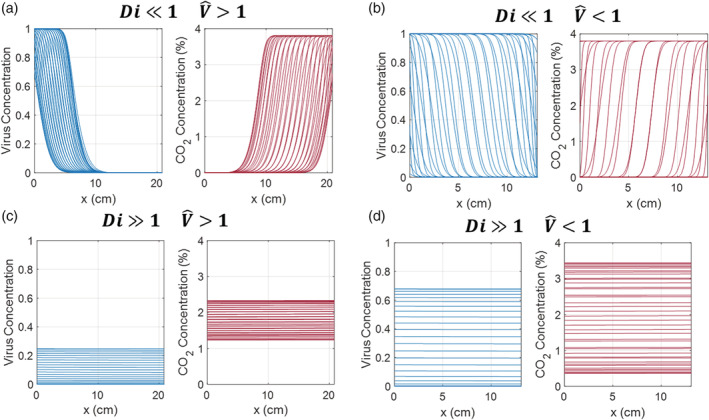
In analogy with reverse‐flow chemical reactors, behavior of a heated mask can be split into different regimes depending on dispersion number Di and reduced volume . (A) The low Di, high limit (“plastic bag limit”) does not allow virus to reach the mouth but does not provide adequate ventilation. (B) The low Di, low limit (“straw limit”) provides ventilation but may allow viral inhalation depending on the viral inactivation rate. This is the most promising regime. (C) The large, well‐mixed limit. Virus and CO2 are well‐mixed within the mask volume regardless of volume. (D) The small, well‐mixed limit. At high Di, there is no bifurcation at so the small, well‐mixed limit displays qualitatively similar behavior to the large, well‐mixed limit, with temporal fluctuations in virus and CO2 concentration during the breath cycle but near‐zero spatial concentration gradients [Color figure can be viewed at wileyonlinelibrary.com]
Given the flow rate of human breath and dispersion coefficients of air in porous media, the dispersion number in the proposed mask designs is likely to be small regardless of the exact mask volume and operating temperature, so the well‐mixed cases with Di ≫ 1 are not immediately physically relevant. Nonetheless, it is important to compare the problem of heated mask design problem to these regimes of reverse‐flow reactor transport. In a general sense, we can see that the ideal heated mask would impede virus transport but not CO2 transport, combining filtration and thermal inactivation to act in the “plastic bag” limit toward virus particles but the “straw” limit toward exhaled CO2.
3.3. Pressure drop and viral impedance
The success of the proposed mask in inactivating SARS‐CoV‐2 relies on achieving viral impedance, as captured by K p , without exceeding a maximum pressure drop. The structure and solidity of the mask mesh are critically important for both criteria. Specifically, the pressure drop constraint specifies a minimum mesh size for a given mask volume, while the mesh size dictates the expected viral impedance value, K p . As shown in Figure 6A,B, our analysis suggests that in a 300 ml mask with a solidity of 0.1 and a copper mesh with diameter 0.1 mm will likely be able to achieve a viral impedance value of K p = 2. This supports the conclusion that our proposed mask, with a size of 300 ml at an operating temperature of 90°C, will be able to cause a 3‐log reduction in viral concentration.
FIGURE 6.
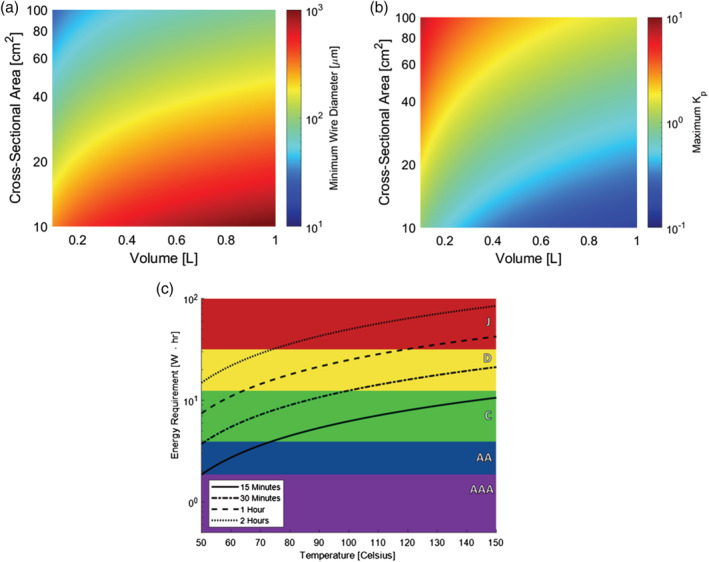
(A) Minimum allowable mesh diameter as a function of mask volume and cross‐sectional area. The threshold mesh diameter induces a pressure drop of 60 Pa L−1/s at the maximum breath flow rate of 0.4 liters per second. Mesh solidity is set to 0.1, with wire spacing equal to 3.2 times the wire diameter. Coarser meshes are required in larger masks to obey the pressure drop constraint, while meshes with higher cross‐sectional area (and lower aspect ratio) can tolerate finer meshes without exceeding the maximum pressure drop. For the final design case, with a volume of 300 ml and a cross‐sectional area of 50 cm2, a mesh size of 0.1 mm is ideal. (B) Maximum achievable partition coefficient, K p , as a function of mask volume and cross‐sectional area. The partition coefficient is calculated as the ratio of the adsorption rate to the desorption rate, where k ads is calculated from fiber efficiencies while a conservative value of k des = 1 s −1 is assumed. It is likely that a mask with a volume of 300 ml and an aspect ratio of 3 can achieve a K p of 2, allowing for 3‐log reduction in SARS‐CoV‐2 transport. (C) Energy requirement of 300 ml mask vs. average temperature. The energy requirement for a given amount of time is compared against the total power supply of standard commercial batteries that have the following power capacities and weights 47 : AAA, 1.87 W h and 12 g; AA, 3.9 W h and 24 g; C, 12.3 W h and 65 g; D, 31.5 W h and 135 g; and J, 540 W h and 272 g [Color figure can be viewed at wileyonlinelibrary.com]
With respect to pressure drop, we set an upper bound of 60 Pa L−1/s at maximum flow, a conservative lower threshold for noticeable inspiratory resistance. 48 , 49 We take the interior of the mask to be filled with a mesh composed of stacked screens of cross‐woven fibers. The mesh is defined by two variables—the fiber diameter, d w , and fiber spacing, s w —where the distance between stacked screens is taken to be equal to this fiber spacing, as shown in Figure S2. The pressure drop across a single layer of mesh screen under oscillatory flow is predicted from an empirical correlation 50 :
| (20) |
where ρ is the fluid density, U max the maximum superficial velocity during the oscillatory flow cycle, and Re d is the Reynolds number based on the wire diameter. The solidity of the screen, α , is defined as the complement of the mesh porosity. For the specified geometry, the solidity of a single screen is equal to:
| (21) |
The average solidity of the stacked fiber screens is then given as:
| (22) |
The pressure drop across more than a single mesh—in this case, across the porous interior of a mask—is taken to scale linearly with the number of mesh screens present, and thus scales linearly with length. 51 Given a mesh solidity of 0.1, the minimum wire diameter before the pressure drop constraint is violated for a mask design of some volume and cross‐sectional area is shown in Figure 6A.
Given a wire diameter of 0.1 mm, it is likely that a partition coefficient of K p = 2, which is required to achieve 3‐log reduction in virus concentration, can be achieved. The maximum value of the partition coefficient, K p , is shown as a function of wire diameter and cross‐sectional area in Figure 6B. This predicted value depends on estimates for both the adsorption rate, k ads , and the desorption rate, k des . The adsorption rate can be calculated as shown below:
| (23) |
where η f is a single‐fiber efficiency. Captured particles are retained by Van der Waals forces, 52 but the mechanism by which they come into contact with the filter medium is dependent on filter and particle geometry. For coronavirus particles, which have a diameter of roughly 100 nm, the dominant mechanism of capture is through Brownian diffusion. 53 The governing parameter for this diffusive mechanism is the Péclet number, defined as the ratio of convective to diffusive transport rates:
| (24) |
where d w is the filter fiber diameter, and D is the diffusion coefficient of the particle. The single fiber efficiency due to diffusion is obtained from an appropriate correlation such as that proposed by Wang et al 54 :
| (25) |
The diffusion coefficient for the particle is obtained from the Stokes‐Einstein equation:
| (26) |
where k B T is the product of the Boltzmann constant and temperature, μ is the fluid dynamic viscosity, d p the diameter of the particle, and C s the Cunningham slip correction factor:
| (27) |
where K n is the Knudsen number of the particle defined as:
| (28) |
where λ is the mean free path of a gas molecule in the fluid. For air, and assuming ideality, the mean free path is obtained from the following correlation:
| (29) |
where R is the gas constant, is the diameter of nitrogen, the dominant molecular species in air, N A is Avogadro's number, and P the pressure.
The desorption rate, by contrast, is less well‐known, so we assume a conservative value of k des = 1 s−1 in our calculations. The desorption rate can likely be tuned by various mechanisms. One approach to tailor the desorption rate of captured particles includes making use of the natural oscillatory flow within the mask. Pulsed air flow can effectively cause particle desorption, and is used industrially to clean surfaces from particle debris. 47 , 55 Mechanical stimulus of the mesh could actively control particle desorption, 56 where optical 57 and pneumatic 58 actuation of these structures is also possible. Applied electric fields can also be used in the same way. By applying an electric field to a conductive mesh, an electrostatic desorption force can be induced. 59 This principle has been applied with success to biological filtration membranes with a continuously applied electrical field, 60 as well with pulsed electric fields to remove microbial surface contamination. 61
Given these estimates for the adsorption and desorption rate, a partition coefficient K p of 2 is achievable for a 300 ml mask with a 0.1 mm mesh for a mask cross‐sectional area of 50 cm2, as shown in Figure 6B. From this analysis of adsorption and desorption rates and mechanisms, then, we see that the necessary viral impedance is likely achievable within the pressure drop and volume constraints of the design process, even though a cross‐sectional area of 50 cm2 fixes a different aspect ratio (AR = 0.85) than the specified aspect ratio of 3. In general, there is a tradeoff between mask volume and achievable viral impedance. The attainable value of K p is a strong function of the cross‐sectional area of the mask. A smaller cross‐sectional area produces higher superficial velocities of flow, resulting in a larger value of the adsorption rate constant. However, these higher velocities also induce large pressure drop, and limit the maximum volume of mesh. Thus, at a given temperature, a smaller volume mask with a larger value of K p may be equally able to achieve a desired viral reduction as a larger mask with a lower value of K p—where ultimately a smaller mask volume would be the overall preferable option due to lower required energy consumption and smaller profile.
3.4. Heating and safety
Heating the mask requires continuous power input to maintain a set temperature. The incorporation of a power supply within any mask design requires considerations and tradeoff between the duration of power supply and the bulk and weight it adds to the design. Figure 6C shows the power supply required of a 300 ml mask over a range of set temperatures. This energy requirement is compared against the capacity of standard consumer batteries. For a moderately heated mask of 90°C, operation for an hour requires 19.5 W‐h, which can be supplied by two C batteries (130 g total), six AA batteries (120 g total), or 12 AAA batteries (108 g total). Because of the substantial battery demands, it is expected that a heated mask could be used during relatively short (<1 h) periods in particularly crowded situations, though the power requirements could be decreased dramatically with improvements to heat integration within the mask and thermal insulation to ambient air. Furthermore, rechargeable batteries or battery packs could be used instead of single‐use batteries to provide a lower cost and long‐term way to power the mask.
With respect to mask safety, continuous inhalation of and exposure to heated air and heating elements are matters of concern for the overall comfort and safety of any heated mask design. Appropriate insulation is necessary to limit the surface temperature of the mask—either on the face, or outwards—as well as minimize heat loss. Low‐density but high thermally insulating neoprene is one material well‐suited out of which the mask may be constructed. Ultrainsulating neoprene with thermal conductivity as low as 0.03 W m−1 K−1 has recently been constructed, by incorporating noble gases into neoprene foam. 62 Further, neoprene is heat‐resistant up to temperatures of 135°C, 63 making it an ideal material for use in the high‐temperature regions of the mask.
Minimizing the temperature of inlet air, which is exposed to the face and inhaled, is also necessary to provide a safe and comfortable mask. Continual inhalation of air exceeding 125 °F (52°C) has been shown to be painful for humans. 64 Accordingly, any mask design must incorporate a system to appropriately cool down air before inhalation. The reduction in temperature of inhaled air can be accomplished through incorporation of low thermal diffusivity materials at the inlet and outlet of the heated chamber, while respecting the overall pressure drop constraint for the comfort of the mask wearer. The regions of the mask containing these thermal masses would not be actively heated, but instead retain the thermal energy of the heated air, cooling it down before exiting the mask. This type of thermal design is discussed in the Supporting Information. Notably, for a 300 ml mask heated to an average temperature of 90°C, the electric power consumption may be able to be reduced from 19.5 to 8.8 W.
3.5. Further improvements
There are mechanisms beyond thermal viral inactivation that may further improve the mask design. Coating the mesh with a layer of a metal such as copper or iron, which as ions have been shown widely to inactivate viruses and bacteria, 65 , 66 may improve mask performance. Anti‐pathogenic polymeric 67 or non‐polymeric 68 coatings may also increase the inactivation rate of adsorbed pathogens. Physical patterning, either on the microscale or nanoscale, could also lead to enhanced rate of inactivation, 69 , 70 as could the incorporation of UV light 71 with due caution about the hazards of ozone on human health. 72
The long lifetime of the designed mask relies on its continued ability to inactivate and adsorb viral particles. The use of a small wire spacing within the mesh would minimize the potential of larger particles—such as dust or other debris that can be as large as 100 microns in diameter—to cake or block individual pores on the filter. 73 The cyclic nature of breath, too, presents a natural mechanism of filter clearing. Exhalation, when the flow reverses direction within the mask, would backwash the filter medium, potentially releasing and expelling any particle contaminants present. 74 In general, care must be taken to design a system, which is able to retain, inactivate, and then emit that inactivated pathogen of interest without irreversibly capturing other contaminants. In the case where periodic replacement of the mesh material within the mask is necessary, a cheaper and less complex mesh material would be favored. We anticipate that a heated mask will maintain its fit and relative sterility over time, allowing it to be more reusable than an N95 respirator. While an N95 respirator can be reused only a handful of times before the fit deteriorates, 75 a heavier, thicker, and more durable heated mask will likely maintain performance better with repeated use. We anticipate that the flexibility of neoprene would allow a heated mask to maintain its fit better than an N95 ventilator upon donning and doffing. Additionally, a heated mask is less likely to become contaminated between uses, requiring fewer sanitization processes that reduce N95 effectiveness. 76 Experimental validation of a heated neoprene/copper mask would be needed to confirm its continued performance over time.
4. CONCLUSIONS
We have computationally analyzed the effectiveness of a heated face mask for thermal inactivation of the novel coronavirus, SARS‐CoV‐2. This constitutes the first quantitative analysis of face mask air purification by thermal inactivation of a pathogen. Relevant design choices for a heated mask include the mask volume, operating temperature, aspect ratio, and the diameter and spacing of fibers within the mask. Parameters, which cannot be changed, or which follow from the design choices above, include the tidal volume and frequency of human breath, kinetics of coronavirus inactivation, human comfort and safety limits, power requirements, and the degree to which particles are impeded within the mask, as modeled by the partition coefficient K p.
We have introduced a framework to consider these factors in mask design optimization, with an optimal mask volume of 300 ml at an operating temperature of 90°C. This mask can achieve a 3‐log reduction in virus concentration with K p = 2, or 6‐log reduction in virus concentration with K p = 5. These values of the partition coefficient can likely be achieved without excessive pressure drop in a copper mesh with a wire diameter of roughly 0.6 mm. In general, we note a tradeoff between mask temperature and volume; the dependence of maximum mask volume on mesh material and spacing by the pressure drop constraint; and the presence of different regimes in heated mask design, which we call the plastic bag, straw, and well‐mixed limits, on the basis of different dimensionless groups by analogy with reverse‐flow chemical reactors. Given physical and safety limits, heated masks are promising options to protect against transmission of COVID‐19 if coupled with thermoelectric cooling and thermally insulating liner materials. Future work, including experimental study with heated mask prototypes or more extensive 3D computational fluid dynamics simulations, will shed more light on the exact volume, temperature, and mesh size that is most promising for heated mask design, as well as the materials and battery systems that are most capable of achieving target viral inactivation.
AUTHOR CONTRIBUTIONS
Samuel Faucher: Investigation; writing‐original draft; writing‐review & editing. Daniel Lundberg: Investigation; writing‐original draft; writing‐review & editing. Xinyao Liang: Investigation; writing‐original draft; writing‐review & editing. Xiaojia Jin: Investigation; writing‐original draft. Rosalie Phillips: Visualization. Dorsa Parviz: Investigation; writing‐original draft. Jacopo Buongiorno: Project administration; supervision. Michael Strano: Project administration; supervision.
Notation
- A
frequency factor (1/s)
- A c
mask flow area (m2)
- c
specific heat of copper (W m/K)
- c p
specific heat at constant pressure of the fluid (J/(kg K))
- C
virus concentration (mol/L)
- C 0
virus concentration in the bulk air (mol/L)
- C s
Cunningham slip correction factor (dimensionless)
diameter of nitrogen (m)
- d p
diameter of virus particle (m)
- d w
fiber diameter (m)
- D
diffusion coefficient of the virus particle (m2/s)
- D e
dispersion coefficient (m2/s)
- Di
dispersion number
- E a
activation energy for virus thermal inactivation (kJ/mol)
- F B
body force (N)
- F E
electrostatic force (N)
- F V
Van der Waals force (N)
- h eff
effective heat‐transfer coefficient (W/m2/K)
- h f
free convective heat‐transfer coefficient for air on the outside surface of the mask (W/(m2 K))
- k
first‐order rate constant for virus thermal inactivation (1/s)
- k ads
virus adsorption rate constant (1/s)
- k B
Boltzmann constant (J/K)
- k des
virus desorption rate constant (1/s)
- k ins
thermal conductivity of insulating material (neoprene) (W/(m K))
- k m
effective thermal conductivity (W/(m K))
- K p
virus partition coefficient
- K n
Knudsen number of the particle
- L
mask length (m)
- L ins
thickness of insulating material (m)
mass flow rate of the fluid (kg/s)
- N A
Avogadro's number
- P m
mask perimeter (m)
- P
pressure (Pa)
Péclet number
- ΔP
pressure drop across a single layer of mesh screen under oscillatory flow (Pa)
- q
heat production per unit volume (W/m3)
- r
virus thermal inactivation rate (mol/(L s))
- R
gas constant (J/(K mol))
- Re d
Reynolds number based on the wire diameter
- s w
fiber spacing (m)
- t
time (s)
- T
temperature (K)
- T amb
ambient temperature (K)
- U
velocity (m/s)
- U 0
superficial velocity of the fluid (m/s)
- U max
maximum air flow velocity within the mask (m/s)
- U vir
effective virus velocity (m/s)
- U p
particle velocity (m/s)
- V mask
mask volume (L)
- V T
tidal volume (L)
reduced volume: ratio of mask volume to tidal volume
- W
imposed electric power (W)
- x
position along the mask (m)
- α
solidity of the screen
- α ′
average solidity of the stacked fiber screens
- η f
single fiber efficiency
- φ
porosity of the mesh
- Λ
filtration efficiency of the porous mesh
- λ
mean free path of a gas molecule in the fluid (m)
- μ
fluid dynamic viscosity (Pa s)
- ρ
fluid density (kg/m3)
- τ
period of human breath (s)
- exh
exhalation
- f
fluid phase (virus‐laden air)
- inh
inhalation
- s
solid phase (copper mesh)
Supporting information
Appendix S1. Supporting Information.
ACKNOWLEDGMENTS
The authors acknowledge the Office of Naval Research (ONR) under award N00014‐16‐1‐2144 for their support in the analysis of thermal materials design. Samuel Faucher and Daniel James Lundberg acknowledge support by the National Science Foundation Graduate Research Fellowship under Grant No. 1122374 and Grant No. 1745302, respectively.
Faucher S, Lundberg DJ, Liang XA, et al. A virucidal face mask based on the reverse‐flow reactor concept for thermal inactivation of SARS‐CoV‐2. AIChE J. 2021;67:e17250. 10.1002/aic.17250
Funding information Division of Graduate Education, Grant/Award Numbers: 1122374, 1745302; Office of Naval Research, Grant/Award Number: N00014‐16‐1‐2144
DATA AVAILABILITY STATEMENT
The data and code that support the findings of this study are available from the corresponding author upon request.
REFERENCES
- 1. Cheng VCC, Wong SC, Chuang VWM, et al. The role of community‐wide wearing of face mask for control of coronavirus disease 2019 (COVID‐19) epidemic due to SARS‐CoV‐2. J Infect. 2020;81:107‐114. 10.1016/j.jinf.2020.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Leung NHL, Chu DKW, Shiu EYC, et al. Respiratory virus shedding in exhaled breath and efficacy of face masks. Nat Med. 2020;26(5):676‐680. 10.1038/s41591-020-0843-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Nogee D, Tomassoni A. Concise communication: Covid‐19 and the N95 respirator shortage: closing the gap. Infect Control Hosp Epidemiol. 2020;41:1‐1. 10.1017/ice.2020.124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Howard J, Huang A, Li Z, et al. An evidence review of face masks against COVID‐19. Proc Natl Acad Sci USA. 2021;118(4):1‐12. 10.1073/pnas.2014564118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. TSI . Mechanisms of Filtration for High Efficiency Fibrous Filters. Shoreview, MN: TSI Inc.; 2012;041:1‐4. [Google Scholar]
- 6. Khinast J, Luss D. Mapping regions with different bifurcation diagrams of a reverse‐flow reactor. AIChE J. 1997;43(8):2034‐2047. 10.1002/aic.690430812. [DOI] [Google Scholar]
- 7. Salinger AG, Eigenberger G. The direct calculation of periodic states of the reverse flow reactor—II. Multiplicity and instability. Chem Eng Sci. 1996;51(21):4915‐4922. 10.1016/0009-2509(96)00327-2. [DOI] [Google Scholar]
- 8. Viecco GA, Caram HS. The spherical reverse flow reactor. Chem Eng Sci. 2002;57(18):4005‐4025. 10.1016/S0009-2509(02)00310-X. [DOI] [Google Scholar]
- 9. Budhi YW. Reverse Flow Reactor Operation for Control of Catalyst Surface Coverage; Eindhoven, Netherlands: Technische Universiteit Eindhoven; 2005. [Google Scholar]
- 10. Cottrell FG. Purifying gases and apparatus therefor. http://www.google.com/patents/US2121733%5Cnhttp://patentimages.storage.googleapis.com/pdfs/US2121733.pdf. Accessed October 13, 2020.
- 11. Zagoruiko AN. The reverse‐flow operation of catalytic reactors: history and prospects. Curr Top Catal. 2017;10(May):113‐129. https://www.researchgate.net/publication/258208737. Accessed October 13, 2020. [Google Scholar]
- 12. Van Sint AM, Nijssen RC. A novel reverse flow reactor coupling endothermic and exothermic reactions: an experimental study. Chem Eng Sci. 2002;57(22–23):4967‐4985. 10.1016/S0009-2509(02)00276-2. [DOI] [Google Scholar]
- 13. Abraham JP, Plourde BD, Cheng L. Using heat to kill SARS‐CoV‐2. Rev Med Virol. 2020;30(5):1‐3. 10.1002/rmv.2115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Kampf G, Voss A, Scheithauer S. Inactivation of coronaviruses by heat. J Hosp Infect. 2020;105:348‐349. 10.1016/j.jhin.2020.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Hessling M, Hoenes K, Lingenfelder C. Selection of parameters for thermal coronavirus inactivation—a data‐based recommendation. GMS Hyg Infect Control. 2020;15:1‐7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Knio ZO, Shelton JA, O'Gara T. Heated air delivery by micro‐sauna: an experimental treatment prototype concept for coronavirus disease 2019. Cureus. 2020;12(5):1‐5. 10.7759/cureus.8162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Recommended guidance for extended use and limited reuse of N95 filtering facepiece respirators in healthcare settings | NIOSH | CDC.
- 18. Strategies for optimizing the supply of N95 Respirators: COVID‐19 | CDC.
- 19. Fischer EP, Fischer MC, Grass D, Henrion I, Eric W, Warren SW. Low‐cost measurement of facemask efficacy for filtering expelled droplets during speech. Sci Adv. 2020;3083:1‐11. 10.1101/2020.06.19.20132969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Cramer A, Tian E, Yu SH, et al. Disposable n95 masks pass qualitative fit‐test but have decreased filtration efficiency after cobalt‐60 gamma irradiation. medRxiv. 2020:10–14.doi: 10.1101/2020.03.28.20043471 [DOI] [PMC free article] [PubMed]
- 21. Fisher EM, Shaffer RE. Considerations for recommending extended use and limited reuse of filtering facepiece respirators in health care settings. J Occup Environ Hyg. 2014;11(8):115‐128. 10.1080/15459624.2014.902954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Lin TH, Chen CC, Huang SH, Kuo CW, Lai CY, Lin WY. Filter quality of electret masks in filtering 14.6–594 nm aerosol particles: effects of five decontamination methods. PLoS One. 2017;12(10):1‐15. 10.1371/journal.pone.0186217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Livingston E, Desai A, Berkwits M. Sourcing personal protective equipment during the COVID‐19 pandemic. JAMA ‐ J Am Med Assoc. 2020;323(19):1912‐1914. 10.1001/jama.2020.5317. [DOI] [PubMed] [Google Scholar]
- 24. Gilbert R, Auchincloss JH, Brodsky J, Boden W. Changes in tidal volume, frequency, and ventilation induced by their measurement. J Appl Physiol. 1972;33(2):252‐254. 10.1152/jappl.1972.33.2.252. [DOI] [PubMed] [Google Scholar]
- 25. Kim JH, Roberge RJ, Powell JB, Shaffer RE, Ylitalo CM, Sebastian JM. Pressure drop of filtering facepiece respirators: How low should we go?. International Journal of Occupational Medicine and Environmental Health. 2015;28(1):71–80. 10.13075/ijomeh.1896.00153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Colby SM, Kabilan S, Jacob RE, Kuprat AP, Einstein DR, Corley RA. Comparison of realistic and idealized breathing patterns in computational models of airflow and vapor dosimetry in the rodent upper respiratory tract. Inhal Toxicol. 2016;28(4):192‐202. 10.3109/08958378.2016.1150367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Chin AWH, Chu JTS, Perera MRA, et al. Stability of SARS‐CoV‐2 in different environmental conditions. Lancet Microbe. 2020;1(1):e10. 10.1016/s2666-5247(20)30003-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Yap TF, Liu Z, Shveda RA, Preston DJ. A predictive model of the temperature‐dependent inactivation of coronaviruses. ChemRxiv; July 2020. doi: 10.26434/chemrxiv.12152970.v4 [DOI] [PMC free article] [PubMed]
- 29. Jiang Y, Zhang H, Wippold JA, et al. Sub‐second heat inactivation of coronavirus. bioRxiv; October 2020:2020.10.05.327528. doi: 10.1101/2020.10.05.327528 [DOI]
- 30. Deen WM. Analysis of Transport Phenomena. 2nd ed.; Oxford, England: Oxford University Press; 2011. [Google Scholar]
- 31. Chen BH, Manna BB, Hines JW. Dispersion of liquid in a column packed with screen cylinders. Ind Eng Chem Process Des Dev. 1971;10(3):341‐346. 10.1021/i260039a011. [DOI] [Google Scholar]
- 32. Nauman EB, Mallikarjun R. Generalized boundary conditions for the axial dispersion model. Chem Eng J. 1983;26(3):231‐237. 10.1016/0300-9467(83)80018-5. [DOI] [Google Scholar]
- 33. Pearson JRA. A note on the "Danckwerts" boundary conditions for continuous flow reactors. Chem Eng Sci. 1959;10(4):281‐284. 10.1016/0009-2509(59)80063-4. [DOI] [Google Scholar]
- 34. Nield DA, Bejan A, Nield DA, Bejan A. Heat transfer through a porous medium. Convection in Porous Media. New York, NY: Springer International Publishing; 2017:37‐55. 10.1007/978-3-319-49562-0_2. [DOI] [Google Scholar]
- 35. Jegatheesan V, Vigneswaran S. Deep bed filtration: mathematical models and observations. Crit Rev Environ Sci Technol. 2005;35(6):515‐569. 10.1080/10643380500326432. [DOI] [Google Scholar]
- 36. Bradford SA, Torkzaban S. Colloid transport and retention in unsaturated porous media: a review of interface‐, collector‐, and pore‐scale processes and models. Vadose Zo J. 2008;7(2):667‐681. 10.2136/vzj2007.0092. [DOI] [Google Scholar]
- 37. Chiang H‐W, Tien C. Dynamics of deep‐bed filtration. Part I: analysis of two limiting situations. AIChE J. 1985;31(8):1349‐1359. 10.1002/aic.690310814. [DOI] [Google Scholar]
- 38. Chiang H‐W, Tien C. Dynamics of deep‐bed filtration. Part II: experiment. AIChE J. 1985;31(8):1360‐1371. 10.1002/aic.690310815. [DOI] [Google Scholar]
- 39. Yuan H, Shapiro AA. Modeling non‐Fickian transport and hyperexponential deposition for deep bed filtration. Chem Eng J. 2010;162(3):974‐988. 10.1016/j.cej.2010.07.003. [DOI] [Google Scholar]
- 40. Fatt I. The network model of porous media. Trans AIME. 1956;207(01):144‐181. 10.2118/574-g. [DOI] [Google Scholar]
- 41. Bryant SL, King PR, Mellor DW. Network model evaluation of permeability and spatial correlation in a real random sphere packing. Transp Porous Media. 1993;11(1):53‐70. 10.1007/BF00614635. [DOI] [Google Scholar]
- 42. Bijeljic B, Muggeridge AH, Blunt MJ. Pore‐scale modeling of longitudinal dispersion. Water Resour Res. 2004;40(11):1‐9. 10.1029/2004WR003567. [DOI] [Google Scholar]
- 43. Joekar‐Niasar V, Hassanizadeh SM. Analysis of fundamentals of two‐phase flow in porous media using dynamic pore‐network models: a review. Crit Rev Environ Sci Technol. 2012;42(18):1895‐1976. 10.1080/10643389.2011.574101. [DOI] [Google Scholar]
- 44. Yang H, Balhoff MT. Pore‐network modeling of particle retention in porous media. AIChE J. 2017;63(7):3118‐3131. 10.1002/aic.15593. [DOI] [Google Scholar]
- 45. OSHA . Carbon Dioxide Health Hazard Information Sheet. FSIS Environmental, Safety and Health Group 2010;1:2‐4. https://www.osha.gov/dts/chemicalsampling/data/CH_225400.html. Accessed October 13, 2020. [Google Scholar]
- 46. Mosley G. Sterility assurance level (SAL): the term and its definition continues to cause confusion in the industry. Pharm Microbiol Forum Newsl. 2008;14(5):1‐15. [Google Scholar]
- 47. Ziskind G, Yarin LP, Peles S, Gutfinger C. Experimental investigation of particle removal from surfaces by pulsed air jets. Aerosol Sci Tech. 2002;36(5):652‐659. 10.1080/02786820252883883. [DOI] [Google Scholar]
- 48. Kim JH, Roberge RJ, Powell JB, Shaffer RE, Ylitalo CM, Sebastian JM. Pressure drop of filtering facepiece respirators: how low should we go? Int J Occup Med Environ Health. 2015;28(1):71‐80. 10.13075/ijomeh.1896.00153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Electronic code of federal regulations: fiber definitions. U.S. Government Printing Office. http://www.ecfr.gov. Published 2021.
- 50. Wakeland RS, Keolian RM. Measurements of resistance of individual square‐mesh screens to oscillating flow at low and intermediate Reynolds numbers. J Fluids Eng Trans ASME. 2003;125(5):851‐862. 10.1115/1.1601254. [DOI] [Google Scholar]
- 51. Sun H, Bu S, Luan Y. A high‐precision method for calculating the pressure drop across wire mesh filters. Chem Eng Sci. 2015;127:143‐150. 10.1016/j.ces.2015.01.023. [DOI] [Google Scholar]
- 52. Kirsh VA. The effect of van der Waals' forces on aerosol filtration with fibrous filters. Colloid J. 2000;62(6):714‐720. 10.1023/A:1026678725025. [DOI] [Google Scholar]
- 53. Wang CS, Otani Y. Removal of nanoparticles from gas streams by fibrous filters: a review. Ind Eng Chem Res. 2013;52(1):5‐17. 10.1021/ie300574m. [DOI] [Google Scholar]
- 54. Wang J, Chen DR, Pui DYH. Modeling of filtration efficiency of nanoparticles in standard filter media. J Nanopart Res. 2007;9(1):109‐115. 10.1007/s11051-006-9155-9. [DOI] [Google Scholar]
- 55. Soemoto K, Wakimoto T, Katoh K. Removal of fine particles on a wall by high‐frequency turbulence added air flow. Int J Flow Control. 2013;5(1):47‐58. 10.1260/1756-8250.5.1.47. [DOI] [Google Scholar]
- 56. Zhang S, Zhang S, Zuo P, et al. Anti‐biofouling and self‐cleaning surfaces featured with magnetic artificial cilia. ACS Appl Mater Interfaces. 2020;12(24):27726‐27736. 10.1021/acsami.0c05403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Van Oosten CL, Bastiaansen CWM, Broer DJ. Printed artificial cilia from liquid‐crystal network actuators modularly driven by light. Nat Mater. 2009;8(8):677‐682. 10.1038/nmat2487. [DOI] [PubMed] [Google Scholar]
- 58. Gorissen B, De Volder M, Reynaerts D. Pneumatically‐actuated artificial cilia array for biomimetic fluid propulsion. Lab Chip. 2015;15(22):4348‐4355. 10.1039/c5lc00775e. [DOI] [PubMed] [Google Scholar]
- 59. Poortinga AT, Smit J, Van Der Mei HC, Busscher HJ. Electric field induced desorption of bacteria from a conditioning film covered substratum. Biotechnol Bioeng. 2001;76(4):395‐399. 10.1002/bit.10129. [DOI] [PubMed] [Google Scholar]
- 60. Huang J, Wang Z, Zhang J, Zhang X, Ma J, Wu Z. A novel composite conductive microfiltration membrane and its anti‐fouling performance with an external electric field in membrane bioreactors. Sci Rep. 2015;5(9268):1–8. 10.1038/srep09268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Feng T, Wu J, Chai K, Yang P. The anti‐biofouling behavior of high voltage pulse electric field (HPEF) mediated by carbon fiber composite coating in seawater. Bioelectrochemistry. 2018;123:137‐144. 10.1016/j.bioelechem.2018.04.015. [DOI] [PubMed] [Google Scholar]
- 62. Moran JL, Cottrill AL, Benck JD, et al. Noble‐gas‐infused neoprene closed‐cell foams achieving ultra‐low thermal conductivity fabrics. RSC Adv. 2018;8(38):21389‐21398. 10.1039/c8ra04037k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Shanks RA, Kong I. General purpose elastomers: structure, chemistry, physics and performance. Advanced Structured Materials. Vol 11. Berlin, Heidelberg: Springer; 2013:11‐45. 10.1007/978-3-642-20925-3_2. [DOI] [Google Scholar]
- 64. Killick EM. Physiological response to breathing hot air. J Hyg (Lond). 1932;32(3):332‐339. 10.1017/S0022172400018052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Sagripanti JL, Routson LB, Lytle CD. Virus inactivation by copper or iron ions alone and in the presence of peroxide. Appl Environ Microbiol. 1993;59(12):4374‐4376. 10.1128/aem.59.12.4374-4376.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Grass G, Rensing C, Solioz M. Metallic copper as an antimicrobial surface. Appl Environ Microbiol. 2011;77(5):1541‐1547. 10.1128/AEM.02766-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Haldar J, An D, De Cienfuegos LÁ, Chen J, Klibanov AM. Polymeric coatings that inactivate both influenza virus and pathogenic bacteria. Proc Natl Acad Sci USA. 2006;103(47):17667‐17671. 10.1073/pnas.0608803103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Lin Q, Lim JYC, Xue K, et al. Sanitizing agents for virus inactivation and disinfection. View. 2020;1(2):1‐26. 10.1002/viw2.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Mann EE, Manna D, Mettetal MR, et al. Surface micropattern limits bacterial contamination. Antimicrob Resist Infect Control. 2014;3(1):1‐8. 10.1186/2047-2994-3-28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Michalska M, Gambacorta F, Divan R, et al. Tuning antimicrobial properties of biomimetic nanopatterned surfaces. Nanoscale. 2018;10(14):6639‐6650. 10.1039/c8nr00439k. [DOI] [PubMed] [Google Scholar]
- 71. Buonanno M, Welch D, Shuryak I, Brenner DJ. Far‐UVC light (222 nm) efficiently and safely inactivates airborne human coronaviruses. Sci Rep. 2020;10(1):1‐8. 10.1038/s41598-020-67211-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Lippmann M. Health effects of ozone a critical review. J Air Pollut Control Assoc. 1989;39(5):672‐695. 10.1080/08940630.1989.10466554. [DOI] [PubMed] [Google Scholar]
- 73. Richards T. Particle clogging in porous media: filtration of a smectite solution. 2010:1–31.
- 74. Zong Q, Liu Z, Liu H, Yang H. Backwashing performance of self‐cleaning screen filters in drip irrigation systems. PLoS One. 2019;14(12):1‐18. 10.1371/journal.pone.0226354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Bergman MS, Viscusi DJ, Zhuang Z, Palmiero AJ, Powell JB, Shaffer RE. Impact of multiple consecutive donnings on filtering facepiece respirator fit. Am J Infect Control. 2012;40(4):375‐380. 10.1016/j.ajic.2011.05.003. [DOI] [PubMed] [Google Scholar]
- 76. Juang PSC, Tsai P. N95 respirator cleaning and reuse methods proposed by the inventor of the N95 mask material. J Emerg Med. 2020;58(5):817‐820. 10.1016/j.jemermed.2020.04.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1. Supporting Information.
Data Availability Statement
The data and code that support the findings of this study are available from the corresponding author upon request.


