Abstract
In terrain analysis and hydrological modeling, surface depressions (or sinks) in a digital elevation model (DEM) are commonly treated as artifacts and thus filled and removed to create a depressionless DEM. Various algorithms have been developed to identify and fill depressions in DEMs during the past decades. However, few studies have attempted to delineate and quantify the nested hierarchy of actual depressions, which can provide crucial information for characterizing surface hydrologic connectivity and simulating the fill-merge-spill hydrological process. In this paper, we present an innovative and efficient algorithm for delineating and quantifying nested depressions in DEMs using the level-set method based on graph theory. The proposed level-set method emulates water level decreasing from the spill point along the depression boundary to the lowest point at the bottom of a depression. By tracing the dynamic topological changes (i.e., depression splitting/merging) within a compound depression, the level-set method can construct topological graphs and derive geometric properties of the nested depressions. The experimental results of two fine-resolution Light Detection and Ranging-derived DEMs show that the raster-based level-set algorithm is much more efficient (~150 times faster) than the vector-based contour tree method. The proposed level-set algorithm has great potential for being applied to large-scale ecohydrological analysis and watershed modeling.
Introduction
Surface depressions, also known as sinks or pits, are abundant in digital elevation models (DEMs). In traditional hydrological modeling, surface depressions in a coarse-resolution DEM are commonly treated as artifacts and thus filled and removed to generate a so-called depressionless DEM, which can then be used to generate a fully connected stream network. In reality, however, surface depressions in DEMs are commonly a combination of spurious and actual terrain features (Lindsay and Creed 2006). It is also common to see that small depressions are nested within a larger compound depression, forming a nested hierarchical structure. Spurious depressions typically result from data noise, interpolation error, and the limited resolution of DEMs (Li et al. 2011; Woodrow et al. 2016). During the past decade, Light Detection and Ranging (LiDAR) technology has increasingly been used to acquire elevation data and produce fine-resolution DEMs. Therefore, it is no longer justifiable to treat all depressions in DEMs as artifacts and simply eliminate them from hydrological analysis. LiDAR-derived DEMs can capture and represent actual surface depressions, especially in glaciated and karst landscapes (Lang and McCarty 2009; Huang et al. 2014; Wu et al. 2014; Wu, Deng, et al. 2016; Wu and Lane 2016). For example, the Prairie Pothole Region of North America is dotted with millions of depressional wetlands, which are typically small and shallow. These wetlands provide important ecological and hydrological functions (Cohen et al. 2016; Evenson et al. 2016; Rains et al. 2016; Vanderhoof et al. 2016; Vanderhoof et al. 2017; Waz and Creed 2017; Wu and Lane 2017; Wu 2018). It is critical to delineate these wetland depressions, integrate them into hydrological modeling, and assess their impacts on downstream waters (USEPA 2015; Lane et al. 2018).
Various algorithms for identifying and filling depressions have been developed in the past decades. These algorithms can be generally grouped into three categories: depression filling (Jenson and Domingue 1988; Planchon and Darboux 2002; Wang and Liu 2006), depression breaching (Soille 2004; Lindsay and Dhun 2015), and hybrid methods combining both filling and breaching approaches (Martz and Garbrecht 1999; Lindsay 2016a). Depression filling algorithms remove depressions by raising the elevation value of a depression cell in a DEM to the “spill elevation” — the minimum elevation value that a grid cell needs to be raised in order to spill out from that cell to an outlet cell on the edge of the DEM (Wang and Liu 2006). In contrast, depression breaching algorithms lower the elevation value of grid cells that are adjacent to the depression cells (Lindsay 2016a). The priority-flood algorithm proposed by Wang and Liu (2006) is one of the most widely used depression filling algorithms implemented in common geographic information system (GIS) software packages. The algorithm works by flooding DEM cells inwards from the outlet cells on the DEM edges using a priority queue data structure to determine the sequence of cells to be flooded. A number of variants of the priority-flood algorithm have been proposed to increase the computational efficiency and deal with flat areas in DEMs (Barnes et al. 2014; Yu et al. 2014; Zhou et al. 2016).
To date, most depression filling or breaching approaches focus on identifying and removing depressions from DEMs. Although it is possible to distinguish actual depressions from spurious depressions based on certain thresholds (e.g., size, depth, volume) (Lindsay 2009, 2016b), few studies have attempted to delineate and quantify the nested hierarchy of actual depressions, which can provide crucial information for characterizing surface hydrologic connectivity and simulating the fill-merge-spill hydrological process (Shaw et al. 2013; Leibowitz et al. 2016; Wu and Lane 2017). Wu et al. (2015) proposed a vector-based approach for delineating the nested hierarchy of depressions and characterizing their topological structure using a “localized contour tree” method. The algorithm operates by generating contours on a DEM and automatically identifying concentric contours associated with depressions. The localized contour tree method has been adopted and adapted to detect and delineate various landscape features, such as depressional wetlands (Wu and Lane 2016, 2017), karst sinkholes (Wu, Deng, et al. 2016), glaciated drumlins (Wang et al. 2017), coastal properties (Wu, Su, et al. 2016), urban centers (Chen et al. 2017), and individual tree crowns (Wu, Yu, et al. 2016). Nevertheless, this vector-based approach has limitations. First, information is lost during the raster-to-vector contouring process. Some shallow depressions might not show up on the contour map if the depth of depressions is smaller than the user-specified contour interval. Consequently, these shallow depressions might not be detectable because they are not represented in the contour map. This is particularly an issue for DEMs with relatively flat terrains. Second, this vector-based method assumes that all depressions are closed-loop depressions represented by a series of concentric contours. This might not be the case for those depressions located along the DEM edges or internal depressions not enclosed by closed contours. Third, the contour tree method is computationally demanding due to the fact the numerous vector contours might be generated and processed, making it difficult to apply the method to a large geographic area. Therefore, there remains a need for an efficient method that can delineate nested surface depressions and quantify their geometric and topological properties at watershed and landscape scales.
In this paper, we present an innovative and efficient raster-based algorithm for delineating and quantifying nested depressions in DEMs using level-set method based on graph theory. The proposed level-set method emulates water level decreasing from the spill point along the depression boundary to the lowest point at the bottom of a depression. By tracing the dynamic topological changes (i.e., depression splitting/merging) within a compound depression, the level-set method can construct topological graphs and derive geometric properties of the nested depressions. It should be noted that our proposed method is not a depression filling algorithm. Instead, it offers a good alternative to traditional depression filling approaches, particularly when the information about the nested hierarchical structure of depressions is desirable.
Methodology
Outline
Our proposed level-set method for delineating and quantifying nested depressions is an automated approach consisting of several steps: (1) DEM filtering; (2) identifying depressions using the priority-flood algorithm; (3) delineating nested depressions using the level-set method; and (4) characterizing nested depressions. DEM filtering is an image preprocessing step to smooth the LiDAR DEM and suppress data noise. The depression filling algorithm (i.e., priority-flood) is then used to extract a subset of the smoothed DEM consisting of only depression pixels. Based on the subset DEM, the level-set method can delineate nested depressions, characterize their hierarchical structure, and compute geometric properties. The details of each computational step are described below.
DEM Filtering
All digital elevation data contain some level of error and uncertainty resulting from various sources of error, such as data collection, processing, and interpolation (Fisher and Tate 2006). In general, DEM errors can be grouped into two categories: systematic and random errors (Liu and Jezek 1999). Systematic errors are usually corrected before the DEM is released (Li et al. 2011). Random errors are relatively difficult to discern. As a result, they are usually not corrected and still exist in the DEM. Therefore, it is a common practice to suppress “data noise” by smoothing the DEM before using it for terrain analysis and hydrological modeling. Some of the commonly used filters for smoothing DEMs include the median and mean filters, which are available in most GIS software packages, such as the Focal Statistics tool in ArcGIS (Redlands, California). The Whitebox Geospatial Analysis Tools, an open-source GIS software package, offers more advanced filters, such as the Gaussian filter, adaptive filter, and K-Nearest mean filter (Lindsay 2016b). Hereafter, we will refer to the processed or smoothed DEM using the 3 × 3 median filter as the original DEM for all subsequent analysis.
Identifying Depressions Using the Priority-Flood Algorithm
After generating the smoothed DEM, we use the priority-flood algorithm (Wang and Liu 2006; Zhou et al. 2016) to identify and fill the sinks in the DEM, which results in a filled DEM free of sinks (i.e., a depressionless DEM). Then we subtract the original DEM from the depressionless DEM to create an elevation difference grid in which each cell value represents the depression depth. The grid cells with an elevation difference value of 0 are non-depression cells, which can be eliminated from further analysis. Subsequently, the elevation difference grid is converted to a binary image, in which a value of 1 represents depression cells (elevation change > 0), whereas a value of 0 represents non-depression cells. Each depression is composed of a varying number of connected cells with a value of 1. By applying the region-group algorithm (van der Walt et al. 2014), information about each depression (e.g., size, volume, and depth) can be obtained. Since depressions in a DEM are commonly a combination of actual and artifact depressions (Lindsay and Creed 2006), one can set certain thresholds (e.g., size and depth), which could be informed by the root-mean-square error (RMSE) of the DEM’s source, to remove those small and shallow depressions that are assumed to be artifacts from the binary image. Finally, the refined binary image is used as a mask to clip the original DEM, resulting in a subset DEM representing the population of assumed existing depressions, which will be used as the input to the level-set algorithm to delineate the nested hierarchy of depressions.
Delineating Nested Depressions Using Level-Set Method
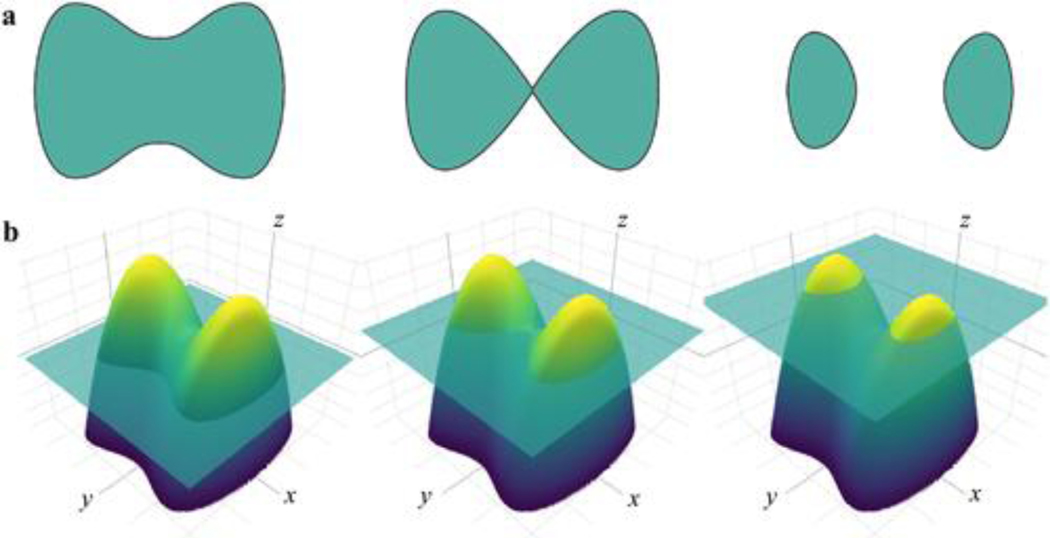
The level-set method was first proposed by Osher and Sethian (1988) to compute and track the motion of an interface (i.e., a curve or surface) evolving over time according to a speed function in two- or three-dimensional space. It has been widely used in many disciplines, such as image segmentation and object recognition, computational geometry, computer vision, and computational fluid dynamics (Osher and Fedkiw 2001; Zhang et al. 2010; Tang et al. 2013; Van Dijk et al. 2013; Li et al. 2016). Figure 1 illustrates the key ideas about the level-set method. In Figure 1a, we see that a shape is undergoing deformation by splitting into two (from left to right). Alternatively, we can also see it as two shapes expanding and merging (from right to left). Although we only show three shapes here, one can imagine that the deformation process is a continuous motion that can result in numerous shapes. To keep track of the shape changes and describe the deformation numerically, one would need to parameterize the boundary of the shape and follow its evolution. It may seem intuitive to evolve explicitly the boundary points based on certain parameters (e.g., moving direction and speed). However, there are some drawbacks to using this approach. Assuming that there is an initial set of points defining the evolving boundary, points will need to be removed or inserted in the boundary when it is shrinking or expanding, and the distance between boundary points should be kept small enough to ensure a smooth evolution. This could become a challenging task during algorithm implementation, particularly when there is a topological change (e.g., splitting and merging of shapes).
Figure 1.
Illustration of the level-set method for numerical analysis of shapes and surfaces. (a) A shape undergoing deformation by splitting into two parts. (b) Modeling the evolution of the shape shown in (a) through its level-set function.
To overcome the challenge mentioned above, the level-set method was proposed (Osher and Sethian 1988). Instead of explicitly evolving the boundary of a shape, we indirectly evolve an xy plane and a surface, and the boundary of the shape is defined as all the points where the xy plane intersects the surface. For example, the hypothetical surface in Figure 1b is the graph of a level-set function (φ) determining the shapes in Figure 1a. The light-green square in Figure 1b represents the xy plane. The boundary of the shape can then be defined implicitly as the zero-level set (φ = 0), while the interior of the shape is the set of points in the xy plane where the level-set is positive (φ > 0). Similarly, the exterior of the shape is defined as the set of points in the xy plane where the level-set is negative (φ < 0). By merely moving the xy plane upward or downward (see Figure 1b) and deriving the zero-level set (i.e., the intersection of the xy plane and the surface), topological changes (e.g., splitting and merging) of the shape can be handled naturally without having to explicitly parameterize the evolution of the shape itself. This example shows that it can be much easier to model the evolution of a shape through its level-set function than the shape directly, especially when the shape undergoes complicated deformations involving topological change. This advantage of the level-set method makes it an efficient and effective tool for modeling time-varying objects, such as topographic depressions in a DEM where depressions can merge as water level increases during wet periods or split as water level decreases during dry periods.
To adopt the level-set method for delineating the nested hierarchy of topographic depressions in DEMs, we define the level-set function φ to have the following properties: (1)
where z represents a point (x, y) on the surface; E(z) is the surface elevation of point z; and his the elevation of the xy plane intersecting the surface. In essence, the level-set function with these two properties transforms a surface into a binary image. When intersecting the surface with the xy plane, surface points above the xy plane are labeled as 0, whereas surface points beneath the xy plane are labeled as 1. The resulting binary image identifies the inundated region based on the elevation of the xy plane, which can vary between the lowest point and the highest point of the depression.
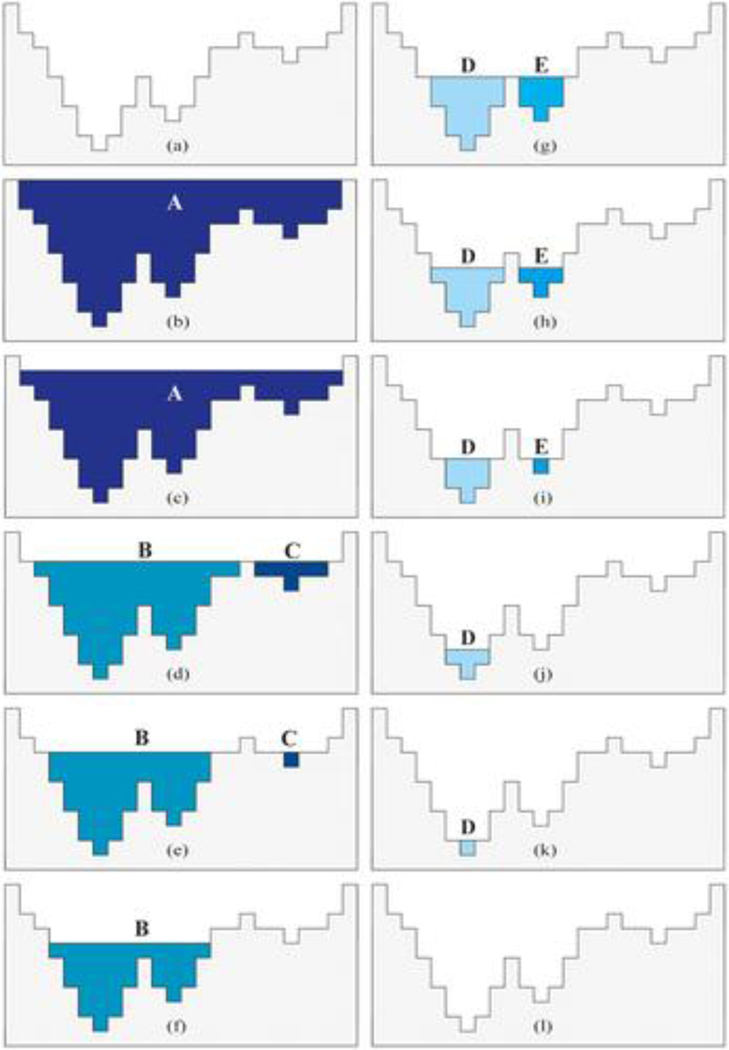
Figure 2 illustrates the procedure for identifying nested depressions using the level-set method. Given the hypothetical compound depression shown in Figure 2a, our goal was to identify each individual depression nested within this compound depression and characterize its topological relationship (i.e., the nested hierarchy). Our proposed level-set method emulates water level decreasing from the spill point along the depression boundary (see Figure 2b) to the lowest point at the bottom of the depression (see Figure 2l). In other words, we emulate the depression changing from a fully inundated condition to a totally dry condition. Assuming that the water level is decreasing (i.e., the xy plane is moving downward) at a constant rate, the key step of the level-set method is to identify the elevation where topological change occurs. In the example shown in Figure 2, there are two occurrences of topological change, namely Figure 2c, 2d, 2f, and 2g. Depression A in Figure 2c splits into Depressions B and C in Figure 2d, while Depression B in Figure 2f splits into Depressions D and E in Figure 2g. The other figures are intermediate steps where no topological change occurs. By tracing the dynamic topological changes (splitting and merging) within the compound depression, the level-set method can construct topological graphs and derive geometric attributes of the nested depressions.
Figure 2.
Illustration of the level-set method for delineating nested depressions. (a)–(l) The level-set method emulates water level decreasing from the spill point along the depression boundary to the lowest point at the bottom of the depression.
Characterizing Nested Depressions
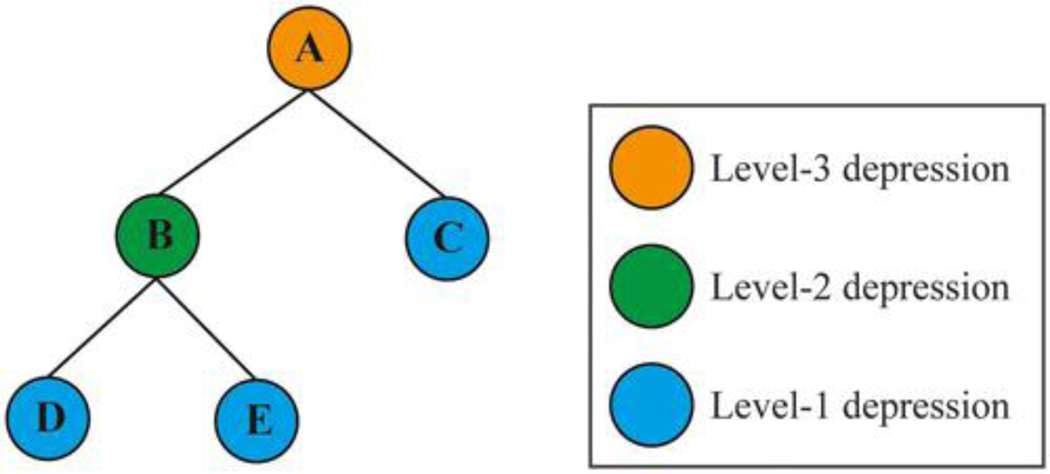
The nested hierarchy of a compound depression can be represented using a tree graph, which we refer to as the depression tree. Figure 3 shows the corresponding depression tree representation for the compound depression shown in Figure 2. The depression tree consists of a set of nodes and links. Each node represents one depression, whereas the links between nodes represent the containment relationship between depressions. In general, there are three types of nodes: leaf node, root node, and internal node. All leaf nodes represent the lowest level (i.e., Level-1) depression, whereas the root node represents the highest level depression. Each leaf node has exactly one node above it, which is called the internal node. Each internal node represents a higher level depression than the depressions beneath it. The root node can be seen as the highest level internal node. Note that a depression tree can be composed of multiple leaf nodes and internal nodes. However, each depression tree can only have one root node, which represents the maximum extent of the depression complex. The depression tree graph is built up by emulating the inundation process of rising water within the depression complex. When multiple depressions merge, a higher level depression is formed. For example, the merger of two Level-1 depressions results in a Level-2 depression, whereas the merger of a Level-1 depression and a Level-2 depression results in a Level-3 depression (see Figure 3). The depression tree graph gives a compact and concise representation for the compound depression. Each depression tree represents one disjoint depression (simple or compound depression). An entire area can be composed of a set of trees, which is appropriately called a forest.
Figure 3.
A depression tree representation of the compound depression shown in Figure 2.
Algorithm Implementation
We have implemented the proposed level-set algorithm using Python, which is a cross-platform programming language that runs on multiple operating systems, such as Linux, Windows, and Mac OS. Several scientific libraries are used for the algorithm, including NumPy (van der Walt et al. 2011), SciPy, scikit-image (van der Walt et al. 2014), and matplotlib. Additionally, the Geospatial Data Abstraction Library is used to read and write DEM files. The source code of our proposed level-set algorithm is publicly available for download at http://gishub.org/2018-JAWRA (accessed May 25, 2018). The user only needs to provide an input DEM, specify an output directory, and set three parameters, including the minimum depression size, minimum depression depth, and slicing interval (i.e., the elevation interval at which the xy plane is moving downward from the spill point to the lowest point within a depression). The program then executes the level-set algorithm automatically to derive and characterize the nested hierarchy of depressions. The output datasets include a depression ID image, a depression-level image, a depression-polygon shapefile, and a comma-separated value (CSV) file storing information about each depression (i.e., depression unique ID, hierarchical level, size, volume, mean depth, maximum depth, lowest elevation, spill elevation, nested depression IDs).
Experimental Results
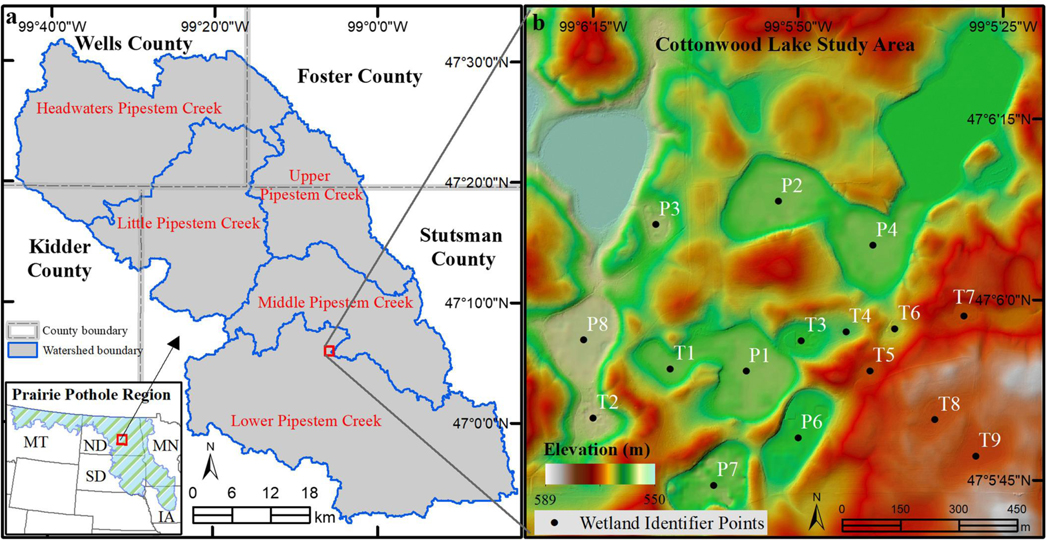
We conducted two experiments to evaluate the performance of the level-set algorithm, which were conducted on a 64-bit Linux machine with a quad-core Intel i7-7700 CPU and 16 GB RAM. The test datasets included a 0.5-m resolution LiDAR DEM with topobathy for the Cottonwood Lake Study Area (CLSA) and a 1-m resolution LiDAR DEM for the Pipestem watershed in the Prairie Pothole Region of North Dakota (see Figure 4). Both test datasets can be downloaded with the algorithm source code for reproducible research through the download link provided in the Algorithm Implementation section.
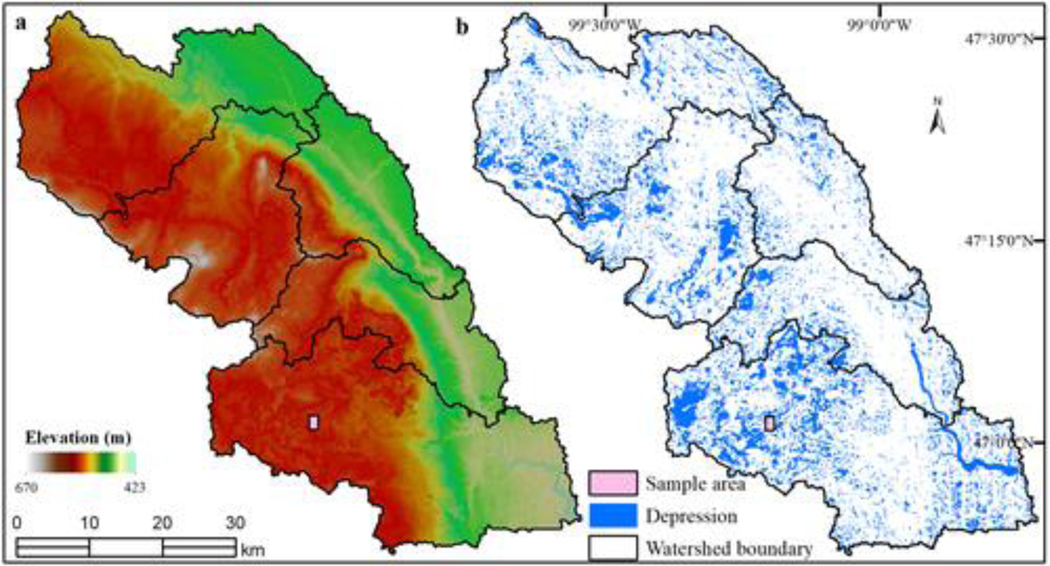
Figure 4.
(a) Location map of the Pipestem watershed in the Prairie Pothole Region of North Dakota. (b) Shaded relief map of LiDAR DEM with topobathy for the Cottonwood Lake Study Area (CLSA) in North Dakota; wetlands identified with the T and P prefix are typified by temporary and permanent flood regimes, respectively (e.g., Winter and Rosenberry 1998). LiDAR, Light Detection and Ranging; DEM, digital elevation model; MT, Montana; ND, North Dakota; SD, South Dakota; MN, Minnesota; IA, Iowa.
Case Study 1:
Bathymetric LiDAR DEM for Cottonwood Lake
The case study area of our first experiment is the CLSA, which is located in Stutsman County, North Dakota (see Figure 4). The CLSA is one of the three long-term wetland ecosystem monitoring sites established by the United States Geological Survey (USGS) in the Prairie Pothole Region of North America (Mushet and Euliss 2012). It has been an active research area for the past decades (e.g., Winter and Rosenberry 1998; Huang et al. 2011; Mushet and Euliss 2012; LaBaugh et al. 2016; Chu 2017; Wu and Lane 2017; Neff and Rosenberry 2018). Field-based wetland identifier points (see Figure 4b) were established by CLSA USGS researchers to aid in the identification of wetlands and facilitate research that investigates the impacts of land use change and natural climate variability on the wetland ecosystem in the Prairie Pothole Region (Mushet and Erickson 2017). The extensive history (1979–2015) of data collection on water surface elevations for these wetlands (Mushet et al. 2016) makes the CLSA a great case study area for studying surface hydrologic connectivity of the prairie wetland ecosystems.
The airborne LiDAR data for the CLSA we used in this experiment was collected on May 17, 2008. The LiDAR data were processed by USGS personnel to produce an initial bare-earth DEM (Mushet et al. 2017). Additional DEM processing to incorporate the bathymetry of the study wetlands (see wetland identifier points in Figure 4b) was done using survey-grade global positioning system data collected by soundings of the bottom of each wetland (Mushet et al. 2017). The refined LiDAR-derived DEM with topobathy was produced with a 0.5-m pixel resolution. The RMSE vertical accuracy of the LiDAR DEM was 6.5 cm tested against control points (Mushet et al. 2017). We selected a 1.3 × 1.3 km study area encompassing the CLSA from the LiDAR DEM to test the level-set algorithm. The shaded relief map of the LiDAR DEM with topobathy is shown in Figure 4b. The elevation in this study area ranges from 550.4 to 589.3 m, with an average elevation of 565.6 m and a standard deviation of 7.1 m.
To delineate the nested hierarchy of depressions in CLSA using the level-set method, we set three parameters, including the minimum depression size (2,000 m2), minimum depression depth (0.3 m), and slicing interval (0.2 m). The parameters of the minimum depression size and minimum depression depth were chosen based on the fact that all CLSA wetlands (see wetland identifier points in Figure 4b) are larger than 2,000 m2 and deeper than 0.3 m (Mushet and Erickson 2017). Similar to the contour interval parameter in the vector-based contour tree method (Wu et al. 2015), we suggest that the slicing interval should not be smaller than the DEM vertical accuracy. Setting the slicing interval as two to three times of the DEM vertical accuracy is recommended. Using the parameters mentioned above, the level-set algorithm was then executed to automatically delineate and characterize nested depressions. The average running time of the level-set algorithm was 0.75 s, which is ~150 times faster than the vector-based contour tree method that took 117 s for the same DEM. The resulting images of unique depressions and their corresponding depression hierarchy from the level-set algorithm are shown in Figure 5a, and 5b, respectively. The algorithm also exports the geometrical and topological attributes of each individual depression (see Figure 5a) as a CSV file (Table 1).
Figure 5.

Delineation of nested depressions in the CLSA using the level-set method. (a) Image of individual depressions overlaid on DEM hillshade. (b) Image of depression hierarchy overlaid on DEM hillshade. (c) Black and white aerial photograph acquired on July 2, 1957. (d) Four-band (Red, Green, Blue, and Near-infrared [RGBN]) aerial photograph acquired on July 31, 2012 (source of aerial photographs: North Dakota GIS Hub Data Portal).
Table 1.
Characteristics of nested depressions in CLSA (see Figure 5a)
| Depression ID | Level | Area (m2) | Volume (m3) | Mean depth (m) | Maximum depth (m) | Lowest elevation (m) | Spill elevation (m) | Children IDs | Region ID |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 226,232 | 666,183 | 2.94 | 5.16 | 558.11 | 563.28 | [2, 3] | 1 |
| 2 | 2 | 175,406 | 218,509 | 1.25 | 2.96 | 558.11 | 561.08 | [4, 5] | 1 |
| 3 | 1 | 2,736 | 438 | 0.16 | 0.31 | 560.96 | 561.08 | 1 | |
| 4 | 1 | 33,901 | 34,478 | 1.02 | 1.76 | 558.11 | 559.88 | 1 | |
| 5 | 1 | 32,710 | 27,463 | 0.84 | 1.44 | 558.43 | 559.88 | 1 | |
| 6 | 1 | 2,548 | 588 | 0.23 | 0.56 | 556.18 | 556.74 | 2 | |
| 7 | 1 | 3,643 | 527 | 0.14 | 0.41 | 560.91 | 561.32 | 3 | |
| 8 | 1 | 56,564 | 20,290 | 0.36 | 0.43 | 551.32 | 551.75 | 4 | |
| 9 | 1 | 4,245 | 2,326 | 0.55 | 1.12 | 557.05 | 558.17 | 5 | |
| 10 | 1 | 27,623 | 30,946 | 1.12 | 2.04 | 555.00 | 557.04 | 6 | |
| 11 | 3 | 98,493 | 311,711 | 3.16 | 5.46 | 557.93 | 563.39 | [12, 13] | 7 |
| 12 | 2 | 55,592 | 77,730 | 1.40 | 2.46 | 557.93 | 560.39 | [14, 15] | 7 |
| 13 | 1 | 2,624 | 863 | 0.33 | 0.69 | 559.70 | 560.39 | 7 | |
| 14 | 1 | 25,798 | 13,677 | 0.53 | 1.06 | 557.93 | 558.99 | 7 | |
| 15 | 1 | 3,909 | 596 | 0.15 | 0.43 | 558.56 | 558.99 | 7 | |
| 16 | 1 | 3,336 | 727 | 0.22 | 0.66 | 569.52 | 570.18 | 8 | |
| 17 | 1 | 2,042 | 337 | 0.16 | 0.38 | 568.32 | 568.70 | 9 | |
| 18 | 1 | 2,228 | 613 | 0.27 | 0.80 | 569.53 | 570.33 | 10 | |
| 19 | 1 | 6,277 | 2,684 | 0.43 | 1.09 | 556.00 | 557.09 | 11 | |
| 20 | 2 | 63,461 | 191,783 | 3.02 | 5.69 | 558.00 | 563.69 | [21, 22] | 12 |
| 21 | 1 | 29,264 | 65,802 | 2.25 | 3.29 | 560.00 | 563.29 | 12 | |
| 22 | 1 | 31,666 | 101,089 | 3.19 | 5.29 | 558.00 | 563.29 | 12 | |
| 23 | 1 | 10,232 | 4,882 | 0.48 | 1.29 | 577.00 | 578.30 | 13 | |
| 24 | 1 | 19,938 | 23,678 | 1.19 | 2.20 | 576.19 | 578.39 | 14 |
In total, 24 individual depressions were detected in CLSA (see Figure 5a), the hierarchical level of which ranged from Level-1 to Level-3 (see Figure 5b). The number of Level-1, Level-2, and Level-3 depressions was 19, 3, and 2, respectively (Table 1). As shown in the “Region ID” column in Table 1, these 24 individual depressions formed 14 disjoint depression complexes (i.e., depressions resulting from the fully filled condition). A region associated with multiple individual depressions indicates that the region is a compound depression with a varying number of depressions nested inside, whereas a region associated with only one depression indicates that the region is a simple depression without nested depressions. In Figure 5a, for example, we can see that Depressions ID-4 (Wetland P2) and ID-5 (Wetland P4) are nested within Depression ID-2. Similarly, Depressions ID-14 (Wetland P1) and ID-15 (Wetland T1) are nested within Depression ID-12. The information about the topological relationships between depressions is recorded in the “Children IDs” column of the exported CSV file (see Table 1).
The fill-merge-spill hydrological processes among wetland depressions can be inferred from the depression hierarchy image (Figure 5b) and further validated using high-resolution aerial photographs (Figures 5c, 5d). For example, Wetlands P2 and P4 used to be disjoint wetlands during relatively dry periods in the 1950s (see Figure 5c). However, these two wetlands have undergone fill-merge hydrological processes to form a larger wetland complex (see Figure 5d) due to the extended wet period in this region since the 1990s (McKenna et al. 2017).
Case Study 2:
Topographic LiDAR DEM for Pipestem Watershed
To test the applicability of the proposed level-set algorithm for delineating nested depressions from DEMs at watershed and landscape scales, we chose the Pipestem River watershed in the state of North Dakota (see Figure 4a). The Pipestem watershed (2,770 km2) is an 8-digit Hydrologic Unit Code consisting of five subwatersheds, including the Headwaters Pipestem Creek, Little Pipestem Creek, Upper Pipestem Creek, Middle Pipestem Creek, and Lower Pipestem Creek. Land use and land cover of the Pipestem watershed included wetlands (12.7%), hay and pasture (13.1%), herbaceous (25.9%), and cultivated crops (44.1%) (Homer et al. 2015). According to the National Wetlands Inventory developed for this region in the 1980s, there were 32,023 wetland polygons distributed across the Pipestem watershed, with a total wetland area of 279.5 km2 (USFWS 2010). The median wetland size is only 1,770 m2 and the ponding depth of most wetlands is <1 m. Due to its sensitivity to land use change and natural climate variability, the Pipestem watershed is increasingly being used by researchers as a test watershed to study wetland hydrologic connectivity and its impacts on downstream waters (e.g., USEPA 2015; Evenson et al. 2016; Wu and Lane 2016, 2017; Nasab et al. 2017; Brooks et al. 2018; Neff and Rosenberry 2018).
The LiDAR data for the Pipestem watershed we used in this experiment were acquired in late October and early November of 2011 as part of the data acquisition campaign of James River Basin LiDAR Phase 2. We downloaded the LiDAR data from the North Dakota LiDAR Dissemination Mapservice (http://lidar.swc.nd.gov/, accessed May 25, 2018). The bare-earth LiDAR DEM can be downloaded by image tiles (2 × 2 km) with 1-m pixel resolution. The RMSE vertical accuracy of the LiDAR DEM is 15 cm. The Pipestem watershed consists of 785 DEM tiles (22.5 GB). To increase computational efficiency and reduce the dataset to a manageable size, we resampled the image tiles to 3-m resolution and mosaicked them to create a seamless LiDAR DEM (24,813 rows × 25,782 columns; file size: 2.4 GB) for the Pipestem watershed. The shaded relief map of the LiDAR DEM is shown in Figure 6a. The elevation in the watershed ranges from 423.9 to 670.7 m, with an average elevation of 534.2 m and a standard deviation of 44.2 m. Most wetland depressions are concentrated in the hummocky terrain areas on the west side of the watershed (see red areas in Figure 6a).
Figure 6.
(a) Shaded relief map of LiDAR DEM for the Pipestem watershed, North Dakota. (b) Delineation of nested depressions using the level-set method (min size = 100 m2; interval = 0.2 m).
Based on the 3-m LiDAR DEM, we delineated depressions for the Pipestem watershed using the level-set algorithm with a minimum depression size of 100 m2, a minimum depression depth of 0.3 m, and a slicing interval of 0.2 m, which are similar to the parameters used in the vector-based contour tree method for this region (Wu and Lane 2017). In total, the Pipestem watershed contained 54,849 depressions across 15 depression hierarchical levels (Table 2). The number of Level-1, Level-2, and Level-3 depressions was 47,255, 5,413, and 1,093, respectively, which accounted for 98.01% of the total number of depressions. After all possible fill-merge-spill processes, the Pipestem watershed ended up with 33,421 depression complexes (regions) at the final stage (Figure 6b). A sample area illustrating such fill-merge-spill hydrological processes within the watershed is shown in Figure 7. In addition to characterizing the nested hierarchy of depressions, the level-set algorithm also computed various properties of each depression, such as depression area, volume, depth, lowest elevation, spill elevation, children depressions, etc. (see Table 1). These properties can provide crucial information for fine-scale hydrological analysis and watershed modeling in the Prairie Pothole Region.
Table 2.
Depression delineation results for Pipestem watershed using level-set method (min depression size = 100 m2; min depression depth = 0.3 m; slicing interval = 0.2 m)
| Depression level | Frequency | Percentage |
|---|---|---|
| 1 | 47,255 | 86.15 |
| 2 | 5,413 | 9.87 |
| 3 | 1,093 | 1.99 |
| 4 | 422 | 0.77 |
| 5 | 206 | 0.38 |
| 6 | 122 | 0.22 |
| 7 | 78 | 0.14 |
| 8 | 62 | 0.11 |
| 9 | 48 | 0.09 |
| 10 | 36 | 0.07 |
| 11 | 33 | 0.06 |
| 12 | 27 | 0.05 |
| 13 | 20 | 0.04 |
| 14 | 18 | 0.03 |
| 15 | 16 | 0.03 |
Figure 7.
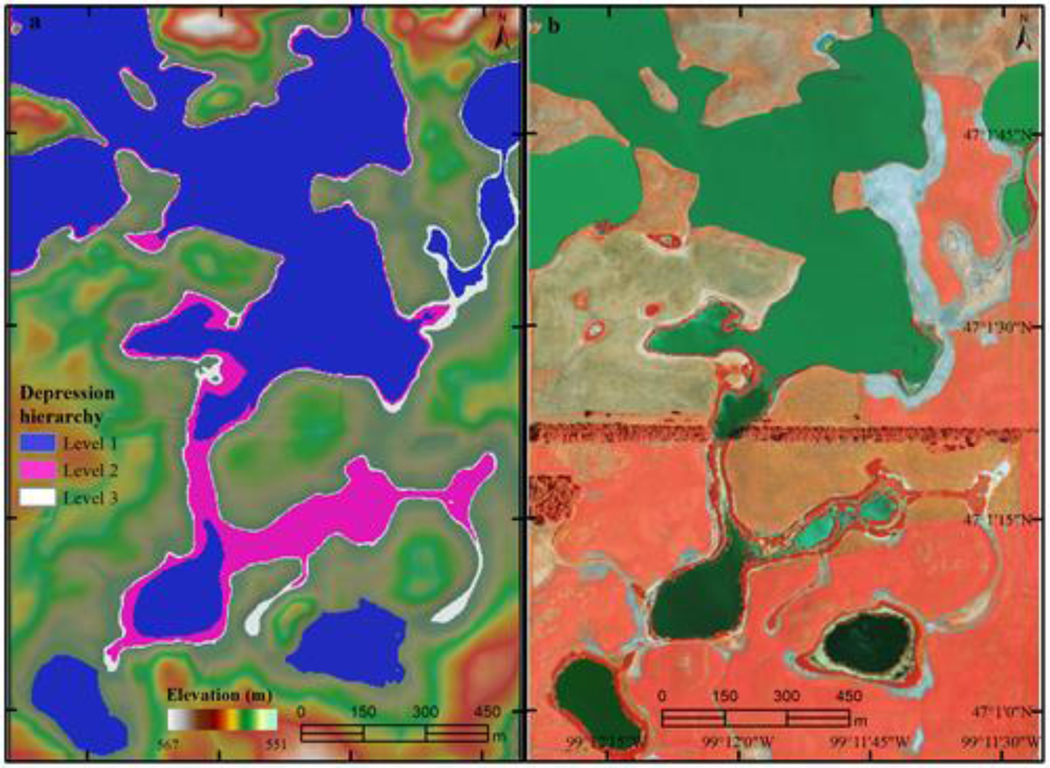
Sample area marked by the pink rectangle in Figure 6. (a) Nested depressions overlaid on the shaded relief map. (b) Four-band (RGBN) aerial photograph acquired on July 31, 2012.
Using the specified parameters mentioned above (minimum depression size = 100 m2; slicing interval = 0.2 m), the level-set algorithm took 281 s to delineate nested depressions for the Pipestem watershed, which is ~160 times faster than the vector-based contour tree method that took 12 h 38 min 34 s. To test the computational efficiency of the level-set algorithm and evaluate the impacts of different parameters on delineation results, we ran the algorithm with different sets of parameters (see Table 3). By increasing the minimum depression size from 100 to 2,000 m2 while keeping the slicing interval at 0.2 m, the running time of the level-set algorithm decreased from 281.0 to 225.5 s. Increasing the slicing interval from 0.2 to 0.4 m also reduced the computation time. Based on our experiments, the slicing interval is the most influential factor that affects computation time, while the minimum depression size controls the number of depressions being detected. By increasing the depression size from 100 to 2,000 m2, the number of depressions delineated for the watershed dramatically decreased from 54,849 to 24,564, i.e., a 55.2% decrease. The dramatic decrease could be attributed to the fact that many small wetlands “fall out” by increasing depression size, and thus are no longer captured by the analysis. The median depth of depressions ranged from 0.25 to 0.37 m.
Table 3.
Comparison of depression delineation results for Pipestem watershed using level-set method with different parameters
| Parameters | Run time (s) | Number of depressions | Median size (m2) | Median volume (m3) | Median depth (m) |
|---|---|---|---|---|---|
| Min size = 100 m2; interval = 0.2 m | 281.0 | 54,849 | 2,034 | 266 | 0.25 |
| Min size = 500 m2; interval = 0.2 m | 270.0 | 43,606 | 2,628 | 395 | 0.30 |
| Min size = 1,000 m2; interval = 0.2 m | 253.4 | 39,897 | 2,835 | 448 | 0.31 |
| Min size = 2,000 m2; interval = 0.2 m | 225.5 | 24,564 | 5,409 | 1,062 | 0.37 |
| Min size = 100 m2; interval = 0.4 m | 175.2 | 42,813 | 2,367 | 347 | 0.29 |
| Min size = 500 m2; interval = 0.4 m | 167.9 | 38,490 | 2,646 | 414 | 0.31 |
| Min size = 1,000 m2; interval = 0.4 m | 167.1 | 36,800 | 2,754 | 439 | 0.32 |
| Min size = 2,000 m2; interval = 0.4 m | 163.0 | 22,672 | 5,220 | 1,041 | 0.37 |
Discussion
Our raster-based approach for delineating nested depressions using the level-set method is much more computationally efficient than the vector-based contour tree approach (Wu et al. 2015). For the vector-based approach, generating contours on a high-resolution LiDAR DEM with a small contour interval can be computationally intensive. Iterating through the contours to determine their spatial relationships (e.g., adjacency, containment, disjoint) and construct contour tree graphs is even more computationally intensive. Additionally, the initial contour tree graphs need to be simplified in order to remove intermediate nodes, resulting in depression tree graphs composed of critical nodes only (Wu et al. 2015). These drawbacks make it difficult to apply the vector-based contour tree approach to a large-volume DEM. In contrast, our raster-based approach based on the level-set method is much more computationally efficient. The significant improvement in performance partly benefits from several Python scientific libraries (e.g., NumPy, SciPy, scikit-image), which handle numerical computation efficiently. In particular, the image processing library scikit-image enables us to perform various image processing tasks efficiently, such as image segmentation, object extraction, and measuring objects’ properties.
It should be noted that the results of delineation of nested depressions from DEMs can be influenced by several factors, such as the DEM pixel resolution, data acquisition date, slicing interval, minimum depression size, and minimum depression depth. Although we only used fine-resolution LiDAR-derived DEMs for the two experimental cases, our proposed level-set method can also be applied to any coarse- or medium-resolution DEMs, such as the Space Shuttle Radar Topography Mission 30-m resolution DEM, Advanced Spaceborne Thermal Emission and Reflection Radiometer Global DEM, USGS National Elevation Dataset, among others. These coarse-resolution DEM datasets can be used to delineate and characterize nested depressions in locations where fine-resolution DEMs are not available. However, small depressions might not be detectable due to the limitation of pixel resolution, let alone the characterization of the nested hierarchy.
DEMs derived from bathymetric LiDAR are optimal datasets for delineating nested depressions using our proposed method, as the underwater basin morphology is readily available for detection and delineation. Otherwise, LiDAR data acquired during dry periods are preferable to those acquired during wet periods. The reason for this is that LiDAR sensors operating in the near-infrared spectrum generally cannot penetrate water (Wu and Lane 2016). Therefore, it would be infeasible to delineate individual depressions that are nested within a larger compound depression that has already been inundated. It is important to note that while the 2008 LiDAR for CLSA (see Case Study 1) was augmented by depth surveys, the 2011 LiDAR over the larger area (including Pipestem watershed) is not and 2011 is also associated with a wetter period of record. Therefore, using the 2011 LiDAR DEM is likely underestimating the depression hierarchical levels and the number of depressions, especially lower level depressions (e.g., Level-1 depressions).
Depending on the user-specified thresholds (i.e., minimum depression size, minimum depression depth, slicing interval), the number of depressions delineated from the same DEM can vary. The smaller these thresholds, the more depressions can be detected and the higher the computational cost, and vice versa. Setting appropriate minimum depression size and minimum depression depth can be an effective way to distinguish actual and artifact depressions (Lindsay and Creed 2006). Importantly, the slicing interval should not be smaller than the DEM vertical accuracy. Otherwise, many small and shallow depressions might be delineated, which could be artifact depressions resulting from data noise and interpolation error (Li et al. 2011). It should be noted that our proposed level-set method is insensitive to the DEM pre-filtering, as we can set a minimum depression size to eliminate those isolated pit cells. However, the pre-filtering does improve the boundary shape of depressions delineated using our proposed method. Without the pre-filtering, the boundary of depressions delineated from LiDAR DEMs might look very jagged and irregular. With the depressions delineated from LiDAR-derived DEMs, additional ancillary datasets (e.g., LiDAR intensity imagery, aerial photographs, satellite images) can be employed to identify potential wetland depressions and facilitate wetland inundation mapping in wetland-dominated landscapes (Huang et al. 2014; Wu et al. 2014; Vanderhoof et al. 2016; Wu and Lane 2016).
The level-set method can also be employed to model natural phenomena exhibiting a dynamic behavior (e.g., expansion/contraction, appearance/disappearance, splitting/merging), such as drought events, air pollution, and urban heat islands (see Zhu et al. 2017). It is also worth noting that the proposed level-set method for delineating and characterizing surface depressions can be easily adapted to delineate elevated landscape features, such as hills, buildings, and trees (see Wu, Yu, et al. 2016; Wang et al. 2017; Wu et al. 2017). Simply flip the DEM — elevated features then become depressional features, which can be delineated and characterized using the proposed algorithm.
Conclusions
Topographic depressions are abundant on Earth’s surface. These depressions possess important ecological and hydrological functions. Identification, delineation, and quantification of surface depressions can provide critical information for many environmental applications, such as wetland conservation and management, surface water mapping, hydrologic connectivity analysis, and watershed modeling. The increasing availability of fine-resolution DEMs derived from LiDAR data makes it possible to obtain detailed information about surface depressions, which would not have been possible with traditional coarse-resolution DEMs. In this paper, we present an innovative and efficient algorithm for delineating and quantifying nested depressions in DEMs using the level-set method based on graph theory. The proposed level-set method emulates water level decreasing from the spill point at the depression edge to the lowest sink point at the bottom of a depression. By tracing the dynamic topological changes (i.e., depression splitting/merging) within a compound depression, the level-set method can construct a topological hierarchy and derive geometric attributes of the nested depressions. The experimental results show that the proposed raster-based level-set algorithm is much more efficient (~150 times faster) than the vector-based contour tree method for delineating nested depressions. The proposed level-set algorithm has been implemented using the open-source Python programming language, and the algorithm source code is publicly available. It has great potential for being applied to large-scale hydrological modeling and analysis. It can also be adapted to delineate and characterize elevated landscape features (e.g., buildings, trees, and cockpit karst), which have a hierarchical representation in DEMs.
Acknowledgments
We thank the three anonymous reviewers for their constructive comments and suggestions. We also thank Dr. David Mushet from the U.S. Geological Survey Northern Prairie Wildlife Research Center for providing the 0.5-m resolution LiDAR DEM with topobathy for the CLSA. This article has been reviewed in accordance with the U.S. Environmental Protection Agency’s peer and administrative review policies and approved for publication. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government. Statements in this publication reflect the authors’ professional views and opinions and should not be construed to represent any determination or policy of the U.S. Environmental Protection Agency.
Literature Cited
- Barnes R, Lehman C, and Mulla D. 2014. “ Priority-Flood: An Optimal Depression-Filling and Watershed-Labeling Algorithm for Digital Elevation Models.” Computers & Geosciences 62: 117–27. [Google Scholar]
- Brooks JR, Mushet DM, Vanderhoof MK, Leibowitz SG, Christensen JR, Neff BP,Rosenberry DO, Rugh WD, and Alexander LC. 2018. “ Estimating Wetland Connectivity to Streams in the Prairie Pothole Region: An Isotopic and Remote Sensing Approach.” Water Resources Research 54: 955–77. 10.1002/2017WR021016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Z, Yu B, Song W, Liu H, Wu Q, Shi K, and Wu J. 2017. “ A New Approach for Detecting Urban Centers and Their Spatial Structure with Nighttime Light Remote Sensing.” IEEE Transactions on Geoscience and Remote Sensing 55: 6305–19. [Google Scholar]
- Chu X. 2017. “ Delineation of Pothole-Dominated Wetlands and Modeling of Their Threshold Behaviors.” Journal of Hydrologic Engineering 22: D5015003. 10.1061/(ASCE)HE.1943-5584.0001224. [DOI] [Google Scholar]
- Cohen MJ, Creed IF, Alexander L, Basu NB, Calhoun AJK, Craft C, D’Amico E, DeKeyser E,Fowler L, Golden HE, Jawitz JW, Kalla P, Kirkman LK, Lane CR, Lang M, Leibowitz SG,Lewis DB, Marton J, McLaughlin DL, Mushet DM, Raanan-Kiperwas H, Rains MC, Smith L, and Walls SC. 2016. “ Do Geographically Isolated Wetlands Influence Landscape Functions?” Proceedings of the National Academy of Sciences of the United States of America 113: 1978–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evenson GR, Golden HE, Lane CR, and D’Amico E. 2016. “ An Improved Representation of Geographically Isolated Wetlands in a Watershed-Scale Hydrologic Model.” Hydrological Processes 30: 4168–84. [Google Scholar]
- Fisher PF, and Tate NJ. 2006. “ Causes and Consequences of Error in Digital Elevation Models.” Progress in Physical Geography 30: 467–89. [Google Scholar]
- Homer C, Dewitz J, Yang L, and Jin S. 2015. “ Completion of the 2011 National Land Cover Database for the Conterminous United States–Representing a Decade of Land Cover Change Information.” Photogrammetric Engineering and Remote Sensing 81: 345–54. [Google Scholar]
- Huang C, Peng Y, Lang M, Yeo I-Y, and McCarty G. 2014. “ Wetland Inundation Mapping and Change Monitoring Using Landsat and Airborne LiDAR Data.” Remote Sensing of Environment 141:231–42. [Google Scholar]
- Huang S, Dahal D, Young C, Chander G, and Liu S. 2011. “ Integration of Palmer Drought Severity Index and Remote Sensing Data to Simulate Wetland Water Surface from 1910 to 2009 in Cottonwood Lake Area, North Dakota.” Remote Sensing of Environment 115: 3377–89. [Google Scholar]
- Jenson SK, and Domingue JO. 1988. “ Extracting Topographic Structure from Digital Elevation Data for Geographic Information System Analysis.” Photogrammetric Engineering and Remote Sensing 54: 1593–600. [Google Scholar]
- LaBaugh JW, Mushet DM, Rosenberry DO, Euliss NH, Goldhaber MB, Mills CT, andNelson RD. 2016. “ Changes in Pond Water Levels and Surface Extent Due to Climate Variability Alter Solute Sources to Closed-Basin Prairie-Pothole Wetland Ponds, 1979 to 2012.” Wetlands 36:343–55. [Google Scholar]
- Lane CR, Leibowitz SG, Autrey BC, LeDue SD, and Alexander LC. 2018. “ Hydrological, Physical, and Chemical Functions and Connectivity of Non-Floodplain Wetlands to Downstream Waters: A Review.” Journal of the American Water Resources Association 54: 346–71. 10.1111/1752-1688.12633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lang MW, and McCarty GW. 2009. “ Lidar Intensity for Improved Detection of Inundation Below the Forest Canopy.” Wetlands 29: 1166–78. [Google Scholar]
- Leibowitz SG, Mushet DM, and Newton WE. 2016. “ Intermittent Surface Water Connectivity: Fill and Spill vs. Fill and Merge Dynamics.” Wetlands 36: 323–42. [Google Scholar]
- Li S, MacMillan RA, Lobb DA, McConkey BG, Moulin A, and Fraser WR. 2011. “ Lidar DEM Error Analyses and Topographic Depression Identification in a Hummocky Landscape in the Prairie Region of Canada.” Geomorphology 129: 263–75. [Google Scholar]
- Li Z, Shi W, Myint SW, Lu P, and Wang Q. 2016. “ Semi-Automated Landslide Inventory Mapping from Bitemporal Aerial Photographs Using Change Detection and Level Set Method.” Remote Sensing of Environment 175: 215–30. [Google Scholar]
- Lindsay JB 2009. “ Geomorphometry in TAS GIS.” In Developments in Soil Science, edited by Hengl T and Reuter HI, 367–86. Amsterdam, The Netherlands: Elsevier. [Google Scholar]
- Lindsay JB 2016a. “ Efficient Hybrid Breaching-Filling Sink Removal Methods for Flow Path Enforcement in Digital Elevation Models.” Hydrological Processes 30: 846–57. [Google Scholar]
- Lindsay JB 2016b. “ Whitebox GAT: A Case Study in Geomorphometric Analysis.” Computers & Geosciences 95: 75–84. [Google Scholar]
- Lindsay JB, and Creed IF. 2006. “ Distinguishing Actual and Artefact Depressions in Digital Elevation Data.” Computers and Geosciences 32: 1192–204. [Google Scholar]
- Lindsay JB, and Dhun K. 2015. “ Modelling Surface Drainage Patterns in Altered Landscapes Using LiDAR.” International Journal of Geographical Information Science 29: 397–411. [Google Scholar]
- Liu H, and Jezek KC. 1999. “ Investigating DEM Error Patterns by Directional Variograms and Fourier Analysis.” Geographical Analysis 31: 249–66. [Google Scholar]
- Martz LW, and Garbrecht J. 1999. “ An Outlet Breaching Algorithm for the Treatment of Closed Depressions in a Raster DEM.” Computers & Geosciences 25: 835–44. [Google Scholar]
- McKenna OP, Mushet DM, Rosenberry DO, and LaBaugh JW. 2017. “ Evidence for a Climate-Induced Ecohydrological State Shift in Wetland Ecosystems of the Southern Prairie Pothole Region.” Climatic Change 145: 273–87. [Google Scholar]
- Mushet DM, and Erickson SF. 2017. “ Cottonwood Lake Study Area — Wetland Identifier Points: U.S. Geological Survey Data Release.” 10.5066/f7d798n0. [DOI] [Google Scholar]
- Mushet DM, and Euliss NH 2012. The Cottonwood Lake Study Area, A Long-Term Wetland Ecosystem Monitoring Site. Reston, VA: U.S. Geological Survey. https://pubs.er.usgs.gov/publication/fs20123040. [Google Scholar]
- Mushet DM, Rosenberry DO, Euliss NH, and Solensky MJ. 2016. “ Cottonwood Lake Study Area — Water Surface Elevations: U.S. Geological Survey Data Release.” 10.5066/f7707zj6. [DOI] [Google Scholar]
- Mushet DM, Roth CL, and Scherff EJ. 2017. “ Cottonwood Lake Study Area — Digital Elevation Model with Topobathy: U.S. Geological Survey Data Release.” 10.5066/f7v69gtd. [DOI] [Google Scholar]
- Nasab MT, Singh V, and Chu X. 2017. “ SWAT Modeling for Depression-Dominated Areas: How Do Depressions Manipulate Hydrologic Modeling?” Water 9: 58. [Google Scholar]
- Neff BP, and Rosenberry DO. 2018. “ Groundwater Connectivity of Upland-Embedded Wetlands in the Prairie Pothole Region.” Wetlands 38: 51–63. [Google Scholar]
- Osher S, and Fedkiw RP. 2001. “ Level Set Methods: An Overview and Some Recent Results.” Journal of Computational Physics 169: 463–502. [Google Scholar]
- Osher S, and Sethian JA. 1988. “ Fronts Propagating with Curvature-Dependent Speed: Algorithms Based on Hamilton-Jacobi Formulations.” Journal of Computational Physics 79: 12–49. [Google Scholar]
- Planchon O, and Darboux F. 2002. “ A Fast, Simple and Versatile Algorithm to Fill the Depressions of Digital Elevation Models.” Catena 46: 159–76. [Google Scholar]
- Rains MC, Leibowitz SG, Cohen MJ, Creed IF, Golden HE, Jawitz JW, Kalla P, Lane CR,Lang MW, and McLaughlin DL. 2016. “ Geographically Isolated Wetlands Are Part of the Hydrological Landscape.” Hydrological Processes 30: 153–60. [Google Scholar]
- Shaw DA, Pietroniro A, and Martz LW. 2013. “ Topographic Analysis for the Prairie Pothole Region of Western Canada.” Hydrological Processes 27: 3105–14. [Google Scholar]
- Soille P. 2004. “ Optimal Removal of Spurious Pits in Grid Digital Elevation Models.” Water Resources Research 40: W12509. [Google Scholar]
- Tang S, Dong P, and Buckles BP. 2013. “ Three-Dimensional Surface Reconstruction of Tree Canopy from Lidar Point Clouds Using a Region-Based Level Set Method.” International Journal of Remote Sensing 34: 1373–85. [Google Scholar]
- USEPA (U.S. Environmental Protection Agency). 2015. Connectivity of Streams and Wetlands to Downstream Waters: A Review and Synthesis of the Scientific Evidence (Final Report). Washington, D.C.: U.S. Environmental Protection Agency. EPA/600/R-14/475F. https://cfpub.epa.gov/ncea/risk/recordisplay.cfm?deid=296414. [Google Scholar]
- USFWS (U.S. Fish and Wildlife Service). 2010. National Wetlands Inventory Website. Washington, D.C.: U.S. Department of the Interior, Fish and Wildlife Service. http://www.fws.gov/wetlands/. [Google Scholar]
- Vanderhoof MK, Alexander LC, and Todd MJ. 2016. “ Temporal and Spatial Patterns of Wetland Extent Influence Variability of Surface Water Connectivity in the Prairie Pothole Region, United States.” Landscape Ecology 31: 805–24. [Google Scholar]
- Vanderhoof MK, Christensen JR, and Alexander LC. 2017. “ Patterns and Drivers for Wetland Connections in the Prairie Pothole Region, United States.” Wetlands Ecology and Management 25:275–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walt S, Colbert SC, and Varoquaux G. 2011. “ The NumPy Array: A Structure for Efficient Numerical Computation.” arXiv [cs.MS]. http://arxiv.org/abs/1102.1523. [Google Scholar]
- Walt S, Schönberger JL, Nunez-Iglesias J, Boulogne F, Warner JD, Yager N, Gouillart E, Yu T, and Scikit-Image Contributors. 2014. “ Scikit-Image: Image Processing in Python.” PeerJ 2: e453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dijk NP, Maute K, Langelaar M, and Van Keulen F. 2013. “ Level-Set Methods for Structural Topology Optimization: A Review.” Structural and Multidisciplinary Optimization 48: 437–72. [Google Scholar]
- Wang L, and Liu H. 2006. “ An Efficient Method for Identifying and Filling Surface Depressions in Digital Elevation Models for Hydrologic Analysis and Modelling.” International Journal of Geographical Information Science 20: 193–213. [Google Scholar]
- Wang S, Wu Q, and Ward D. 2017. “ Automated Delineation and Characterization of Drumlins Using a Localized Contour Tree Approach.” International Journal of Applied Earth Observation and Geoinformation 62: 144–56. [Google Scholar]
- Waz A, and Creed IF. 2017. “ Automated Techniques to Identify Lost and Restorable Wetlands in the Prairie Pothole Region.” Wetlands 37: 1079–91. [Google Scholar]
- Winter TC, and Rosenberry DO. 1998. “ Hydrology of Prairie Pothole Wetlands During Drought and Deluge: A 17-Year Study of the Cottonwood Lake Wetland Complex in North Dakota in the Perspective of Longer Term Measured and Proxy Hydrological Record.” Climatic Change 40: 189–209. [Google Scholar]
- Woodrow K, Lindsay JB, and Berg AA. 2016. “ Evaluating DEM Conditioning Techniques, Elevation Source Data, and Grid Resolution for Field-Scale Hydrological Parameter Extraction.” Journal of Hydrology 540: 1022–29. [Google Scholar]
- Wu B, Yu B, Wu Q, Huang Y, Chen Z, and Wu J. 2016. “ Individual Tree Crown Delineation Using Localized Contour Tree Method and Airborne LiDAR Data in Coniferous Forests.” International Journal of Applied Earth Observation and Geoinformation 52: 82–94. [Google Scholar]
- Wu B, Yu B, Wu Q, Yao S, Zhao F, Mao W, and Wu J. 2017. “ A Graph-Based Approach for 3D Building Model Reconstruction from Airborne LiDAR Point Clouds.” Remote Sensing 9: 92. [Google Scholar]
- Wu Q. 2018. “ GIS and Remote Sensing Applications in Wetland Mapping and Monitoring.” InComprehensive Geographic Information Systems, edited by Huang B, 140–57. Oxford: Elsevier. 10.1016/b978-0-12-409548-9.10460-9. [DOI] [Google Scholar]
- Wu Q, Deng C, and Chen Z. 2016. “ Automated Delineation of Karst Sinkholes from LiDAR-Derived Digital Elevation Models.” Geomorphology 266: 1–10. [Google Scholar]
- Wu Q, and Lane CR. 2016. “ Delineation and Quantification of Wetland Depressions in the Prairie Pothole Region of North Dakota.” Wetlands 36: 215–27. [Google Scholar]
- Wu Q, and Lane CR. 2017. “ Delineating Wetland Catchments and Modeling Hydrologic Connectivity Using Lidar Data and Aerial Imagery.” Hydrology and Earth System Sciences 21: 3579–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Q, Lane C, and Liu H. 2014. “ An Effective Method for Detecting Potential Woodland Vernal Pools Using High-Resolution LiDAR Data and Aerial Imagery.” Remote Sensing 6: 11444–67. [Google Scholar]
- Wu Q, Liu H, Wang S, Yu B, Beck R, and Hinkel K. 2015. “ A Localized Contour Tree Method for Deriving Geometric and Topological Properties of Complex Surface Depressions Based on High-Resolution Topographical Data.” International Journal of Geographical Information Science 29:2041–60. [Google Scholar]
- Wu Q, Su H, Sherman DJ, Liu H, Wozencraft JM, Yu B, and Chen Z. 2016. “ A Graph-Based Approach for Assessing Storm-Induced Coastal Changes.” International Journal of Remote Sensing 37: 4854–73. [Google Scholar]
- Yu WB, Su C, Yu CN, Wang XZ, Feng CJ, and Zhang XC. 2014. “ An Efficient Algorithm for Depression Filling and Flat-Surface Processing in Raster DEMs.” IEEE Geoscience and Remote Sensing Letters 11: 2198–202. [Google Scholar]
- Zhang K, Zhang L, Song H, and Zhou W. 2010. “ Active Contours with Selective Local or Global Segmentation: A New Formulation and Level Set Method.” Image and Vision Computing 28: 668–76. [Google Scholar]
- Zhou G, Sun Z, and Fu S. 2016. “ An Efficient Variant of the Priority-Flood Algorithm for Filling Depressions in Raster Digital Elevation Models.” Computers & Geosciences 90: 87–96. [Google Scholar]
- Zhu R, Guilbert E, and Wong MS. 2017. “ Object-Oriented Tracking of the Dynamic Behavior of Urban Heat Islands.” International Journal of Geographical Information Science 31: 405–24. [Google Scholar]