Automated Artery Localization and Vessel Wall Segmentation using Tracklet Refinement and Polar Conversion

Abstract

Quantitative analysis of blood vessel wall structures is important to study atherosclerotic diseases and assess cardiovascular event risks. To achieve this, accurate identification of vessel luminal and outer wall contours is needed. Computer-assisted tools exist, but manual preprocessing steps, such as region of interest identification and/or boundary initialization, are still needed. In addition, prior knowledge of the ring shape of vessel walls has not been fully explored in designing segmentation methods. In this work, a fully automated artery localization and vessel wall segmentation system is proposed. A tracklet refinement algorithm was adapted to robustly identify the artery of interest from a neural network-based artery centerline identification architecture. Image patches were extracted from the centerlines and converted in a polar coordinate system for vessel wall segmentation. The segmentation method used 3D polar information and overcame problems such as contour discontinuity, complex vessel geometry, and interference from neighboring vessels. Verified by a large (>32000 images) carotid artery dataset collected from multiple sites, the proposed system was shown to better automatically segment the vessel wall than traditional vessel wall segmentation methods or standard convolutional neural network approaches. In addition, a segmentation uncertainty score was estimated to effectively identify slices likely to have errors and prompt manual confirmation of the segmentation. This robust vessel wall segmentation system has applications in different vascular beds and will facilitate vessel wall feature extraction and cardiovascular risk assessment.

I. INTRODUCTION

Atherosclerotic cardiovascular disease is a leading cause of death worldwide [1]. Angiographic techniques are commonly used to depict luminal stenosis resulting from atherosclerosis progression. However, they often under- or over-estimate the underlying disease burden due to expansive or restrictive arterial wall remodeling [2]. Black-blood vessel wall magnetic resonance imaging (MRI) has allowed for direct visualization of atherosclerotic lesions in major arterial beds [3], [4] without ionizing radiation or contrast media. Arterial wall segmentation in vessel wall MRI provides a quantitative analysis of atherosclerotic burden, which can be exploited for monitoring disease progression in serial studies and clinical trials [5], [6].

Considering the anatomical variations of arteries, MRI signal complexity, and flow artifacts, most previous studies, including quantitative analysis of the vessel wall, rely on manual segmentation. In manual review, inner and outer boundaries of arterial walls (lumen and outer wall) visible in the axial planes on each slice of the MR images need to be drawn on each slice [7], which is tedious and subject to reader variability [8]. Unlike brain tumors or larger human organs, where locating the region of interest for segmentation is relatively easy, the vessel wall is usually 1 millimeter in thickness and takes less than 0.1% of space in the image. In addition, the size of arteries may change along the slices, and the artery might be tortuous with many bifurcations. Correct identification of the region containing the artery of interest is usually needed prior to vessel wall segmentation; for example, zooming in to the region, including the common carotid artery (CCA) or internal carotid artery (ICA) for carotid vessel wall analysis facilitates segmenting the thin vessel wall region. Semi-automated or automated methods have been proposed to segment vessel walls, such as using active contour models by Yuan et al. [9] and Adams et al. [10], an active shape model by Underhill et al. [11], or using graph cut by Arias-Lorza et. al. [12]–[14]. Another category of methods segment the vessel wall area by classifying pixels into vessel wall regions and non-vessel wall regions using machine learning models [15], [16]. Manually locating the artery of interest is required for most segmentation methods, but some methods try to automatically locate arteries by referring to registered MR angiography, in which lumen areas are better visualized [17]. In addition, Hough circle detection has been attempted to detect arterial centers, under the assumption that arteries are circular in shape [18]. These methods reduce some manual steps and show reasonable agreement for images with high vessel wall contrast. However, three major problems remain for existing methods: 1) extensive human input is still needed for most methods, including contour initialization [9], [10], seed point initialization [11]–[13], [15], [16], and registration of image sequences [17]; 2) feedback from the automated segmentation models, for example, the level of confidence in the segmentation, which might be useful for clinicians to check problematic slices to ensure the segmentation quality, is usually not available; and 3) due to the limited number of annotated samples in a specific vascular region, the robustness of the algorithm has not been fully explored in previous studies.

Recently, deep learning-based methods have shown superior performance in cardiovascular applications when compared to traditional methods, including retinal blood vessel segmentation [19] and coronary artery segmentation [20]. In our previous works, the convolutional auto-encoder (CAE) demonstrates a high agreement with manual contours of the lumen [21] and outer wall [22]. However, several major obstacles exist, preventing our deep learning-based algorithms from being effectively used: (1) the target artery cannot be automatically identified in the presence of multiple arteries; (2) some prior knowledge, for example, vessel wall contours should be closed rings, is not used (see Figure 1 for a problematic case); and (3) information from neighboring slices is not well used to refine the segmentation results.

Fig. 1.

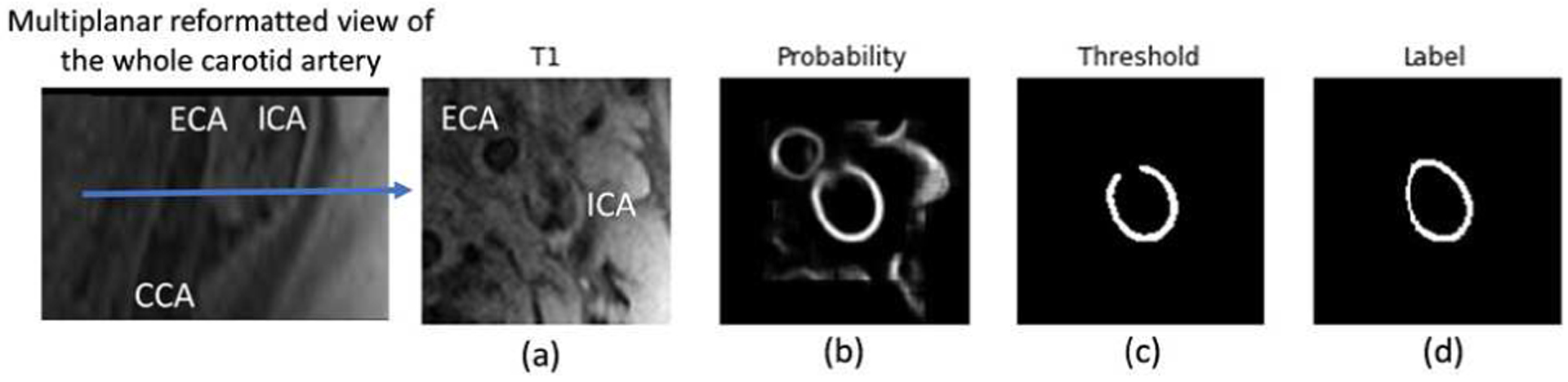
Exemplary problems encountered previously in CAE [22]. (a) Original vessel wall image with flow artifacts and external carotid artery (ECA) coexisting with the ICA. (b) Probability map from prediction. The ECA is visible in the region of interest for the ICA (the target artery) vessel wall segmentation, leading to both arteries having a high probability. (c) Broken vessel wall segmentation due to weak signal in a portion of the vessel wall region. (d) Human labeling.

In this study, we overcame the above challenges with a two-step fully automated vessel wall analysis workflow. A localization approach using tracklet refinement was developed to first robustly identify the lumen center of arteries along image slices to provide regions of interest for the subsequent vessel wall segmentation. Unlike the commonly used Cartesian coordinate-based segmentation methods, we proposed to transform the ring-shaped vessel wall to a polar coordinate system to ensure the continuity and accuracy of vessel wall boundaries. From the consistency of predictions from different rotations, an uncertainty score can be derived to effectively estimate the segmentation performance.

In summary, the major contributions of this work are in three areas:

1. We proposed a fully automated vessel wall segmentation workflow for black blood vessel wall MRI without any manual intervention. The use of an artery localization architecture to identify artery centerlines before vessel wall segmentation avoids the step of selecting the region of interests for arteries. The use of the convolutional neural network (CNN) model for segmentation does not require wall boundary initialization.

2. We proposed to segment the vessel wall by boundary regression in the polar coordinate system. We extensively explored different polar regression architectures and compared them with the state-of-the-art Cartesian segmentation methods. Polar regression provided unique benefits, including better vessel wall continuity and improved segmentation, which is especially needed in challenging slices near arterial bifurcations where the artery shape is no longer circular.

3. By predicting boundary coordinates from rotated polar patches, sub-pixel level segmentation is available. More importantly, by combining boundary regression results from rotated patches, our method can also yield uncertainty scores to inform users of possible mistakes.

The rest of this paper is organized as follows: in Section II, we give a detailed description of the methodologies contained in our proposed localization and segmentation system. The experimental data setup and simulation results are given in Section III, followed by the Discussion in Section IV. The conclusion is drawn in Section V.

II. PROPOSED LOCALIZATION AND SEGMENTATION METHODOLOGIES

The workflow for the proposed localization and segmentation methodologies is shown in Figure 2.

Fig. 2.

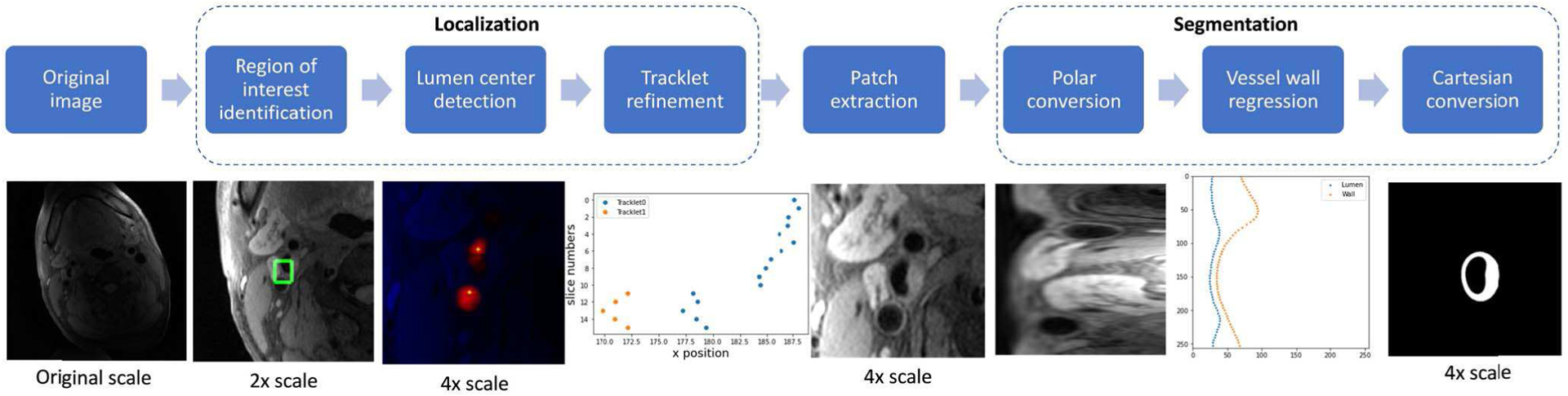
Workflow for proposed localization and segmentation methodologies.

A. LUMEN CENTER LOCALIZATION

The purpose of the localization task is to automatically identify the lumen center of each image slice to provide the region of interest for the subsequent vessel wall segmentation. Tracking the artery across consecutive images spatially is a similar task to temporal object tracking in a video. Therefore, a tracking-by-detection approach was adopted in our localization scheme, which included three steps: region of interest identification, lumen center detection, and tracklet refinement.

For region of interest identification, a Yolo V2 detector [23] based on CNN was used to predict bounding boxes (minimum encompassing rectangles covering whole artery regions) of arteries in each image slice. The original weights of the Yolo detector were used to further train the model in artery detection. Yolo V2 was selected because it is time efficient and generally accurate [23]. Other detectors might also be suitable for this purpose and we did not optimize this step for this project.

Accurate patch extraction from the lumen center is important for polar conversion. However, the center of bounding boxes from the Yolo detector may not be the same as the geometric lumen center when the arterial shape is not a perfect circle (Figure 3B shows an example). Instead, we predicted centers of the lumen near the bounding boxes using the following steps. First, a 2D U-net [24] was trained to predict the minimum distance to the nearest non-lumen area for each pixel. Then, the predicted minimum distance map was thresholded using Otsu’s method [25] and divided into connected components based on pixel connectivity. Components having no overlap with the bounding box were removed, and the centers of the remaining components were used to represent each possible lumen. The value of the minimum distance map at each lumen center was used as the confidence score for the centers. 2D U-net was selected as a popular model for image-to-image conversion, and Otsu’s method was used as a conventional method for thresholding. Other competing methods may also serve the same purpose.

Fig. 3.

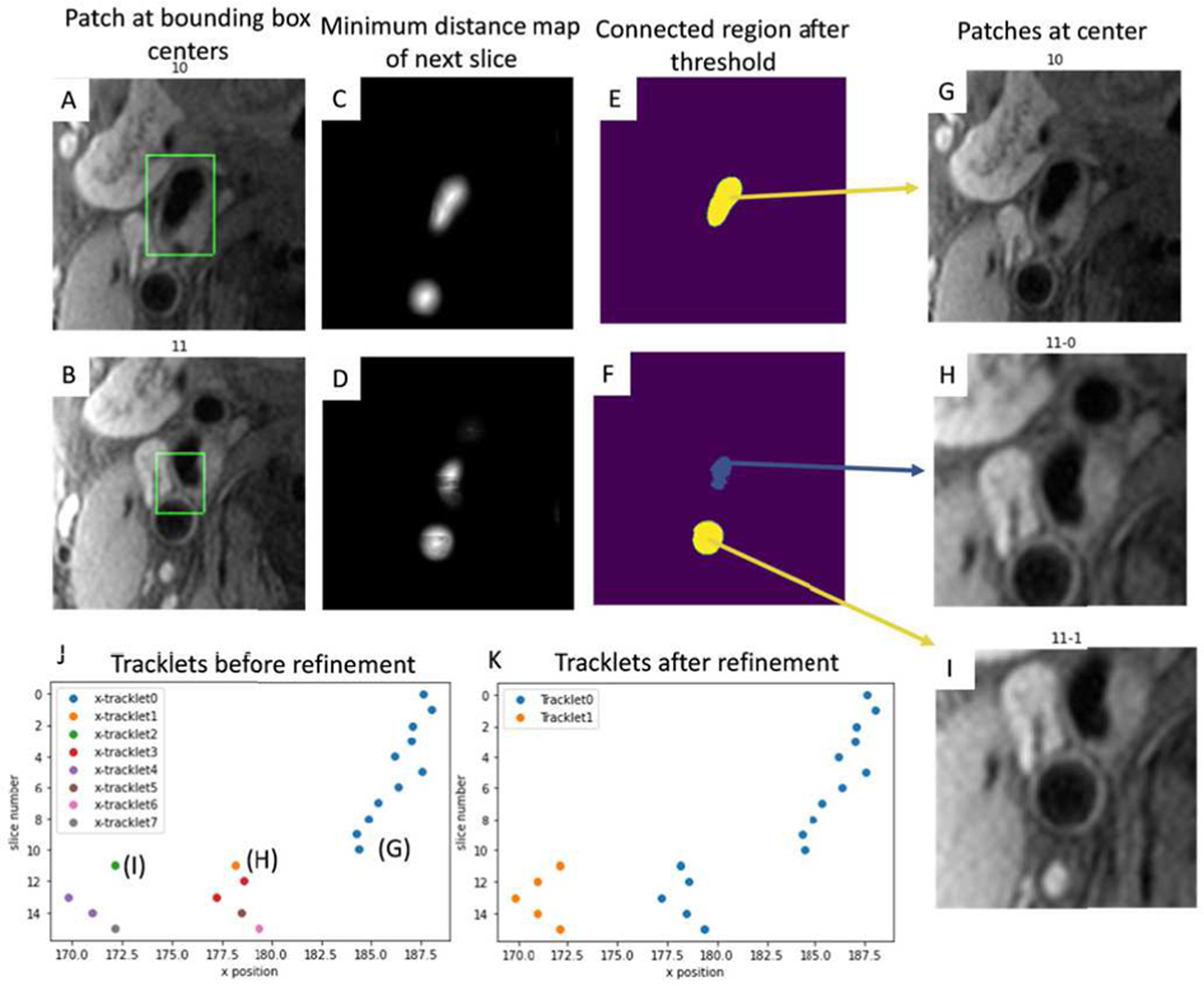
A, B: Bounding boxes detected by Yolo V2 at slices 10 and 11 to identify rough artery locations. C, D: Minimum distance map predictions. E, F: Connected regions showing overlap with bounding boxes after threshold of C and D. G: Patch from the connected region center (as lumen centers) of E. H, I: Patches from two connected region centers from F. J: Lumen centers of all slices form tracklets (x position vs z position). K: Tracklets after refinement. The longest tracklet (blue) on each side of the carotid artery is used as the centerline for segmentation.

When no, or multiple, lumen centers were identified for some slices, a tracking method (tracklet refinement algorithm) was used to infer the missing centers or remove centers corresponding to veins/arteries not of interest. First, a series of closely matching (based on intensities along the path between centers) neighboring centers were defined as a short tracklet. All short tracklets formed a collection of K = {T₁, T₂, …, T_i. Tracklet T_i with z_t,i − z_h,i + 1 neighboring centers was represented with head and tail centers T_i = (h_i, t_i) = ([x_h,i, y_h,i, z_h,i,], [x_t,i, y_t,i, z_t,i]). Short tracklets were then merged for longer tracklets by a connection loss L (T_i, T_j) defined as the feature distance between head and tail of each pair of tracklets,

$$L\left(T_i,T_j\right)=\{\begin{array}{ll}\infty ,\hfill & z_{h,i}>z_{h,j}\hfill \\ {\Vert F\left(C\left(t_i\right)\right)-F\left(C\left(h_j\right)\right)\Vert }^2,\hfill & z_{h,i}\le z_{h,j}\hfill \end{array}$$ (1)

C is a function to crop the in-plane image patch of 128*128 at the center of h or t. F is a CNN feature extraction network with 5 convolution layers, 5 max pooling layers, and a fully connected layer of 64 nodes as the output. Triplet loss [26] L_t (A, P, N) was used to train the feature extraction network, where the anchor and positive patches were extracted from ground truth lumen centers at the head and tail of the tracklets, and the negative patch was extracted from the same slice as the positive patch but at (one of) the center(s) of connected component(s) not encompassing lumen centers (an example is shown in Figure 4).

$$L_t(A,P,N)=\text{max}(\parallel F(A)-F(P){\parallel }^2-\parallel F(A)-F(N){\parallel }^2+\propto ,0).$$ (2)

∝ is the margin between positive and negative pairs. The default value of 0.4 was used for ∝ in this study.

Fig. 4.

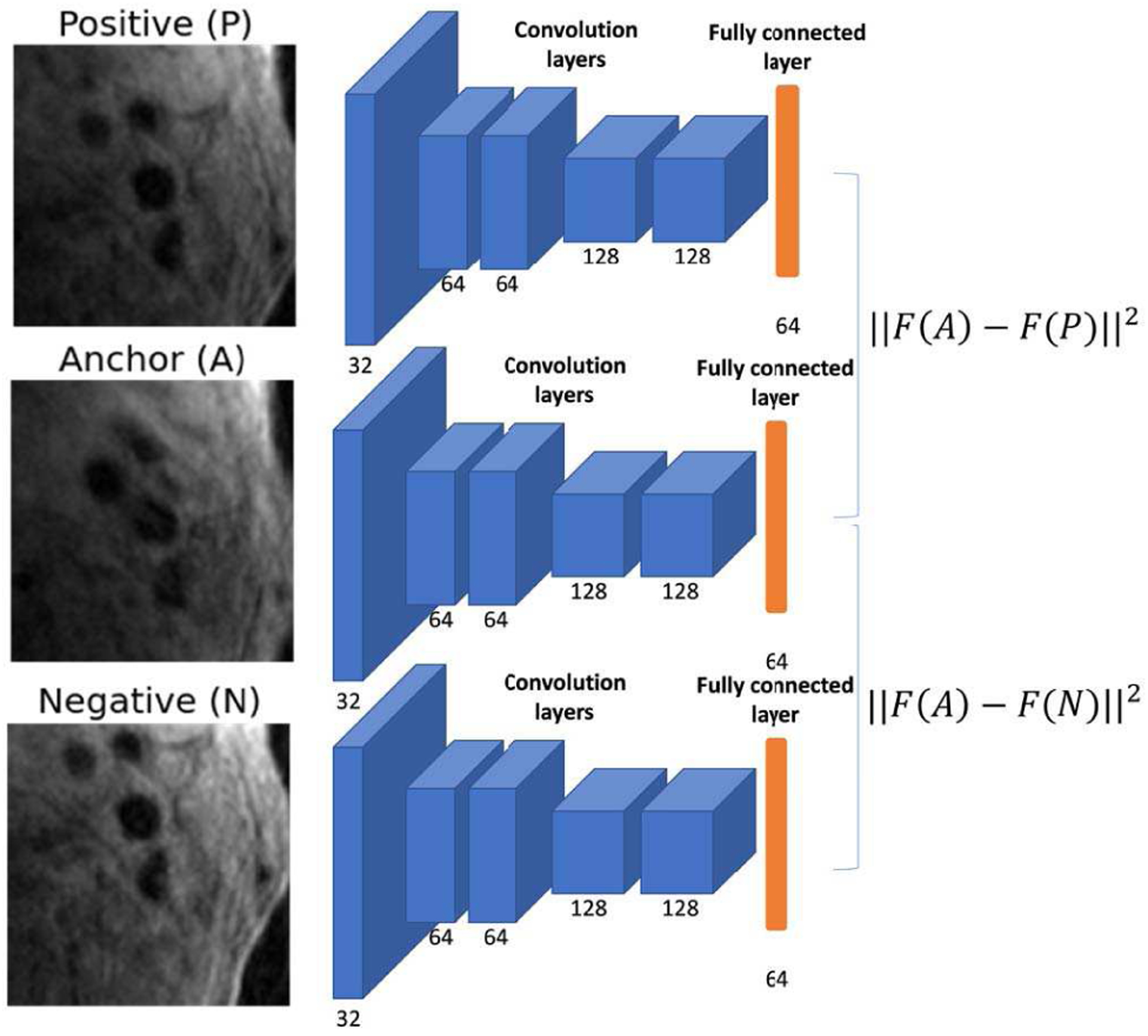
Feature extraction network and triplet loss for identifying pairs of tracklets to merge. Number of kernels are shown in each convolution layer.

Tracklets were pairwise calculated for connection losses, and the pair (i, j) with mutual minimum loss among all merge options were connected. min_i {L (T_i, T_j) | Tj ∈ K} = min _j {L {T_i, T_j | T_i ∈ K}. During tracklet merging, missing lumen centers between slice z_h,i and z_h,j were linearly inter-polated by T_i, T_j. Center confidence scores within the tracklet were summed up, and the tracklets with the top score on each side of the carotid artery were considered as the target centerline. An example of using tracklet refinement to find the centerline when there are multiple centers for connection is shown in Figure 3.

Image patches $\widehat{P}[y,x]$ of h*w (128*128 in this study) were cropped along the centerline and enlarged 4 times (manual vessel wall review standard) using bilinear interpolation for subsequent vessel wall segmentation.

B. MOTIVATION FOR USING THE POLAR COORDINATE SYSTEM FOR VESSEL WALL SEGMENTATION

Vessel walls are typically ring shapes with two contours in each axial slice, with the lumen contour always inside the outer wall contour. Two problems exist using traditional Cartesian based CNN methods for segmentation (Figure 1 as an example). 1) Complete contours of vessel walls cannot be continuously segmented if part of the vessel wall does not have strong enough prediction results. 2) Nearby arteries or veins are also segmented due to their similar signal patterns.

These two problems can be easily solved if images are converted to a polar coordinate system for boundary regression.1) Compared with pixel wise segmentation in a 2D Cartesian space (degree of freedom: 16*h*w), contour identification in the polar system only needs to predict the polar boundary coordinates, which are distances from the lumen center to N points along the lumen and outer wall contours (degree of freedom: 2 * N). The segmentation task becomes easier after polar conversion. In addition, contour continuity can be easily ensured as long as the predicted outer wall distance is larger than the lumen distance for each point. 2) Neighboring arteries or veins appear very different from the target artery after polar conversion, and therefore they can be more easily discriminated by the CNN.

Polar boundary coordinates predicted from the polar image can be converted back to Cartesian coordinates and the final segmentation mask can be acquired by filling the region between two contours.

C. POLAR REGRESSION CNN ARCHITECTURE

The polar image patches P[t, r] with the size of 2h * 2w were converted from Cartesian image patches $\widehat{P}[y,x]$ with the polar center at [2h, 2w], using the polar transformation relation of $P[t,r]=f(\widehat{P}[y,x])$. The polar conversion equations used in this study are in the supplementary material.

Considering the patch size, available training sample size, and the difficulty of the regression task, a CNN architecture (Polar-Reg) with 14 convolutional layers and 6 max pooling layers was used for polar regression (architecture is shown in Figure 5). The last fully connected layer had 2t nodes, which were the polar boundary coordinates R_l (P), R_o(P) in t directions. Then the boundary coordinates were converted to the Cartesian system ${\widehat{R}}_{l,o}(y,x)=f^{-1}\left(R_{l,o}(P)\right)$. The regions between boundaries ${\widehat{R}}_{l,o}(y,x)$ were filled with 1 as the binary segmentation mask $S{\widehat{M}}_r(P)$.

Fig. 5.

CNN architecture for polar regression. Number of kernels are shown in each convolution layer. Each convolution layer was followed by a batch normalization layer and a rectified linear unit. The depth channel is not drawn for simplicity. Each rotated polar patch regresses boundary coordinates in t = 256 directions. The predicted coordinates from different angles were averaged for smoothness, and their standard deviation was used to estimate boundary consistency, as the segmentation confidence score. Finally, the polar boundary coordinates were converted back to the Cartesian coordinate system and the regions between lumen and outer wall contours were used as the segmentation result.

The Polar IoU loss [27], an IoU loss [28] in the polar coordinate system was used as the loss function for the regression.

$$\mathit{\text{Loss}}=\text{log}\frac{{\sum }_{i=1}^n{d}_{\mathit{\text{min}}}}{{\sum }_{i=1}^n{d}_{\mathit{\text{max}}}},$$ (3)

d_min and d_max are the smaller and larger boundary coordinates along one of the n directions from the ground truth and prediction.

The Adam optimizer [29] was used to control the learning rate.

To incorporate neighboring slice information, patches centered at [x, y, z±1] were concatenated in the depth dimension in CNN architecture. If slice z±1 did not exist, the current slice would be repeated. For simplicity, the depth channel is not drawn in Figure 5.

D. PATCH ROTATION

A polar patch rotation method was proposed for both data augmentation and prediction combinations.

Data augmentation is needed for better training with limited samples. Traditional augmentation methods, such as rotation and offsetting, are not suitable for polar patches. Considering the boundless property of polar patch along the angle directions, we proposed to augment polar patches as

$$P_{\alpha }^{\prime }[t,r]=\{\begin{array}{ll}P[2*h-\alpha +t,r],\hfill & t<\alpha \hfill \\ P[t-\alpha ,r],\hfill & t\ge \alpha ,\hfill \end{array}$$ (4)

where α is a random integer from 0 to 2 * h. Combined with vertical flipping, 4 * h times samples can be acquired for training.

During the prediction stage, multiple rotated polar patches were combined to ensure boundary smoothness. Rotated patches with α_i = i * G, i = 1, 2, …, ⌊2 * h/G⌋ were generated and their prediction results were averaged to be the final probability map and boundary coordinates. G is the predefined step size for predictions (10 was empirically selected in this study, see supplementary material).

Final lumen and outer wall boundary coordinates from the regression B_l and B_w were calculated as

$$B_{l,o}[t]=R_{l,o}(P[t])=\frac{1}{2*\frac{h}{G}}\sum _i{R}_{l,o}\left(P_{{\alpha }_i}^{\prime }\left[g\left(t-{\alpha }_i\right)\right]\right).$$ (5)

where $g(x)=\{\begin{array}{c}x+2*h,x<0\\ x,x\ge 0\end{array}$.

Vessel wall contours in Cartesian coordinate system were

$${\widehat{B}}_{l,o}(x,y)=f^{-1}\left(B_{l,o}(t)\right).$$ (6)

E. QUANTIFYING THE UNCERTAINTY IN SEGMENTATION

We observed that our vessel wall segmentation, with good agreement with manual labels, demonstrated clear boundaries and a simple ring shape on MR images, and thus the segmentation neural network reliably generated consistent vessel wall boundaries from rotated patches with any α_i; in other words, $R_{l,o}\left(P_{{\alpha }_i}^{\prime }\left[g\left(t-{\alpha }_i\right)\right]\right)$ should be constants with all possible α_i.

Based on this, we proposed lumen and wall consistency scores $Cs{t}_{l,o}(P)$ to quantify segmentation uncertainty.

$$Cs{t}_{l,o}(P)=1-\frac{1}{2*h}\sum _t\left(\frac{1}{\sqrt{\frac{1}{12}}}\sqrt{\frac{1}{2*\frac{h}{G}}\sum _{\alpha }{\left(\frac{R_{l,o}\left(P_{\alpha }^{\prime }[t]\right)-B_{l,o}[t]}{2*w}\right)}^2}\right).$$ (7)

Boundary coordinates were normalized between 0 to 1, and the variation of predictions from different patches was evaluated by the ratio of the standard deviation of boundaries predicted from different patches, to the worst case when all the predictions were random $(\sqrt{1/12})$. The range of consistency was between 0 (random) to 1 (perfectly consistent). The worst case scenario is unlikely to happen, which means the score is usually high.

F. ITERATIVE CENTERLINE REFINEMENT FROM SEGMENTATION

Polar patches used for training were converted from perfect lumen centers, which was not the case for testing data, leading to inferior segmentations in prediction. Even refined from the localization module, the centerline can still be further improved from the center deviations calculated from the predicted polar boundaries. The center deviations can be reduced iteratively from the angle of $\frac{{360}^{\circ }}{2h}\varnothing$ with the largest differences of polar coordinates from opposite directions.

$$\{\begin{array}{l}\varnothing =\mathit{\text{argmax}}\left(|B_l[\varnothing ]-B_l[\varnothing +h]|\right)\hfill \\ \Delta x=\text{cos}\left(B_l[\varnothing ]-B_l[\varnothing +h]\right)\hfill \\ \Delta y=\text{sin}\left(B_l[\varnothing ]-B_l[\varnothing +h]\right)\hfill \end{array}$$ (8)

By adjusting the x₁ = x₀+Δ x, y₁ = y₀+ Δy, a new $\widehat{P}[y,x]$ with a better polar center can be extracted for another round of segmentation. The process was iterated until the deviations were below the imaging resolution or the max iteration was reached.

III. EXPERIMENTAL DATA SETUP AND RESULTS

A. MR IMAGES

Data were collected following institutional review board guidelines. Informed consents were obtained from all study participants.

The carotid dataset included T1-weighted (T1W) carotid artery images from 954 subjects with recent ischemic stroke or transient ischemic attack, which were collected from the CARE-II study from multiple sites [30], and 203 asymptomatic subjects from a clinical trial (NCT00851500) from the Kowa Research Institute [31], [32].

Detailed imaging parameters are shown in the supplementary material.

B. HUMAN LABELING

Lumen and outer walls were delineated manually by trained reviewers with 3+ years’ experience in cardiovascular MR imaging using a custom-designed software package (CASCADE) [33]. Image slices with poor image quality were excluded from review and all the labeled slices were also peer reviewed to ensure labeling quality. Each image slice was rated with an image quality level of adequate, good, or excellent. A human reviewer required about one hour to annotate a single subject’s carotid artery scan.

The CARE-II and Kowa datasets were pooled and randomly divided into 925 subjects (80%; 26008 image slices) as the training set, 116 subjects (10%; 3215 image slices) as the validation set, and 116 subjects (10%; 3406 image slices) as the testing set. The test set was not used in any way until the model design was finalized.

C. FEASIBILITY ANALYSIS OF POLAR REGRESSION FOR VESSEL WALL SEGMENTATION

As a proof of concept that vessel wall segmentation by polar regression is feasible without much loss of accuracy during the polar conversion, we analyzed the upper limit of Dice Similarity Coefficient (DSC) [34] between segmentation from converted polar boundary coordinates and the ground truth segmentation. In addition, DSC with different choices of t was evaluated. We used t = 256 in our models with the mean DSC of 0.9630, indicating the loss of information by polar conversion was not our concern considering our current performance in segmentation. More discussions were presented in the supplementary material.

D. ABLATION STUDY AND COMPARISON METHODS

To evaluate the model complexity on segmentation performance, a deeper regression model with Resnet 101 [35] was evaluated for performance improvements. The model (Polar-Res-Reg) was built by connecting the last two layers of the Polar-Reg to the last fully connected layer from a Resnet trained with initial weights on the ImageNet dataset [36].

To evaluate the contribution of neighboring slices to segmentation improvements, P [t, r] were repeated three times (Polar-Res-Reg-Single) as the input to train the same segmentation neural network as Polar-Res-Reg.

The proposed Polar-Reg model used polar patches to regress polar boundary coordinates. To evaluate the contributions of polar inputs and outputs, we designed the Cart-Reg model which predicted polar boundary coordinates from Cartesian patches, and Cart-Cart-Reg model which predicted Cartesian coordinates from Cartesian patches.

To evaluate the effect of accurate polar centers on the performance of vessel wall segmentation, the Polar-Reg model was tested directly on bounding box centers (without tracklet refinement). To evaluate the effectiveness of the iterative center adjustment from segmentation, Polar-Reg-Once allowed only one segmentation per vessel wall.

Cartesian based segmentation methods (existing methods are usually in this category) were also compared, including the popular neural network models 3D U-net [24] (previously adopted in vessel wall segmentation [22]), Mask-RCNN [37] (Resnet 101 backbone, pretrained on the ImageNet [36] dataset). These methods were trained and tested using the same datasets and settings as our polar models.

We also compared the performance with a state-of-the-art non-CNN vessel wall segmentation method, Optimal front segmentation (Opfront) [14], which is based on the graph cut algorithm.

E. EVALUATION METRICS

To better reflect the performance of each module, we first used the ground truth lumen centers to evaluate the vessel wall segmentation, then we used the lumen center localization module to generate centerlines for vessel wall segmentation, and evaluated both the localization and segmentation.

For the localization evaluation, mean absolute distance (MAD) between predicted lumen centers with ground truth centers, number of false negatives (no lumen center in a slice) and false positives (more than one center in a slice) were calculated before and after the tracklet refinement.

Performance of the segmentation was evaluated by the DSC, and Degree of Similarity (DoS) [38], both of which ranged from 0 (mismatch) to 1 (perfect match). Detailed definitions are in the supplementary material. DSC > 0.7 indicates excellent agreement [39]. DSC for lumen (DSC^Inner: area within the lumen contour), complete vessel (DSC^Outer: area within the outer wall contour) and vessel wall (DSC^VW: area between the lumen and outer wall contours) were evaluated separately. DoS for lumen and outer walls were also evaluated separately as DoS^Lumen, DoS^Wall. In addition, vascular features from predicted and ground truth contours were calculated and compared. Representative and clinically important vascular features were selected, including max wall thickness, mean wall thickness, lumen area, and wall area. Absolute mean difference and intraclass correlation coefficient between predicted and ground truth vascular features were calculated.

F. VALIDATION ON CONSISTENCY SCORES

Independent associations between consistency scores and DSC^VW were evaluated using Spearman’s partial rank correlation coefficients. The correlation between a combination of scores and DSC^VW was summarized using R-squared from a linear model with rank-transformed scores as predictor variables and DSC^VW as the outcome variable. These analyses were conducted at the slice level, so generalized estimating equations (GEEs) were used to test associations and compare models while accounting for non-independence between slices from the same subject. Please also refer to the supplementary material for sensitivity evaluation of consistency scores.

G. HARDWARE AND SOFTWARE SETUP

Model training and evaluation were performed on workstations (Intel® Xeon® CPU E5–1650 v4 @3.6GHz 6 cores, 64 GB Memory) with an NVIDIA Titan Xp (evaluation) / V (training) GPU. Tensorflow [40] and Keras were used as the deep learning platform in this study.

H. PERFORMANCE ON TEST SET

For the segmentation based on ground truth lumen centers, the superior performance of polar regression models compared with other models in vessel wall segmentation and vascular feature quantification is shown in TABLE 1 and TABLE 2. As an example, the segmentation results by each method on two image slices are shown in Figure 6. Polar regression models had better performance than the segmentation models (U-Net, Mask-RCNN), in both lumen and outer walls, indicating segmentation from boundary regression was more effective than predicting probability maps. The deeper regression network (Polar-Res-Reg with 45.0M parameters) had slightly better performance than the shallower regression model (Polar-Reg model with 4.6M parameters). Network architectures with neighboring slices as inputs were better than single slice inputs. The traditional method (Opfront) cannot handle vessel walls with weak signal contrasts, and in most cases cannot ensure ring shapes, so DoS was not evaluated.

TABLE I.

Carotid vessel wall segmentation performance compared with other methods

Model	DSCVW	DSCInner	DSCouter	DoSLumen	DoSwall	Number of slices with failed segmentation	Processing time (s)	Number of parameters in network
Polar-Res-Reg	0.860	0.961	0.962	0.921	0.864	0	0.757	44,989,224
Polar-Res-Reg-Single	0.841	0.955	0.954	0.901	0.838	0	0.891	44,989,224
Polar-Reg	0.848	0.957	0.959	0.907	0.843	0	0.738	4,639,104
Cart-Reg	0.828	0.950	0.952	0.883	0.800	0	0.092	4,639,104
Cart-Cart-Reg	0.807	0.943	0.943	0.841	0.738	0	0.080	6,212,480
Mask R-CNN [40]	0.792	0.940	0.940	0.654	0.565	81	0.138	63,733,406
Cartesian U-net [24]	0.774	0.922	0.941	0.647	0.517	194	0.103	4,094,817
Opfront [14]	0.531	0.822	0.878	N/A	N/A	N/A	38.717	N/A

Segmentations are all based on ground truth lumen centers. Slices which failed in finding ring shape contours were considered failed segmentation, and were excluded from evaluations. The metric with the best performance is shown in bold.

TABLE II.

Carotid vessel wall features quantified from segmentation compared with other methods

	Max Wall Thickness		Mean Wall Thickness		Lumen Area		Wall Area
	MAD	ICC (Cl)	MAD	ICC (Cl)	MAD	ICC (Cl)	MAD	ICC (Cl)
Polar-Res-Reg	0.890	0.896 (0.8870.904)	0.484	0.886 (0.8780.893)	25.715	0.985 (0.9840.986)	40.404	0.984 (0.9830.985)
Polar-Reg	0.964	0.874 (0.8640.883)	0.521	0.870 (0.8620.878)	28.439	0.981 (0.9790.982)	42.703	0.981 (0.9790.983)
Cart-Reg	1.145	0.817 (0.7980.833)	0.542	0.829 (0.8180.840)	32.521	0.972 (0.9690.975)	54.296	0.966 (0.9610.970)
Mask R-CNN [39]	1.264	0.653 (0.6320.672)	0.701	0.509 (0.4730.543)	32.171	0.942 (0.9380.945)	62.567	0.907 (0.8850.924)
Cartesian U-Net [24]	1.071	0.810 (0.7980.822)	0.565	0.808 (0.7280.859)	45.065	0.935 (0.9230.945)	52.460	0.949 (0.9450.952)

MAD: mean absolute difference, lower better. ICC (Cl): intraclass correlation coefficient (with 95% confidence interval), higher better.

Segmentations are all based on ground truth lumen centers. Slices which failed in finding ring shape contours were considered failed segmentation, and were excluded from evaluations. The metric with the best performance is shown in bold.

Fig. 6.

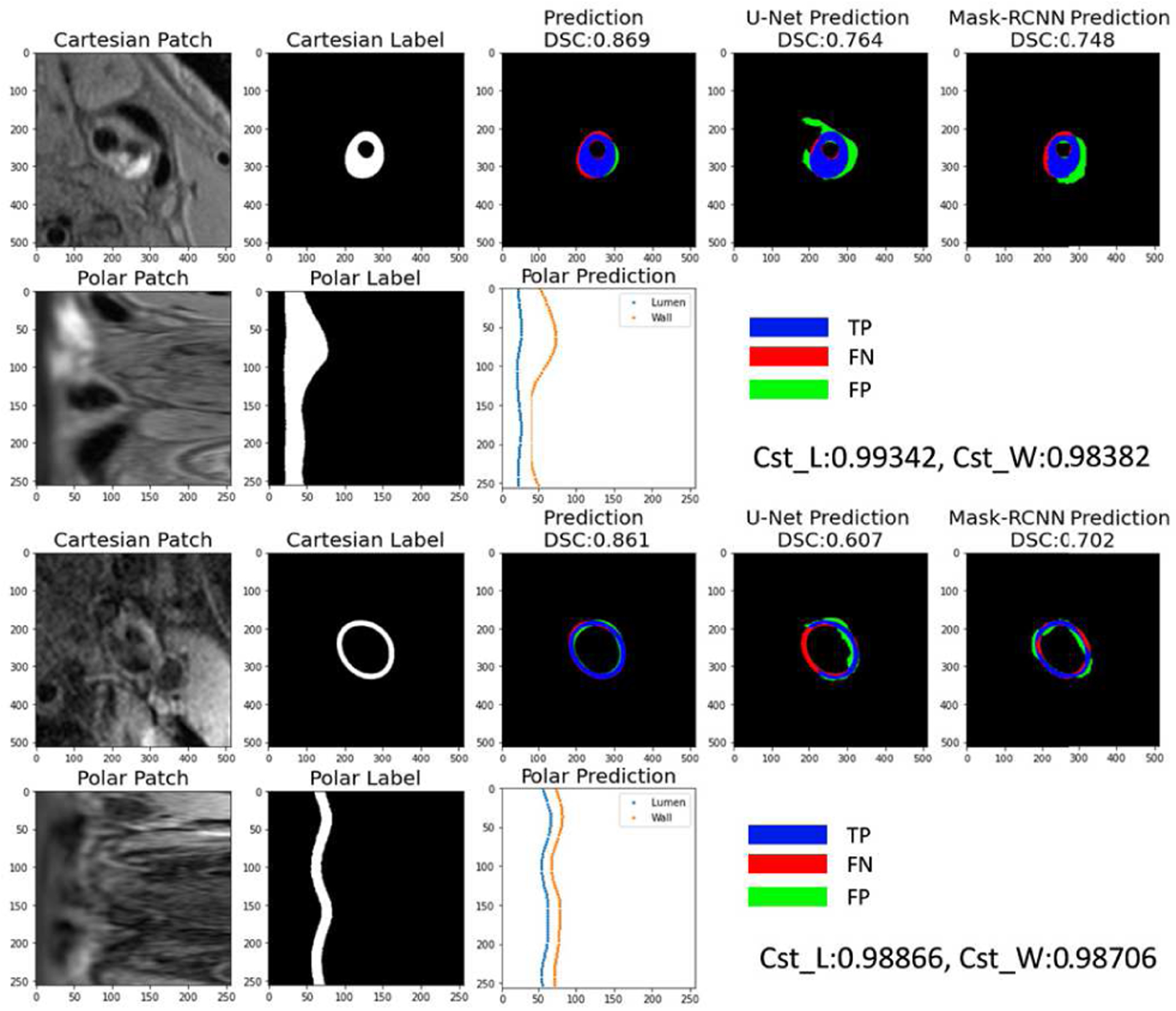
Examples of vessel wall segmentations at slices near the carotid bifurcation. Original Cartesian patches were converted to polar patches (first column) for prediction of boundary coordinates in the polar coordinate system (middle bottom plot). Coordinates were converted back to Cartesian system and the region between the two contours was filled as the segmentation (middle top plot). To better display the segmentation difference with manual labels (second column), regions were displayed as blue (TP, correct segmentation region), green (FP, wrong segmented region), and red (FN, not segmented region). Segmentation from two Cartesian methods (U-Net [24] and Mask R-CNN [40]) were compared in the last two columns. Cartesian segmentations might have segmented the wrong artery (top) or a broken vessel wall (bottom). For patches with low contrast (bottom), the consistency scores from the polar model (Polar-Seg- Reg is used as an example) were relatively low, indicating possible lower segmentation performance, so manual checking might be required.

The localization evaluation results are shown in TABLE 5, after tracklet refinement, 31 (0.9%) FN centers and 211 (6.2%) FP centers from the carotid dataset were all corrected. The MAD improved from 2.60 to 1.58 pixels.

TABLE V.

Lumen center localization performance before and after tracklet refinement

		MAD (pixel)	#FN	# FP
Carotid N=3406	Before refinement	2.60	31 (0.9%)	211 (6.2%)
	After refinement	1.58	0 (0.0%)	0 (0.0%)

MAD: Mean absolute distance between predicted lumen centers with ground truth centers. #FN: number of false negatives (no lumen centers at one slice). #FP: false positives (more than one centers at a slice)

The joint localization and segmentation results are shown in Table 4. Polar regression based on refined centerlines had better performance than when based directly on bounding box centers. Polar-Reg achieved the best performance in terms of MAD and most other segmentation metrics compared to the other methods. Generally, performance was worse than predictions based on perfect lumen centers.

TABLE IV.

Joint vessel wall localization and segmentation performance compared with other methods

Centerline	Model	MAD (pixel)	DSCVW	DSCInner	DSCouter	DoSLumen	DoSwall	Number of slices with failed segmentation	Processing time (s)
Original	Polar-Reg	2.18	0.756	0.908	0.921	0.741	0.652	31	0.811
Refined	Polar-Reg-Once	1.96	0.765	0.916	0.926	0.754	0.663	0	0.832
Refined	Polar-Reg	1.32	0.768	0.918	0.927	0.758	0.669	0	1.647
Refined	Polar-Res-Reg	2.43	0.767	0.911	0.924	0.757	0.696	0	1.124
Refined	Cart-Reg	1.59	0.748	0.902	0.923	0.710	0.698	0	0.108
Refined	Cart-Cart-Reg	1.96	0.713	0.884	0.906	0.656	0.608	0	0.554
Refined	Mask-RCNN [40]	1.73	0.731	0.900	0.913	0.722	0.642	178	0.150
Refined	Cartesian U-Net [24]	3.05	0.583	0.807	0.846	0.578	0.533	1272	0.440

The original centerline was from bounding box centers. Slices which failed in finding ring shape contours were considered failed segmentation, and were excluded from evaluations. The metric with the best performance is shown in bold.

The number of slices and the mean DSC-VW in each of the image quality levels are shown in TABLE 3. Better image quality led to higher DSC-VW, but even for slices with only adequate image quality, the polar regression models still generated contours with DSC-VW over 0.694.

TABLE III.

DSC-vw from slices with different image qualities of Carotid arteries

	Image quality
	Adequate	Good	Excellent
Number of slices	621	2483	302
Polar-Reg with ground truth center	0.802	0.861	0.880
Polar -Reg with localized center	0.694	0.778	0.809

Lastly, the uncertainty of segmentation was quantified using the consistency scores. Lumen and wall consistency scores had a mean value of 0.99195±0.00813 and 0.98757±0.01222 for the Polar-Reg model. Both consistency scores, except wall consistency for Polar-Res-Reg, showed significant contributions in predicting DSC^VW, indicating lower scores were likely to generate a worse segmentation mask compared with the ground truth. Wall consistency had strong relations with lumen consistency, so its partial correlation was lower in the regression model. Quantitative results between models are shown in TABLE 6.

TABLE VI.

Quantitative comparison of carotid segmentation uncertainty predicted by models

Models	Lumen Consistency		Wall Consistency		R square
	Correlation	P value	Correlation	P value
Polar-Res-Reg	0.244	<le-5	−0.043	0.060	0.139
Polar-Reg	0.132	<le-5	0.047	0.045	0.115
Cart-Reg	0.230	<le-5	0.195	0.013	0.232

Correlation: partial correlation coefficient from Spearman’s method. P value: from Generalized Estimating Equations. R square: from a linear model with rank-transformed scores as predictor variables and DSC^VW as the outcome variable

IV. DISCUSSION

In this study, fully automated vessel wall segmentation was achieved with high accuracy by effectively using a localization model to detect lumen centers using a tracking-by-detection approach and a regression model to segment vessel wall in the polar coordinate system. The step of artery localization avoids the manual procedure to select the region for artery analysis so that the vessel wall can be analyzed without human intervention. Traditional vessel wall segmentation methods are susceptible to poor image quality, only providing reasonable results when both lumen and outer wall boundaries have high contrast. Our proposed deep learning-based method extracted useful boundary information from more than 32,000 slices of manually drawn vessel wall contours with various levels of image quality. We believe our dataset encompasses a wide spectrum of atherosclerosis as well as healthy arteries and is capable of training a robust deep learning model with good generalizability. The use of the polar regression CNN architecture is an ideal approach, incorporating the prior knowledge of vessel wall structures (e.g., ring shape, lumen in the center), and outperforms our previous deep learning segmentation method [22] based on the Cartesian coordinate system. The use of multiple CNN models sequentially (predicting minimum distance map by CNN, merging tracklets with CNN features, then CNN based regression on polar patches along the artery centerlines) mimics the human behavior in vessel wall review, thus this CNN analysis system is not a black box and easily understandable. However, if the CNN model is trained end-toend directly for classification of vascular diseases from images [41], [42], prediction results are not easily explainable and errors are not clearly identifiable, especially for challenging images. In this paper, we focused on determining whether accurate and fully automated vessel wall analysis based on polar regression was feasible as a proof-of-concept. The choice of specific algorithms or models needs to be further explored to fully optimize vessel wall segmentation performance.

Both consistency scores were shown to provide independent and critical information in identifying problematic slices in segmentation, which can be useful in guiding humans to examine only the slices with higher likelihoods of possible errors and ensure high segmentation quality.

The method proposed to segment carotid arteries is also applicable to other vascular beds. One example was the popliteal arteries [43]. We used a publicly accessible popliteal artery dataset [44] to test the generalizability of our model on a large popliteal artery dataset in which there are challenging cases where some vessel wall boundaries are unclear and vein/branching artery co-exists near the artery of interest. Comprehensive validation and feasibility assessment of our method on popliteal vessel wall quantification was discussed in [45].

There are existing automated tracking-based vessel centerline extraction methods for coronary arteries from computed tomography angiography data [46]–[48]. However, due to the very different images and applications compared with MR vessel wall image analysis in our study, no comparisons were made.

The application of deep learning methods in vessel wall segmentation might have a profound impact on MR vessel wall image analysis. As a research tool, with accurately segmented vessel wall areas from an automated method, quantitative vessel wall features can be extracted to enhance our understanding of atherosclerosis progression from large population studies, for which time-consuming manual or semi-automated methods are not achievable. Clinically, a fast screening tool can be developed to automatically identify high-risk patients for further detailed examination in a time-efficient manner. After choosing a proper threshold for better sensitivity over specificity, the quantitative vessel wall features along with the confidence scores can largely reduce the burden for clinicians by prioritizing patients urgently requiring medical care and giving initial evaluations for the carotid scans.

A limitation of the polar methods is the extra calculation time, mainly for polar conversions, compared with Cartesian methods. GPU acceleration for polar conversion may be attempted in the future. Additionally, only the relatively straight carotid and popliteal arteries were evaluated in this study. However, the method has the potential to be adapted to MRI data of more tortuous arteries (e.g., intracranial arteries) with the combination of robust artery tracing and cross-sectional slicing methods [49].

V. CONCLUSION

A deep learning system for vessel wall localization and segmentation has been developed with tracklet refinement and polar transformation. Compared with traditional methods, the proposed system avoids human intervention and demonstrates better performance in accurate segmentation of vessel wall areas, as well as providing consistency scores to indicate possible errors. It has the potential to facilitate research on atherosclerosis and assist radiologists in image review.

Biographies

Li Chen received the B.S. degree in Electrical Engineering from Fudan University in 2016. He is currently a PhD candidate in the department of Electrical and Computer Engineering in University of Washington.

His research interests include medical image processing and machine learning.

Jie Sun received the M.D. degree from Peking Union Medical College (Beijing, China) in 2009. He was a postdoctoral fellow and then an acting instructor in the Department of Radiology at the University of Washington. Since 2019, he has been a research assistant professor with the Department of Radiology. His research interests include development, validation, and translation of cardiovascular imaging techniques and imaging-based clinical research. He has authored more than 50 journal articles and book chapters. Dr. Sun’s awards and honors include the Mentored Clinical & Population Research Award (American Heart Association) and the Translation Research Scholar Award (Institute of Translational Health Sciences)

Gador Canton received her PhD degree in Mechanical Engineering from UC San Diego in 2004. She is a mechanical engineer with extensive expertise in analyzing biomedical problems from an engineering perspective (+10 years).

Specialties: R&D, Experimental Flow Mechanics, Computational Fluid Dynamics, Magnetic Resonance Imaging, Cardiovascular Mechanics, Biofluid Mechanics

Niranjan Balu is a Research Assistant Professor in the Department of Radiology at the University of Washington. He currently leads the Imaging Physics Group at Dr. Chun Yuan’s Vascular Imaging Lab where he manages the MRI aspect of large NIH sponsored multicenter studies and multicenter pharmaceutical trials. His research interests include MR pulse sequence design, image processing and their application to clinical cardiovascular MRI. His current research is focused on developing new MRI techniques to reduce quantitative measurement variability in vessel wall MRI and development of fast sequences to facilitate translation of vessel wall MRI to the clinic.

Daniel S. Hippe is a statistician in the UW Department of Radiology with numerous collaborations within Radiology—including with the Vascular Imaging Lab, the Quantitative Breasting Imaging Lab—and with research groups and departments outside Radiology, including I-LABS, the Nghiem Lab, Radiation Oncology, Dermatology, Cardiology, and Pediatrics. He received his BS in Electrical Engineering in 2004 and MS in Statistics in 2011, both from the University of Washington. He enjoys working with investigators across a wide variety of disciplines and continually learning about different areas of medicine. The use of imaging is the common theme which connects the wide range of projects he works on.

Xihai Zhao received the MD degree in Medical Imaging from Harbin Medical University in 1999, MS degree in Radiology from Shanghai Jiao Tong University School of Medicine in 2004, and PhD degree in Radiology from Chinese PLA Postgraduate Medical School in 2007.

He devoted most of his time to medical research in assessment of the cardiovascular risk of Chinese population by characterizing the atherosclerosis disease in multiple vascular beds, including intracranial artery, carotid artery, aortic arch, and femoral artery, with state-of-the art MR vessel wall imaging techniques. In this field, he has published over 110 research articles in the top peer-reviewed journals on cardiovascular disease and imaging, including Stroke, ATVB, JCMR, JAHA, Atherosclerosis, AJNR, European Radiology, MRM, and JMRI.

Rui Li received the BS and PhD degrees from department of Electronic Engineering, Tsinghua University, China (2000, 2005).

His research Interest focuses on cardiovascular magnetic resonance imaging technique development, including plaque imaging and 4D flow imaging.

Thomas S. Hatsukami is a board certified surgeon at the Vascular Laboratories at Harborview and UW Medical Center, the UW’s V. Paul Gavora and Helen S. and John A. Schilling Endowed Chair in Vascular Surgery and a UW professor of Surgery.

Dr. Hatsukami strives to create active partnerships with his patients to achieve the best possible outcomes.

Dr. Hatsukami earned his M.D. from the UCLA. He has an internationally recognized research program using magnetic resonance imaging techniques to characterize high-risk atherosclerotic plaque, identify novel biomarkers for atherosclerosis and assess pharmacological therapy to stabilize and reduce plaque in the arteries.

Jenq-Neng Hwang received the BS and MS degrees, both in electrical engineering from the National Taiwan University, Taipei, Taiwan, in 1981 and 1983 separately. He then received his Ph.D. degree from the University of Southern California. In the summer of 1989, Dr. Hwang joined the Department of Electrical and Computer Engineering (ECE) of the University of Washington in Seattle, where he has been promoted to Full Professor since 1999. He served as the Associate Chair for Research from 2003 to 2005, and from 2011–2015. He also served as the Associate Chair for Global Affairs from 2015–2020. He is currently the International Programs Lead in the ECE Department. He is the founder and co-director of the Information Processing Lab., which has won several AI City Challenges awards in the past years. He has written more than 380 journal, conference papers and book chapters in the areas of machine learning, multimedia signal processing, computer vision, and multimedia system integration and networking, including an authored textbook on “Multimedia Networking: from Theory to Practice,” published by Cambridge University Press. Dr. Hwang has close working relationship with the industry on artificial intelligence and machine learning.

Dr. Hwang received the 1995 IEEE Signal Processing Society’s Best Journal Paper Award. He is a founding member of Multimedia Signal Processing Technical Committee of IEEE Signal Processing Society and was the Society’s representative to IEEE Neural Network Council from 1996 to 2000. He is currently a member of Multimedia Technical Committee (MMTC) of IEEE Communication Society and also a member of Multimedia Signal Processing Technical Committee (MMSP TC) of IEEE Signal Processing Society. He served as associate editors for IEEE T-SP, T-NN and T-CSVT, T-IP and Signal Processing Magazine(SPM). He is currently on the editorial board of ZTE Communications, ETRI, IJDMB and JSPS journals. He sserved as the Program Co-Chair of IEEE ICME 2016 and was the Program Co-Chairs of ICASSP 1998 and ISCAS 2009. Dr. Hwang is a fellow of IEEE since 2001.

Chun Yuan received his B.S. in physics at Beijing Normal University and his Ph.D. in Biomedical Physics at the University of Utah. He became Senior Research Analyst of GE Medical Systems immediately thereafter. He has pioneered multiple high-resolution MRI techniques to detect vulnerable atherosclerotic plaques and led numerous MRI studies examining carotid atherosclerosis. He is a member of the editorial board for the following Journals: JACC CV imaging, Journal of Cardiovascular MR, and the Journal of Geriatric Cardiology. He also serves as manuscript reviewer for about 30 other peer-reviewed journals involving magnetic resonance, arteriosclerosis, stroke and cardiovascular sciences.

Through his stint in the University of Washington, he has mentored 50 postdocs who have moved on to become professors, chief research scientists, clinician-researchers, heads of departments and other positions of responsibility in both private and government or public institutions in the USA, China, Germany, and around the world.

Because of his expertise in the field of cardiovascular imaging and magnetic resonance, he has been an invited speaker or keynote speaker, lecturer, moderator or faculty for many international and US meetings in the imaging field. He has over 300 articles in peer-reviewed journals. His research is supported by several NIH and private grants and currently supervises several postdoctoral fellows, research scientists and graduate students, as well as teaches courses in Bioengineering and Radiology.