Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Feb 18;92(6):4451–4458. doi: 10.1021/acs.analchem.9b05420

Multivariate Curve Resolution for 2D Solid-State NMR spectra

Francesco Bruno †,‡, Roberto Francischello §,∥, Giovanni Bellomo †,‡, Lucia Gigli †,‡, Alessandra Flori ⊥, Luca Menichetti §,⊥, Leonardo Tenori †, Claudio Luchinat †,‡, Enrico Ravera †,‡,*
PMCID: PMC7997113  PMID: 32069028

Abstract

graphic file with name ac9b05420_0006.jpg

We present a processing method, based on the multivariate curve resolution approach (MCR), to denoise 2D solid-state NMR spectra, yielding a substantial S/N ratio increase while preserving the lineshapes and relative signal intensities. These spectral features are particularly important in the quantification of silicon species, where sensitivity is limited by the low natural abundance of the 29Si nuclei and by the dilution of the intrinsic protons of silica, but can be of interest also when dealing with other intermediate-to-low receptivity nuclei. This method also offers the possibility of coprocessing multiple 2D spectra that have the signals at the same frequencies but with different intensities (e.g.: as a result of a variation in the mixing time). The processing can be carried out on the time-domain data, thus preserving the possibility of applying further processing to the data. As a demonstration, we have applied Cadzow denoising on the MCR-processed FIDs, achieving a further increase in the S/N ratio and more effective denoising also on the transients at longer indirect evolution times. We have applied the combined denoising on a set of experimental data from a lysozyme–silica composite.

Introduction

Sensitivity is one of the largest limitations in solid-state nuclear magnetic resonance (ssNMR) and becomes more severe as the gyromagnetic ratio and the natural abundance of the investigated nucleus decrease. Under these conditions, the signal intensity is low and, quite often, the low relaxation mechanisms efficiency requires experiments with long recovery delays. One relevant example is 29Si NMR. Silicon is the second most abundant element by mass on earth,1 has relevant functions in living organisms,2 and a large share of its compounds are solid.329Si-solid-state NMR is, therefore, an election technique for a plethora of applications, but faces some silicon intrinsic limitations. 29Si can be described as a diluted isotope with medium sensitivity:4 the natural isotopic abundance is 4.7% and the frequency with respect to 1H is 19.9%; therefore, the receptivity of 29Si is roughly twice that of 13C in natural abundance. However, the overall sensitivity of 29Si NMR is often negatively impacted by the absence of nuclei with higher gyromagnetic ratios in the vicinity, rendering the relaxation times prohibitively long. This latter problem can be overcome by paramagnetic doping, at the price of altering the chemical composition of the sample.5−8

The low sensitivity, as is always the case in NMR,9 is due to the low Boltzmann population difference among the ground and excited states. One way to increase this difference is to increase the static magnetic field; commercial instruments with fields as high as 28.2 T (1.2 GHz 1H Larmor frequency) are now available.10 However, not only are high field magnets more expensive than low field magnets because of the different manufacturing processes, but their operational costs are also higher, so that, overall, the price per experiment gets significantly higher even when moving from 16.4 to 18.8 T (from 700 to 800 MHz). Another option is to use larger amounts of sample, but (a) the amount of sample is likely limited, (b) small rotors need to be used to increase the maximal achievable spinning speed and thus the resolution,11 and (c) more components may be present, imposing a strong dilution on the species of interest.12,13 Proton detection, available at high spinning frequency, can be used to increase the sensitivity,11,14,15 but this is necessarily limited to proton-rich materials. Dynamic nuclear polarization (DNP) is also a viable route to study silicon-based materials,16−19 but the equipment is more expensive than standard NMR. An interesting application of ultrafast acquisition based on gradient encoding has been proposed for high resolution magic-angle-spinning (MAS) of soft solids,20,21 but the applicability to rigid solids is also hardware-limited. Hence, methods based on data processing, rather than on data acquisition, might be welcome in preparatory studies, before the actual measurements performed at higher fields and/or using DNP. Consistent efforts are indeed devoted to the development of processing methods that allow for signal extraction from noisy spectra, in this and in different areas of NMR. These efforts led to several options to reduce noise: wavelet transform,22 Savitzky-Golay,23 random QR denoising,24 singular spectrum analysis,25 and Cadzow filtering.26,27 Each of these methodologies, however, has its own benefits and drawbacks.

We here propose for the first time the use of multivariate curve resolution (MCR) for denoising applications in ssNMR. MCR is a chemometric method primarily developed to recover pure components information from data of complex mixtures.28−31 Initially developed for UV–Vis spectroscopy,32 MCR has been then successfully applied to resolve data from a plethora of different analytical techniques,33 first of all chromatography, but also chemical reaction monitoring,34 spectroscopic imaging,35 environmental monitoring,36 and analysis of “omics” data sets, such as genomic37 and metabolomic data.38 It has also been applied to the deconvolution of 2D solution NMR data of reaction mixtures.39 MCR has the same aim as the blind-source-separation method, the applications of which to NMR are discussed in refs (40−43). We here show that this processing is extremely beneficial for ssNMR spectra. We also demonstrate that it can be also successfully applied to the simultaneous denoising of spectra of the same sample acquired at different mixing times, therefore offering the opportunity for also using the spectra with the lowest S/N ratio from a series.

Finally, while this method would be fully compatible with denoising the processed spectra,39 we have applied it for denoising time-domain data, thus preserving the possibility of applying further processing to the data. In particular, we have applied the Cadzow denoising to further increase the S/N ratio, as it appears to be well suited for ssNMR spectroscopy.27 This latter point turns out to be particularly relevant. Finally, through the whole process, quantitative information is preserved.

Experimental Section

Experimental Data

Solid-state NMR experiments were recorded on a Bruker Avance II spectrometer operating at 700 MHz 1H Larmor frequency (16.4 T), corresponding to 139 MHz 29Si Larmor frequency. The spectrometer is equipped with a 3.2 BVT MAS probehead in double resonance mode. The pulse lengths are 2.4 and 4.7 μs for 1H and 29Si, respectively. Cross-polarization was achieved by matching the k = 1 Hartmann–Hahn condition.44 The spectral windows for the different nuclei were 60 and 249 ppm for 1H and 29Si, respectively. During the 1H magnetization evolution under the chemical shift in the indirect dimension of heteronuclear correlation experiments, the PMLG decoupling sequence was used to suppress 1H–1H dipolar couplings.45,46 Spectra were acquired with CPMG echo train acquisition,47 and then the echoes were coadded.

Synthetic Data

Synthetic data were generated over the same spectral window as the experimental data. The spectra in the series of three (see below) comprise of up to nine cross-peaks of variable intensities and line widths in the indirect dimension (SI Table S1).

Data Processing

Indicating the features of the MCR algorithm according to the standard chemometric nomenclature, MCR decomposes the experimental data matrix D into a “Concentration” matrix C and a “Spectra” matrix S, and the part of the data that is not reproduced by the factorization contributes to the residual matrix E (see eq 2 in the Results and Discussion section). The factorization has been accomplished through alternating least-squares,28 starting from the purest variables48 estimate for the matrix C in the time domain. The number of components is set to 4, with 10% of the most intense signal as threshold for the noise.28 We have implemented the MCR algorithm in Python, but there are several implementations available in, for example, MATLAB.49 The operation is repeated until convergence, which is evaluated on the spectral norm of the difference between the matrices associated with two consecutive steps, and the optimization ends when the norm in any of the matrices goes below 10–5.

All spectra were processed using the NMR PIPE class from the NMRGlue library,50 with the parameters reported in SI Table S2.

The S/N ratio was estimated dividing the maximum signal intensity by the standard deviation of the noise, calculated as follows:

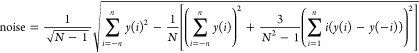graphic file with name ac9b05420_m001.jpg 1

where N is the total number of points in the noise region, n = (N – 1)/2 and y(i) is the ith point in the noise region. As a representative noise region, we selected a slice of the spectrum where no signal is present.

Results and Discussion

Application of the MCR Algorithm

According to the standard nomenclature used in chemometrics, MCR decomposes the data matrix D into a “concentration” matrix C and a “spectra” matrix S, leaving behind a residuals matrix E:

graphic file with name ac9b05420_m002.jpg 2

Intuitively, in a 2D NMR spectrum there is no variation in concentrations, but rather in the signal intensities because of indirect evolution. Therefore, the resulting matrix C contains the time evolutions of the indirect dimension, and the resulting matrix S contains the FIDs of the direct dimension. Given that we wanted to demonstrate that this method is applicable regardless of the line shape of the peaks, we limited the input of prior information to the analysis: no forward model (e.g.: using Gaussians for modeling the peaks), nor any regularization (e.g.: non-negativity of the spectra in the frequency domain, or smoothness), for either the FIDs or evolutions, were applied. Therefore, the factorization was obtained through a simple alternating least-squares approach:28−30 at the kth iteration, the values for Ck and Sk are obtained as

graphic file with name ac9b05420_m003.jpg
graphic file with name ac9b05420_m004.jpg

and

graphic file with name ac9b05420_m005.jpg

where “+” denotes the Moore-Penrose pseudoinverse. The initial guess for the indirect evolution matrix, C0, was obtained through the purest variables algorithm.48

We have used four components for the factorization, as this number ensures the best S/N with the least amount of bias and without increasing the number of iterations needed for optimization (see SI Table S3 for more details). Therefore, ST is a complex matrix of dimension 4 × N, and C a complex matrix of dimension M × 4 where N and M are the number of points in the direct and indirect dimension respectively (see SI Table S2).

As already mentioned, a very important feature of MCR is that several spectra can be coprocessed with a common basis of FIDs (see below).

Denoising on a Single Synthetic Spectrum

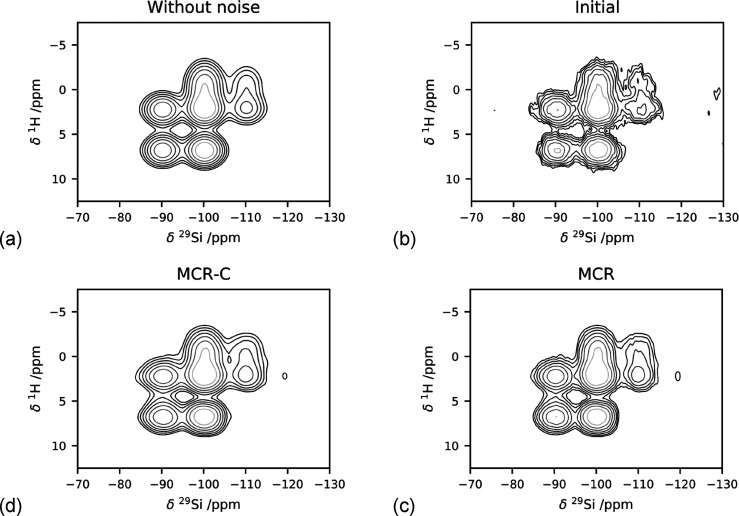
The method was first tested on a single synthetic spectrum (Figure 1a). The peak positions, line widths, and intensities are given in Table 1. Gaussian noise was added to the spectrum (Figure 1b), yielding a S/N ratio of 46.

Figure 1.

Figure 1

Open in a new tab

(a) Synthetic spectrum without noise and (b) synthetic spectrum with noise applied, (c-d) result of the processing of the (b) spectrum: (c) spectrum reconstructed with MCR and (d) spectrum reconstructed with MCR after application of Cadzow denoising.

Table 1. S/N Ratio in the Different Spectra Across the Different Processing Steps.

  spectrum
step A B C
initial S/N 45 45 47
  single coprocessed single coprocessed single coprocessed
MCR S/N 106 206 221 150 250 153
MCR+Cadzow S/N 130 253 237 191 299 195
Open in a new tab

The denoising increases the S/N ratio to 221 after MCR and 237 after Cadzow denoising. Importantly, it does not alter the relative intensities of the peaks (SI Figure S1). To be noted that the Cadzow denoising gives more emphasis to the earlier points of the time domain and requires additional exponential apodization,27 therefore it imposes a modest line broadening to the reconstructed spectrum, which manifests itself in the bias observed in the difference trace (SI Figure S1, bottom panel).

Denoising on Multiple Synthetic Spectra

The power of the MCR method is that it can handle simultaneously multiple data matrices, and it is therefore ideal for coprocessing series of spectra. This is particularly relevant in the case of spectra that are acquired by varying some experimental parameter which impacts the overall sensitivity, causing some of the spectra of the series to have a significantly lower signal-to-noise ratio. This is somewhat similar to the frequency selection in non-uniformly sampled (NUS) processing as described, for instance, in refs (51−56) or the application to deconvolution of complex mixtures through multidimensional NMR.42,54 The synthetic test is designed to match the behavior of three spectra acquired on the same sample increasing, for example, the mixing time, therefore altering the signals intensities but not their line widths or positions.

MCR has been applied imposing the 1H spectrum to be common to all three experiments and allowing for variations in the 29Si intensities. The physical meaning of this constraint is that in all three experiments the proton source is the same and the difference resides in the efficiency of the 1H–29Si transfer as a function of the mixing time. The results are given in SI Figure S2. The improvement in the S/N ratio in the three experiments is quite large (see Table 1) and, as we had observed for the single spectrum, the shape and the relative intensities of the peaks are preserved (SI Figure S3).

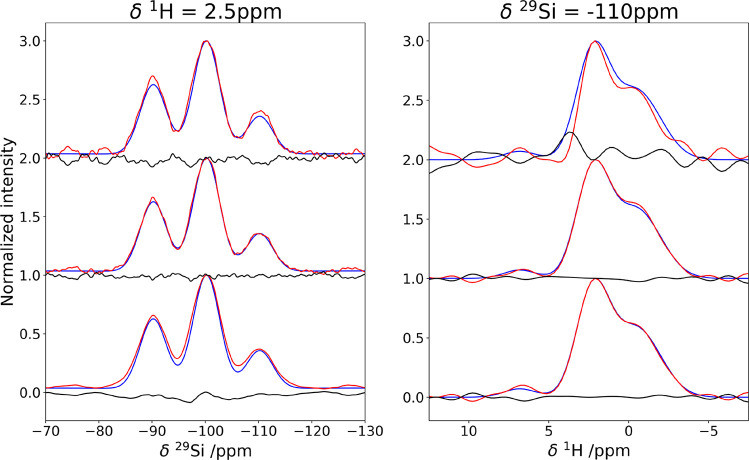
It is interesting to observe that, while the S/N ratio improves less for spectra B and C when they are coprocessed with A, the S/N ratio of A is largely improved when the spectra are coprocessed. At the same time, the reconstruction of all three spectra shows a higher adherence to the noiseless spectrum with respect to the individually processed spectra (Figure 2).

Figure 2.

Figure 2

Open in a new tab

Impact of the coprocessing in the denoising of the synthetic spectrum B. In all panels, the blue trace corresponds to the noiseless spectrum. The denoising steps are listed from top to bottom: (top) initial spectrum-red trace and difference-black trace, (middle) MCR-reconstructed spectrum-red trace and difference-black trace, (bottom) MCR+Cadzow reconstructed spectrum-red trace and difference-black trace.

The Impact of Denoising on Experimental Spectra

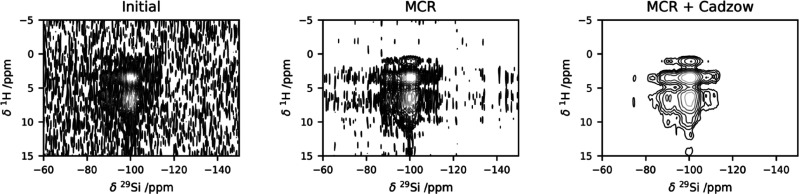
Given that the quantitative information on the spectra appears to be preserved across the denoising steps, we have applied the same procedure to experimental data sets, acquired on a silica-lysozyme composite.19,57 The target spectra are 1H–29Si HETCOR with Lee Goldburg homonuclear decoupling during the indirect dimension (Figure 3). Further examples are described in SI Figures S4 and S5.

Figure 3.

Figure 3

Open in a new tab

Effect of denoising on a low S/N experimental spectrum. From left to right: initial experimental spectrum, spectrum reconstructed with MCR and spectrum reconstructed with MCR after application of Cadzow denoising.

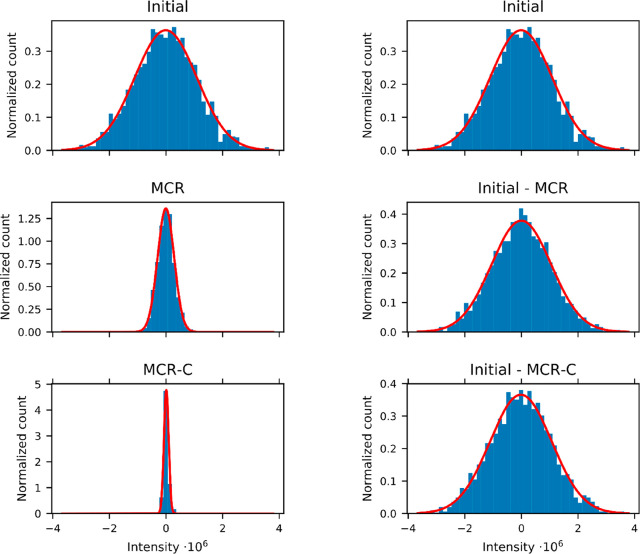
It is also extremely important to evaluate the properties of the noise, to verify that it does not change significantly during the denoising procedure. To do so, we have evaluated the difference between the initial spectrum and the processed ones and evaluated the noise distribution (Figure 4 and SI Table S3). The noise extracted from the spectra remains Gaussian. The noise distribution width is greatly decreased in the “signal” spectra (i.e.: the FT of the CST matrix), whereas the noise distribution width in the “error” spectrum (i.e.: the FT of the E matrix) remains the same as the noise of the initial spectrum, indicating that no part of the signal is discarded into the noise.

Figure 4.

Figure 4

Open in a new tab

Distribution of the intensities along the points of the row of the spectrum extracted at 50 ppm, which contains only noise, representing the noise in the initial spectrum (initial) and after application of combined denoising. Left–intensity in the “signal” spectrum CST; Right–intensity in the “noise” spectrum E. The red curves are the best fitting Gaussian distributions that approximates the intensities, their parameters are given in SI Table S3.

MCR is ideally versed toward processing of two-dimensional spectra, handling several transients at the same time, whereas other denoising methods, like Cadzow denoising, work on single transients. Therefore, one can expect that the order used to apply the different denoising schemes has an impact on the reconstruction. To test this, we have inverted the order of the processing steps (SI Figure S6) and we have found that, while the impact of MCR and Cadzow yields similar improvements in S/N ratio (from 9 to 32 and 33, respectively), MCR is able to improve the Cadzow procedure when applied first (80 for Cadzow+MCR and 99 for MCR+Cadzow).

Combined Denoising on a Set of Experimental Spectra

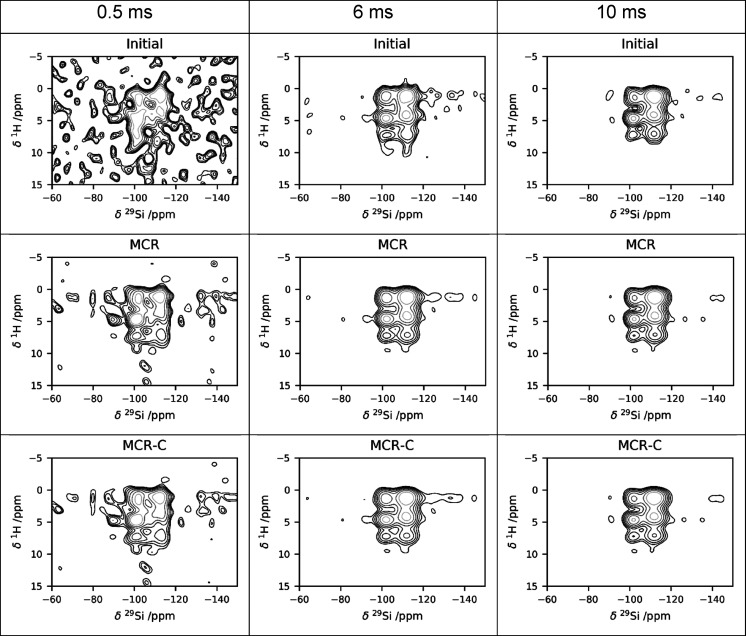
We have also applied the combined denoising to a series of 1H–29Si HETCOR spectra acquired with different contact times (0.5, 6, and 10 ms, respectively). All the echoes in the CPMG were coadded, and the resulting S/N ratio of the three spectra is 9, 42, and 60, respectively. The MCR processing increases the S/N ratio to 26, 119, and 160, and the subsequent application of Cadzow denoising further increases it to 28, 123, and 177. The results are shown in Figure 5.

Figure 5.

Figure 5

Open in a new tab

Denoising of a series of experimental spectra, acquired at different contact times: from left to right 0.5, 6, and 10 ms, respectively. (Top row) initial spectra, (central row) MCR-reconstructed spectra, (bottom row) MCR+Cadzow reconstructed spectra.

Conclusions

We have presented the use of MCR for denoising of low sensitivity solid-state NMR two-dimensional spectra. Our results demonstrate that this denoising approach preserves the quantitative information on the cross-peak intensity, yielding an improvement in the S/N ratio of around a factor of 3. Furthermore, it is robust to high levels of noise. We have also demonstrated that the intrinsic ability of MCR to coprocess multiple spectra can be used to improve the reconstruction of the spectra with the lowest S/N ratio across a series of spectra; this is particularly relevant in the case of spectra acquired on the same sample, altering some parameters in the pulse sequence, for example, varying the cross-polarization contact time across different experiments. We stress that we have applied the MCR method to time-domain data, therefore preserving the applicability of other denoising schemes, and even improving their performance, increasing the S/N ratio up to a factor of 9. Finally, our results have been obtained without imposing prior knowledge in the form of regularization of additional constraints,42 and thus demonstrate that this method is applicable on systems or experiments that are not described by simple forward models. Therefore, this application is not limited to 29Si MAS NMR, but can be applied to other nuclei of moderate or low receptivity, and also on multidimensional experiments acquired on static samples, where sensitivity is limited by the fact that the signal is spread over complicated powder patterns.58−63

We foresee that MCR can be generally extended to data sets of higher dimensionality and NUS sampled data.

Acknowledgments

This work has been supported by the Fondazione Cassa di Risparmio di Firenze, the Italian Ministero della Salute through the grant GR- 2016-02361586, and the Italian Ministero dell’Istruzione, dell’Università e della Ricerca through the “Progetto Dipartimenti di Eccellenza 2018-2022” to the Department of Chemistry “Ugo Schiff” of the University of Florence, and the University of Florence through the “Progetti Competitivi per Ricercatori”. The authors acknowledge the support and the use of resources of Instruct-ERIC, a landmark ESFRI project, and specifically the CERM/CIRMMP Italy center.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.analchem.9b05420.

  • Tables S1–S4, Figures S1–S6 (PDF)

Author Present Address

# (G.B.) Laboratory of Clinical Neurochemistry, Neurology Clinic, University of Perugia, Piazzale Lucio Severi 1/8, 06132 Perugia (PG), Italy.

The authors declare no competing financial interest.

Dedication

We dedicate this work to the memory of Prof. Stefano Caldarelli, a brilliant mind, a very imaginative scientist, and a very dear friend. This dedication is further motivated by the fact that this work has been triggered by a discussion with him at the EMBO Workshop “Challenges for magnetic resonance in life sciences” in Principina Terra a few months before his untimely passing.

Supplementary Material

ac9b05420_si_001.pdf (1.4MB, pdf)

References

  1. Cox P. A.The Elements. Their Origin, Abundance, and Distribution., 1989. [Google Scholar]
  2. Bertini I.; Gray H. B.; Stiefel E. I.; Valentine J. S.. Biological Inorganic Chemistry; University Science Books: Sausalito, CA, 2006. [Google Scholar]
  3. Greenwood N. N.; Earnshaw A.. Chemistry of the Elements; Pergamon Press, Oxford, 1984. [Google Scholar]
  4. Harris R. K.; Mann B. E.. NMR and the Periodic Table; Academic Press: London, 1978. [Google Scholar]
  5. Wickramasinghe N. P.; Ishii Y. Sensitivity Enhancement, Assignment, and Distance Measurement in 13C Solid-State NMR Spectroscopy for Paramagnetic Systems under Fast Magic Angle Spinning. J. Magn. Reson. 2006, 181 (2), 233–243. 10.1016/j.jmr.2006.05.008. [DOI] [PubMed] [Google Scholar]
  6. Sun S.; Yan S.; Guo C.; Li M.; Hoch J. C.; Williams J. C.; Polenova T. A Timesaving Strategy for MAS NMR Spectroscopy by Combining Non-Uniform Sampling and Paramagnetic Relaxation Assisted Condensed Data Collection. J. Phys. Chem. B 2012, 116 (46), 13585–13596. 10.1021/jp3005794. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Parthasarathy S.; Nishiyama Y.; Ishii Y. Sensitivity and Resolution Enhanced Solid-State NMR for Paramagnetic Systems and Biomolecules under Very Fast Magic Angle Spinning. Acc. Chem. Res. 2013, 46 (9), 2127–2135. 10.1021/ar4000482. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Kocman V.; Di Mauro G. M.; Veglia G.; Ramamoorthy A. Use of Paramagnetic Systems to Speed-up NMR Data Acquisition and for Structural and Dynamic Studies. Solid State Nucl. Magn. Reson. 2019, 102, 36–46. 10.1016/j.ssnmr.2019.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Fujiwara T.; Ramamoorthy A.. How Far Can the Sensitivity of NMR Be Increased? In Annual Reports on NMR Spectroscopy; Elsevier, 2006; Vol. 58, pp 155–175. 10.1016/S0066-4103(05)58003-7. [DOI] [Google Scholar]
  10. Banci L.; Barbieri L.; Calderone V.; Cantini F.; Cerofolini L.; Ciofi-Baffoni S.; Felli I. C.; Fragai M.; Lelli M.; Luchinat C.; et al. Biomolecular NMR at 1.2 GHz. ArXiv191007462 Phys. 2019.
  11. McNeill S. A.; Gor’kov P. L.; Struppe J.; Brey W. W.; Long J. R. Optimizing SsNMR Experiments for Dilute Proteins in Heterogeneous Mixtures at High Magnetic Fields. Magn. Reson. Chem. 2007, 45 (S1), S209–S220. 10.1002/mrc.2146. [DOI] [PubMed] [Google Scholar]
  12. Dvinskikh S.; Dürr U.; Yamamoto K.; Ramamoorthy A. A High-Resolution Solid-State NMR Approach for the Structural Studies of Bicelles. J. Am. Chem. Soc. 2006, 128 (19), 6326–6327. 10.1021/ja061153a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Bertini I.; Luchinat C.; Parigi G.; Ravera E. SedNMR: On the Edge between Solution and Solid-State NMR. Acc. Chem. Res. 2013, 46 (9), 2059–2069. 10.1021/ar300342f. [DOI] [PubMed] [Google Scholar]
  14. Zhang R.; Damron J.; Vosegaard T.; Ramamoorthy A. A Cross-Polarization Based Rotating-Frame Separated-Local-Field NMR Experiment under Ultrafast MAS Conditions. J. Magn. Reson. 2015, 250, 37–44. 10.1016/j.jmr.2014.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Ravera E.; Cerofolini L.; Martelli T.; Louka A.; Fragai M.; Luchinat C. 1H-Detected Solid-State NMR of Proteins Entrapped in Bioinspired Silica: A New Tool for Biomaterials Characterization. Sci. Rep. 2016, 6, 27851. 10.1038/srep27851. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lelli M.; Gajan D.; Lesage A.; Caporini M. A.; Vitzthum V.; Miéville P.; Héroguel F.; Rascón F.; Roussey A.; Thieuleux C.; et al. Fast Characterization of Functionalized Silica Materials by Silicon-29 Surface-Enhanced NMR Spectroscopy Using Dynamic Nuclear Polarization. J. Am. Chem. Soc. 2011, 133 (7), 2104–2107. 10.1021/ja110791d. [DOI] [PubMed] [Google Scholar]
  17. Lafon O.; Rosay M.; Aussenac F.; Lu X.; Trébosc J.; Cristini O.; Kinowski C.; Touati N.; Vezin H.; Amoureux J.-P. Beyond the Silica Surface by Direct Silicon-29 Dynamic Nuclear Polarization. Angew. Chem., Int. Ed. 2011, 50 (36), 8367–8370. 10.1002/anie.201101841. [DOI] [PubMed] [Google Scholar]
  18. Thankamony A. S. L.; Lafon O.; Lu X.; Aussenac F.; Rosay M.; Trébosc J.; Vezin H.; Amoureux J.-P. Solvent-Free High-Field Dynamic Nuclear Polarization of Mesoporous Silica Functionalized with TEMPO. Appl. Magn. Reson. 2012, 43 (1–2), 237–250. 10.1007/s00723-012-0364-3. [DOI] [Google Scholar]
  19. Ravera E.; Michaelis V. K.; Ong T.-C.; Keeler E. G.; Martelli T.; Fragai M.; Griffin R. G.; Luchinat C. Biosilica-Entrapped Enzymes Studied by Using Dynamic Nuclear-Polarization-Enhanced High-Field NMR Spectroscopy. ChemPhysChem 2015, 16 (13), 2751–2754. 10.1002/cphc.201500549. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. André M.; Piotto M.; Caldarelli S.; Dumez J.-N. Ultrafast High-Resolution Magic-Angle-Spinning NMR Spectroscopy. Analyst 2015, 140 (12), 3942–3946. 10.1039/C5AN00653H. [DOI] [PubMed] [Google Scholar]
  21. Rouger L.; Yon M.; Sarou-Kanian V.; Fayon F.; Dumez J.-N.; Giraudeau P. Ultrafast Acquisition of 1H-1H Dipolar Correlation Experiments in Spinning Elastomers. J. Magn. Reson. 2017, 277, 30–35. 10.1016/j.jmr.2017.02.005. [DOI] [PubMed] [Google Scholar]
  22. Antoine J.-P.; Chauvin C.; Coron A. Wavelets and Related Time-Frequency Techniques in Magnetic Resonance Spectroscopy. NMR Biomed. 2001, 14 (4), 265–270. 10.1002/nbm.699. [DOI] [PubMed] [Google Scholar]
  23. Vivó-Truyols G.; Schoenmakers P. J. Automatic Selection of Optimal Savitzky–Golay Smoothing. Anal. Chem. 2006, 78 (13), 4598–4608. 10.1021/ac0600196. [DOI] [PubMed] [Google Scholar]
  24. Chiron L.; van Agthoven M. A.; Kieffer B.; Rolando C.; Delsuc M.-A. Efficient Denoising Algorithms for Large Experimental Datasets and Their Applications in Fourier Transform Ion Cyclotron Resonance Mass Spectrometry. Proc. Natl. Acad. Sci. U. S. A. 2014, 111 (4), 1385–1390. 10.1073/pnas.1306700111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Ghanati R.; Kazem Hafizi M.; Mahmoudvand R.; Fallahsafari M. Filtering and Parameter Estimation of Surface-NMR Data Using Singular Spectrum Analysis. J. Appl. Geophys. 2016, 130, 118–130. 10.1016/j.jappgeo.2016.04.005. [DOI] [Google Scholar]
  26. Laurent G.; Woelffel W.; Barret-Vivin V.; Gouillart E.; Bonhomme C. Denoising Applied to Spectroscopies – Part I: Concept and Limits. Appl. Spectrosc. Rev. 2019, 54 (7), 602–630. 10.1080/05704928.2018.1523183. [DOI] [Google Scholar]
  27. Man P. P.; Bonhomme C.; Babonneau F. Denoising NMR Time-Domain Signal by Singular-Value Decomposition Accelerated by Graphics Processing Units. Solid State Nucl. Magn. Reson. 2014, 61–62, 28–34. 10.1016/j.ssnmr.2014.05.001. [DOI] [PubMed] [Google Scholar]
  28. Tauler R. Multivariate Curve Resolution Applied to Second Order Data. Chemom. Intell. Lab. Syst. 1995, 30 (1), 133–146. 10.1016/0169-7439(95)00047-X. [DOI] [Google Scholar]
  29. Tauler R.; Smilde A.; Kowalski B. Selectivity, Local Rank, Three-Way Data Analysis and Ambiguity in Multivariate Curve Resolution. J. Chemom. 1995, 9 (1), 31–58. 10.1002/cem.1180090105. [DOI] [Google Scholar]
  30. Tauler R. Calculation of Maximum and Minimum Band Boundaries of Feasible Solutions for Species Profiles Obtained by Multivariate Curve Resolution. J. Chemom. 2001, 15 (8), 627–646. 10.1002/cem.654. [DOI] [Google Scholar]
  31. Ruckebusch C.; Blanchet L. Multivariate Curve Resolution: A Review of Advanced and Tailored Applications and Challenges. Anal. Chim. Acta 2013, 765, 28–36. 10.1016/j.aca.2012.12.028. [DOI] [PubMed] [Google Scholar]
  32. Lawton W. H.; Sylvestre E. A. Self Modeling Curve Resolution. Technometrics 1971, 13 (3), 617–633. 10.1080/00401706.1971.10488823. [DOI] [Google Scholar]
  33. de Juan A.; Tauler R. Multivariate Curve Resolution (MCR) from 2000: Progress in Concepts and Applications. Crit. Rev. Anal. Chem. 2006, 36 (3–4), 163–176. 10.1080/10408340600970005. [DOI] [Google Scholar]
  34. Garrido M.; Rius F. X.; Larrechi M. S. Multivariate Curve Resolution–Alternating Least Squares (MCR-ALS) Applied to Spectroscopic Data from Monitoring Chemical Reactions Processes. Anal. Bioanal. Chem. 2008, 390 (8), 2059–2066. 10.1007/s00216-008-1955-6. [DOI] [PubMed] [Google Scholar]
  35. Duponchel L.; Elmi-Rayaleh W.; Ruckebusch C.; Huvenne J. P. Multivariate Curve Resolution Methods in Imaging Spectroscopy: Influence of Extraction Methods and Instrumental Perturbations. J. Chem. Inf. Comput. Sci. 2003, 43 (6), 2057–2067. 10.1021/ci034097v. [DOI] [PubMed] [Google Scholar]
  36. Tauler R.; Lacorte S.; Guillamón M.; Cespedes R.; Viana P.; Barceló D. CHEMOMETRIC MODELING OF MAIN CONTAMINATION SOURCES IN SURFACE WATERS OF PORTUGAL. Environ. Toxicol. Chem. 2004, 23 (3), 565. 10.1897/03-176b. [DOI] [PubMed] [Google Scholar]
  37. Jaumot J.; Tauler R.; Gargallo R. Exploratory Data Analysis of DNA Microarrays by Multivariate Curve Resolution. Anal. Biochem. 2006, 358 (1), 76–89. 10.1016/j.ab.2006.07.028. [DOI] [PubMed] [Google Scholar]
  38. Puig-Castellví F.; Alfonso I.; Tauler R. Untargeted Assignment and Automatic Integration of 1 H NMR Metabolomic Datasets Using a Multivariate Curve Resolution Approach. Anal. Chim. Acta 2017, 964, 55–66. 10.1016/j.aca.2017.02.010. [DOI] [PubMed] [Google Scholar]
  39. Jaumot J.; Marchán V.; Gargallo R.; Grandas A.; Tauler R. Multivariate Curve Resolution Applied to the Analysis and Resolution of Two-Dimensional [ 1 H, 15 N] NMR Reaction Spectra. Anal. Chem. 2004, 76 (23), 7094–7101. 10.1021/ac049509t. [DOI] [PubMed] [Google Scholar]
  40. Nuzillard D.; Nuzillard J.-M. Application of Blind Source Separation to 1-D and 2-D Nuclear Magnetic Resonance Spectroscopy. IEEE Signal Process. Lett. 1998, 5 (8), 209–211. 10.1109/97.704974. [DOI] [Google Scholar]
  41. Toumi I.; Torrésani B.; Caldarelli S. Effective Processing of Pulse Field Gradient NMR of Mixtures by Blind Source Separation. Anal. Chem. 2013, 85 (23), 11344–11351. 10.1021/ac402085x. [DOI] [PubMed] [Google Scholar]
  42. Toumi I.; Caldarelli S.; Torrésani B. A Review of Blind Source Separation in NMR Spectroscopy. Prog. Nucl. Magn. Reson. Spectrosc. 2014, 81, 37–64. 10.1016/j.pnmrs.2014.06.002. [DOI] [PubMed] [Google Scholar]
  43. Cherni A.; Piersanti E.; Anthoine S.; Chaux C.; Shintu L.; Yemloul M.; Torrésani B. Challenges in the Decomposition of 2D NMR Spectra of Mixtures of Small Molecules. Faraday Discuss. 2019, 218, 459–480. 10.1039/C9FD00014C. [DOI] [PubMed] [Google Scholar]
  44. Marks D.; Vega S. J. Magn. Reson., Ser. A 1996, 118, 157–172. 10.1006/jmra.1996.0024. [DOI] [Google Scholar]
  45. Vinogradov E.; Madhu P. K.; Vega S. Proton Spectroscopy in Solid State Nuclear Magnetic Resonance with Windowed Phase Modulated Lee–Goldburg Decoupling Sequences. Chem. Phys. Lett. 2002, 354 (3), 193–202. 10.1016/S0009-2614(02)00060-X. [DOI] [Google Scholar]
  46. Leskes M.; Thakur R. S.; Madhu P. K.; Kurur N. D.; Vega S. Bimodal Floquet Description of Heteronuclear Dipolar Decoupling in Solid-State Nuclear Magnetic Resonance. J. Chem. Phys. 2007, 127 (2), 024501 10.1063/1.2746039. [DOI] [PubMed] [Google Scholar]
  47. Wiench J. W.; Lin V. S.-Y.; Pruski M. 29Si NMR in Solid State with CPMG Acquisition under MAS. J. Magn. Reson. 2008, 193 (2), 233–242. 10.1016/j.jmr.2008.05.007. [DOI] [PubMed] [Google Scholar]
  48. Windig Willem.; Guilment Jean. Interactive Self-Modeling Mixture Analysis. Anal. Chem. 1991, 63 (14), 1425–1432. 10.1021/ac00014a016. [DOI] [Google Scholar]
  49. Jaumot J.; Gargallo R.; de Juan A.; Tauler R. A Graphical User-Friendly Interface for MCR-ALS: A New Tool for Multivariate Curve Resolution in MATLAB. Chemom. Intell. Lab. Syst. 2005, 76 (1), 101–110. 10.1016/j.chemolab.2004.12.007. [DOI] [Google Scholar]
  50. Helmus J. J.; Jaroniec C. P. Nmrglue: An Open Source Python Package for the Analysis of Multidimensional NMR Data. J. Biomol. NMR 2013, 55 (4), 355–367. 10.1007/s10858-013-9718-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Hiller S.; Ibraghimov I.; Wagner G.; Orekhov V. Y. Coupled Decomposition of Four-Dimensional NOESY Spectra. J. Am. Chem. Soc. 2009, 131 (36), 12970–12978. 10.1021/ja902012x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Matsuki Y.; Eddy M. T.; Griffin R. G.; Herzfeld J. Rapid Three-Dimensional MAS NMR Spectroscopy at Critical Sensitivity. Angew. Chem., Int. Ed. 2010, 49 (48), 9215–9218. 10.1002/anie.201003329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Stanek J.; Augustyniak R.; Koźmiński W. Suppression of Sampling Artefacts in High-Resolution Four-Dimensional NMR Spectra Using Signal Separation Algorithm. J. Magn. Reson. 2012, 214, 91–102. 10.1016/j.jmr.2011.10.009. [DOI] [PubMed] [Google Scholar]
  54. Balsgart N. M.; Mulbjerg M.; Guo Z.; Bertelsen K.; Vosegaard T. High Throughput Identification and Quantification of Phospholipids in Complex Mixtures. Anal. Chem. 2016, 88 (4), 2170–2176. 10.1021/acs.analchem.5b03798. [DOI] [PubMed] [Google Scholar]
  55. Kosiński K.; Stanek J.; Górka M. J.; Żerko S.; Koźmiński W. Reconstruction of Non-Uniformly Sampled Five-Dimensional NMR Spectra by Signal Separation Algorithm. J. Biomol. NMR 2017, 68 (2), 129–138. 10.1007/s10858-017-0095-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Shchukina A.; Urbańczyk M.; Kasprzak P.; Kazimierczuk K. Alternative Data Processing Techniques for Serial NMR Experiments. Concepts Magn. Reson., Part A 2017, 46A (2), e21429 10.1002/cmr.a.21429. [DOI] [Google Scholar]
  57. Luckarift H. R.; Dickerson M. B.; Sandhage K. H.; Spain J. C. Rapid, Room-Temperature Synthesis of Antibacterial Bionanocomposites of Lysozyme with Amorphous Silica or Titania. Small 2006, 2 (5), 640–643. 10.1002/smll.200500376. [DOI] [PubMed] [Google Scholar]
  58. Hester R. K.; Ackerman J. L.; Neff B. L.; Waugh J. S. Separated Local Field Spectra in NMR: Determination of Structure of Solids. Phys. Rev. Lett. 1976, 36 (18), 1081–1083. 10.1103/PhysRevLett.36.1081. [DOI] [Google Scholar]
  59. Zhang P.; Dunlap C.; Florian P.; Grandinetti P. J.; Farnan I.; Stebbins J. F. Silicon Site Distributions in an Alkali Silicate Glass Derived by Two-Dimensional 29Si Nuclear Magnetic Resonance. J. Non-Cryst. Solids 1996, 204 (3), 294–300. 10.1016/S0022-3093(96)00601-1. [DOI] [Google Scholar]
  60. Marassi F. M.; Opella S. J. [No Title Found]. J. Biomol. NMR 2002, 23 (3), 239–242. 10.1023/A:1019887612018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Ramamoorthy A.; Wei Y.; Lee D.-K.. PISEMA Solid-State NMR Spectroscopy. In Annu. Rep. NMR Spectrosc.; Elsevier, 2004; Vol. 52, pp 1–52. 10.1016/S0066-4103(04)52001-X. [DOI] [Google Scholar]
  62. Wu C. H.; Opella S. J. Proton-Detected Separated Local Field Spectroscopy. J. Magn. Reson. 2008, 190 (1), 165–170. 10.1016/j.jmr.2007.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Jayanthi S.; Ramanathan K. V. 2n-SEMA-a Robust Solid State Nuclear Magnetic Resonance Experiment for Measuring Heteronuclear Dipolar Couplings in Static Oriented Systems Using Effective Transverse Spin-Lock. J. Chem. Phys. 2010, 132 (13), 134501. 10.1063/1.3336815. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ac9b05420_si_001.pdf (1.4MB, pdf)

Articles from Analytical Chemistry are provided here courtesy of American Chemical Society

RESOURCES