Abstract
This research proposes a new type of Grey Wolf optimizer named Gradient-based Grey Wolf Optimizer (GGWO). Using gradient information, we accelerated the convergence of the algorithm that enables us to solve well-known complex benchmark functions optimally for the first time in this field. We also used the Gaussian walk and Lévy flight to improve the exploration and exploitation capabilities of the GGWO to avoid trapping in local optima. We apply the suggested method to several benchmark functions to show its efficiency. The outcomes reveal that our algorithm performs superior to most existing algorithms in the literature in most benchmarks. Moreover, we apply our algorithm for predicting the COVID-19 pandemic in the US. Since the prediction of the epidemic is a complicated task due to its stochastic nature, presenting efficient methods to solve the problem is vital. Since the healthcare system has a limited capacity, it is essential to predict the pandemic's future trend to avoid overload. Our results predict that the US will have almost 16 million cases by the end of November. The upcoming peak in the number of infected, ICU admitted cases would be mid-to-end November. In the end, we proposed several managerial insights that will help the policymakers have a clearer vision about the growth of COVID-19 and avoid equipment shortages in healthcare systems.
Keywords: COVID-19, Pandemic modeling, Grey wolf optimizer, Gradient search
1. Introduction
Scientists employ optimization in almost every research field. Optimization is a significant challenge in science and engineering, mainly due to the complexity of problems on the one hand and the shortcomings of classical approaches, on the other hand. Random Search Algorithms (RSA) are one of the most efficient means of solving complex real-world problems (Zabinsky, 2010, Solis and Wets, 1981, Hong and Nelson, 2007). These algorithms sacrifice optimality to find a high-quality near-optimal solution in a short time. The main feature of these methods is randomness embedded in their framework during the iterations of the algorithm. RSAs are more flexible and easier to apply compared to traditional methods in terms of implementation complexity. Metaheuristics are one group of the main RSAs that have been widely used to resolve complex optimization problems. Some of the most recent metaheuristic algorithms are Grey Wolf Optimizer (GWO), Salp Swarm Algorithm (SSA), and Coronavirus Herd Immunity Optimizer (CHIO).
Healthcare science is one of the main fields in which optimization makes a remarkable improvement. In December 2019, a new virus named SARS-Cov-2 emerged in China that causes severe respiratory disease (COVID-19). The virus spread rapidly to more than 213 countries resulting in 22,185,755 cases and 780,369 deaths. Improvement in modeling the COVID-19 outbreak will significantly help the authorities in decision making. Besides, these insights enable us to optimally distribute resources and side-step equipment shortages in hospitals and save humans’ lives. Prediction of the COVID-19 pandemic is challenging due to its stochastic nature and complexity.
(Zhang, Ma, & Wang, 2020) proposed a piecewise Poisson formulation to study the recent cases of the COVID-19 pandemic. Using the suggested model, the researchers projected the peak of the epidemic. (Chimmula & Zhang, 2020) presented a deep learning-based method using Long-Short Term Memory (LSTM) to forecast the progress of the COVID-19 outbreak. The authors also aimed at estimating the possible ending point of the epidemic. The offered methodologies have several limitations that make their outcomes inapplicable. LSTM needs a large amount of memory, making the computational tests a challenging task. Besides, scientists should provide enormous data to train the LSTM. Moreover, the suggested method cannot forecast either the number of cases with life-threatening symptoms or the number of asymptomatic cases. Furthermore, LSTM cannot estimate essential epidemiological statistics, including the reproduction rate. (Arora, Kumar, & Panigrahi, 2020)utilized a deep learning-based method using LSTM to forecast India's forthcoming COVID-19 cases. Their offered method has the same limitations as the method suggested by Chimmula and Zhang (2020), which makes their forecasts valid for a short period. Many researchers utilized LSTM and machine learning techniques to forecast the future pandemic scenarios in several countries; however, most of them have the same limitations ((Abebe, 2020, Alamo et al., 2020, da Silva et al., 2020, Garcia et al., 2020, Lalmuanawma et al., 2020, Panwar et al., 2020, Peng and Nagata, 2020); ; ; ; ; ; ).
One of the most recent models to define the pandemic is the SIDARTHE model. The model was first presented in a paper by Giordano et al. (2020). The authors claimed that the formulation is able to project the future trend of the outbreak over a more extended period of time. Besides, the model provides the policymakers and healthcare professionals with vital epidemiological information such as reproduction rate. Although the model is very efficient in predicting future trends, the scientists highlighted that solving the model optimally is complicated due to its unique characteristics.
As mentioned earlier, solving complex optimization problems using metaheuristics is easier compared to classical methods. Grey Wolf Optimizer (GWO) is one of the most recent and efficient metaheuristic algorithms in the literature. GWO is inspired by the hunting behavior of Grey wolves in nature. The GWO performs acceptably in exploration by adapting the search radius of the wolves in the first iterations. It maintains a good diversity among the wolves to avoid local optima. However, we could improve the exploration ability of the GWO to enhance its ability to search the solution space more intelligently (Long et al., 2018). The lack of efficient exploration ability in GWO is apparent from its results in multimodal benchmark functions (Mirjalili et al., 2014). Besides, to enhance the algorithm to efficiently exploit the solution space, we should add some new operators to the algorithm. The GWO performs average in the exploration of the solution space, considering its results in composite benchmarks in which other algorithms dominate GWO in most benchmarks (Mirjalili et al. 2014). Random movements such as Gaussian and Lévy walks in the exploration phase will remarkably increase the exploration ability of the algorithm.
In the exploitation phase, the GWO uses random movements on a tiny scale that do not necessarily guarantee an improvement in the best solution. Using gradient information that always guarantees improvement in the best solution will significantly improve the performance of GWO. GWO is applied successfully to many optimization problems in different fields such as text document clustering (Rashaideh et al. 2018), feature selection (Abdel-Basset et al. 2020), predicting the strength of concretes (Golafshani et al. 2020), biodiesel production (Samuel et al. 2020), multi-objective flexible job-shop scheduling problem (Zhu and Zhou 2020), and three-dimensional path planning for UAVs (Dewangan et al. 2019). For more detailed information about applications of GWO, please see Faris et al. (2018).
In this research, we present a new algorithm called Gradient-based Grey Wolf Optimizer (GGWO) that enables scientists to solve many real-world optimization problems. In our algorithm, we utilize the advantages of the gradient that presents valuable information about the solution space. In many optimization problems, gradient information is available or could be estimated. Using gradient information, we explore the solution space more intelligently by considering the gradient direction in our search process, leading us to the optimal or a good near-optimal solution. Almost all metaheuristic algorithms ignore the gradient information, which increases the probability of getting trapped in local optima. This motivated us to add the gradient in one of the most efficient algorithms to improve the exploration and exploitation abilities of the method. Considering gradient information, we accelerate the algorithm that enables us to solve well-known complex benchmark functions optimally for the first time in the field.
Besides, we use deep mathematical concepts such as Gaussian walk and Lévy flights to improve the search efficiency of our method. The proposed contributions enable the suggested algorithm to avoid local optima. Our computational results on several benchmarks demonstrate the superiority of our algorithm to other algorithms in the literature. Moreover, we apply several statistical tests to determine significant differences in the performance of the algorithm compared to state-of-the-art methodologies. Moreover, we apply the devised algorithm to forecast the spread of the pandemic in the United States, with most cases of COVID-19 (https://www.worldometers.info/coronavirus). Our results predicted the maximum number of infected and hospitalized cases in the United States that will happen in mid-to-end November 2020. Besides, we perform further analysis to project future scenarios. We also measured the effect of the implemented restrictions by the government.
We have organized the remainder of this paper as follows: Section 2 provides a detailed literature review. Section 3 proposes a new methodology to solve optimization problems based on gradient information and random walks. In Section 4, we carry out computational experiments on challenging benchmarks using our algorithm. Section 5 presents an application of our methodology for forecasting the spread of the COVID-19 outbreak. In Section 6, we analyzed the uncertainty in the future spread of the pandemic. Section 7 concludes the paper, including an outlook on future research avenues.
2. Survey on the relevant literature
The underlying idea of most of the metaheuristic algorithms is to mimic a swarm behavior of nature. Mirjalili et al. (2016) divided metaheuristics into three categories: Swarm Algorithms (SAs), Evolutionary Algorithms (EAs), and Physics-based Algorithms (PAs). EAs, PAs, and SAs mimic the evolution process, law of physics on particles, and swarm behavior, respectively (Khalilpourazari and Pasandideh 2019). Some of the most recent algorithms in this area are categorized in Table 1 .
Table 1.
Classification of metaheuristic algorithms.
| Evolutionary algorithms | Physics-based algorithms | Swarm Based algorithms | Other Population-based algorithms |
|---|---|---|---|
| Genetic Programming (GP) (Koza and Koza, 1992) | Simulated annealing (Van Laarhoven and Aarts, 1987) | Particle Swarm Optimization (PSO) (Clerc and Kennedy, 2002, Kennedy and Eberhart, 1995) | Stochastic Fractal Search (SFS) (Salimi 2015) |
| Estimation of distribution algorithm (EDA) (Wang et al. 2013) | Galaxy-based Search Algorithm (GBSA) (Kaveh et al., 2020) | Artificial Bee Colony (ABC) (Karaboga and Basturk 2007) | Sine Cosine Algorithm (SCA) (Mirjalili, 2016a) |
| Biogeography Based Optimizer (BBO) (Ergezer et al., 2008) | Simulated Annealing (SA) (Cerby, 1985, Kirkpatrick et al., 1983) | Ant Lion Optimization Algorithm (ALO) (Mirjalili, 2015b) | Coronavirus Optimization Algorithm (COA) (Martínez-Álvarez et al. 2020) |
| Degree-Descending Search Strategy (DDS) (Cui et al. 2018) | Thermal exchange optimization (Kaveh and Dadras 2017) | Dynamic Virtual Bats Algorithm (Topal and Altun 2016) | Sine–Cosine Crow Search Algorithm (SCCSA) (Khalilpourazari and Pasandideh 2019) |
| Evolutionary Programming (EP) (Fogel et al. 1966) | Central Force Optimization (CFO) (Formato 2007) | Salp Swarm Algorithm (SSA) (Mirjalili et al. 2017) | Gradient-Based Optimizer (GBO) (Ahmadianfar et al., 2020) |
| Genetic Algorithms (GA) (Holland 1992) | Curved Space Optimization (CSO) (Moghaddam et al., 2012) | Grey Wolf Optimizer (GWO) (Mirjalili et al. 2014) | Lightning Search Algorithm (LSA) (Shareef et al. 2015) |
| Evolution Strategy (ES) (Rechenberg, 1978, Huning, 1976) | Charged System Search (CSS) (Kaveh and Talatahari 2010) | Dragonfly Algorithm (DA) (Mirjalili, 2016b) | Water Cycle Algorithm (WCA) (Eskandar et al. 2012) |
| Differential Evolution (DE) (Price 2013) | Gravitational Search Algorithm (GSA) (Rashedi et al. 2009) | Cuckoo Search (CS) (Yang and Deb 2009) | Virus colony search (Li et al. 2016) |
| Black Hole Mechanics Optimization (BHMO) (Kaveh et al., 2020) | Crow Search Algorithm (CSA) (Askarzadeh 2016) | Water Cycle Moth Flame Optimization (WCMFO) (Khalilpourazari and Khalilpourazary 2019) | |
| Black Hole (BH) algorithm (Hatamlou 2013) | Grasshopper Optimization Algorithm (Saremi et al. 2017) | Coronavirus herd immunity optimizer (CHIO) (Al-Betar et al. 2020) | |
| Multi-Verse Optimization (MVO) Algorithm (Mirjalili et al. 2016) | Moth-Flame Optimization (MFO) (Mirjalili, 2015a) | Adaptive β-hill climbing for optimization (Al-Betar et al. 2019) | |
| Small-World Optimization Algorithm (SWOA) (Du et al. 2006) | Whale Optimization Algorithm (WOA) (Mirjalili et al., 2016) | β-hill climbing algorithm (Al-Betar et al. 2017) | |
| Tabu search (Glover and Laguna, 1999) |
Based on the classification of Mirjalili et al. (2016), our algorithm is in the category of the swarm-based algorithms; however, this is not the only classification in the literature. For instance, based on blum and roli (2003), metaheuristics could be classified based on different perspectives such as nature-inspired vs. non-nature inspired, population-based vs. single point search, dynamic vs. static objective function, one vs. various neighborhood structures, and memory usage vs. memory-less methods. Based on the latter classification, our algorithm is in the class of population-based nature-inspired algorithms with the static objective function. The readers are referred to Blum and Roli (2003) for more details regarding the latter classifications.
Grey Wolf Optimizer (GWO) is one of the most efficient algorithms in solving complex optimization problems. The GWO performs acceptably in exploration by modifying the distance between grey wolves in the first iterations. It maintains a proper distance and diversity between the wolves to avoid local optima. However, the exploration ability of the GWO could be significantly improved (Long et al., 2018). Using random movements like Gaussian and Lévy walks during the exploration phase will remarkably increase the exploration ability of the algorithm. However, GWO suffers from a lack of an efficient exploitation ability (Bansal and Singh, 2020, Long et al., 2018). In the exploitation phase, the GWO uses random movements on a tiny scale that do not necessarily guarantee an improvement in the best solution. However, gradient information, which always guarantees improvement in the best solution, will significantly improve the performance of GWO. In this research, we enhanced the GWO by adding new operators to search the solution space using the gradient information for the first time. We called the algorithm Gradient-based Grey Wolf Optimizer (GGWO). The gradient provides valuable information about the solution space and enables the GGWO to achieve highly accurate results. Gradient information and new operators meaningfully enhanced the performance of the GGWO in exploiting the neighborhood of the best solution.
Moreover, we apply a Gaussian walk and Lévy flight at the end of each iteration to enhance exploration. These features enable GGWO to avoid local optima while maintaining proper exploitation throughout the optimization process. We demonstrate the superiority of our methodology on some benchmarks using robust statistical tests. Furthermore, as an application, we use our proposed algorithm to forecast the spread of the COVID-19 pandemic in the US. Our results show that our algorithm could predict the future trends of the pandemic.
3. Designing an accelerated Grey Wolf Optimizer
We will first illustrate the fundamentals of Grey Wolf Optimizer (GWO), then we will accelerate the GWO using gradient information and Gaussian and Lévy flights.
3.1. Grey Wolf Optimizer
GWO, recently proposed by Mirjalili et al. (2014), is inspired by grey wolves' hunting strategies in nature. Generally speaking, grey wolves are hierarchically categorized into four classes: Alpha, Beta, Delta, and Omega (Abdel-Basset et al. 2020). The Alpha is the dominant wolf in the pack. He/she makes all the decisions in the swarm. Other swarm members must comply with his/her decision. Besides, the only wolves that breed in the swarm are Alphas. Beta wolves’ assist Alpha and communicate between Alpha wolves and other wolves. Beta wolf is the best nominee for being Alpha if one of the Alpha wolves dies or is too old to manage the swarm. The Beta fulfills the orders of the Alpha but also controls other wolves of the swarm. Omega wolves represent the lowest-ranked grey wolves (Dhargupta et al. 2020). Omega wolves always follow other high-ranking wolves. Wolves that are not included in the Alpha, Beta, or Omega class are named Delta wolves. The Deltas manage the Omega wolves while assisting Alpha and Beta.
Like many other swarm intelligence-based algorithms, GWO starts optimization by initializing a population. Then, after determining the dominant members, the wolves update their location in the solution space around the target. We apply Eqs.(1) to (2) to simulate the encircling process:
| (1) |
| (2) |
In Eqs. (1)-(2), t shows the current iteration and and are coefficients. Besides and represent position vectors of prey and a grey wolf, respectively. Coefficients and are calculated as follows:
| (3) |
| (4) |
where decreases linearly throughout iterations in the range of 2 to 0 and and are random numbers in [0,1]. Based on the values of parameter, which linearly decreases throughout iterations from 2 to 0, GWO performs exploration or exploitation. In cases which the value of is greater than 1 or less than −1, the GWO performs exploration by diverging the wolves from the best solution. In addition, if the GWO performs exploitation by ensuring that the wolves move toward the best solution. We note that is a random parameter that ensures random movements of the wolves around the best solution obtained so far using Eq. (5). To mathematically state the hunting process and show how Omegas follow other dominant wolves, we use Eqs. (5)–(7):
| (5) |
| (6) |
| (7) |
The GWO performs the above actions repeatedly to find a near-optimal solution for the problem until a stopping criterion is met.
3.2. Accelerated Gradient-based Grey Wolf Optimizer
To perform fine in terms of exploration, an algorithm should maintain an appropriate balance between exploration and exploitation. GWO searches the solution space by updating the position of the dominated wolves regarding the position of Alpha, Beta, and Delta. By reducing the parameter over iterations, GWO aims at exploration in the first iterations and then focuses on exploiting in the last iterations. Besides, adjusting this parameter helps the GWO avoid trapping in local optima.
This paper adds two novel features to GWO to enhance its performance and propose a novel algorithm called Gradient-Based Grey Wolf Optimizer (GGWO). First, we propose a new procedure to use gradient information to improve the algorithm's exploitation and exploration abilities. In many optimization problems, the gradient will provide valuable information about the shape of the solution space by determining the steepest slope at each point in the solution space. We move particles to the nearest local optima using gradient information while maintaining a proper exploration ability. Such updating operators enable GWO to search the solution space more efficiently and enhance the exploration ability of the algorithm to side-step local optima. We propose the following new updating formulations for Omega wolves. We note that eq.(8) is based on the given illustrations in (Pahnehkolaei et al., 2017).
| (8) |
where i is the index of decision variables in the optimization problem, and n is the number of grey wolves. The terms and show the largest positive and the smallest negative slopes for each dimension at each iteration of the algorithm. Whereas is a continuous parameter determined in (0,1]. In the above formulation, we update the using equation (9) as follows (Pahnehkolaei et al., 2017):
| (9) |
Based on the given illustrations in Pahnehkolaei et al. (2017), it is apparent that:
| (10) |
In some optimization problems, the gradient of the problem may be unknown due to the non-differentiability of the objective function or discrete characteristics of the decision variables. In order to handle those problems, we present the following equation (Pahnehkolaei et al., 2017):
| (11) |
The second contribution that we have added to GWO is the use of Gaussian walk and Lévy flight. These two are random walks to increase randomness in the GGWO and boost its exploration ability. Lévy flight and Gaussian walks create self-similar clusters (trajectories) but differ significantly in structure. The cluster created by the lévy flight contains several islands (sets of short steps) connected by long excursions (Chakrabarti et al., 2006). However, the Gaussian walk creates a denser and smaller cluster (within the same number of iterations) that consists of many small steps (Mousavirad and Ebrahimpour-Komleh, 2017, Yang, 2014). Random selection of these two methods enhances the exploration capability of the GGWO by helping the algorithm avoid local optima. Therefore, GGWO switches randomly between Lévy flight and Gaussian walks to use the advantage of both (Salimi 2015). In the proposed GGWO, we use the following formulations to update the position of Omega wolves in the solution space at the end of each iteration:
| (12) |
| (13) |
where and present the best solution and standard deviation of the Gaussian distribution, respectively. GGWO changes the Gaussian parameter as and reduces the length of steps over iterations by setting where l is the iteration number. The expression is the new position of the wolf and is its current position. Besides, and are random numbers in (0,1]. The Lévy flight is computed by Eq. (14):
| (14) |
where and are random numbers in (0,1]. The term is a constant equal to 1.5. In Eqn. (13), we compute by:
| (15) |
Based on the given illustrations, the main framework of the GGWO is the same as GWO; however, with some significant changes. For instance, first, instead of the classical GWO operators, the GGWO uses a combination of the original operators and gradient-based operators to update the position of the wolves. Besides, we need to add a new feature to the GGWO (a function) to calculate the gradient of the objective function at each point of the solution space. Moreover, we use Gaussian walk and Lévy flight to increase randomness at the end of each iteration, which significantly improved the exploration and exploitation by using both long and short steps to move the particles in the solution space. The pseudo-code of the GGWO is presented as follows:
|
We also present the flowchart of the GGWO in Fig. 1 .
Fig. 1.
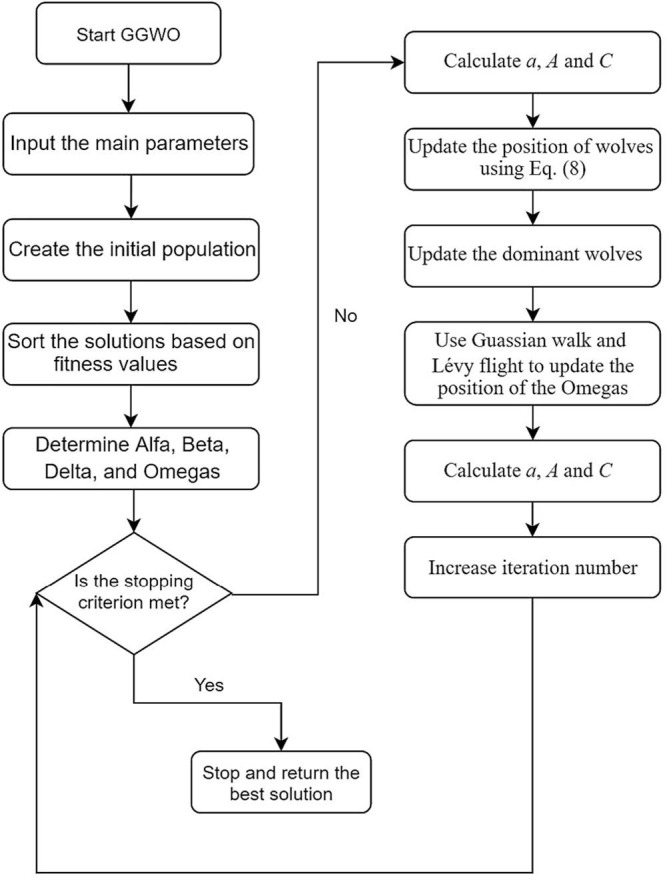
Flowchart of the offered GGWO.
4. Results and discussion
In order to evaluate the efficiency of the offered GGWO, we compare it with well-known algorithms in the literature, including Grey Wolf Optimizer (GWO), Gradient-based Water Cycle Algorithm (GWCA), Artificial Bee Colony (ABC), Gravitational Search Algorithm (GSA), hybrid Particle Swarm Optimization Gravitational Search Algorithm (PSOGSA), Particle Swarm Optimization (PSO), Salp Swarm Algorithm (SSA), Sine-Cosine Algorithm (SCA), and Moth-Flame Optimization (MFO). Table 2 provides the values of the parameters of the algorithms. We implement the experiments considering two different dimensions, 30 and 50, to enhance the benchmark functions' complexity. In all the tests, we consider a maximum NFEs of 30,000 as the stopping condition. We also set the control parameter to 0.9 in all tests. We repeat the solution process by each algorithm 50 times to enhance the accuracy of the results. Besides, we report the average, standard deviation, best, and worst values of the objective functions for each test problem and each algorithm. Table 3 presents the used benchmarks. These benchmarks are known as complex benchmarks in the literature (Lozano et al., 2011, Liao et al., 2015).
Table 2.
Main parameters of the algorithms.
| Algorithm | parameter | value | Algorithm | parameter | value |
|---|---|---|---|---|---|
| GWCA (Pahnehkolaei et al. 2017) | parameter | 0.9 | PSO (Clerc, M and Kennedy 2002) | parameter | 2 |
| dmax | 0.001 | parameter | 2 | ||
| Nsr | 4 | Inertial weight | Linearly decreases from 0.6 to 0.3 | ||
| ABC (Karaboga 2005) | number of onlookers | 0.5*pop | GSA (Rashedi et al. 2009) | Rnorm | 2 |
| number of employed bees | 0.5*pop | Rpower | 1 | ||
| number of scouts | 1 | Alpha and G0 | 20 and 100 | ||
| GGWO | parameter | 0.9 | MFO (Mirjalili, 2015b) | parameter | Linearly decreases from −1 |
| parameter | Linearly decreases from 2 to 0 | parameter | 1 | ||
| GWO (Mirjalili et al. 2014) | parameter | Linearly decreases from 2 to 0 | SCA (Mirjalili et al. 2016) | parameter | Linearly decreases from 2 to 0 |
| PSOGSA (Mirjalili and Hashim 2010) | parameter | 0.5 | SSA (Mirjalili et al. 2017) | parameter | Not an input, determined during optimization |
| parameter | 1.5 | ||||
| Remaining parameters | As of GSA and PSO |
Table 3.
Benchmark functions.
| Function | Formulation | Range | D |
|---|---|---|---|
| Ackley | f1(x) = | 30,50 | |
| Rastrigin | f2(x) = | 30,50 | |
| Sphere | f3(x) = | 30,50 | |
| Griewank | f4(x) = | 30,50 | |
| High ConditionedElliptic | f5(x) = | 30,50 | |
| Rosenbrock | f6(x) = | 30,50 | |
| Shifted Ackley | f7(x) = 20exp | 30,50 | |
| Shifted Rastrigin | f8(x) = | 30,50 | |
| Shifted Sphere | f9(x) = | 30,50 | |
| Shifted Griewank | f10(x) = | 30,50 | |
| Shifted HighConditionedElliptic | f11(x) = | 30,50 | |
| ShiftedRosenbrock | f12(x) = | 30,50 |
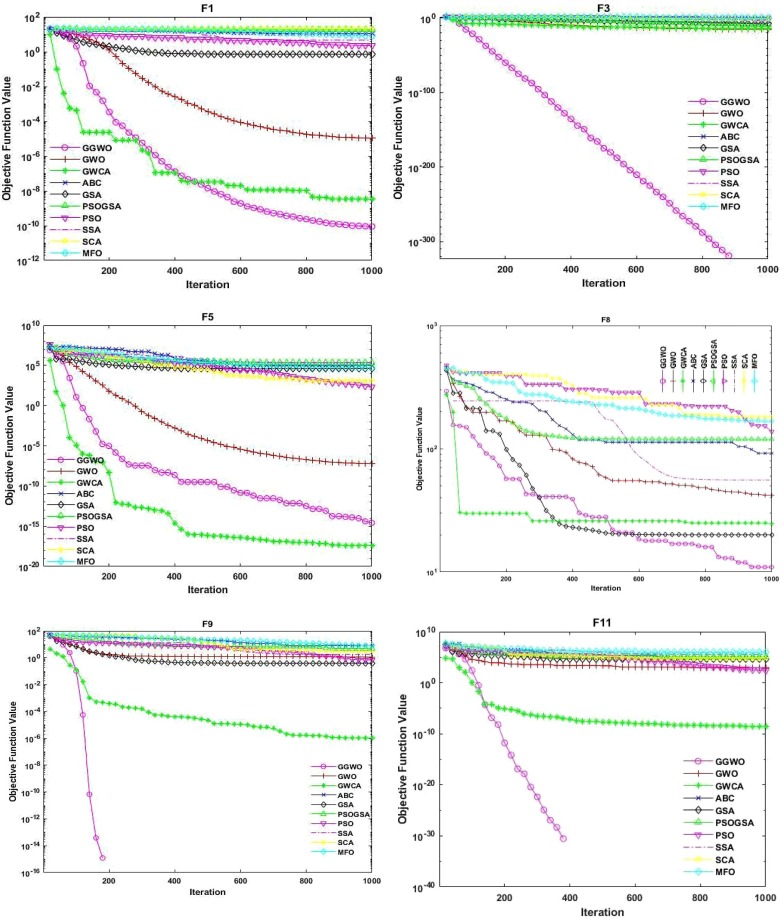
In the first four benchmark functions (F1, F2, F3, and F4) in dimension 30, the outcomes in Table 4 show that our proposed method, GGWO performs significantly better than all the other algorithms in D30. The results in Table 5 show the superiority of GGWO over other algorithms in these benchmarks in D50 as well. Our proposed algorithm provides considerably better solutions in F1-F4 than any other algorithm due to its advanced operators to maximize exploration and exploitation abilities. Fig. 2 shows that the GGWO avoids trapping in local optima and rapidly reaches the optimal solution for the problems. Besides, GGWO offers significantly lower average, best, worst, and StDev of objective function value for these benchmarks compared to other algorithms.
Table 4.
Results of the simulations in 30 dimensions.
| MFO | 14.15397 | 8.396961 | 8.71E-08 | 2.00E + 01 | 149.93231 | 3.21E + 01 | 98.57154 | 2.27E + 02 | 2.666667 | 6.914918 | 2.98E-08 | 20 | 21.09083 | 45.48769 | 4.47E-14 | 180.2163 | 542387.86 | 542451.75 | 70214.2 | 2706358.3 | 2,680,335 | 14592674.1 | 1.189283 | 7,994,325 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCA | 14.29482 | 8.284824 | 3.08E-08 | 2.02E + 01 | 3.6824603 | 8.55E + 00 | 1.01E-11 | 2.83E + 01 | 1.59E-05 | 2.70E-05 | 6.81E-08 | 0.000108 | 0.08646 | 0.2018043 | 3.02E-12 | 0.850527 | 8.57E-06 | 4.68E-05 | 6.83E-18 | 0.000291 | 28.36875 | 1.409943 | 27.11928 | 33.39472 |
| SSA | 1.520216 | 0.923497 | 1.76E-05 | 3.222505 | 58.238599 | 1.64E + 01 | 2.79E + 01 | 8.95E + 01 | 1.79E-05 | 1.72E-06 | 1.39E-05 | 2.11E-05 | 0.008941 | 0.0094284 | 1.52E-08 | 0.039202 | 23856.1263 | 11888.77 | 2781.57 | 48046.444 | 333.7611 | 604.09280 | 23.15309 | 2309.699 |
| PSO | 6.07E-07 | 2.64E-06 | 2.79E-11 | 1.41E-05 | 39.599863 | 6.66E + 00 | 27.85883 | 5.37E + 01 | 5.87E-08 | 2.50E-07 | 2.02E-11 | 1.38E-06 | 0.011078 | 0.010589 | 0 | 0.049282 | 1.44E-11 | 7.60E-11 | 1.26E-18 | 4.17E-10 | 50.051 | 27.905481 | 15.03268 | 85.36001 |
| PSOGSA | 11.6611 | 8.345575 | 2.11E-10 | 19.38025 | 131.5994 | 41.05358 | 61.68735 | 209.9356 | 2.666667 | 6.914918 | 2.75E-10 | 20 | 33.15244 | 50.22736 | 0 | 180.4868 | 41346.57 | 124323.0 | 3.21E-06 | 529831.7 | 3151.067 | 16416.77 | 14.20298 | 90023.83 |
| GSA | 6.23E-09 | 1.25E-09 | 4.85E-09 | 1.14E-08 | 24.24192 | 7.713473 | 13.9294 | 44.7730 | 8.67E-09 | 1.79E-09 | 5.80E-09 | 1.31E-08 | 0.082105 | 0.190495 | 0 | 1.025695 | 241.9223 | 159.920 | 40.904 | 719.373 | 36.1634 | 40.7528 | 24.0738 | 233.399 |
| ABC | 7.78298 | 1.02873 | 4.727577 | 9.587644 | 70.24234 | 10.32227 | 41.16908 | 92.06869 | 1.51191 | 6.15E-01 | 0.593387 | 2.68743 | 1.461505 | 0.268137 | 1.076298 | 2.169038 | 7706.80 | 5264.083 | 804.9848 | 20380.170 | 5105.301 | 2839.1764 | 974.2829 | 12450.14 |
| GWCA | 1.07E-15 | 5.84E-15 | 0 | 3.20E-14 | 0 | 0 | 0 | 0 | 2.36E-29 | 1.29E-28 | 1.23E-45 | 7.04E-28 | 0 | 0 | 0 | 0 | 9.45E-66 | 5.18E-65 | 1.56E-154 | 2.84E-64 | 1.62E-24 | 7.46E-24 | 0 | 4.08E-23 |
| GWO | 8.64E-15 | 2.75E-15 | 7.11E-15 | 1.42E-14 | 0.253528 | 9.75E-01 | 0 | 4.34E + 00 | 2.28E-62 | 3.68E-62 | 2.71E-64 | 1.59E-61 | 0.002502 | 0.0084466 | 0 | 0.044127 | 7.46E-121 | 1.67E-120 | 8.71E-125 | 7.99E-120 | 26.43985 | 0.62575 | 25.09341 | 27.93068 |
| GGWO | 0 | 0 | 0.00E + 00 | 0.00E + 00 | 0 | 0 | 0 | 0 | 0.00E + 00 | 0.00E + 00 | 0 | 0 | 0 | 0 | 0 | 0 | 1.83E-44 | 7.04E-44 | 2.09E-48 | 3.81E-43 | 34.85498 | 27.24732 | 23.46658 | 147.9126 |
| Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | |
| F1 | F2 | F3 | F4 | F5 | F6 |
| MFO | 8.24452 | 7.647263 | 5.38E-08 | 19.36775 | 147.56100 | 31.37337 | 55.71759 | 1.93E+02 | 2.02E+00 | 6.17E+00 | 1.72E-08 | 20.77365 | 26.3487 | 46.67469 | 8.99E-15 | 171.03153 | 526409.36 | 788901.1 | 7121.1631 | 3,677,252 | 24584.675 | 40160.65 | 6.028516 | 97478.38 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCA | 3.82560 | 0.263284 | 3.181999186 | 4.236515 | 80.68202 | 21.67571 | 46.14895 | 131.4449 | 2.181049 | 0.195076 | 1.813314 | 2.71688 | 2.048136 | 0.200311 | 1.714016 | 2.5636 | 11300.144 | 4919.088 | 4364.6324 | 25798.35 | 1579.4940 | 729.624 | 619.937 | 4580.251 |
| SSA | 2.20E+00 | 9.17E-01 | 2.07E-05 | 4.298275 | 62.814945 | 19.05743 | 2.89E+01 | 105.4653 | 1.72E-05 | 2.10E-06 | 1.23E-05 | 2.14E-05 | 0.013608 | 0.016441 | 1.92E-08 | 0.078470 | 27888.185 | 15809.66 | 5121.0405 | 62981.94 | 118.949 | 260.1012 | 24.5781 | 1404.456 |
| PSO | 1.37E-08 | 3.46E-08 | 3.60E-11 | 1.88E-07 | 41.323920 | 10.27609 | 2.19E+01 | 59.69746 | 1.23E-08 | 4.69E-08 | 2.48E-11 | 2.58E-07 | 0.006484 | 0.008487 | 0 | 0.03196 | 4.67E-11 | 1.93E-10 | 1.10E-19 | 1.02E-09 | 44.56550 | 30.6383 | 7.104455 | 103.615 |
| PSOGSA | 1.27E+01 | 7.72E+00 | 2.09E-10 | 19.4627 | 130.1343 | 3.17E+01 | 7.36E+01 | 197.9958 | 1.36E+00 | 5.177062 | 2.82E-10 | 20.712 | 32.66406 | 43.75126 | 0 | 99.19931 | 70235.0059 | 198201.4 | 1.07E-06 | 920733.9 | 2251076.86 | 1,229,469 | 17.17134 | 6,734,709 |
| GSA | 6.38E-09 | 1.01E-09 | 4.52E-09 | 9.15E-09 | 27.22869 | 5.514884 | 1.69E+01 | 41.78826 | 8.39E-09 | 1.28E-09 | 5.83E-09 | 1.14E-08 | 0.078723 | 0.103276 | 0 | 0.50500 | 243.352 | 164.8371 | 27.1468 | 658.5043 | 35.59113 | 46.26933 | 20.27133 | 264.3985 |
| ABC | 6.87411 | 1.10026 | 4.57E+00 | 9.122293 | 70.35375 | 9.115818 | 42.18886 | 81.53446 | 1.337828 | 0.438737 | 0.441513 | 2.456872 | 1.549616 | 0.33096 | 1.089729 | 2.32780 | 6974.676 | 5005.006 | 523.0540 | 23425.73 | 4974.3077 | 3151.212 | 1626.709 | 13565.01 |
| GWCA | 0.031295 | 0.170983 | 1.56E-07 | 0.936517 | 6.007273 | 7.630498 | 0 | 25.86894 | 1.72E-15 | 2.63E-15 | 5.55E-17 | 1.40E-14 | 0.064927 | 0.183418 | 9.21E-11 | 1.01610 | 7.67E-27 | 3.38E-26 | 0 | 1.86E-25 | 43.10708 | 25.15395 | 27.43943 | 110.0079 |
| GWO | 1.77128 | 0.409414 | 1.089748892 | 2.734984 | 14.50399 | 6.74869 | 4.87896 | 30.3255 | 0.735554 | 0.266815 | 0.299032 | 1.44783 | 1.142719 | 0.176141 | 0.748066 | 1.52756 | 1545.0258 | 1139.612 | 170.0078 | 5516.087 | 253.92733 | 242.061 | 36.21686 | 1292.285 |
| GGWO | 1.942059 | 0.435974 | 4.16E-06 | 2.495867 | 2.653285 | 3.308464 | 0 | 12.9344 | 0 | 0 | 0 | 0 | 0.015744 | 0.014757 | 1.56E-11 | 0.04916 | 0 | 0 | 0 | 0 | 32.40043 | 17.36383 | 17.90934 | 84.31829 |
| Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | |
| F7 | F8 | F9 | F10 | F11 | F12 |
Table 5.
Computational results in dimension 50.
| MFO | 18.86403 | 3.129202 | 2.846973 | 19.9633 | 273.0153 | 54.26109 | 152.2283 | 359.3914 | 11.54425 | 12.86791 | 0.000632 | 28.28427 | 57.22312 | 64.8810 | 1.87E-06 | 270.9139 | 2,570,794 | 1,892,066 | 115043.3 | 6,491,725 | 800,426 | 2,439,969 | 80.7810 | 8,003,304 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCA | 1.56E + 01 | 8.767169 | 4.50E-04 | 20.4345 | 2.57E + 01 | 3.52E + 01 | 0.00026 | 132.586 | 0.08209 | 0.13338 | 5.81E-05 | 0.548486 | 0.247561 | 0.32939 | 7.83E-05 | 0.952744 | 0.38588 | 0.980396 | 8.27E-06 | 3.5341 | 4952.241 | 6071.786 | 49.06581 | 23217.09 |
| SSA | 2.41E + 00 | 0.67627 | 3.24E-05 | 3.57424 | 8.50E + 01 | 2.76E + 01 | 33.8286 | 140.2889 | 2.99E-05 | 1.22E-06 | 2.79E-05 | 3.28E-05 | 0.009848 | 0.00998 | 5.92E-08 | 0.036919 | 42706.08 | 20507.34 | 17742.4 | 98336.71 | 76.9411 | 109.9943 | 44.79358 | 643.8471 |
| PSO | 9.81E-02 | 0.373198 | 1.18E-06 | 1.47E + 00 | 9.26E + 01 | 2.03E + 01 | 62.68241 | 1.53E + 02 | 2.56E-05 | 3.56E-05 | 3.35E-07 | 0.000149 | 0.004186 | 0.008477 | 4.30E-13 | 0.03934 | 2.98E-07 | 8.91E-07 | 2.05E-09 | 4.91E-06 | 94.89612 | 55.11365 | 27.04189 | 249.9203 |
| PSOGSA | 1.58E + 11 | 5.483801 | 4.11E-10 | 19.6161 | 2.29E + 02 | 3.38E + 01 | 156.2079 | 293.5112 | 2 | 6.102572 | 5.70E-10 | 20 | 60.13315 | 64.11064 | 0 | 180.336 | 299933.2 | 1,141,383 | 0.134512 | 4,498,815 | 2,667,924 | 1,461,248 | 37.49836 | 800,359 |
| GSA | 3.80E-09 | 3.88E-10 | 2.97E-09 | 4.78E-09 | 30.0477 | 6.719748 | 18.90422 | 41.78827 | 7.04E-09 | 5.68E-10 | 5.95E-09 | 8.11E-09 | 1.44335 | 0.727960 | 0.350652 | 3.30963 | 244.6193 | 151.415 | 78.73644 | 761.5141 | 44.75936 | 0.528158 | 44.04607 | 46.45274 |
| ABC | 10.99270 | 1.291766 | 7.86104 | 12.71119 | 168.097 | 20.5388 | 116.4862 | 204.640 | 5.25385 | 1.01402 | 3.93371 | 7.454158 | 5.93384 | 2.449968 | 1.531393 | 11.31384 | 90773.92 | 38735.38 | 30262.28 | 163447.5 | 43158.95 | 24904.52 | 7121.636 | 82301.65 |
| GWCA | 4.74E-16 | 1.23E-15 | 0 | 3.55E-15 | 0 | 0.00E + 00 | 0 | 0.00E + 00 | 4.21E-30 | 1.28E-29 | 2.71E-44 | 4.38E-29 | 0 | 0 | 0 | 0 | 2.90E-58 | 1.06E-57 | 8.07E-91 | 4.17E-57 | 8.95E-24 | 2.60E-23 | 0 | 1.28E-22 |
| GWO | 1.43E-14 | 2.18E-15 | 1.07E-14 | 2.13E-14 | 1.260281 | 4.796155 | 0 | 18.9042 | 1.06E-54 | 2.10E-54 | 5.16E-56 | 8.67E-54 | 0.001723 | 0.005711 | 0 | 0.022141 | 3.88E-105 | 1.37E-104 | 2.39E-109 | 5.42E-104 | 46.75566 | 0.702115 | 46.11286 | 48.56676 |
| GGWO | 1.18E-16 | 6.49E-16 | 0 | 3.55E-15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2.34E-36 | 1.09E-35 | 3.50E-40 | 5.99E-35 | 62.18671 | 51.01123 | 44.42791 | 279.2602 |
| Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | |
| F1 | F2 | F3 | F4 | F5 | F6 |
| MFO | 17.96136 | 3.045411 | 2.57947 | 19.41094 | 280.7398 | 54.5312 | 207.1563 | 423.467 | 9.82966 | 12.70863 | 0.00037 | 35.5646 | 48.3729 | 61.78711 | 1.32E-05 | 186.1236 | 2,069,598 | 1356684.6 | 398587.8 | 7,605,752 | 7,821,421 | 32,471,414 | 2.032239 | 1.67E+08 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCA | 4.521862 | 0.546814 | 4.047869 | 6.377384 | 193.6459 | 33.18219 | 136.1962 | 258.4204 | 3.36659 | 0.362941 | 2.84272 | 4.44995 | 3.468887 | 0.446900 | 2.68606 | 4.625300 | 50080.83 | 18612.17 | 16444.15 | 86449.89 | 31723.78 | 95236.72 | 3659.787 | 531,852 |
| SSA | 2.538247 | 0.538350 | 1.374312 | 3.333027 | 82.51514 | 23.03776 | 33.82857 | 136.309 | 3.04E-05 | 1.96E-06 | 2.68E-05 | 3.44E-05 | 0.004104 | 0.006345 | 4.17E-08 | 0.022126 | 46914.21 | 22315.88 | 19700.93 | 92357.54 | 131.4435 | 166.5185 | 41.48509 | 640.1873 |
| PSO | 2.21E-05 | 3.27E-05 | 7.98E-07 | 0.000131 | 99.33005 | 17.65016 | 68.6521 | 136.309 | 2.58E-05 | 5.52E-05 | 1.40E-06 | 0.000287 | 0.00394 | 0.005661 | 5.76E-14 | 0.017226 | 1.92E-06 | 6.67E-06 | 7.99E-10 | 3.61E-05 | 91.01528 | 38.9426 | 39.82111 | 172.8936 |
| PSOGSA | 15.9417 | 3.092674 | 2.85818 | 19.29966 | 231.3938 | 41.25106 | 159.193 | 313.4414 | 7.22E-10 | 4.51E-11 | 6.45E-10 | 8.38E-10 | 51.6887 | 57.03139 | 1.11E-16 | 185.8100 | 9289.844 | 50629.72 | 0.064453 | 277356.2 | 54.55684 | 24.25274 | 38.37738 | 131.1459 |
| GSA | 3.89E-09 | 4.05E-10 | 3.28E-09 | 4.58E-09 | 28.45582 | 4.671152 | 18.90422 | 38.80337 | 7.16E-09 | 1.11E-09 | 5.59E-09 | 1.11E-08 | 1.901848 | 0.89989 | 0.078681 | 4.461654 | 327.9037 | 208.638 | 61.2343 | 798.1094 | 45.61572 | 5.515901 | 44.35261 | 74.80706 |
| ABC | 10.8829 | 1.227730 | 8.23459 | 12.73090 | 167.5958 | 16.70806 | 129.7736 | 191.6545 | 5.11762 | 1.12580 | 3.12082 | 7.55719 | 5.907881 | 2.50211 | 1.57466 | 10.73243 | 104725.1 | 58102.98 | 14737.57 | 228,529 | 57467.26 | 48491.88 | 8973.947 | 227428.3 |
| GWCA | 0.39543 | 0.704873 | 1.49E-07 | 2.140674 | 8.68934 | 14.20356 | 0 | 36.81349 | 1.58E-15 | 1.32E-15 | 2.04E-16 | 5.95E-15 | 0.05428 | 0.117440 | 8.49E-07 | 0.578953 | 3.75E-25 | 1.60E-24 | 1.08E-32 | 8.78E-24 | 65.17494 | 28.98188 | 47.47152 | 193.4626 |
| GWO | 2.245981 | 0.245903 | 1.69206 | 2.621921 | 39.81563 | 13.17458 | 12.74205 | 69.08735 | 1.1938 | 0.33094 | 0.60971 | 2.080546 | 1.41276 | 0.18717 | 1.140895 | 1.843354 | 6132.125 | 3531.791 | 1200.19 | 12604.24 | 669.3124 | 227.4713 | 346.0705 | 1187.163 |
| GGWO | 2.44568 | 0.192152 | 2.07810 | 2.769214 | 3.681349 | 4.181849 | 0 | 12.9344 | 0 | 0 | 0 | 0 | 0.03344 | 0.09759 | 5.75E-11 | 0.52315 | 0 | 0 | 0 | 0 | 54.44438 | 30.41612 | 44.70562 | 214.3801 |
| Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | Average | Std Dev | Best | Worst | |
| F7 | F8 | F9 | F10 | F11 | F12 |
Fig. 2.
Convergence plot of the algorithms in dimension 30.
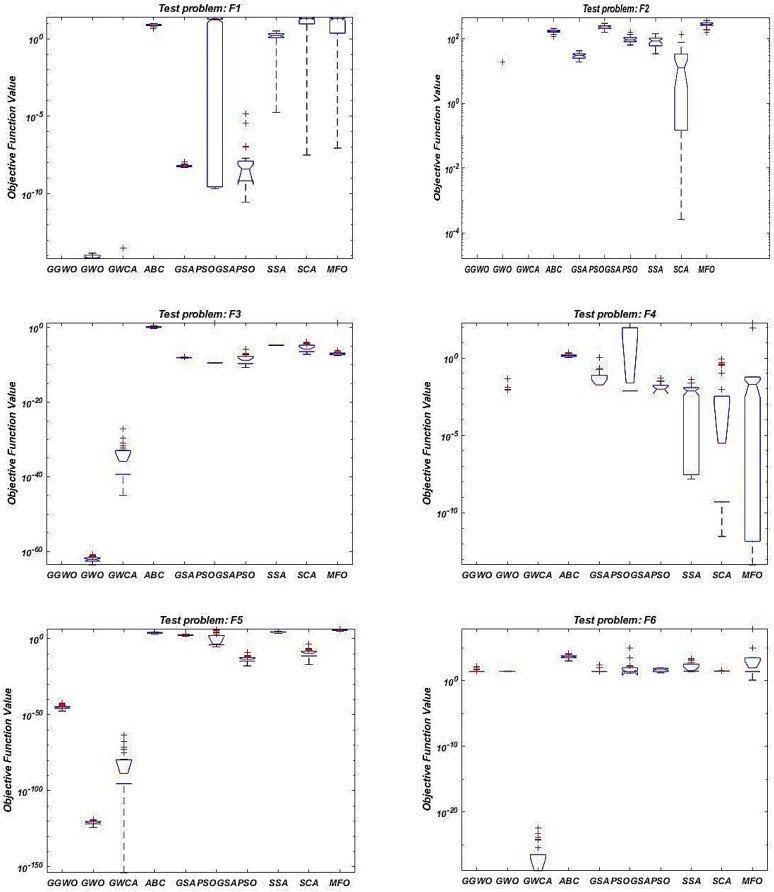
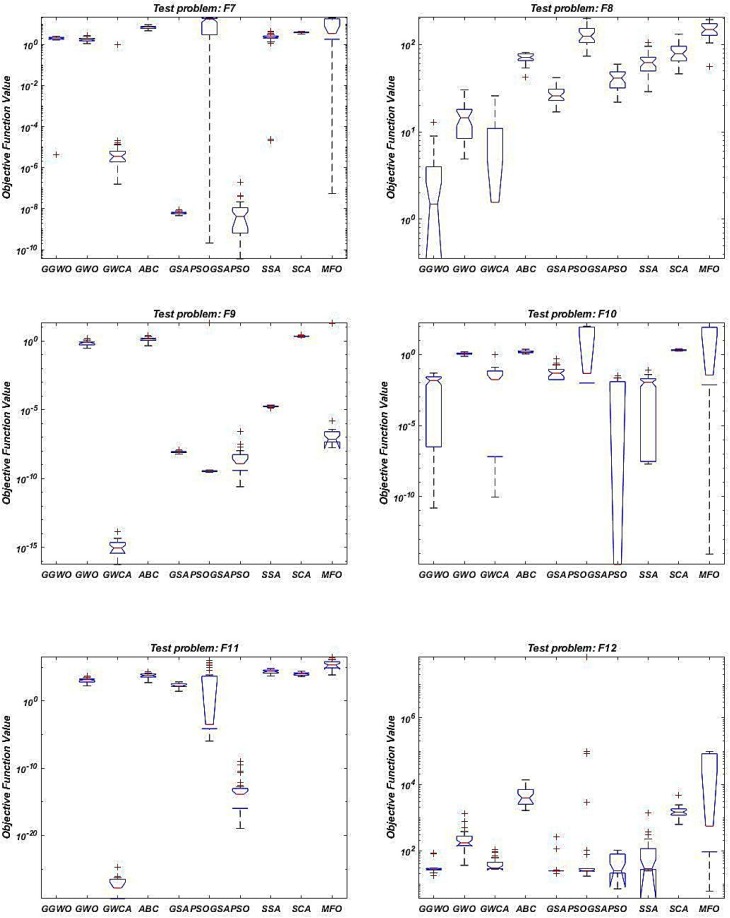
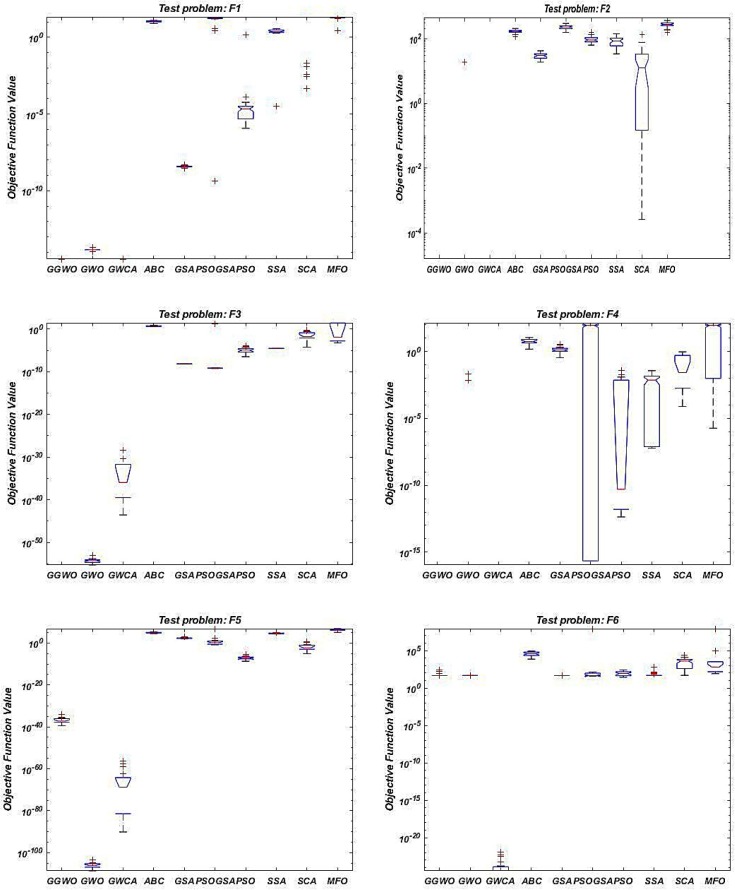
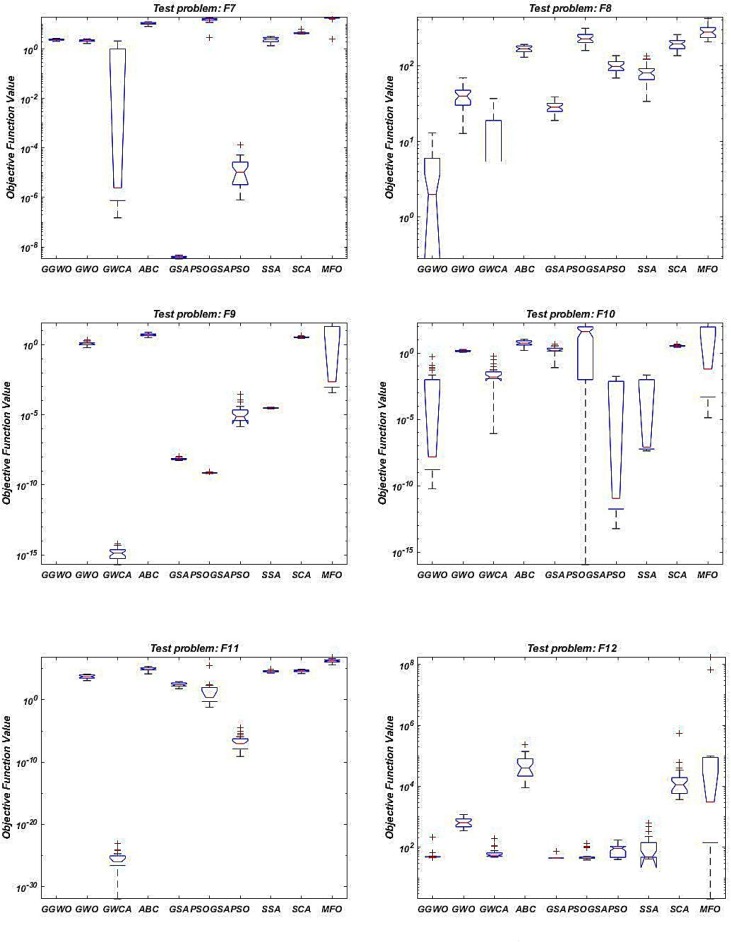
Fig. 3a, Fig. 3b, Fig. A1, Fig. A2 in the Appendix show the boxplots of the results in which GGWO presents significantly lower and narrower charts. The offered GGWO performs very well in F5, F6, and F7 benchmarks in dimension 30 considering average, best, worst, and StDev of results compared to other methods based on Table 4. In addition, in dimension 50, GGWO achieves the third optimum (lowest) results, as shown in Table 5. Moreover, in F5 from Fig. 2, GGWO’s convergence curve shows its exploration and exploitation capabilities and efficiency in avoiding local optima.
Fig. 3a.
Dimension 30 boxplots.
Fig. 3b.
Dimension 30 boxplots.
Fig. A1.
Dimension 50 boxplots.
Fig. A2.
Dimension 50 boxplots.
The results in Table 4 show that our designed algorithm performs meaningfully better than all the other methods in F8 and F9 for dimension 30. This is because GGWO has a significantly lower average compared to the other algorithms. Besides, based on the best, worst, and standard deviation of the objective function, we could conclude that the GGWO is the best solution approach for this benchmark. In addition, Table 5 shows that for F8 and F9 in dimension 50, GGWO has significantly lower results considering average, best, worst, and standard deviation of the objective function. Therefore, GGWO is a reliable and robust algorithm since it has consistent performance and could find a promising solution in all repetitions. Besides, in F8 and F9, GGWO makes a perfect trade-off amid both exploration and exploitation based on the data provided in Fig. 2. Although the other algorithms got trapped in local optima, GGWO could achieve global optima quicker without trapping in local optima.
Considering F10 and F12 in dimension 30, the GGWO performs the best. Besides, for dimension 50, GGWO performs well in terms of average, best, worst, and standard deviation of the objective function. In F11 for dimension 30, GGWO performs outstanding comparing to all the other methods. It has significantly lower average, SD, best, and worst values than the other algorithms based on results in Table 4. Besides, in F11 for dimension 50, GGWO’s performance is much promising than other algorithms in terms of average, best, worst, and SD from Table 5. Furthermore, based on Fig. 2, in F11, GGWO ensures the right balance amid exploration and exploitation. In contrast to the other algorithms that get trapped in local optima, GGWO reaches the global optima.
To draw a reliable conclusion and demonstrate the superiority of the offered algorithm, statistical tests are conducted in this section. For this purpose, we apply Tukey’s multiple comparison tests to discover significant differences in the performance of the algorithms. Fig. 3a, Fig. 3b, Fig. A1, Fig. A2 in the Appendix show the results of Tukey’s multiple comparison tests schematically. Based on Fig. 3a, Fig. 3b for dimension 30 and 50, the results of comparing the boxplot of the GGWO to other algorithms for the first four benchmarks (F1, F2, F3, and F4) show that the boxplot of the GGWO is significantly lower and thinner than all the other algorithm. In F5, F6, F7, F8, F10, and F12, the boxplots of the GGWO are lower than most of the algorithms, especially in F9 and F11, the box plot of the GGWO is a line at zero. This is because GGWO obtained the global optima of the benchmarks in all repetitions. These results show that the proposed algorithm not only performs remarkably but also performs significantly robust and reliable.
Table 6a, Table 6b, Table 6c present the outcomes of Tukey’s multiple comparison tests for objective function values of the benchmarks in dimension 30 and 50. Based on the results, in F1 and F2 for dimension 30 and 50, all the tests show p-values less than 0.05, except for the second row. This indicates that there are significant differences between the performances of the compared algorithms. Therefore, our proposed algorithm performs significantly better than all other algorithms (GWO, ABC, GSA, PSOGSA, PSO, SSA, SCA, and MFO) in terms of objective function value at 95% confidence level except for GWCA. However, based on the average, best, worst, and SD values, we observe that the GGWO performs much better than GWCA in F1 and F2 (Table 4). Our proposed method accomplishes outstanding results in F3 and F5 for dimensions 30 and 50 compared to other solution methods.
Table 6a.
Results of Tukey’s multiple comparison test for dimensions 30 and 50.
| Dimension 30 | Dimension 50 | ||||||
|---|---|---|---|---|---|---|---|
| Benchmark | Comparison | P-value | Significant difference | Benchmark | Comparison | P-value | Significant difference |
| F1 | GGWO-GWO | 2.56E-13 | Yes | F1 | GGWO-GWO | 1.81E-13 | Yes |
| GGWO-GWCA | 0.33371 | No | GGWO-GWCA | 0.1694 | No | ||
| GGWO-ABC | 1.21E-12 | Yes | GGWO-ABC | 1.71E-12 | Yes | ||
| GGWO-GSA | 1.21E-12 | Yes | GGWO-GSA | 1.71E-12 | Yes | ||
| GGWO-PSOGSA | 1.21E-12 | Yes | GGWO-PSOGSA | 1.71E-12 | Yes | ||
| GGWO-PSO | 1.21E-12 | Yes | GGWO-PSO | 1.71E-12 | Yes | ||
| GGWO-SSA | 1.21E-12 | Yes | GGWO-SSA | 1.71E-12 | Yes | ||
| GGWO-SCA | 1.21E-12 | Yes | GGWO-SCA | 1.71E-12 | Yes | ||
| GGWO-MFO | 1.21E-12 | Yes | GGWO-MFO | 1.71E-12 | Yes | ||
| F2 | GGWO-GWO | 0.16074 | Yes | F2 | GGWO-GWO | 0.1608 | Yes |
| GGWO-GWCA | Nan | No | GGWO-GWCA | Nan | No | ||
| GGWO-ABC | 1.20E-12 | Yes | GGWO-ABC | 1.21E-12 | Yes | ||
| GGWO-GSA | 1.18E-12 | Yes | GGWO-GSA | 1.21E-12 | Yes | ||
| GGWO-PSOGSA | 1.20E-12 | Yes | GGWO-PSOGSA | 1.21E-12 | Yes | ||
| GGWO-PSO | 1.20E-12 | Yes | GGWO-PSO | 1.21E-12 | Yes | ||
| GGWO-SSA | 1.20E-12 | Yes | GGWO-SSA | 1.21E-12 | Yes | ||
| GGWO-SCA | 1.20E-12 | Yes | GGWO-SCA | 1.21E-12 | Yes | ||
| GGWO-MFO | 1.20E-12 | Yes | GGWO-MFO | 1.21E-12 | Yes | ||
| F3 | GGWO-GWO | 1.21E-12 | Yes | F3 | GGWO-GWO | 1.20E-12 | Yes |
| GGWO-GWCA | 1.21E-12 | Yes | GGWO-GWCA | 1.20E-12 | Yes | ||
| GGWO-ABC | 1.21E-12 | Yes | GGWO-ABC | 1.20E-12 | Yes | ||
| GGWO-GSA | 1.21E-12 | Yes | GGWO-GSA | 1.20E-12 | Yes | ||
| GGWO-PSOGSA | 1.20E-12 | Yes | GGWO-PSOGSA | 1.20E-12 | Yes | ||
| GGWO-PSO | 1.21E-12 | Yes | GGWO-PSO | 1.20E-12 | Yes | ||
| GGWO-SSA | 1.21E-12 | Yes | GGWO-SSA | 1.20E-12 | Yes | ||
| GGWO-SCA | 1.21E-12 | Yes | GGWO-SCA | 1.20E-12 | Yes | ||
| GGWO-MFO | 1.20E-12 | Yes | GGWO-MFO | 1.20E-12 | Yes | ||
| F4 | GGWO-GWO | 0.041926 | Yes | F4 | GGWO-GWO | 0.081493 | No |
| GGWO-GWCA | Nan | No | GGWO-GWCA | Nan | No | ||
| GGWO-ABC | 1.21E-12 | Yes | GGWO-ABC | 1.20E-12 | Yes | ||
| GGWO-GSA | 3.45E-07 | Yes | GGWO-GSA | 1.20E-12 | Yes | ||
| GGWO-PSOGSA | 5.76E-11 | Yes | GGWO-PSOGSA | 5.72E-11 | Yes | ||
| GGWO-PSO | 1.70E-08 | Yes | GGWO-PSO | 1.20E-12 | Yes | ||
| GGWO-SSA | 1.21E-12 | Yes | GGWO-SSA | 1.20E-12 | Yes | ||
| GGWO-SCA | 1.21E-12 | Yes | GGWO-SCA | 1.20E-12 | Yes | ||
| GGWO-MFO | 1.21E-12 | Yes | GGWO-MFO | 1.20E-12 | Yes | ||
Table 6b.
Results of Tukey’s multiple comparison test for dimensions 30 and 50.
| Dimension 30 | Dimension 50 | ||||||
|---|---|---|---|---|---|---|---|
| Benchmark | Comparison | P-value | Significant difference | Benchmark | Comparison | P-value | Significant difference |
| F5 | GGWO-GWO | 3.02E-11 | Yes | F5 | GGWO-GWO | 2.98E-11 | Yes |
| GGWO-GWCA | 3.02E-11 | Yes | GGWO-GWCA | 2.98E-11 | Yes | ||
| GGWO-ABC | 3.02E-11 | Yes | GGWO-ABC | 2.98E-11 | Yes | ||
| GGWO-GSA | 3.02E-11 | Yes | GGWO-GSA | 2.98E-11 | Yes | ||
| GGWO-PSOGSA | 3.02E-11 | Yes | GGWO-PSOGSA | 2.98E-11 | Yes | ||
| GGWO-PSO | 3.02E-11 | Yes | GGWO-PSO | 2.98E-11 | Yes | ||
| GGWO-SSA | 3.02E-11 | Yes | GGWO-SSA | 2.98E-11 | Yes | ||
| GGWO-SCA | 3.02E-11 | Yes | GGWO-SCA | 2.98E-11 | Yes | ||
| GGWO-MFO | 3.02E-11 | Yes | GGWO-MFO | 2.98E-11 | Yes | ||
| F6 | GGWO-GWO | 1.75E-05 | Yes | F6 | GGWO-GWO | 0.000167 | Yes |
| GGWO-GWCA | 2.11E-11 | Yes | GGWO-GWCA | 1.94E-11 | Yes | ||
| GGWO-ABC | 3.02E-11 | Yes | GGWO-ABC | 2.98E-11 | Yes | ||
| GGWO-GSA | 0.40354 | No | GGWO-GSA | 0.063459 | No | ||
| GGWO-PSOGSA | 0.83026 | No | GGWO-PSOGSA | 0.5394 | No | ||
| GGWO-PSO | 0.22823 | No | GGWO-PSO | 0.051812 | No | ||
| GGWO-SSA | 3.83E-06 | Yes | GGWO-SSA | 8.62E-05 | Yes | ||
| GGWO-SCA | 9.51E-06 | Yes | GGWO-SCA | 4.57E-10 | Yes | ||
| GGWO-MFO | 0.007959 | Yes | GGWO-MFO | 9.65E-10 | Yes | ||
| F7 | GGWO-GWO | 0.012111 | Yes | F7 | GGWO-GWO | 0.003828 | Yes |
| GGWO-GWCA | 1.04E-10 | Yes | GGWO-GWCA | 3.60E-11 | Yes | ||
| GGWO-ABC | 2.86E-11 | Yes | GGWO-ABC | 2.95E-11 | Yes | ||
| GGWO-GSA | 2.86E-11 | Yes | GGWO-GSA | 2.95E-11 | Yes | ||
| GGWO-PSOGSA | 0.000222 | Yes | GGWO-PSOGSA | 2.95E-11 | Yes | ||
| GGWO-PSO | 2.86E-11 | Yes | GGWO-PSO | 2.95E-11 | Yes | ||
| GGWO-SSA | 0.013165 | Yes | GGWO-SSA | 0.3552 | No | ||
| GGWO-SCA | 2.86E-11 | Yes | GGWO-SCA | 2.95E-11 | Yes | ||
| GGWO-MFO | 0.006316 | Yes | GGWO-MFO | 7.21E-11 | Yes | ||
| F8 | GGWO-GWO | 6.44E-10 | Yes | F8 | GGWO-GWO | 3.09E-11 | Yes |
| GGWO-GWCA | 0.17834 | No | GGWO-GWCA | 0.2345 | No | ||
| GGWO-ABC | 2.31E-11 | Yes | GGWO-ABC | 2.80E-11 | Yes | ||
| GGWO-GSA | 2.31E-11 | Yes | GGWO-GSA | 2.78E-11 | Yes | ||
| GGWO-PSOGSA | 2.31E-11 | Yes | GGWO-PSOGSA | 2.80E-11 | Yes | ||
| GGWO-PSO | 2.31E-11 | Yes | GGWO-PSO | 2.80E-11 | Yes | ||
| GGWO-SSA | 2.31E-11 | Yes | GGWO-SSA | 2.80E-11 | Yes | ||
| GGWO-SCA | 2.31E-11 | Yes | GGWO-SCA | 2.80E-11 | Yes | ||
| GGWO-MFO | 2.31E-11 | Yes | GGWO-MFO | 2.80E-11 | Yes | ||
Table 6c.
Results of Tukey’s multiple comparison test for dimensions 30 and 50.
| Dimension 30 | Dimension 50 | ||||||
|---|---|---|---|---|---|---|---|
| Benchmark | Comparison | P-value | Significant difference | Benchmark | Comparison | P-value | Significant difference |
| F9 | GGWO-GWO | 1.21E-12 | Yes | F9 | GGWO-GWO | 1.21E-12 | Yes |
| GGWO-GWCA | 1.21E-12 | Yes | GGWO-GWCA | 1.21E-12 | Yes | ||
| GGWO-ABC | 1.21E-12 | Yes | GGWO-ABC | 1.21E-12 | Yes | ||
| GGWO-GSA | 1.21E-12 | Yes | GGWO-GSA | 1.21E-12 | Yes | ||
| GGWO-PSOGSA | 1.21E-12 | Yes | GGWO-PSOGSA | 1.21E-12 | Yes | ||
| GGWO-PSO | 1.21E-12 | Yes | GGWO-PSO | 1.21E-12 | Yes | ||
| GGWO-SSA | 1.21E-12 | Yes | GGWO-SSA | 1.21E-12 | Yes | ||
| GGWO-SCA | 1.21E-12 | Yes | GGWO-SCA | 1.21E-12 | Yes | ||
| GGWO-MFO | 1.21E-12 | Yes | GGWO-MFO | 1.21E-12 | Yes | ||
| F10 | GGWO-GWO | 3.02E-11 | Yes | F10 | GGWO-GWO | 0.000587 | Yes |
| GGWO-GWCA | 0.20095 | No | GGWO-GWCA | 3.02E-11 | Yes | ||
| GGWO-ABC | 3.02E-11 | Yes | GGWO-ABC | 4.50E-11 | Yes | ||
| GGWO-GSA | 0.004215 | Yes | GGWO-GSA | 0.002052 | Yes | ||
| GGWO-PSOGSA | 0.023234 | Yes | GGWO-PSOGSA | 0.001114 | Yes | ||
| GGWO-PSO | 0.000182 | Yes | GGWO-PSO | 0.099258 | No | ||
| GGWO-SSA | 0.44642 | No | GGWO-SSA | 3.02E-11 | Yes | ||
| GGWO-SCA | 3.02E-11 | Yes | GGWO-SCA | 1.87E-05 | Yes | ||
| GGWO-MFO | 0.039167 | Yes | GGWO-MFO | 0.000587 | Yes | ||
| F11 | GGWO-GWO | 1.21E-12 | Yes | F11 | GGWO-GWO | 1.21E-12 | Yes |
| GGWO-GWCA | 4.57E-12 | Yes | GGWO-GWCA | 1.21E-12 | Yes | ||
| GGWO-ABC | 1.21E-12 | Yes | GGWO-ABC | 1.21E-12 | Yes | ||
| GGWO-GSA | 1.21E-12 | Yes | GGWO-GSA | 1.21E-12 | Yes | ||
| GGWO-PSOGSA | 1.21E-12 | Yes | GGWO-PSOGSA | 1.21E-12 | Yes | ||
| GGWO-PSO | 1.21E-12 | Yes | GGWO-PSO | 1.21E-12 | Yes | ||
| GGWO-SSA | 1.21E-12 | Yes | GGWO-SSA | 1.21E-12 | Yes | ||
| GGWO-SCA | 1.21E-12 | Yes | GGWO-SCA | 1.21E-12 | Yes | ||
| GGWO-MFO | 1.21E-12 | Yes | GGWO-MFO | 1.21E-12 | Yes | ||
| F12 | GGWO-GWO | 4.08E-11 | Yes | F12 | GGWO-GWO | 3.02E-11 | Yes |
| GGWO-GWCA | 8.88E-06 | Yes | GGWO-GWCA | 3.32E-06 | Yes | ||
| GGWO-ABC | 3.02E-11 | Yes | GGWO-ABC | 3.02E-11 | Yes | ||
| GGWO-GSA | 1.87E-05 | Yes | GGWO-GSA | 1.17E-09 | Yes | ||
| GGWO-PSOGSA | 0.030317 | Yes | GGWO-PSOGSA | 0.000225 | Yes | ||
| GGWO-PSO | 0.29047 | No | GGWO-PSO | 0.004033 | Yes | ||
| GGWO-SSA | 0.05012 | No | GGWO-SSA | 0.43764 | No | ||
| GGWO-SCA | 3.02E-11 | Yes | GGWO-SCA | 3.02E-11 | Yes | ||
| GGWO-MFO | 2.39E-08 | Yes | GGWO-MFO | 1.85E-08 | Yes | ||
In F4 for dimension 30, GGWO performs statistically better than the other algorithms. Likewise, in the same benchmark for dimension 50, GGWO achieves better results than other methods. Based on the average, best, worst, and SD values in this benchmark, we determine that the GGWO performs much better than GWO and GWCA in F4 (in Table 4). In F6 and F7 for dimension 30, GGWO performs significantly better than all the other algorithms. For dimension 50, GGWO performs better than all the other algorithms except SSA. However, based on the average, best, worst, and SD values, the GGWO outperforms SSA in solving F7 (in Table 4). In F8 for dimension 30 and 50, GGWO outperforms most of the other algorithms. Besides, considering the average, SD, best, and worst cases, GGWO beats GWCA (in Table 4). In F9, F10, F11 and F12, in dimensions 30 and 50, GGWO outperforms other state-of-the-art algorithms.
In this section, we perform more in-depth statistical tests, such as Friedman’s test, to make a consistent conclusion. Friedman’s test discovers extensive differences among algorithms at a 95% confidence level. It is one of the most famous and widely used statistical tests to compare algorithms in the literature. Table 7, Table 8 show the Friedman tests’ scores for each algorithm considering algorithms’ performance in all dimensions. In Friedman’s test, the lower the score, the more effective the method is. In Table 9, Table 10 , we assigned a rank for each algorithm in each benchmark function based on the scores obtained in Table 7, Table 8. Results of Table 9, Table 10 disclosed that for both dimensions 30 and 50, the proposed algorithm ranked first in most of the benchmark functions, including F1, F2, F3, F4, F8, F9, and F11. Considering F5, F6, and F10, GGWO ranked third. In F7, GGWO performs better than five algorithms for both dimensions 30 and 50. Besides, GGWO ranked fourth and third in dimensions 30 and 50, respectively.
Table 7.
Friedman’s test for dimension 30.
| Algorithm | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GGWO | GWO | GWCA | ABC | GSA | PSOGSA | PSO | SSA | SCA | MFO | |
| F1 | 10.3333 | 25.1667 | 11 | 73.8 | 44.0333 | 69.5333 | 42.2667 | 62.4 | 84.7667 | 81.7 |
| F2 | 15.1667 | 16.5667 | 15.1667 | 76.4 | 42.4 | 87.2 | 60.6333 | 58.9 | 39.9 | 92.6667 |
| F3 | 5.5 | 15.5 | 25.5 | 92.8333 | 50.7667 | 46 | 45.9 | 80.3333 | 74.5 | 68.1667 |
| F4 | 18.5 | 24.5333 | 18.5 | 90.1667 | 54.9833 | 69.4667 | 50.15 | 57.6 | 54.2667 | 66.8333 |
| F5 | 25.5 | 5.93333 | 15.0667 | 74.8333 | 63.0333 | 61.3667 | 36.5667 | 83.1 | 44.6333 | 94.9667 |
| F6 | 37.76 | 47.3 | 5.5 | 92.6 | 35.5667 | 46.8333 | 49.7333 | 67.3667 | 59.1667 | 63.1667 |
| F7 | 50.33 | 46.4667 | 29.1 | 83.8667 | 13.1333 | 73.9333 | 11.5667 | 55.6667 | 72.8333 | 68.1 |
| F8 | 9.166 | 24.7333 | 13.9667 | 66.0333 | 35.7333 | 87.5667 | 46.5 | 60.4667 | 69.9667 | 90.8667 |
| F9 | 5.5 | 75.1333 | 15.5 | 82.9667 | 43.4333 | 31.9667 | 34.7 | 63.8333 | 93.4 | 58.5667 |
| F10 | 32.5333 | 70.2333 | 37.9 | 79.1667 | 43.0833 | 54.5833 | 17.3333 | 30.2333 | 88.0667 | 51.8667 |
| F11 | 5.66667 | 52.9667 | 15.3333 | 65.8 | 42.5667 | 49.1667 | 25.5 | 81.8667 | 72.7667 | 93.3667 |
| F12 | 32.3 | 65.6 | 45.4333 | 90.7333 | 20.1333 | 29.3667 | 27 | 42.3 | 80.1 | 72.0333 |
Table 8.
Friedman’s test for dimension 50.
| Algorithm | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GGWO | GWO | GWCA | ABC | GSA | PSOGSA | PSO | SSA | SCA | MFO | |
| F1 | 10 | 25.5 | 11 | 69.5 | 35.8333 | 76.4 | 46.0333 | 58.2667 | 86.2333 | 86.2333 |
| F2 | 15.1667 | 16.7 | 15.1667 | 73.5333 | 46.0667 | 88.0667 | 56 | 67.0667 | 35.7667 | 91.4667 |
| F3 | 5.5 | 15.5 | 25.5 | 89.8333 | 44.5 | 41.0333 | 56.8667 | 62.1667 | 78.7333 | 85.3667 |
| F4 | 15.5 | 19.6833 | 15.5 | 84.5 | 74.7667 | 66.2167 | 42.3333 | 52.3333 | 58.4333 | 75.7333 |
| F5 | 25.5 | 5.5 | 15.5 | 83.5333 | 64.7 | 57.4 | 35.5 | 76.2667 | 46.3333 | 94.7667 |
| F6 | 36 | 44.6667 | 5.5 | 93.1667 | 27.1 | 40.3667 | 50.7333 | 50.5667 | 78.5 | 78.4 |
| F7 | 47.0333 | 41.4667 | 19.3333 | 76.2667 | 5.5 | 86.2667 | 22.0333 | 47.9333 | 66.1667 | 93 |
| F8 | 11.35 | 33 | 12.5833 | 68.8667 | 25.6333 | 84.7 | 52.8333 | 47.7 | 75.8 | 92.5333 |
| F9 | 5.5 | 71.5 | 15.5 | 90.7667 | 35.5 | 25.5 | 47.2 | 53.8 | 82.2333 | 77.5 |
| F10 | 23.9333 | 59.1 | 38.9667 | 84.2 | 64.4333 | 59.3667 | 15.3667 | 23.2 | 76.8333 | 59.6 |
| F11 | 5.5 | 55.1667 | 15.5 | 81.1667 | 44.4667 | 37.8667 | 25.5 | 71.4333 | 72.9 | 95.5 |
| F12 | 32.3667 | 69.6333 | 42.6333 | 90.7 | 14.4667 | 18.0667 | 42.8 | 39.3667 | 82.9333 | 72.0333 |
Table 9.
Ranking of the algorithms based on Friedman’s test for dimension 30.
| Algorithm | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GGWO | GWO | GWCA | ABC | GSA | PSOGSA | PSO | SSA | SCA | MFO | |
| F1 | 1 | 3 | 2 | 8 | 5 | 7 | 4 | 6 | 10 | 9 |
| F2 | 1 | 3 | 2 | 8 | 5 | 9 | 6 | 7 | 4 | 10 |
| F3 | 1 | 2 | 3 | 10 | 6 | 5 | 4 | 9 | 8 | 7 |
| F4 | 1 | 3 | 2 | 10 | 6 | 9 | 4 | 7 | 5 | 8 |
| F5 | 3 | 1 | 2 | 8 | 7 | 6 | 4 | 9 | 5 | 10 |
| F6 | 3 | 5 | 1 | 10 | 2 | 4 | 6 | 9 | 7 | 8 |
| F7 | 5 | 4 | 3 | 10 | 2 | 9 | 1 | 6 | 8 | 7 |
| F8 | 1 | 3 | 2 | 7 | 4 | 9 | 5 | 6 | 8 | 10 |
| F9 | 1 | 8 | 2 | 9 | 5 | 3 | 4 | 7 | 10 | 6 |
| F10 | 3 | 8 | 4 | 9 | 5 | 7 | 1 | 2 | 10 | 6 |
| F11 | 1 | 6 | 2 | 7 | 4 | 5 | 3 | 9 | 8 | 10 |
| F12 | 4 | 7 | 6 | 10 | 1 | 3 | 2 | 5 | 9 | 8 |
| Average | 2.083333 | 4.416667 | 2.583333 | 8.833333 | 4.333333 | 6.333333 | 3.666667 | 6.833333 | 7.666667 | 8.25 |
| Best | 1 | 1 | 1 | 7 | 1 | 3 | 1 | 2 | 4 | 6 |
| Worst | 5 | 8 | 6 | 10 | 7 | 9 | 6 | 9 | 10 | 10 |
Table 10.
Ranking of the algorithms based on Friedman’s test for dimension 50.
| Algorithm | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GGWO | GWO | GWCA | ABC | GSA | PSOGSA | PSO | SSA | SCA | MFO | |
| F1 | 1 | 3 | 2 | 7 | 4 | 8 | 5 | 6 | 9 | 10 |
| F2 | 1 | 3 | 2 | 8 | 5 | 9 | 7 | 6 | 4 | 10 |
| F3 | 1 | 2 | 3 | 10 | 5 | 4 | 6 | 7 | 8 | 9 |
| F4 | 1 | 3 | 2 | 10 | 8 | 7 | 4 | 5 | 6 | 9 |
| F5 | 3 | 1 | 2 | 9 | 7 | 6 | 4 | 8 | 5 | 10 |
| F6 | 3 | 5 | 1 | 10 | 2 | 4 | 7 | 6 | 9 | 8 |
| F7 | 5 | 4 | 2 | 8 | 1 | 9 | 3 | 6 | 7 | 10 |
| F8 | 1 | 4 | 2 | 7 | 3 | 9 | 6 | 5 | 8 | 10 |
| F9 | 1 | 7 | 2 | 10 | 4 | 3 | 5 | 6 | 9 | 8 |
| F10 | 3 | 5 | 4 | 10 | 8 | 6 | 1 | 2 | 9 | 7 |
| F11 | 1 | 6 | 2 | 9 | 5 | 4 | 3 | 7 | 8 | 10 |
| F12 | 3 | 7 | 5 | 10 | 1 | 2 | 6 | 4 | 9 | 8 |
| Average | 2 | 4.166667 | 2.416667 | 9 | 4.416667 | 5.916667 | 4.75 | 5.6666 | 7.583333 | 9.083333 |
| Best | 1 | 1 | 1 | 7 | 1 | 2 | 1 | 2 | 4 | 7 |
| Worst | 5 | 7 | 5 | 10 | 8 | 9 | 7 | 8 | 9 | 10 |
The results in Table 9 also show that the average ranking of the GGWO is 2.083333 and 2 regarding all the benchmark functions in dimensions 30 and 50, respectively. The outcomes rank the GGWO first among all other algorithms. Considering the best case, the GGWO is better than all the other algorithms. In addition, the worst case of GGWO is significantly lower than all the other algorithms. In other words, it obtained the best rank among all solution methods in terms of the best worst-case rank, which shows the robustness of the offered methodology. The results indicate that the GGWO can achieve very competitive outcomes compared to the other novel metaheuristic methods and perform better for most benchmark functions.
5. A case study of the COVID-19 pandemic in the United states
We use one of the most recently developed models to forecast the covid-19 pandemic (Giordano et al., 2020). The model reflects eight states, including susceptible, infected, diagnosed, ailing, recognized, threatened, healed, extinct cases. This formulation takes into account several health states for patients. The recommended formulation consists of several differential equations to demonstrate the outbreak. Table 11 defines the notations used in the model.
Table 11.
Notations of the model.
| Sets | |
|---|---|
| State | |
| Parameters | |
| Transmission rate from an infected case to a susceptible individual. | |
| Transmission rate from a diagnosed to a susceptible individual. | |
| Transmission rate from an ailing to a susceptible individual. | |
| Transmission rate from a recognized person to a susceptible individual. | |
| The detection rate of an individual with no symptoms. | |
| The probability that an infected individual knows that he/she is infected. | |
| The probability that an infected individual does not know that he/she is infected. | |
| The detection rate of an individual with symptoms. | |
| The recovery rate. | |
| The probability of developing life-threatening symptoms. | |
| The probability of developing life-threatening symptoms for a detected case. | |
| Death rate. | |
| Variables | |
| The portion of susceptible individuals | |
| The portion of infected individuals (infected and undetected cases without symptoms). | |
| The fraction of diagnosed individuals(infected and detected cases without symptoms). | |
| The portion of ailing individuals(infected and undetected cases with symptoms). | |
| The portion of recognized individuals(infected and detected cases with symptoms). | |
| The portion of threatened individuals(infected detected cases that developed life-threatening symptoms). | |
| The fraction of recovered individuals. | |
| The fraction of death cases. | |
Therefore, we could propose the following model:
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
The United States is part of the COVID-19 pandemic created by acute respiratory syndrome coronavirus 2 (SARS-CoV-2). The country announced its first community transmission case of COVID-19 in January 2020. Up to date, the US has reported more than 4,918,420 COVID-19 cases and 160,290 death cases, making it the country with the most COVID-19 cases. To optimize the limited resources of the healthcare systems, it is crucial to forecast the pandemic's future trends. This approach will enable managers to estimate the peak of the outbreak and plan for the worst-case scenario. Since COVID-19 is a novel virus, the epidemiological parameters are unknown (Ahamad et al. 2020). Thus, we need to present novel methodologies to model the outbreak.
In the following, we resolve the sum of the mean square error model using the GGWO and attain the optimum result for the model. Fig. 4 displays the convergence of GGWO and the average objective value of the grey wolves over the iterations.
Fig. 4.
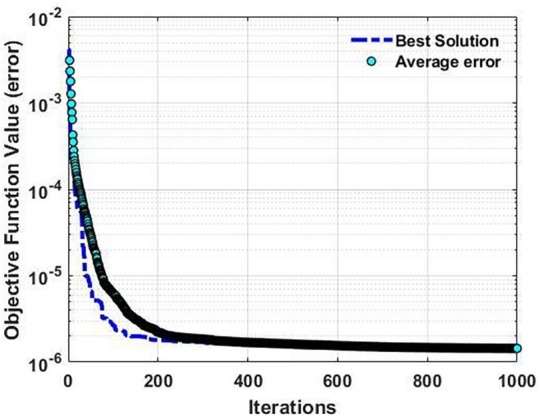
Convergence plot of the GGWO.
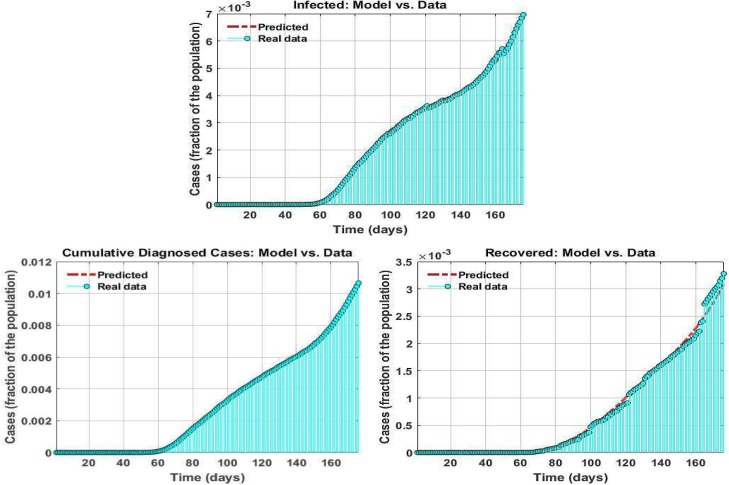
We note that we did not reflect the mean square error of the death cases since the data might be profoundly affected by patients' age, health state, and gender. The data used in this research is available at https://data.humdata.org/dataset/novel-coronavirus-2019-ncov-cases. In Fig. 4, we can observe a perfect trade-off between exploration and exploitation in the performance of the GGWO. Table 12 presents the results of the case study in the US. Fig. 5 describes the accuracy of the predicted model versus real-data. We observe that the offered procedure forecast future trends precisely. It is also noteworthy that the sum of square errors for suggested parameters is 1.44E-06.
Table 12.
Computational results of the case study for the US.
| Stages | Output of model | |||||
|---|---|---|---|---|---|---|
| after May 25 | May 22 to May 25 | Mar 26, to May 22 | Mar 22, to March 26 | Mar 13 to March 22 | Jan 22, to March 13 | |
| 0.126069 | 0.126069 | 0.088807 | 0.442191 | 0.442191 | 0.13946 | |
| 7.22E-05 | 7.22E-05 | 0.004443 | 0.004443 | 0.004443 | 0.002902 | |
| 0.033251 | 0.033251 | 0.02874 | 0.285809 | 0.285809 | 0.036517 | |
| 7.22E-05 | 7.22E-05 | 0.004443 | 0.004443 | 0.004443 | 0.002902 | |
| 0.02025 | 0.017224 | 0.017224 | 0.017224 | 0.019209 | 0.019209 | |
| 0.000193 | 0.022792 | 0.022792 | 0.054364 | 0.054364 | 0.054364 | |
| 0.000193 | 0.022792 | 0.022792 | 0.054364 | 0.054364 | 0.054364 | |
| 0.070311 | 0.070311 | 0.070311 | 0.070311 | 0.070311 | 0.070311 | |
| 0.067394 | 0.067394 | 0.067394 | 0.013641 | 0.013641 | 0.013641 | |
| 0.012395 | 0.012395 | 0.008573 | 0.009172 | 0.009172 | 0.009172 | |
| 0.012395 | 0.012395 | 0.008573 | 0.009172 | 0.009172 | 0.009172 | |
| 0.012395 | 0.012395 | 0.008573 | 0.013641 | 0.013641 | 0.013641 | |
| 0.0003 | 0.008573 | 0.008573 | 0.009172 | 0.009172 | 0.009172 | |
| 0.005631 | 0.005631 | 0.005631 | 0.005856 | 0.005856 | 0.005856 | |
| 0.029214 | 0.029214 | 0.029214 | 0.031166 | 0.031166 | 0.031166 | |
| 0.004884 | 0.004884 | 0.004884 | 0.004884 | 0.004884 | 0.004884 | |
Fig. 5.
Prediction vs. real-data from the US.
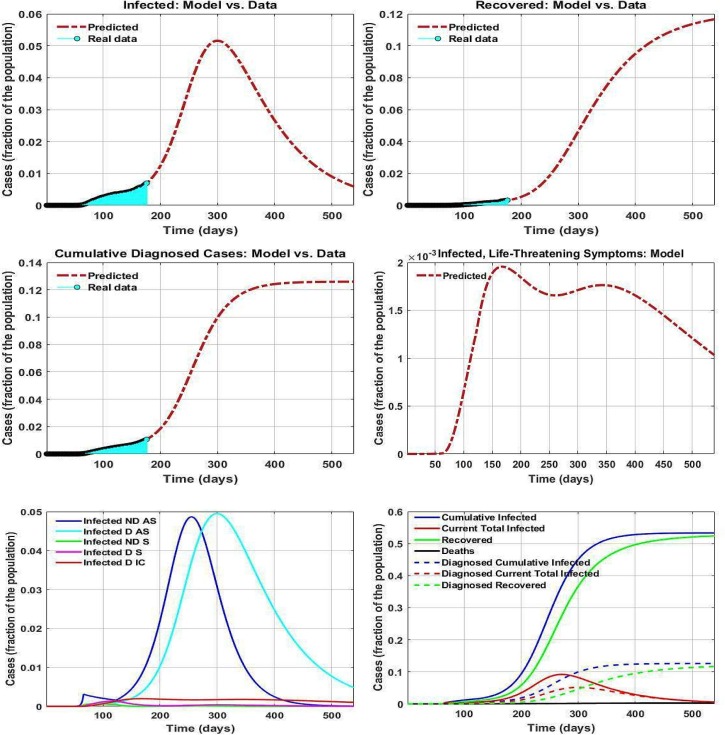
Fig. 6 shows the predicted number of different types of individuals that will develop life-threatening symptoms. Based on the outcomes of our study, we predict that the US will experience the peak of the pandemic in terms of infected cases during mid-November 2020. Our model forecasts that the number of infected cases in the US could reach 16 million by that time. Fig. 6 depicts an accurate prediction on the number of infected cases that develop life-threatening symptoms in the future so that the policymakers and healthcare professionals, and managers could plan for ICU and ventilator allocation.
Fig. 6.
Prediction of future pandemic trends.
During the first stage of the outbreak in the US, the transmission rates were low from January 22 to March 13. Based on our results, the reproduction rate was for this stage. On February 26, 2020, the first community case of the US was reported by The Centers for Disease Control and Prevention (CDC). On March 2, 13, and 16, the US government applied some travel restrictions from 26 European countries and the UK and Ireland, respectively, to contain the spread of the virus. On March 11, 2020, the World Health Organization (WHO) stated the outbreak to be a pandemic. In our study, we consider March 13–22 as the second stage due to the fact that a rapid increase in the number of cases was reported in the country. The reproduction rate was approximately for this stage. As becomes evident, the reproduction number significantly increased in this stage due to community transmission.
On March 19, the testing capacity remarkably increased to detect more infected cases. Since, in this critical time interval, the testing capacity increased, so the detection rate changed from the previous stages. Therefore, we considered March 22–26 as the third stage in our study. During this stage, the reproduction number was which shows exponential growth in this time interval. During the fourth stage, March 26 to May 22, the transmission rates were considerably reduced due to dynamic lockdown and social distancing measures. That is why we observe a meaningful reduction in the reproduction rate for this stage . In the fifth stage, May 22 to May 25, we observe an increase in the transmission rates of the virus since other states start to experience exponential growth in the number of COVID-19 cases. During this stage, the reproduction rate reported . In the last stage, after May 25, we observe an increase in the parameter due to a significant increase in the number of everyday tests resulting in . In the case of continuing the current measures and restrictions, we predicted the future trends of the pandemic in the US over the next 362 days. Fig. 6 presents more details about the model and predictions.
Based on the outcomes, we determined that keeping the current restrictions such as social distancing and partial lockdowns in place will significantly help to slow down the spread of the virus. It worth mentioning that any deviation in the future parameters could significantly affect the predicted trends. Therefore, it is crucial to study the effect of changes in the main parameters of the pandemic on future outcomes.
6. Sensitivity analyses and managerial insights
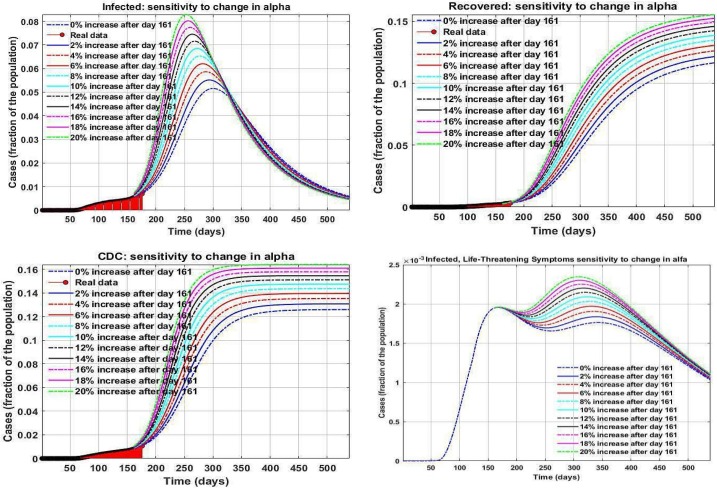
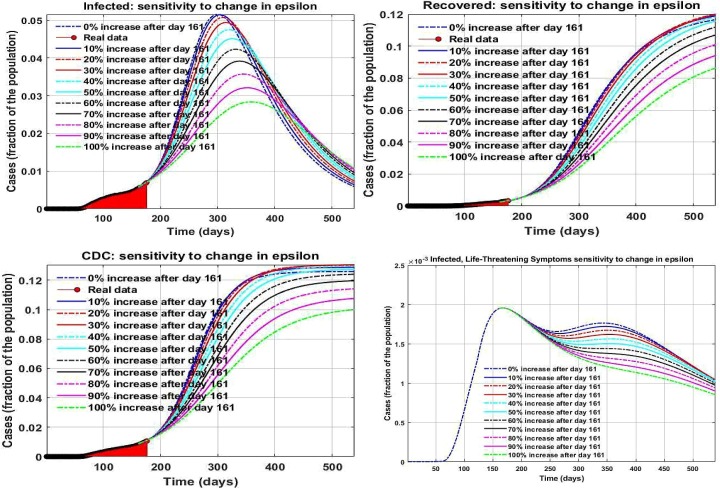
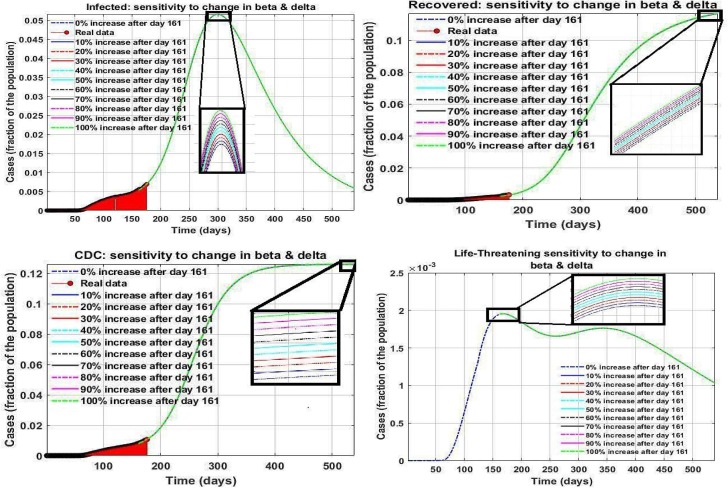
The provided forecast of future pandemic growth in the earlier section considers strict social distancing, behavioral recommendations, and preventing gatherings. However, some businesses are permitted to reopen while continuing social distancing. On the other hand, the pandemic has been started to evolve in more states in the country. Hence, it is vital to discover the effects of reopenings and pandemic growth that create variations in the transmission rates on the upcoming situations. Therefore, we augmented the values of the parameters and explored the outcomes. Such deviations could meaningfully influence the number of cases. We portray the results in Fig. 7, Fig. 8, Fig. 9 . Our results show that the parameter plays a prominent role in the number of infected cases. Increasing parameter surge the number of infected people considerably.
Fig. 7.
Prediction of the infected cases in the US.
Fig. 8.
Prediction of the cumulative diagnosed cases in the US.
Fig. 9.
Prediction of the recovered cases in the US.
Increasing also rises the number of infected people who develop life-threatening symptoms significantly. Therefore, it becomes disclosed that strict measures such as social distancing are the only factors that can decrease this parameter. Increasing more than four percent will result in a new higher peak in the number of patients who need ICU admission. Our results show that the US will experience its peak in the number of infected people from November 1, 2020, to January 10, 2021. Any increase in this parameter of more than 4 percent will create another peak in the number of infected cases who need ICU admission. Therefore, social distancing, wearing masks, and avoiding gatherings are the most critical factors that will help the country pass the peaks. Increasing other parameters such as and have the same effect; however, their influence on the number of infected cases is lower than those of parameter .
Moreover, increasing the value of considerably decreases the portion of infected, recovered, cumulative diagnosed, and death cases. Hence, to contain the virus and stop the pandemic, we can increase testing capacity by at least 40 percent to avoid experiencing another surge of infection who need ICU admission. We discovered that increasing parameter by 100 percent would reduce the total infected case in the upcoming peak by 50 percent. Our study discovered that asymptomatic cases play the most substantial role in spreading the virus.
7. Conclusion and outlook
The original GWO algorithm cannot maintain a proper balance between exploration and exploitation. In this research, we address this issue by presenting a new version of this algorithm, called GGWO, that enables us to solve optimization problems accurately. Our algorithm used the advantages of the gradient that provides valuable information about the solution space. Using gradient information, we accelerated the algorithm that enables us to solve many well-known complex benchmark functions optimally for the first time in the field. Besides, we used deep mathematical concepts such as Gaussian walk and Lévy flight to improve the search efficiency of our methodology. These contributions enabled the proposed algorithm to avoid trapping in local optima. Our computational results on several benchmarks demonstrated the superiority of our algorithm to other algorithms in the literature. Moreover, we applied several robust statistical tests to determine significant differences in the performance of the algorithm compared to state-of-the-art methodologies. Our outcomes revealed that our algorithm is able to solve most benchmarks optimally without trapping in local optima for the first time. Moreover, in instances with dimension 50, Friedman’s test showed that our algorithm's average rank is 2, which is the best average rank among the analyzed algorithms. In 7 out of 12 benchmarks, the proposed algorithm was ranked first.
Moreover, we applied our algorithm for predicting the COVID-19 pandemic in the US. Our results projected the highest number of infected individuals in the United States in mid-November 2020. The results also determined the peak of the number of hospitalized cases. Besides, we performed several analyses to depict upcoming scenarios of the pandemic to help the authorities. The results showed that the transmission rate from an infected person to a susceptible case is the most critical factor in future trends. A surge in this constant would meaningfully raise the total number of cases. Besides, rising the transmission rate from a diagnosed or recognized person to a susceptible case causes a surge in the total number of cases. Moreover, any increase in the value of decreases the total number of cases. Thus, to contain the virus, governments should reduce the infection transmission rate by applying more restrictions on social activities and simultaneously increasing daily tests. Our study revealed that asymptomatic cases have the most significant role in spreading the virus.
As one of the potential research avenues, it would be interesting to take stochasticity and uncertainty into account (Kropat et al., 2011, Özmen et al., 2011, Weber et al., 2011). In addition, considering the effect of information sharing and spread in pandemic growth would be interesting (Belen et al. 2011). Besides, considering other factors such as age, sex, race, and health condition would significantly increase the accuracy of the model. From an algorithmic perspective, presenting a multi-objective version of the proposed algorithm could solve many-objective optimization problems. Moreover, the authorities could use the proposed methodology to optimize resource allocation during the outbreak. Furthermore, healthcare managers could plan for testing kit allocation to test centers using the offered prediction methodology.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Abdel-Basset M., El-Shahat D., El-henawy I., de Albuquerque V., Mirjalili S. A new fusion of grey wolf optimizer algorithm with a two-phase mutation for feature selection. Expert Systems with Applications. 2020;139:112824. doi: 10.1016/j.eswa.2019.112824. [DOI] [Google Scholar]
- Abebe T.H. Forecasting the Number of Coronavirus (COVID-19) Cases in Ethiopia Using Exponential Smoothing Times Series Model. medRxiv. 2020 doi: 10.1101/2020.06.29.20142489. [DOI] [Google Scholar]
- Ahamad M.M., Aktar S., Rashed-Al-Mahfuz M.d., Uddin S., Liò P., Xu H.…Moni M.A. A machine learning model to identify early stage symptoms of SARS-Cov-2 infected patients. Expert Systems with Applications. 2020;160:113661. doi: 10.1016/j.eswa.2020.113661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahmadianfar, I., Bozorg-Haddad, O., & Chu, X. (2020). Gradient-Based Optimizer: A New Metaheuristic Optimization Algorithm. Information Sciences.
- Alamo T., Reina D.G., Millán P. Data-driven methods to monitor, model, forecast and control covid-19 pandemic: Leveraging data science, epidemiology and control theory. arXiv preprint. 2020 arXiv:2006.01731. [Google Scholar]
- Al-Betar M.A., Aljarah I., Awadallah M.A., Faris H., Mirjalili S. Adaptive β-hill climbing for optimization. Soft Computing. 2019;23(24):13489–13512. [Google Scholar]
- Al-Betar M.A., Awadallah M.A., Bolaji A.L.A., Alijla B.O. May). β-hill climbing algorithm for sudoku game. IEEE; 2017. pp. 84–88. [Google Scholar]
- Al-Betar, M. A., Alyasseri, Z. A. A., Awadallah, M. A., & Doush, I. A. (2020). Coronavirus herd immunity optimizer (CHIO). [DOI] [PMC free article] [PubMed]
- Askarzadeh A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Computers & Structures. 2016;169:1–12. [Google Scholar]
- Arora P., Kumar H., Panigrahi B.K. Prediction and analysis of COVID-19 positive cases using deep learning models: A descriptive case study of India. Chaos, Solitons & Fractals. 2020 doi: 10.1016/j.chaos.2020.110017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bansal J.C., Singh S. A better exploration strategy in Grey Wolf Optimizer. Journal of Ambient Intelligence and Humanized Computing. 2021;12(1):1099–1118. [Google Scholar]
- Belen S., Kropat E., Weber G.-W. On the classical Maki-Thompson rumour model in continuous time. Central European Journal of Operations Research. 2011;19(1):1–17. [Google Scholar]
- Blum C., Roli A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM computing surveys (CSUR) 2003;35(3):268–308. [Google Scholar]
- Cerby V. Thermodynamical approach to the travelling salesman problem: An efficient simulation algorithm. Journal of Optimization Theory and Applications. 1985;45:41–51. [Google Scholar]
- Chakrabarti B.K., Chakraborti A., Chatterjee A., (Eds.). Wiley-VCH; 2006. Econophysics and sociophysics: Trends and perspectives. [Google Scholar]
- Chimmula V.K.R., Zhang L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos, Solitons & Fractals. 2020 doi: 10.1016/j.chaos.2020.109864. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clerc M., Kennedy J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE transactions on Evolutionary Computation. 2002;6(1):58–73. [Google Scholar]
- Cui Laizhong, Hu Huaixiong, Yu Shui, Yan Qiao, Ming Zhong, Wen Zhenkun, Lu Nan. DDSE: A novel evolutionary algorithm based on degree-descending search strategy for influence maximization in social networks. Journal of Network and Computer Applications. 2018;103:119–130. [Google Scholar]
- Dewangan Ram Kishan, Shukla Anupam, Godfrey W. Wilfred. Three dimensional path planning using Grey wolf optimizer for UAVs. Applied Intelligence. 2019;49(6):2201–2217. [Google Scholar]
- da Silva R.G., Ribeiro M.H.D.M., Mariani V.C., dos Santos Coelho L. Forecasting Brazilian and American COVID-19 cases based on artificial intelligence coupled with climatic exogenous variables. Chaos, Solitons & Fractals. 2020 doi: 10.1016/j.chaos.2020.110027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhargupta Souvik, Ghosh Manosij, Mirjalili Seyedali, Sarkar Ram. Selective opposition based grey wolf optimization. Expert Systems with Applications. 2020;151:113389. doi: 10.1016/j.eswa.2020.113389. [DOI] [Google Scholar]
- Du H., Wu X., Zhuang J. September). Small-world optimization algorithm for function optimization. Springer; Berlin, Heidelberg: 2006. pp. 264–273. [Google Scholar]
- Ergezer M., Simon D., Du D. Biogeography-based optimization. IEEE Transactions on Evolutionary Computation. 2008;12:702–713. [Google Scholar]
- Eskandar Hadi, Sadollah Ali, Bahreininejad Ardeshir, Hamdi Mohd. Water cycle algorithm–A novel metaheuristic optimization method for solving constrained engineering optimization problems. Computers & Structures. 2012;110-111:151–166. [Google Scholar]
- Faris Hossam, Aljarah Ibrahim, Al-Betar Mohammed Azmi, Mirjalili Seyedali. Grey wolf optimizer: A review of recent variants and applications. Neural computing and applications. 2018;30(2):413–435. [Google Scholar]
- Fogel L.J., Owens A.J., Walsh M.J. John Wiley; London: 1966. Artificial intelligence through simulated evolution. [Google Scholar]
- Garcia L.P., Goncalves A.V., de Andrade M.P., Pedebos L.A., Vidor A.C., Zaina R.…Vargas Amaral F. Estimating underdiagnosis of covid-19 with nowcasting and machine learning: Experience from brazil. medRxiv. 2020 doi: 10.1590/1980-549720210047. [DOI] [PubMed] [Google Scholar]
- Giordano G., Blanchini F., Bruno R., Colaneri P., Di Filippo A., Di Matteo A., Colaneri M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nature Medicine. 2020:1–6. doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glover Fred, Laguna Manuel. Handbook of Combinatorial Optimization. Springer US; Boston, MA: 1999. pp. 2093–2229. [DOI] [Google Scholar]
- Golafshani Emadaldin Mohammadi, Behnood Ali, Arashpour Mehrdad. Predicting the compressive strength of normal and High-Performance Concretes using ANN and ANFIS hybridized with Grey Wolf Optimizer. Construction and Building Materials. 2020;232:117266. doi: 10.1016/j.conbuildmat.2019.117266. [DOI] [Google Scholar]
- Hatamlou Abdolreza. Black hole: A new heuristic optimization approach for data clustering. Information Sciences. 2013;222:175–184. [Google Scholar]
- Holland John H. Genetic algorithms. Scientific American. 1992;267(1):66–72. [Google Scholar]
- Hong L. Jeff, Nelson Barry L. A framework for locally convergent random-search algorithms for discrete optimization via simulation. ACM Transactions on Modeling and Computer Simulation (TOMACS) 2007;17(4):19. doi: 10.1145/1276927.1276932. [DOI] [Google Scholar]
- Huning, A. (1976). Evolutionsstrategie. optimierung technischer systeme nach prinzipien der biologischen evolution.
- Kaveh A., Talatahari S. A novel heuristic optimization method: Charged system search. Acta Mechanica. 2010;213(3-4):267–289. [Google Scholar]
- Kaveh A., Seddighian M.R., Ghanadpour E. Black Hole Mechanics Optimization: A novel meta-heuristic algorithm. Asian Journal of Civil Engineering. 2020;21(7):1129–1149. [Google Scholar]
- Kaveh A., Dadras A. A novel meta-heuristic optimization algorithm: Thermal exchange optimization. Advances in Engineering Software. 2017;110:69–84. [Google Scholar]
- Karaboga Dervis, Basturk Bahriye. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. Journal of global optimization. 2007;39(3):459–471. [Google Scholar]
- Kennedy J., Eberhart R. November). Particle swarm optimization. In Proceedings of ICNN'95-International Conference on Neural Networks. 1995;Vol. 4:1942–1948. [Google Scholar]
- Khalilpourazari S., Pasandideh S.H.R. Sine–cosine crow search algorithm: Theory and applications. Neural Computing and Applications. 2019:1–18. [Google Scholar]
- Khalilpourazari Soheyl, Khalilpourazary Saman. An efficient hybrid algorithm based on Water Cycle and Moth-Flame Optimization algorithms for solving numerical and constrained engineering optimization problems. Soft Computing. 2019;23(5):1699–1722. [Google Scholar]
- Kirkpatrick S., Gelatt C.D., Vecchi M.P. Optimization by simulated annealing. science. 1983;220(4598):671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- Koza J.R., Koza J.R. Vol. 1. MIT press; 1992. (Genetic programming: on the programming of computers by means of natural selection). [Google Scholar]
- Kropat E., Weber G.W., Belen S. Dynamics, games and science I. Springer; Berlin, Heidelberg: 2011. Dynamical Gene-Environment Networks Under Ellipsoidal Uncertainty: Set-Theoretic Regression Analysis Based on Ellipsoidal OR; pp. 545–571. [Google Scholar]
- Lalmuanawma S., Hussain J., Chhakchhuak L. Applications of machine learning and artificial intelligence for Covid-19 (SARS-CoV-2) pandemic: A review. Chaos, Solitons & Fractals. 2020 doi: 10.1016/j.chaos.2020.110059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long Wen, Jiao Jianjun, Liang Ximing, Tang Mingzhu. An exploration-enhanced grey wolf optimizer to solve high-dimensional numerical optimization. Engineering Applications of Artificial Intelligence. 2018;68:63–80. [Google Scholar]
- Lozano M., Molina D., Herrera F. Editorial scalability of evolutionary algorithms and other metaheuristics for large-scale continuous optimization problems. Soft Computing. 2011;15(11):2085–2087. [Google Scholar]
- Li Mu Dong, Zhao Hui, Weng Xing Wei, Han Tong. A novel nature-inspired algorithm for optimization: Virus colony search. Advances in Engineering Software. 2016;92:65–88. [Google Scholar]
- Liao Tianjun, Molina Daniel, Stützle Thomas. Performance evaluation of automatically tuned continuous optimizers on different benchmark sets. Applied Soft Computing. 2015;27:490–503. [Google Scholar]
- Martínez-Álvarez, F., Asencio-Cortés, G., Torres, J. F., Gutiérrez-Avilés, D., Melgar-García, L., Pérez-Chacón, R., ... & Troncoso, A. (2020). Coronavirus Optimization Algorithm: A bioinspired metaheuristic based on the COVID-19 propagation model. arXiv preprint arXiv:2003.13633. [DOI] [PubMed]
- Mirjalili Seyedali, Mirjalili Seyed Mohammad, Hatamlou Abdolreza. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Computing and Applications. 2016;27(2):495–513. [Google Scholar]
- Mirjalili Seyedali, Mirjalili Seyed Mohammad, Lewis Andrew. Grey wolf optimizer. Advances in engineering software. 2014;69:46–61. [Google Scholar]
- Mirjalili Seyedali. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Computing and Applications. 2016;27(4):1053–1073. [Google Scholar]
- Mirjalili Seyedali. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowledge-based systems. 2015;89:228–249. [Google Scholar]
- Mirjalili Seyedali. SCA: A sine cosine algorithm for solving optimization problems. Knowledge-based systems. 2016;96:120–133. [Google Scholar]
- Mirjalili S., Hashim S.Z.M. December). A new hybrid PSOGSA algorithm for function optimization. IEEE; 2010. pp. 374–377. [Google Scholar]
- Mirjalili Seyedali, Saremi Shahrzad, Mirjalili Seyed Mohammad, Coelho Leandro dos S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Systems with Applications. 2016;47:106–119. [Google Scholar]
- Mirjalili Seyedali. The ant lion optimizer. Advances in engineering software. 2015;83:80–98. [Google Scholar]
- Mirjalili Seyedali, Gandomi Amir H., Mirjalili Seyedeh Zahra, Saremi Shahrzad, Faris Hossam, Mirjalili Seyed Mohammad. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Advances in Engineering Software. 2017;114:163–191. [Google Scholar]
- Moghaddam, F. F., Moghaddam, R. F., & Cheriet, M. (2012). Curved space optimization: a random search based on general relativity theory. arXiv preprint arXiv:1208.2214.
- Mousavirad S.J., Ebrahimpour-Komleh H. Human mental search: A new population-based metaheuristic optimization algorithm. Applied Intelligence. 2017;47(3):850–887. doi: 10.1007/s10489-017-0903-6. [DOI] [Google Scholar]
- Özmen Ayşe, Weber Gerhard Wilhelm, Batmaz İnci, Kropat Erik. RCMARS: Robustification of CMARS with different scenarios under polyhedral uncertainty set. Communications in Nonlinear Science and Numerical Simulation. 2011;16(12):4780–4787. [Google Scholar]
- Pahnehkolaei Seyed Mehdi Abedi, Alfi Alireza, Sadollah Ali, Kim Joong Hoon. Gradient-based water cycle algorithm with evaporation rate applied to chaos suppression. Applied Soft Computing. 2017;53:420–440. [Google Scholar]
- Panwar H., Gupta P.K., Siddiqui M.K., Morales-Menendez R., Singhvvv V. Application of deep learning for fast detection of COVID-19 in X-Rays using nCOVnet. Chaos, Solitons & Fractals. 2020 doi: 10.1016/j.chaos.2020.109944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng Y., Nagata M.H. An empirical overview of nonlinearity and overfitting in machine learning using COVID-19 data. Chaos, Solitons & Fractals. 2020 doi: 10.1016/j.chaos.2020.110055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price K.V. Springer; Berlin, Heidelberg: 2013. Differential evolution. In Handbook of Optimization; pp. 187–214. [Google Scholar]
- Rashedi Esmat, Nezamabadi-pour Hossein, Saryazdi Saeid. GSA: A gravitational search algorithm. Information sciences. 2009;179(13):2232–2248. [Google Scholar]
- Rashaideh, H., Sawaie, A., Al-Betar, M. A., Abualigah, L. M., Al-Laham, M. M., Ra’ed, M., & Braik, M. (2018). A grey wolf optimizer for text document clustering. Journal of Intelligent Systems, 29(1), 814-830.
- Rechenberg I. Simulations methoden in der Medizin und Biologie. Springer; Berlin, Heidelberg: 1978. Evolutions strategien; pp. 83–114. [Google Scholar]
- Formato Richard A. Formato. Central force optimization: A new metaheuristic with applications in applied electromagnetics. Prog Electromagn Res. 2007;77:425–491. [Google Scholar]
- Salimi Hamid. Stochastic fractal search: A powerful metaheuristic algorithm. Knowledge-Based Systems. 2015;75:1–18. [Google Scholar]
- Samuel Olusegun David, Okwu Modestus O., Oyejide Oluwayomi J., Taghinezhad Ebrahim, Afzal Asif, Kaveh Mohammad. Optimizing biodiesel production from abundant waste oils through empirical method and grey wolf optimizer. Fuel. 2020;281:118701. doi: 10.1016/j.fuel.2020.118701. [DOI] [Google Scholar]
- Saremi Shahrzad, Mirjalili Seyedali, Lewis Andrew. Grasshopper optimisation algorithm: Theory and application. Advances in Engineering Software. 2017;105:30–47. [Google Scholar]
- Shareef Hussain, Ibrahim Ahmad Asrul, Mutlag Ammar Hussein. Lightning search algorithm. Applied Soft Computing. 2015;36:315–333. [Google Scholar]
- Solis Francisco J., Wets Roger J.-B. Minimization by random search techniques. Mathematics of operations research. 1981;6(1):19–30. [Google Scholar]
- Topal Ali Osman, Altun Oguz. A novel meta-heuristic algorithm: Dynamic virtual bats algorithm. Information Sciences. 2016;354:222–235. [Google Scholar]
- Van Laarhoven P.J., Aarts E.H. Simulated annealing: Theory and applications. Springer; Dordrecht: 1987. Simulated annealing; pp. 7–15. [Google Scholar]
- Wang Sheng-yao, Wang Ling, Liu Min, Xu Ye. An effective estimation of distribution algorithm for solving the distributed permutation flow-shop scheduling problem. International Journal of Production Economics. 2013;145(1):387–396. [Google Scholar]
- Weber Gerhard-Wilhelm, Defterli Ozlem, Alparslan Gök Sırma Zeynep, Kropat Erik. Modeling, inference and optimization of regulatory networks based on time series data. European Journal of Operational Research. 2011;211(1):1–14. [Google Scholar]
- Yang, X. S., & Deb, S. (2009, December). Cuckoo search via Lévy flights. In 2009 World congress on nature & biologically inspired computing (NaBIC) (pp. 210-214). IEEE.
- Yang X.-S. Elsevier; 2014. Nature-inspired optimization algorithms (First edition) [Google Scholar]
- Zabinsky, Z. B. (2010). Random search algorithms. Wiley encyclopedia of operations research and management science.
- Zhu Zhenwei, Zhou Xionghui. An efficient evolutionary grey wolf optimizer for multi-objective flexible job shop scheduling problem with hierarchical job precedence constraints. Computers & Industrial Engineering. 2020;140:106280. doi: 10.1016/j.cie.2020.106280. [DOI] [Google Scholar]
- Zhang X., Ma R., Wang L. Predicting turning point, duration and attack rate of COVID-19 outbreaks in major Western countries. Chaos, Solitons & Fractals. 2020 doi: 10.1016/j.chaos.2020.109829. [DOI] [PMC free article] [PubMed] [Google Scholar]