Colossal anomalous Nernst effect in a correlated noncentrosymmetric kagome ferromagnet

Uranium-based ferromagnet demonstrates notable ability to convert heat to electricity.

Abstract

The transverse voltage generated by a temperature gradient in a perpendicularly applied magnetic field, termed the Nernst effect, has promise for thermoelectric applications and for probing electronic structure. In magnetic materials, an anomalous Nernst effect (ANE) is possible in a zero magnetic field. We report a colossal ANE in the ferromagnetic metal UCo_0.8Ru_0.2Al, reaching 23 microvolts per kelvin. Uranium’s 5f electrons provide strong electronic correlations that lead to narrow bands, a known route to producing a large thermoelectric response. In addition, uranium’s strong spin-orbit coupling produces an intrinsic transverse response in this material due to the Berry curvature associated with the relativistic electronic structure. Theoretical calculations show that in UCo_0.8Ru_0.2Al at least 148 Weyl nodes, and two nodal lines, exist within 60 millielectron volt of the Fermi level. This work demonstrates that magnetic actinide materials can host strong Nernst and Hall responses due to their combined correlated and topological nature.

INTRODUCTION

Because electrons carry both heat and charge, the transport of one is necessarily related to the other. Thermoelectric applications aim to exploit this fact by converting heat or charge flow into electric voltages or temperature gradients (1, 2). In the presence of a magnetic field, transverse responses are possible. It has been argued that the transverse geometry allows one to convert heat into electrical energy much more efficiently than the conventional longitudinal geometry (1, 3, 4). In conventional materials, however, the amplitude of the transverse anomalous Nernst effect (ANE) has been too small to realize practical thermoelectric devices.

Recently, it has been recognized that the Berry curvature associated with the Bloch waves of electrons generates an additional and potentially very large transverse response in magnetic materials (5–9). This is exemplified by the full-Heusler ferromagnet Co₂MnGa whose ANE at room temperature is 6 μV/K and reaches to a record 8 μV/K at T = 400 K (3). This value is larger than typical ferromagnets, and theoretical calculations reveal that the large ANE is a consequence of the intrinsic Berry curvature contribution. After the triumph of Co₂MnGa, a natural question arises: Can one further enhance or maximize the size of the ANE for applications or due to fundamental constraints? Here, we examine a uranium compound, which has multiple favorable attributes for enhancing the Berry curvature and ANE, and we find an ANE, which is even four times larger than found in Co₂MnGa.

The Nernst Effect is related to the thermoelectric ($\overline{\mathrm{\alpha }}$) and conductivity ($\overline{\mathrm{\sigma }}$) tensors through the expression ${\mathit{S}}_{\mathit{xy}}=-{\mathit{E}}_{\mathit{y}}/{\nabla }_{\mathit{x}}\mathit{T}=({\mathrm{\sigma }}_{\mathit{xx}}{\mathrm{\alpha }}_{\mathit{xy}}-{\mathrm{\sigma }}_{\mathit{xy}}{\mathrm{\alpha }}_{\mathit{xx}})/({\mathrm{\sigma }}_{\mathit{xx}}^2+{\mathrm{\sigma }}_{\mathit{xy}}^2)$. The transverse contribution to the thermoelectric and conductivity tensors is directly connected to the Berry curvature Ω_B through

$${\mathrm{\sigma }}_{\mathit{xy}}=-\frac{{\mathit{e}}^2}{\mathrm{ħ}}{\int }_{\text{BZ}}\frac{{\mathit{d}}^3\mathit{k}}{{(2\mathrm{\pi })}^3}\mathit{f}(\mathit{k}){\mathrm{\Omega }}_{\mathit{B}}(\mathit{k})$$ (1)

$${\mathrm{\alpha }}_{\mathit{xy}}=\frac{{\mathit{ek}}_{\mathit{B}}}{\mathrm{ħ}}{\int }_{\text{BZ}}\frac{{\mathit{d}}^3\mathit{k}}{{(2\mathrm{\pi })}^3}\mathit{s}(\mathit{k}){\mathrm{\Omega }}_{\mathit{B}}(\mathit{k})$$ (2)

where k_B is the Boltzmann’s constant, e is the charge of an electron, ħ is the Planck’s constant h divided by 2π, f(k) is the Fermi-Dirac distribution function, s(k) = − f(k) ln (f(k)) − (1 − f(k)) ln (1 − f(k)), and ∫_BZ is the integration over the Brillouin zone. At low temperatures, these two quantities are related through the Mott formula (10, 11).

An examination of these equations reveals that large Berry curvatures and small Fermi energies E_F will generate large Hall and Nernst effects, in general. As elaborated on below, to enhance the Berry curvature contribution to the ANE and anomalous Hall effect (AHE), we therefore look for a system with the following properties: (i) a large spin-orbit coupling (SOC), (ii) strong electronic correlations, (iii) ferromagnetic order, and (iv) a kagome lattice structure.

The Berry curvature depends strongly on the SOC. Increasing the strength of the SOC increases the potential occurrence of band inversions, which generate regions of potentially diverging Berry curvature in the Brillouin zone. Depending on the symmetry of the inverted bands, nodal lines and/or Dirac or Weyl nodes may appear. In general, the strength of the SOC increases with increasing atomic number, and hence, we look for materials near the bottom of the periodic table.

To maximize the effects of larger SOC requires multiple bands to reside in the vicinity of the Fermi energy. This can be accomplished through strong electronic correlations, which will shift multiple band crossing points closer to the Fermi energy, thereby enhancing the Berry curvature. Furthermore, the renormalized band structures due to electronic correlations lead to smaller effective Fermi energies, which is known to promote large Seebeck and Nernst responses (12, 13). The need for both strong correlations and large SOC leads us naturally to heavy fermion systems composed of 4f and 5f elements.

Without broken time-reversal symmetry, a transverse Hall or Nernst response is identically zero. Hence, in the absence of an applied magnetic field, magnetic order is required for a finite ANE or AHE. Although possible in a system with antiferromagnetic order (8, 9, 14, 15), the requisite absence of symmetries is guaranteed in a ferromagnetic system.

In a system with antiferromagnetic interactions, magnetic frustration present in a kagome lattice can lead to additional band renormalization. Although magnetic frustration is presumably absent in a ferromagnetic material, the unrenormalized hopping on a kagome lattice coincidentally produces one flat band. Perhaps this explains, in part, why large AHE and ANE responses have been recently observed in a number of kagome compounds (6, 16–19).

In our exploration of materials, we found that the layered distorted kagome lattice system UCo_1−xRu_xAl in the ZrNiAl structure type (shown in Fig. 1A) satisfies all the above criteria. In addition, the crystal structure is noncentrosymmetric, which can generate pairs of Weyl nodes with opposite chiralities. By themselves, such Weyl nodes do not contribute to the AHE and ANE, but they can be further split by the magnetic order. Both parent compounds UCoAl and URuAl are paramagnetic, but much of their solid solution UCo_1−xRu_xAl is ferromagnetic (20, 21). Members of the entire alloy series show relatively large Sommerfeld coefficients γ of ∼50 mJ/mol K² (21–24), indicating that charge carriers are moderately heavy. Magnetic x-ray and photoemission measurements also certify the presence of electronic correlations (25, 26). Furthermore, previous work has shown substantial anomalous Hall conductivity (AHC) for dopings close to the quantum-phase transition (21). Here, we examine x = 0.2 with a critical temperature (T_c) of 56 K, close to the optimal value in the series.

Fig. 1. Crystal structure and theoretical calculations of UCo_0.8Ru_0.2Al.

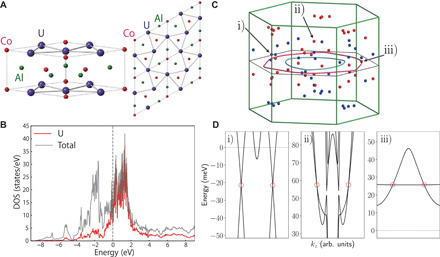
(A) Crystal structure of UCo_{1 − x}Ru_xAl. Left: The unit cell of UCoAl viewed from the [111] direction. A Co atom is replaced by a Ru atom upon doping. Right: The top view of UCoAl. The solid bonds indicate the tilted kagome layer formed by uranium atoms. (B) Density of states (DOS) including partial DOS for UCo_0.8Ru_0.2Al. (C) Nodal lines and Weyl points within ±60 meV of the Fermi energy in UCo_0.8Ru_0.2Al. For clarity, Weyl pairs with a k_z separation < 0.2 2π/c are not shown. (D) Band plots for examples of (i) type I, (ii) type II, and (iii) critically tilted Weyl points (red circles), identified with arrows in (C), plotted on the interval −2k_W < k_z < 2k_W, where 2k_W is the Weyl pair separation along the k_z direction.

RESULTS

Our spin-polarized theoretical calculations including SOC support our initial conjecture. A partial density of states of UCo_0.8Ru_0.2Al shown in Fig. 1B reveals a narrow band of uranium f-states dominating the electronic structure near E_F. Electronic correlations are expected to further reduce this bandwidth (24). The magnitude of the calculated AHC due to the Berry curvature is found to be ∼2000 ohm⁻¹cm⁻¹, although the value as well as sign, is highly sensitive to details of the electronic structure (24). The origin of this large AHC is due to the dominant flat 5f uranium bands creating a remarkable number of topological features close to E_F. Figure 1C shows the location of a subset of the Weyl nodes in the Brillouin zone that are within ±60 meV of the Fermi level. There are at least 148 Weyl points, which is, by far, larger than other Weyl materials. There exist both type I and type II Weyl nodes, as well as a few that are proximate to a Lifshitz transition between the two types (see Fig. 1D). Such a “quantum-critical” Weyl node was argued to be the origin of the large Nernstresponse in Co₂MnGa (3). We additionally find two topological nodal lines close to E_F within the σ_z mirror plane (Fig. 1C). These nodal lines arise at the crossing of bands belonging to distinct irreducible representations of the mirror plane point group and are protected against perturbations by the existence of mirror symmetry. While these nodal lines are substantial sources of Berry curvature, they will not contribute to ${\mathrm{\Omega }}_{\mathit{xy}}^{\mathit{z}}$. We note that first-principles calculations of the electronic structure of uranium compounds is notoriously challenging, but the main observation of an incredibly large number of Weyl nodes and Berry curvature found here is independent of the details of the electronic structure [see (24)].

The temperature dependence of the longitudinal resistivity ρ_xx and the Seebeck coefficient S_xx of a single crystal of UCo_0.8Ru_0.2Al is shown in Fig. 2. A kink is observed in both ρ_xx and S_xx at the ferromagnetic T_c = 56 K. The sample is a bad metal as reflected by the large residual resistivity (105 μ ohm cm). A longitudinal conductivity σ_xx of ∼9500 ohm⁻¹cm⁻¹, which falls within the moderately dirty regime where σ_xx = 3 × 10³ −5 × 10⁵ ohm⁻¹cm⁻¹, is the first indication that the transverse transport will be dominated by the intrinsic contribution (27). In the T = 0 limit, the S_xx/T gives a value of 0.9 μV/K². This suggests a Fermi temperature of ∼470 K (12), consistent with a Fermi temperature of 930 K estimated by specific heat (24). We also note that the ratio of the experimental Sommerfeld coefficient to the computed value based on density functional theory implies a mass renormalization of ∼3 (24).

Fig. 2. Longitudinal transport and magnetization properties of single crystalline UCo_0.8Ru_0.2Al.

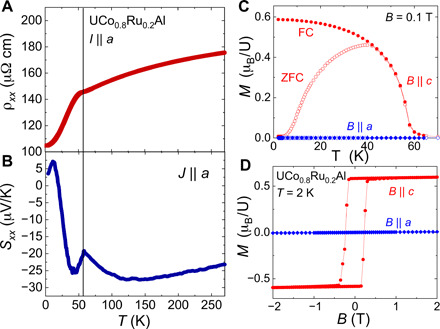
(A) Electrical resistivity ρ versus temperature T with the current I ∥ a. The vertical solid line indicates the ferromagnetic critical temperature. (B) Seebeck coefficient S_xx versus T with the heat current J ∥ a. (C) Temperature dependence of the field-cooled (FC) and zero-field-cooled (ZFC) magnetization M per formula unit for B ∥ c (red) and B ∥ a (blue) in an applied field B = 0.1 T. (D) Field dependence of the magnetization M(H) at T = 2 K.

The temperature- and field-dependent magnetization of UCo_0.8Ru_0.2Al is shown in Fig. 2. The system shows very strong Ising-type magnetic anisotropy, with the easy axis along the c axis. The saturation magnetic moment of 0.59 μ_B/U is consistent with a previous study (20) and implies that the uranium 5f electrons are rather strongly hybridized with ligand electrons. A small field of B = 0.1 T is enough to polarize the magnetic moments during field cooling (FC). Thus, we take the transverse responses (Hall, Nernst, and Righi-Leduc effects) with FC and B = 0.1 T conditions, which is small enough to render the ordinary contributions as negligible.

The field and temperature dependence of the Hall, Nernst, and Righi-Leduc effects are shown in Fig. 3. For the field dependence, they all show a step-like behavior similar to the magnetization. The saturated response at high fields in the ordered state confirms that the transverse effects are dominated by the anomalous contribution, and the ordinary component is negligibly small. Consequently, the transverse response discussed in the remainder of the paper implicitly refers to the anomalous component. The vanishing transverse response as the temperature exceeds T_c is also consistent with this picture.

Fig. 3. Colossal anomalous transverse responses from UCo_0.8Ru_0.2Al with B∥c.

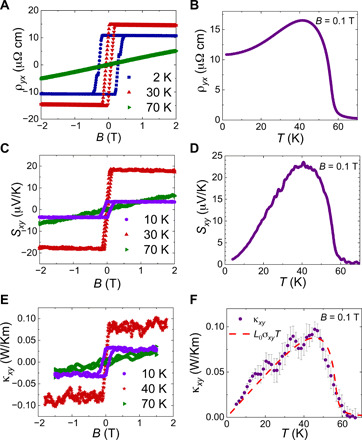
(A and B) Hall effect ρ_xy as a function of magnetic field B and temperature T, respectively. (C and D) Nernst effect S_xy as a function of B and T, respectively. (E and F) Thermal Hall (Righi-Leduc) effect κ_xy as a function of B and T, respectively. The red dashed line in (F) is the expected thermal Hall conductivity based on the electrical Hall conductivity if the Wiedemann-Franz law is satisfied. All temperature-dependent data were taken with B = 0.1 T.

The anomalous Hall effect of UCo_0.8Ru_0.2Al is found to be very large, as shown in Fig. 3 (A and B). At T = 40 K, ρ_xy is −16 μ ohm cm, which decreases to −11 μ ohm cm at T = 2 K, corresponding to a conductivity of σ_xy = 980 ohm⁻¹ cm⁻¹. These values are similar to that of Co₂MnGa and Co₃Sn₂S₂ and among the largest values for ferromagnetic metals (3, 16).

Next, we display our primary result, a colossal ANE. While the anomalous Hall resistivity is as large as in Co₂MnGa and Co₃Sn₂S₂, more unexpectedly, the ANE is found to be colossal in UCo_0.8Ru_0.2Al, reaching 23 μV/K at T= 40 K (Fig. 3, C and D). To the best of our knowledge, this is approximately three to four times larger than the current record value of 6 to 8 μV/K held by Co₂MnGa (3). Furthermore, in UCo_0.8Ru_0.2Al, the magnitude of S_xy at 40 K is comparable to the Seebeck coefficient. Consequently, the anomalous Nernst angle tan (θ_N) = ∣ S_xy/S_xx∣ reaches 0.92 at 41 K, where both S_xx and S_xy have extrema with values of −25.5 and 23.5 μV/K, respectively.

Figure 3 (E and F) displays the anomalous thermal Hall conductivity κ_xy of UCo_0.8Ru_0.2Al as a function of field and temperature. To check the validity of the anomalous Wiedemann-Franz (WF) law $L_0=\frac{{\mathrm{\kappa }}_{\mathit{xy}}}{{\mathrm{\sigma }}_{\mathit{xy}}T}$ where ${\mathit{L}}_0=\frac{{\mathrm{\pi }}^2{\mathit{k}}_{\mathit{B}}^2}{3{\mathit{e}}^2}$ = 2.44 × 10⁻⁸ W ohm/K², we compared κ_xy with L₀σ_xyT (Fig. 3F). We find that they overlap each other very well, and thus, the WF law is valid. The validity of a transverse WF law indicates that the anomalous transverse entropy and charge flow are governed by the intrinsic contribution from the Berry curvature (8, 15).

DISCUSSION

The AHC as a function of T/T_c for a variety of materials with large transverse responses in heat and charge (15, 28–30) is shown in Fig. 4A. The AHC of UCo_0.8Ru_0.2Al is almost temperature-independent below T = 0.5 T_c. This implies that the AHC is independent of scattering rate, which is an additional support that the intrinsic contribution dominates the transverse response in this system. At T = 2 K, ∣σ_xy∣ reaches 980 ohm⁻¹ cm⁻¹ in UCo_0.8Ru_0.2Al, which is comparable to Co₂MnGa, one of the largest intrinsic AHC known. The AHC from SrRuO₃ and Mn₃Ge is almost one order of magnitude smaller than that of UCo_0.8Ru_0.2Al. The anomalous Peltier conductivity α_xy as a function of T/T_c for these materials is shown in Fig. 4B. The Peltier coefficient is the sum of two contributions σ_xxS_xx and σ_xyS_xx. In UCo_0.8Ru_0.2Al, σ_xxS_xy ≫ σ_xyS_xx (see the Supplementary Materials). In sharp contrast to the fact that σ_xy of UCo_0.8Ru_0.2Al is comparable to that of Co₂MnGa and Co₃Sn₂S₂, α_xy of UCo_0.8Ru_0.2Al is roughly three to four times larger than that of Co₂MnGa, the current record holder for α_xy, and Co₃Sn₂S₂. α_xy of SrRuO₃ and Mn₃Ge are notably smaller.

Fig. 4. Anomalous Hall and Peltier conductivity of various magnets.

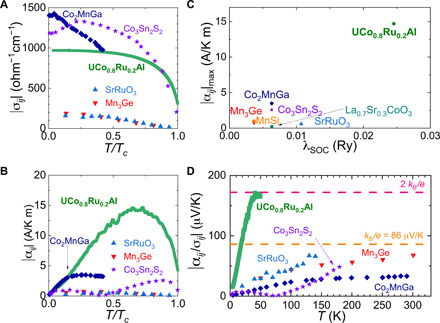
(A) AHC σ_ij and (B) anomalous Peltier conductivity α_ij as a function of normalized temperature T/T_c (green line). For comparison, other materials with large anomalous contributions are also shown. (C) The maximum value of α_ij for various compounds compared with the strength of the SOC of the magnetic element (31). The compounds include UCo_0.8Ru_0.2Al (this work, green circle), Co₂MnGa (blue diamond) (28), Co₃Sn₂S₂ (purple star) (30), SrRuO₃ (29) (cyan upper triangle), La_0.7Sr_0.3CoO₃ (light green square) (29), Mn₃Ge (red lower triangle) (15), and MnSi (orange hexagon) (49). (D) Plot of α_ij/σ_ij versus T. Orange and pink dashed lines indicate k_B/e and 2 k_B/e, respectively.

Why is α_ij so large in UCo_0.8Ru_0.2Al? In Fig. 4C we plot the maximal value of ∣α_ij∣ versus λ_SOC for various compounds. λ_SOC is estimated from atomic calculations of the magnetic element (31, 32). Despite this very rough estimate for the strength of the SOC in these materials, Fig. 4C supports our original conjecture that a large SOC increases the possibility for more band inversions, which can create a large Berry curvature contribution to anomalous transverse response functions (33).

A large SOC alone, however, is insufficient to explain the remarkable properties of UCo_0.8Ru_0.2Al, because the maximal contribution from any pair of bands to the AHE is e²/hc, where c is the c-axis lattice constant, and in this limit, one expects a vanishing ANE. Instead, our electronic structure calculations shown in Fig. 1 reveal that there are many bands in the vicinity of the Fermi energy. This is a consequence of the nature of the 5f electrons in uranium. Furthermore, electronic correlations will further renormalize the bands leading to smaller effective Fermi energies, which is known to enhance thermoelectric properties (12). Notably, the Sommerfeld coefficient of the heat capacity γ is substantially larger for UCo_0.8Ru_0.2Al (41 mJ/mol K²) compared to Co₂MnGa (12 mJ/mol K²) (3). Thus, it is the combination of the small effective Fermi energy and the large SOC that leads to multiple topological features within the energy window set by the SOC and that enables the remarkably large values of both σ_ij and α_ij in UCo_0.8Ru_0.2Al.

It is interesting to ask which specific features of the electronic structure are most responsible for the large ANE in UCo_0.8Ru_0.2Al. UCo_0.8Ru_0.2Al crystallizes in the nonsymmorphic space group 189. From basic symmetry considerations, this space group has been argued to have a variety of interesting topological features, including Weyl nodes (34–37), nodal lines (38–41), and triple points (42, 43). All of these features appear in our electronic structure calculations (24). Notably, one set of critically tilted Weyl points lies 25 meV above E_f, corresponding to a doping of x ∼ 0.07 in the rigid band picture. For this set of Weyl nodes, we compute values of σ_xy ∼ 1200 ohm⁻¹ cm⁻¹ and α_xy ∼ 20 A(K m)⁻¹ at that energy, which may be shifted as a consequence of electronic correlations. Another possibility is that electronic correlations pin the Weyl nodes to the chemical potential as has been suggested in some Weyl-Kondo semimetals (44). Additional measurements, such as angle-resolved photoemission spectroscopy, will be required to confirm the identity of the most relevant topological features in UCo_0.8Ru_0.2Al.

Last, we consider the relationship between σ_ij and α_ij. From the Mott relation, which is valid in the T = 0 limit, a large α_ij/T implies that σ_ij can be enhanced by appropriately tuning the chemical potential. As temperature is increased, the relationship between σ_ij and α_ij is less straight forward. Behnia et al. (28) have argued, however, that the ratio of α_ij/σ_ij is bounded by the ratio of natural units k_B/e = 86 μV/K, which reflects the fact that the Peltier coefficient represents the transport of entropy, while the Hall coefficient represents the transport of charge. For UCo_0.8Ru_0.2Al, α_ij/σ_ij reaches 170 μV/K at T = 47 K, as shown in Fig. 4D. This supports the notion that multiple bands are simultaneously contributing to the large Nernst response in UCo_0.8Ru_0.2Al.

In conclusion, we have found a colossal ANE in UCo_0.8Ru_0.2Al. The simultaneous presence of strong SOC and electronic correlations drives narrow bands leading to a gigantic Nernst response and presents an exciting blueprint for how to develop magnetic topological metals for thermoelectric applications.

MATERIALS AND METHODS

A single crystal of nominal composition UCo_0.8Ru_0.2Al was grown by the Czochralski method in a tri-arc furnace. The crystal structure was confirmed to have the P$\overline{6}2\mathit{m}$ (# 189) space group with the ZrNiAl structure type. Powder and single-crystal diffraction was performed to confirm the crystal structure and the phase purity of the samples. The sample was oriented, and the quality was further checked by the x-ray Laue method with a photosensitive detector in backscattering geometry. The measured magnetic properties are in good agreement with previous studies, further confirming the sample quality.

Electronic structure calculations were performed using the local spin density approximation, yielding a ferromagnetic ground state, within the framework of the full potential linear muffin tin orbital method with SOC (45). This approximation has been previously used to study UCoAl (25, 46) and other uranium compounds in the same structural family (47). Experimental lattice constants were used (48), and doping dependence was handled using a rigid band approximation.

Weyl points and other topological features were located, and their topology was verified in a single-shot method (43). An initial coarse k-grid of 30 × 30 × 30 was used to locate candidate sources/sinks of Berry curvature flux, whose positions were iteratively refined by repeating the procedure on 2 × 2 × 2 grids within each k-cube. Additional details can be found in (24).

Transport, thermoelectric, and thermal transport measurements were performed in the same setup. A temperature gradient was generated by a 10-kilohm chip resistor attached to one end of the sample and measured by homemade thermocouples with the calibrated table made of Fe-doped gold and chromel. The other end of the sample was attached to a sapphire substrate that was physically clamped to an oxygen-free copper cold finger. Conventional steady-state measurements were performed to measure the thermoelectic power and thermal conductivity. The heating power was carefully monitored so that the thermal and thermoelectric responses were linear with the heating power.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/13/eabf1467/DC1