Abstract
Reducing the peak time of an epidemic disease in order for slowing down the eventual dynamics and getting prepared for the unavoidable epidemic wave is utmost significant to fight against the risks of a contagious epidemic disease. To serve to this purpose, the well-documented infection model of SIR is examined in the current research to propose an analytical approach for providing an explicit formula associated with a straightforward computation of peak time of outbreak. Initially, the time scale from the relevant autonomous SIR epidemic model is formulated analytically via an integral based on the fractions of susceptible and infected compartments. Afterwards, through a series expansion of the logarithmic term of the resultant integrand, the peak time is shown to rely upon the fraction of susceptible, the infectious ratio as well as the initial fractions of ill and susceptible individuals. The approximate expression is shown to rigorously capable of capturing the time threshold of illness for an epidemic from the semi-time SIR epidemiology. Otherwise, it is also successful to predict the peak time from a past history of a disease when all-time epidemic model is adopted. Accuracy of the derived expressions are initially confirmed by direct comparisons with recently reported approximate formulas in the literature. Several other epidemic disease samples including the COVID-19 often studied in the recent literature are eventually attacked with favourable performance of the presented formulae for assessing the peak time occurrence of an epidemic. A quick evaluation of the peak time of a disease certainly enables the governments to take early effective epidemic precautions.
Keywords: Epidemic, SIR model, Peak thresholds, Peak time, COVID-19
1. Introduction
Rapid emergence and spread of a deadly disease wave originated from a local region can easily threaten the rest of the globe in this global world from the experienced outbreaks so far. Therefore, early understanding of the critical parameters of an epidemic disease is significant to take necessary precautions in order for controlling hazardous epidemiological impacts. This attracted many researchers from the scientific community to develop new mathematical tools to model epidemic contractions as well as to predict threshold parameters from them [1]. In an aim to reduce the amplitude of the epidemic peak, one of the important thresholds is the peak time of a spreading infectious disease which is the essential target of the present effort.
The mathematical SIR model of epidemiology initiated as early as in 20th century in [2] is one of the most widely recognized and studied models after the simple logistic differential equation of Bernoulli [3]. The main reason is that it is not complicated and can be applicable to a variety of illnesses existing in the world including the flu, influenza, fever, measles, malaria, smallpox, plague, cholera, predator–prey interaction of phages and bacteria, sexually transmitted diseases like HIV, Zika and Ebola, and coronavirus-based diseases like SARS and COVID-19, among many others, provided that the initial vulnerable people and infected people are known with infection and recovery rates.
A great deal of theoretical and numerical research has been implemented so far on the SIR model, hence the present work has only a limited space to cite a small percentage focusing mostly on the recent publications. To start with, not only the classical numerical integration schemes [3] were used to simulate the SIR model system, but some further semi-analytical approaches were employed, too; such as, the differential transformation method [4], the variational iteration method [5] and the Adomian decomposition method [6]. An analytical prediction was given in [7] for the S(E)IR epidemic model, whose rigorous validation and comparisons with the full simulations were not implemented. It was shown in [8] that if the susceptibles are represented as a finite multi-exponential or a logistic function, a closed form solution to the SIR model can be given. Using the SIR model, the model predictions were compared to data for the Bombay plague epidemic, the English boys school epidemic and the Eyam plague outbreak in [9]. [10] proposed an analytical parametric form solution of SIR epidemic model and showed that the numerical solution reproduces their analytical solution. The classical SIR model and its potential application areas were later reviewed in [11]. [12] connected the SIR model through a sexual contact network and direct contact vector to explain the sexual transmission and spread of diseases. The epidemic model based on Bailey’s continuous differential system was solved analytically in [13], which was later extended to time scales. [14] aimed at approximating the recovery rate, infection rate, and the loss of immunity rate by comparing the SIR relevant models with real world data. Especially, COVID-19 in Italy from February 15th to April 6th was studied. SIR and SEIR epidemic models were used to predict the peak time of COVID-19 in Egypt in [15]. It was suggested that the peak time will be delayed by mitigation strategies and other lockdown measures will help delay the expected peak. [16] highlighted the analogy between the dynamics of disease transmission in the conventional SIR model and chemical reaction kinetics. Time evolution of the COVID-19 pandemic in Italy by a Gauss error function and Monte Carlo simulations was reported in [17]. The numerical results in [18] based on the SIR model pointed to the fact that tracing early detection and isolation of infecteds are more efficient than those based on social distancing, which is of high premise in treating COVID-19. The COVID-19 epidemic in Italy was comprehensively studied in [19] to assess the epidemic size and its timescale from the SIR and SIR-type models (A-SIR). Asymptotically consistent series expansion technique was applied in the research papers [20] and [21] to SEIR models in order to accelerate the convergence of series, but no estimates for the peak times were given. Infection peak predictions of coronavirus disease in Japan were computed through full numerical simulations of the S(E)IR model in [22]. In [23] S(E)IR models were criticized for not being able to provide adequate predictions of the time to peak. However, in real computations, deterministic and stochastic approaches are better being simultaneously used to predict the thresholds. Indeed, from the deterministic models, we should rely on the epidemic peak thresholds coming out of the SIR model. A rather fruitful approach was adopted in the recent publication [24] to construct an analytic solution for the all-time SIR model with time-dependent infection rate. The differential rate of infections during a single wave captured by the Gauss model was also addressed regarding the COVID-19 pandemic disease. The global asymptotical stability analysis was considered in a continuous reactor in [25] for a mathematical dynamical system involving both deterministic and stochastic SIR epidemic models.
As highlighted from the above cited literature, predicting the thresholds of an infectious illness in order for realizing the peak time right from the beginning of an outbreak is of vital importance to assess how an epidemic will turn into an harmful phenomenon in the end. Nevertheless, reducing the epidemic models can most effectively be fulfilled if precise knowledge of the peak time is known. This was commonly achieved so far by numerically simulating the full system of SIR model by different techniques of integration. The main objective of the current work is to derive formulas from which the peak time of a disease can be obtained without requirement of use of the entire system of equations during computer simulations. This is accomplished by first presenting an integral expression of the infection time from the SIR model. An elaborative and accessible formula is then extracted from the series expansion making use of the leading term approximation only. Adding the first order term to the expansion, an improved and more accurate formula involving the hyperbolic and logarithmic functions is also devised. Hence, through series expansion around the initial susceptible fraction, the results are the first-order and second-order approximate analytical expressions involving the hyperbolic and logarithmic functions, for the peak time of a disease given the epidemic parameters. This is a useful result that can be readily incorporated into future studies and codes. Accuracy of the formulas are initially verified on recently published approximate methods. A number of tests are eventually performed on the recently studied SIR models with a great success. In addition, the values found for the peak time of COVID-19 infection in countries like Japan, Korea, Italy and Iran, are very close to the exact values. By the help of quick evaluation of peak time from the presented formulae, the early effective epidemic precautions, such as the isolation, the tracing, the social distancing and, if necessary, the lockdown can be taken by the governments.
2. Governing equations
The traditional SIR mathematical model of epidemiology is well-known as a compartmental-based epidemiological model, thus we briefly outline the model here. A cumulative number of individuals consisting of susceptible (S), infected (I) and recovered (R) is thought in different compartments. Only a vivid interaction between the susceptible and ill is permitted through the productive contact . As a result, defining as the constant rate of susceptibles to become ill per time per population, as the constant rate of ills to turn into a recovered patient (dead/immune) per time, and also under certain common assumptions [2], [3] and [18], the initial value problem among the three species is expressed via the SIR epidemiologic nonlinear mathematical model
| (1a) |
| (1b) |
| (1c) |
where stands for initial number of susceptible, ill and recovered, respectively. On defining the fractions or density functions
and , the model in (1a)–(1c) can be rewritten as
| (2a) |
| (2b) |
| (2c) |
3. Epidemic thresholds at the peak time
Making use of Eqs. (2a)–(2b), we obtain the sum of infection and susceptible densities
| (3) |
To facilitate the understanding, since it is difficult to solve analytically in the time domain, it is noted that to obtain solution (3) it is necessary to eliminate differential in system (2a)–(2c), and then integrate the first two equations.
At the peak time of an endemic disease (most probably the pandemic), Eq. (2b) dictates the number of susceptible and hence, using (2b), (3), the peak time thresholds are given by ([26])
| (4a) |
| (4b) |
| (4c) |
Although the extreme values are worked out in system (4a)–(4c), the critical peak time leading to these extrema is not known yet. However, the time of the autonomous system (2a)–(2c) can be solved by means of integrating equation (2a) in the manner
| (5) |
Keeping the system (2a)–(2c) in mind, the denominator of the integrand in (5) can never vanish at a finite time. Consequently, considering (4a)–(4c), the peak time of an epidemic/pandemic disease takes place at the location yielding
| (6) |
Altogether, the data in (6) and (4a)–(4c) present the peak time thresholds, but it is unfortunately impossible to analytically evaluate from (6) due to the appearance of logarithmic term. It is noted here that the initial number of susceptibles has the largest value in the interval of integration. Therefore, series expansion of the logarithmic term around and integrating the resulting integrands will yield the following first and second order term approximates, given as Eqs. (7a), (7b) in Box I,
Box I.
| (7a) |
| (7b) |
being valid for the magnitudes of order and , respectively. Hence, for those values of (and also from (6)) not departing far from , the formulae in (7a)–(7b) result in higher accuracy.
As clear from (6) or (7a)–(7b), the peak time of epidemic depends on the infection and recovery rates as well as the initial loadings. However, defining the most significant controlling parameter of the epidemic disease, the reproductive number as a result of combining the infection rate and the recovery rate
| (8) |
it is further possible to express the peak time of a disease in the subsequent forms as Eqs. (9a), (9b) in Box II.
Box II.
| (9a) |
| (9b) |
Having known a very small portion of initially ill people at the beginning of a contagious disease, since contribution from the term is negligible, a further refined version of the peak times can be written by virtue of as Eqs. (10a), (10b) in Box III.
Box III.
| (10a) |
| (10b) |
It is worth to mention that since the analytical estimates above for the epidemic peak time are obtained from the exact integral formula from Eq. (6), small errors/uncertainities in the epidemic parameters would result in small errors in the final results.
4. Results and discussion
Before presenting further results, we initially compare the performance of our formulas of peak endemic time in (7a)–(7b) and (9a)–(9b) with those from the approximate formulas recently derived in [18] and [19]. The goal of [18] was to reduce the amplitude of the epidemic peak of COVID-19 by estimating the peak time from an approximant valid for reproduction number less than . For a true comparison, the reader better look at Table 1 on page 5 of [18]. The predictive formulae in [18], [19] are actually given respectively in the forms
The above comparative Table 1 is a clear evidence pointing to the better accuracy of our formulae. Note that the exact values are given by the symbol . For all the magnitudes of the reproduction number shown, moderate and large values of epidemic peak times (as large as 1592) are accurately predicted by the presented relations here in (7a)–(7b). On the other hand, it is apparent that the approximation obtained in [19] making use of the Taylor expansion of the number of recovered individuals is not as accurate as ours; even worse, the approximation of the former can badly diverge for some parameter range listed in the Table 1 (possibly owing to the argument exceeding unity), see the first line with a cross mark. So, the present formulas provide rather more fruitful knowledge than incremental numeric improvements.
Table 1.
Comparison of peak infection times with those obtained from the approximations in [18], [19] denoted by superscripts . Superscripts and 1, 2 refer, respectively, to the numerical integration of system (2a)–(2c) and approximate formulae in (7a)–(7b). The initial fractions of ill/vulnerable people are and .
| 0.3333 | 0.1111 | 2.9999 | 58.3916 | 49.5168 | x | 56.2219 | 57.5961 |
| 0.2222 | 0.1111 | 1.9999 | 108.623 | 92.9849 | 109.852 | 103.616 | 107.265 |
| 0.3333 | 0.1667 | 1.9999 | 72.4152 | 61.9899 | 73.2349 | 69.0776 | 71.5097 |
| 0.1667 | 0.1111 | 1.4999 | 198.465 | 169.956 | 39.5469 | 187.458 | 197.987 |
| 0.3333 | 0.2222 | 1.4999 | 99.2323 | 84.9781 | 19.7735 | 93.7290 | 98.9845 |
| 0.1333 | 0.1111 | 1.1999 | 425.688 | 359.499 | 91.1995 | 396.225 | 422.914 |
| 0.3333 | 0.2778 | 1.1999 | 170.275 | 143.800 | 36.4798 | 158.490 | 169.165 |
| 0.3333 | 0.3222 | 1.0345 | 549.133 | 425.794 | 178.491 | 489.759 | 547.955 |
| 0.1149 | 0.1111 | 1.0345 | 1592.48 | 1234.80 | 517.625 | 1420.30 | 1589.07 |
We should also remark here that Kröger and Schlickeiser [24] constructed accurate analytical approximants of the peak epidemic time as illustrated in their Fig. 5. However, a close look through their analysis proves that the model they consider is the all-time SIR model meaning that the initial data should match the time data, as given on page 4 Section 2.2 in their paper. Based on their approach, the peak time formula presented by Eq. (59) (see page 15 in [24]) in their paper requires the past (), present () and future () knowledge of the illness. Since initially at time , the infected and recovered data must be zero, at time neither the infected not the recovered data can be zero in the all-time model pursued in [24], which puts a severe restriction on the peak time estimate. Their Fig. 5 was in fact generated with a non-zero recovereds at . Because of these facts, they did not compare their formula with the literature, since most of the research in the literature is based on the semi-time SIR model with , which may involve a vanishing recovered initially at time . Our model is also about the semi-time SIR model (even though it accurately estimates the past history in some cases), which results in peak time epidemic formulae successfully reproducing many published data in the literature including the COVID-19 disease, to be evidenced later on. Based on the above arguments, there is no basis to make a direct comparison of the all-time model of [24] with the semi-time model of the present case.
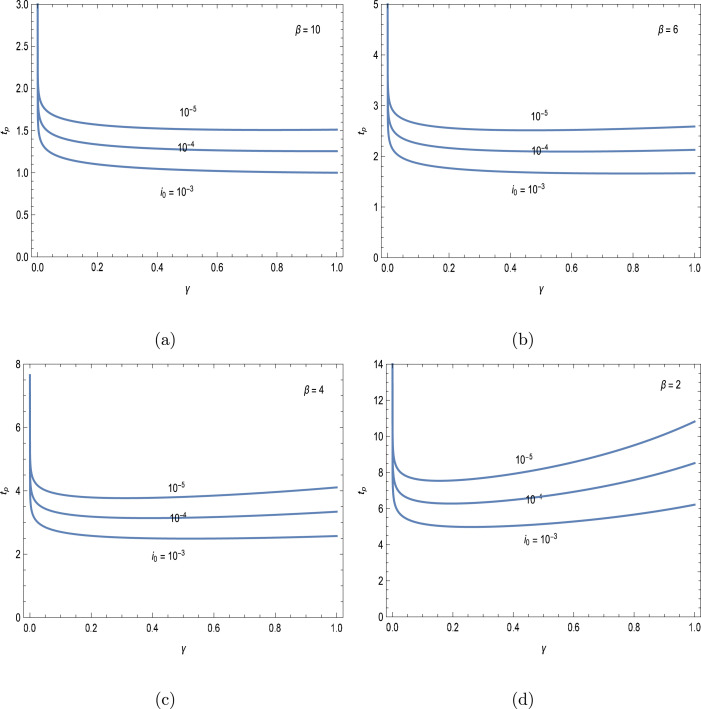
Assuming no initially recovereds, the variation of peak times against recovery rate for some selected epidemic parameters is demonstrated in Figs. 1(a–d). It is clear that the peak time is short enough as the initial fraction of ill is large, otherwise, smaller fractions give rise to larger peak time of epidemic, a well-documented fact in the studied literature. Another striking feature from Figs. 1(a–d) is that increase in the infection rate will absolutely reduce the infection peak time, since the reproduction number is high in this case leading to an intense spread of the disease among the susceptibles. It is not surprising that the peak tends to infinity as limits to zero, since in that case everybody in the community will become ill with a peak susceptible tending to zero, which is possible for infinite times. It is also anticipated from the figures that nearly unaltered peak times are attained for large infectious conditions for the moderate recovery rates. On the other hand, the peak time curve rises up again after falling for smaller values having reached a minimum at a certain . Having determined the local extremum with respect to of the first approximation in (7a), this minimum takes place at the location where the following relation holds
| (11) |
As a result, all the possible scenarios on the epidemic peak time are readily grasped from the formulae presented in (7a)–(7b) for given set of epidemic parameters without having to resort to numerical simulations.
Fig. 1.
Epidemic peak time against the recovery rate for three initial fractions of ill. (a) , (b) , (c) and (c) .
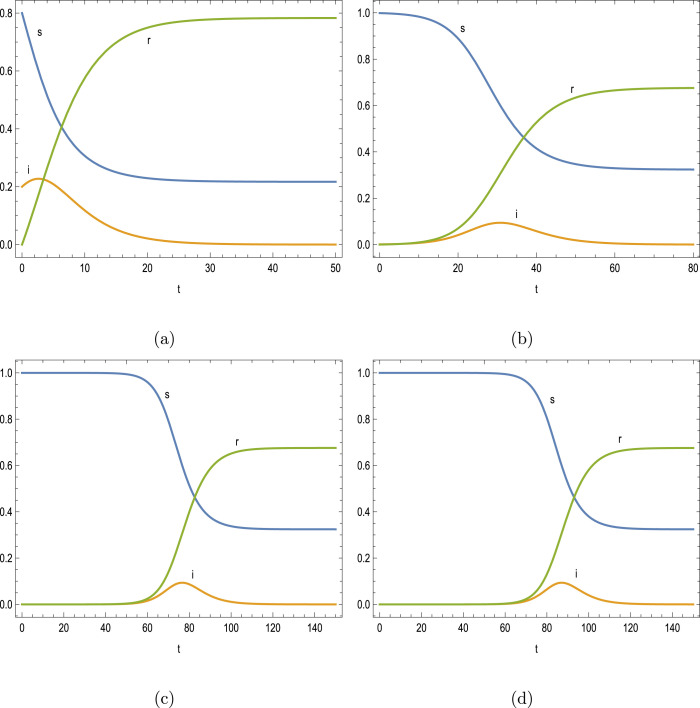
It is now time to test the performance of peak time predictions in (7a)–(7b), (9a)–(9b) for large to small reproduction numbers prescribing the initial values and against full numerical simulations, from which the following Fig. 2, Fig. 3, Fig. 4 were obtained. It should be recalled that outbreak takes place if resulting in a positive peak time, otherwise no spread of illness occurs, but with a potential past history peak at negative time. Figs. 2(a–c) reveal the evolution of epidemic for the parameters and with no initial recovered case. The actual peak thresholds from (4a)–(4c), (6), and the predicted peak times from (7a)–(7b) are summarized in Table 2. It is fascinating to observe that the peak times of epidemic at very large values of reproduction numbers are successfully estimated from our approximates. The short peak times at large reproduction number is fully consistent with the results displayed in Figs. 1(a–d).
Fig. 2.
Time development of infectious disease corresponding to the parameters and . (a) , (b) and (c) .
Fig. 3.
Time development of infectious disease corresponding to the parameters and . (a) , (b) , (c) and (d) .
Fig. 4.
Time development of infectious disease corresponding to the parameters and . (a) , (b) and (c) .
Table 2.
Peak time thresholds for and .
| 0.2 | 8 | 0.1 | 0.6921 | 0.2079 | 0.4078 | 0.3868 | 0.3960 |
| 9.999 | 0.1 | 0.6697 | 0.2303 | 1.5442 | 1.5116 | 1.5264 | |
| 10 | 0.1 | 0.6697 | 0.2303 | 2.3023 | 2.2792 | 2.2939 |
The scenario of contagious outbreak is exhibited next in Figs. 3(a–d) for the parameters and . The relevant epidemic parameters can also be inferred from Table 3 for the associated thresholds. Small to larger peak times corresponding to the small reproduction number are also successfully captured by the presented formulas in (7a)–(7b).
Table 3.
Peak time thresholds for and .
| 0.2 | 1.333 | 0.6 | 0.2274 | 0.1726 | 2.6371 | 2.5541 | 2.6259 |
| 1.665 | 0.6 | 0.0941 | 0.3059 | 30.776 | 27.936 | 30.147 | |
| 1.667 | 0.6 | 0.0935 | 0.3065 | 76.620 | 73.982 | 76.294 | |
| 1.667 | 0.6 | 0.0935 | 0.3065 | 87.038 | 85.495 | 87.807 |
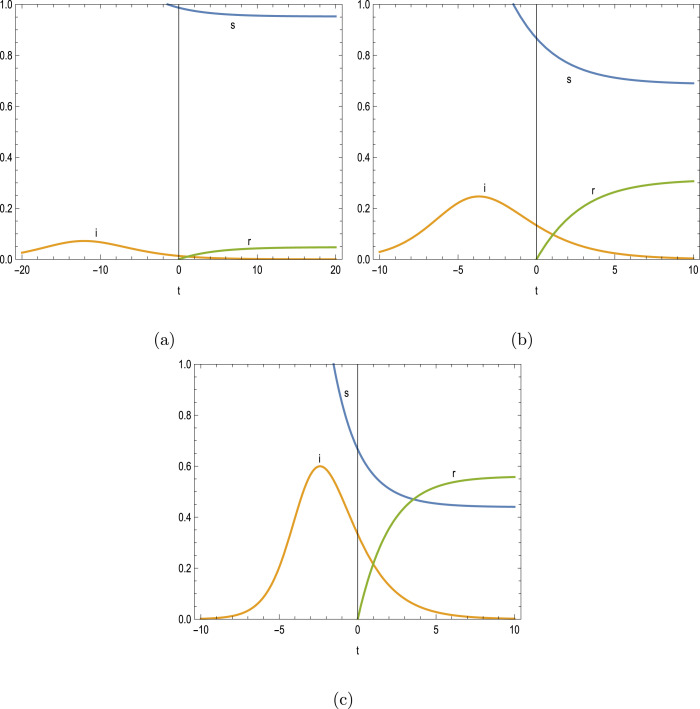
When the epidemic cannot start off with , the disease is dying out in time, but the peak has already occurred in the past time, as physically realized from Figs. 4(a–c), corresponding to parameters and , for instance. A summary of critical parameters is also listed in Table 4. Even in this circumstance, the derived formulae in (7a)–(7b) are able to correctly predict the past peak time of disease. Knowing time is also significant to understand the stage at which the epidemic situation prolongs and how far it is from the peak.
Table 4.
Peak time thresholds for and .
| 0.013 | 0.7331 | 0.0720 | −12.070 | −10.038 | −12.614 |
| 0.133 | 0.6439 | 0.2465 | −3.672 | −3.173 | −3.859 |
| 0.333 | 0.4953 | 0.5997 | −2.397 | −2.042 | −2.689 |
In Table 5, we provide further comparisons of actual peak disease times versus approximate ones for various epidemiological problems studied in the open literature by the researchers. The good fit of approximates for the peak times given in the present study is once more witnessed from these quantitative results for a range of reproduction numbers. A particular attention should be paid to those peak times predicted excellently by the present approach connected with the traditional high school influenza example given in almost every epidemiology textbooks, see for instance [8], [11] and [1] (with 763 school boys, 3 of them are initially infected) and the Hong Kong flu with open simulator in [27] (with 7.9 million people of New York, 10 of them are initially contracted).
Table 5.
Comparison of peak infection times from the models studied in some open literature as stated.
| Reference | ||||||||
|---|---|---|---|---|---|---|---|---|
| [10] | 0.45 | 0.02 | 0.3333 | 0.4444 | 10 | 9.514 | 9.197 | 9.325 |
| [8] | 1.66 | 0.4545 | 0.0039 | 0.9948 | 3.633 | 5.503 | 5.142 | 5.355 |
| [14] | 0.9178 | 0.7068 | 0.9999 | 1.298 | 55.620 | 52.585 | 55.231 | |
| [9] | 4.6291 | 2.82 | 0.0268 | 0.9732 | 1.597 | 1.428 | 1.256 | 1.390 |
| [27] | 0.5 | 0.30 | 0.9999 | 1.666 | 64.230 | 61.274 | 63.586 | |
| [12] | 10 | 1 | 0.05 | 0.95 | 9.5 | 0.5886 | 0.5597 | 0.5723 |
| [16] | 2 | 1 | 0.9999 | 2 | 11.376 | 10.820 | 11.225 |
We eventually display in Table 6 the peak times of COVID-19 pandemic disease in the capital cities of some countries mentioned. It is recalled that the fitting parameters are taken from the website [28]. It can be mathematically justified that since the factor is too small in the infection case of Korea, the exact integral in (6) results in an excellent match with the approximates in (7a)–(7b). Other peak times are also well-recovered at desired sensitivity.
Table 6.
Comparison of peak infection times of COVID-19 in some capitals. The initial fractions of ill/vulnerable people are and .
| Japan | 0.1391 | 0.0184 | 7.565 | 91.124 | 88.361 | 89.695 |
| Korea | 0.1947 | 132.033 | 132.033 | 132.033 | ||
| Italy | 0.2569 | 0.0141 | 18.160 | 49.141 | 48.223 | 48.577 |
| Iran | 0.5961 | 0.0802 | 7.429 | 21.274 | 20.623 | 20.939 |
5. Conclusions
Evaluation of peak time of an infection from the epidemiological mathematical SIR model is considered within the current investigation. The goal is, rather to determine explicit analytical formula for the epidemic peak time, in the absence of which it has to be computed from the full numerical simulations, as has been implemented by the researchers so far. Many important conclusions can be drawn from such a formula during a real time epidemic disease via playing with the characteristic parameters of a running epidemic, otherwise heavy computations from numerical simulations are required. Particularly, if the calculation of peak time is required as a subroutine in an iterative procedure to estimate parameters, it will be called several times, and its numerical evaluation can become rather expensive. Thus, and analytic replacement as given here can enable more efficient calculations.
To achieve the target, the peak time of an outbreak is initially formulated in terms of an integral from the system of equations of SIR model. Since an anti-derivative of the pertinent integrand is not possible to directly evaluate, a series expansion around the initial susceptible fraction is fulfilled yielding first-order and second-order approximate analytical expressions for the peak time representations of an epidemic disease given the epidemic parameters. The peak time of a disease is straightforwardly accessible when the initial fractions of susceptibles, and infection/recovery rates are prescribed. The well-known characteristic features of peak time of an epidemic disease studied so far from the SIR model are now transparent from the presented explicit formulae. Accuracy of the obtained expressions is initially tested against the recently given formulas in [18] and [19]. Not only the peak time of an epidemic disease is well-predicted from the presented formulae, but also the peak time from the past history of the disease is well-captured for the peak time of an endemic disease. A series of epidemic disease problems from the available models in the open literature are predicted with good accuracy from the given formulas. In particular, the COVID-19 peak times under given local epidemic parameters of countries like, Japan, Korea, Italy and Iran are accurately estimated, which had to be numerically simulated otherwise in the previously published papers.
Since many epidemiological models are only differentiations of the basic SIR model, the present approach may also be adopted in other class of models that predict the spread of diseases in order to capture the peak time of an epidemic disease, which warrants further investigation. Hence, new formulas can be obtained incorporating the effects of incubation period, growth/decay/homogeneity of population, recovered individuals again in the susceptible category, etc.
Declaration of Competing Interest
The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Communicated by V.M. Perez-Garcia
References
- 1.Murray J.D. Springer-Verlag; 2002. Mathematical Biology I, An Introduction; pp. 325–326. [Google Scholar]
- 2.Kermack W.O., McKendrick A.G. Proc. R. Soc. A. 1927;115:700. [Google Scholar]
- 3.Brauer F., Castillo-Chavez C. Springer-Verlag; 2001. Mathematical Models in Population Biology and Epidemiology; pp. 273–332. [Google Scholar]
- 4.Batiha A.-M., Batiha B. Aust. J. Basic Appl. Sci. 2011;5:3122. [Google Scholar]
- 5.Rafei M., Daniali H., Ganji D.D. Appl. Math. Comput. 2007;186:1701. [Google Scholar]
- 6.Biazar J. Appl. Math. Comput. 2006;173:1101. [Google Scholar]
- 7.Feng Z. Math. Biosci. Eng. 2007;4:675. doi: 10.3934/mbe.2007.4.675. [DOI] [PubMed] [Google Scholar]
- 8.T.M. Balkew, (Electronic theses and dissertations), East Tennessee State University, 2010.
- 9.http://www.math.unm.edusulskymathcampApplyData.
- 10.Harko T., Lobo F.S.N., Mak M.K. Appl. Math. Comput. 2014;236:184. [Google Scholar]
- 11.Rodrigues H.S. Int. J. Appl. Math. Inf. 2016;10:92. [Google Scholar]
- 12.Miller J.C. Inf. Dis. Model. 2017;2:35. doi: 10.1016/j.idm.2016.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bohner M., Streipert S., Torres D.F.M. Nonlinear Anal. Hybrid Syst. 2019;32:228. [Google Scholar]
- 14.Cano C. Louisiana Tech University; 2020. Louisiana Tech Digital Commons. [Google Scholar]
- 15.10.1101/2020.04.30.20086751. [DOI]
- 16.Simon C.M. PeerJ. Phys. Chem. 2020;2 [Google Scholar]
- 17.Ciufolini I., Paolozzi A. Eur. Phys. J. Plus. 2020;135:355. doi: 10.1140/epjp/s13360-020-00383-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cadoni M. Chaos Solitons Fractals. 2020;138 doi: 10.1016/j.chaos.2020.109940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cadoni M., Gaeta G. Physica D. 2020;411 doi: 10.1016/j.physd.2020.132626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Barlow N.S., Weinstein S.J. Physica D. 2020;408 doi: 10.1016/j.physd.2020.132540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Weinstein S.J., Holland M.S., Rogers K.E., Barlow N.S. Physica D. 2020;411 doi: 10.1016/j.physd.2020.132633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kuniya T. J. Clin. Med. 2020;9:789. doi: 10.3390/jcm9030789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Castro M., Ares S., Cuesta J.A., Manrubia S. Proc. Natl. Acad. Sci. USA. 2020;117 doi: 10.1073/pnas.2007868117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kroger M., Schlickeiser R. J. Phys. A. 2021;53 [Google Scholar]
- 25.Hajji M.E., Sayari S., Zaghdani A. J. Korean Math. Soc. 2021;58:45. [Google Scholar]
- 26.Hethcote H.W. SIAM Rev. 2000;42:599. [Google Scholar]
- 27.https://www.math.duke.edu/education/ccp/materials/diffcalc/sir/index.html.
- 28.https://www.lewuathe.com/covid-19-dynamics-with-sir-model.html.