Adhesion strength and contractility enable metastatic cells to become adurotactic

SUMMARY

Significant changes in cell stiffness, contractility, and adhesion, i.e., mechanotype, are observed during a variety of biological processes. Whether cell mechanics merely change as a side effect of or driver for biological processes is still unclear. Here, we sort genotypically similar metastatic cancer cells into strongly adherent (SA) versus weakly adherent (WA) phenotypes to study how contractility and adhesion differences alter the ability of cells to sense and respond to gradients in material stiffness. We observe that SA cells migrate up a stiffness gradient, or durotax, while WA cells largely ignore the gradient, i.e., adurotax. Biophysical modeling and experimental validation suggest that differences in cell migration and durotaxis between weakly and strongly adherent cells are driven by differences in intra-cellular actomyosin activity. These results provide a direct relationship between cell phenotype and durotaxis and suggest how, unlike other senescent cells, metastatic cancer cells navigate against stiffness gradients.

INTRODUCTION

Durotaxis is a form of directional cell migration in which cells respond to and move toward extracellular regions of increasing stiffness (DuChez et al., 2019; Lo et al., 2000). Durotactic migration has been observed in a large number of migratory cells of mesenchymal lineage and is almost universally reported to occur in both 2D and 3D environments in the direction of increasing stiffness (DuChez et al., 2019; Joaquin et al., 2016; Novikova et al., 2017), with some speculation that it may occur in reverse (Isomursu et al., 2020; Singh et al., 2014). While multi-que migrational responses may occur in vivo (Lara Rodriguez and Schneider, 2013), as the majority of tumors progress, their microenvironment gradually becomes stiffer than the surrounding stroma (Lachowski et al., 2017; McKenzie et al., 2018). This suggests that the ability to move against stiffness gradients seems to be highly relevant at least in some cancers. Therefore, a breakdown in the normal processes regulating durotaxis may contribute to cancer cells developing different sensitivities to stiffness gradients leading to an increase in metastatic potential.

Several mechanisms have been proposed for the molecular basis of durotaxis (Sawada et al., 2006; Sunyer et al., 2016), but how and when these molecular interactions are transduced into a directed force along or against a stiffness gradient is unclear. Computational and mathematical models have bridged gaps in our understanding of how cell mechanics and the microenvironment affect the speed, persistence (Danuser et al., 2013; Holmes and Edelstein-Keshet, 2012; Kim et al., 2018; Mak et al., 2017; Schlüter et al., 2012; Yeoman and Katira, 2018), and emergent behaviors such as durotaxis (Feng et al., 2019; Mak et al., 2015; Novikova et al., 2017; Stefanoni et al., 2011). However, a number of these models make additional a priori assumptions about how intra-cellular processes are differentially affected by stiffness in order to show durotactic behavior (Shatkin et al., 2020). Additionally, co-occurrence of durotaxis, adurotaxis, or anti-durotaxis in similar cell populations, as might occur in metastatic tumors, is difficult to explain by current models.

We hypothesize that mechanotypic heterogeneity across and within cell populations might be responsible for differential durotactic behavior in these populations. In recent work, we found that adhesion strength acted as a physical marker that sorted isogenic cells into weakly and strongly adhesive cell groups that were more versus less contractile and migratory (Beri et al., 2020), respectively. RNA sequencing further showed transcriptional differences characteristic of distinct mechanotypes that sorted patient outcomes in The Cancer Genome Atlas (TCGA); patients with the weakly adhesive gene signatures relapsed at a rate 2-fold higher than the strongly adhesive gene signatures. Such differences could contribute to durotactic differences not previously observed, and here we show that mechanotypic differences are the proximate driver for differential rigidity sensing and adurotactic behavior.

RESULTS

Adhesion dynamics define an adurotactic phenotype

Here, we report that weakly adherent populations of various types of cancers cells are significantly less durotactic than their strongly adherent counterparts, potentially explaining how tumor cells migrate down stiffness gradients. Using the parallel plate flow chamber (PPFC) (Beri et al., 2020), cells are isolated based on adhesion strength and seeded onto photopatterned hydrogels with alternating soft and stiff elasticity profiles that match Young’s moduli of softer stromal and stiffer tumor extracellular matrix (ECM) for each type of cancer (Figures 1A and 1B), i.e., 0.3 and 1.5 kPa for mammary (Cox and Erler, 2011; Paszek et al., 2005), 4 and 20 kPa for lung (Burgstaller et al., 2017; Pankova et al., 2019; White, 2015), and 10 and 30 kPa for prostate (Ahn et al., 2010; Krupski et al., 2010; Zhai et al., 2010). When cells were plated on these gradients and observed by time-lapse video microscopy (Videos S1, S2, and S3), we found that strongly adherent (SA) cells on average migrate significantly slower than their weakly adherent (WA) counterparts for mammary, lung, and prostate cancer cell lines (Figure 1C; Figure S1A) on stiff substrates, and slightly slower on softer substrates. Although slower, SA cells for each cell type were more likely to durotax and less likely to undergo adurotaxis than WA subpopulations(Figure 1D; Figure S1B); quantitatively, the durotactic odds ratio is calculated as the ratio of the odds that a SA cell is durotactic to the odds that a WA cells is durotactic. We found that this ratio was between 1.75 and 3 for durotaxis. Conversely for adurotaxis, that ratio was between 0.66 and 0.33 across all cell lines, which indicates that SA cells durotax and WA cells adurotax. Consistent with phenotype differences, we observe accumulation only of the SA cells over 24 h in culture on patterned substrates as SA cells moved from a random distribution to one biased toward stiffer regions (Figure 1E; Figure S1C; Video S4). These behaviors again are largely conserved across cell lines from multiple tumor types, albeit with varying degrees of effect such that accumulation is most robust for a mammary cell line. While the effects are the same, variability may be due in part to inherent mechanotype differences. For example, cells sort into WA and SA subpopulations at different shear stress in the PPFC; lung tumor cells are less adherent overall with the SA fraction sorting at >180 dynes/cm², while prostate and mammary lines require >500 dynes/cm² to sort their SA fraction.

Figure 1. Weakly adherent cells exhibit higher adurotactic behavior.

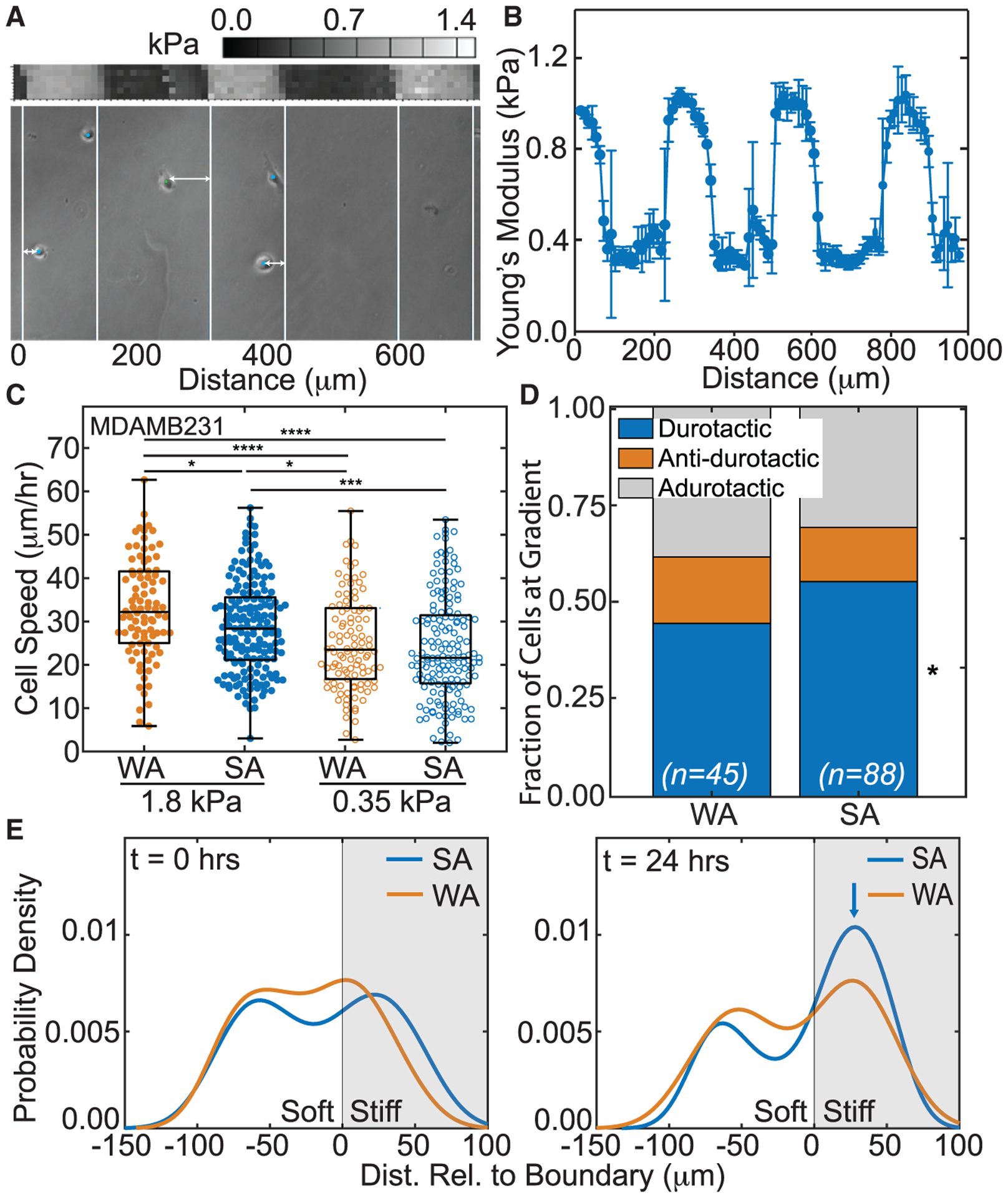
(A) Bright-field image of cells (dots) with lines to indicate transitions between soft and stiff substrate regions of step-gradient hydrogels (bottom). Double-headed arrows indicate the distance relative to the closest gradient or boundary. Atomic force microscopy (AFM) map is also shown (center) with corresponding color map (top). Position is indicated in micrometers.

(B) Plot of average substrate stiffness versus position for step-gradient hydrogels (n > 3). Error bars represent standard deviation.

(C) MDA-MB-231 cell speed on soft or stiff side of step-gradient hydrogels is plotted. Data are shown for cells sorted by adhesion strength, i.e., weakly (orange) versus strongly (blue), and cells on softer (open) versus stiffer (closed) regions. (n > 144 cells for each condition from triplicate experiments). *p < 0.05, ***p < 10⁻³, ****p < 10⁻⁴ were determined by one-way ANOVA with Tukey test for multiple comparisons for the indicated comparisons.

(D) For adhesion-sorted MDA-MB-231 cells that encounter the step gradient, the fraction of durotactic, anti-durotactic, and adurotactic behavior is plotted. Data represent n = 45 of 144 WA cells and 88 of 237 cells that crossed the gradient over triplicate experiments. Comparisons made using a Fisher’s exact test for the same migration behavior between WA and SA cells, *p < 0.05.

(E) At 0 and 24 h, probability density function of MDA-MB-231 cell distribution (calculated using the unbounded kernel density function) versus hydrogel position is shown for weakly (orange) versus strongly (blue) adherent cells from triplicate experiments. The stiffer region is shaded in gray. Blue arrow indicates a peak in the strongly adherent cell distribution at 24 h.

To understand what gives rise to mechanotype, we first measured traction forces across adhesion-sorted cell lines. We found that weakly adherent tumor cells exhibit higher traction forces—measured for prostate cell lines on both single modulus soft and stiff substrates (Figure S2A) and for mammary cell lines on single modulus stiff substrates mimicking their fibrotic niche (Figure 2A); the lung cell lines were generally less adherent, and thus we did not observe significant traction differences (Figure S2A). This general trend, however, may appear counterintuitive: first, that weakly adherent cells generate stronger forces, and second, that cells generating stronger forces show decreased durotaxis and increased adurotaxis. We note that, as WA cells approached the gradient from either side, their velocities are dependent on distance to the boundary irrespective of the side they are approaching from, while SA cell speed generally increases moving from softer to stiffer substrates (Figure S2B). This suggests possible traction force redistribution along the cell length for the WA cells as they move across the stiffness gradient. We also noted that focal adhesion sizes were stiffness dependent for SA cells, while focal adhesion sizes for WA were the similar on either stiffness (Figures S3A and S3B). These observations suggest that adurotaxis could arise from a lack of change in balance between adhesion dynamics, redistribution of traction forces across the stiffness gradient, or both. Conversely, what does not appear to regulate durotaxis are differences in cytokine expression; blotting of 105 cytokines showed only 4 that were expressed above background and none were differentially expressed (Figure S3C).

Figure 2. Higher forces on catch bonds leads to adurotactic behavior.

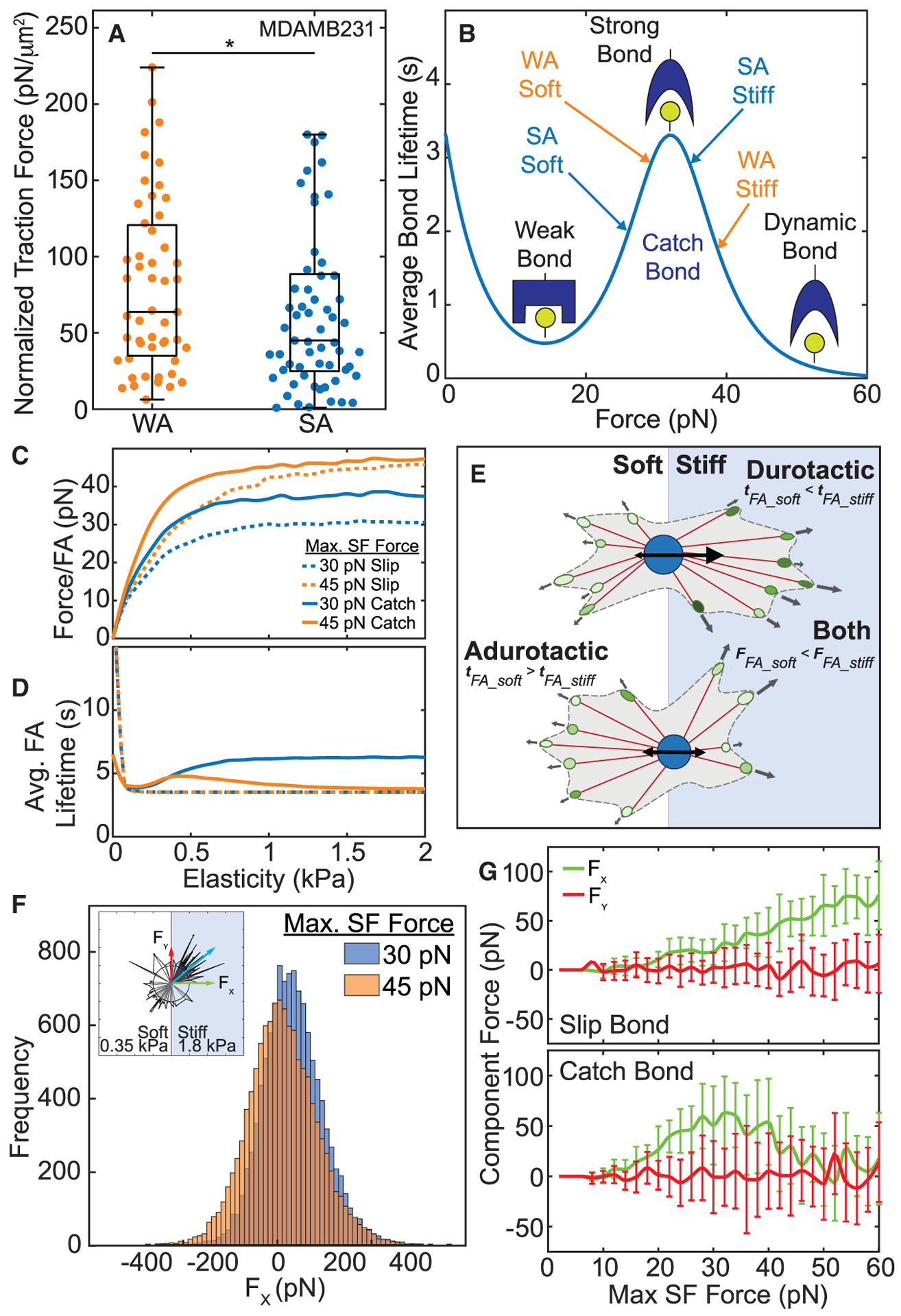
(A) Traction force, normalized to cell area, is plotted for MDA-MB-231 cells on single-modulus hydrogels. Data are shown for weakly (orange) versus strongly (blue) adherent cells, (n > 50). *p < 0.05 was determined by one-way ANOVA with Tukey test for multiple comparisons.

(B) Schematic of bond lifetime versus force with bond states for weakly (orange) versus strongly (blue) adherent cells as used in the computational model.

(C) Force/FA versus substrate elasticity for catch (solid lines) and slip bonds (dashed lines) comparing 30 pN max SF force (blue) and 45 pN max SF force (orange), predicted by computational model.

(D) Average FA lifetime plotted versus substrate elasticity for the same simulations.

(E) Schematic of cells migrating over a step gradient. For durotactic cells, higher tractions and longer bond lifetimes on the stiff side drive adhesion maturation and net migration toward the stiffer substrate. For adurotactic cells, tractions balance across the boundary due to longer bond lifetimes on the soft side of the step gradient.

(F) Histogram of all X component forces simulated over 1 h for a cell fixed at a step gradient, comparing 30 pN max SF force (blue) and 45 pN max SF force (orange). Inset shows model cell with protruding stress fibers and X component force (green arrow), Y component force (red arrow), and resultant force (blue arrow).

(G) X and Y component forces versus max SF force for slip bonds (top) and catch bonds (bottom) from the computational model. Colors match the arrows in inset for Figure 2E. Error bars represent standard deviation.

To test the above suggestions, we employed a focal adhesion maturation and traction force generation model dependent on catch bond dynamics between cell-adhesion proteins and the substrate (Figure 2B). In this model, polymerizing actin fibers bind to substrate bound adhesion proteins, mature into actin-myosin stress fibers (SFs) and focal adhesions (FAs), and generate traction forces between the cell and the substrate. The focal adhesions grow/shrink via addition/dissociation of individual integrin-substrate bonds and SF recruitment in a force-dependent manner. Stress fibers are limited by the maximum force that each one can generate, i.e., max SF force, and ideally corresponds to the myosin stall force of collectively contracting heads against the actin stress fiber; max SF force is reached exponentially as the stress fiber pulls against the substrate (Schwarz et al., 2006). The substrate stiffness in this model controls the rate of force increase in the stress fibers (Equation 5), which in turn alters the force generated in each stress fiber dependent on the associated integrin-substrate adhesion lifetime. The forces driving cell migration are obtained by vectorially summing forces in all the FA bound SFs within the cell at any given instant. Using this model, we compared the effect of integrin catch and slip bonds dynamics (Fusco et al., 2017) on the force per adhesion and on focal adhesion lifetimes as a function of substrate stiffness for cells with different max SF force (assigned from prior observations of SF force [Schwarz et al., 2006]). As a function of substrate stiffness, both catch and slip bonds show increased force per focal adhesion, with catch bonds generating and sustaining higher forces due to bond strengthening and recruitment of secondary stress fibers (Figure 2C). For focal adhesion lifetimes, lifetimes with slip bond dynamics remained constant across relevant substrate stiffness. For catch bonds, however, lower max SF forces saturated focal adhesion lifetimes at higher values whereas higher max SF forces exhibit a small peak near normal mammary stiffness and then drop to saturate at a lower value at higher stiffnesses (Figure 2D). These data suggest that max SF force and stiffness-dependent values for FA lifetimes optimize cell-migration forces for a given mechanotype. To test the predicted changes in adhesion lifetimes based on substrate stiffness, we applied a range of shear stress to cells cultured on substrates resembling normal and pathological mammary stiffness using a population-based adhesion assay (Boettiger, 2007). We found that cells selected on glass as weakly but not strongly adherent could modulate their average adhesion strength and become more adherent in softer conditions (Figure S3D). These results align with model predictions based on catch-bond dynamics between the cell-adhesion receptors and the substrate (solid lines in Figure 2D). Since average FA lifetime is more substrate stiffness sensitive for weakly adherent cells and identical to strongly adherent cells on softer substrates, these data suggest that weakly adherent cells are less adherent and primed to migrate on stiffer substrates with lower FA lifetimes. These correlations will next be explored in a cell-based model to understand mechanotype mechanisms.

Actomyosin contractility defines adhesion phenotype and explains migration behavior

In this model framework (Figures S4A and S4B), we compared a range of max SF forces, finding that 30 pN indeed corresponds to peak bond lifetime at high substrate stiffness but that at higher max SF force, softer substrates experience longer bond lifetimes. We also found monotonically increasing force per adhesion for catch bonds, consistent with higher traction forces seen experimentally in WA cells (Figure 2A). Bond lifetimes were insensitive to stiffness for slip bonds, while force per adhesion increased monotonically as with catch bonds (Figure S4C). The relationship between average bond lifetime and substrate elasticity suggests that by increasing max SF force, a scenario could arise in which a cell’s catch bonds are more stable adhesions on a softer substrate (Figure 2E). Stress fibers attached to those adhesion sites would have more time to pull a WA cell in the direction of the softer substrate, balancing numerous shorter-lived forces in focal adhesions on the stiffer region. To illustrate this, we fixed a cell at the step gradient interface and measured force generated parallel (F_x) and perpendicular (F_y) to the gradient. On average, cells with 30 pN max SF force had a positive F_x, indicating that the overall force on the cell is pulling it toward the stiffer substrate, whereas cells with 45 pN max SF force had neutral F_x, suggesting the cell would behave adurotactically (Figure 2F). This scenario requires cell-surface adhesions to behave as catch bonds, which appears reasonable (Kong et al., 2009; Morikis et al., 2017; Zhu and Chen, 2013). We would also note that when slip bond dynamics are used, it results in cells with higher max SF force to durotax (Figure 2G), which would be at odds with experimental results where WA cells are more contractile but less durotactic than SA cells.

The main input required for this model is the max SF force of the WA and SA mammary cells, but with this difference cell-migration speeds and traction forces match experimental observations with the small exception of migration speeds of SA cells on soft substrates, which go up slightly according to the model (Figures 3A and 3B; Videos S5 and S6). While a fine tuning of other model parameters can fix the disparity, we focus only on the effect of max SF force here and maintain other parameter values at those commonly found in literature. Additionally, just this difference in max SF force enables the model to correctly predict durotactic differences (Figure 3C) and the accumulation of SA cells on stiffer substrates versus uniform distribution of WA cells across the gradient over 24 h for mammary cells (Figure 3D; Video S7). Importantly, when substrate stiffness is altered to resemble the prostate cancer stiffness gradient (Ahn et al., 2010; Krupski et al., 2010; Zhai et al., 2010), mammary cell parameters (Table S1) cause SA cells to not durotax (Figure S4D). However, when substrate stiffness range is maintained, i.e., 0.35 to 1.8 kPa, but the gradient made more shallow, we do not observe changes in cell accumulation on the stiff region of the substrate for SA cells; i.e., they continue to durotax; for WA cells under the same conditions, they still fail to accumulate (Figure S4E). Thus, it would appear that durotactic and adurotactic behaviors may not be very sensitive to gradient magnitude but rather the mere presence of a gradient.

Figure 3. Differential bond stiffness affect tractions to induce adurotaxis.

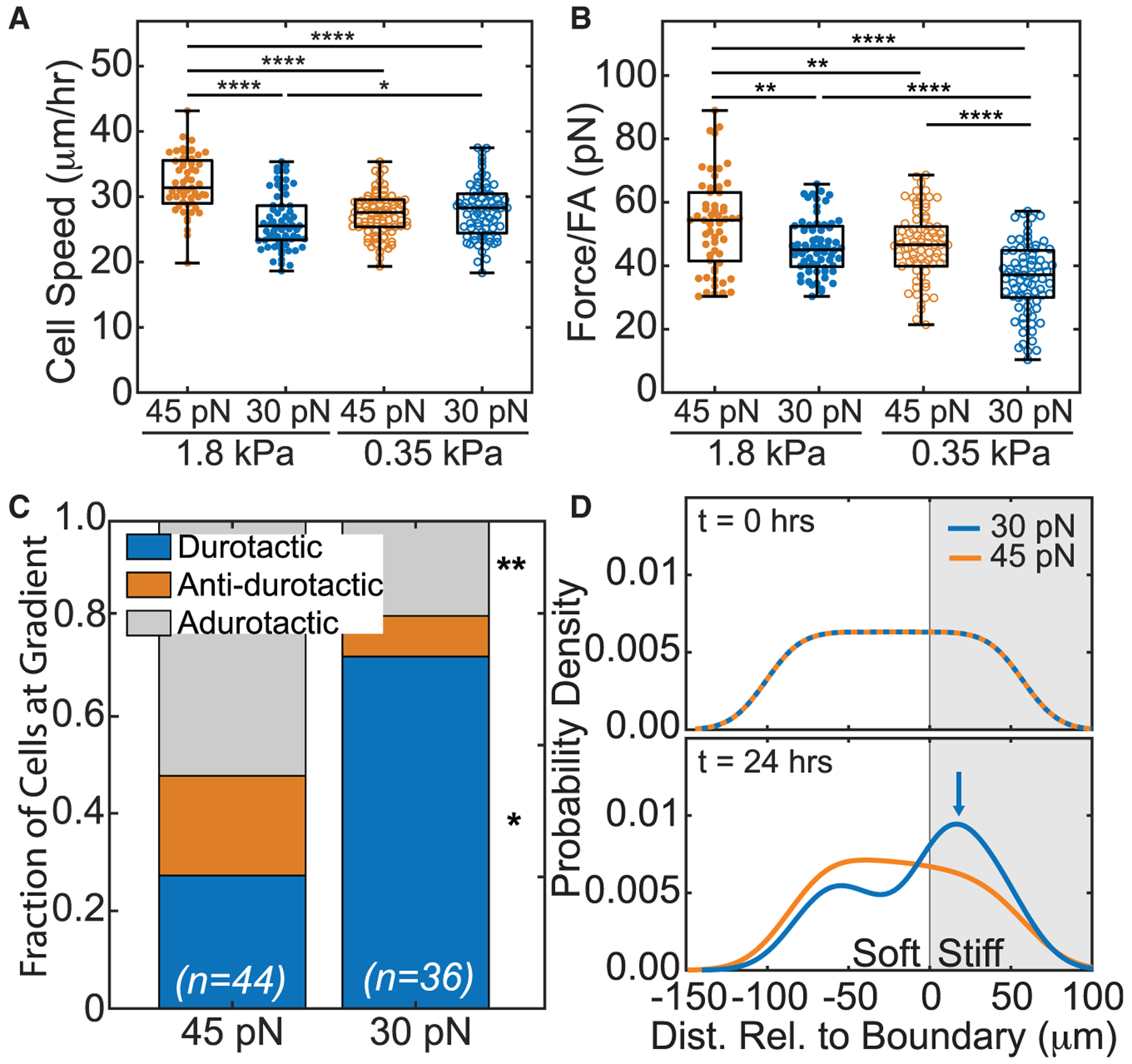
(A) Model cell speed on simulated on soft or stiff side of step gradient is plotted. Data are shown for cells of differing max SF force, i.e., 45 pN (orange) versus 30 pN (blue), and cells on softer (open) versus stiffer (closed) regions. (n = 100 cells for each simulation).

(B) Average traction force per focal adhesion, as determined from the computational model, is plotted for 45 pN (orange) and 30 pN (blue) max SF force (n = 100 cells for each condition). *p < 0.05, **p < 10⁻², ***p < 10⁻³, ****p < 10⁻⁴ were determined by one-way ANOVA with Tukey test for multiple comparisons for the indicated comparisons in (A) and (B).

(C) For model cells that encounter the step gradient, the fraction of durotactic, anti-durotactic, and adurotactic behavior is plotted. Data represent n = 44 of 100 and 36 of 100 cells simulated at 45 and 30 pN, respectively; those not counted did not interact with the gradient. Comparisons made using a Fisher’s exact test for the same migration behavior between 30 and 45 pN conditions, *p < 0.05 and **p < 0.01.

(D) At 0 and 24 h, the model probability density function (PDF) of cell distribution versus simulated hydrogel position is shown for cells with 45 pN (orange) versus 30 pN (blue) max SF force. The stiffer region is shaded in gray. Blue arrow indicates a peak in the 30 pN cell distribution at 24 h. *p < 0.05, **p < 10⁻², ****p < 10⁻⁴ were determined by paired Student’s t test for the indicated comparisons unless otherwise stated.

Adurotactic phenotype is titratable by myosin activity

The dependence of durotaxis on a change max SF forces implies that the number of active myosin motors per SF filament could affect behavior; prior work suggests that such differences could impart control over cell migration and stiffness (Koenderink et al., 2009). To validate such control in our system, we reduced the number of active myosin motors within a cell, i.e., SF force, finding that it increases the durotactic tendency of cells as predicted by the model between 30 and 45 pN (Figure 4A). Furthermore, we tested this experimentally by inhibiting the myosin II activity of WA mammary cells with blebbistatin. Cell speed decreased for blebbistatin treated cells on soft and stiff substrates (Figure 4B), resulting in similar velocities as untreated SA cells. Furthermore, treated cells are 2-fold more likely to migrate from the soft substrate into the stiff substrate and much less likely to exhibit antidurotactic migration (Figure 4C). WA mammary cells also showed a dose-dependent response to blebbistatin treatment, wherein the WA phenotype became more durotactic, resembling the durotactic behavior of SA cells (Figure 4D). Conversely, SA mammary cells also showed a dose-dependent response to lysophosphatidic acid treatment, wherein the SA phenotype became less durotactic, resembling the adurotactic behavior of WA cells (Figure 4E). These data confirm the suggestion that max SF force, as produced by the number of active myosin motors per SF filament, enables WA cells to exhibit less durotaxis and is a mechanical argument for why WA cells metastasize.

Figure 4. Tuning contractility modulates adurotaxis in adhesion-sorted cells.

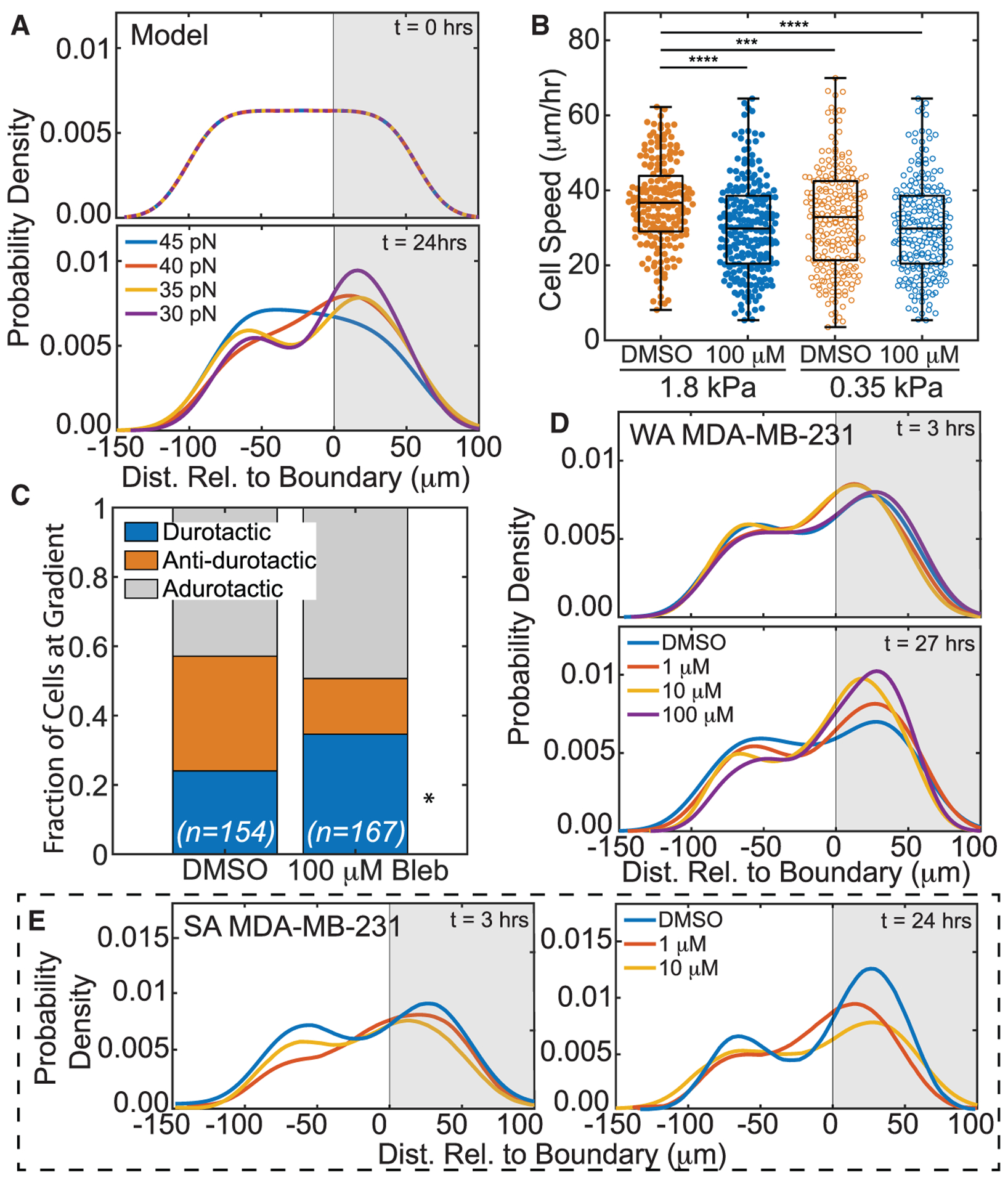
(A) Model PDF of cell distribution versus simulated hydrogel position as predicted for 30 (purple), 35 (yellow), 40 (red), and 45 pN (blue) max SF forces at t = 0 and t = 24 h. Durotactic tendency increased with decreasing max SF force.

(B) Weakly adherent MDA-MB-231 cell speed on soft or stiff side of step-gradient hydrogels for cells is plotted. Data are shown for blebbistatin-treated and nontreated cells, i.e., DMSO (orange) versus 100 μM (blue), and cells on softer (open) versus stiffer (closed) regions. (n > 245 cells for each condition from triplicate experiments). ***p < 10⁻³, ****p < 10⁻⁴ were determined by one-way ANOVA with Tukey test for multiple comparisons for the indicated comparisons.

(C) For treated and nontreated weakly adherent MDA-MB-231 cells that encounter the step gradient, the fraction of durotactic, anti-durotactic, and adurotactic behavior is plotted. Data represent n = 154 of 256 DMSO-treated and 167 of 245 blebbistatin-treated cells over triplicate experiments; those not counted did not interact with the gradient. Comparisons were made using a Fisher’s exact test for the same migration behavior between treated and DMSO, *p < 0.05.

(D) Weakly adherent MDA-MB-231 PDF of cell distribution was plotted versus hydrogel position for blebbistatin treatment of 100 μM (purple), 10 μM (yellow), 1 μM (red), or DMSO (blue) at t = 3 and t = 27 h.

(E) Strongly adherent MDA-MB-231 PDF of cell distribution was plotted versus hydrogel position for LPA treatment of 10 μM (yellow), 1 μM (red), or DMSO (blue) at t = 3 and t = 24 h.

DISCUSSION

The findings of this work help explain how a metastatic cell’s distinct mechanotype correlates to the paradoxical migration down a stiffness gradient that occurs during cancer metastasis. Cancer cells isolated by their adhesion strength from a seemingly isogenic population exhibit consistent behavior across different cell lines from vastly different cancer types; moreover, each cancer type exhibits adurotaxis in their tumor-specific niche, which change dramatically for step gradient strength (between 3- and 5-fold) and gradient range (from 0.3 to 30 kPa). Despite these differences, greater contractility in weakly adherent cells is conserved and led to decreased durotactic behavior that is not directly governed by lack of rigidity sensing, as evidenced by slow down at the gradient boundary. From previous work, RNA sequencing shows a distinct underlying phenotype for weakly versus strongly adherent cells with differences in cytoskeletal protein expression, which relates to decreased progression-free and disease-free intervals when compared to the gene expression signatures of human patients (Beri et al., 2020). A weakly adherent cell’s ability to migrate against stiffness gradients connects this observation to the material properties of the niche, which contribute to its increased metastatic potential.

Computational modeling suggests that mechanotype differences in weakly and strongly adherent cells arises from increased contractility. Furthermore, it demonstrates that catch bonds are a necessary component for the diverging migratory behaviors seen in metastatic cells. Interestingly, catch-bond dynamics have been largely left out of most cell-migration and FA dynamics models until recently (Tan et al., 2020). Additionally, the model is able to simulate cells that exhibit both durotaxis and adurotaxis without relying on any a priori assumptions about how rigidity sensing mechanisms are uniquely dependent on substrate stiffness (Novikova et al., 2017). Actomyosin activity within in single stress fiber largely determines the stress a single bond experiences (Koenderink et al., 2009), with substrate stiffness affecting maximum force loading rate. The biphasic nature of catch bond lifetime allows cancer cells to become more migratory and less durotactic with increased contractility, which likely contributes to the greater metastatic potential as well as sets population stability as observed experimentally (Beri et al., 2020). That being said, while our data suggest a cytoskeletally driven mechanism, it does not rule out confounding issues from adhesion location, composition, or dynamics.

While material properties change between tumors (Ahn et al., 2010; Burgstaller et al., 2017; Cox and Erler, 2011; Krupski et al., 2010; Pankova et al., 2019; Paszek et al., 2005; White, 2015; Zhai et al., 2010) and can be affected by cancer treatment (Miller et al., 2018), we found that durotactic behavior and migration speed can be tuned by actomyosin contractility, without any direct tweaks to protein expression levels. This suggests that the differences in migratory behavior are indeed linked directly to cell mechanotype within its niche. This may also explain why drugs that specifically target proteins involved in cell contractility are so effective at reducing invasion and metastasis. Yet tumors are heterogeneous and likely contain cells that encompass a range of actomyosin activities. Additionally, the ECM surrounding tumors show dynamic, nonlinear properties, which are known to influence the outcome of tumor progression and metastasis (Chaudhuri et al., 2020; Malandrino et al., 2019; Münster et al., 2013). These heterogeneities and tumor plasticity could present some key challenges to drug development. While our current in vitro and in silico models do not focus on these parameters, our results suggest that future metastatic modeling should couple adhesion dynamics, stress fiber considerations, and heterogeneity in cellular and ECM mechanics when identifying the lowest effective dose required to prevent metastasis.

INCLUSION AND DIVERSITY

One or more of the authors of this paper self-identifies as an under-represented ethnic minority in science and received support from a program designed to increase minority representation in science. The author list of this paper includes contributors from the location where the research was conducted who participated in the data collection, design, analysis, and/or interpretation of the work.

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Adam Engler (aengler@ucsd.edu).

Materials availability

Photopatterned polyacrylamide gels generated in this study will be made available on request.

Data and code availability

The MATLAB code used to track cell migration for brightfield images, analyze focal adhesion immunofluorescence images, simulate cell migration, and test the model is available via Github (https://github.com/compactmatterlab/Durotaxis). The MATLAB code for adhesion analysis is also available via Github (https://github.com/englea52/Englerlab).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Cell culture

Human metastatic cell lines used in this study include MDA-MB-231 (mammary, female 51 years), PC-3 (prostate, male 62 years), and NCI-H1299 (lung, male 43 years). MDA-MB-231 cells were cultured in DMEM, 10% FBS, and 1% antibiotic/antimycotic; PC-3 cells were cultured in F-12K, 10% FBS, and 1% penicillin/streptomycin; NCI-H1299 cells cultured in RPMI 1640, 10% FBS, and 1% antibiotic/antimycotic. All cells were purchased from ATCC and authenticated by morphology, growth curve, and isoenzyme analysis. PCR was used to verify cultures were free of Mycoplasma, and cells were not used beyond passage 11. Media reagents were purchased from Life Technologies.

METHOD DETAILS

Fabrication of step-gradient polyacrylamide gels

We used a two-step photopolymerization method described previously (Happe et al., 2017) to produce hydrogels with alternating elasticity profiles. Acrylamide concentrations of the prepolymer solutions were modified to obtain elasticities matching that of the tumor and stromal environment of each type of cancer. For breast cancer hydrogels, 3% acrylamide (3.7% for lung, 6.4% for prostate) and 0.4% bis-acrylamide were used for the first prepolymer solution, which was polymerized between a methacrylated 18mm coverslip and a chlorosilanated glass slide by exposing to ultraviolet light (350 nm) for 5 minutes, using 2-hydroxy-4’-(2-hydroxyethoxy)-2-methylpropiophenone (0.5%) as the photo-initiator. The PA hydrogel was removed from the chlorosilanated glass slide and dehydrated for 1 hour on a hot plate at 30 C prior to rehydrating with a 2% acrylamide (3.7% for lung, 3.2% for prostate) and 0.4% bis-acrylamide prepolymer solution. The rehydrated gel was again exposed to UV light for 5 min through a high-resolution chrome patterned photomask 200 μm dark stripes and 100 μm clear stripes. The Young’s moduli of each region were validated using atomic force microscopy.

The hydrogels were then placed in a 12-well plate on top of 50 μl of 2 mg/ml of collagen I to adhere the coverslip to the bottom of the well. After the collagen polymerized, the gels were immersed in a solution of sulfosuccinimidyl 6-(4’-azido-2′-nitrophenylamino)hexanoate (0.2 mg/ml, Sulfo-SANPAH; Pierce) dissolved in 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid buffer (pH 8.4, 50 mM) and exposed to UV light (350 nm) for 10 minutes. After washing several times with PBS, the functionalized surface of the gels was coated with collagen I (150 μg/ml) by incubating overnight at 37 C.

Isolating weakly and strongly adherent cells

Weakly and strongly adherent cells were isolated at varying shear stresses using a parallel plate flow chamber (Beri et al., 2020). To ensure sufficient spacing between individual cells, MDA-MB-231 and NCI-H1299 cells were seeded at ~1800 cells/cm² onto a fibronectin (2 μg/cm²) coated glass plate and incubated overnight. PC-3 cells were found to detach more consistently on a collagen I (1 μg/cm²) coated glass plate and seeded lower at 1500 cells/cm². For each cell line, PBS free of magnesium and calcium and with 4.5 g/L of dextrose was used to shear cells. Shear stresses used to detach the weakly adherent (WA) population were selected to collect about 20,000 cells at a given flow rate (3 min at 30 dynes/cm² for MDA-MB-231, 3 min at 60 dynes/cm² for PC-3 and NCI-H1299 cells). The strongly adherent (SA) population was collected after washing away the intermediate population at a higher shear stress (2 min 500 at dynes/cm² for MDA-MB-231, 5 min at 300 dynes/cm² for NCI-H1299, and 2 min at 750 dynes/cm² for PC-3), and detaching the remaining SA population using 0.25% trypsin-EDTA. Media was then pumped though the device to neutralize the trypsin and collect the SA cells. Collected cells were then seeded onto hydrogels and allowed to adhere for at least 2 hours prior to imaging.

Population-based adhesion assay

Cells were seeded onto 0.35 and 1.8 kPa hydrogels attached to 25 mm glass coverslips that were functionalized with 10 μg/mL human fibronectin. Cells were seeded at a density ~1,800 cells/cm² to minimize cell-cell contact. Cells attached to coverslips for a minimum of 12 hr using appropriate cell culture media at which time they were then mounted on a custom-built spinning-disk device (Boettiger, 2007), submerged into temperature-controlled PBS free of magnesium and calcium and with 4.5 g/L of dextrose, and exposed to a range of fluid sheer–depending on rotational speed–for 5 min. Once spun, cells were then fixed with 3.7% formaldehyde. Cell nuclei were then stained with 4’,6-Diamidino-2-Phenylindole (DAPI, 1:2500) and imaged using a CSU-X1 confocal scanner unit (Yokogawa), QuantEM:512SC camera (Photometrics), and MS-2000-WK multi-axis stage controller (Applied Scientific Instrumentation) on a Nikon Ti-S microscope. Metamorph 7.6 software and a custom-written MATLAB script (https://github.com/englea52/EnglerLab, MathWorks, Natick, MA) was used to stitched together 1500 individual images of nuclei and quantify average cell adhesion, i.e., τ₅₀, which is defined as the shear stress at which 50% of the initial cell population is removed by shear stress. Shear stress was calculated based on Equation 1:

$$\tau =\frac{4}{5}r\sqrt{\rho \mu {\omega }^3}$$ (Equation 1)

where r is the radial position from the center of the disk, ρ is the buffer density, μ is the buffer viscosity, and ω is the rotational velocity.

2D migration assays

Isolated cells were seeded at ~1500 cells/well onto step-gradient gels fixed in a 12-well plate and allowed to adhere for no more than 2 hours to ensure a random distribution across the step-gradient at the start of imaging. The cells were imaged over 24 hours using a Nikon Eclipse Ti-S microscope equipped with a temperature and CO₂ controller (Pathology Devices Inc., LiveCell). Images at multiple cell positions were taken in brightfield at 10x every 15 minutes. Cell trajectories were collected and analyzed using a custom MATLAB script (https://github.com/compactmatterlab/Durotaxis, MathWorks, Natick, MA). To prevent biases due to differences in cell division on soft or stiff substrates, daughter cells were excluded in trajectory analysis. From cell trajectories, we categorized cell migration as durotactic, anti-durotactic, or adurotactic, meaning that cells migrated across the substrate stiffness boundary only from soft to stiff, only from stiff to soft, or crossed the boundary multiple times, respectively; cells never approaching the boundary were not categorized. Trajectories were used to determine the distance between each cell and its closest soft-stiff boundary and plot the distribution of cells across the boundary. For cell migrating under drug treatment, cells were treated with either DMSO, 1μM, 10μM, or 100μM (S)4’nitroBlebbistatin (24171, Cayman Chemical Co.) or lysophosphatidic acid and imaged 3 hours after treatment for up to 24 hours.

Traction force microscopy

Traction forces were measured as previously described and calculated using a custom MATLAB script(Lo Sardo et al., 2018). Cells were seeded on to single-modulus polyacrylamide hydrogels with an elasticity matching their respective tumor microenvironment. Prepolymer solutions contained 2% (v/v) of 0.2 μm diameter 580/605 FluoSpheres microspheres (Invitrogen). Gels were prepared as we previously described (Beri et al., 2020) in 24-well glass bottom plates (Cellvis). Cell were seeded at ~5,000 cells per well and allowed to adhere for at least 3 hours. Brightfield images were taken at 60x to obtain cell areas as measured in ImageJ. Bead images were then captured every minute for 30 minutes. Reference images were then taken after removing the cells with 10% (v/v) Triton X solution. Traction forces were determined from the traction stress map and normalized to cell area.

Computational modeling

To understand how durotaxis and adurotaxis can occur due to differences in cell contractility and adhesion dynamics, we built a computational model that incorporates focal adhesion formation, stress fiber (SF) mediated force generation, and catch or slip bond dynamics between the cell receptors and surface adhesion sites. This model is described in detail below -

• 1A cell is defined by a central point. A random number of stress fibers, obtained from a Poisson distribution with mean μ_SF, are generated about the central point. Each stress fiber has an initial length equal to the radius of the cell (5 μm) and is oriented radially. The angular distribution of these stress fiber is uniform from 0 to 2π radian.
• 2
  These stress fibers can then grow in length radially based on the rate of actin polymerization (v_{act_L} if along the leading edge, defined by a region within −π/2 and π/2 radians of the cell migration direction, or v_{act_T} if in the direction of the trailing edge, a region complimentary to the leading edge) or shrink in length based on the rate of depolymerization (v_ret). (Initial cell migration direction is picked randomly, though this changes as described in part 7). The stress fibers switch from polymerization to depolymerization sporadically at time intervals generated from an exponential random number based on an average retraction time (t_ret), while depolymerization stops when the stress fiber reaches a minimum length (assumed to be the cell radius). The polymerizing and depolymerizing stress fibers are free to diffuse angularly about the cell center, with a diffusion coefficient dependent on the length of the SF (Heyes, 2019), Equation 2.

  $$D_{\mathit{\text{rot}}}=\frac{3k_{B}Tln\left(L/d_{\mathit{\text{act}}}\right)}{\pi \eta L^3}$$ (Equation 2)

Here k_B is Boltzmann’s constant, T is temperature, L is the length of the actin filament, d_act is the diameter of an F-actin, and η is the viscosity of the cytoplasm.

• 3
  Both polymerizing and depolymerizing SFs can bind to the substrate at their free end and begin to form a focal adhesion via integrin-substate bonds. This arrests the growth, shrinking and diffusion of the SF. The newly formed ECM-integrin-SF complex may be comprised of solely an adaptor protein (i.e., paxillin (Schaller, 2001), zyxin (Hansen and Kwiatkowski, 2013), etc. (Legate et al., 2006; Wu, 2005; Wu and Dedhar, 2001)), an adaptor protein with a stress sensor protein (i.e., vinculin (Grashoff et al., 2010; Rio et al., 2009), talin (Burridge and Guilluy, 2016; Rio et al., 2009)), or branched (i.e., Apr2/3 (Goley and Welch, 2006)) with some combination of adaptor and tension sensor proteins. The dynamics of these protein interactions are modeled by first determining the SF-integrin-ECM binding probability, calculated by Equation 3,

  $$P_{\mathit{\text{on}}}=1-{\text{e}}^{-\Delta t{k}_{\mathit{\text{on}}}}$$ (Equation 3)

where Δt is the model’s timestep and k_on is the assembly rate of the SF-integrin-ECM complex. The number of integrins bound to the SF is determined stochastically using the Poisson distribution with an average given by the average number of integrins/F-actin (μ_Int). We assume stress fibers with more than one integrin have a branching protein already bound to the SF prior to assembly of the complex. Likewise, each integrin has a certain probability (P_tal) of being bound to a stress sensor protein prior to complex assembly.

• 4
  Integrin-ECM bonds have a certain probability of unbinding based on the applied load on each bond via the SF and the catch or slip bond dynamics measured experimentally by Kong et al. (Kong et al., 2009) and calculated by Equation 4,

  $$P_{\mathit{\text{off}}}=1-e^{-\Delta t{k}_{\mathit{\text{off}}}(f)}$$ (Equation 4a)

  $$k_{\mathit{\text{off}}}(f)={\left[A{e}^{\raisebox{1ex}{$-f\xi $}\!\left/ \!\raisebox{-1ex}{$k_{B}T$}\right.}+{\left(B{e}^{\raisebox{1ex}{$f\xi $}\!\left/ \!\raisebox{-1ex}{$k_{B}T$}\right.}+C{e}^{\raisebox{1ex}{$-f\xi $}\!\left/ \!\raisebox{-1ex}{$k_{B}T$}\right.}\right)}^{-1}\right]}^{-1}\mathit{\text{for catch}}$$ (Equation 4b)

  $$k_{\mathit{\text{off}}}(f)=K_0{\text{e}}^{f/F_b}\mathit{\text{for slip}}$$ (Equation 4c)

where A, B, and C are constants, ξ is the unbinding length, and f is the load on an individual bond. For slip bonds, K₀ is the unloaded off rate and F_b is the characteristic bond rupture force (Bangasser and Odde, 2013). When a single SF is bound to multiple integrin-ECM bonds, the SF forces is distributed equally across each of these bonds.

• 5
  The SF force increases exponentially with time based on Equation 5, as derived in (Schwarz et al., 2006)

  $$F=F_S\left(1-e^{\raisebox{1ex}{$-v_0{K}_{ecm}t$}\!\left/ \!\raisebox{-1ex}{$F_S$}\right.}\right)$$ (Equation 5)

where F_S is the max SF force, determined by the myosin motor force (F_myo) times the number of myosin motors (n_myo). v₀ is the myosin sliding velocity and K_ecm is the underlying ECM stiffness. The model is based on the linear force velocity relationship of molecular motors such as non-muscle myosin II, (Howard, 2001) and a simple two-spring model. The stiffness of the ECM is converted from the user defined Young’s modulus (E_stiff, E_soft) by multiplying the modulus with a characteristic length (set to 0.1 μm) based on the order of magnitude for molecular sensing of myosin and related motor protein structures, e.g., thin filaments. The ECM stiffness value is spatially varied to simulate the photopatterned PA gels with a gradient length (L_grad) of 10μm between the soft and stiff regions, as determined from AFM measurements. The stiffness of the protein complexes involved in the ECM bond is neglected as they are an order of magnitude stiffer than the underlying substrate.

• 6
  If a tension sensor protein experiences a sufficiently large force f > F_thres it opens actin binding sites for recruiting new SFs (Grashoff et al., 2010; Rio et al., 2009), leading to FA growth and maturation. A new SFs (not one of the existing SFs) will bind to this open site with a given probability determined by Equation 6,

  $$P_{\mathit{\text{Act}}}=1-e^{-t_{SF}{K}_{\mathit{\text{Act}}}}$$ (Equation 6)

where t_SF is the time the binding site has been open and K_Act is the SF binding rate. Number of new SFs that can be recruited is limited by a finite max number of SFs possible in the cell (n_SF). The new stress fibers are not explicitly simulated as the initial free SFs described in part 2, but are included as newly formed ECM-Integrin-SF complexes described in part 3, within the vicinity of and parallel to the recruiting ECM-Integrin-SF complex.

• 7
  The forces at all bound ECM-Integrin-SF complexes are then summed $\left(\sum \overrightarrow{F}\right)$ to get the net force on the cell, which is divided by the friction factor due to bound integrins to calculate the distance the cell will move before the next time step, Equation 7.

  $$\overrightarrow{d}=\Delta t\frac{\sum {\overrightarrow{F}}_i}{n_b\Pi }$$ (Equation 7)

where F is force the force generated by each SF, n_b number of active integrin bonds, and Π is the friction factor for an individual bond. The direction of migration also determines the new leading and trailing edges of the cell.

• 8SF ends attached to active integrin bonds remain stationary in space as the cell moves. ECM-Integrin-SF complexes deteriorate if all integrin-ECM bonds an SF is attached to are broken. When no ECM-Integrin-SF complexes remain attached in the FA, the FA is dissolved releasing a free SF into the cell. The position of the free SF end is updated with the cell position before the next iteration begins.
• 9During any timestep, the dynamics of the free SFs (SFs not bound to integrins) are determined as described in part 2.

Values for each parameter used in this model are shown in Table S1. We simulate 24 hours of cell migration, and track the cells position relative to the soft/stiff boundary as in the time-lapse microscopy images, (Supplemental Information, Video S3). The model loops through the flow schematic in Figure S4A and described in detail above, with each loop comprising a single timestep.

Immunofluorescence staining and FA analysis

MDA-MB-231 cells were seeded onto single moduli gels (either 0.48 kPa or 1.8 kPa) and allowed to adhere overnight. Cells were washed with PBS with cations and fixed with 4% paraformaldehyde for 10 minutes. Fixed cells were then stained with deep red cell mask in PBS (1:1000 v/v; Thermofisher Scientific) for 10 minutes. 0.1% TritonX in PBS was used to permeabilize the cells for 10 minutes. Blocking was done with PBS supplemented with FBS (10% v/v, Gemini Bio) for 20 minutes at room temperature. Cells were incubated overnight at 4 C with primary paxillin antibody (1:500; ab32084, Abcam) in blocking buffer. Gels were then washed with blocking buffer and incubated with secondary Alexa Fluor 488-conjugated antibody (1:500; A11008, Invitrogen) and rhodamine phalloidin (1:3000, R415, Thermofisher Scientific) for 1 hour at room temperature, followed by Hoechst 33342 (1:2000; Invitrogen) in DI water for 10 minutes. Coverslips were then mounted onto slides with Flouromount-G (Southern Biotech). Samples were imaged using a Zeiss LSM 780 confocal microscope (Zeiss) with a 63x oil-immersion objective. A custom MATLAB script was used to measure cell area and size and number of focal adhesions.

Cytokine antibody array

Media was analyzed using the Proteome Profiler Human XL Cytokine Array (R&D Systems). Briefly, membranes were blocked for 1 hour using array buffer, and media was then combined with array buffer overnight at 4°C with rocking. Membranes were washed, incubated with the antibody cocktail diluted for 1 hour, washed, and incubated with streptavidin-HRP for 30 minutes, and finally treated with chemiluminescent reagent mix; membranes were exposed to film and imaged. Pixel quantification was performed in ImageJ and normalized to positive and loading controls. Conditioned media for SA and WA cells on 0.35 and 1.8 kPa substrates were normalized to internal loading control spots and plotted against each other.

QUANTIFICATION AND STATISTICAL ANALYSIS

Comparisons for migration speeds and traction forces were done using a two-tailed unpaired t test or one-way ANOVA with Tukey test for multiple comparisons for the indicated comparisons where appropriate and as indicated. Categorical comparisons for durotactic, anti-durotactic, and adurotactic cells were done using a Fisher’s exact test using definitions from the 2D migration assay section of this manuscript; again, durotactic cells were defined as cells that are on the soft region at the start of the time lapse and migrated to the stiff in the 24 hours of imaging, and vice versa for anti-durotactic. Adurotactic cells were defined as cells that crossed the boundary at some point during imaging and returned to the substrate they started on. Probability density estimations were calculated using MATLAB’s kernel smoothing function and plotted to visualize cell distributions at the start of imaging (t = 0 h) and after 24 hours of imaging (t = 24 h). The theoretical optimum bandwidth for the kernel smoothing function was used to generate reasonably smooth curves. Despite potential errors near the edges of the bounded region (−57.5 to 85 μm of the boundary), to reduce sensitivity to sampling error, we chose to use an unbounded KDE. This does not affect the cell density estimation near the stiffness gradient. P values for all analyses, *, p < 0.05; **, p < 0.01; ***, p < 0.001; and ****, p < 0.0001. Outliers were removed only in plotting using MATLAB’s quartiles method, so box-and-whisker plots remove points outside the whisker ends, defined by 1.5 interquartile ranges above the upper quartile or below the lower quartile. Other error bars were expressed as mean ± SD. Statistical analyses were done using MATLAB.

KEY RESOURCES TABLE

REAGENT OR RESOURCE	SOURCE	IDENTIFIER
Antibodies
Rabbit monoclonal Anti-Paxillin	Abcam	Cat#ab32084; RRID: AB_779033
Goat polyclonal anti-Rabbit	ThermoFisher Scientific	Cat#A-11008; RRID: AB_143165
Chemicals, peptides, and recombinant proteins
(S)4’nitroBlebbistatin	Cayman Chemical Co.	Cat#24171; CAS: 1621326-32-6
Oleoyl-L-α-lysophosphatidic acid sodium salt	Sigma Aldrich	Cat#L7260; CAS: 22556-62-3
Rhodamine Phalloidin	ThermoFisher Scientific	Cat#R415; CAS: 219920-04-4
Hoechst 33342	Invitrogen	Cat#H3570; CAS: 23491-52-3
Sulfosuccinimidyl 6-(4’-azido-2’-nitrophenylamino)hexanoate	CovaChem	Cat#13414-5×5; CAS: 102568-43-4
2-hydroxy-4’-(2-hydroxyethoxy)-2-methylpropiophenone	Sigma Aldrich	Cat#410896-10G; CAS: 106797-53-9
Deposited data
Raw and analyzed data	This paper	N/A
Experimental models: cell lines
Human: MDA-MB-231 metastatic breast cancer cell line	ATCC	ATCC HTB-26
Human: PC-3 metastatic prostate cancer cell line	ATCC	ATCC CRL-1435
Human: NCI-H1299 metastatic lung cancer cell lien	ATCC	ATCC CRL-5803
Software and algorithms
Cell Tracking Script	MATLAB, This paper	https://github.com/compactmatterlab/Durotaxis
Computational Cell Migration Model	MATLAB, This paper	https://github.com/compactmatterlab/Durotaxis
Cell Adhesion Script	MATLAB, This paper	https://github.com/englea52/EnglerLab
ImageJ	(Schneider et al., 2012)	https://imagej.nih.gov/ij/
Particle image velocimetry script	Lo Sardo et al., 2018	N/A
Other
Step-gradient polyacrylamide gels	Happe et al., 2017	N/A
Parallel plate flow chamber	Beri et al., 2020	N/A
Spinning Disc Assay	Boettiger, 2007	N/A
Proteome Profiler Human XL Cytokine Array	R&D Systems	Cat# ARY022B